Theoretische Grundlagen des Software Engineering
|
|
|
- Clemens Fürst
- vor 10 Jahren
- Abrufe
Transkript
1 Theoretische Grundlagen des Software Engineering 12: Termersetzungssysteme
2 Reduktionssysteme Definition: Reduktionssystem Ein Reduktionssystem ist ein Tupel (A, ) Dabei gilt: A ist eine beliebige Menge (die Trägermenge) A A ist eine zweistellige Relation über A (die Reduktionsrelation) 2
3 Ausprägungen Abstrakte Reduktionssysteme Universelle Grundlagen Wortersetzungssysteme Berechenbarkeitstheorie/Grammatiken/Turing- Maschinen Termersetzungssysteme Theorembeweisen, Programmsynthese, Funktionale Programmiersprachen Polynom-Rewriting Computer-Algebra (Buchbergers Algorithmus/Gröbner-Basen) Graph- Rewriting Verallgemeinerung von Termersetzung, Modellbasierte Entwicklung 3
4 Termersetzungssysteme 4
5 Termersetzungssysteme Idee Reduktionssystem (A, ) A: Menge von Termen : Endlich beschrieben durch Regeln und Gleichungen 5
6 Beispiel Betrachte folgendes Regelwerk: 1. add(x, 0) x 2. add(x, s(y)) s(add(x, y)) Idee: Spezifiziere Addition 0 repräsentiert 0 N s ist die Nachfolgerfunktion ( +1 ) s i (0) repräsentiert i N 6
7 Beispiel (fortgesetzt) (1)add(x, 0) x (2) add(x, s(y)) s(add(x, y)) add(s(s(0)), add(s(0), s(s(0)))) (1) add(s(s(0)), s(add(s(0), s(0))))) (1) add(s(s(0)), s(s(add(s(0), 0))))) (2) add(s(s(0)), s(s(s(0)))) (1) s(add(s(s(0)), s(s(0)))) (1) s(s(add(s(s(0)), s(0)))) (1) s(s(s(add(s(s(0)), 0)))) (2) s(s(s(s(s(0))))) 7
8 Beispiel (fortgesetzt) (1)add(x, 0) x (2) add(x, s(y)) s(add(x, y)) add(s(s(0)), s(add(s(0), s(0))))) add(s(s(0)), s(s(add(s(0), 0))))) s(s(s(s(s(0))))) vs. add(s(s(0)), s(add(s(0), s(0))))) s(add(s(s(0)), add(s(0), s(0)))) s(add(s(s(0)), s(add(s(0), 0)))) s(s(add(s(s(0)), add(s(0), 0)))) s(s(add(s(s(0)), s(0)))) s(s(s(add(s(s(0)), 0)))) s(s(s(s(s(0))))) 8
9 Variablen und Funktionssymbole Definition: Variablenmenge V V ist eine abzählbare Menge (von Variablensymbolen) Definition: Signatur Σ Eine Signatur Σ ist eine Menge von Funktionssymbolen mit assoziierter Stelligkeit Strikt analog zur Prädikatenlogik, nur ohne Prädikatssymbole 9
10 Variablen und Funktionssymbole Anmerkungen Wir verlangen, dass V, Σ disjunkt sind Funktionssymbole haben ein Stelligkeit n 0 Schreibweise: f n oder arity(f ) = n Oft implizit ersichtlich aus der Verwendung Funktionsssymbole mit Stelligkeit n = 0 heißen Konstanten Konvention für die Vorlesung: Variablen: x, y, z, x 1, y s,... Konstanten: a, b, c, d,... Funktionssymbole: f, g, h... 10
11 Terme Definition Gegeben: Σ, V Term(Σ, V ) ist die kleinste Menge mit: V Term(Σ, V ) Wenn f Σ mit Stelligkeit n t 1,..., t n Term(Σ, V ) dann f (t 1,..., t n ) Term(Σ) Term(Σ, V ) ist die Menge der Terme über Σ und V 11
12 Terme als Bäume 1! f 2 1 g y 2 1 f(g(f(a,g(x))),y) = 11 f a g 112 Pos(t)={!, 1, 2, 11,111, 112, 1121} 1 x
13 Positionen Definition: Positionen in Termen Positionen (oder Stellen) sind Worte über N und bezeichnen Teilterme eines Terms. Sei t Term(F, V ). Die Menge Pos(t) ist rekursiv definiert: Pos(t) = {ɛ} falls t V Ansonsten gilt: t = f (t 1,..., ts n ) für f n F und t 1,..., t n Term(F, V ). Dann ist Pos(s) = {ɛ} Pos(t i ) 1 i n 13
14 Teilterme Definition: Teilterme und Positionen Sei t Term(Σ, V ) und p Pos(t). Der Teilterm von t an Stelle p, t p ist rekursiv definiert wie folgt: Fall 1: p = ɛ. Dann ist t p = t Fall 2: p = iq. Dann hat t die Form f (t 1,..., t m ) und es gilt t iq = t i q s ist ein Teilterm von t, falls p Pos(t) : s = t p s ist ein echter Teilterm von t, falls p Pos(t) : p ɛ und s = t p 14
15 1! f 2 Teilterme und Positionen 1 g y a 1 11 f 1 2 g x t = f (g(f (a, g(x))), y) t 2 = y t 112 = g(f (a, g(x))) 12 = f (a, (g(x)) 2 = g(x) t 11 = f (a, g(x)) 15
16 Termersetzung Definition Seien s, t Term(Σ, V ) und p Pos(t) t[s] P ist der der Term, der entsteht, wenn t p in t durch s ersetzt wird. Formal: Induktive Definition über p Fall 1 (p = ɛ): Dann gilt t[s] ɛ = s Fall 2 (p = iq und t = f (t 1,..., t n )): Dann gilt: f (t 1,..., t n )[s] iq = f (t i,..., t i [s] q,... t n ) 16
17 Termersetzung Beispiele Sei t = f (g(f (a, g(x))), y) t[b] 11 = f (g(b), y) t[g(g(a))] 2 = f (g(f (a, g(x))), g(g(a))) t[f (c, c)] ɛ = f (c, c) 17
18 Eigenschaften von Positionen Lemma (Pos- 1) Seien s, t, r Term(Σ, V ) und seien p, q N. Dann gilt: (a) : Wenn pq Pos(t), dann p Pos(t) (b) : Wenn pq Pos(t), dann (t p ) q = t pq 18
19 Variablenmenge Definition: Variablenmenge eines Terms Sei t Term(Σ, V ). Die Variablenmenge von t ist die Menge der in t vorkommenden Variablen, also: Var(t) = {t p p Pos(t)} V Beispiele: Var(x) = {x} Var(f (g(a), b)) = Var(f (g(x), y)) = {x, y} 19
20 Grundterme Definition Die Menge der Grundterme über Σ ist Term(Σ, ) Schreibweise: Term(Σ) Es gilt: Term(Σ) = {t Term(Σ, V ) Var(t) = } Der Begriff grund wird mit gleicher Bedeutung ( variablenfrei ) auf auf Tupel, Regeln, Gleichungen, und Mengen von Termen angewendet! 20
21 Terme und Grundterme Σ = {f 2, g 1, a 0, b 0 } V = {x, y, z} f(x, z) f(x, f(y, z)) z x f(g(g(b)), f(g(g(g(a))), g(g(b)))) g(g(x)) g(b) g(f(a, g(b))) f(a, f(b, b)) a Term(Σ, V ) f(a, g(g(g(f(b, y))))) f(x, f(x, x)) g(g(f(x, y))) Term(Σ) 21
22 Regeln und Gleichungen Definition Seien Σ und V gegeben. Eine Gleichung (über Term(Σ, V )) ist ein Tupel (s, t) Term(Σ, V ) Term(Σ, V ). Wir schreiben die Gleichung (s, t) als s t Gleichungen sind ungerichtet, d.h. s t ist implizit äquivalent to t s Eine Regel (über Term(Σ, V )) ist ein Tupel (s, t) Term(Σ, V ) Term(Σ, V ). Wir schreiben die Regel (s, t) als s t Regeln sind gerichtet! Die Seiten einer Regel heißen linke Seite (left hand side, LHS) und rechte Seite (right hand side RHS) 22
23 Substitutionen (1) Definition Seien Σ und V gegeben. Eine Substitution ist eine Funktion σ : V Term(Σ, V ) mit der Eigenschaft, dass {x σ(x) x} endlich ist. Dom(σ) = {x σ(x) x} heißt die Domäne von σ Anschaulich: Eine Substitution ersetzt (endlich viele) Variablen durch Terme Beachte: V Term(Σ, V ) - Substitutionen können also auch Variablen einsetzen Schreibweise: σ = {x t 1, y t 2 } Aus unklaren Gründen findet man in der Literatur oft xσ statt σ(x) 23
24 Substitutionen (2) Substitutionen können auch auf Terme, Gleichungen und Regeln angewendet werden: Definition Eine Substitution σ wird rekursiv fortgesetzt zu einer Funktion σ : Term(Σ, V ) Term(Σ, V ) durch σ(f (t 1,..., t n ) = f (σ(t 1,..., σ(t n )) Effektiv werden die Variablen im Term ersetzt. Substitutionen werden auf Regeln und Gleichungen fortgesetzt: σ(s t) = σ(s) σ(t) σ(s t) = σ(s) σ(t) Erinnerung: σ(m) = {σ(e) e M} für Mengen kennen wir schon! 24
25 Beispiel Sei σ 1 = {x f (a), y a, z x} Sei σ 2 = {x y, y z, z x} σ 1 (f (g(x), f (y, g(z)))) =f (σ 1 (g(x)), σ 1 (f (y, g(z)))) =f (g(σ 1 (x)), f (σ 1 (y), σ 1 (g(z)))) =f (g(f (a)), f (a, g(σ 1 (z)))) =f (g(f (a)), f (a, g(x))) σ 2 (f (g(x), f (y, g(z)))) =f (σ 2 (g(x)), σ 2 (f (y, g(z)))) =f (g(σ 2 (x)), f (σ 2 (y), σ 2 (g(z)))) =f (g(y), f (z, g(σ 2 (z)))) =f (g(f (a)), f (a, g(x))) 25
26 Instanz, Match Definition Seien s, t Term(Σ, V ) und seit σ eine Substitution. Wenn σ(s) = t gilt, so heißt σ ein Match von s auf t t eine Instanz von s Sei nun t eine Instanz von s Wenn s keine Instanz von t ist, so heißt t eine echte Instanz von s 26
27 Instanz, Match Beispiel s t Match? Echte Instanz? x f (a, b) σ = {x f (a, b)} Ja x g(x) σ = {x g(x)} Ja g(y) g(x) σ = {y x} Nein, {x y} f (x, g(x)) f (a, x) Nein - f (x, g(y)) f (a, g(b)) σ = {x a, y b} Ja f (x, g(x)) f (a, h(a)) Nein - Wenn ein Match existiert, so ist er (auf den beteiligten Variablen) eindeutig! 27
28 Matching Frage: Wie findet man einen Match? Idee: Traversiere s und t in Vorordnung, baue (Repräsentation von) Substitution σ Situationen: s ist eine Variable Fall 1: s ist in σ nicht gebunden: Erweitere σ um s t Fall 2: s ist gebunden, σ(s) = t: Ok, matcht schon Fall 3: s ist gebunden, σ(s) t: Es gibt keinen Match! s ist von der Form f (s 1,..., s n ) Fall 1: t ist von der Form f (t 1,..., t n): Mache mit den s i, t i weiter Fall 2 : t ist von anderer Form: Es gibt keinen Match! 28
29 Matching def matchterms ( s, t, sigma = { } ) : i f isvar ( s ) : i f not s in sigma : sigma [ s ] = t return sigma e l i f sigma [ s ] == t : return sigma else : return None e l i f isvar ( t ) : return None e l i f getfun ( s )! = getfun ( t ) : return None else : for s, t in z i p ( getargs ( s ), getargs ( t ) ) : i f matchterms ( s, t, sigma ) == None : return None return sigma 29
30 Matching Anmerkungen Matching wird in vielen modenen Programmiersprachen eingesetzt: Haskell F# Python Aber auch: Finden der richtigen Methode bei Polymorphismus in C++ Matching wird in fast allen symbolischen Systemen eingesetzt: Expertensystem Planungssysteme Theorembeweiser Computeralgebrasystemen IDE s ( Intellisense ) 30
31 Was ist ein Reduktionssystem? Ein Reduktionssystem ist ein Tupel (A, ) Hier: A ist Menge der Terme über einer Signatur Was ist mit? 31
32 Rewrite- Relation Definition Seien Σ, V gegeben und sei R eine Menge von Regeln über Term(Σ, V ). R definiert the Rewrite- Relation R auf Term(Σ, V ) wie folgt: s R t gdw p Pos(s), l r R, σ : s p = σ(l) und t = s[σ(r)] p Wenn die linke Seite einer Regel auf einen Teilterm matched, kann dieser durch die instanziierte rechte Seite ersetzt werden 32
33 Programme als Terme (Beispiel) Beispielprogramm def fak1 ( a ) : i f a==0: return 1 else : return a fak1 ( a 1) 33
34 Beispiel: Programme als Terme (Signatur Σ) arg 2 Konstruktor für Argumentlisten stmt 2 Konstruktor für Befehlslisten end 0 Listenende fcall 2 Funktionsaufruf def 3 Kodiert def return 1 Kodiert return equal 2 Kodiert == mult 2 Kodiert * minus 2 Kodiert - fak1 0 Name aus dem Programm a 0 Name aus dem Programm 0 0 Konstante aus dem Programm 1 0 Konstante aus dem Programm 34
35 Programme als Terme (Kodiertes Program) def ( fak1, arg ( a, end ), stmt ( i f ( equal ( a, 0 ), stmt ( return ( 1 ), end ), stmt ( return ( mult ( a, f c a l l ( fak1, arg ( minus ( a, 1 ) ), end ) ), end ), end ) 35
36 Programme als Terme (Rewriting) Mögliche Anwendung: Optimierung mult(x, 0) 0 mult(0, x) 0 mult(x, 1) x mult(1, x) x minus(x, 0) x... aber auch denkbar: Regeln, die nutzlose else- Statements entfernen Regeln, die konstante Ausdrücke auswerten Regeln, die tote if/else Zweige entfernen 36
37 Zusammenfassung Beispiel: Rewrite-System Terme Positionen Grundterme Substitutionen Matching Instanzen Matching-Algorithmus Definition Rewrite- Relation R Anwendungsbeispiel: Programm als Term 37
38 Aufgaben - Zeigen Sie Lemma (Pos- 1 (b)): Sei t Term(Σ, V ) und pq Pos(t). Dann gilt: (t p ) q = t pq. - Welche der folgenden Term sind Instanzen/echte Instanzen voneinander? Geben Sie jeweils den Match an. t 1 = h(f (x, a), g(x)), t 2 = h(x, f (y, g(x))), t 3 = x, t 4 = h(f (y, z), g(z)) - Betrachten Sie R = {f (f (x, y), z) f (x, f (y, z)), f (x, i(x)) e, f (x, e) e}. Bestimmen Sie alle R Normalformen der folgenden Terme: f (f (a, i(a)), z) f (f (x, i(y)), e) f (f (e, i(e)), i(e)) 38
Theoretische Grundlagen des Software Engineering
 Theoretische Grundlagen des Software Engineering 11: Abstrakte Reduktionssysteme [email protected] Reduktionssysteme Definition: Reduktionssystem Ein Reduktionssystem ist ein Tupel (A, ) Dabei gilt: A
Theoretische Grundlagen des Software Engineering 11: Abstrakte Reduktionssysteme [email protected] Reduktionssysteme Definition: Reduktionssystem Ein Reduktionssystem ist ein Tupel (A, ) Dabei gilt: A
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Terme stehen für Namen von Objekten des Diskursbereichs (Subjekte, Objekte des natürlichsprachlichen Satzes)
 Prädikatenlogik Man kann den natürlichsprachlichen Satz Die Sonne scheint. in der Prädikatenlogik beispielsweise als logisches Atom scheint(sonne) darstellen. In der Sprache der Prädikatenlogik werden
Prädikatenlogik Man kann den natürlichsprachlichen Satz Die Sonne scheint. in der Prädikatenlogik beispielsweise als logisches Atom scheint(sonne) darstellen. In der Sprache der Prädikatenlogik werden
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Semantik von Formeln und Sequenzen
 Semantik von Formeln und Sequenzen 33 Grundidee der Verwendung von Logik im Software Entwurf Syntax: Menge von Formeln = Axiome Ax K ist beweisbar Formel ϕ beschreiben Korrektkeit Vollständigkeit beschreibt
Semantik von Formeln und Sequenzen 33 Grundidee der Verwendung von Logik im Software Entwurf Syntax: Menge von Formeln = Axiome Ax K ist beweisbar Formel ϕ beschreiben Korrektkeit Vollständigkeit beschreibt
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Umgekehrte Kurvendiskussion
 Umgekehrte Kurvendiskussion Bei einer Kurvendiskussion haben wir eine Funktionsgleichung vorgegeben und versuchen ihre 'Besonderheiten' herauszufinden: Nullstellen, Extremwerte, Wendepunkte, Polstellen
Umgekehrte Kurvendiskussion Bei einer Kurvendiskussion haben wir eine Funktionsgleichung vorgegeben und versuchen ihre 'Besonderheiten' herauszufinden: Nullstellen, Extremwerte, Wendepunkte, Polstellen
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Informatik I WS 07/08 Tutorium 24
 Info I Tutorium 24 Informatik I WS 07/08 Tutorium 24 3.2.07 astian Molkenthin E-Mail: [email protected] Web: http://infotut.sunshine2k.de Organisatorisches / Review is zum 2.2 müssen alle Praxisaufgaben
Info I Tutorium 24 Informatik I WS 07/08 Tutorium 24 3.2.07 astian Molkenthin E-Mail: [email protected] Web: http://infotut.sunshine2k.de Organisatorisches / Review is zum 2.2 müssen alle Praxisaufgaben
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Zusammenfassung. Satz. 1 Seien F, G Boolesche Ausdrücke (in den Variablen x 1,..., x n ) 2 Seien f : B n B, g : B n B ihre Booleschen Funktionen
 Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 6 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Satz 1 Seien F, G Boolesche Ausdrücke
Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 6 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Satz 1 Seien F, G Boolesche Ausdrücke
Erfüllbarkeit und Allgemeingültigkeit
 Theoretische Informatik: Logik, M. Lange, FB16, Uni Kassel: 3.3 Aussagenlogik Erfüllbarkeit 44 Erfüllbarkeit und Allgemeingültigkeit Def.: eine Formel ϕ heißt erfüllbar, wennesein I gibt, so dass I = ϕ
Theoretische Informatik: Logik, M. Lange, FB16, Uni Kassel: 3.3 Aussagenlogik Erfüllbarkeit 44 Erfüllbarkeit und Allgemeingültigkeit Def.: eine Formel ϕ heißt erfüllbar, wennesein I gibt, so dass I = ϕ
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen 19
 Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann [email protected]
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann [email protected]
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Mathematischer Vorbereitungskurs für Ökonomen
 Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Gleichungen Inhalt: 1. Grundlegendes 2. Lineare Gleichungen 3. Gleichungen mit Brüchen
Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Gleichungen Inhalt: 1. Grundlegendes 2. Lineare Gleichungen 3. Gleichungen mit Brüchen
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
 9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
Satz. Für jede Herbrand-Struktur A für F und alle t D(F ) gilt offensichtlich
 Herbrand-Strukturen und Herbrand-Modelle Sei F eine Aussage in Skolemform. Dann heißt jede zu F passende Struktur A =(U A, I A )eineherbrand-struktur für F, falls folgendes gilt: 1 U A = D(F ), 2 für jedes
Herbrand-Strukturen und Herbrand-Modelle Sei F eine Aussage in Skolemform. Dann heißt jede zu F passende Struktur A =(U A, I A )eineherbrand-struktur für F, falls folgendes gilt: 1 U A = D(F ), 2 für jedes
Lernziele: Ausgleichstechniken für binäre Bäume verstehen und einsetzen können.
 6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
1 Aussagenlogik und Mengenlehre
 1 Aussagenlogik und engenlehre 1.1 engenlehre Definition (Georg Cantor): nter einer enge verstehen wir jede Zusammenfassung von bestimmten wohl unterschiedenen Objekten (m) unserer Anschauung oder unseres
1 Aussagenlogik und engenlehre 1.1 engenlehre Definition (Georg Cantor): nter einer enge verstehen wir jede Zusammenfassung von bestimmten wohl unterschiedenen Objekten (m) unserer Anschauung oder unseres
Grundlagen der Künstlichen Intelligenz
 Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
4. AUSSAGENLOGIK: SYNTAX. Der Unterschied zwischen Objektsprache und Metasprache lässt sich folgendermaßen charakterisieren:
 4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
3. Grundlagen der Linearen Programmierung
 3. Grundlagen der linearen Programmierung Inhalt 3. Grundlagen der Linearen Programmierung Lineares Programm Grafische Lösung linearer Programme Normalform Geometrie linearer Programme Basislösungen Operations
3. Grundlagen der linearen Programmierung Inhalt 3. Grundlagen der Linearen Programmierung Lineares Programm Grafische Lösung linearer Programme Normalform Geometrie linearer Programme Basislösungen Operations
Verhindert, dass eine Methode überschrieben wird. public final int holekontostand() {...} public final class Girokonto extends Konto {...
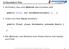 PIWIN I Kap. 8 Objektorientierte Programmierung - Vererbung 31 Schlüsselwort: final Verhindert, dass eine Methode überschrieben wird public final int holekontostand() {... Erben von einer Klasse verbieten:
PIWIN I Kap. 8 Objektorientierte Programmierung - Vererbung 31 Schlüsselwort: final Verhindert, dass eine Methode überschrieben wird public final int holekontostand() {... Erben von einer Klasse verbieten:
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK
 TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK WS 11/12 Einführung in die Informatik II Übungsblatt 2 Univ.-Prof. Dr. Andrey Rybalchenko, M.Sc. Ruslán Ledesma Garza 8.11.2011 Dieses Blatt behandelt
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK WS 11/12 Einführung in die Informatik II Übungsblatt 2 Univ.-Prof. Dr. Andrey Rybalchenko, M.Sc. Ruslán Ledesma Garza 8.11.2011 Dieses Blatt behandelt
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen.
 13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
Kapitel 7 Dr. Jérôme Kunegis. Logische Kalküle. WeST Web Science & Technologies
 Kapitel 7 Dr. Jérôme Kunegis Logische Kalküle WeST Web Science & Technologies Lernziele Grundideen des Domain-Relationenkalküls (DRK) und des Tupel-Relationenkalküls (TRK) Relationale Datenbank als Formelmenge
Kapitel 7 Dr. Jérôme Kunegis Logische Kalküle WeST Web Science & Technologies Lernziele Grundideen des Domain-Relationenkalküls (DRK) und des Tupel-Relationenkalküls (TRK) Relationale Datenbank als Formelmenge
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand
 Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
der Eingabe! Haben Sie das Ergebnis? Auf diesen schwarzen Punkt kommen wir noch zu sprechen.
 Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie [email protected]
 Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie [email protected] Interpreter für funktionale Sprache
Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie [email protected] Interpreter für funktionale Sprache
Also kann nur A ist roter Südler und B ist grüner Nordler gelten.
 Aufgabe 1.1: (4 Punkte) Der Planet Og wird von zwei verschiedenen Rassen bewohnt - dem grünen und dem roten Volk. Desweiteren sind die Leute, die auf der nördlichen Halbkugel geboren wurden von denen auf
Aufgabe 1.1: (4 Punkte) Der Planet Og wird von zwei verschiedenen Rassen bewohnt - dem grünen und dem roten Volk. Desweiteren sind die Leute, die auf der nördlichen Halbkugel geboren wurden von denen auf
Aufgaben zur Flächenberechnung mit der Integralrechung
 ufgaben zur Flächenberechnung mit der Integralrechung ) Geben ist die Funktion f(x) = -x + x. a) Wie groß ist die Fläche, die die Kurve von f mit der x-chse einschließt? b) Welche Fläche schließt der Graph
ufgaben zur Flächenberechnung mit der Integralrechung ) Geben ist die Funktion f(x) = -x + x. a) Wie groß ist die Fläche, die die Kurve von f mit der x-chse einschließt? b) Welche Fläche schließt der Graph
Skript und Aufgabensammlung Terme und Gleichungen Mathefritz Verlag Jörg Christmann Nur zum Privaten Gebrauch! Alle Rechte vorbehalten!
 Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt 4
 Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter H. Schmitt David Farago, Christoph Scheben, Mattias Ulbrich Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt
Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. Dr. Peter H. Schmitt David Farago, Christoph Scheben, Mattias Ulbrich Formale Systeme, WS 2012/2013 Lösungen zu Übungsblatt
Objektorientierte Programmierung für Anfänger am Beispiel PHP
 Objektorientierte Programmierung für Anfänger am Beispiel PHP Johannes Mittendorfer http://jmittendorfer.hostingsociety.com 19. August 2012 Abstract Dieses Dokument soll die Vorteile der objektorientierten
Objektorientierte Programmierung für Anfänger am Beispiel PHP Johannes Mittendorfer http://jmittendorfer.hostingsociety.com 19. August 2012 Abstract Dieses Dokument soll die Vorteile der objektorientierten
Einführung in. Logische Schaltungen
 Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen
 Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Absolute Stetigkeit von Maßen
 Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
11.3 Komplexe Potenzreihen und weitere komplexe Funktionen
 .3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
.3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
Vorkurs Mathematik Übungen zu Polynomgleichungen
 Vorkurs Mathematik Übungen zu en 1 Aufgaben Lineare Gleichungen Aufgabe 1.1 Ein Freund von Ihnen möchte einen neuen Mobilfunkvertrag abschließen. Es gibt zwei verschiedene Angebote: Anbieter 1: monatl.
Vorkurs Mathematik Übungen zu en 1 Aufgaben Lineare Gleichungen Aufgabe 1.1 Ein Freund von Ihnen möchte einen neuen Mobilfunkvertrag abschließen. Es gibt zwei verschiedene Angebote: Anbieter 1: monatl.
! " # $ " % & Nicki Wruck worldwidewruck 08.02.2006
 !"# $ " %& Nicki Wruck worldwidewruck 08.02.2006 Wer kennt die Problematik nicht? Die.pst Datei von Outlook wird unübersichtlich groß, das Starten und Beenden dauert immer länger. Hat man dann noch die.pst
!"# $ " %& Nicki Wruck worldwidewruck 08.02.2006 Wer kennt die Problematik nicht? Die.pst Datei von Outlook wird unübersichtlich groß, das Starten und Beenden dauert immer länger. Hat man dann noch die.pst
Vorname: Nachname: Matrikelnummer: E-Mail-Addresse: Studiengang (bitte genau einen ankreuzen): Master of SSE Erasmus Sonstige:
 RHEINISCH- WESTFÄLISCHE TECHNISCHE HOCHSCHULE AACHEN LEHR- UND FORSCHUNGSGEBIET INFORMATIK II RWTH Aachen D-52056 Aachen GERMANY http://www-i2.informatik.rwth-aachen.de/lufgi2/tes06/ LuFG Informatik II
RHEINISCH- WESTFÄLISCHE TECHNISCHE HOCHSCHULE AACHEN LEHR- UND FORSCHUNGSGEBIET INFORMATIK II RWTH Aachen D-52056 Aachen GERMANY http://www-i2.informatik.rwth-aachen.de/lufgi2/tes06/ LuFG Informatik II
Probleme beim Arbeiten mit Variablen, Termen und Gleichungen
 Probleme beim Arbeiten mit Variablen, Termen und Gleichungen Tage des Unterrichts in Mathematik, Naturwissenschaften und Technik Rostock 2010 Prof. Dr. Hans-Dieter Sill, Universität Rostock, http://www.math.uni-rostock.de/~sill/
Probleme beim Arbeiten mit Variablen, Termen und Gleichungen Tage des Unterrichts in Mathematik, Naturwissenschaften und Technik Rostock 2010 Prof. Dr. Hans-Dieter Sill, Universität Rostock, http://www.math.uni-rostock.de/~sill/
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
Lernmaterial für die Fernuni Hagen effizient und prüfungsnah
 Lernmaterial für die Fernuni Hagen effizient und prüfungsnah www.schema-f-hagen.de Sie erhalten hier einen Einblick in die Dokumente Aufgaben und Lösungen sowie Erläuterungen Beim Kauf erhalten Sie zudem
Lernmaterial für die Fernuni Hagen effizient und prüfungsnah www.schema-f-hagen.de Sie erhalten hier einen Einblick in die Dokumente Aufgaben und Lösungen sowie Erläuterungen Beim Kauf erhalten Sie zudem
Logik für Informatiker
 Logik für Informatiker 2. Aussagenlogik Teil 3 30.04.2012 Viorica Sofronie-Stokkermans Universität Koblenz-Landau e-mail: [email protected] 1 Letztes Mal Aussagenlogik Syntax: welche Formeln? Semantik:
Logik für Informatiker 2. Aussagenlogik Teil 3 30.04.2012 Viorica Sofronie-Stokkermans Universität Koblenz-Landau e-mail: [email protected] 1 Letztes Mal Aussagenlogik Syntax: welche Formeln? Semantik:
Lineare Differentialgleichungen erster Ordnung erkennen
 Lineare Differentialgleichungen erster Ordnung In diesem Kapitel... Erkennen, wie Differentialgleichungen erster Ordnung aussehen en für Differentialgleichungen erster Ordnung und ohne -Terme finden Die
Lineare Differentialgleichungen erster Ordnung In diesem Kapitel... Erkennen, wie Differentialgleichungen erster Ordnung aussehen en für Differentialgleichungen erster Ordnung und ohne -Terme finden Die
Codierungsverfahren SS 2011. Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur
 Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur Wie die zyklischen BCH-Codes zur Mehrbitfehler-Korrektur eignen sich auch die sehr verwandten Reed-Solomon-Codes (= RS-Codes) zur Mehrbitfehler-Korrektur.
Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur Wie die zyklischen BCH-Codes zur Mehrbitfehler-Korrektur eignen sich auch die sehr verwandten Reed-Solomon-Codes (= RS-Codes) zur Mehrbitfehler-Korrektur.
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
2. Universelle Algebra
 2. Universelle Algebra Die Theorie der universellen Algebra verallgemeinert die Theorien der klassischen Algebren. Obwohl ursprünglich nur eine Sorte betrachtet wurde, werden wir hier gleich den mehrsortigen
2. Universelle Algebra Die Theorie der universellen Algebra verallgemeinert die Theorien der klassischen Algebren. Obwohl ursprünglich nur eine Sorte betrachtet wurde, werden wir hier gleich den mehrsortigen
Der Vollstreckungsbescheid. 12 Fragen und Antworten
 Der Vollstreckungsbescheid 12 Fragen und Antworten Was bewirkt der Vollstreckungsbescheid eigentlich? Anerkennung der Schuld durch eine neutrale, eine richterliche Instanz Kein späterer Widerspruch möglich
Der Vollstreckungsbescheid 12 Fragen und Antworten Was bewirkt der Vollstreckungsbescheid eigentlich? Anerkennung der Schuld durch eine neutrale, eine richterliche Instanz Kein späterer Widerspruch möglich
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume?
 Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden [email protected] WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden [email protected] WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Gleichungen und Ungleichungen
 Gleichungen Ungleichungen. Lineare Gleichungen Sei die Gleichung ax = b gegeben, wobei x die Unbekannte ist a, b reelle Zahlen sind. Diese Gleichung hat als Lösung die einzige reelle Zahl x = b, falls
Gleichungen Ungleichungen. Lineare Gleichungen Sei die Gleichung ax = b gegeben, wobei x die Unbekannte ist a, b reelle Zahlen sind. Diese Gleichung hat als Lösung die einzige reelle Zahl x = b, falls
Kombinatorische Optimierung
 Juniorprof. Dr. Henning Meyerhenke 1 Henning Meyerhenke: KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Vorlesung 1 Programm des
Juniorprof. Dr. Henning Meyerhenke 1 Henning Meyerhenke: KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Vorlesung 1 Programm des
Internet online Update (Internet Explorer)
 Um Ihr Consoir Beta immer schnell und umkompliziert auf den aktuellsten Stand zu bringen, bieten wir allen Kunden ein Internet Update an. Öffnen Sie Ihren Internetexplorer und gehen auf unsere Internetseite:
Um Ihr Consoir Beta immer schnell und umkompliziert auf den aktuellsten Stand zu bringen, bieten wir allen Kunden ein Internet Update an. Öffnen Sie Ihren Internetexplorer und gehen auf unsere Internetseite:
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
 Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Java Kurs für Anfänger Einheit 5 Methoden
 Java Kurs für Anfänger Einheit 5 Methoden Ludwig-Maximilians-Universität München (Institut für Informatik: Programmierung und Softwaretechnik von Prof.Wirsing) 22. Juni 2009 Inhaltsverzeichnis Methoden
Java Kurs für Anfänger Einheit 5 Methoden Ludwig-Maximilians-Universität München (Institut für Informatik: Programmierung und Softwaretechnik von Prof.Wirsing) 22. Juni 2009 Inhaltsverzeichnis Methoden
3. LINEARE GLEICHUNGSSYSTEME
 176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
IRF2000 Application Note Lösung von IP-Adresskonflikten bei zwei identischen Netzwerken
 Version 2.0 1 Original-Application Note ads-tec GmbH IRF2000 Application Note Lösung von IP-Adresskonflikten bei zwei identischen Netzwerken Stand: 27.10.2014 ads-tec GmbH 2014 IRF2000 2 Inhaltsverzeichnis
Version 2.0 1 Original-Application Note ads-tec GmbH IRF2000 Application Note Lösung von IP-Adresskonflikten bei zwei identischen Netzwerken Stand: 27.10.2014 ads-tec GmbH 2014 IRF2000 2 Inhaltsverzeichnis
Formelsammlung zur Kreisgleichung
 zur Kreisgleichung Julia Wolters 6. Oktober 2008 Inhaltsverzeichnis 1 Allgemeine Kreisgleichung 2 1.1 Berechnung des Mittelpunktes und Radius am Beispiel..... 3 2 Kreis und Gerade 4 2.1 Sekanten, Tangenten,
zur Kreisgleichung Julia Wolters 6. Oktober 2008 Inhaltsverzeichnis 1 Allgemeine Kreisgleichung 2 1.1 Berechnung des Mittelpunktes und Radius am Beispiel..... 3 2 Kreis und Gerade 4 2.1 Sekanten, Tangenten,
Theoretische Grundlagen der Informatik WS 09/10
 Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
Tangentengleichung. Wie lautet die Geradengleichung für die Tangente, y T =? Antwort:
 Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Was ist Sozial-Raum-Orientierung?
 Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Übung zur Algebra WiSe 2008/2009, Blatt 1
 Aufgabe 1: Zeigen Sie, dass die Untergruppe der Permutationsmatrizen in GL(n, R) isomorph zur symmetrischen Gruppe S n ist. Es sei Perm n die Menge der Permutationsmatrizen in GL(n, R). Der Isomorphismus
Aufgabe 1: Zeigen Sie, dass die Untergruppe der Permutationsmatrizen in GL(n, R) isomorph zur symmetrischen Gruppe S n ist. Es sei Perm n die Menge der Permutationsmatrizen in GL(n, R). Der Isomorphismus
Wurzeln als Potenzen mit gebrochenen Exponenten. Vorkurs, Mathematik
 Wurzeln als Potenzen mit gebrochenen Exponenten Zur Einstimmung Wir haben die Formel benutzt x m n = x m n nach der eine Exponentialzahl potenziert wird, indem man die Exponenten multipliziert. Dann sollte
Wurzeln als Potenzen mit gebrochenen Exponenten Zur Einstimmung Wir haben die Formel benutzt x m n = x m n nach der eine Exponentialzahl potenziert wird, indem man die Exponenten multipliziert. Dann sollte
Lösen von linearen Gleichungssystemen mit zwei Unbekannten:
 Lösen von linearen Gleichungssystemen mit zwei Unbekannten: 1. Additions- und Subtraktionsverfahren 3x = 7y 55 + 5x 3x = 7y 55 7y 5x + 2y = 4 3 5 werden, dass die Variablen links und die Zahl rechts vom
Lösen von linearen Gleichungssystemen mit zwei Unbekannten: 1. Additions- und Subtraktionsverfahren 3x = 7y 55 + 5x 3x = 7y 55 7y 5x + 2y = 4 3 5 werden, dass die Variablen links und die Zahl rechts vom
Vorlesung. Funktionen/Abbildungen 1
 Vorlesung Funktionen/Abbildungen 1 1 Grundlagen Hinweis: In dieser Vorlesung werden Funktionen und Abbildungen synonym verwendet. In der Schule wird eine Funktion häufig als eindeutige Zuordnung definiert.
Vorlesung Funktionen/Abbildungen 1 1 Grundlagen Hinweis: In dieser Vorlesung werden Funktionen und Abbildungen synonym verwendet. In der Schule wird eine Funktion häufig als eindeutige Zuordnung definiert.
Nichtlineare Optimierung ohne Nebenbedingungen
 Kapitel 2 Nichtlineare Optimierung ohne Nebenbedingungen In diesem Abschnitt sollen im wesentlichen Verfahren zur Bestimmung des Minimums von nichtglatten Funktionen in einer Variablen im Detail vorgestellt
Kapitel 2 Nichtlineare Optimierung ohne Nebenbedingungen In diesem Abschnitt sollen im wesentlichen Verfahren zur Bestimmung des Minimums von nichtglatten Funktionen in einer Variablen im Detail vorgestellt
Anleitung: Einrichtung der Fritz!Box 7272 mit VoIP Telefonanschluss
 Schließen Sie die AVM Fritz!Box, wie auf dem der Fritz!Box beiliegenden Schaubild beschrieben, an. Starten Sie den Internet Explorer oder einen beliebigen Browser (Mozilla Firefox, Google Chrome, Safari)
Schließen Sie die AVM Fritz!Box, wie auf dem der Fritz!Box beiliegenden Schaubild beschrieben, an. Starten Sie den Internet Explorer oder einen beliebigen Browser (Mozilla Firefox, Google Chrome, Safari)
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Markovketten. Bsp. Page Ranking für Suchmaschinen. Wahlfach Entscheidung unter Risiko und stat. Datenanalyse 07.01.2015
 Markovketten Markovketten sind ein häufig verwendetes Modell zur Beschreibung von Systemen, deren Verhalten durch einen zufälligen Übergang von einem Systemzustand zu einem anderen Systemzustand gekennzeichnet
Markovketten Markovketten sind ein häufig verwendetes Modell zur Beschreibung von Systemen, deren Verhalten durch einen zufälligen Übergang von einem Systemzustand zu einem anderen Systemzustand gekennzeichnet
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Darstellungsformen einer Funktion
 http://www.flickr.com/photos/sigfrid/348144517/ Darstellungsformen einer Funktion 9 Analytische Darstellung: Eplizite Darstellung Funktionen werden nach Möglichkeit eplizit dargestellt, das heißt, die
http://www.flickr.com/photos/sigfrid/348144517/ Darstellungsformen einer Funktion 9 Analytische Darstellung: Eplizite Darstellung Funktionen werden nach Möglichkeit eplizit dargestellt, das heißt, die
Statistische Thermodynamik I Lösungen zur Serie 1
 Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
DIFFERENTIALGLEICHUNGEN
 DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
Theorie der Informatik
 Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Grammatiken. Einführung
 Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
2.11 Kontextfreie Grammatiken und Parsebäume
 2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
