Kapitel 7: Benutzerdefinierte Datentypen
|
|
|
- Alexa Brandt
- vor 10 Jahren
- Abrufe
Transkript
1 Kapitel 7: Benutzerdefinierte Datentypen Andreas Abel LFE Theoretische Informatik Institut für Informatik Ludwig-Maximilians-Universität München 10. Juni 2011 Quelle: Martin Wirsing, Benutzerdefinierte Datentypen Foliensatz ProMo SS 2010 Andreas Abel (LMU) Datentypen / 38
2 Einführung Einführende Fragen Wie definiere ich komplexe Datenstrukturen in SML? Z.B. Eine Datei-Verzeichnis-Struktur? Ist list in SML fest eingebaut oder kann ich Listen selbst definieren? Welche Datenstruktur verwende ich zur Repräsentation von abstrakter Syntax (z.b. SML-Typausdrücke)? Andreas Abel (LMU) Datentypen / 38
3 Einführung Inhalt 1 Einführung 2 Aufzählungstypen 3 Partialität und der Typ option 4 Rekursive Datentypen 5 Binärbäume 6 Linearisierung von Bäumen 7 Breitendurchlauf 8 Arithmetische Ausdrücke 9 Abstrakte Syntaxbäume Andreas Abel (LMU) Datentypen / 38
4 Aufzählungstypen Aufzählungstypen Eine Vergleichfunktion hat drei mögliche Ergebnisse: kleiner, gleich, oder größer. Diese Alternativen repräsentieren wir durch einen Aufzählungstypen: datatype CMP = LT EQ GT Diese Anweisung erzeugt eine neue Typkonstante CMP und drei neue Werte (Konstruktoren) LT, EQ, GT vom Typ CMP. Damit implementieren wir eine Vergleichsfunktion auf Zeichen: fun comparechar(x : char, y : char) : CMP = if x > y then GT else if x = y then EQ else LT Andreas Abel (LMU) Datentypen / 38
5 Aufzählungstypen Verarbeitung von Aufzählungen Die Konstruktoren von Aufzählungen werden mit pattern matching unterschieden. type a comparison = a * a -> CMP fun comparelex(cmpa : a comparison, cmpb : b comparison) : ( a * b) comparison = fn ((a1,b1),(a2,b2)) => case cmpa(a1,a2) of GT => GT LT => LT EQ => cmpb(b1,b2) Diese Funktion höherer Ordnung vergleicht ein Paar (a1,b1) mit einem Paar (a2,b2) lexikographisch, wobei die ersten Komponenten mit Vergleichsfunktion cmpa und die zweiten mit cmpb verglichen werden. Andreas Abel (LMU) Datentypen / 38
6 Aufzählungstypen Selbstgestrickter Listenvergleich Eine polymorphe Vergleichsfunktion für Listen: fun comparelist(cmp : a comparison) : a list comparison = fn ([], [] ) => EQ ([], ys ) => LT (xs, [] ) => GT (x::xs, y::ys) => comparelex (cmp,comparelist cmp) ((x,xs),(y,ys)) Vergleichsfunktion für Strings als Zeichenlisten: val comparecharlist = comparelist comparechar fun comparestring(s,t) = comparecharlist (String.explode s, String.explode t) Andreas Abel (LMU) Datentypen / 38
7 Partialität und der Typ option Optionale Ergebnisse Folgender Typ ist in der Standardbibliothek von SML vordefiniert: datatype a option = NONE SOME of a Erzeugt Konstruktoren: NONE : a option und SOME : a -> a option. Man verwenden ihn als Rückgabetyp für partielle Funktionen (anstatt eine Ausnahme zu werfen). Z.B. Holen eines Wertes aus einer Assoziationsliste: fun lookup (key: a, assoclist: ( a * b) list): b option = let fun loop [] = NONE loop ((k,v)::l) = if k = key then SOME v else loop l in loop assoclist end Achtung! Wegen des Gleichheitstests k = key muss der Schlüsseltyp ein Gleichheitstyp (engl. equality type) a sein. Andreas Abel (LMU) Datentypen / 38
8 Partialität und der Typ option Verarbeitung von optionalen Werten Undefiniertheit NONE kann mittels pattern matching abgefangen werden: fun lookupwithdefault (default : b, key : a, assoclist : ( a * b) list) : b = case lookup(key, assoclist) of SOME v => v NONE => default Andreas Abel (LMU) Datentypen / 38
9 Partialität und der Typ option Disjunkte Vereinigung Polymorphe Datentypen können auch mehrere Typparameter haben. Z.B. Typ der disjunkten Vereinigung: datatype ( a, b) either = Left of a Right of b Hiermit können wir informative Fehlermeldungen zurückgeben: fun division (n:int, m:int) : (string,int) either = if m = 0 then Left "division by zero" else Right (n div m) fun resulttostring (Left err) = err resulttostring (Right n ) = Int.toString n Andreas Abel (LMU) Datentypen / 38
10 Rekursive Datentypen Rekursive Datentypen Datentyp-Deklarationen dürfen rekursiv sein, d.h. der gerade definierte Typ darf in den Typen seiner Konstruktoren vorkommen. Bekanntes Beispiel ist der Typ der Listen: datatype a list = nil cons of a * a list Wechselseitige Rekursion mittels datatype... and... type name = string type url = string datatype file = File of name Dir of directory and directory = Local of name * file list Remote of url Andreas Abel (LMU) Datentypen / 38
11 Rekursive Datentypen Typen mit nur einem Konstruktor SML expandiert Typsynonyme wie type name = string. datatype file = Dir of directory File of string datatype directory = Local of string * file list Remote of string Um die Unterscheidung von name und url zu forcieren, verwenden wir einen wrapper ( Umschlag ). datatype name = Name of string datatype url = Url of string datatype file =... Nun lautet die Antwort von SML: datatype file = Dir of directory File of name datatype directory = Local of name * file list Remote of url Andreas Abel (LMU) Datentypen / 38
12 Rekursive Datentypen Datentypdeklaration (allgemein) Die allgemeine Form einer Datentypdeklaration in SML is datatype D 1 = cd 1,1... cd 1,n1 and... and D m = cd m,1... cd m,nm wobei jedes D i eine der Formen 1 identifier, 2 a identifier, oder 3 ( a_1,..., a_k) identifier annimmt und jedes cd i,j eine der Formen 1 c (Konstruktor ohne Argument), oder 2 c of typ (Konstruktor mit Argument vom Typ typ). Einfaches Beispiel: Listen datatype a list = nil cons of a * a list Andreas Abel (LMU) Datentypen / 38
13 Binärbäume Binärbäume Ist A eine Menge, so wird die Menge A der Binärbäume mit Knotenmarkierungen in A (oder einfach Binärbäume über A) induktiv definiert durch: 1 Der leere Baum ε ist in A. 2 Sind l und r in A und x in A, so ist das Tripel (l, x, r) in A. Alternativ kann man die Mengen A n der Binärbäume mit Höhe (Tiefe) kleiner n rekursiv definieren durch: 1 A 0 = (kein Baum hat negative Höhe). 2 A n+1 = {ε} {(l, x, r) x A, l, r A n }. Man beweist leicht A n A n+1 (Kumulativität. A = n N A n ist der Limes der Folge A 0, A 1,... Die Höhe (Tiefe) eines Baums t ist das kleinste n, so dass t A n+1. Andreas Abel (LMU) Datentypen / 38
14 Binärbäume Terminologie für Bäume x heißt Wurzel oder (Wurzel)beschriftung von (l, x, r). l heißt linker und r rechter Unterbaum von (l, x, r). Ein Binärbaum der Form (ε, x, ε) heißt Blatt. ε heißt leerer Baum, jeder andere Baum ist nichtleer. Die Knoten und Teilbäume eines Binärbaums sind rekursiv definiert: 1 Der leere Baum ε hat keine Knoten und nur sich selbst als Teilbaum. 2 Die Knoten von (l, x, r) sind x plus die Knoten von l und r. Die Teilbäume von (l, x, r) sind (l, x, r) plus die Teilbäume von l und r. Sei [x] definiert als Abkürzung für ein Blatt (ε, x, ε) und t = (([2], 3, ([5], 8, ε)), 6, (ε, 8, [4])) t hat Knoten {2, 3, 5, 8, 6, 4} und Teilbäume {t, (([2], 3, ([5], 8, ε)), (ε, 8, [4])), ([5], 8, ε), [2], [4], [5], ε}. Andreas Abel (LMU) Datentypen / 38
15 Binärbäume Typische Darstellung eines Binärbaumes Wurzel: 6 Blätter: 2, 5, Andreas Abel (LMU) Datentypen / 38
16 Binärbäume Binärbäume in SML Binärbäume sind ein Beispiel eines rekursiven Datentyps: datatype a tree = Empty (* leerer Baum *) Node of a tree * a * a tree (* Knoten *) fun leaf x = Node(Empty, x, Empty) (* Blatt *) val t = Node(Node(leaf 2, 3, Node(leaf 5, 8, Empty)), 6, Node(Empty, 8, leaf 4)) In der Antwort von SML wird der Baum nicht vollständig ausgegeben: val t = Node (Node (Node #,3,Node #),6,Node (Empty,8,Node #)) : int tree Datenstrukturen werden nur bis zur Tiefe Control.Print.printDepth gedruckt. Diesen Wert können wir setzen, z.b. Control.Print.printDepth := 10; Andreas Abel (LMU) Datentypen / 38
17 Binärbäume Standardfunktionen für Binärbäume Projektionen (partiell, undefiniert auf Empty!) fun label (Node(_,x,_)) = x fun left (Node(l,_,_)) = l fun right (Node(_,_,r)) = r Test auf leerer Baum. Schlechte Implementierung: fun isempty t = (t = Empty) Warning: calling polyequal val isempty = fn : a tree -> bool Funktioniert nur für Gleichheitstypen a. Besser: fun isempty (Empty) = true isempty (Node _) = false val isempty = fn : a tree -> bool Andreas Abel (LMU) Datentypen / 38
18 Binärbäume Rekursion auf Bäumen Höhe eines Baumes: fun height (Empty) = 0 height (Node(l,_,r)) = 1 + Int.max (height l, height r) Eine Funktion f auf alle Beschriftungen anwenden: fun maptree f (Empty) = Empty maptree f (Node(l,x,r)) = let val l = maptree f l val x = f x val r = maptree f r in Node(l,x,r ) end Beachte: maptree f t erzeugt einen komplett neuen Baum! maptree (fn x => x) t liefert eine Kopie von t. Andreas Abel (LMU) Datentypen / 38
19 Linearisierung von Bäumen Linearisierung Mit Hilfe eines Baumdurchlaufs (engl. tree traversal) können wir alle Markierungen in einer Liste aufsammeln. Die Reihenfolge der Listenelemente hängt von der Art des Durchlaufs ab: 1 Vorordnung (engl. preorder) 2 Symmetrische Ordnung (engl. inorder) 3 Nachordnung (engl. postorder) Andreas Abel (LMU) Datentypen / 38
20 Linearisierung von Bäumen Vorordnung Zuerst Markierung, dann linker, dann rechter Teilbaum. fun preorder (Empty) = [] preorder (Node(l,x,r)) = preorder preorder r Andreas Abel (LMU) Datentypen / 38
21 Linearisierung von Bäumen Symmetrische Ordnung Zuerst linker Teilbaum, dann Markierung, dann rechter Teilbaum. fun inorder (Empty) = [] inorder (Node(l,x,r)) = inorder inorder r Andreas Abel (LMU) Datentypen / 38
22 Linearisierung von Bäumen Nachordnung Zuerst linker, dann rechter Teilbaum, dann Markierung. fun postorder (Empty) = [] postorder (Node(l,x,r)) = postorder postorder [x] Andreas Abel (LMU) Datentypen / 38
23 Linearisierung von Bäumen Generischer Tiefendurchlauf Alle Durchläufe bearbeiten die Teilbäume unabhängig voneinander. Das zugrundeliegende Schema heißt Tiefendurchlauf (engl. depth-first) fun foldtree (n : b * a * b -> b)(e : b) : a tree -> b = let fun loop (Empty) = e loop (Node(l,x,r)) = n (loop l, x, loop r) in loop end Die drei Baumlinearisierungen sind Instanzen davon: fun preorder fun inorder fun postorder t = foldtree (fn (l,x,r) => r) [] t t = foldtree (fn (l,x,r) => r) [] t t = foldtree (fn (l,x,r) => [x]) [] t Andreas Abel (LMU) Datentypen / 38
24 Breitendurchlauf Breitendurchlauf Beim Breitendurchlauf (engl. breadth-first traversal) werden die Teilbäume nicht unabhängig behandelt Der Baum wird schichtenweise abgearbeitet. Andreas Abel (LMU) Datentypen / 38
25 Breitendurchlauf Breitendurchlauf Nach Entfernen der 1 bleiben zwei Teilbäume: Nach Entfernen von 2 und 3 drei Teilbäume: Andreas Abel (LMU) Datentypen / 38
26 Breitendurchlauf Breitendurchlauf Verallgemeinerung: Breitendurchlauf eines Waldes (engl. forest), einer Liste von Bäumen. fun uproot (ts : a tree list) : a list * a tree list = case ts of ([]) => ([],[]) (Empty :: ts) => uproot ts (Node(l,x,r) :: ts) => let val (xs, ts ) = uproot ts in (x :: xs, l :: r :: ts ) end uproot (dt. Entwurzeln) zerlegt eine Liste von Bäumen in eine Liste der Wurzeln und eine Liste der Teilbäume. Andreas Abel (LMU) Datentypen / 38
27 Breitendurchlauf Breitendurchlauf Beim Breitendurchlauf durch einen Wald sammeln wir erst die Wurzeln und dann durchlaufen wir rekursiv die Teilbäume. fun breadthforest ([]) = [] breadthforest (ts) = let val (xs, ts ) = uproot ts in breadthforest ts end fun breadthfirst t = breadthforest [t] Andreas Abel (LMU) Datentypen / 38
28 Arithmetische Ausdrücke Arithmetische Ausdrücke als Bäume Beispiel: Ein Mathe-Nachhilfe-Programm für Grundschüler. Es druckt zufällig einen arithmetischen Ausdruck wie (5 + 3) 2, und vergleicht den Lösungsvorschlag mit dem Wert des Ausdrucks (hier: 16). Die Zahlen sollen einstellig sein und die Operationen + und. Den Ausdruck können wir intern als Binärbaum repräsentieren. Richtig: Falsch: Andreas Abel (LMU) Datentypen / 38
29 Arithmetische Ausdrücke Arithmetische Ausdrücke als Binärbäume Es gibt drei Typen von Knotenmarkierungen: Zahl, +, *. datatype Label = Num of int Plus Times type Expr = Label tree Beispiel: val a1 = Node(Node(leaf(Num 5), Plus, leaf(num 3)), Times, leaf(num 2)) Andreas Abel (LMU) Datentypen / 38
30 Arithmetische Ausdrücke Auswertung Den Wert des Ausdrucks berechnen wir rekursiv: fun eval (Empty) = 0 eval (Node(_, Num n, _)) = n eval (Node(l, Plus, r)) = eval l + eval r eval (Node(l, Times, r)) = eval l * eval r Wir sagen, eval (dt. auswerten) interpretiert den Ausdruck. val a1v = eval a1 val a1v = 16 : int Übung: Implementieren Sie eval als Instanz von foldtree! Andreas Abel (LMU) Datentypen / 38
31 Arithmetische Ausdrücke Ausdrücke ausdrucken Eine andere Interpretation des Ausdrucks ist seine Repräsentation as Zeichenkette. fun exprtostring (Empty) = "" exprtostring (Node(_, Num n, _)) = Int.toString n exprtostring (Node(l, Plus, r)) = "(" ^ exprtostring l ^ " + " ^ exprtostring r ^ ")" exprtostring (Node(l, Times, r)) = "(" ^ exprtostring l ^ " * " ^ exprtostring r ^ ")" val a1s = "((5 + 3) * 2)" : string Übung: Implementieren Sie exprtostring als Instanz von foldtree! Übung: Schreiben Sie eine bessere Ausgabefunktion, die Klammern nur verwendet wenn nötig! Andreas Abel (LMU) Datentypen / 38
32 Arithmetische Ausdrücke Ungültige Ausdrücke Die Binärbaum-Repräsentation erlaubt ungültige Ausdrücke (engl. malformed expressions) val bad = Node(Node(leaf Plus, Num 5, leaf(num 3)), Times, leaf(num 2)) Zahlen sollen nur als Blattknoten auftreten! Operationen nur als innere Knoten! Andreas Abel (LMU) Datentypen / 38
33 Arithmetische Ausdrücke Arithmetische Ausdrücke als Datentyp Wir definieren einen speziellen Baumtyp expr: datatype expr = Num of int Plus of expr * expr Times of expr * expr val a2 = Times(Plus(Num 5, Num 3)), Num 2) Die Ausdrucksrepräsentation ist ökonomischer. Die Funktionsdefinitionen sind auch klarer! fun eval (Num n) = n eval (Plus (l,r)) = eval l + eval r eval (Times (l,r)) = eval l * eval r Andreas Abel (LMU) Datentypen / 38
34 Abstrakte Syntaxbäume Typausdrücke als Bäume Auch Typausdrücke repräsentiert man als Bäume: Beispiel: α ((α β) β) α β α β Andreas Abel (LMU) Datentypen / 38
35 Abstrakte Syntaxbäume Typausdrücke als Bäume Wie würden wir Typinferenz selbst implementieren? Zuerst müssen wir Typausdrücke reprasentieren: Variablen a, b, c,... zählen wir einfach durch als 0,1,2,...: type tyvar = int Typkonstanten wie int,string,... repräsentieren wir durch ihren Namen: type tybas = string (* "int", "string", "real", "bool" *) Typausdrücke sind Binärbaume mit speziellen Blättern: datatype tyexp = TyVar of tyvar (* a, b,... *) TyBas of tybas (* int, string,... *) TyArr of tyexp * tyexp (* A -> B *) Andreas Abel (LMU) Datentypen / 38
36 Abstrakte Syntaxbäume Drucken von Typausdrücken Wir drucken die ersten 26 Typvariablen als a, b,..., z und die restlichen als a0, a1, a2,... fun tyvartostring (n) = " " ^ (if n < 26 then Char.toString(chr(n + 97)) else "a" ^ Int.toString(n - 26)) Funktionstypen müssen wir Klammern: fun tytostring (TyVar a) = tyvartostring a tytostring (TyBas b) = b tytostring (TyArr(A,B)) = "(" ^ tytostring A ^ " -> " ^ tytostring B ^ ")" val ty1 = TyArr (TyVar 0, TyArr (TyArr (TyVar 0, TyVar 1), TyVar 1)) val ty1s = tytostring ty1 val ty1s = "( a -> (( a -> b) -> b))" : string Andreas Abel (LMU) Datentypen / 38
37 Abstrakte Syntaxbäume Substitution in Typausdrücken Eine Substitution σ = [A/α, B/β] repräsentieren wir als Liste von Paaren [(0,A),(1,B)]. type tysubst = (tyvar * tyexp) list Substitution Aσ ersetzt in A alle Typvariablen α durch σ(α), falls jenes definiert ist. fun substty (A : tyexp, sigma : tysubst) : tyexp = let fun loop (TyVar a) = lookupwithdefault(tyvar a, a, sigma) loop (TyBas b) = TyBas b loop (TyArr(B,C) = TyArr (loop B, loop C) in loop A end Andreas Abel (LMU) Datentypen / 38
38 Abstrakte Syntaxbäume Zusammenfassung Benutzerdefinierte Datentypen: Aufzählungen, option, Listen, Bäume. Binärbäume. Tiefen- und Breitendurchlauf. Ausdrücke und Interpretation. Andreas Abel (LMU) Datentypen / 38
Idee: Wenn wir beim Kopfknoten zwei Referenzen verfolgen können, sind die Teillisten kürzer. kopf Eine Datenstruktur mit Schlüsselwerten 1 bis 10
 Binäre Bäume Bäume gehören zu den wichtigsten Datenstrukturen in der Informatik. Sie repräsentieren z.b. die Struktur eines arithmetischen Terms oder die Struktur eines Buchs. Bäume beschreiben Organisationshierarchien
Binäre Bäume Bäume gehören zu den wichtigsten Datenstrukturen in der Informatik. Sie repräsentieren z.b. die Struktur eines arithmetischen Terms oder die Struktur eines Buchs. Bäume beschreiben Organisationshierarchien
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Programmierung und Modellierung
 Programmierung und Modellierung Terme, Suchbäume und Pattern Matching Martin Wirsing in Zusammenarbeit mit Moritz Hammer SS 2009 2 Inhalt Kap. 7 Benutzerdefinierte Datentypen 7. Binärer Suchbaum 8. Anwendung:
Programmierung und Modellierung Terme, Suchbäume und Pattern Matching Martin Wirsing in Zusammenarbeit mit Moritz Hammer SS 2009 2 Inhalt Kap. 7 Benutzerdefinierte Datentypen 7. Binärer Suchbaum 8. Anwendung:
Lernziele: Ausgleichstechniken für binäre Bäume verstehen und einsetzen können.
 6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
Kapiteltests zum Leitprogramm Binäre Suchbäume
 Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
368 4 Algorithmen und Datenstrukturen
 Kap04.fm Seite 368 Dienstag, 7. September 2010 1:51 13 368 4 Algorithmen und Datenstrukturen Java-Klassen Die ist die Klasse Object, ein Pfeil von Klasse A nach Klasse B bedeutet Bextends A, d.h. B ist
Kap04.fm Seite 368 Dienstag, 7. September 2010 1:51 13 368 4 Algorithmen und Datenstrukturen Java-Klassen Die ist die Klasse Object, ein Pfeil von Klasse A nach Klasse B bedeutet Bextends A, d.h. B ist
Binäre Bäume Darstellung und Traversierung
 Binäre Bäume Darstellung und Traversierung Name Frank Bollwig Matrikel-Nr. 2770085 E-Mail [email protected] Datum 15. November 2001 0. Vorbemerkungen... 3 1. Terminologie binärer Bäume... 4 2.
Binäre Bäume Darstellung und Traversierung Name Frank Bollwig Matrikel-Nr. 2770085 E-Mail [email protected] Datum 15. November 2001 0. Vorbemerkungen... 3 1. Terminologie binärer Bäume... 4 2.
Datenstrukturen & Algorithmen
 Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Erwin Grüner 09.02.2006
 FB Psychologie Uni Marburg 09.02.2006 Themenübersicht Folgende Befehle stehen in R zur Verfügung: {}: Anweisungsblock if: Bedingte Anweisung switch: Fallunterscheidung repeat-schleife while-schleife for-schleife
FB Psychologie Uni Marburg 09.02.2006 Themenübersicht Folgende Befehle stehen in R zur Verfügung: {}: Anweisungsblock if: Bedingte Anweisung switch: Fallunterscheidung repeat-schleife while-schleife for-schleife
Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie [email protected]
 Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie [email protected] Interpreter für funktionale Sprache
Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie [email protected] Interpreter für funktionale Sprache
13. Binäre Suchbäume
 1. Binäre Suchbäume Binäre Suchbäume realiesieren Wörterbücher. Sie unterstützen die Operationen 1. Einfügen (Insert) 2. Entfernen (Delete). Suchen (Search) 4. Maximum/Minimum-Suche 5. Vorgänger (Predecessor),
1. Binäre Suchbäume Binäre Suchbäume realiesieren Wörterbücher. Sie unterstützen die Operationen 1. Einfügen (Insert) 2. Entfernen (Delete). Suchen (Search) 4. Maximum/Minimum-Suche 5. Vorgänger (Predecessor),
Datenstrukturen und Algorithmen
 Datenstrukturen und Algorithmen VO 708.031 Bäume [email protected] 1 Inhalt der Vorlesung 1. Motivation, Einführung, Grundlagen 2. Algorithmische Grundprinzipien 3. Sortierverfahren 4. Halden
Datenstrukturen und Algorithmen VO 708.031 Bäume [email protected] 1 Inhalt der Vorlesung 1. Motivation, Einführung, Grundlagen 2. Algorithmische Grundprinzipien 3. Sortierverfahren 4. Halden
Tutorium Algorithmen & Datenstrukturen
 June 16, 2010 Binärer Baum Binärer Baum enthält keine Knoten (NIL) besteht aus drei disjunkten Knotenmengen: einem Wurzelknoten, einem binären Baum als linken Unterbaum und einem binären Baum als rechten
June 16, 2010 Binärer Baum Binärer Baum enthält keine Knoten (NIL) besteht aus drei disjunkten Knotenmengen: einem Wurzelknoten, einem binären Baum als linken Unterbaum und einem binären Baum als rechten
Was bisher geschah. deklarative Programmierung. funktionale Programmierung (Haskell):
 Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK
 TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK WS 11/12 Einführung in die Informatik II Übungsblatt 2 Univ.-Prof. Dr. Andrey Rybalchenko, M.Sc. Ruslán Ledesma Garza 8.11.2011 Dieses Blatt behandelt
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK WS 11/12 Einführung in die Informatik II Übungsblatt 2 Univ.-Prof. Dr. Andrey Rybalchenko, M.Sc. Ruslán Ledesma Garza 8.11.2011 Dieses Blatt behandelt
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens [email protected] Überblick Grundlagen Definitionen Elementare Datenstrukturen Rekursionen Bäume 2 1 Datenstruktur Baum Definition eines Baumes
Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens [email protected] Überblick Grundlagen Definitionen Elementare Datenstrukturen Rekursionen Bäume 2 1 Datenstruktur Baum Definition eines Baumes
Einführung in die Programmierung
 : Inhalt Einführung in die Programmierung Wintersemester 2008/09 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering Fakultät für Informatik TU Dortmund - mit / ohne Parameter - mit / ohne Rückgabewerte
: Inhalt Einführung in die Programmierung Wintersemester 2008/09 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering Fakultät für Informatik TU Dortmund - mit / ohne Parameter - mit / ohne Rückgabewerte
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
DATENSTRUKTUREN UND ZAHLENSYSTEME
 DATENSTRUKTUREN UND ZAHLENSYSTEME RALF HINZE Institute of Information and Computing Sciences Utrecht University Email: [email protected] Homepage: http://www.cs.uu.nl/~ralf/ March, 2001 (Die Folien finden
DATENSTRUKTUREN UND ZAHLENSYSTEME RALF HINZE Institute of Information and Computing Sciences Utrecht University Email: [email protected] Homepage: http://www.cs.uu.nl/~ralf/ March, 2001 (Die Folien finden
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Algorithmik II. a) Fügen Sie in einen anfangs leeren binären Baum die Schlüsselfolge 20, 28, 35, 31, 9, 4, 13, 17, 37, 25 ein.
 Aufgabe 10 Binäre Bäume a) Fügen Sie in einen anfangs leeren binären Baum die Schlüsselfolge, 28, 35, 31, 9, 4,, 17, 37, 25 ein. 1. Einfügen von : 3. Einfugen von 35: 2. Einfügen von 28: 28 28 10. Einfügen
Aufgabe 10 Binäre Bäume a) Fügen Sie in einen anfangs leeren binären Baum die Schlüsselfolge, 28, 35, 31, 9, 4,, 17, 37, 25 ein. 1. Einfügen von : 3. Einfugen von 35: 2. Einfügen von 28: 28 28 10. Einfügen
Folge 19 - Bäume. 19.1 Binärbäume - Allgemeines. Grundlagen: Ulrich Helmich: Informatik 2 mit BlueJ - Ein Kurs für die Stufe 12
 Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Informatik II Bäume. Beispiele. G. Zachmann Clausthal University, Germany [email protected]. Stammbaum. Stammbaum. Stammbaum
 lausthal Beispiele Stammbaum Informatik II. Zachmann lausthal University, ermany [email protected]. Zachmann Informatik - SS 06 Stammbaum Stammbaum / Parse tree, Rekursionsbaum Parse tree, Rekursionsbaum
lausthal Beispiele Stammbaum Informatik II. Zachmann lausthal University, ermany [email protected]. Zachmann Informatik - SS 06 Stammbaum Stammbaum / Parse tree, Rekursionsbaum Parse tree, Rekursionsbaum
Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen:
 Ein- und Ausgabe Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen: fun p r i n t T r e e printa t = c a s e t o f Leaf a => ( p r i n t Leaf ; printa a ) Node ( l, a, r ) => ( p r i n
Ein- und Ausgabe Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen: fun p r i n t T r e e printa t = c a s e t o f Leaf a => ( p r i n t Leaf ; printa a ) Node ( l, a, r ) => ( p r i n
Funktionale Programmierung
 Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
Formale Spezialisierungstechniken. am Beispiel des binären Baums. Hybride Programmiersprachen Daniel Krompass Berlin, 2009
 Formale Spezialisierungstechniken am Beispiel des binären Baums. Hybride Programmiersprachen Daniel Krompass Berlin, 2009 Spezialisierungsarten (Typbeziehungen erster Art) X stellt Methoden und Eigenschaften
Formale Spezialisierungstechniken am Beispiel des binären Baums. Hybride Programmiersprachen Daniel Krompass Berlin, 2009 Spezialisierungsarten (Typbeziehungen erster Art) X stellt Methoden und Eigenschaften
Java Einführung Operatoren Kapitel 2 und 3
 Java Einführung Operatoren Kapitel 2 und 3 Inhalt dieser Einheit Operatoren (unär, binär, ternär) Rangfolge der Operatoren Zuweisungsoperatoren Vergleichsoperatoren Logische Operatoren 2 Operatoren Abhängig
Java Einführung Operatoren Kapitel 2 und 3 Inhalt dieser Einheit Operatoren (unär, binär, ternär) Rangfolge der Operatoren Zuweisungsoperatoren Vergleichsoperatoren Logische Operatoren 2 Operatoren Abhängig
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Algorithmen und Datenstrukturen Suchbaum
 Algorithmen und Datenstrukturen Suchbaum Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Motivation Datenstruktur zur Repräsentation dynamischer Mengen
Algorithmen und Datenstrukturen Suchbaum Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Motivation Datenstruktur zur Repräsentation dynamischer Mengen
Objektorientierte Programmierung
 Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Übungen 19.01.2012 Programmieren 1 Felix Rohrer. Übungen
 Übungen if / else / else if... 2... 2 Aufgabe 2:... 2 Aufgabe 3:... 2 Aufgabe 4:... 2 Aufgabe 5:... 2 Aufgabe 6:... 2 Aufgabe 7:... 3 Aufgabe 8:... 3 Aufgabe 9:... 3 Aufgabe 10:... 3 switch... 4... 4 Aufgabe
Übungen if / else / else if... 2... 2 Aufgabe 2:... 2 Aufgabe 3:... 2 Aufgabe 4:... 2 Aufgabe 5:... 2 Aufgabe 6:... 2 Aufgabe 7:... 3 Aufgabe 8:... 3 Aufgabe 9:... 3 Aufgabe 10:... 3 switch... 4... 4 Aufgabe
KONSTRUKTION VON ROT-SCHWARZ-BÄUMEN
 KONSTRUKTION VON ROT-SCHWARZ-BÄUMEN RALF HINZE Institut für Informatik III Universität Bonn Email: [email protected] Homepage: http://www.informatik.uni-bonn.de/~ralf Februar, 2001 Binäre Suchbäume
KONSTRUKTION VON ROT-SCHWARZ-BÄUMEN RALF HINZE Institut für Informatik III Universität Bonn Email: [email protected] Homepage: http://www.informatik.uni-bonn.de/~ralf Februar, 2001 Binäre Suchbäume
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Informatik Grundlagen, WS04, Seminar 13
 Informatik Grundlagen, WS04, Seminar 13 Informatik Informatik Grundlagen, Seminar 13 WS04 1 Was wir heute besprechen Nachbesprechen von Übungsblatt 11 Rekursion Grundprinzipien Übung Besprechung Übungsblatt
Informatik Grundlagen, WS04, Seminar 13 Informatik Informatik Grundlagen, Seminar 13 WS04 1 Was wir heute besprechen Nachbesprechen von Übungsblatt 11 Rekursion Grundprinzipien Übung Besprechung Übungsblatt
1. Einfach verkettete Liste unsortiert 2. Einfach verkettete Liste sortiert 3. Doppelt verkettete Liste sortiert
 Inhalt Einführung 1. Arrays 1. Array unsortiert 2. Array sortiert 3. Heap 2. Listen 1. Einfach verkettete Liste unsortiert 2. Einfach verkettete Liste sortiert 3. Doppelt verkettete Liste sortiert 3. Bäume
Inhalt Einführung 1. Arrays 1. Array unsortiert 2. Array sortiert 3. Heap 2. Listen 1. Einfach verkettete Liste unsortiert 2. Einfach verkettete Liste sortiert 3. Doppelt verkettete Liste sortiert 3. Bäume
Typdeklarationen. Es gibt in Haskell bereits primitive Typen:
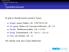 Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
Funktionale Programmierung ALP I. Funktionen höherer Ordnung. Teil 2 SS 2013. Prof. Dr. Margarita Esponda. Prof. Dr.
 ALP I Funktionen höherer Ordnung Teil 2 SS 2013 Funktionen höherer Ordnung Nehmen wir an, wir möchten alle Zahlen innerhalb einer Liste miteinander addieren addall:: (Num a) => [a -> a addall [ = 0 addall
ALP I Funktionen höherer Ordnung Teil 2 SS 2013 Funktionen höherer Ordnung Nehmen wir an, wir möchten alle Zahlen innerhalb einer Liste miteinander addieren addall:: (Num a) => [a -> a addall [ = 0 addall
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
4. Lernen von Entscheidungsbäumen. Klassifikation mit Entscheidungsbäumen. Entscheidungsbaum
 4. Lernen von Entscheidungsbäumen Klassifikation mit Entscheidungsbäumen Gegeben sei eine Menge von Objekten, die durch /Wert- Paare beschrieben sind. Jedes Objekt kann einer Klasse zugeordnet werden.
4. Lernen von Entscheidungsbäumen Klassifikation mit Entscheidungsbäumen Gegeben sei eine Menge von Objekten, die durch /Wert- Paare beschrieben sind. Jedes Objekt kann einer Klasse zugeordnet werden.
Programmiertechnik II
 Bäume Symboltabellen Suche nach Werten (items), die unter einem Schlüssel (key) gefunden werden können Bankkonten: Schlüssel ist Kontonummer Flugreservierung: Schlüssel ist Flugnummer, Reservierungsnummer,...
Bäume Symboltabellen Suche nach Werten (items), die unter einem Schlüssel (key) gefunden werden können Bankkonten: Schlüssel ist Kontonummer Flugreservierung: Schlüssel ist Flugnummer, Reservierungsnummer,...
Wiederholung ADT Menge Ziel: Verwaltung (Finden, Einfügen, Entfernen) einer Menge von Elementen
 Was bisher geschah abstrakter Datentyp : Signatur Σ und Axiome Φ z.b. ADT Menge zur Verwaltung (Finden, Einfügen, Entfernen) mehrerer Elemente desselben Typs Spezifikation einer Schnittstelle Konkreter
Was bisher geschah abstrakter Datentyp : Signatur Σ und Axiome Φ z.b. ADT Menge zur Verwaltung (Finden, Einfügen, Entfernen) mehrerer Elemente desselben Typs Spezifikation einer Schnittstelle Konkreter
1. Probeklausur zu Programmierung 1 (WS 07/08)
 Fachschaft Informatikstudiengänge Fachrichtung 6.2 Informatik Das Team der Bremser 1. Probeklausur zu Programmierung 1 (WS 07/08) http://fsinfo.cs.uni-sb.de Name Matrikelnummer Bitte öffnen Sie das Klausurheft
Fachschaft Informatikstudiengänge Fachrichtung 6.2 Informatik Das Team der Bremser 1. Probeklausur zu Programmierung 1 (WS 07/08) http://fsinfo.cs.uni-sb.de Name Matrikelnummer Bitte öffnen Sie das Klausurheft
Theorie der Informatik
 Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Serienbrieferstellung in Word mit Kunden-Datenimport aus Excel
 Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
Anwendungsbeispiele Buchhaltung
 Rechnungen erstellen mit Webling Webling ist ein Produkt der Firma: Inhaltsverzeichnis 1 Rechnungen erstellen mit Webling 1.1 Rechnung erstellen und ausdrucken 1.2 Rechnung mit Einzahlungsschein erstellen
Rechnungen erstellen mit Webling Webling ist ein Produkt der Firma: Inhaltsverzeichnis 1 Rechnungen erstellen mit Webling 1.1 Rechnung erstellen und ausdrucken 1.2 Rechnung mit Einzahlungsschein erstellen
Diana Lange. Generative Gestaltung Operatoren
 Diana Lange Generative Gestaltung Operatoren Begriffserklärung Verknüpfungsvorschrift im Rahmen logischer Kalküle. Quelle: google Operatoren sind Zeichen, die mit einer bestimmten Bedeutung versehen sind.
Diana Lange Generative Gestaltung Operatoren Begriffserklärung Verknüpfungsvorschrift im Rahmen logischer Kalküle. Quelle: google Operatoren sind Zeichen, die mit einer bestimmten Bedeutung versehen sind.
Wurzeln als Potenzen mit gebrochenen Exponenten. Vorkurs, Mathematik
 Wurzeln als Potenzen mit gebrochenen Exponenten Zur Einstimmung Wir haben die Formel benutzt x m n = x m n nach der eine Exponentialzahl potenziert wird, indem man die Exponenten multipliziert. Dann sollte
Wurzeln als Potenzen mit gebrochenen Exponenten Zur Einstimmung Wir haben die Formel benutzt x m n = x m n nach der eine Exponentialzahl potenziert wird, indem man die Exponenten multipliziert. Dann sollte
Verarbeitung unendlicher Datenstrukturen Jetzt können wir z.b. die unendliche Liste aller geraden Zahlen oder aller Quadratzahlen berechnen:
 Verarbeitung unendlicher Datenstrukturen Jetzt können wir z.b. die unendliche Liste aller geraden Zahlen oder aller Quadratzahlen berechnen: take 1 0 ( f i l t e r ( fn x => x mod 2=0) nat ) ; val it =
Verarbeitung unendlicher Datenstrukturen Jetzt können wir z.b. die unendliche Liste aller geraden Zahlen oder aller Quadratzahlen berechnen: take 1 0 ( f i l t e r ( fn x => x mod 2=0) nat ) ; val it =
15 Optimales Kodieren
 15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
3.2 Binäre Suche. Usr/local/www/ifi/fk/menschen/schmid/folien/infovk.ppt 1
 3.2 Binäre Suche Beispiel 6.5.1: Intervallschachtelung (oder binäre Suche) (Hier ist n die Anzahl der Elemente im Feld!) Ein Feld A: array (1..n) of Integer sei gegeben. Das Feld sei sortiert, d.h.: A(i)
3.2 Binäre Suche Beispiel 6.5.1: Intervallschachtelung (oder binäre Suche) (Hier ist n die Anzahl der Elemente im Feld!) Ein Feld A: array (1..n) of Integer sei gegeben. Das Feld sei sortiert, d.h.: A(i)
Der Aufruf von DM_in_Euro 1.40 sollte die Ausgabe 1.40 DM = 0.51129 Euro ergeben.
 Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Objektorientierte Programmierung
 Universität der Bundeswehr Fakultät für Informatik Institut 2 Priv.-Doz. Dr. Lothar Schmitz FT 2006 Zusatzaufgaben Lösungsvorschlag Objektorientierte Programmierung Lösung 22 (Java und UML-Klassendiagramm)
Universität der Bundeswehr Fakultät für Informatik Institut 2 Priv.-Doz. Dr. Lothar Schmitz FT 2006 Zusatzaufgaben Lösungsvorschlag Objektorientierte Programmierung Lösung 22 (Java und UML-Klassendiagramm)
Übungskomplex Felder (1) Eindimensionale Felder Mehrdimensionale Felder
 Übungskomplex Felder (1) Eindimensionale Felder Mehrdimensionale Felder Hinweise zur Übung Benötigter Vorlesungsstoff Ab diesem Übungskomplex wird die Kenntnis und praktische Beherrschung der Konzepte
Übungskomplex Felder (1) Eindimensionale Felder Mehrdimensionale Felder Hinweise zur Übung Benötigter Vorlesungsstoff Ab diesem Übungskomplex wird die Kenntnis und praktische Beherrschung der Konzepte
Einführung in die Informatik: Programmierung und Software-Entwicklung, WS 11/12. Kapitel 13. Bäume. Bäume
 1 Kapitel 13 Ziele 2 Den Begriff des Baums in der Informatik kennenlernen als verkettete Datenstruktur repräsentieren können Rekursive Funktionen auf n verstehen und schreiben können Verschiedene Möglichkeiten
1 Kapitel 13 Ziele 2 Den Begriff des Baums in der Informatik kennenlernen als verkettete Datenstruktur repräsentieren können Rekursive Funktionen auf n verstehen und schreiben können Verschiedene Möglichkeiten
Einführung in die Java- Programmierung
 Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger [email protected] WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger [email protected] WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Hilfe zur Urlaubsplanung und Zeiterfassung
 Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Grundlagen der Programmierung Prof. H. Mössenböck. 3. Verzweigungen
 Grundlagen der Programmierung Prof. H. Mössenböck 3. Verzweigungen If-Anweisung n > 0? j n if (n > 0) x = x / n; ohne else-zweig x x / n j max x x > y? n max y if (x > y) max = x; else max = y; mit else-zweig
Grundlagen der Programmierung Prof. H. Mössenböck 3. Verzweigungen If-Anweisung n > 0? j n if (n > 0) x = x / n; ohne else-zweig x x / n j max x x > y? n max y if (x > y) max = x; else max = y; mit else-zweig
Objektorientierte Programmierung. Kapitel 12: Interfaces
 12. Interfaces 1/14 Objektorientierte Programmierung Kapitel 12: Interfaces Stefan Brass Martin-Luther-Universität Halle-Wittenberg Wintersemester 2012/13 http://www.informatik.uni-halle.de/ brass/oop12/
12. Interfaces 1/14 Objektorientierte Programmierung Kapitel 12: Interfaces Stefan Brass Martin-Luther-Universität Halle-Wittenberg Wintersemester 2012/13 http://www.informatik.uni-halle.de/ brass/oop12/
teischl.com Software Design & Services e.u. [email protected] www.teischl.com/booknkeep www.facebook.com/booknkeep
 teischl.com Software Design & Services e.u. [email protected] www.teischl.com/booknkeep www.facebook.com/booknkeep 1. Erstellen Sie ein neues Rechnungsformular Mit book n keep können Sie nun Ihre eigenen
teischl.com Software Design & Services e.u. [email protected] www.teischl.com/booknkeep www.facebook.com/booknkeep 1. Erstellen Sie ein neues Rechnungsformular Mit book n keep können Sie nun Ihre eigenen
SEP 114. Design by Contract
 Design by Contract SEP 114 Design by Contract Teile das zu entwickelnde Programm in kleine Einheiten (Klassen, Methoden), die unabhängig voneinander entwickelt und überprüft werden können. Einheiten mit
Design by Contract SEP 114 Design by Contract Teile das zu entwickelnde Programm in kleine Einheiten (Klassen, Methoden), die unabhängig voneinander entwickelt und überprüft werden können. Einheiten mit
Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))?
![Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))?](/thumbs/24/4200701.jpg) Fragen f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Wozu evaluiert [f [ ], f [ ]]? Weiteres Beispiel: f [ ] y = [
Fragen f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Wozu evaluiert [f [ ], f [ ]]? Weiteres Beispiel: f [ ] y = [
Erweiterung der Aufgabe. Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen:
 VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Informatik 11 Kapitel 2 - Rekursive Datenstrukturen
 Fachschaft Informatik Informatik 11 Kapitel 2 - Rekursive Datenstrukturen Michael Steinhuber König-Karlmann-Gymnasium Altötting 15. Januar 2016 Folie 1/77 Inhaltsverzeichnis I 1 Datenstruktur Schlange
Fachschaft Informatik Informatik 11 Kapitel 2 - Rekursive Datenstrukturen Michael Steinhuber König-Karlmann-Gymnasium Altötting 15. Januar 2016 Folie 1/77 Inhaltsverzeichnis I 1 Datenstruktur Schlange
5.2 Neue Projekte erstellen
 5.2 Neue Projekte erstellen Das Bearbeiten von bestehenden Projekten und Objekten ist ja nicht schlecht wie aber können Sie neue Objekte hinzufügen oder gar völlig neue Projekte erstellen? Die Antwort
5.2 Neue Projekte erstellen Das Bearbeiten von bestehenden Projekten und Objekten ist ja nicht schlecht wie aber können Sie neue Objekte hinzufügen oder gar völlig neue Projekte erstellen? Die Antwort
Institut für Programmierung und Reaktive Systeme 25. August 2014. Programmier-Labor. 04. + 05. Übungsblatt. int binarysearch(int[] a, int x),
![Institut für Programmierung und Reaktive Systeme 25. August 2014. Programmier-Labor. 04. + 05. Übungsblatt. int binarysearch(int[] a, int x), Institut für Programmierung und Reaktive Systeme 25. August 2014. Programmier-Labor. 04. + 05. Übungsblatt. int binarysearch(int[] a, int x),](/thumbs/29/13862323.jpg) Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme 25. August 2014 Programmier-Labor 04. + 05. Übungsblatt Aufgabe 21: a) Schreiben Sie eine Methode
Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme 25. August 2014 Programmier-Labor 04. + 05. Übungsblatt Aufgabe 21: a) Schreiben Sie eine Methode
Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung: Lösungsvorschlag
 Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 9 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 9 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Algorithmen und Datenstrukturen SS09
 Foliensatz 8 Michael Brinkmeier Technische Universität Ilmenau Institut für Theoretische Informatik Sommersemester 29 TU Ilmenau Seite / 54 Binärbäume TU Ilmenau Seite 2 / 54 Binäre Bäume Bäume und speziell
Foliensatz 8 Michael Brinkmeier Technische Universität Ilmenau Institut für Theoretische Informatik Sommersemester 29 TU Ilmenau Seite / 54 Binärbäume TU Ilmenau Seite 2 / 54 Binäre Bäume Bäume und speziell
Programmieren in C. Felder, Schleifen und Fließkommaarithmetik. Prof. Dr. Nikolaus Wulff
 Programmieren in C Felder, Schleifen und Fließkommaarithmetik Prof. Dr. Nikolaus Wulff Addition von Zahlen 1 2 3 4 5 #include int main() { int x,y,z,sum; x = 1; y = 2; z = 4; sum = x + y + z;
Programmieren in C Felder, Schleifen und Fließkommaarithmetik Prof. Dr. Nikolaus Wulff Addition von Zahlen 1 2 3 4 5 #include int main() { int x,y,z,sum; x = 1; y = 2; z = 4; sum = x + y + z;
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Kap. 4.2: Binäre Suchbäume
 Kap. 4.2: Binäre Suchbäume Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 11. VO DAP2 SS 2009 26. Mai 2009 1 Zusätzliche Lernraumbetreuung Morteza Monemizadeh:
Kap. 4.2: Binäre Suchbäume Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 11. VO DAP2 SS 2009 26. Mai 2009 1 Zusätzliche Lernraumbetreuung Morteza Monemizadeh:
Datentypen. Agenda für heute, 4. März, 2010. Pascal ist eine streng typisierte Programmiersprache
 Agenda für heute, 4. März, 2010 Zusammengesetzte if-then-else-anweisungen Datentypen Pascal ist eine streng typisierte Programmiersprache Für jeden Speicherplatz muss ein Datentyp t (Datenformat) t) definiert
Agenda für heute, 4. März, 2010 Zusammengesetzte if-then-else-anweisungen Datentypen Pascal ist eine streng typisierte Programmiersprache Für jeden Speicherplatz muss ein Datentyp t (Datenformat) t) definiert
Informatik 2 Labor 2 Programmieren in MATLAB Georg Richter
 Informatik 2 Labor 2 Programmieren in MATLAB Georg Richter Aufgabe 3: Konto Um Geldbeträge korrekt zu verwalten, sind zwecks Vermeidung von Rundungsfehlern entweder alle Beträge in Cents umzuwandeln und
Informatik 2 Labor 2 Programmieren in MATLAB Georg Richter Aufgabe 3: Konto Um Geldbeträge korrekt zu verwalten, sind zwecks Vermeidung von Rundungsfehlern entweder alle Beträge in Cents umzuwandeln und
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Binäre Suchbäume (binary search trees, kurz: bst)
 Binäre Suchbäume (binary search trees, kurz: bst) Datenstruktur zum Speichern einer endlichen Menge M von Zahlen. Genauer: Binärbaum T mit n := M Knoten Jeder Knoten v von T ist mit einer Zahl m v M markiert.
Binäre Suchbäume (binary search trees, kurz: bst) Datenstruktur zum Speichern einer endlichen Menge M von Zahlen. Genauer: Binärbaum T mit n := M Knoten Jeder Knoten v von T ist mit einer Zahl m v M markiert.
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Eine Baumstruktur sei folgendermaßen definiert. Eine Baumstruktur mit Grundtyp Element ist entweder
 Programmieren in PASCAL Bäume 1 1. Baumstrukturen Eine Baumstruktur sei folgendermaßen definiert. Eine Baumstruktur mit Grundtyp Element ist entweder 1. die leere Struktur oder 2. ein Knoten vom Typ Element
Programmieren in PASCAL Bäume 1 1. Baumstrukturen Eine Baumstruktur sei folgendermaßen definiert. Eine Baumstruktur mit Grundtyp Element ist entweder 1. die leere Struktur oder 2. ein Knoten vom Typ Element
Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer
 Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer Klassendiagramme Ein Klassendiagramm dient in der objektorientierten Softwareentwicklung zur Darstellung von Klassen und den Beziehungen,
Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer Klassendiagramme Ein Klassendiagramm dient in der objektorientierten Softwareentwicklung zur Darstellung von Klassen und den Beziehungen,
II. Grundlagen der Programmierung. 9. Datenstrukturen. Daten zusammenfassen. In Java (Forts.): In Java:
 Technische Informatik für Ingenieure (TIfI) WS 2005/2006, Vorlesung 9 II. Grundlagen der Programmierung Ekkart Kindler Funktionen und Prozeduren Datenstrukturen 9. Datenstrukturen Daten zusammenfassen
Technische Informatik für Ingenieure (TIfI) WS 2005/2006, Vorlesung 9 II. Grundlagen der Programmierung Ekkart Kindler Funktionen und Prozeduren Datenstrukturen 9. Datenstrukturen Daten zusammenfassen
R ist freie Software und kann von der Website. www.r-project.org
 R R ist freie Software und kann von der Website heruntergeladen werden. www.r-project.org Nach dem Herunterladen und der Installation von R kann man R durch Doppelklicken auf das R-Symbol starten. R wird
R R ist freie Software und kann von der Website heruntergeladen werden. www.r-project.org Nach dem Herunterladen und der Installation von R kann man R durch Doppelklicken auf das R-Symbol starten. R wird
Praktische Informatik 3: Einführung in die Funktionale Programmierung Vorlesung vom 10.11.2010: Rekursive Datentypen
 Rev. 1152 1 [23] Praktische Informatik 3: Einführung in die Funktionale Programmierung Vorlesung vom 10.11.2010: Rekursive Datentypen Christoph Lüth & Dennis Walter Universität Bremen Wintersemester 2010/11
Rev. 1152 1 [23] Praktische Informatik 3: Einführung in die Funktionale Programmierung Vorlesung vom 10.11.2010: Rekursive Datentypen Christoph Lüth & Dennis Walter Universität Bremen Wintersemester 2010/11
SS 2010. Björn Berezowski B.Sc. Marco Münch B.Sc. Michael Roth B.Sc. Repetitorium PG 1. Übungsblatt. 1 Übung - Probeklausur SS 2010 Typ Prof.
 SS 2010 Björn Berezowski B.Sc. Marco Münch B.Sc. Michael Roth B.Sc. Repetitorium PG 1 Übungsblatt 1 Übung - Probeklausur SS 2010 Typ Prof.Humm Aufgabe : Bank-Verwaltungs-System In dieser Klausur werden
SS 2010 Björn Berezowski B.Sc. Marco Münch B.Sc. Michael Roth B.Sc. Repetitorium PG 1 Übungsblatt 1 Übung - Probeklausur SS 2010 Typ Prof.Humm Aufgabe : Bank-Verwaltungs-System In dieser Klausur werden
Beispiele: (Funktionen auf Listen) (3) Bemerkungen: Die Datenstrukturen der Paare (2) Die Datenstrukturen der Paare
 Beispiele: (Funktionen auf Listen) (3) Bemerkungen: 5. Zusammenhängen der Elemente einer Liste von Listen: concat :: [[a]] -> [a] concat xl = if null xl then [] else append (head xl) ( concat (tail xl))
Beispiele: (Funktionen auf Listen) (3) Bemerkungen: 5. Zusammenhängen der Elemente einer Liste von Listen: concat :: [[a]] -> [a] concat xl = if null xl then [] else append (head xl) ( concat (tail xl))
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann [email protected]
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann [email protected]
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Java 7. Elmar Fuchs Grundlagen Programmierung. 1. Ausgabe, Dezember 2011 JAV7
 Java 7 Elmar Fuchs Grundlagen Programmierung 1. Ausgabe, Dezember 2011 JAV7 5 Java 7 - Grundlagen Programmierung 5 Kontrollstrukturen In diesem Kapitel erfahren Sie wie Sie die Ausführung von von Bedingungen
Java 7 Elmar Fuchs Grundlagen Programmierung 1. Ausgabe, Dezember 2011 JAV7 5 Java 7 - Grundlagen Programmierung 5 Kontrollstrukturen In diesem Kapitel erfahren Sie wie Sie die Ausführung von von Bedingungen
Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert
 Beamen in EEP Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert Zuerst musst du dir 2 Programme besorgen und zwar: Albert, das
Beamen in EEP Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert Zuerst musst du dir 2 Programme besorgen und zwar: Albert, das
WS 2008/09. Diskrete Strukturen
 WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
Programmieren I. Kapitel 7. Sortieren und Suchen
 Programmieren I Kapitel 7. Sortieren und Suchen Kapitel 7: Sortieren und Suchen Ziel: Varianten der häufigsten Anwendung kennenlernen Ordnung Suchen lineares Suchen Binärsuche oder Bisektionssuche Sortieren
Programmieren I Kapitel 7. Sortieren und Suchen Kapitel 7: Sortieren und Suchen Ziel: Varianten der häufigsten Anwendung kennenlernen Ordnung Suchen lineares Suchen Binärsuche oder Bisektionssuche Sortieren
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Übungen für Woche 10
 Übungen für Woche 10 Martin Rubey 12. Januar 2011 Die folgenden Übungen sollen den Umgang mit Backtracking und kombinatorischen Spezies näherbringen. Genaue Hinweise gibt es erst auf Seite 5. Zur Erinnerung:
Übungen für Woche 10 Martin Rubey 12. Januar 2011 Die folgenden Übungen sollen den Umgang mit Backtracking und kombinatorischen Spezies näherbringen. Genaue Hinweise gibt es erst auf Seite 5. Zur Erinnerung:
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T:
 Binäre Bäume Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T: BinTree [T: TYPE]: DATATYPE empty: empty? node (key: T, left:bibtree, right:bibtree):
Binäre Bäume Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T: BinTree [T: TYPE]: DATATYPE empty: empty? node (key: T, left:bibtree, right:bibtree):
I.1 Die Parrot Assemblersprache
 I.1 Die Parrot Assemblersprache Die virtuelle CPU Parrot ermöglicht die Verarbeitung der Parrot Assemblersprache (PASM). Zum Einstieg soll ein erstes Beispiel die Ausführung einer PASM-Datei zeigen. Legen
I.1 Die Parrot Assemblersprache Die virtuelle CPU Parrot ermöglicht die Verarbeitung der Parrot Assemblersprache (PASM). Zum Einstieg soll ein erstes Beispiel die Ausführung einer PASM-Datei zeigen. Legen
