Übung: Computergrafik 1
|
|
|
- Ralf Pfaff
- vor 9 Jahren
- Abrufe
Transkript
1 Prof. Dr. Andreas Butz Prof. Dr. Ing. Axel Hoppe Dipl.-Medieninf. Dominikus Baur Dipl.-Medieninf. Sebastian Boring Übung: Computergrafik 1 Geometrische Primitive OpenGL Zeichenarten Kurven
2 Primitive Übung Computergrafik 1 SoSe
3 2D Objekte Beispiel: glbegin(gl_polygon); glcolor3f(1.0f, 0.0f, 0.0f); // red glvertex3f(-1.0f, -1.0f, 0.0f); glvertex3f(1.0f, -1.0f, 0.0f); glcolor3f(0.0f, 0.0f, 1.0f); // blue glvertex3f(1.0f, 1.0f, 0.0f); glvertex3f(-1.0f, 1.0f, 0.0f); glend(); Weitere Formen: GL_POINTS, GL_LINES (je 2 Punkte verbunden) GL_LINE_STRIP, GL_LINE_LOOP GL_QUADS, GL_POLYGON, GL_TRIANGLES, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN, GL_QUAD_STRIP 3D-Objekte müssen aus 2D-Objekten zusammengesetzt werden (s. Übungsblatt) (Quelle: Übung Computergrafik 1 SoSe
4 2D Objekte Beispiele: GL_POINTS GL_LINES GL_LINE_STRIP GL_LINE_LOOP GL_QUADS GL_POLYGON (Quelle: Übung Computergrafik 1 SoSe
5 2D Objekte GL_TRIANGLES GL_TRIANGLE_STRIP GL_TRIANGLE_FAN GL_QUAD_STRIP 6 (Quelle: Übung Computergrafik 1 SoSe
6 glbegin - glend, glvertex Innerhalb eines glbegin... glend Blocks dürfen nur bestimmte gl- Befehle vorkommen, u.a. glcolor, glvertex, gltexcoord glvertex muss innerhalb von glbegin/glend aufgerufen werden! Varianten: glvertex2f(x, y) - z wird auf 0 gesetzt glvertex3f(x, y, z) glvertex4f(x, y, z, w) - manipuliert zusätzlich die homogene Komponente des Vektors glvertex3fv( v ) übergibt einen Pointer auf einen Vektor Übung Computergrafik 1 SoSe
7 Würfel in OpenGL Übung Computergrafik 1 SoSe
8 Primitivmanipulation Wie Punkte und Linien gezeichnet werden lässt sich mit bestimmten Befehlen manipulieren: glcolor3f/glcolor4f setzt einen Farbwert glpointsize(float) bestimmt die Dicke von Punkten glenable(gl_point_smooth) aktiviert Kantenglättung gllinewidth(float) bestimmt die Dicke von Linien glenable(gl_line_smooth) aktiviert Kantenglättung Übung Computergrafik 1 SoSe
9 Primitivmanipulation II Wie Punkte und Linien gezeichnet werden lässt sich mit bestimmten Befehlen manipulieren: gllinestipple(int, short) erzeugt ein Muster in der Linie (muss mit glenable(gl_line_stipple) aktiviert werden) Der 16-Bit Short Wert bestimmt das Muster (Bit gesetzt -> Pixel wird gezeichnet, Bit nicht gesetzt -> Pixel wird nicht gezeichnet Durch Angabe eines Faktors lässt sich das Muster strecken Übung Computergrafik 1 SoSe
10 Primitivmanipulation III Wie Punkte und Linien gezeichnet werden lässt sich mit bestimmten Befehlen manipulieren: glpolygonstipple(glubyte*) erzeugt ein Muster in einem Polygon (Pointer auf 32 x 32 Bit Array) (muss mit glenable(gl_polygon_stipple) aktiviert werden) (Quelle: Übung Computergrafik 1 SoSe
11 Primitivmanipulation IV Wie Punkte und Linien gezeichnet werden lässt sich mit bestimmten Befehlen manipulieren: glpolygonmode(face, mode) beeinflusst, wie Polygone gezeichnet werden: face bestimmt den Teil des Polygons (GL_FRONT, GL_BACK, GL_FRONT_AND_BACK) mode gibt den Zeichenmodus für den gewählten Teil an (GL_POINT, GL_LINE, GL_FILL) Achtung! Vertices die gegen den Uhrzeigersinn gezeichnet werden gelten als vorne, im Uhrzeigersinn als hinten! Übung Computergrafik 1 SoSe
12 Primitivmanipulation V Übung Computergrafik 1 SoSe
13 OpenGL Zeichenmodi Primitive lassen sich in OpenGL auf vier verschiedene Arten zeichnen: Im sogenannten immediate mode mit glbegin/glend Performanceeinbußen! Nicht vorhanden in OpenGL 3.x und OpenGL ES mit vorkompilierten Display Lists Performant aber statisch (auch nicht unterstützt in OpenGL ES) mit Vertex Arrays oder interleaved Arrays Dynamisch aber nicht performant mit Vertex Buffer Objects (VBOs) Performant und dynamisch (Quelle: Übung Computergrafik 1 SoSe
14 OpenGL Display Lists Display Lists speichern eine Reihe von OpenGL-Befehlen, kompilieren sie und schicken sie an die Grafikkarte => weniger Overhead, höhere Performance Fast alle Befehle sind erlaubt (anders als in glbegin/glend) GLuint glgenlists(range) erstellt neue Display Listen und gibt die Nummer der ersten Liste zurück glnewlist(list, mode) beginnt eine neue Liste (mode ist entweder GL_COMPILE oder GL_COMPILE_AND_EXECUTE) glendlist() beendet die aktuelle Liste glcalllist(list) führt die Anweisungen der Liste aus Übung Computergrafik 1 SoSe
15 OpenGL Display Lists... Übung Computergrafik 1 SoSe
16 OpenGL Vertex Arrays Nachteile der Display Lists: Keine Änderungen mehr möglich nach Kompilieren Redundanz in den Vertices Lösung: Vertex Arrays Verfügbar für verschiedene Operationen: glvertexpointer (Vertices) glnormalpointer (Normalen) glcolorpointer (Farben) glindexpointer (Indizes) gltexcoordpointer (Texturkoordinaten) gledgeflagpointer (Edge Flags) Übung Computergrafik 1 SoSe
17 OpenGL Vertex Arrays Für alle glxxpointer-befehle gleiche Syntax: glvertexpointer(int size, enum type, sizei stride, void* pointer) size Koordinatenzahl im Array (2,3,4) type Datentyp (GL_INT, GL_FLOAT, GL_DOUBLE, etc.) stride Abstand zwischen einzelnen Elementen im Array in Bytes (z.b. stride = 4 bei GL_FLOAT (4 Byte) um nur jeden zweiten Vertex zu nehmen) pointer Der Pointer auf den Speicherbereich der das Array enthält Übung Computergrafik 1 SoSe
18 OpenGL Vertex Arrays Weitere Befehle für Vertex Arrays: glenableclientstate(gl_vertex_array) aktiviert Vertex Arrays gldisableclientstate(gl_vertex_array) deaktiviert sie wieder gldrawarrays(mode, offset, size) zeichnet ein Vertex Array mode entspricht GL_LINES, GL_QUADS, etc. (s.o.) offset erstes Element des Arrays (normalerweise 0) size Anzahl der Elemente im Vertex Array Übung Computergrafik 1 SoSe
19 OpenGL Vertex Arrays Übung Computergrafik 1 SoSe
20 OpenGL Vertex Arrays Jeder Punkt in dem Würfel ist weiterhin viermal im Array vertreten Daher lassen sich auch Indizes zum Zeichnen von Vertex Arrays angeben gldrawelements(mode, count, type, indices) mode entspricht GL_LINES, GL_QUADS, etc. (s.o.) count Anzahl der Elemente die gerendert werden sollen type Datentyp des Index Arrays (GL_UNSIGNED_BYTE, GL_SHORT, GL_INT, etc.) indices Pointer auf das Index Array Übung Computergrafik 1 SoSe
21 OpenGL Vertex Arrays Übung Computergrafik 1 SoSe
22 OpenGL Interleaved Arrays Um Vertices in verschiedenen Farben zu zeichnen brauchen wir wieder zwei Arrays, eins für die Vertices, eins für die Farben Diese Daten lassen sich auch in einem Interleaved Array kombinieren, d.h. abwechselnd Farbwerte und Vertex-Koordinaten Der Befehl glinterleavedarrays (format, stride, pointer) kümmert sich darum, dass der Client State richtig ist und dass alle internen Arrays passend gefüllt werden. format Das Format des Interleaved Arrays stride Abstand in Bytes zwischen einzelnen Elementen (d.h. Punkte, Farben, etc.) pointer Ein Pointer auf das Interleaved Array format setzt sich folgendermaßen zusammen: GL_XXX[_YYY][_ZZZ][_AAA] mit Tripeln {V C T N} {2 3 4} {F D} Vertex, Color, Texture Coords, Normals 2, 3, 4 Elemente im Array pro Vertex, etc. Float, Double Übung Computergrafik 1 SoSe
23 OpenGL Interleaved Arrays (Quelle: Übung Computergrafik 1 SoSe
24 OpenGL VBOs Vertex Buffer Objects (VBOs) bilden die Brücke zwischen Display Lists und Vertex Arrays Sie werden auf der Grafikkarte gehalten (keine Verluste durch Übertragung) können aber trotzdem leicht geändert werden glgenbuffersarb(glsizei n, GLuint* ids) erzeugt neue VBOs glbindbufferarb(target, id) target entweder GL_ARRAY_BUFFER_ARB (Vertices, Farben) oder GL_ELEMENT_ARRAY_BUFFER_ARB (Indizes) id des VBOs glbufferdataarb(target, size, void* data, usage) size Größe des Arrays in Bytes usage Nutzung des VBOs: GL_STATIC_DRAW_ARB wird nicht geändert GL_DYNAMIC_DRAW_ARB wird evtl. geändert GL_STREAM_DRAW_ARB wird jedes Frame geändert Übung Computergrafik 1 SoSe
25 OpenGL VBOs VBOs zu zeichnen funktionert (fast) genauso wie bei Vertex Arrays: Laden des jeweiligen VBOs mit glbindbufferarb Aktivieren des GL_VERTEX_ARRAY Client states Laden des Arrays aus dem VBO mit glvertexpointer (allerdings mit leerem (=0) Pointer!) Zeichnen mit gldrawarrays, gldrawelements Deaktivieren des VBOs mit glbindbufferarb mit leerem Pointer Übung Computergrafik 1 SoSe
26 OpenGL VBOs (Quelle: Übung Computergrafik 1 SoSe
27 OpenGL VBOs (Quelle: Übung Computergrafik 1 SoSe
28 Primitive mit GLU Übung Computergrafik 1 SoSe
29 GLU Primitive Die Hilfsbibliothek GLU bietet verschiedene vorgefertigte Primitive die auf Quadriken basieren Eine Quadrik ist eine Fläche deren Punkte durch eine Formel wie x 2 + y 2 + z 2 = r 2 beschrieben werden Neue Quadrikenobjekte werden mit dem Befehl GLUquadricObj* glunewquadric() erzeugt. GLU kümmert sich um die Details der darunterliegen Quadrik. Übung Computergrafik 1 SoSe
30 GLU Primitive Verfügbare Primitive in GLU sind (u.a.): glucylinder (quad, base, top, height, slices, stacks) zeichnet einen Zylinder entlang der Z-Achse base Zylinderradius bei z = 0 top Zylinderradius bei z = height height Höhe des Zylinders slices Aufteilungen um die z-achse herum stacks Aufteilungen die z-achse entlang glusphere (quad, radius, slices, stacks) zeichnet eine Kugel um den Ursprung radius Radius der Kugel slices Aufteilungen um die z-achse herum stacks Aufteilungen die z-achse entlang Übung Computergrafik 1 SoSe
31 GLU Primitive Übung Computergrafik 1 SoSe
32 Kurven Übung Computergrafik 1 SoSe
33 Bézierkurven Übung Computergrafik 1 SoSe
34 Bézierkurven n = 1 linear n =2 quadratisch n = 3 kubisch (Quelle: Übung Computergrafik 1 SoSe
35 OpenGL Bézierkurven Die Punkte, die auf einer Bézierkurve liegen lassen sich in OpenGL automatisch in beliebiger Granularität berechnen glmap1f(target, u1, u2, stride, order, *points) target Werte die durch die Funktion berechnet werden sollen (z.b. GL_MAP1_VERTEX_3, GL_MAP1_NORMAL) u1, u2 Untere und obere Grenze (0, 1 bieten sich an) stride Abstand in floats/doubles zwischen Kontrollpunkten im Array order Ordnung der Kurve (= Grad + 1) points Array mit Kontrollpunkten glevalcoord1f (u) berechnet einen Punkt der Kurve u Die Position auf der Kurve (liegt zwischen u1 und u2) Übung Computergrafik 1 SoSe
36 OpenGL Bézierkurven (Quelle: Übung Computergrafik 1 SoSe
37 NURBS Non-uniform Rational B-Splines sind die Verallgemeinerung von Bézierkurven Dienen der Beschreibung von beliebig geformten Flächen im Raum Definition über Kontrollpunkte und Knoten Der Knotenvektor definiert den Einfluss der einzelnen Kontrollpunkte auf die jeweiligen Punkte der Kurve Es müssen immer Kontrollpunkte + Grad der Kurve + 1 Knoten angegeben werden (Quelle: Übung Computergrafik 1 SoSe
38 OpenGL NURBS (Quelle: Übung Computergrafik 1 SoSe
39 OpenGL NURBS (Quelle: Übung Computergrafik 1 SoSe
40 Mathe Übung Computergrafik 1 SoSe
41 Normalen Die Normale einer Ebene bzw. eines Vektorpaars ist derjenige Vektor der darauf senkrecht steht (und ungleich 0 ist) Bestimmung entweder über lineares Gleichungssystem oder Kreuzprodukt: (Quelle: Übung Computergrafik 1 SoSe
42 Winkel zwischen zwei Vektoren Das Skalarprodukt zweier Vektoren erzeugt einen Skalar als Ergebnis und kann folgendermaßen berechnet werden: Dadurch lassen sich u.a. die Länge (der Betrag) eines Vektors bestimmen: Oder der Winkel zwischen zwei Vektoren: (Quelle: Übung Computergrafik 1 SoSe
43 Literatur Weiterführende Literatur g/sdk/docs /man/ James Van Verth, Lars Bishop: Essential Mathematics for Games and Interactive Applications: A Programmer's Guide OpenGL Redbook : NeHe OpenGL Tutorials: Song Ho Ahn Tutorials: Übung Computergrafik 1 SoSe
OpenGL 2.0 Vertex Arrays
 OpenGL 2.0 Vertex Arrays Boguslaw Sylla Interaktive 3D-Computergrafik SS 2010 Hochschule RheinMain Inhalt des Vortrags 1 Ein- / Ausschalten von Arrays EnableClientState, DisableClientState 2 Spezifizieren
OpenGL 2.0 Vertex Arrays Boguslaw Sylla Interaktive 3D-Computergrafik SS 2010 Hochschule RheinMain Inhalt des Vortrags 1 Ein- / Ausschalten von Arrays EnableClientState, DisableClientState 2 Spezifizieren
7.1 Polygon Offset. Anwendung - Darstellung von Polygonen als Teil von Oberflächen - Beispiel: Gradlinien auf der Erde - Schwierigkeit:
 7.1 Polygon Offset Anwendung - Darstellung von Polygonen als Teil von Oberflächen - Beispiel: Gradlinien auf der Erde - Schwierigkeit: - Polygone sollen einmal als Fläche und einmal in Wireframe-Darstellung
7.1 Polygon Offset Anwendung - Darstellung von Polygonen als Teil von Oberflächen - Beispiel: Gradlinien auf der Erde - Schwierigkeit: - Polygone sollen einmal als Fläche und einmal in Wireframe-Darstellung
3D Programmierpraktikum: Szenegraphen und Texturierung
 3D Programmierpraktikum: Szenegraphen und Praktikum 3D Programmierung Sebastian Boring, Otmar Hilliges Donnerstag, 1. Juni 2006 LMU München Medieninformatik Boring/Hilliges 3D Programmierpraktikum SS2006
3D Programmierpraktikum: Szenegraphen und Praktikum 3D Programmierung Sebastian Boring, Otmar Hilliges Donnerstag, 1. Juni 2006 LMU München Medieninformatik Boring/Hilliges 3D Programmierpraktikum SS2006
Einführung in die API OpenGL
 Einführung in die API OpenGL LMU München - LFE Medieninformatik Folie 1 Überblick Was ist OpenGL? OpenGL und Windows 3D Grafik Grundlagen OpenGL benutzen Transformationen, Licht, Texture Mapping Ein kleines
Einführung in die API OpenGL LMU München - LFE Medieninformatik Folie 1 Überblick Was ist OpenGL? OpenGL und Windows 3D Grafik Grundlagen OpenGL benutzen Transformationen, Licht, Texture Mapping Ein kleines
OpenGL auf Mac OS X und ios
 OpenGL auf Mac OS X und ios Torsten Kammer 28.4.2011 CocoaHeads Aachen Grundlagen API für hardwarebeschleunigte 3D-Grafik Kann auch für schnelles 2D verwendet werden Grundlage von Core Image, Core Animation,
OpenGL auf Mac OS X und ios Torsten Kammer 28.4.2011 CocoaHeads Aachen Grundlagen API für hardwarebeschleunigte 3D-Grafik Kann auch für schnelles 2D verwendet werden Grundlage von Core Image, Core Animation,
Modellierung. Oliver Hartmann
 Modellierung Oliver Hartmann [email protected] Inhalt Boolesche Operationen Splines B-Splines Bezier-Kurven NURBS Anwendung Sculpting Volumengrafik Marching Cubes Ray Casting Texture Mapping Boolesche
Modellierung Oliver Hartmann [email protected] Inhalt Boolesche Operationen Splines B-Splines Bezier-Kurven NURBS Anwendung Sculpting Volumengrafik Marching Cubes Ray Casting Texture Mapping Boolesche
Tim Pommerening v0.0.1 (ohne Gewähr) Seite 1 von 6
 Tim Pommerening v0.0.1 (ohne Gewähr) Seite 1 von 6 Formelsammlung: GDV Bezeichnung Gefülltes regelmäßiges n-eck Formel /** * Zeichnet ein gefülltes n-eck. * x0, y0 : Koordinaten des Mittelpunkts. * r0
Tim Pommerening v0.0.1 (ohne Gewähr) Seite 1 von 6 Formelsammlung: GDV Bezeichnung Gefülltes regelmäßiges n-eck Formel /** * Zeichnet ein gefülltes n-eck. * x0, y0 : Koordinaten des Mittelpunkts. * r0
Grafikprogrammierung mit OpenGL
 Technische Universität Dresden Dresden, August 2003 Fakultät Informatik Institut für Software- und Multimediatechnik Lehrheft Computergrafik Herausgabe: K. Hoedt W. Mascolus Fakultät Informatik Lehrheft
Technische Universität Dresden Dresden, August 2003 Fakultät Informatik Institut für Software- und Multimediatechnik Lehrheft Computergrafik Herausgabe: K. Hoedt W. Mascolus Fakultät Informatik Lehrheft
Geometrische Primitive und Hidden Surface Removal
 C A R L V O N O S S I E T Z K Y Geometrische Primitive und Hidden Surface Removal Johannes Diemke Übung im Modul OpenGL mit Java Wintersemester 2010/2011 Wiederholung Geometrische Primitive in OpenGL Mit
C A R L V O N O S S I E T Z K Y Geometrische Primitive und Hidden Surface Removal Johannes Diemke Übung im Modul OpenGL mit Java Wintersemester 2010/2011 Wiederholung Geometrische Primitive in OpenGL Mit
Erste Schritte in OpenGL
 Erste Schritte in OpenGL Modelierung Aus Punkten werden geometrische Körper Komplexe Objeckte werden aus meheren einfachen Objeckten erstellt Dazu müssen Vertexes (Punkte) im virtuellen Raum angefordnet
Erste Schritte in OpenGL Modelierung Aus Punkten werden geometrische Körper Komplexe Objeckte werden aus meheren einfachen Objeckten erstellt Dazu müssen Vertexes (Punkte) im virtuellen Raum angefordnet
Computergrafik II. OpenGL Einführung
 Computergrafik II OpenGL Einführung OpenGL Rein prozedurales Interface Keine direkten Klassen/Objekte Verwaltung von OpenGL-Strukturen mittels Identifier Explizites funktionales Erzeugen/Löschen von Objekten
Computergrafik II OpenGL Einführung OpenGL Rein prozedurales Interface Keine direkten Klassen/Objekte Verwaltung von OpenGL-Strukturen mittels Identifier Explizites funktionales Erzeugen/Löschen von Objekten
Grafikprogrammierung (Echtzeitrendering)
 (Echtzeitrendering) erfordert Unterstützung für beide Aufgaben der Computergrafik Geometrische Modellierung Datenstrukturen für geometrische Modelle Schnittstellen für deren Kombination Bildsynthese Rendering
(Echtzeitrendering) erfordert Unterstützung für beide Aufgaben der Computergrafik Geometrische Modellierung Datenstrukturen für geometrische Modelle Schnittstellen für deren Kombination Bildsynthese Rendering
Darstellung runder Objekte in OpenGL ES. 1 Darstellung eines Zylinders oder Kegels. Inhaltsverzeichnis. Berechnen der Punkte.
 Seite 1 von 9 Darstellung runder Objekte in OpenGL ES Inhaltsverzeichnis Darstellung runder Objekte in OpenGL ES...1 1Darstellung eines Zylinders oder Kegels...1 Berechnen der Punkte...1 Darstellung als
Seite 1 von 9 Darstellung runder Objekte in OpenGL ES Inhaltsverzeichnis Darstellung runder Objekte in OpenGL ES...1 1Darstellung eines Zylinders oder Kegels...1 Berechnen der Punkte...1 Darstellung als
Technische Universität Dresden Fakultät Informatik Prof. Dr.-Ing.habil. Orlamünder. OpenGL. OpenGL. OpenGL000
 000 Konzepte der ist ein Software-Interface zur Hardware. Zweck ist die Darstellung von zwei- und dreidimensionalen Objekten mittels eines Bildspeichers. Diese Objekte sind entweder Images, die aus Pixeln
000 Konzepte der ist ein Software-Interface zur Hardware. Zweck ist die Darstellung von zwei- und dreidimensionalen Objekten mittels eines Bildspeichers. Diese Objekte sind entweder Images, die aus Pixeln
Computergraphik I Die Graphik-Pipeline &
 Computergraphik I Die Graphik-Pipeline & Einführung in OpenGL 3+ G. Zachmann University of Bremen, Germany cgvr.informatik.uni-bremen.de OpenGL OpenGL ist ein Software-Interface für Graphik-Hardware mit
Computergraphik I Die Graphik-Pipeline & Einführung in OpenGL 3+ G. Zachmann University of Bremen, Germany cgvr.informatik.uni-bremen.de OpenGL OpenGL ist ein Software-Interface für Graphik-Hardware mit
Texture Mapping. Texturen
 Grundlagen - Eine Textur ist ein Bild, das auf eine Oberfläche einer Geometrie aufgebracht ist - erlauben eine realistischere Darstellung von Oberflächen - können auf alle Primitive, nicht nur Polygone
Grundlagen - Eine Textur ist ein Bild, das auf eine Oberfläche einer Geometrie aufgebracht ist - erlauben eine realistischere Darstellung von Oberflächen - können auf alle Primitive, nicht nur Polygone
Übung: Computergrafik 1
 Prof. Dr. Andreas Butz Prof. Dr. Ing. Axel Hoppe Dipl.-Medieninf. Dominikus Baur Dipl.-Medieninf. Sebastian Boring Übung: Computergrafik 1 Fouriertransformation Organisatorisches Neue Abgabefrist für Blatt
Prof. Dr. Andreas Butz Prof. Dr. Ing. Axel Hoppe Dipl.-Medieninf. Dominikus Baur Dipl.-Medieninf. Sebastian Boring Übung: Computergrafik 1 Fouriertransformation Organisatorisches Neue Abgabefrist für Blatt
OpenGL. Rendering: (Wiedergabe, Darstellung): Erzeugg. digitaler (Pixel-)Bilder aus log.-mathem. Modell-Beschreibungen.
 OpenGL Grafik-Bibliothek mit einigen hundert Befehlen gl...() (div. Ausführungen) angeschlossener Aufsatz : OpenGL Utility Library (GLU), ca. 50 Befehle glu...() Plattform-unabhängig (Hardware, Fenster-/
OpenGL Grafik-Bibliothek mit einigen hundert Befehlen gl...() (div. Ausführungen) angeschlossener Aufsatz : OpenGL Utility Library (GLU), ca. 50 Befehle glu...() Plattform-unabhängig (Hardware, Fenster-/
Übung Computergrafik 3
 Übung Computergrafik 3 1.Übungsblatt: Geometrie Stephan Groß (Dank an Irini Schmidt und Jakob Bärz) Institut für Computervisualistik Universität Koblenz-Landau 6. Juli 2011 Aufgabe 1: Fragezeichen Gegeben:
Übung Computergrafik 3 1.Übungsblatt: Geometrie Stephan Groß (Dank an Irini Schmidt und Jakob Bärz) Institut für Computervisualistik Universität Koblenz-Landau 6. Juli 2011 Aufgabe 1: Fragezeichen Gegeben:
Approximationsverfahren für die Kurvendarstellung
 Approximationsverfahren für die Kurvendarstellung (a) Bézier-Kurven spezielle Form polynomialer Kurven spezifiziert durch n+1 Kontrollpunkte P 0, P 1,..., P n Kurve läuft nicht durch alle Kontrollpunkte,
Approximationsverfahren für die Kurvendarstellung (a) Bézier-Kurven spezielle Form polynomialer Kurven spezifiziert durch n+1 Kontrollpunkte P 0, P 1,..., P n Kurve läuft nicht durch alle Kontrollpunkte,
Texture Mapping Beispiel. Universität Frankfurt
 Texture Mapping Beispiel Texture Mapping Warum? - Detailreiche Oberfläche ohne zusätzliche Polygone Texturen I - 1D-Texturen - 2D-Texturen - 3D-Texturen Element der Textur: Texel Texturen II - Änderung
Texture Mapping Beispiel Texture Mapping Warum? - Detailreiche Oberfläche ohne zusätzliche Polygone Texturen I - 1D-Texturen - 2D-Texturen - 3D-Texturen Element der Textur: Texel Texturen II - Änderung
Einführung in GLSL - OpenGL Shading Language. Athanasios Karamalis
 Einführung in GLSL - OpenGL Shading Language Athanasios Karamalis Allgemein zur Shader-Programmierung Vor 2001 konnte nur die sogenannte Fixed Functionality der Graphik API und Graphikkarte verwendet werden
Einführung in GLSL - OpenGL Shading Language Athanasios Karamalis Allgemein zur Shader-Programmierung Vor 2001 konnte nur die sogenannte Fixed Functionality der Graphik API und Graphikkarte verwendet werden
Grafikprogrammierung mit OpenGL I
 Grafikprogrammierung mit OpenGL I Proseminar Computergrafik Sommersemester 2 TU Dresden Johannes Völker Matrikelnummer: 3478976 [email protected] Dozent: Wilfried Mascolus Lehrstuhl für Computergraphik
Grafikprogrammierung mit OpenGL I Proseminar Computergrafik Sommersemester 2 TU Dresden Johannes Völker Matrikelnummer: 3478976 [email protected] Dozent: Wilfried Mascolus Lehrstuhl für Computergraphik
Abitur 2013 Mathematik Geometrie V
 Seite 1 http://www.abiturloesung.de/ Seite Abitur 1 Mathematik Geometrie V Teilaufgabe b ( BE) Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massiven Beton, der die
Seite 1 http://www.abiturloesung.de/ Seite Abitur 1 Mathematik Geometrie V Teilaufgabe b ( BE) Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massiven Beton, der die
Modellierung und Programmierung 1
 Modellierung und Programmierung 1 Prof. Dr. Sonja Prohaska Computational EvoDevo Group Institut für Informatik Universität Leipzig 19. November 2015 Gültigkeitsbereich (Scope) von Variablen { int m; {
Modellierung und Programmierung 1 Prof. Dr. Sonja Prohaska Computational EvoDevo Group Institut für Informatik Universität Leipzig 19. November 2015 Gültigkeitsbereich (Scope) von Variablen { int m; {
3D Programmierpraktikum: Schattenberechnung in Echtzeit
 3D Programmierpraktikum: Schattenberechnung in Echtzeit Praktikum 3D Programmierung Sebastian Boring, Otmar Hilliges Donnerstag, 20. Juli 2006 LMU München Medieninformatik Boring/Hilliges 3D Programmierpraktikum
3D Programmierpraktikum: Schattenberechnung in Echtzeit Praktikum 3D Programmierung Sebastian Boring, Otmar Hilliges Donnerstag, 20. Juli 2006 LMU München Medieninformatik Boring/Hilliges 3D Programmierpraktikum
Übungsstunde 8 zu Computergrafik 1
 Institut für Computervisualistik Universität Koblenz 14. und 15. Januar 2013 Inhaltsverzeichnis 1 Wiederholung - Beleuchtung Gouraud-Shading Phong-Shading Flat-Shading Vergleich 2 - Idee in OpenGL Texturfilterung
Institut für Computervisualistik Universität Koblenz 14. und 15. Januar 2013 Inhaltsverzeichnis 1 Wiederholung - Beleuchtung Gouraud-Shading Phong-Shading Flat-Shading Vergleich 2 - Idee in OpenGL Texturfilterung
Programmierpraktikum 3D Computer Grafik
 Prof. Andreas Butz, Dipl.Inf. Otmar Hilliges Programmierpraktikum 3D Computer Grafik Dynamische Schattenberechnung Agenda Der Stencil-Puffer Der 1-bit Stencil-Puffer Der 8-bit Stencil-Puffer Volumetrische
Prof. Andreas Butz, Dipl.Inf. Otmar Hilliges Programmierpraktikum 3D Computer Grafik Dynamische Schattenberechnung Agenda Der Stencil-Puffer Der 1-bit Stencil-Puffer Der 8-bit Stencil-Puffer Volumetrische
WiMa-Praktikum 1. Woche 8
 WiMa-Praktikum 1 Universität Ulm, Sommersemester 2017 Woche 8 Lernziele In diesem Praktikum sollen Sie üben und lernen: Besonderheiten der For-Schleife in Matlab Wiederholung des Umgangs mit Matrizen und
WiMa-Praktikum 1 Universität Ulm, Sommersemester 2017 Woche 8 Lernziele In diesem Praktikum sollen Sie üben und lernen: Besonderheiten der For-Schleife in Matlab Wiederholung des Umgangs mit Matrizen und
Eine Einführung in OpenGL
 Eine Einführung in OpenGL Inhaltsverzeichnis 1 Übersicht 2 1.1 Was ist OpenGL?........................... 2 1.2 Was leistet OpenGL?......................... 2 2 Erste Schritte mit OpenGL 3 2.1 Grundstrukturen...........................
Eine Einführung in OpenGL Inhaltsverzeichnis 1 Übersicht 2 1.1 Was ist OpenGL?........................... 2 1.2 Was leistet OpenGL?......................... 2 2 Erste Schritte mit OpenGL 3 2.1 Grundstrukturen...........................
CGVert. Projekt. 3D-Scannen. Multimarker Tracking. Triangulierung. Low-Cost Scanner P 4. Ball-Erkennung. 3D Positionsbestimmung. Kalmanfilter. CGVert.
 Seminar-Vortrag Projektgruppen der Vertiefung Computergrafik (Vorträge am 29.11.2006 ab 8.50Uhr) Themenauswahl Bis heute (25.10.2006) um 16.00Uhr Vortrag Am 29.11.2006 Dauer: 30min Medium Beamer und/oder
Seminar-Vortrag Projektgruppen der Vertiefung Computergrafik (Vorträge am 29.11.2006 ab 8.50Uhr) Themenauswahl Bis heute (25.10.2006) um 16.00Uhr Vortrag Am 29.11.2006 Dauer: 30min Medium Beamer und/oder
Java 3D. Linien, Flächen und Objekte Axel Bartsch, Okt. 2002
 Java 3D Linien, Flächen und Objekte Axel Bartsch, Okt. 2002 Virtual World Koordinaten System Grundlagen zur Definition visueller Objekte Shape3D Unterklasse der Leaf-Klasse Eigenschaften des visuellen
Java 3D Linien, Flächen und Objekte Axel Bartsch, Okt. 2002 Virtual World Koordinaten System Grundlagen zur Definition visueller Objekte Shape3D Unterklasse der Leaf-Klasse Eigenschaften des visuellen
Computergrafik Universität Osnabrück, Henning Wenke,
 Computergrafik Universität Osnabrück, Henning Wenke, 2012-06-18 Kapitel XIII Texturing Definition: Textur (Computergrafik) Geometrieunabhängige Oberflächeneigenschaft Typischerweise höher aufgelöst als
Computergrafik Universität Osnabrück, Henning Wenke, 2012-06-18 Kapitel XIII Texturing Definition: Textur (Computergrafik) Geometrieunabhängige Oberflächeneigenschaft Typischerweise höher aufgelöst als
Grafikprogrammierung mit OpenGL
 Grafikprogrammierung mit OpenGL Proseminar Computergrafik Sommersemester 2009 Dozent: Wilfried Mascolus Lehrstuhl für Computergraphik und Visualisierung Fakultät Informatik Sebastian Hubl Matrikelnummer:
Grafikprogrammierung mit OpenGL Proseminar Computergrafik Sommersemester 2009 Dozent: Wilfried Mascolus Lehrstuhl für Computergraphik und Visualisierung Fakultät Informatik Sebastian Hubl Matrikelnummer:
Aufgaben und Lösungen
 Aufgaben und Lösungen c Michael Bender, Manfred Brill Oktober 005 Sie finden in diesem Dokument alle Aufgaben und die zugehörigen Lösungen aus Michael Bender, Manfred Brill: Computergrafik. Auflage, Hanser
Aufgaben und Lösungen c Michael Bender, Manfred Brill Oktober 005 Sie finden in diesem Dokument alle Aufgaben und die zugehörigen Lösungen aus Michael Bender, Manfred Brill: Computergrafik. Auflage, Hanser
Workshop: Einführung in die 3D-Computergrafik. Julia Tolksdorf Thies Pfeiffer Christian Fröhlich Nikita Mattar
 Workshop: Einführung in die 3D-Computergrafik Julia Tolksdorf Thies Pfeiffer Christian Fröhlich Nikita Mattar 1 Organisatorisches Tagesablauf: Vormittags: Theoretische Grundlagen Nachmittags: Bearbeitung
Workshop: Einführung in die 3D-Computergrafik Julia Tolksdorf Thies Pfeiffer Christian Fröhlich Nikita Mattar 1 Organisatorisches Tagesablauf: Vormittags: Theoretische Grundlagen Nachmittags: Bearbeitung
Arrays. Einleitung. Deklarieren einer Array Variablen
 Arrays Einleitung bisher jede Variable einzeln deklariert: 12 3 14 12 32 32 3 32 5 3 double sum; int count; ÿ Sie können Zweck und Aufbau von Array-Datentypen erklären ÿ Sie können einen Array korrekt
Arrays Einleitung bisher jede Variable einzeln deklariert: 12 3 14 12 32 32 3 32 5 3 double sum; int count; ÿ Sie können Zweck und Aufbau von Array-Datentypen erklären ÿ Sie können einen Array korrekt
9. Vektoren. (auch Felder/array)
 9. Vektoren (auch Felder/array) Motivation Hat man mehrere Objekte gleichen Datentyps, so kann man sie explizit deklarieren, wenn die Anzahl bekannt ist double x1,x2,x3,x4; Nachteile: versagt, -wenn die
9. Vektoren (auch Felder/array) Motivation Hat man mehrere Objekte gleichen Datentyps, so kann man sie explizit deklarieren, wenn die Anzahl bekannt ist double x1,x2,x3,x4; Nachteile: versagt, -wenn die
Abstand messen. Misst den Abstand zwischen 2 Punkten. Punktefang beachten! Die Auswahl erlaubt auch den Abstand zweier Flächen zu ermitteln. 1.
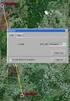 HBB Engineering GmbH Salzstraße 9 D-83454 Anger Telefon +49 (0)8656-98488-0 Telefax +49 (0)8656-98488-88 [email protected] www.hbb-engineering.de Abstand messen Version: UNIGRAPHICS/NX 8.5 Ersteller:
HBB Engineering GmbH Salzstraße 9 D-83454 Anger Telefon +49 (0)8656-98488-0 Telefax +49 (0)8656-98488-88 [email protected] www.hbb-engineering.de Abstand messen Version: UNIGRAPHICS/NX 8.5 Ersteller:
Übungsblatt 1: Lösungswege und Lösungen
 Übungsblatt : Lösungswege und Lösungen 5..6 ) Hier geht es weniger um mathematisch-strenge Beweise als darum, mit abstrakten Vektoren ohne Komponenten) zu hantieren und damit die Behauptungen plausibel
Übungsblatt : Lösungswege und Lösungen 5..6 ) Hier geht es weniger um mathematisch-strenge Beweise als darum, mit abstrakten Vektoren ohne Komponenten) zu hantieren und damit die Behauptungen plausibel
3. Aufgabe: Bitmap-Datei
 1 Einleitung 3. Aufgabe: Bitmap-Datei In dieser Programmieraufgabe soll eine Grafik erstellt und gespeichert werden. Es wurde das Bitmap-Format von Microsoft gewählt, da es recht einfach erstellt und von
1 Einleitung 3. Aufgabe: Bitmap-Datei In dieser Programmieraufgabe soll eine Grafik erstellt und gespeichert werden. Es wurde das Bitmap-Format von Microsoft gewählt, da es recht einfach erstellt und von
Übung: Computergrafik 1
 Prof. Dr. Andreas Butz Prof. Dr. Ing. Axel Hoppe Dipl.-Medieninf. Dominikus Baur Dipl.-Medieninf. Sebastian Boring Übung: Computergrafik MDIs in Qt Farbmodelle MDIs Übung Computergrafik SoSe 2009 2 Multiple
Prof. Dr. Andreas Butz Prof. Dr. Ing. Axel Hoppe Dipl.-Medieninf. Dominikus Baur Dipl.-Medieninf. Sebastian Boring Übung: Computergrafik MDIs in Qt Farbmodelle MDIs Übung Computergrafik SoSe 2009 2 Multiple
Vektor-Multiplikation Vektor- Multiplikation
 Vektor- Multiplikation a d c b Thema: Schultyp: Vorkenntnisse: Bearbeitungsdauer: Vektor-Multiplikation: Vektorprodukt Mittelschule, Berufsschule, Fachhochschule Elementare Programmierkenntnisse, Geometrie,
Vektor- Multiplikation a d c b Thema: Schultyp: Vorkenntnisse: Bearbeitungsdauer: Vektor-Multiplikation: Vektorprodukt Mittelschule, Berufsschule, Fachhochschule Elementare Programmierkenntnisse, Geometrie,
Praktikum: Spieleengine im Eigenbau
 Seite 1/17 Praktikum Spieleengine im Eigenbau Alexander Weggerle, Tobias Bäuerle 19.10.09 http://www.saschawillems.de Praktikum: Spieleengine im Eigenbau Seite 2/17 Praktikum Spieleengine im Eigenbau Alexander
Seite 1/17 Praktikum Spieleengine im Eigenbau Alexander Weggerle, Tobias Bäuerle 19.10.09 http://www.saschawillems.de Praktikum: Spieleengine im Eigenbau Seite 2/17 Praktikum Spieleengine im Eigenbau Alexander
Methoden und Wrapperklassen
 Methoden und Wrapperklassen CoMa-Übung IV TU Berlin 06.11.2012 CoMa-Übung IV (TU Berlin) Methoden und Wrapperklassen 06.11.2012 1 / 24 Themen der Übung 1 Methoden 2 Wrapper-Klassen CoMa-Übung IV (TU Berlin)
Methoden und Wrapperklassen CoMa-Übung IV TU Berlin 06.11.2012 CoMa-Übung IV (TU Berlin) Methoden und Wrapperklassen 06.11.2012 1 / 24 Themen der Übung 1 Methoden 2 Wrapper-Klassen CoMa-Übung IV (TU Berlin)
Grundlagen der 3D-Computergrafik Programmieren mit OpenGL
 Grundlagen der 3DComputergrafik Programmieren mit OpenGL Marc Wagner [email protected] 13. November 1998 Was ist OpenGL? OpenGL (Open Graphics Library) ist ein Softwareinterface zum
Grundlagen der 3DComputergrafik Programmieren mit OpenGL Marc Wagner [email protected] 13. November 1998 Was ist OpenGL? OpenGL (Open Graphics Library) ist ein Softwareinterface zum
Wertebereich und Genauigkeit der Zahlendarstellung
 Wertebereich und Genauigkeit der Zahlendarstellung Sowohl F als auch C kennen bei ganzen und Floating Point-Zahlen Datentypen verschiedener Genauigkeit. Bei ganzen Zahlen, die stets exakt dargestellt werden
Wertebereich und Genauigkeit der Zahlendarstellung Sowohl F als auch C kennen bei ganzen und Floating Point-Zahlen Datentypen verschiedener Genauigkeit. Bei ganzen Zahlen, die stets exakt dargestellt werden
OpenGL for Java OpenGL for Java Prof. Dr. V. Stahl
 OpenGL for Java Ziele Bewegte Simulationen grafisch darstellen können (effizient, realistisch, dreidimensional) Grundfunktionen von OpenGL beherrschen Mathematische Voraussetzungen für Computer Grafik
OpenGL for Java Ziele Bewegte Simulationen grafisch darstellen können (effizient, realistisch, dreidimensional) Grundfunktionen von OpenGL beherrschen Mathematische Voraussetzungen für Computer Grafik
Programmieren in C. Speicher anfordern, Unions und Bitfelder. Prof. Dr. Nikolaus Wulff
 Programmieren in C Speicher anfordern, Unions und Bitfelder Prof. Dr. Nikolaus Wulff Vergleich: Felder und Strukturen Felder müssen Elemente vom selben Typ enthalten. Strukturen können Elemente unterschiedlichen
Programmieren in C Speicher anfordern, Unions und Bitfelder Prof. Dr. Nikolaus Wulff Vergleich: Felder und Strukturen Felder müssen Elemente vom selben Typ enthalten. Strukturen können Elemente unterschiedlichen
Freiformkurven und Freiformflächen in Solid Edge
 Freiformkurven und Freiformflächen in Solid Edge Allgemeine Anmerkungen zu Kurven oder Skizze in eine 2D Umgebung. Dort können mit dem Menüpunkt Kurve bzw In Kurve umwandeln B-Splinekurven erzeugt werden.
Freiformkurven und Freiformflächen in Solid Edge Allgemeine Anmerkungen zu Kurven oder Skizze in eine 2D Umgebung. Dort können mit dem Menüpunkt Kurve bzw In Kurve umwandeln B-Splinekurven erzeugt werden.
Computer Graphics Shader
 Computer Graphics Shader Sven Janusch Inhalt Fixed Function Pipeline Programmable Pipeline Implementierung Applikation Beispiel Sven Janusch 2 Fixed Function Pipeline T&L Pipeline (Transformation and Lighting)
Computer Graphics Shader Sven Janusch Inhalt Fixed Function Pipeline Programmable Pipeline Implementierung Applikation Beispiel Sven Janusch 2 Fixed Function Pipeline T&L Pipeline (Transformation and Lighting)
2.2 Kollineare und koplanare Vektoren
 . Kollineare und koplanare Vektoren Wie wir schon gelernt haben, können wir einen Vektor durch Multiplikation mit einem Skalar verlängern oder verkürzen. In Abbildung 9 haben u und v die gleiche Richtung,
. Kollineare und koplanare Vektoren Wie wir schon gelernt haben, können wir einen Vektor durch Multiplikation mit einem Skalar verlängern oder verkürzen. In Abbildung 9 haben u und v die gleiche Richtung,
UIKit (Cocoa Touch) Framework für ios Apps. Objective C. Model View Controller Pattern
 ios Rendering ios Architektur UIKit (Cocoa Touch) A composable, reusable, declarative, real-world inspired animation, and interaction system Framework für ios Apps Objective C Model View Controller Pattern
ios Rendering ios Architektur UIKit (Cocoa Touch) A composable, reusable, declarative, real-world inspired animation, and interaction system Framework für ios Apps Objective C Model View Controller Pattern
- Für die beiden zu überblendenden Farben (source und destination) werden Blending-Faktoren besimmt (S r
 3.2 Blending Anwendung - Kombination der Farbinformation eines neu zu zeichnenden Objekts (Source) mit der Farbinformation, die bereits im Framebuffer gespeichert ist (Destination) - Darstellung teilweise
3.2 Blending Anwendung - Kombination der Farbinformation eines neu zu zeichnenden Objekts (Source) mit der Farbinformation, die bereits im Framebuffer gespeichert ist (Destination) - Darstellung teilweise
OpenGL Transformationen: Modeling
 OpenGL Transformationen: Modeling transponiert! Punkt-Trfn = Matrizen-Multiplikationen von links (s.o.): v neu = T n (... ) T 2 T 1 v alt = T gesamt v alt OpenGL: Laden mat[16]: glloadmatrix{fd}(mat) Matrizen-Multiplikation:
OpenGL Transformationen: Modeling transponiert! Punkt-Trfn = Matrizen-Multiplikationen von links (s.o.): v neu = T n (... ) T 2 T 1 v alt = T gesamt v alt OpenGL: Laden mat[16]: glloadmatrix{fd}(mat) Matrizen-Multiplikation:
Programmieren I. Arrays Heusch 7.2 Ratz Institut für Angewandte Informatik
 Programmieren I Arrays Heusch 7.2 Ratz 5.1 KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Arrays: Definition Arrays (dt. Felder) dienen zum Speichern mehrerer gleichartiger Daten
Programmieren I Arrays Heusch 7.2 Ratz 5.1 KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Arrays: Definition Arrays (dt. Felder) dienen zum Speichern mehrerer gleichartiger Daten
Computeranwendung und Programmierung (CuP)
 Computeranwendung und Programmierung (CuP) ArrayList 0 1 2 Obj0 Obj1 size() - 1 15.12.2014 CuP - VO 2 Auer 1 ArrayList import java.util.arraylist; ArrayList buchliste; buchliste = new ArrayList();
Computeranwendung und Programmierung (CuP) ArrayList 0 1 2 Obj0 Obj1 size() - 1 15.12.2014 CuP - VO 2 Auer 1 ArrayList import java.util.arraylist; ArrayList buchliste; buchliste = new ArrayList();
Einstieg in die Informatik mit Java
 1 / 34 Einstieg in die Informatik mit Java Klassen mit Instanzmethoden Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 34 1 Definition von Klassen 2 Methoden 3 Methoden
1 / 34 Einstieg in die Informatik mit Java Klassen mit Instanzmethoden Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 34 1 Definition von Klassen 2 Methoden 3 Methoden
Texture Based Direct Volume Rendering
 Texture Based Direct Volume Rendering Vorlesung: "Advanced Topics in Computer Graphics" [email protected] 1 Agenda 1. Einleitung Volume Rendering 1.1. Volumendatensatz 1.2. Volumenintegral 1.3. Image order
Texture Based Direct Volume Rendering Vorlesung: "Advanced Topics in Computer Graphics" [email protected] 1 Agenda 1. Einleitung Volume Rendering 1.1. Volumendatensatz 1.2. Volumenintegral 1.3. Image order
3D Programmierpraktikum: Geometrische Transformationen, Materialien und Beleuchtung
 3D Programmierpraktikum: Geometrische Transformationen, Materialien und Beleuchtung Praktikum 3D Programmierung Sebastian Boring, Otmar Hilliges Donnerstag, 8. Mai 26 LMU München Medieninformatik Boring/Hilliges
3D Programmierpraktikum: Geometrische Transformationen, Materialien und Beleuchtung Praktikum 3D Programmierung Sebastian Boring, Otmar Hilliges Donnerstag, 8. Mai 26 LMU München Medieninformatik Boring/Hilliges
Vektoren - Basiswechsel
 Vektoren - Basiswechsel Grundprinzip Für rein geometrische Anwendungen verwendet man üblicherweise die Standardbasis. Damit ergibt sich in den Zahlenangaben der Koordinaten kein Unterschied zu einem Bezug
Vektoren - Basiswechsel Grundprinzip Für rein geometrische Anwendungen verwendet man üblicherweise die Standardbasis. Damit ergibt sich in den Zahlenangaben der Koordinaten kein Unterschied zu einem Bezug
Mathematische Grundlagen für die Vorlesung. Differentialgeometrie
 Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Computergrafik 1 Übung
 Prof. Dr. Andreas Butz Dipl.-Medieninf. Hendrik Richter Dipl.-Medieninf. Raphael Wimmer Computergrafik Übung Wiederholung Lineare Algebra: Vektoren, Matrizen, Transformationen in D und 3D Computergrafik
Prof. Dr. Andreas Butz Dipl.-Medieninf. Hendrik Richter Dipl.-Medieninf. Raphael Wimmer Computergrafik Übung Wiederholung Lineare Algebra: Vektoren, Matrizen, Transformationen in D und 3D Computergrafik
Zugriff auf Matrizen. Anhängen von Elementen. Punktweise Operatoren. Vektoren und Matrizen in MATLAB II
 Zugriff auf Matrizen. Anhängen von Elementen. Punktweise Operatoren. Vektoren und Matrizen in MATLAB II Matrixzugriff Wir wollen nun unsere Einführung in die Arbeit mit Vektoren und Matrizen in MATLAB
Zugriff auf Matrizen. Anhängen von Elementen. Punktweise Operatoren. Vektoren und Matrizen in MATLAB II Matrixzugriff Wir wollen nun unsere Einführung in die Arbeit mit Vektoren und Matrizen in MATLAB
Parallele Algorithmen in der Bildverarbeitung
 Seminar über Algorithmen - SoSe 2009 Parallele Algorithmen in der Bildverarbeitung von Christopher Keiner 1 Allgemeines 1.1 Einleitung Parallele Algorithmen gewinnen immer stärker an Bedeutung. Es existieren
Seminar über Algorithmen - SoSe 2009 Parallele Algorithmen in der Bildverarbeitung von Christopher Keiner 1 Allgemeines 1.1 Einleitung Parallele Algorithmen gewinnen immer stärker an Bedeutung. Es existieren
H. Gruber, R. Neumann. Erfolg im Mathe-Abi. Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen
 H. Gruber, R. Neumann Erfolg im Mathe-Abi Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen Inhaltsverzeichnis Inhaltsverzeichnis Themen des Pflichtteils... Analysis Von der Gleichung
H. Gruber, R. Neumann Erfolg im Mathe-Abi Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen Inhaltsverzeichnis Inhaltsverzeichnis Themen des Pflichtteils... Analysis Von der Gleichung
Display-Listen, Blending, Antialiasing, Nebel. Display-Listen
 Display-Listen Warum werden Display-Listen eingesetzt? - Display-Listen speichern eine Sequenz von OpenGL-Kommandos - Ermöglicht sehr einfach die mehrmalige Darstellung der gleichen Geometrie - Ermöglicht
Display-Listen Warum werden Display-Listen eingesetzt? - Display-Listen speichern eine Sequenz von OpenGL-Kommandos - Ermöglicht sehr einfach die mehrmalige Darstellung der gleichen Geometrie - Ermöglicht
Tutorial. Übungsblatt CAD: Faltwerkdach für Bühne
 Tutorial Übungsblatt CAD: Faltwerkdach für Bühne 1. REVERSE FOLDING Für das Reverse Folding nimmt man eine gefaltete Ebene schneidet diese mit einer geeigneten schrägen Ebene α in zwei Teile und spiegelt
Tutorial Übungsblatt CAD: Faltwerkdach für Bühne 1. REVERSE FOLDING Für das Reverse Folding nimmt man eine gefaltete Ebene schneidet diese mit einer geeigneten schrägen Ebene α in zwei Teile und spiegelt
Programmierkurs C++ Variablen und Datentypen
 Programmierkurs C++ Variablen und Datentypen Prof. Dr. Stefan Fischer Institut für Telematik, Universität zu Lübeck http://www.itm.uni-luebeck.de/people/fischer #2 Überblick Welche Datentypen gibt es in
Programmierkurs C++ Variablen und Datentypen Prof. Dr. Stefan Fischer Institut für Telematik, Universität zu Lübeck http://www.itm.uni-luebeck.de/people/fischer #2 Überblick Welche Datentypen gibt es in
Übung: Computergrafik 1
 Prof. Dr. Andreas Butz Prof. Dr. Ing. Axel Hoppe Dipl.-Medieninf. Dominikus Baur Dipl.-Medieninf. Sebastian Boring Übung: Computergrafik 1 Filtern im Frequenzraum Segmentierung Organisatorisches Klausuranmeldung
Prof. Dr. Andreas Butz Prof. Dr. Ing. Axel Hoppe Dipl.-Medieninf. Dominikus Baur Dipl.-Medieninf. Sebastian Boring Übung: Computergrafik 1 Filtern im Frequenzraum Segmentierung Organisatorisches Klausuranmeldung
Analytische Geometrie mit dem Voyage 1
 Analytische Geometrie mit dem Voyage. Vektoren Vektoren lassen sich definieren in eckigen Klammern. Setzt man ein Semikolon zwischen die einzelnen Komponenten, so ergibt sich ein Spaltenvektor. Ein Spaltenvektor
Analytische Geometrie mit dem Voyage. Vektoren Vektoren lassen sich definieren in eckigen Klammern. Setzt man ein Semikolon zwischen die einzelnen Komponenten, so ergibt sich ein Spaltenvektor. Ein Spaltenvektor
Jörn Loviscach Hochschule Bremen
 Programmierbare Hardware-Shader Jörn Loviscach Hochschule Bremen Überblick Vertex- und Pixel-Shader Anwendungsbeispiele fx-dateien Anwendungsbeispiele Zusammenfassung Puffer Vertex- und Pixel-Shader Hardware-Renderpipeline
Programmierbare Hardware-Shader Jörn Loviscach Hochschule Bremen Überblick Vertex- und Pixel-Shader Anwendungsbeispiele fx-dateien Anwendungsbeispiele Zusammenfassung Puffer Vertex- und Pixel-Shader Hardware-Renderpipeline
12 Übungen zu Gauß-Algorithmus
 Aufgaben zum Vorkurs B S. 2 Übungen zu Gauß-Algorithmus 2x x 2 = 7x +, 5x 2 = 7 Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: 2x x 2 = x +2x 2 = 2 2x x 2 = 7x +, 5x 2 =, 5 x 2x 2 = x +x 2 = 5 2x +x 2 = 4
Aufgaben zum Vorkurs B S. 2 Übungen zu Gauß-Algorithmus 2x x 2 = 7x +, 5x 2 = 7 Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: 2x x 2 = x +2x 2 = 2 2x x 2 = 7x +, 5x 2 =, 5 x 2x 2 = x +x 2 = 5 2x +x 2 = 4
LABORÜBUNG MATLAB/OCTAVE
 LABORÜBUNG MATLAB/OCTAVE 1. Riemannsche Summen mit MATLAB/Octave Riemannsche Summen lassen sich sehr einfach mit MATLAB/Octave berechnen. Das Vorgehen ist das folgende: (i) die Breite x der Teilintervallen
LABORÜBUNG MATLAB/OCTAVE 1. Riemannsche Summen mit MATLAB/Octave Riemannsche Summen lassen sich sehr einfach mit MATLAB/Octave berechnen. Das Vorgehen ist das folgende: (i) die Breite x der Teilintervallen
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
C++ - Objektorientierte Programmierung Konstruktoren und Destruktoren
 C++ - Objektorientierte Programmierung Konstruktoren und Destruktoren hat eine Kantenlänge hat eine Füllfarbe Kantenlänge setzen Füllfarbe lesen Volumen berechnen Leibniz Universität IT Services Anja Aue
C++ - Objektorientierte Programmierung Konstruktoren und Destruktoren hat eine Kantenlänge hat eine Füllfarbe Kantenlänge setzen Füllfarbe lesen Volumen berechnen Leibniz Universität IT Services Anja Aue
Sie braucht weniger Speicherplatz als das Polygon und
 Kapitel 7 Kurven Die bisher besprochenen 2D-Objekte haben bis auf den Kreis den Nachteil, daß sie im weitesten Sinne eckig sind. Wenn ein Objekt mit runder Form verlangt wird, z.b. ein Herz, ein Schiffsrumpf,
Kapitel 7 Kurven Die bisher besprochenen 2D-Objekte haben bis auf den Kreis den Nachteil, daß sie im weitesten Sinne eckig sind. Wenn ein Objekt mit runder Form verlangt wird, z.b. ein Herz, ein Schiffsrumpf,
Programmierkurs C++ Datenstrukturen Seite 1
 Programmierkurs C++ Datenstrukturen Seite 1 3 Datenstrukturen 3.1 Arrays Zur Wiederholung als Strukturelement der Programmierung gehört auf der Seite der Datenstrukturen die Liste. Eine Liste kann auf
Programmierkurs C++ Datenstrukturen Seite 1 3 Datenstrukturen 3.1 Arrays Zur Wiederholung als Strukturelement der Programmierung gehört auf der Seite der Datenstrukturen die Liste. Eine Liste kann auf
Praktikum Computergrafik
 Praktikum Computergrafik Steven Schlegel Abteilung für Bild- und Signalverarbeitung Betreuer: Steven Schlegel ([email protected]) Einführung in OpenGL und GLSL OpenGL OpenGL (Open Graphics
Praktikum Computergrafik Steven Schlegel Abteilung für Bild- und Signalverarbeitung Betreuer: Steven Schlegel ([email protected]) Einführung in OpenGL und GLSL OpenGL OpenGL (Open Graphics
Lineare Algebra - Übungen 1 WS 2017/18
 Prof. Dr. A. Maas Institut für Physik N A W I G R A Z Lineare Algebra - Übungen 1 WS 017/18 Aufgabe P1: Vektoren Präsenzaufgaben 19. Oktober 017 a) Zeichnen Sie die folgenden Vektoren: (0,0) T, (1,0) T,
Prof. Dr. A. Maas Institut für Physik N A W I G R A Z Lineare Algebra - Übungen 1 WS 017/18 Aufgabe P1: Vektoren Präsenzaufgaben 19. Oktober 017 a) Zeichnen Sie die folgenden Vektoren: (0,0) T, (1,0) T,
CalcVectorPC v Veröffentlicht 2016 Copyright S-cubic GmbH. Krebsbachstr. 12 D Bergisch Gladbach
 CalcVectorPC v1.0.0 CalcVectorPC v1.0.0 Veröffentlicht 2016 Copyright 2016 S-cubic GmbH Krebsbachstr. 12 D-51429 Bergisch Gladbach Tel +49 (0) 2204 9160 30 Fax +49 (0) 2204 9199 416 email: [email protected]
CalcVectorPC v1.0.0 CalcVectorPC v1.0.0 Veröffentlicht 2016 Copyright 2016 S-cubic GmbH Krebsbachstr. 12 D-51429 Bergisch Gladbach Tel +49 (0) 2204 9160 30 Fax +49 (0) 2204 9199 416 email: [email protected]
Ausgabe:
 Aufgabe 2.10: Schreiben Sie ein Programm, das zunächst die Quadratzahlen zu den Zahlen 1-10 mit Hilfe einer While- Schleife und danach die Quadratzahlen zu den Zahlen 3, 6, 9,.., 30 mit Hilfe einer For-Schleife
Aufgabe 2.10: Schreiben Sie ein Programm, das zunächst die Quadratzahlen zu den Zahlen 1-10 mit Hilfe einer While- Schleife und danach die Quadratzahlen zu den Zahlen 3, 6, 9,.., 30 mit Hilfe einer For-Schleife
JAVA BASICS. 2. Primitive Datentypen. 1. Warum Java? a) Boolean (logische Werte wahr & falsch)
 JAVA BASICS 2. Primitive Datentypen 1. Warum Java? weit verbreitet einfach und (relativ) sicher keine Pointer (?) keine gotos kein Präprozessor keine globalen Variablen garbage collection objekt-orientiert
JAVA BASICS 2. Primitive Datentypen 1. Warum Java? weit verbreitet einfach und (relativ) sicher keine Pointer (?) keine gotos kein Präprozessor keine globalen Variablen garbage collection objekt-orientiert
Grundlagen der 3D-Grafik
 Seminar Programmierung von Grafikkarten Grundlagen der 3D-Grafik 8.5.26 Dominik Bossdorf Christian Schulze Marco Sebastiao 1 Inhalt Grafikhardware Rendering Pipeline am Beispiel OpenGL 3D Theorie mit homogenen
Seminar Programmierung von Grafikkarten Grundlagen der 3D-Grafik 8.5.26 Dominik Bossdorf Christian Schulze Marco Sebastiao 1 Inhalt Grafikhardware Rendering Pipeline am Beispiel OpenGL 3D Theorie mit homogenen
