Einschrittverfahren Das Eulersche Polygonzugverfahren Wir betrachten die Anfangswertaufgabe. y = f(x, y), y(a) = y 0, (1)
|
|
|
- Christian Schulze
- vor 7 Jahren
- Abrufe
Transkript
1 Einschrittverfahren Das Eulersche Polygonzugverfahren Wir betrachten die Anfangswertaufgabe y = f(x, y), y(a) = y 0, () wobei die Lösung y im Intervall [a, b] gesucht ist. Dabei kann y auch vektorwertig, also () ein Differentialgleichungssystem erster Ordnung sein. Einschrittverfahren --
2 Es sei a = x 0 < x < x 2 <... < x N =: b eine (nicht notwendig äquidistante) Zerlegung von [a, b]. Wir nehmen diese Zerlegung zunächst als gegeben an. Tatsächlich wird die Folge der x j im Verfahren mitbestimmt und an das Verhalten der Lösung der Anfangswertaufgabe angepasst. Da f(x n, y(x n )) gerade die Steigung y (x n ) der gesuchten Lösung y(x) von () ist, gilt näherungsweise bei nicht zu großer Schrittweite h n := x n+ x n h n (y(x n+ ) y(x n )) f(x n, y(x n )), d.h. y(x n+ ) = y(x n ) + h n f(x n, y(x n )) + ε n. (2) Einschrittverfahren -2-
3 Wir vernachlässigen nun in (2) den Fehler ε n. Dann wird die entstehende Gleichung nicht mehr durch die Lösung y(x n ) von () an den Knoten x n erfüllt, sondern nur noch durch Näherungswerte y n für y(x n ). Wir bestimmen also die y n ausgehend von y 0 durch das Verfahren y n+ = y n + h n f(x n, y n ), n = 0,,..., N, (3) wobei h n := x n+ x n ist. Definition Das durch (3) beschriebene Verfahren zur approximativen Lösung der Anfangswertaufgabe () heißt das Eulersche Polygonzugverfahren. Es wurde 768 von L. Euler beschrieben. Einschrittverfahren -3-
4 6 5 4 y 3 3 y 2 2 y y 0 0 x 0 x x 2 x Knotenpunkte und Näherungswerte Einschrittverfahren -4-
5 Beispiel y = y 2, y(0.8) = 5, x [0.8,.8] 6 besitzt die Lösung y(x) = 2 x. Mit den äquidistanten Schrittweiten h = 00, 200 und 400 liefert das Verfahren (3) Näherungen, deren Fehler in der folgenden Tabelle enthalten sind. Einschrittverfahren -5-
6 Tabelle : Fehlertabelle x N = 00 N = 200 N = E E E E E 4.79E E E E E 3.76E E E 3 3.3E 3.57E E E E E E E E 2.7E E E E 2.69E E 7.38E E E 2.08E.08E Man liest aus der Tabelle ab, dass die Fehler bei Halbierung der Schrittweite ebenfalls halbiert werden. Einschrittverfahren -6-
7 Wir wollen nun im allgemeinen Fall den entstandenen Fehler abschätzen. Dieser setzt sich aus zwei Anteilen zusammen: Wir haben im n-ten Schritt die Lösung y(x n+ ; x n, y(x n )) der Differentialgleichung y = f(x, y) mit dem Anfangswert y(x n ) an der Stelle x n zu bestimmen. Statt dessen betrachten wir die Anfangswertaufgabe y = f(x, y), y(x n ) = y n mit dem falschen Anfangswert y n, und wir lösen diese auch nur näherungsweise, indem wir den Abbruchfehler vernachlässigen. Tatsächlich werden bei der Realisierung des Verfahrens auf einem Rechner noch bei der Auswertung von f(x n, y n ) und den Rechenoperationen Rundungsfehler gemacht. Diese wollen wir aber bei den folgenden Betrachtungen außer Acht lassen. Einschrittverfahren -7-
8 Wir schreiben das Polygonzugverfahren in der Form y n+ y n h n f(x n, y n ) = 0. (4) Setzt man hier an Stelle der Werte y n die Werte y(x n ) der Lösung von () an den Knoten x n ein, so erhält man (vgl. (2)) y(x n+ ) y(x n ) h n f(x n, y(x n )) =: ε(x n, h n ). (5) Definition ε(x n, h n ) heißt der lokale Fehler (auch Abbruchfehler) des Polygonzugverfahrens an der Stelle x n bei der Schrittweite h n. Einschrittverfahren -8-
9 Subtrahiert man die Gleichung (4) von (5), so folgt y(x n+ ) y n+ = y(x n ) y n +h n (f(x n, y(x n )) f(x n, y n ))+ε(x n, h n ). (6) Definition δ n+ := y(x n+ ) y n+ heißt der Fehler oder (zur besseren Unterscheidung) globale Fehler des Polygonzugverfahrens an der Stelle x n+. Einschrittverfahren -9-
10 Um den globalen Fehler abschätzen zu können, setzen wir voraus, dass f auf [a, b] IR einer globalen Lipschitz Bedingung f(x, y) f(x, z) L y z für alle y, z IR und alle x [a, b] bzgl. y genügt. Eine Lipschitz Bedingung in einem Rechteck (wie im Satz von Picard Lindelöf) würde auch genügen. Man müsste dann nur aufpassen, dass die Näherungslösungen dieses Rechteck nicht verlassen. Einschrittverfahren -0-
11 Dann folgt aus (6) mit der Dreiecksungleichung und ε n := ε(x n, h n ) δ n+ ( + Lh n ) δ n + ε n, (7) und durch vollständige Induktion erhält man hieraus n n δ n δ 0 + ε j exp h j L, (8) j=0 denn für n = 0 ist diese Aussage trivial, und ist (8) für ein n < N erfüllt, so folgt j=0 δ n+ ( + Lh n ) δ n + ε n exp(lh n ) δ n + ε n n n exp(lh n ) δ 0 + ε j exp h j L + ε n j=0 j=0 Einschrittverfahren --
12 = δ 0 + n ε j exp n h j L + ε n δ 0 + j=0 n ε j exp j=0 n h j L j=0 j=0 Es ist n j=0 h j N j=0 h j = b a und δ 0 = y(a) y 0 = 0. Daher folgt N δ n e (b a)l ε j. Bis auf eine multiplikative Konstante lässt sich der globale Fehler also durch die Summe der lokalen Fehler abschätzen. j=0 Einschrittverfahren -2-
13 Wir setzen nun weiter voraus, dass die Lösung y von () zweimal stetig differenzierbar ist. Dies ist z.b. erfüllt, wenn die rechte Seite f stetig differenzierbar in einer offenen Menge ist, die enthält. {(x, y(x)) : a x b} Dann gilt nach dem Taylorschen Satz für den lokalen Fehler ε j = y(x j + h j ) y(x j ) h j y (x j ) = 2 h2 jy (x j + θ j h j ) mit einem θ j (0, ), und daher folgt für den globalen Fehler Einschrittverfahren -3-
14 δ n N 2 e(b a)l j=0 h 2 j y (x j + θ j h j ) 2 e(b a)l max a x b y (x) N j=0 h 2 j 2 e(b a)l max a x b y (x) max j=0,...,n h j N j=0 h j 2 (b a) e(b a)l max a x b y (x) =: C max j=0,...,n h j max j=0,...,n h j mit einer von den gewählten Schrittweiten h n unabhängigen Konstante C. Einschrittverfahren -4-
15 Hieraus liest man ab, dass bei Halbierung der Schrittweiten der Fehler ebenfalls halbiert wird. Man liest ferner ab, dass man O(δ ) Schritte des Polygonzugverfahrens aufwenden muss, um den globalen Fehler δ zu erreichen (für den Fehler δ = 0 6 also c 0 6 Schritte). Dies zeigt, dass das Eulersche Polygonzugverfahren für die Praxis nicht geeignet ist und dass man schnellere Verfahren benötigt. Wie im Falle der Quadratur wird man in der Praxis nicht mit vorgegebenen Schrittweiten rechnen, sondern die Schrittweite dem Lösungsverhalten anpassen. Dabei schätzt man wie bei den adaptiven Quadraturformeln den lokalen Fehler mit Hilfe einer zweiten Formel. Einschrittverfahren -5-
16 2.5 van der Pol Gleichung; µ= Einschrittverfahren -6-
17 3 van der Pol Gleichung (Ableitung); µ= Einschrittverfahren -7-
18 2.5 van der Pol Gleichung; µ=; Schrittweitenkontrolle Einschrittverfahren -8-
19 3 van der Pol Gleichung (Ableitung); µ= Einschrittverfahren -9-
20 2 van der Pol Gleichung; µ= Einschrittverfahren -20-
21 2 van der Pol Gleichung (Ableitung); µ= Einschrittverfahren -2-
22 2 van der Pol Gleichung; µ= Einschrittverfahren -22-
23 2 van der Pol Gleichung (Ableitung); µ= Einschrittverfahren -23-
24 Wir verwenden hierzu zwei Schritte des Polygonzugverfahrens mit halber Schrittweite: ỹ n+ 2 = y n + h n 2 f(x n, y n ) ỹ n+ = ỹ n+ 2 + h n 2 f(x n + h n 2, ỹ n+ 2 ) = y n + h n 2 f(x n, y n ) + h n 2 f(x n + h n 2, y n + h n 2 f(x n, y n )). Für den lokalen Fehler gilt mit der Lösung z(x) der Anfangswertaufgabe y = f(x, y), y(x n ) = y n (im Falle z C 3 [a, b]) nach dem Taylorschen Satz ε(x n, h n ) = z(x n + h n ) (y n + h n f(x n, y n )) = z(x n ) + h n z (x n ) + 2 h2 nz (x n ) + O(h 3 n) z(x n ) h n z (x n ) Einschrittverfahren -24-
25 = 2 h2 nz (x n ) + O(h 3 n) (9) und genauso für die zusammengesetzte Formel ε(x n, h n ) = z(x n + h n ) ỹ n+ = y n + h n f(x n, y n ) + 2 h2 nz (x n ) + O(h 3 n) y n h n 2 f(x n, y n ) h n 2 (f(x n, y n ) + h n 2 x f(x n, y n ) + h n 2 y f(x n, y n )f(x n, y n ) + O(h 2 n)) = 4 h2 nz (x n ) + O(h 3 n) wegen z (x) = d dx f(x, z(x)) = x f(x, z(x)) + y f(x, z(x)) z (x). Einschrittverfahren -25-
26 Durch Subtraktion dieser beiden Formeln erhält man ỹ n+ y n+ = 4 h2 nz (x n ) + O(h 3 n). Setzt man dies in (9) unter Vernachlässigung des O(h 3 n)-terms ein, so erhält man die Schätzung für den lokalen Fehler ε(x n, h n ) φ(x n, h n ) := 2(ỹ n+ y n+ ). (0) Einschrittverfahren -26-
27 Zugleich erhält man mit ŷ n+ := 2ỹ n+ y n+ = y n + h n f(x n + 2 h n, y n + h n 2 f(x n, y n )) () eine Näherung für y(x n + h n ) mit dem lokalen Fehler ˆε(x n, h n ) = 2 ε(x n, h n ) ε(x n, h n ) = O(h 3 n). Verfahren mit dieser Eigenschaft werden wir Verfahren der Ordnung 2 nennen. Einschrittverfahren -27-
28 Die Formel (0) verwenden wir nun zur Schrittweitensteuerung: Wir geben uns eine Toleranz τ > 0 vor und bestimmen die Schrittweite in jedem Schritt so, dass gilt. lokaler Fehler τ (2) Approximieren wir ε(x n, h) durch ε(x n, h) γh 2, so kann man γ durch einen Probeschritt der Länge H schätzen: γ H 2 ε(x n, H). Die optimale Wahl der Schrittweite wäre nach (2) τ = ε(x n, h) γ h 2 h2 H 2 ε(x n, H), d.h. τ h = H ε(x n, H). Einschrittverfahren -28-
29 Der folgende MATLAB-Programmteil verwendet eine ähnliche Schrittweitenkontrolle bei gegebenen Startwerten x und y und gegebener Probeschrittlänge h: v=.e-5*ones(,n); z = f(x,y); while h>0 y = y + h*z; y2 = y + h/2*z; y2 = y2 + h/2 * f(x+h/2,y2); d=max(v,max(abs(y),abs(y))); phi = 2 * norm((y2 - y)./d); hneu = h * min(max(0.9*sqrt(tol/phi),0.2),0); if phi > tol h = hneu; else x = x + h; y = 2*y2 - y; (*) z = f(x,y); h = min(b-x,hneu); end, end Einschrittverfahren -29-
30 Bemerkung Es wurde der absolute Fehler durch den relativen Fehler ersetzt. Ferner wurde dabei der Betrag des Funktionswerts nach unten komponentenweise durch 0 5 begrenzt. Zusätzlich wurde die optimale Schrittweite hneu mit dem Faktor 0.9 verkleinert. Dies verringert die Wahrscheinlichkeit, dass der nächste Schritt verworfen wird. Schließlich wurde durch den minimalen Faktor 0.2 und den maximalen Faktor 0 dafür gesorgt, dass die Schrittweiten von Schritt zu Schritt sich nicht zu stark ändern. Die gewählten Konstanten 0.9, 0.2 und 0 lassen sich durch keine Theorie begründen, sondern haben sich in Codes bewährt. Einschrittverfahren -30-
31 Bemerkung: Nach unserer Herleitung müsste in der Zeile ( ) y = y stehen. Da man aber ohne Mehrkosten die bessere Näherung y = 2 y2 y (Formel der Ordnung 2) zur Verfügung hat, verwendet man diese. Unsere Fehlerschätzung ist damit in der Regel pessimistisch. Beispiel y = y 2, y(0.8) = 5 6. Mit τ = e 3 benötigt man 6 Funktionsauswertungen für die numerische Lösung im Intervall [0.8,.8]. Der maximale absolute Fehler ist dabei.6 0 2, der maximale relative Fehler 3.2e 3, die maximale benutzte Schrittweite ist und die minimale Schrittweite ist Die nächste Abbildung zeigt die berechneten Punkte; die Schrittweite wird kleiner bei größerer Steigung. Um dieselbe Genauigkeit mit äquidistanter Schrittweite zu erreichen, benötigt man 2776 Funktionsauswertungen. Einschrittverfahren -3-
32 Schrittweitenkontrolle Einschrittverfahren -32-
33 Allgemeine Einschrittverfahren Das behandelte Polygonzugverfahren ist die einfachste Methode der großen Klasse der Einschrittverfahren, bei denen die Näherung y n+ an dem neuen Punkt x n+ := x n + h n allein aus der Näherung y n an der Stelle x n und der Schrittweite h n berechnet wird. Einschrittverfahren haben also die folgende Gestalt mit einer Verfahrensfunktion Φ. y n+ = y n + h n Φ(x n, y n, h n ) (3) Einschrittverfahren -33-
34 Um die Güte von Einschrittverfahren zu beurteilen, führen wir die folgenden Begriffe ein: Definition: Es sei z(x) die Lösung der Anfangswertaufgabe Dann heißt z = f(x, z(x)), z(x n ) = y n. ε(h) := z(x n + h) y n h Φ(x n, y n, h) der lokale Fehler des durch (3) definierten Verfahrens. Das Verfahren (3) heißt konsistent, falls ε(h) = o(h) gilt, es heißt von der Ordnung p, wenn ε(h) = O(h p+ ) gilt. Einschrittverfahren -34-
35 Satz 2.9: Es seien sie Näherungen y n von y(x n ) mit dem Einschrittverfahren berechnet. y n+ = y n + h n Φ(x n, y n, h n ), n = 0,,..., N, Erfüllt die Verfahrensfunktion Φ eine Lipschitz Bedingung bzgl. y in [a, b] IR (es genügt eine Umgebung der Lösung) Φ(x, y, h) Φ(x, z, h) Λ y z (4) und ist das Einschrittverfahren konsistent von der Ordnung p so gilt für den globalen Fehler y(x + h) y(x) hφ(x, y(x), h) C h p+, (5) δ n = y n y(x n ) C(b a)e Λ(b a) h p, mit h := max j=0,...,n h j. (6) Einschrittverfahren -35-
36 Beweis: Mit wörtlich demselben Beweis wie für das Polygonzugverfahren erhält man aus (3) und (4) n n δ n exp h j Λ ε j, j=0 j=0 und mit (5) folgt δ n exp n j=0 h j Λ n j=0 Ch p+ j exp (Λ(b a)) C max j=0,...,n hp j C(b a)e Λ(b a) h p. n j=0 h j Einschrittverfahren -36-
37 Bemerkung Die Lipschitz Bedingung für die Verfahrensfunktion Φ erhält man in vielen Fällen aus der Lipschitz Bedingung für die rechte Seite f. Bemerkung Wie beim Übergang von den Quadraturformeln zu summierten Quadraturformeln verliert man beim Übergang vom lokalen zum globalen Fehler eine h-potenz. Einschrittverfahren -37-
38 Beispiel [Polygonzugverfahren] (Euler 768) Das einfachste Einschrittverfahren ist das Eulersche Polygonzugverfahren Φ(x, y, h) = f(x, y). Einschrittverfahren -38-
39 Beispiel [Verbessertes Polygonzugverfahren] (Coriolis 837, Runge 895) Wir haben dieses Verfahren bereits durch Extrapolation aus dem Polygonzugverfahren mit den Schrittweiten h und h 2 y n+ = y n + h n f hergeleitet (vgl. ()): ( x n + h n 2, y n + h ) n 2 f(x n, y n ). Geometrisch kann man dieses Verfahren so interpretieren: Es wird zunächst eine Schätzung y n+ = y n + h ( n 2 2 f(x n, y n ) für y x n + h ) n ( 2 ermittelt, und die hiermit berechnete Näherung f x n + h ) n 2, y n+ 2 y ( x n + h ) n für die Steigung von y im ganzen Intervall [x n, x n + h n ] 2 verwendet. Einschrittverfahren -39-
40 y n+ y n x n x n+ Verbessertes Polygonzugverfahren Einschrittverfahren -40-
41 Wir haben bereits gesehen, dass das verbesserte Polygonzugverfahren die Ordnung 2 besitzt. Erfüllt f eine Lipschitzbedingung so erfüllt auch die Verfahrensfunktion wegen f(x, y) f(x, z) L y z, Φ(x, y, h) = f(x + 0.5h, y + 0.5hf(x, y)) Φ(x, y, h) Φ(x, z, h) = f(x + 0.5h, y + 0.5hf(x, y)) f(x + 0.5h, z + 0.5hf(x, z)) L y + 0.5hf(x, y) (z + 0.5hf(x, z)) L( y z + 0.5h f(x, y) f(x, z) ) L( y z + 0.5hL y z ) L( + 0.5(b a)l) y z =: Λ y z eine Lipschitz Bedingung. Nach Satz 2.9 ist das verbesserte Polygonzugverfahren also ein Verfahren der Ordnung 2. Einschrittverfahren -4-
42 Beispiel Eine naheliegende Idee, Verfahren höherer Ordnung zu entwickeln, liefert der Taylorsche Satz. Ist f differenzierbar, so erhält man wegen und y (x) = d dx f(x, y(x)) = f x(x, y(x)) + f y (x, y(x))y (x) = f x (x, y(x)) + f y (x, y(x))f(x, y(x)) y(x n + h) = y(x n ) + hy (x n ) + 2 h2 y (x n ) + O(h 3 ) = y n + hf(x n, y n ) + 2 h2 (f x (x n, y n ) + f y (x n, y n )f(x n, y n )) + O(h 3 ) mit Φ(x, y, h) = f(x, y) + 0.5h(f x (x, y) + f y (x, y)f(x, y)) ein Einschrittverfahren der Ordnung 2. Nachteil ist, dass man die Ableitung der rechten Seite benötigt, deren Auswertung häufig aufwendiger ist als die der Funktion. Einschrittverfahren -42-
43 Beispiel [Verfahren von Heun] (Heun 900) Dem verbesserten Polygonzugverfahren verwandt ist das Verfahren von Heun, das in der Literatur machmal auch Verbessertes Polygonzugverfahren genannt wird. Man verwendet den Mittelwert zweier Näherungen k := f(x n, y n ), k 2 := f(x n + h n, y n + h n k ) für die Steigung von y im Intervall [x n, x n+ ] und setzt hiermit k + k 2 y n+ = y n + h n. 2 Dieses Verfahren entspricht der Quadratur des Integrals in y(x n+ ) y(x n ) = x n+ f(t, y(t)) dt mit der Trapezregel, wenn man den unbekannten Punkt (x n+, y(x n+ )) ersetzt durch (x n+, y n + h n f(x n, y n )). x n Einschrittverfahren -43-
44 3.5 y n y n x n x n Verfahren von Heun Einschrittverfahren -44-
45 Mit dem Taylorschen Satz kann man zeigen, dass für den lokalen Fehler ε(h) = z(x n +h) y n h 2 (f(x n, y n )+f(x n +h, y n +h f(x n, y n ))) = O(h 3 ) gilt, dass das Verfahren von Heun also wie das verbesserte Polygonzugverfahren die Ordnung 2 besitzt. Einschrittverfahren -45-
46 Beispiel [explizite Runge Kutta Verfahren] (Kutta 90) Explizite Runge Kutta Verfahren sind Verallgemeinerungen des verbesserten Polygonzugverfahrens und des Verfahrens von Heun. Es wird ein gewichtetes Mittel von Approximationen der Steigung der Lösung y im Intervall [x n, x n+ ] bestimmt und hiermit ein Schritt der Länge h n ausgeführt. Es sei k := f(x n, y n ) j k j := f(x n + α j h n, y n + h n s y n+ := y n + h n γ j k j. j= l= β jl k l ), j = 2,..., s (7) Die Koeffizienten α j, β jl, γ j werden dabei so gewählt, dass das Verfahren möglichst hohe Ordnung hat. s heißt die Stufe des Runge Kutta Verfahrens. Einschrittverfahren -46-
47 Als Beispiel betrachten wir die Herleitung von zweistufigen Runge Kutta Verfahren. Es gilt y n+ = y n + h(γ k + γ 2 k 2 ) = y n + h(γ f(x n, y n ) + γ 2 f(x n + α 2 h, y n + hβ 2 f(x n, y n ))). (8) Wir bestimmen die Parameter γ, γ 2, α 2 und β 2 so, dass das Verfahren möglichst große Ordnung hat. Ist f C 2 (und damit y C 3 ), so gilt nach dem Taylorschen Satz y(x + h) = y(x) + hy (x) + 2 h2 y (x) + 6 h3 y (x) + o(h 3 ) = y(x) + hf(x, y(x)) + ) 2 h2( f x (x, y(x)) + f y (x, y(x))f(x, y(x)) + 6 h3[ f xx + 2ff xy + f 2 f yy + f x f y + ff 2 y ] (x, y(x)) + o(h 3 ) Einschrittverfahren -47-
48 und y(x) + h(γ f(x, y(x)) + γ 2 f(x + α 2 h, y(x) + hβ 2 f(x, y(x)))) = y(x) + hγ f(x, y(x)) + hγ 2 [f + α 2 hf x + β 2 hf y f + 2 (α 2h) 2 f xx +α 2 β 2 h 2 f xy f + 2 (β 2h) 2 f 2 f yy ](x, y(x)) + o(h 3 ). Subtraktion und Ordnen nach Potenzen von h liefert y(x + h) y(x) h(γ f(x, y(x)) + γ 2 f(x + α 2 h, y(x) + hβ 2 f(x, y(x)))) = h( γ γ 2 )f(x, y(x)) + 2 h2[ ( 2γ 2 α 2 )f x + ( 2γ 2 β 2 )ff y ](x, y(x)) + 6 h3[ ( 3γ 2 α2)f 2 xx + 2( 3γ 2 α 2 β 2 )f xy f ] +( 3γ 2 β2)f 2 yy f 2 + f x f y + ffy 2 (x, y(x)) + o(h 3 ). Einschrittverfahren -48-
49 Da bei keiner Wahl der Parameter der Koeffizient bei h 3 für alle Funktionen f verschwindet, können wir keine höhere Konvergenzordnung als 2 erreichen. Für Verfahren der Ordnung 2 muss gelten γ + γ 2 =, 2γ 2 α 2 =, 2γ 2 β 2 =. (9) Dieses nichtlineare System von 3 Gleichungen in 4 Unbekannten besitzt unendlich viele Lösungen. Wählt man γ 2 als freien Parameter, so erhält man die Lösungsschar γ = γ 2, α 2 = β 2 = 2γ 2, γ 2 0. (20) Die bereits betrachteten Verfahren der Ordnung 2 sind hierin enthalten. Für γ 2 = erhält man das verbesserte Polygonzugverfahren, für γ 2 = 0.5 das Verfahren von Heun. Einschrittverfahren -49-
50 Unter Verwendung von (9) geht der Term bei h 3 über in 6 (( 3 )(f xx + 2ff xy + f 2 f yy ) + f x f y + ff 4γ y)(x, 2 y(x)). (2) 2 Hier ist die Summe der Beträge der Koeffizienten vor den partiellen Ableitungen minimal für γ 2 = 3 4. In diesem Sinne ist also die folgende Formel unter den Methoden (8) optimal: y n+ = y n + 4 h n ( f(x n, y n ) + 3f(x n h n, y n + 2 ) 3 h nf(x n, y n )). (22) Damit ist nicht gesagt, dass (22) unter allen möglichen Formeln (8) bei Anwendung auf eine spezielle Differentialgleichung das kleinste führende Fehlerglied hat, da sich in der Entwicklung von y(x + h) y(x) hφ(x, y(x)) Terme mit entgegengesetztem Vorzeichen kompensieren können. Andere Optimalitätskriterien sind denkbar (vgl. Grigorieff). Einschrittverfahren -50-
51 Beispiel Wir betrachten erneut y = y 2, y(0.8) = 5, x [0.8,.8]. 6 Dann erhält man mit dem verbesserten Polygonzugverfahren, dem Verfahren von Heun, dem optimalen Verfahren aus (22) und dem mit dem Taylorschen Satz entwickelten Verfahren die Fehler der folgenden Tabelle: Einschrittverfahren -5-
52 Tabelle 2: Verfahren der Ordnung 2 h verb. Poly. Heun optimal Taylor /5.0e e 9.58e.6e + 0 /0 4.34e 3.38e 4.02e 5.25e /20.47e.07e.34e.86e / e e e e 2 /80.4e e 3.02e 2.5e 2 / e e e e 3 / e e e e 4 /640.89e 4.27e 4.48e e 4 / e 5 3.7e e e 5 Einschrittverfahren -52-
53 Bevor wir Verfahren größerer Ordnung als 2 angeben, schicken wir einige Bemerkungen voraus über die mit einem s-stufigen Verfahren erreichbare Konsistenzordnung. Diese Frage ist keinesfalls leicht zu beantworten, da die beim Taylorabgleich entstehenden Bedingungsgleichungen nichtlinear in den Parametern sind. Eine sorgfältige Untersuchung mit Hilfe von Ordnungsbäumen findet man in Hairer, Nørsett, Wanner. Die Zahl der zu erfüllenden Gleichungen steigt mit wachsender Ordnung p sehr stark an, wie die folgende Tabelle zeigt: Ordnung p Zahl der Gleichungen Dabei wurden die Gleichungen k j= β kj = α k, k = 2,..., m, die wir stets als erfüllt annehmen, nicht mitgezählt. Einschrittverfahren -53-
54 Gibt man die Ordnung p vor und bestimmt dazu die Stufenzahl s des Runge Kutta Verfahrens minimal, so gilt der folgende Zusammenhang p s Man sieht, dass sich mit wachsender Ordnung das Verhältnis von erreichbarer Ordnung p zur Zahl der dazu nötigen Stufen (also zur Zahl der Funktionsauswertungen in jedem Schritt) verschlechtert. Entwickelt man (7) bis zu Termen mit h 2, so sieht man unmittelbar: Satz 2.8 Das Einschrittverfahren (7) ist genau dann konsistent, wenn gilt s j= γ j =. Einschrittverfahren -54-
55 Wir betrachten nun den Fall s = 4: Eine etwas mühsame Taylorentwicklung (ähnlich wie im Fall s = 2; vgl. Gear, p. 32 ff) zeigt, dass man in der Darstellung des lokalen Fehlers durch keine Wahl der Parameter den Koeffizienten bei h 5 unabhängig von f zum Verschwinden bringen kann. Es ist also die Ordnung p = 4 erreichbar. Die acht Bedingungen der 0 Parameter (3 Gleichungen zur Bestimmung der Parameter α j nicht mitgerechnet) lauten: Einschrittverfahren -55-
56 = γ + γ 2 + γ 3 + γ 4 2 = α 2 γ 2 + α 3 γ 3 + α 4 γ 4 3 = α2γ α3γ α4γ = α2γ α3γ α4γ = α 3 β 43 γ 4 + α 2 β 42 γ 4 + α 2 β 32 γ 3 8 = α 3 α 4 β 43 γ 4 + α 2 α 4 β 42 γ 4 + α 2 α 3 β 32 γ 3 2 = α3β 2 43 γ 4 + α2β 2 42 γ 4 + α2β 2 32 γ 3 24 = α 2 β 32 β 43 γ 4. Einschrittverfahren -56-
57 Die Parameter sind durch die vorstehenden Gleichungen nicht eindeutig bestimmt. Wir geben 3 verschiedene Formeln an. Dabei verwenden wir das folgende Koeffiziententableau, mit dem man Runge Kutta Verfahren auf übersichtliche Weise darstellen kann: 0 α 2 β 2 α 3. β 3 β 32 α s β s β s2... β s,s γ γ 2... γ s γ s. Einschrittverfahren -57-
58 Die uns bekannten Verfahren der Ordnung 2 kann man damit so schreiben Verfahren von Heun verb. Polygonzugverfahren optimales Verfahren Einschrittverfahren -58-
59 Am bekanntesten ist wohl das klassische Runge Kutta Verfahren (895) der Ordnung Ausführlich geschrieben lautet dieses k = f(x n, y n ) ( k 2 = f x n + h n 2, y n + h ) n 2 k ( k 3 = f x n + h n 2, y n + h ) n 2 k 2 k 4 = f(x n + h n, y n + h n k 3 ) k + 2k 2 + 2k 3 + k 4 y n+ = y n + h n. 6 Einschrittverfahren -59-
60 Weitere Verfahren der Ordnung 4 sind die 3/8 Regel (Kutta 90) und die optimale Formel von Kuntzmann (Kuntzmann 959) Einschrittverfahren -60-
61 Die 3/8-Regel verallgemeinert die Newtonsche 3/8-tel Regel (oder Keplersche Fassregel oder pulcherima) der numerischen Integration. Die Formel von Kuntzmann erhält man ähnlich wie im Falle s = 2, indem man die Parameter so bestimmt, dass die Summe der Beträge der Koeffizienten im führenden Fehlerglied von y(x+h) y(x) hφ(x, y(x)) minimal wird. Die klassische Runge Kutta Regel ist die bekannteste, die 3/8-Regel häufig die genaueste der expliziten Runge Kutta Verfahren der Ordnung 4. Einschrittverfahren -6-
62 Beispiel Wir betrachten erneut y = y 2, y(0.8) = 5, x [0.8,.8]. 6 Dann erhält man mit dem klassischen Runge Kutta Verfahren, der 3/8 Regel und dem optimalen Verfahren von Kuntzmann die Fehler der folgenden Tabelle Tabelle 3: Verfahren der Ordnung 4 h klassisch 3/8 Regel Kuntzmann /5 3.52e e e 2 /0 3.39e e 3 3.5e 3 / e e e 4 /40.65e 5.43e 5.67e 5 /80.05e e 7.03e 6 / e e e 8 / e e e 9 Einschrittverfahren -62-
63 Eine Schrittweitensteuerung kann man für die Runge Kutta Verfahren prinzipiell wie für das Polygonzugverfahren durchführen. Um den Fehler zu schätzen, kann man zwei Schritte mit der halben Schrittweite ausführen. Im Falle der klassischen Runge Kutta Verfahren hat man dabei die Funktion f an 7 zusätzlichen Punkten auszuwerten, so dass man in jedem Schritt insgesamt Funktionsauswertungen benötigt. Mit wesentlich weniger Aufwand kommt man bei den eingebetteten Runge Kutta Formeln aus: Einschrittverfahren -63-
64 Die Idee ist ähnlich wie bei den Kronrod-Formeln zur Quadratur von einer Runge Kutta Formel der Stufe s mit den Zuwächsen k,..., k s und der Ordnung p auszugehen und hierzu bei erhöhter Stufenzahl σ weitere k s+,..., k σ zu bestimmen, so dass die Formel ỹ n+ = y n + h n ( s γ j k j + σ γ j k j ) j= j=s+ eine höhere Ordnung q als die Ausgangsformel hat. Dann gilt für die lokalen Fehler ε = C h p+ + O(h p+2 ) und ε = O(h q+ ) = O(h p+2 ), d.h. ỹ n+ y n+ = C h p+ + O(h p+2 ), und hiermit kann man bei vorgegebener Toleranz die optimale Schrittweite wie vorher schätzen. Einschrittverfahren -64-
65 Man führt also einen Probeschritt der Länge H aus, erhält hieraus C ỹn+(h) y n+ (H) H p+, und die Forderung ε(x n, h) C h p+ = τ liefert die neue Schrittweite h = H ( ) /(p+) τ. ỹ n+ (H) y n+ (H) Einschrittverfahren -65-
66 Wir geben einige eingebettete Formelpaare an: Fehlberg (Ordnungen p = 2, q = 3) p = 2 2 q = Einschrittverfahren -66-
67 England (Ordnungen p = 4, q = 5) p = q = Einschrittverfahren -67-
68 Verner (Ordnungen p = 5, q = 6) p = q = Einschrittverfahren -68-
69 Wie beim Polygonzugverfahren mit Schrittweitensteuerung verwendet man bei diesen sehr frühen Formelpaaren im weiteren Verlauf der Integration die Näherung für das Verfahren höherer Ordnung, obwohl der Fehler für das Verfahren niedrigerer Ordnung geschätzt wurde. Für diese Näherung liegt dann zwar keine Fehlerschätzung vor, aber ein Anwender wird sich wohl kaum beschweren, wenn der Code eine höhere Genauigkeit liefert als die Geforderte. Neuere Formelpaare wurden so konstruiert, dass die neue Näherung y n+ in x n+ so gewählt ist, dass das im nächsten Schritt benötigte k = f(x n+, y n+ ) bereits im letzten Schritt berechnet wurde. Verfahren dieses Typs werden als FSAL-Verfahren (first evaluation of f for the next step same as last of the current step). Bei ihnen bekommt man in jedem erfolgreichen Schritt eine Auswertung der rechten Seite geschenkt. Einschrittverfahren -69-
70 Das bekannteste und wohl am häufigsten verwendete Verfahren, das auch in der ODE-Suite von MATLAB als ODE45 implementiert ist, ist das Formelpaar von Dormand und Prince, das Runge-Kutta Verfahren der Ordnungen 4 und 5 kombiniert. Für etwas schwächere Genauigkeitsanforderungen wird eine Kombination von Verfahren der Ordnungen 2 und 3 von Bogacki und Shampine in der ODE-Suite von MATLAB als ODE23 bereitgestellt. Einschrittverfahren -70-
71 Bogacki und Shampine (Ordnungen p = 2, q = 3) p = q = Einschrittverfahren -7-
72 Dormand und Prince (Ordnungen p = 4, q = 5) p = q = Einschrittverfahren -72-
73 Beispiel y = y 2, y(0.8) = 5 6. Um die Lösung y(x) = im Punkte b =.8 mit höchstens 2 x dem absoluten Fehler zu approximieren, benötigt man mit dem Formelpaar von Fehlberg 38 Funktionsauswertungen, mit dem von England 96, mit dem von Verner 84, mit dem Paar von Dormand und Prince 49 und mit dem Paar von Bogacki und Shampine 87 Funktionsauswertungen. Einschrittverfahren -73-
74 Extrapolationsverfahren Wir betrachten das Einschrittverfahren y n+ = y n + hφ(x n, y n, h) (23) der Ordnung p. Ist die Schrittfunktion Φ genügend oft differenzierbar (dies ist bei Runge Kutta Methoden eine Forderung an die Glattheit der rechten Seite f der Differentialgleichung ()), so gilt für den lokalen Fehler y(x + h) y(x) hφ(x, y(x), h) = N+ j=p+ d j (x)h j + O(h N+2 ). (24) Einschrittverfahren -74-
75 Es sei y h (x) := y n die Näherung von y(a + nh), die man mit n äquidistanten Schritten mit dem Verfahren (23) erhält. Dann hat der globale Fehler die Größe O(h p ). Wir zeigen, dass es eine Funktion e p gibt, so dass der globale Fehler geschrieben werden kann als Dazu betrachten wir die Funktion y h (x) y(x) = e p (x)h p + O(h p+ ). (25) ŷ h (x) := y h (x) e p (x)h p (26) als die Näherung, die man mit n Schritten eines Einschrittverfahrens erhalten hat. ŷ n+ = ŷ n + hˆφ(x n, ŷ n, h) (27) Einschrittverfahren -75-
76 Es gilt ŷ n+ = y n+ e p (x n + h)h p = y n + hφ(x n, y n, h) e p (x n + h)h p = ŷ n + hφ(x n, ŷ n + e p (x n )h p, h) e p (x n + h)h p + e p (x n )h p, und daher ist die Schrittfunktion ˆΦ(x, ŷ, h) = Φ(x, ŷ + e p (x)h p, h) (e p (x + h) e p (x))h p. (28) Einschrittverfahren -76-
77 Für den lokalen Fehler erhält man y(x + h) y(x) hˆφ(x, y(x), h) = y(x + h) y(x) hφ(x, y(x) + e p (x)h p, h) + (e p (x + h) e p (x))h p ( = y(x + h) y(x) h Φ(x, y(x), h) + ) y Φ(x, y(x), h)e p(x)h p + O(h p+ ) +(e p (x + h) e p (x))h p = d p+ (x)h p+ y Φ(x, y(x), 0)e p(x)h p+ + e p(x)h p+ + O(h p+2 ), und wegen Φ(x, y(x), 0) = lim h 0 y(x + h) y(x) h = y (x) = f(x, y(x)), d.h. y Φ(x, y(x), 0) = f(x, y(x)) y Einschrittverfahren -77-
78 folgt schließlich y(x + h) y(x) hˆφ(x, y(x), h) ( = d p+ (x) ) y f(x, y(x))e p(x) + e p(x) h p+ + O(h p+2 ). (29) Damit wird durch (27) ein Verfahren der Ordnung p + definiert, falls e p Lösung der Anfangswertaufgabe e p(x) = y f(x, y(x))e p(x) d p+ (x), e p (a) = 0, (30) ist. Einschrittverfahren -78-
79 Nach Satz 2.9 gilt in diesem Fall d.h. ŷ h y(x) = O(h p+ ), y h (x) y(x) = e p (x)h p + O(h p+ ). (3) Das obige Vorgehen kann man mit dem Einschrittverfahren (27) mit der Schrittfunktionen ˆΦ wiederholen. Es hat die Konsistenzordnung p + und erfüllt y ˆΦ(x, y(x), 0) = f(x, y(x)). y Man erhält schließlich Einschrittverfahren -79-
80 Satz 2.2 Die Schrittfunktion Φ des Einschrittverfahrens (23) sei hinreichend glatt, und es gelte für den lokalen Fehler die Entwicklung (24). Dann besitzt der globale Fehler eine asymptotische Entwicklung y h (x) y(x) = N j=p e j (x)h j + E h (x)h N+, (32) wobei die e j Lösungen linearer Anfangswertaufgaben der Gestalt (30) sind und E h beschränkt auf [a, b] ist. Einschrittverfahren -80-
81 Satz 2.2 wurde nur für äquidistante Schritte der Länge h bewiesen. Bei unterschiedlichen Schrittlängen nehmen wir an, dass es eine Funktion τ : [a, b] IR + gibt, so dass die Schrittlängen x n+ x n = τ(x n )h (33) von einem Parameter h abhängen. Dann geht die Entwicklung des lokalen Fehlers über in y(x + τ(x)h) y(x) hτ(x)φ(x, y(x), τ(x)h) = N+ j=p+ d j (x)τ(x) j h j + O(h N+2 ), (34) und mit ähnlichen Schlüssen wie oben erhält man, dass Satz 2.2 auch bei variabler Schrittweite richtig bleibt. Einschrittverfahren -8-
82 Satz 2.2 ist die Grundlage für Extrapolationsverfahren. Wir betrachten das Einschrittverfahren (23) für die Anfangswertaufgabe (). Es sei H > 0 eine Basisschrittlänge. Wir wählen eine Folge positiver ganzer Zahlen und definieren hierzu die Schrittweiten n < n 2 < n 3 <... (35) h j := H n j. Eine häufige Wahl ist die Romberg Folge, 2, 4, 8, 6, 32,..., oder die Bulirsch Folge, 2, 3, 4, 6, 8, 2, 6, 24, 32,.... Diese beiden Folgen haben sich bei der Extrapolation zur numerischen Integration bewährt, da man dann mit der zusammengesetzten Trapezregel auf jeweils vorher berechnete Trapezsummen zurückgreifen kann, und so ohne großen zusätzlichen Aufwand Näherungen für kleine Schrittweiten bestimmen kann. Bei Anfangswertaufgaben ist dies nicht der Fall, und hier ist häufig die harmonische Folge, 2, 3, 4, 5, 6,... die beste Wahl. Einschrittverfahren -82-
83 Ist eine Näherung y n für y(x n ) bereits bekannt, so berechnen wir mit n j Schritten der äquidistanten Schrittweite h j Näherungen y hj (x n + H) =: T j, (36) für y(x n + H) und benutzen diese, um durch Extrapolation eine bessere Näherung für y(x n + H) zu bestimmen. Dazu berechnen wir das Interpolationspolynom das die Bedingungen p(h) = η 0 + η p h p + η p+ h p η p+k 2 h p+k 2, (37) p(h i ) = T i,, i = j, j, j 2,..., j k +, (38) erfüllt, und wählen p(0) = η 0 =: T j,k (39) als neue Näherung. (38) ist ein lineares System von k Gleichungen zur Bestimmung der k Unbekannten η 0, η p,..., η p+k 2. Einschrittverfahren -83-
84 Offensichtlich kann T j,k als Näherungswert aus einem Einschrittverfahren mit der Schrittweite H gedeutet werden. Satz 2.22 Besitzt das Basisverfahren (23) die Konsistenzordnung p, so hat das Einschrittverfahren, das T j,k durch Interpolation bestimmt, die Konsistenzordnung p + k. Beweis: Berechnet man die T i, ausgehend vom Punkt (x, y(x)), so gilt nach Satz 2.2 (mit N = p + k ) T i, = y(x+h)+e p (x+h)h p i +...+e p+k 2(x+H)h p+k 2 i + i (40) mit i = e p+k (x + H)h p+k i + E hi (x + H)h p+k i. Einschrittverfahren -84-
85 Wegen e p+k (x) = 0 gilt e p+k (x + H) = O(H), und wegen h i H folgt i = O(H p+k ). Ferner gilt nach (37) und (38) Daher gilt T i, = η 0 + η p h p i η p+k 2h p+k 2 i. ( ) p ( ) p+k 2 H H (η 0 y(x+h))+(η p e p (x+h)) +...+(η p+k 2 e p+k 2(x+H)) = i. n i n i (4) Einschrittverfahren -85-
86 (4) ist ein lineares Gleichungssystem von k Gleichungen zur Bestimmung der k Unbekannten η 0 y(x + H), (η p e p (x + H))H p,..., (η p+k 2 e p+k 2 (x + H))H p+k 2, und die Koeffizientenmatrix hat die Gestalt /n p j /n p+ j... /n p+k 2 j A = /n p j /n p+ j... /n p+k 2 j /n p j k+ /n p+ j k+... /n p+k 2 j k+ Mit ähnlichen Argumenten wie in Mathematik I für die Vandermondesche Determinante sieht man ein, dass die Matrix A regulär ist. Daher folgt η 0 y(x + H) A max i = O(H k+p ). i Einschrittverfahren -86-
87 Ist T i, gegeben, so kann man die T j,k mit dem Neville Aitken Schema T j,k+ = T j,k + T j,k T j,k (n j /n j k ) (42) (vgl. Mathematik II) auf effiziente Weise bestimmen. Man erhält die Werte T T 2 T 22 T 3 T 32 T 33 T 4 T 42 T 43 T Ein großer Vorteil der Extrapolationsmethoden ist, dass in der ersten Spalte Näherungen der Ordnung p stehen, in der zweiten der Ordnung p +, in der dritten der Ordnung p + 2 usw. Man kann die Spalten als die Ergebnisse eingebetteter Verfahren auffassen. Damit erhält man eine billige Möglichkeit der Schrittweitenkontrolle. Einschrittverfahren -87-
88 Wählt man eine große Zahl von Spalten in dem Neville Aitken Schema, also eine große Ordnung, so hat man als Preis zu zahlen, dass man sehr viele Funktionsauswertungen für einen Schritt vornehmen muss. Andererseits wird man bei großer Konsistenzordnung große Schritte ausführen können, um eine vorgegebene Genauigkeit zu erreichen. Ist A k die Zahl der nötigen Funktionsauswertungen, um T k,k auszuwerten und H k die optimale Schrittlänge im nächsten Schritt, so ist W k := A k H k die Arbeit pro Einheitsschritt. Man wird nun nicht nur die Schrittlänge optimal wählen, sondern zugleich die Ordnung des Verfahrens, so dass W k minimal wird. Methoden zur Ordnungs- und Schrittweitenkontrolle sind in Hairer, Nørsett, Wanner beschrieben und in dem FORTRAN77 Code ODEX umgesetzt. Einschrittverfahren -88-
89 Das angegebene Verfahren von Dormand und Prince wird für geringe Genauigkeitsanforderungen (relativer Fehler: ) als die effizienteste Methode angesehen. Für höhere Genauigkeitsanforderungen (relativer Fehler: ) gilt ein Verfahren der Ordnung 8, das ebenfalls von Dormand und Prince publiziert wurde, mit einem Fehlerschätzer der Ordnung 5 und einer Korrektur der Ordnung 3, die von Hairer und Wanner vorgestellt wurden, als geeignet. Für sehr hohe Genauigkeitsanforderungen muss man Extrapolationsverfahren verwenden. Einschrittverfahren -89-
90 FORTRAN77 Codes der Methoden von Dormand und Prince und das Extrapolationsverfahren ODEX sind in dem Buch von Hairer, Nörsett, Wanner abgedruckt. Man kann diese (oder auch C Versionen) erhalten unter In MATLAB sind als eingebettete Runge Kutta Methoden für nichtsteife Anfangswertaufgaben das Verfahren von Dormand und Prince der Ordnung 4 als ODE45 und für den Fall, dass keine sehr hohe Genauigkeit benötigt wird, das Verfahren von Bogacki und Shampine der Ordnung 2 als ODE23 implementiert. Einschrittverfahren -90-
91 ODEX wurde von D. Abendroth in MATLAB übertragen und kann von geladen werden. Weitere Sortware findet man in der Spiegelung der NETLIB in der elib des ZIB in den Unterverzeichnissen ode und odepack. Einschrittverfahren -9-
92 Das Konrad Zuse Zentrum für Informationsverarbeitung (ZIB), Berlin, stellt das ODELab zur Verfügung. Es enthält eine Reihe von Lösern für Anfangswertaufgaben, mit denen die Verfahren getestet werden können. Das ODELab ist unter zugänglich. Einschrittverfahren -92-
Numerische Simulation 1
 Numerische Simulation Heinrich Voß Technische Universität Hamburg Harburg Arbeitsbereich Mathematik 2007 27.03.202: Ich bedanke mich bei Dominik Zobel für eine Reihe von Korrekturen 2 Inhaltsverzeichnis
Numerische Simulation Heinrich Voß Technische Universität Hamburg Harburg Arbeitsbereich Mathematik 2007 27.03.202: Ich bedanke mich bei Dominik Zobel für eine Reihe von Korrekturen 2 Inhaltsverzeichnis
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
KAPITEL 10. Numerische Integration
 KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Numerische Methoden 7. Übungsblatt
 Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
11. Einschrittverfahren
 H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
(a), für i = 1,..., n.
 .4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
.4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
Übungsblatt 4 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Übungsblatt 4 Musterlösung Aufgabe 7 (Nullstellen als Eigenwerte) Die Polynome {S n } n=0,,2,, S n P n, mit führem Koeffizienten eins, heißen Orthogonalpolynome
Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Übungsblatt 4 Musterlösung Aufgabe 7 (Nullstellen als Eigenwerte) Die Polynome {S n } n=0,,2,, S n P n, mit führem Koeffizienten eins, heißen Orthogonalpolynome
Numerische Verfahren
 Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 15.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren Numerische
Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 15.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren Numerische
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
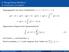 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 23
 Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Klassische Polynom Interpolation.
 Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
1/26. Integration. Numerische Mathematik 1 WS 2011/12
 1/26 Integration Numerische Mathematik 1 WS 2011/12 Notation 2/26 Die Abbildung I b a : C([a, b]) R gegeben durch Ia b (f ) := beschreibt die Integration. b a f (x)dx, Um das Integral I(f ) zu approximieren
1/26 Integration Numerische Mathematik 1 WS 2011/12 Notation 2/26 Die Abbildung I b a : C([a, b]) R gegeben durch Ia b (f ) := beschreibt die Integration. b a f (x)dx, Um das Integral I(f ) zu approximieren
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Institut für Geometrie und Praktische Mathematik Multiple-Choice-Test NumaMB F08 (30 Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine
RWTH Aachen Institut für Geometrie und Praktische Mathematik Multiple-Choice-Test NumaMB F08 (30 Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine
Numerik für Ingenieure I Wintersemester 2008
 1 / 32 Numerik für Ingenieure I Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 23.1.2009 2 / 32 Wiederholung Stückweise Polynominterpolation Stückweise lineare Interpolierende
1 / 32 Numerik für Ingenieure I Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 23.1.2009 2 / 32 Wiederholung Stückweise Polynominterpolation Stückweise lineare Interpolierende
Zweite Prüfung zur Vorlesung
 Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Lokaler Fehler y = y 2, y(0.2) = 5/9, Lösung: y = 1 Fehler nach dem 1. Schritt
 Lokaler Fehler y = y, y(.) = /9, Lösung: y = Fehler nach dem. Schritt ( t) 4 Fehler 6 8 4 (I) Euler explizit (II) Euler implizit (IIIa) Crank Nicolson (IIIb) Heun (IVa) Euler modifiziert (IVb) Euler mod.
Lokaler Fehler y = y, y(.) = /9, Lösung: y = Fehler nach dem. Schritt ( t) 4 Fehler 6 8 4 (I) Euler explizit (II) Euler implizit (IIIa) Crank Nicolson (IIIb) Heun (IVa) Euler modifiziert (IVb) Euler mod.
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
Differentiell-algebraische Gleichungen vom Index 1
 Differentiell-algebraische Gleichungen vom Index 1 Beispiel: Das ungedämpfte mathematische Pendel (der Länge 1 und der Masse 1) wird unter Verwendung des Auslenkwinkels ϕ bekanntlich beschrieben durch
Differentiell-algebraische Gleichungen vom Index 1 Beispiel: Das ungedämpfte mathematische Pendel (der Länge 1 und der Masse 1) wird unter Verwendung des Auslenkwinkels ϕ bekanntlich beschrieben durch
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
Numerik gewöhnlicher Differentialgleichungen. Übung 8 - Lösungsvorschlag
 Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Institut für Geometrie und Praktische Mathematik Diplom VP Numerik 13. September 004 Aufgabe 1 10 0 40 Gegeben sei die Matrix A = 80 10 10. 10 5 5 (6 Punkte) a) Skalieren (Zeilenäquilibrierung)
RWTH Aachen Institut für Geometrie und Praktische Mathematik Diplom VP Numerik 13. September 004 Aufgabe 1 10 0 40 Gegeben sei die Matrix A = 80 10 10. 10 5 5 (6 Punkte) a) Skalieren (Zeilenäquilibrierung)
Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK. K. Taubert Universität Hamburg SS08
 Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK K. Taubert Universität Hamburg SS8 Linearisierung 2 LINEARISIERUNG und das VERHALTEN VON LÖSUNGEN NICHTLINEARER DIFFERENTIALGLEICHUNGEN
Theorie und Numerik von Differentialgleichungen mit MATLAB und SIMULINK K. Taubert Universität Hamburg SS8 Linearisierung 2 LINEARISIERUNG und das VERHALTEN VON LÖSUNGEN NICHTLINEARER DIFFERENTIALGLEICHUNGEN
Mathematik. für das Ingenieurstudium. 10 Funktionen mit mehreren Variablen. Jürgen Koch Martin Stämpfle.
 10 Funktionen mit mehreren Variablen www.mathematik-fuer-ingenieure.de 2010 und, Esslingen Dieses Werk ist urheberrechtlich geschützt. Alle Rechte, auch die der Übersetzung, des Nachdruckes und der Vervielfältigung
10 Funktionen mit mehreren Variablen www.mathematik-fuer-ingenieure.de 2010 und, Esslingen Dieses Werk ist urheberrechtlich geschützt. Alle Rechte, auch die der Übersetzung, des Nachdruckes und der Vervielfältigung
Diplom VP Numerik 27. August 2007
 Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Diplom VP Numerik 28. August 2006
 Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Klausur Numerische Mathematik (für Elektrotechniker), 24. Februar 2016
 Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Numerische Integration
 Heinrich Voss voss@tu-harburg.de Hamburg University of Technology Institute for Numerical Simulation TUHH Heinrich Voss Kapitel 3 2010 1 / 87 In vielen Fällen ist es nicht möglich, ein gegebenes Integral
Heinrich Voss voss@tu-harburg.de Hamburg University of Technology Institute for Numerical Simulation TUHH Heinrich Voss Kapitel 3 2010 1 / 87 In vielen Fällen ist es nicht möglich, ein gegebenes Integral
Diplom VP Informatik / Numerik 2. September 2002
 Diplom VP Informatik / Numerik. September 00 Aufgabe Gegeben sei das lineare Gleichungssystem A x = b mit 0 4 0 0 0 0 A = 4 0 0 0 0 0 0 0 0 und b = 4 4 8 5. Punkte a Berechnen Sie die Cholesky Zerlegung
Diplom VP Informatik / Numerik. September 00 Aufgabe Gegeben sei das lineare Gleichungssystem A x = b mit 0 4 0 0 0 0 A = 4 0 0 0 0 0 0 0 0 und b = 4 4 8 5. Punkte a Berechnen Sie die Cholesky Zerlegung
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Nichtlineare Gleichungssysteme
 Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Exakte Differentialgleichungen
 Kapitel 4 Exakte Differentialgleichungen 4.1 Kurvenscharen Sei D R 2 ein offenes und zusammenhängendes Gebiet. Dann kann man zu jeder D einfach überdeckenden Kurvenschar eine Differentialgleichung erster
Kapitel 4 Exakte Differentialgleichungen 4.1 Kurvenscharen Sei D R 2 ein offenes und zusammenhängendes Gebiet. Dann kann man zu jeder D einfach überdeckenden Kurvenschar eine Differentialgleichung erster
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
8 Numerik gewöhnlicher Differentialgleichungen
 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 03 8 Numerik gewöhnlicher Differentialgleichungen 8. Grundlagen In der Numerik von gewöhnlichen Differentialgleichungen werden vorwiegend Aufgaben folgender
8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 03 8 Numerik gewöhnlicher Differentialgleichungen 8. Grundlagen In der Numerik von gewöhnlichen Differentialgleichungen werden vorwiegend Aufgaben folgender
Rheinisch-Westfälische Technische Hochschule. Gegeben seien eine gewöhnliche Dierentialgleichung (DGL) und ein Anfangswert. γ l K l.
 Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
D-MAVT NUMERISCHE MATHEMATIK FS 14 K. Nipp, A. Hiltebrand Lösung vom Test 1
 D-MAVT NUMERISCHE MATHEMATIK FS 4 K. Nipp, A. Hiltebrand Lösung vom Test. Sei eps die Maschinengenauigkeit in Matlab. Dann gilt: eps/4 = Richtig / Falsch + eps/2 = Richtig / Falsch 8 + eps = 8 Richtig
D-MAVT NUMERISCHE MATHEMATIK FS 4 K. Nipp, A. Hiltebrand Lösung vom Test. Sei eps die Maschinengenauigkeit in Matlab. Dann gilt: eps/4 = Richtig / Falsch + eps/2 = Richtig / Falsch 8 + eps = 8 Richtig
Übungen zu Splines Lösungen zu Übung 20
 Übungen zu Splines Lösungen zu Übung 20 20.1 Gegeben seien in der (x, y)-ebene die 1 Punkte: x i 6 5 4 2 1 0 1 2 4 5 6 y i 1 1 1 1 1 + 5 1 + 8 4 1 + 8 1 + 5 1 1 1 1 (a) Skizzieren Sie diese Punkte. (b)
Übungen zu Splines Lösungen zu Übung 20 20.1 Gegeben seien in der (x, y)-ebene die 1 Punkte: x i 6 5 4 2 1 0 1 2 4 5 6 y i 1 1 1 1 1 + 5 1 + 8 4 1 + 8 1 + 5 1 1 1 1 (a) Skizzieren Sie diese Punkte. (b)
NICHTRESTRINGIERTE OPTIMIERUNG
 3 NICHTRESTRINGIERTE OPTIMIERUNG Die Aufgabe, mit der wir uns im Folgen beschäftigen werden, ist die Lösung von Minimierungsproblemen der Form minimiere f(x) in R n, (3.1) wobei f : R n R eine gegebene
3 NICHTRESTRINGIERTE OPTIMIERUNG Die Aufgabe, mit der wir uns im Folgen beschäftigen werden, ist die Lösung von Minimierungsproblemen der Form minimiere f(x) in R n, (3.1) wobei f : R n R eine gegebene
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHE- MIE UND LEBENSMITTELCHEMIE
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHE- MIE UND LEBENSMITTELCHEMIE Differentialrechnung für Funktionen mehrerer
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHE- MIE UND LEBENSMITTELCHEMIE Differentialrechnung für Funktionen mehrerer
Klausur zur Vordiplom-Prüfung
 Technische Universität Hamburg-Harburg SS Arbeitsbereich Mathematik Dr. Jens-Peter M. Zemke Klausur zur Vordiplom-Prüfung Numerische Verfahren. Juli Sie haben Minuten Zeit zum Bearbeiten der Klausur. Bitte
Technische Universität Hamburg-Harburg SS Arbeitsbereich Mathematik Dr. Jens-Peter M. Zemke Klausur zur Vordiplom-Prüfung Numerische Verfahren. Juli Sie haben Minuten Zeit zum Bearbeiten der Klausur. Bitte
Übungsblatt 1 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi
![Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi](/thumbs/92/110521610.jpg) Funktionentheorie, Woche 7 Eigenschaften holomorpher Funktionen 7.1 Ganze Funktionen Definition 7.1 Eine Funktion f : C C, die holomorph ist auf C, nennt man eine ganze Funktion. Bemerkung 7.1.1 Als Folge
Funktionentheorie, Woche 7 Eigenschaften holomorpher Funktionen 7.1 Ganze Funktionen Definition 7.1 Eine Funktion f : C C, die holomorph ist auf C, nennt man eine ganze Funktion. Bemerkung 7.1.1 Als Folge
Inexakte Newton Verfahren
 Kapitel 3 Inexakte Newton Verfahren 3.1 Idee inexakter Newton Verfahren Wir betrachten weiterhin das nichtlineare Gleichungssystem F (x) = mit einer zumindest stetig differenzierbaren Funktion F : R n
Kapitel 3 Inexakte Newton Verfahren 3.1 Idee inexakter Newton Verfahren Wir betrachten weiterhin das nichtlineare Gleichungssystem F (x) = mit einer zumindest stetig differenzierbaren Funktion F : R n
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei die Matrix
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Nichtlineare Gleichungen in einer und mehreren Unbekannten
 Gleichungen in einer und mehreren Unbekannten 2. Vorlesung 170004 Numerische Methoden I Clemens Brand 26. Februar 2009, Gliederung,, Gleichungen in einer Variablen Was ist... Wie geht... eine lineare (nichtlineare,
Gleichungen in einer und mehreren Unbekannten 2. Vorlesung 170004 Numerische Methoden I Clemens Brand 26. Februar 2009, Gliederung,, Gleichungen in einer Variablen Was ist... Wie geht... eine lineare (nichtlineare,
Name: Matrikel-Nr.: 1
 Name: Matrikel-Nr.: 1 2 Name: Matrikel-Nr.: 3 Aufgabe 1. Zeigen Sie per vollständiger Induktion, dass für alle n N gilt: n k=1 k(k + 1) 2 = n(n + 1)(n + 2). 6 3 Punkte 4 Name: Matrikel-Nr.: 5 Aufgabe 2.
Name: Matrikel-Nr.: 1 2 Name: Matrikel-Nr.: 3 Aufgabe 1. Zeigen Sie per vollständiger Induktion, dass für alle n N gilt: n k=1 k(k + 1) 2 = n(n + 1)(n + 2). 6 3 Punkte 4 Name: Matrikel-Nr.: 5 Aufgabe 2.
1 Einführung, Terminologie und Einteilung
 Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Serie 13: Online Test
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
3. Lineare Mehrschrittverfahren 3.1 Begriffe
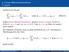 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
Analysis II. Aufgaben zum Stoff der Analysis I und II Lösungsvorschlag
 Prof Dr H Garcke, D Depner SS 9 NWF I - Mathematik 1979 Universität Regensburg Aufgabe 1 Analysis II Aufgaben zum Stoff der Analysis I und II Lösungsvorschlag i Erinnern Sie sich an die Konvergenzkriterien
Prof Dr H Garcke, D Depner SS 9 NWF I - Mathematik 1979 Universität Regensburg Aufgabe 1 Analysis II Aufgaben zum Stoff der Analysis I und II Lösungsvorschlag i Erinnern Sie sich an die Konvergenzkriterien
Anwendungen der Differentialrechnung
 KAPITEL 3 Anwendungen der Differentialrechnung 3.1 Lokale Maxima und Minima Definition 16: Sei f : D R eine Funktion von n Veränderlichen. Ein Punkt x heißt lokale oder relative Maximalstelle bzw. Minimalstelle
KAPITEL 3 Anwendungen der Differentialrechnung 3.1 Lokale Maxima und Minima Definition 16: Sei f : D R eine Funktion von n Veränderlichen. Ein Punkt x heißt lokale oder relative Maximalstelle bzw. Minimalstelle
ETHZ, D-MATH. Numerische Methoden D-PHYS, WS 2015/16 Dr. V. Gradinaru
 ETHZ, D-MATH Prüfung Numerische Methoden D-PHYS, WS 5/6 Dr. V. Gradinaru..6 Prüfungsdauer: 8 Minuten Maximal erreichbare Punktzahl: 6. Der van-der-pol Oszillator ( Punkte) Der van-der-pol Oszillator kann
ETHZ, D-MATH Prüfung Numerische Methoden D-PHYS, WS 5/6 Dr. V. Gradinaru..6 Prüfungsdauer: 8 Minuten Maximal erreichbare Punktzahl: 6. Der van-der-pol Oszillator ( Punkte) Der van-der-pol Oszillator kann
Öffnen Sie den Klausurbogen erst nach Aufforderung! Mathematische Grundlagen II (CES) SS 2017 Klausur
 Prof. Dr. Manuel Torrilhon Prof. Dr. Sebastian Noelle Öffnen Sie den Klausurbogen erst nach Aufforderung! Zugelassene Hilfsmittel: Mathematische Grundlagen II (CES) SS 2017 Klausur 07.08.2017 Dokumentenechtes
Prof. Dr. Manuel Torrilhon Prof. Dr. Sebastian Noelle Öffnen Sie den Klausurbogen erst nach Aufforderung! Zugelassene Hilfsmittel: Mathematische Grundlagen II (CES) SS 2017 Klausur 07.08.2017 Dokumentenechtes
Beispiel für eine periodische Spline-Interpolationsfunktion: Wir betrachten f(x) = sin(πx) und geben die folgenden Stützstellen und Stützwerte vor:
 5 Splineinterpolation Beispiel für eine periodische Spline-Interpolationsfunktion: Wir betrachten f(x) sin(πx) und geben die folgenden Stützstellen und Stützwerte vor: x i 3 f i Damit ist n 5, h Forderung
5 Splineinterpolation Beispiel für eine periodische Spline-Interpolationsfunktion: Wir betrachten f(x) sin(πx) und geben die folgenden Stützstellen und Stützwerte vor: x i 3 f i Damit ist n 5, h Forderung
19. Januar Universität Erlangen-Nürnberg Department Mathematik PD Dr. Markus Bause. . Danach liefert die Gauss-Elinination. .
 Universität Erlangen-Nürnberg Department Mathematik PD Dr Markus Bause Numerik I 9 Januar A Gegeben sei die Matrix A = a Führen Sie eine Zeilenskalierung der Matrix durch Klausur b Bestimmen Sie mit Hilfe
Universität Erlangen-Nürnberg Department Mathematik PD Dr Markus Bause Numerik I 9 Januar A Gegeben sei die Matrix A = a Führen Sie eine Zeilenskalierung der Matrix durch Klausur b Bestimmen Sie mit Hilfe
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
1 2 x x x x x x2 + 83
 Polynominterpolation Aufgabe 1 Gegeben sei die Wertetabelle i 0 1 2 3 x i 0 1 2 4 f i 3 1 2 7 a) Bestimmen Sie das Interpolationspolynom von Lagrange durch die obigen Wertepaare. b) Interpolieren Sie die
Polynominterpolation Aufgabe 1 Gegeben sei die Wertetabelle i 0 1 2 3 x i 0 1 2 4 f i 3 1 2 7 a) Bestimmen Sie das Interpolationspolynom von Lagrange durch die obigen Wertepaare. b) Interpolieren Sie die
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Polynominterpolation. Allgemeines Problem: Beispiel 1 (Teil 1):
 . Großübung Polynominterpolation Allgemeines Problem: Aufgrund gegebener Messwerte (Paare aus Werten i und Funktionswerten f( i )) soll ein Funktionsverlauf rekonstruiert bzw. zumeist angenähert werden.
. Großübung Polynominterpolation Allgemeines Problem: Aufgrund gegebener Messwerte (Paare aus Werten i und Funktionswerten f( i )) soll ein Funktionsverlauf rekonstruiert bzw. zumeist angenähert werden.
Probeklausur. 1 Stetigkeit [7 Punkte] 2 Differenzierbarkeit [10 Punkte] Ferienkurs Analysis 2 für Physiker SS Karolina Stoiber Aileen Wolf
![Probeklausur. 1 Stetigkeit [7 Punkte] 2 Differenzierbarkeit [10 Punkte] Ferienkurs Analysis 2 für Physiker SS Karolina Stoiber Aileen Wolf Probeklausur. 1 Stetigkeit [7 Punkte] 2 Differenzierbarkeit [10 Punkte] Ferienkurs Analysis 2 für Physiker SS Karolina Stoiber Aileen Wolf](/thumbs/76/73718518.jpg) Karolina Stoiber Aileen Wolf Ferienkurs Analysis 2 für Physiker SS 26 A Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar
Karolina Stoiber Aileen Wolf Ferienkurs Analysis 2 für Physiker SS 26 A Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar
Gewöhnliche Differentialgleichungen Woche 6. Existenz nach Picard-Lindelöf
 d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
Das Trust-Region-Verfahren
 Das Trust-Region-Verfahren Nadine Erath 13. Mai 2013... ist eine Methode der Nichtlinearen Optimierung Ziel ist es, das Minimum der Funktion f : R n R zu bestimmen. 1 Prinzip 1. Ersetzen f(x) durch ein
Das Trust-Region-Verfahren Nadine Erath 13. Mai 2013... ist eine Methode der Nichtlinearen Optimierung Ziel ist es, das Minimum der Funktion f : R n R zu bestimmen. 1 Prinzip 1. Ersetzen f(x) durch ein
9 Höhere partielle Ableitungen und die Taylorformel
 Vorlesung SS 29 Analsis 2 Prof Dr Siegfried Echterhoff 9 Höhere partielle Ableitungen und die Talorformel Definition 91 Sei U R n offen, f : U R m eine Funktion Dann heißt f 2-mal partiell differenzierbar,
Vorlesung SS 29 Analsis 2 Prof Dr Siegfried Echterhoff 9 Höhere partielle Ableitungen und die Talorformel Definition 91 Sei U R n offen, f : U R m eine Funktion Dann heißt f 2-mal partiell differenzierbar,
Lösung Semesterendprüfung
 MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
Klausurlösung Einführung in Numerische Methoden und FEM Universität Siegen, Department Maschinenbau,
 Universität Siegen, Department Maschinenbau, 7.7. Aufgabe y 3 l 3 3 F l l x Das dargestellte Fachwerk soll statisch mit Hilfe der FEM untersucht werden. Die Knoten und Elemente sind in der Abbildung nummeriert.
Universität Siegen, Department Maschinenbau, 7.7. Aufgabe y 3 l 3 3 F l l x Das dargestellte Fachwerk soll statisch mit Hilfe der FEM untersucht werden. Die Knoten und Elemente sind in der Abbildung nummeriert.
Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen
 Kapitel XII Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen 53 Implizite Funktionen und allgemeine partielle Differenzierbarkeit 54 Der Umkehrsatz 55 Lokale Extrema unter Nebenbedingungen,
Kapitel XII Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen 53 Implizite Funktionen und allgemeine partielle Differenzierbarkeit 54 Der Umkehrsatz 55 Lokale Extrema unter Nebenbedingungen,
Differentialgleichungen
 Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
eps für alle x D. 4. Die Zahl 256 ist in M(2, 4, 6, 6) exakt darstellbar.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
