Basteln und Zeichnen
|
|
|
- Ralph Krüger
- vor 8 Jahren
- Abrufe
Transkript
1 Titel des Arbeitsblatts Seite Inhalt 1 Falte eine Hexentreppe 2 Falte eine Ziehharmonika 3 Die Schatzinsel 4 Das Quadrat und seine Winkel 5 Senkrechte und parallele Linien 6 Ein Scherenschnitt 7 Bastle Formen 8 Wir zeichnen Dreiecke 9 Wir zeichnen Quadrate 10 Noch mehr Dreiecke und Vierecke 11 Wie viele Dreiecke und Quadrate siehst du? 12 Hinweise und Lösungen 13 Kopiervorlage Bastle Formen 15 Kopiervorlage Wir zeichnen Dreiecke und Vierecke 16 für Mathematik und Geometrie Seite 1
2 Falte eine Hexentreppe 2 Papierstreifen in verschiedenen Farben ca. 40 cm lang und 4 cm breit, Klebstoff. Nimm die beiden Papierstreifen und klebe ihre Enden im rechten Winkel wie auf dem Foto aufeinander. Der helle Streifen liegt unterhalb. Warte bis der Klebstoff trocken ist. Falte den unterhalb liegenden hellen Streifen über den darüber liegenden dunklen Streifen. Danach liegt der dunkle Streifen unterhalb und wird anschließend über den hellen Streifen gefaltet. So faltest du weiter, bis die Streifen zu Ende sind. Klebe den vorletzten Abschnitt mit dem letzten Abschnitt zusammen. Warte bis der Klebstoff trocken ist. Wenn du die Faltung auseinanderziehst, erhältst du eine Hexentreppe. Hier ist die Hexentreppe der Körper eines Schmetterlings. für Mathematik und Geometrie Seite 2
3 Falte eine Ziehharmonika ein Blatt Papier im Format DIN A4 und dein Übungsheft. Falten und zählen. Kannst du das Blatt wie auf den Fotos falten? Damit dir das gelingt, musst du manchmal das Papier drehen oder wenden, dann eine Faltlinie öffnen und nach der anderen Seite falten. Wie viele Faltlinien musst du für die fertige Ziehharmonika machen? Wie viele Rechtecke hat die Ziehharmonika? Schreibe das Ergebnis in dein Übungsheft. Wenn du Hilfe brauchst, schaue die Fotos unten genau an. Hier siehst du eine Möglichkeit die Ziehharmonika zu falten. für Mathematik und Geometrie Seite 3
4 Die Schatzinsel ein Blatt Papier im Format DIN A4. Vier Piraten wollen den Plan einer Schatzinsel mit zwei magischen Linien in vier ungefähr gleich große Teile teilen. Kannst du ihnen helfen? Reiße den Rand des Papiers weg. Jetzt hast du den Plan der Schatzinsel. Falte das Papier so, dass eine gerade Linie den Plan teilt. Falte das Papier so, dass diese Linie auf sich zu liegen kommt. Du hast nun einen rechten Winkel gefaltet (Foto links unten). Öffnest du die Faltlinien, so teilen zwei gerade Linien den Plan der Schatzinsel in vier Teile (Foto rechts unten). Was sollst du dir merken? Du kannst aus einem Stück Papier einen rechten Winkel falten. Die beiden Faltlinien heißen senkrecht zueinander. Zwei senkrechte Linien schließen einen rechten Winkel ein. für Mathematik und Geometrie Seite 4
5 Das Quadrat und seine Winkel ein quadratisches Blatt Papier (21 cm x 21 cm) und als Werkzeug einen rechten Winkel, den du aus dem Plan der Schatzinsel gefaltet hast. Lege den rechten Winkel in eine Ecke des Quadrats. Was beobachtest du? Reiße das quadratische Blatt Papier in fünf Teile. Lege die vier Teile mit den Ecken des Quadrats zusammen. Was beobachtest du? Was sollst du dir merken? Der Winkel in einem Eckpunkt eines Quadrats ist ein rechter Winkel. Vier rechte Winkel bilden einen vollen Winkel. Zusatzaufgabe: Mache dasselbe mit einem rechteckigen Blatt Papier. für Mathematik und Geometrie Seite 5
6 Senkrechte und parallele Linien ein Blatt Papier im Format DIN A4. Reiße den Rand weg. Falte das Papier einmal. Danach falte das Papier so, dass diese Linie auf sich zu liegen kommt. Öffne diese Faltlinie und falte an einer anderen Stelle eine neue Linie so, dass die erste Linie wieder auf sich zu liegen kommt. Öffne alle Faltlinien. Was kannst du beobachten? Was sollst du dir merken? Die beiden zur ersten Linie senkrechten Linien liegen parallel zueinander. Zwei parallele Linien haben überall den gleichen Abstand. für Mathematik und Geometrie Seite 6
7 Ein Scherenschnitt ein quadratisches Blatt Papier (21 cm x 21 cm), ein Geodreieck, einen Bleistift und eine Schere. Falte das Quadrat zu einem Dreieck. Danach falte das Dreieck noch zweimal zu einem Dreieck. Zeichne auf dem zuletzt gefalteten Dreieck mit deinem Geodreieck die Mittellinie des Dreiecks, links und rechts der Mittellinie parallele Linien im Abstand 15 mm, die Linie im Abstand 15 mm von der Grundlinie und die beiden Dreiecke wie auf dem Foto. Schneide nun aus dem gefalteten Papier die beiden eingezeichneten Dreiecke aus. Dein Scherenschnitt ist fertig. Falte ihn auf. Kannst du auch die beiden anderen Figuren falten? Probiere es aus. für Mathematik und Geometrie Seite 7
8 Bastle Formen Pfeifenputzer, Trinkhalme und Schere. Nimm die Vorlage und wähle eine Form aus. Zähle die Seiten ab und schneide genau so viele Trinkhalmstücke zurecht. Fädle die Trinkhalmstücke auf einen Pfeifenputzer auf. Biege deine Form wie auf der Vorlage. Bastle alle Formen! Was sollst du dir merken? Die Formen heißen Dreieck, Quadrat, Fünfeck, Sechseck und Achteck. für Mathematik und Geometrie Seite 8
9 Wir zeichnen Dreiecke ein Geodreieck oder ein Lineal, einen Bleistift und Buntstifte. Markiere die Ecken der Dreiecke farbig. Übertrage die Ecken in den rechten Raster. Zeichne die Dreiecke im rechten Raster ein. Verwende dazu dein Geodreieck oder dein Lineal! für Mathematik und Geometrie Seite 9
10 Wir zeichnen Quadrate ein Geodreieck oder ein Lineal, einen Bleistift und Buntstifte. Markiere die Ecken der Quadrate farbig. Übertrage die Ecken in den rechten Raster. Zeichne die Quadrate im rechten Raster ein. Verwende dazu dein Geodreieck oder dein Lineal! für Mathematik und Geometrie Seite 10
11 Noch mehr Dreiecke und Vierecke ein Geodreieck oder ein Lineal und einen Bleistift. Zeichnen und zählen. Die erste Figur besteht aus Vierecken. Markiere die Ecken der Vierecke im linken Raster farbig. Übertrage die Ecken in den rechten Raster. Zeichne die Figur mit dem Lineal oder Geodreieck im rechten Raster ein. Die Figur hat Ecken. Es sind Vierecke zu sehen. Die zweite Figur besteht aus Dreiecken. Mache es wie oben. Die zweite Figur hat Ecken. Es sind Dreiecke zu sehen. für Mathematik und Geometrie Seite 11
12 Wie viele Dreiecke und Quadrate siehst du? ein Geodreieck oder ein Lineal und einen Bleistift. Zeichnen und zählen. Die Figur bestehen aus Dreiecken und Quadraten. Markiere die Ecken der Dreiecke im linken Raster farbig. Übertrage die Ecken in den rechten Raster. Zeichne die Figur mit dem Lineal oder Geodreieck im rechten Raster ein. Es sind Dreiecke und Quadrate sind zu sehen. Mache es für die zweite Figur wie oben. In der zweiten Figur sind... Dreiecke und... Quadrate zu sehen. für Mathematik und Geometrie Seite 12
13 Hinweise und Lösungen Bezug zum Lehrplan Erfassen und Beschreiben einfacher geometrischer Figuren Untersuchen von Flächen Spielerisches Gestalten von Flächen Rechte Winkel Parallele Geraden Hantieren mit Zeichengeräten Zählen, Konzentration Saubere Durchführung von Zeichnungen Das Quadrat und seine Winkel (Seite 5) Beobachtungen zu Lege den gefalteten Winkel auf die Ecke des Quadrats können sein: Der gefaltete rechte Winkel deckt jede Ecke des Quadrats genau ab. Die Faltlinien liegen genau auf den Kanten des Quadrats. Beobachtungen zu Lege die vier Quadratteile mit Ecken zusammen können sein: Die vier Teile passen genau zusammen. Es bleibt keine Lücke. Senkrechte und parallele Linien (Seite 6) Beobachtungen zu Öffne die Faltlinien können sein: Es gibt nun zwei Linien, die zur ersten Linie senkrecht sind. Die Strecke auf der Senkrechten kann längs der neuen Linien verschoben werden. Die beiden Linien haben gleichen Abstand. Ein Scherenschnitt (Seite 7) Drei bis vier Kinder können das Arbeitsblatt als Vorlage verwenden. Für jedes Kind soll ein quadratisches Papier bereit liegen. Zusatzfragen: Welche Spiegelungen sind möglich? Welche Linien sind Spiegelachsen? Jede Faltlinie ist Symmetrielinie des Scherenschnitts. Bastle Formen (Seite 8) Das Arbeitsblatt Bastle Formen kann für zwei bis drei Kinder als Vorlage aufgelegt werden. Von der Kopiervorlage Bastle Formen können zwei Kinder die Formen auch ausschneiden. Damit die Kinder beim Basteln auch einige Eigenschaften der Formen kennen lernen, sind weitere Fragestellungen und Arbeitsaufträge zu Bastle Formen möglich: Was liegt der Seite eines Dreiecks, eines Vierecks, usw.... gegenüber? Bei Vielecken mit ungerader Eckenzahl liegt einer Seite immer eine Ecke gegenüber, bei Vielecken mit gerader Eckenanzahl liegt einer Seite immer eine parallele Seite gegenüber. Drücke das Quadrat, das Fünfeck, das Sechseck und das Achteck leicht zusammen. Was beobachtest du? Alle Figuren verändern ihr Aussehen. Drücke ein Dreieck leicht zusammen. Was beobachtest du? Das Dreieck bleibt stabil. für Mathematik und Geometrie Seite 13
14 Wir zeichnen Dreiecke, Quadrate und Vierecke (Seite 9 12) Für all diese Aufgaben ist das Zeichnen am Raster Voraussetzung. Jedes Arbeitsblatt kann zwei Kindern als Vorlage dienen. Zum Zeichnen kann für jedes Kind die Kopiervorlage Raster vorbereitet werden. Damit die Kinder die Figuren richtig in den rechten Raster übertragen, müssen sie vorher die Position der Ecken im Raster auszählen daher auch der Auftrag, die Ecken farbig zu markieren. Es können sowohl die Linien als auch die Kästchen gezählt werden. Z.B.: Die Ecke liegt auf der 4. Linie von oben und auf der 3. Linie von links. Oder: Die Ecke liegt 3 Einheiten von oben und 2 Einheiten von links (vgl. auch die Fotos von Seite 9). Noch mehr Dreiecke und Vierecke (Seite 11) Sobald ein Punkt Ecke eines Vierecks ist, wird er als genau eine Ecke gezählt unabhängig davon, ob er Ecke von weiteren Vierecken ist. Figur 1 hat 13 Ecken und 9 Vierecke. Punkte: 4 Punkte sind Ecken von nur einem Viereck, 8 Punkte sind Ecken von je 3 Vierecken und ein Punkt, der Mittelpunkt, ist Ecke von 4 Vierecken. Vierecke: Auch 9 Vierecke kann als Lösung vorgeschlagen werden. 8 Farben reichen um die Vierecke auszumalen, aber alle 8 Vierecke zusammen bilden ein achtfärbiges Quadrat. Figur 2 hat 13 Ecken und 16 Dreiecke. Wie viele Dreiecke und Quadrate siehst du? (Seite 12) Figur 1: Es sind 8 Dreiecke und 2 Quadrate zu sehen. Auch 16 Dreiecke kann als Lösung vorgeschlagen werden. 8 Farben reichen um die Dreiecke auszumalen, aber je zwei benachbarte Dreiecke bilden je ein neues zweifärbiges Dreieck (ein halbes Quadrat). Figur 2: Hier sind 12 Dreiecke und 4 Quadrate zu sehen. für Mathematik und Geometrie Seite 14
15 Kopiervorlage Bastle Formen für Mathematik und Geometrie Seite 15
16 Kopiervorlage Raster für Mathematik und Geometrie Seite 16
Falte den letzten Schritt wieder auseinander. Knick die linke Seite auseinander, sodass eine Öffnung entsteht.
 MATERIAL 2 Blatt farbiges Papier (ideal Silber oder Weiß) Schere Lineal Stift Kleber Für das Einhorn benötigst du etwa 16 Minuten. SCHRITT 1, TEIL 1 Nimm ein einfarbiges, quadratisches Stück Papier. Bei
MATERIAL 2 Blatt farbiges Papier (ideal Silber oder Weiß) Schere Lineal Stift Kleber Für das Einhorn benötigst du etwa 16 Minuten. SCHRITT 1, TEIL 1 Nimm ein einfarbiges, quadratisches Stück Papier. Bei
Wassily Kandinsky: Structure joyeuse. Beschreibe die Figuren und zeichne sie aus freier Hand in dein Heft.
 6 Flächen Wie heißen die Figuren? a) Dreiecke Viereck d) Quadrat b) Kreis Quadrate e) Dreiecke Rechteck c) Rechtecke Viereck f) Kreis Wassily Kandinsky: Structure joyeuse Lege Vierecke. a) Nimm vier gleich
6 Flächen Wie heißen die Figuren? a) Dreiecke Viereck d) Quadrat b) Kreis Quadrate e) Dreiecke Rechteck c) Rechtecke Viereck f) Kreis Wassily Kandinsky: Structure joyeuse Lege Vierecke. a) Nimm vier gleich
Falten regelmäßiger Vielecke
 Blatt 1 Gleichseitige Dreiecke Ausgehend von einem quadratischen Stück Papier kann man ohne weiteres Werkzeug viele interessante geometrische Figuren nur mit den Mitteln des Papierfaltens (Origami) erzeugen.
Blatt 1 Gleichseitige Dreiecke Ausgehend von einem quadratischen Stück Papier kann man ohne weiteres Werkzeug viele interessante geometrische Figuren nur mit den Mitteln des Papierfaltens (Origami) erzeugen.
2.4 Achsensymmetrie. Achsensymmetrie entdecken. Name:
 Name: Klasse: Datum: Achsensymmetrie entdecken Öffne die Datei 2_4_Spielkarte.ggb. 1 Bewege den blauen Punkt nach Lust und Laune. Beschreibe deine Beobachtungen. Beschreibe, wie sich der grüne Punkt bewegt,
Name: Klasse: Datum: Achsensymmetrie entdecken Öffne die Datei 2_4_Spielkarte.ggb. 1 Bewege den blauen Punkt nach Lust und Laune. Beschreibe deine Beobachtungen. Beschreibe, wie sich der grüne Punkt bewegt,
DOWNLOAD VORSCHAU. Bilderrahmen und Bilderhalter. zur Vollversion. Alltagsgegenstände fantasievoll gestalten. Gerlinde Blahak
 DOWNLOAD Gerlinde Blahak Bilderrahmen und Bilderhalter Alltagsgegenstände fantasievoll gestalten auszug aus dem Originaltitel: Lehrerhinweise zu den einzelnen Projekten Haltevorrichtung für Bilder Zeitaufwand:
DOWNLOAD Gerlinde Blahak Bilderrahmen und Bilderhalter Alltagsgegenstände fantasievoll gestalten auszug aus dem Originaltitel: Lehrerhinweise zu den einzelnen Projekten Haltevorrichtung für Bilder Zeitaufwand:
Fröbelstern Fotofaltkurs Schritt für Schritt aus der Zeitschrift LC 431, Seite 64/65
 OZ-Verlags-GmbH Papierstreifen. Die Enden des vierten gefalteten Papierstreifens weiter durch den zweiten gefalteten Streifen oben ziehen. 1 Die vier Papierstreifen jeweils waagerecht in der Mitte falten.
OZ-Verlags-GmbH Papierstreifen. Die Enden des vierten gefalteten Papierstreifens weiter durch den zweiten gefalteten Streifen oben ziehen. 1 Die vier Papierstreifen jeweils waagerecht in der Mitte falten.
Definition und Begriffe
 Merkblatt: Das Dreieck Definition und Begriffe Das Dreieck ist ein Vieleck. In der Ebene ist es die einfachste Figur, die von geraden Linien begrenzt wird. Ecken: Jedes Dreieck hat drei Ecken, die meist
Merkblatt: Das Dreieck Definition und Begriffe Das Dreieck ist ein Vieleck. In der Ebene ist es die einfachste Figur, die von geraden Linien begrenzt wird. Ecken: Jedes Dreieck hat drei Ecken, die meist
Bastelanleitung für Daumenkinos
 Bastelanleitung für Daumenkinos Bastelmaterial: 1 Schere 1 Lineal 1 Bleistift (Kugelschreiber oder Feinliner) 1 Radiergummi verschiedene Buntstifte Papier oder Bastelkarton Gummibänder Büroklammern 1.
Bastelanleitung für Daumenkinos Bastelmaterial: 1 Schere 1 Lineal 1 Bleistift (Kugelschreiber oder Feinliner) 1 Radiergummi verschiedene Buntstifte Papier oder Bastelkarton Gummibänder Büroklammern 1.
Bei Konstruktionen dürfen nur die folgenden Schritte durchgeführt werden : Beliebigen Punkt auf einer Geraden, Strecke oder Kreislinie zeichnen.
 Geometrie I. Zeichnen und Konstruieren ================================================================== 1.1 Der Unterschied zwischen Zeichnen und Konstruieren Bei der Konstruktion einer geometrischen
Geometrie I. Zeichnen und Konstruieren ================================================================== 1.1 Der Unterschied zwischen Zeichnen und Konstruieren Bei der Konstruktion einer geometrischen
Öffnen Sie die Albelli Gestaltungssoftware
 In 10 Schritten zu Ihrem ersten Fotobuch Anleitung Ab Windowsversion 7.4 1 Wählen Sie Ihre besten Fotos aus. Wenn Sie wissen, welche Fotos Sie verwenden möchten, speichern Sie sie am besten in einem Ordner
In 10 Schritten zu Ihrem ersten Fotobuch Anleitung Ab Windowsversion 7.4 1 Wählen Sie Ihre besten Fotos aus. Wenn Sie wissen, welche Fotos Sie verwenden möchten, speichern Sie sie am besten in einem Ordner
Minis im Museum. Begleitmaterial zum Thema Fische für Kitas und Grundschulen. ozeaneum.de
 Minis im Museum Begleitmaterial zum Thema Fische für Kitas und Grundschulen Kontakt Museumspädagogik: OZEANEUM Stralsund GmbH Hafenstraße 11 18439 Stralsund Tel.: +49 (0) 3831 2650 690 Fax: +49 (0) 3831
Minis im Museum Begleitmaterial zum Thema Fische für Kitas und Grundschulen Kontakt Museumspädagogik: OZEANEUM Stralsund GmbH Hafenstraße 11 18439 Stralsund Tel.: +49 (0) 3831 2650 690 Fax: +49 (0) 3831
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Vergleichsarbeiten in 3. Grundschulklassen. Mathematik. Aufgabenheft 1
 Vergleichsarbeiten in 3. Grundschulklassen Mathematik Aufgabenheft 1 Name: Klasse: Herausgeber: Projekt VERA (Vergleichsarbeiten in 3. Grundschulklassen) Universität Koblenz-Landau Campus Landau Fortstraße
Vergleichsarbeiten in 3. Grundschulklassen Mathematik Aufgabenheft 1 Name: Klasse: Herausgeber: Projekt VERA (Vergleichsarbeiten in 3. Grundschulklassen) Universität Koblenz-Landau Campus Landau Fortstraße
Thema: Winkel in der Geometrie:
 Thema: Winkel in der Geometrie: Zuerst ist es wichtig zu wissen, welche Winkel es gibt: - Nullwinkel: 0 - spitzer Winkel: 1-89 (Bild 1) - rechter Winkel: genau 90 (Bild 2) - stumpfer Winkel: 91-179 (Bild
Thema: Winkel in der Geometrie: Zuerst ist es wichtig zu wissen, welche Winkel es gibt: - Nullwinkel: 0 - spitzer Winkel: 1-89 (Bild 1) - rechter Winkel: genau 90 (Bild 2) - stumpfer Winkel: 91-179 (Bild
MINT-Schülerinnen-Camp 25. 28. September 2003 in Berlin. Entwurf und Bau einer stabilen Brücke aus Papier - Technisches Experiment
 Sabrina Evers TU Braunschweig Sabrina.Evers@tu-bs.de MINT-Schülerinnen-Camp 25. 28. September 2003 in Berlin Entwurf und Bau einer stabilen Brücke aus Papier - Technisches Experiment 1. Teil 1 Erforschung
Sabrina Evers TU Braunschweig Sabrina.Evers@tu-bs.de MINT-Schülerinnen-Camp 25. 28. September 2003 in Berlin Entwurf und Bau einer stabilen Brücke aus Papier - Technisches Experiment 1. Teil 1 Erforschung
Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert
 Beamen in EEP Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert Zuerst musst du dir 2 Programme besorgen und zwar: Albert, das
Beamen in EEP Das sogenannte Beamen ist auch in EEP möglich ohne das Zusatzprogramm Beamer. Zwar etwas umständlicher aber es funktioniert Zuerst musst du dir 2 Programme besorgen und zwar: Albert, das
Unser Bücherkatalog: Worum geht s?
 Unser Bücherkatalog: Worum geht s? Die Buchbeschreibung ist dein wichtigstes Hilfsmittel, um anderen Lust darauf zu machen, ein Buch zu lesen. Es ist aber gar nicht so einfach, eine gute Buchbeschreibung
Unser Bücherkatalog: Worum geht s? Die Buchbeschreibung ist dein wichtigstes Hilfsmittel, um anderen Lust darauf zu machen, ein Buch zu lesen. Es ist aber gar nicht so einfach, eine gute Buchbeschreibung
1. Software installieren 2. Software starten. Hilfe zum Arbeiten mit der DÖHNERT FOTOBUCH Software
 1. Software installieren 2. Software starten Hilfe zum Arbeiten mit der DÖHNERT FOTOBUCH Software 3. Auswahl 1. Neues Fotobuch erstellen oder 2. ein erstelltes, gespeichertes Fotobuch laden und bearbeiten.
1. Software installieren 2. Software starten Hilfe zum Arbeiten mit der DÖHNERT FOTOBUCH Software 3. Auswahl 1. Neues Fotobuch erstellen oder 2. ein erstelltes, gespeichertes Fotobuch laden und bearbeiten.
Grundlegende Geometrie - Vorlesung mit integriertem Praxiskurs. 09.02. Klausur (08-10 Uhr Audimax, HS 1)
 Vorlesungsübersicht Wintersemester 2015/16 Di 08-10 Audimax Grundlegende Geometrie - Vorlesung mit integriertem Praxiskurs Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier
Vorlesungsübersicht Wintersemester 2015/16 Di 08-10 Audimax Grundlegende Geometrie - Vorlesung mit integriertem Praxiskurs Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier
Euch fällt mit Sicherheit noch viel mehr ein!
 MEMOBOARD Dieses Memoboard ist vielseitig einsetzbar. Es passt in dein persönliches Nähzimmer, denn du kannst daran alle deine Ideen und Bilder sammeln. Es passt in das Büro deines Liebsten, denn er kann
MEMOBOARD Dieses Memoboard ist vielseitig einsetzbar. Es passt in dein persönliches Nähzimmer, denn du kannst daran alle deine Ideen und Bilder sammeln. Es passt in das Büro deines Liebsten, denn er kann
Sich einen eigenen Blog anzulegen, ist gar nicht so schwer. Es gibt verschiedene Anbieter. www.blogger.com ist einer davon.
 www.blogger.com Sich einen eigenen Blog anzulegen, ist gar nicht so schwer. Es gibt verschiedene Anbieter. www.blogger.com ist einer davon. Sie müssen sich dort nur ein Konto anlegen. Dafür gehen Sie auf
www.blogger.com Sich einen eigenen Blog anzulegen, ist gar nicht so schwer. Es gibt verschiedene Anbieter. www.blogger.com ist einer davon. Sie müssen sich dort nur ein Konto anlegen. Dafür gehen Sie auf
Comic Life 2.x. Fortbildung zum Mediencurriculum
 Comic Life 2.x Fortbildung zum Mediencurriculum - 1 - Comic Life Eine kurze Einführung in die Bedienung von Comic Life 2.x. - 2 - Starten von Comic Life Bitte starte das Programm Comic Life. Es befindet
Comic Life 2.x Fortbildung zum Mediencurriculum - 1 - Comic Life Eine kurze Einführung in die Bedienung von Comic Life 2.x. - 2 - Starten von Comic Life Bitte starte das Programm Comic Life. Es befindet
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Leichte-Sprache-Bilder
 Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Schritt für Schritt zu tollen Origami-Figuren
 Schritt für Schritt zu tollen Origami-Figuren Für Anfänger: Schmetterling Benötigtes Material: Papier-Quadrat in beliebiger Farbe (80 g/m 2, ca. 20x20cm) Schritt 1: Falten Sie das Faltblatt als Dreieck,
Schritt für Schritt zu tollen Origami-Figuren Für Anfänger: Schmetterling Benötigtes Material: Papier-Quadrat in beliebiger Farbe (80 g/m 2, ca. 20x20cm) Schritt 1: Falten Sie das Faltblatt als Dreieck,
Eignungstest Mathematik
 Eignungstest Mathematik Klasse 4 Datum: Name: Von Punkten wurden Punkte erreicht Zensur: 1. Schreibe in folgende Figuren die Bezeichnungen für die jeweilige Figur! Für eine Rechteck gibt ein R ein, für
Eignungstest Mathematik Klasse 4 Datum: Name: Von Punkten wurden Punkte erreicht Zensur: 1. Schreibe in folgende Figuren die Bezeichnungen für die jeweilige Figur! Für eine Rechteck gibt ein R ein, für
Wir sparen Strom. Turbinchens Schulstunde. Infoblatt
 Infoblatt Wir sparen Strom Wir wissen schon, dass wir für viele Dinge im Leben Strom brauchen: für die Waschmaschine, für den Elektroherd, für den Computer, das Licht etc.! Strom aus der Steckdose kostet
Infoblatt Wir sparen Strom Wir wissen schon, dass wir für viele Dinge im Leben Strom brauchen: für die Waschmaschine, für den Elektroherd, für den Computer, das Licht etc.! Strom aus der Steckdose kostet
Auf Diät Wie Sie Ihre Entwicklung verschlanken. Job Merkblätter. Einmal drucken pro Team
 Auf Diät Wie Sie Ihre Entwicklung verschlanken The Bottleneck Game Job Merkblätter Einmal drucken pro Team Deutsche Version von Martin Heider (http://infomar.de/) und Pierluigi Pugliese (http://www.connexxo.com)
Auf Diät Wie Sie Ihre Entwicklung verschlanken The Bottleneck Game Job Merkblätter Einmal drucken pro Team Deutsche Version von Martin Heider (http://infomar.de/) und Pierluigi Pugliese (http://www.connexxo.com)
Unterschrift des Absenders. Brieftext
 Dr. Bindseiler ist angesäuert als er Gisis Brief an Anja findet. Aber er ist mehr über die Form des Briefes entsetzt als über den Inhalt: Du übst wohl schon für die nächste Schlechtschreibreform?, fragt
Dr. Bindseiler ist angesäuert als er Gisis Brief an Anja findet. Aber er ist mehr über die Form des Briefes entsetzt als über den Inhalt: Du übst wohl schon für die nächste Schlechtschreibreform?, fragt
3. Verpackungskünstler. Berechnungen am Quader, Umgang mit Termen, räumliche Vorstellung
 Berechnungen am Quader, Umgang mit Termen, räumliche Vorstellung Päckchen, die man verschenken möchte, werden gerne mit Geschenkband verschnürt. Dazu wird das Päckchen auf seine größte Seite gelegt, wie
Berechnungen am Quader, Umgang mit Termen, räumliche Vorstellung Päckchen, die man verschenken möchte, werden gerne mit Geschenkband verschnürt. Dazu wird das Päckchen auf seine größte Seite gelegt, wie
9 Auto. Rund um das Auto. Welche Wörter zum Thema Auto kennst du? Welches Wort passt? Lies die Definitionen und ordne zu.
 1 Rund um das Auto Welche Wörter zum Thema Auto kennst du? Welches Wort passt? Lies die Definitionen und ordne zu. 1. Zu diesem Fahrzeug sagt man auch Pkw oder Wagen. 2. kein neues Auto, aber viel billiger
1 Rund um das Auto Welche Wörter zum Thema Auto kennst du? Welches Wort passt? Lies die Definitionen und ordne zu. 1. Zu diesem Fahrzeug sagt man auch Pkw oder Wagen. 2. kein neues Auto, aber viel billiger
Primarschule Birmensdorf PIA Anleitungen Word. Bevor du mit Schreiben beginnen kannst, musst du dein Word- Dokument einrichten.
 Word einrichten Bevor du mit Schreiben beginnen kannst, musst du dein Word- Dokument einrichten. Starte ein Word Dokument, indem du auf das blaue W drückst. Wähle Ansicht 1, gehe zu Symbolleiste 2 und
Word einrichten Bevor du mit Schreiben beginnen kannst, musst du dein Word- Dokument einrichten. Starte ein Word Dokument, indem du auf das blaue W drückst. Wähle Ansicht 1, gehe zu Symbolleiste 2 und
Papierverbrauch im Jahr 2000
 Hier findest du Forschertipps. Du kannst sie allein oder in der kleinen Gruppe mit anderen Kindern bearbeiten! Gestaltet ein leeres Blatt, schreibt Berichte oder entwerft ein Plakat. Sprecht euch in der
Hier findest du Forschertipps. Du kannst sie allein oder in der kleinen Gruppe mit anderen Kindern bearbeiten! Gestaltet ein leeres Blatt, schreibt Berichte oder entwerft ein Plakat. Sprecht euch in der
Fülle das erste Bild "Erforderliche Information für das Google-Konto" vollständig aus und auch das nachfolgende Bild.
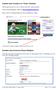 Erstellen eines Fotoalbum mit "Picasa"-Webalben Wie es geht kannst Du hier in kleinen Schritten nachvollziehen. Rufe im Internet folgenden "LINK" auf: http://picasaweb.google.com Jetzt musst Du folgendes
Erstellen eines Fotoalbum mit "Picasa"-Webalben Wie es geht kannst Du hier in kleinen Schritten nachvollziehen. Rufe im Internet folgenden "LINK" auf: http://picasaweb.google.com Jetzt musst Du folgendes
Ein süsses Experiment
 Ein süsses Experiment Zuckerkristalle am Stiel Das brauchst du: 250 Milliliter Wasser (entspricht etwa einer Tasse). Das reicht für 4-5 kleine Marmeladengläser und 4-5 Zuckerstäbchen 650 Gramm Zucker (den
Ein süsses Experiment Zuckerkristalle am Stiel Das brauchst du: 250 Milliliter Wasser (entspricht etwa einer Tasse). Das reicht für 4-5 kleine Marmeladengläser und 4-5 Zuckerstäbchen 650 Gramm Zucker (den
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Lernen an Stationen Thema: Flächenberechnung
 Lernen an Stationen Thema: Flächenberechnung 8. Jahrgang Mathematics is a way of thinking, not a collection of facts! Ausgehend von dieser grundsätzlichen Überzeugung sollte ein Unterricht zum Thema Flächenberechnung
Lernen an Stationen Thema: Flächenberechnung 8. Jahrgang Mathematics is a way of thinking, not a collection of facts! Ausgehend von dieser grundsätzlichen Überzeugung sollte ein Unterricht zum Thema Flächenberechnung
Kartei zum Lesetagebuch Nr. 2. Kartei zum Lesetagebuch Nr. 1. Kartei zum Lesetagebuch Nr. 4. Kartei zum Lesetagebuch Nr. 3.
 Kartei zum Lesetagebuch Nr. 1 Buchempfehlung Kartei zum Lesetagebuch Nr. 2 Die traurigste Stelle Überlege, wem das Buch gefallen könnte! Schreibe auf, wem du das Buch empfehlen würdest und erkläre warum!
Kartei zum Lesetagebuch Nr. 1 Buchempfehlung Kartei zum Lesetagebuch Nr. 2 Die traurigste Stelle Überlege, wem das Buch gefallen könnte! Schreibe auf, wem du das Buch empfehlen würdest und erkläre warum!
Kurzanleitung Messer machen
 Kurzanleitung Messer machen Für einen Bausatz benötigen Sie die folgenden Materialien: Messerklinge Passung Rentierhorn Masurbirke Lederstücke Arbeitsschritte: 1. Um die Messerklinge vor Beschädigungen
Kurzanleitung Messer machen Für einen Bausatz benötigen Sie die folgenden Materialien: Messerklinge Passung Rentierhorn Masurbirke Lederstücke Arbeitsschritte: 1. Um die Messerklinge vor Beschädigungen
Licht-Bilder. Schneide dir eine Schablone für Licht aus. Klebe Papier an die Wand. Mache ein großes Licht-Bild. Ein anderes Kind malt es nach.
 Licht-Bilder Können wir auch mit Licht statt mit Schatten Figuren machen? Schneide dir eine Schablone für Licht aus. Klebe Papier an die Wand. Mache ein großes Licht-Bild. Ein anderes Kind malt es nach..
Licht-Bilder Können wir auch mit Licht statt mit Schatten Figuren machen? Schneide dir eine Schablone für Licht aus. Klebe Papier an die Wand. Mache ein großes Licht-Bild. Ein anderes Kind malt es nach..
http://www.olympiade-mathematik.de 2. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 7 Saison 1962/1963 Aufgaben und Lösungen
 2. Mathematik Olympiade Saison 1962/1963 Aufgaben und Lösungen 1 OJM 2. Mathematik-Olympiade Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen soll deutlich erkennbar in logisch und
2. Mathematik Olympiade Saison 1962/1963 Aufgaben und Lösungen 1 OJM 2. Mathematik-Olympiade Aufgaben Hinweis: Der Lösungsweg mit Begründungen und Nebenrechnungen soll deutlich erkennbar in logisch und
Anleitung PDF erstellen aus Word
 Wie erstelle ich ein PDF im individuellen Format? 1. Öffnen Sie ein neues Word-Dokument 2. Ändern Sie die Größe/Format des Word-Dokument Falls Sie eine Faltkarte bedrucken lassen möchten, müssen Sie das
Wie erstelle ich ein PDF im individuellen Format? 1. Öffnen Sie ein neues Word-Dokument 2. Ändern Sie die Größe/Format des Word-Dokument Falls Sie eine Faltkarte bedrucken lassen möchten, müssen Sie das
Steinmikado I. Steinmikado II. Steinzielwerfen. Steinwerfen in Dosen
 Steinmikado I Steinmikado II : ab 4 : ab 4 : 20 Steine : 20 Steine Spielregel : M 10-01 In der Mitte des Raumes schichten wir einen Steinberg auf. Die Aufgabe besteht darin, vom Fuße des Berges jeweils
Steinmikado I Steinmikado II : ab 4 : ab 4 : 20 Steine : 20 Steine Spielregel : M 10-01 In der Mitte des Raumes schichten wir einen Steinberg auf. Die Aufgabe besteht darin, vom Fuße des Berges jeweils
Nina. bei der Hörgeräte-Akustikerin. Musterexemplar
 Nina bei der Hörgeräte-Akustikerin Nina bei der Hörgeräte-Akustikerin Herausgeber: uphoff pr-consulting Alfred-Wegener-Str. 6 35039 Marburg Tel.: 0 64 21 / 4 07 95-0 info@uphoff-pr.de www.uphoff-pr.de
Nina bei der Hörgeräte-Akustikerin Nina bei der Hörgeräte-Akustikerin Herausgeber: uphoff pr-consulting Alfred-Wegener-Str. 6 35039 Marburg Tel.: 0 64 21 / 4 07 95-0 info@uphoff-pr.de www.uphoff-pr.de
Geometrie Klasse 5 Basiswissen und Grundbegriffe der Geometrie
 Geometrie Klasse 5 Basiswissen und Grundbegriffe der Geometrie Skript Beispiele Musteraufgaben Seite 1 Impressum Mathefritz Verlag Jörg Christmann Pfaffenkopfstr. 21E 66125 Saarbrücken verlag@mathefritz.de
Geometrie Klasse 5 Basiswissen und Grundbegriffe der Geometrie Skript Beispiele Musteraufgaben Seite 1 Impressum Mathefritz Verlag Jörg Christmann Pfaffenkopfstr. 21E 66125 Saarbrücken verlag@mathefritz.de
Mit Papier, Münzen und Streichhölzern rechnen kreative Aufgaben zum Umgang mit Größen. Von Florian Raith, Fürstenzell VORANSICHT
 Mit Papier, Münzen und Streichhölzern rechnen kreative Aufgaben zum Umgang mit Größen Von Florian Raith, Fürstenzell Alltagsgegenstände sind gut greifbar so werden beim Rechnen mit ihnen Größen begreifbar.
Mit Papier, Münzen und Streichhölzern rechnen kreative Aufgaben zum Umgang mit Größen Von Florian Raith, Fürstenzell Alltagsgegenstände sind gut greifbar so werden beim Rechnen mit ihnen Größen begreifbar.
Die Größe von Flächen vergleichen
 Vertiefen 1 Die Größe von Flächen vergleichen zu Aufgabe 1 Schulbuch, Seite 182 1 Wer hat am meisten Platz? Ordne die Figuren nach ihrem Flächeninhalt. Begründe deine Reihenfolge. 1 2 3 4 zu Aufgabe 2
Vertiefen 1 Die Größe von Flächen vergleichen zu Aufgabe 1 Schulbuch, Seite 182 1 Wer hat am meisten Platz? Ordne die Figuren nach ihrem Flächeninhalt. Begründe deine Reihenfolge. 1 2 3 4 zu Aufgabe 2
Gefahr erkannt Gefahr gebannt
 Ihre Unfallversicherung informiert Toter Winkel Gefahr erkannt Gefahr gebannt Gesetzliche Unfallversicherung Die Situation Liebe Eltern! Immer wieder kommt es zu schweren Verkehrsunfällen, weil LKW-Fahrer
Ihre Unfallversicherung informiert Toter Winkel Gefahr erkannt Gefahr gebannt Gesetzliche Unfallversicherung Die Situation Liebe Eltern! Immer wieder kommt es zu schweren Verkehrsunfällen, weil LKW-Fahrer
Computeria Rorschach Mit Excel Diagramme erstellen
 Mit Excel Diagramme erstellen 25.12.2010 Roland Liebing Mit Excel Diagramme erstellen Diagramme können Zahlenwerte veranschaulichen, das heisst, mit Hilfe eines Diagramms können Zahlen besser miteinander
Mit Excel Diagramme erstellen 25.12.2010 Roland Liebing Mit Excel Diagramme erstellen Diagramme können Zahlenwerte veranschaulichen, das heisst, mit Hilfe eines Diagramms können Zahlen besser miteinander
Bereich: Mensch, Natur und Kultur bzw. Heimat- und Sachkunde ab Klasse 2 Arbeitszeit: ca. 1 bis 2 Doppelstunden
 Geburtstagskalender Bereich: Mensch, Natur und Kultur bzw. Heimat- und Sachkunde ab Klasse 2 Arbeitszeit: ca. 1 bis 2 Doppelstunden Aufgabe und Motivation Die Unterrichtseinheit Zeiteinteilung und Zeitablauf
Geburtstagskalender Bereich: Mensch, Natur und Kultur bzw. Heimat- und Sachkunde ab Klasse 2 Arbeitszeit: ca. 1 bis 2 Doppelstunden Aufgabe und Motivation Die Unterrichtseinheit Zeiteinteilung und Zeitablauf
Satzhilfen Publisher Seite Einrichten
 Satzhilfen Publisher Seite Einrichten Es gibt verschiedene Möglichkeiten die Seite einzurichten, wir fangen mit der normalen Version an, Seite einrichten auf Format A5 Wählen Sie zunächst Datei Seite einrichten,
Satzhilfen Publisher Seite Einrichten Es gibt verschiedene Möglichkeiten die Seite einzurichten, wir fangen mit der normalen Version an, Seite einrichten auf Format A5 Wählen Sie zunächst Datei Seite einrichten,
Copyright Sophie Streit / Filzweiber /www.filzweiber.at. Fertigung eines Filzringes mit Perlen!
 Fertigung eines Filzringes mit Perlen! Material und Bezugsquellen: Ich arbeite ausschließlich mit Wolle im Kardenband. Alle Lieferanten die ich hier aufliste haben nat. auch Filzzubehör. Zu Beginn möchtest
Fertigung eines Filzringes mit Perlen! Material und Bezugsquellen: Ich arbeite ausschließlich mit Wolle im Kardenband. Alle Lieferanten die ich hier aufliste haben nat. auch Filzzubehör. Zu Beginn möchtest
2. Propädeutische Geometrie Klasse 5/6. Für den Geometrieunterricht ausnützen!
 2. Propädeutische Geometrie Klasse 5/6 2.1 Zur Entwicklung der Schüler Kinder im Alter von 10-12 Jahren sind wissbegierig neugierig leicht zu motivieren anhänglich (Lehrperson ist Autorität) zum Spielen
2. Propädeutische Geometrie Klasse 5/6 2.1 Zur Entwicklung der Schüler Kinder im Alter von 10-12 Jahren sind wissbegierig neugierig leicht zu motivieren anhänglich (Lehrperson ist Autorität) zum Spielen
Spiel und Spaß im Freien. Arbeitsblat. Arbeitsblatt 1. Zeichnung: Gisela Specht. Diese Vorlage darf für den Unterricht fotokopiert werden.
 Spiel und Spaß im Freien Arbeitsblatt 1 Arbeitsblat 1 Zeichnung: Gisela Specht Arbeitsblatt 1 Was kann man mit diesen Dingen machen? Was passt zusammen? Verbinde die richtigen Bildkarten miteinander. 2
Spiel und Spaß im Freien Arbeitsblatt 1 Arbeitsblat 1 Zeichnung: Gisela Specht Arbeitsblatt 1 Was kann man mit diesen Dingen machen? Was passt zusammen? Verbinde die richtigen Bildkarten miteinander. 2
Die neue Aufgabe von der Monitoring-Stelle. Das ist die Monitoring-Stelle:
 Die neue Aufgabe von der Monitoring-Stelle Das ist die Monitoring-Stelle: Am Deutschen Institut für Menschen-Rechte in Berlin gibt es ein besonderes Büro. Dieses Büro heißt Monitoring-Stelle. Mo-ni-to-ring
Die neue Aufgabe von der Monitoring-Stelle Das ist die Monitoring-Stelle: Am Deutschen Institut für Menschen-Rechte in Berlin gibt es ein besonderes Büro. Dieses Büro heißt Monitoring-Stelle. Mo-ni-to-ring
Die Post hat eine Umfrage gemacht
 Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Ebook Schnabelinas Trotzkopf
 Ebook Schnabelinas Trotzkopf Schnabelinas Trotzkopf ist ein schmaler Pulloverschnitt mit überkreuzter Passe. Er ist perfekt, um ihn unter einer Strampelhose zu tragen. Man kann ihn sowohl aus Sweat oder
Ebook Schnabelinas Trotzkopf Schnabelinas Trotzkopf ist ein schmaler Pulloverschnitt mit überkreuzter Passe. Er ist perfekt, um ihn unter einer Strampelhose zu tragen. Man kann ihn sowohl aus Sweat oder
Klinikmütze. Es eignen sich Jersey- oder Interlockstoffe, am Besten mit Elasthananteil.
 Klinikmütze Das Klinik-Mützen-Projekt möchte mit bunten Mützen ein bisschen Farbe in den tristen Klinikalltag bringen und den kleinen Patienten ein Lächeln ins Gesicht zaubern. Die Mützen sollen sowohl
Klinikmütze Das Klinik-Mützen-Projekt möchte mit bunten Mützen ein bisschen Farbe in den tristen Klinikalltag bringen und den kleinen Patienten ein Lächeln ins Gesicht zaubern. Die Mützen sollen sowohl
Zahlenwinkel: Forscherkarte 1. alleine. Zahlenwinkel: Forschertipp 1
 Zahlenwinkel: Forscherkarte 1 alleine Tipp 1 Lege die Ziffern von 1 bis 9 so in den Zahlenwinkel, dass jeder Arm des Zahlenwinkels zusammengezählt das gleiche Ergebnis ergibt! Finde möglichst viele verschiedene
Zahlenwinkel: Forscherkarte 1 alleine Tipp 1 Lege die Ziffern von 1 bis 9 so in den Zahlenwinkel, dass jeder Arm des Zahlenwinkels zusammengezählt das gleiche Ergebnis ergibt! Finde möglichst viele verschiedene
Benutzername: Passwort: Nun befindest du dich in einem Bereich, von wo aus du Berichte über Ereignisse schreiben kannst und Fotos dazugeben kannst.
 BERICHTE MIT FOTOS AUF DIE SCHULHOMEPAGE STELLEN Gehe im Internet auf die Seite deiner Schulhomepage. In diesem Skript wird am Beispiel der Homepage der VS Mittersill gearbeitet. http://www.vs-mittersill.salzburg.at
BERICHTE MIT FOTOS AUF DIE SCHULHOMEPAGE STELLEN Gehe im Internet auf die Seite deiner Schulhomepage. In diesem Skript wird am Beispiel der Homepage der VS Mittersill gearbeitet. http://www.vs-mittersill.salzburg.at
Forschertagebuch Wasser Die Oberflächenspannung
 Forschertagebuch Wasser Die Oberflächenspannung von Forscherauftrag Nr. ❶ ein randvolles Glas Wasser ein Handtuch Becher mit vielen 1-Cent Münzen eine Pipette Denkaufgabe! Was meinst du, passen noch Münzen
Forschertagebuch Wasser Die Oberflächenspannung von Forscherauftrag Nr. ❶ ein randvolles Glas Wasser ein Handtuch Becher mit vielen 1-Cent Münzen eine Pipette Denkaufgabe! Was meinst du, passen noch Münzen
partie 1 52 défis mathématiques pour les classes bilingues (cycle 3) traduit à partir du site de J-L SIGRIST www.jlsigrist.com
 52 défis mathématiques pour les classes bilingues (cycle 3) partie 1 traduit à partir du site de J-L SIGRIST www.jlsigrist.com par ILTIS Stéphane STUDER Yann-Noël HEINTZ Yannick Wie viele Vierecke siehst
52 défis mathématiques pour les classes bilingues (cycle 3) partie 1 traduit à partir du site de J-L SIGRIST www.jlsigrist.com par ILTIS Stéphane STUDER Yann-Noël HEINTZ Yannick Wie viele Vierecke siehst
Deutsches Rotes Kreuz. Kopfschmerztagebuch von:
 Deutsches Rotes Kreuz Kopfschmerztagebuch Kopfschmerztagebuch von: Hallo, heute hast Du von uns dieses Kopfschmerztagebuch bekommen. Mit dem Ausfüllen des Tagebuches kannst Du mehr über Deine Kopfschmerzen
Deutsches Rotes Kreuz Kopfschmerztagebuch Kopfschmerztagebuch von: Hallo, heute hast Du von uns dieses Kopfschmerztagebuch bekommen. Mit dem Ausfüllen des Tagebuches kannst Du mehr über Deine Kopfschmerzen
Diese Anleitung zeigt dir, wie du eine Einladung mit Microsoft Word gestalten kannst.
 Diese Anleitung zeigt dir, wie du eine Einladung mit Microsoft Word gestalten kannst. Bevor es losgeht Wenn du mal etwas falsch machst ist das in Word eigentlich kein Problem! Den Rückgängig-Pfeil (siehe
Diese Anleitung zeigt dir, wie du eine Einladung mit Microsoft Word gestalten kannst. Bevor es losgeht Wenn du mal etwas falsch machst ist das in Word eigentlich kein Problem! Den Rückgängig-Pfeil (siehe
changenow THE PLAN Die 7 Brillen der Vergangenheit
 André Loibl s changenow THE PLAN Die 7 Brillen der Vergangenheit a Kanga Publication 2013 André Loibl www.changenow.de 1. Wo bist Du jetzt? Auf einer Skala von 1-10: Wie sehr beeinflusst Dich das Ereignis?
André Loibl s changenow THE PLAN Die 7 Brillen der Vergangenheit a Kanga Publication 2013 André Loibl www.changenow.de 1. Wo bist Du jetzt? Auf einer Skala von 1-10: Wie sehr beeinflusst Dich das Ereignis?
1 Schritt für Schritt zu Ihrem eigenen Etikett
 1 Schritt für Schritt zu Ihrem eigenen Etikett 1.1 Einleitung Wir lieben es, wenn Dinge aufeinander abgestimmt sind. Warum? Weil s einfach besser wird, wenn s wirklich passt. Deshalb gibt es von Festool
1 Schritt für Schritt zu Ihrem eigenen Etikett 1.1 Einleitung Wir lieben es, wenn Dinge aufeinander abgestimmt sind. Warum? Weil s einfach besser wird, wenn s wirklich passt. Deshalb gibt es von Festool
Spielmaterial. Hallo! Ich bin der kleine AMIGO und zeige euch, wie dieses Spiel funktioniert. Viel Spaß! von Liesbeth Bos
 Kissenschlacht_Regel.qxp:Layout 1 19.05.2010 12:00 Uhr Seite 1 Hallo! Ich bin der kleine AMIGO und zeige euch, wie dieses Spiel funktioniert. Viel Spaß! von Liesbeth Bos Spieler: 2 4 Personen Alter: ab
Kissenschlacht_Regel.qxp:Layout 1 19.05.2010 12:00 Uhr Seite 1 Hallo! Ich bin der kleine AMIGO und zeige euch, wie dieses Spiel funktioniert. Viel Spaß! von Liesbeth Bos Spieler: 2 4 Personen Alter: ab
Anleitung So klappt der Downloadschnitt
 Anleitung So klappt der Downloadschnitt Liebe Kundin, lieber Kunde, bitte nehmen Sie sich einen Augenblick Zeit um diese Anleitung zu lesen. Sie enthält nützliche Tipps und Tricks zum Thema Downloadschnitte
Anleitung So klappt der Downloadschnitt Liebe Kundin, lieber Kunde, bitte nehmen Sie sich einen Augenblick Zeit um diese Anleitung zu lesen. Sie enthält nützliche Tipps und Tricks zum Thema Downloadschnitte
Was man mit dem Computer alles machen kann
 Was man mit dem Computer alles machen kann Wie komme ich ins Internet? Wenn Sie einen Computer zu Hause haben. Wenn Sie das Internet benutzen möchten, dann brauchen Sie ein eigenes Programm dafür. Dieses
Was man mit dem Computer alles machen kann Wie komme ich ins Internet? Wenn Sie einen Computer zu Hause haben. Wenn Sie das Internet benutzen möchten, dann brauchen Sie ein eigenes Programm dafür. Dieses
Meine Lernplanung Wie lerne ich?
 Wie lerne ich? Zeitraum Was will ich erreichen? Wie? Bis wann? Kontrolle Weiteres Vorgehen 17_A_1 Wie lerne ich? Wenn du deine gesteckten Ziele nicht erreicht hast, war der gewählte Weg vielleicht nicht
Wie lerne ich? Zeitraum Was will ich erreichen? Wie? Bis wann? Kontrolle Weiteres Vorgehen 17_A_1 Wie lerne ich? Wenn du deine gesteckten Ziele nicht erreicht hast, war der gewählte Weg vielleicht nicht
BIA-Wissensreihe Teil 4. Mind Mapping Methode. Bildungsakademie Sigmaringen
 BIA-Wissensreihe Teil 4 Mind Mapping Methode Bildungsakademie Sigmaringen Inhalt Warum Mind Mapping? Für wen sind Mind Maps sinnvoll? Wie erstellt man Mind Maps? Mind Mapping Software 3 4 5 7 2 1. Warum
BIA-Wissensreihe Teil 4 Mind Mapping Methode Bildungsakademie Sigmaringen Inhalt Warum Mind Mapping? Für wen sind Mind Maps sinnvoll? Wie erstellt man Mind Maps? Mind Mapping Software 3 4 5 7 2 1. Warum
PhotoFiltre: Fotokorrektur schnell und einfach
 PhotoFiltre: Fotokorrektur schnell und einfach Mit PhotoFiltre können Sie jede Art von Fotonachbearbeitung schnell und einfach durchführen, für den Privatanwender, selbst für den anspruchsvollen das perfekte
PhotoFiltre: Fotokorrektur schnell und einfach Mit PhotoFiltre können Sie jede Art von Fotonachbearbeitung schnell und einfach durchführen, für den Privatanwender, selbst für den anspruchsvollen das perfekte
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Geld Verdienen im Internet leicht gemacht
 Geld Verdienen im Internet leicht gemacht Hallo, Sie haben sich dieses E-book wahrscheinlich herunter geladen, weil Sie gerne lernen würden wie sie im Internet Geld verdienen können, oder? Denn genau das
Geld Verdienen im Internet leicht gemacht Hallo, Sie haben sich dieses E-book wahrscheinlich herunter geladen, weil Sie gerne lernen würden wie sie im Internet Geld verdienen können, oder? Denn genau das
Mathematik VERA-8 in Bayern Testheft B: Realschule Wirtschaftsschule
 Mathematik VERA-8 in Bayern Testheft B: Realschule Wirtschaftsschule - 1 - ALLGEMEINE ANWEISUNGEN In diesem Testheft findest du eine Reihe von Aufgaben und Fragen zur Mathematik. Einige Aufgaben sind kurz,
Mathematik VERA-8 in Bayern Testheft B: Realschule Wirtschaftsschule - 1 - ALLGEMEINE ANWEISUNGEN In diesem Testheft findest du eine Reihe von Aufgaben und Fragen zur Mathematik. Einige Aufgaben sind kurz,
Wie kommt der Strom zu uns?
 Infoblatt Wie kommt der Strom zu uns? Bis Strom aus der Steckdose kommt, hat er einen weiten Weg hinter sich. Strom wird im Generator des Kraftwerkes erzeugt. Bestimmt kannst du dir vorstellen, dass hier
Infoblatt Wie kommt der Strom zu uns? Bis Strom aus der Steckdose kommt, hat er einen weiten Weg hinter sich. Strom wird im Generator des Kraftwerkes erzeugt. Bestimmt kannst du dir vorstellen, dass hier
Bilder zum Upload verkleinern
 Seite 1 von 9 Bilder zum Upload verkleinern Teil 1: Maße der Bilder verändern Um Bilder in ihren Abmessungen zu verkleinern benutze ich die Freeware Irfan View. Die Software biete zwar noch einiges mehr
Seite 1 von 9 Bilder zum Upload verkleinern Teil 1: Maße der Bilder verändern Um Bilder in ihren Abmessungen zu verkleinern benutze ich die Freeware Irfan View. Die Software biete zwar noch einiges mehr
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Einen Wiederherstellungspunktes erstellen & Rechner mit Hilfe eines Wiederherstellungspunktes zu einem früheren Zeitpunkt wieder herstellen
 Einen Wiederherstellungspunktes erstellen & Rechner mit Hilfe eines Wiederherstellungspunktes zu einem früheren Zeitpunkt wieder herstellen 1 Hier einige Links zu Dokumentationen im WEB Windows XP: http://www.verbraucher-sicher-online.de/node/18
Einen Wiederherstellungspunktes erstellen & Rechner mit Hilfe eines Wiederherstellungspunktes zu einem früheren Zeitpunkt wieder herstellen 1 Hier einige Links zu Dokumentationen im WEB Windows XP: http://www.verbraucher-sicher-online.de/node/18
Gimp Kurzanleitung. Offizielle Gimp Seite: http://www.gimp.org/
 Gimp Kurzanleitung Offizielle Gimp Seite: http://www.gimp.org/ Inhalt Seite 2 Seite 3-4 Seite 5-6 Seite 7 8 Seite 9 10 Seite 11-12 Ein Bild mit Gimp öffnen. Ein Bild mit Gimp verkleinern. Ein bearbeitetes
Gimp Kurzanleitung Offizielle Gimp Seite: http://www.gimp.org/ Inhalt Seite 2 Seite 3-4 Seite 5-6 Seite 7 8 Seite 9 10 Seite 11-12 Ein Bild mit Gimp öffnen. Ein Bild mit Gimp verkleinern. Ein bearbeitetes
mit dem TeXnicCenter von Andreas Both
 LaTeX mit dem TeXnicCenter Seite 1 von 9 mit dem TeXnicCenter von Andreas Both Diese Dokument soll den Schnelleinstieg von der Installation bis zum ersten LaTeX-Dokument in sehr kurzen (5) Schritten und
LaTeX mit dem TeXnicCenter Seite 1 von 9 mit dem TeXnicCenter von Andreas Both Diese Dokument soll den Schnelleinstieg von der Installation bis zum ersten LaTeX-Dokument in sehr kurzen (5) Schritten und
Formung einer Brustzugabe
 Formung einer Brustzugabe 1 Formung einer Brustzugabe Wenn du eine große Oberweite hast (in deutschen Größen etwa ab C-Körbchen), macht es Sinn, bei einem Oberteil zusätzliches Gestrick als Brustzugabe
Formung einer Brustzugabe 1 Formung einer Brustzugabe Wenn du eine große Oberweite hast (in deutschen Größen etwa ab C-Körbchen), macht es Sinn, bei einem Oberteil zusätzliches Gestrick als Brustzugabe
Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])
![Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])](/thumbs/29/13170670.jpg) 3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
ACDSee Pro 2. ACDSee Pro 2 Tutorials: Übertragung von Fotos (+ Datenbank) auf einen anderen Computer. Über Metadaten und die Datenbank
 Tutorials: Übertragung von Fotos (+ ) auf einen anderen Computer Export der In dieser Lektion erfahren Sie, wie Sie am effektivsten Fotos von einem Computer auf einen anderen übertragen. Wenn Sie Ihre
Tutorials: Übertragung von Fotos (+ ) auf einen anderen Computer Export der In dieser Lektion erfahren Sie, wie Sie am effektivsten Fotos von einem Computer auf einen anderen übertragen. Wenn Sie Ihre
Ein Buch entsteht. Ein langer Weg
 Ein Buch entsteht ilo 2003 Ein langer Weg Wenn ein Schriftsteller oder eine Schriftstellerin eine Geschichte schreibt, dann ist das noch ein langer Weg bis daraus ein Buch wird. Der Autor Alles fängt damit
Ein Buch entsteht ilo 2003 Ein langer Weg Wenn ein Schriftsteller oder eine Schriftstellerin eine Geschichte schreibt, dann ist das noch ein langer Weg bis daraus ein Buch wird. Der Autor Alles fängt damit
Wir lernen PowerPoint - Grundkurs Grußkarten erstellen
 Wir lernen PowerPoint - Grundkurs Grußkarten erstellen Inhalt der Anleitung Seite 1. Geburtstagskarte erstellen 2 6 2. Einladung erstellen 7 1 1. Geburtstagskarte erstellen a) Wir öffnen PowerPoint und
Wir lernen PowerPoint - Grundkurs Grußkarten erstellen Inhalt der Anleitung Seite 1. Geburtstagskarte erstellen 2 6 2. Einladung erstellen 7 1 1. Geburtstagskarte erstellen a) Wir öffnen PowerPoint und
Praktikum Schau Geometrie
 Praktikum Schau Geometrie Intuition, Erklärung, Konstruktion Teil 1 Sehen auf intuitive Weise Teil 2 Formale Perspektive mit Aufriss und Grundriss Teil 3 Ein niederländischer Maler zeigt ein unmögliches
Praktikum Schau Geometrie Intuition, Erklärung, Konstruktion Teil 1 Sehen auf intuitive Weise Teil 2 Formale Perspektive mit Aufriss und Grundriss Teil 3 Ein niederländischer Maler zeigt ein unmögliches
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sowohl die Malstreifen als auch die Neperschen Streifen können auch in anderen Stellenwertsystemen verwendet werden.
 Multiplikation Die schriftliche Multiplikation ist etwas schwieriger als die Addition. Zum einen setzt sie das kleine Einmaleins voraus, zum anderen sind die Überträge, die zu merken sind und häufig in
Multiplikation Die schriftliche Multiplikation ist etwas schwieriger als die Addition. Zum einen setzt sie das kleine Einmaleins voraus, zum anderen sind die Überträge, die zu merken sind und häufig in
ACDSee 2009 Tutorials: Rote-Augen-Korrektur
 In diesem Tutorial lernen Sie den schnellsten Weg zum Entfernen roter Augen von Ihren Fotos mit der Rote-Augen- Korrektur. Die Funktion zur Reduzierung roter Augen ist ein Untermenü des Bearbeitungsmodus.
In diesem Tutorial lernen Sie den schnellsten Weg zum Entfernen roter Augen von Ihren Fotos mit der Rote-Augen- Korrektur. Die Funktion zur Reduzierung roter Augen ist ein Untermenü des Bearbeitungsmodus.
Die Übereckperspektive mit zwei Fluchtpunkten
 Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Diagnostisches Interview zur Bruchrechnung
 Diagnostisches Interview zur Bruchrechnung (1) Tortendiagramm Zeigen Sie der Schülerin/dem Schüler das Tortendiagramm. a) Wie groß ist der Teil B des Kreises? b) Wie groß ist der Teil D des Kreises? (2)
Diagnostisches Interview zur Bruchrechnung (1) Tortendiagramm Zeigen Sie der Schülerin/dem Schüler das Tortendiagramm. a) Wie groß ist der Teil B des Kreises? b) Wie groß ist der Teil D des Kreises? (2)
Mehrere PDF-Dokumente zu einem zusammenfügen
 Mehrere PDF-Dokumente zu einem zusammenfügen Eine Funktion des Programm»PDFCreator«, welches auf allen Computer der Landesverwaltung installiert ist, ermöglicht es dir einfach und schnell mehrere Dateien
Mehrere PDF-Dokumente zu einem zusammenfügen Eine Funktion des Programm»PDFCreator«, welches auf allen Computer der Landesverwaltung installiert ist, ermöglicht es dir einfach und schnell mehrere Dateien
Freebook. Nähanleitung für eine. Ordner- Hülle
 Freebook Nähanleitung für eine Ordner- Hülle Hallo liebe Nähfreundin! Vielen Dank, dass du dich für meine Nähanleitung entschieden hast. In dieser Anleitung werde ich dir Schritt für Schritt zeigen, wie
Freebook Nähanleitung für eine Ordner- Hülle Hallo liebe Nähfreundin! Vielen Dank, dass du dich für meine Nähanleitung entschieden hast. In dieser Anleitung werde ich dir Schritt für Schritt zeigen, wie
JAHRESPRÜFUNG MATHEMATIK. 1. Klassen Kantonschule Reussbühl Luzern. 27. Mai 2014 Zeit: 13:10 14:40 (90 Minuten)
 KLASSE: NAME: VORNAME: Mögliche Punktzahl: 51 48 Pte. = Note 6 Erreichte Punktzahl: Note: JAHRESPRÜFUNG MATHEMATIK 1. Klassen Kantonschule Reussbühl Luzern 7. Mai 014 Zeit: 1:10 14:40 (90 Minuten) Allgemeines
KLASSE: NAME: VORNAME: Mögliche Punktzahl: 51 48 Pte. = Note 6 Erreichte Punktzahl: Note: JAHRESPRÜFUNG MATHEMATIK 1. Klassen Kantonschule Reussbühl Luzern 7. Mai 014 Zeit: 1:10 14:40 (90 Minuten) Allgemeines
Kulturelle Evolution 12
 3.3 Kulturelle Evolution Kulturelle Evolution Kulturelle Evolution 12 Seit die Menschen Erfindungen machen wie z.b. das Rad oder den Pflug, haben sie sich im Körperbau kaum mehr verändert. Dafür war einfach
3.3 Kulturelle Evolution Kulturelle Evolution Kulturelle Evolution 12 Seit die Menschen Erfindungen machen wie z.b. das Rad oder den Pflug, haben sie sich im Körperbau kaum mehr verändert. Dafür war einfach
Kurzanleitung. MEYTON Aufbau einer Internetverbindung. 1 Von 11
 Kurzanleitung MEYTON Aufbau einer Internetverbindung 1 Von 11 Inhaltsverzeichnis Installation eines Internetzugangs...3 Ist mein Router bereits im MEYTON Netzwerk?...3 Start des YAST Programms...4 Auswahl
Kurzanleitung MEYTON Aufbau einer Internetverbindung 1 Von 11 Inhaltsverzeichnis Installation eines Internetzugangs...3 Ist mein Router bereits im MEYTON Netzwerk?...3 Start des YAST Programms...4 Auswahl
Die Beschreibung bezieht sich auf die Version Dreamweaver 4.0. In der Version MX ist die Sitedefinition leicht geändert worden.
 In einer Website haben Seiten oft das gleiche Layout. Speziell beim Einsatz von Tabellen, in denen die Navigation auf der linken oder rechten Seite, oben oder unten eingesetzt wird. Diese Anteile der Website
In einer Website haben Seiten oft das gleiche Layout. Speziell beim Einsatz von Tabellen, in denen die Navigation auf der linken oder rechten Seite, oben oder unten eingesetzt wird. Diese Anteile der Website
Im Zeichen des Lotus Pädagogisches Material zum Schwerpunktthema alle welt 1/2010
 1-8 Im Zeichen des Lotus Pädagogisches Material zum Schwerpunktthema alle welt 1/2010 Religion Thema Schulstufe Lehrplanbezug Ziel Methoden 2. Klasse VS Themenfeld 2.3 Mit Geheimnissen leben Hinter die
1-8 Im Zeichen des Lotus Pädagogisches Material zum Schwerpunktthema alle welt 1/2010 Religion Thema Schulstufe Lehrplanbezug Ziel Methoden 2. Klasse VS Themenfeld 2.3 Mit Geheimnissen leben Hinter die
Bedienungsanleitung Albumdesigner. Neues Projekt: Bestehendes Projekt öffnen:
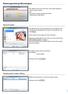 Bedienungsanleitung Albumdesigner Hier wählen Sie aus ob Sie mit einem neuen Album beginnen - Neues Projekt erstellen oder Sie arbeiten an einem bestehenden weiter - Bestehendes Projekt öffnen. Neues Projekt:
Bedienungsanleitung Albumdesigner Hier wählen Sie aus ob Sie mit einem neuen Album beginnen - Neues Projekt erstellen oder Sie arbeiten an einem bestehenden weiter - Bestehendes Projekt öffnen. Neues Projekt:
