Proseminar Komplexe Analysis 1
|
|
|
- Valentin Berg
- vor 5 Jahren
- Abrufe
Transkript
1 Proseminar Komplexe Analysis 1 Michael Kunzinger und Gerald Teschl WS215/16 Bemerkung: Die meisten Beispiele sind aus dem Buch von K. Jänich, Funktionentheorie, Springer. 1. Bereiten Sie eine Kurzpräsentation über die Polardarstellung komplexer Zahlen vor. Zeigen Sie insbesondere, wie Multiplikation, Division und Potenzen in dieser Darstellung aussehen. Zeigen Sie, dass jede komplexe Zahl z genau n verschiedene n-te Wurzeln besitzt und wie diese berechnet werden können. 2. Beweise folgende Eigenschaften des Betrags z = x 2 + y 2, z = x + iy: (a) z 1 z 2 = z 1 z 2. (b) z 1 + z 2 z 1 + z 2 (Dreiecksungleichung). 3. Was versteht man unter Konvergenz von Folgen und Reihen in C? In welchem Zusammenhang stehen diese Begriffe mit dem Betrag komplexer Zahlen bzw. mit der Konvergenz reeller Folgen und Reihen? 4. Sind folgende Reihen konvergent bzw. absolut konvergent? (a) n=1 in n. (b) n=1 1 (1+i) n. 5. Die Exponentialfunktion und die Winkelfunktionen werden in der komplexen Analysis durch die aus der Analysis bekannten Potenreihen (mit komplexem Argument) definiert. Man zeige, dass e iz = cos(z) + i sin(z) für alle z C gilt und leite daraus ab: (a) cos 2 (z) + sin 2 (z) = 1 für alle z C. (b) Re(cos(z)) =?, Im(cos(z)) =?. (c) Kosinus hat nur reelle Nullstellen.
2 PS KA 1 Kunzinger/Teschl WS15/ Man gebe an, für welche a, b R das Polynom u(x, y) = x 2 + 2axy + by 2 Realteil einer ganzen Funktion f ist, also Re(f(x+iy)) = u(x, y) gilt. Man bestimme für jedes solches (a, b) alle zulässigen holomorphen Funktionen. 7. Man beschreibe die durch e z gegebene Abbildung des Rechtecks {x+iy x 1, y π} in C. 8. Ist die komplexe Konjugation z z (komplex) differenzierbar? 9. Man zeige, dass eine holomorphe Funktion mit zusammenhängendem Definitionsbereich, die nur reelle Werte annimmt, konstant sein muss.
3 PS KA 1 Kunzinger/Teschl WS15/ Unter der Länge einer stetig differenzierbaren Kurve : [t, t 1 ] U C = R 2 versteht man bekanntlich die Zahl L() := t1 t (t) dt. Es sei f : U C eine stetige, durch eine Konstante C dem Betrag nach beschränkte Funktion, f(z) C für alle z U, dann gilt f(z)dz C L(). 11. Es sei (t) = (x(t), y(t)), t [, 1], eine geschlossene differenzierbare Kurve. Nach einem bekannten Lemma, das wir hier aber als Definition lesen wollen, ist für geschlossene Kurven F () := x dy = 1 x(t)y (t)dt der von umlaufene Flächeninhalt. Was bedeutet demnach das Kurvenintegral zdz für eine geschlossenen Kurve in C? 12. Zeigen Sie: Wenn f(z) eine Stammfunktion F (z) besitzt, dann ist F (z) = F (z ) + f(z)dz für jeden differenzierbaren Weg von z nach z. Versuchen Sie eine Stammfunktion F (z) von f(z) = 1 z zu definieren indem Sie dz F (z) = z, mit einer differenzierbaren Kurve von z = 1 bis z, setzen. Berechnen Sie F (z) für z C\(, ]. Kann es auch eine Stammfunktion auf ganz C\{} geben? Hinweis: Zur Berechnung des Integrals bieten sich Polarkoordinaten an. Setzen Sie z = re iϕ, ϕ ( π, π) und integrieren Sie zunächst entlang der reellen Achse von 1 nach r und dann entlang des Kreisbogens von r nach z.
4 PS KA 1 Kunzinger/Teschl WS15/ Es sei f(z) := (z 1 i) 2 sin(z). Man bestimme den Konvergenzradius der Potenzreihe um z =. 14. Man berechne z 1 =2 sin(z) z 4 dz. 15. Man beweise, dass in einem sternförmigen Gebiet jede holomorphe Funktion eine Stammfunktion besitzt. 16. Sei f eine ganze nichtkonstante Funktion. Man beweise, dass die Bildmenge f(c) dicht in C liegt.
5 PS KA 1 Kunzinger/Teschl WS15/ Es sei n N, und r und c seien zwei positive reelle Zahlen. Für die ganze Funktion f gelte die Abschätzung f(z) c z n für alle z C mit z r. Man zeige, dass dann f ein Polynom höchstens n-ten Grades ist. 18. Sei z eine Nullstelle einer holomorphen Funktion f. Man zeige: Genau dann kann man aus f lokal bei z die k-te Wurzel ziehen (d.h. eine in einer Umgebung von z holomorphe Funktion h mit (h(z)) k = f(z) finden), wenn k die Ordnung der Nullstelle teilt. 19. Sei U R offen in R und f : U R reell analytisch, d.h. überall in U lokal in eine Potenzreihe entwickelbar. Man zeige, dass es eine in C offene Menge U mit U R = U und eine holomorphe Funktion f : U C mit f U = f gibt. Kann man im Falle U = ( 1, 1) immer U = {z z < 1} wählen? 2. Fresnel Integrale: Man zeige, dass sin(x 2 )dx = gilt, indem man das Wegintegral R exp( z 2 )dz cos(x 2 )dx = 2π untersucht. Dabei ist R folgender geschlossener Weg: Die gerade Verbindung von nach R, der Kreisbogen von R nach Re iπ/4, die gerade Verbindung von Re iπ/4 zurück nach. (Hinweis: R e x2 dx = π kann als bekannt vorausgesetzt werden.) 4
6 PS KA 1 Kunzinger/Teschl WS15/ Man beweise, dass das Maximumsprinzip nicht nur für f(z), sondern auch für Re(f(z)) und Im(f(z)) gilt. 22. Man schließe aus dem Schwarz schen Lemma, dass eine biholomorphe, d.h. bijektiv und in beiden Richtungen holomorphe Abbildung der offenen Einheitskreisscheibe E auf sich, welche außerdem den Nullpunkt festlässt, eine Drehung sein muss. 23. Sei f : E E eine biholomorphe Abbildung der offenen Einheitskreisscheibe E. Zeige, dass f(z) = λ z a 1 az für ein a E und ein λ mit λ = 1 ist. z a (Hinweis: Zeige, dass f a (z) = 1 az die offenen Einheitskreisscheibe auf sich selbst abbildet und verwende dann Aufgabe 22.) 24. Für die folgenden Beispiele holomorpher Funktionen auf E\{} = {z < z < 1} behandle man die isolierte Singularität so: Ist die Singularität hebbar, so hebe man sie, ist sie ein Pol, bestimme man den Hauptteil, und ist sie wesentlich, so bestimme man für alle genügend kleinen ε > das Bild von {z < z < ε} unter der Funktion: a) 1 1 e z, b) e 1 sin(z) z, c). z
7 PS KA 1 Kunzinger/Teschl WS15/ Die Funktion f : G C sei meromorph. Man zeige, dass die logarithmische Ableitung von f ebenfalls meromorph ist und höchstens Pole erster Ordnung hat. Berechne den Grenzwert lim (z z ) f (z) z z f(z), z G. Es sei z eine isolierte Singularität von f(z). Man zeige, dass z kein Pol von exp(f(z)) ist. 26. Man bestimme die Laurententwicklung von f(z) := im Kreisring {z r < z < R} für (a) r = und R = 1, (b) r = 1 und R = 2, (c) r = 2 und R =. 1 z(z 1)(z 2) (Hinweis: Partialbruchzerlegung und geometrische Reihe.) 27. Man bestimme die Automorphismen der komplexen Ebene, d.h. die biholomorphen Abbildungen von C auf sich. (Hinweis: Wende für einen Automophismus f den Satz von Casorati Weierstraß auf f( 1 z ) an und benütze Aufgabe 17.) 28. Für eine Funktion f sei sowohl f(z) als auch f( 1 z ) meromorph in C. Zeige dass f(z) = p(z) q(z) mit zwei Polynomen p(z) und q(z) gilt. (Hinweis: Kann f unendlich viele Pole haben? Lokal können sich die Pole von f ja nicht häufen, aber wie sieht es mit aus? Wie kann man die Pole beheben? Sind alle endlichen Pole behoben, kann es dann noch eine wesentliche Singularität bei geben?)
8 PS KA 1 Kunzinger/Teschl WS15/ Sei G C\{} ein einfach zusammenhängendes Gebiet. Man zeige, dass es eine holomorphe Funktion f : G C mit e f(z) = z für alle z G gibt und dass dann {f +2πik k Z} die Menge aller holomorphen Funktionen auf G mit dieser Eigenschaft ist ( Zweige des Logarithmus auf G). 3. Man formuliere und beweise eine analoge Aussage über die holomorphen Funktionen f mit e f(z) = g(z) für eine gegebene nirgends verschwindende holomorphe Funktion g auf G. 31. Für gegebene n, k Z und < r 1 bestimme man die Umlaufzahl der durch (t) := e int + re ikt definierten geschlossenen Kurve (t) : [, 2π] C\{} um den Nullpunkt. (Hinweis: Man defomiere stetig wobei Anfangs- und Endpunkt nicht fest bleiben müessen, solange nur die Kurve geschlossen bleibt.) 32. Sei : [t, t 1 ] C\{} eine geschlossene, an einem Punkt der positiven reellen Halbachse beginnende Kurve. Für k N werde die Auswahl eines Wertes k (t) für die k-te Wurzel von (t) durch k (t ) > und die Stetigkeit von k : [t, t 1 ] C festgelegt. Man berechne das dementsprechend aufgefasste Integral k zdz k aus k, (t ) und der Umlaufzahl ν (). (Hinweis: z = exp( 1 k log( z ) + arg(z)). Wie sieht eine lokale Stammfunktion aus?) i k
9 PS KA 1 Kunzinger/Teschl WS15/ Welche Werte kann das Integral dz 1 + z 2 für geschlossene Kurven in C\{±i} annehmen? 34. Man berechne mit Hilfe des Residuenkalküls: (a): (c): x 2 x 4 + 6x dx x sin(x) x 2 + a 2 dx, a > (b): cos(x) x 2 + a 2 dx, a >
10 PS KA 1 Kunzinger/Teschl WS15/ Man berechne mit Hilfe des Residuenkalküls: (a): (c): π/2 sin(x) dx (b): x dx 1 + sin 2 (x) dx x 1 + x 2 dx 36. Für rationale Funktionen R(z) ohne Pole auf der abgeschlossenen positiven Halbgeraden R + und mit einer mindestens doppelten Nullstelle bei leite man eine Residuenformel für R(x)dx her, indem man den Residuensatz auf R(z) ln(z) in der positiv geschlitzten Ebene geeignet anwendet.
11 PS KA 1 Kunzinger/Teschl WS15/ Seien ω 1, ω 2 C reell-linear unabhängig und f eine auf C meromorphe nichtkonstante doppelt periodische Funktion mit den Perioden ω 1 und ω 2, d.h. mit der Eigenschaft f(z + ω 1 ) = f(z + ω 2 ) = f(z) für alle z. Man zeige, dass f auf dem Fundamentalbereich F := {λ 1 ω 1 + λ 2 ω 2 λ i < 1} ebensoviele Polstellen wie Nullstellen hat (gezählt jeweils mit Vielfachheit). (Hinweis: Integrieren Sie f (z)/f(z) über den Rand des Fundamentalbereichs.) 38. Sei P (z) := z n + a n 1 z n a. Man beweise: Gilt P (z) 1 für alle z mit z = 1, so folgt P (z) = z n. (Hinweis: Q t (z) = z n tp (z) hat für t < 1 alle Nullstellen im Einheitskreis und es wäre doch recht sonderbar wenn für t 1 eine davon nach springen könnte. Um das auszuschließen, wähle man einen größeren Kreis auf dem Q 1 (z) nicht verschwindet und berufe sich auf die stetige Abhängigkeit des Null- und Polstellen zählenden Integrals von t.) 39. Es sei G ein beschränktes Gebiet, und G bezeichne dessen abgeschlossene Hülle. Auf G sei eine Folge (f n ) n 1 stetiger, auf G sogar holomorpher Funktionen gegeben, welche auf G\G gleichmäßig konvergiert. Man zeige, dass dann die Folge auf ganz G gleichmäßig konvergiert. (Hinweis: Maximumsprinzip.)
12 PS KA 1 Kunzinger/Teschl WS15/ Man zeige, dass für Re(z) > 1 durch ζ(z) := eine holomorphe Funktion (die Riemann sche ζ-funktion) gegeben ist und gebe eine Reihendarstellung für ζ (z) an. n=1 41. Aus der Partialbruchzerlegung für π 2 sin(πz) 2 1 n z π cot(πz) = 1 z + in kompakter Konvergenz auf C \ Z. 42. Man zeige sin(πz) = e g(z) z n=1 leite man her, dass 2z z 2 n 2 (1 z2 n 2 ) mit einer ganzen Funktion g(z). Um g(z) zu bestimmen betrachte die logarithmische Ableitung und vergleiche mit Aufgabe 41. Für die dann noch fehlende Konstante betrachte die Ableitung bei. n=1 (Hinweis: Für den ersten Teil verwende Aufgabe 3.)
Proseminar Komplexe Analysis 1
 Proseminar Komplexe Analysis 1 Bernhard Lamel und Gerald Teschl SS27 Bemerkung: Die meisten Beispiel sind aus dem Buch von K. Jähnich, Funktionentheorie, Springer. 1. Beweise folgende Eigenschaften des
Proseminar Komplexe Analysis 1 Bernhard Lamel und Gerald Teschl SS27 Bemerkung: Die meisten Beispiel sind aus dem Buch von K. Jähnich, Funktionentheorie, Springer. 1. Beweise folgende Eigenschaften des
4 Anwendungen des Cauchyschen Integralsatzes
 4 Anwendungen des Cauchyschen Integralsatzes Satz 4. (Cauchysche Integralformel) Es sei f : U C komplex differenzierbar und a {z C; z z 0 r} U. Dann gilt f(a) = z z 0 =r z a dz. a z 0 9 Beweis. Aus dem
4 Anwendungen des Cauchyschen Integralsatzes Satz 4. (Cauchysche Integralformel) Es sei f : U C komplex differenzierbar und a {z C; z z 0 r} U. Dann gilt f(a) = z z 0 =r z a dz. a z 0 9 Beweis. Aus dem
Themen Potenzreihen Laurentreihen Residuenkalkül
 5 Reihenentwicklungen und der Residuensatz Themen Potenzreihen Laurentreihen Residuenkalkül folgen 5.1 Potenzreihen und Taylorreihen Satz Sei und sei f(z) = a n (z z 0 ) n, a n, n=0 R = 1 lim sup n a n,
5 Reihenentwicklungen und der Residuensatz Themen Potenzreihen Laurentreihen Residuenkalkül folgen 5.1 Potenzreihen und Taylorreihen Satz Sei und sei f(z) = a n (z z 0 ) n, a n, n=0 R = 1 lim sup n a n,
D-MATH Funktionentheorie HS 2018 Prof. Michael Struwe. Lösungen Serie 8. Laurentreihen, isolierte Singularitäten, meromorphe Funktionen
 D-MATH Funktionentheorie HS 208 Prof. Michael Struwe Lösungen Serie 8 Laurentreihen, isolierte Singularitäten, meromorphe Funktionen. Bestimmen Sie die Laurentreihenentwicklung der folgenden Funktionen:
D-MATH Funktionentheorie HS 208 Prof. Michael Struwe Lösungen Serie 8 Laurentreihen, isolierte Singularitäten, meromorphe Funktionen. Bestimmen Sie die Laurentreihenentwicklung der folgenden Funktionen:
Funktionentheorie, Woche 11. Funktionen mit Singularitäten Meromorphe Funktionen
 Funktionentheorie, Woche Funktionen mit Singularitäten. Meromorphe Funktionen Definition. Sei U C offen und sei f : U gilt, nennt man f meromorph auf U: Ĉ eine Funktion. Wenn folgendes. P = f ( hat keine
Funktionentheorie, Woche Funktionen mit Singularitäten. Meromorphe Funktionen Definition. Sei U C offen und sei f : U gilt, nennt man f meromorph auf U: Ĉ eine Funktion. Wenn folgendes. P = f ( hat keine
c r Addiert man nun beide Reihendarstellungen, so folgt f (ζ) Nach dem Cauchyschen Integralsatz gilt dann auch
 Residuen V Beweis Einsetzen in das Kurvenintegral über c r ergibt demnach f (ζ) 2πi ζ z dζ = f (ζ) 2πi (ζ z 0 ) c r k= c r k+ dζ Addiert man nun beide Reihendarstellungen, so folgt a k (z z 0 ) k, r z
Residuen V Beweis Einsetzen in das Kurvenintegral über c r ergibt demnach f (ζ) 2πi ζ z dζ = f (ζ) 2πi (ζ z 0 ) c r k= c r k+ dζ Addiert man nun beide Reihendarstellungen, so folgt a k (z z 0 ) k, r z
Komplexe Funktionen für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg SoSe 214 Dr K Rothe Komplexe Funktionen für Studierende der Ingenieurwissenschaften Aufgaben und Theoriehinweise zu Blatt 6 Komplexe Funktionen, K Rothe,
Fachbereich Mathematik der Universität Hamburg SoSe 214 Dr K Rothe Komplexe Funktionen für Studierende der Ingenieurwissenschaften Aufgaben und Theoriehinweise zu Blatt 6 Komplexe Funktionen, K Rothe,
6.7 Isolierte Singularitäten
 6.7 Isolierte Singularitäten Definition: Eine analytische Funktion f hat in einem Punkt a C eine isolierte Singularität, falls f in einem Kreisring B r (a) \ {a} = {z C : 0 < z a < r} für r > 0, definiert
6.7 Isolierte Singularitäten Definition: Eine analytische Funktion f hat in einem Punkt a C eine isolierte Singularität, falls f in einem Kreisring B r (a) \ {a} = {z C : 0 < z a < r} für r > 0, definiert
Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi
![Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi](/thumbs/92/110521610.jpg) Funktionentheorie, Woche 7 Eigenschaften holomorpher Funktionen 7.1 Ganze Funktionen Definition 7.1 Eine Funktion f : C C, die holomorph ist auf C, nennt man eine ganze Funktion. Bemerkung 7.1.1 Als Folge
Funktionentheorie, Woche 7 Eigenschaften holomorpher Funktionen 7.1 Ganze Funktionen Definition 7.1 Eine Funktion f : C C, die holomorph ist auf C, nennt man eine ganze Funktion. Bemerkung 7.1.1 Als Folge
Lösungen zur Klausur Funktionentheorie I SS 2005
 Universität Karlsruhe 29 September 25 Mathematisches Institut I Prof Dr M von Renteln Dr C Kaiser Aufgabe en zur Klausur Funktionentheorie I SS 25 Sei S die Möbiustransformation, die durch S(z) = i i z
Universität Karlsruhe 29 September 25 Mathematisches Institut I Prof Dr M von Renteln Dr C Kaiser Aufgabe en zur Klausur Funktionentheorie I SS 25 Sei S die Möbiustransformation, die durch S(z) = i i z
Meromorphe Funktionen
 Kapitel Meromorphe Funktionen Der Satz von Mittag-Leffler Zur Erinnerung: Die holomorphe Funktion f habe in z 0 C eine isolierte Singularität. Liegt eine Polstelle vor, so gibt es eine offene Umgebung
Kapitel Meromorphe Funktionen Der Satz von Mittag-Leffler Zur Erinnerung: Die holomorphe Funktion f habe in z 0 C eine isolierte Singularität. Liegt eine Polstelle vor, so gibt es eine offene Umgebung
Funktionentheorie I. M. Griesemer
 Funktionentheorie I M. Griesemer Übersicht der wichtigsten Definitionen und Sätze der Vorlesung Funktionentheorie I, SS 2001, Fachbereich Mathematik, Johannes Gutenberg - Universität Mainz. Inhalt der
Funktionentheorie I M. Griesemer Übersicht der wichtigsten Definitionen und Sätze der Vorlesung Funktionentheorie I, SS 2001, Fachbereich Mathematik, Johannes Gutenberg - Universität Mainz. Inhalt der
4 Isolierte Singularitäten und Laurentreihen
 35 4 Isolierte Singularitäten und Laurentreihen Wir beginnen mit einer lokalen Beschreibung der Nullstellen holomorpher Funktionen. 4. Lokale Beschreibung von Nullstellen. Sei U C offen, f : U C holomorph
35 4 Isolierte Singularitäten und Laurentreihen Wir beginnen mit einer lokalen Beschreibung der Nullstellen holomorpher Funktionen. 4. Lokale Beschreibung von Nullstellen. Sei U C offen, f : U C holomorph
5.1 Anwendung auf die Berechnung uneigentlicher
 Kapitel 5 Anwendungen des Residuenkalküls Wie sich am Ende des vorigen Kapitels in Beispiel 4.17 bereits angedeutet hat, bietet der Residuenkalkül ein mächtiges Werkzeug, um uneigentliche Integrale mit
Kapitel 5 Anwendungen des Residuenkalküls Wie sich am Ende des vorigen Kapitels in Beispiel 4.17 bereits angedeutet hat, bietet der Residuenkalkül ein mächtiges Werkzeug, um uneigentliche Integrale mit
2. Klausur zur Funktionentheorie SS 2009
 Aufgabe : Finden Sie ein Beispiel für eine meromorphe Funktion f M(C), die auf den Kreisringen A 0, (0) und A,2 (0) unterschiedliche Laurentreihenentwicklungen besitzt. Beweisen Sie, dass Ihr Beispiel
Aufgabe : Finden Sie ein Beispiel für eine meromorphe Funktion f M(C), die auf den Kreisringen A 0, (0) und A,2 (0) unterschiedliche Laurentreihenentwicklungen besitzt. Beweisen Sie, dass Ihr Beispiel
Ferienkurs Analysis 3 - Funktionentheorie
 Ferienkurs Analysis 3 - Funktionentheorie Ralitsa Bozhanova, Max v. Vopelius 12.08.2009 1 Grundbegriffe und Differenzierbarkeit 1.1 R-lineare und C-lineare Abbildungen C C Da C sowohl VR über R als auch
Ferienkurs Analysis 3 - Funktionentheorie Ralitsa Bozhanova, Max v. Vopelius 12.08.2009 1 Grundbegriffe und Differenzierbarkeit 1.1 R-lineare und C-lineare Abbildungen C C Da C sowohl VR über R als auch
23 Laurentreihen und Residuen
 23 Laurentreihen und Residuen 23. Laurentreihen Ist eine Funktion f in einem Punkt z nicht holomorph (oder nicht einmal definiert), so läßt sich f nicht durch eine Potenzreihe mit Entwicklungspunkt z darstellen.
23 Laurentreihen und Residuen 23. Laurentreihen Ist eine Funktion f in einem Punkt z nicht holomorph (oder nicht einmal definiert), so läßt sich f nicht durch eine Potenzreihe mit Entwicklungspunkt z darstellen.
D-MATH Funktionentheorie HS 2018 Prof. Michael Struwe. Lösungen Serie 5. Korollare der Integralformel von Cauchy
 D-MATH Funktionentheorie HS 08 Prof. Michael Struwe Lösungen Serie 5 Korollare der Integralformel von Cauchy. (a) Berechnen Sie für folgende Funktionen die Taylorreihe bei z 0 und bestimmen Sie den Konvergenzradius.
D-MATH Funktionentheorie HS 08 Prof. Michael Struwe Lösungen Serie 5 Korollare der Integralformel von Cauchy. (a) Berechnen Sie für folgende Funktionen die Taylorreihe bei z 0 und bestimmen Sie den Konvergenzradius.
Übungen zur Vorlesung Funktionentheorie Sommersemester Musterlösung zu Blatt 10. f(z) f(z) dz
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Musterlösung zu Blatt 0 Aufgabe. Berechnen Sie
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Musterlösung zu Blatt 0 Aufgabe. Berechnen Sie
10. Isolierte Singularitäten
 0. Isolierte Singularitäten 57 0. Isolierte Singularitäten Der wichtigste Spezialfall von Laurent-Reihen (und in der Tat auch der, den wir ab jetzt nur noch betrachten werden) ist der, bei dem der innere
0. Isolierte Singularitäten 57 0. Isolierte Singularitäten Der wichtigste Spezialfall von Laurent-Reihen (und in der Tat auch der, den wir ab jetzt nur noch betrachten werden) ist der, bei dem der innere
Übungen zur Funktionentheorie
 Mathematisches Institut SS 29 Universität München Prof. Dr. M. Schottenloher C. Paleani M. Schwingenheuer A. Stadelmaier Übungen zur Funktionentheorie Lösungen zu Übungsblatt. Sei fz) = z ) z 2) 2 eine
Mathematisches Institut SS 29 Universität München Prof. Dr. M. Schottenloher C. Paleani M. Schwingenheuer A. Stadelmaier Übungen zur Funktionentheorie Lösungen zu Übungsblatt. Sei fz) = z ) z 2) 2 eine
3 Meromorphe Funktionen und der Residuenkalkül
 $Id: mero.tex,v 1.3 2016/06/22 16:12:36 hk Exp $ 3 Meromorphe Funktionen und der Residuenkalkül 3.3 Hauptteile und Residuen Am Ende der letzten Sitzung hatten wir die Laurententwicklung einer holomorphen
$Id: mero.tex,v 1.3 2016/06/22 16:12:36 hk Exp $ 3 Meromorphe Funktionen und der Residuenkalkül 3.3 Hauptteile und Residuen Am Ende der letzten Sitzung hatten wir die Laurententwicklung einer holomorphen
Höhere Mathematik II für die Fachrichtung Physik. Lösungsvorschläge zum 11. Übungsblatt
 Institut für Analysis SS17 PD Dr. Peer Christian Kunstmann 7.7.17 Dipl.-Math. Leonid Chaichenets, Johanna Richter, M.Sc. Tobias Ried, M.Sc., Tobias Schmid, M.Sc. Höhere Mathematik II für die Fachrichtung
Institut für Analysis SS17 PD Dr. Peer Christian Kunstmann 7.7.17 Dipl.-Math. Leonid Chaichenets, Johanna Richter, M.Sc. Tobias Ried, M.Sc., Tobias Schmid, M.Sc. Höhere Mathematik II für die Fachrichtung
3.4 Analytische Fortsetzung
 3.4 Analytische Fortsetzung 3.4. Analytische Fortsetzung 49 Es kann vorkommen, dass eine holomorphe Funktion f, definiert durch eine Potenzreihe um den Punkt z 0 mit Konvergenzradius R, über den Rand der
3.4 Analytische Fortsetzung 3.4. Analytische Fortsetzung 49 Es kann vorkommen, dass eine holomorphe Funktion f, definiert durch eine Potenzreihe um den Punkt z 0 mit Konvergenzradius R, über den Rand der
Übungen zur Vorlesung Funktionentheorie Sommersemester Klausurvorbereitungsblatt Lösungsvorschläge
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Dr. Tobias Mai M.Sc. Felix Leid Übungen zur Vorlesung Funktionentheorie Sommersemester 7 Klausurvorbereitungsblatt Lösungsvorschläge (5) Bestimmen
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Dr. Tobias Mai M.Sc. Felix Leid Übungen zur Vorlesung Funktionentheorie Sommersemester 7 Klausurvorbereitungsblatt Lösungsvorschläge (5) Bestimmen
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript
 Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
Prüfungsvorbereitungskurs Höhere Mathematik 3
 Prüfungsvorbereitungskurs Höhere Mathematik 3 Funktionentheorie Marco Boßle Jörg Hörner Mathematik Online Frühjahr 20 PV-Kurs HM 3 Funktionentheorie - Zusammenfassung Grundlagen Komplexe Funktion f (z)
Prüfungsvorbereitungskurs Höhere Mathematik 3 Funktionentheorie Marco Boßle Jörg Hörner Mathematik Online Frühjahr 20 PV-Kurs HM 3 Funktionentheorie - Zusammenfassung Grundlagen Komplexe Funktion f (z)
Einige Standard-Aufgabentypen der Funktionentheorie I
 Matthias Stemmler SS 6 stemmler@mathematik.uni-marburg.de Einige Standard-Aufgabentypen der Funktionentheorie I I. Untersuchung von Funktionen auf komplexe Differenzierbarkeit/Holomorphie gegeben: gesucht:
Matthias Stemmler SS 6 stemmler@mathematik.uni-marburg.de Einige Standard-Aufgabentypen der Funktionentheorie I I. Untersuchung von Funktionen auf komplexe Differenzierbarkeit/Holomorphie gegeben: gesucht:
Mathematik III für Physiker. Vorlesung
 Mathematik III für Physiker Wintersemester /3 Vorlesung..3 Satz 6 (iduensatz) Sei f holomorph in G := C \ {z,..., z N } und G ein geschlossener, stückweise stetig dierenzierbarer Weg. Dann gilt f(ξ)dξ
Mathematik III für Physiker Wintersemester /3 Vorlesung..3 Satz 6 (iduensatz) Sei f holomorph in G := C \ {z,..., z N } und G ein geschlossener, stückweise stetig dierenzierbarer Weg. Dann gilt f(ξ)dξ
10 Logarithmus- und Potenzfunktion
 4 Logarithmus- und Potenzfunktion. Satz: Sei G einfach zusammenhängend, f H(G) und z G. Dann existiert genau eine Stammfunktion F von f mit F(z ) =. Für z G sei γ z ein beliebiger Integrationsweg in G,
4 Logarithmus- und Potenzfunktion. Satz: Sei G einfach zusammenhängend, f H(G) und z G. Dann existiert genau eine Stammfunktion F von f mit F(z ) =. Für z G sei γ z ein beliebiger Integrationsweg in G,
Übungen zur Vorlesung Funktionentheorie Sommersemester Lösungshinweise zum Klausurvorbereitungsblatt. (z) i f. 2xe (x2 +y 2) i2ye (x2 +y 2 ) 2
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Lösungshinweise zum Klausurvorbereitungsblatt (3
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Lösungshinweise zum Klausurvorbereitungsblatt (3
AUFGABEN ZUR FUNKTIONENTHEORIE. von. Prof. Dr. H.-W. Burmann
 AUFGABEN ZUR FUNKTIONENTHEORIE von Prof. Dr. H.-W. Burmann Bei den folgenden Aufgaben handelt es sich um Reste, die bei der Erstellung der Aufgabenblätter übriggeblieben sind. Der Schwierigkeitsgrad der
AUFGABEN ZUR FUNKTIONENTHEORIE von Prof. Dr. H.-W. Burmann Bei den folgenden Aufgaben handelt es sich um Reste, die bei der Erstellung der Aufgabenblätter übriggeblieben sind. Der Schwierigkeitsgrad der
Höhere Mathematik III WS 05/06 Lösungshinweis Aufgabe G 81 Blatt 12
 Höhere Mathematik III WS 5/6 Lösungshinweis Aufgabe G 8 Blatt Rechenweg : Für das komplexe Wegintegral über : t z(t, t [a, b] gilt f(z dz = b a f ( z(t z (t dt. Rechenweg : Ist f stetig differenzierbar
Höhere Mathematik III WS 5/6 Lösungshinweis Aufgabe G 8 Blatt Rechenweg : Für das komplexe Wegintegral über : t z(t, t [a, b] gilt f(z dz = b a f ( z(t z (t dt. Rechenweg : Ist f stetig differenzierbar
6.1 Holomorphe Funktionen und Potenzreihen. n=0 α n (z z 0 ) n mit Konvergenzradius größer oder gleich r existiert und
 Funktionentheorie, Woche 6 Analytische Funktionen 6. Holomorphe Funktionen und Potenzreihen Definition 6. Eine Funktion f : U C C nennt man analytisch in z 0 U, wenn es r > 0 gibt mit B r (z 0 ) U derart,
Funktionentheorie, Woche 6 Analytische Funktionen 6. Holomorphe Funktionen und Potenzreihen Definition 6. Eine Funktion f : U C C nennt man analytisch in z 0 U, wenn es r > 0 gibt mit B r (z 0 ) U derart,
9 Ergänzungen zur Funktionentheorie
 9 Ergänzungen zur Funktionentheorie 9. Herausziehen von Polen und Nullstellen Das folgende Lemma hatten wir an zahlreichen Stellen verwendet, ohne es jemals streng bewiesen zu haben. Lemma 9. Die Funktion
9 Ergänzungen zur Funktionentheorie 9. Herausziehen von Polen und Nullstellen Das folgende Lemma hatten wir an zahlreichen Stellen verwendet, ohne es jemals streng bewiesen zu haben. Lemma 9. Die Funktion
3 Der Riemannsche Abbildungssatz
 24 Biholomorphe Abbildungen 3 Der Riemannsche Abbildungssatz Definition. Sei G C ein Gebiet, G. Eine holomorphe oder meromorphe Funktion f auf U \ { } heißt holomorph (bzw. meromorph) im Unendlichen, falls
24 Biholomorphe Abbildungen 3 Der Riemannsche Abbildungssatz Definition. Sei G C ein Gebiet, G. Eine holomorphe oder meromorphe Funktion f auf U \ { } heißt holomorph (bzw. meromorph) im Unendlichen, falls
2 Der Weierstraßsche Produktsatz
 4 Kapitel Meromorphe Funktionen Der Weierstraßsche Produktsatz Unser nächstes Problem soll sein, zu einer vorgegebenen Menge von Punkten eine holomorphe Funktion zu suchen, die genau in den Punkten Nullstellen
4 Kapitel Meromorphe Funktionen Der Weierstraßsche Produktsatz Unser nächstes Problem soll sein, zu einer vorgegebenen Menge von Punkten eine holomorphe Funktion zu suchen, die genau in den Punkten Nullstellen
X. Funktionentheorie. Übersicht über den Inhalt von Kapitel X: 57. Holomorphe Funktionen. 58. Cauchy-Formeln und Anwendungen
 56 Integralsätze im Raum 273 X. Funktionentheorie Übersicht über den Inhalt von Kapitel X: 57. Holomorphe Funktionen 58. Cauchy-Formeln und Anwendungen 59. Laurent-Entwicklungen und Residuensatz 274 X.
56 Integralsätze im Raum 273 X. Funktionentheorie Übersicht über den Inhalt von Kapitel X: 57. Holomorphe Funktionen 58. Cauchy-Formeln und Anwendungen 59. Laurent-Entwicklungen und Residuensatz 274 X.
Kapitel 24. Entwicklungen holomorpher Funktionen Taylor-Reihen (Potenzreihen und holomorphe Funktionen;
 Kapitel 24 Entwicklungen holomorpher Funktionen Reihenentwicklungen spielen in der Funktionentheorie eine ganz besodere Rolle. Im Reellen wurden Potenzreihen in Kapitel 5.2 besprochen, das komplexe Gegenstück
Kapitel 24 Entwicklungen holomorpher Funktionen Reihenentwicklungen spielen in der Funktionentheorie eine ganz besodere Rolle. Im Reellen wurden Potenzreihen in Kapitel 5.2 besprochen, das komplexe Gegenstück
f heißt komplex differenzierbar oder holomorph auf Ω, wenn f in allen z Ω komplex differenzierbar
 2 Komplexe Analysis n diesem Abschnitt wollen wir einen kurzen Ausflug in die komplexe Analysis die sogenannte Funktionentheorie unternehmen, und zwar wollen wir jetzt komplexe Kurvenintegrale betrachten.
2 Komplexe Analysis n diesem Abschnitt wollen wir einen kurzen Ausflug in die komplexe Analysis die sogenannte Funktionentheorie unternehmen, und zwar wollen wir jetzt komplexe Kurvenintegrale betrachten.
Komplexe Analysis D-ITET. Serie 8
 Dr. T. Bühler M. Wellershoff Frühlingssemester 206 Komplexe Analysis D-ITET Serie 8 ETH Zürich D-MATH Aufgabe 8. Umlaufzahlen Berechnen - Teil I Das Ziel der Aufgabe ist es die Umlaufzahlen in vier Zyklen
Dr. T. Bühler M. Wellershoff Frühlingssemester 206 Komplexe Analysis D-ITET Serie 8 ETH Zürich D-MATH Aufgabe 8. Umlaufzahlen Berechnen - Teil I Das Ziel der Aufgabe ist es die Umlaufzahlen in vier Zyklen
Etwa mehr zu Exponential- und Logarithmusfunktion
 Etwa mehr zu Exponential- und Logarithmusfunktion Will man einen Logarithmus definieren, so liegt es nahe, diesen als Umkehrfunktion zur Exponentialfunktion zu definieren. Solch eine kann es aber nicht
Etwa mehr zu Exponential- und Logarithmusfunktion Will man einen Logarithmus definieren, so liegt es nahe, diesen als Umkehrfunktion zur Exponentialfunktion zu definieren. Solch eine kann es aber nicht
3 Windungszahlen und Cauchysche Integralformeln
 3 3 Windungszahlen und Cauchysche Integralformeln 3. Definition: Sei geschlossener Integrationsweg oder Zyklus mit z 0 C \ Sp. Dann heißt n(, z 0 ) := dz z z 0 Windungszahl (oder: Index, Umlaufszahl) von
3 3 Windungszahlen und Cauchysche Integralformeln 3. Definition: Sei geschlossener Integrationsweg oder Zyklus mit z 0 C \ Sp. Dann heißt n(, z 0 ) := dz z z 0 Windungszahl (oder: Index, Umlaufszahl) von
Kapitel 7. Funktionentheorie. 7.1 Holomorphe und harmonische Funktionen. 1. Definitionen
 Kapitel 7 Funktionentheorie In diesem Kapitel geht es meistens um Funktionen, die auf einem Gebiet G C definiert sind und komplexe Werte annehmen. Nach Lust, Laune und Bedarf wird C mit R identifiziert,
Kapitel 7 Funktionentheorie In diesem Kapitel geht es meistens um Funktionen, die auf einem Gebiet G C definiert sind und komplexe Werte annehmen. Nach Lust, Laune und Bedarf wird C mit R identifiziert,
Lösungskizze zu Übungsblatt 2 (Funktionentheorie und gewöhnliche Differentialgleichungen für Lehramt Gymnasium)
 Mathematisches Institut der Universität München skizze zu Übungsblatt 2 (Funktionentheorie und gewöhnliche Differentialgleichungen für Lehramt Gymnasium) Aufgabe 166 (1 Punkte) Berechnen Sie in den folgenden
Mathematisches Institut der Universität München skizze zu Übungsblatt 2 (Funktionentheorie und gewöhnliche Differentialgleichungen für Lehramt Gymnasium) Aufgabe 166 (1 Punkte) Berechnen Sie in den folgenden
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 3 - Übungen Funktionentheorie - Musterlösung
 Ferienkurs Analysis 3 - Übungen Funktionentheorie - Musterlösung Ralitsa Bozhanova, Ma v. Vopelius.8.9 Differenzierbarkeit (a Sei A (a ij i,j, R. Zeigen Sie, dass die von A durch die Matrimultiplikation
Ferienkurs Analysis 3 - Übungen Funktionentheorie - Musterlösung Ralitsa Bozhanova, Ma v. Vopelius.8.9 Differenzierbarkeit (a Sei A (a ij i,j, R. Zeigen Sie, dass die von A durch die Matrimultiplikation
H.J. Oberle Komplexe Funktionen SoSe Residuensatz
 H.J. Oberle Komplexe Funktionen SoSe 2013 Partialbruch-Zerlegung. 10. Residuensatz Wir setzen unsere Untersuchung der isolierten Singularitäten einer holomorphen Funktion mit einer Methode fort, die komplexe
H.J. Oberle Komplexe Funktionen SoSe 2013 Partialbruch-Zerlegung. 10. Residuensatz Wir setzen unsere Untersuchung der isolierten Singularitäten einer holomorphen Funktion mit einer Methode fort, die komplexe
Funktionentheorie - Zusammenfassung
 Funktionentheorie - Zusammenfassung Diese Zusammenfassung erhebt keinen Anspruch auf Vollständigkeit oder Korrektheit. Solltet ihr Fehler finden oder Ergänzungen haben, teilt sie mir bitte mit: richard.gebauer@student.kit.edu
Funktionentheorie - Zusammenfassung Diese Zusammenfassung erhebt keinen Anspruch auf Vollständigkeit oder Korrektheit. Solltet ihr Fehler finden oder Ergänzungen haben, teilt sie mir bitte mit: richard.gebauer@student.kit.edu
ÜBUNGSBEISPIELE ZUR KOMPLEXEN ANALYSIS. Komplexe Zahlen. (x, y) + (u, v) := (x + u, y + v) (x, y) (u, v) := (xu yv, xv + yu)
 ÜBUNGSBEISPIELE ZUR KOMPLEXEN ANALYSIS ARMIN RAINER Sommersemester 05 Komplexe Zahlen Sei z = i und w = 3 + 4i. Berechne: (a) z + w, zw, z w, w z, z 3, w. (b) z, z, w, w, z, w. Zeige, dass R mit der Addition
ÜBUNGSBEISPIELE ZUR KOMPLEXEN ANALYSIS ARMIN RAINER Sommersemester 05 Komplexe Zahlen Sei z = i und w = 3 + 4i. Berechne: (a) z + w, zw, z w, w z, z 3, w. (b) z, z, w, w, z, w. Zeige, dass R mit der Addition
Musterlösung zur Serie 11
 D-MATH, D-PHYS Funktionentheorie HS 203 Prof. J. Teichmann Musterlösung zur Serie. (a) Die Identitätsfunktion ϕ : Ω C, ϕ(z) = z erfüllt die Bedingungen von Satz 4.7, weshalb es eine holomorphe Funktion
D-MATH, D-PHYS Funktionentheorie HS 203 Prof. J. Teichmann Musterlösung zur Serie. (a) Die Identitätsfunktion ϕ : Ω C, ϕ(z) = z erfüllt die Bedingungen von Satz 4.7, weshalb es eine holomorphe Funktion
Kapitel 4. Der globale Cauchysche Integralsatz
 Kapitel 4 Der globale Cauchysche Integralsatz Die Ergebnisse, die wir im vorigen Kapitel gewonnen haben, leben in der Regel davon, dass über einfach geschlossene Kurven integriert wird. Wie sich die Aussagen
Kapitel 4 Der globale Cauchysche Integralsatz Die Ergebnisse, die wir im vorigen Kapitel gewonnen haben, leben in der Regel davon, dass über einfach geschlossene Kurven integriert wird. Wie sich die Aussagen
1. Übungsblatt zur Funktionentheorie I
 Hannover, den 9. April 24. Übungsblatt zur Funktionentheorie I Abgabe am 26./27. April 24 vor den Stundenübungen Leider können nur die mit Punkten versehenen Aufgaben korrigiert werden. Aufgabe (2,3,5
Hannover, den 9. April 24. Übungsblatt zur Funktionentheorie I Abgabe am 26./27. April 24 vor den Stundenübungen Leider können nur die mit Punkten versehenen Aufgaben korrigiert werden. Aufgabe (2,3,5
Lösungen zum 11. Übungsblatt Funktionentheorie I
 Universität Karlsruhe SS 2005 Mathematisches Institut I Prof. Dr. M. von Renteln Dr. C. Kaiser Lösungen zum 11. Übungsblatt Funktionentheorie I Aufgabe 11.1 a) Nach dem Maximumprinzip nimmt die Funktion
Universität Karlsruhe SS 2005 Mathematisches Institut I Prof. Dr. M. von Renteln Dr. C. Kaiser Lösungen zum 11. Übungsblatt Funktionentheorie I Aufgabe 11.1 a) Nach dem Maximumprinzip nimmt die Funktion
28: Holomorphe Funktionen, Potenzreihen und Laurentreihen
 Einleitung 28: Holomorphe Funktionen, Potenzreihen und Laurentreihen 28.1 Einleitung Wir wissen bereits, dass eine holomorphe Funktion f : M C unendlich oft komplex differenzierbar ist. Für jedes z 0 M
Einleitung 28: Holomorphe Funktionen, Potenzreihen und Laurentreihen 28.1 Einleitung Wir wissen bereits, dass eine holomorphe Funktion f : M C unendlich oft komplex differenzierbar ist. Für jedes z 0 M
Residuen II. Residuen III. Beispiel. Beispiel. f (z) = 1 + z 2. gilt nach 2) , Res (f ; i) = Res (f ; i) = 1 = 1. Die Funktion
 Residuen II Komplexe Partialbruchzerlegung, Residuensatz Für gilt nach 2) Res (f ; i) = 1 2z = 1 z=i 2i f (z) = 1 1 + z 2, Res (f ; i) = 1 2z = 1 z= i 2i Reiner Lauterbach (Universität Hamburg) Komplexe
Residuen II Komplexe Partialbruchzerlegung, Residuensatz Für gilt nach 2) Res (f ; i) = 1 2z = 1 z=i 2i f (z) = 1 1 + z 2, Res (f ; i) = 1 2z = 1 z= i 2i Reiner Lauterbach (Universität Hamburg) Komplexe
3. VORLESUNG,
 1.3.9. Satz (Parametrisierung der Kreislinie). 3. VORLESUNG, 23.04.2009 (i) Die Abbildung p : R S 1, p(ϕ) = e iϕ = cosϕ+isinϕ ist ein Gruppenmorphismus der additiven Gruppe (R,+) auf die multiplikative
1.3.9. Satz (Parametrisierung der Kreislinie). 3. VORLESUNG, 23.04.2009 (i) Die Abbildung p : R S 1, p(ϕ) = e iϕ = cosϕ+isinϕ ist ein Gruppenmorphismus der additiven Gruppe (R,+) auf die multiplikative
Funktionentheorie Nachholklausur
 Prof. Dr. Thomas Vogel Sommersemester 2014 Robert Schmidt 6.10.2014 Funktionentheorie Nachholklausur Nachname: Matrikelnr.: Vorname: Fachsemester: Abschluss: Bachelor, PO 2007 2010 2011 Master, PO 2010
Prof. Dr. Thomas Vogel Sommersemester 2014 Robert Schmidt 6.10.2014 Funktionentheorie Nachholklausur Nachname: Matrikelnr.: Vorname: Fachsemester: Abschluss: Bachelor, PO 2007 2010 2011 Master, PO 2010
Potenzreihenentwicklung im Reellen und Komplexen
 Potenzreihenentwicklung im Reellen und Komplexen Christoph Lassnig 26. Januar 20 Zusammenfassung Dieses Dokument bietet einen kleinen Überblick über Potenzreihen, sowie auf ihnen aufbauenden Sätzen und
Potenzreihenentwicklung im Reellen und Komplexen Christoph Lassnig 26. Januar 20 Zusammenfassung Dieses Dokument bietet einen kleinen Überblick über Potenzreihen, sowie auf ihnen aufbauenden Sätzen und
Abbildung 14: Winkel im Bogenmaß
 Mathematik für Naturwissenschaftler I. (7) Trigonometrische Funktionen (in R): Trigonometrische Funktionen wie sin x und cos x stehen üblicherweise in Zusammenhang mit Winkeln. Während im Alltag Winkel
Mathematik für Naturwissenschaftler I. (7) Trigonometrische Funktionen (in R): Trigonometrische Funktionen wie sin x und cos x stehen üblicherweise in Zusammenhang mit Winkeln. Während im Alltag Winkel
Studienbegleitende Prüfung / Modulprüfung / Diplomprüfung Funktionentheorie I SS 2010 Lösungsvorschläge Version vom
 Studienbegleitende Prüfung / Modulprüfung / Diplomprüfung Funktionentheorie I SS 2010 svorschläge Version vom 2382010 Aufgabe 1 (2+2 Punkte) a) Sei f : C C gegeben durch f(z) := 5 5i 1 2i + ez z Geben
Studienbegleitende Prüfung / Modulprüfung / Diplomprüfung Funktionentheorie I SS 2010 svorschläge Version vom 2382010 Aufgabe 1 (2+2 Punkte) a) Sei f : C C gegeben durch f(z) := 5 5i 1 2i + ez z Geben
Analysis I. 1. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an.
 Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
Tutor: Martin Friesen, Übungsblatt 3 - Funktionentheorie, Prof. G. Hemion
 Tutor: Martin Friesen, martin.friesen@gmx.de Übungsblatt 3 - Funktionentheorie, Prof. G. Hemion. Die Exponentialfunktion ist exp z Wie in der reellen Analysis werden auch die trigonometrischen Funktionen
Tutor: Martin Friesen, martin.friesen@gmx.de Übungsblatt 3 - Funktionentheorie, Prof. G. Hemion. Die Exponentialfunktion ist exp z Wie in der reellen Analysis werden auch die trigonometrischen Funktionen
Residuum. Für eine in einer punktierten Kreisscheibe D\{a} analytische Funktion f definiert man das Residuum im Punkt a als.
 Residuum Für eine in einer punktierten Kreisscheibe D\{a} analytische Funktion f definiert man das Residuum im Punkt a als Res Res f = 1 f (z) dz, z=a a 2πi wobei C : t a + re it, 0 t 2π, ein entgegen
Residuum Für eine in einer punktierten Kreisscheibe D\{a} analytische Funktion f definiert man das Residuum im Punkt a als Res Res f = 1 f (z) dz, z=a a 2πi wobei C : t a + re it, 0 t 2π, ein entgegen
6 Komplexe Integration
 6 Komplexe Integration Ziel: Berechne für komplexe Funktion f : D W C Integral der Form f(z)dz =? wobei D C ein Weg im Definitionsbereich von f. Fragen: Wie ist ein solches komplexes Integral sinnvollerweise
6 Komplexe Integration Ziel: Berechne für komplexe Funktion f : D W C Integral der Form f(z)dz =? wobei D C ein Weg im Definitionsbereich von f. Fragen: Wie ist ein solches komplexes Integral sinnvollerweise
2.5 Komplexe Wurzeln. Mathematik für Naturwissenschaftler I 2.5
 Mathematik für Naturwissenschaftler I 2.5 Die Periodizität von e z ist der Grund, warum im Komplexen Logarithmen etwas schwieriger zu behandeln sind als im Reellen: Der natürliche Logarithmus ist die Umkehrung
Mathematik für Naturwissenschaftler I 2.5 Die Periodizität von e z ist der Grund, warum im Komplexen Logarithmen etwas schwieriger zu behandeln sind als im Reellen: Der natürliche Logarithmus ist die Umkehrung
Funktionentheorie 1 - Übung SS 2015 Marcel Marohn
 Funktionentheorie 1 - Übung SS 2015 Marcel Marohn 7. April 2015 Inhaltsverzeichnis 1 Der topologische Raum C 3 1.1 Grundlagen über Komplexe Zahlen...................... 3 1.2 Topologische Grundbegriffe..........................
Funktionentheorie 1 - Übung SS 2015 Marcel Marohn 7. April 2015 Inhaltsverzeichnis 1 Der topologische Raum C 3 1.1 Grundlagen über Komplexe Zahlen...................... 3 1.2 Topologische Grundbegriffe..........................
6.1 Komplexe Funktionen
 118 6 Funktionentheorie 6.1 Komplexe Funktionen Wir kennen die komplexen Zahlen als Erweiterung des Körpers der reellen Zahlen. Man postuliert die Existenz einer imaginären Größe i mit der Eigenschaft
118 6 Funktionentheorie 6.1 Komplexe Funktionen Wir kennen die komplexen Zahlen als Erweiterung des Körpers der reellen Zahlen. Man postuliert die Existenz einer imaginären Größe i mit der Eigenschaft
(b) Folgern Sie, dass f auf C \{±i} keine Stammfunktion besitzt, indem Sie f entlang einer passenden Kreislinie mit Mittelpunkt in i integrieren.
 Musterlösung noch: Funktionentheorie Aufgabe 2.5 (Holomorphe Stammfunktion. Sei f : C \{±i} C gegeben durch f( + 2. (a Zeigen Sie, dass f ( + i eine Stammfunktion auf K 2 (i besitt. Hinweis: Zeigen Sie
Musterlösung noch: Funktionentheorie Aufgabe 2.5 (Holomorphe Stammfunktion. Sei f : C \{±i} C gegeben durch f( + 2. (a Zeigen Sie, dass f ( + i eine Stammfunktion auf K 2 (i besitt. Hinweis: Zeigen Sie
4 Der globale Cauchysche Integralsatz 56
 Inhaltsverzeichnis Vorbemerkung ii 0 Abbildungen f : U lc lc, (x, y) f(x, y) 2 1 Holomorphe Funktionen 10 2 Kurvenintegrale 18 3 Die Stammfunktion 27 3.1 Stammfunktionen und der Cauchysche Integralsatz........
Inhaltsverzeichnis Vorbemerkung ii 0 Abbildungen f : U lc lc, (x, y) f(x, y) 2 1 Holomorphe Funktionen 10 2 Kurvenintegrale 18 3 Die Stammfunktion 27 3.1 Stammfunktionen und der Cauchysche Integralsatz........
Typ der Residuum Funktion Test Singularität bei a bei a. ; a = i, Res(f; i) = lim z 2 +1 (z i)(z+i) z i 2i
 A: Berechnung von Residuen (f Singularität in a, meist f = g, g, h analytisch in a) h Typ der Residuum Funktion Test Singularität bei a bei a. f(z) lim(z a)f(z) = hebbar z a f(z) = sin z, a = ; lim zf(z)
A: Berechnung von Residuen (f Singularität in a, meist f = g, g, h analytisch in a) h Typ der Residuum Funktion Test Singularität bei a bei a. f(z) lim(z a)f(z) = hebbar z a f(z) = sin z, a = ; lim zf(z)
Anleitung 6 Komplexe Funktionen für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg SoSe 20 Dr. Hanna Peywand Kiani Anleitung 6 Komplexe Funktionen für Studierende der Ingenieurwissenschaften Cauchy Integralformeln, Taylor-Reihen, Singularitäten,
Fachbereich Mathematik der Universität Hamburg SoSe 20 Dr. Hanna Peywand Kiani Anleitung 6 Komplexe Funktionen für Studierende der Ingenieurwissenschaften Cauchy Integralformeln, Taylor-Reihen, Singularitäten,
13. Übungsblatt zur Mathematik III für ETiT, WI(ET), IST, CE, LaB-ET, Sport-Wiss
 Fachbereich Mathematik Prof. Dr. H.-D. Alber Dr. N. Kraynyukova Dipl.-Ing. A. Böttcher WS / 3. Januar 3. Übungsblatt zur Mathematik III für ETiT, WI(ET), IST, CE, LaB-ET, Sport-Wiss Gruppenübung Aufgabe
Fachbereich Mathematik Prof. Dr. H.-D. Alber Dr. N. Kraynyukova Dipl.-Ing. A. Böttcher WS / 3. Januar 3. Übungsblatt zur Mathematik III für ETiT, WI(ET), IST, CE, LaB-ET, Sport-Wiss Gruppenübung Aufgabe
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. Michael Wolf Daniel Stilck França Stefan Huber Zentralübung Z7.. Komplexe Wegintegrale TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Berechnen Sie die folgenden Integrale: (a cos(z e z z
Prof. Dr. Michael Wolf Daniel Stilck França Stefan Huber Zentralübung Z7.. Komplexe Wegintegrale TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Berechnen Sie die folgenden Integrale: (a cos(z e z z
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Hans Joachim Oberle Universität Hamburg. Komplexe Funktionen. Vorlesung an der TUHH im Sommersemester 2013 Freitags, 9:45-11:15, Audimax II
 Hans Joachim Oberle Universität Hamburg Komplexe Funktionen Vorlesung an der TUHH im Sommersemester 2013 Freitags, 9:45-11:15, Audimax II Literatur. R. Ansorge, H.J. Oberle, K. Rothe, T. Sonar: Mathematik
Hans Joachim Oberle Universität Hamburg Komplexe Funktionen Vorlesung an der TUHH im Sommersemester 2013 Freitags, 9:45-11:15, Audimax II Literatur. R. Ansorge, H.J. Oberle, K. Rothe, T. Sonar: Mathematik
Der kleine Satz von Picard und seine Anwendungen
 Der kleine Satz von Picard und seine Anwendungen Jens Ole Hein 16. Oktober 2013 Inhaltsverzeichnis 1 Kleiner Picardscher Satz 2 1.1 Eine äquivalente Aussage............................... 2 1.2 Kleiner
Der kleine Satz von Picard und seine Anwendungen Jens Ole Hein 16. Oktober 2013 Inhaltsverzeichnis 1 Kleiner Picardscher Satz 2 1.1 Eine äquivalente Aussage............................... 2 1.2 Kleiner
Höhere Mathematik Vorlesung 8
 Höhere Mathematik Vorlesung 8 Mai 2017 ii In der Mathematik versteht man die Dinge nicht. Man gewöhnt sich nur an sie. John von Neumann 8 Funktionentheorie Komplexe Zahlen Jede komplexe Zahl besitzt eine
Höhere Mathematik Vorlesung 8 Mai 2017 ii In der Mathematik versteht man die Dinge nicht. Man gewöhnt sich nur an sie. John von Neumann 8 Funktionentheorie Komplexe Zahlen Jede komplexe Zahl besitzt eine
Analytische Zahlentheorie
 4. April 005. Übungsblatt Aufgabe (4 Punkte Sei k N. Beweisen Sie, dass f : N C mit f(n := n k streng multiplikativ ist. Sei τ die Funktion, die der natürlichen Zahl n die Anzahl der Teiler von n zuordnet
4. April 005. Übungsblatt Aufgabe (4 Punkte Sei k N. Beweisen Sie, dass f : N C mit f(n := n k streng multiplikativ ist. Sei τ die Funktion, die der natürlichen Zahl n die Anzahl der Teiler von n zuordnet
1. Aufgabe 9 Punkte. Musterlösung Analysis III f. Ing., 09. Oktober Partialbruchzerlegung: 4 z 1 1. (z 1)(z +3) =
 Musterlösung Analysis III f. Ing., 09. Oktober 0. Aufgabe 9 Punkte Partialbruchzerlegung: (z )(z +3) z z +3 Um eine im Ringgebiet < z < 5 konvergente Laurent-Reihe zu erhalten, entwickelt man den Term
Musterlösung Analysis III f. Ing., 09. Oktober 0. Aufgabe 9 Punkte Partialbruchzerlegung: (z )(z +3) z z +3 Um eine im Ringgebiet < z < 5 konvergente Laurent-Reihe zu erhalten, entwickelt man den Term
Funktionentheorie I - Prüfungsprotokolle Skript Dr. Herzog
 Funktionentheorie I - Prüfungsprotokolle Skript Dr. Herzog 1 Komplexe Zahlen 2 Topologische Begriffe Offene Menge Abgeschlossene Menge Kompakte Teilmenge: Überdeckungskompaktheit 3 Die Riemann sche Zahlenkugel
Funktionentheorie I - Prüfungsprotokolle Skript Dr. Herzog 1 Komplexe Zahlen 2 Topologische Begriffe Offene Menge Abgeschlossene Menge Kompakte Teilmenge: Überdeckungskompaktheit 3 Die Riemann sche Zahlenkugel
6.8 Residuenkalkül. Ziel: Weitere Verallgemeinerung auf mehrere Löcher L 1,..., L N. Kapitel 6: Komplexe Integration Γ 1
 6.8 Residuenkalkül Erinnerung: Sei f analytisch auf einem zweifach zusammenhängenden Gebiet G, d.h. G besitzt genau ein Loch L. Weiterhin seien und zwei positiv orientierte geschlossene Wege, die das Loch
6.8 Residuenkalkül Erinnerung: Sei f analytisch auf einem zweifach zusammenhängenden Gebiet G, d.h. G besitzt genau ein Loch L. Weiterhin seien und zwei positiv orientierte geschlossene Wege, die das Loch
86 Klassifizierung der isolierten Singularitäten holomorpher
 86 Klassifizierung der isolierten Singularitäten holomorpher Funktionen 86. Isolierte Singulariäten holomorpher Funktionen 86.3 Klassifizierung der isolirerten Singularitäten 86.5 Charakterisierung hebbarer
86 Klassifizierung der isolierten Singularitäten holomorpher Funktionen 86. Isolierte Singulariäten holomorpher Funktionen 86.3 Klassifizierung der isolirerten Singularitäten 86.5 Charakterisierung hebbarer
Kapitel 5. Die trigonometrischen Funktionen Die komplexen Zahlen Folgen und Reihen in C
 Kapitel 5. Die trigonometrischen Funktionen 5.1. Die komplexen Zahlen 5.. Folgen und Reihen in C 5.10. Definition. Eine Folge (c n n N komplexer Zahlen heißt konvergent gegen c C, falls zu jedem ε > 0
Kapitel 5. Die trigonometrischen Funktionen 5.1. Die komplexen Zahlen 5.. Folgen und Reihen in C 5.10. Definition. Eine Folge (c n n N komplexer Zahlen heißt konvergent gegen c C, falls zu jedem ε > 0
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Wachstumsverhalten ganzer Funktionen. Inhaltsverzeichnis
 Wachstumsverhalten ganzer Funktionen Vortrag zum Seminar zur Funktionentheorie, 11.6.212 Simon Langer Inhaltsverzeichnis 1 Einleitung 2 2 Wachstumsverhalten ganzer Funktionen 3 3 Ganze Funktionen endlicher
Wachstumsverhalten ganzer Funktionen Vortrag zum Seminar zur Funktionentheorie, 11.6.212 Simon Langer Inhaltsverzeichnis 1 Einleitung 2 2 Wachstumsverhalten ganzer Funktionen 3 3 Ganze Funktionen endlicher
Übungen Analysis I WS 03/04
 Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Höhere Mathematik Vorlesung 9
 Höhere Mathematik Vorlesung 9 Mai 2017 ii Be yourself, everyone else is already taken. Osar Wilde 9 Integralrehnung im Komplexen Das Riemannshe Integral einer komplexwertigen Funktion: Sei f : [a, b] C
Höhere Mathematik Vorlesung 9 Mai 2017 ii Be yourself, everyone else is already taken. Osar Wilde 9 Integralrehnung im Komplexen Das Riemannshe Integral einer komplexwertigen Funktion: Sei f : [a, b] C
Prof. D. Salamon Funktionentheorie ETH Zürich MATH, PHYS 27. Oktober Musterlösung 5
 Prof. D. Salamon Funktionentheorie ETH Zürich MATH, PHYS 27. Oktober 2009 Musterlösung 5 1. Sei f : C C eine holomorphe Funktion, so dass f(z) < z n für ein n N und alle hinreichend grossen z. Dann ist
Prof. D. Salamon Funktionentheorie ETH Zürich MATH, PHYS 27. Oktober 2009 Musterlösung 5 1. Sei f : C C eine holomorphe Funktion, so dass f(z) < z n für ein n N und alle hinreichend grossen z. Dann ist
1.3 Isolierte Singularitäten
 6.3 Isolierte Singularitäten Definition Sei U C offen, z 0 U und f : U \ {z 0 } C holomorph. Dann nennt man z 0 eine isolierte Singularität von f. Zunächst einmal ist z 0 nur eine Definitionslücke für
6.3 Isolierte Singularitäten Definition Sei U C offen, z 0 U und f : U \ {z 0 } C holomorph. Dann nennt man z 0 eine isolierte Singularität von f. Zunächst einmal ist z 0 nur eine Definitionslücke für
Examenskurs Analysis Probeklausur I
 Georg Tamme Sommersemester 14 Examenskurs Analysis Probeklausur I 5.6.14 F1II1. Sei f : C C eine ganze Funktion. Entscheiden Sie, ob die folgenden Behauptungen wahr sind. Begründen Sie Ihre Antwort jeweils
Georg Tamme Sommersemester 14 Examenskurs Analysis Probeklausur I 5.6.14 F1II1. Sei f : C C eine ganze Funktion. Entscheiden Sie, ob die folgenden Behauptungen wahr sind. Begründen Sie Ihre Antwort jeweils
Funktionentheorie. Wolfram Decker
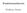 Funktionentheorie Wolfram Decker Inhaltsverzeichnis Kapitel. Grundlagen 7 1. Komplexe Zahlen 7 1.1. Der Körper C 7 1.2. Konjugation 7 1.3. Euklidischer Abstand, C als metrischer Raum 8 1.4. Zusammenhang
Funktionentheorie Wolfram Decker Inhaltsverzeichnis Kapitel. Grundlagen 7 1. Komplexe Zahlen 7 1.1. Der Körper C 7 1.2. Konjugation 7 1.3. Euklidischer Abstand, C als metrischer Raum 8 1.4. Zusammenhang
Folgen, Reihen, Potenzreihen, Exponentialfunktion
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
3 Der Cauchysche Integralsatz
 3 Der Cauchysche Integralsatz Die in der Funktionentheorie meist vorkommenden Integrale (insbesondere im Cauchyschen Integralsatz) sind Kurvenintegrale und wie folgt definiert: Definition Sei U C, f :
3 Der Cauchysche Integralsatz Die in der Funktionentheorie meist vorkommenden Integrale (insbesondere im Cauchyschen Integralsatz) sind Kurvenintegrale und wie folgt definiert: Definition Sei U C, f :
8. Die Nullstellen der Zeta-Funktion
 8.. Wie vorher sei ( s ξ(s = π s/ Γ ζ(s. ξ ist meromorph in ganz C, hat Pole (erster Ordnung nur bei s = und s = und genügt der Funktionalgleichung ξ(s = ξ( s. Daraus folgt: Für Re s < hat die Zeta-Funktion
8.. Wie vorher sei ( s ξ(s = π s/ Γ ζ(s. ξ ist meromorph in ganz C, hat Pole (erster Ordnung nur bei s = und s = und genügt der Funktionalgleichung ξ(s = ξ( s. Daraus folgt: Für Re s < hat die Zeta-Funktion
3 Meromorphe Funktionen und der Residuenkalkül
 $Id: mero.tex,v.5 203/05/4 3:0:42 hk Exp hk $ 3 Meromorphe Funktionen und der Residuenkalkül 3.2 Isolierte Singularitäten In der letzten Sitzung hatten wir die drei Typen isolierter Singularitäten und
$Id: mero.tex,v.5 203/05/4 3:0:42 hk Exp hk $ 3 Meromorphe Funktionen und der Residuenkalkül 3.2 Isolierte Singularitäten In der letzten Sitzung hatten wir die drei Typen isolierter Singularitäten und
6. VORLESUNG,
 27 6. VORLESUNG, 1.5.217 2.2.9. Beispiel. Die Funktion f : C C, f(z) = 1 hat keine Stammfuntkion, da z dz (2.9) z =. B 1 () B 1 () Hätte f eine Stammfunktion, so wäre das Integral Null. Die Formel (2.9)
27 6. VORLESUNG, 1.5.217 2.2.9. Beispiel. Die Funktion f : C C, f(z) = 1 hat keine Stammfuntkion, da z dz (2.9) z =. B 1 () B 1 () Hätte f eine Stammfunktion, so wäre das Integral Null. Die Formel (2.9)
