Logik und Beweisbarkeit
|
|
|
- Günter Gerhardt
- vor 5 Jahren
- Abrufe
Transkript
1 Logik und Beweisbarkeit VL 08 Martin Mundhenk Univ. Jena, Institut für Informatik 11. Januar 2019
2 Teil 3: Berechenbarkeitstheorie 1. Aussagenlogik 2. Arithmetik 3. Berechenbarkeitstheorie VL08: URM-berechenbare Funktionen und die These von Church VL09: Entscheidbare und semi-entscheidbare Mengen VL10: Reduzierbarkeit VL11: Beweissysteme 4. Unvollständigkeitssätze ( Literatur: Nigel Cutland: Computability (Cambridge University Press) )
3 VL 8 Übersicht 3.8 Unlimited Register Machines Es wird das Computer-Modell URM (Unlimited Register Machine) vorgestellt, mit dem man Funktionen auf den natürlichen Zahlen berechnen kann. Wir werden für allerlei Funktionen zeigen, wie sie von URM-Programmen berechnet werden können. Das ist (leider) technisch recht aufwendig, überzeugt uns aber davon, dass man alles, was von einem Computer-Modell erwarten kann, auch vom URM-Modell erreicht wird. Das behauptet auch die These von Church und Turing, nach der man alles, was man in diesem Modell berechnen kann, auch intuitiv berechnen kann. Das erlaubt uns für die Zukunft, auch intuitiv statt formal zu argumentieren (wenn wir die Fallstricke der intuitiven Argumentation im Auge behalten).
4 VL 9 Übersicht 3.9 Entscheidbare und semi-entscheidbare Mengen Unser Ziel ist ja, einen Unterschied zwischen der Menge arithm. Formeln, die mit den Peano-Axiomen bewiesen werden können und der Menge arithm. Formeln, die vom Standard-Modell N erfüllt werden zu zeigen. Dazu übertragen wir den Begriff der Berechenbarkeit bzw. Nicht-Berechenbarkeit auf Mengen und erhalten die Begriffe entscheidbare Menge semi-entscheidbare Menge Uns interessieren besonders die semi-entscheidbaren Mengen, die nicht entscheidbar sind. Diese Eigenschaft ist auch der gesuchte Unterschied zwischen den beiden o.g. Mengen (aber das kommt erst in einer späteren Vorlesung).
5 VL 10 Übersicht 3.11 Beweissysteme Wir kennen das Beweissystem der Robinson-Arithmetik und anderer Arithmetiken. Wir wissen, wie man Formeln mittels Natürlichem Schließen herleiten kann. Die Axiome-Mengen, aus denen wir Formeln hergeleitet haben, waren stets entscheidbar. Diese Erfahrung nutzen wir jetzt, um zwei allgemeine (abstrakte) Begriffe von Beweissystemen zu definieren, die in die Begriffswelt der berechenbaren Funktionen passen und die uns bekannten Beweissysteme enthalten. Interessanterweise stellen sich die mit diesen Beweissystemen herleitbaren Formelmengen als genau die semi-entscheidbaren Mengen heraus. Das wird sich später als die gesuchte Eigenschaft der Robinson-/Peano-Arithmetik herausstellen.
6 Vorlesung 8: URM-berechenbare Funktionen und die These von Church und Turing 3. Berechenbarkeitstheorie VL08: URM-berechenbare Funktionen und die These von Church URM-berechenbare Funktionen Die These von Church und Turing Kodierung von URM-Programmen durch Zahlen Nicht alle Funktionen sind URM-berechenbar Universelle URM-Programme VL09: Entscheidbare und semi-entscheidbare Mengen VL10: Reduzierbarkeit VL11: Beweissysteme ( Literatur: Nigel Cutland: Computability (Cambridge University Press) )
7 8.1 URM-berechenbare Funktionen und die These von Church und Turing In diesem Abschnitt wird das Computer-Modell URM vorgestellt, mit dem man Funktionen auf den natürlichen Zahlen in berechenbare Funktionen (d.h. solche, für die es ein URM-Programm gibt) und nicht-berechenbare Funktionen (d.h. solche, für die es kein URM-Programm gibt) unterscheiden kann. Wir werden für allerlei Funktionen zeigen, wie sie von URM-Programmen berechnet werden können. Das ist (leider) technisch recht aufwendig, überzeugt uns aber davon, dass man alles, was von einem Computer-Modell erwarten kann, auch vom URM-Modell erreicht wird. Am Ende steht die These von Church und Turing, nach der man alles, was man in diesem Modell berechnen kann, auch intuitiv berechnen kann. Das erlaubt uns für die Zukunft davor, intuitiv statt formal zu argumentieren (wenn wir die Fallstricke der intuitiven Argumentation kennen)
8 Definition 8.1 (Syntax von URM-Programmen) Eine Unlimited Register Machine (URM) besteht aus Registern R 0, R 1, R 2,..., R k (für k N), die jeweils eine nat. Zahl speichern können und einem URM-Programm. Ein URM-Programm ist eine endliche Folge von Zahlen, die zeilenweise mit den angegebenen Mnemonics dargestellt werden. a, b, c stehen für beliebige natürliche Zahlen. Zeile Wirkung R a = a setze Register R a auf 0 R a += a addiere 1 zum Register R a if R a == R b : goto c a 5 b 7 c falls Register R a und R b den gleichen Inhalt haben, dann springe zu Zeile c des Programms Sei m das Maximum aller a, b, die in den Zeilen des URM-Programms P vorkommen. Dann benutzt P (höchstens) die Register R 0, R 1,..., R m, und man sagt: P ist URM-Programm mit m Registern (plus Ausgaberegister R 0 )
9 Beispiele für URM-Programme Register gleichsetzen (und abkürzende Schreibweisen benutzen) 0: R 0 = 0 1: if R 0 == R 1 : goto 4 2: R 0 += 1 3: if R 0 == R 0 : goto 1 opiere den Inhalt von R 1 nach R 0.
10 3.8.4 Beispiele für URM-Programme Register gleichsetzen (und abkürzende Schreibweisen benutzen) 0: R 0 = 0 1: if R 0 == R 1 : goto 4 2: R 0 += 1 3: goto 1 Kopiere den Inhalt von R 1 nach R 0. Abkürzende Schreibweisen: goto a springe zu Zeile a des Programms Bei Benutzung abkürzender Schreibweisen weiß man, wie man die Programme ohne abkürzende Schreibweisen schreiben kann.
11 3.8.4 Beispiele für URM-Programme Register gleichsetzen (und abkürzende Schreibweisen benutzen) 0: R 0 = 0 1: while R 0!= R 1 : 2: R 0 += 1 Kopiere den Inhalt von R 1 nach R 0. Abkürzende Schreibweisen: goto a springe zu Zeile a des Programms while R a!= R b : (klar, Schleifenrumpf wird durch Einrückung gekennzeichnet) Bei Benutzung abkürzender Schreibweisen weiß man, wie man die Programme ohne abkürzende Schreibweisen schreiben kann.
12 Beispiele für URM-Programme Register gleichsetzen (und abkürzende Schreibweisen benutzen) 0: R 0 = 0 1: while R 0!= R 1 : 2: R 0 += 1 Kopiere den Inhalt von R 1 nach R 0. R b = 0 while R b!= R a : R b += 1 Kopiere den Inhalt von R a nach R b. Abkürzende Schreibweisen: goto a springe zu Zeile a des Programms while R a!= R b : (klar, Schleifenrumpf wird durch Einrückung gekennzeichnet) R b = R a kopiere Inhalt von R a nach R b Bei Benutzung abkürzender Schreibweisen weiß man, wie man die Programme ohne abkürzende Schreibweisen schreiben kann.
13 Addieren Addiere die Inhalte der Register R a und R b und schreibe das Ergebnis nach R c. R c = R a R t = 0 while R b!= R t : R c += 1 R t += 1 Abkürzende Schreibweise: R c = R a + R b
14 Multiplizieren und Potenzieren R t = 0 R c = 0 while R b!= R t : R c = R c + R a R t += 1 R t = 0 R c = 0 R c += 1 while R b!= R t : R c = R c R a R t += 1 Abk.: R c = R a R b Abk.: R c = R Rb a
15 Dekrementieren und subtrahieren Die Subtraktion auf den natürlichen Zahlen ist { a. a b, falls a > b b = 0, sonst R a = 0 R t = 0 if R b == R t : goto Ende R t += 1 while R b!= R t : R a += 1 R t += 1 R z = 0 R a = R b R s = R c while R s!= R z : R a = R a -1 R s = R s -1 Abk.: R a = R b -1 Ende Abk.: R a = R b - R c die Nummer der ersten Programmzeile hinter dem Programm 3.8.7
16 Vorzeichenfunktionen sig(x) = { 1, falls x > 0 0, falls x = 0 sig(x) = 1 sig(x) R a = 0 R c = R b while R c!= R a : R a += 1 R c = R a Abk.: R a = sig(r b ) R t = sig(r b ) R s = 0 R s += 1 R a = R s - R t Abk.: R a = sig(r b )
17 3.8.9 Vergleiche R a > R b = { 1, falls R a > R b 0, sonst R a R b = R a > R b + 1 R c = R a - R b R c = sig(r c ) Abk.: R c = R a > R b R t = R b R t += 1 R c = R a > R t Abk.: R c = R b R a
18 Aussagenlogische Verknüpfungen R a und R b = { 1, falls R a > 0 und R b > 0 0, sonst R c = R a R b R c = sig(r c ) Abk.: R c = R a R b nicht R a = { 1, falls R a = 0 0, sonst R a oder R b = { 1, falls R a > 0 oder R b > 0 0, sonst R c = sig(r a ) R c = R a + R b R c = sig(r c ) Abk.: R c =!R a Abk.: R c = R a R b
19 Ausdrücke auswerten Es ist intuitiv klar, dass arithmetisch-logische Ausdrücke als URM-Programme geschrieben werden können. Beispiel: R c = R a + sig(r a (R b 2)) ist Abkürzung für R t = 0 R t += 1 R t += 1 R t = R b - R t R t = R a R t R t = sig(r t ) R c = R a + R t
20 Schleifen mit beliebigen Bedingungen while <Ausdruck> : P ist Abkürzung für R t = <Ausdruck> R z = 0 while R t!= R z : P R t = <Ausdruck>
21 if then else if <Ausdruck> : P else : Q ist Abkürzung für R i = 0 R z = 0 while <Ausdruck>!(R i > R z ) : P R i += 1 R i = 0 while <Ausdruck>!(R i > R z ) : Q R i += 1
22 Ganzzahlige Division und Rest R t = R a R c = 0 while R t R b : R t = R t - R b R c += 1 R t = R a / R b R s = R t R b R c = R a - R s Abk.: R c = R a mod R b Abk.: R c = R a / R b
23 Primzahlen R c = 0 if R a > 1 : R t = 2 while R a mod R t : R t += 1 if!(r t ==R a ) : R c += 1 Abk.: R c = R a ist Primzahl R b = 2 R t = 1 while R a > R t : R b += 1 R s = R b ist Primzahl R t = R t + R s Abk.: R b = R a -te Primzahl
24 Potenzen von Teilern finden maximale Potenz von t als Faktor von n = max{k tk teilt n} R c = 0 while! ( R a mod Rb Rc+1 ) : R c += 1 Abk.: R c = maxpotenz von R b in R a
25 URM-Programme Semantik Definition 8.2 (Konfiguration eines URM-Programms) Sei P ein URM-Programm mit k Registern. Eine Konfiguration von P ist ein Element von N k+2. Eine Konfiguration (c 0,..., c k, c k+1 ) enthält eines URM-Programms P = (I 0,..., I m ) die Inhalte c 0,..., c k der Register R 0,..., R k und die Nummer c k+1 (Programmzähler) der nächsten auszuführenden Programmzeile I ck+1.
26 Definition 8.3 (Konfigurationsübergangsrelation P ) Sei P = (I 0, I 1,..., I s 1 ) ein URM-Programm mit k Registern, und c = (c 0,..., c k, pz) sowie c = (c 0,..., c k, pz ) seien zwei Konfigurationen von P. Es gilt c P c gdw. pz < s und I pz = R a = 0, c a = 0, c i = c i für i a, und pz = pz + 1, oder I pz = R a += 1, c a = c a + 1, c i = c i für i a, und pz = pz + 1, oder I pz = if R a == R b : goto c, c i = c i für alle i, und ca = c b und pz = c, oder ca c b und pz = pz + 1. P ist die reflexive und transitive Hülle von P.
27 URM-berechenbare Funktionen Definition 8.4 (URM-berechenbare Funktionen) Eine partielle Funktion f : N k N ist URM-berechenbar, falls es ein URM-Programm P = (I 0,..., I s 1 ) mit l k Registern gibt, so dass für alle a 1,..., a k N gilt: 1. Wenn f (a 1,..., a k ) definiert ist, dann gibt es c 1,..., c l, pz N mit pz s, so dass P (0, a 1,..., a k, 0,..., 0, 0) (f (a }{{} 1,..., a k ), c 1,..., c l, pz) }{{} Startkonfiguration von P(a 1,..., a k) Endkonfiguration ( umgangssprachlich: die Berechnung P(a 1,..., a k ) hält mit f (a 1,..., a k ) als Inhalt von Register R 0 ). 2. Wenn f (a 1,..., a k ) undefiniert ist, dann gilt für jede Konfiguration c = (c 0,..., c l, pz ) mit (0, a 1,..., a k, 0,..., 0, 0) P c, dass pz < s ( umgangssprachlich: die Berechnung P(a 1,..., a k ) hält nicht ).
28 Die These von Church und Turing Es gibt eine Vielzahl formaler Begriffe der Berechenbarkeit (z.b. URM-Berechenbarkeit, Turing-Berechenbarkeit, µ-rek., λ-b., Post-B.,... ), von denen man formal zeigen kann, dass sie äquivalent sind. Man kennt keine Funktion, die intuitiv berechenbar ist und nicht URM-berechenbar (... ) ist. These von Church und Turing Die im intuitiven Sinne berechenbaren Funktionen sind genau die URM-berechenbaren Funktionen.
29 Kodierung von URM-Programmen durch Zahlen Jedes URM-Programm lässt sich als eine natürliche Zahl darstellen. Wir schreiben dann auch P i für das Programm, das durch die Zahl i dargestellt wird. Um das zeigen zu können, brauchen wir ein paar Kodierungsfunktionen.
30 Kodierung von URM-Programmen durch Zahlen mittels τ Tupel (r 1, r 2,..., r k ) N k können kodiert werden mittels τ : N k 0 N mit τ(r 1, r 2,..., r k ) = p0 k p r i i, wobei p i die i-te Primzahl ist (p 0 = 2). i 1 Bsp.: (1, 2, 3, 4) wird kodiert durch τ(1, 2, 3, 4) = = Lemma 8.5 (τ ist eine berechenbare Kodierungsfunktion) Obige Funktion τ : N k 0 N ist injektiv und URM-berechenbar.
31 Kodierung von URM-Programmen Wir hatten bereits Zeilen von URM-Programmen als Zahlen definiert (und sie mittels umgangssprachlicher Abkürzungen beschrieben). Zeile umgangssprachlich R a = 0 R a += 1 if R a == R b : goto c als Zahl a a a 5 b 7 c Ein URM-Programm P = (I 0, I 1,..., I s 1 ) ist ein Tupel von Zahlen. Seine Kodierung als natürliche Zahl ist τ(p) = τ(i 0, I 1,..., I s 1 ). Bem.: Jede Programmzeile ist eine Zahl 1.
32 Beispiel: von der Zahl zum URM-Programm und weiter zur Funktion Zahl n : = τ(144, 60, 100) URM-Programm τ 1 (n) : if R 0 == R 0 : goto 0 R 1 += 1 R 2 = 0 Die Funktion ϕ (1) : N N ist die überall undefinierte Funktion, d.h. für alle n N gilt: ϕ (1) (n) ist undefiniert.
33 Da τ nicht surjektiv ist, hat τ kein Inverses auf N. Wir bezeichnen mit τ 1 URM eine Erweiterung von τ 1, die jede natürliche Zahl auf ein URM-Programm abbildet. τ 1 URM (n) = (I 1,..., I s ) mit s = max{i 2 i teilt n} und max{i pj i teilt n}, falls das Maximum i I j = eine Programmzeile ist if R 0 == R 0 : goto j, sonst (Endlosschleife) Z.B. ist τ 1 URM (n) für jedes ungerade n das leere Programm. Das stört uns nicht, da uns ausreicht, dass τ injektiv ist
34 Definition 8.6 (Bezeichnungen von Programmen und Funktionen) Sei n N. P n ist das URM-Programm mit τ 1 URM (n) = P n. (Für jedes n N gibt es ein URM-Programm P n.) ϕ (k) n bezeichnet die Funktion N k N, die durch das URM-Programm P n berechnet wird. Für ϕ (1) n schreiben wir auch ϕ n.
35 8.4 Eine Funktion, die nicht URM-berechenbar ist Definiere ψ : N N mit ψ(n) = { 0, falls ϕn (n) = 1 1, sonst Satz 8.7 ψ ist nicht URM-berechenbar. Beweis: Annahme: ψ ist URM-berechenbar, d.h. ψ = ϕ m für ein m N. Dann gilt ψ(m) = 1 Def. ψ ϕ m (m) 1 ϕm=ψ ψ(m) 1 und ψ(m) 1 ϕ m (m) = 1 ψ(m) = 1. Insgesamt: ψ(m) = 1 ψ(m) 1 d
36 Universelle Programme Satz 8.8 Es gibt ein universelles URM-Programm U, das beliebige URM-Programme simulieren kann. Das heißt U(i, x) hält genau dann, wenn P i (x) hält, und wenn P i (x) hält, dann liefert U(i, x) das gleiche Ergebnis in Register R 0. Den Satz kann man mit Benutzung der These von Church und Turing leicht beweisen. Im folgenden Exkurs wird ein universelles URM-Programm konstruiert (also die Beweisidee ohne Benutzng der These von Church und Turing).
37 Was haben wir in dieser Vorlesung gelernt? Alles, was man intuitiv mit natürlichen Zahlen berechnen kann, kann man auch formal mit URM-Programmen berechnen. D.h. für jede intuitiv berechenbare Funktion gibt es ein URM-Programm, das sie berechnet. Jedes URM-Programm lässt sich durch eine natürliche Zahl darstellen. Wir benutzen diese Zahl auch, um die durch das Programm berechnete Funktion darzustellen. Es gibt ein universelles URM-Programm. Es gibt Funktionen, die nicht URM-berechenbar sind.
38 Exkurs: Das universelle Programm U (k) simuliert die Berechnung k-stelliger Funktionen. Es erhält als Eingabe e, x 1,..., x k und berechnet die gleiche Ausgabe wie P e (x 1,..., x k ) bzw. hält nicht. Der Algorithmus arbeitet grob gesagt wie folgt. Eingabe e, x 1,..., x k der Programmcode steht bereits in R 1 schreibe den Registercode von 0, x 1,..., x k nach R 2 setze R 3 auf 0 (d.h. R 3 enthält den Programmzähler) solange der Programmzähler R 3 < Anzahl Zeilen des Programms in R 1 : simuliere den durch den Programmzähler bestimmten Befehl des Programmcodes in R 1 auf dem Registercode in R 2 und setze den Programmzähler R 3 entsprechend um schreibe den Inhalt von Register 0 aus dem Konfigurationscode nach R 0
39 Der Programmcode und der Registercode Der Programmcode eines Programms (I 0, I 1,..., I k 1 ) ist τ(i 0, I 1,..., I p ). Die Anzahl der Zeilen des Programms mit Programmcode m ist γ 1 (m). Der Registercode kodiert die Inhalte aller Register einer URM. Jedes Programm benutzt eine feste Zahl R 0, R 1, R 2,..., R k von Ein- und Ausgaberegistern. Alle Registerinhalte r 0, r 1, r 2,..., r k beim Start des Programms können als k kodiert werden. i=0 p r0 i Damit sind auch die übrigen Register mit Inhalt 0 korrekt kodiert.
40 Lies den Inhalt eines Registers aus dem Registercode in R 2 Dekodiere aus dem Registercode in R 2 den Inhalt des Registers, dessen Index in R b steht, und schreibe ihn nach R c. R t = R 2 R c = 0 R u = R b -te Primzahl while R t mod R u == 0 : R t = R t / R u R c += 1 Abk.: R c = Register R Rb aus Registercode R 2
41 Schreibe den Inhalt eines Registers im Registercode in R a Schreibe im Registercode in R a den Inhalt von R c in das Register, dessen Index in R b steht. R t = R b -te Primzahl (Teil 1: setze das Register im Registercode auf 0) while!(r a mod R t ==0) : R a = R a / R t R s = R c (Teil 2: setze das Register im Registercode auf R c) while R s : R a = R a R t R s = R s -1 Abk.: R a = schreibe R c als Reg. R Rb in R a
42 Berechne den Registercode beim Start der Simulation Der Inhalt der Register R 2,..., R k+1 wird als Registercode (für Register (R 0, )R 1,..., R k ) nach R 2 geschrieben. R t = 1 (am Anfang sind alle Register 0, also ist der Reg.code 1) R i = 2 (der Index des nächsten zu kodierenden Registers) R b = 1 (der Index des nächsten Registers im Konfig.code) R t = schreibe R i als Reg. R Rb in R t R i = 3 (der Index des nächsten zu kodierenden Registers) R b = 2 (der Index des nächsten Registers im Konfig.code) R t = schreibe R i als Reg. R Rb in R t. R i = k + 1 (der Index des nächsten zu kodierenden Registers) R b = k (der Index des nächsten Registers im Konfig.code) R t = schreibe R i als Reg. R Rb in R t R 2 = R t Abk.: R 2 = Kodierung von 0, R 2,..., R k+1
43 Bsp.: nach der Dekodierung von if R 10 == R 8 : goto 6 ist R 4 = 2, R 5 = 10, R 6 = 8 und R 7 = 6 nach der Dekodierung von R 13 += 1 ist R 4 = 1, R 5 = 13, R 6 = 0 und R 7 = Dekodierung des Zeilencodes Jede Zeile eines URM-Programms wird als Zahl kodiert (Zeilencode). Zeile umgangssprachlich als Zahl R a = a R a += 1 if R a == R b : goto c a a 5 b 7 c Der Programmcode ist die Kodierung eines Tupels von Zeilencodes. Das universelle Programm dekodiert den Zeilencode, indem es seine Bestandteile in die Register R 4, R 5, R 6 und R 7 schreibt.
44 Dekodiere aus dem Programmcode in R a die Zeile, deren Nummer in R b steht, und schreibe sie nach R c. R t = R a R c = 0 R p = R b +1 R u = R p -te Primzahl while R t mod R u == 0 : R t = R t / R u R c += 1 Abk.: R c = Zeile R b aus Programmcode R a
45 Dekodiere aus dem Programmcode in R 1 die Zeile, deren Nummer in R b steht, und schreibe ihre Bestandteile nach R 4,..., R 7. R c = Zeile R b aus Programmcode R 1 R s = 2 R 4 = maxpotenz von R s in R c R s = 3 R 5 = maxpotenz von R s in R c R s = 5 R 6 = maxpotenz von R s in R c R s = 7 R 7 = maxpotenz von R s in R c (falls der Zeilencode nicht korrekt war, wird die Simulation in eine Endlosschleife gehen) if R c /(2 R4 3 R5 5 R6 7 R7 ) > 1 or ( R 4 < 2 and R 6 + R 7 > 0 ) : R 4 = 3 Abk.: decode next line from program code in R 1
46 Simulation der einzelnen URM-Befehle: R x = 0 sim[r R5 = 0]: simuliere R R5 = 0, d.h. setze im Registercode in R 2 den Inhalt des Registers, dessen Index in R 5 steht, auf 0. R z = 0 R 2 = schreibe R z als Reg. R R5 in R 2 R 3 += 1 (Programmzähler+1)
47 Simulation der einzelnen URM-Befehle: R x += 1 sim[r R5 += 1]: simuliere R R5 += 1, d.h. addiere 1 im Registercode in R 2 zum Inhalt des Registers, dessen Index in R 5 steht. R t = R 5 -te Primzahl R 2 = R 2 R t R 3 += 1 (Programmzähler+1)
48 Simulation der URM-Befehle: if R x == R y : goto z sim[if R R5 == R R6 : goto R 7 ]: simuliere if R b == R c : goto d, d.h. setze den Programmzähler in R 3 auf den Inhalt von R 7, falls im Registercode in R 2 die Register, deren Indizes in R 5 und R 6 stehen, den gleichen Inhalt haben. Anderenfalls wird nur der Programmzähler hochgezählt. R a = Register R R5 aus Registercode R 2 R b = Register R R6 aus Registercode R 2 if R a ==R b : R 3 = R 7 else : R 3 += 1
49 Das universelle Programm U (k) U (k) (e, x 1,..., x k ) simuliert P e (x 1,..., x k ) und berechnet ϕ e (x 1,..., x k ). (bereite die Simulation vor) R 2 = Kodierung von 0, R 2,..., R k+1 R 3 = 0 (setze Programmzähler auf 0) R 8 = 2 (wir brauchen zweimal eine 2) (simuliere jeden Schritt des Programms) while R 3 < maxpotenz von R 8 in R 1 : decode next line from program code in R 1 if R 4 ==0 : sim[r R5 = 0] if R 4 ==1 : sim[r R5 += 1] if R 4 ==2 : sim[if R R5 == R R6 : goto R 7 ] (schreibe das Ergebnis der Simulation nach R 0) R 0 = maxpotenz von R 4 in R 8
Logik und Beweisbarkeit
 Logik und Beweisbarkeit VL 10 Martin Mundhenk Univ. Jena, Institut für Informatik 22. Januar 2019 Vorlesung 11: Beweissysteme 3. Berechenbarkeitstheorie VL08: URM-berechenbare Funktionen und die These
Logik und Beweisbarkeit VL 10 Martin Mundhenk Univ. Jena, Institut für Informatik 22. Januar 2019 Vorlesung 11: Beweissysteme 3. Berechenbarkeitstheorie VL08: URM-berechenbare Funktionen und die These
Logik und Beweisbarkeit
 Logik und Beweisbarkeit Einleitung Martin Mundhenk Univ. Jena, Institut für Informatik. Februar 0 Einleitung: U ber Sinn und Form Symbolisches Addieren Al-Chwarizmi (etwa 8 80) Problem: Was ist MMMDCCCXCIX
Logik und Beweisbarkeit Einleitung Martin Mundhenk Univ. Jena, Institut für Informatik. Februar 0 Einleitung: U ber Sinn und Form Symbolisches Addieren Al-Chwarizmi (etwa 8 80) Problem: Was ist MMMDCCCXCIX
1.5 Turing-Berechenbarkeit
 A.M. Turing (1937): Maschinenmodell zur exakten Beschreibung des Begriffs effektiv berechenbar Stift Mensch a c b b Rechenblatt a b b c Lese-/Schreibkopf endliche Kontrolle Turingmaschine Eine Turingmaschine
A.M. Turing (1937): Maschinenmodell zur exakten Beschreibung des Begriffs effektiv berechenbar Stift Mensch a c b b Rechenblatt a b b c Lese-/Schreibkopf endliche Kontrolle Turingmaschine Eine Turingmaschine
1.5 Turing-Berechenbarkeit
 A.M. Turing (1937): Maschinenmodell zur exakten Beschreibung des Begriffs effektiv berechenbar Stift Mensch a c b b Rechenblatt a b b c Lese-/Schreibkopf endliche Kontrolle Turingmaschine Eine Turingmaschine
A.M. Turing (1937): Maschinenmodell zur exakten Beschreibung des Begriffs effektiv berechenbar Stift Mensch a c b b Rechenblatt a b b c Lese-/Schreibkopf endliche Kontrolle Turingmaschine Eine Turingmaschine
LOOP-Programme: Syntaktische Komponenten
 LOOP-Programme: Syntaktische Komponenten LOOP-Programme bestehen aus folgenden Zeichen (syntaktischen Komponenten): Variablen: x 0 x 1 x 2... Konstanten: 0 1 2... Operationssymbole: + Trennsymbole: ; :=
LOOP-Programme: Syntaktische Komponenten LOOP-Programme bestehen aus folgenden Zeichen (syntaktischen Komponenten): Variablen: x 0 x 1 x 2... Konstanten: 0 1 2... Operationssymbole: + Trennsymbole: ; :=
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Halteproblem/Kodierung von Turing-Maschinen
 Halteproblem/Kodierung von Turing-Maschinen Unser Ziel ist es nun zu zeigen, dass das sogenannte Halteproblem unentscheidbar ist. Halteproblem (informell) Eingabe: Turing-Maschine M mit Eingabe w. Frage:
Halteproblem/Kodierung von Turing-Maschinen Unser Ziel ist es nun zu zeigen, dass das sogenannte Halteproblem unentscheidbar ist. Halteproblem (informell) Eingabe: Turing-Maschine M mit Eingabe w. Frage:
Dank. Theoretische Informatik II. Teil II. Registermaschinen. Vorlesung
 Dank Vorlesung Theoretische Informatik II Bernhard Beckert Institut für Informatik Diese Vorlesungsmaterialien basieren zum Teil auf den Folien zu den Vorlesungen von Katrin Erk (gehalten an der Universität
Dank Vorlesung Theoretische Informatik II Bernhard Beckert Institut für Informatik Diese Vorlesungsmaterialien basieren zum Teil auf den Folien zu den Vorlesungen von Katrin Erk (gehalten an der Universität
Logik und Beweisbarkeit
 Logik und Beweisbarkeit Folien zur Vorlesung im Sommersemester 2016 Teil 1 Martin Mundhenk Univ. Jena, Institut für Informatik 12. April 2016 Vorlesung Logik und Beweisbarkeit (Sommer 2016) 1. Aussagenlogik
Logik und Beweisbarkeit Folien zur Vorlesung im Sommersemester 2016 Teil 1 Martin Mundhenk Univ. Jena, Institut für Informatik 12. April 2016 Vorlesung Logik und Beweisbarkeit (Sommer 2016) 1. Aussagenlogik
Algorithmen und Komplexität, Teil II: Berechenbarkeit und Komplexität
 Algorithmen und Komplexität, Teil II: Berechenbarkeit und Komplexität Ralph Keusch 21. November 2017 Berechenbarkeitstheorie RAM-Maschine 1: M 1 1 2: M 0 1 3: M 0 M 0 M 1 4: M 2 M 2 M 1 5: GOTO 3 IF M
Algorithmen und Komplexität, Teil II: Berechenbarkeit und Komplexität Ralph Keusch 21. November 2017 Berechenbarkeitstheorie RAM-Maschine 1: M 1 1 2: M 0 1 3: M 0 M 0 M 1 4: M 2 M 2 M 1 5: GOTO 3 IF M
Grundlagen der Theoretischen Informatik: Übung 10
 Grundlagen der Theoretischen Informatik: Übung 10 Joachim Selke Fachgebiet Theoretische Informatik Universität Hannover 20. Januar 2005 Turing-Maschinen als Rechenmaschinen gegeben sei eine Funktion f
Grundlagen der Theoretischen Informatik: Übung 10 Joachim Selke Fachgebiet Theoretische Informatik Universität Hannover 20. Januar 2005 Turing-Maschinen als Rechenmaschinen gegeben sei eine Funktion f
Unentscheidbarkeitssätze der Logik
 Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Unentscheidbarkeitssätze der Logik Elmar Eder () Unentscheidbarkeitssätze der Logik 1 / 30 Die Zahlentheorie ist nicht formalisierbar Satz (Kurt Gödel) Zu jedem korrekten formalen System der Zahlentheorie
Unvollständigkeit der Arithmetik
 Unvollständigkeit der Arithmetik Slide 1 Unvollständigkeit der Arithmetik Hans U. Simon (RUB) Email: simon@lmi.rub.de Homepage: http://www.ruhr-uni-bochum.de/lmi Unvollständigkeit der Arithmetik Slide
Unvollständigkeit der Arithmetik Slide 1 Unvollständigkeit der Arithmetik Hans U. Simon (RUB) Email: simon@lmi.rub.de Homepage: http://www.ruhr-uni-bochum.de/lmi Unvollständigkeit der Arithmetik Slide
Berechenbarkeit und Komplexität
 Teil II: Berechenbarkeit und Komplexität Algorithmen und Komplexität 22. November 2016 Berechenbarkeitstheorie RAM-Maschine 1: M 1 1 2: M 0 1 3: M 0 M 0 M 1 4: M 2 M 2 M 1 5: GOTO 3 IF M 2 > 0. M 2 : M
Teil II: Berechenbarkeit und Komplexität Algorithmen und Komplexität 22. November 2016 Berechenbarkeitstheorie RAM-Maschine 1: M 1 1 2: M 0 1 3: M 0 M 0 M 1 4: M 2 M 2 M 1 5: GOTO 3 IF M 2 > 0. M 2 : M
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie WS 11/12 155 Überblick Zunächst einmal definieren wir formal den Begriff
Ein formales Berechnungsmodell: Turingmaschinen. Turingmaschinen 26 / 62
 Ein formales Berechnungsmodell: Turingmaschinen Turingmaschinen 26 / 62 Ein formales Rechnermodell Bisher haben wir abstrakt von Algorithmen bzw. Programmen gesprochen und uns dabei JAVA- oder C++-Programme
Ein formales Berechnungsmodell: Turingmaschinen Turingmaschinen 26 / 62 Ein formales Rechnermodell Bisher haben wir abstrakt von Algorithmen bzw. Programmen gesprochen und uns dabei JAVA- oder C++-Programme
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 139 Unentscheidbarkeit Überblick Zunächst einmal definieren wir formal
VL-11: LOOP und WHILE Programme I. (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger
 VL-11: LOOP und WHILE Programme I (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger WS 2017, RWTH BuK/WS 2017 VL-11: LOOP und WHILE Programme I 1/46 Organisatorisches Nächste Vorlesung: Mittwoch,
VL-11: LOOP und WHILE Programme I (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger WS 2017, RWTH BuK/WS 2017 VL-11: LOOP und WHILE Programme I 1/46 Organisatorisches Nächste Vorlesung: Mittwoch,
Berechenbarkeit und Komplexität Vorlesung 10
 Berechenbarkeit und Komplexität Vorlesung 10 Prof. Dr. Wolfgang Thomas Lehrstuhl Informatik 7 RWTH Aachen 27. November 2014 Wolfgang Thomas, Informatik 7 () Vorlesung Berechenbarkeit und Komplexität 27.
Berechenbarkeit und Komplexität Vorlesung 10 Prof. Dr. Wolfgang Thomas Lehrstuhl Informatik 7 RWTH Aachen 27. November 2014 Wolfgang Thomas, Informatik 7 () Vorlesung Berechenbarkeit und Komplexität 27.
Wiederholung. Organisatorisches. VL-11: LOOP und WHILE Programme I. (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger
 Organisatorisches VL-11: LOOP und WHILE Programme I (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger Nächste Vorlesung: Mittwoch, November 29, 14:15 15:45 Uhr, Roter Hörsaal Webseite: http://algo.rwth-aachen.de/lehre/ws1718/buk.php
Organisatorisches VL-11: LOOP und WHILE Programme I (Berechenbarkeit und Komplexität, WS 2017) Gerhard Woeginger Nächste Vorlesung: Mittwoch, November 29, 14:15 15:45 Uhr, Roter Hörsaal Webseite: http://algo.rwth-aachen.de/lehre/ws1718/buk.php
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Grundlagen der Programmierung (Vorlesung 24)
 Grundlagen der Programmierung (Vorlesung 24) Ralf Möller, FH-Wedel Vorige Vorlesung Anwendung im Bereich Compilerbau Inhalt dieser Vorlesung Turing-Maschinen Berechenbarkeitstheorie, Halteproblem Lernziele
Grundlagen der Programmierung (Vorlesung 24) Ralf Möller, FH-Wedel Vorige Vorlesung Anwendung im Bereich Compilerbau Inhalt dieser Vorlesung Turing-Maschinen Berechenbarkeitstheorie, Halteproblem Lernziele
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12 Die Registermaschine (random access machine, RAM) 0 I 0 1 I 1 2 I 2 m I m Programm
Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12 Die Registermaschine (random access machine, RAM) 0 I 0 1 I 1 2 I 2 m I m Programm
Theoretische Informatik SS 03 Übung 3
 Theoretische Informatik SS 03 Übung 3 Aufgabe 1 a) Sind die folgenden Funktionen f : partiell oder total: f(x, y) = x + y f(x, y) = x y f(x, y) = x y f(x, y) = x DIV y? Hierbei ist x DIV y = x y der ganzzahlige
Theoretische Informatik SS 03 Übung 3 Aufgabe 1 a) Sind die folgenden Funktionen f : partiell oder total: f(x, y) = x + y f(x, y) = x y f(x, y) = x y f(x, y) = x DIV y? Hierbei ist x DIV y = x y der ganzzahlige
GTI. Hannes Diener. 18. Juni. ENC B-0123,
 GTI Hannes Diener ENC B-0123, diener@math.uni-siegen.de 18. Juni 1 / 32 Als Literatur zu diesem Thema empfiehlt sich das Buch Theoretische Informatik kurzgefasst von Uwe Schöning (mittlerweile in der 5.
GTI Hannes Diener ENC B-0123, diener@math.uni-siegen.de 18. Juni 1 / 32 Als Literatur zu diesem Thema empfiehlt sich das Buch Theoretische Informatik kurzgefasst von Uwe Schöning (mittlerweile in der 5.
Theoretische Informatik 1
 Theoretische Informatik 1 Die Komplexitätsklasse P David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Äquivalenz von RM und TM Äquivalenz, Sätze Simulation DTM
Theoretische Informatik 1 Die Komplexitätsklasse P David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Äquivalenz von RM und TM Äquivalenz, Sätze Simulation DTM
Berechenbarkeit und Komplexität Vorlesung 11
 Berechenbarkeit und Komplexität Vorlesung 11 Prof. Dr. Wolfgang Thomas Lehrstuhl Informatik 7 RWTH Aachen 7. Dezember 2014 Wolfgang Thomas, Informatik 7 () Vorlesung Berechenbarkeit und Komplexität 7.
Berechenbarkeit und Komplexität Vorlesung 11 Prof. Dr. Wolfgang Thomas Lehrstuhl Informatik 7 RWTH Aachen 7. Dezember 2014 Wolfgang Thomas, Informatik 7 () Vorlesung Berechenbarkeit und Komplexität 7.
Berechenbarkeit. Serie 4. Die Seminaraufgaben werden in den Übungen vom bis besprochen.
 Universität Leipzig Institut für Informatik Sommersemester 2018 Prof. Dr. Andreas Maletti Gustav Grabolle Mirko Schulze Aufgaben zur Lehrveranstaltung Berechenbarkeit Serie 4 Hinweise: Abgabeschluss für
Universität Leipzig Institut für Informatik Sommersemester 2018 Prof. Dr. Andreas Maletti Gustav Grabolle Mirko Schulze Aufgaben zur Lehrveranstaltung Berechenbarkeit Serie 4 Hinweise: Abgabeschluss für
Einführung in die mathematische Logik
 Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 19 Entscheidbarkeit und Berechenbarkeit In der letzten Vorlesung haben wir verschiedene mathematische Operationen
Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 19 Entscheidbarkeit und Berechenbarkeit In der letzten Vorlesung haben wir verschiedene mathematische Operationen
THEORETISCHE INFORMATIK UND LOGIK
 THEORETISCHE INFORMATIK UND LOGIK 3. Vorlesung: WHILE und LOOP Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 12. April 2017 Was bisher geschah... Grundbegriffe, die wir verstehen und erklären
THEORETISCHE INFORMATIK UND LOGIK 3. Vorlesung: WHILE und LOOP Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 12. April 2017 Was bisher geschah... Grundbegriffe, die wir verstehen und erklären
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik 0 KIT 17.05.2010 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik nationales Forschungszentrum Vorlesung in am
Theoretische Grundlagen der Informatik 0 KIT 17.05.2010 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik nationales Forschungszentrum Vorlesung in am
Diskrete Strukturen Kapitel 5: Algebraische Strukturen (Gruppen)
 WS 2015/16 Diskrete Strukturen Kapitel 5: Algebraische Strukturen (Gruppen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
WS 2015/16 Diskrete Strukturen Kapitel 5: Algebraische Strukturen (Gruppen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
Theoretische Informatik für Wirtschaftsinformatik und Lehramt
 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Entscheidungsprobleme Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität Erlangen-Nürnberg
Theoretische Informatik für Wirtschaftsinformatik und Lehramt Entscheidungsprobleme Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität Erlangen-Nürnberg
Mächtigkeit von WHILE-Programmen
 Mächtigkeit von WHILE-Programmen und rekursive Funktionen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 16. November 2010 Berthold Vöcking, Informatik 1 () Vorlesung
Mächtigkeit von WHILE-Programmen und rekursive Funktionen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 16. November 2010 Berthold Vöcking, Informatik 1 () Vorlesung
Falls H die Eingabe verwirft, so wissen wir, dass M bei Eingabe w nicht hält. M hält im verwerfenden Haltezustand. Beweis:
 1 Unentscheidbarkeit 2 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 #include char *s="include
1 Unentscheidbarkeit 2 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 #include char *s="include
Fragen 1. Muss eine DTM ein Wort zu Ende gelesen haben, um es zu akzeptieren? a) Ja! b) Nein!
 4 Turingmaschinen Eingabeband nicht nur lesen, sondern auch schreiben kann und die zudem mit ihrem Lese-Schreib-Kopf (LSK) nach links und rechts gehen kann. Das Eingabeband ist zudem in beide Richtungen
4 Turingmaschinen Eingabeband nicht nur lesen, sondern auch schreiben kann und die zudem mit ihrem Lese-Schreib-Kopf (LSK) nach links und rechts gehen kann. Das Eingabeband ist zudem in beide Richtungen
1.2 LOOP-, WHILE- und GOTO-Berechenbarkeit
 Die Programmiersprache LOOP (i) Syntaktische Komponenten: Variable: x 0, x 1, x 2,... Konstanten: 0, 1, 2,... Trennsymbole: ; := Operationszeichen: + Schlüsselwörter: LOOP DO END (ii) LOOP-Programme: Wertzuweisungen:
Die Programmiersprache LOOP (i) Syntaktische Komponenten: Variable: x 0, x 1, x 2,... Konstanten: 0, 1, 2,... Trennsymbole: ; := Operationszeichen: + Schlüsselwörter: LOOP DO END (ii) LOOP-Programme: Wertzuweisungen:
Vorlesung Diskrete Strukturen Die natürlichen Zahlen
 Vorlesung Diskrete Strukturen Die natürlichen Zahlen Bernhard Ganter WS 2009/10 Alles ist Zahl? Wenn in der modernen Mathematik alles auf Mengen aufgebaut ist, woher kommen dann die Zahlen? Sind Zahlen
Vorlesung Diskrete Strukturen Die natürlichen Zahlen Bernhard Ganter WS 2009/10 Alles ist Zahl? Wenn in der modernen Mathematik alles auf Mengen aufgebaut ist, woher kommen dann die Zahlen? Sind Zahlen
Typen von Programmiersprachen
 Typen von Programmiersprachen Berechenbarkeitstheorie: Formalisierung des intuitiven Berechenbarkeitsbegriffs man kann vier Typen von Programmiersprachen zum Berechnen von Zahlenfunktionen unterscheiden:
Typen von Programmiersprachen Berechenbarkeitstheorie: Formalisierung des intuitiven Berechenbarkeitsbegriffs man kann vier Typen von Programmiersprachen zum Berechnen von Zahlenfunktionen unterscheiden:
Übungen zur VP Mathematische Logik
 Übungen zur VP Mathematische Logik Alexander Bors 1. März 2017 Werden je nach Bedarf im Laufe des Semesters noch um weitere Übungen ergänzt. Übungen zur naiven Mengenlehre von Cantor (Vorlesung 1) Übung
Übungen zur VP Mathematische Logik Alexander Bors 1. März 2017 Werden je nach Bedarf im Laufe des Semesters noch um weitere Übungen ergänzt. Übungen zur naiven Mengenlehre von Cantor (Vorlesung 1) Übung
2. Imperative Programmierung und Berechenbarkeit - Registermaschinen -
 2. Imperative Programmierung und Berechenbarkeit - Registermaschinen - 2.1 Definition 2.2 Loop-Programme 2.3 While Programme 2.4 While Programme und rekursive Funktionen Im Wesentlichen: Tafel! Maschinenmodell
2. Imperative Programmierung und Berechenbarkeit - Registermaschinen - 2.1 Definition 2.2 Loop-Programme 2.3 While Programme 2.4 While Programme und rekursive Funktionen Im Wesentlichen: Tafel! Maschinenmodell
Semantik von Programmiersprachen SS 2017
 Lehrstuhl für Programmierparadigmen Denis Lohner Sebastian Ullrich denis.lohner@kit.edu sebastian.ullrich@kit.edu Semantik von Programmiersprachen SS 2017 http://pp.ipd.kit.edu/lehre/ss2017/semantik Lösungen
Lehrstuhl für Programmierparadigmen Denis Lohner Sebastian Ullrich denis.lohner@kit.edu sebastian.ullrich@kit.edu Semantik von Programmiersprachen SS 2017 http://pp.ipd.kit.edu/lehre/ss2017/semantik Lösungen
Der Satz von Rice. Dann ist C(S) eine unentscheidbare Menge.
 Der Satz von Rice Satz: Sei R die Klasse der (Turing-) berechenbaren Funktionen, S eine nichttriviale Teilmenge von R und C(S) ={w Mw berechnet eine Funktion aus S}. Dann ist C(S) eine unentscheidbare
Der Satz von Rice Satz: Sei R die Klasse der (Turing-) berechenbaren Funktionen, S eine nichttriviale Teilmenge von R und C(S) ={w Mw berechnet eine Funktion aus S}. Dann ist C(S) eine unentscheidbare
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 15.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 15.07.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen und Diskrete Strukturen Aufgaben zur Vorbereitung der Klausur
 Technische Universität Ilmenau WS 2008/2009 Institut für Mathematik Informatik, 1.FS Dr. Thomas Böhme Aufgabe 1 : Grundlagen und Diskrete Strukturen Aufgaben zur Vorbereitung der Klausur Gegeben sind die
Technische Universität Ilmenau WS 2008/2009 Institut für Mathematik Informatik, 1.FS Dr. Thomas Böhme Aufgabe 1 : Grundlagen und Diskrete Strukturen Aufgaben zur Vorbereitung der Klausur Gegeben sind die
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17.November 2011 INSTITUT FÜR THEORETISCHE 0 KIT 17.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17.November 2011 INSTITUT FÜR THEORETISCHE 0 KIT 17.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 11 15. Juli 2010 Einführung in die Theoretische
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 11 15. Juli 2010 Einführung in die Theoretische
Vorlesung Diskrete Strukturen Die natürlichen Zahlen
 Vorlesung Diskrete Strukturen Die natürlichen Zahlen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul Einführung
Vorlesung Diskrete Strukturen Die natürlichen Zahlen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul Einführung
6.4 Entscheidbarkeit. nein sein müssen, ist klar. THEO 6.4 Entscheidbarkeit 205/307 c Ernst W. Mayr
 6.4 Entscheidbarkeit Wortproblem Leerheit Äquivalenz Schnittproblem Typ 3 ja ja ja ja DCFL ja ja ja nein (*) Typ 2 ja ja nein (*) nein Typ 1 ja nein (*) nein nein Typ 0 nein (*) nein nein nein (*) Diese
6.4 Entscheidbarkeit Wortproblem Leerheit Äquivalenz Schnittproblem Typ 3 ja ja ja ja DCFL ja ja ja nein (*) Typ 2 ja ja nein (*) nein Typ 1 ja nein (*) nein nein Typ 0 nein (*) nein nein nein (*) Diese
Syntax von LOOP-Programmen
 LOOP-Berechenbarkeit Syntax von LOOP-Programmen Definition LOOP-Programme bestehen aus: Variablen: x 0, x 1, x 2, x 3,... Konstanten: 0, 1, 2, 3,... Trennsymbolen:; und := Operationen: + und Befehlen:
LOOP-Berechenbarkeit Syntax von LOOP-Programmen Definition LOOP-Programme bestehen aus: Variablen: x 0, x 1, x 2, x 3,... Konstanten: 0, 1, 2, 3,... Trennsymbolen:; und := Operationen: + und Befehlen:
Turing-Maschinen: Ein abstrakes Maschinenmodell
 Wann ist eine Funktion (über den natürlichen Zahlen) berechenbar? Intuitiv: Wenn es einen Algorithmus gibt, der sie berechnet! Was heißt, eine Elementaroperation ist maschinell ausführbar? Was verstehen
Wann ist eine Funktion (über den natürlichen Zahlen) berechenbar? Intuitiv: Wenn es einen Algorithmus gibt, der sie berechnet! Was heißt, eine Elementaroperation ist maschinell ausführbar? Was verstehen
Universelle Maschinen und universelle Funktionen
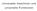 Universelle Maschinen und universelle Funktionen UNIVERSELLE FUNKTIONEN DEFINITION. Sei F eine Klasse von partiellen Funktionen über N. Eine partielle Funktion ϕ (n+1) ist n-universell für F, wenn (i)
Universelle Maschinen und universelle Funktionen UNIVERSELLE FUNKTIONEN DEFINITION. Sei F eine Klasse von partiellen Funktionen über N. Eine partielle Funktion ϕ (n+1) ist n-universell für F, wenn (i)
LOOP-Programme: Syntaktische Komponenten
 LOOP-Programme: Syntaktische Komponenten LOOP-Programme bestehen aus folgenden Zeichen (syntaktischen Komponenten): Variablen: x 0 x 1 x 2... Konstanten: 0 1 2... Operationssymbole: + Trennsymbole: ; :=
LOOP-Programme: Syntaktische Komponenten LOOP-Programme bestehen aus folgenden Zeichen (syntaktischen Komponenten): Variablen: x 0 x 1 x 2... Konstanten: 0 1 2... Operationssymbole: + Trennsymbole: ; :=
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik 0 KIT 07.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik nationales Forschungszentrum Vorlesung in am
Theoretische Grundlagen der Informatik 0 KIT 07.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik nationales Forschungszentrum Vorlesung in am
Satz 1.18 (Kompaktheitssatz der Aussagenlogik)
 Satz 1.18 (Kompaktheitssatz der Aussagenlogik) Σ F ist erfüllbar genau dann, wenn jede endliche Teilmenge von Σ erfüllbar ist. Σ F ist unerfüllbar genau dann, wenn es eine unerfüllbare endliche Teilmenge
Satz 1.18 (Kompaktheitssatz der Aussagenlogik) Σ F ist erfüllbar genau dann, wenn jede endliche Teilmenge von Σ erfüllbar ist. Σ F ist unerfüllbar genau dann, wenn es eine unerfüllbare endliche Teilmenge
Lösungsmenge L I = {x R 3x + 5 = 9} = L II = {x R 3x = 4} = L III = { }
 Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Funktionale Programmierung ALP I. λ Kalkül WS 2012/2013. Prof. Dr. Margarita Esponda. Prof. Dr. Margarita Esponda
 ALP I λ Kalkül WS 2012/2013 Berechenbarkeit - inspiriert durch Hilbert's Frage - im Jahr 1900, Paris - Internationaler Mathematikerkongress Gibt es ein System von Axiomen, aus denen alle Gesetze der Mathematik
ALP I λ Kalkül WS 2012/2013 Berechenbarkeit - inspiriert durch Hilbert's Frage - im Jahr 1900, Paris - Internationaler Mathematikerkongress Gibt es ein System von Axiomen, aus denen alle Gesetze der Mathematik
Berechenbarkeit. Script, Kapitel 2
 Berechenbarkeit Script, Kapitel 2 Intuitiver Berechenbarkeitsbegriff Turing-Berechenbarkeit WHILE-Berechenbarkeit Church sche These Entscheidungsprobleme Unentscheidbarkeit des Halteproblems für Turingmaschinen
Berechenbarkeit Script, Kapitel 2 Intuitiver Berechenbarkeitsbegriff Turing-Berechenbarkeit WHILE-Berechenbarkeit Church sche These Entscheidungsprobleme Unentscheidbarkeit des Halteproblems für Turingmaschinen
Wir suchen Antworten auf die folgenden Fragen: Was ist Berechenbarkeit? Wie kann man das intuitiv Berechenbare formal fassen?
 Einige Fragen Ziel: Wir suchen Antworten auf die folgenden Fragen: Wie kann man das intuitiv Berechenbare formal fassen? Was ist ein Algorithmus? Welche Indizien hat man dafür, dass ein formaler Algorithmenbegriff
Einige Fragen Ziel: Wir suchen Antworten auf die folgenden Fragen: Wie kann man das intuitiv Berechenbare formal fassen? Was ist ein Algorithmus? Welche Indizien hat man dafür, dass ein formaler Algorithmenbegriff
Einführung in die Berechenbarkeitstheorie
 Einführung in die Berechenbarkeitstheorie Timo Kötzing 4. November 2013 1 Einleitung Dieses Dokument bietet eine kurze Einführung in die Grundlagen der Berechenbarkeitstheorie (für eine Ausführliche Behandlung
Einführung in die Berechenbarkeitstheorie Timo Kötzing 4. November 2013 1 Einleitung Dieses Dokument bietet eine kurze Einführung in die Grundlagen der Berechenbarkeitstheorie (für eine Ausführliche Behandlung
Berechenbarkeitstheorie 19. Vorlesung
 1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Erinnerung:
1 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Erinnerung:
8. Der Äquivalenzsatz
 8. Der Äquivalenzsatz ÄQUIVALENZSATZ. Für eine (partielle) Funktion f : N n N sind folgende Aussagen äquivalent: f ist (partiell) Turing-berechenbar. f wird von einer k-band-turingmaschine berechnet (k
8. Der Äquivalenzsatz ÄQUIVALENZSATZ. Für eine (partielle) Funktion f : N n N sind folgende Aussagen äquivalent: f ist (partiell) Turing-berechenbar. f wird von einer k-band-turingmaschine berechnet (k
THEORETISCHE INFORMATIK UND LOGIK
 Was bisher geschah... Grundbegriffe, die wir verstehen und erklären können: DTM, NTM, Entscheider, Aufzähler, berechenbar/entscheidbar, semi-entscheidbar, unentscheidbar, Church-Turing-These THEORETISCHE
Was bisher geschah... Grundbegriffe, die wir verstehen und erklären können: DTM, NTM, Entscheider, Aufzähler, berechenbar/entscheidbar, semi-entscheidbar, unentscheidbar, Church-Turing-These THEORETISCHE
ALP I Turing-Maschine
 ALP I Turing-Maschine Teil I WS 2012/2013 Äquivalenz vieler Berechnungsmodelle Alonzo Church λ-kalkül Kombinatorische Logik Alan Turing Turing-Maschine Mathematische Präzisierung Effektiv Berechenbare
ALP I Turing-Maschine Teil I WS 2012/2013 Äquivalenz vieler Berechnungsmodelle Alonzo Church λ-kalkül Kombinatorische Logik Alan Turing Turing-Maschine Mathematische Präzisierung Effektiv Berechenbare
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 7.07.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik Turingmaschinen und rekursiv aufzählbare Sprachen (V) 7.07.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Theoretische Informatik 1
 Theoretische Informatik 1 Registermaschine David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Registermaschinen Algorithmusbegriff konkretisiert formale Beschreibung
Theoretische Informatik 1 Registermaschine David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Registermaschinen Algorithmusbegriff konkretisiert formale Beschreibung
Registermaschine (RAM), Church-Turing-These. Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen
 Registermaschine (RAM), Church-Turing-These Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 22 Registermaschinen (RAM) Programm b c(0) c(1) c(2) c(3) c(4)...
Registermaschine (RAM), Church-Turing-These Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 22 Registermaschinen (RAM) Programm b c(0) c(1) c(2) c(3) c(4)...
Kontrollfluss. man Verzweigungen und Sprünge. o bisher linear (von oben nach unten) o Für interessante Programme braucht
 Kontrollanweisungen Kontrollfluss o bisher linear (von oben nach unten) o Für interessante Programme braucht man Verzweigungen und Sprünge Kontrollfluss o bisher linear (von oben nach unten) o Für interessante
Kontrollanweisungen Kontrollfluss o bisher linear (von oben nach unten) o Für interessante Programme braucht man Verzweigungen und Sprünge Kontrollfluss o bisher linear (von oben nach unten) o Für interessante
Einführung in die mathematische Logik
 Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 22 Repräsentierbarkeit in einer Theorie Wir haben schon in der zwanzigsten Vorlesung davon gesprochen, wann eine arithmetische
Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 22 Repräsentierbarkeit in einer Theorie Wir haben schon in der zwanzigsten Vorlesung davon gesprochen, wann eine arithmetische
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier
 Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/17 Rekursions- und Lerntheorie
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/17 Rekursions- und Lerntheorie
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen
 Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Einführung in Berechenbarkeit, Komplexität und Formale Sprachen V8, 5.11.09 Willkommen zur Vorlesung Einführung in Berechenbarkeit, Komplexität und Formale Sprachen Friedhelm Meyer auf der Heide 1 Rückblick
Notengebung. Teilnote Kreuzerlliste: 60% 69% 4; 70% 79% 3; 80% 89% 2; 90% 100% 1. Falls Sie weitere Fragen haben, bitte melden Sie sich bei mir.
 Notengebung Die Gesamtnote für die Übung ergibt sich je zur Hälfte aus der Teilnote Kreuzerlliste und der Teilnote Zwischentest, gerundet auf freundliche Weise; für eine positive Benotung müssen beide
Notengebung Die Gesamtnote für die Übung ergibt sich je zur Hälfte aus der Teilnote Kreuzerlliste und der Teilnote Zwischentest, gerundet auf freundliche Weise; für eine positive Benotung müssen beide
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Berechenbarkeit und Komplexität: Mächtigkeit von Programmiersprachen: WHILE- und LOOP-Programme
 Berechenbarkeit und Komplexität: Mächtigkeit von Programmiersprachen: WHILE- und LOOP-Programme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 29. November 2007 Turing-mächtige
Berechenbarkeit und Komplexität: Mächtigkeit von Programmiersprachen: WHILE- und LOOP-Programme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität 29. November 2007 Turing-mächtige
Informatik III. Arne Vater Wintersemester 2006/ Vorlesung
 Informatik III Arne Vater Wintersemester 2006/07 11. Vorlesung 30.11.2006 1 Beziehungen zwischen den Sprachen Jede reguläre Sprache ist eine kontextfreie Sprache. Jede kontextfreie Sprache ist eine entscheidbare
Informatik III Arne Vater Wintersemester 2006/07 11. Vorlesung 30.11.2006 1 Beziehungen zwischen den Sprachen Jede reguläre Sprache ist eine kontextfreie Sprache. Jede kontextfreie Sprache ist eine entscheidbare
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier
 Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/16 Rekursions- und Lerntheorie
Rekursions- und Lerntheorie WiSe 2010/11; Univ. Trier Henning Fernau Universität Trier fernau@uni-trier.de Rekursions- und Lerntheorie, Fernau, Universität Trier, WiSe 2010 1/16 Rekursions- und Lerntheorie
Formale Methoden 2. Gaetano Geck Lehrstuhl I Logik in der Informatik WS 2015/2016
 Formale Methoden 2 Gaetano Geck Lehrstuhl I Logik in der Informatik WS 2015/2016 Teil 3: Kodierung 1 Motivation 2 Exkurs Grundlagen formaler Sprachen 3 Grundlagen 4 Beispielkodierungen FM2 (WS 2014/15,
Formale Methoden 2 Gaetano Geck Lehrstuhl I Logik in der Informatik WS 2015/2016 Teil 3: Kodierung 1 Motivation 2 Exkurs Grundlagen formaler Sprachen 3 Grundlagen 4 Beispielkodierungen FM2 (WS 2014/15,
Theoretische Informatik für Wirtschaftsinformatik und Lehramt
 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Universelle Turingmaschinen und Church sche These Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander
Theoretische Informatik für Wirtschaftsinformatik und Lehramt Universelle Turingmaschinen und Church sche These Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander
3. RAM als Rechnermodell
 3. RAM als Rechnermodell Motivation Wir möchten Berechnungsvorschriften (Algorithmen) formal beschreiben und deren Eigenschaften wie Korrektheit und Laufzeit analysieren Rechnermodell abstrahiert vom verwendeten
3. RAM als Rechnermodell Motivation Wir möchten Berechnungsvorschriften (Algorithmen) formal beschreiben und deren Eigenschaften wie Korrektheit und Laufzeit analysieren Rechnermodell abstrahiert vom verwendeten
Achim Feldmeier, 23. Juni : Penrose nimmt dieses Argument auf in Shadows of the Mind.
 Können Menschen mehr (Mathematik) als Computer? Turing - Penrose - Searle Achim Feldmeier, 23. Juni 2008 1931: Gödel beweist den Unvollständigkeitssatz. 1937: Turing beweist das Halteproblem. 1961: Lucas
Können Menschen mehr (Mathematik) als Computer? Turing - Penrose - Searle Achim Feldmeier, 23. Juni 2008 1931: Gödel beweist den Unvollständigkeitssatz. 1937: Turing beweist das Halteproblem. 1961: Lucas
Mengen. (Nicht-) Elemente einer Menge { 3, 4 } { 1, { 2 }, { 3, 4 }, { 5 } } 3 { 1, { 2 }, { 3, 4 }, { 5 } }
 Mengen Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor) Notation 1. Aufzählung aller Elemente: { 1,
Mengen Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor) Notation 1. Aufzählung aller Elemente: { 1,
Programm heute. Algorithmen und Datenstrukturen (für ET/IT) Definition Algorithmus. Wie beschreibt man Algorithmen?
 Programm heute Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2015 1 Einführung Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München 2 Grundlagen von Algorithmen
Programm heute Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2015 1 Einführung Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München 2 Grundlagen von Algorithmen
Theorie der Informatik. Theorie der Informatik P und NP Polynomielle Reduktionen NP-Härte und NP-Vollständigkeit
 Theorie der Informatik 13. Mai 2015 20. P, NP und polynomielle Reduktionen Theorie der Informatik 20. P, NP und polynomielle Reduktionen 20.1 P und NP Malte Helmert Gabriele Röger 20.2 Polynomielle Reduktionen
Theorie der Informatik 13. Mai 2015 20. P, NP und polynomielle Reduktionen Theorie der Informatik 20. P, NP und polynomielle Reduktionen 20.1 P und NP Malte Helmert Gabriele Röger 20.2 Polynomielle Reduktionen
Theoretische Informatik
 Theoretische Informatik Prof. Meer, Dr. Gengler Aufgabenblatt 12 Besprechung in KW 03 / Abgabe in KW 04 Heften Sie unbedingt alle Blätter Ihrer Lösung zusammen und geben Sie oben auf dem ersten Blatt Ihren
Theoretische Informatik Prof. Meer, Dr. Gengler Aufgabenblatt 12 Besprechung in KW 03 / Abgabe in KW 04 Heften Sie unbedingt alle Blätter Ihrer Lösung zusammen und geben Sie oben auf dem ersten Blatt Ihren
Kapitel 2. Elementare Zahlentheorie Primfaktorzerlegung
 Kapitel 2. Elementare Zahlentheorie 2.1. Primfaktorzerlegung Menge der ganzen Zahlen Z = {..., 3, 2, 1, 0, 1, 2, 3,...} Addition Inverse Multiplikation Z Z Z, Z Z, Z Z Z, (a, b) a + b a a (a, b) a b Ausgezeichnete
Kapitel 2. Elementare Zahlentheorie 2.1. Primfaktorzerlegung Menge der ganzen Zahlen Z = {..., 3, 2, 1, 0, 1, 2, 3,...} Addition Inverse Multiplikation Z Z Z, Z Z, Z Z Z, (a, b) a + b a a (a, b) a b Ausgezeichnete
Algorithmen und Datenstrukturen (für ET/IT)
 Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2016 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Programm heute 1 Einführung 2 Grundlagen von Algorithmen
Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2016 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Programm heute 1 Einführung 2 Grundlagen von Algorithmen
Mengen. Eigenschaften. Spezielle Mengen (1) Prominente Mengen. ! Mengenzugehörigkeit
 Mengen! Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor)! Notation 1. Aufzählung aller Elemente: {
Mengen! Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor)! Notation 1. Aufzählung aller Elemente: {
Entscheidungsprobleme
 Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge U Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Entscheidungsprobleme übliche Formulierung gegeben: Eingabe x aus einer Grundmenge U Frage: Hat x eine bestimmte Eigenschaft P? Beispiel: gegeben: Frage: n N Ist n eine Primzahl? Formalisierung: Grundmenge
Automaten, Formale Sprachen und Berechenbarkeit I Wichtige Begriffe
 Automaten, Formale Sprachen und Berechenbarkeit I Wichtige Begriffe Eine partielle Funktion ist eine Relation f A B; für jedes x dom(f) gibt es ein y range(f) mit x f y; wir schreiben statt f A B und x
Automaten, Formale Sprachen und Berechenbarkeit I Wichtige Begriffe Eine partielle Funktion ist eine Relation f A B; für jedes x dom(f) gibt es ein y range(f) mit x f y; wir schreiben statt f A B und x
Übung zur Vorlesung Berechenbarkeit und Komplexität
 RWTH Aachen Lehrgebiet Theoretische Informatik Reidl Ries Rossmanith Sanchez Tönnis WS 2012/13 Übungsblatt 7 26.11.2012 Übung zur Vorlesung Berechenbarkeit und Komplexität Aufgabe T15 Entwickeln Sie ein
RWTH Aachen Lehrgebiet Theoretische Informatik Reidl Ries Rossmanith Sanchez Tönnis WS 2012/13 Übungsblatt 7 26.11.2012 Übung zur Vorlesung Berechenbarkeit und Komplexität Aufgabe T15 Entwickeln Sie ein
Theoretische Informatik 1
 Theoretische Informatik 1 Teil 2 Bernhard Nessler Institut für Grundlagen der Informationsverabeitung TU Graz SS 2007 Übersicht 1 Codierung, Gödelisierung Paare, Tupel, Listen Überabzählbarkeit 2 Ist universell?
Theoretische Informatik 1 Teil 2 Bernhard Nessler Institut für Grundlagen der Informationsverabeitung TU Graz SS 2007 Übersicht 1 Codierung, Gödelisierung Paare, Tupel, Listen Überabzählbarkeit 2 Ist universell?
13. Woche: NP-Vollständigkeit Satz von Cook-Levin Anwendungen in der Kryptographie
 13 Woche: NP-Vollständigkeit Satz von Cook-Levin Anwendungen in der Kryptographie 13 Woche: NP-Vollständigkeit, Satz von Cook-Levin, Anwendungen 276/ 333 N P-Vollständigkeit Ḋefinition NP-vollständig Sei
13 Woche: NP-Vollständigkeit Satz von Cook-Levin Anwendungen in der Kryptographie 13 Woche: NP-Vollständigkeit, Satz von Cook-Levin, Anwendungen 276/ 333 N P-Vollständigkeit Ḋefinition NP-vollständig Sei
