Charakterisierungen spezieller windschiefer Regelflächen durch die Normalkrümmung ausgezeichneter Flächenkurven
|
|
|
- Adolph Max Melsbach
- vor 5 Jahren
- Abrufe
Transkript
1 arxiv: v1 [math.dg] 25 Apr 2014 Charakterisierungen spezieller windschiefer Regelflächen durch die Normalkrümmung ausgezeichneter Flächenkurven Stylianos S. Stamatakis Abteilung für Mathematik der Aristoteles Universität Thessaloniki GR Thessaloniki, Griechenland Abstract We consider ruled surfaces in the three-dimensional Euclidean space and some geometrically distinguished families of curves on them whose normal curvature has a concrete form. The aim of this paper is to find and classify all ruled surfaces with the mentioned property MSC 2010: 53A25, 53A05 Keywords: Ruled surfaces, normal curvature, principal curvatures, Edlingersurfaces, helicoid 1 Einleitung Geometrisch ausgezeichnete Kurvenscharen auf windschiefen Regelfächen des euklidischen Raumes R 3 sind von verschiedenen Autoren vielfach untersucht worden. Eine Reihe von Resultaten ergeben sich, wenn man fordert, dass die betrachtete Kurvenschar eine zusätzliche Eigenschaft besitzt. Die vorliegende Arbeit liefert einen Beitrag zu diesem Themenkreis. Wir betrachten spezielle Kurvenscharen auf einer windschiefen Regelfläche und nehmen an, dass die Normalkrümmung längs jeder dieser Kurven eine bestimmte Gestalt besitzt. Unser Ziel ist die Klassifikation der Regelflächen mit der geforderten Eigenschaft. Im euklidischen Raum R 3 sei Φ eine reguläre und von torsalen Erzeugenden freie Regelfläche mit der Striktionslinie s = s(u) und dem Erzeugendeneinheitsvektor 1
2 e(u). Φ sei über dem Definitionsgebiet G := I R (I R offenes Intervall) von der Klasse C 3. Eine Parameterdarstellung von Φ lautet dann (1) x(u,v) = s(u)+ve(u), u I, v R. Wegen der Annahme gilt (2) s (u), e (u) = 0 u I, wobei Strich Ableitung nach u und, das Standard-Skalarprodukt im Raume R 3 bedeuten. Den Parameter u wählen wir so, dass (3) e (u) = 1 u I gilt. Längs der Striktionslinie betrachten wir das begleitende Dreibein{e(u), n(u), z(u)}, wobei n(u) := e (u) der Zentralnormalenvektor und z(u) := e(u) n(u) der Zentraltangentenvektor von Φ ist. Es gelten folgende Ableitungsgleichungen : (4) e (u) = n(u), n (u) = e(u) + k(u) z(u), z (u) = k(u) n(u), wobei (5) k(u) = (e(u), e (u), e (u)) die konische Krümmung von Φ bedeutet. Für den Drall δ(u) und die Striktion σ(u) von Φ haben wir (6) δ(u) = (e(u), e (u), s (u)), σ(u) := (e(u), s (u)) ( π < σ π,signσ = signδ). Die Funktionen k(u), δ(u) und σ(u) bilden bekanntlich ein vollständiges Invariantensystem von Φ (vgl. [3], 2 2 S.19). Die Koordinatenfunktionen g ij bzw. h ij des ersten bzw. zweiten Fundamentaltensors bezüglich der (lokalen) Koordinaten u 1 := u, u 2 := v lauten ( ) v (g ij ) = 2 +δ 2 (λ 2 +1) δλ δλ 1 (7) ( ) [kv (h ij ) = 1 2 +δ v+δ 2, (k λ)] δ w δ 0 mit w := v 2 +δ 2. Für die Gaußsche Krümmung K und die mittlere Krümmung H von Φ gelten die Beziehungen (8) K = δ2 w 4, H = kv2 +δ v +δ 2 (k +λ) 2w 3, 2
3 wobei λ := cotσ gesetzt wurde. Eine windschiefe Regelfläche Φ, deren sämtliche Schmiegquadriken Drehhyperboloide sind, bezeichnet man bekanntlich als Edlinger-Fläche [2], [3]. Hinreichende und notwendige Bedingungen dafür sind die Beziehungen ([1], S.103) (9) δ = kλ+1 = 0. Es handelt sich um eine konstant gedrallte Regelfläche mit der Striktionslinie als Krümmugslinie. Die Kurven konstanten Striktionsabstandes, d.h. die Kurven v = konst., sind in diesem Fall Krümmungslinien von Φ. Die andere Krümmungslinienschar wird durch [k 2 v 2 +δ 2 (k 2 +1)]du δkdv = 0 bestimmt. Die zugehörigen Normalkrümmungen der beiden Krümmungslinien(Hauptkrümmungen) lauten (10) k 1 = k(u)w 1, k 2 = δ2 (u) k(u) w 3. 2 Der Fall der Hauptkrümmungen Im folgenden betrachten wir ausschließlich windschiefe Regelflächen des Raumes R 3 mit der Parameterdarstellung (1), die die Voraussetzungen (2) und (3) erfüllen. Ausgehend von (10) stellen wir zunächst die Aufgabe, alle Regelflächen zu bestimmen, deren eine Hauptkrümmung die Gestalt (11) k i = f(u)w n, n Z, f(u) C 0 (I), i = 1 oder 2, besitzt. Es ist offenbar f(u) 0 u I, denn Φ ist windschief. Für die Normalkrümmung in Richtung du : dv findet man unter Beachtung von (7) (12) k N = 1 w [kv2 +δ v +δ 2 (k λ)] du 2 +2δdudv [v 2 +δ 2 (λ 2 +1)] du 2 +2δλdudv+dv 2, woraus mit (11) [f w n+1 [v 2 +δ 2 (λ 2 +1)]+kv 2 +δ v +δ 2 (k λ)]du 2 +2δ(f λw n+1 1)dudv+f w n+1 dv 2 = 0 folgt. Diese in du : dv quadratische Gleichung besitzt genau dann eine Lösung, wenn ihre Diskriminante verschwindet: (13) f 2 w 2n+4 +f [kv 2 +δ v +δ 2 (k +λ)]w n+1 δ 2 = 0 u I, v R. 3
4 Es sei zunächst n = 0. Dann erhalten wir aus (13) f 4 (v 2 +δ 2 ) 4 2f 2 δ 2 (v 2 +δ 2 ) 2 +δ 4 f 2 [kv 2 +δ v +δ 2 (k +λ)] 2 (v 2 +δ 2 ) = 0. Auf der linken Seite steht ein Polynom achten Grades in v, das für jedes u I und unendlich viele Werte v R zu erfüllen ist. Durch Koeffizientenvergleich mit dem Nullpolynom ergibt sich f = 0, also ein Widerspruch. Wir unterscheiden nun folgende Fälle: Fall I: Es sei n ungerade. Die Beziehung (13) erhält die Gestalt (14) Q(v) : = f [kv 2 +δ v +δ 2 (k +λ)](v 2 +δ 2 ) n+1 2 +f 2 (v 2 +δ 2 ) n+2 δ 2 = 0 u I, v R. Ist n 1, so liefert das Verschwinden des Koeffizienten des höchsten Grades des Polynoms Q(v) f = 0, was nicht möglich ist. Es sei n = 1. Dann wird (14) Q(v) = f 2 (v 2 +δ 2 )+f [kv 2 +δ v +δ 2 (k +λ)] δ 2 = 0. Aus dem Verschwinden der Koeffizienten des Polynoms Q(v) erhalten wir d.h. Φ muss eine Edlinger-Fläche sein. f = k, δ = kλ+1 = 0, Es sei n = 3 und k 1 die Hauptkrümmung, die die Gestalt (11) besitzt, d.h. k 1 = f(u)w 3. Dann erhalten wir aus (8) für die andere Hauptkrümmung k 2 = f (u)w 1 mit f (u) := δ2 (u) f(u), d.h. eine Hauptkrümmung von Φ hat die Gestalt (11), wobei n = 1 ist. Wie wir im vorangehenden Fall gesehen haben, ist Φ wieder eine Edlinger-Fläche. Der Fall n 5 führt auf einen Widerspruch, wie man leicht feststellen kann. Fall II: Es sei n gerade. Für n = 2 folgt aus (13) Q(v) := f 2 [kv 2 +δ v +δ 2 (k +λ)] 2 (f 2 δ 2 ) 2 (v 2 +δ 2 ) = 0 u I, v R. Das Verschwinden des Koeffizienten f 2 k 2 der Potenz höchsten Grades des Polynoms Q(v) liefert k = 0. Aus dem Verschwinden der übrigen Koeffizienten folgt f 2 δ 2 (f 2 δ 2 ) 2 = 2f 2 δ 2 δ λ = f 2 δ 4 λ 2 δ 2 (f 2 δ 2 ) 2 = 0, 4
5 woraus wir δ = λ = 0 und f = ±δ erhalten. Es handelt sich also in diesem Fall um eine Wendelfläche. Die Fälle n 2 und n 4 führen auf Widersprüche, wie man leicht zeigen kann. Wir fassen unsere Ergebnisse zusammen: Proposition 1 Es sei Φ R 3 eine windschiefe C 3 -Regelfläche, deren eine Hauptkrümmung die Gestalt (11) besitzt. Dann gilt eine der folgenden Eigenschaften: (a) n = 1, f(u) = k(u) und Φ ist eine Edlinger-Fläche. (b) n = 2, f(u) = ±δ(u) und Φ ist eine Wendelfläche. (c) n = 3, f(u) = δ 2 (u)k 1 (u) und Φ ist eine Edlinger-Fläche. Aus diesem Satz folgt unmittelbar folgendes Corollary 2 Es sei Φ R 3 eine windschiefe C 3 -Regelfläche, zwischen deren Hauptkrümmungen die Beziehung (15) δ 2 k 3 1 +k4 k 2 = 0 bestehe. Dann ist Φ eine Edlinger-Fläche. Proof. Auf Grund von (8) und (15) folgt und daraus Wegen Satz 1 ist aber k 4 1 = k4 w 4 k 1 = ±kw 1. k 1 = kw 1. Somit besitzt die Hauptkrümmung k 1 die Gestalt (11), wobei n = 1 ist. Daher ist Φ eine Edlinger-Fläche. 3 Der Fall der Normalkrümmung Darüer hinaus betrachten wir weitere geometrisch ausgezeichnete Kurvenscharen auf Φ, längs deren die Normalkrümmung die Gestalt (16) k N = f(u)w n, n Z, f(u) C 0 (I) besitzt. Unser Ziel ist die Bestimmung dieser Regelflächen Es sei S 1 die Schar der Kurven konstanten Striktionsabstandes. Nach (12) lautet die Normalkrümmung längs einer Kurve von S 1 (17) k N = 1 w kv2 δ v +δ 2 (k λ) v 2 +δ 2 (λ 2 +1) 5
6 und hat genau dann die Gestalt (16), wenn (18) f w n+1 [v 2 +δ 2 (λ 2 +1)]+kv 2 +δ v+δ 2 (k λ) = 0. Offensichtlich ist genau dann f = 0, wenn (19) kv 2 +δ v +δ 2 (k λ) = 0 identisch in v gilt, d.h. genau dann, wenn also wenn Φ eine Wendelfläche ist. k = δ = λ = 0, Es sei nun f 0. Für n = 1 folgt aus (18) Q(v) := f[v 2 +δ 2 (λ 2 +1)]+kv 2 +δ v +δ 2 (k λ) = 0. Das Verschwinden der Koeffizienten des Polynoms Q(v) liefert f = k, δ = 0, λ(kλ+1) = 0. Somit ist die Regelfläche Φ entweder ein konstant gedralltes Orthoid (δ = λ = 0) oder eine Edlinger-Fläche (δ = kλ+1 = 0). Für n > 1 folgt aus (18) Q(v) := f 2 (v 2 +δ 2 ) n+1 [v 2 +δ 2 (λ 2 +1)] 2 [kv 2 +δ v +δ 2 (k λ)] 2 = 0. Aus dem Verschwinden des Koeffizienten des höchsten Grades des Polynoms Q(v) folgt f = 0. Dies ist aber nicht möglich. Für n < 1 folgt aus (18) Q(v) := (v 2 +δ 2 ) n 1 [kv 2 +δ v +δ 2 (k λ)] 2 f 2 [v 2 +δ 2 (λ 2 +1)] 2 = 0. Das Verschwinden des Koeffizienten des höchsten Grades des Polynoms Q(v) liefert k = 0 und demnach (20) Q(v) = (v 2 +δ 2 ) n 1 (δ v δ 2 λ) 2 f 2 [v 2 +δ 2 (λ 2 +1)] 2 = 0. Ist n = 2, so erhält Q(v) die Gestalt (21) Q(v) = (v 2 +δ 2 )(δ v δ 2 λ) 2 f 2 [v 2 +δ 2 (λ 2 +1)] 2 = 0. Aus dem Verschwinden der Koeffizienten von Q(v) folgt f = 0, also ein Widerspruch. Für n < 2 liefert das Verschwinden des Koeffizienten des höchsten Grades des Polynoms Q(v) in (20) δ = 0 und daher (22) Q(v) = δ 4 λ 2 (v 2 +δ 2 ) n 1 f 2 [v 2 +δ 2 (λ 2 +1)] 2 = 0. 6
7 Für n = 3 ist Q(v) = δ 4 λ 2 (v 2 +δ 2 ) 2 f 2 [v 2 +δ 2 (λ 2 +1)] 2 = 0. Aus dem Verschwinden der Koeffizienten des Polynoms Q(v) folgt wieder f = 0, also ein Widerspruch. Für n < 3 erhalten wir aus (22) was ebenfalls unmöglich ist. Somit ist folgender Satz bewiesen: λ = f = 0, Proposition 3 Die Normalkrümmung längs der Kurven konstanten Striktionsabstandes einer windschiefen C 3 -Regelfläche Φ R 3 besitze die Gestalt (16). Dann gilt eine der folgenden Eigenschaften: (a) f = 0 und Φ ist eine Wendelfläche. (b) n = 1,f(u) = k(u) und Φ ist ein konstant gedralltes Orthoid oder eine Edlinger-Fläche Es sei S 2 die Schar der Orthogonaltrajektorien der Schar S 1. Sie ist durch [v 2 +δ 2 (λ 2 +1)]du+δλdv = 0 bestimmt. Nach (12) lautet die zugehörige Normalkrümmung (23) k N = 1 w 3 δ2 λ [(kλ+2)v 2 +δ λv+δ 2 (λ 2 +kλ+2)] v 2 +δ 2 (λ 2 +1) und hat genau dann die Gestalt (16), wenn gilt (24) f w n+3 [v 2 +δ 2 (λ 2 +1)]+δ 2 λ[(kλ+2)v 2 +δ λv+δ 2 (λ 2 +kλ+2)] = 0. Es ist f = 0 genau dann, wenn λ[(kλ+2)v 2 +δ λv +δ 2 (λ 2 +kλ+2)] = 0 identisch in v gilt. Wäre λ 0, so würden wir folgern kλ+2 = δ λ = δ 2 (λ 2 +kλ+2) = 0, was nicht möglich ist. Somit ist f = 0 genau dann, wenn λ = 0, d.h. wenn Φ ein Orthoid ist. Es sei nun fλ 0. Für n = 3 folgt aus (24) (25) Q(v) := f [v 2 +δ 2 (λ 2 +1)]+δ 2 λ[(kλ+2)v 2 +δ λv+δ 2 (λ 2 +kλ+2)] = 0. 7
8 Aus dem Verschwinden der Koeffizienten des Polynoms Q(v) erhalten wir f = δ 2 λ(kλ+2), δ = 0, kλ+1 = 0, somit haben wir f = δ 2 λ und die Regelfläche Φ ist eine Edlinger-Fläche. Man überzeugt sich leicht, dass die Fälle n > 3 und n < 3 auf Widersprüche führen. Somit gilt der Proposition 4 Die Normalkrümmung längs der Orthogonaltrajektorien der Kurven konstanter Striktionsabstandes einer windschiefen C 3 -Regelfläche Φ R 3 besitze die Gestalt (16). Dann gilt eine der folgenden Eigenschaften: (a) f = 0 und Φ ist ein Orthoid. (b) n = 3, f(u) = δ 2 (u)k 1 (u) und Φ ist eine Edlinger-Fläche Es sei S 3 die Schar der Orthogonaltrajektorien der Erzeugenden, die durch δλdu+dv = 0 bestimmt ist. Nach (12) lautet die zugehörige Normalkrümmung (26) k N = kv2 δ v δ 2 (k +λ) w 3 und hat genau dann die Gestalt (16), wenn gilt (27) f w n+3 +kv 2 +δ v +δ 2 (k +λ) = 0. Es ist f = 0 genau dann, wenn (19) identisch in v gilt, d.h. genau dann, wenn also wenn Φ eine Wendelfläche ist. k = λ = δ = 0, Es sei nun f 0. Für n = 3 folgt aus (27) (28) Q(v) := kv 2 +δ v+δ 2 (k +λ)+f = 0. Das Verschwinden der Koeffizienten des Polynoms Q(v) liefert f = δ 2 λ, k = 0, δ = 0. Somit ist die Regelfläche Φ ein konstant gedralltes Konoid. Für n = 2 folgt aus (27) Q(v) := f 2 (v 2 +δ 2 ) [kv 2 +δ v+δ 2 (k +λ)] 2 = 0. Aus dem Verschwinden der Koeffizienten des Polynoms Q(v) folgt k = 0, f 2 = δ 2, δ λ = 0, f 2 = δ 2 λ 2 = 0, 8
9 also f = 0, d.h. ein Widerspruch. Für n = 1 folgt aus (27) Q(v) := f(v 2 +δ 2 )+kv 2 +δ v +δ 2 (k +λ) = 0. Aus dem Verschwinden der Koeffizienten des Polynoms Q(v) folgt f = k,δ = 0,λ = 0. Somit ist Φ ein konstant gedralltes Orthoid. Die Fälle n 0 und n 4 führen auf Widersprüche, wie man leicht zeigen kann. Daher gilt: Proposition 5 Die Normalkrümmung längs der Orthogonaltrajektorien der Erzeugenden einer windschiefen C 3 -Regelfläche Φ R 3 besitze die Gestalt (16). Dann gilt eine der folgenden Eigenschaften: (a) f = 0 und Φ ist eine Wendelfläche. (b) n = 3, f(u) = δ 2 (u)λ(u) und Φ ist ein konstant gedralltes Konoid. (c) n = 1, f(u) = k(u) und Φ ist ein konstant gedralltes Orthoid Es sei S 4 die Schar der Kurven konstanter Gaußscher Krümmung, d.h. die Schar der Kurven längs denen die Gaußsche Krümmung konstant ist [4]. Sie ist durch δ (δ 2 v 2 )du+2δvdv = 0 bestimmt. Nach (12) lautet die zugehörige Normalkrümmung (29) k N = 1 w 4δ2 v[kv 3 +δ 2 (k λ)v +δ 2 δ ] A wobei A = ( 4δ 2 +δ 2) v 4 +4δ 2 δ λv 3 +2δ 2[ 2δ 2( λ 2 +1 ) δ 2] v 2 4δ 4 δ λv+δ 4 δ 2 gesetzt wurde, und hat genau dann die Gestalt (16), wenn gilt: (30) f w n+1 [(4δ 2 +δ 2)v 4 +4δ 2 δ λv 3 +2δ 2 [2δ 2 (λ 2 +1) δ 2]v 2 4δ 4 δ λv+δ 4 δ 2]+4δ 2 v[kv 3 +δ 2 (k λ)v+δ 2 δ ] = 0. Es ist f = 0 genau dann, wenn kv 3 +δ 2 (k λ)v+δ 2 δ = 0 identisch in v erfüllt ist, d.h. genau dann, wenn k = λ = δ = 0, also wenn Φ eine Wendelfläche ist. 9
10 Es sei im Folgenden f 0. Für n = 1 folgt aus (30) (31) Die Koeffizienten Q(v) := f [(4δ 2 +δ 2)v 4 +4δ 2 δ λv 3 +2δ 2 [2δ 2 (λ 2 +1) δ 2]v 2 4δ 4 δ λv +δ 4 δ 2]+4δ 2 v[kv 3 +δ 2 (k λ)v+δ 2 δ ] = 0. a 4 := f (4δ 2 +δ 2)+4δ 2 k, a 3 := 4f δ 2 δ λ, a 2 := 2f δ 2 [2δ 2 (λ 2 +1) δ 2]+4δ 4 (k λ), a 1 := 4f δ 4 δ λ+4δ 4 δ, a 0 := f δ 4 δ 2 des Polynoms Q(v) müssen verschwinden. Aus a 0 = 0 folgt δ = 0 und sodann aus a 2 = a 4 = 0, dass f = k, λ(kλ+1) = 0 gilt. Folglich ist die Regelfläche Φ entweder ein konstant gedralltes Orthoid (δ = λ = 0) oder eine Edlinger-Fläche (δ = kλ+1 = 0). Die Fälle n > 1 und n < 1 führen auf Widersprüche. Wir haben somit folgenden Satz bewiesen: Proposition 6 Die Normalkrümmung längs der Kurven konstanten Gaußscher Krümmung einer windschiefen C 3 -Regelfläche Φ R 3 besitze die Gestalt (16). Dann gilt eine der folgenden Eigenschaften: (a) f = 0 und Φ ist eine Wendelfläche. (b) n = 1, f(u) = k(u) und Φ ist ein konstant gedralltes Orthoid oder eine Edlinger-Fläche. Folgende Tabelle gibt eine Übersicht über die obigen Resultate. Normalkrümmung der Gestalt k N = f w n längs einer der Krümmungslinien der Kurven konstanten Striktionsabstandes der Orthogonaltrajektorien der Kurven konstanten Striktionsabstandes der Orthogonaltrajektorien der Erzeugenden der Kurven konstanter Gaußscher Krümmung f n Art der Regelfläche k ±δ δ 2 k 1 0 k δ 2 k k δ 2 λ 0 k Edlinger-Fläche Wendelfläche Edlinger-Fläche Wendelfläche konstant gedralltes Orthoid oder Edlinger-Fläche Orthoid Edlinger-Fläche Wendelfläche konstant gedralltes Orthoid konstant gedralltes Konoid Wendelfläche konstant gedralltes Orthoid oder Edlinger-Fläche 10
11 References [1] H. Brauner: Über Strahlflächen von konstantem Drall. Monatsh. Math. 63 (1959), [2] R. Edlinger: Über Regelflächen, deren sämtliche oskulierenden Hyperboloide Drehhyperboloide sind. S.-B. Akad. Wiss. Wien 132 (1923), [3] J. Hoschek: Liniengeometrie. Bibliographisches Institut, Zürich [4] H. Sachs: Einige Kennzeichnungen der Edlinger-Flächen. Monatsh. Math. 77 (1973),
Lineare Algebra II 6. Übungsblatt
 Lineare Algebra II 6 Übungsblatt Fachbereich Mathematik SS 2011 Prof Dr Kollross 18/19 Mai 2011 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minimalpolynom) Bestimmen Sie das Minimalpolynom der
Lineare Algebra II 6 Übungsblatt Fachbereich Mathematik SS 2011 Prof Dr Kollross 18/19 Mai 2011 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minimalpolynom) Bestimmen Sie das Minimalpolynom der
Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik II für biw/ciw/mach/mage/vt
 Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
[5], [0] v 4 = + λ 3
![[5], [0] v 4 = + λ 3 [5], [0] v 4 = + λ 3](/thumbs/62/48038195.jpg) Aufgabe 9. Basen von Untervektorräumen. Bestimmen Sie Basen von den folgenden Untervektorräumen U K des K :. K = R und U R = span,,,,,.. K = C und U C = span + i, 6, i. i i + 0. K = Z/7Z und U Z/7Z = span
Aufgabe 9. Basen von Untervektorräumen. Bestimmen Sie Basen von den folgenden Untervektorräumen U K des K :. K = R und U R = span,,,,,.. K = C und U C = span + i, 6, i. i i + 0. K = Z/7Z und U Z/7Z = span
Fachbereich Mathematik/Informatik 16. Juni 2012 Prof. Dr. H. Brenner. Mathematik für Anwender II. Testklausur mit Lösungen
 Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Lösung - Serie 24. D-MAVT/D-MATL Analysis II FS 2018 Dr. Andreas Steiger. 1. Welche der folgenden Differenzialgleichungen ist linear? (y 2) 2 = y.
 D-MAVT/D-MATL Analysis II FS 018 Dr. Andreas Steiger Lösung - Serie 4 1. Welche der folgenden Differenzialgleichungen ist linear? (a) (y ) = y (b) y + y 1 x + y 1 + x = 1 x (c) y = xy x y (d) y + y + y
D-MAVT/D-MATL Analysis II FS 018 Dr. Andreas Steiger Lösung - Serie 4 1. Welche der folgenden Differenzialgleichungen ist linear? (a) (y ) = y (b) y + y 1 x + y 1 + x = 1 x (c) y = xy x y (d) y + y + y
Spline-Räume - B-Spline-Basen
 Spline-Räume - B-Spline-Basen René Janssens 4. November 2009 René Janssens () Spline-Räume - B-Spline-Basen 4. November 2009 1 / 56 Übersicht 1 Erster Abschnitt: Räume von Splinefunktionen Grundlegende
Spline-Räume - B-Spline-Basen René Janssens 4. November 2009 René Janssens () Spline-Räume - B-Spline-Basen 4. November 2009 1 / 56 Übersicht 1 Erster Abschnitt: Räume von Splinefunktionen Grundlegende
Kapitel 11 Eigenwerte und Eigenvektoren
 Kapitel Eigenwerte und Eigenvektoren. Problem der Diagonalisierbarkeit Es sei wieder K gleich R oder. Eine n n)-matrix A mit Koeffizienten aus K wird als diagonalisierbar bezeichnet, wenn es eine invertierbare
Kapitel Eigenwerte und Eigenvektoren. Problem der Diagonalisierbarkeit Es sei wieder K gleich R oder. Eine n n)-matrix A mit Koeffizienten aus K wird als diagonalisierbar bezeichnet, wenn es eine invertierbare
Klausur Mathematik I
 Klausur Mathematik I (E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). September 7 (Hans-Georg Rück) Aufgabe (6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft Re(z) = und (z
Klausur Mathematik I (E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). September 7 (Hans-Georg Rück) Aufgabe (6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft Re(z) = und (z
Differentialgeometrie von Kurven und Flächen
 Differentialgeometrie von Kurven und Flächen Inhaltsverzeichnis:. Hilfsmittel Fritzsche 2. Parametrisierte Kurven Ballnus, 29.0. 3. Ebene Krümmung Ballnus, 05.. 4. Raumkurven Stergiou, 2.. 5. Globale Eigenschaften
Differentialgeometrie von Kurven und Flächen Inhaltsverzeichnis:. Hilfsmittel Fritzsche 2. Parametrisierte Kurven Ballnus, 29.0. 3. Ebene Krümmung Ballnus, 05.. 4. Raumkurven Stergiou, 2.. 5. Globale Eigenschaften
Lösungen zur Serie 5
 Dr. P. Thurnheer Grundlagen der Mathematik I ETH Zürich D-CHAB, D-BIOL (Analysis B) FS 10 Lösungen zur Serie 5 1. a) Die erste Kurve ist eine Kardioide (Herzkurve). i) Wenn man t durch t erstezt, kriegt
Dr. P. Thurnheer Grundlagen der Mathematik I ETH Zürich D-CHAB, D-BIOL (Analysis B) FS 10 Lösungen zur Serie 5 1. a) Die erste Kurve ist eine Kardioide (Herzkurve). i) Wenn man t durch t erstezt, kriegt
Differentialgeometrische Eigenschaften von Kurven und Flächen
 Kapitel 5 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen
Kapitel 5 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
a 0 +a 1 x+a 2 x n=0 a n x n := lim
 1 Taylor-Entwicklung 1.1 Potenzreihen Def.: Ein Ausdruck der Form a 0 +a 1 +a +... a n n := lim k k a n n, (1) mit einer (unendlichen) Folge reeller Konstanten a 0,a 1,a,... ( Koeffizienten ) und einer
1 Taylor-Entwicklung 1.1 Potenzreihen Def.: Ein Ausdruck der Form a 0 +a 1 +a +... a n n := lim k k a n n, (1) mit einer (unendlichen) Folge reeller Konstanten a 0,a 1,a,... ( Koeffizienten ) und einer
3 Vektorräume abstrakt
 Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
Mathematik I+II Frühlingsemester 2019 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren
 Mathematik I+II Frühlingsemester 219 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 46 8. Lineare Algebra: 5. Eigenwerte und
Mathematik I+II Frühlingsemester 219 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 46 8. Lineare Algebra: 5. Eigenwerte und
Lösungen der Probleme aus der dritten bis fünften Werkstatt
 Die WURZEL Werkstatt Mathematik Lösungen der Probleme aus der dritten bis fünften Werkstatt Es ist eine Binsenweisheit: Man kann nicht allein durch Zuschauen Mathematik erlernen. Nur im Umgang mit komplexen
Die WURZEL Werkstatt Mathematik Lösungen der Probleme aus der dritten bis fünften Werkstatt Es ist eine Binsenweisheit: Man kann nicht allein durch Zuschauen Mathematik erlernen. Nur im Umgang mit komplexen
2 Die Dimension eines Vektorraums
 2 Die Dimension eines Vektorraums Sei V ein K Vektorraum und v 1,..., v r V. Definition: v V heißt Linearkombination der Vektoren v 1,..., v r falls es Elemente λ 1,..., λ r K gibt, so dass v = λ 1 v 1
2 Die Dimension eines Vektorraums Sei V ein K Vektorraum und v 1,..., v r V. Definition: v V heißt Linearkombination der Vektoren v 1,..., v r falls es Elemente λ 1,..., λ r K gibt, so dass v = λ 1 v 1
Lösung zu Serie [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich:
![Lösung zu Serie [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich: Lösung zu Serie [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich:](/thumbs/67/57409595.jpg) Lineare Algebra D-MATH, HS 04 Prof. Richard Pink Lösung zu Serie. [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich: a) F (X) := X 5 X in R[X] und C[X]. b) F (X) := X 4 +X 3 +X in
Lineare Algebra D-MATH, HS 04 Prof. Richard Pink Lösung zu Serie. [Aufgabe] Faktorisieren Sie die folgenden Polynome so weit wie möglich: a) F (X) := X 5 X in R[X] und C[X]. b) F (X) := X 4 +X 3 +X in
eine vom Nullvektor verschiedene Lösung hat. r heisst in diesem Fall Eigenvektor der Matrix A zum Eigenwert λ.
 Eigenwert, Eigenvektor In der Regel hat bei einer linearen Abbildung das Bild eines Vektors eine andere Richtung als das Original r. Bei der Untersuchung der geometrischen Eigenschaften von linearen Abbildungen
Eigenwert, Eigenvektor In der Regel hat bei einer linearen Abbildung das Bild eines Vektors eine andere Richtung als das Original r. Bei der Untersuchung der geometrischen Eigenschaften von linearen Abbildungen
Mathematische Grundlagen für die Vorlesung. Differentialgeometrie
 Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
D-MAVT Lineare Algebra I HS 2017 Prof. Dr. N. Hungerbühler. Lösungen Serie 14: Ferienserie
 D-MAVT Lineare Algebra I HS 7 Prof. Dr. N. Hungerbühler Lösungen Serie 4: Ferienserie . Finden Sie ein Erzeugendensystem des Lösungsraums L R 5 des Systems x + x x 3 + 3x 4 x 5 = 3x x + 4x 3 x 4 + 5x 5
D-MAVT Lineare Algebra I HS 7 Prof. Dr. N. Hungerbühler Lösungen Serie 4: Ferienserie . Finden Sie ein Erzeugendensystem des Lösungsraums L R 5 des Systems x + x x 3 + 3x 4 x 5 = 3x x + 4x 3 x 4 + 5x 5
Implizite Funktionen. Ist für eine stetig differenzierbare Funktion f : R n R m R n. so lässt sich das Gleichungssystem
 Implizite Funktionen Ist für eine stetig differenzierbare Funktion f : R n R m R n f (x, y ) = (0,..., 0) t, det f x (x, y ) 0, so lässt sich das Gleichungssystem f k (x 1,..., x n, y 1,..., y m ) = 0,
Implizite Funktionen Ist für eine stetig differenzierbare Funktion f : R n R m R n f (x, y ) = (0,..., 0) t, det f x (x, y ) 0, so lässt sich das Gleichungssystem f k (x 1,..., x n, y 1,..., y m ) = 0,
3. Übungsblatt zur Lineare Algebra I für Physiker
 Fachbereich Mathematik Prof. Dr. Mirjam Dür Dipl. Math. Stefan Bundfuss. Übungsblatt zur Lineare Algebra I für Physiker WS 5/6 6. Dezember 5 Gruppenübung Aufgabe G (Basis und Erzeugendensystem) Betrachte
Fachbereich Mathematik Prof. Dr. Mirjam Dür Dipl. Math. Stefan Bundfuss. Übungsblatt zur Lineare Algebra I für Physiker WS 5/6 6. Dezember 5 Gruppenübung Aufgabe G (Basis und Erzeugendensystem) Betrachte
Lösungen zu den Hausaufgaben zur Analysis II
 Christian Fenske Lösungen zu den Hausaufgaben zur Analysis II Blatt 6 1. Seien 0 < b < a und (a) M = {(x, y, z) R 3 x 2 + y 4 + z 4 = 1}. (b) M = {(x, y, z) R 3 x 3 + y 3 + z 3 = 3}. (c) M = {((a+b sin
Christian Fenske Lösungen zu den Hausaufgaben zur Analysis II Blatt 6 1. Seien 0 < b < a und (a) M = {(x, y, z) R 3 x 2 + y 4 + z 4 = 1}. (b) M = {(x, y, z) R 3 x 3 + y 3 + z 3 = 3}. (c) M = {((a+b sin
Klausur zur Geometrie für Bachelor und Lehramt
 Klausur zur Geometrie für Bachelor und Lehramt Aufgabe ( Punkt) Lösung Aufgabe Kurzfragen (jeweils Punkte) (a) Skizzieren Sie qualitativ eine ebene Kurve c : R R mit Krümmung κ(t) = t (b) Ist die ebene
Klausur zur Geometrie für Bachelor und Lehramt Aufgabe ( Punkt) Lösung Aufgabe Kurzfragen (jeweils Punkte) (a) Skizzieren Sie qualitativ eine ebene Kurve c : R R mit Krümmung κ(t) = t (b) Ist die ebene
4 Eigenwerte und Eigenvektoren
 4 Eigenwerte und Eigenvektoren Sei V {0} ein K Vektorraum und f : V V K linear. Definition: Ein Eigenwert von f ist ein Element λ K, für die es einen Vektor v 0 in V gibt, so dass f(v) = λ v. Sei nun λ
4 Eigenwerte und Eigenvektoren Sei V {0} ein K Vektorraum und f : V V K linear. Definition: Ein Eigenwert von f ist ein Element λ K, für die es einen Vektor v 0 in V gibt, so dass f(v) = λ v. Sei nun λ
ETH Zürich Musterlösungen Basisprüfung Sommer 2014 D-MAVT & D-MATL Analysis I & II Prof. Dr. Urs Lang
 ETH Zürich Musterlösungen asisprüfung Sommer 14 D-MAVT & D-MATL Analysis I & II Prof. Dr. Urs Lang 1. a I. I n 1 1 e r dr e r 1 e 1. 1 r n e r dr r n e r 1 n r n 1 e r dr e ni n 1, für n 1. b Wegen der
ETH Zürich Musterlösungen asisprüfung Sommer 14 D-MAVT & D-MATL Analysis I & II Prof. Dr. Urs Lang 1. a I. I n 1 1 e r dr e r 1 e 1. 1 r n e r dr r n e r 1 n r n 1 e r dr e ni n 1, für n 1. b Wegen der
3.5 Duale Vektorräume und Abbildungen
 3.5. DUALE VEKTORRÄUME UND ABBILDUNGEN 103 3.5 Duale Vektorräume und Abbildungen Wir wollen im Folgenden auch geometrische Zusammenhänge mathematisch beschreiben und beginnen deshalb jetzt mit der Einführung
3.5. DUALE VEKTORRÄUME UND ABBILDUNGEN 103 3.5 Duale Vektorräume und Abbildungen Wir wollen im Folgenden auch geometrische Zusammenhänge mathematisch beschreiben und beginnen deshalb jetzt mit der Einführung
Lineare Algebra für D-ITET, D-MATL, RW. Beispiellösung für Serie 6. Aufgabe 6.1. Dr. V. Gradinaru K. Imeri. Herbstsemester 2018.
 Dr. V. Gradinaru K. Imeri Herbstsemester 8 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie 6 Aufgabe 6. Multiple Choice: Online abzugeben. 6.a) (i) Welche der folgenden
Dr. V. Gradinaru K. Imeri Herbstsemester 8 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie 6 Aufgabe 6. Multiple Choice: Online abzugeben. 6.a) (i) Welche der folgenden
Analysis I. 1. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
Wichtige Kenntnisse der Linearen Algebra
 Wichtige Kenntnisse der Linearen Algebra In Kapitel 3 der Vorlesung werden wir sehen (und in Kapitel 6 vertiefen, dass zur Beschreibung von Quantensystemen mathematische Begriffe aus dem Gebiet der Linearen
Wichtige Kenntnisse der Linearen Algebra In Kapitel 3 der Vorlesung werden wir sehen (und in Kapitel 6 vertiefen, dass zur Beschreibung von Quantensystemen mathematische Begriffe aus dem Gebiet der Linearen
Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen
 Kapitel XII Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen 53 Implizite Funktionen und allgemeine partielle Differenzierbarkeit 54 Der Umkehrsatz 55 Lokale Extrema unter Nebenbedingungen,
Kapitel XII Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen 53 Implizite Funktionen und allgemeine partielle Differenzierbarkeit 54 Der Umkehrsatz 55 Lokale Extrema unter Nebenbedingungen,
Zusatzmaterial zu Kapitel 6
 ZU KAPITEL 62: METHODEN ZUR STABILITÄTSPRÜFUNG Zusatzmaterial zu Kapitel 6 Zu Kapitel 62: Methoden zur Stabilitätsprüfung Einleitung Bei der Feststellung der asymptotischen Stabilität (siehe Kapitel 63)
ZU KAPITEL 62: METHODEN ZUR STABILITÄTSPRÜFUNG Zusatzmaterial zu Kapitel 6 Zu Kapitel 62: Methoden zur Stabilitätsprüfung Einleitung Bei der Feststellung der asymptotischen Stabilität (siehe Kapitel 63)
Flächen und ihre Krümmungen
 Flächen und ihre Krümmungen Teilnehmer: Levi Borodenko Anna Heinrich Jochen Jacobs Robert Jendersie Tanja Lappe Manuel Radatz Maximilian Rogge Käthe-Kollwitz-Oberschule, Berlin Käthe-Kollwitz-Oberschule,
Flächen und ihre Krümmungen Teilnehmer: Levi Borodenko Anna Heinrich Jochen Jacobs Robert Jendersie Tanja Lappe Manuel Radatz Maximilian Rogge Käthe-Kollwitz-Oberschule, Berlin Käthe-Kollwitz-Oberschule,
Institut für Analysis WS 2017/18 PD Dr. Peer Christian Kunstmann Dipl.-Math. Leonid Chaichenets Tobias Ried, M.Sc.
 Institut für Analysis WS 07/8 PD Dr. Peer Christian Kunstmann 0..07 Dipl.-Math. Leonid Chaichenets Tobias Ried, M.Sc. Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zum 0. Übungsblatt
Institut für Analysis WS 07/8 PD Dr. Peer Christian Kunstmann 0..07 Dipl.-Math. Leonid Chaichenets Tobias Ried, M.Sc. Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zum 0. Übungsblatt
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 22 Algebraische Körpererweiterung Satz 1. Sei K L eine Körpererweiterung und sei f L ein Element. Dann sind folgende Aussagen
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 22 Algebraische Körpererweiterung Satz 1. Sei K L eine Körpererweiterung und sei f L ein Element. Dann sind folgende Aussagen
7.6.5 Gaußsche Krümmung K und mittlere Krümmung H
 7.6.5 Gaußsche Krümmung K und mittlere Krümmung H Im folgenden sei stets Φ : x(u, v), (u, v) G, eine reguläre C 2 -Fläche. Dann ist an jeder Stelle (u, v) G für jede Flächenrichtung nach 7.6.3 t = a 1
7.6.5 Gaußsche Krümmung K und mittlere Krümmung H Im folgenden sei stets Φ : x(u, v), (u, v) G, eine reguläre C 2 -Fläche. Dann ist an jeder Stelle (u, v) G für jede Flächenrichtung nach 7.6.3 t = a 1
Lineare Algebra. 5. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Lineare Algebra. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching October 2, 207 Erinnerung Definition. Ein Skalarprodukt ist eine Abbildung, : E n E n E, v, w v, w = n k= v
Lineare Algebra. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching October 2, 207 Erinnerung Definition. Ein Skalarprodukt ist eine Abbildung, : E n E n E, v, w v, w = n k= v
Reihenentwicklungen von Lösungen (I) 1 Einleitung
 Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 22.11.2011 Carmen Freuen Ziel dieses Vortrages ist es, die Reihenentwicklung von Lösungen linearer Differentialgleichungen vorzustellen und zu untersuchen.
Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 22.11.2011 Carmen Freuen Ziel dieses Vortrages ist es, die Reihenentwicklung von Lösungen linearer Differentialgleichungen vorzustellen und zu untersuchen.
02. Vektorräume und Untervektorräume
 02. Vektorräume und Untervektorräume Wir kommen nun zur eigentlichen Definition eines K-Vektorraums. Dabei ist K ein Körper (bei uns meist R oder C). Informell ist ein K-Vektorraum eine Menge V, auf der
02. Vektorräume und Untervektorräume Wir kommen nun zur eigentlichen Definition eines K-Vektorraums. Dabei ist K ein Körper (bei uns meist R oder C). Informell ist ein K-Vektorraum eine Menge V, auf der
11. Darstellung von Kurven und Flächen
 H.J. Oberle Approximation WS 23/4. Darstellung von Kurven und Flächen Bézier Kurven. Unser Ziel ist es, polynomiale Kurven auf dem Rechner möglichst effizient darzustellen. Hierzu nutzen wir die Basisdarstellung
H.J. Oberle Approximation WS 23/4. Darstellung von Kurven und Flächen Bézier Kurven. Unser Ziel ist es, polynomiale Kurven auf dem Rechner möglichst effizient darzustellen. Hierzu nutzen wir die Basisdarstellung
Geometrische Form des Additionstheorems
 Geometrische Form des Additionstheorems Jae Hee Lee 29. Mai 2006 Zusammenfassung Der Additionstheorem lässt sich mithilfe des Abelschen Theorems elegant beweisen. Dieser Beweis und die Isomorphie zwischen
Geometrische Form des Additionstheorems Jae Hee Lee 29. Mai 2006 Zusammenfassung Der Additionstheorem lässt sich mithilfe des Abelschen Theorems elegant beweisen. Dieser Beweis und die Isomorphie zwischen
Lösungsskizze zur Wiederholungsserie
 Lineare Algebra D-MATH, HS Prof. Richard Pink Lösungsskizze zur Wiederholungsserie. [Aufgabe] Schreibe die lineare Abbildung f : Q Q 5, x +x +x x x +x +6x f x := x +x +8x x x +x +x. x +x +5x als Linksmultiplikation
Lineare Algebra D-MATH, HS Prof. Richard Pink Lösungsskizze zur Wiederholungsserie. [Aufgabe] Schreibe die lineare Abbildung f : Q Q 5, x +x +x x x +x +6x f x := x +x +8x x x +x +x. x +x +5x als Linksmultiplikation
Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II. x 2
 Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II Wiederholungsblatt: Analysis Sommersemester 2011 W. Werner, F. Springer erstellt von: Max Brinkmann Aufgabe 1: Untersuchen Sie, ob die
Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II Wiederholungsblatt: Analysis Sommersemester 2011 W. Werner, F. Springer erstellt von: Max Brinkmann Aufgabe 1: Untersuchen Sie, ob die
Mathematik Semester 3 / Arbeitsblatt f (x) = x x 3 4 x. 5 x 3 20 x. x 2 1
 9.2 Aufgaben Aufgabe 16.39 aus dem Buch. 1. f (x) = x4 + 1 x 3 + x 4. f (x) = x4 1 2 x 3 8 x 2. f (x) = x3 + 1 x 3 4 x 5. f (x) = x5 + 1 5 x 3 20 x 3. f (x) = 4 x2 x 2 + 1 6. f (x) = x2 2 x 2 7. f (x)
9.2 Aufgaben Aufgabe 16.39 aus dem Buch. 1. f (x) = x4 + 1 x 3 + x 4. f (x) = x4 1 2 x 3 8 x 2. f (x) = x3 + 1 x 3 4 x 5. f (x) = x5 + 1 5 x 3 20 x 3. f (x) = 4 x2 x 2 + 1 6. f (x) = x2 2 x 2 7. f (x)
Vorlesung 27. Der projektive Raum. Wir werden den projektiven Raum zunehmend mit mehr Strukturen versehen.
 Vorlesung 27 Der projektive Raum Definition 1. Sei K ein Körper. Der projektive n-dimensionale Raum P n K besteht aus allen Geraden des A n+1 K durch den Nullpunkt, wobei diese Geraden als Punkte aufgefasst
Vorlesung 27 Der projektive Raum Definition 1. Sei K ein Körper. Der projektive n-dimensionale Raum P n K besteht aus allen Geraden des A n+1 K durch den Nullpunkt, wobei diese Geraden als Punkte aufgefasst
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung
 Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Lineare Algebra II 11. Übungsblatt
 Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof. Dr. Ulrich Reif
 14 Oktober 2008 1 Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof Dr Ulrich Reif Inhalt: 1 Vektorrechnung 2 Lineare Gleichungssysteme 3 Matrizenrechnung 4 Lineare Abbildungen 5 Eigenwerte
14 Oktober 2008 1 Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof Dr Ulrich Reif Inhalt: 1 Vektorrechnung 2 Lineare Gleichungssysteme 3 Matrizenrechnung 4 Lineare Abbildungen 5 Eigenwerte
1 Euklidische und unitäre Vektorräume
 1 Euklidische und unitäre Vektorräume In diesem Abschnitt betrachten wir reelle und komplexe Vektorräume mit Skalarprodukt. Dieses erlaubt uns die Länge eines Vektors zu definieren und (im Fall eines reellen
1 Euklidische und unitäre Vektorräume In diesem Abschnitt betrachten wir reelle und komplexe Vektorräume mit Skalarprodukt. Dieses erlaubt uns die Länge eines Vektors zu definieren und (im Fall eines reellen
i j m f(y )h i h j h m
 10 HÖHERE ABLEITUNGEN UND ANWENDUNGEN 56 Speziell für k = 2 ist also f(x 0 + H) = f(x 0 ) + f(x 0 ), H + 1 2 i j f(x 0 )h i h j + R(X 0 ; H) mit R(X 0 ; H) = 1 6 i,j,m=1 i j m f(y )h i h j h m und passendem
10 HÖHERE ABLEITUNGEN UND ANWENDUNGEN 56 Speziell für k = 2 ist also f(x 0 + H) = f(x 0 ) + f(x 0 ), H + 1 2 i j f(x 0 )h i h j + R(X 0 ; H) mit R(X 0 ; H) = 1 6 i,j,m=1 i j m f(y )h i h j h m und passendem
Tutorium: Diskrete Mathematik
 Tutorium: Diskrete Mathematik Vorbereitung der Abschlussklausur am 16.02.2017 (Teil 2, Lösungen 15. Februar 2017 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler 15. Februar
Tutorium: Diskrete Mathematik Vorbereitung der Abschlussklausur am 16.02.2017 (Teil 2, Lösungen 15. Februar 2017 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler 15. Februar
Kurventheorie. 1.1 Parameterdarstellung. 1.2 Reguläre Kurven
 Diese kleine Formelsammlung ist ein Hilfsmittel für die studienbegleitende Prüfung am 30. August 2012. Sie ist kein Ersatz für eine Vorlesungsmitschrift. Die Formelsammlung wird einseitig im Format DIN
Diese kleine Formelsammlung ist ein Hilfsmittel für die studienbegleitende Prüfung am 30. August 2012. Sie ist kein Ersatz für eine Vorlesungsmitschrift. Die Formelsammlung wird einseitig im Format DIN
Der Fundamentalsatz der Algebra. 1 Motivation
 Vortrag im Rahmen des Proseminars zur Analysis, 24. April 2006 Micha Bittner Motivation Den ersten des Fundamentalsatzes der Algebra erbrachte C.F. Gauss im Jahr 799 im Rahmen seiner Dissertation. Heute
Vortrag im Rahmen des Proseminars zur Analysis, 24. April 2006 Micha Bittner Motivation Den ersten des Fundamentalsatzes der Algebra erbrachte C.F. Gauss im Jahr 799 im Rahmen seiner Dissertation. Heute
Differentialgeometrie II
 Differentialgeometrie II Zusammenfassung von Tilmann Bitterberg HfT-Stuttgart, den 9. Juli 2001 Inhaltsverzeichnis 15 Regelflächen 3 15.1 Darstellung von Regelflächen......................... 3 15.2 Begleitendes
Differentialgeometrie II Zusammenfassung von Tilmann Bitterberg HfT-Stuttgart, den 9. Juli 2001 Inhaltsverzeichnis 15 Regelflächen 3 15.1 Darstellung von Regelflächen......................... 3 15.2 Begleitendes
Hauptachsentransformation: Eigenwerte und Eigenvektoren
 Hauptachsentransformation: Eigenwerte und Eigenvektoren die bisherigen Betrachtungen beziehen sich im Wesentlichen auf die Standardbasis des R n Nun soll aufgezeigt werden, wie man sich von dieser Einschränkung
Hauptachsentransformation: Eigenwerte und Eigenvektoren die bisherigen Betrachtungen beziehen sich im Wesentlichen auf die Standardbasis des R n Nun soll aufgezeigt werden, wie man sich von dieser Einschränkung
Mathematik II Frühlingsemester 2015 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren
 Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Folgerungen aus dem Auflösungsatz
 Folgerungen aus dem Auflösungsatz Wir haben in der Vorlesung den Satz über implizite Funktionen (Auflösungssatz) kennen gelernt. In unserer Formulierung lauten die Resultate: Seien x 0 R m, y 0 R n und
Folgerungen aus dem Auflösungsatz Wir haben in der Vorlesung den Satz über implizite Funktionen (Auflösungssatz) kennen gelernt. In unserer Formulierung lauten die Resultate: Seien x 0 R m, y 0 R n und
x 3 Genau dann liegt ein Punkt X mit dem Ortsvektor x auf g, wenn es ein λ R gib,t so dass
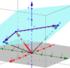 V. Geradengleichungen in Parameterform 5. Definition ---------------------------------------------------------------------------------------------------------------- x 3 v a x x x Definition und Satz :
V. Geradengleichungen in Parameterform 5. Definition ---------------------------------------------------------------------------------------------------------------- x 3 v a x x x Definition und Satz :
18 λ 18 + λ 0 A 18I 3 = / Z 2 Z 2 Z Z Z 1
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
1. und 2. Fundamentalform
 1. und 2. Fundamentalform regulärer Flächen Proseminar Differentialgeometrie Von Daniel Schliebner Herausgabe: 05. Dezember 2007 Daniel Schliebner 1. und 2. Fundamentalform regulärer Flächen Seite 1 6.1
1. und 2. Fundamentalform regulärer Flächen Proseminar Differentialgeometrie Von Daniel Schliebner Herausgabe: 05. Dezember 2007 Daniel Schliebner 1. und 2. Fundamentalform regulärer Flächen Seite 1 6.1
Eine Kennzeichnung der Kugel.
 Eine Kennzeichnung der Kugel. Von W. SCHERRER (Bern). (Als Manuskript eingegangen am 27. Dezember 1939.) Einleitung. Die ausgezeichnete Stellung der Kugel als Aichfläche der Euklidischen Metrik findet
Eine Kennzeichnung der Kugel. Von W. SCHERRER (Bern). (Als Manuskript eingegangen am 27. Dezember 1939.) Einleitung. Die ausgezeichnete Stellung der Kugel als Aichfläche der Euklidischen Metrik findet
ε δ Definition der Stetigkeit.
 ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
Basistext Geraden und Ebenen
 Basistext Geraden und Ebenen Parameterdarstellung Geraden Eine Gerade ist durch zwei Punkte P und Q, die auf der Geraden liegen, eindeutig festgelegt. Man benötigt zur Darstellung den Vektor. Dieser wird
Basistext Geraden und Ebenen Parameterdarstellung Geraden Eine Gerade ist durch zwei Punkte P und Q, die auf der Geraden liegen, eindeutig festgelegt. Man benötigt zur Darstellung den Vektor. Dieser wird
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16
 Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16 21. Januar 2016 Definition 8.1 Eine Menge R zusammen mit zwei binären Operationen
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16 21. Januar 2016 Definition 8.1 Eine Menge R zusammen mit zwei binären Operationen
Über die Bestimmung der linearen Teiler einer algebraischen Form.
 Über die Bestimmung der linearen Teiler einer algebraischen Form. Von F. HOCEVAR aus Graz. In den zahlreichen Arbeiten über die linearen Teiler der Formen beschäftigte man sich bisher in der Regel nur
Über die Bestimmung der linearen Teiler einer algebraischen Form. Von F. HOCEVAR aus Graz. In den zahlreichen Arbeiten über die linearen Teiler der Formen beschäftigte man sich bisher in der Regel nur
Angewandte Geometrie Semestralprüfung am 5. Juli 2005, Uhr
 Technische Universität München SS 2005 Zentrum Mathematik Blatt 7 apl. Prof. Dr. J. Hartl Angewandte Geometrie Semestralprüfung am 5. Juli 2005, 12.00-1.0 Uhr 1. In einem dreidimensionalen euklidischen
Technische Universität München SS 2005 Zentrum Mathematik Blatt 7 apl. Prof. Dr. J. Hartl Angewandte Geometrie Semestralprüfung am 5. Juli 2005, 12.00-1.0 Uhr 1. In einem dreidimensionalen euklidischen
Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen.
 10.1. Ebene Kurven Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen. Parameterdarstellungen einer Kurve sind stetige
10.1. Ebene Kurven Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen. Parameterdarstellungen einer Kurve sind stetige
Vorlesung 12 Differentialgeometrie: Grundlagen 49. Definition 4.25 Die Zweite Fundamentalform ordnet jedem Punkt die Bilinearform
 Vorlesung 2 Differentialgeometrie: Grundlagen 49 Wir werden jetzt κ(v) durch Untersuchung von d p N bestimmen. Dazu beobachten wir zunächst, das aus dn(v) N folgt, dass es zu jedem v T p U ein w T p U
Vorlesung 2 Differentialgeometrie: Grundlagen 49 Wir werden jetzt κ(v) durch Untersuchung von d p N bestimmen. Dazu beobachten wir zunächst, das aus dn(v) N folgt, dass es zu jedem v T p U ein w T p U
Lineare Algebra II (SS 13)
 Lineare Algebra II (SS 13) Bernhard Hanke Universität Augsburg 03.07.2013 Bernhard Hanke 1 / 16 Selbstadjungierte Endomorphismen und der Spektralsatz Definition Es sei (V,, ) ein euklidischer oder unitärer
Lineare Algebra II (SS 13) Bernhard Hanke Universität Augsburg 03.07.2013 Bernhard Hanke 1 / 16 Selbstadjungierte Endomorphismen und der Spektralsatz Definition Es sei (V,, ) ein euklidischer oder unitärer
Lösungsvorschlag zur Nachklausur zur Analysis
 Prof Dr H Garcke, D Depner SS 09 NWF I - Mathematik 080009 Universität Regensburg Lösungsvorschlag zur Nachklausur zur Analysis Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz und berechnen Sie
Prof Dr H Garcke, D Depner SS 09 NWF I - Mathematik 080009 Universität Regensburg Lösungsvorschlag zur Nachklausur zur Analysis Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz und berechnen Sie
Aufgabe K1: Potential einer Hohlkugel ( = 11 Punkte)
 Aufgabe K: Potential einer Hohlkugel ( + 7 + = Punkte) (a) Leiten Sie die integrale Form der Maxwell Gleichungen der Elektrostatik aus den entsprechenden differentiellen Gleichungen her. Differentielle
Aufgabe K: Potential einer Hohlkugel ( + 7 + = Punkte) (a) Leiten Sie die integrale Form der Maxwell Gleichungen der Elektrostatik aus den entsprechenden differentiellen Gleichungen her. Differentielle
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Gegenbeispiele in der Wahrscheinlichkeitstheorie
 Gegenbeispiele in der Wahrscheinlichkeitstheorie Mathias Schaefer Universität Ulm 26. November 212 1 / 38 Übersicht 1 Normalverteilung Definition Eigenschaften Gegenbeispiele 2 Momentenproblem Definition
Gegenbeispiele in der Wahrscheinlichkeitstheorie Mathias Schaefer Universität Ulm 26. November 212 1 / 38 Übersicht 1 Normalverteilung Definition Eigenschaften Gegenbeispiele 2 Momentenproblem Definition
Skalarprodukte im Funktionenraum und orthogonale Funktionen
 1 Skalarprodukte im Funktionenraum und orthogonale Funktionen Im Allgemeinen muss ein reelles Skalarprodukt (, ) (wir betrachten reelle Funktionen) folgende Eigenschaften ausweisen: Bilinearität (Linearität
1 Skalarprodukte im Funktionenraum und orthogonale Funktionen Im Allgemeinen muss ein reelles Skalarprodukt (, ) (wir betrachten reelle Funktionen) folgende Eigenschaften ausweisen: Bilinearität (Linearität
Apl. Prof. Dr. N. Knarr Musterlösung , 120min
 Apl. Prof. Dr. N. Knarr Musterlösung 4.3.25, 2min Aufgabe ( Punkte) Es sei S := {(x, y, z) R 3 z = x 2 + y 2, z 2}. (a) (6 Punkte) Berechnen Sie den Flächeninhalt von S. (b) (4 Punkte) Berechnen Sie die
Apl. Prof. Dr. N. Knarr Musterlösung 4.3.25, 2min Aufgabe ( Punkte) Es sei S := {(x, y, z) R 3 z = x 2 + y 2, z 2}. (a) (6 Punkte) Berechnen Sie den Flächeninhalt von S. (b) (4 Punkte) Berechnen Sie die
Vektorprodukt. Satz: Für a, b, c V 3 und λ IR gilt: = a b + a c (Linearität) (Linearität) b = λ
 Vektorprodukt Satz: Für a, b, c V 3 und λ IR gilt: 1 a b = b a (Anti-Kommutativität) ( ) 2 a b + c ( 3 a λ ) b = λ = a b + a c (Linearität) ( a ) b (Linearität) Satz: Die Koordinatendarstellung des Vektorprodukts
Vektorprodukt Satz: Für a, b, c V 3 und λ IR gilt: 1 a b = b a (Anti-Kommutativität) ( ) 2 a b + c ( 3 a λ ) b = λ = a b + a c (Linearität) ( a ) b (Linearität) Satz: Die Koordinatendarstellung des Vektorprodukts
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Der Differenzialquotient Teil 1 Mth 33
 Aus FUNKSCHAU 5/1956, im Original -spaltig. Digitalisiert 11/016 von Eike Grund für http://www.radiomuseum.org mit freundlicher Genehmigung der FUNKSCHAU-Redaktion. Die aktuellen Ausgaben der FUNKSCHAU
Aus FUNKSCHAU 5/1956, im Original -spaltig. Digitalisiert 11/016 von Eike Grund für http://www.radiomuseum.org mit freundlicher Genehmigung der FUNKSCHAU-Redaktion. Die aktuellen Ausgaben der FUNKSCHAU
13 Polynome und Nullstellen
 60 II. Differentialrechnung 13 Polynome und Nullstellen Lernziele: Resultat: Zwischenwertsatz Methoden: Raten von Nullstellen, Euklidischer Algorithmus, Horner-Schema Kompetenzen: Bestimmung von Nullstellen
60 II. Differentialrechnung 13 Polynome und Nullstellen Lernziele: Resultat: Zwischenwertsatz Methoden: Raten von Nullstellen, Euklidischer Algorithmus, Horner-Schema Kompetenzen: Bestimmung von Nullstellen
Die zweite Fundamentalform und Krümmungen
 Kapitel 6 Die zweite Fundamentalform und Krümmungen 6.1 Die zweite Fundamentalform Im Abschnitt 5.2 wurde das Normalenvektorfeld N einer regulär parametrisierten Fläche X : U R 2 R 3 definiert. Durch die
Kapitel 6 Die zweite Fundamentalform und Krümmungen 6.1 Die zweite Fundamentalform Im Abschnitt 5.2 wurde das Normalenvektorfeld N einer regulär parametrisierten Fläche X : U R 2 R 3 definiert. Durch die
M U = {x U f 1 =... = f n k (x) = 0}, (1)
 Aufgabe 11. a) Es sei M = {(x, y, z) R 3 f 1 = xy = 0; f = yz = 0}. Der Tangentialraum T x M muss in jedem Punkt x M ein R-Vektorraum sein und die Dimension 1 besitzen, damit diese Menge M eine Untermannigfaltigkeit
Aufgabe 11. a) Es sei M = {(x, y, z) R 3 f 1 = xy = 0; f = yz = 0}. Der Tangentialraum T x M muss in jedem Punkt x M ein R-Vektorraum sein und die Dimension 1 besitzen, damit diese Menge M eine Untermannigfaltigkeit
8.5 Symmetrische Polynome, Diskriminate und Resultante
 332 85 Symmetrische Polynome, Diskriminate und Resultante Ein weiteres Verfahren zur Feststellung, ob mehrfache Wurzeln vorliegen, ist die Betrachtung der Diskriminante, deren Einführung jetzt vorbereitet
332 85 Symmetrische Polynome, Diskriminate und Resultante Ein weiteres Verfahren zur Feststellung, ob mehrfache Wurzeln vorliegen, ist die Betrachtung der Diskriminante, deren Einführung jetzt vorbereitet
Lösungsskizzen der Klausur zur Linearen Algebra im Herbst 2015
 sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
Höhere Mathematik für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 05/06 08.0.06 Höhere Mathemati für die Fachrichtung Physi Lösungsvorschläge zum 9. Übungsblatt
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 05/06 08.0.06 Höhere Mathemati für die Fachrichtung Physi Lösungsvorschläge zum 9. Übungsblatt
8 Eigenwerttheorie I 8. EIGENWERTTHEORIE I 139. Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet:
 8. EIGENWERTTHEORIE I 139 8 Eigenwerttheorie I Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet: K[x] = Abb[N, K] = {P ; P = a n x n + a n 1 x n 1 + + a 0 ; a
8. EIGENWERTTHEORIE I 139 8 Eigenwerttheorie I Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet: K[x] = Abb[N, K] = {P ; P = a n x n + a n 1 x n 1 + + a 0 ; a
Übungen zur Vorlesung Funktionentheorie Sommersemester Musterlösung zu Blatt 10. f(z) f(z) dz
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Musterlösung zu Blatt 0 Aufgabe. Berechnen Sie
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Musterlösung zu Blatt 0 Aufgabe. Berechnen Sie
10.6. Implizite ebene Kurven und Tangenten
 0.6. Implizite ebene Kurven und Tangenten Im Gegensatz zu expliziten Darstellungen sind weder implizite noch Parameterdarstellungen einer Kurve eindeutig. Der Übergang von impliziten zu expliziten Darstellungen
0.6. Implizite ebene Kurven und Tangenten Im Gegensatz zu expliziten Darstellungen sind weder implizite noch Parameterdarstellungen einer Kurve eindeutig. Der Übergang von impliziten zu expliziten Darstellungen
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 8
 D-MAVT/D-MATL Analysis I HS 017 Dr. Andreas Steiger Lösung - Serie 8 1. MC-Aufgaben Online-Abgabe) 1. Sei z := exp π 6 i) 5 + b i). Für welches b R ist z eine reelle Zahl? a) 1 b) c) 1 5 d) 5 e) Keines
D-MAVT/D-MATL Analysis I HS 017 Dr. Andreas Steiger Lösung - Serie 8 1. MC-Aufgaben Online-Abgabe) 1. Sei z := exp π 6 i) 5 + b i). Für welches b R ist z eine reelle Zahl? a) 1 b) c) 1 5 d) 5 e) Keines
Mathematik II: Übungsblatt 03 : Lösungen
 N.Mahnke Mathematik II: Übungsblatt 03 : Lösungen Verständnisfragen 1. Was bestimmt die erste Ableitung einer Funktion f : D R R im Punkt x 0 D? Die erste Ableitung einer Funktion bestimmt deren Steigung
N.Mahnke Mathematik II: Übungsblatt 03 : Lösungen Verständnisfragen 1. Was bestimmt die erste Ableitung einer Funktion f : D R R im Punkt x 0 D? Die erste Ableitung einer Funktion bestimmt deren Steigung
Lineare Algebra II. Bonusaufgabe B. 1. Betrachten Sie das Standard-Skalarprodukt im R 3 : R 3 R 3 R
 Bonusaufgabe B 1. Betrachten Sie das Standard-Skalarprodukt im R 3 : R 3 R 3 R a 1 a 2, b 1 3 b 2 := a i b i = a 1 b 1 + a 2 b 2 + a 3 b 3. a 3 b 3 i=1 Rufen Sie sich die folgenden Zusammenhänge in Erinnerung:
Bonusaufgabe B 1. Betrachten Sie das Standard-Skalarprodukt im R 3 : R 3 R 3 R a 1 a 2, b 1 3 b 2 := a i b i = a 1 b 1 + a 2 b 2 + a 3 b 3. a 3 b 3 i=1 Rufen Sie sich die folgenden Zusammenhänge in Erinnerung:
Prüfungsteil B, Aufgabengruppe 2: Geometrie
 Bundesabitur Mathematik: Bayern 01 Aufgabe 1 a) 1. SCHRITT: VEKTOR CH BESTIMMEN CH = ( 8 108 ) ( 10) = ( 0 ). 3. SCHRITT: LÄNGE DES VEKTORS BERECHNEN CH = ( ) + 3 =. 3. SCHRITT: BERECHNUNG DES FLÄCHENINHALTS
Bundesabitur Mathematik: Bayern 01 Aufgabe 1 a) 1. SCHRITT: VEKTOR CH BESTIMMEN CH = ( 8 108 ) ( 10) = ( 0 ). 3. SCHRITT: LÄNGE DES VEKTORS BERECHNEN CH = ( ) + 3 =. 3. SCHRITT: BERECHNUNG DES FLÄCHENINHALTS
Übungsaufgaben zu den mathematischen Grundlagen von KM
 TUM, Institut für Informatik WS 2003/2004 Prof Dr Thomas Huckle Andreas Krahnke, MSc Dipl-Inf Markus Pögl Übungsaufgaben zu den mathematischen Grundlagen von KM 1 Bestimmen Sie die Darstellung von 1 4
TUM, Institut für Informatik WS 2003/2004 Prof Dr Thomas Huckle Andreas Krahnke, MSc Dipl-Inf Markus Pögl Übungsaufgaben zu den mathematischen Grundlagen von KM 1 Bestimmen Sie die Darstellung von 1 4
Lineare Algebra II 3. Übungsblatt
 Lineare Algebra II 3. Übungsblatt Fachbereich Mathematik SS 2011 Prof. Dr. Kollross 27./28. April 2011 Susanne Kürsten Tristan Alex Minitest Aufgabe M1 (Formale Polynome) Betrachten Sie die folgenden Polynome
Lineare Algebra II 3. Übungsblatt Fachbereich Mathematik SS 2011 Prof. Dr. Kollross 27./28. April 2011 Susanne Kürsten Tristan Alex Minitest Aufgabe M1 (Formale Polynome) Betrachten Sie die folgenden Polynome
Musterlösung zur Klausur Differentialgeometrie für die Fachrichtung Geodäsie
 Karlsruher Institut für Technologie KIT) 4. März 20 Institut für Algebra und Geometrie PD Dr. Gabriele Link Musterlösung zur Klausur Differentialgeometrie für die Fachrichtung Geodäsie Aufgabe. Kurventheorie.
Karlsruher Institut für Technologie KIT) 4. März 20 Institut für Algebra und Geometrie PD Dr. Gabriele Link Musterlösung zur Klausur Differentialgeometrie für die Fachrichtung Geodäsie Aufgabe. Kurventheorie.
9. Primitivwurzeln. O. Forster: Einführung in die Zahlentheorie
 9. Primitivwurzeln 9.1. Satz. Sei G eine zyklische Gruppe der Ordnung m und g G ein erzeugendes Element. Das Element a := g k, k Z, ist genau dann ein erzeugendes Element von G, wenn k zu m teilerfremd
9. Primitivwurzeln 9.1. Satz. Sei G eine zyklische Gruppe der Ordnung m und g G ein erzeugendes Element. Das Element a := g k, k Z, ist genau dann ein erzeugendes Element von G, wenn k zu m teilerfremd
y f(t)dt in eine Taylorreihe um (0,0). Für welche (x,y) konvergiert diese Reihe gegen F(x,y)? x 5! x7 7! +... = 2 3! x ! x !
 Wolfgang Erben (1. Januar 016) WS 01 Analysis Aufgabe 1. (6 Punkte) Gegeben sei die Funktion f () sinh sin a) Zeigen Sie, dass f () für alle 0 durch eine Potenzreihe um 0 dargestellt werden kann. Geben
Wolfgang Erben (1. Januar 016) WS 01 Analysis Aufgabe 1. (6 Punkte) Gegeben sei die Funktion f () sinh sin a) Zeigen Sie, dass f () für alle 0 durch eine Potenzreihe um 0 dargestellt werden kann. Geben
5 5 5 Abbildung : Raumkurve Abbildung 5: Tangente t existiert nur dann, wenn _ ~x(t ) = ist. Ein Punkt mit f _x; _y; _zg = f; ; g heißt ein regulärer
 3 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen zu geben.
3 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen zu geben.
