Reihenentwicklungen von Lösungen (I) 1 Einleitung
|
|
|
- Ludo Burgstaller
- vor 5 Jahren
- Abrufe
Transkript
1 Vortrag zum Seminar Gewöhnliche Differentialgleichungen, Carmen Freuen Ziel dieses Vortrages ist es, die Reihenentwicklung von Lösungen linearer Differentialgleichungen vorzustellen und zu untersuchen. Dabei sei vorab angemerkt, dass die Aussagen der Ausarbeitung alle für den reellen Zahlenbereich getroffen worden sind. Es finden sich jedoch analoge Aussagen für den Fall, dass die Variablen komplex sind. 1 Einleitung Motivation Viele naturwissenschaftliche Fragestellungen (in der Physik, Mathematik, etc.) führen uns zu Differentialgleichungen, welche nicht in einer geschlossenen Form lösbar sind. Damit sind solche Differentialgleichungen gemeint, deren Lösung weder durch Polynome, noch durch rationale Funktionen, Logarithmen, Exponentialfunktionen oder ähnlichem ausgedrückt werden können. Betrachtet man beispielsweise die Gleichung ( ) y = sin(y) y als mögliche Modellierung eines gedämpften Pendels, so stellt man fest, dass diese nicht elementar lösbar ist. Für viele solcher Gleichungen ist es allerdings möglich, die Lösung als Potenzreihe der Form n=0 a n (z z 0 ) n, z R mit den festen Konstanten a n, z 0 R für n N darzustellen 1 und die entsprechenden Koeffizienten a n zu bestimmen. Dieser Lösungsansatz soll im Folgenden insbesondere anhand linearer Differentialgleichungen zweiter Ordnung vorgestellt werden. 1 Zur Definition vgl. Krieg, A., Analysis I, Kapitel III (4.1)
2 1 Einleitung Im folgenden Satz wollen wir einige bekannte Eigenschaften von Potenzreihen darstellen. Bekanntes und Grundlegendes (1.1) Satz (Eigenschaften von Potenzreihen) Es seien t 0, a n R für n N und die Potenzreihe f : R R t n=0 a n (t t 0 ) n gegeben. (i) Jede Potenzreihe n=0 a n (t t 0 ) n hat einen Konvergenzradius R 0 und konvergiert absolut für (t t 0 ) < R. 2 (ii) Es sei f (t) = n=0 a n (t t 0 ) n und (t t 0 ) < R. Dann gilt für k 1: f (k) (t)= n=k n (n 1)... (n k + 1) a n (t t 0 ) n k. Insbesondere hat auch die k-te Ableitung den Konvergenzradius R. 3 (iii) Falls a, b aus dem Konvergenzintervall R stammen, so gilt: b a f (s) ds = n=0 a n b a sn ds. 4 (iv) Eindeutigkeitssatz für Potenzreihen: Falls n=0 c n (t t 0 ) n eine weitere Potenzreihe mit Konvergenzradius R > 0 ist und { } für (t t 0 ) < min R, R gilt n=0 a n (t t 0 ) n = n=0 c n (t t 0 ) n, dann gilt a n = c n für alle n N. (v) Addition von Potenzreihen: Es seien f (t) = n=0 a n (t t 0 ) n und g(t) = n=0 c n (t t 0 ) n konvergente Potenzreihen. 2 Vgl. Krieg, A., Analysis I, Kapitel III (4.5) und (2.1) 3 Vgl. Krieg, A., Analysis II, Kapitel VII (2.10) 4 Vgl. Krieg, A., Analysis II, Kapitel VII (2.7) 2
3 1 Einleitung Dann gilt: f (t) + g(t) = n=0 (a n + c n ) (t t 0 ) n überall dort, wo beide Potenzreihen konvergieren. 5 (vi) Multiplikation von Potenzreihen: Es seien f (t) = n=0 a n (t t 0 ) n und g(t) = n=0 c n (t t 0 ) n konvergente Potenzreihen. Dann gilt: f (t) g(t) = n=0 p n (t t 0 ) n mit p n = a n c 0 + a n 1 c a 0 c n. Diese Potenzreihe konvergiert für alle t R für die f und g konvergieren. 6 (1.2) Satz (Majorantenkriterium) Es sei k=1 a k eine Reihe mit a k R für alle k N. Gegeben sei eine konvergente reelle Reihe k=1 c k mit c k R für k N. Wenn es ein N N und ein M R + gibt, so dass a k M c k für alle k N, dann ist k=1 a k absolut konvergent. (1.3) Satz (Quotientenkriterium) Gegeben sei eine Reihe k=1 a k mit a k R, a k = 0 für alle k N. Sei also 0 r R. Dann gilt: r := lim inf a k+1 k a, R k := lim sup a k+1 k a, k (i) Aus R < 1 folgt die absolute Konvergenz der Reihe k=1 a k. (ii) Aus r > 1 folgt die Divergenz der Reihe k=1 a k. 5 Vgl. Krieg, A., Analysis I, Kapitel III (1.6) 6 Vgl. Krieg, A., Analysis I, Kapitel III (2.14) 3
4 2 Problemstellung (1.4) Definition (analytisch) Es sei I R (oder I C) ein Intervall. Dann heißt die Funktion f : I R analytisch im Punkt a I, falls f eine Reihendarstellung f (t) = n=0 c n (t a) n mit c n R für n N mit Entwicklungspunkt a und positivem Konvergenzradius R besitzt. 2 Problemstellung Als Einstieg in die Thematik soll uns die Gleichung ( ) dienen, welche wir mit einer einfachen, aber relativ umständlichen Methode lösen werden. Mit Hilfe dieser Methode kann man auch einige nichtlineare Gleichungen lösen. Zusätzlich zu unserer Differentialgleichung seien folgende Anfangsbedingungen gegeben: y(0) = π 4, y (0) = 0. Nach Vorlesung (Kapitel II (5.1)) wissen wir, dass es zu den gegebenen Anfangsbedingungen eine eindeutige Lösung gibt, da man das gegebene System in ein System erster Ordnung transformieren kann und sich die eindeutige Lösung dann als Folge aus Kapitel I, Satz (6.11) ergibt. Außerdem kann man die Lösung als Potenzreihe um t = 0 entwickeln 7. Doch wie erhält man diese Reihe, die die vorgegebenen Anfangsbedingungen erfüllt? Wenn die Lösung der Differentialgleichung ( ) als Potenzreihe darstellbar ist, dann muss jede Ableitung im Punkt t = 0 existieren. Eine mögliche Lösung ϕ hat somit die Taylor- 7 Krieg, A., Walcher, S. Gewöhnliche Differentialgleichungen. Kapitel II (5.1) 4
5 2 Problemstellung entwicklung um 0: ϕ(t) = ϕ(0) + ϕ (0) t + ϕ (0) 2! t ϕn (0) n! t n = Für t < R (Konvergenzradius) konvergiert diese Reihe gegen ϕ(t). 8 ϕ (k) (t 0)k (0) k! k=0 Durch die Anfangswertbedingungen wissen wir, dass ϕ(0) = π 4, d.h. die Lösung verläuft durch den Punkt (0, π 4 ) mit Steigung 0, da ϕ (0) = 0 gilt. Angenommen, dass ϕ die Lösung der Differentialgleichung ( ) ist, so liefert Einsetzen in die Differentialgleichung: ϕ (t) = sin(ϕ(t)) ϕ (t). Setzt man t = 0 folgt daraus: ϕ (0) = sin(ϕ(0)) ϕ (0) = sin( π 4 ) 0 = 2 2 = 1 2. Weitere Reihenwerte ergeben sich durch differenzieren der Differentialgleichung: ϕ (3) (t) = cos(ϕ(t)) ϕ (t) ϕ (t). Einsetzen von t = 0 liefert hier: ϕ (3) (0) = 2 2 = 1 2. Die vierte Ableitung ergibt: ϕ (4) (t) = sin(ϕ(t)) ϕ (t) 2 cos(ϕ(t)) ϕ (t) ϕ (t). Einsetzen von t = 0 liefert: ϕ (4) (0) = Zusätzlich ist die Anfangswertbedingung ϕ (0) = 0 gegeben, woraus ϕ (0) t = 0 folgt. Auf diese Weise kann man rekursiv alle Reihenglieder im Punkt t = 0 ermitteln: 8 Vgl. Krieg, A., Analysis I, Kapitel V (3.11) 5
6 ϕ(t) = π 2 t 2 }{{} 4 } 2 {{ 2! } =ϕ(0) =ϕ t (0) 2 2! + 2 t 3 2 3! }{{} =ϕ (3) (0) t 3 3! Problematik: 1. Die Methode ist sehr umständlich und es wird im Allgemeinen immer schwieriger, das nächste Reihenglied zu bestimmen. 2. Selbst wenn es gelingt ϕ (n) (0) für jedes n N zu bestimmen, ist es im Allgemeinen unmöglich die Konvergenz der erhaltenen Reihe zu zeigen und damit die Methode zu rechtfertigen. 3. Man kann eine Lösung erhalten, die nicht die ursprüngliche Gleichung löst. Betrachtet man hierzu beispielsweise die Gleichung y = f (t) mit exp( 1/t 2 ) (t = 0) f (t) = 0 (t = 0) Angenommen ϕ ist eine Lösung von y = f (t) mit ϕ(0) = 0, die als konvergente Reihe darstellbar ist, dann folgt daraus, dass alle Koeffizienten dieser Reihe gleich Null sein müssen, denn es gilt: a n = f (n) (0) = 0 für n N. (mit Differenzenquotienten nachweisbar). Daraus ergibt sich n=0 a n t n = 0. Mit Satz (1.1) (v) folgt, dass die Reihe somit der Nullfunktion entsprechen muss. Die Nullfunktion ist allerdings keine Lösung der gegebenen Differentialgleichung. Bevor wir nun eine Methode studieren mit der wir eine Reihenentwicklung von Lösungen linearer Differentialgleichungen erhalten ohne auf die oben genannten Probleme zu stoßen, stellen wir zunächst ein nützliches Lemma vor. 6
7 (1.5) Lemma Es seien f, g : R R analytische Funktionen im Punkt a, gegeben durch die Potenzreihen f (t) = n=p c n (t a) n, g(t) = n=q d n (t a) n, t R mit p, q N, c n, d n R für n N. Außerdem sei p < q und c p = 0, d q = 0. (Diese Annahme sorgt dafür, dass die Reihe von f mit dem Term (t a) p und die Reihe von g mit dem Term (t a) q beginnt.) Dann sind die Funktionen f und g linear unabhängig auf jedem Intervall I R auf dem beide Reihen konvergieren. Beweis Nehmen wir an, die Funktionen f und g seien konvergent auf einem Intervall I R. Zudem seien die Funktionen linear abhängig auf diesem Intervall I. Dann existieren nach Definition von linearer Abhängigkeit Konstanten A und B (mit A = 0 oder B = 0 ), sodass für jedes t I gilt: A f (t) + B g(t) = A c n (t a) n + B d n (t a) n = 0 n=p n=q Addiert man diese beide Reihen nun gliedweise (vgl. Satz (1.1) vi.), dann ergibt sich für die daraus resultierende Potenzreihe: A c p (t a) p + B d q (t a) q + A c p+1 (t a) p+1 + B d q+1 (t a) q = A c p (t a) p A c q 1 (t a) q 1 + n=q (A c n + B d n ) (t a) n = 0 Da p < q gilt, hat der Term A c p (t a) p die niedrigste Ordnung (folgt aus Koeffizientenvergleich in den Potenzen von (t a)). Aus diesem Koeffizientenvergleich der Potenzen von (t a) schließen wir nun, dass A = 0 gilt. Dann gilt aber auch: für alle t I. B d n (t a) n = A c n (t a) n n=q n=p }{{} =0 7
8 Daraus folgt aber, dass B = 0 sein muss (vgl. Satz (1.1) (v) und d q = 0 nach Voraussetzung). Damit folgt dann auch schon, dass A = B = 0 gilt. Dies widerspricht jedoch der Annahme, dass f und g linear abhängig sind. Nun kann auch ein einfaches Beispiel angegeben werden. (1.6) Beispiel Nachdem wir diese Aussage kennengelernt haben, studieren wir ein spezifisches Problem: Wir möchten gerne folgende Differentialgleichung lösen: y ty = 0 (1) Die zugehörigen Anfangsbedingungen seien gegeben durch ϕ(0) = a, ϕ (0) = b mit a, b R. Da es keine Lösung in einer geschlossenen Form gibt (muss akzeptiert werden), versuchen wir die Lösung zu erhalten, indem wir einen Potenzreihenansatz machen. Diese Methode beginnt mit der Annahme, dass die gesuchte Lösung ϕ analytisch ist im Punkt t = 0. (Wären die Anfangsbedingungen für t = t 0 gegeben, würden wir mit der Annahme beginnen, dass ϕ analytisch ist im Punkt t = t 0 ). Aus der Annahme folgt, dass ϕ : R R in eine Potenzreihe der Form ϕ(t) = c 0 + c 1 t c k t k +... = c k t k mit c k R für k N (2) k=0 entwickelt werden kann. Diese Potenzreihe konvergiert für t < A, mit einer zu bestimmenden positiven Konstante A. Aufgabe ist es nun, die Koeffizienten c k der Potenzreihe so zu bestimmen, dass ϕ sowohl die Gleichung (1) als auch die zugehörigen Anfangsbedingungen erfüllt. 8
9 Falls nun die Potenzreihe (2) eine Lösung von (1) darstellt, dann muss diese Potenzreihe zweimal differenzierbar sein (ansonsten kann sie unmöglich die Differentialgleichung erfüllen). Wir erhalten: ϕ (t) = c c 2 t k c k t k = ϕ (t) = 2 c c 3 t +... = k=1 k=2 Multiplizieren wir des weiteren ϕ mit t, so erhalten wir: k c k t k 1, k (k 1) c k t k 2, t R t R (3) t ϕ(t) = c 0 t + c 1 t c k t k = c k t k+1, t R (4) k=0 Setzen wir (3) und (4) nun in die ursprüngliche Differentialgleichung (1) ein, so ergibt sich: ϕ (t) t ϕ(t) = k (k 1) c k t k 2 c k t k+1 (5) k=2 k=0 Betrachten wir die erste Reihe von (5) so fällt auf, dass diese mit dem konstanten Term 2 c 2 beginnt. Um beide Reihen kombinieren zu können, separieren wir diesen konstanten Term von der ersten Reihe und führen bei der zweiten Reihe eine Indexverschiebung aus. Dafür sei k = n 3 und für die zweite Reihe ergibt sich somit: c k t k+1 = k=0 c n 3 t n 2, t R. (6) n=3 Da der Index nicht von Bedeutung ist, ersetzen wir nun wiederum n durch k. Im nächsten Schritt fahren wir erst mal nur formal fort, d.h. die Gültigkeit der Umformungen wird später gesichert, indem wir die Konvergenz der Reihen nachweisen. 9
10 Damit ergibt sich (5) erneut als: ϕ (t) t ϕ(t) = 2 c 2 + = 2 c 2 + k=3 k=3 k (k 1) c k t k 2 c k 3 t k 2 k=3 [k (k 1) c k c k 3 ]t k 2, t R. Angenommen die Umformungen waren bis hierhin gerechtfertigt, dann ist ϕ genau dann eine Lösung der gegebenen Differentialgleichung (1), wenn die Koeffizienten c k folgende Gleichung erfüllen: 2 c 2 + k=3 [k (k 1) c k c k 3 ]t k 2 = 0 Wegen des Eindeutigkeitssatzes für Potenzreihen (siehe Satz (1.1) v.) müssen alle Koeffizienten 0 ergeben. Damit ergibt sich: 2 c 2 = 0 bzw. k (k 1) c k c k 3 = 0 (k = 3, 4, 5,...). Solche Relationen kann man nun dazu benutzen, die Koeffizienten c k rekursiv zu bestimmen: 2 c 2 = 0 c 2 = 0 Für k=3 gilt: 3 2 c 3 c 0 = 0 c 3 = c 0 Für k=4 gilt: 4 3 c 4 c 1 = 0 c 4 = c 1 Auf die gleiche Weise erhält man weitere Werte der Reihe: 10
11 c 5 = c 2 = 0 c 6 = c 3 = c 7 = c 4 = c c 1... Im Allgemeinen lassen sich diese Reihenwerte nun wie folgt darstellen: c 2 = 0 c 3 = 1 3! c 0 c 4 = 2 4! c 1 c 5 = 0 c 6 = 1 4 6! c 0 c 7 = 2 5 7! c 1. c 3 m+2 = 0 c 3 m = (3 m 2) (3 m)! (3 m 1) c 0 c 3 m+1 = c (3 m + 1 1)! Diese Reihenwerte lassen sich durch Induktion verifizieren: Induktion für c 3 m+2 : IA) Es sei c 3 m+2 = 0. Für m = 0 ist c 2 = 0. IV) Die Behauptung gelte für ein beliebiges, aber festes m N 0. IS) m m + 1 c (3m+5) 3 c 3(m+1)+2 = c 3m+5 = (3m + 5) ((3m + 5) 1) = c 3m+2 (3m + 5) (3m + 4) IV 0 = (3m + 5) (3m + 4) = 0 Induktion für c 3 m : IA) Es sei c 3 m = (3 m 2) (3 m)! c 0. Für m = 1 ist c 3 = c 0. IV) Die Behauptung gelte für ein beliebiges, aber festes m N. 11
12 IS) m m + 1 c (3m+3) 3 c 3(m+1) = c 3m+3 = (3m + 3) ((3m + 3) 1) = c 3m (3m + 3) (3m + 2) IV (3m 2) = (3m)! (3m + 3) (3m + 2) c (3m 2) (3(m + 1) 2) 0 = (3m)! (3m + 3) (3m + 2) (3m + 1) c 0 = (3m 2) (3(m + 1) 2) (3(m + 1))! c 0 Induktion für c 3m+1 : IA) Es sei c 3 m+1 = (3 m 1) (3 m+1)! c 1. Für m = 1 ist c 4 = c 1. IV) Die Behauptung gelte für ein beliebiges, aber festes m N. IS) m m + 1 c (3m+4) 3 c 3(m+1)+1 = c 3m+4 = (3m + 4) ((3m + 4) 1) = c 3m+1 (3m + 4) (3m + 3) IV (3m 1) = (3m + 1)! (3m + 4) (3m + 3) c (3m 1) (3(m + 1) 1) = (3m + 1)! (3m + 4) (3m + 3) (3m + 2) c (3m 1) (3(m + 1) 1) = c (3(m + 1) + 1 1)! Damit werden alle möglichen Koeffizienten der Reihe durch c 0 und c 1 dargestellt. Diese kann man nun mit Hilfe der Anfangsbedingungen ϕ(0) = a, ϕ (0) = b bestimmen. Denn es gilt: ϕ(0) = c 0 + c c = a c 0 = a bzw. ϕ (0) = c c c = b c 1 = b (vgl.(2), (3)) Damit erhält man, vorausgesetzt alle Umformungen waren gerechtfertigt, eine Lösung der Form: 12
13 ϕ(t) = a [1 + m=1 ( (3 m 2) t 3 m ] (3 m)! }{{} =c 3 m t 3 m + b [t + m= (3 m 1) t 3 m+1 ]. (3 m + 1)! }{{} =c 3 m+1 t 3 m+1 Um zu prüfen, ob alle Annahmen gerechtfertigt waren, zeigen wir nun die Konvergenz beider Reihen mit Hilfe des Quotientenkriteriums 9 : Gegeben sei die Reihe m=1 Dann gilt: lim m (3 m 2) (3 m)! (3 (m + 1) 2) (3 (m + 1))! t 3m mit (3 m 2) (3 m)! = 0. t 3(m+1) (3 m)! (3 m 2) t 3m = lim m 3 m + 1 (3m + 3) (3m + 2) (3m + 1)) t3 = lim m 1 (3m + 3) (3m + 2) t3 = 0 Da 0 < 1 gilt, folgt damit die absolute Konvergenz der Reihe. Für die zweite Reihe m= (3 m 1) (3 m+1)! t 3m+1 mit (3 m 1) (3 m+1)! = 0 gilt: lim m (3 (m + 1) 1) (3 (m + 1) + 1)! t 3(m+1)+1 (3 m + 1)! (3 m 1)t 3m+1 3 m + 2 = lim m (3 m + 3) (3 m + 4) (3 m + 2) 1 t3 = lim m (3 m + 4) (3 m + 3) t3 = 0 Da 0 < 1 gilt, folgt damit die absolute Konvergenz der Reihe auf R. Mit der gezeigten Konvergenz wissen wir, dass alle getroffenen Annahmen für alle t R gerechtfertigt waren. Außerdem wissen wir durch Lemma (3.1.), dass die beiden Reihen ϕ 1 (t) = 1 + m=1 ϕ 2 (t) = t + m= (3 m 2) (3 m)! t 3 m und (3 m 1) (3 m+1)! 9 Vgl. Krieg, A., Analysis I, Kapitel III (2.6) t 3 m+1 linear unabhängig sind. 13
14 Deswegen ist, falls a, b R als willkürliche Konstanten festgesetzt sind, eine allgemeine Lösung der Gleichung (1) gegeben durch a ϕ 1 (t) + b ϕ 2 (t). Es sei angemerkt, dass für eine gute Approximation der Lösung (für kleine t) nur eine relativ geringe Anzahl Terme nötig ist. Für große Werte von t (z.b. t = 10)konvergiert die Reihe zu langsam, um von praktischem Nutzen zu sein. (1.7) Satz Es sei I R ein Intervall, a, b R und die Funktionen p, q, f : I R seien analytisch im Punkt t 0 I. Betrachtet wird die Differentialgleichung y + p(t)y + q(t)y = f (t). Dann gibt es eine eindeutige Lösung ϕ der Differentialgleichung, welche die Anfangsbedingungen ϕ(t 0 ) = a, ϕ (t 0 ) = b erfüllt. Diese Lösung ist analytisch im Punkt t = t 0 und ihre Reihenentwicklung ϕ(t) = k=0 c k(t t 0 ) k mit t I, c k R für k N konvergiert mindestens für diejenigen Werte, für die die Potenzreihenentwicklungen von p, q und f für den Entwicklungspunkt t 0 konvergieren. Die entsprechenden Koeffizienten c k können rekursiv durch direkte Substitution bestimmt werden. Wichtig: Es ist zu beachten, dass die Differentialgleichung unbedingt in der oben genannten Form gegeben sein muss (mit Leitkoeffizient 1). Anmerkung: Der Beweis dieses Satzes wird im nächsten Vortrag vorgestellt. Hier stellen wir nur eine Anwendung des Satzes vor. 14
15 Die Legendregleichung (1.8) Beispiel (Legendregleichung) Gegeben sei die Gleichung (1 t 2 ) y 2 t y + α (α + 1) y = 0, wobei α R eine gegebene Konstante ist. Zu prüfen ist nun, ob die Lösung einen Potenzreihenansatz um den Punkt t = 0 besitzt. Um Satz (3.3) anwenden zu können, ist es zielführend die Gleichung zuerst durch (1 t 2 ) zu dividieren ( t = ±1). Es ergibt sich: y 2 t 1 t 2 y + α (α + 1) 1 t 2 y = 0 Diese Gleichung ist für t = 1 und t = 1 wohldefiniert. Nutzen wir die Bezeichnungen aus Satz (3.3), so ist unser Entwicklungspunkt gegeben durch t 0 = 0. Weiter erhalten wir für die in t = t 0 analytischen Funktionen p, q und f : p(t) = 2 t, q(t) = α (α+1) und f (t) = 0. Man stellt überdies fest, dass man p und q als 1 t 2 1 t 2 konvergente Potenzreihen für t < 1 entwickeln kann: Mit der geometrischen Reihe 10 ergibt sich: p(t) = 2 t 1 t 2 = 2 t q(t) = t 2 k k=0 α (α + 1) 1 t 2 = α (α + 1) t 2 k k=0 Für jede Wahl von a, b R existiert nach Satz (3.3) eine eindeutige analytische Lösung ϕ der Legendregleichung, die die Anfangsbedingungen ϕ(0) = a, ϕ (0) = b erfüllt. Außerdem konvergiert die Reihenentwicklung von ϕ für t < vgl.krieg, A., Analysis I, Kapitel III (1.4) 15
16 Aus der Legendre- Gleichung (1 t 2 ) y 2 t y + α (α + 1) y = 0 ergibt sich mit dem Ansatz aus Beispiel (3.2) : ϕ(t) = c k t k k=0 sowie, ϕ (t) = c c 2 t k c k t k = k c k t k 1 k=1 ϕ (t) = 2 c c 3 t k (k 1) c k t k = k (k 1) c k t k 2. k=2 In den folgenden Schritten gehen wir zunächst wieder rein formal vor; die Rechtfertigung der Umformungen wird später gegeben. Setzen wir nun ϕ(t), ϕ (t), ϕ (t) in die Differentialgleichung ein, ergibt sich: (1 t 2 ) k=0 k (k 1) c k t k 2 2 t k=2 (k + 2) (k + 1) c k+2 t k k c k t k 1 + α (α + 1) k=1 k (k 1)c k t k 2 k=2 c k t k = 0 k=0 k c k t k + α (α + 1) k=1 c k t k = 0 k=0 Für den Koeffizienten von t k (k 2) erhalten wir damit: (k + 2) (k + 1) c k+2 k (k 1) c k 2 k c k + α (α + 1) c k = 0 bzw. c k+2 = k (k + 1) α (α + 1) (k + 2) (k + 1) c k Für k = 0 bzw. k = 1 ergibt sich aus der obigen Gleichung: k = 0 : 2 c 2 + α (α + 1) c 0 =0 k = 1 : 6 c 3 2 c 1 + α (α + 1) c 1 =0 Für die Anfangsbedingungen ϕ(0) = 1 = c 0, ϕ (0) = 0 = c 1 verschwinden alle ungera- 16
17 den Koeffizienten und man erhält: c 0 = ϕ(0) = α (α + 1) α (α + 1) α (α + 1) c 2 = c 2 0 = 1 = (3 2 α (α + 1)) (3 2 α (α + 1)) ( α (α + 1)) c 4 = c 3 2 = = α (α + 1) + α 2 (α + 1) 2 = α (α3 + 2α 2 5α 6) α (α 2) (α + 1) (α + 3) = Allgemein erhält man: c 2 k = ( 1) k α... (α 2 k + 2) (α + 1)... (α + 2 k 1) für k 1. (2 k)! Induktion für c 2 k : IA) Es sei c 2 k = ( 1) k α... (α 2 k+2) (α+1)... (α+2 k 1) (2 k)! für k = 1. IV) Die Behauptung gelte für ein beliebiges, aber festes k N, k 1. IS) k k + 1 2k(2k + 1) α(α + 1) c 2(k+1) = c 2 k+2 = (2k + 1) (2k + 2) = α2 + α 2k (2k + 1) c (2k + 1) (2k + 2) 2k (α 2k) (α + 2k + 1) = (2k + 1) (2k + 2) c 2k = (α 2(k + 1) + 2) (α + 2(k + 1) 1) (2k + 1) (2k + 2) c 2k c 2k IV = ( 1) k+1 α... (α 2k + 2) (α + 1)... (α + 2k 1) (α 2(k + 1) + 2) (α + 2(k + 1) 1) (2(k + 1))! = ( 1)k+1 α... (α 2k + 2)(α 2(k + 1) + 2) (α + 1)... (α + 2k 1)(α + 2(k + 1) 1) (2(k + 1))! 17
18 Falls α 0 und gerade ist, bzw. α < 0 und ungerade ist, ist die Lösung der Legendre- Gleichung durch folgendes Polynom gegeben: ϕ(t) = 1 + k=1 c 2 k t 2 k = 1 + k=1 ( 1) k α... (α 2 k + 2) (α + 1)... (α + 2 k 1) (2 k)! t 2 k ϕ(t) ist ein Polynom, da für α = 2 m, m N folgt: c 2k = 0 für k m + 1, da der Faktor α 2k + 2 = 0 ist für k = m + 1. Damit ist ϕ(t) ein Polynom vom Grad 2m. Die ersten geraden, so genannten Legendre- Polynome sind: α = 0 ϕ(t) = 1 α = 2 ϕ(t) = 1 3 t 2 α = 4 ϕ(t) = 1 10 t t4 Für die Anfangsbedingungen ϕ(0) = c 0 = 0, ϕ (0) = c 1 = 1 erhalten wir aus Gleichung (7): c 0 = c 2 =... = 0, d.h. alle geraden Koeffizienten sind 0. Weiter ergibt sich für die ungeraden Koeffizienten: c 1 = ϕ(0) = α (α + 1) c 3 = c 2 1 = 2 α2 α (α 1) (α + 2) 1 = α (α + 1) (12 α (α + 1)) ( (α 1) (α + 2)) c 5 = c 5 3 = = (α 1) (α + 2) ( 12 + α (α + 1)) (α 1) (α 3) (α + 2) (α + 4) = Allgemein erhält man: c 2 k+1 = ( 1) k (α 1)... (α 2 k + 1) (α + 2)... (α + 2 k) für k 1. (2 k + 1)! 18
19 Beweis per Induktion: Induktion für c 2 k+1 : IA) Es sei c 2 k+1 = ( 1) k (α 1)... (α 2 k+1) (α+2)... (α+2 k) (2 k+1)! für k = 1. IV)Die Behauptung gelte für ein beliebiges, aber festes k N, k 1. IS) k k + 1 (2k + 1) (2k + 2) α(α + 1) c 2(k+1)+1 = c (2 k+1)+2 = (2k + 3) (2k + 2) = α2 + α 2(k + 1) (2k + 1) c (2k + 3) (2k + 2) 2k+1 (α (2k + 1)) (α + 2(k + 1)) = c (2k + 3) (2k + 2) 2k+1 (α 2(k + 1) + 1) (α + 2(k + 1)) = c (2k + 3) (2k + 2) 2k+1 c 2k+1 IV = ( 1) k+1 (α 1)... (α 2k + 1) (α 2(k + 1) + 1) (α + 2)... (α + 2k) (α + 2(k + 1)) (2(k + 1) + 1)! Falls α > 0 und ungerade ist, bzw. α < 0 und gerade ist, ist die Lösung der Legendregleichung durch folgendes Polynom gegeben: ϕ(t) = t + = t + k=1 k=1 c 2 k+1 t 2 k+1 ( 1) k ϕ(t) ist ein Polynom, da (α 1)... (α 2 k + 1) (α + 2)... (α + 2 k) (2 k + 1)! t 2 k+1. für α = 2 m 1, m N folgt: c 2k+1 = 0 für k m, da der Faktor α 2k + 1 = 0 ist für k = m. Damit ist die Lösung ϕ(t) der Legendregleichung ein Polynom vom Grad 2m 1. Diese Polynome, welche die Legendregleichung lösen, werden auch Legendre- Polynome genannt. 19
20 Die ersten ungeraden Legendre-Polynome sind: α = 1 α = 3 α = 5 ϕ(t) = t ϕ(t) = t 5 3 t3 ϕ(t) = t 14 3 t t5 Es ist gezeigt, dass die Legendre- Gleichung (1 t 2 ) y 2 t y + α (α + 1) y = 0, für eine nicht negative ganze Zahl α = n ein Polynom vom Grad n N als Lösung besitzt. Da wir ein Polynom als Lösung erhalten, ist die Konvergenz der Lösung natürlich auf ganz R gegeben. Satz (3.3) liefert nur Konvergenz auf t < 1; der Konvergenzbereich kann somit größer sein als im Satz angegeben. Damit sind die ersten 5 Legendre- Polynome (geschrieben P n (t) bei Grad n) gegeben durch: P 0 (t) = 1 (α = 0) P 1 (t) = t (α = 1) P 2 (t) P 3 (t) = 1 2 (1 3 t2 ) (α = 2) = 3 2 (t 5 3 t3 ) (α = 3) P 4 (t) = 3 8 (1 10 t t4 ) (α = 4) P 5 (t) = 15 8 (t 14 3 t t5 ) (α = 5) Diese Polynome erhält man, indem man den Vorfaktor der Legendre-Polynome so wählt, dass P n (1) = 1 ergibt. Anwendung der Legendre Polynome Die vorgestellten Legendre-Polynome sind insbesondere in der Physik von großem Interesse. 20
21 Anwendungsbsp: : Die Multipolentwicklung des elektrostatischen Potentials einer räumlich beschränkten Ladungsverteilung. 21
22 4 Literatur Anschauung Legendre Polynome 4 Literatur Brauer, F. /Nohel, J. A.: Ordinary Differential Equations. New York, Amsterdam Seite Skripte: Krieg, A.: Analysis I. RWTH Aachen Krieg, A.: Analysis II. RWTH Aachen Krieg, A./Walcher, S.: Gewöhnliche Differentialgleichungen. RWTH Aachen
Reihenentwicklung II. 1 Potenzreihenentwicklung von Lösungen
 Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 29.11.2011 Julia Rittich In dem vorherigen Vortrag haben wir erfahren, dass in vielen Anwendungsproblemen eine Differentialgleichung nicht in geschlossener
Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 29.11.2011 Julia Rittich In dem vorherigen Vortrag haben wir erfahren, dass in vielen Anwendungsproblemen eine Differentialgleichung nicht in geschlossener
5 Potenzreihenansatz und spezielle Funktionen
 5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
konvergent falls eine allgemeine ("gutmütige") Funktion. Frage: kann man sie in der darstellen mittels einer Potenzreihe in
 C5 Funktionen: Taylorreihen & Fourieranalysis C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen
C5 Funktionen: Taylorreihen & Fourieranalysis C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen
konvergent falls Sei eine allgemeine ("gutmütige") Funktion. Frage: kann man sie in der Nähe des Punktes darstellen mittels einer Potenzreihe in
 C5 Funktionen: Reihenentwicklungen C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen lässt sich
C5 Funktionen: Reihenentwicklungen C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen lässt sich
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
a 0 +a 1 x+a 2 x n=0 a n x n := lim
 1 Taylor-Entwicklung 1.1 Potenzreihen Def.: Ein Ausdruck der Form a 0 +a 1 +a +... a n n := lim k k a n n, (1) mit einer (unendlichen) Folge reeller Konstanten a 0,a 1,a,... ( Koeffizienten ) und einer
1 Taylor-Entwicklung 1.1 Potenzreihen Def.: Ein Ausdruck der Form a 0 +a 1 +a +... a n n := lim k k a n n, (1) mit einer (unendlichen) Folge reeller Konstanten a 0,a 1,a,... ( Koeffizienten ) und einer
Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik II für biw/ciw/mach/mage/vt
 Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Höhere Mathematik I für die Fachrichtung Physik. Lösungsvorschläge zum 12. Übungsblatt
 Institut für Analysis WS07/8 Prof. Dr. Dirk Hundertmark 6..08 Dr. Michal Je Höhere Mathematik I für die Fachrichtung Physik Lösungsvorschläge zum. Übungsblatt Aufgabe 68: a Es sei c irgendeine Zahl zwischen
Institut für Analysis WS07/8 Prof. Dr. Dirk Hundertmark 6..08 Dr. Michal Je Höhere Mathematik I für die Fachrichtung Physik Lösungsvorschläge zum. Übungsblatt Aufgabe 68: a Es sei c irgendeine Zahl zwischen
Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen
 Proseminar Lineare Algebra SS10 Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen Simon Strahlegger Heinrich-Heine-Universität Betreuung: Prof. Dr. Oleg Bogopolski Inhaltsverzeichnis:
Proseminar Lineare Algebra SS10 Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen Simon Strahlegger Heinrich-Heine-Universität Betreuung: Prof. Dr. Oleg Bogopolski Inhaltsverzeichnis:
Analysis I. 3. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Leitfaden a tx t
 Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Staatsexamen Herbst 2017 Differential- und Integralrechnung, Thema I
 Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Vorlesung Mathematik 2 für Ingenieure (Sommersemester 2016)
 1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
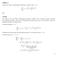 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Anleitung zu Blatt 2, Analysis II
 Fachbereich Mathematik der Universität Hamburg Dr. H. P. Kiani Anleitung zu Blatt 2, Analysis II SoSe 202 Funktionenfolgen, Potenzreihen I Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur
Fachbereich Mathematik der Universität Hamburg Dr. H. P. Kiani Anleitung zu Blatt 2, Analysis II SoSe 202 Funktionenfolgen, Potenzreihen I Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur
Lösung - Serie 25. D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger
 D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
Analysis I. 7. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Aufgaben und Lösungen Ausarbeitung der Übungsstunde zur Vorlesung Analysis I
 Aufgaben und en Ausarbeitung der Übungsstunde zur Vorlesung Analysis I Wintersemester 2008/2009 Übung 6 Einleitung Eventuell auftretende Fragen zum Übungsblatt sollen beantwortet werden. Dazu ist es erforderlich,
Aufgaben und en Ausarbeitung der Übungsstunde zur Vorlesung Analysis I Wintersemester 2008/2009 Übung 6 Einleitung Eventuell auftretende Fragen zum Übungsblatt sollen beantwortet werden. Dazu ist es erforderlich,
Mathematik für Anwender I
 Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 17 Potenzreihen Definition 17.1. Es sei (c n ) n N eine Folge von reellen Zahlen und x eine weitere reelle Zahl. Dann heißt
Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 17 Potenzreihen Definition 17.1. Es sei (c n ) n N eine Folge von reellen Zahlen und x eine weitere reelle Zahl. Dann heißt
Klausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 4.3.3 Klausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((4+3+3 Punkte a Welche
Karlsruher Institut für Technologie (KIT Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 4.3.3 Klausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((4+3+3 Punkte a Welche
Technische Universität München Zentrum Mathematik. Übungsblatt 7
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
Kapitel 24. Entwicklungen holomorpher Funktionen Taylor-Reihen (Potenzreihen und holomorphe Funktionen;
 Kapitel 24 Entwicklungen holomorpher Funktionen Reihenentwicklungen spielen in der Funktionentheorie eine ganz besodere Rolle. Im Reellen wurden Potenzreihen in Kapitel 5.2 besprochen, das komplexe Gegenstück
Kapitel 24 Entwicklungen holomorpher Funktionen Reihenentwicklungen spielen in der Funktionentheorie eine ganz besodere Rolle. Im Reellen wurden Potenzreihen in Kapitel 5.2 besprochen, das komplexe Gegenstück
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
27 Taylor-Formel und Taylor-Entwicklungen
 136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
3. Folgen und Reihen. 3.1 Folgen und Grenzwerte. Denition 3.1 (Folge) Kapitelgliederung
 Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
1 Reihen von Zahlen. Inhalt:
 5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
Funktionenfolgen, Potenzreihen, Exponentialfunktion
 Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Höhere Mathematik II. Variante A
 Lehrstuhl II für Mathematik Prof Dr E Triesch Höhere Mathematik II SoSe 5 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter (Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof Dr E Triesch Höhere Mathematik II SoSe 5 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter (Vorder- und Rückseite
April (Voll-) Klausur Analysis I für Ingenieure. Rechenteil
 April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
Höhere Mathematik für Physiker II
 Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
Musterlösungen zu Blatt 15, Analysis I
 Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
7 KONVERGENTE FOLGEN 35. inf M = Infimum von M. bezeichnet haben. Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt.
 7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
2.12 Potenzreihen. 1. Definitionen. 2. Berechnung 2.12. POTENZREIHEN 207. Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen.
 2.2. POTENZREIHEN 207 2.2 Potenzreihen. Definitionen Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen. Eine Potenzreihe mit Entwicklungspunkt x 0 ist eine Reihe a n x x 0 n. Es gilt: es
2.2. POTENZREIHEN 207 2.2 Potenzreihen. Definitionen Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen. Eine Potenzreihe mit Entwicklungspunkt x 0 ist eine Reihe a n x x 0 n. Es gilt: es
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Meromorphe Funktionen
 Kapitel Meromorphe Funktionen Der Satz von Mittag-Leffler Zur Erinnerung: Die holomorphe Funktion f habe in z 0 C eine isolierte Singularität. Liegt eine Polstelle vor, so gibt es eine offene Umgebung
Kapitel Meromorphe Funktionen Der Satz von Mittag-Leffler Zur Erinnerung: Die holomorphe Funktion f habe in z 0 C eine isolierte Singularität. Liegt eine Polstelle vor, so gibt es eine offene Umgebung
SS 2016 Höhere Mathematik für s Studium der Physik 21. Juli Probeklausur. Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert.
 SS 6 Höhere Mathematik für s Studium der Physik. Juli 6 Probeklausur Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert. Fragen Sei (X, d) ein metrischer Raum. Beantworten Sie die nachfolgenden
SS 6 Höhere Mathematik für s Studium der Physik. Juli 6 Probeklausur Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert. Fragen Sei (X, d) ein metrischer Raum. Beantworten Sie die nachfolgenden
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript
 Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
10 Kriterien für absolute Konvergenz von Reihen
 10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
Analysis I. 6. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
HM I Tutorium 5. Lucas Kunz. 24. November 2016
 HM I Tutorium 5 Lucas Kunz 24. November 206 Inhaltsverzeichnis Theorie 2. Definition einer Reihe.............................. 2.2 Wichtige Reihen................................. 2.3 Limites inferior
HM I Tutorium 5 Lucas Kunz 24. November 206 Inhaltsverzeichnis Theorie 2. Definition einer Reihe.............................. 2.2 Wichtige Reihen................................. 2.3 Limites inferior
Potenzreihen. Potenzreihen sind Funktionenreihen mit einer besonderen Gestalt.
 Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
8. 2A. Integration von Potenzreihen
 8. 2A. Integration von Potenzreihen Wie wir schon mehrfach sahen, sind Potenzreihen ein unentbehrliches Werkzeug für viele Berechnungen in der Ingenieurmathematik. Glücklicherweise darf man Potenzreihen
8. 2A. Integration von Potenzreihen Wie wir schon mehrfach sahen, sind Potenzreihen ein unentbehrliches Werkzeug für viele Berechnungen in der Ingenieurmathematik. Glücklicherweise darf man Potenzreihen
Analysis I. 4. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
2 k k 1 k(k + 1) = 2n+1. n = 0 = k(k + 1) = 2n+1 n n. = 2 n+1 n + 2 (n + 1)(n + 2) + n. (n + 1)(n + 2)
 Prof. Hesse Höhere Mathematik I und II Musterlösung 7. 0. 0, 80min Aufgabe (3 Punkte) Zeigen Sie mit vollständiger Induktion: Für alle n N gilt n k= k k k(k + ) = n+ n +. Induktionsanfang: k= Induktionsschluss
Prof. Hesse Höhere Mathematik I und II Musterlösung 7. 0. 0, 80min Aufgabe (3 Punkte) Zeigen Sie mit vollständiger Induktion: Für alle n N gilt n k= k k k(k + ) = n+ n +. Induktionsanfang: k= Induktionsschluss
Algebraische Kurven. Vorlesung 25
 Prof. Dr. H. Brenner Osnabrück SS 2012 Algebraische Kurven Vorlesung 25 Lösung in Potenzreihen für algebraische Kurven Sei F 0 ein Polynom, das die ebene algebraische Kurve C beschreibe, und sei P = (0,0)
Prof. Dr. H. Brenner Osnabrück SS 2012 Algebraische Kurven Vorlesung 25 Lösung in Potenzreihen für algebraische Kurven Sei F 0 ein Polynom, das die ebene algebraische Kurve C beschreibe, und sei P = (0,0)
P n (1) P j (1) + ε 2, j=0. P(1) P j (1) + ε 2 < ε. log(1+x) =
 Zu ε > 0 gibt es ein N N mit P n (1) P j (1) < ε/2 für j,n > N, also gilt Es folgt (1 x) n 1 j=n+1 und schließlich mit n x j P n (1) P j (1) (1 x) ε 2 P n (1) P n (x) (1 x) P(1) P(x) (1 x) für x hinreichend
Zu ε > 0 gibt es ein N N mit P n (1) P j (1) < ε/2 für j,n > N, also gilt Es folgt (1 x) n 1 j=n+1 und schließlich mit n x j P n (1) P j (1) (1 x) ε 2 P n (1) P n (x) (1 x) P(1) P(x) (1 x) für x hinreichend
REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert
![REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert](/thumbs/55/37057337.jpg) Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Fourier-Reihen: Definitionen und Beispiele
 Fourier-Reihen: Definitionen und Beispiele Die Fourieranalysis beschäftigt sich mit dem Problem Funktionen in Kosinus und Sinus zu entwickeln. Diese Darstellungen sind in der Mathematik sowie in der Physik
Fourier-Reihen: Definitionen und Beispiele Die Fourieranalysis beschäftigt sich mit dem Problem Funktionen in Kosinus und Sinus zu entwickeln. Diese Darstellungen sind in der Mathematik sowie in der Physik
Musterlösung Klausur zu Analysis II. Verständnisteil
 Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Mathematik I - Woche 10
 Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
Klausur - Analysis I Lösungsskizzen
 Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit und falsche Aussagen mit. Es sind keine Begründungen
Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit und falsche Aussagen mit. Es sind keine Begründungen
11. Übungsblatt zur Mathematik I für Maschinenbau
 Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 200/ 2.0.-28.0. Aufgabe G (Grenzwertberechnung)
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 200/ 2.0.-28.0. Aufgabe G (Grenzwertberechnung)
Ferienkurs Analysis 1
 Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
Folgen und Reihen. Folgen. Inhalt. Mathematik für Chemiker Teil 1: Analysis. Folgen und Reihen. Reelle Funktionen. Vorlesung im Wintersemester 2014
 Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Aufgabensammlung zur Analysis 1
 Analysis 1 18.12.2017 Prof. Dr. H. Koch Dr. F. Gmeineder Abgabe: Keine Abgabe. Aufgabensammlung zur Analysis 1 Anmerkungen: Das vorliegende Blatt enthält eine Auswahl von Aufgaben, die auf Klausuren zur
Analysis 1 18.12.2017 Prof. Dr. H. Koch Dr. F. Gmeineder Abgabe: Keine Abgabe. Aufgabensammlung zur Analysis 1 Anmerkungen: Das vorliegende Blatt enthält eine Auswahl von Aufgaben, die auf Klausuren zur
HM I Tutorien 6 und 7
 HM I Tutorien 6 und 7 Lucas Kunz. Dezember 207 und 8. Dezember 207 Inhaltsverzeichnis Vorwort 2 2 Theorie 2 2. Definition einer Reihe.............................. 2 2.2 Absolute Konvergenz..............................
HM I Tutorien 6 und 7 Lucas Kunz. Dezember 207 und 8. Dezember 207 Inhaltsverzeichnis Vorwort 2 2 Theorie 2 2. Definition einer Reihe.............................. 2 2.2 Absolute Konvergenz..............................
Mathematik I. k=0 c k(x a) k bilden die Teilpolynome n k=0 c k(x a) k polynomiale Approximationen für die Funktion f
 Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 30 Zu einer konvergenten Potenzreihe f(x) = c k(x a) k bilden die Teilpolynome n c k(x a) k polynomiale Approximationen für die Funktion
Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 30 Zu einer konvergenten Potenzreihe f(x) = c k(x a) k bilden die Teilpolynome n c k(x a) k polynomiale Approximationen für die Funktion
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
Kapitel 6. Exponentialfunktion
 Kapitel 6. Exponentialfunktion 6.1. Potenzreihen In Kap. 4 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Kapitel 6. Exponentialfunktion 6.1. Potenzreihen In Kap. 4 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
6.5 Die Taylor-Reihe. Start: Erinnerung an den Satz über die geometrische Reihe. Für die endliche geometrische Reihe gilt die Summenformel
 6.5 Die Taylor-Reihe Start: Erinnerung an den Satz über die geometrische Reihe. Für die endliche geometrische Reihe gilt die Summenformel N q n = qn+ q für q C \ {}. Für q < ist die unendliche geometrische
6.5 Die Taylor-Reihe Start: Erinnerung an den Satz über die geometrische Reihe. Für die endliche geometrische Reihe gilt die Summenformel N q n = qn+ q für q C \ {}. Für q < ist die unendliche geometrische
5. Vorlesung Wintersemester
 5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
Analysis I Lösung von Serie 14. Um die Inhomogene DGl zu lösen, müssen wir partikuläre Lösungen finden. (a) Wir machen den Ansatz:
 d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
Die komplexe Exponentialfunktion und die Winkelfunktionen
 Die komplexe Exponentialfunktion und die Winkelfunktionen In dieser Zusammenfassung werden die für uns wichtigsten Eigenschaften der komplexen und reellen Exponentialfunktion sowie der Winkelfunktionen
Die komplexe Exponentialfunktion und die Winkelfunktionen In dieser Zusammenfassung werden die für uns wichtigsten Eigenschaften der komplexen und reellen Exponentialfunktion sowie der Winkelfunktionen
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 26 1. Folgen R. Steuding (HS-RM)
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 26 1. Folgen R. Steuding (HS-RM)
Mathematik IT 3 (Analysis) Probeklausur
 Mathematik IT (Analysis) Probeklausur Datum: 08..0, Zeit: :5 5:5 Name: Matrikelnummer: Vorname: Geburtsdatum: Studiengang: Aufgabe Nr. 5 Σ Punkte Soll 5 9 7 Punkte Ist Lösungen ohne begründeten Lösungsweg
Mathematik IT (Analysis) Probeklausur Datum: 08..0, Zeit: :5 5:5 Name: Matrikelnummer: Vorname: Geburtsdatum: Studiengang: Aufgabe Nr. 5 Σ Punkte Soll 5 9 7 Punkte Ist Lösungen ohne begründeten Lösungsweg
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Analysis I. 2. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching March 5, 07 Erinnerung (Euler Formel). e iϕ = cos ϕ + i sin ϕ. Die Polarform von z = x + iy C sei Euler Formel z
Analysis I. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching March 5, 07 Erinnerung (Euler Formel). e iϕ = cos ϕ + i sin ϕ. Die Polarform von z = x + iy C sei Euler Formel z
Ferienkurs Analysis 1, SoSe Unendliche Reihen. Florian Beye August 15, 2008
 Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Maclaurinsche Reihe 1-E1. Ma 2 Lubov Vassilevskaya
 Maclaurinsche Reihe 1-E1 Colin Maclaurin Colin Maclaurin (1698-1746), schottischer Mathematiker, der Erfinder der nach ihm benannten Maclaurinschen Reihe und Mitentwickler der Euler-Maclaurin-Formel. 1-E
Maclaurinsche Reihe 1-E1 Colin Maclaurin Colin Maclaurin (1698-1746), schottischer Mathematiker, der Erfinder der nach ihm benannten Maclaurinschen Reihe und Mitentwickler der Euler-Maclaurin-Formel. 1-E
Mathematisches Institut der Universität Heidelberg Prof. Dr. E. Freitag /Thorsten Heidersdorf. Probeklausur
 Mathematisches Institut der Universität Heidelberg Prof. Dr. E. Freitag /Thorsten Heidersdorf Probeklausur Diese Probeklausur soll a) als Test für euch selber dienen, b) die Vorbereitung auf die Klausur
Mathematisches Institut der Universität Heidelberg Prof. Dr. E. Freitag /Thorsten Heidersdorf Probeklausur Diese Probeklausur soll a) als Test für euch selber dienen, b) die Vorbereitung auf die Klausur
9 Konvergenz und absolute Konvergenz von Reihen
 9 Konvergenz und absolute Konvergenz von Reihen 9.2 Konvergenz von Reihen 9.5 Monotoniekriterium für Reihen 9.6 Konvergenzkriterium von Cauchy für Reihen 9.9 Rechenregeln für konvergente Reihen 9.10 Absolute
9 Konvergenz und absolute Konvergenz von Reihen 9.2 Konvergenz von Reihen 9.5 Monotoniekriterium für Reihen 9.6 Konvergenzkriterium von Cauchy für Reihen 9.9 Rechenregeln für konvergente Reihen 9.10 Absolute
Kapitel 1. Holomorphe Funktionen
 Kapitel 1 Holomorphe Funktionen Zur Erinnerung: I IR sei ein offenes Intervall, und sei z 0 I. Eine Funktion f : I IR heißt differenzierbar in z 0, falls der Limes fz fz 0 lim =: f z 0 z z 0 z z 0 existiert.
Kapitel 1 Holomorphe Funktionen Zur Erinnerung: I IR sei ein offenes Intervall, und sei z 0 I. Eine Funktion f : I IR heißt differenzierbar in z 0, falls der Limes fz fz 0 lim =: f z 0 z z 0 z z 0 existiert.
KAPITEL 9. Funktionenreihen
 KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
Übungen Ingenieurmathematik
 Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Analysis I. 1. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Kapitel 3. Konvergenz von Folgen und Reihen
 Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
Klausur - Analysis I Lösungsskizzen
 Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
Abschlussklausur , 10:30 bis 13:30
 FU Berlin: SoSe 18 (Mathematik I, Weber) Abschlussklausur 26.7.2018, 10:30 bis 13:30 Name: Matrikelnummer: Unterschrift: Bewertung (vom Dozenten auszufüllen): Aufgabe 1 2 3 4 5 6 7 8 Summe Maximal erreichbare
FU Berlin: SoSe 18 (Mathematik I, Weber) Abschlussklausur 26.7.2018, 10:30 bis 13:30 Name: Matrikelnummer: Unterschrift: Bewertung (vom Dozenten auszufüllen): Aufgabe 1 2 3 4 5 6 7 8 Summe Maximal erreichbare
Folgen und Reihen Folgen
 Folgen und Reihen 30307 Folgen Einstieg: Wir beginnen mit einigen Beispielen für reelle Folgen: (i),, 4, 8, 6, (ii) 4,, 6, 3, 7, (iii) 0,,,, 3,, (iv), 3, 7,,, Aufgabe : Setzt die Zahlenfolgen logisch fort
Folgen und Reihen 30307 Folgen Einstieg: Wir beginnen mit einigen Beispielen für reelle Folgen: (i),, 4, 8, 6, (ii) 4,, 6, 3, 7, (iii) 0,,,, 3,, (iv), 3, 7,,, Aufgabe : Setzt die Zahlenfolgen logisch fort
Rechenoperationen mit Folgen. Rekursion und Iteration.
 Rechenoperationen mit Folgen. Die Menge aller Folgen in V bildet einen Vektorraum, V N, für den die Addition und skalare Multiplikation wie folgt definiert sind. (a n ) n N + (b n ) n N := (a n + b n )
Rechenoperationen mit Folgen. Die Menge aller Folgen in V bildet einen Vektorraum, V N, für den die Addition und skalare Multiplikation wie folgt definiert sind. (a n ) n N + (b n ) n N := (a n + b n )
8.1 Begriffsbestimmung
 8 Gewöhnliche Differentialgleichungen 8 Gewöhnliche Differentialgleichungen 8.1 Begriffsbestimmung Wir betrachten nur Differentialgleichungen für Funktionen einer (reellen) Variablen. Definition: Für eine
8 Gewöhnliche Differentialgleichungen 8 Gewöhnliche Differentialgleichungen 8.1 Begriffsbestimmung Wir betrachten nur Differentialgleichungen für Funktionen einer (reellen) Variablen. Definition: Für eine
ANALYSIS 2 VERSION 26. Juni 2018
 ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
Mathematik I HM I A. SoSe Variante A
 Prof. Dr. E. Triesch Mathematik I SoSe 08 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur die Antworten
Prof. Dr. E. Triesch Mathematik I SoSe 08 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur die Antworten
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppitz, Dr. I. Rybak 14. Gruppenübung zur Vorlesung Höhere Mathematik 1 Sommersemester 009 Prof. Dr. M. Stroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe
P. Engel, T. Pfrommer S. Poppitz, Dr. I. Rybak 14. Gruppenübung zur Vorlesung Höhere Mathematik 1 Sommersemester 009 Prof. Dr. M. Stroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe
Stroppel Musterlösung , 180min. Aufgabe 1 (4 Punkte) Bestimmen Sie die folgenden Grenzwerte und Funktionengrenzwerte.
 Stroppel Musterlösung 3908, 80min Aufgabe 4 Punkte) Bestimmen Sie die folgenden Grenzwerte und Funktionengrenzwerte a) 4n 3 9 lim b) lim n n + n) n + )5n 4) c) lim x 0 sinlnx + )) sinhx) a) Es ist lim
Stroppel Musterlösung 3908, 80min Aufgabe 4 Punkte) Bestimmen Sie die folgenden Grenzwerte und Funktionengrenzwerte a) 4n 3 9 lim b) lim n n + n) n + )5n 4) c) lim x 0 sinlnx + )) sinhx) a) Es ist lim
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
Invertieren von Potenzreihen
 Invertieren von Potenzreihen Sei E(x) die Erzeugende Funktion der Reihe, 0, 0, 0,.... E(x) ist neutrales Element der Multiplikation von Potenzreihen. Definition Inverses einer Potenzreihe Sei A(x), B(x)
Invertieren von Potenzreihen Sei E(x) die Erzeugende Funktion der Reihe, 0, 0, 0,.... E(x) ist neutrales Element der Multiplikation von Potenzreihen. Definition Inverses einer Potenzreihe Sei A(x), B(x)
(b) Bestimmen Sie mit Hilfe des Newton-Verfahrens eine Nullstelle von f auf 6 Nachkommastellen
 Mathematik I für Naturwissenschaften Dr. Christine Zehrt 5.10.18 Übung 6 (für Pharma/Geo/Bio) Uni Basel Besprechung der Lösungen: 9. Oktober 018 in den Übungsstunden Aufgabe 1 GebenSieohneTaschenrechnereineNäherungvon
Mathematik I für Naturwissenschaften Dr. Christine Zehrt 5.10.18 Übung 6 (für Pharma/Geo/Bio) Uni Basel Besprechung der Lösungen: 9. Oktober 018 in den Übungsstunden Aufgabe 1 GebenSieohneTaschenrechnereineNäherungvon
Polynomiale Approximation. und. Taylor-Reihen
 Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Identitätssatz für Potenzreihen
 Identitätssatz für Potenzreihen Satz 3.56 Seien f (z) = a n z n und g(z) = b n z n zwei Potenzreihen mit positiven Konvergenzradien R f > 0 und R g > 0. Gilt f (z) = g(z) für alle z mit 0 z < min{r f,
Identitätssatz für Potenzreihen Satz 3.56 Seien f (z) = a n z n und g(z) = b n z n zwei Potenzreihen mit positiven Konvergenzradien R f > 0 und R g > 0. Gilt f (z) = g(z) für alle z mit 0 z < min{r f,
3.3. KONVERGENZKRITERIEN 67. n+1. a p und a n. beide nicht konvergent, so gilt die Aussage des Satzes 3.2.6
 3.3. KONVERGENZKRITERIEN 67 und l n+1 wiederum als kleinsten Wert, so dass A 2n+2 = A 2n+1 + l n+1 k=l n < A. Alle diese Indizes existieren und damit ist eine Folge {A k } k N definiert. Diese Folge konvergiert
3.3. KONVERGENZKRITERIEN 67 und l n+1 wiederum als kleinsten Wert, so dass A 2n+2 = A 2n+1 + l n+1 k=l n < A. Alle diese Indizes existieren und damit ist eine Folge {A k } k N definiert. Diese Folge konvergiert
Lösen von Differentialgleichungen durch Reihenentwicklung
 Lösen von Differentialgleichungen durch Reihenentwicklung Thomas Wassong FB17 Mathematik Universität Kassel 30. April 2008 Einführung Reihen in der Mathematik Reihen zum Lösen von Differentialgleichungen
Lösen von Differentialgleichungen durch Reihenentwicklung Thomas Wassong FB17 Mathematik Universität Kassel 30. April 2008 Einführung Reihen in der Mathematik Reihen zum Lösen von Differentialgleichungen
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
