Kapitel 6: Dynamic Shortest Path
|
|
|
- Willi Gerstle
- vor 5 Jahren
- Abrufe
Transkript
1 Kapitel 6: Dynamic Shortest Path 6. Einführung 6. SSSP von Ramalingam & Reps VO Algorithm Engineering Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS Organisatorisches zur Übung wichtig: Dienstags-Übung vom 9. Mai wird verschoben auf 5. Juni Donnerstags-Übung: Einteilung der Aufgabenbearbeitung für Übungsblatt 3: Aufgabe : Gruppe 6 Aufgabe : Gruppen und Aufgabe 3: Gruppen 9, und 5./3. VO 5./. Mai 007 Nachlese Oberwolfach Seminar on Algorithm Engineering TSP-Buch hier! Achtung: falsche Flipfolge für Lin-Kernighan im Buch, Fig. 5.5 passt nicht mit Flipfolge korrekt (Bill Cook): Fall.: flip(a,base), flip(base,b), flip(b,s), Fall.: flip(s,b), flip(b,a) Dritte flip()-sequenz: 3er Austausche Wähle einen Nachbarn b von next(a) entfernt (a,next(a). Fall: b liegt zwischen next(base) und a: Betrachte Alternativen für flip()-sequenzen:.: <flip(a,base), flip(base,b),flip(b,s)> entfernt zusätzlich (b,next(b)).: <flip(s,b), flip(b,a)>, wobei b=prev(b) zu Beginn entfernt zusätzlich (prev(b),b) flip(s,b) base a=next(a) a flip(b,a) base next(a) a s= next(base) s 3 b b=prev(b) neu: Achtung Fehler im Buch b b Pino Italiano (Rom): A Theoretician knows: Theory and Practice are quite the same! A Practitioner knows: Theory and Practice are quite different! Nachlese Oberwolfach Seminar on Algorithm Engineering Rajeev Raman (London): In my theoretical papers I have always written: it is easy to do this and that. Now I have tried to implement it, and it was not clear how to do this at all. Jetzt HIER: 3. Übungsblatt über Suffix Arrays Aufgabenzuordnung für die Donnerstag-Gruppe: s. Web für Dienstags-Gruppe: heute Leonardo da Vinci: Der vitruvianische Mensch, 9 5 6
2 Überblick 5. Einführung Dynamische Graphalgorithmen Dynamische Komplexitätsmaße Dijkstra s SSSP-Algorithmus Analyse: Korrektheit und Laufzeit Literatur für diese VO G. Ramalingam und T. Reps: On the computational complexity of dynamic graph problems. Theoretical Computer Science 58, 996, SSSP von Ramalingam & Reps Einführung SP-Teilgraph für SSSP Algorithmus Dynamic SSSP Laufzeit-Analyse 7 8 Dynamische Graphalgorithmen Dynamische Graphalgorithmen Ein dynamischer Algorithmus erhält eine gegebene Eigenschaft P eines gewichteten Graphen während dynamischer Änderungen des Graphen, z.b. Einfügen neuer Kanten, Entfernen von Kanten und Kosten-Änderungen der Kanten Anforderungen an einen dynamischen Algorithmus: schnelle Beantwortung von Anfragen auf Eigenschaft P schnelle Bearbeitung von Update-Operationen, d.h. schneller als ein statischer Algorithmus, der jedesmal alles von vorn berechnen muss 9 Wir betrachten o.e. nur Kosten-Änderungen der Kanten. Ein dynamischer Algorithmus heißt voll-dynamisch (full dynamic) wenn er für Erhöhungen als auch für Verminderungen von Kantenkosten geeignet ist. Sonst heißt er teil-dynamisch (partially dynamic). 0 Dynamische Komplexitätsmaße Amortisiert: Worst-Case in Größe des Inputs, wobei der Durchschnitt über eine Folge von Operationen genommen wird. Alternativ: Worst-Case in Größe der Änderungen bzgl. des Inputs und des Outputs Worst Case bzgl. der I/O-Änderungen Ein Knoten heißt modifiziert (modified), wenn er oder eine inzidente Kante einen neuen Input-Wert bekommen hat oder eingefügt oder entfernt wurde. Ein Knoten heißt betroffen (affected), wenn er entweder neu eingefügt wurde oder er durch die Änderung einen neuen Output-Wert bekommen hat. CHANGED:={Menge aller modifizierten oder betroffenen Knoten} Sei δ = CHANGED Sei δ = δ +Anzahl der zu CHANGED inzidenten Kanten So viele Änderungen sind mindestens notwendig notwendige Laufzeit
3 Worst Case bzgl. der I/O-Änderungen Kürzeste Wege Probleme Ein dynamischer Algorithmus heißt beschränkt (bounded), wenn die benötigte Zeit für einen Update Schritt durch eine Funktion in δ beschränkt ist. Sonst heißt er unbeschränkt (unbounded). Ein dynamisches Problem heißt unbeschränkt (unbounded), wenn kein dynamischer beschränkter Algorithmus existiert. HIER: ein beschränkter dynamischer SSSP Algorithmus 3 Single-Source Shortest Path (SSSP) Geg.: Graph G=(V,E) mit Kantenkosten w R, keine negativen Kreise, s V Gesucht: Kürzeste (s,v)-wege in G für alle v V All-Pairs Shortest Path (APSP) Geg.: Graph G=(V,E) mit Kantenkosten w R, keine negativen Kreise Gesucht: Kürzeste Wege zwischen allen Knotenpaaren (Distanzmatrix) Dijkstra s Algorithmus Dijkstra s Algorithmus Graph G gerichtet mit Kantenkosten w 0 Sei M = große Zahl Sei dist(v) die Distanzmatrix Q sei Prioritätswarteschlange mit Operationen InsertPrioQ(v,dist(v)): fügt v ein mit Priorität dist(v) ExtractMinQ(): Gibt das Minimum zurück und entfernt es aus Q DecreasePrioQ(v, dist(v)): Aktualisiert die Priorität von v in Q auf dist(v) 5 Q ; dist[s]=0; InsertPrioQ(s,0) // S {s} Für alle Knoten x s: Setze dist[x]=m; InsertPrioQ(x,M) Solange Q : x ExtractMinQ(); // Addiere x zu S; Für alle Kanten (x,y), die x verlassen: Falls dist[y] > dist[x]+w[x,y]: Setze dist[y] dist[x]+w(x,y); DecreasePrioQ(y,dist[y]) Return dist[] : edge relaxation. edge scanning 6 Analyse: Korrektheit Induktion: Nach jeder Iteration ist V in Mengen aufgeteilt: S und T:=V\S Ind.-Ann.: () Für x S ist dist(x)=länge des kürzesten (s,x)-weges () für x T ist dist(x)=länge des kürzesten (s,x)-weges bei dem jeder Knoten außer x zu S gehört. Ind.-Schritt: Knoten x mit kleinstem dist-wert wird in S aufgenommen. Ist korrekt, denn: Falls ein kürzerer Weg existieren würde, dann würde dieser einen ersten Knoten in T benutzen; aber dieser müßte weiter weg von s sein, denn sein dist-wert ist größer als der von x. Die edge relaxation sorgt dafür, dass () erfüllt ist. 7 Analyse: Laufzeit Sei n= V und m= E T = n*t(insertprioq()) + n*t(extractminq()) + m*t(decreaseprioq()) Binärer Heap für Q: O( (n+m) log n ) T(InsertPrioQ())=O(log n) T(ExtractMinQ())=O(log n) T(DecreasePrioQ())=O(log n) Fibonacci Heap für Q: O(m+n log n) T(InsertPrioQ())=O() T(ExtractMinQ())=O(log n) amortisiert T(DecreasePrioQ())=O() amortisiert 8 3
4 5. Algorithmus von Ramalingam & Reps Betrachte folgendes kürzestes Wegeproblem: Single-Source Shortest Path (SSSP) Geg.: Graph G=(V,E) mit Kantenkosten c w R, >0 keine negativen Kreise, ts V Gesucht: Kürzeste (v,t) (s,v)-wege in G für alle v V 5. Algorithmus von Ramalingam & Reps Geg.: Gerichteter Graph G=(V,E) mit positiven Kantenkosten c(e) R, t V, sowie Sequenz der folgenden Operationen: delete_edge(v,w): entferne die Kante (v,w) aus G insert_edge(v,w,c): füge die Kante (v,w) in G ein dist(v): gib die Distanz zwischen Knoten v und t zurück path(v): gib den kürzesten Weg von v nach t aus, falls einer existiert. 9 Damit sind auch die folgenden Operationen simulierbar: increase_weight(e,c ): erhöhe die Kosten von Kante e auf c decrease_weight(e,c ): reduziere Kosten der Kante e auf c (durch delete_edge und insert_edge) 0 Definitionen Ein Teilgraph T von G heißt kürzester-wege-baum für G mit Senke t, falls Tist ein gerichteter Baum mit Wurzel t V(T)ist die Menge aller Knoten, die t erreichen können, und für jede Kante in T gilt: dist(u) = dist(v)+c(u,v) Definitionen Eine Kante heißt SP-Kante, wenn sie auf einem kürzesten Weg von v nach t liegt für ein v V. Eine Kante ist also genau dann SP-Kante, wenn gilt: dist(u) = dist(v)+c(u,v) Sei SP(G) der durch die Menge aller SP-Kanten induzierte Teilgraph von G (der kürzeste-wege Teilgraph). Jeder kürzeste Weg in G ist in SP(G) enthalten und umgekehrt: Jeder Weg in SP(G) ist ein kürzester Weg in G. Da die Kantengewichte alle positiv sind, ist SP(G) ein gerichteter, azyklischer Graph. Delete_edge(v,w): G G Ein Knoten in G heißt betroffen, wenn der Wert dist G (v) dist G (v) ist. Eine SP-Kante (x,y) heißt betroffen durch die delete_edge(v,w) Operation, wenn kein Pfad in G von x nach t existiert, der die Kante (x,y) benutzt und Länge dist alt (x) besitzt. Delete_edge(v,w): G G Ein Knoten in G heißt betroffen, wenn der Wert dist G (v) dist G (v) ist. Eine SP-Kante (x,y) heißt betroffen durch die delete_edge(v,w) Operation, wenn kein Pfad in G von x nach t existiert, der die Kante (x,y) benutzt und Länge dist alt (x) besitzt. G: 8 w 5 v 7 3 t Beobachtungen in SP(G) (x,y) ist betroffen y ist betroffen Knoten x v ist betroffen alle ausgehenden SP-Kanten von x sind betroffen Knoten v selbst ist betroffen (v,w) die einzige ausgehende SP-Kante ist 3
5 Algorithmus Delete_edge(v,w) Phase von Delete_edge(v,w) Phase : Bestimme die Menge aller betroffenen Knoten und Kanten Entferne die betroffenen Kanten von SP(G) Phase : Berechne neue dist-werte aller betroffenen Knoten Aktualisiere SP(G) Menge der betroffenen Knoten = Menge der Knoten, die im Graphen SP(G)-(v,w) keine Verbindung zur Senke t besitzen. Algorithmus-Idee: Aufruf von Top-Sort, wenn outdegree von v in SP(G ) = 0. Speichere SP(G) durch Adjazenzlisten: in(v)+out(v), oder nicht explizite Speicherung, sondern durch Test: dist(x) == dist(y)+c(x,y) 5 6 Phase von Delete_edge(v,w) Sei A die Menge der nicht-betroffenen Knoten Ziel: Berechne dist(x) für alle Knoten in B=V \ A Algorithmus-Idee: Kontrahiere A zu einem Knoten t und ersetze die Kanten (x,y) durch (x,t ) mit Kosten c(x,y)+dist(y) Aufruf von Dijkstra für den neuen Graphen c(5,7)+dist(7) G: w 5 v 7 5 c(5,)+dist() A 3 t v 3 8 c(3,)+dist() 7 Algorithmus Delete_edge(v,w). Falls (v,w) SP(G) dann:. Entferne (v,w) aus SP(G) und E; dekrementiere outdegsp(v) 3. Falls outdegsp(v)==0 dann: // Phase. WorkSet={v}; AffectVert= 5. Solange WorkSet do: 6. Wähle und entferne Knoten u aus WorkSet 7. AffectVert = AffectVert {u} 8. Für jeden Knoten x mit (x,u) 9. Entferne (x,u) aus SP(G); dekrement. outdegsp(x) 0. Falls outdegsp(x)==0 dann:. WorkSet = WorkSet {x} 8 Algorithmus Delete_edge(v,w) ff. Q= // Phase 3. Für jeden Knoten a AffectVert do:. dist(a) = min({c(a,b)+dist(b) (a,b) E und b AffectVert)} M 5. Falls dist(a) M dann: 6. InsertQ(a,dist(a)) 7. Solange Q do: 8. a ExtractMin(Q) 9. Für jeden Knoten b Succ(a) mit c(a,b)+dist(b)==dist(a) 0. Füge (a,b) in SP(G) ein; inkrementiere outdegsp(a). Für jeden Knoten b Pred(a) mit c(b,a)+dist(a)<dist(b). dist(b) = c(b,a)+dist(a) 3. AktualisiereHeapQ(b,dist(b)) 9 Laufzeitanalyse Phase : Anzahl der Iterationen: δ Eine Iteration für Knoten u benötigt O( Pred(u) ) Gesamt: O( δ ) Phase : mit Fibonacci Heaps Insert + Decrease_key: O() amortisiert ExtractMin O(log p) mit p=anzahl der Elemente im Heap Anzahl der Iterationen: höchstens δ Gesamt: O( δ + δ log δ ) Laufzeit: O( δ + δ log δ ) 30 5
6 Insert_edge(v,w): G G Beobachtung: Wenn u betroffen ist, dann sehen alle kürzesten Wege in G von u nach t folgendermaßen aus: (kürzester (u,v)-weg, Kante (v,w), kürzester (w,s)-weg) u ist betroffen dist G (u,v)+c(v,w)+dist G (w) < dist G (u) G: 8 w 5 7 v 3 t Algorithmus Insert_edge(v,w) Idee: Benutze Dijkstra s Algorithmus für Menge der betroffenen Knoten mit Key: dist(x)-dist(v) für alle x Betrachte kürzesten-wege Baum T v für Knoten v (Wurzel): Sei x beliebiger Knoten, u: Elter von x in T v Wenn x betroffen ist, dann muß auch u betroffen sein, denn sonst: ex. kürzester Weg P von u nach t ohne Kante (v,w); dann ist Weg ((x,u),p) auch kürzester Weg; x wäre nicht betroffen. Menge der betroffenen Knoten bilden zusammenhängenden Teilbaum von T v mit Wurzel v w G: 5 v 7 3 t 8 betroffene Knoten: 3 betroffene Knoten: 3 Algorithmus Insert_edge((v,w),c). Insert edge (v,w) in G, setze Kosten c(v,w). Q= 3. Falls c(v,w)+dist(w)<dist(v) dann:. dist(v)= c(v,w)+dist(w) 5. InsertHeapQ(v,0) 6. Sonst Falls c(v,w)+dist(w) == dist(v) dann: 7. Füge (v,w) in SP(G) ein 8. outdeg(v)++ 33 Algorithmus Insert_edge((v,w),c) ff 9. Solange Q : 0. u ExtractMin(Q). Entferne alle ausgehenden Kanten von u in SP(G) und update outdeg(u). Für jeden Knoten x Succ(u): 3. Falls c(u,x)+dist(x) == dist(u) dann:. Füge (u,x) in SP(G) ein und aktualisiere outdeg(u) 5. Für jeden Knoten x Pred(u): 6. Falls c(x,u)+dist(u) < dist(x) dann: 7. dist(x)= c(x,u)+dist(u) 8. Aktualisiere/InsertHeapQ(x,dist(x)-dist(v)) 9. Sonst Falls c(x,u)+dist(u) == dist(x) 0. Füge (x,u) in SP(G) ein und aktualisiere outdeg(x) 3 Laufzeitanalyse Zusammenfassung mit Fibonacci Heaps Insert + Decrease_key: O() amortisiert ExtractMin: O(log p) mit p=anzahl der Elemente im Heap Anzahl der Iterationen: höchstens δ Gesamt: O( δ + δ log δ ) Theorem: Es gibt einen beschränkten dynamischen Algorithmus für das SSSP-Problem mit Laufzeit O( δ + δ log δ ) für jede Update- Operation delete_edge(v,w) und insert_edge(v,w,c). Laufzeit: O( δ + δ log δ )
Kap. 7: Dynamische Algorithmen für kürzeste Wege
 Kap. 7: Dynamische Algorithmen für kürzeste Wege Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 27./28. VO A&D WS 08/09 3./5. Februar 2009 1 Ankündigung
Kap. 7: Dynamische Algorithmen für kürzeste Wege Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 27./28. VO A&D WS 08/09 3./5. Februar 2009 1 Ankündigung
Ankündigung für SS09. Überblick. Ankündigung für SS09. Literatur für Experimente. Literatur für diese VO
 Kap. 7: Dynamische Algorithmen für kürzeste Wege Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS Fakultät für Informatik, TU Dortmund 7./8. VO A&D WS 08/09 3./5. Februar 009 Ankündigung
Kap. 7: Dynamische Algorithmen für kürzeste Wege Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS Fakultät für Informatik, TU Dortmund 7./8. VO A&D WS 08/09 3./5. Februar 009 Ankündigung
Kürzeste (billigste) Wege
 Kürzeste (billigste) Wege 1. Kürzeste (billigste) Wege Gerichteter Graph G = (V, E) Kostenfunktion c : E R 1 2 1 3 3 2 4 4 2 6 6 5 3 2 Entfernung zwischen zwei Knoten Kosten eines Wegs P = v 0, v 1,...,
Kürzeste (billigste) Wege 1. Kürzeste (billigste) Wege Gerichteter Graph G = (V, E) Kostenfunktion c : E R 1 2 1 3 3 2 4 4 2 6 6 5 3 2 Entfernung zwischen zwei Knoten Kosten eines Wegs P = v 0, v 1,...,
Kap. 6.6: Kürzeste Wege
 Kap. 6.6: Kürzeste Wege Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 1./. VO DAP SS 009./9. Juli 009 1 Nachtest für Ausnahmefälle Di 1. Juli 009, 16:00 Uhr,
Kap. 6.6: Kürzeste Wege Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 1./. VO DAP SS 009./9. Juli 009 1 Nachtest für Ausnahmefälle Di 1. Juli 009, 16:00 Uhr,
Kap. 6.6: Kürzeste Wege
 0.0.00 Nachtest für Ausnahmefälle Kap..: Kürzeste Wege Professor Dr. Lehrstuhl für Algorithm Engineering, LS Fakultät für Informatik, TU Dortmund./. VO DAP SS 00./. Juli 00 Di. Juli 00, :00 Uhr, OH, R.
0.0.00 Nachtest für Ausnahmefälle Kap..: Kürzeste Wege Professor Dr. Lehrstuhl für Algorithm Engineering, LS Fakultät für Informatik, TU Dortmund./. VO DAP SS 00./. Juli 00 Di. Juli 00, :00 Uhr, OH, R.
Kürzeste Wege. Ein Startknoten, nichtnegative Gewichte
 Kürzeste Wege Gegeben ein Digraph D = (V, A) mit Bogengewichten c(a). Aufgabe: Finde einen Weg W von einem Knoten zu allen anderen oder zu einem bestimmten mit c(w) minimal. Problem: negative Gewichte
Kürzeste Wege Gegeben ein Digraph D = (V, A) mit Bogengewichten c(a). Aufgabe: Finde einen Weg W von einem Knoten zu allen anderen oder zu einem bestimmten mit c(w) minimal. Problem: negative Gewichte
Kapitel 6: Dynamic Shortest Path
 Kapitel 6: Dynamic Shortest Path 6.4 Experimentelle Analyse VO Algorithm Engineering Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 18. VO 12. Juni 2007 Literatur für diese VO C.
Kapitel 6: Dynamic Shortest Path 6.4 Experimentelle Analyse VO Algorithm Engineering Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 18. VO 12. Juni 2007 Literatur für diese VO C.
1 Kürzeste Pfade in Graphen
 Praktikum Algorithmen-Entwurf (Teil 3) 03.11.2011 1 1 Kürzeste Pfade in Graphen Es sei ein gerichteter Graph G = (V, E) mit V = n Knoten, E = m Kanten und Kantengewichten c : E R gegeben. Ein Pfad in G
Praktikum Algorithmen-Entwurf (Teil 3) 03.11.2011 1 1 Kürzeste Pfade in Graphen Es sei ein gerichteter Graph G = (V, E) mit V = n Knoten, E = m Kanten und Kantengewichten c : E R gegeben. Ein Pfad in G
Fortgeschrittene Netzwerk- und Graph-Algorithmen
 Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Vorlesung 2 KÜRZESTE WEGE
 Vorlesung 2 KÜRZESTE WEGE 34 Kürzeste Wege im Graphen Motivation! Heute:! Kürzeste Wege von einem Knoten (SSSP)! Kürzeste Wege zwischen allen Knotenpaaren (APSP)! Viele Anwendungen:! Navigationssysteme!
Vorlesung 2 KÜRZESTE WEGE 34 Kürzeste Wege im Graphen Motivation! Heute:! Kürzeste Wege von einem Knoten (SSSP)! Kürzeste Wege zwischen allen Knotenpaaren (APSP)! Viele Anwendungen:! Navigationssysteme!
Algorithmen & Komplexität
 Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Kürzeste Pfade Problem Gegeben Netzwerk: Graph G = (V, E), Gewichtsfunktion w: E N Zwei Knoten: s, t Kantenzug/Weg
Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Kürzeste Pfade Problem Gegeben Netzwerk: Graph G = (V, E), Gewichtsfunktion w: E N Zwei Knoten: s, t Kantenzug/Weg
Lernmodul 7 Algorithmus von Dijkstra
 Folie 1 von 30 Lernmodul 7 Algorithmus von Dijkstra Quelle: http://www.map24.de Folie 2 von 30 Algorithmus von Dijkstra Übersicht Kürzester Weg von A nach B in einem Graphen Problemstellung: Suche einer
Folie 1 von 30 Lernmodul 7 Algorithmus von Dijkstra Quelle: http://www.map24.de Folie 2 von 30 Algorithmus von Dijkstra Übersicht Kürzester Weg von A nach B in einem Graphen Problemstellung: Suche einer
Grundlagen: Algorithmen und Datenstrukturen
 Grundlagen: Algorithmen und Datenstrukturen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Sommersemester 00
Grundlagen: Algorithmen und Datenstrukturen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Sommersemester 00
Grundlagen: Algorithmen und Datenstrukturen
 Grundlagen: Algorithmen und Datenstrukturen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Sommersemester H.
Grundlagen: Algorithmen und Datenstrukturen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Sommersemester H.
p = (v 0, v 1,..., v k )
 1 Routenlaner Hamburg 300 km 200 km Berlin 450 km Köln 200 km 400 km Frankfurt 50 km 200 km 150 km Mannheim Saarbrücken 100 km 250 km Stuttgart 200 km Dresden 300 km Nürnberg 200 km München Berechne den
1 Routenlaner Hamburg 300 km 200 km Berlin 450 km Köln 200 km 400 km Frankfurt 50 km 200 km 150 km Mannheim Saarbrücken 100 km 250 km Stuttgart 200 km Dresden 300 km Nürnberg 200 km München Berechne den
Graphalgorithmen 2. Dominik Paulus Dominik Paulus Graphalgorithmen / 47
 Graphalgorithmen Dominik Paulus.0.01 Dominik Paulus Graphalgorithmen.0.01 1 / 7 1 Spannbäume Kruskal Prim Edmonds/Chu-Liu Datenstrukturen Fibonacci-Heap Union/Find Kürzeste Pfade Dijkstra Bellman-Ford
Graphalgorithmen Dominik Paulus.0.01 Dominik Paulus Graphalgorithmen.0.01 1 / 7 1 Spannbäume Kruskal Prim Edmonds/Chu-Liu Datenstrukturen Fibonacci-Heap Union/Find Kürzeste Pfade Dijkstra Bellman-Ford
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Kürzeste Wege Maike Buchin 4. und 6.7.2017 Einführung Motivation: Bestimmung von kürzesten Wegen ist in vielen Anwendungen, z.b. Routenplanung, ein wichtiges Problem. Allgemeine
Vorlesung Datenstrukturen Kürzeste Wege Maike Buchin 4. und 6.7.2017 Einführung Motivation: Bestimmung von kürzesten Wegen ist in vielen Anwendungen, z.b. Routenplanung, ein wichtiges Problem. Allgemeine
Überblick. Kap. 1.4: Minimum Weight Perfect Matching. 1.3 Blüten-Schrumpf Algorithmus für Maximum Matching
 Kap. 1.4: Minimum Weight Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 4. VO 6. November 2006 Überblick kurze Wiederholung: 1.2 Blüten-Schrumpf-Algorithmus für Perfektes Matching
Kap. 1.4: Minimum Weight Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 4. VO 6. November 2006 Überblick kurze Wiederholung: 1.2 Blüten-Schrumpf-Algorithmus für Perfektes Matching
10 Kürzeste Pfade SSSP-Problem
 In diesem Kapitel setzen wir uns mit der Berechnung von kürzesten Pfaden in einem Graphen auseinander. Definition 10.1 (Pfadgewichte). i) Das Gewicht eines Pfades p = (v 0, v 1,..., v k ) ist die Summe
In diesem Kapitel setzen wir uns mit der Berechnung von kürzesten Pfaden in einem Graphen auseinander. Definition 10.1 (Pfadgewichte). i) Das Gewicht eines Pfades p = (v 0, v 1,..., v k ) ist die Summe
2. Das single-source-shortest-path-problem
 . Das single-source-shortest-path-problem Zunächst nehmen wir an, dass d 0 ist. Alle kürzesten Pfade von a nach b sind o.b.d.a. einfache Pfade.. Dijkstra s Algorithmus Gegeben: G = (V, A), (A = V V ),
. Das single-source-shortest-path-problem Zunächst nehmen wir an, dass d 0 ist. Alle kürzesten Pfade von a nach b sind o.b.d.a. einfache Pfade.. Dijkstra s Algorithmus Gegeben: G = (V, A), (A = V V ),
8.4 Digraphen mit negativen Kantengewichten Grundsätzliches Betrachte Startknoten s und einen Kreis C mit Gesamtlänge < 0.
 8.4 Digraphen mit negativen Kantengewichten 8.4.1 Grundsätzliches Betrachte Startknoten s und einen Kreis C mit Gesamtlänge < 0. k 4 5 1 s 1 3 2 C k 0 k 3 1 1 1 k 1 k 2 v Sollte ein Pfad von s nach C und
8.4 Digraphen mit negativen Kantengewichten 8.4.1 Grundsätzliches Betrachte Startknoten s und einen Kreis C mit Gesamtlänge < 0. k 4 5 1 s 1 3 2 C k 0 k 3 1 1 1 k 1 k 2 v Sollte ein Pfad von s nach C und
Algo&Komp. - Wichtige Begriffe Mattia Bergomi Woche 6 7
 1 Kürzeste Pfade Woche 6 7 Hier arbeiten wir mit gewichteten Graphen, d.h. Graphen, deren Kanten mit einer Zahl gewichtet werden. Wir bezeichnen die Gewichtsfunktion mit l : E R. Wir wollen einen kürzesten
1 Kürzeste Pfade Woche 6 7 Hier arbeiten wir mit gewichteten Graphen, d.h. Graphen, deren Kanten mit einer Zahl gewichtet werden. Wir bezeichnen die Gewichtsfunktion mit l : E R. Wir wollen einen kürzesten
Effiziente Algorithmen und Datenstrukturen: Kürzeste Wege
 Effiziente Algorithmen und Datenstrukturen: Kürzeste Wege Kürzeste Wege Zentrale Frage: Wie komme ich am schnellsten von A nach B? B A Kürzeste Wege Zentrale Frage: Wie komme ich am schnellsten von A nach
Effiziente Algorithmen und Datenstrukturen: Kürzeste Wege Kürzeste Wege Zentrale Frage: Wie komme ich am schnellsten von A nach B? B A Kürzeste Wege Zentrale Frage: Wie komme ich am schnellsten von A nach
3.2 Generischer minimaler Spannbaum-Algorithmus
 3.2 Generischer minimaler Spannbaum-Algorithmus Initialisiere Wald F von Bäumen, jeder Baum ist ein singulärer Knoten (jedes v V bildet einen Baum) while Wald F mehr als einen Baum enthält do wähle einen
3.2 Generischer minimaler Spannbaum-Algorithmus Initialisiere Wald F von Bäumen, jeder Baum ist ein singulärer Knoten (jedes v V bildet einen Baum) while Wald F mehr als einen Baum enthält do wähle einen
2. November Gradfolgen Zusammenhang Kürzeste Wege. H. Meyerhenke: Algorithmische Methoden zur Netzwerkanalyse 37
 2. November 2011 Gradfolgen Zusammenhang Kürzeste Wege H. Meyerhenke: Algorithmische Methoden zur Netzwerkanalyse 37 Satz von Erdős und Gallai Eine Partition einer natürlichen Zahl ist genau dann die Gradfolge
2. November 2011 Gradfolgen Zusammenhang Kürzeste Wege H. Meyerhenke: Algorithmische Methoden zur Netzwerkanalyse 37 Satz von Erdős und Gallai Eine Partition einer natürlichen Zahl ist genau dann die Gradfolge
9 Minimum Spanning Trees
 Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
Kap. 6.5: Minimale Spannbäume ff
 Kap. 6.: Minimale Spannbäume ff Professor Dr. Karsten Klein Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 20. VO 2. TEIL DAP2 SS 2009 2. Juli 2009 SS08 1 Überblick 6.:
Kap. 6.: Minimale Spannbäume ff Professor Dr. Karsten Klein Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 20. VO 2. TEIL DAP2 SS 2009 2. Juli 2009 SS08 1 Überblick 6.:
Algorithmen I. Prof. Jörn Müller-Quade Institut für Theoretische Informatik Web: https://crypto.iti.kit.edu/index.php?
 Algorithmen I Prof. Jörn Müller-Quade 19.6.1 Institut für Theoretische Informatik Web: https://crypto.iti.kit.edu/index.php?id=99 (Folien von Peter Sanders) KIT Institut für Theoretische Informatik 1 Organisatorisches
Algorithmen I Prof. Jörn Müller-Quade 19.6.1 Institut für Theoretische Informatik Web: https://crypto.iti.kit.edu/index.php?id=99 (Folien von Peter Sanders) KIT Institut für Theoretische Informatik 1 Organisatorisches
3. Minimale Spannbäume. Definition 99 T heißt minimaler Spannbaum (MSB, MST) von G, falls T Spannbaum von G ist und gilt:
 3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e),
3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e),
Algorithmen und Komplexität Teil 1: Grundlegende Algorithmen
 Algorithmen und Komplexität Teil 1: Grundlegende Algorithmen WS 08/09 Friedhelm Meyer auf der Heide Vorlesung 6, 28.10.08 Friedhelm Meyer auf der Heide 1 Organisatorisches Prüfungsanmeldung bis 30.10.
Algorithmen und Komplexität Teil 1: Grundlegende Algorithmen WS 08/09 Friedhelm Meyer auf der Heide Vorlesung 6, 28.10.08 Friedhelm Meyer auf der Heide 1 Organisatorisches Prüfungsanmeldung bis 30.10.
Graphalgorithmen II. Sebastian Ehrenfels Sebastian Ehrenfels Graphalgorithmen II / 44
 Graphalgorithmen II Sebastian Ehrenfels 4.6.2013 Sebastian Ehrenfels Graphalgorithmen II 4.6.2013 1 / 44 Inhalt 1 Datenstrukturen Union-Find Fibonacci-Heap 2 Kürzeste wege Dijkstra Erweiterungen Bellman-Ford
Graphalgorithmen II Sebastian Ehrenfels 4.6.2013 Sebastian Ehrenfels Graphalgorithmen II 4.6.2013 1 / 44 Inhalt 1 Datenstrukturen Union-Find Fibonacci-Heap 2 Kürzeste wege Dijkstra Erweiterungen Bellman-Ford
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen Lerneinheit : Kürzeste Pfade in Graphen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 016.6.01 Einleitung Diese Lerneinheit beschäftigt
Algorithmen und Datenstrukturen Lerneinheit : Kürzeste Pfade in Graphen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 016.6.01 Einleitung Diese Lerneinheit beschäftigt
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 20 (23.7.2014) All Pairs Shortest Paths, String Matching (Textsuche) Algorithmen und Komplexität Vorlesungsevaluation Sie sollten alle eine
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 20 (23.7.2014) All Pairs Shortest Paths, String Matching (Textsuche) Algorithmen und Komplexität Vorlesungsevaluation Sie sollten alle eine
Grundlagen der Algorithmen und Datenstrukturen Kapitel 10
 Grundlagen der Algorithmen und Datenstrukturen Kapitel 0 Christian Scheideler + Helmut Seidl SS 009 5.06.09 Kapitel 0 Kürzeste Wege Zentrale Frage: Wie komme ich am schnellsten von A nach B? B A 5.06.09
Grundlagen der Algorithmen und Datenstrukturen Kapitel 0 Christian Scheideler + Helmut Seidl SS 009 5.06.09 Kapitel 0 Kürzeste Wege Zentrale Frage: Wie komme ich am schnellsten von A nach B? B A 5.06.09
Algorithmen & Komplexität
 Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Kapitel 4: Datenstrukturen Kapitel 4.2: Union-Find-Strukturen Union-Find-Strukturen Gegeben: Datensätze
Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Kapitel 4: Datenstrukturen Kapitel 4.2: Union-Find-Strukturen Union-Find-Strukturen Gegeben: Datensätze
Programmierkurs Python II
 Programmierkurs Python II Stefan Thater & Michaela Regneri Universität des Saarlandes FR 4.7 Allgemeine Linguistik (Computerlinguistik) Übersicht Topologische Sortierung (einfach) Kürzeste Wege finden
Programmierkurs Python II Stefan Thater & Michaela Regneri Universität des Saarlandes FR 4.7 Allgemeine Linguistik (Computerlinguistik) Übersicht Topologische Sortierung (einfach) Kürzeste Wege finden
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
4.2 Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition 4.2.1
 Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
Organisatorisches. Programmierpraktikum Das Canadian Traveller Problem. Organisatorisches. Organisatorisches
 Organisatorisches Programmierpraktikum Das Canadian Traveller Problem Rainer Schrader Birgit Engels Anna Schulze Zentrum für Angewandte Informatik Köln. April 006 Prof. Dr. Rainer Schrader Tel.: 470-600
Organisatorisches Programmierpraktikum Das Canadian Traveller Problem Rainer Schrader Birgit Engels Anna Schulze Zentrum für Angewandte Informatik Köln. April 006 Prof. Dr. Rainer Schrader Tel.: 470-600
Grundlagen Algorithmen und Datenstrukturen TUM Sommersemester 2011 (2) Dozent: Hanjo Täubig
 Grundlagen Algorithmen und Datenstrukturen TUM Sommersemester 2011 (2) Dozent: Hanjo Täubig Janosch Maier 3. August 2011 Inhaltsverzeichnis 1 Sortieren 3 1.1 Externes Sortieren..........................
Grundlagen Algorithmen und Datenstrukturen TUM Sommersemester 2011 (2) Dozent: Hanjo Täubig Janosch Maier 3. August 2011 Inhaltsverzeichnis 1 Sortieren 3 1.1 Externes Sortieren..........................
Vorlesung 2 KÜRZESTE WEGE
 Vorlesung 2 KÜRZESTE WEGE 45 Kürzeste Wege im Graphen Motivation! Heute:! Kürzeste Wege von einem Knoten (SSSP)! Distanzen zwischen allen Knotenpaaren (APD)! Viele Anwendungen:! Navis! Netzwerkrouting!...
Vorlesung 2 KÜRZESTE WEGE 45 Kürzeste Wege im Graphen Motivation! Heute:! Kürzeste Wege von einem Knoten (SSSP)! Distanzen zwischen allen Knotenpaaren (APD)! Viele Anwendungen:! Navis! Netzwerkrouting!...
8. A & D - Heapsort. Werden sehen, wie wir durch geschicktes Organsieren von Daten effiziente Algorithmen entwerfen können.
 8. A & D - Heapsort Werden sehen, wie wir durch geschicktes Organsieren von Daten effiziente Algorithmen entwerfen können. Genauer werden wir immer wieder benötigte Operationen durch Datenstrukturen unterstützen.
8. A & D - Heapsort Werden sehen, wie wir durch geschicktes Organsieren von Daten effiziente Algorithmen entwerfen können. Genauer werden wir immer wieder benötigte Operationen durch Datenstrukturen unterstützen.
Algorithmen und Datenstrukturen (für ET/IT)
 Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2018 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München Organisatorisches: Keine Vorlesung nächste Woche wegen
Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2018 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München Organisatorisches: Keine Vorlesung nächste Woche wegen
Datenstrukturen und Algorithmen (SS 2013)
 Datenstrukturen und Algorithmen (SS 2013) Übungsblatt 10 Abgabe: Montag, 08.07.2013, 14:00 Uhr Die Übungen sollen in Gruppen von zwei bis drei Personen bearbeitet werden. Schreiben Sie die Namen jedes
Datenstrukturen und Algorithmen (SS 2013) Übungsblatt 10 Abgabe: Montag, 08.07.2013, 14:00 Uhr Die Übungen sollen in Gruppen von zwei bis drei Personen bearbeitet werden. Schreiben Sie die Namen jedes
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 17 (8.7.2014) Minimale Spannbäume II Union Find, Prioritätswarteschlangen Algorithmen und Komplexität Minimaler Spannbaum Gegeben: Zus. hängender,
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 17 (8.7.2014) Minimale Spannbäume II Union Find, Prioritätswarteschlangen Algorithmen und Komplexität Minimaler Spannbaum Gegeben: Zus. hängender,
Informatik II, SS 2016
 Informatik II - SS 208 (Algorithmen & Datenstrukturen) Vorlesung 4 (..208) Graphenalgorithmen III Algorithmen und Komplexität Bäume Gegeben: Zusammenhängender, ungerichteter Graph G = V, E Baum: Zusammenhängender,
Informatik II - SS 208 (Algorithmen & Datenstrukturen) Vorlesung 4 (..208) Graphenalgorithmen III Algorithmen und Komplexität Bäume Gegeben: Zusammenhängender, ungerichteter Graph G = V, E Baum: Zusammenhängender,
Kürzeste Pfade. Organisatorisches. VL-17: Kürzeste Pfade. (Datenstrukturen und Algorithmen, SS 2017) Walter Unger
 Organisatorisches VL-17: Kürzeste Pfade (Datenstrukturen und Algorithmen, SS 2017) Walter Unger Vorlesung: Gerhard Woeginger (Zimmer 4024 im E1) Sprechstunde: Mittwoch 11:15 12:00 Übungen: Tim Hartmann,
Organisatorisches VL-17: Kürzeste Pfade (Datenstrukturen und Algorithmen, SS 2017) Walter Unger Vorlesung: Gerhard Woeginger (Zimmer 4024 im E1) Sprechstunde: Mittwoch 11:15 12:00 Übungen: Tim Hartmann,
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 018/19 1. Vorlesung Minimale Spannbäume Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Motivation ) Kantengewichte w : E R >0 ) w(e ) := e E w(e)
1 Algorithmen und Datenstrukturen Wintersemester 018/19 1. Vorlesung Minimale Spannbäume Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Motivation ) Kantengewichte w : E R >0 ) w(e ) := e E w(e)
Kap. 5: Graphen. Carsten Gutwenger Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund. 17. VO DAP2 SS
 Kap. 5: Graphen Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 17. VO DAP2 SS 2009 23. Juni 2008 1 Motivation Warum soll ich heute hier bleiben? Graphen sind wichtig und
Kap. 5: Graphen Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 17. VO DAP2 SS 2009 23. Juni 2008 1 Motivation Warum soll ich heute hier bleiben? Graphen sind wichtig und
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 2016/17 19. Vorlesung Kürzeste Wege & Dijkstras Algorithmus Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Wozu kürzeste Wege? 2 3-8 Modellierung
1 Algorithmen und Datenstrukturen Wintersemester 2016/17 19. Vorlesung Kürzeste Wege & Dijkstras Algorithmus Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Wozu kürzeste Wege? 2 3-8 Modellierung
Informatik II, SS 2018
 Informatik II - SS 2018 (Algorithmen & Datenstrukturen) Vorlesung 15b (13.06.2018) Graphenalgorithmen IV Algorithmen und Komplexität Prims MST-Algorithmus A = while A ist kein Spannbaum do e = u, v ist
Informatik II - SS 2018 (Algorithmen & Datenstrukturen) Vorlesung 15b (13.06.2018) Graphenalgorithmen IV Algorithmen und Komplexität Prims MST-Algorithmus A = while A ist kein Spannbaum do e = u, v ist
Datenstrukturen und Algorithmen
 Datenstrukturen und Algorithmen Jedes Programm verwendet Datenstrukturen und Algorithmen um seine Aufgabe zu erfüllen Diese müssen offenbar zunächst sorgfältig dem speziellen Problem entsprechend ausgewählt
Datenstrukturen und Algorithmen Jedes Programm verwendet Datenstrukturen und Algorithmen um seine Aufgabe zu erfüllen Diese müssen offenbar zunächst sorgfältig dem speziellen Problem entsprechend ausgewählt
16. All Pairs Shortest Path (ASPS)
 . All Pairs Shortest Path (ASPS) All Pairs Shortest Path (APSP): Eingabe: Gewichteter Graph G=(V,E) Ausgabe: Für jedes Paar von Knoten u,v V die Distanz von u nach v sowie einen kürzesten Weg a b c d e
. All Pairs Shortest Path (ASPS) All Pairs Shortest Path (APSP): Eingabe: Gewichteter Graph G=(V,E) Ausgabe: Für jedes Paar von Knoten u,v V die Distanz von u nach v sowie einen kürzesten Weg a b c d e
Effiziente Algorithmen I
 9. Präsenzaufgabenblatt, WiSe 2013/14 Übungstunden am 13.01. & 15.01.2014 Aufgabe Q Gegeben sei ein Fluss-Netzwerk mit Digraph D = (V, A), Knotenkapazitäten c(u, v) 0, Quelle s und Senke t. Kann sich der
9. Präsenzaufgabenblatt, WiSe 2013/14 Übungstunden am 13.01. & 15.01.2014 Aufgabe Q Gegeben sei ein Fluss-Netzwerk mit Digraph D = (V, A), Knotenkapazitäten c(u, v) 0, Quelle s und Senke t. Kann sich der
Fortgeschrittene Netzwerk- und Graph-Algorithmen
 Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Algorithmen und Datenstrukturen (ESE) Entwurf, Analyse und Umsetzung von Algorithmen (IEMS) WS 2013 / 2014 Vorlesung 13, Donnerstag, 30.
 Algorithmen und Datenstrukturen (ESE) Entwurf, Analyse und Umsetzung von Algorithmen (IEMS) WS 0 / 04 Vorlesung, Donnerstag, 0. Januar 0 (Kürzeste Wege, Dijkstras Algorithmus) Junior-Prof. Dr. Olaf Ronneberger
Algorithmen und Datenstrukturen (ESE) Entwurf, Analyse und Umsetzung von Algorithmen (IEMS) WS 0 / 04 Vorlesung, Donnerstag, 0. Januar 0 (Kürzeste Wege, Dijkstras Algorithmus) Junior-Prof. Dr. Olaf Ronneberger
Datenstrukturen. Mariano Zelke. Sommersemester 2012
 Datenstrukturen Mariano Zelke Sommersemester 2012 Tiefensuche: Die globale Struktur Der gerichtete oder ungerichtete Graph G werde durch seine Adjazenzliste A repräsentiert. Im Array besucht wird vermerkt,
Datenstrukturen Mariano Zelke Sommersemester 2012 Tiefensuche: Die globale Struktur Der gerichtete oder ungerichtete Graph G werde durch seine Adjazenzliste A repräsentiert. Im Array besucht wird vermerkt,
Algorithmen für Routenplanung 2. Sitzung, Sommersemester 2012 Thomas Pajor 23. April 2012
 Algorithmen für Routenplanung 2. Sitzung, Sommersemester 2012 Thomas Pajor INSTITUT FÜR THEORETISCHE INFORMATIK ALGORITHMIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und nationales
Algorithmen für Routenplanung 2. Sitzung, Sommersemester 2012 Thomas Pajor INSTITUT FÜR THEORETISCHE INFORMATIK ALGORITHMIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und nationales
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 2016/17 19. Vorlesung Kürzeste Wege & Dijkstras Algorithmus Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Ergebnisse des 1. Kurztests 14 12 10
1 Algorithmen und Datenstrukturen Wintersemester 2016/17 19. Vorlesung Kürzeste Wege & Dijkstras Algorithmus Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Ergebnisse des 1. Kurztests 14 12 10
Graphalgorithmen II. Werner Sembach Werner Sembach Graphalgorithmen II / 22
 Graphalgorithmen II Werner Sembach 14.04.2014 Werner Sembach Graphalgorithmen II 14.04.2014 1 / 22 Übersicht Datenstrukturen Union-Find Fibonacci-Heap Werner Sembach Graphalgorithmen II 14.04.2014 2 /
Graphalgorithmen II Werner Sembach 14.04.2014 Werner Sembach Graphalgorithmen II 14.04.2014 1 / 22 Übersicht Datenstrukturen Union-Find Fibonacci-Heap Werner Sembach Graphalgorithmen II 14.04.2014 2 /
Kürzeste und Schnellste Wege
 Ideen und Konzepte der Informatik Kürzeste und Schnellste Wege Wie funktioniert ein Navi? Kurt Mehlhorn Schnellste Wege Routen finden im Navi Karten und Graphen Schnellste und kürzeste Wege sind das gleiche
Ideen und Konzepte der Informatik Kürzeste und Schnellste Wege Wie funktioniert ein Navi? Kurt Mehlhorn Schnellste Wege Routen finden im Navi Karten und Graphen Schnellste und kürzeste Wege sind das gleiche
Bipartites Matching. Gegeben: Ein bipartiter, ungerichteter Graph (V 1, V 2, E). Gesucht: Ein Matching (Paarung) maximaler Kardinalität.
 Netzwerkalgorithmen Bipartites Matching (Folie 90, Seite 80 im Skript) Gegeben: Ein bipartiter, ungerichteter Graph (V, V, E). Gesucht: Ein Matching (Paarung) maximaler Kardinalität. Ein Matching ist eine
Netzwerkalgorithmen Bipartites Matching (Folie 90, Seite 80 im Skript) Gegeben: Ein bipartiter, ungerichteter Graph (V, V, E). Gesucht: Ein Matching (Paarung) maximaler Kardinalität. Ein Matching ist eine
25. Minimale Spannbäume
 695 25. Minimale Spannbäume Motivation, Greedy, Algorithmus von Kruskal, Allgemeine Regeln, Union-Find Struktur, Algorithmus von Jarnik, Prim, Dijkstra, Fibonacci Heaps [Ottman/Widmayer, Kap. 9.6, 6.2,
695 25. Minimale Spannbäume Motivation, Greedy, Algorithmus von Kruskal, Allgemeine Regeln, Union-Find Struktur, Algorithmus von Jarnik, Prim, Dijkstra, Fibonacci Heaps [Ottman/Widmayer, Kap. 9.6, 6.2,
Informatik II, SS 2016
 Informatik II - SS 2016 (Algorithmen & Datenstrukturen) Vorlesung 11 (1.6.2016) Binäre Suchbäume III Algorithmen und Komplexität Tiefe eines binären Suchbaums Worst-Case Laufzeit der Operationen in binären
Informatik II - SS 2016 (Algorithmen & Datenstrukturen) Vorlesung 11 (1.6.2016) Binäre Suchbäume III Algorithmen und Komplexität Tiefe eines binären Suchbaums Worst-Case Laufzeit der Operationen in binären
Datenstrukturen und Algorithmen 2. Klausur SS 2001
 UNIVERSITÄT PADERBORN FACHBEREICH 7 (MATHEMATIK INFORMATIK) Datenstrukturen und Algorithmen 2. Klausur SS 200 Lösungsansätze Dienstag, 8. September 200 Name, Vorname:...................................................
UNIVERSITÄT PADERBORN FACHBEREICH 7 (MATHEMATIK INFORMATIK) Datenstrukturen und Algorithmen 2. Klausur SS 200 Lösungsansätze Dienstag, 8. September 200 Name, Vorname:...................................................
Informatik II: Algorithmen & Datenstrukturen. Blättern Sie nicht um bevor Sie dazu aufgefordert werden!
 Albert-Ludwigs-Universität Institut für Informatik Prof. Dr. F. Kuhn Informatik II: Algorithmen & Datenstrukturen Montag, 29. August, 2014, 14:00 17:00 Name:...........................................................
Albert-Ludwigs-Universität Institut für Informatik Prof. Dr. F. Kuhn Informatik II: Algorithmen & Datenstrukturen Montag, 29. August, 2014, 14:00 17:00 Name:...........................................................
Erinnerung VL
 Erinnerung VL.6.16 Graphtraversierung (DFS, topologische Sortierung und mehr) Kürzeste Wege: Problemstellung, Algorithmen Analoger Algorithmus Dijkstras Algorithmus: Idee, Korrektheit Heute: mehr zu Dijkstra,
Erinnerung VL.6.16 Graphtraversierung (DFS, topologische Sortierung und mehr) Kürzeste Wege: Problemstellung, Algorithmen Analoger Algorithmus Dijkstras Algorithmus: Idee, Korrektheit Heute: mehr zu Dijkstra,
Algorithmen II Vorlesung am
 Algorithmen II Vorlesung am 07..0 Minimale Schnitte in Graphen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales Forschungszentrum
Algorithmen II Vorlesung am 07..0 Minimale Schnitte in Graphen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales Forschungszentrum
Effiziente Algorithmen und Datenstrukturen I. Kapitel 9: Minimale Spannbäume
 Effiziente Algorithmen und Datenstrukturen I Kapitel 9: Minimale Spannbäume Christian Scheideler WS 008 19.0.009 Kapitel 9 1 Minimaler Spannbaum Zentrale Frage: Welche Kanten muss ich nehmen, um mit minimalen
Effiziente Algorithmen und Datenstrukturen I Kapitel 9: Minimale Spannbäume Christian Scheideler WS 008 19.0.009 Kapitel 9 1 Minimaler Spannbaum Zentrale Frage: Welche Kanten muss ich nehmen, um mit minimalen
11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME
 Algorithmen und Datenstrukturen 11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME Algorithmen und Datenstrukturen - Ma5hias Thimm (thimm@uni-koblenz.de) 1 Algorithmen und Datenstrukturen 11.1. BERECHNUNG MAXIMALER FLÜSSE
Algorithmen und Datenstrukturen 11. GRAPHEN 3 FLÜSSE UND SPANNBÄUME Algorithmen und Datenstrukturen - Ma5hias Thimm (thimm@uni-koblenz.de) 1 Algorithmen und Datenstrukturen 11.1. BERECHNUNG MAXIMALER FLÜSSE
Algorithmen und Datenstrukturen Kapitel 9. und
 Algorithmen und Datenstrukturen Kapitel 9 Minimale Spannbäume und Kürzeste Pfade Frank Heitmann heitmann@informatik.uni-hamburg.de 9. Dezember 01 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/13
Algorithmen und Datenstrukturen Kapitel 9 Minimale Spannbäume und Kürzeste Pfade Frank Heitmann heitmann@informatik.uni-hamburg.de 9. Dezember 01 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/13
9. Natürliche Suchbäume
 Bäume Bäume sind. Natürliche Suchbäume [Ottman/Widmayer, Kap..1, Cormen et al, Kap. 12.1-12.] Verallgemeinerte Listen: Knoten können mehrere Nachfolger haben Spezielle Graphen: Graphen bestehen aus Knoten
Bäume Bäume sind. Natürliche Suchbäume [Ottman/Widmayer, Kap..1, Cormen et al, Kap. 12.1-12.] Verallgemeinerte Listen: Knoten können mehrere Nachfolger haben Spezielle Graphen: Graphen bestehen aus Knoten
Kap. 4.7 Skiplisten. 14./15. VO DAP2 SS /16. Juni 2009
 Kap. 4.7 Skiplisten Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 14./15. VO DAP2 SS 2008 9./16. Juni 2009 1 2. Übungstest Termin: Di 16. Juni 2009 im AudiMax,
Kap. 4.7 Skiplisten Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 14./15. VO DAP2 SS 2008 9./16. Juni 2009 1 2. Übungstest Termin: Di 16. Juni 2009 im AudiMax,
Datenstrukturen und Algorithmen SS07
 Datenstrukturen und Algorithmen SS0 Datum:.6.200 Michael Belfrage mbe@student.ethz.ch belfrage.net/eth Programm von Heute Minimaler Spannbaum (MST) Challenge der Woche Fibonacci Heap Minimaler Spannbaum
Datenstrukturen und Algorithmen SS0 Datum:.6.200 Michael Belfrage mbe@student.ethz.ch belfrage.net/eth Programm von Heute Minimaler Spannbaum (MST) Challenge der Woche Fibonacci Heap Minimaler Spannbaum
Vorlesung Algorithmische Geometrie. Streckenschnitte. Martin Nöllenburg INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK
 Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 24.04.2011 Überlagern von Kartenebenen Beispiel: Gegeben zwei verschiedene Kartenebenen,
Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 24.04.2011 Überlagern von Kartenebenen Beispiel: Gegeben zwei verschiedene Kartenebenen,
18. Natürliche Suchbäume
 Wörterbuchimplementationen 1. Natürliche Suchbäume [Ottman/Widmayer, Kap..1, Cormen et al, Kap. 12.1-12.] Hashing: Implementierung von Wörterbüchern mit erwartet sehr schnellen Zugriffszeiten. Nachteile
Wörterbuchimplementationen 1. Natürliche Suchbäume [Ottman/Widmayer, Kap..1, Cormen et al, Kap. 12.1-12.] Hashing: Implementierung von Wörterbüchern mit erwartet sehr schnellen Zugriffszeiten. Nachteile
Dies ist gerade der konstruktive Schritt beim Aufbau von Binomialbäumen.
 Linken von Bäumen: Zwei Bäume desselben Wurzel-Rangs werden unter Einhaltung der Heap-Bedingung verbunden. Sind k 1 und k 2 die Wurzeln der zwei zu linkenden Bäume, so wird ein neuer Baum aufgebaut, dessen
Linken von Bäumen: Zwei Bäume desselben Wurzel-Rangs werden unter Einhaltung der Heap-Bedingung verbunden. Sind k 1 und k 2 die Wurzeln der zwei zu linkenden Bäume, so wird ein neuer Baum aufgebaut, dessen
24. Minimale Spannbäume
 Problem Gegeben: Ungerichteter, zusammenhängender, gewichteter Graph G = (V, E, c). 4. Minimale Spannbäume Gesucht: Minimaler Spannbaum T = (V, E ), E E, so dass e E c(e) minimal. Motivation, Greedy, Algorithmus
Problem Gegeben: Ungerichteter, zusammenhängender, gewichteter Graph G = (V, E, c). 4. Minimale Spannbäume Gesucht: Minimaler Spannbaum T = (V, E ), E E, so dass e E c(e) minimal. Motivation, Greedy, Algorithmus
Datenstrukturen & Algorithmen Lösungen zu Blatt 4 FS 15
 Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Institut für Theoretische Informatik 18. März
Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Institut für Theoretische Informatik 18. März
Kap. 4.7 Skiplisten. 15./16. VO DAP2 SS /10. Juni 2008
 Kap. 4.7 Skiplisten Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 15./16. VO DAP2 SS 2008 5./10. Juni 2008 1 Proseminare WS 2008/09 Anmeldefrist: Montag 16.06.
Kap. 4.7 Skiplisten Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 15./16. VO DAP2 SS 2008 5./10. Juni 2008 1 Proseminare WS 2008/09 Anmeldefrist: Montag 16.06.
Maximale s t-flüsse in Planaren Graphen
 Maximale s t-flüsse in Planaren Graphen Vorlesung Algorithmen für planare Graphen 6. Juni 2017 Guido Brückner INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg
Maximale s t-flüsse in Planaren Graphen Vorlesung Algorithmen für planare Graphen 6. Juni 2017 Guido Brückner INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg
Von Aachen nach Halle...
 Von Aachen nach Halle... Koeln? Aachen Halle 14. 6. 15. 6. 16. 6. Saarbruecken? Effiziente Algorithmen fr Graphtraversierungen Ulrich Meyer p. 3 Von Aachen nach Halle... Koeln? Aachen Halle 14. 6. 15.
Von Aachen nach Halle... Koeln? Aachen Halle 14. 6. 15. 6. 16. 6. Saarbruecken? Effiziente Algorithmen fr Graphtraversierungen Ulrich Meyer p. 3 Von Aachen nach Halle... Koeln? Aachen Halle 14. 6. 15.
Das EM-Modell. Vorlesung 3: Lubys Algorithmus. Graphenalgorithmen und lineare Algebra Hand in Hand
 Vorlesung 3: Lubys Algorithmus Das EM-Modell 85 Nachsatz: Halbringnotation! Auch Bücher enthalten Fehler...! A op 1.op 2 v: Abkürzung für Matrix-Vektor-Multiplikation! Vereinbarung für Reihenfolge: A +.*
Vorlesung 3: Lubys Algorithmus Das EM-Modell 85 Nachsatz: Halbringnotation! Auch Bücher enthalten Fehler...! A op 1.op 2 v: Abkürzung für Matrix-Vektor-Multiplikation! Vereinbarung für Reihenfolge: A +.*
Kürzeste-Wege-Algorithmen und Datenstrukturen
 Kürzeste-Wege-Algorithmen und Datenstrukturen Institut für Informatik Universität zu Köln SS 2009 Teil 1 Inhaltsverzeichnis 1 Kürzeste Wege 2 1.1 Voraussetzungen................................ 2 1.2
Kürzeste-Wege-Algorithmen und Datenstrukturen Institut für Informatik Universität zu Köln SS 2009 Teil 1 Inhaltsverzeichnis 1 Kürzeste Wege 2 1.1 Voraussetzungen................................ 2 1.2
Algorithmentechnik - U bung 3 4. Sitzung Tanja Hartmann 03. Dezember 2009
 Algorithmentechnik - U bung 3 4. Sitzung Tanja Hartmann 03. Dezember 2009 I NSTITUT F U R T HEORETISCHE I NFORMATIK, P ROF. D R. D OROTHEA WAGNER KIT Universita t des Landes Baden-Wu rttemberg und nationales
Algorithmentechnik - U bung 3 4. Sitzung Tanja Hartmann 03. Dezember 2009 I NSTITUT F U R T HEORETISCHE I NFORMATIK, P ROF. D R. D OROTHEA WAGNER KIT Universita t des Landes Baden-Wu rttemberg und nationales
Grundzüge von Algorithmen und Datenstrukturen, WS 15/16: Lösungshinweise zum 13. Übungsblatt
 U N S A R I V E R S A V I E I T A S N I S S Grundzüge von Algorithmen und Datenstrukturen, WS /6: Lösungshinweise zum 3. Übungsblatt Christian Hoffmann, Fabian Bendun Aufgabe 3. (a) Sei j i + = n die Größe
U N S A R I V E R S A V I E I T A S N I S S Grundzüge von Algorithmen und Datenstrukturen, WS /6: Lösungshinweise zum 3. Übungsblatt Christian Hoffmann, Fabian Bendun Aufgabe 3. (a) Sei j i + = n die Größe
Übersicht. Datenstrukturen und Algorithmen. Das Rechenproblem: kürzeste Pfade. Übersicht. Vorlesung 17: Kürzeste Pfade (K24) Bellman-Ford Dijkstra
 Datenstrukturen und Algorithmen Vorlesung 17: (K) Joost-Pieter Katoen Lehrstuhl für Informat Software Modeling and Verification Group http://moves.rwth-aachen.de/teaching/ss-15/dsal/ 1. Juni 15 1 Joost-Pieter
Datenstrukturen und Algorithmen Vorlesung 17: (K) Joost-Pieter Katoen Lehrstuhl für Informat Software Modeling and Verification Group http://moves.rwth-aachen.de/teaching/ss-15/dsal/ 1. Juni 15 1 Joost-Pieter
Vorlesung Algorithmische Geometrie. Streckenschnitte. Martin Nöllenburg INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK
 Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 22.04.2014 Überlagern von Kartenebenen Beispiel: Gegeben zwei verschiedene Kartenebenen,
Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 22.04.2014 Überlagern von Kartenebenen Beispiel: Gegeben zwei verschiedene Kartenebenen,
Kürzeste Wegealgorithmen
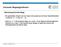 Kürzeste Wegealgorithmen Berechnung kürzester Wege Ein gewichteter Graph G ist ein Tupel (V,E) zusammen mit einer Gewichtsfunktion f, wobei E V V und f: E Seien u,v V. Ein kürzester Weg von u nach v ist
Kürzeste Wegealgorithmen Berechnung kürzester Wege Ein gewichteter Graph G ist ein Tupel (V,E) zusammen mit einer Gewichtsfunktion f, wobei E V V und f: E Seien u,v V. Ein kürzester Weg von u nach v ist
Vorlesung Algorithmische Geometrie. Streckenschnitte. Martin Nöllenburg INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK
 Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 24.04.2011 Überlagern von Kartenebenen Beispiel: Gegeben zwei verschiedene Kartenebenen,
Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 24.04.2011 Überlagern von Kartenebenen Beispiel: Gegeben zwei verschiedene Kartenebenen,
Richtig oder falsch? Richtig oder falsch? Richtig oder falsch? Mit dynamischer Programmierung ist das Knapsack- Problem in Polynomialzeit lösbar.
 Gegeben sei ein Netzwerk N = (V, A, c, s, t) wie in der Vorlesung. Ein maximaler s-t-fluss kann immer mit Hilfe einer Folge von höchstens A Augmentationsschritten gefunden werden. Wendet man den Dijkstra-Algorithmus
Gegeben sei ein Netzwerk N = (V, A, c, s, t) wie in der Vorlesung. Ein maximaler s-t-fluss kann immer mit Hilfe einer Folge von höchstens A Augmentationsschritten gefunden werden. Wendet man den Dijkstra-Algorithmus
Datenstrukturen und Algorithmen
 Prof. Dr. Erika Ábrahám Datenstrukturen und Algorithmen 1/1 Datenstrukturen und Algorithmen Vorlesung 14: Prof. Dr. Erika Ábrahám Theorie Hybrider Systeme Informatik 2 http://ths.rwth-aachen.de/teaching/ss-14/
Prof. Dr. Erika Ábrahám Datenstrukturen und Algorithmen 1/1 Datenstrukturen und Algorithmen Vorlesung 14: Prof. Dr. Erika Ábrahám Theorie Hybrider Systeme Informatik 2 http://ths.rwth-aachen.de/teaching/ss-14/
Grundlagen der Algorithmen und Datenstrukturen Kapitel 6
 Grundlagen der Algorithmen und Datenstrukturen Kapitel 6 Christian Scheideler + Helmut Seidl SS 2009 25.05.09 Kapitel 6 1 Priority Queue M: Menge von Elementen Jedes Element e identifiziert über key(e).
Grundlagen der Algorithmen und Datenstrukturen Kapitel 6 Christian Scheideler + Helmut Seidl SS 2009 25.05.09 Kapitel 6 1 Priority Queue M: Menge von Elementen Jedes Element e identifiziert über key(e).
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein
 Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
5.5 Prioritätswarteschlangen
 5.5 Prioritätswarteschlangen LIFO- und FIFO-Warteschlangen entfernen Werte aus der Warteschlange in Abhängigkeit davon, wann sie in diese eingefügt wurden Prioritätswartschlangen interpretieren die Werte
5.5 Prioritätswarteschlangen LIFO- und FIFO-Warteschlangen entfernen Werte aus der Warteschlange in Abhängigkeit davon, wann sie in diese eingefügt wurden Prioritätswartschlangen interpretieren die Werte
