Dynamische Optimierung
|
|
|
- Helene Holzmann
- vor 9 Jahren
- Abrufe
Transkript
1 Dynamische Optimierung Michaela Nettekoven Abteilung für Quantitative Betriebswirtschaftslehre und Operations Research Wirtschaftsuniversität Wien 21. Januar 2005 Unter dynamischer Optimierung versteht man eine generelle mathematische Methode zur Lösung mehrstuger Entscheidungsprozesse. Die Güte einer Entscheidung wird dabei nicht an ihrer momentanen Wirkung, sondern an ihrem Einuss auf den Prozess als Ganzes gesehen. So entscheidet beispielsweise ein Schachspieler dynamisch gut, wenn er bei einem Zug nicht nur direkte Vorteile, sondern auch Möglichkeiten in späteren Zügen berücksichtigt. Je nachdem, ob die Entscheidungen zu bestimmten (diskreten) Zeitpunkten oder kontinuierlich getroen werden, spricht man von diskreten oder stetigen dynamischen Programmen. Diskrete dynamische Programme sind typischerweise mit Dienzengleichungen verknüpft, stetige dynamische Programme mit Dierentialgleichungen. Die dynamische Programmierung wurde in den 50er Jahren von Richard Bellman begründet (Bellman'sches Optimalitätsprinzip, Bellman'sche Rekursionsgleichungen). Anwendungsgebiete der dynamischen Optimierung nden sich z.b. in Produktionsplanung, Lagerhaltung, Wachstumstheorie, usw. Von der Problemstellung her ergeben sich Beziehungen zur Kontrolltheorie, zur Variationsrechnung und zu dynamischen Spielen. In der dynamischen Programmierung werden Optimierungsprobleme rekursiv gelöst. Obwohl die Grundidee einfach ist, ist die Formulierung der Rekursionsgleichungen oft schwierig, da es anders als in der linearen Optimierung keine Standardform gibt, sondern die Gleichungen an das spezielle Problem angepasst werden müssen. Daher werden im Folgenden verschiedene Modellbeispiele vorgestellt, anhand derer die Methoden der dynamischen Programmierung gezeigt werden. 1 Einführungsbeispiel: Das Postkutschenproblem Ein Goldsucher möchte zur Zeit des amerikanischen Goldrauschs (Mitte des 19. Jahrhunderts) mit der Postkutsche von Missouri nach Kalifornien reisen. Dem Goldsucher stehen verschiedene Routen zur Auswahl, insgesamt erfordert die Reise drei Zwischenstopps (vgl. Abbildung 1). Die Kosten der einzelnen Etappen sind ebenfalls in Abbildung 1 gegeben. Der Goldsucher möchte nun die billigste Reiseroute von Missouri (A) nach Kalifornien (J) nden. Im allgemeinen ist es nicht optimal, jeweils die billigste Teilstrecke zu wählen! 1
2 7 B E H A C F J I D G 5 3 Abbildung 1: Reiserouten und Kosten beim Postkutschenproblem Eine Möglichkeit zur Problemlösung besteht darin, alle möglichen Routen zu bestimmen und die entsprechenden Kosten zu berechnen. Mit Hilfe der dynamischen Programmierung kann die optimale Lösung aber mit wesentlich weniger Rechenaufwand ermittelt werden. Dabei wird das groÿe Gesamtproblem in kleine Teilprobleme zerlegt. Der Graph, der das Postkutschenproblem beschreibt, besteht aus 5 Schichten, diese bezeichnet man auch als Stufen n des Problems: n = 1, 2,..., 5. Die verschiedenen Orte, die durch die Buchstaben A bis J gekennzeichnet sind, bezeichnet man als Zustände. In Stufe 1 gibt es also nur einen Zustand, nämlich A, in Stufe 2 sind die Zustände B, C und D, usw. bis zur Stufe 5 mit dem Zustand J. Die Zustände in den einzelnen Stufen n bezeichnet man auch als x n. In jeder der Stufen n = 1,..., 4 ist die Entscheidung darüber zu treen, welche weitere Route gewählt wird, d.h. welcher Zustand x n+1 in der nächsten Stufe eintreten wird (z.b. ob vom Zustand x 2 =D der Zustand x 3 =E, F oder G erreicht wird). Bezeichne f n (x n, x n+1 ) die Gesamtkosten der besten Strategie für die verbleibenden Stufen, wenn der Goldsucher sich derzeit in Zustand x n bendet und als Folgezustand x n+1 wählt. Sei x n+1 derjenige Folgezustand x n+1, der f n (x n, x n+1 ) minimiert, und sei f n(x n ) der entsprechende Funktionswert: f n(x n ) = min x n+1 f n (x n, x n+1 ) = f n (x n, x n+1) wobei f n (x n, x n+1 ) = unmittelbare Kosten beim Übergang von x n nach x n minimale zukünftige Kosten von x n+1 bis zum Endzustand = c xn,x n+1 + f n+1(x n+1 ) Das Ziel ist es, die minimalen Gesamtkosten f 1 (x 1 ) = f 1 (A) und die entsprechende Reiseroute zu nden. Die dynamische Optimierung ermittelt dabei nacheinander f 4 (x 4 ), f 3 (x 3 ), f 2 (x 2 ) und schlieÿlich f 1 (x 1 ) (Rückwärtsinduktion). Danach wird, beginnend beim Ausgangspunkt, die optimale Route zusammengesetzt (Vorwärtsrechnung). 2
3 Die Lösung des Problems beginnt beim letzten Teilproblem: Angenommen, der Goldsucher ist in Stufe 4 (Zustand H oder I), wie hoch sind die Kosten für die verbleibende Wegstrecke? Da man sich in der vorletzten Stufe bendet, ergibt sich sofort die Lösung: Für n = 4 gilt: aktueller minimale optimaler Zustand Folgekosten Folgezustand x 4 f4 (x 4 ) x 5 H 3 J I 4 J Für n = 3 sind ein paar Berechnungen erforderlich: aktueller Kosten bei Weg nach J über minimale optimaler Zustand f 3 (x 3, x 4 ) = c x3,x 4 + f4 (x 4 ) Folgekosten Folgezustand x 3 H I f3 (x 3 ) x 4 E 1+3=4 4+4=8 4 H F 6+3=9 3+4=7 7 I G 3+3=6 3+4=7 6 H Angenommen, der Goldsucher bendet sich auf Stufe 2 im Zustand B. Die nächsten möglichen Zustände sind E, F oder G. Wählt er E als Folgezustand und danach die kostenminimale Route (d.h. von E weiter nach H und J), so kommen zu den unmittelbaren Kosten von c B,E =7 die minimalen Folgekosten, ausgehend vom Zustand E, hinzu, die in der obigen Tabelle berechnet wurden: f 3 (E) = 4. Damit ergibt sich Tabelle für n = 2: Zuletzt für n = 1: aktueller Kosten bei Weg nach J über minimale optimaler Zustand f 2 (x 2, x 3 ) = c x2,x 3 + f3 (x 3 ) Folgekosten Folgezustand x 2 E F G f2 (x 2 ) x 3 B 7+4=11 4+7=11 6+6=12 11 E,F C 3+4=7 2+7=9 4+6=10 7 E D 4+4=8 1+7=8 5+6=11 8 E,F aktueller Kosten bei Weg nach J über minimale optimaler Zustand f 1 (x 1, x 2 ) = c x1,x 2 + f2 (x 2 ) Folgekosten Folgezustand x 1 B C D f1 (x 1 ) x 2 A 2+11=13 4+7=11 3+8=11 11 C,D Die drei optimalen Reiserouten verursachen demnach Gesamtkosten in Höhe von jeweils 11 und lauten A C E H J D E H J F I J 3
4 2 Charakteristika dynamischer Optimierungsprobleme Dynamische Programme weisen typischerweise folgende Merkmale auf: ˆ Das Problem kann in einzelne Stufen n, n = 1,..., N, zerlegt werden. Auch unendlich viele Stufen sind möglich. ˆ In jeder Stufe n = 1,..., N 1 ist eine Entscheidung u n, u n Ω n, zu treen. ˆ Jeder Stufe n sind bestimmte Zustände x n, x n X n, zugeordnet. Die Anzahl der Zustände kann je nach Problemstellung endlich oder unendlich sein. ˆ Jede auf der Stufe n getroene Entscheidung u n hat zwei Auswirkungen: Der direkte Eekt zeigt sich durch den unmittelbaren Beitrag zur Zielfunktion (z.b. die Reisekosten von B nach E im Postkutschenbeispiel), der indirekte Eekt manifestiert sich durch den durch diese Entscheidung erreichten Folgezustand auf Stufe n+1: x n+1 = h n (x n, u n ). Um langfristige Optimalität zu gewährleisten, müssen sowohl direkter als auch indirekter Effekt berücksichtigt werden. Im Postkutschenproblem bestand die Entscheidung u n in der Auswahl des nächsten Zustands x n+1. Hier wurden zur Vereinfachung u n mit x n+1 identiziert und in der Notation unterdrückt (reduzierte Modellformulierung). ˆ Die Lösungsmethode liefert eine optimale Entscheidungspolitik: Für jeden Zustand in jeder Stufe wird die jeweils optimale weitere Strategie ermittelt. Wenn es den Goldsucher im Postkutschenbeispiel durch bestimmte Umstände z.b. in den Ort G verschlägt (der nicht in der optimalen Reiseroute enthalten ist), kann er trotzdem sofort seine weitere optimale Route wählen: über H nach J. Diese zusätzliche Information ist v.a. für Sensitivitätsanalysen hilfreich. ˆ Bei gegebenem Zustand ist die optimale Entscheidungsfolge für den Rest des Problems unabhängig von den zuvor getroenen Entscheidungen, d.h. alle für ein Subproblem relevanten Informationen sind im aktuellen Zustand subsumiert (Optimalitätsprinzip der dynamischen Programmierung). Die Wegstrecke, die der Goldsucher wählen sollte, wenn er beispielsweise in Ort F ist, hängt nicht davon ab, wie er nach F gelangt ist. ˆ Der Algorithmus beginnt bei der letzten Stufe des Problems und sucht für dieses Teilproblem die optimale Lösung. ˆ Aus der optimalen Lösung für die Stufe n+1 wird mit Hilfe einer rekursiven Beziehung die optimale Lösung für die Stufe n ermittelt. Diese Rekursionsgleichung lautet im Postkutschenproblem (bei Gleichsetzung von u n und x n+1 ): f n(x n ) = min x n+1 { cxn,x n+1 + f n+1(x n+1 ) } Die konkrete Form der Rekursionsgleichung (Bellman'sche Rekursionsgleichung) hängt vom jeweiligen Problem ab. Allgemein lautet sie f n(x n ) = min u n { g(xn, u n ) + f n+1(x n+1 ) } 4
5 Stufe n x n u n Stufe n+1 x n+1 Abbildung 2: Deterministisches dynamisches Programm bzw. für Maximierungsprobleme f n(x n ) = max u n { g(xn, u n ) + f n+1(x n+1 ) }, wobei die Funktion g(, ) den unmittelbaren Beitrag von u n zur Zielfunktion beschreibt. ˆ Ist der Algorithmus auf Stufe 1 angelangt, ist das gesamte Problem gelöst. Bellman'sches Optimalitätsprinzip der dynamischen Programmierung: Die optimale Entscheidungspolitik hat die Eigenschaft, dass unabhängig vom jeweiligen Anfangszustand und den bisherigen Entscheidungen die restlichen Entscheidungen eine optimale Politik für das verbleibende Teilproblem darstellen. Anders ausgedrückt, unabhängig davon, wie ein bestimmter Zustand x n der n-ten Stufe im Intervall [0, N] erreicht wurde, müssen die Entscheidungen u n,..., u N für das noch zu durchlaufende Intervall [n, N] so gewählt werden, dass mit x n als Anfangszustand eine optimale Lösung für das Intervall [n, N] erreicht wird. Jede Teilfolge der optimalen Entscheidungsfolge ist optimal. Der groÿe Vorteil der dynamischen Programmierung besteht in der Rechenzeitersparnis gegenüber der bloÿen Enumeration. Beim Postkutschenproblem gibt es insgesamt 18 mögliche Reiserouten. Berechnet man für jeden Weg die entsprechenden Kosten und sucht dann die billigste Route aus, muss man insgesamt 54 Additionen (3 pro Weg) und 17 Vergleiche durchführen. Bei der Lösung als dynamisches Problem sind lediglich 3+9+6=18 Additionen und 11 Vergleiche durchzuführen. Je mehr Stufen und Zustände pro Stufe ein Problem aufweist, umso gröÿer wird die Ersparnis im Vergleich zur vollständigen Enumeration: bei einem Problem mit 10 Stufen, 10 Zuständen pro Stufe und 10 möglichen Entscheidungsalternativen pro Zustand gibt es verschiedene Wege, der Algorithmus der dynamischen Programmierung kommt jedoch mit 1000 Rechenoperationen (10 für jeden Zustand in jeder Stufe) aus. Dynamische Programmen können in deterministische und stochastische dynamische Programme unterteilt werden. Bei deterministischen dynamischen Programmen ist der Folgezustand x n+1 vollständig durch den aktuellen Zustand x n und die getroene Entscheidung u n bestimmt (Abbildung 2). Im Gegensatz dazu wird bei stochastischen dynamischen Programmen (Markov'sche Entscheidungsprobleme) der Folgezustand der nächsten Stufe durch den aktuellen Zustand, die aktuelle Entscheidung und eine Wahrscheinlichkeitsverteilung bestimmt (vgl. Abbildung 3). 5
6 Stufe n Entscheidung x n u n p 1 Stufe n p 2. p S 1 p S S-1 7 S Abbildung 3: Stochastisches dynamisches Programm 3 Deterministische dynamische Programme: Beispiele 3.1 Zuteilung von Ärzteteams Die Weltgesundheitsorganisation möchte Ärzteteams in drei verschiedene unterentwickelte Länder schicken, um die ärztliche Versorgung der Bevölkerung zu verbessern. Insgesamt stehen 5 Teams zur Verfügung. In der folgenden Tabelle ist angegeben, welche Auswirkungen (zusätzlich erwartete Personen-Lebensjahre in 1.000) der Einsatz von Ärzteteams hat: zusätzliche Personen-Lebensjahre in Anzahl Land Teams Wie sollten die Teams auf die drei Länder aufgeteilt werden? Formulierung: Die drei Länder können als die Stufen des Problems aufgefasst werden. Die Entscheidungsvariablen u n beschreiben, wie viele Teams in das jeweilige Land geschickt werden. Die Zustände in den einzelnen Stufen werden von den Entscheidungen beeinusst. Sie beschreiben, wie viele Teams noch nicht zugeteilt wurden und für die nächsten Länder noch zur Verfügung stehen. Daher gibt es zu Beginn des Problems in Stufe 1, wenn noch keine Teams 6
7 Abbildung 4: Zuteilung Ärzteteams zugeteilt wurden, nur einen Zustand x 1 = 5. Für Stufe 2 bzw 3 gilt x 2 = x 1 u 1 = 5 u 1 bzw. x 3 = x 2 u 2. Am Ende sollen alle Teams eingeteilt sein, daher gilt x 4 = 0. Abbildung 4 beschreibt das Problem. Bezeichne p i (u i ) die in der Tabelle gegebenen Auswirkungen, wenn u i Arzteteams in Land i gesendet werden. Ziel ist es, die Variablen u i so zu wählen, dass 3 i=1 p i(u i ) maximiert wird, wobei 3 i=1 u i = 5 gelten muss und die u i nichtnegative ganzzahlige Variablen sind. Damit ergibt sich für eine beliebige Stufe n f n (x n, u n ) = p n (u n ) + max u n+1,...,u 3 3i=n u i = xn 3 i=n+1 p i (u i ). Mit f n(x n ) = max f n (x n, u n ) u n=0,1,...,x n 7
8 gilt dann und damit die rekursive Beziehung Lösung: f n(x n ) = f n(x n, u n ) = p n (u n ) + f n+1(x n u n ), { max pn (u n ) + f u n =0,1,...,x n n+1(x n u n ) }. Für die letzte Stufe gilt f 4 (0) = 0, damit ergibt sich für Stufe 3 Stufe 2: Stufe 1: aktueller maximaler optimale optimaler Zustand Folgebeitrag Entscheidung Folgezustand x 3 f3 (x 3 ) u 3 x akt. ZF-Beitrag bei u 2 Teams in Land 2 max. opt. opt. Zustand f 2 (x 2, u 2 ) = p 2 (u 2 ) + f3 (x 2 u 2 ) FB Entsch. FZ x f2 (x 2 ) u 2 x , 1 2, akt. ZF-Beitrag bei u 1 Teams in Land 1 max. opt. opt. Zustand f 1 (x 1, u 1 ) = p 1 (u 1 ) + f2 (x 1 u 1 ) FB Entsch. FZ x f1 (x 1 ) u 1 x Die optimale Zuteilung lautet also ein Team in Land 1, drei in Land 2 und eines in Land 3. Dieses Beispiel illustriert einen häugen Typ dynamischer Programme, bei dem eine beschränkte Ressource auf verschiedene Aktivitäten aufgeteilt werden soll. Diese Sichtweise erinnert natürlich an das Standardproblem der linearen Optimierung, trotzdem gibt es einige wichtige Unterschiede: 8
9 ˆ Im obigen dynamischen Problem wird nur eine Ressource aufgeteilt. Prinzipiell ist es auch möglich, mit mehreren Ressourcen zu arbeiten, die Lösungsmethode wird aber sehr schnell inezient. Im Gegensatz dazu können lineare Programme sehr viele Ressourcen bzw. Nebenbedingungen in ezienter Weise berücksichtigen. ˆ Die Formulierung eines solchen Problems als dynamisches Programm ist weitaus allgemeiner als ein lineares Programm. Von den vier Voraussetzungen der linearen Optimierung (Proportionalität, Additivität, Teilbarkeit und Sicherheit) muss nur die Bedingung der Additivität erfüllt sein (bzw. das Analogon für Produkte (statt Summen) von Funktionen), damit das Bellman'sche Optimalitätsprinzip gilt. Proportionalität: wird von fast allen dynamischen Programmen verletzt (auch im obigen Beispiel, siehe die Tabelle mit den zusätzlichen Lebensjahren). Teilbarkeit: Sehr oft sind die Entscheidungsvariablen ganzzahlig. Meistens wird das Problem sogar komplexer, wenn beliebige Teilbarkeit der Variablen gefordert wird. Sicherheit: Auch wenn wir hier nur deterministische Probleme behandeln, sind in der Praxis vor allem stochastische dynamische Programme verbreitet. Auch das obige Zuteilungsproblem lieÿe sich realitätsnäher durch ein stochastisches Programm beschreiben. 4 Übungsaufgaben 1. EVN will in NÖ Transformatoren aufstellen. Jeder Transformator kann an mehreren Stellen positioniert werden. Je nach gewählter Stelle ergeben sich unterschiedliche Arbeitskosten. Zwischen den Transformatoren werden Leitungen gelegt, so dass zusätzliche Kosten entstehen (siehe Abbildung). Finden Sie mittels dynamischer Programmierung die kostengünstigste Variante. 2. Eine Studentin hat noch 7 Tage bis zum Beginn der Prüfungswoche, in der sie alle vier Prüfungen, zu denen sie antritt, gleich am ersten Tag hat. Sie möchte die verbleibende Lernzeit so eektiv wie möglich aufteilen. Sie braucht mindestens einen Tag für jedes Fach, und sie möchte sich täglich nur auf ein Fach konzentrieren. Die Studentin beschlieÿt, die Aufteilung mittels dynamischer Programmierung vorzunehmen, um die Gesamtpunkte- 9
10 zahl der vier Prüfungen zu maximieren. Sie schätzt die Punkteanzahl bei entsprechender Aufteilung folgendermaÿen ein: geschätzte Punkteanzahl Anzahl der Kurs Lerntage Lösen Sie dieses Problem mittels Dynamischer Programmierung. 3. Der Preis eines neuen Autos beträgt 10000, die jährlichen Instandhaltungskosten und Wiederverkaufswerte sind in nachstehender Tabelle angeführt. Bestimmen Sie unter der Annahme, dass Sie jetzt ein neues Auto besitzen, mittels Dynamischer Programmierung eine replacement-politik, mit der Sie die minimalen Kosten aus Besitz und Instandhaltung eines Autos für die nächsten 6 Jahre erzielen. (Gehen Sie davon aus, dass Sie nach Ende dieser 6 Jahre kein Auto besitzen.) Alter des Autos (Jahre) Wiederverkaufswert Instandhaltungskosten (Jahr 1) (Jahr 2) (Jahr 3) (Jahr 4) (Jahr 5) (Jahr 6) 10
Dynamische Optimierung
 Dynamische Optimierung Mike Hüftle 28. Juli 2006 Inhaltsverzeichnis 1 Einleitung 2 1.1.................................... 2 2 Dynamisches Optimierungmodell 3 2.1 Grundmodell der dynamischen Optimierung............
Dynamische Optimierung Mike Hüftle 28. Juli 2006 Inhaltsverzeichnis 1 Einleitung 2 1.1.................................... 2 2 Dynamisches Optimierungmodell 3 2.1 Grundmodell der dynamischen Optimierung............
4. Dynamische Optimierung
 4. Dynamische Optimierung Allgemeine Form dynamischer Optimierungsprobleme 4. Dynamische Optimierung Die dynamische Optimierung (DO) betrachtet Entscheidungsprobleme als eine Folge voneinander abhängiger
4. Dynamische Optimierung Allgemeine Form dynamischer Optimierungsprobleme 4. Dynamische Optimierung Die dynamische Optimierung (DO) betrachtet Entscheidungsprobleme als eine Folge voneinander abhängiger
14. Das Minimumprinzip
 H.J. Oberle Variationsrechnung u. Optimale Steuerung SoSe 2008 14. Das Minimumprinzip In diesem Abschnitt behandeln wir die Idee der dynamischen Programmierung, die auf Bellmann 31 (1957) zurückgeht und
H.J. Oberle Variationsrechnung u. Optimale Steuerung SoSe 2008 14. Das Minimumprinzip In diesem Abschnitt behandeln wir die Idee der dynamischen Programmierung, die auf Bellmann 31 (1957) zurückgeht und
(Lineare) stochastische Optimierung
 (Lineare) stochastische Optimierung Bsp: Aus zwei Sorten Rohöl wird Benzin und Heizöl erzeugt. Die Produktivität sowie der Mindestbedarf (pro Woche) und die Kosten sind in folgender Tabelle angegeben:
(Lineare) stochastische Optimierung Bsp: Aus zwei Sorten Rohöl wird Benzin und Heizöl erzeugt. Die Produktivität sowie der Mindestbedarf (pro Woche) und die Kosten sind in folgender Tabelle angegeben:
Einführung in die Wirtschaftsinformatik VO WS 2008 / 2009
 Einführung in die Wirtschaftsinformatik VO WS 2008 / 2009 Daten Modelle Steuerung Wilfried Grossmann Teil 3: Steuerung Mathematische Modelle werden häufig dazu verwendet um ein optimales Verhalten zu bestimmen
Einführung in die Wirtschaftsinformatik VO WS 2008 / 2009 Daten Modelle Steuerung Wilfried Grossmann Teil 3: Steuerung Mathematische Modelle werden häufig dazu verwendet um ein optimales Verhalten zu bestimmen
Theoretische Informatik. Exkurs: Komplexität von Optimierungsproblemen. Optimierungsprobleme. Optimierungsprobleme. Exkurs Optimierungsprobleme
 Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
3.2 Lineare Optimierung (Entscheidungen unter Sicherheit)
 3. Lineare Optimierung (Entscheidungen unter Sicherheit) Betrachtet wird hier der Fall Θ = (bzw. die Situation u(a, ϑ) bzw. l(a,ϑ) konstant in ϑ Θ für alle a A). Da hier keine Unsicherheit über die Umweltzustände
3. Lineare Optimierung (Entscheidungen unter Sicherheit) Betrachtet wird hier der Fall Θ = (bzw. die Situation u(a, ϑ) bzw. l(a,ϑ) konstant in ϑ Θ für alle a A). Da hier keine Unsicherheit über die Umweltzustände
3. Das Reinforcement Lernproblem
 3. Das Reinforcement Lernproblem 1. Agierender Agent in der Umgebung 2. Discounted Rewards 3. Markov Eigenschaft des Zustandssignals 4. Markov sche Entscheidung 5. Werte-Funktionen und Bellman sche Optimalität
3. Das Reinforcement Lernproblem 1. Agierender Agent in der Umgebung 2. Discounted Rewards 3. Markov Eigenschaft des Zustandssignals 4. Markov sche Entscheidung 5. Werte-Funktionen und Bellman sche Optimalität
Algorithmen I - Tutorium 28 Nr. 12
 Algorithmen I - Tutorium 28 Nr. 12 20.07.2017: Spaß mit Dynamischer und Linearer Programmierung Marc Leinweber [email protected] INSTITUT FÜR THEORETISCHE INFORMATIK (ITI), PROF. DR. JÖRN
Algorithmen I - Tutorium 28 Nr. 12 20.07.2017: Spaß mit Dynamischer und Linearer Programmierung Marc Leinweber [email protected] INSTITUT FÜR THEORETISCHE INFORMATIK (ITI), PROF. DR. JÖRN
1 Zahlentheorie. 1.1 Kongruenzen
 3 Zahlentheorie. Kongruenzen Der letzte Abschnitt zeigte, daß es sinnvoll ist, mit großen Zahlen möglichst einfach rechnen zu können. Oft kommt es nicht darauf, an eine Zahl im Detail zu kennen, sondern
3 Zahlentheorie. Kongruenzen Der letzte Abschnitt zeigte, daß es sinnvoll ist, mit großen Zahlen möglichst einfach rechnen zu können. Oft kommt es nicht darauf, an eine Zahl im Detail zu kennen, sondern
Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber
 Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Sitzplatznr.: Wiederholungsklausur zur Vorlesung Operations Research im Wintersemester
Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Sitzplatznr.: Wiederholungsklausur zur Vorlesung Operations Research im Wintersemester
Lösungen von Übungsblatt 12
 Lösungen von Übungsblatt 12 Algorithmen (WS 2018, Ulrike von Luxburg) Lösungen zu Aufgabe 1 Eine (kanonische) Möglichkeit, die Branch-Schritte auszuführen ergibt sich wie folgt: Das ursprüngliche Problem
Lösungen von Übungsblatt 12 Algorithmen (WS 2018, Ulrike von Luxburg) Lösungen zu Aufgabe 1 Eine (kanonische) Möglichkeit, die Branch-Schritte auszuführen ergibt sich wie folgt: Das ursprüngliche Problem
3.3 Optimale binäre Suchbäume
 3.3 Optimale binäre Suchbäume Problem 3.3.1. Sei S eine Menge von Schlüsseln aus einem endlichen, linear geordneten Universum U, S = {a 1,,...,a n } U und S = n N. Wir wollen S in einem binären Suchbaum
3.3 Optimale binäre Suchbäume Problem 3.3.1. Sei S eine Menge von Schlüsseln aus einem endlichen, linear geordneten Universum U, S = {a 1,,...,a n } U und S = n N. Wir wollen S in einem binären Suchbaum
Das Problem des Handlungsreisenden
 Seite 1 Das Problem des Handlungsreisenden Abbildung 1: Alle möglichen Rundreisen für 4 Städte Das TSP-Problem tritt in der Praxis in vielen Anwendungen als Teilproblem auf. Hierzu gehören z.b. Optimierungsprobleme
Seite 1 Das Problem des Handlungsreisenden Abbildung 1: Alle möglichen Rundreisen für 4 Städte Das TSP-Problem tritt in der Praxis in vielen Anwendungen als Teilproblem auf. Hierzu gehören z.b. Optimierungsprobleme
Abbildung 1: Graphische Lösung der ersten Übungsaufgabe
 Lösungen zu den Übungsaufgaben im Kapitel 1 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier 1. Lösen Sie die folgende lineare Optimierungsaufgabe
Lösungen zu den Übungsaufgaben im Kapitel 1 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier 1. Lösen Sie die folgende lineare Optimierungsaufgabe
Teil II Optimierung. Modellgestützte Analyse und Optimierung Kap. 5 Einführung Optimierung. Peter Buchholz 2006
 Teil II Optimierung Gliederung 5 Einführung, Klassifizierung und Grundlagen 6 Lineare Optimierung 7 Nichtlineare Optimierung 8 Dynamische Optimierung (dieses Jahr nur recht kurz) (9 Stochastische Optimierungsmethoden
Teil II Optimierung Gliederung 5 Einführung, Klassifizierung und Grundlagen 6 Lineare Optimierung 7 Nichtlineare Optimierung 8 Dynamische Optimierung (dieses Jahr nur recht kurz) (9 Stochastische Optimierungsmethoden
8. Reinforcement Learning
 8. Reinforcement Learning Einführung 8. Reinforcement Learning Wie können Agenten ohne Trainingsbeispiele lernen? Auch kennt der Agent zu Beginn nicht die Auswirkungen seiner Handlungen. Stattdessen erhält
8. Reinforcement Learning Einführung 8. Reinforcement Learning Wie können Agenten ohne Trainingsbeispiele lernen? Auch kennt der Agent zu Beginn nicht die Auswirkungen seiner Handlungen. Stattdessen erhält
Stochastische dynamische Optimierung
 Bisher: Neuer Zustand s 0 auf Stufe n +1istdurchaltenZustands auf Stufe n und Aktion a eindeutig bestimmt. s 0 = z n (s, a) Jetzt: Neuer Zustand s 0 ist zusätzlich vom Zufall abhängig. Genauer: Zufallsvariable,
Bisher: Neuer Zustand s 0 auf Stufe n +1istdurchaltenZustands auf Stufe n und Aktion a eindeutig bestimmt. s 0 = z n (s, a) Jetzt: Neuer Zustand s 0 ist zusätzlich vom Zufall abhängig. Genauer: Zufallsvariable,
Polynome. Analysis 1 für Informatik
 Gunter Ochs Analysis 1 für Informatik Polynome sind reelle Funktionen, die sich ausschlieÿlich mit den Rechenoperation Addition, Subtraktion und Multiplikation berechnen lassen. Die allgemeine Funktionsgleichung
Gunter Ochs Analysis 1 für Informatik Polynome sind reelle Funktionen, die sich ausschlieÿlich mit den Rechenoperation Addition, Subtraktion und Multiplikation berechnen lassen. Die allgemeine Funktionsgleichung
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
Aufgabe 1: Berechnen Sie für den in Abbildung 1 gegebenen Graphen den. Abbildung 1: Graph für Flussproblem in Übungsaufgabe 1
 Lösungen zu den Übungsaufgaben im Kapitel 4 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier Aufgabe 1: Berechnen Sie für den in Abbildung
Lösungen zu den Übungsaufgaben im Kapitel 4 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier Aufgabe 1: Berechnen Sie für den in Abbildung
Fachbereich Wirtschaftswissenschaften Professur f. Quantitativen Methoden Prof. Dr. Dietrich Ohse
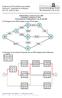 Fachbereich Wirtschaftswissenschaften Professur f. Quantitativen Methoden Prof. Dr. Dietrich Ohse Diplomprüfung / Sommersemester 24 Quantitative Methoden der BWL Musterlösung der Prüfungsklausur vom. Juli
Fachbereich Wirtschaftswissenschaften Professur f. Quantitativen Methoden Prof. Dr. Dietrich Ohse Diplomprüfung / Sommersemester 24 Quantitative Methoden der BWL Musterlösung der Prüfungsklausur vom. Juli
Operations Research II (Nichtlineare und dynamische Optimierung)
 Operations Research II (Nichtlineare und dynamische Optimierung) 5. April 007 Frank Köller,, Hans-Jörg von Mettenheim & Michael H. Breitner 8.4.007 # Nichtlineare Optimierung: Überblick Allgemeine Form:
Operations Research II (Nichtlineare und dynamische Optimierung) 5. April 007 Frank Köller,, Hans-Jörg von Mettenheim & Michael H. Breitner 8.4.007 # Nichtlineare Optimierung: Überblick Allgemeine Form:
(3D-)Extrema unter Nebenbedingungen. Problemstellung (lokale Optimierung)
 (3D-)Extrema unter Nebenbedingungen Wir beschränken uns wieder (meistens) auf Funktionen von zwei Variablen x, y. Bei drei oder mehr Variablen x 1,..., x n sind die gleichen Techniken analog anwendbar,
(3D-)Extrema unter Nebenbedingungen Wir beschränken uns wieder (meistens) auf Funktionen von zwei Variablen x, y. Bei drei oder mehr Variablen x 1,..., x n sind die gleichen Techniken analog anwendbar,
Dynamische Optimierung im Dienstleistungsbereich
 Dynamische Optimierung im Dienstleistungsbereich Univ.-Prof. Dr. Jochen Gönsch Universität Duisburg-Essen Mercator School of Management Lehrstuhl für Betriebswirtschaftslehre, insb. Service Operations
Dynamische Optimierung im Dienstleistungsbereich Univ.-Prof. Dr. Jochen Gönsch Universität Duisburg-Essen Mercator School of Management Lehrstuhl für Betriebswirtschaftslehre, insb. Service Operations
3.2.5 Dualität der linearen Optimierung I
 3..5 Dualität der linearen Optimierung I Jedem linearen Programm in Standardform kann ein sogenanntes duales Programm zugeordnet werden. Es entsteht dadurch, daß man von einem Minimierungsproblem zu einem
3..5 Dualität der linearen Optimierung I Jedem linearen Programm in Standardform kann ein sogenanntes duales Programm zugeordnet werden. Es entsteht dadurch, daß man von einem Minimierungsproblem zu einem
Probeklausur Optimierung
 Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Dr. Nico Düvelmeyer Hamburg, 4. Juli 2011 Probeklausur Optimierung Bitte selber ausfüllen: Name: (darf anonymisiert werden)
Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Dr. Nico Düvelmeyer Hamburg, 4. Juli 2011 Probeklausur Optimierung Bitte selber ausfüllen: Name: (darf anonymisiert werden)
2 Polynome und rationale Funktionen
 Gleichungen spielen auch in der Ingenieurmathematik eine große Rolle. Sie beschreiben zum Beispiel Bedingungen, unter denen Vorgänge ablaufen, Gleichgewichtszustände, Punktmengen. Gleichungen für eine
Gleichungen spielen auch in der Ingenieurmathematik eine große Rolle. Sie beschreiben zum Beispiel Bedingungen, unter denen Vorgänge ablaufen, Gleichgewichtszustände, Punktmengen. Gleichungen für eine
Dynamische Programmierung. Problemlösungsstrategie der Informatik
 als Problemlösungsstrategie der Informatik und ihre Anwedung in der Diskreten Mathematik und Graphentheorie Fabian Cordt Enisa Metovic Wissenschaftliche Arbeiten und Präsentationen, WS 2010/2011 Gliederung
als Problemlösungsstrategie der Informatik und ihre Anwedung in der Diskreten Mathematik und Graphentheorie Fabian Cordt Enisa Metovic Wissenschaftliche Arbeiten und Präsentationen, WS 2010/2011 Gliederung
Perlen der Informatik I Wintersemester 2012 Aufgabenblatt 7
 Technische Universität München WS 2012 Institut für Informatik Prof. Dr. H.-J. Bungartz Prof. Dr. T. Huckle Prof. Dr. M. Bader Kristof Unterweger Perlen der Informatik I Wintersemester 2012 Aufgabenblatt
Technische Universität München WS 2012 Institut für Informatik Prof. Dr. H.-J. Bungartz Prof. Dr. T. Huckle Prof. Dr. M. Bader Kristof Unterweger Perlen der Informatik I Wintersemester 2012 Aufgabenblatt
Graphentheorie. Kürzeste Wege. Kürzeste Wege. Kürzeste Wege. Rainer Schrader. 25. Oktober 2007
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 25. Oktober 2007 1 / 20 2 / 20 Wir werden Optimierungsprobleme vom folgenden Typ betrachten: gegeben eine Menge X und eine Funktion
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 25. Oktober 2007 1 / 20 2 / 20 Wir werden Optimierungsprobleme vom folgenden Typ betrachten: gegeben eine Menge X und eine Funktion
Average-Case-Komplexität
 Exkurs Average-Case-Komplexität Das eben gestellte Problem kann man auch effizienter lösen Algorithmus prefixaverages2(x) s = 0.0 for i in range(0,n): s += X[i] A[i] = s / (i + 1) return A O(1) n O(1)
Exkurs Average-Case-Komplexität Das eben gestellte Problem kann man auch effizienter lösen Algorithmus prefixaverages2(x) s = 0.0 for i in range(0,n): s += X[i] A[i] = s / (i + 1) return A O(1) n O(1)
Einführung in die Objektorientierte Programmierung Vorlesung 17: Dynamische Programmierung. Sebastian Küpper
 Einführung in die Objektorientierte Programmierung Vorlesung 17: Dynamische Programmierung Sebastian Küpper Redundanz Rekursiver Lösungen Rekursion kann elegante Bescheibungen zur Problemlösung ergeben
Einführung in die Objektorientierte Programmierung Vorlesung 17: Dynamische Programmierung Sebastian Küpper Redundanz Rekursiver Lösungen Rekursion kann elegante Bescheibungen zur Problemlösung ergeben
Über- und unterbestimmte
 Über- und unterbestimmte Systeme (verallgemeinerte Lösungen) Über- und unterbestimmte Systeme Ax = b ist genau dann für alle b R m eindeutig lösbar, wenn m = n und rk A = n. Falls m n oder rk A < min{m,
Über- und unterbestimmte Systeme (verallgemeinerte Lösungen) Über- und unterbestimmte Systeme Ax = b ist genau dann für alle b R m eindeutig lösbar, wenn m = n und rk A = n. Falls m n oder rk A < min{m,
Inhalt. 8.1 Motivation. 8.2 Optimierung ohne Nebenbedingungen. 8.3 Optimierung unter Nebenbedingungen. 8.4 Lineare Programmierung
 8. Optimierung Inhalt 8.1 Motivation 8.2 Optimierung ohne Nebenbedingungen 8.3 Optimierung unter Nebenbedingungen 8.4 Lineare Programmierung 8.5 Kombinatorische Optimierung 2 8.1 Motivation Viele Anwendungen
8. Optimierung Inhalt 8.1 Motivation 8.2 Optimierung ohne Nebenbedingungen 8.3 Optimierung unter Nebenbedingungen 8.4 Lineare Programmierung 8.5 Kombinatorische Optimierung 2 8.1 Motivation Viele Anwendungen
Eigenschaften von LPs
 2 Lineare Programmierung Eigenschaften von LPs Eigenschaften von LPs Definition 24 Eine Menge K IR n heißt konvex gdw für je zwei Punkte Punkte x (1) K und x (2) K auch jeder Punkt mit 0 λ 1 zu K gehört
2 Lineare Programmierung Eigenschaften von LPs Eigenschaften von LPs Definition 24 Eine Menge K IR n heißt konvex gdw für je zwei Punkte Punkte x (1) K und x (2) K auch jeder Punkt mit 0 λ 1 zu K gehört
Angewandte Stochastik
 Angewandte Stochastik Dr. C.J. Luchsinger 13 Allgemeine Theorie zu Markov-Prozessen (stetige Zeit, diskreter Zustandsraum) Literatur Kapitel 13 * Grimmett & Stirzaker: Kapitel 6.9 Wie am Schluss von Kapitel
Angewandte Stochastik Dr. C.J. Luchsinger 13 Allgemeine Theorie zu Markov-Prozessen (stetige Zeit, diskreter Zustandsraum) Literatur Kapitel 13 * Grimmett & Stirzaker: Kapitel 6.9 Wie am Schluss von Kapitel
Lineare (Un-)Gleichungen und lineare Optimierung
 Lineare (Un-)Gleichungen und lineare Optimierung Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-6020 Innsbruck, Österreich [email protected] 1 Einleitung In der linearen
Lineare (Un-)Gleichungen und lineare Optimierung Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-6020 Innsbruck, Österreich [email protected] 1 Einleitung In der linearen
P-Median Problem. Michael Enser Anzahl der ausgewählten Standorte oder Mediane
 P-Median Problem Michael nser 4..20 Inhaltsverzeichnis Allgemeines p-median-problem. Allgemeine ention............................. 2.2 in kleines eispiel.............................. 2 2 -median Problem
P-Median Problem Michael nser 4..20 Inhaltsverzeichnis Allgemeines p-median-problem. Allgemeine ention............................. 2.2 in kleines eispiel.............................. 2 2 -median Problem
1 Der Simplex Algorithmus I
 1 Nicoletta Andri 1 Der Simplex Algorithmus I 1.1 Einführungsbeispiel In einer Papiermühle wird aus Altpapier und anderen Vorstoffen feines und grobes Papier hergestellt. Der Erlös pro Tonne feines Papier
1 Nicoletta Andri 1 Der Simplex Algorithmus I 1.1 Einführungsbeispiel In einer Papiermühle wird aus Altpapier und anderen Vorstoffen feines und grobes Papier hergestellt. Der Erlös pro Tonne feines Papier
Substitutionsverfahren
 Substitutionsverfahren 1 Motivation Wir stehen vor folgendem Problem: In unserem Betrieb kann unsere einzige Maschine Produkt A in zwei Stunden und Produkt B in einer Stunde produzieren. Die Maschine läuft
Substitutionsverfahren 1 Motivation Wir stehen vor folgendem Problem: In unserem Betrieb kann unsere einzige Maschine Produkt A in zwei Stunden und Produkt B in einer Stunde produzieren. Die Maschine läuft
3. Der größte gemeinsame Teiler
 Chr.Nelius: Zahlentheorie (SoSe 2016) 18 3. Der größte gemeinsame Teiler (3.1) DEF: a und b seien beliebige ganze Zahlen. a) Eine ganze Zahl t heißt gemeinsamer Teiler von a und b, wenn gilt t a und t
Chr.Nelius: Zahlentheorie (SoSe 2016) 18 3. Der größte gemeinsame Teiler (3.1) DEF: a und b seien beliebige ganze Zahlen. a) Eine ganze Zahl t heißt gemeinsamer Teiler von a und b, wenn gilt t a und t
Dynamische Optimierung. Kapitel 4. Dynamische Optimierung. Peter Becker (H-BRS) Operations Research II Wintersemester 2014/15 160 / 206
 Kapitel 4 Dynamische Optimierung Peter Becker (H-BRS) Operations Research II Wintersemester 2014/15 160 / 206 Inhalt Inhalt 4 Dynamische Optimierung Allgemeiner Ansatz und Beispiele Stochastische dynamische
Kapitel 4 Dynamische Optimierung Peter Becker (H-BRS) Operations Research II Wintersemester 2014/15 160 / 206 Inhalt Inhalt 4 Dynamische Optimierung Allgemeiner Ansatz und Beispiele Stochastische dynamische
Algorithmen und Datenstrukturen 1 Kapitel 3
 Algorithmen und Datenstrukturen 1 Kapitel 3 Technische Fakultät [email protected] Vorlesung, U. Bielefeld, Winter 2005/2006 3.6 Dynamische Programmierung Die rekursive Problemzerlegung kann
Algorithmen und Datenstrukturen 1 Kapitel 3 Technische Fakultät [email protected] Vorlesung, U. Bielefeld, Winter 2005/2006 3.6 Dynamische Programmierung Die rekursive Problemzerlegung kann
Approximationsalgorithmen. 19. Dezember / 28
 Approximationsalgorithmen 19. Dezember 2017 1 / 28 Optimierungsprobleme Das Ziel: Bearbeite schwierige Optimierungsprobleme der Form opt y f (x, y) so dass L(x, y). Die Zielfunktion f (x, y) ist zu minimieren
Approximationsalgorithmen 19. Dezember 2017 1 / 28 Optimierungsprobleme Das Ziel: Bearbeite schwierige Optimierungsprobleme der Form opt y f (x, y) so dass L(x, y). Die Zielfunktion f (x, y) ist zu minimieren
5. Der größte gemeinsame Teiler
 Chr.Nelius: Zahlentheorie (SoSe 2017) 22 5. Der größte gemeinsame Teiler (5.1) DEF: a und b seien beliebige ganze Zahlen. a) Eine ganze Zahl t heißt gemeinsamer Teiler von a und b, wenn gilt t a und t
Chr.Nelius: Zahlentheorie (SoSe 2017) 22 5. Der größte gemeinsame Teiler (5.1) DEF: a und b seien beliebige ganze Zahlen. a) Eine ganze Zahl t heißt gemeinsamer Teiler von a und b, wenn gilt t a und t
Dualitätssätze der linearen Optimierung
 Kapitel 9 Dualitätssätze der linearen Optimierung Sei z = c T x min! Ax = b 9.1 x 0 mit c, x R n, b R m, A R m n ein lineares Programm. Definition 9.1 Duales lineares Programm. Das lineare Programm z =
Kapitel 9 Dualitätssätze der linearen Optimierung Sei z = c T x min! Ax = b 9.1 x 0 mit c, x R n, b R m, A R m n ein lineares Programm. Definition 9.1 Duales lineares Programm. Das lineare Programm z =
Grundlagen der Mathematik
 Universität Hamburg Winter 2016/17 Fachbereich Mathematik Janko Latschev Grundlagen der Mathematik Lösungsskizzen 2 Präsenzaufgaben (P2) Wir betrachten drei Teilmengen der natürlichen Zahlen: - A = {n
Universität Hamburg Winter 2016/17 Fachbereich Mathematik Janko Latschev Grundlagen der Mathematik Lösungsskizzen 2 Präsenzaufgaben (P2) Wir betrachten drei Teilmengen der natürlichen Zahlen: - A = {n
Inhalt. 1. Einführung in die Informatik. 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele.
 1. Einführung in die Informatik Inhalt 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele Peter Sobe 1 Einführende Beispiele 2. Algorithmen Täglich werden Verarbeitungsvorschriften
1. Einführung in die Informatik Inhalt 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele Peter Sobe 1 Einführende Beispiele 2. Algorithmen Täglich werden Verarbeitungsvorschriften
Betriebliche Optimierung
 Betriebliche Optimierung Joachim Schauer Institut für Statistik und OR Uni Graz Joachim Schauer ( Institut für Statistik und OR Uni Graz Betriebliche ) Optimierung 1 / 22 1 Das Travelling Salesperson Problem
Betriebliche Optimierung Joachim Schauer Institut für Statistik und OR Uni Graz Joachim Schauer ( Institut für Statistik und OR Uni Graz Betriebliche ) Optimierung 1 / 22 1 Das Travelling Salesperson Problem
Computer Science Department - High Performance and Web Computing Group. Optimierungsprobleme
 Optimierungsprobleme Häufig in Alltagssituationen anzutreffen (z.b. Kauf eines Gerätes) Optimierungsprobleme (OPs) sind Probleme, die i.a. viele zulässige Lösungen besitzen Jeder Lösung ist ein bestimmter
Optimierungsprobleme Häufig in Alltagssituationen anzutreffen (z.b. Kauf eines Gerätes) Optimierungsprobleme (OPs) sind Probleme, die i.a. viele zulässige Lösungen besitzen Jeder Lösung ist ein bestimmter
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Multiplikation langer Zahlen
 Multiplikation langer Zahlen Aljoscha Rudawski 20.5.2017 Inhaltsverzeichnis 1 Einleitung 1 2 Multiplikation nach Lehrbuch 1 2.1 Addition langer Zahlen............................. 2 2.2 Multiplikation
Multiplikation langer Zahlen Aljoscha Rudawski 20.5.2017 Inhaltsverzeichnis 1 Einleitung 1 2 Multiplikation nach Lehrbuch 1 2.1 Addition langer Zahlen............................. 2 2.2 Multiplikation
Lineare (Un-)Gleichungen und lineare Optimierung
 Lineare (Un-)Gleichungen und lineare Optimierung Franz Pauer Institut für Mathematik Universität Innsbruck Lehrer/innen/fortbildungstag Wien 2010 9. April 2010 Eine Maximumsaufgabe Eine Firma stellt aus
Lineare (Un-)Gleichungen und lineare Optimierung Franz Pauer Institut für Mathematik Universität Innsbruck Lehrer/innen/fortbildungstag Wien 2010 9. April 2010 Eine Maximumsaufgabe Eine Firma stellt aus
Universität Basel Wirtschaftswissenschaftliches Zentrum. Zufallsvariablen. Dr. Thomas Zehrt
 Universität Basel Wirtschaftswissenschaftliches Zentrum Zufallsvariablen Dr. Thomas Zehrt Inhalt: 1. Einführung 2. Zufallsvariablen 3. Diskrete Zufallsvariablen 4. Stetige Zufallsvariablen 5. Erwartungswert
Universität Basel Wirtschaftswissenschaftliches Zentrum Zufallsvariablen Dr. Thomas Zehrt Inhalt: 1. Einführung 2. Zufallsvariablen 3. Diskrete Zufallsvariablen 4. Stetige Zufallsvariablen 5. Erwartungswert
Optimierung. Vorlesung 08
 Optimierung Vorlesung 08 Heute Dualität Ganzzahligkeit Optimierung der Vorlesung durch Evaluierung 2 Das duale LP Das primale LP Maximiere c T x unter Ax b, x R d 0. wird zu dem dualen LP Minimiere b T
Optimierung Vorlesung 08 Heute Dualität Ganzzahligkeit Optimierung der Vorlesung durch Evaluierung 2 Das duale LP Das primale LP Maximiere c T x unter Ax b, x R d 0. wird zu dem dualen LP Minimiere b T
Anwendungen dynamischer Programmierung in der Biologie
 Anwendungen dynamischer Programmierung in der Biologie Überblick Algorithmus zum Finden der wahrscheinlichsten Sekundärstruktur eines RNS Moleküls Sequence Alignment Verbesserung von Sequence Alignment
Anwendungen dynamischer Programmierung in der Biologie Überblick Algorithmus zum Finden der wahrscheinlichsten Sekundärstruktur eines RNS Moleküls Sequence Alignment Verbesserung von Sequence Alignment
Aufgabe 1: Betrachtet werde das Matrixspiel mit der Auszahlungsmatrix a. 1. Für welche Werte von a gibt es ein Nash sches Gleichgewicht?
 Lösungen zu den Übungsaufgaben im Kapitel 7 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier Aufgabe : Betrachtet werde das Matrixspiel mit
Lösungen zu den Übungsaufgaben im Kapitel 7 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier Aufgabe : Betrachtet werde das Matrixspiel mit
Die Taylorreihe einer Funktion
 Kapitel 6 Die Taylorreihe einer Funktion Dieser Abschnitt beschäftigt sich mit Taylorreihen, Taylorpolynomen und der Restgliedabschätzung für Taylorpolynome. Die Taylorreihe einer reellen Funktion ist
Kapitel 6 Die Taylorreihe einer Funktion Dieser Abschnitt beschäftigt sich mit Taylorreihen, Taylorpolynomen und der Restgliedabschätzung für Taylorpolynome. Die Taylorreihe einer reellen Funktion ist
Reinforcement Learning
 Universität Potsdam Institut für Informatik Lehrstuhl Maschinelles Lernen Reinforcement Learning Uwe Dick Inhalt Problemstellungen Beispiele Markov Decision Processes Planen vollständige MDPs Lernen unbekannte
Universität Potsdam Institut für Informatik Lehrstuhl Maschinelles Lernen Reinforcement Learning Uwe Dick Inhalt Problemstellungen Beispiele Markov Decision Processes Planen vollständige MDPs Lernen unbekannte
Lineare Gleichungssysteme
 Christian Serpé Universität Münster 14. September 2011 Christian Serpé (Universität Münster) 14. September 2011 1 / 56 Gliederung 1 Motivation Beispiele Allgemeines Vorgehen 2 Der Vektorraum R n 3 Lineare
Christian Serpé Universität Münster 14. September 2011 Christian Serpé (Universität Münster) 14. September 2011 1 / 56 Gliederung 1 Motivation Beispiele Allgemeines Vorgehen 2 Der Vektorraum R n 3 Lineare
2.6 Theorie des Haushalts
 .6 Theorie des Haushalts WS 007/08 Nutzenfunktionen und Indifferenzkurven Nutzenfunktion: Hilfsmittel, um Präferenzen zu beschreiben Eine Präferenzordnung lässt sich unter den obigen Annahmen über eine
.6 Theorie des Haushalts WS 007/08 Nutzenfunktionen und Indifferenzkurven Nutzenfunktion: Hilfsmittel, um Präferenzen zu beschreiben Eine Präferenzordnung lässt sich unter den obigen Annahmen über eine
7. LINEARISIERUNG UND DAS DIFFERENTIAL
 63 Dieses Skript ist ein Auszug mit Lücken aus Einführung in die mathematische Behandlung der Naturwissenschaften I von Hans Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie das Buch auch
63 Dieses Skript ist ein Auszug mit Lücken aus Einführung in die mathematische Behandlung der Naturwissenschaften I von Hans Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie das Buch auch
Die duale Simplexmethode
 Kapitel 0 Die duale Simplexmethode Bei der dualen Simplexmethode ist eine Startlösung oftmals leichter angebbar als bei der Simplexmethode für das ursprüngliche lineare Programm, da man keine Nichtnegativitätsanforderungen
Kapitel 0 Die duale Simplexmethode Bei der dualen Simplexmethode ist eine Startlösung oftmals leichter angebbar als bei der Simplexmethode für das ursprüngliche lineare Programm, da man keine Nichtnegativitätsanforderungen
Aussage: richtig falsch
 Aufgabe 1: Multiple Choice (10 unkte) Folgende Aussagen sind entweder richtig oder falsch! Kreuzen Sie jeweils direkt hinter der Aussage eines der Kästchen an! Stimmt Ihre Bewertung einer Aussage so gibt
Aufgabe 1: Multiple Choice (10 unkte) Folgende Aussagen sind entweder richtig oder falsch! Kreuzen Sie jeweils direkt hinter der Aussage eines der Kästchen an! Stimmt Ihre Bewertung einer Aussage so gibt
1 Lineare Optimierung, Simplex-Verfahren
 1 Lineare Optimierung, Simplex-Verfahren 1.1 Einführung Beispiel: In einer Fabrik werden n Produkte A 1, A 2,..., A n hergestellt. Dazu werden m Rohstoffe B 1, B 2,..., B m (inklusive Arbeitskräfte und
1 Lineare Optimierung, Simplex-Verfahren 1.1 Einführung Beispiel: In einer Fabrik werden n Produkte A 1, A 2,..., A n hergestellt. Dazu werden m Rohstoffe B 1, B 2,..., B m (inklusive Arbeitskräfte und
Dynamische Programmierung
 Dynamische Programmierung Claudia Gerhold 9.5.6 Claudia Gerhold Dynamische Programmierung 9.5.6 / 4 Agenda Einführung Dynamische Programmierung Top-Down Ansatz mit Memoization Bottom-Up Ansatz 3 Anwendungsbeispiele
Dynamische Programmierung Claudia Gerhold 9.5.6 Claudia Gerhold Dynamische Programmierung 9.5.6 / 4 Agenda Einführung Dynamische Programmierung Top-Down Ansatz mit Memoization Bottom-Up Ansatz 3 Anwendungsbeispiele
Diskret oder kontinuierlich modellieren?
 Diskret oder kontinuierlich modellieren? Franz Pauer, Florian Stampfer Institut für Fachdidaktik und Institut für Mathematik Universität Innsbruck Lehrer/innen/fortbildungstag Wien 2017 21. April 2017
Diskret oder kontinuierlich modellieren? Franz Pauer, Florian Stampfer Institut für Fachdidaktik und Institut für Mathematik Universität Innsbruck Lehrer/innen/fortbildungstag Wien 2017 21. April 2017
Kurseinheit 2»Dualität und weiterführende Methoden«
 Inhaltsübersicht 1 Gliederung Kurseinheit 1»Simpleverfahren«1. Einleitung 1.1. Einordnung und Übersicht des Stoffes 1.2. Einführendes Beispiel und Grundlagen 2. Lineare Gleichungssysteme 2.1. Die allgemeine
Inhaltsübersicht 1 Gliederung Kurseinheit 1»Simpleverfahren«1. Einleitung 1.1. Einordnung und Übersicht des Stoffes 1.2. Einführendes Beispiel und Grundlagen 2. Lineare Gleichungssysteme 2.1. Die allgemeine
Teil I. Lineare Optimierung
 Teil I Lineare Optimierung 5 Kapitel 1 Grundlagen Definition 1.1 Lineares Optimierungsproblem, lineares Programm. Eine Aufgabenstellung wird lineares Optimierungsproblem oder lineares Programm genannt,
Teil I Lineare Optimierung 5 Kapitel 1 Grundlagen Definition 1.1 Lineares Optimierungsproblem, lineares Programm. Eine Aufgabenstellung wird lineares Optimierungsproblem oder lineares Programm genannt,
U. Rausch, 2010 Ganze Zahlen 1
 U. Rausch, 2010 Ganze Zahlen 1 Ganze Zahlen 1 Einleitung Als ganze Zahlen bezeichnet man die natürlichen Zahlen 1, 2,, 4,..., die Null 0 und die negativen ganzen Zahlen 1, 2,, 4,... Wir verabreden die
U. Rausch, 2010 Ganze Zahlen 1 Ganze Zahlen 1 Einleitung Als ganze Zahlen bezeichnet man die natürlichen Zahlen 1, 2,, 4,..., die Null 0 und die negativen ganzen Zahlen 1, 2,, 4,... Wir verabreden die
(Technisch: Setze alle Skalarprodukte der allgemeinen Lösung mit den Basisvektoren des Kerns gleich Null eindeutige leastsqares Lösung)
 Lineare Optimierung Unterbestimmte LGS und Optimierung Bei lösbaren unterbestimmten linearen Gleichungssystemen haben wir die Qual der Wahl in Abhängigkeit von den freien Parametern (Anzahl = Anzahl Unbekannte
Lineare Optimierung Unterbestimmte LGS und Optimierung Bei lösbaren unterbestimmten linearen Gleichungssystemen haben wir die Qual der Wahl in Abhängigkeit von den freien Parametern (Anzahl = Anzahl Unbekannte
Datenstrukturen & Algorithmen
 Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Dynamische Programmierung Einführung Ablaufkoordination von Montagebändern Längste gemeinsame Teilsequenz Optimale
Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Dynamische Programmierung Einführung Ablaufkoordination von Montagebändern Längste gemeinsame Teilsequenz Optimale
3 Iterative Lösung von sequentiellen Entscheidungsprozessen
 3 Iterative Lösung von sequentiellen Entscheidungsprozessen Die Behandlung bewertete Marov-Kette diente dem Ziel, sequentielle Entscheidungsprozesse, die sich aus Marov-Ketten herleiten lassen, untersuchen
3 Iterative Lösung von sequentiellen Entscheidungsprozessen Die Behandlung bewertete Marov-Kette diente dem Ziel, sequentielle Entscheidungsprozesse, die sich aus Marov-Ketten herleiten lassen, untersuchen
Algebra und Zahlentheorie I (WS03/04), Lösungen zu Blatt 12
 Algebra und Zahlentheorie I (WS03/04), Lösungen zu Blatt 12 Aufgabe 1. (Division mit Rest in Polynomringen) Es sei R ein kommutativer Ring {0} und R[X] ein Polynomring in der Unbestimmten X über R. Ferner
Algebra und Zahlentheorie I (WS03/04), Lösungen zu Blatt 12 Aufgabe 1. (Division mit Rest in Polynomringen) Es sei R ein kommutativer Ring {0} und R[X] ein Polynomring in der Unbestimmten X über R. Ferner
Optimieren unter Nebenbedingungen
 Optimieren unter Nebenbedingungen Hier sucht man die lokalen Extrema einer Funktion f(x 1,, x n ) unter der Nebenbedingung dass g(x 1,, x n ) = 0 gilt Die Funktion f heißt Zielfunktion Beispiel: Gesucht
Optimieren unter Nebenbedingungen Hier sucht man die lokalen Extrema einer Funktion f(x 1,, x n ) unter der Nebenbedingung dass g(x 1,, x n ) = 0 gilt Die Funktion f heißt Zielfunktion Beispiel: Gesucht
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2007 11. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik [email protected] Das Rucksack-Problem Ein Dieb, der einen Safe
Algorithmen und Datenstrukturen 2 Sommersemester 2007 11. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik [email protected] Das Rucksack-Problem Ein Dieb, der einen Safe
Lineare Optimierungsaufgaben - eine Einführung
 Lineare Optimierungsaufgaben - eine Einführung Aufgabenstellung, Beispiele, graphisches Lösen und Trafo auf Normalform Vortragsskript von Lorenz Fischer Operations Research bedeutet die Suche nach einer
Lineare Optimierungsaufgaben - eine Einführung Aufgabenstellung, Beispiele, graphisches Lösen und Trafo auf Normalform Vortragsskript von Lorenz Fischer Operations Research bedeutet die Suche nach einer
4. ggt und kgv. Chr.Nelius: Zahlentheorie (SS 2007) 9
 Chr.Nelius: Zahlentheorie (SS 2007) 9 4. ggt und kgv (4.1) DEF: Eine ganze Zahl g heißt größter gemeinsamer Teiler (ggt) zweier ganzer Zahlen a und b, wenn gilt: GGT 0 ) g 0 GGT 1 ) g a und g b GGT 2 )
Chr.Nelius: Zahlentheorie (SS 2007) 9 4. ggt und kgv (4.1) DEF: Eine ganze Zahl g heißt größter gemeinsamer Teiler (ggt) zweier ganzer Zahlen a und b, wenn gilt: GGT 0 ) g 0 GGT 1 ) g a und g b GGT 2 )
Betriebswirtschaftliche Optimierung
 Institut für Statistik und OR Uni Graz 1 Das Travelling Salesperson Problem 2 Das Travelling Salesperson Problem Zentrales Problem der Routenplanung Unzählige wissenschaftliche Artikel theoretischer sowie
Institut für Statistik und OR Uni Graz 1 Das Travelling Salesperson Problem 2 Das Travelling Salesperson Problem Zentrales Problem der Routenplanung Unzählige wissenschaftliche Artikel theoretischer sowie
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2009 11. Vorlesung Uwe Quasthoff Universität Leipzig Institut für Informatik [email protected] Das Rucksack-Problem Ein Dieb, der einen
Algorithmen und Datenstrukturen 2 Sommersemester 2009 11. Vorlesung Uwe Quasthoff Universität Leipzig Institut für Informatik [email protected] Das Rucksack-Problem Ein Dieb, der einen
Unimodularität. Kapitel 1. Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206
 Kapitel 1 Unimodularität Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206 Inhalt 1 Unimodularität Total unimodulare Matrizen Inzidenzmatrix Optimierungsprobleme auf Graphen Peter
Kapitel 1 Unimodularität Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206 Inhalt 1 Unimodularität Total unimodulare Matrizen Inzidenzmatrix Optimierungsprobleme auf Graphen Peter
Nachtermin 2003 Nichttechnik 12. Analysis
 Die reellen Funktionen f : xa f (x); D = R a a f a Nachtermin 2003 Nichttechnik 12 Analysis 1 2 f a (x) = (x + 4x a) mit a R 4 sind die ersten Ableitungen der Funktionen Der Graph einer solchen Funktion
Die reellen Funktionen f : xa f (x); D = R a a f a Nachtermin 2003 Nichttechnik 12 Analysis 1 2 f a (x) = (x + 4x a) mit a R 4 sind die ersten Ableitungen der Funktionen Der Graph einer solchen Funktion
Zentralübung Diskrete Wahrscheinlichkeitstheorie (zur Vorlesung Prof. Esparza)
 SS 2013 Zentralübung Diskrete Wahrscheinlichkeitstheorie (zur Vorlesung Prof. Esparza) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2013ss/dwt/uebung/ 10. Mai 2013
SS 2013 Zentralübung Diskrete Wahrscheinlichkeitstheorie (zur Vorlesung Prof. Esparza) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2013ss/dwt/uebung/ 10. Mai 2013
