Musterlösung zur Probeklausur zur Kombinatorik
|
|
|
- Irma Meinhardt
- vor 7 Jahren
- Abrufe
Transkript
1 UNIVERSITÄT ULM Institut für Zahlentheorie und Wahrscheinlichkeitstheorie Musterlösung zur Probeklausur zur Kombinatorik Prof. Dr. Helmut Maier, Hans- Peter Reck Gesamtpunktzahl: 00 Punkte Freitag,. Dezember 2009, 2:00 Uhr. Wieviele Möglichkeiten gibt es, die Buchstaben der folgenden Wörter umzuordnen? (a) MEMMINGEN Das Wort Memmingen hat neun Buchstaben, also gibt es grundsätzlich 9! Umordnungen. Da aber der Buchstabe m dreimal, e und n zweimal und i und g je einmal auftreten, reduzieren sich die Umordnungen um diejenigen Weisen, wo dieselben Buchstaben lediglich vertauscht werden. Insgesamt ergeben sich (b) MAMMAMIA 9! 3! 2! 2!!! = 9! = 520 Anordnungen. 24 Hier haben wir ein Wort mit acht Buchstaben, das mit dem Buchstaben m viermal enthält, den Buchstaben a dreimal und einmal i. Also haben wir (c) MISSISSIPPI 8! 4! 3!! = 8! = 280 Anordnungen In diesem Wort kommen vier s, vier i zwei p und ein m vor. Insgesamt liegen damit! 4! 4! 2!! =! 56 = Anordnungen vor. (9 Punkte) 2. Eine ID- Nummer (Identifikationsnummer) bestehe aus einer Folge von drei Buchstaben, die dem Alphabet A,..., Z und einer Folge von fünf Ziffern, die der Menge {0,,..., 9} entnommen werden. Wieveiel Möglichkeiten gibt es, wenn für die Ziffern Wiederholungen zulässig sind, für die Buchstaben aber nicht?
2 Für die drei Buchstaben sind keine Wiederholungen zulässig, also gibt es für den ersten Buchstaben 26 Möglichkeiten, für den zweiten noch 25 und den dritten 24. Bei den Buchstaben haben wir keine Einschränkung, also immer 0 Möglichkeiten. Insgesamt sind es = Variationen. (5 Punkte) 3. Auf einem Regal sollen drei rote und drei schwarze (unterscheidbare) Bücher aufgestellt werden. Wieviel Möglichkeiten gibt es, wenn (a) keine Einschränkungen über die Anordnung gemacht werden? Wenn es keine Einschränkungen gibt, dann bleiben für das erste Buch sechs Plätze zur Auswahl, für das zweite fünf, usw.: es gibt also 6! = 720 Anordnungen. (b) die schwarzen Bücher nebeneinander stehen sollen? Stehen die schwarzen nebeneinander, haben wir hier 3! Anordnungen innerhalb des schwarzen Blocks. Betrachten wir das linke Buch dieses Blocks, gibt es vier Möglichkeiten, dieses zu platzieren, damit der schwarze Block zusammen bleibt. Für die roten gibt es dann entsprechend 3! Möglichkeiten. Insgesamt ergeben sich hier 4 3! 3! = 44 Anordnungen. (c) rote und schwarze Bücher einander abwechseln sollen? In diesem Fall haben wir ein festgelegtes Farbmuster, abhängig nur von der Frage mit welcher Farbe man links beginnt (Faktor zwei). Für das linke Buch gibt es drei Möglichkeiten (Anzahl der Bücher der gewählten Farbe), für das nächste drei (Anzahl der andersfarbigen), das nächste zwei (verbleibende Anzahl der erstgewählten Farbe),..., die letzten beiden sind dann festgelegt. Wir erhalten: 2 3! 3! = 72 Anordnungen. (2 Punkte) 4. Aus 35 Teilnehmern einer Tombola sollen sieben Gewinner ausgewählt werden. Auf wieviele Arten ist dies möglich? Aus 35 Teilnehmern werden sieben ohne Zurücklegen und ohne Reihenfolge ausgewählt. Wir nutzen den Binomialkoeffizienten und erhalten ( ) = = ! verschiedene Arten. (5 Punkte) 5. Von einer Gruppe von 25 Studenten sprechen 20 englisch, 2 französisch und drei Latein. Dabei sprechen englisch und französisch, zwei englisch und Latein, einer französisch und Latein und ein Student spricht alle drei Fremdsprachen. Wie viele Studenten gibt es, 2
3 die keine dieser drei Fremdsprachen sprechen? Nach dem Einschluß- Auschluß- Prinzip berechnen wir N(EF L) = 25 E F L = 25 ( E + F + L E F E L F L + E F L ) = 25 ( ) = = 3 Drei Studenten sprechen keine dieser Fremdsprachen. (0 Punkte) 6. Es sei (a n ) mit 0 n < eine Folge kompleer Zahlen. Gib an, welcher der folgenden Ausdrücke (a) die erzeugende Funktion bzw. Die erzeugende Funktion wird durch den Ausdruck a n n dargestellt. (b) die eponentielle erzeugende Funktion Die eponentiell erzeugende Funktion stellt der Ausdruck k=0 a k k k! dar. der Folge (a n ) darstellt? sin(a n ) a n n k=0 a k k k! e an. (6 Punkte) 7. In einer Geldkasse befinden sich 5 Ein- Euro- Münzen und acht Zwei- Euro- Münzen. es sei a n die Anzahl der Möglichkeiten, einen Betrag von n Euro zusammenzusetzen. (a) Gib die erzeugende Funktion der Folge (a n ) an. Die erzeugende Reihe, um einen Betrag von n Euro aus den Ein- Euro- Münzen zusammenzustellen, beträgt A() = Für die Zwei- Euro- Münzen ergibt sich B() = Damit gilt für die erzeugende Reihe für eine Zusammenstellung aus allen vorhandenen Münzen C() = A()B() = ( ) ( ) =
4 (b) Auf wieviele Weisen kann ein Betrag von sieben Euro zusammengesetzt werden? Anhand des Koeffizienten von 7 sehen wir sofort, daß es vier Möglichkeiten gibt. Dies entspricht den Kombinationen , , und schließlich mit sieben einzelnen Euro- Stücken. (2 Punkte) 8. Eine Folge liegt in folgender Rekursionsdarstellung vor: a 0 =, a = 2 und a n = 2a n a n 2. (a) Gib die erzeugende Funktion der Folge (a n ) und einen geschlossenen Ausdruck für a n an. Zur Untersuchung dieser Folge betrachten wir die erzeugende Reihe f() von a n : Mit den Anfangswerten a 0 = und a = 2 und der Rekursionsformel a n = 2a n a n 2 erhalten wir: f() = a n n = a n n = (2a n a n 2 ) n = a n n a n 2 n = = a n n 2 a n n 2 n= a n n a n 2 n 2 = (f() ) + 2 f() = + 2 f() 2 f(), also Wir wissen, daß f() = = ( ) 2. = n und daß ( ) = ist. Somit muß auch ( ) n = ( ) 2 ( ) = ( ) 2 4
5 gelten. Die Summe läßt sich gliedweise differenzieren und wir erhalten ( ) n = n n = (n + ) n. n= (b) Bestimme a 280. Damit gilt a n = n + und somit a 280 = 28. (7 Punkte) 9. Gib zu jeder der folgenden Partitionen die konjugierte Partition an. Welche der Partitionen ist selbstkonjugiert? (a) 2 = Das Ferrers- Diagramm dieser Partition hat folgende Gestalt: Konjugiert ergibt dies folgendes Diagramm und damit die Partition 2 = (b) 7 = In diesem Fall haben wir folgendes Ferrers- Diagramm: Dies ist symmetrisch, und damit ist diese Partition selbstkonjugiert. (c) 23 = Nun liegt folgendes Ferrers- Diagramm vor: 5
6 Gespiegelt ergibt es also die Partition 23 = (2 Punkte) 0. Wie heißt der Satz vom Ramsey? Es seien p, q, r natürliche Zahlen mit r, p r und q r. Dann eistiert die Ramseyzahl R(p, q, r). Unter der Ramseyzahl R(p, q, r) versteht man die natürliche Zahl mit der folgenden Eigenschaft: Es sei N R(p, q, r) und S eine Menge mit S = N. Die Menge aller r- elementigen Teilmengen von S werde in zwei Klassen α und β geteilt. Dann gibt es eine monochromatische Teilmenge S α von der Farbe α mit S α = p oder eine monochromatische Teilmenge S β von der Farbe β mit S β = q. Man sagt: S hat die Ramseyeigenschaft. Es sei N < R(p, q, r). Dann gibt es eine Menge S mit S = N und eine Einteilung der Menge der r- elementigen Teilmengen von S in Klassen α und β, so daß es weder eine monochromatische p- elementige Teilmenge von S von der Farbe α, noch eine monochromatische q- elementige Teilmenge von der Farbe β gibt. (2 Punkte) Viel Erfolg!
Counting-Übungen (SS4) Felix Rohrer. Grundlagen des Zählens. 1. KR, Abschnitt 5.1, Aufgabe 7: I. KR, Abschnitt 5.1, Aufgabe 15:
 Counting-Übungen (SS4) Felix Rohrer Grundlagen des Zählens 1. KR, Abschnitt 5.1, Aufgabe 7:? Es gibt 17'576 Monogramme 17576 (1.1) I. KR, Abschnitt 5.1, Aufgabe 15: Wörter mit 1 Zeichen + Wörter mit 2
Counting-Übungen (SS4) Felix Rohrer Grundlagen des Zählens 1. KR, Abschnitt 5.1, Aufgabe 7:? Es gibt 17'576 Monogramme 17576 (1.1) I. KR, Abschnitt 5.1, Aufgabe 15: Wörter mit 1 Zeichen + Wörter mit 2
Skript zur Vorlesung. Kombinatorik. Wintersemester 2009/10. Prof. Dr. Helmut Maier Dipl.-Math. Hans- Peter Reck
 Skript zur Vorlesung Kombinatorik Wintersemester 2009/10 Prof. Dr. Helmut Maier Dipl.-Math. Hans- Peter Reck Institut für Zahlentheorie und Wahrscheinlichkeitstheorie Universität Ulm Inhaltsverzeichnis
Skript zur Vorlesung Kombinatorik Wintersemester 2009/10 Prof. Dr. Helmut Maier Dipl.-Math. Hans- Peter Reck Institut für Zahlentheorie und Wahrscheinlichkeitstheorie Universität Ulm Inhaltsverzeichnis
Kombinatorik. Dr. Lucia Draque Penso. Universität Ulm. Dr. Lucia Draque Penso (Universität Ulm) Kombinatorik 1 / 18
 Kombinatorik Dr. Lucia Draque Penso Universität Ulm Dr. Lucia Draque Penso (Universität Ulm) Kombinatorik 1 / 18 Elfte Vorlesung Dr. Lucia Draque Penso (Universität Ulm) Kombinatorik / 18 Formale Potenzreihe
Kombinatorik Dr. Lucia Draque Penso Universität Ulm Dr. Lucia Draque Penso (Universität Ulm) Kombinatorik 1 / 18 Elfte Vorlesung Dr. Lucia Draque Penso (Universität Ulm) Kombinatorik / 18 Formale Potenzreihe
Musterlösung zur Probeklausur zur Angewandten Diskreten Mathematik
 UNIVERSITÄT ULM Institut für Zahlentheorie und Wahrscheinlichkeitstheorie Musterlösung zur Probeklausur zur Angewandten Diskreten Mathematik Prof. Dr. Helmut Maier, Hans- Peter Reck Gesamtpunktzahl: 100
UNIVERSITÄT ULM Institut für Zahlentheorie und Wahrscheinlichkeitstheorie Musterlösung zur Probeklausur zur Angewandten Diskreten Mathematik Prof. Dr. Helmut Maier, Hans- Peter Reck Gesamtpunktzahl: 100
2 Kombinatorik. 56 W.Kössler, Humboldt-Universität zu Berlin
 2 Kombinatorik Aufgabenstellung: Anzahl der verschiedenen Zusammenstellungen von Objekten. Je nach Art der zusätzlichen Forderungen, ist zu unterscheiden, welche Zusammenstellungen als gleich, und welche
2 Kombinatorik Aufgabenstellung: Anzahl der verschiedenen Zusammenstellungen von Objekten. Je nach Art der zusätzlichen Forderungen, ist zu unterscheiden, welche Zusammenstellungen als gleich, und welche
Universität Basel Wirtschaftswissenschaftliches Zentrum. Kombinatorik. Dr. Thomas Zehrt. Inhalt: 1. Endliche Mengen 2. Einfache Urnenexperimente
 Universität Basel Wirtschaftswissenschaftliches Zentrum Kombinatorik Dr. Thomas Zehrt Inhalt: 1. Endliche Mengen 2. Einfache Urnenexperimente 2 Teil 1 Endliche Mengen Eine endliche Menge M ist eine Menge,
Universität Basel Wirtschaftswissenschaftliches Zentrum Kombinatorik Dr. Thomas Zehrt Inhalt: 1. Endliche Mengen 2. Einfache Urnenexperimente 2 Teil 1 Endliche Mengen Eine endliche Menge M ist eine Menge,
Kombinatorik. Jörn Loviscach. Versionsstand: 31. Oktober 2009, 17:22. 1 Begriff Kombinatorik; Zahl aller Teilmengen
 Kombinatorik Jörn Loviscach Versionsstand: 31. Oktober 2009, 17:22 1 Begriff Kombinatorik; Zahl aller Teilmengen Die Kombinatorik ein recht kleines Gebiet der Mathematik befasst sich mit dem Abzählen von
Kombinatorik Jörn Loviscach Versionsstand: 31. Oktober 2009, 17:22 1 Begriff Kombinatorik; Zahl aller Teilmengen Die Kombinatorik ein recht kleines Gebiet der Mathematik befasst sich mit dem Abzählen von
Bei der Berechnung von Laplace-Wahrscheinlichkeiten muss man die Mächtigkeit von Ergebnisräumen und Ereignissen bestimmen.
 VI. Kombinatorik ================================================================== 6.1 Einführung --------------------------------------------------------------------------------------------------------------
VI. Kombinatorik ================================================================== 6.1 Einführung --------------------------------------------------------------------------------------------------------------
SS 2016 Torsten Schreiber
 SS 01 Torsten Schreiber 15 Ein lineares Gleichungssystem besteht immer aus einer Anzahl an Variablen und Gleichungen. Die Zahlen vor den Variablen werden in der sogenannten zusammen gefasst und die Zahlen
SS 01 Torsten Schreiber 15 Ein lineares Gleichungssystem besteht immer aus einer Anzahl an Variablen und Gleichungen. Die Zahlen vor den Variablen werden in der sogenannten zusammen gefasst und die Zahlen
Kombinatorik ================================================================== bzw. + B. Dann gibt es 8 9 = 72 verschiedene Auswahlmöglichkeiten.
 Kombinatorik ================================================================== Produktregel (Zählprinzip) : A B = A B Additionsregel (Regel vom Ein- und Ausschluß) : bzw. A = A A B = A + B A B Beispiele
Kombinatorik ================================================================== Produktregel (Zählprinzip) : A B = A B Additionsregel (Regel vom Ein- und Ausschluß) : bzw. A = A A B = A + B A B Beispiele
Kombinatorik. Je nachdem, ob diese Randbedingungen erfüllt sein müssen oder nicht, lassen sich 6 Grundaufgaben unterscheiden: Wiederholung
 Kombinatorik In der Kombinatorik beschäftigt man sich damit die verschiedenen Möglichkeiten der Auswahl und Anordnung von Elementen aus endlichen Mengen zu untersuchen und insbesondere die Anzahl dieser
Kombinatorik In der Kombinatorik beschäftigt man sich damit die verschiedenen Möglichkeiten der Auswahl und Anordnung von Elementen aus endlichen Mengen zu untersuchen und insbesondere die Anzahl dieser
Vorlesung. Prof. Janis Voigtländer Übungsleitung: Dennis Nolte. Mathematische Strukturen Sommersemester 2017
 Vorlesung Mathematische Strukturen Sommersemester 017 Prof. Janis Voigtländer Übungsleitung: Dennis Nolte Kombinatorik: Einführung Es folgt eine Einführung in die abzählende Kombinatorik. Dabei geht es
Vorlesung Mathematische Strukturen Sommersemester 017 Prof. Janis Voigtländer Übungsleitung: Dennis Nolte Kombinatorik: Einführung Es folgt eine Einführung in die abzählende Kombinatorik. Dabei geht es
Vorkurs Mathematik. Christoph Hindermann. Mengenlehre und Kombinatorik
 Kapitel 1 Christoph Hindermann Vorkurs Mathematik 1 1.1.1 Begriff der Menge Eine Menge ist eine Zusammenfassung bestimmer, wohl unterscheidbarer Objekte unserer Anschauung oder unseres Denkens. Die Objekte
Kapitel 1 Christoph Hindermann Vorkurs Mathematik 1 1.1.1 Begriff der Menge Eine Menge ist eine Zusammenfassung bestimmer, wohl unterscheidbarer Objekte unserer Anschauung oder unseres Denkens. Die Objekte
Sachrechnen/Größen WS 14/15-
 Kapitel Daten & Wahrscheinlichkeit 3.1 Kombinatorische Grundlagen 3.2 Kombinatorik & Wahrscheinlichkeit in der Grundschule 3.3 Daten Darstellen 3.1 Kombinatorische Grundlagen Verschiedene Bereiche der
Kapitel Daten & Wahrscheinlichkeit 3.1 Kombinatorische Grundlagen 3.2 Kombinatorik & Wahrscheinlichkeit in der Grundschule 3.3 Daten Darstellen 3.1 Kombinatorische Grundlagen Verschiedene Bereiche der
Wahrscheinlichkeitstheorie Aufgaben mit Lösungen. Jörg Gayler, Lubov Vassilevskaya
 Wahrscheinlichkeitstheorie Aufgaben mit Lösungen Jörg Gayler, Lubov Vassilevskaya i Inhaltsverzeichnis Kombinatorisches Rechnen. Formelsammlung.................................... 2. Fakultät : Definition,
Wahrscheinlichkeitstheorie Aufgaben mit Lösungen Jörg Gayler, Lubov Vassilevskaya i Inhaltsverzeichnis Kombinatorisches Rechnen. Formelsammlung.................................... 2. Fakultät : Definition,
4. Kombinatorik *) In der Kombinatorik werden drei wichtige Symbole benötigt: o n! o (n) k o
 *) Die Berechnung der Wahrscheinlichkeit im Laplace-Experiment wirkt zunächst einfach. Man muss einfach die Anzahl der günstigen Fälle durch die Anzahl der möglichen Fälle teilen. Das Feststellen dieser
*) Die Berechnung der Wahrscheinlichkeit im Laplace-Experiment wirkt zunächst einfach. Man muss einfach die Anzahl der günstigen Fälle durch die Anzahl der möglichen Fälle teilen. Das Feststellen dieser
Kombinatorik. Diskrete Strukturen. Sommersemester Uta Priss ZeLL, Ostfalia. Hausaufgaben Kombinatorik Beispielaufgaben
 Kombinatorik Diskrete Strukturen Uta Priss ZeLL, Ostfalia Sommersemester 2016 Diskrete Strukturen Kombinatorik Slide 1/13 Agenda Hausaufgaben Kombinatorik Beispielaufgaben Diskrete Strukturen Kombinatorik
Kombinatorik Diskrete Strukturen Uta Priss ZeLL, Ostfalia Sommersemester 2016 Diskrete Strukturen Kombinatorik Slide 1/13 Agenda Hausaufgaben Kombinatorik Beispielaufgaben Diskrete Strukturen Kombinatorik
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Statistik I für Humanund Sozialwissenschaften
 Statistik I für Humanund Sozialwissenschaften 3. Übung Lösungsvorschlag Gruppenübung G 8 a) Ein Professor möchte herausfinden, welche 5 seiner insgesamt 8 Mitarbeiter zusammen das kreativste Team darstellen.
Statistik I für Humanund Sozialwissenschaften 3. Übung Lösungsvorschlag Gruppenübung G 8 a) Ein Professor möchte herausfinden, welche 5 seiner insgesamt 8 Mitarbeiter zusammen das kreativste Team darstellen.
Permutation = Anordnung aller Elemente einer Menge, Kombination = Auswahl von einigen aus vielen Elementen, Variation = Auswahl und Anordnung.
 Kombinatorik Was ist Kombinatorik? Die 92 natürlichen chemischen Elemente sind die mathematischen Elemente der Menge chemisches Periodensystem. Ebenso sind die zehn Ziffern 0 9 eine Menge, jede Ziffer
Kombinatorik Was ist Kombinatorik? Die 92 natürlichen chemischen Elemente sind die mathematischen Elemente der Menge chemisches Periodensystem. Ebenso sind die zehn Ziffern 0 9 eine Menge, jede Ziffer
Kombinatorik. 1. Beispiel: Wie viele fünfstellige Zahlen lassen sich aus den fünf Ziffern in M = {1;2;3;4;5} erstellen?
 1 Kombinatorik Aus einer Grundgesamtheit mit n Elementen wird eine Stichprobe k Elementen entnommen. Dabei kann die Stichprobe geordnet oder ungeordnet sein. "Geordnet" bedeutet, dass die Reihenfolge der
1 Kombinatorik Aus einer Grundgesamtheit mit n Elementen wird eine Stichprobe k Elementen entnommen. Dabei kann die Stichprobe geordnet oder ungeordnet sein. "Geordnet" bedeutet, dass die Reihenfolge der
Kombinatorik BEISPIEL: WIE VIELE MÖGLICHKEITEN GIBT ES, EINE DREISTELLIGE ZAHL MIT DEN ZIFFERN 3
 Kombinatorik Die Kombinatorik beschäftigt sich damit, verschiedene mögliche Auswahlen und Anordnungen von Elementen aus endlichen Mengen zu untersuchen. Insbesondere wird die Anzahl dieser berechnet. BEISPIEL:
Kombinatorik Die Kombinatorik beschäftigt sich damit, verschiedene mögliche Auswahlen und Anordnungen von Elementen aus endlichen Mengen zu untersuchen. Insbesondere wird die Anzahl dieser berechnet. BEISPIEL:
Zentralübung zur Vorlesung Diskrete Strukturen
 WS 2010/11 Zentralübung zur Vorlesung Diskrete Strukturen Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2010ws/ds/uebung/ 22. Dezember 2010 ZÜ DS ZÜ IX Übersicht: 1.
WS 2010/11 Zentralübung zur Vorlesung Diskrete Strukturen Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2010ws/ds/uebung/ 22. Dezember 2010 ZÜ DS ZÜ IX Übersicht: 1.
Mathematische Strukturen Sommersemester Vorlesung. Kombinatorik: Einführung. Ziehen aus Urnen
 Vorlesung Mathematische Strukturen Sommersemester 07 Prof. Janis Voigtländer Übungsleitung: Dennis Nolte : Einführung Es folgt eine Einführung in die abzählende. Dabei geht es darum, die Elemente einer
Vorlesung Mathematische Strukturen Sommersemester 07 Prof. Janis Voigtländer Übungsleitung: Dennis Nolte : Einführung Es folgt eine Einführung in die abzählende. Dabei geht es darum, die Elemente einer
AUFGABEN ZUR KOMBINATORIK (1)
 --- --- AUFGABEN ZUR KOMBINATORIK (). Zum Würfeln wird ein Tetraeder benutzt, das auf seinen vier Seiten mit,, und beschriftet ist. Als Ergebnis zählt diejenige Augenzahl, die auf der Grundfläche steht.
--- --- AUFGABEN ZUR KOMBINATORIK (). Zum Würfeln wird ein Tetraeder benutzt, das auf seinen vier Seiten mit,, und beschriftet ist. Als Ergebnis zählt diejenige Augenzahl, die auf der Grundfläche steht.
WS 2016/17 Diskrete Strukturen Kapitel 3: Kombinatorik (1)
 WS 2016/17 Diskrete Strukturen Kapitel 3: Kombinatorik (1) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 3: Kombinatorik (1) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Wahrscheinlichkeitsrechnung
 Abiturvorbereitung Wahrscheinlichkeitsrechnung S. 1 von 9 Wahrscheinlichkeitsrechnung Kombinatorik Formeln für Wahrscheinlichkeiten Bedingte Wahrscheinlichkeiten Zusammenfassung wichtiger Begriffe Übungsaufgaben
Abiturvorbereitung Wahrscheinlichkeitsrechnung S. 1 von 9 Wahrscheinlichkeitsrechnung Kombinatorik Formeln für Wahrscheinlichkeiten Bedingte Wahrscheinlichkeiten Zusammenfassung wichtiger Begriffe Übungsaufgaben
Elemente der Stochastik (SoSe 2016) 5. Übungsblatt
 Dr. M. Weimar 02.05.2016 Elemente der Stochasti (SoSe 2016) 5. Übungsblatt Aufgabe 1 (4 Punte) Beweisen sie, dass die Potenzmenge P(A) einer beliebigen endlichen Menge A genau P(A) 2 A Elemente enthält!
Dr. M. Weimar 02.05.2016 Elemente der Stochasti (SoSe 2016) 5. Übungsblatt Aufgabe 1 (4 Punte) Beweisen sie, dass die Potenzmenge P(A) einer beliebigen endlichen Menge A genau P(A) 2 A Elemente enthält!
Mathematik für Informatiker I, WS 2007/08 Musterlösung zur freiwilligen Zwischenklausur vom 4. Dezember 2007
 1 Mathematik für Informatiker I, WS 007/08 Musterlösung zur freiwilligen Zwischenklausur vom 4. Dezember 007 1. Ist die Permutation f ( 1 3 4 5 6 7 8 ) 9 7 3 1 6 5 4 9 8 gerade oder ungerade? Wie lautet
1 Mathematik für Informatiker I, WS 007/08 Musterlösung zur freiwilligen Zwischenklausur vom 4. Dezember 007 1. Ist die Permutation f ( 1 3 4 5 6 7 8 ) 9 7 3 1 6 5 4 9 8 gerade oder ungerade? Wie lautet
Kombinatorik: Einführung. Vorlesung Mathematische Strukturen. Sommersemester Ziehen aus Urnen. Ziehen aus Urnen
 Kombinatorik: Einführung Vorlesung Mathematische Strukturen Sommersemester 04 Prof. Barbara König Übungsleitung: Henning Kerstan Es folgt eine Einführung in die Kombinatorik. Dabei geht es darum, die Elemente
Kombinatorik: Einführung Vorlesung Mathematische Strukturen Sommersemester 04 Prof. Barbara König Übungsleitung: Henning Kerstan Es folgt eine Einführung in die Kombinatorik. Dabei geht es darum, die Elemente
W.12 Kombinatorik 1. vermischte Aufgaben zu Vertauschungsmöglichkeiten ( )
 1 Die Kombinatorik ist die Lehre von den Vertauschungsmöglichkeiten. Da man eigentlich fast jede Wahrscheinlichkeit mit irgendwelchen Vertauschungsmöglichkeiten multiplizieren muss, ist es naheliegend,
1 Die Kombinatorik ist die Lehre von den Vertauschungsmöglichkeiten. Da man eigentlich fast jede Wahrscheinlichkeit mit irgendwelchen Vertauschungsmöglichkeiten multiplizieren muss, ist es naheliegend,
Das Urnenmodell. Anatoli Maier; Gregor Steinschulte; Mussie Mengstab; Robert Grendysa; Stephane Kom Djike / / / /
 Das Urnenmodell Hausarbeit Mathe III (Prof. Kästner, Friedberg) Anatoli Maier; Gregor Steinschulte; Mussie Mengstab; Robert Grendysa; Stephane Kom Djike 876522 / 900265 / 885568 / 875921 / 932424 Wintersemester
Das Urnenmodell Hausarbeit Mathe III (Prof. Kästner, Friedberg) Anatoli Maier; Gregor Steinschulte; Mussie Mengstab; Robert Grendysa; Stephane Kom Djike 876522 / 900265 / 885568 / 875921 / 932424 Wintersemester
Unter dem Symbol n! (gelesen n Fakultät) versteht man das Produkt der natürlichen Zahlen von 1 bis n.
 Die Fakultät Definition: Unter dem Symbol n! (gelesen n Fakultät) versteht man das Produkt der natürlichen Zahlen von 1 bis n. n! = 1 2 3... (n 2) (n 1) n Zusätzlich wird definiert 0! = 1 Wie aus der Definition
Die Fakultät Definition: Unter dem Symbol n! (gelesen n Fakultät) versteht man das Produkt der natürlichen Zahlen von 1 bis n. n! = 1 2 3... (n 2) (n 1) n Zusätzlich wird definiert 0! = 1 Wie aus der Definition
Elemente der Stochastik (SoSe 2016) 4. Übungsblatt
 Dr. M. Weimar 26.04.2016 Elemente der Stochastik (SoSe 2016) 4. Übungsblatt Aufgabe 1 (1+1+2=4 Punkte) Eine Autofahrerin verursacht einen Unfall und begeht Fahrerflucht. Ein Zeuge will sich die Nummer
Dr. M. Weimar 26.04.2016 Elemente der Stochastik (SoSe 2016) 4. Übungsblatt Aufgabe 1 (1+1+2=4 Punkte) Eine Autofahrerin verursacht einen Unfall und begeht Fahrerflucht. Ein Zeuge will sich die Nummer
Abitur 2011 G9 Abitur Mathematik GK Stochastik IV
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2011 G9 Abitur Mathematik GK Stochastik IV In einer bayerischen Großstadt findet das jährliche Volksfest statt. Die Attraktion ist die Achterbahn mit
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2011 G9 Abitur Mathematik GK Stochastik IV In einer bayerischen Großstadt findet das jährliche Volksfest statt. Die Attraktion ist die Achterbahn mit
Technische Universität München. Kombinatorik. Christian Fuchs
 Kombinatorik Christian Fuchs 1.Definition Kombinatorik 2.Grundlegende Zählmethoden 3.Binomialkoeffizienten 4.Permutationen 5.Stirling-Zahlen 6.Catalan-Zahlen 7.Zahlpartitionen 8.Aufgaben 9.Literatur Technische
Kombinatorik Christian Fuchs 1.Definition Kombinatorik 2.Grundlegende Zählmethoden 3.Binomialkoeffizienten 4.Permutationen 5.Stirling-Zahlen 6.Catalan-Zahlen 7.Zahlpartitionen 8.Aufgaben 9.Literatur Technische
Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Mayr)
 WS 2011/12 Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Mayr) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2011ws/ds/uebung/ 14. Dezember 2011 ZÜ DS ZÜ IX
WS 2011/12 Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Mayr) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2011ws/ds/uebung/ 14. Dezember 2011 ZÜ DS ZÜ IX
Kombinatorik. 1. Permutationen 2. Variationen 3. Kombinationen. ad 1) Permutationen. a) Permutationen von n verschiedenen Elementen
 Kombinatorik Zur Berechnung der Wahrscheinlichkeit eines zusammengesetzten Ereignisses ist oft erforderlich, zwei verschiedene Anzahlen zu berechnen: die Anzahl aller Elementarereignisse und die Anzahl
Kombinatorik Zur Berechnung der Wahrscheinlichkeit eines zusammengesetzten Ereignisses ist oft erforderlich, zwei verschiedene Anzahlen zu berechnen: die Anzahl aller Elementarereignisse und die Anzahl
Kombinatorik: Einführung. Vorlesung Mathematische Strukturen. Sommersemester Ziehen aus Urnen. Ziehen aus Urnen
 Kombinatorik: Einführung Vorlesung Mathematische Strukturen Sommersemester 05 Prof. Barbara König Übungsleitung: Dennis Nolte Es folgt eine Einführung in die Kombinatorik. Dabei geht es darum, die Elemente
Kombinatorik: Einführung Vorlesung Mathematische Strukturen Sommersemester 05 Prof. Barbara König Übungsleitung: Dennis Nolte Es folgt eine Einführung in die Kombinatorik. Dabei geht es darum, die Elemente
Kombinatorik. smo osm. Thomas Huber, Viviane Kehl. Inhaltsverzeichnis. Aktualisiert: 1. Dezember 2015 vers Divide and Conquer 2
 Schweizer Mathematik-Olympiade smo osm Kombinatorik Thomas Huber, Viviane Kehl Aktualisiert: 1. Dezember 2015 vers. 1.0.0 Inhaltsverzeichnis 1 Divide and Conquer 2 2 Die vier fundamentalen Auswahlprozesse
Schweizer Mathematik-Olympiade smo osm Kombinatorik Thomas Huber, Viviane Kehl Aktualisiert: 1. Dezember 2015 vers. 1.0.0 Inhaltsverzeichnis 1 Divide and Conquer 2 2 Die vier fundamentalen Auswahlprozesse
Blatt 5: Kombinatorik MAE 3. Urnenmodelle
 School of Engineering Winterthur Zürcher Hochschule für Angewandte Wissenschaften Blatt 5: Kombinatorik MAE 3 Urnenmodelle Geben Sie zu jeder der beschriebenen Situationen an, wie viele Elemente (k) ausgewählt
School of Engineering Winterthur Zürcher Hochschule für Angewandte Wissenschaften Blatt 5: Kombinatorik MAE 3 Urnenmodelle Geben Sie zu jeder der beschriebenen Situationen an, wie viele Elemente (k) ausgewählt
WS 2015/16 Diskrete Strukturen Kapitel 3: Kombinatorik (3)
 WS 2015/16 Diskrete Strukturen Kapitel 3: Kombinatorik (3) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
WS 2015/16 Diskrete Strukturen Kapitel 3: Kombinatorik (3) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
Berechnung von Teilmengen
 Berechnung von Teilmengen Satz Anzahl der Teilmengen 2 n = n k=0 k=0 ( ) n k Beweis Korollar aus Binomischem Lehrsatz (1 + 1) n = n ( n k=0 k) 1 k 1 n k. Oder kombinatorisch: Sei M Menge mit M = n. Die
Berechnung von Teilmengen Satz Anzahl der Teilmengen 2 n = n k=0 k=0 ( ) n k Beweis Korollar aus Binomischem Lehrsatz (1 + 1) n = n ( n k=0 k) 1 k 1 n k. Oder kombinatorisch: Sei M Menge mit M = n. Die
Kombinatorik - kurz. Ronald Balestra CH Zürich
 Kombinatorik - kurz Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch 14. Mai 2012 Inhaltsverzeichnis 1 Um was geht s? 1 1.1 Allgemeines Zählprinzip....................... 2 1.2 Permutationen............................
Kombinatorik - kurz Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch 14. Mai 2012 Inhaltsverzeichnis 1 Um was geht s? 1 1.1 Allgemeines Zählprinzip....................... 2 1.2 Permutationen............................
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
1 Begriff Kombinatorik; Zahl aller Teilmengen
 6 Kombinatorik Jörn Loviscach Versionsstand: 2. Dezember 2011, 16:25 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.j3l7h.de/videos.html This work
6 Kombinatorik Jörn Loviscach Versionsstand: 2. Dezember 2011, 16:25 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.j3l7h.de/videos.html This work
Zufallsauswahlen aus endlichen Grundgesamtheiten
 Zufallsauswahlen aus endlichen Grundgesamtheiten In der statistischen Praxis kommt dem Ziehen von Stichproben größte Bedeutung zu, da in vielen Fällen die Untersuchung der Grundgesamtheit zu teuer oder
Zufallsauswahlen aus endlichen Grundgesamtheiten In der statistischen Praxis kommt dem Ziehen von Stichproben größte Bedeutung zu, da in vielen Fällen die Untersuchung der Grundgesamtheit zu teuer oder
Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge zu Übungsblatt 1
 TUM, Zentrum Mathematik Lehrstuhl für Mathematische Physik WS 2013/ Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weidner Tutoraufgaben: Einführung in die Wahrscheinlichkeitstheorie svorschläge zu
TUM, Zentrum Mathematik Lehrstuhl für Mathematische Physik WS 2013/ Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weidner Tutoraufgaben: Einführung in die Wahrscheinlichkeitstheorie svorschläge zu
Kombinatorik. Worum geht es in diesem Modul?
 Kombinatorik Worum geht es in diesem Modul? Permutationen Binomialkoeffizienten Variation und Kombination Stichproben ohne Zurücklegen mit Berücksichtigung der Reihenfolge Stichproben mit Zurücklegen mit
Kombinatorik Worum geht es in diesem Modul? Permutationen Binomialkoeffizienten Variation und Kombination Stichproben ohne Zurücklegen mit Berücksichtigung der Reihenfolge Stichproben mit Zurücklegen mit
Aufgabe 1. Übung Wahrscheinlichkeitsrechnung Markus Kessler Seite 1 von 8. Die Ereignisse A, B und C erfüllen die Bedingungen
 Ü b u n g 1 Aufgabe 1 Die Ereignisse A, B und C erfüllen die Bedingungen P(A) = 0. 7, P(B) = 0. 6, P(C) = 0. 5 P(A B) = 0. 4, P(A C) = 0. 3, P(B C) = 0. 2, P(A B C) = 0. 1 Bestimmen Sie P(A B), P(A C),
Ü b u n g 1 Aufgabe 1 Die Ereignisse A, B und C erfüllen die Bedingungen P(A) = 0. 7, P(B) = 0. 6, P(C) = 0. 5 P(A B) = 0. 4, P(A C) = 0. 3, P(B C) = 0. 2, P(A B C) = 0. 1 Bestimmen Sie P(A B), P(A C),
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16
 Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16 12. November 2015 Satz 3.16 (Binomischer Lehrsatz) Seien a, b R. Dann gilt für alle
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16 12. November 2015 Satz 3.16 (Binomischer Lehrsatz) Seien a, b R. Dann gilt für alle
Inhaltsverzeichnis (Ausschnitt)
 6 Diskrete Wahrscheinlichkeitsräume Inhaltsverzeichnis (Ausschnitt) 6 Diskrete Wahrscheinlichkeitsräume Laplacesche Wahrscheinlichkeitsräume Kombinatorik Allgemeine diskrete Wahrscheinlichkeitsräume Deskriptive
6 Diskrete Wahrscheinlichkeitsräume Inhaltsverzeichnis (Ausschnitt) 6 Diskrete Wahrscheinlichkeitsräume Laplacesche Wahrscheinlichkeitsräume Kombinatorik Allgemeine diskrete Wahrscheinlichkeitsräume Deskriptive
Der Binomische Lehrsatz, die Binomialkoeffizienten und das PASCALsche Dreieck
 1 Der Binomische Lehrsatz, die Binomialkoeffizienten und das PASCALsche Dreieck Wir kennen die beiden binomischen Formeln: Sie sind ein Sonderfall des Binomischen Lehrsatzes: Wir sehen, dass die Potenzen
1 Der Binomische Lehrsatz, die Binomialkoeffizienten und das PASCALsche Dreieck Wir kennen die beiden binomischen Formeln: Sie sind ein Sonderfall des Binomischen Lehrsatzes: Wir sehen, dass die Potenzen
Grundlagen der Mathematik I Lösungsvorschlag zum 13. Übungsblatt
 Mathematisches Institut der Universität München Wintersemester 2013/14 Daniel Rost Lukas-Fabian Moser Grundlagen der Mathematik I Lösungsvorschlag zum 13. Übungsblatt Aufgabe 1. injektive. Es wird sich
Mathematisches Institut der Universität München Wintersemester 2013/14 Daniel Rost Lukas-Fabian Moser Grundlagen der Mathematik I Lösungsvorschlag zum 13. Übungsblatt Aufgabe 1. injektive. Es wird sich
Stochastik (Laplace-Formel)
 Stochastik (Laplace-Formel) Übungen Spielwürfel oder Münzen werden ideal (oder fair) genannt, wenn jedes Einzelereignis mit gleicher Wahrscheinlichkeit erwartet werden kann. 1. Ein idealer Spielwürfel
Stochastik (Laplace-Formel) Übungen Spielwürfel oder Münzen werden ideal (oder fair) genannt, wenn jedes Einzelereignis mit gleicher Wahrscheinlichkeit erwartet werden kann. 1. Ein idealer Spielwürfel
II Wahrscheinlichkeitsrechnung
 251 1 Hilfsmittel aus der Kombinatorik Wir beschäftigen uns in diesem Abschnitt mit den Permutationen, Kombinationen und Variationen. Diese aus der Kombinatorik stammenden Abzählmethoden sind ein wichtiges
251 1 Hilfsmittel aus der Kombinatorik Wir beschäftigen uns in diesem Abschnitt mit den Permutationen, Kombinationen und Variationen. Diese aus der Kombinatorik stammenden Abzählmethoden sind ein wichtiges
2. Hausübung Diskrete Mathematik SS 2003
 2. Hausübung Diskrete Mathematik SS 2003 Lösungsvorschläge 6. Zunächst bestimmen wir die Anzahl der verschiedenen möglichen Ergebnisse für die Differenzen a i a j. Wegen 1 a 1 < < a 21 100 gibt es 99 Möglichkeiten
2. Hausübung Diskrete Mathematik SS 2003 Lösungsvorschläge 6. Zunächst bestimmen wir die Anzahl der verschiedenen möglichen Ergebnisse für die Differenzen a i a j. Wegen 1 a 1 < < a 21 100 gibt es 99 Möglichkeiten
Grundbegrie der Wahrscheinlichkeitsrechnung
 Die Benutzung dieser Materialien ist auf Herbst 2017 beschränkt. Diese Hilfsmaterialien sind nur für unseren Studenten gemeint, dürfen also nicht weiterverteilt werden. Grundbegrie der Wahrscheinlichkeitsrechnung
Die Benutzung dieser Materialien ist auf Herbst 2017 beschränkt. Diese Hilfsmaterialien sind nur für unseren Studenten gemeint, dürfen also nicht weiterverteilt werden. Grundbegrie der Wahrscheinlichkeitsrechnung
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik. Klausurvorbereitung
 Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl.-Math. S. König, Dipl.-Math. A. Würfl, Klausurvorbereitung Die Klausur zum Propädeutikum Diskrete
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl.-Math. S. König, Dipl.-Math. A. Würfl, Klausurvorbereitung Die Klausur zum Propädeutikum Diskrete
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik - WS 11/12. Klausurvorbereitung
 Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik - WS 11/12 Prof. Dr. A. Taraz, Dr. O. Cooley, Klausurvorbereitung Die Klausur zum Propädeutikum Diskrete Mathematik findet
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik - WS 11/12 Prof. Dr. A. Taraz, Dr. O. Cooley, Klausurvorbereitung Die Klausur zum Propädeutikum Diskrete Mathematik findet
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 12. Dezember 2012 1 Kombinatorik Fakultät Binomialkoeffizienten Urnenmodelle 2 Definition Fakultät Die Zahl n! =
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 12. Dezember 2012 1 Kombinatorik Fakultät Binomialkoeffizienten Urnenmodelle 2 Definition Fakultät Die Zahl n! =
Die Formel für Kombinationen wird verwendet, wenn
 1. Übung: Kombinatorik Aufgabe 1 Die Formel für Kombinationen wird verwendet, wenn a) Alle n Elemente angeordnet werden sollen. b) Aus n Elementen k Elemente gezogen werden sollen. c) Die Reihenfolge der
1. Übung: Kombinatorik Aufgabe 1 Die Formel für Kombinationen wird verwendet, wenn a) Alle n Elemente angeordnet werden sollen. b) Aus n Elementen k Elemente gezogen werden sollen. c) Die Reihenfolge der
Vollständige Induktion. Analysis I. Guofang Wang. Universität Freiburg
 Universität Freiburg 26.10.2011 Vollständige Induktion Wir unterbrechen jetzt die Diskussion der Axiome der reellen Zahlen, um das Beweisverfahren der vollständigen Induktion kennenzulernen. Wir setzen
Universität Freiburg 26.10.2011 Vollständige Induktion Wir unterbrechen jetzt die Diskussion der Axiome der reellen Zahlen, um das Beweisverfahren der vollständigen Induktion kennenzulernen. Wir setzen
Kombinatorik. Hallo Welt Philip Kranz. 12. Juli Philip Kranz () Kombinatorik 12. Juli / 47
 Kombinatorik Hallo Welt 2011 Philip Kranz 12. Juli 2011 Philip Kranz () Kombinatorik 12. Juli 2011 1 / 47 Inhalt 1 Einführung 2 Grundlagen Permutationen Variationen Kombinationen Binomialkoeffizient /
Kombinatorik Hallo Welt 2011 Philip Kranz 12. Juli 2011 Philip Kranz () Kombinatorik 12. Juli 2011 1 / 47 Inhalt 1 Einführung 2 Grundlagen Permutationen Variationen Kombinationen Binomialkoeffizient /
Grundlagen der Mathematik
 Universität Hamburg Winter 2016/17 Fachbereich Mathematik Janko Latschev Lösungsskizzen 8 Grundlagen der Mathematik Präsenzaufgaben (P13) Primfaktorzerlegungen Die Primfaktorzerlegungen lauten: a) 66 =
Universität Hamburg Winter 2016/17 Fachbereich Mathematik Janko Latschev Lösungsskizzen 8 Grundlagen der Mathematik Präsenzaufgaben (P13) Primfaktorzerlegungen Die Primfaktorzerlegungen lauten: a) 66 =
Relationen. Ein wichtiger Spezialfall ist der, dass die Mengen identisch sind:
 Relationen Es seien zwischen und und Mengen. Eine (binäre) Relation ist eine Teilmenge von. Ein wichtiger Spezialfall ist der, dass die Mengen identisch sind: und Eine binäre Relation auf einer Menge ist
Relationen Es seien zwischen und und Mengen. Eine (binäre) Relation ist eine Teilmenge von. Ein wichtiger Spezialfall ist der, dass die Mengen identisch sind: und Eine binäre Relation auf einer Menge ist
Binomialkoeffizient. Gymnasium Immensee Stochastik, 5. Klassen. Bettina Bieri
 Binomialkoeffizient Gymnasium Immensee Stochastik, 5. Klassen Bettina Bieri 7. Februar 7 Inhaltsverzeichnis Nötiges Vorwissen: Fakultäten. Definition: Fakultät......................... spezielle Fakuläten.........................3
Binomialkoeffizient Gymnasium Immensee Stochastik, 5. Klassen Bettina Bieri 7. Februar 7 Inhaltsverzeichnis Nötiges Vorwissen: Fakultäten. Definition: Fakultät......................... spezielle Fakuläten.........................3
Stochastik. Grundwissenskatalog G8-Lehrplanstandard
 GRUNDWISSEN MATHEMATIK Stochastik Grundwissenskatalog G8-Lehrplanstandard Basierend auf den Grundwissenskatalogen des Rhöngymnasiums Bad Neustadt und des Kurt-Huber-Gymnasiums Gräfelfing J O H A N N E
GRUNDWISSEN MATHEMATIK Stochastik Grundwissenskatalog G8-Lehrplanstandard Basierend auf den Grundwissenskatalogen des Rhöngymnasiums Bad Neustadt und des Kurt-Huber-Gymnasiums Gräfelfing J O H A N N E
WS 2014/15 Diskrete Strukturen Kapitel 3: Kombinatorik (2)
 WS 2014/15 Diskrete Strukturen Kapitel 3: Kombinatorik (2) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_14
WS 2014/15 Diskrete Strukturen Kapitel 3: Kombinatorik (2) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_14
Wahrscheinlichkeitsrechnung für die Mittelstufe
 Wahrscheinlichkeitsrechnung für die Mittelstufe Wir beginnen mit einem Beispiel, dem Münzwurf. Es wird eine faire Münze geworfen mit den Seiten K (für Kopf) und Z (für Zahl). Fair heißt, dass jede Seite
Wahrscheinlichkeitsrechnung für die Mittelstufe Wir beginnen mit einem Beispiel, dem Münzwurf. Es wird eine faire Münze geworfen mit den Seiten K (für Kopf) und Z (für Zahl). Fair heißt, dass jede Seite
KOMPETENZHEFT ZUR KOMBINATORIK
 KOMPETENZHEFT ZUR KOMBINATORIK. Aufgabenstellungen Aufgabe.. Beim Schach können zwei Türme einander schlagen, wenn sie in derselben Reihe oder in derselben Spalte stehen. Rechts siehst du eine Möglichkeit,
KOMPETENZHEFT ZUR KOMBINATORIK. Aufgabenstellungen Aufgabe.. Beim Schach können zwei Türme einander schlagen, wenn sie in derselben Reihe oder in derselben Spalte stehen. Rechts siehst du eine Möglichkeit,
Zählprinzip und Baumdiagramm (Aufgaben)
 Gymnasium Pegnitz Grundwissen JS 5 17. Juni 2007 Zählprinzip und Baumdiagramm (Aufgaben) 1.,,Nur einmal zweimal - Ein Würfelspiel für 2 oder mehr Spieler Jeder Spieler würfelt so lange, bis eine Zahl zum
Gymnasium Pegnitz Grundwissen JS 5 17. Juni 2007 Zählprinzip und Baumdiagramm (Aufgaben) 1.,,Nur einmal zweimal - Ein Würfelspiel für 2 oder mehr Spieler Jeder Spieler würfelt so lange, bis eine Zahl zum
Folien der 16. Vorlesungswoche
 Folien der 16. Vorlesungswoche Nachschlag Kombinatorik: Erzeugende Funktionen Kombinatorik ist die Kunst des intelligenten Abzählens endlicher Mengen. Obwohl die behandelten Probleme einfach und elementar
Folien der 16. Vorlesungswoche Nachschlag Kombinatorik: Erzeugende Funktionen Kombinatorik ist die Kunst des intelligenten Abzählens endlicher Mengen. Obwohl die behandelten Probleme einfach und elementar
1 Grundlagen Wahrscheinlichkeitsrechung
 1 Grundlagen Wahrscheinlichkeitsrechung 1.1 Grundbegriffe Alle möglichen Ereignisse eines Zufallsexperiments fassen wir in einer Ereignismenge Ω zusammen. Ereignisse sind Teilmengen von Ω. Umfasst das
1 Grundlagen Wahrscheinlichkeitsrechung 1.1 Grundbegriffe Alle möglichen Ereignisse eines Zufallsexperiments fassen wir in einer Ereignismenge Ω zusammen. Ereignisse sind Teilmengen von Ω. Umfasst das
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 3. November 2010 1 Kombinatorik Fakultät Binomialkoeffizienten Urnenmodelle 2 Definition Tabellen Fakultät, Beispiel
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 3. November 2010 1 Kombinatorik Fakultät Binomialkoeffizienten Urnenmodelle 2 Definition Tabellen Fakultät, Beispiel
Aufgaben zur Kombinatorik
 Aufgaben zur Kombinatorik Aufgabe 34 Kombinatorik: Kombinationen Wie viele verschiedene Zusammenstellungen von genau 5 Buchstaben können aus den 26 Buchstaben des Alphabets gebildet werden, wenn Wiederholungen
Aufgaben zur Kombinatorik Aufgabe 34 Kombinatorik: Kombinationen Wie viele verschiedene Zusammenstellungen von genau 5 Buchstaben können aus den 26 Buchstaben des Alphabets gebildet werden, wenn Wiederholungen
Tutorium: Diskrete Mathematik
 Tutorium: Diskrete Mathematik Vorbereitung der Bonusklausur am 24.11.2016 (Teil 2) 23. November 2016 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler 23. November 2016
Tutorium: Diskrete Mathematik Vorbereitung der Bonusklausur am 24.11.2016 (Teil 2) 23. November 2016 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler 23. November 2016
Relationen. Es seien A und B Mengen. Eine (binäre) Relation zwischen A und B ist eine Teilmenge von A B.
 Mathematik I für Informatiker Relationen auf einer Menge p. 1 Relationen Es seien A und B Mengen. Eine (binäre) Relation zwischen A und B ist eine Teilmenge von A B. Ein wichtiger Spezialfall ist der,
Mathematik I für Informatiker Relationen auf einer Menge p. 1 Relationen Es seien A und B Mengen. Eine (binäre) Relation zwischen A und B ist eine Teilmenge von A B. Ein wichtiger Spezialfall ist der,
Basen von Schnitt und Summe berechnen
 Basen von Schnitt und Summe berechnen 1 / 8 Voraussetzung Es seien U 1, U 2 Untervektorräume von K n. Wir wollen Basen des Schnittes U 1 U 2 und der Summe bestimmen. U 1 + U 2 2 / 8 Bezeichnung Der Einfachheit
Basen von Schnitt und Summe berechnen 1 / 8 Voraussetzung Es seien U 1, U 2 Untervektorräume von K n. Wir wollen Basen des Schnittes U 1 U 2 und der Summe bestimmen. U 1 + U 2 2 / 8 Bezeichnung Der Einfachheit
Aufgabe Summe Note Punkte
 Fachhochschule Südwestfalen - Meschede Prof. Dr. Henrik Schulze Klausur Ingenieurmathematik am 9. März 7 - Musterlösung Name Matr.-Nr. Vorname Unterschrift Aufgabe 4 5 6 7 Summe Note Punkte Die Klausur
Fachhochschule Südwestfalen - Meschede Prof. Dr. Henrik Schulze Klausur Ingenieurmathematik am 9. März 7 - Musterlösung Name Matr.-Nr. Vorname Unterschrift Aufgabe 4 5 6 7 Summe Note Punkte Die Klausur
Surjektive, injektive und bijektive Funktionen.
 Kapitel 1: Aussagen, Mengen, Funktionen Surjektive, injektive und bijektive Funktionen. Definition. Sei f : M N eine Funktion. Dann heißt f surjektiv, falls die Gleichung f(x) = y für jedes y N mindestens
Kapitel 1: Aussagen, Mengen, Funktionen Surjektive, injektive und bijektive Funktionen. Definition. Sei f : M N eine Funktion. Dann heißt f surjektiv, falls die Gleichung f(x) = y für jedes y N mindestens
Kombinatorik kompakt. Stochastik WS 2016/17 1
 Kombinatorik kompakt Stochastik WS 2016/17 1 Übersicht Auswahl/Kombinationen von N aus m Elementen Statistische unterscheidbare ununterscheidbare Physik Objekte (gleiche) Objekte ( ohne m N m+n 1 ) N mit
Kombinatorik kompakt Stochastik WS 2016/17 1 Übersicht Auswahl/Kombinationen von N aus m Elementen Statistische unterscheidbare ununterscheidbare Physik Objekte (gleiche) Objekte ( ohne m N m+n 1 ) N mit
1 Quadratische Funktionen Potenzfunktionen Potenzrechengesetze... 15
 A Wahrscheinlichkeiten Seite Kombinatorische Zählverfahren... Pascal sches Dreieck... 5 Binomialkoeffizient... 8 Vierfeldertafel... 9 5 Bedingte Wahrscheinlichkeiten... B Potenzfunktionen Quadratische
A Wahrscheinlichkeiten Seite Kombinatorische Zählverfahren... Pascal sches Dreieck... 5 Binomialkoeffizient... 8 Vierfeldertafel... 9 5 Bedingte Wahrscheinlichkeiten... B Potenzfunktionen Quadratische
( ) ( ) ( ) ( ) P B s s s s s s s s s s s P B P A s s s s s
 " # $%& '% %.) Ergebnisraum Fritz und Emil spielen gegeneinander Tischtennis. Fritz gewinnt einen Satz mit der Wahrscheinlichkeit von s Spielstärke Fritz) Es gilt folgende Vereinbarung: Sieger ist, wer
" # $%& '% %.) Ergebnisraum Fritz und Emil spielen gegeneinander Tischtennis. Fritz gewinnt einen Satz mit der Wahrscheinlichkeit von s Spielstärke Fritz) Es gilt folgende Vereinbarung: Sieger ist, wer
Übungen zur Kombinatorik (Laplace)
 1. In einem Beutel sind 10 Spielmarken enthalten, die von 0 bis 9 nummeriert sind. X sei das Ereignis, dass man zufällig die Marke 5 oder 8 herausholt, Y das Ereignis, dass eine größere Zahl als 5 gezogen
1. In einem Beutel sind 10 Spielmarken enthalten, die von 0 bis 9 nummeriert sind. X sei das Ereignis, dass man zufällig die Marke 5 oder 8 herausholt, Y das Ereignis, dass eine größere Zahl als 5 gezogen
= 5! 2! = 60 6 ) = 924
 Kombinatorik Aufgabe 1 In einer Urne befinden sich fünf Kugeln in jeweils verschiedenen Farben. Es sollen drei Kugeln ohne Zurücklegen und unter Beachtung der Reihenfolge gezogen werden. Wie viele Möglichkeiten
Kombinatorik Aufgabe 1 In einer Urne befinden sich fünf Kugeln in jeweils verschiedenen Farben. Es sollen drei Kugeln ohne Zurücklegen und unter Beachtung der Reihenfolge gezogen werden. Wie viele Möglichkeiten
Was braucht mehr Glück... ein Lotto - Sechser? oder ein Royalflush
 Was braucht mehr Glück... ein Lotto - Sechser? oder ein Royalflush 1 Ein Fachschaftstag U1a Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch Name: Vorname: 8. Oktober 2016 Inhaltsverzeichnis 1 Die
Was braucht mehr Glück... ein Lotto - Sechser? oder ein Royalflush 1 Ein Fachschaftstag U1a Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch Name: Vorname: 8. Oktober 2016 Inhaltsverzeichnis 1 Die
Diskrete Strukturen. Hausaufgabe 1 (5 Punkte)
 Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 007/08 Lösungsblatt 7
Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 007/08 Lösungsblatt 7
Abitur 2017 Mathematik Stochastik III
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2017 Mathematik Stochastik III Teilaufgabe Teil A 2 (3 BE) Ein Glücksrad hat drei Sektoren, einen blauen, einen gelben und einen roten. Diese sind unterschiedlich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2017 Mathematik Stochastik III Teilaufgabe Teil A 2 (3 BE) Ein Glücksrad hat drei Sektoren, einen blauen, einen gelben und einen roten. Diese sind unterschiedlich
Statistik Einführung // Wahrscheinlichkeitstheorie 3 p.2/58
 Statistik Einführung Wahrscheinlichkeitstheorie Kapitel 3 Statistik WU Wien Gerhard Derflinger Michael Hauser Jörg Lenneis Josef Leydold Günter Tirler Rosmarie Wakolbinger Statistik Einführung // Wahrscheinlichkeitstheorie
Statistik Einführung Wahrscheinlichkeitstheorie Kapitel 3 Statistik WU Wien Gerhard Derflinger Michael Hauser Jörg Lenneis Josef Leydold Günter Tirler Rosmarie Wakolbinger Statistik Einführung // Wahrscheinlichkeitstheorie
Unterrichtsplanung zur Einführung des Binomialkoeffizienten und der Binomialverteilung
 Unterrichtsplanung zur Einführung des Binomialkoeffizienten und der Binomialverteilung Einleitung: Im Folgenden soll ein Unterrichtskonzept zur Einführung der Begriffe Binomialkoeffizient und Binomialverteilung
Unterrichtsplanung zur Einführung des Binomialkoeffizienten und der Binomialverteilung Einleitung: Im Folgenden soll ein Unterrichtskonzept zur Einführung der Begriffe Binomialkoeffizient und Binomialverteilung
3. Ein Schachclub hat 9 Mitglieder. Wie viele Spielpaarungen sind möglich?
 Kombinatorik Produktregel 1. Auf einer Tagung werden 18 Vorträge gehalten, von denen je 3 parallel laufen. Wie viele Möglichkeiten haben die Tagungsteilnehmer, ihr eigenes Programm zusammenzustellen? 2.
Kombinatorik Produktregel 1. Auf einer Tagung werden 18 Vorträge gehalten, von denen je 3 parallel laufen. Wie viele Möglichkeiten haben die Tagungsteilnehmer, ihr eigenes Programm zusammenzustellen? 2.
3. Kombinatorik Modelltheoretische Wahrscheinlichkeiten Regeln der Kombinatorik
 3. Kombinatorik Modelltheoretische Wahrscheinlichkeiten lassen sich häufig durch Abzählen der günstigen und möglichen Fällen lösen. Kompliziertere Fragestellungen bedürfen aber der Verwendung mathematischer
3. Kombinatorik Modelltheoretische Wahrscheinlichkeiten lassen sich häufig durch Abzählen der günstigen und möglichen Fällen lösen. Kompliziertere Fragestellungen bedürfen aber der Verwendung mathematischer
Symmetrien und Winkel
 1 10 Symmetrien 301 Zeichne Grossbuchstaben des Alphabets, sortiert nach vier Typen: achsensymmetrisch punktsymmetrisch achsen- und punktsymmetrisch weder achsen- noch punktsymmetrisch Trage bei den symmetrischen
1 10 Symmetrien 301 Zeichne Grossbuchstaben des Alphabets, sortiert nach vier Typen: achsensymmetrisch punktsymmetrisch achsen- und punktsymmetrisch weder achsen- noch punktsymmetrisch Trage bei den symmetrischen
Kombinatorik. Matthias Bayerlein Matthias Bayerlein Kombinatorik / 34
 Kombinatorik Matthias Bayerlein 25.6.2010 Matthias Bayerlein Kombinatorik 25.6.2010 1 / 34 Überblick Grundlagen aus der Schule Spezielle Zahlenfolgen Zusammenfassung Matthias Bayerlein Kombinatorik 25.6.2010
Kombinatorik Matthias Bayerlein 25.6.2010 Matthias Bayerlein Kombinatorik 25.6.2010 1 / 34 Überblick Grundlagen aus der Schule Spezielle Zahlenfolgen Zusammenfassung Matthias Bayerlein Kombinatorik 25.6.2010
Wiederholung. Operationen auf Mengen. Relationen, Abbildungen/Funktionen. Beweistechniken: Landau-Notation A B, A Å B, A B, A \ B, P(A)
 Wiederholung Operationen auf Mengen A B, A Å B, A B, A \ B, P(A) Relationen, Abbildungen/Funktionen Reflexiv, symmetrisch, antisymmetrisch, transitiv Injektiv, surjektiv, bijektiv Beweistechniken: Indirekter
Wiederholung Operationen auf Mengen A B, A Å B, A B, A \ B, P(A) Relationen, Abbildungen/Funktionen Reflexiv, symmetrisch, antisymmetrisch, transitiv Injektiv, surjektiv, bijektiv Beweistechniken: Indirekter
Stochastik Kombinatorik
 Stochastik Kombinatorik In der Kombinatorik werden Techniken behandelt, mit deren Hilfe ohne direktes Abzählen die Anzahl möglicher Ausgänge bei einem Experiment bestimmt werden können. Wie viele Einstellungen
Stochastik Kombinatorik In der Kombinatorik werden Techniken behandelt, mit deren Hilfe ohne direktes Abzählen die Anzahl möglicher Ausgänge bei einem Experiment bestimmt werden können. Wie viele Einstellungen
Kombinatorik. Cusanus-Gymnasium Wittlich Permutationen. Wie viele Möglichkeiten gibt es 10 Personen in eine Reihe auf 10 Sitze zu setzen?
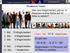 Permutationen Wie viele Möglichkeiten gibt es 10 Personen in eine Reihe auf 10 Sitze zu setzen? 1. Sitz : 10 Möglichkeiten 2. Sitz : 9 Möglichkeiten 3. Sitz : 8 Möglichkeiten. 9. Sitz : 2 Möglichkeiten
Permutationen Wie viele Möglichkeiten gibt es 10 Personen in eine Reihe auf 10 Sitze zu setzen? 1. Sitz : 10 Möglichkeiten 2. Sitz : 9 Möglichkeiten 3. Sitz : 8 Möglichkeiten. 9. Sitz : 2 Möglichkeiten
