Theoretische Informatik I
|
|
|
- Kilian Linden
- vor 9 Jahren
- Abrufe
Transkript
1 Theoretische Informatik I Einheit 2.4 Reguläre Ausdrücke 1. Anwendungen 2. Syntax und Semantik 3. Vereinfachungsregeln 4. Beziehung zu endlichen Automaten
2 Eine algebraische Beschreibung für Sprachen Automaten beschreiben Abarbeitung von Sprachen Operationale Semantik: Symbole führen zu Zustandsänderungen Bestimme Worte bzw. Symbolketten werden durch Zustände akzeptiert Für Automaten ist Sprache ˆ= Menge der akzeptierten Worte Wie beschreibt man Eigenschaften von Worten? Deklarative Semantik: äußere Form von Zeichenreihen einer Sprache z.b. Worte haben eine führende Null, dann beliebig viele Einsen Anwendungen brauchen präzise Beschreibungssprache für Worte Grundeinheiten von Programmiersprachen, Suchmuster für Browser,... Reguläre Ausdrücke als formale Syntax Kurze, prägnante Beschreibung des Aufbaus der Worte einer Sprache z.b. 01 : Zuerst eine Null, dann beliebig viele Einsen Theoretische Informatik I 2: 1 Reguläre Ausdrücke
3 Reguläre Ausdrücke beschreiben Sprachen Ausdrücke für einfache Grundmengen Leere Menge Sprache, die nur das leere Wort enthält Sprache, die nur das Symbol a Σ enthält Ausdrücke für Komposition von Mengen Vereinigung L M von Sprachen Verkettung L M von Sprachen L M = {w Σ u L. v M. w = uv} (Kleene sche) Hülle L von Sprachen L n = {w Σ u 1,.., u n L. w = u 1..u n } (n N) (L 0 = {}) L = n 0 Ln = {w Σ n N. u 1,.., u n L. w = u 1..u n } Reguläre Ausdrücke sind nicht selbst Mengen Nur eine syntaktische Beschreibungsform, die ein Computer versteht Theoretische Informatik I 2: 2 Reguläre Ausdrücke
4 Anwendung: Suchmuster in Unix grep searches files for lines containing a match to a given pattern A regular expression is a pattern that describes a set of strings. Regular expressions are constructed by using various operators to combine smaller expressions. Fundamental building blocks are expressions that match a single character. A bracket expression is a list of characters enclosed by [ and ]. It matches any single character in that list. For example, [ ] matches any single digit. Within a bracket expression, a range expression consists of two characters separated by a hyphen. It matches any single character that sorts between the two characters. For example, in the default C locale, [a-d] is equivalent to [abcd]. Certain named classes of characters are predefined within bracket expressions. They are [:alnum:], [:alpha:], [:cntrl:], [:digit:],... The period. matches any single character. The caret ^ and the dollar sign $ are metacharacters that match the empty string... A regular expression may be followed by one of several repetition operators:?: The preceding item is optional and matched at most once. *: The preceding item will be matched zero or more times. + The preceding item will be matched one or more times. Two regular expressions may be concatenated; the resulting regular expression matches any string concatenating two substrings that match the subexpressions. Two regular expressions may be joined by the infix operator The resulting regular expression matches any string matching either subexpression. Theoretische Informatik I 2: 3 Reguläre Ausdrücke
5 Anwendung: Lexikalische Analyse Wichtigster Grundbestandteil von Compilern Reguläre Ausdrücke beschreiben Token Logische Grundeinheiten von Programmiersprachen z.b. Schlüsselwörter, Bezeichner, Dezimalzahlen,... Lexer transformieren reguläre Ausdrücke in Analyseprogramme Analyse kann die Token der Programmiersprache identifizieren Zugrundeliegende Technik: Umwandlung regulärer Ausdrücke in DEAs Theoretische Informatik I 2: 4 Reguläre Ausdrücke
6 Reguläre Ausdrücke präzisiert Syntax: Terme über Σ {,,+,,,(,)},, und a (für alle a Σ) sind reguläre Ausdrücke Sind E und F reguläre Ausdrücke, dann auch E+F, E F, E und (E) Semantik: Sprachen über Σ L(E): Sprache des regulären Ausdrucks E, induktiv definiert L( ) =, L() = {}, L(a) = {a} (für alle a Σ) L(E+F ) = L(E) L(F ), L(E F ) = L(E) L(F ), L(E ) = (L(E)), L((E)) = L(E) Konventionen E F wird üblicherweise als EF abgekürzt Definitorische Abkürzungen: E + EE, [a 1...a n ] a a n Prioritätsregelungen ermöglichen es, überflüssige Klammern wegzulassen ( Sternoperator ) bindet stärker als, und dies stärker als + Verkettung und Vereinigung + sind assoziativ Theoretische Informatik I 2: 5 Reguläre Ausdrücke
7 Sprachen vs. Ausdrücke Sprachen sind Mengen Abstraktes Semantisches Konzept: Ungeordnete Kollektion von Worten Beschreibung von Mengen (auf Folie, Tafel,...) benötigt textuelle Notation Notation benutzt Kurzschreibweisen wie,, für Mengenoperationen... aber ist selbst nur ein Hilfsmittel zur Kommunikation Reguläre Ausdrücke sind Terme Syntaktisches Konstrukt: Struktur, die ein Computer versteht Reguläre Ausdrücke werden zur Beschreibung von Sprachen benutzt und sind ähnlich zur Standardnotation von Mengen Reguläre Ausdrücke sind selbst keine Mengen Unterscheide Ausdruck E von Sprache des Ausdrucks L(E) Man verzichtet auf den Unterschied wenn der Kontext eindeutig ist Theoretische Informatik I 2: 6 Reguläre Ausdrücke
8 Entwicklung regulärer Ausdrücke Beschreibe Menge aller Worte, in denen 0 und 1 abwechseln 1. Regulärer Ausdruck für die Sprache {01} 0 repräsentiert {0}, 1 repräsentiert {1} Also ist L(01) = L(0) L(1) = {0} {1} = {01} 2. Erzeuge {01, 0101, ,...} durch Sternbildung L((01) ) = L(01) = {01} = {01, 0101, ,...} 3. Manche Worte nicht erfaßt Start mit Eins statt Null: (10) Start und Ende mit Null: (01) 0 Start und Ende mit Eins: (10) 1 Vollständiger Ausdruck: (01) + (10) + (01) 0 + (10) 1 4. Es geht auch kürzer Optional 1 am Anfang oder 0 am Ende: (+1)(01) (+0) Theoretische Informatik I 2: 7 Reguläre Ausdrücke
9 Algebraische Gesetze für regulärer Ausdrücke Hilfsmittel zur Vereinfachung regulärer Ausdrücke Äquivalenz von Ausdrücken E = F, falls L(E) = L(F ) E äquivalent zu F Was beweist (01) + (10) + (01) 0 + (10) 1 = (+1)(01) (+0)? Algebraische Gesetze erlauben Umschreiben in äquivalente Ausdrücke Assoziativität von und + (E F ) G = E (F G): L((E F ) G) = L(E F ) L(G) = L(E) L(F ) L(G) = L(E) L(F G) = L(E (F G)) (E+F )+G = E+(F +G): L((E+F )+G) = L(E+F ) L(G) = L(E) L(F ) L(G) =... = L(E+(F +G)) Kommutativität von + E+F = F +E: L(E+F ) = = L(E) L(F ) = L(F ) L(E) = L(F +E) Kommutativität von gilt nicht: = L(01) = {01} {10} = L(10) Theoretische Informatik I 2: 8 Reguläre Ausdrücke
10 Algebraische Gesetze II Einheiten und Annihilatoren +E = E = E+, E = E = E, E = = E Distributivgesetze (E+F ) G = E G+F G: L((E+F ) G) = (L(E) L(F )) L(G) = {w Σ u L(E) L(F ). v L(G).w = uv} = {w Σ u L(E). v L(G).w = uv u L(F ). v L(G).w = uv} = {w Σ u L(E). v L(G).w = uv} {w Σ u L(F ). v L(G).w = uv} = L(E) L(G) L(F ) L(G) = L(E G+F G) G (E+F ) = G E + G F Idempotenz von + E+E = E Hüllengesetze (E ) = E, =, = E + = E E = E E, E = + E + Theoretische Informatik I 2: 9 Reguläre Ausdrücke
11 Beweismethodik für algebraische Gesetze Beispiel: Nachweis von (E+F ) = (E F ) Sei w L((E+F ) ) Dann w = w 1..w k mit w i L(E) oder w i L(F ) für alle i Dann w = w 1..w k mit w i L(E F ) für alle i Also w L((E F ) ) Beweis benötigt keine Information über E und F Man könnte genausogut konkrete Symbole verwenden (E+F ) = (E F ) gilt weil (a+b) = (a b ) gilt Allgemeines Beweisprinzip E regulärer Ausdruck mit Metavariablen F 1,..,F m (für Sprachen L 1,..,L m ) C entsprechender Ausdruck mit Symbolen a 1,..a m statt der F i w L(E) ist zerlegbar in w = w 1..w k mit w i L ji g.d.w. v=a j1..a jk L(C) Beweis durch strukturelle Induktion über Aufbau regulärer Ausdrücke Prüfverfahren für E = F ersetzt alle Metavariablen durch Symbole a Σ und testet dann Gleichheit der konkreten Ausdrücke später Theoretische Informatik I 2: 10 Reguläre Ausdrücke
12 Umwandlung regulärer Ausdrücke in Automaten Sprachen regulärer Ausdrücke sind endlich erkennbar Für jeden regulären Ausdruck E gibt es einen -NEA A mit A hat genau einen akzeptierenden Zustand q f Der Startzustand von A ist in keinem δ A (q, a) enthalten Für alle a Σ ist δ A (q f, a) = L(E) = L(A) Beweis durch strukturelle Induktion über Aufbau der regulären Ausdrücke Induktionsanfänge Start Für E = wähle A = Start Für E = wähle A = Start Für E = a wähle A = a Korrektheit offensichtlich, da jeweils maximal ein Zustandsübergang Theoretische Informatik I 2: 11 Reguläre Ausdrücke
13 Umwandlung regulärer Ausdrücke in Automaten Induktionsannahme: seien A 1 und A 2 -NEAs für E 1 und E 2 Induktionsschritt Für E = E 1 +E 2 wähle A = Start Automat A 1 Automat A 2 Für E = E 1 E 2 wähle A = Start Automat A 1 Automat A 2 Für E = E1 Start wähle A = Automat A 1 Für E = (E 1 ) wähle A = A 1 Theoretische Informatik I 2: 12 Reguläre Ausdrücke
14 Korrektheit der Umwandlungen Klammern ändern nichts Es ist L((E 1 )) = L(E 1 ) = L(A 1 ) = L(A) Verkettung ist Verschaltung von Automaten Start Automat A 1 Automat A 2 Es gilt w L(E 1 E 2 ) w L(E 1 ) L(E 2 ) = L(A 1 ) L(A 2 ) u L(A 1 ). v L(A 2 ).w = uv u, v Σ.w = uv q f,1 ˆδ1 (q 0,1, u) q f,2 ˆδ2 (q 0,2, v) u, v Σ.w = uv q 0,2 ˆδ(q0,1, u) q f,2 ˆδ(q0,2, v) (q 0,2 -Hülle(q f,1 )) q f,2 ˆδ(q0,1, w) (Definition ˆδ) w L(A) Argument ist umkehrbar, also w L(A) w L(E 1 E 2 ) Sternbildung und Vereinigung in Übungen? Theoretische Informatik I 2: 13 Reguläre Ausdrücke
15 Umwandlung regulärer Ausdrücke am Beispiel Konstruiere endlichen Automaten für (0+1) 1(0+1) Teilautomat für (0+1) 0 1 Teilautomat für (0+1) Automat für (0+1) 1(0+1) Start Elimination von -Übergängen ,1 Theoretische Informatik I 2: 14 Reguläre Ausdrücke
16 Umwandlung von Automaten in Reguläre Ausdrücke Gegeben A = ({q 1,..., q n }, Σ, δ, q 1, {q f1,.., q fm }) Definiere Ausdrücke für Pfade durch A R (k) ij : Regulärer Ausdruck für Menge der Worte w mit ˆδ(q i, w) = q j so daß für alle v w (v w) gilt: ˆδ(qi, v)=q n n k (Abarbeitung von w berührt keinen Zustand größer als k) Setze die R (k) ij Per Definition ist R (n) ij Setze R = R (n) 1f R (n) 1f m zu Ausdruck für L(A) zusammen ein Ausdruck für Worte w mit ˆδ(q i, w) = q j Dann gilt L(R) = m j=1 {w Σ ˆδ(q 1, w) = q fj } = {w Σ q {q f1,.., q fm }. ˆδ(q 1, w) = q} = L(A) Theoretische Informatik I 2: 15 Reguläre Ausdrücke
17 Iterative Bestimmung der Ausdrücke R (k) ij Basisfall R 0 ij : Pfadlänge 0 (nur für i=j): L(R 0 ii) Pfad darf zwischendurch keine Zustände berühren Pfadlänge 1: {a Σ δ(q i, a) = q j } L(R 0 ij ) Ergebnis: R 0 ii = + a a k, R0 ij = + a a k (i j) wobei {a 1,.., a k } = {a Σ δ(q i, a)=q j } Schrittfall R k ij (0<k n) Worte w L(Rij), k deren Pfad q k nicht enthält: L(Rij k 1 ) L(Rij) k Worte w L(Rij k ), deren Pfad q k enthält: Zerlege w in uz 1..z p v mit ˆδ(q i, u)=q k l p.ˆδ(q k, z l )=q k ˆδ(q k, v)=q j Ergebnis: R k ij = Rk 1 ij + R k 1 ik (R k 1 kk ) R k 1 kj Theoretische Informatik I 2: 16 Reguläre Ausdrücke
18 Umwandlung von Automaten am Beispiel Basisfall R 0 11 = + 1 R 0 12 = 0 R 0 21 = R 0 22 = Stufe 1 Start 1 q 1 R11 1 = R R11(R 0 11) 0 R11 0 = ( + 1)( + 1) ( + 1) 1 R12 1 = R R11(R 0 11) 0 R12 0 = 0 + ( + 1)( + 1) R21 1 = R R21(R 0 11) 0 R11 0 = + ( + 1) ( + 1) R22 1 = R R21(R 0 11) 0 R12 0 = ( + 1) Stufe 2 R11 2 = R R12(R 1 22) 1 R21 1 = (+0+1) 1 R12 2 = R R12(R 1 22) 1 R22 1 = (+0+1) (+0+1) 1 0(0+1) R21 2 = R R22(R 1 22) 1 R21 1 = + (+0+1)(+0+1) R22 2 = R R22(R 1 22) 1 R22 1 = (+0+1) + (+0+1)(+0+1) (+0+1) (0+1) 0 0,1 Regulärer Ausdruck des Automaten: 1 0(0+1) q 2 Theoretische Informatik I 2: 17 Reguläre Ausdrücke
19 Eine effizientere Umwandlungsmethode Direkte Umwandlung ist sehr aufwendig Es müssen n 3 Ausdrücke R k ij erzeugt werden Ausdrücke Rij k können viermal so groß wie die Rk 1 ij werden Ohne Vereinfachung der Rij k sind bis zu n 3 4 n Symbole zu erzeugen Optimierung des Verfahrens: vermeide Vielfachkopien der R k 1 ij Effizienterer Zugang: Elimination von Zuständen Statt Pfade zu verlängern, lege Zustände des Automaten zusammen Ersetze Übergänge q i a Σ q j durch Übergänge mit regulären Ausdrücken Schrittweise Umwandlung erzeugt regulären Ausdruck des Automaten Technisches Hilfsmittel: RA-Automaten Überführungsfunktion δ arbeitet auf regulären Ausdrücken A akzeptiert w, wenn es einen Pfad w = v 1..v m von q 0 zu einem q F gibt und alle v i in der Sprache des entsprechenden regulären Ausdrucks liegen Konsistente Formalisierung mühsam und ohne Erkenntnisgewinn Theoretische Informatik I 2: 18 Reguläre Ausdrücke
20 Zustandselimination in RA-Automaten R 1,m q 1 Q 1 R 1,1 S s P 1 p 1 q 1 R 1,1 + Q 1 S P 1 R 1,m + Q 1 S P m p 1 Q k P m q k R k,m p m R k,1 Eliminiere Zustand s mit Vorgängern q 1,.., q k und Nachfolgern p 1,.., p n q k R k,1 + Q k S P 1 R k,m + Q k S P m p m Eliminiere Pfad von q 1 nach p 1 über s: R 1,1 + Q 1 S P 1. Eliminiere Pfad von q 1 nach p m über s: R 1,m + Q 1 S P m Eliminiere Pfad von q k nach p 1 über s: R k,1 + Q k S P 1. Eliminiere Pfad von q k nach p m über s: R k,m + Q k S P m Theoretische Informatik I 2: 19 Reguläre Ausdrücke
21 Umwandlung durch Zustandselimination 1. Transformiere Automaten in RA-Automaten Ersetze Beschriftungen mit Symbolen a Σ durch reguläre Ausdrücke 2. Für q F eliminiere alle Zustände außer q 0 und q Iterative Anwendung des Eliminationsverfahrens 3. Bilde regulären Ausdruck aus finalem Automaten Start q 0 q: R R S T U (R + SU T ) SU Start q 0 =q: R 4. Vereinige Ausdrücke aller Endzustände Bilde Summe aller entstandenen regulären Ausdrücke Theoretische Informatik I 2: 20 Reguläre Ausdrücke
22 Umwandlung durch Zustandselimination am Beispiel Start 1 q 1 0 0,1 q 2 Transformiere in RA-Automaten Start 0 Keine Zustände zu eliminieren q 1 Bilde regulären Ausdruck aus finalem Automaten Extrahierter Ausdruck: (1 + 0(0+1) ) 0(0+1) Nach Vereinfachung: 1 0(0+1) q 2 Theoretische Informatik I 2: 21 Reguläre Ausdrücke
23 Umwandlung durch Zustandselimination am Beispiel Start 0,1 A 1 B 0,1 C 0,1 D Transformiere in RA-Automaten 0+1 Start A Elimination von Zustand B 0+1 Start 1(0+1) 0+1 C A B C D Elimination von Zustand C für Endzustand D 0+1 Start 1(0+1)(0+1) (0+1) 1(0+1)(0+1) D A Elimination von Zustand D für Endzustand C 0+1 Start 1(0+1) (0+1) 1(0+1) C A Gesamter Ausdruck: (0+1) 1(0+1) + (0+1) 1(0+1)(0+1) D Theoretische Informatik I 2: 22 Reguläre Ausdrücke
24 Reguläre Ausdrücke Zusammenfassung Algebraische Notation für Sprachen,, Symbole des Alphabets, Vereinigung, Verkettung, Sternoperator Äquivalent zu endlichen Automaten Gut zum Nachweis algebraischer Gesetze von Sprachen Anwendung in Programmiersprachen und Suchmaschinen Transformation in endliche Automaten Iterative Konstruktion von -NEAs Nachträgliche Optimierung durch Elimination von -Übergängen Transformation von Automaten in Ausdrücke Konstruktion von Ausdrücken für Verarbeitungspfade im Automaten Konstruktion durch Elimination von Zuständen in RA Automaten Nachträgliche Optimierungen durch Anwendung algebraischer Gesetze Theoretische Informatik I 2: 23 Reguläre Ausdrücke
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Automatentheorie und formale Sprachen
 Automatentheorie und formale Sprachen VL 4 Reguläre Ausdrücke und reguläre Sprachen Kathrin Hoffmann 10. April 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 10.4. 2012 114 Aufgabe 13:
Automatentheorie und formale Sprachen VL 4 Reguläre Ausdrücke und reguläre Sprachen Kathrin Hoffmann 10. April 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 10.4. 2012 114 Aufgabe 13:
Theoretische Informatik I
 Theoretische Informatik I Rückblick Theoretische Informatik I 1. Mathematische Methoden 2. Reguläre Sprachen 3. Kontextfreie Sprachen Themen der Theoretischen Informatik I & II Mathematische Methodik in
Theoretische Informatik I Rückblick Theoretische Informatik I 1. Mathematische Methoden 2. Reguläre Sprachen 3. Kontextfreie Sprachen Themen der Theoretischen Informatik I & II Mathematische Methodik in
Satz (Abschluß unter der Stern-Operation)
 Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Zusammenfassung der letzten LVA. Endliche Automaten mit Epsilon-Übergängen. Inhalte der Lehrveranstaltung (cont d)
 Zusammenfassung der letzten LVA Ein nichtdeterministischer endlicher Automat (NEA) ist ein 5-Tupel (Q, Σ, δ, S, F), sodass Q eine endliche Menge von Zustände Σ eine endliche Menge, das Eingabealphabet;
Zusammenfassung der letzten LVA Ein nichtdeterministischer endlicher Automat (NEA) ist ein 5-Tupel (Q, Σ, δ, S, F), sodass Q eine endliche Menge von Zustände Σ eine endliche Menge, das Eingabealphabet;
Berechenbarkeit und Komplexität Endliche Automaten
 Berechenbarkeit und Komplexität Endliche Automaten Wolfgang Schreiner [email protected] Research Institute for Symbolic Computation (RISC) Johannes Kepler University, Linz, Austria
Berechenbarkeit und Komplexität Endliche Automaten Wolfgang Schreiner [email protected] Research Institute for Symbolic Computation (RISC) Johannes Kepler University, Linz, Austria
äußere Klammern können entfallen, ebenso solche, die wegen Assoziativität von + und Konkatenation nicht notwendig sind:
 3. Reguläre Sprachen Bisher wurden Automaten behandelt und Äquivalenzen zwischen den verschiedenen Automaten gezeigt. DEAs erkennen formale Sprachen. Gibt es formale Sprachen, die nicht erkannt werden?
3. Reguläre Sprachen Bisher wurden Automaten behandelt und Äquivalenzen zwischen den verschiedenen Automaten gezeigt. DEAs erkennen formale Sprachen. Gibt es formale Sprachen, die nicht erkannt werden?
Theoretische Informatik I
 Theoretische Informatik I Einheit 2.5 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibung des Aufbaus von Sprachen Mathematische Mengennotation Beschreibung durch Eigenschaften
Theoretische Informatik I Einheit 2.5 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibung des Aufbaus von Sprachen Mathematische Mengennotation Beschreibung durch Eigenschaften
2 2 Reguläre Sprachen. 2.2 Endliche Automaten. Übersicht
 Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Reguläre Sprachen und endliche Automaten
 Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden kann.
 Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Theoretische Informatik I
 heoretische Informatik I Einheit 2 Endliche Automaten & Reguläre Sprachen. Deterministische endliche Automaten 2. Nichtdeterministische Automaten 3. Reguläre Ausdrücke 4. Grammatiken 5. Eigenschaften regulärer
heoretische Informatik I Einheit 2 Endliche Automaten & Reguläre Sprachen. Deterministische endliche Automaten 2. Nichtdeterministische Automaten 3. Reguläre Ausdrücke 4. Grammatiken 5. Eigenschaften regulärer
Theoretische Informatik I
 heoretische Informatik I Einheit 2 Endliche Automaten & Reguläre Sprachen. Deterministische endliche Automaten 2. Nichtdeterministische Automaten 3. Reguläre Ausdrücke 4. Grammatiken 5. Eigenschaften regulärer
heoretische Informatik I Einheit 2 Endliche Automaten & Reguläre Sprachen. Deterministische endliche Automaten 2. Nichtdeterministische Automaten 3. Reguläre Ausdrücke 4. Grammatiken 5. Eigenschaften regulärer
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier [email protected] 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier [email protected] 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Diskrete Mathematik. Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl
 OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
Proseminar Automatentheorie. Thema: Berry Sethi Algorithmus. Von Christopher Haas
 Proseminar Automatentheorie Thema: Berry Sethi Algorithmus Von Christopher Haas Inhaltsangabe Allgemeines/Notation Ableitung regulärer Ausdruck Intuitiv Definition Beispiele Das Brzozowski-Verfahren Markierungsverfahren
Proseminar Automatentheorie Thema: Berry Sethi Algorithmus Von Christopher Haas Inhaltsangabe Allgemeines/Notation Ableitung regulärer Ausdruck Intuitiv Definition Beispiele Das Brzozowski-Verfahren Markierungsverfahren
Induktive Definition
 Rechenregeln A B = B A A (B C) = (A B) C A (B C) = (A B) C A (B C) = A B A C (B C) A = B A C A {ε} A = A A {ε} = A (A {ε}) = A (A ) = A A A = A + A A = A + A + {ε} = A Beispiel. Real-Zahlen = {0,..., 9}
Rechenregeln A B = B A A (B C) = (A B) C A (B C) = (A B) C A (B C) = A B A C (B C) A = B A C A {ε} A = A A {ε} = A (A {ε}) = A (A ) = A A A = A + A A = A + A + {ε} = A Beispiel. Real-Zahlen = {0,..., 9}
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Automaten und Coinduktion
 Philipps-Univestität Marburg Fachbereich Mathematik und Informatik Seminar: Konzepte von Programmiersprachen Abgabedatum 02.12.03 Betreuer: Prof. Dr. H. P. Gumm Referentin: Olga Andriyenko Automaten und
Philipps-Univestität Marburg Fachbereich Mathematik und Informatik Seminar: Konzepte von Programmiersprachen Abgabedatum 02.12.03 Betreuer: Prof. Dr. H. P. Gumm Referentin: Olga Andriyenko Automaten und
Theoretische Grundlagen des Software Engineering
 Theoretische Grundlagen des Software Engineering 5: Reguläre Ausdrücke und Grammatiken [email protected] Software Systems Engineering Reguläre Sprachen Bisher: Charakterisierung von Sprachen über Automaten
Theoretische Grundlagen des Software Engineering 5: Reguläre Ausdrücke und Grammatiken [email protected] Software Systems Engineering Reguläre Sprachen Bisher: Charakterisierung von Sprachen über Automaten
Beispiel Produktautomat
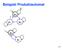 Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
 Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier [email protected] 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier [email protected] 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 20.
 Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Reguläre Ausdrücke und Sprachen
 KAPITEL 3 Reguläre Ausdrücke und Sprachen Wir beginnen dieses Kapitel mit der Einführung einer Notation namens»reguläre Ausdrücke«. Bei diesen Ausdrücken handelt es sich um eine andere Art von sprachdefinierender
KAPITEL 3 Reguläre Ausdrücke und Sprachen Wir beginnen dieses Kapitel mit der Einführung einer Notation namens»reguläre Ausdrücke«. Bei diesen Ausdrücken handelt es sich um eine andere Art von sprachdefinierender
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 19.
 Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Professur für Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Professur für Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Homomorphismen. Defnition: Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen:
 Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Theorie der Informatik. Theorie der Informatik. 2.1 Äquivalenzen. 2.2 Vereinfachte Schreibweise. 2.3 Normalformen. 2.
 Theorie der Informatik 24. Februar 2014 2. Aussagenlogik II Theorie der Informatik 2. Aussagenlogik II 2.1 Äquivalenzen Malte Helmert Gabriele Röger 2.2 Vereinfachte Schreibweise Universität Basel 24.
Theorie der Informatik 24. Februar 2014 2. Aussagenlogik II Theorie der Informatik 2. Aussagenlogik II 2.1 Äquivalenzen Malte Helmert Gabriele Röger 2.2 Vereinfachte Schreibweise Universität Basel 24.
Kapitel 2: Formale Sprachen Gliederung
 Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
DisMod-Repetitorium Tag 4
 DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
Formale Sprachen und endliche Automaten
 Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
 Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Das Pumping Lemma: Ein Anwendungsbeispiel
 Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
Theoretische Informatik II
 Theoretische Informatik II Einheit 4.2 Modelle für Typ-0 & Typ-1 Sprachen 1. Nichtdeterministische Turingmaschinen 2. Äquivalenz zu Typ-0 Sprachen 3. Linear beschränkte Automaten und Typ-1 Sprachen Maschinenmodelle
Theoretische Informatik II Einheit 4.2 Modelle für Typ-0 & Typ-1 Sprachen 1. Nichtdeterministische Turingmaschinen 2. Äquivalenz zu Typ-0 Sprachen 3. Linear beschränkte Automaten und Typ-1 Sprachen Maschinenmodelle
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Einführung in die Computerlinguistik reguläre Sprachen und endliche Automaten
 Einführung in die Computerlinguistik reguläre Sprachen und endliche Automaten Dozentin: Wiebke Petersen 03.11.2009 Wiebke Petersen Einführung CL (WiSe 09/10) 1 Formal language Denition Eine formale Sprache
Einführung in die Computerlinguistik reguläre Sprachen und endliche Automaten Dozentin: Wiebke Petersen 03.11.2009 Wiebke Petersen Einführung CL (WiSe 09/10) 1 Formal language Denition Eine formale Sprache
Lösung zur Klausur. Grundlagen der Theoretischen Informatik im WiSe 2003/2004
 Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Die Nerode-Relation und der Index einer Sprache L
 Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Automaten und formale Sprachen. Lösungen zu den Übungsblättern
 Automaten und formale Sprachen zu den Übungsblättern Übungsblatt Aufgabe. (Sipser, exercise.3) M = ({q, q2, q3, q4, q5}, {u, d}, δ, q3, {q3}) δ: u d q q q 2 q 2 q q 3 q 3 q 2 q 4 q 4 q 3 q 5 q 5 q 4 q
Automaten und formale Sprachen zu den Übungsblättern Übungsblatt Aufgabe. (Sipser, exercise.3) M = ({q, q2, q3, q4, q5}, {u, d}, δ, q3, {q3}) δ: u d q q q 2 q 2 q q 3 q 3 q 2 q 4 q 4 q 3 q 5 q 5 q 4 q
Reguläre Ausdrücke. Michael Jäger. 4. April 2017
 Reguläre Ausdrücke Michael Jäger 4. April 2017 Zeichenketten und Sprachen Ein Alphabet ist eine endliche Menge von Symbolen. Beispiele: 1. Σ 1 = {0, 1} 2. Σ 2 = {a, b, c, d, e, f, g, h, i, j, k, l, m,
Reguläre Ausdrücke Michael Jäger 4. April 2017 Zeichenketten und Sprachen Ein Alphabet ist eine endliche Menge von Symbolen. Beispiele: 1. Σ 1 = {0, 1} 2. Σ 2 = {a, b, c, d, e, f, g, h, i, j, k, l, m,
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier [email protected] 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier [email protected] 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Suche nach einem solchen Kreis. Endlichkeitstest. Vereinigung und Durchschnitt. Abschlusseigenschaften
 Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
1 Eliminieren von ɛ-übergängen
 1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
Automaten und formale Sprachen Klausurvorbereitung
 Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Reguläre Ausdrücke und Sprachen
 Reguläre Ausdrücke und Sprachen 3.1 Reguläre Ausdrücke.............................. 114 3.2 Endliche Automaten und reguläre Ausdrücke..... 122 3.3 Anwendungen regulärer Ausdrücke.............. 140 3.4
Reguläre Ausdrücke und Sprachen 3.1 Reguläre Ausdrücke.............................. 114 3.2 Endliche Automaten und reguläre Ausdrücke..... 122 3.3 Anwendungen regulärer Ausdrücke.............. 140 3.4
Kapitel 2: Formale Sprachen Gliederung. 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie
 Gliederung. Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen (noch weiter) 2.3. Kontextfreie Sprachen 2/4,
Gliederung. Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen (noch weiter) 2.3. Kontextfreie Sprachen 2/4,
Das Pumping-Lemma Formulierung
 Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
2.3 Abschlusseigenschaften
 2.3 Abschlusseigenschaften 2.3 Abschlusseigenschaften In diesem Abschnitt wollen wir uns mit Abschlusseigenschaften der regulären Sprachen, d.h. mit der Frage, ob, gegeben eine Operation und zwei reguläre
2.3 Abschlusseigenschaften 2.3 Abschlusseigenschaften In diesem Abschnitt wollen wir uns mit Abschlusseigenschaften der regulären Sprachen, d.h. mit der Frage, ob, gegeben eine Operation und zwei reguläre
Übungsblatt 6. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2 Lösungsblatt 2 3. Mai 2 Einführung in die Theoretische Informatik Hinweis:
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2 Lösungsblatt 2 3. Mai 2 Einführung in die Theoretische Informatik Hinweis:
Einführung in die Computerlinguistik reguläre Sprachen und endliche Automaten
 Einführung in die Computerlinguistik reguläre Sprachen und endliche Automaten Dozentin: Wiebke Petersen May 3, 2010 Wiebke Petersen Einführung CL (SoSe2010) 1 Operationen auf Sprachen Seien L Σ und K Σ
Einführung in die Computerlinguistik reguläre Sprachen und endliche Automaten Dozentin: Wiebke Petersen May 3, 2010 Wiebke Petersen Einführung CL (SoSe2010) 1 Operationen auf Sprachen Seien L Σ und K Σ
Lexikalische Programmanalyse der Scanner
 Der Scanner führt die lexikalische Analyse des Programms durch Er sammelt (scanned) Zeichen für Zeichen und baut logisch zusammengehörige Zeichenketten (Tokens) aus diesen Zeichen Zur formalen Beschreibung
Der Scanner führt die lexikalische Analyse des Programms durch Er sammelt (scanned) Zeichen für Zeichen und baut logisch zusammengehörige Zeichenketten (Tokens) aus diesen Zeichen Zur formalen Beschreibung
Induktionsbeweise. Induktionsbeweis: Beweisprinzip. Induktionsbeweis: Bestandeile
 Induktionsbeweise in den formalen Sprachen Induktionsbeweise Induktionsbeweise beruhen auf dem Induktionsprinzip (5. Peano-Axiom) Wir wenden Induktionsbeweise typischerweise für rekursiv/induktiv definierte
Induktionsbeweise in den formalen Sprachen Induktionsbeweise Induktionsbeweise beruhen auf dem Induktionsprinzip (5. Peano-Axiom) Wir wenden Induktionsbeweise typischerweise für rekursiv/induktiv definierte
Grammatiken. Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V. Startsymbol S V. Kurzschreibweise G = (V, Σ, P, S)
 Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Diskrete Mathematik. Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom
 Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
Automaten und Formale Sprachen ε-automaten und Minimierung
 Automaten und Formale Sprachen ε-automaten und Minimierung Ralf Möller Hamburg Univ. of Technology Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik, Vieweg Verlag 2 Danksagung
Automaten und Formale Sprachen ε-automaten und Minimierung Ralf Möller Hamburg Univ. of Technology Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik, Vieweg Verlag 2 Danksagung
ist ein regulärer Ausdruck.
 Dr. Sebastian Bab WiSe 12/13 Theoretische Grlagen der Informatik für TI Termin: VL 11 vom 22.11.2012 Reguläre Ausdrücke Reguläre Ausdrücke sind eine lesbarere Notation für Sprachen Denition 1 (Regulärer
Dr. Sebastian Bab WiSe 12/13 Theoretische Grlagen der Informatik für TI Termin: VL 11 vom 22.11.2012 Reguläre Ausdrücke Reguläre Ausdrücke sind eine lesbarere Notation für Sprachen Denition 1 (Regulärer
3.0 VU Formale Modellierung
 3.0 VU Formale Modellierung Gernot Salzer Arbeitsbereich Theoretische Informatik und Logik Institut für Computersprachen SS 206 Inhalt 0. Überblick. Organisation 2. Was bedeutet Modellierung? 3. Aussagenlogik
3.0 VU Formale Modellierung Gernot Salzer Arbeitsbereich Theoretische Informatik und Logik Institut für Computersprachen SS 206 Inhalt 0. Überblick. Organisation 2. Was bedeutet Modellierung? 3. Aussagenlogik
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Sommersemester 2016 20.04.2016 Viorica Sofronie-Stokkermans e-mail: [email protected] 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Grundlagen der Theoretischen Informatik Sommersemester 2016 20.04.2016 Viorica Sofronie-Stokkermans e-mail: [email protected] 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Theoretische Informatik. Reguläre Sprachen und Automaten
 Theoretische Informatik Reguläre Sprachen und Automaten Reguläre Sprachen Reguläre Ausdrücke und Sprachen Gleichungen Syntaxdiagramme Erweiterungen Anwendungen Reguläre Ausdrücke über Σ Syntax: Konstante
Theoretische Informatik Reguläre Sprachen und Automaten Reguläre Sprachen Reguläre Ausdrücke und Sprachen Gleichungen Syntaxdiagramme Erweiterungen Anwendungen Reguläre Ausdrücke über Σ Syntax: Konstante
Worterkennung in Texten speziell im Compilerbau 20. April Frank Heitmann 2/64
 Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann [email protected] Wir haben mittlerweile einiges
Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann [email protected] Wir haben mittlerweile einiges
Formalismen für REG. Formale Grundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen. Das Pumping Lemma. Abschlusseigenschaften
 Formalismen für RE Formale rundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen Frank Heitmann [email protected] Satz Zu jeder regulären Sprache L gibt es einen DFA A mit L(A) =
Formalismen für RE Formale rundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen Frank Heitmann [email protected] Satz Zu jeder regulären Sprache L gibt es einen DFA A mit L(A) =
Logik Vorlesung 5: Grundlagen Resolution
 Logik Vorlesung 5: Grundlagen Resolution Andreas Maletti 21. November 2014 Überblick Inhalt 1 Motivation und mathematische Grundlagen 2 Aussagenlogik Syntax und Semantik Äquivalenz und Normalformen Weitere
Logik Vorlesung 5: Grundlagen Resolution Andreas Maletti 21. November 2014 Überblick Inhalt 1 Motivation und mathematische Grundlagen 2 Aussagenlogik Syntax und Semantik Äquivalenz und Normalformen Weitere
Ein Fragment von Pascal
 Ein Fragment von Pascal Wir beschreiben einen (allerdings sehr kleinen) Ausschnitt von Pascal durch eine kontextfreie Grammatik. Wir benutzen das Alphabet Σ = {a,..., z, ;, :=, begin, end, while, do} und
Ein Fragment von Pascal Wir beschreiben einen (allerdings sehr kleinen) Ausschnitt von Pascal durch eine kontextfreie Grammatik. Wir benutzen das Alphabet Σ = {a,..., z, ;, :=, begin, end, while, do} und
Berechenbarkeitstheorie 1. Vorlesung
 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Zentrale Themen
Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Zentrale Themen
2.2 Reguläre Sprachen Endliche Automaten
 2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
a b b a Alphabet und Wörter - Zusammengefasst Formale Grundlagen der Informatik 1 Kapitel 2 Endliche Automaten und reguläre Sprachen
 Formale Grundlagen der Informatik Kapitel 2 und reguläre Sprachen Frank Heitmann [email protected] 5. April 26 Frank Heitmann [email protected] /52 Alphabet und Wörter
Formale Grundlagen der Informatik Kapitel 2 und reguläre Sprachen Frank Heitmann [email protected] 5. April 26 Frank Heitmann [email protected] /52 Alphabet und Wörter
Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken
 1 / 15 Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken Prof. Dr. Hans Kleine Büning FG Wissensbasierte Systeme WS 08/09 2 / 15 Deterministischer endlicher Automat (DEA) Definition 1:
1 / 15 Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken Prof. Dr. Hans Kleine Büning FG Wissensbasierte Systeme WS 08/09 2 / 15 Deterministischer endlicher Automat (DEA) Definition 1:
Einführung in die Computerlinguistik reguläre Sprachen und endliche Automaten
 Einführung in die Computerlinguistik reguläre Sprachen und endliche Automaten Dozentin: Wiebke Petersen May 3, 2010 Wiebke Petersen Einführung CL (SoSe2010) 1 Operationen auf Sprachen Seien L Σ und K Σ
Einführung in die Computerlinguistik reguläre Sprachen und endliche Automaten Dozentin: Wiebke Petersen May 3, 2010 Wiebke Petersen Einführung CL (SoSe2010) 1 Operationen auf Sprachen Seien L Σ und K Σ
Automatentheorie und formale Sprachen reguläre Ausdrücke
 Automatentheorie und formale Sprachen reguläre Ausdrücke Dozentin: Wiebke Petersen 6.5.2009 Wiebke Petersen Automatentheorie und formale Sprachen - SoSe09 1 Formal language Denition A formal language L
Automatentheorie und formale Sprachen reguläre Ausdrücke Dozentin: Wiebke Petersen 6.5.2009 Wiebke Petersen Automatentheorie und formale Sprachen - SoSe09 1 Formal language Denition A formal language L
Algorithmen auf Sequenzen
 Algorithmen auf Sequenzen Vorlesung von Prof. Dr. Sven Rahmann im Sommersemester 2008 Kapitel 4 Reguläre Ausdrücke Webseite zur Vorlesung http://ls11-www.cs.tu-dortmund.de/people/rahmann/teaching/ss2008/algorithmenaufsequenzen
Algorithmen auf Sequenzen Vorlesung von Prof. Dr. Sven Rahmann im Sommersemester 2008 Kapitel 4 Reguläre Ausdrücke Webseite zur Vorlesung http://ls11-www.cs.tu-dortmund.de/people/rahmann/teaching/ss2008/algorithmenaufsequenzen
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 3 14. Mai 2010 Einführung in die Theoretische
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 3 14. Mai 2010 Einführung in die Theoretische
Dank. Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Reguläre Ausdrücke als Suchmuster für grep
 Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Einführung in die Computerlinguistik Satz von Kleene
 Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 10.5.2010 Wiebke Petersen Einführung CL (SoSe2010) 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von
Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 10.5.2010 Wiebke Petersen Einführung CL (SoSe2010) 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von
Automatentheorie und Formale Sprachen
 Automatentheorie und Formale Sprachen ÜBUNGEN Kathrin Hoffmann SoSe 2012 Hoffmann (HAW Hamburg) AF SoSe 2012 1 Übung Ü1 Vorstellungsrunde Mengenoperationen Mengenfamilien Formale Sprachen DEA Vorstellungsrunde:
Automatentheorie und Formale Sprachen ÜBUNGEN Kathrin Hoffmann SoSe 2012 Hoffmann (HAW Hamburg) AF SoSe 2012 1 Übung Ü1 Vorstellungsrunde Mengenoperationen Mengenfamilien Formale Sprachen DEA Vorstellungsrunde:
Theoretische Informatik I
 Theoretische Informatik I Einheit 1 Mathematische Methodik 1. Formale Modelle 2. Beweistechniken 3. Wichtige Grundbegriffe Methodik des Problemlösens Klärung der Voraussetzungen Welche Begriffe sind zum
Theoretische Informatik I Einheit 1 Mathematische Methodik 1. Formale Modelle 2. Beweistechniken 3. Wichtige Grundbegriffe Methodik des Problemlösens Klärung der Voraussetzungen Welche Begriffe sind zum
