Automatentheorie und formale Sprachen
|
|
|
- Kajetan Brandt
- vor 9 Jahren
- Abrufe
Transkript
1 Automatentheorie und formale Sprachen VL 4 Reguläre Ausdrücke und reguläre Sprachen Kathrin Hoffmann 10. April 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
2 Aufgabe 13: Gegeben Σ = {0, 1} und der folgende NEA: Konstruieren Sie bitte den DEA, der dieselbe Sprache erkennt. Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
3 Lösung von Aufgabe 13 Teilmengenkonstruktion ergibt: 0 1 {q0} {q0, q1, q3} {q0} {q0, q1, q3} {q0, q1, q2, q3} {q0} {q0, q1, q2, q3} {q0, q1, q2, q3} {q0} und als Diagramm: Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
4 Spontanität Weitere Modellierungshilfe: ɛ-übergänge ɛ kennzeichnet die leere Zeichenreihe ɛ = 0 Σ 0 = {ɛ} Σ = Σ 0 Σ 1 Σ 2 Σ 3... Σ = Σ + {ɛ} ɛ Übergang bedeutet: Wechsel des Zustands ohne Konsumierung eines Zeichens Wie der Nicht-Determinismus eine Art zusätzlicher Freiheitsgrad wird beim NEA eingesetzt: ɛ-nea Auch ɛ-neas sind äquivalent zu DEAs Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
5 ɛ-nea Definition Ein nicht-deterministischer, endlicher ɛ-automat E = (Q E, Σ E, δ E, q 0, F E ) besteht aus einer nichtleeren, endlichen Zustandsmenge Q E einem endlichen Eingabealphabet Σ E einer Übergangsfunktion δ E : Q E (Σ E {ɛ}) P(Q E ) einem Startzustand q 0 und einer Menge von (akzeptierenden) Endzuständen F E Q E Bemerkung ɛ-übergänge sind Übergänge ohne explizite Eingabe, so genannte spontane Übergänge. Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
6 Beispiel Welche Sprache erkennt dieser ɛ-nea A? Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
7 Beispiel Welche Sprache erkennt dieser ɛ-nea A? Lösung L(A) = {ɛ, b} Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
8 ɛ-hülle Definition Gegeben ɛ-nea E = (Q, Σ, δ, q 0, F) dann ist die ɛ-hülle eines Zustandes q Q rekursiv definiert durch: q ɛ-hülle(q) Ist p ɛ-hülle(q) und r δ(p, ɛ), dann ist auch r ɛ-hülle(q). BSP: ɛ-hülle(q0) = {q0, q1, q2, q3, q4} ɛ-hülle(q1) = {q1, q3, q4} ɛ-hülle(q2) = {q2} Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
9 Aufgabe 14: Gegeben der ɛ-nea E. Geben Sie bitte L(E) an. Berechnen Sie bitte die ɛ-hüllen der Zustände. Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
10 Aufgabe 14: Gegeben der ɛ-nea E. Geben Sie bitte L(E) an. Berechnen Sie bitte die ɛ-hüllen der Zustände. Lösung L(E) = {b n n 0} ɛ-hülle(q0) = {q0, q2, q4, q3} ɛ-hülle(q1) = {q1} ɛ-hülle(q2) = {q2, q4} ɛ-hülle(q3) = {q2, q3, q4} ɛ-hülle(q4) = {q4} Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
11 Erweiterte Übergangsfunktion Die erweiterte Übergangfunktion δ : Q Σ P(Q) des ɛ-nea E = (Q, Σ, q 0, δ, F) ist die sequentielle Anwendung von δ auf ein Wort wx mit w Σ und x Σ und ist rekursiv definiert durch: δ(q, ɛ) = ɛ-hülle(q) δ(q, wx) = ɛ-hülle( δ(q, x)) q δ(q,w) wobei ɛ-hülle(s) = ɛ-hülle(q) mit S Q q S Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
12 Beispiel: Berechnung von δ(q0, bba) δ(q0, ɛ) = ɛ-hülle(q0) = {q0, q3} Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
13 Beispiel: Berechnung von δ(q0, bba) δ(q0, ɛ) = ɛ-hülle(q0) = {q0, q3} δ(q0, b) = ɛ-hülle( δ(q, b)) q δ(q0,ɛ) = ɛ-hülle(δ(q0, b) δ(q3, b)) = ɛ-hülle({q0, q4}) = {q0, q3, q4} Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
14 Beispiel: Berechnung von δ(q0, bba) δ(q0, b) = {q0, q3, q4} δ(q0, bb) = ɛ-hülle( q δ(q0,b) δ(q, b)) = ɛ-hülle(δ(q0, b) δ(q3, b) δ(q4, b)) = ɛ-hülle({q0, q4}) = {q0, q3, q4} Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
15 Beispiel: Berechnung von δ(q0, bba) δ(q0, bb) = {q0, q3, q4} δ(q0, bba) = ɛ-hülle( q δ(q0,bb) δ(q, a)) = ɛ-hülle(δ(q0, a) δ(q3, a) δ(q4, a)) = ɛ-hülle({q1, q2, q4}) = {q1, q2, q4} weil {q1, q2, q4} F = {q2} ist also bba L(A) Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
16 Äquivalenz DEA und ɛ-nea DEA konstruieren ähnlich wie beim NEA: Teilmengenkonstruktion modifiziert Satz 2.22 aus [HMU02]: Eine Sprache L wird genau dann von einem ɛ-nea akzeptiert, wenn L von einem DEA akzeptiert wird. Beweisidee: Wie NEA, also Nachweis, dass Übergangsfunktionen sich entsprechen Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
17 DEA aus ɛ-nea konstruieren Sei ɛ-nea E = (Q E, Σ E, δ E, q 0, F E ) gegeben, dann gibt es den DEA D = (Q D, Σ D, δ D, q D, F D ) mit Q D = {S S Q und S = ɛ-hülle(s)} die Menge aller abgeschlossenen ɛ-hüllen Σ D = Σ N dasselbe Alphabet q D = ɛ-hülle(q 0 ) die ɛ-hülle des Startzustandes δ D : P(Q D ) Σ P(Q D ) mit δ D (S, x) = ɛ-hülle( q S δ E (q, x)) für S P(Q D ) und x Σ D die Übergangsfunktion, die jeder Menge von Zuständen, die im NEA möglich sind, genau die ɛ-hülle der Menge der möglichen Folgezustände im NEA zuordnet F D = {S S Q D und S F E } die Teilmengen von Q D mit mindestens einem Endzustand Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
18 Aufgabe 15: Konstruieren Sie bitte einen äquivalenten DEA. Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
19 Aufgabe 15: Konstruieren Sie bitte einen äquivalenten DEA. Lösung b {q0, q2, q3, q4} {q1, q2, q4} {q1, q2, q4} {q1, q2, q4} Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
20 Zusammenfassung: Endliche Automaten Endliche Automaten bilden ein simples Berechnungsmodell. Es gibt DEAs, NEAs und ɛ-neas. Sie sich gleich ausdrucksmächtig. Ein endlicher Automat ist zustandsorientiert und arbeitet ein Wort von links nach rechts Zeichen für Zeichen ab. Das wird durch Konfigurationen oder die erweiterte Übergangsfunktion beschrieben. Endliche Automaten akzeptieren Sprachen. Diese Sprachen nennt man regulär. Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
21 Thema 4 Reguläre Ausdrücke und reguläre Sprachen Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 128
22 Übersicht Praktische Anwendung regulärer Ausdrücke Syntax und Semantik Rechenregeln Äquivalenz zu endlichen Automaten Pumping Lemma für reguläre Sprachen Abschlusseigenschaften regulärer Sprachen Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 129
23 Was sind reguläre Ausdrücke? Notation zur deklarativen Definition einer Sprache Beispiel: Erforderliche Operationen: Vereinigung Verkettung Unendliche Verkettung in UNIX-Tools, in Programmiersprachen wie Perl, PHP, Javascript, in Editoren wie UltraEdit, jedit verschiedene Dialekte, aber gleiche Grundstruktur (hier wie [HMU]) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 130
24 Reguläre Ausdrücke in der Praxis Beschreibung von Datentypen in XML Schema <xsd:simpletype name="usstate"> <xsd:restriction base="xsd:string"> <xsd:pattern value="ak AL AR"/> <!-- and so on... --> </xsd:restriction> </xsd:simpletype> <!-- Stock Keeping Unit: a product identifier- <xsd:simpletype name="sku"> <xsd:restriction base="xsd:string"> <xsd:pattern value="\d{3}-[a-z]{2}"/> </xsd:restriction> </xsd:simpletype> Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 131
25 Reguläre Ausdrücke in der Praxis XML Dokument Typ Definitionen: Inhaltsmodelle <!ELEMENT chapter (title, subtitle?, (graphic table), sectio Unix grep grep a1* datei Suche nach Zeichenketten, die a, a1, a11, a lauten grep ˆ[0-9][0-9]*$ datei Suche nach Zeilen in datei, die nur Ziffern enthalten oder leer sind grep a[bc]+d datei Suche in datei nach Zeichenketten, die mit a anfangen, danach mindestens ein b oder c haben und mit d aufhören Generatoren für lexikalische Analysekomponenten: lex, flex, jflex Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 132
26 WDH: Operationen auf Sprachen Verkettung von Sprachen: V W = {vw v V, w W } rekursive Verkettung von Sprachen (auch Potenz von Sprachen): V 0 = {ɛ} und V n+1 = V n V für n 0 (Kleene-)Stern von V ist V = i 0 V i Vereinigung, Schnitt, Komplement und Differenz von Sprachen Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 133
27 Reguläre Ausdrücke Definition Sei Σ ein Alphabet. Dann sind, ɛ und x für jedes x Σ reguläre Ausdrücke über Σ. Sind r und s reguläre Ausdrücke über Σ, dann auch (r s), (r + s) und r. Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 134
28 Reguläre Ausdrücke Definition Sei Σ ein Alphabet. Dann sind, ɛ und x für jedes x Σ reguläre Ausdrücke über Σ. Sind r und s reguläre Ausdrücke über Σ, dann auch (r s), (r + s) und r. BSP: für Σ = {a, b, c} Reguläre Ausdrücke (RA): (ɛ + (a b)) = ɛ + ab (a + b ) (a + b) (b (a (cb) )) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 134
29 Reguläre Ausdrücke Definition Sei Σ ein Alphabet. Dann sind, ɛ und x für jedes x Σ reguläre Ausdrücke über Σ. Sind r und s reguläre Ausdrücke über Σ, dann auch (r s), (r + s) und r. BSP: für Σ = {a, b, c} Reguläre Ausdrücke (RA): (ɛ + (a b)) = ɛ + ab (a + b ) (a + b) (b (a (cb) )) Klammerregeln bindet stärker als stärker als +. Gleichrangige von links nach rechts. Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 134
30 Rekursive Definition der Sematik Sprachen regulärer Ausdrücke Definition Für jeden regulären Ausdruck r über Σ definieren wir eine reguläre Sprache L(r) Σ : L( ) = L(ɛ) = {ɛ} L(x) = {x} für x Σ L(r s) = L(r) L(s) L(r + s) = L(r) L(s) L(r ) = L(r) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 135
31 Rekursive Definition der Sematik Sprachen regulärer Ausdrücke Definition Für jeden regulären Ausdruck r über Σ definieren wir eine reguläre Sprache L(r) Σ : L( ) = L(ɛ) = {ɛ} L(x) = {x} für x Σ L(r s) = L(r) L(s) L(r + s) = L(r) L(s) L(r ) = L(r) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 135
32 Rekursive Definition der Sematik Sprachen regulärer Ausdrücke Definition Für jeden regulären Ausdruck r über Σ definieren wir eine reguläre Sprache L(r) Σ : L( ) = L(ɛ) = {ɛ} L(x) = {x} für x Σ L(r s) = L(r) L(s) L(r + s) = L(r) L(s) L(r ) = L(r) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 135
33 Rekursive Definition der Sematik Sprachen regulärer Ausdrücke Definition Für jeden regulären Ausdruck r über Σ definieren wir eine reguläre Sprache L(r) Σ : L( ) = L(ɛ) = {ɛ} L(x) = {x} für x Σ L(r s) = L(r) L(s) L(r + s) = L(r) L(s) L(r ) = L(r) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 135
34 Rekursive Definition der Sematik Sprachen regulärer Ausdrücke Definition Für jeden regulären Ausdruck r über Σ definieren wir eine reguläre Sprache L(r) Σ : L( ) = L(ɛ) = {ɛ} L(x) = {x} für x Σ L(r s) = L(r) L(s) L(r + s) = L(r) L(s) L(r ) = L(r) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 135
35 Rekursive Definition der Sematik Sprachen regulärer Ausdrücke Definition Für jeden regulären Ausdruck r über Σ definieren wir eine reguläre Sprache L(r) Σ : L( ) = L(ɛ) = {ɛ} L(x) = {x} für x Σ L(r s) = L(r) L(s) L(r + s) = L(r) L(s) L(r ) = L(r) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 135
36 Rekursive Definition der Sematik Sprachen regulärer Ausdrücke Definition Für jeden regulären Ausdruck r über Σ definieren wir eine reguläre Sprache L(r) Σ : L( ) = L(ɛ) = {ɛ} L(x) = {x} für x Σ L(r s) = L(r) L(s) L(r + s) = L(r) L(s) L(r ) = L(r) BSP: für Σ = {a, b, c} Reguläre Ausdrücke (RA): L(ɛ + ab) = {ɛ, ab} L(a + b ) = {a, ɛ, b, bb, bbb,...} L((a + b) ) = {ɛ, a, b, aa, ab, bb, abb,...} L(b a(bc) ) = {a, ba, abc, bbabcbcb,...} Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 135
37 Rekursive Definition der Sematik Sprachen regulärer Ausdrücke Definition Für jeden regulären Ausdruck r über Σ definieren wir eine reguläre Sprache L(r) Σ : L( ) = L(ɛ) = {ɛ} L(x) = {x} für x Σ L(r s) = L(r) L(s) L(r + s) = L(r) L(s) L(r ) = L(r) BSP: für Σ = {a, b, c} Reguläre Ausdrücke (RA): L(ɛ + ab) = {ɛ, ab} L(a + b ) = {a, ɛ, b, bb, bbb,...} L((a + b) ) = {ɛ, a, b, aa, ab, bb, abb,...} L(b a(bc) ) = {a, ba, abc, bbabcbcb,...} Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 135
38 Rekursive Definition der Sematik Sprachen regulärer Ausdrücke Definition Für jeden regulären Ausdruck r über Σ definieren wir eine reguläre Sprache L(r) Σ : L( ) = L(ɛ) = {ɛ} L(x) = {x} für x Σ L(r s) = L(r) L(s) L(r + s) = L(r) L(s) L(r ) = L(r) BSP: für Σ = {a, b, c} Reguläre Ausdrücke (RA): L(ɛ + ab) = {ɛ, ab} L(a + b ) = {a, ɛ, b, bb, bbb,...} L((a + b) ) = {ɛ, a, b, aa, ab, bb, abb,...} L(b a(bc) ) = {a, ba, abc, bbabcbcb,...} Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 135
39 Rekursive Definition der Sematik Sprachen regulärer Ausdrücke Definition Für jeden regulären Ausdruck r über Σ definieren wir eine reguläre Sprache L(r) Σ : L( ) = L(ɛ) = {ɛ} L(x) = {x} für x Σ L(r s) = L(r) L(s) L(r + s) = L(r) L(s) L(r ) = L(r) BSP: für Σ = {a, b, c} Reguläre Ausdrücke (RA): L(ɛ + ab) = {ɛ, ab} L(a + b ) = {a, ɛ, b, bb, bbb,...} L((a + b) ) = {ɛ, a, b, aa, ab, bb, abb,...} L(b a(bc) ) = {a, ba, abc, bbabcbcb,...} Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 135
40 Beispiel: Bildung eines regulären Ausdrucks Regulärer Ausdruck für die Sprache L, die aus Wörtern besteht, die abwechselnd 0 s und 1 s enthalten: L(0) = {0} und L(1) = {1} Verkettung: L(0 1) = L(01) = L(0) L(1) = {01} Kleenesche Hülle: L((01) ) = (L(01)) = {ɛ, 01, 0101, ,...} Vereinigung: L((01) + (10) ) = L((01) ) + L((10) ) = {ɛ, 01, 10, 0101, 1010,...} Die Wörter mit ungerader Anzahl von Zeichen: L((01) + (10) + 1(01) + 0(10) ) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 136
41 Beispiel: Bildung eines regulären Ausdrucks Regulärer Ausdruck für die Sprache L, die aus Wörtern besteht, die abwechselnd 0 s und 1 s enthalten: L(0) = {0} und L(1) = {1} Verkettung: L(0 1) = L(01) = L(0) L(1) = {01} Kleenesche Hülle: L((01) ) = (L(01)) = {ɛ, 01, 0101, ,...} Vereinigung: L((01) + (10) ) = L((01) ) + L((10) ) = {ɛ, 01, 10, 0101, 1010,...} Die Wörter mit ungerader Anzahl von Zeichen: L((01) + (10) + 1(01) + 0(10) ) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 136
42 Beispiel: Bildung eines regulären Ausdrucks Regulärer Ausdruck für die Sprache L, die aus Wörtern besteht, die abwechselnd 0 s und 1 s enthalten: L(0) = {0} und L(1) = {1} Verkettung: L(0 1) = L(01) = L(0) L(1) = {01} Kleenesche Hülle: L((01) ) = (L(01)) = {ɛ, 01, 0101, ,...} Vereinigung: L((01) + (10) ) = L((01) ) + L((10) ) = {ɛ, 01, 10, 0101, 1010,...} Die Wörter mit ungerader Anzahl von Zeichen: L((01) + (10) + 1(01) + 0(10) ) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 136
43 Beispiel: Bildung eines regulären Ausdrucks Regulärer Ausdruck für die Sprache L, die aus Wörtern besteht, die abwechselnd 0 s und 1 s enthalten: L(0) = {0} und L(1) = {1} Verkettung: L(0 1) = L(01) = L(0) L(1) = {01} Kleenesche Hülle: L((01) ) = (L(01)) = {ɛ, 01, 0101, ,...} Vereinigung: L((01) + (10) ) = L((01) ) + L((10) ) = {ɛ, 01, 10, 0101, 1010,...} Die Wörter mit ungerader Anzahl von Zeichen: L((01) + (10) + 1(01) + 0(10) ) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 136
44 Beispiel: Bildung eines regulären Ausdrucks Regulärer Ausdruck für die Sprache L, die aus Wörtern besteht, die abwechselnd 0 s und 1 s enthalten: L(0) = {0} und L(1) = {1} Verkettung: L(0 1) = L(01) = L(0) L(1) = {01} Kleenesche Hülle: L((01) ) = (L(01)) = {ɛ, 01, 0101, ,...} Vereinigung: L((01) + (10) ) = L((01) ) + L((10) ) = {ɛ, 01, 10, 0101, 1010,...} Die Wörter mit ungerader Anzahl von Zeichen: L((01) + (10) + 1(01) + 0(10) ) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 136
45 Beispiel: Bildung eines regulären Ausdrucks Regulärer Ausdruck für die Sprache L, die aus Wörtern besteht, die abwechselnd 0 s und 1 s enthalten: L(0) = {0} und L(1) = {1} Verkettung: L(0 1) = L(01) = L(0) L(1) = {01} Kleenesche Hülle: L((01) ) = (L(01)) = {ɛ, 01, 0101, ,...} Vereinigung: L((01) + (10) ) = L((01) ) + L((10) ) = {ɛ, 01, 10, 0101, 1010,...} Die Wörter mit ungerader Anzahl von Zeichen: L((01) + (10) + 1(01) + 0(10) ) Bemerkung: Übliche Vereinfachung ist (01) + (10) + 1(01) + 0(10), obwohl L((01) + (10) + 1(01) + 0(10) ) gemeint ist. Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 136
46 Aufgabe 16: 1 Bitte beschreiben Sie mit einem regulären Ausdruck, die Sprache über dem Alphabet {a, b, c}, deren Wörter mindestens ein a und ein b enthalten. 2 Bitte beschreiben Sie folgende Sprache: (1 + ɛ)(00 1) 0 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 137
47 Aufgabe 16: 1 Bitte beschreiben Sie mit einem regulären Ausdruck, die Sprache über dem Alphabet {a, b, c}, deren Wörter mindestens ein a und ein b enthalten. 2 Bitte beschreiben Sie folgende Sprache: (1 + ɛ)(00 1) 0 Lösung 1 c a(a + c) b(a + b + c) + c b(b + c) a(a + b + c) 2 L((1 + ɛ)(00 1) 0 ) = {w w {u11v u, v {0, 1} }} also die Sprache, deren Wörte keine zwei aufeinander folgende 1 en enthalten Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 137
48 Hausaufgabe 17: Bitte beschreiben Sie mit einem regulären Ausdruck, die Sprache über dem Alphabet {0, 1}, so dass in den Wörter alle direkt aufeinander folgender Nullen (Nuller-Folgen) vor allen Einser-Folgen stehen. BSP: 00011, , Anders ausgedrückt: anfangs nur einzelne 1 en, dann nur einzelne 0 en Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 138
49 Hausaufgabe 17: Bitte beschreiben Sie mit einem regulären Ausdruck, die Sprache über dem Alphabet {0, 1}, so dass in den Wörter alle direkt aufeinander folgender Nullen (Nuller-Folgen) vor allen Einser-Folgen stehen. BSP: 00011, , Anders ausgedrückt: anfangs nur einzelne 1 en, dann nur einzelne 0 en Lösung (10 + 0) (ɛ + 1)(01 + 1) (ɛ + 0) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 138
50 Alternative RA für dieselbe Sprache RA für die Sprache L, die aus Wörtern besteht, die abwechselnd 0 s und 1 s enthalten (01) + (10) + 0(10) + 1(01) (ɛ + 1)(01) (ɛ + 0) Äquivalenz regulärer Ausdrücke Zwei reguläre Ausdrücke sind äquivalent, wenn sie dieselbe Sprache beschreiben Welche Äquivalenzumformungen gibt es? Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 139
51 Assoziativität und Kommutativität Satz mit Beweisidee Seien r, s und t reguläre Ausdrücke und R := L(r), S := L(s) und T := L(t) die dazugehörigen Sprachen, dann gelten: Kommutativgesetz der Vereinigung: r + s = s + r weil R S = S R Assoziativgesetz der Vereinigung: (r + s) + t = r + (s + t) weil (R S) T = R (S T ) Assoziativgesetz der Verkettung: (r s) t = r (s t) weil (R S) T = R (S T ) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 140
52 Einheiten Die Einheit bezüglich eines Operators ist ein Wert, für den gilt, dass bei Anwendung des Operators auf die Einheit und auf einen anderen Wert der andere Wert das Ergebnis bildet: Identitätsgesetz der Vereinigung: ist Einheit bezüglich der Vereinigung: + r = r + = r weil R = R = R Identitätsgesetz der Verkettung: ɛ ist Einheit bezüglich der Verkettung: ɛr = rɛ = r weil {ɛ} R = R {ɛ} = R Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 141
53 Annihilatoren und Idempotenz Der Annihilator bezüglich eines Operators ist ein Wert, für den gilt, dass bei Anwendung des Operators auf den Annihilator und auf einen anderen Wert der Annihilator das Ergebnis bildet. ist Annihilator bezüglich der Verkettung: r = r = weil R = R = Ein Operator heißt idempotent, wenn seine Anwendung auf zwei Operanden mit demselben Wert eben diesen Wert als Ergebnis hat. Idempotenzgesetz der Vereinigung: r + r = r Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 142
54 Distributivgesetze Linkes Distributivgesetz der Verkettung bezüglich der Vereinigung: r(s + t) = rs + rt Rechtes Distributivgesetz der Verkettung bezüglich der Vereinigung: (s + t)r = sr + tr Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 143
55 Gesetze bezüglich Hüllenbildung (r ) = r = ɛ ɛ = ɛ r+ := rr = r r r = r + + ɛ r? := ɛ + r Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 144
56 Aufgabe 18: Bitte vereinfachen Sie die folgenden reguläre Ausdrücke: 1 (1 + ɛ) + (11 (10 ) ) 2 ((1010) + (10) )(1 + ) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 145
57 Aufgabe 18: Bitte vereinfachen Sie die folgenden reguläre Ausdrücke: 1 (1 + ɛ) + (11 (10 ) ) 2 ((1010) + (10) )(1 + ) Lösung 1 (1 + ɛ) + (11 (10 ) ) = 1 + ɛ = ɛ ((1010) + (10) )(1 + ) = ((1010) + (10) )1 = (10) 1 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 145
58 Endliche Automaten und reguläre Ausdrücke EAs und RAs beschreiben dieselben Sprachen: Beweisplan für die Äquivalenz: Reguläre Sprachen Noch zu zeigen Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 146
59 DEA = RA: k-pfad Idee: Pfade in einem DEA auf Basis der Kantenbeschriftungen in RA überführen Zustände des DEA werden in 1, 2,..., n umbenannt Der k-pfad R (k) bezeichnet den RA, dessen Sprache ij genau die Wörter umfasst, die den Beschriftungen der Pfade von Zustand i nach Zustand j entsprechen, wobei kein Zustand mit einem Namen > k durchlaufen werden darf. Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 147
60 k-pfade durch den Automaten Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 148
61 k-pfade durch den Automaten Reguläre Ausdrücke ij k-pfad reg. Ausdruck 11 ɛ ɛ für direkten Weg von i nach j (über höchstens 0) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 148
62 k-pfade durch den Automaten Reguläre Ausdrücke ij k-pfad reg. Ausdruck 11 ɛ ɛ für direkten Weg von i nach j (über höchstens 0) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 148
63 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke ij für den Weg über höchstens 1 von i nach j k-pfad reg. Ausdruck ɛ Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 148
64 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke ij für den Weg über höchstens 1 von i nach j k-pfad reg. Ausdruck ɛ Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 148
65 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ k-pfad reg. Ausdruck ɛ Reguläre Ausdrücke R (2) ij k-pfad reg. Ausdruck R (2) 11 1 R (2) (0 + 1) R (2) 21 R (2) 22 (0 + 1) für den Weg über 2 von i nach j Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 148
66 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ k-pfad reg. Ausdruck ɛ Reguläre Ausdrücke R (2) für den Weg über 2 von i nach j ij k-pfad reg. Ausdruck R (2) 11 1 R (2) (0 + 1) Alle Wörter mit mind. einer 0 R (2) 21 R (2) 22 (0 + 1) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 148
67 Induktive Berechnung der Pfade R (k) ij lässt sich aus R (k 1) ij berechnen Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 149
68 DEA = RA Zustände des DEA werden in 1, 2,..., n umbenannt R (k) bezeichnet den RA, dessen Sprache ij genau die Zeichenreihen umfasst, die den Beschriftungen der Pfade von Zustand i nach Zustand j entsprechen, wobei kein Zustand mit einem Namen > k durchlaufen werden darf. Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 150
69 DEA = RA Zustände des DEA werden in 1, 2,..., n umbenannt R (k) bezeichnet den RA, dessen Sprache ij genau die Zeichenreihen umfasst, die den Beschriftungen der Pfade von Zustand i nach Zustand j entsprechen, wobei kein Zustand mit einem Namen > k durchlaufen werden darf. R (k) ij lässt sich aus R (k 1) ij berechnen Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 150
70 DEA = RA Zustände des DEA werden in 1, 2,..., n umbenannt R (k) bezeichnet den RA, dessen Sprache ij genau die Zeichenreihen umfasst, die den Beschriftungen der Pfade von Zustand i nach Zustand j entsprechen, wobei kein Zustand mit einem Namen > k durchlaufen werden darf. R (k) ij lässt sich aus R (k 1) ij R (k) ij = R (k 1) ij berechnen + R (k 1) ik (R (k 1) ) R (k 1) kk kj RA ist die Summe aller R (k) mit 1 dem Startzustand und f F 1f einem Endzustand f F Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 150 R n 1f
71 k-pfade durch den Automaten Reguläre Ausdrücke ij k-pfad reg. Ausdruck 11 ɛ ɛ für direkten Weg von i nach j (über höchstens 0) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
72 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck reg. Ausdruck R(0) 11 (R(0) 11 ) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
73 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck 11 ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
74 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck 11 ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
75 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) R(0) 11 (R(0) 11 ) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
76 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck 11 ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1)(ɛ + 1) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
77 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck 11 ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1)(ɛ + 1) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
78 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck 11 ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1)(ɛ + 1) R(0) 21 (R(0) 11 ) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
79 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck 11 ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1) 22 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
80 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck 11 ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1) 22 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
81 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck 11 ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1) R(0) 21 (R(0) 11 ) 12 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
82 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck 11 ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1) 22 ɛ (ɛ + 1) 0 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
83 k-pfade durch den Automaten k-pfad reg. Ausdruck 11 ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij = + ij ij i1 (R(0) 11 ) 1j k-pfad ind. Pfadausdruck vereinf. Ausdruck 11 ɛ (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1)(ɛ + 1) (ɛ + 1) (ɛ + 1) 22 ɛ (ɛ + 1) 0 ɛ Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
84 k-pfade durch den Automaten k-pfad reg. Ausdruck k-pfad vereinf. Ausdruck ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij R (2) = + ij ij i2 (R(1) 22 ) 2j k-pfad ind. Pfadausdruck reg. Ausdruck R (2) R(1) 12 (R(1) 22 ) 21 R (2) 12 R (2) 21 R (2) 22 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
85 k-pfade durch den Automaten k-pfad reg. Ausdruck k-pfad vereinf. Ausdruck ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij R (2) = + ij ij i2 (R(1) 22 ) 2j k-pfad ind. Pfadausdruck reg. Ausdruck R (2) (ɛ ) 1 R (2) 12 R (2) 21 R (2) 22 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
86 k-pfade durch den Automaten k-pfad reg. Ausdruck k-pfad vereinf. Ausdruck ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij R (2) = + ij ij i2 (R(1) 11 ) 2j k-pfad ind. Pfadausdruck reg. Ausdruck R (2) (ɛ ) 1 R (2) R(1) 12 (R(1) 22 ) 22 R (2) 21 R (2) 22 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
87 k-pfade durch den Automaten k-pfad reg. Ausdruck k-pfad vereinf. Ausdruck ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij R (2) = + ij ij i2 (R(1) 22 ) 2j k-pfad ind. Pfadausdruck reg. Ausdruck R (2) (ɛ ) 1 R (2) (ɛ ) (ɛ ) 1 0(0 + 1) R (2) 21 R (2) 22 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
88 k-pfade durch den Automaten k-pfad reg. Ausdruck k-pfad vereinf. Ausdruck ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij R (2) = + ij ij i2 (R(1) 22 ) 2j k-pfad ind. Pfadausdruck reg. Ausdruck R (2) (ɛ ) 1 R (2) (ɛ ) (ɛ ) 1 0(0 + 1) R (2) R(1) 22 (R(1) 22 ) 21 R (2) 22 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
89 k-pfade durch den Automaten k-pfad reg. Ausdruck k-pfad vereinf. Ausdruck ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij R (2) = + ij ij i2 (R(1) 22 ) 2j k-pfad ind. Pfadausdruck reg. Ausdruck R (2) (ɛ ) 1 R (2) (ɛ ) (ɛ ) 1 0(0 + 1) R (2) 21 + (ɛ )(ɛ ) R (2) 22 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
90 k-pfade durch den Automaten k-pfad reg. Ausdruck k-pfad vereinf. Ausdruck ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij R (2) = + ij ij i2 (R(1) 22 ) 2j k-pfad ind. Pfadausdruck reg. Ausdruck R (2) (ɛ ) 1 R (2) (ɛ ) (ɛ ) 1 0(0 + 1) R (2) 21 + (ɛ )(ɛ ) R (2) R(1) 22 (R(1) 22 ) 22 Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
91 k-pfade durch den Automaten k-pfad reg. Ausdruck k-pfad vereinf. Ausdruck ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij R (2) = + ij ij i2 (R(1) 22 ) 2j k-pfad ind. Pfadausdruck reg. Ausdruc R (2) (ɛ ) 1 R (2) (ɛ ) (ɛ ) 1 0(0 + 1) R (2) 21 + (ɛ )(ɛ ) R (2) 22 (ɛ ) + (ɛ )(ɛ ) (ɛ ) (0 + 1) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
92 k-pfade durch den Automaten k-pfad reg. Ausdruck k-pfad vereinf. Ausdruck ɛ ɛ Reguläre Ausdrücke für den Weg über höchstens 1 von i nach j: ij R (2) = + ij ij i2 (R(1) 22 ) 2j k-pfad ind. Pfadausdruck reg. Ausdruc R (2) (ɛ ) 1 R (2) (ɛ ) (ɛ ) 1 0(0 + 1) R (2) 21 + (ɛ )(ɛ ) R (2) 22 (ɛ ) + (ɛ )(ɛ ) (ɛ ) (0 + 1) Hoffmann (HAW Hamburg) Thema 4 Reguläre Ausdrücke und reguläre Sprachen 151
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Automatentheorie und Formale Sprachen
Automatentheorie und Formale Sprachen ÜBUNGEN Kathrin Hoffmann SoSe 2012 Hoffmann (HAW Hamburg) AF SoSe 2012 1 Übung Ü1 Vorstellungsrunde Mengenoperationen Mengenfamilien Formale Sprachen DEA Vorstellungsrunde:
Zusammenfassung der letzten LVA. Endliche Automaten mit Epsilon-Übergängen. Inhalte der Lehrveranstaltung (cont d)
Zusammenfassung der letzten LVA Ein nichtdeterministischer endlicher Automat (NEA) ist ein 5-Tupel (Q, Σ, δ, S, F), sodass Q eine endliche Menge von Zustände Σ eine endliche Menge, das Eingabealphabet;
Induktive Definition
Rechenregeln A B = B A A (B C) = (A B) C A (B C) = (A B) C A (B C) = A B A C (B C) A = B A C A {ε} A = A A {ε} = A (A {ε}) = A (A ) = A A A = A + A A = A + A + {ε} = A Beispiel. Real-Zahlen = {0,..., 9}
Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken
1 / 15 Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken Prof. Dr. Hans Kleine Büning FG Wissensbasierte Systeme WS 08/09 2 / 15 Deterministischer endlicher Automat (DEA) Definition 1:
äußere Klammern können entfallen, ebenso solche, die wegen Assoziativität von + und Konkatenation nicht notwendig sind:
3. Reguläre Sprachen Bisher wurden Automaten behandelt und Äquivalenzen zwischen den verschiedenen Automaten gezeigt. DEAs erkennen formale Sprachen. Gibt es formale Sprachen, die nicht erkannt werden?
Reguläre Ausdrücke. Michael Jäger. 4. April 2017
Reguläre Ausdrücke Michael Jäger 4. April 2017 Zeichenketten und Sprachen Ein Alphabet ist eine endliche Menge von Symbolen. Beispiele: 1. Σ 1 = {0, 1} 2. Σ 2 = {a, b, c, d, e, f, g, h, i, j, k, l, m,
Diskrete Mathematik. Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl
OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
Diskrete Mathematik. Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom
Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
2 2 Reguläre Sprachen. 2.2 Endliche Automaten. Übersicht
Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Theoretische Grundlagen der Informatik
Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Berechenbarkeitstheorie 1. Vorlesung
Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Zentrale Themen
Automatentheorie und formale Sprachen
Automatentheorie und formale Sprachen Zusammenfassung Kathrin Hoffmann 27. Juni 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 27.6. 2012 329 Kontextsensitive Grammatiken und Sprachen
Einführung in die Computerlinguistik Satz von Kleene
Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 5. Foliensatz Wiebke Petersen Einführung CL 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen
1 Eliminieren von ɛ-übergängen
1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
Kapitel 2: Formale Sprachen Gliederung
Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
Satz von Kleene. (Stephen C. Kleene, ) Wiebke Petersen Einführung CL 2
Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen endlichen Automaten akzeptiert wird ist regulär und jede reguläre Sprache wird von einem deterministischen endlichen
Automaten und formale Sprachen Klausurvorbereitung
Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Formale Sprachen und endliche Automaten
Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Einführung in die Computerlinguistik Satz von Kleene
Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 5. Foliensatz Wiebke Petersen Einführung CL 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier [email protected] 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden kann.
Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Das Pumping Lemma: Ein Anwendungsbeispiel
Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
Theoretische Informatik für Medieninformatiker
Theoretische Informatik für Medieninformatiker Jan Johannsen Lehrveranstaltung im Sommersemester 27 / 6 Organisatorisches: Jede Lehrveranstaltungsstunde gliedert sich in einen Vorlesungsteil, dessen Länge
Satz (Abschluß unter der Stern-Operation)
Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Homomorphismen. Defnition: Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen:
Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Automaten und Formale Sprachen SoSe 2013 in Trier
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier [email protected] 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Kapitel 1 Automaten: Die Grundlagen und Methoden... 23
Vorwort...................................................... 17 Vorwort zur deutschen Auflage.............................. 21 Kapitel 1 Automaten: Die Grundlagen und Methoden..... 23 1.1 Wozu dient das
Übersicht. 3 3 Kontextfreie Sprachen
Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} c) {abcabc} d) {abcbc, abc, a} c) {aa, ab, ba, bb} d) {{aa}, {ab}, {ba}, {bb}}
2 Endliche Automaten Fragen 1. Was ergibt sich bei {a, bc} {de, fg}? a) {abc, defg} b) {abcde, abcfg} c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} 2. Was ergibt sich bei {abc, a} {bc, λ}?
FORMALE SYSTEME. 8. Vorlesung: Minimale Automaten. TU Dresden, 6. November Markus Krötzsch Lehrstuhl Wissensbasierte Systeme
FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
Beispiel Produktautomat
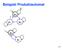Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
Suche nach einem solchen Kreis. Endlichkeitstest. Vereinigung und Durchschnitt. Abschlusseigenschaften
Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Automaten und Formale Sprachen SoSe 2013 in Trier
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier [email protected] 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
3.0 VU Formale Modellierung
3.0 VU Formale Modellierung Gernot Salzer Arbeitsbereich Theoretische Informatik und Logik Institut für Computersprachen SS 206 Inhalt 0. Überblick. Organisation 2. Was bedeutet Modellierung? 3. Aussagenlogik
Automatentheorie und formale Sprachen
Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Die Nerode-Relation und der Index einer Sprache L
Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Grundbegriffe der Informatik Tutorium 33
Tutorium 33 02.02.2017 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Gliederung 1 2 3 Ein ist ein Tupel A = (Z, z 0, X, f, Y, h)
Reguläre Sprachen und endliche Automaten
Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
Übungen zur Vorlesung Modellierung WS 2003/2004 Blatt 11 Musterlösungen
Dr. Theo Lettmann Paderborn, den 9. Januar 24 Abgabe 9. Januar 24 Übungen zur Vorlesung Modellierung WS 23/24 Blatt Musterlösungen AUFGABE 7 : Es sei der folgende partielle deterministische endliche Automat
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Worterkennung in Texten speziell im Compilerbau 20. April Frank Heitmann 2/64
Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann [email protected] Wir haben mittlerweile einiges
ist ein regulärer Ausdruck.
Dr. Sebastian Bab WiSe 12/13 Theoretische Grlagen der Informatik für TI Termin: VL 11 vom 22.11.2012 Reguläre Ausdrücke Reguläre Ausdrücke sind eine lesbarere Notation für Sprachen Denition 1 (Regulärer
Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2 Lösungsblatt 2 3. Mai 2 Einführung in die Theoretische Informatik Hinweis:
Grundlagen der Theoretischen Informatik
Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Lexikalische Analyse, Tokenizer, Scanner
Lexikalische Analyse, Tokenizer, Scanner Frühe Phase des Übersetzers Aufgabenteilung: Scanner (lokale) Zeichen (Symbol-)Analyse Parser Syntax-Analyse Aufgabe des Scanners: Erkennung von: Zahlen, Bezeichner,
5.2 Endliche Automaten
114 5.2 Endliche Automaten Endliche Automaten sind Turingmaschinen, die nur endlichen Speicher besitzen. Wie wir bereits im Zusammenhang mit Turingmaschinen gesehen haben, kann endlicher Speicher durch
2. Gegeben sei folgender nichtdeterministischer endlicher Automat mit ɛ-übergängen:
Probeklausur Automatentheorie & Formale Sprachen WiSe 2012/13, Wiebke Petersen Name: Matrikelnummer: Aufgabe A: Typ3-Sprachen 1. Konstruieren Sie einen endlichen Automaten, der die Sprache aller Wörter
Software Engineering Ergänzung zur Vorlesung
Ergänzung zur Vorlesung Prof. Dr. Markus Müller-Olm WS 2008 2009 2.6.1 Endliche und reguläre Sprachen Endliche und reguläre Sprache: fundamental in vielen Bereichen der Informatik: theorie Formale Sprachen
THIA - Übungsblatt 2.
THIA - Übungsblatt 2. Aufgabe 12 (Eine einfache Sprache). Endliche Ziffernfolgen, die mit einer 0 beginnen, auf die mindestens eine weitere Ziffer folgt, wobei nur die Ziffern 0,..., 7 vorkommen, sollen
Algorithmen mit konstantem Platzbedarf: Die Klasse REG
Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
Es gibt drei unterschiedliche Automaten:
Automatentheorie Es gibt drei unterschiedliche Automaten: 1. Deterministische Endliche Automaten (DEA) 2. Nichtdeterministische Endliche Automaten (NEA) 3. Endliche Automaten mit Epsilon-Übergängen (ε-
DisMod-Repetitorium Tag 4
DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
Formale Sprachen und Automaten
Avant Propos Formale Sprachen und Automaten Sie [die Theorie der formalen Sprachen] ist ein Musterbeispiel einer informatischen Theorie, weil es ihr gelingt, einen großen Bestand an Einsichten und Zusammenhängen
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Theoretische Grundlagen der Informatik
Theoretiche Grundlagen der Informatik KIT 24.1.211 Univerität de Dorothea Lande Baden-Württemberg Wagner - Theoretiche und Grundlagen der Informatik nationale Forchungzentrum Vorleung in am der 2.Oktober
Das Pumping-Lemma Formulierung
Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 3 14. Mai 2010 Einführung in die Theoretische
Theoretische Informatik I
heoretische Informatik I Einheit 2 Endliche Automaten & Reguläre Sprachen. Deterministische endliche Automaten 2. Nichtdeterministische Automaten 3. Reguläre Ausdrücke 4. Grammatiken 5. Eigenschaften regulärer
Endliche Automaten Jörg Roth 101
Endliche Automaten Jörg Roth 101 Wir wollen im Folgenden die Abschlusseigenschaften regulärer Sprachen betrachten. Fragestellung: Wenn wir reguläre Sprachen haben, welche binären und unären Operationen
Formale Methoden 1. Gerhard Jäger 16. Januar Uni Bielefeld, WS 2007/2008 1/19
1/19 Formale Methoden 1 Gerhard Jäger [email protected] Uni Bielefeld, WS 2007/2008 16. Januar 2008 2/19 Reguläre Ausdrücke vierte Art (neben Typ-3-Grammatiken, deterministischen und nicht-deterministischen
Theoretische Informatik I
Theoretische Informatik I Einheit 2.4 Reguläre Ausdrücke 1. Anwendungen 2. Syntax und Semantik 3. Vereinfachungsregeln 4. Beziehung zu endlichen Automaten Eine algebraische Beschreibung für Sprachen Automaten
2.2 Reguläre Sprachen Endliche Automaten
2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 19.
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Professur für Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Kurz-Skript zur Theoretischen Informatik I
Kurz-Skript zur Theoretischen Informatik I Inhaltsverzeichnis 1 Grundlagen 2 2 Reguläre Ausdrücke 4 3 Endliche Automaten 5 3.1 Vollständige endliche Automaten................................... 6 3.2 ε
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier [email protected] 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Grundlagen der theoretischen Informatik
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Automatentheorie und formale Sprachen rechtslineare Grammatiken
Automatentheorie und formale Sprachen rechtslineare Grammatiken Dozentin: Wiebke Petersen 17.6.2009 Wiebke Petersen Automatentheorie und formale Sprachen - SoSe09 1 Pumping lemma for regular languages
Proseminar Automatentheorie. Thema: Berry Sethi Algorithmus. Von Christopher Haas
Proseminar Automatentheorie Thema: Berry Sethi Algorithmus Von Christopher Haas Inhaltsangabe Allgemeines/Notation Ableitung regulärer Ausdruck Intuitiv Definition Beispiele Das Brzozowski-Verfahren Markierungsverfahren
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Kapitel 2: Formale Sprachen Gliederung. 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie
Gliederung. Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen (noch weiter) 2.3. Kontextfreie Sprachen 2/4,
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 20.
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Grundlagen der Theoretischen Informatik, SoSe 2008
2. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 1 Einelementiges Alphabet (4 Punkte) (a) Geben
Theoretische Grundlagen der Informatik
Theoretische Grundlagen der Informatik Rolf Socher ISBN 3-446-22987-6 Leseprobe Weitere Informationen oder Bestellungen unter http://www.hanser.de/3-446-22987-6 sowie im Buchhandel Einführung.. 13 2 Endliche
Grundlagen der Informatik. Prof. Dr. Stefan Enderle NTA Isny
Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
Einführung in die Computerlinguistik Satz von Kleene
Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 10.5.2010 Wiebke Petersen Einführung CL (SoSe2010) 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von
Typ-0-Sprachen und Turingmaschinen
Typ-0-Sprachen und Turingmaschinen Jean Vancoppenolle Universität Potsdam Einführung in formale Sprachen und Automaten Dr. Thomas Hanneforth (Präsentation aus Foliensätzen von Dr. Thomas Hanneforth und
Automaten, Spiele, und Logik
Automaten, Spiele, und Logik Woche 2 25. April 2014 Inhalt der heutigen Vorlesung 1. Reguläre Ausdrücke 2. der Satz von Kleene 3. Brzozowski Methode 4. grep und perl Reguläre Ausdrücke Rekursive Definition,
Theoretische Informatik I
Theoretische Informatik I Rückblick Theoretische Informatik I 1. Mathematische Methoden 2. Reguläre Sprachen 3. Kontextfreie Sprachen Themen der Theoretischen Informatik I & II Mathematische Methodik in
Kontextfreie Sprachen werden von PDAs akzeptiert
Kontextfreie Sprachen werden von PDAs akzeptiert Sei G = (Σ, V, S, P) eine kontextfreie Grammatik. Dann gibt es einen PDA A mit L(A) = L(G). Der PDA A arbeitet mit nur einem Zustand q 0, besitzt das Kelleralphabet
Automatentheorie und Formale Sprachen
Automatentheorie und Formale Sprachen Mengen, Alphabete, Wörter, formale Sprachen Dozentin: Wiebke Petersen 29.4.2009 Wiebke Petersen Automatentheorie und formale Sprachen SoSe 09 Mengen Definition 1.