Algorithmen und Datenstrukturen
|
|
|
- Gerhard Arnim Holtzer
- vor 9 Jahren
- Abrufe
Transkript
1 Algorithmen und Datenstrukturen Prof. Dr. Ralf Möller Universität zu Lübeck Institut für Informationssysteme Tanya Braun (Übungen) sowie viele Tutoren
2 Teilnehmerkreis und Voraussetzungen Studiengänge Bachelor Informatik Bachelor/Master Mathematik in Medizin und Lebenswissenschaften Bachelor Medieninformatik Bachelor Medizinische Ingenieurwissenschaft Bachelor Medizinische Informatik Voraussetzungen Einführung in die Programmierung Lineare Algebra und Diskrete Strukturen 1 2
3 Organisatorisches: Übungen Start: Montag, 18. April 2015 Übungen: Montags Anmeldung über Moodle nach dieser Veranstaltung Übungsaufgaben stehen jeweils kurz nach der Vorlesung am Freitag über Moodle bereit Aufgaben sollen in einer 2-er Gruppe bearbeitet werden Abgabe der Lösungen erfolgt bis Donnerstag in der jeweils folgenden Woche nach Ausgabe bis 12 Uhr in der IFIS- Teeküche (1 Kasten pro Gruppe) Bitte unbedingt Namen, Matrikelnummern und Übungsgruppennummern auf Abgaben vermerken 3
4 Organisatorisches: Prüfung Die Eintragung in den Kurs und in eine Übungsgruppe ist Voraussetzung, um an dem Modul Algorithmen und Datenstrukturen teilnehmen zu können und Zugriff auf die Unterlagen zu erhalten Am Ende des Semesters findet eine Klausur statt Voraussetzung zur Teilnahme an der Klausur sind mindestens 50% der gesamtmöglichen Punkte aller Übungszettel 4
5 Literatur Th. Cormen, C.E. Leiserson, R. Rivest, C. Stein, Algorithmen: Eine Einführung, 4. Auflage, Oldenbourg, 2013 M. Dietzfelbinger, K. Mehlhorn, P. Sanders Algorithmen und Datenstrukturen - Die Grundwerkzeuge, Springer, 2014 R. Sedgewick, K. Wayne, Algorithmen und Datenstrukturen, 4. Auflage, Pearson,
6 Literatur T. Ottmann, P. Widmayer, Algorithmen und Datenstrukturen, Spektrum 1997 U. Schöning, Algorithmen - kurz gefasst, Spektrum,
7 Ausblick über IFIS Module Bachelor-Programm Algorithmen und Datenstrukturen Datenbanken Non-Standard-Datenbanken Master-Programm Webbasierte Informationssysteme Datenmanagement Mobile und verteilte Datenbanken Semantic Web Web and Data Science Foundations of Ontologies and Databases for Information Systems Web Mining Agents 7
8 Allgemeine Lernziele in diesem Kurs Weg vom Problem zum Algorithmus gehen können Auswahl eines Algorithmus aus Alternativen unter Bezugnahme auf vorliegende Daten und deren Struktur Entwicklung eines Algorithmus mitsamt geeigneter Datenstrukturen (Terminierung, Korrektheit,...) Analyse von Algorithmen durchführen Anwachsen der Laufzeit bei Vergrößerung der Eingabe Erste Schritte in Bezug auf die Analyse von Problemen gehen können Ja, Probleme sind etwas anderes als Algorithmen! Probleme können in gewisser Weise schwer sein Prüfung, ob Algorithmus optimal 8
9 Beispielproblem: Summe der Elemente eines Feldes A[1..n] bestimmen Algorithmus? summe(a) = n A[i] Aufwand? i=1 Wenn A n Elemente hat, n Schritte! Der Aufwand wird linear genannt
10 Spezialisierung des Problems Vorwissen: A[i] = i Das Problem wird sehr viel einfacher! 10
11 Ausnutzen der Einschränkung Summe jedes Paares: Paare: 101 * 50 = 5050 Lösungsverfahren: function summe-2(a) n ß length(a) return (n+1)*(n/2) Nach Carl Friedrich Gauß (ca. 1786) Aufwand? Konstant, d.h. hängt (idealisiert!) nicht von n ab Entwurfsmuster: Ein-Schritt-Berechnung 11
12 Algorithmen: Notation durch Programme Annahme: Serielle Ausführung Vgl. Vorlesung Einführung in die Programmierung Variablen, Felder A[...] Zuweisungen ß (oder auch := ) Fallunterscheidungen if... then... else... Vergleich und Berechnungen für Bedingungstest Schleifen while... do, for... do Vergleich und Berechnungen für Bedingungstest procedure, function Auf Folien wird der jeweilige Skopus durch Einrückung ausgedrückt 12
13 Ein erstes Problem: Summe der Elemente Gegeben: A[1..n] : N Feld (Array) A von n Zahlen aus N (natürliche Zahlen) Gesucht: Transformation S von A, so dass gilt: summe = Σ i {1,...,n} A[i] Also: Gesucht ist ein Verfahren S, so dass { P } S { Q } gilt (Notation nach Hoare) Vorbedingung: P: true (keine Einschränkung) Nachbedingung: Q: summe = Σ i {1,...,n} A[i] C.A.R. Hoare, An axiomatic basis for computer programming. Communications of the ACM, Vol. 12, S ,
14 Ein zweites Problem: Summe der Elemente Gegeben: A[1..n] : N Feld (Array) A von n Zahlen aus N (natürliche Zahlen) Gesucht: Transformation S von A, so dass gilt: summe-2 = Σ i {1,...,n} A[i] Also: Gesucht ist ein Verfahren S, so dass { P } S { Q } gilt (Notation nach Hoare) Vorbedingung: P: A[i] = i Nachbedingung: Q: summe-2 = Σ i {1,...,n} A[i] C.A.R. Hoare, An axiomatic basis for computer programming. Communications of the ACM, Vol. 12, S ,
15 Ein erstes Problem: In-situ-Sortierproblem Gegeben: A[1..n] : N Feld (Array) A von n Zahlen aus N (natürliche Zahlen) Gesucht: Transformation S von A, so dass gilt: 1 i<j n: A[i] A[j] Nebenbedingung: Es wird intern kein weiteres Feld gleicher (oder auch nur fast gleicher Größe) verwendet Also: Gesucht ist ein Verfahren S, so dass { P } S { Q } gilt (Notation nach Hoare) Vorbedingung: P = true (keine Einschränkung) Nachbedingung: Q = 1 i<j n: A[i] A[j] Nebenbedingung: nur konstant viel zusätzlicher Speicher (feste Anzahl von Hilfsvariablen) C.A.R. Hoare, An axiomatic basis for computer programming. Communications of the ACM, Vol. 12, S ,
16 In-situ-Sortieren: Problemanalyse Felder erlauben wahlfreien Zugriff auf Elemente Zugriffszeit für ein Feld konstant (d.h. sie hängt nicht vom Indexwert ab) Idealisierende Annahme (gilt nicht für moderne Computer) Es gibt keine Aussage darüber, ob die Feldinhalte schon sortiert sind, eine willkürliche Reihenfolge haben, oder umgekehrt sortiert sind Vielleicht lassen sich solche erwarteten Eingaben aber in der Praxis feststellen Aufwand das Problem zu lösen: Man kann leicht sehen, dass jedes Element falsch positioniert sein kann Mindestaufwand im allgemeinen Fall: n Bewegungen Maximalaufwand in Abhängigkeit von n? 16
17 Aufwand zur Lösung eines Problems Gegeben ein Problem (hier: In-situ-Sortierproblem) Damit verbundene Fragen: Wie langsam muss ein Algorithmus sein, damit alle möglichen Probleminstanzen korrekt gelöst werden? Oder: Wenn wir schon einen Algorithmus haben, können wir noch einen substantiell besseren finden? Jedes Eingabefeld A stellt eine Probleminstanz dar Notwendiger Aufwand in Abhängigkeit von der Eingabegröße heißt Komplexität eines Problems Anzahl der notwendigen Verarbeitungsschritte in Abhängigkeit der Größe der Eingabe (hier: Anzahl der Elemente des Feldes A) Komplexität durch jeweils schlimmste Probleminstanz bestimmt Einzelne Probleminstanzen können evtl. weniger Schritte benötigen 17
18 Beispiel 2: Sortierung Gegeben: A = [4, 7, 3, 5, 9, 1] Gesucht: In-situ-Sortierverfahren (aufsteigend) Aufgabe: Entwickle Idee A 1: procedure Insertion-Sort(A) 2: for j 2tolength(A) do 3: key A[j] 4:. Insert A[j] into the sorted sequence A[1..j 1] 5: i j 1 6: while i>0anda[i] >keydo 7: A[i +1] A[i] 8: i i 1 9: A[i +1] key j 18
19 Entwurfsmuster / Entwurfsverfahren Schrittweise Berechnung Beispiel: Bestimmung der Summe eines Feldes durch Aufsummierung von Feldelementen Ein-Schritt-Berechnng Beispiel: Bestimmung der Summe eines Feldes ohne die Feldelemente selbst zu betrachten (geht nur unter Annahmen) Verkleinerungsprinzip Beispiel: Sortierung eines Feldes Unsortierter Teil wird immer kleiner, letztlich leer Umgekehrt: Sortierter Teil wird immer größer, umfasst am Ende alles à Sortierung erreicht 19
20 Zusammenfassung: Entwurfsmuster In dieser Vorlesungseinheit: Schrittweise Berechnung Ein-Schritt-Berechnung Verkleinerungsprinzip Nächste Vorlesung Teile und Herrsche Später : Vollständige Suchverfahren (z.b. Rücksetzen, Verzweigen und Begrenzen) Approximative Such- und Berechnungsverfahren (z.b. gierige Suche) Schrittweise Annäherung Dynamisches Programmieren (Berechnung von Teilen und deren Kombination, Wiederverwendung von Zwischenergebnissen) 20
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Prof. Dr. Ralf Möller Universität zu Lübeck Institut für Informationssysteme Stefan Werner (Übungen) sowie viele Tutoren Teilnehmerkreis und Voraussetzungen Studiengänge
Algorithmen und Datenstrukturen Prof. Dr. Ralf Möller Universität zu Lübeck Institut für Informationssysteme Stefan Werner (Übungen) sowie viele Tutoren Teilnehmerkreis und Voraussetzungen Studiengänge
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Wintersemester 2012/13 1. Vorlesung Kapitel 1: Sortieren Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Das Problem Eingabe Gegeben: eine Folge A = a 1, a 2,..., a
Algorithmen und Datenstrukturen Wintersemester 2012/13 1. Vorlesung Kapitel 1: Sortieren Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Das Problem Eingabe Gegeben: eine Folge A = a 1, a 2,..., a
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Wintersemester 2013/14 1. Vorlesung Kapitel 1: Sortieren Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Das Problem Eingabe Gegeben: eine Folge A = a 1, a 2,..., a
Algorithmen und Datenstrukturen Wintersemester 2013/14 1. Vorlesung Kapitel 1: Sortieren Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Das Problem Eingabe Gegeben: eine Folge A = a 1, a 2,..., a
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen A1. Organisatorisches Marcel Lüthi and Gabriele Röger Universität Basel 28. Februar 2018 Organisatorisches Personen: Dozenten Marcel Lüthi Gabriele Röger Dozenten Dr. Marcel
Algorithmen und Datenstrukturen A1. Organisatorisches Marcel Lüthi and Gabriele Röger Universität Basel 28. Februar 2018 Organisatorisches Personen: Dozenten Marcel Lüthi Gabriele Röger Dozenten Dr. Marcel
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Übung 1 Stephan Friedrichs Technische Universität Braunschweig, IBR 31. Oktober 2013 Programm für Heute 1 Organisatorisches 2 Übung Probleme und Instanzen Algorithmen (Pseudocode,
Algorithmen und Datenstrukturen Übung 1 Stephan Friedrichs Technische Universität Braunschweig, IBR 31. Oktober 2013 Programm für Heute 1 Organisatorisches 2 Übung Probleme und Instanzen Algorithmen (Pseudocode,
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Einleitung und Grundlagen Maike Buchin 18.4.2017 Verantwortliche Dozentin Organisation der Übungen Übungsleiter Korrekteure Maike Buchin [email protected] Raum NA 1/70 Sprechzeiten:
Vorlesung Datenstrukturen Einleitung und Grundlagen Maike Buchin 18.4.2017 Verantwortliche Dozentin Organisation der Übungen Übungsleiter Korrekteure Maike Buchin [email protected] Raum NA 1/70 Sprechzeiten:
Informatik 1 (WS 2018/2019)
 Informatik 1 (WS 2018/2019) Klaus Berberich ([email protected]) Wolfgang Braun ([email protected]) 0. Organisatorisches Dozenten Klaus Berberich ([email protected]) Sprechstunde
Informatik 1 (WS 2018/2019) Klaus Berberich ([email protected]) Wolfgang Braun ([email protected]) 0. Organisatorisches Dozenten Klaus Berberich ([email protected]) Sprechstunde
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 2014/15 3. Vorlesung Laufzeitanalyse Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Recap: Diskutieren Sie mit Ihrer NachbarIn! 1. 2. 3. Was sind
1 Algorithmen und Datenstrukturen Wintersemester 2014/15 3. Vorlesung Laufzeitanalyse Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Recap: Diskutieren Sie mit Ihrer NachbarIn! 1. 2. 3. Was sind
Algorithmen und Datenstrukturen CS1017
 Algorithmen und Datenstrukturen CS1017 Th. Letschert TH Mittelhessen Gießen University of Applied Sciences Organisatorisches und Einführung Lehrpersonal Dozent Dr. Letschert Tutoren Alissia Sauer Jonas
Algorithmen und Datenstrukturen CS1017 Th. Letschert TH Mittelhessen Gießen University of Applied Sciences Organisatorisches und Einführung Lehrpersonal Dozent Dr. Letschert Tutoren Alissia Sauer Jonas
Datenstrukturen. Sommersemester Kapitel 1: Motivation / Grundlagen. Steffen Lange
 Datenstrukturen Sommersemester 2010 Steffen Lange 1/1, Folie 1 2010 Prof. Steffen Lange - HDa/FbI - Datenstrukturen Organisatorisches Vorlesung wöchentlich; zwei Blöcke Folien im Netz (/* bitte zur Vorlesung
Datenstrukturen Sommersemester 2010 Steffen Lange 1/1, Folie 1 2010 Prof. Steffen Lange - HDa/FbI - Datenstrukturen Organisatorisches Vorlesung wöchentlich; zwei Blöcke Folien im Netz (/* bitte zur Vorlesung
ADS. 1. Vorlesung. Techniken der Programmentwicklung Prof. Dr. Wolfgang Schramm
 ADS 1. Vorlesung Techniken der Programmentwicklung Prof. Dr. Wolfgang Schramm 6.10.2016 ORGANISATORISCHES Algorithmen & Datenstrukturen Prof. Dr. Wolfgang Schramm Der Dozent 2 Prof. Dr. Wolfgang Schramm
ADS 1. Vorlesung Techniken der Programmentwicklung Prof. Dr. Wolfgang Schramm 6.10.2016 ORGANISATORISCHES Algorithmen & Datenstrukturen Prof. Dr. Wolfgang Schramm Der Dozent 2 Prof. Dr. Wolfgang Schramm
Datenstrukturen, Algorithmen und Programmierung 2
 Datenstrukturen, Algorithmen und Programmierung 2 Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 1. VO SS 2008 8. April 2008 Petra Mutzel Kurzvorstellung
Datenstrukturen, Algorithmen und Programmierung 2 Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 1. VO SS 2008 8. April 2008 Petra Mutzel Kurzvorstellung
Algorithmen und Datenstrukturen (für ET/IT)
 Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2017 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München Programm heute 1 Einführung 2 Grundlagen von Algorithmen
Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2017 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München Programm heute 1 Einführung 2 Grundlagen von Algorithmen
Informatik II: Algorithmen und Datenstrukturen SS 2013
 Informatik II: Algorithmen und Datenstrukturen SS 2013 Vorlesung 1a, Dienstag, 16. April 2013 (Organisatorisches, Programmierumgebung, Sortieren) Prof. Dr. Hannah Bast Lehrstuhl für Algorithmen und Datenstrukturen
Informatik II: Algorithmen und Datenstrukturen SS 2013 Vorlesung 1a, Dienstag, 16. April 2013 (Organisatorisches, Programmierumgebung, Sortieren) Prof. Dr. Hannah Bast Lehrstuhl für Algorithmen und Datenstrukturen
Problem: Gegeben Spezifikation (P,Q) und Implementierung S Gesucht formaler (automatisierbarer?) Beweis, dass S (P,Q) erfüllt.
 Formale Verifikation von Algorithmen 1.3 Verifikation Problem: Gegeben Spezifikation (P,Q) und Implementierung S Gesucht formaler (automatisierbarer?) Beweis, dass S (P,Q) erfüllt. Bisher nicht möglich
Formale Verifikation von Algorithmen 1.3 Verifikation Problem: Gegeben Spezifikation (P,Q) und Implementierung S Gesucht formaler (automatisierbarer?) Beweis, dass S (P,Q) erfüllt. Bisher nicht möglich
Übung Algorithmen und Datenstrukturen
 Übung Algorithmen und Datenstrukturen Sommersemester 2016 Patrick Schäfer, Humboldt-Universität zu Berlin Agenda 1. Vorstellen des vierten Übungsblatts 2. Vorbereitende Aufgaben für das vierte Übungsblatt
Übung Algorithmen und Datenstrukturen Sommersemester 2016 Patrick Schäfer, Humboldt-Universität zu Berlin Agenda 1. Vorstellen des vierten Übungsblatts 2. Vorbereitende Aufgaben für das vierte Übungsblatt
4.3 Verifikation von Aussagen über Algorithmen
 4.3 Verifikation von Aussagen über Algorithmen Hoaresche Logik: Kalkül zum Beweisen von Aussagen über Algorithmen und Programme, Programm-Verifikation, [C.A.R. Hoare, 1969]. Mod - 4.51 Statische Aussagen
4.3 Verifikation von Aussagen über Algorithmen Hoaresche Logik: Kalkül zum Beweisen von Aussagen über Algorithmen und Programme, Programm-Verifikation, [C.A.R. Hoare, 1969]. Mod - 4.51 Statische Aussagen
Kapitel 10. Komplexität von Algorithmen und Sortieralgorithmen
 Kapitel 10 Komplexität von Algorithmen und Sortieralgorithmen Arrays 1 Ziele Komplexität von Algorithmen bestimmen können (in Bezug auf Laufzeit und auf Speicherplatzbedarf) Sortieralgorithmen kennenlernen:
Kapitel 10 Komplexität von Algorithmen und Sortieralgorithmen Arrays 1 Ziele Komplexität von Algorithmen bestimmen können (in Bezug auf Laufzeit und auf Speicherplatzbedarf) Sortieralgorithmen kennenlernen:
Informatikgrundlagen (WS 2016/2017)
 Informatikgrundlagen (WS 2016/2017) Klaus Berberich ([email protected]) Wolfgang Braun ([email protected]) 0. Organisatorisches Dozenten Klaus Berberich ([email protected]) Sprechstunde
Informatikgrundlagen (WS 2016/2017) Klaus Berberich ([email protected]) Wolfgang Braun ([email protected]) 0. Organisatorisches Dozenten Klaus Berberich ([email protected]) Sprechstunde
Übersicht Datenstrukturen und Algorithmen. Literatur. Algorithmus: Wikipedia Definition. Vorlesung 1: Einführung. Prof. Dr.
 Übersicht Datenstrukturen und Vorlesung 1: Prof. Dr. Erika Ábrahám Theorie Hybrider Systeme Informatik 2 http://ths.rwth-aachen.de/teaching/ss-14/ datenstrukturen-und-algorithmen/ Diese Präsentation verwendet
Übersicht Datenstrukturen und Vorlesung 1: Prof. Dr. Erika Ábrahám Theorie Hybrider Systeme Informatik 2 http://ths.rwth-aachen.de/teaching/ss-14/ datenstrukturen-und-algorithmen/ Diese Präsentation verwendet
Kapitel 9. Komplexität von Algorithmen und Sortieralgorithmen
 1 Kapitel 9 Komplexität von Algorithmen und Sortieralgorithmen Ziele 2 Komplexität von Algorithmen bestimmen können (in Bezug auf Laufzeit und auf Speicherplatzbedarf) Sortieralgorithmen kennenlernen:
1 Kapitel 9 Komplexität von Algorithmen und Sortieralgorithmen Ziele 2 Komplexität von Algorithmen bestimmen können (in Bezug auf Laufzeit und auf Speicherplatzbedarf) Sortieralgorithmen kennenlernen:
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 7 (21.5.2014) Binäre Suche, Hashtabellen I Algorithmen und Komplexität Abstrakte Datentypen : Dictionary Dictionary: (auch: Maps, assoziative
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 7 (21.5.2014) Binäre Suche, Hashtabellen I Algorithmen und Komplexität Abstrakte Datentypen : Dictionary Dictionary: (auch: Maps, assoziative
2. Grundlagen. Beschreibung von Algorithmen durch Pseudocode. Korrektheit von Algorithmen durch Invarianten.
 2. Grundlagen Beschreibung von Algorithmen durch Pseudocode. Korrektheit von Algorithmen durch Invarianten. Laufzeitverhalten beschreiben durch O-Notation. 1 Beispiel Minimum-Suche Eingabe bei Minimum
2. Grundlagen Beschreibung von Algorithmen durch Pseudocode. Korrektheit von Algorithmen durch Invarianten. Laufzeitverhalten beschreiben durch O-Notation. 1 Beispiel Minimum-Suche Eingabe bei Minimum
Dynamisches Programmieren - Problemstruktur
 Dynamisches Programmieren - Problemstruktur Optimale Substruktur: Optimale Lösung enthält optimale Lösungen von Teilproblemen. Bsp.: Kürzester Weg im Graphen, LCS (s. etwa Folie 42 der letzten Vorlesung)
Dynamisches Programmieren - Problemstruktur Optimale Substruktur: Optimale Lösung enthält optimale Lösungen von Teilproblemen. Bsp.: Kürzester Weg im Graphen, LCS (s. etwa Folie 42 der letzten Vorlesung)
Algorithmen & Komplexität
 Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik Was ist ein Algorithmus? Ein Algorithmus ist eine eindeutige Handlungsvorschrift, [bestehend] aus endlich vielen, wohldefinierten
Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik Was ist ein Algorithmus? Ein Algorithmus ist eine eindeutige Handlungsvorschrift, [bestehend] aus endlich vielen, wohldefinierten
Tutoraufgabe 1 (Hoare-Kalkül):
 Prof. aa Dr. J. Giesl Programmierung WS16/17 F. Frohn, J. Hensel, D. Korzeniewski Allgemeine Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus der gleichen Kleingruppenübung (Tutorium) bearbeitet
Prof. aa Dr. J. Giesl Programmierung WS16/17 F. Frohn, J. Hensel, D. Korzeniewski Allgemeine Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus der gleichen Kleingruppenübung (Tutorium) bearbeitet
Grundlagen der Programmierung (Vorlesung 24)
 Grundlagen der Programmierung (Vorlesung 24) Ralf Möller, FH-Wedel Vorige Vorlesung Anwendung im Bereich Compilerbau Inhalt dieser Vorlesung Turing-Maschinen Berechenbarkeitstheorie, Halteproblem Lernziele
Grundlagen der Programmierung (Vorlesung 24) Ralf Möller, FH-Wedel Vorige Vorlesung Anwendung im Bereich Compilerbau Inhalt dieser Vorlesung Turing-Maschinen Berechenbarkeitstheorie, Halteproblem Lernziele
Aufgabe 8. 1 Arbeitsweise illustrieren. 2 Korrektheitsbeweis führen. 3 Laufzeitanalyse durchführen.
 Aufgabe 8 Betrachten Sie den folgenden Algorithmus namens Bubble-Sort. Bubble-Sort(A[1..n]): 1 for i 1 to length(a) 1 2 do for j length(a) downto i + 1 3 do if A[j 1] > A[j] 4 then A[j 1] A[j] 1 Arbeitsweise
Aufgabe 8 Betrachten Sie den folgenden Algorithmus namens Bubble-Sort. Bubble-Sort(A[1..n]): 1 for i 1 to length(a) 1 2 do for j length(a) downto i + 1 3 do if A[j 1] > A[j] 4 then A[j 1] A[j] 1 Arbeitsweise
C. A. R. Hoare. An Axiomatic Basis for Computer Programming. Nicolas Schelp. Proseminar Assertions SS 2007
 C. A. R. Hoare An Axiomatic Basis for Computer Programming Nicolas Schelp Proseminar Assertions SS 2007 Inhalt Motivation Kurze Biographie Der Hoare-Kalkül Axiome und Inferenzregeln des Hoare-Kalküls Die
C. A. R. Hoare An Axiomatic Basis for Computer Programming Nicolas Schelp Proseminar Assertions SS 2007 Inhalt Motivation Kurze Biographie Der Hoare-Kalkül Axiome und Inferenzregeln des Hoare-Kalküls Die
Übung Algorithmen und Datenstrukturen
 Übung Algorithmen und Datenstrukturen Sommersemester 2016 Patrick Schäfer, Humboldt-Universität zu Berlin Organisation Vorlesung: Montag 11 13 Uhr Marius Kloft RUD 26, 0 115 Mittwoch 11 13 Uhr Marius Kloft
Übung Algorithmen und Datenstrukturen Sommersemester 2016 Patrick Schäfer, Humboldt-Universität zu Berlin Organisation Vorlesung: Montag 11 13 Uhr Marius Kloft RUD 26, 0 115 Mittwoch 11 13 Uhr Marius Kloft
Algorithmen und Datenstrukturen
 Universität Innsbruck Institut für Informatik Zweite Prüfung 16. Oktober 2008 Algorithmen und Datenstrukturen Name: Matrikelnr: Die Prüfung besteht aus 8 Aufgaben. Die verfügbaren Punkte für jede Aufgabe
Universität Innsbruck Institut für Informatik Zweite Prüfung 16. Oktober 2008 Algorithmen und Datenstrukturen Name: Matrikelnr: Die Prüfung besteht aus 8 Aufgaben. Die verfügbaren Punkte für jede Aufgabe
Datenstrukturen und Algorithmen Beispiellösung zu Heimübungsblatt 7. Abbildung 1: Das Array A als Baum (vgl. Foliensatz 16, Folie 3)
 Aufgabe 3 a) Wir verwenden zur Lösung den Algorithmus Build-Heap 1, dieser verwendet die Funktion Heapify. Unser Array A ist gegeben durch [7, 10,, 5, 5,, 3, 3, 17]. 10 5 5 3 17 7 Abbildung 1: Das Array
Aufgabe 3 a) Wir verwenden zur Lösung den Algorithmus Build-Heap 1, dieser verwendet die Funktion Heapify. Unser Array A ist gegeben durch [7, 10,, 5, 5,, 3, 3, 17]. 10 5 5 3 17 7 Abbildung 1: Das Array
QuickSort ist ein Sortieralgorithmus, der auf der Idee des Teile & Beherrsche beruht, und das gegebene Array an Ort und Stelle (in place) sortiert
 4.3.6 QuickSort QuickSort ist ein Sortieralgorithmus, der auf der Idee des Teile & Beherrsche beruht, und das gegebene Array an Ort und Stelle (in place) sortiert QuickSort teilt das gegebene Array anhand
4.3.6 QuickSort QuickSort ist ein Sortieralgorithmus, der auf der Idee des Teile & Beherrsche beruht, und das gegebene Array an Ort und Stelle (in place) sortiert QuickSort teilt das gegebene Array anhand
Übungen zur Vorlesung Datenstrukturen und Algorithmen SS 07 Beispiellösung Blatt 5
 Kamil Swierkot Paderborn, den 01.06.2007 Aufgabe 17 Übungen zur Vorlesung Datenstrukturen und Algorithmen SS 07 Beispiellösung Blatt 5 Bei der Optimierungsvariante des SubSetSum Problems wird bei der Eingabe
Kamil Swierkot Paderborn, den 01.06.2007 Aufgabe 17 Übungen zur Vorlesung Datenstrukturen und Algorithmen SS 07 Beispiellösung Blatt 5 Bei der Optimierungsvariante des SubSetSum Problems wird bei der Eingabe
6 Quicksort. die mittlere Laufzeit Θ(n log n) beträgt und. die in der asymptotischen Notation verborgenen Konstanten sehr klein sind.
 Algorithmen und Datenstrukturen 132 6 Quicksort In diesem Abschnitt wird Quicksort, ein weiterer Sortieralgorithmus, vorgestellt. Trotz einer eher langsamen Worst-Case Laufzeit von Θ(n 2 ) ist Quicksort
Algorithmen und Datenstrukturen 132 6 Quicksort In diesem Abschnitt wird Quicksort, ein weiterer Sortieralgorithmus, vorgestellt. Trotz einer eher langsamen Worst-Case Laufzeit von Θ(n 2 ) ist Quicksort
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Sortieren fortgesetzt Maike Buchin 16.5.2017 5.6 Brechen der Unteren Schranke nur Vergleichen erlauben keine Algorithmen mit Laufzeit schneller als O(n log n) stattdessen: Struktur
Vorlesung Datenstrukturen Sortieren fortgesetzt Maike Buchin 16.5.2017 5.6 Brechen der Unteren Schranke nur Vergleichen erlauben keine Algorithmen mit Laufzeit schneller als O(n log n) stattdessen: Struktur
Übung zu Algorithmen und Datenstrukturen (für ET/IT)
 Übung zu Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2017 Rüdiger Göbl, Mai Bui Computer Aided Medical Procedures Technische Universität München Fibonacci Zahlen Fibonacci Folge Die Fibonacci
Übung zu Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2017 Rüdiger Göbl, Mai Bui Computer Aided Medical Procedures Technische Universität München Fibonacci Zahlen Fibonacci Folge Die Fibonacci
Student: Alexander Carls Matrikelnummer: Aufgabe: Beschreibung des euklidischen Algorithmus Datum:
 Berufsakademie Stuttgart / Außenstelle Horb Studienbereich Technik Studiengang Informationstechnik Kurs IT2006, 2.Semester Dozent: Olaf Herden Student: Alexander Carls Matrikelnummer: 166270 Aufgabe: Beschreibung
Berufsakademie Stuttgart / Außenstelle Horb Studienbereich Technik Studiengang Informationstechnik Kurs IT2006, 2.Semester Dozent: Olaf Herden Student: Alexander Carls Matrikelnummer: 166270 Aufgabe: Beschreibung
1. Übung Algorithmen I
 Timo Bingmann, Christian Schulz INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS 1 KIT Timo Universität Bingmann, des LandesChristian Baden-Württemberg Schulz und nationales Forschungszentrum in der
Timo Bingmann, Christian Schulz INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS 1 KIT Timo Universität Bingmann, des LandesChristian Baden-Württemberg Schulz und nationales Forschungszentrum in der
Definition der Hilfsprädikate
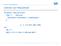 Denition der Hilfsprädikate fct sorted = (seq nat s) bool: if #s < 2 then true else rst(s) rst(rest(s)) sorted(rest(s)) a s = ( nat k: k#a = k#s) mit k# = 0 k# j s = if k == j then 1+ k#s else k#s 1 Annotierte
Denition der Hilfsprädikate fct sorted = (seq nat s) bool: if #s < 2 then true else rst(s) rst(rest(s)) sorted(rest(s)) a s = ( nat k: k#a = k#s) mit k# = 0 k# j s = if k == j then 1+ k#s else k#s 1 Annotierte
Komplexität von Algorithmen:
 Komplexität von Algorithmen: Ansatz: Beschreiben/erfassen der Komplexität über eine Funktion, zur Abschätzung des Rechenaufwandes abhängig von der Größe der Eingabe n Uns interessiert: (1) Wie sieht eine
Komplexität von Algorithmen: Ansatz: Beschreiben/erfassen der Komplexität über eine Funktion, zur Abschätzung des Rechenaufwandes abhängig von der Größe der Eingabe n Uns interessiert: (1) Wie sieht eine
Informatik II. Willkommen zur Vorlesung! Das Team. Übungsbetrieb. Vorlesung am D-BAUG der ETH Zürich
 Willkommen zur Vorlesung! Informatik II Vorlesung am D-BAUG der ETH Zürich Vorlesungshomepage: http://lec.inf.ethz.ch/baug/informatik2/2018/ Felix Friedrich & Hermann Lehner FS 2018 1 2 Das Team Dozenten
Willkommen zur Vorlesung! Informatik II Vorlesung am D-BAUG der ETH Zürich Vorlesungshomepage: http://lec.inf.ethz.ch/baug/informatik2/2018/ Felix Friedrich & Hermann Lehner FS 2018 1 2 Das Team Dozenten
Sortieralgorithmen. Jan Pöschko. 18. Januar Problemstellung Definition Warum Sortieren?... 2
 Jan Pöschko 18. Januar 2007 Inhaltsverzeichnis 1 Problemstellung 2 1.1 Definition................................... 2 1.2 Warum Sortieren?.............................. 2 2 Einfache Sortieralgorithmen
Jan Pöschko 18. Januar 2007 Inhaltsverzeichnis 1 Problemstellung 2 1.1 Definition................................... 2 1.2 Warum Sortieren?.............................. 2 2 Einfache Sortieralgorithmen
Beispiellösung zu den Übungen Datenstrukturen und Algorithmen SS 2008 Blatt 5
 Robert Elsässer Paderborn, den 15. Mai 2008 u.v.a. Beispiellösung zu den Übungen Datenstrukturen und Algorithmen SS 2008 Blatt 5 AUFGABE 1 (6 Punkte): Nehmen wir an, Anfang bezeichne in einer normalen
Robert Elsässer Paderborn, den 15. Mai 2008 u.v.a. Beispiellösung zu den Übungen Datenstrukturen und Algorithmen SS 2008 Blatt 5 AUFGABE 1 (6 Punkte): Nehmen wir an, Anfang bezeichne in einer normalen
Präsenzübung Datenstrukturen und Algorithmen SS 2014
 Prof. aa Dr. E. Ábrahám F. Corzilius, S. Schupp, T. Ströder Präsenzübung Datenstrukturen und Algorithmen SS 2014 Vorname: Nachname: Studiengang (bitte genau einen markieren): Informatik Bachelor Informatik
Prof. aa Dr. E. Ábrahám F. Corzilius, S. Schupp, T. Ströder Präsenzübung Datenstrukturen und Algorithmen SS 2014 Vorname: Nachname: Studiengang (bitte genau einen markieren): Informatik Bachelor Informatik
Algorithmen und Datenstrukturen (AuD) Prof. Dr. Claudia Eckert und Dr. Thomas Stibor
 Algorithmen und Datenstrukturen (AuD) Prof. Dr. Claudia Eckert und Dr. Thomas Stibor Organisatorisches: Vorlesung 4 SWS, Zentralübung 2 SWS: 6 Credit Points Mi 9:45 11:15 Raum 1200 (Vorlesung) Do 8:00
Algorithmen und Datenstrukturen (AuD) Prof. Dr. Claudia Eckert und Dr. Thomas Stibor Organisatorisches: Vorlesung 4 SWS, Zentralübung 2 SWS: 6 Credit Points Mi 9:45 11:15 Raum 1200 (Vorlesung) Do 8:00
Aufgabe (Schreibtischtest, lexikographische Ordnung)
 Aufgabe (Schreibtischtest, lexikographische Ordnung) Führen Sie einen Schreibtischtest für den Algorithmus Bubblesort aus der VL für die folgenden Eingabe-Arrays durch. Geben Sie das Array S nach jedem
Aufgabe (Schreibtischtest, lexikographische Ordnung) Führen Sie einen Schreibtischtest für den Algorithmus Bubblesort aus der VL für die folgenden Eingabe-Arrays durch. Geben Sie das Array S nach jedem
Elementare Sortierverfahren
 Algorithmen und Datenstrukturen I Elementare Sortierverfahren Fakultät für Informatik und Mathematik Hochschule München Letzte Änderung: 18.03.2018 18:16 Inhaltsverzeichnis Sortieren.......................................
Algorithmen und Datenstrukturen I Elementare Sortierverfahren Fakultät für Informatik und Mathematik Hochschule München Letzte Änderung: 18.03.2018 18:16 Inhaltsverzeichnis Sortieren.......................................
Vorlesung Programmieren
 Vorlesung Programmieren Organisation Dr. Dennis Pfisterer Institut für Telematik, Universität zu Lübeck http://www.itm.uni-luebeck.de/people/pfisterer Ziele dieser Veranstaltung Ziel: Wissen, wie man Computerprogramme
Vorlesung Programmieren Organisation Dr. Dennis Pfisterer Institut für Telematik, Universität zu Lübeck http://www.itm.uni-luebeck.de/people/pfisterer Ziele dieser Veranstaltung Ziel: Wissen, wie man Computerprogramme
Algorithmen und Datenstrukturen (für ET/IT)
 Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2018 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München Organisatorisches: Keine Vorlesung nächste Woche wegen
Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 2018 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München Organisatorisches: Keine Vorlesung nächste Woche wegen
Übung Algorithmen I
 Übung Algorithmen I 24.5.17 Sascha Witt [email protected] (Mit Folien von Lukas Barth, Julian Arz, Timo Bingmann, Sebastian Schlag und Christoph Striecks) Organisatorisches Übungsklausur Am 21.06.2017
Übung Algorithmen I 24.5.17 Sascha Witt [email protected] (Mit Folien von Lukas Barth, Julian Arz, Timo Bingmann, Sebastian Schlag und Christoph Striecks) Organisatorisches Übungsklausur Am 21.06.2017
{P} S {Q} {P} S {Q} {P} S {Q} Inhalt. Hoare-Kalkül. Hoare-Kalkül. Hoare-Tripel. Hoare-Tripel. Hoare-Tripel
 Inhalt Hoare-Kalkül Formale Verifizierung Hoare-Kalkül while-sprache Terminierung Partielle / totale Korrektheit 4.0 Hoare-Kalkül entwickelt von C.A.R. (Tony) Hoare (britischer Informatiker), 1969 formales
Inhalt Hoare-Kalkül Formale Verifizierung Hoare-Kalkül while-sprache Terminierung Partielle / totale Korrektheit 4.0 Hoare-Kalkül entwickelt von C.A.R. (Tony) Hoare (britischer Informatiker), 1969 formales
Suchen und Sortieren
 Suchen und Sortieren Suchen Sortieren Mischen Zeitmessungen Bewertung von Sortier-Verfahren Seite 1 Suchverfahren Begriffe Suchen = Bestimmen der Position (Adresse) eines Wertes in einer Datenfolge Sequentielles
Suchen und Sortieren Suchen Sortieren Mischen Zeitmessungen Bewertung von Sortier-Verfahren Seite 1 Suchverfahren Begriffe Suchen = Bestimmen der Position (Adresse) eines Wertes in einer Datenfolge Sequentielles
Algorithmen und Datenstrukturen II
 Algorithmen und Datenstrukturen II Große Übung #1 Arne Schmidt 19.04.2016 Organisatorisches Arne Schmidt Große Übung 2 Homepage Aktuelle Informationen, Hausaufgaben, Slides auf: https://www.ibr.cs.tu-bs.de/courses/ss17/aud2/
Algorithmen und Datenstrukturen II Große Übung #1 Arne Schmidt 19.04.2016 Organisatorisches Arne Schmidt Große Übung 2 Homepage Aktuelle Informationen, Hausaufgaben, Slides auf: https://www.ibr.cs.tu-bs.de/courses/ss17/aud2/
Algorithmen und Datenstrukturen
 Rheinisch-Westfälische Technische Hochschule Aachen Lehrstuhl für Informatik VI Algorithmen und Datenstrukturen Vorlesungsmitschrift zur Vorlesung im SS 2004 Prof. Dr.-Ing. H. Ney Letzte Überarbeitung:
Rheinisch-Westfälische Technische Hochschule Aachen Lehrstuhl für Informatik VI Algorithmen und Datenstrukturen Vorlesungsmitschrift zur Vorlesung im SS 2004 Prof. Dr.-Ing. H. Ney Letzte Überarbeitung:
Kapitel 9. Komplexität von Algorithmen und Sortieralgorithmen
 Kapitel 9 Komplexität von Algorithmen und Sortieralgorithmen Arrays 1 Ziele Komplexität von Algorithmen bestimmen können (in Bezug auf Laufzeit und auf Speicherplatzbedarf) Sortieralgorithmen kennenlernen:
Kapitel 9 Komplexität von Algorithmen und Sortieralgorithmen Arrays 1 Ziele Komplexität von Algorithmen bestimmen können (in Bezug auf Laufzeit und auf Speicherplatzbedarf) Sortieralgorithmen kennenlernen:
Übung Algorithmen und Datenstrukturen
 Übung Algorithmen und Datenstrukturen Sommersemester 2017 Patrick Schäfer, Humboldt-Universität zu Berlin Agenda: Sortierverfahren 1. Schreibtischtest 2. Stabilität 3. Sortierung spezieller Arrays 4. Untere
Übung Algorithmen und Datenstrukturen Sommersemester 2017 Patrick Schäfer, Humboldt-Universität zu Berlin Agenda: Sortierverfahren 1. Schreibtischtest 2. Stabilität 3. Sortierung spezieller Arrays 4. Untere
Prof. Dr. Margarita Esponda
 Algorithmen und Programmieren II Sortieralgorithmen imperativ Teil I Prof. Dr. Margarita Esponda Freie Universität Berlin Sortieralgorithmen Bubble-Sort Insert-Sort Selection-Sort Vergleichsalgorithmen
Algorithmen und Programmieren II Sortieralgorithmen imperativ Teil I Prof. Dr. Margarita Esponda Freie Universität Berlin Sortieralgorithmen Bubble-Sort Insert-Sort Selection-Sort Vergleichsalgorithmen
9. Rekursion. 1 falls n 1 n (n 1)!, andernfalls. Experiment: Die Türme von Hanoi. Links Mitte Rechts. Mathematische Rekursion
 Experiment: Die Türme von Hanoi. Rekursion Mathematische Rekursion, Terminierung, der Aufrufstapel, Beispiele, Rekursion vs. Iteration Links Mitte Rechts Mathematische Rekursion Viele mathematische Funktionen
Experiment: Die Türme von Hanoi. Rekursion Mathematische Rekursion, Terminierung, der Aufrufstapel, Beispiele, Rekursion vs. Iteration Links Mitte Rechts Mathematische Rekursion Viele mathematische Funktionen
Kapitel 3: Sortierverfahren Gliederung
 Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
Algorithmen I. Dennis Hofheinz. Übungen: Lukas Barth und Lisa Kohl. Institut für theoretische Informatik Web: https://crypto.iti.kit.
 Algorithmen I Dennis Hofheinz Übungen: Lukas Barth und Lisa Kohl Institut für theoretische Informatik Web: https://crypto.iti.kit.edu/algo-sose16 (Folien von Peter Sanders) KIT Institut für Theoretische
Algorithmen I Dennis Hofheinz Übungen: Lukas Barth und Lisa Kohl Institut für theoretische Informatik Web: https://crypto.iti.kit.edu/algo-sose16 (Folien von Peter Sanders) KIT Institut für Theoretische
Übung zu Algorithmen und Datenstrukturen (für ET/IT)
 Übung zu Algorithmen und Datenstrukturen (für ET/IT) Wintersemester 2012/13 Jakob Vogel Computer-Aided Medical Procedures Technische Universität München Komplexität von Programmen Laufzeit kann näherungsweise
Übung zu Algorithmen und Datenstrukturen (für ET/IT) Wintersemester 2012/13 Jakob Vogel Computer-Aided Medical Procedures Technische Universität München Komplexität von Programmen Laufzeit kann näherungsweise
Teil 2 - Softwaretechnik. Modul: Programmierung B-PRG Grundlagen der Programmierung 1 Teil 2. Übersicht. Softwaretechnik
 Grundlagen der Programmierung 1 Modul: Programmierung B-PRG Grundlagen der Programmierung 1 Teil 2 Softwaretechnik Prof. Dr. O. Drobnik Professur Architektur und Betrieb verteilter Systeme Institut für
Grundlagen der Programmierung 1 Modul: Programmierung B-PRG Grundlagen der Programmierung 1 Teil 2 Softwaretechnik Prof. Dr. O. Drobnik Professur Architektur und Betrieb verteilter Systeme Institut für
Übung Algorithmen I
 Übung Algorithmen I 18.5.16 Lukas Barth [email protected] (Mit Folien von Julian Arz, Timo Bingmann, Sebastian Schlag und Christoph Striecks) Roadmap Sortieren Kleine Wiederholung Visualisierungen Adaptives
Übung Algorithmen I 18.5.16 Lukas Barth [email protected] (Mit Folien von Julian Arz, Timo Bingmann, Sebastian Schlag und Christoph Striecks) Roadmap Sortieren Kleine Wiederholung Visualisierungen Adaptives
Informatik II Sortieren
 lausthal Sortieralgorithmen Informatik II Sortieren Preprocessing fürs Suchen sind für kommerzielle Anwendungen häufig die Programmteile, die die meiste Rechenzeit verbrauchen viele raffinierte Methoden
lausthal Sortieralgorithmen Informatik II Sortieren Preprocessing fürs Suchen sind für kommerzielle Anwendungen häufig die Programmteile, die die meiste Rechenzeit verbrauchen viele raffinierte Methoden
Objektorientierte Programmierung VL: Prof. Dr. Marco Block-Berlitz - Freie Universität Berlin Proinformatik III
 Objektorientierte Programmierung VL: Prof. Dr. Marco Block-Berlitz - Freie Universität Berlin Proinformatik III Text: Hinnerk van Bruinehsen - Grafiken: Jens Fischer powered by SDS.mint SoSe 2011 1 Teil
Objektorientierte Programmierung VL: Prof. Dr. Marco Block-Berlitz - Freie Universität Berlin Proinformatik III Text: Hinnerk van Bruinehsen - Grafiken: Jens Fischer powered by SDS.mint SoSe 2011 1 Teil
Anwendungsbeispiel MinHeap
 Anwendungsbeispiel MinHeap Uns seien n ganze Zahlen gegeben und wir möchten darin die k größten Zahlen bestimmen; zudem gelten, dass n deutlich größer als k ist Wir können das Problem mit Laufzeit in O(n
Anwendungsbeispiel MinHeap Uns seien n ganze Zahlen gegeben und wir möchten darin die k größten Zahlen bestimmen; zudem gelten, dass n deutlich größer als k ist Wir können das Problem mit Laufzeit in O(n
Abgabe: (vor der Vorlesung) Aufgabe 2.1 (P) O-Notation Beweisen Sie die folgenden Aussagen für positive Funktionen f und g:
 TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK Lehrstuhl für Sprachen und Beschreibungsstrukturen SS 2009 Grundlagen: Algorithmen und Datenstrukturen Übungsblatt 2 Prof. Dr. Helmut Seidl, S. Pott,
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK Lehrstuhl für Sprachen und Beschreibungsstrukturen SS 2009 Grundlagen: Algorithmen und Datenstrukturen Übungsblatt 2 Prof. Dr. Helmut Seidl, S. Pott,
Übung Algorithmen und Datenstrukturen
 Übung Algorithmen und Datenstrukturen Sommersemester 2015 Marc Bux, Humboldt-Universität zu Berlin Organisation Vorlesung: Montag 11 13 Uhr Ulf Leser RUD 26, 0 115 Mittwoch 11 13 Uhr Ulf Leser RUD 26,
Übung Algorithmen und Datenstrukturen Sommersemester 2015 Marc Bux, Humboldt-Universität zu Berlin Organisation Vorlesung: Montag 11 13 Uhr Ulf Leser RUD 26, 0 115 Mittwoch 11 13 Uhr Ulf Leser RUD 26,
Datenstrukturen sind neben Algorithmen weitere wichtige Bausteine in der Informatik
 5. Datenstrukturen Motivation Datenstrukturen sind neben Algorithmen weitere wichtige Bausteine in der Informatik Eine Datenstruktur speichert gegebene Daten und stellt auf diesen bestimmte Operationen
5. Datenstrukturen Motivation Datenstrukturen sind neben Algorithmen weitere wichtige Bausteine in der Informatik Eine Datenstruktur speichert gegebene Daten und stellt auf diesen bestimmte Operationen
8.1.3 Operation Build-Max-Heap Operation zur Konstruktion eines Heaps Eingabe: Feld A[1..n], n = länge(a) BUILD-MAX-HEAP (A)
![8.1.3 Operation Build-Max-Heap Operation zur Konstruktion eines Heaps Eingabe: Feld A[1..n], n = länge(a) BUILD-MAX-HEAP (A) 8.1.3 Operation Build-Max-Heap Operation zur Konstruktion eines Heaps Eingabe: Feld A[1..n], n = länge(a) BUILD-MAX-HEAP (A)](/thumbs/61/46182525.jpg) Stand der Vorlesung: Datenstruktur Heap: fast vollständiger Binärbaum MaxHeap: sortierter Heap, größtes Element an Wurzel Sortierverfahren: HeapSort: Sortieren eines Feldes A[1.. n] Idee: in place: Feld
Stand der Vorlesung: Datenstruktur Heap: fast vollständiger Binärbaum MaxHeap: sortierter Heap, größtes Element an Wurzel Sortierverfahren: HeapSort: Sortieren eines Feldes A[1.. n] Idee: in place: Feld
