KONSTRUKTION VON MASSEN
|
|
|
- Meike Straub
- vor 9 Jahren
- Abrufe
Transkript
1 KONSTRUKTION VON MASSEN MARCUS HEITEL 1. Einleitung Wir wollen im Folgenden das Lebesguemaß konstruieren. Dieses soll die Eigenschaft λ ( [a, b = b a für a, b R besitzen. Nun ist ein Maß aber auf einer σ-algebra definiert (hier die Borel-σ-Algebra, welche nicht nur Intervalle aus R enthält. Wie wir sehen werden, bietet der Fortsetzungssatz von Carathéodory die Möglichkeit dieses Maß zu konstruieren. 2. Prämaß Als erstes benötigen wir ein paar neue Begriffe, unter anderem den Begriff des Prämaßes. Dieses soll ein allgemeiner Begriff als das Maß, das heißt, es ist nicht nur auf σ-algebren definiert, sondern auch auf Ringen. Im Folgenden sei Ω eine beliebige Menge. Definition 2.1. Ein Ring (über Ω R P(Ω ist ein Menge von Teilmengen von Ω derart, dass gilt: (i R (ii A, B R A B R (iii A, B R A\B R Bemerkung 2.2. Der in Definition 2.1 definierte Ring R ist ein Unterring von (P(Ω,, im Sinne der Algebra mit der Verknüpfung als Addition und als Mutliplikation, denn A B = (A\B (B\A und A B = A\(A\B. Satz 2.3. Algebren sind genau die Ringe, die die Grundmenge Ω enthalten. Beweis. Sei F eine Algebra. Ω = C F nach (i und (ii. Folglich enthält jede Algebra die Menge Ω. Weiter gilt A B F nach (iii und A\B = A B C = (A C B C F nach (iii und (ii. Sei nun R ein Ring, der Ω enthält, dann gilt: = Ω\Ω R, A C = Ω\A R für A R und A B R für A, B R per Definition eines Ringes. Definition 2.4. Sei R ein Ring. Ein Inhalt ist eine Abbildung µ : R [0, ] derart, dass gilt: (i µ( = 0 (ii A i R paarweise disjunkt µ( A i = µ(a i 1 (i 1,..., n}
2 2 MARCUS HEITEL Definition 2.5. Sei R ein Ring. Ein Prämaß ist eine Abbildung µ : R [0, ] derart, dass gilt: (i µ( = 0 (ii A i R paarweise disjunkt (i N, sodass µ( A i = µ(a i A i R (gilt i.a. nicht! (σ-additivität Bemerkung 2.6. Ein Prämaß ist kein Maß. Beschränkt man ein Prämaß auf eine σ-algebra, so ist es auch ein Maß. Beispiel 2.7. (Lebegue sches Prämaß Sei R = [a, b a b, a, b R} die Menge aller endlichen Vereinigungen von halboffenen Intervallen in R und λ : R [0, ] definiert durch λ( = 0 und für A = [a i, b i R gilt: λ(a = (b i a i Dabei ist a i < b i und [a i, b i disjunkt für i 1,..., n}. Dann ist R ein Ring und λ ein Prämaß auf R und wird als Lebegue sches Prämaß bezeichnet. Bemerkung 2.8. Das Lebesgue sches Prämaß kann mit dem Fortsetzungssatz zum Lebesguemaß fortgesetzt werden. 3. Äußeres Maß Ziel ist es nun ein Prämaß zu einem Maß auf einer σ-algebra fortzusetzen. Dafür brauchen wir Mengen, die messbar sind. Carathéodory zeigte die Messbarkeit von Mengen mit einer Abbildung, die auf der ganzen Potenzmenge definiert ist - das sogenannte äußere Maß. Definition 3.1. Ein äußeres Maß auf P(Ω ist eine Mengenfunktion ν : P(Ω [0, ] derart, dass gilt: (i ν( = 0 (ii A B Ω gilt: ν(a ν(b (Monotonie (iii Sei (A i i N P(Ω eine Folge, dann gilt ν( A i ν(a i (σ-subadditivität Bemerkung 3.2. Ein äußeres Maß ist kein Maß. Beispiel 3.3. (Erzeugtes äußeres Maß Ist durch µ auf einer Algebra oder einem Ring R ein Prämaß gegeben, so gilt: µ (A = inf µ(ãi } Ãi R, A à i, A P(Ω ist ein äußeres Maß, welches wir das von µ erzeugte äußeres Maß nennen. Beweis. (i µ ( = inf µ(ãi à i R, } Ãi = µ( = 0,denn = Ã\à R (à R
3 KONSTRUKTION VON MASSEN 3 ( A i R : (ii Sei A B Ω, dann ist B := (Ãi R : A } Ãi und damit auch µ (A = inf µ(ãi à i R, A Ãi inf µ( B i Bi R, A B B i } = µ (B } B } Ãi A := (iii Sei (A i i N P(Ω. Definiere U(A i als Menge aller Folgen ( A ij j N R, welche A i überdecken. Sei weiter obda µ (A i < U(A i. Sei ε > 0. i N ( A ij j N U(A i mit µ (A i + 2 i ε j=1 µ( A ij (i fest Die Doppelfolge (Ãij i,j N liegt dann in U ( A i µ ( A i (ii i,j=1 µ(ãij µ (A i + ε Weil ε > 0 beliebig war, folgt die Behauptung. Bemerkung 3.4. Im letzten Beispiel gilt der Beweis auch für einen Inhalt, nicht nur für Prämaße. Deshalb kann man auch durch Inhalte äußere Maße erzeugen. Im Beweis des Fortsetzungssatzes werden wir aber ein Prämaß betrachten, weshalb das obige Beispiel auch so gewählt wurde. 4. Der Fortsetzungssatz von Carathéodory Wir werden im Folgenden eine σ-algebra konstruieren, auf der das äußere Maß zu einem Maß wird. Dabei werden die Mengen, die sich in dieser σ-algebra befinden, durch folgende Definition ausgezeichnet: Definition 4.1. Sei ν ein äußeres Maß auf P(Ω und A Ω. Dann heißt A ν-messbar, falls B Ω gilt: ν(b = ν(a B + ν(b \ A Die Menge aller ν-messbaren Mengen wird mit Σ ν bezeichnet. Satz 4.2. (Carathéodory 1 Σ ν ist eine σ-algebra und ν Σν ist ein Maß. Beweis. Wir rechnen zuerst die Axiome einer Algebra nach: (i Σ ν, denn ν(b = ν( B + ν(b \ (B Ω (ii Sei A Σ ν A C Σ ν, denn: ν(b = ν(a B + ν(b \ A = ν(b \ A C + ν(a C B (B Ω (iii Seien A 1, A 2 Σ ν. Dann gilt nach Definition 4.1 insbesondere für die Wahl von B A 2 statt B mit B Ω : ν(b A 2 = ν((b A 2 A 1 + ν((b A 2 \A 1 Ebenso folgt mit der Wahl von B\(A 1 A 2 anstelle von B: ν ( B\(A 1 A 2 ( (B\(A1 = ν A 2 ( (B\(A1 A 2 + ν A 2 \A 2 = ν ( B (A C 1 A C 2 A 2 + ν ( B (A C 1 A C 2 A C 2 = ν ( (B A C 1 A 2 (B A 2 A C 2 + ν ( (B A C 1 A C 2 (B A C 2 = ν ( (B A 2 \A 1 + ν(b\a2 1 Constantin Carathéodory( : griechischer Mathematiker
4 4 MARCUS HEITEL Zusammen erhält man: ν(b = ν(b A 2 + ν(b\a 2 = ν ( (B A 2 A 1 + ν ( (B A2 \A 1 + ν ( B\(A 1 A 2 ν ( (B A 2 \A 1 = ν ( (B (A 1 A 2 + ν ( B\(A 1 A 2 (A 1 A 2 Σ ν und damit gilt mit (ii: (A 1 A 2 = (A C 1 A C 2 C Σ ν Also ist Σ ν eine Algebra. Als nächstes zeigen wir, dass ν endlich additiv ist. A 1, A 2 Σ ν mit A 1 A 2 = dann gilt mit der Definition der ν-messbarkeit für die Wahl von B (A 1 A 2 statt allgemeinem B Ω: ν ( B (A 1 A 2 ( (B = ν(b A 1 + ν (A1 A 2 \A 1 = ν(b A 1 + ν (B ( (A 1 A C 1 (A 2 A C 1 = ν(b A 1 + ν ( B (A 2 \A 1 = ν(b A 1 + ν(b A 2 Für B = Ω folgt dann ν(a 1 A 2 = ν(a 1 + ν(a 2 Nun wollen wir zeigen, dass es sich sogar um eine σ-algebra handelt. Seien A i Σ ν und A := i N A i. Da wir eine Algebra haben, gilt: n A i Σ ν (n N. Weiter folgt mit der endlichen Additivität und C n := n A i für B Ω ν(b = ν(b C n +ν(b\c n = ν(b\c n + ν(b A i ν(b\a+ ν(b A i Lassen wir nun n laufen, so erhalten wir: ν(b ν(b\a + ν(b A i und aufgrund der Subadditivität von ν ν(b ν(b A + ν(b\a ν(b\a + ν(b A i Deshalb müssen die Ungleichungen Gleichungen gewesen sein, womit gilt ν(b = ν(b A + ν(b\a Damit ist A Σ ν und Σ ν eine σ-algebra. ν ist ein Maß, was aus ( mit B = A folgt (σ-additivität. Satz 4.3. (Fortsetzungssatz von Carathéodory Gilt ν = µ von Beispiel 3.3, so enthält Σ ν den Ring R, auf der das Prämaß µ defniert ist und ν R = µ. Beweis. Für A R und B Ω gilt µ (A = µ(a und aus der Subadditivität folgt µ (B µ (A B + µ (B \ A Zu ε > 0 existiert eine Folge (A i i N R mit B i N A i und µ (A i µ (B + ε (nach der Definition von µ. Aus der Subadditivität von µ folgt dann: µ (B A µ (A i A = µ(a i A, (
5 und wir erhalten damit: KONSTRUKTION VON MASSEN 5 µ (B\A µ (A i \A = µ(a i \A µ (B µ (B A + µ (B\A (µ(a i A + (µ(a i \A = µ(a i µ (B + ε Weil ε > 0 beliebig war, folgt A Σ ν und ν R = µ Bemerkung 4.4. Es ist nicht nötig, dass µ ein Prämaß ist, es kann auch ein Inhalt sein. Das Prämaß wurde dennoch verwendet, weil so umgekehrt gezeigt werden kann, dass zu jedem Prämaß auf einem Ring auch eine σ- Algebra existiert, die den Ring umfasst und ein Maß, welches eingeschränkt auf den Ring gleich dem Prämaß ist. Mithilfe des Fortsetzungssatzes kann das Lebesgue sche Prämaß aus Beispiel 2.7 zum Lebesguemaß fortgesetzt werden. Eine weitere Anwendung ist das Zeigen der Existenz von Produktmaßen. Satz 4.5. (Eindeutigkeitssatz Es sei E P(Ω eine durchschnittsstabile Familie, das heißt für A, B E gilt auch A B E. Σ = σ(e sei die von E erzeugte σ-algebra. Seien weiter µ, ν : Σ [0, ] Maße derart, dass µ(e = ν(e E E. Es gebe E k E mit µ(e k < sodass Ω = k N E k. Dann ist µ = ν. Bemerkung 4.6. Der Eindeutigkeitssatz liefert zusammen mit dem Fortsetzungssatz auf einem -stabilen Erzeuger eine eindeutige Fortsetzung von σ-endichem (R, µ auf (Σ ν, ν Σν. Literatur [Bal10] Werner Balser, Maßtheorie, Skript zur Vorlesung an der Universität Ulm, cantor.mathematik.uni-ulm.de/m5/balser/skripten/masstheorie.pdf, [Bau92] Heinz Bauer, Maß- und Integrationstheorie, de Gruyter Lehrbuch, Berlin, [Bog07] Vladimir I. Bogachev, Measure Theory, Springer Verlag, [Els08] Jürgen Elstrodt, Maß- und Integrationstheorie, Springer Verlag, 2008.
2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit
 2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit a) Fortsetzungssatz, Eindeutigkeit Es wird gezeigt, dass jedes Prämaß µ auf einem Ring R zu einem Maß µ auf A(R) fortgesetzt werden kann, d.h. µ kann
2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit a) Fortsetzungssatz, Eindeutigkeit Es wird gezeigt, dass jedes Prämaß µ auf einem Ring R zu einem Maß µ auf A(R) fortgesetzt werden kann, d.h. µ kann
Universität Leipzig, SoSo 2013
 Vorlesung Wahrscheinlichkeitstheorie I Universität Leipzig, SoSo 2013 Prof. Dr. Max v. Renesse [email protected] Sprechstunde: Di 13.15-14.45, A 337 Übungen: Mo 11.15 -- 12.45 A 314 K. Zimmermann
Vorlesung Wahrscheinlichkeitstheorie I Universität Leipzig, SoSo 2013 Prof. Dr. Max v. Renesse [email protected] Sprechstunde: Di 13.15-14.45, A 337 Übungen: Mo 11.15 -- 12.45 A 314 K. Zimmermann
1 Das Lebesgue-Maß. 1.1 Etwas Maßtheorie. Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}.
 1 Das Lebesgue-Maß 1.1 Etwas Maßtheorie Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}. Definition 1.1. Ein nichtleeres Mengensystem A P(X) heißt σ-algebra, wenn: (A1) X A (A2) Wenn
1 Das Lebesgue-Maß 1.1 Etwas Maßtheorie Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}. Definition 1.1. Ein nichtleeres Mengensystem A P(X) heißt σ-algebra, wenn: (A1) X A (A2) Wenn
Existenz des Lebesgue-Borel-Maßes
 A Existenz des Lebesgue-Borel-Maßes In diesem (nicht prüfungsrelevanten) Anhang tragen wir u.a. die Existenz des Lebesgue- Borel-Maßes nach. 52 Es empfiehlt sich, diesen Anhang erst nach Kapitel 5 zu lesen
A Existenz des Lebesgue-Borel-Maßes In diesem (nicht prüfungsrelevanten) Anhang tragen wir u.a. die Existenz des Lebesgue- Borel-Maßes nach. 52 Es empfiehlt sich, diesen Anhang erst nach Kapitel 5 zu lesen
Metrische äußere Maße, Borel-Maße
 Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
σ-algebren, Definition des Maßraums
 σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Reelle Analysis. Vorlesungsskript. Enno Lenzmann, Universität Basel. 11. Oktober 2013
 Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
Skript zur Vorlesung Analysis 3
 Skript zur Vorlesung Analysis 3 Wintersemester 2013/2014 Prof. Dr. Benjamin Schlein Inhaltsverzeichnis 1 Masstheorie 2 1.1 σ-algebren.................................. 6 1.2 Masse.....................................
Skript zur Vorlesung Analysis 3 Wintersemester 2013/2014 Prof. Dr. Benjamin Schlein Inhaltsverzeichnis 1 Masstheorie 2 1.1 σ-algebren.................................. 6 1.2 Masse.....................................
Musterlösung Analysis 3 - Maßtherorie
 Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1)
Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1)
Lehrstuhl IV Stochastik & Analysis. Stochastik II. Wahrscheinlichkeitstheorie I. Skriptum nach einer Vorlesung von Hans-Peter Scheffler
 Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Das Lebesgue-Maß im R p
 Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
A. Maß- und Integrationstheorie
 A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
Lemma (Eigenschaften elementarer Mengen) 1. Jede elementare Menge lässt sich als disjunkte Vereinigung halboffener Intervalle schreiben.
 12.3. DIE LEBESGUE ALGEBRA 19 Bemerkung 12.3.2 (Bezeichnungen) Im Buch von Bauer [2] werden elementare Mengen als Figuren bezeichnet. Wir folgen mit unserer Nomenklatur Rudin [15]. Natürlich kann man auf
12.3. DIE LEBESGUE ALGEBRA 19 Bemerkung 12.3.2 (Bezeichnungen) Im Buch von Bauer [2] werden elementare Mengen als Figuren bezeichnet. Wir folgen mit unserer Nomenklatur Rudin [15]. Natürlich kann man auf
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang. Lösung - Serie 2. + A k = A c k Ac k 0
 D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
Maßtheorie. Skript zur Vorlesung von Prof. Dr. Michael Kohler. Sommersemester 2005 und Wintersemester 2005/2006
 Maßtheorie Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2005 und Wintersemester 2005/2006 1 1 Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Länge / Fläche
Maßtheorie Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2005 und Wintersemester 2005/2006 1 1 Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Länge / Fläche
Wahrscheinlichkeitstheorie und Maßtheorie
 KAPITEL 7 Wahrscheinlichkeitstheorie und Maßtheorie 7.1. Vorüberlegungen Die folgenden drei Beispiele sind Spezialfälle des Oberbegriffs Maß. Beispiel 7.1.1 (Verteilung der Ladung oder der Masse). Man
KAPITEL 7 Wahrscheinlichkeitstheorie und Maßtheorie 7.1. Vorüberlegungen Die folgenden drei Beispiele sind Spezialfälle des Oberbegriffs Maß. Beispiel 7.1.1 (Verteilung der Ladung oder der Masse). Man
Skriptbausteine zur Vorlesung Maßtheorie
 Skriptbausteine zur Vorlesung Maßtheorie Vorlesender: Prof. Dr. Bernd Hofmann Der folgende Text soll die Nacharbeit der Vorlesung erleichtern und dabei an Definitionen, Sätze und Beispiele erinnern. Das
Skriptbausteine zur Vorlesung Maßtheorie Vorlesender: Prof. Dr. Bernd Hofmann Der folgende Text soll die Nacharbeit der Vorlesung erleichtern und dabei an Definitionen, Sätze und Beispiele erinnern. Das
Der Satz von Lusin. Markus Schuster Juni 2012 Universita t Ulm
 Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Universita t Ulm Maßtheorie Seminar 2012 Seite 2 Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Inhaltsverzeichnis Motivation Definitionen Der Satz
Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Universita t Ulm Maßtheorie Seminar 2012 Seite 2 Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Inhaltsverzeichnis Motivation Definitionen Der Satz
Hausdorff-Maß und Hausdorff-Dimension. Jens Krüger
 Hausdorff-Maß und Hausdorff-Dimension Jens Krüger Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen aus der Maßtheorie 3 3 Die Konstruktion des Hausdorff-Maßes 4 4 Eigenschaften des Hausdorff-Maßes und Hausdorff-Dimension
Hausdorff-Maß und Hausdorff-Dimension Jens Krüger Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen aus der Maßtheorie 3 3 Die Konstruktion des Hausdorff-Maßes 4 4 Eigenschaften des Hausdorff-Maßes und Hausdorff-Dimension
Lösungsvorschlag zu den Hausaufgaben der 3. Übung
 FAKULTÄT FÜR MATHEMATIK Prof. Dr. Patrizio Neff 30.0.204 Lösungsvorschlag zu den Hausaufgaben der 3. Übung Aufgabe : (6 Punte) Welche der folgenden Tupel sind Maßräume? Beweisen Sie Ihre Behauptung. {
FAKULTÄT FÜR MATHEMATIK Prof. Dr. Patrizio Neff 30.0.204 Lösungsvorschlag zu den Hausaufgaben der 3. Übung Aufgabe : (6 Punte) Welche der folgenden Tupel sind Maßräume? Beweisen Sie Ihre Behauptung. {
Übungen zur Analysis 3
 Mathematisches Institut der Universität München Prof. Dr. Franz Merkl Wintersemester 013/01 Blatt 17.10.013 Übungen zur Analysis 3.1ε σ-subadditivität. a Es sei µ ein Inhalt auf einer Mengenalgebra A.
Mathematisches Institut der Universität München Prof. Dr. Franz Merkl Wintersemester 013/01 Blatt 17.10.013 Übungen zur Analysis 3.1ε σ-subadditivität. a Es sei µ ein Inhalt auf einer Mengenalgebra A.
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
Kapitel I. Maßtheorie
 Aufgabenvorschläge für das Proseminar zur Maß- und Integrationstheorie (WS 10/11) Shantanu Dave & Günther Hörmann Kapitel I. Maßtheorie zu 1. Maße und σ-algebren 1 Sei Ω eine Menge. Zeige: (a) Ist A eine
Aufgabenvorschläge für das Proseminar zur Maß- und Integrationstheorie (WS 10/11) Shantanu Dave & Günther Hörmann Kapitel I. Maßtheorie zu 1. Maße und σ-algebren 1 Sei Ω eine Menge. Zeige: (a) Ist A eine
Grundlagen Mengenlehre, Maßtheorie
 Grundlagen Mengenlehre, Maßtheorie 12. März 2011 1 Grundlagen der Mengenlehre - Rechnen mit Mengen Im folgenden bezeichnen wir mit P(X) die Menge aller Teilmengen von X, die sogenannte Potenzmenge von
Grundlagen Mengenlehre, Maßtheorie 12. März 2011 1 Grundlagen der Mengenlehre - Rechnen mit Mengen Im folgenden bezeichnen wir mit P(X) die Menge aller Teilmengen von X, die sogenannte Potenzmenge von
Aufgaben zu Kapitel 0
 Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Meßbare Funktionen. bilden die Grundlage der Integrationstheorie. Definition 24.1 :
 24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
Ferienkurs in Maß- und Integrationstheorie
 Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS-
 ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS- und WAHRSCHEINLICHKEITSTHEORIE im SS 2014 Übung Maß- und Integrationstheorie (SS 2014) 1 Aufgabe 1 (σ-algebra)
ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS- und WAHRSCHEINLICHKEITSTHEORIE im SS 2014 Übung Maß- und Integrationstheorie (SS 2014) 1 Aufgabe 1 (σ-algebra)
Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie
 Dr. Christoph Luchsinger Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie Allgemeine Masse Herausgabe des Übungsblattes: Woche 13, Abgabe der Lösungen: Woche 14 (bis Freitag, 16.15 Uhr), Besprechung:
Dr. Christoph Luchsinger Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie Allgemeine Masse Herausgabe des Übungsblattes: Woche 13, Abgabe der Lösungen: Woche 14 (bis Freitag, 16.15 Uhr), Besprechung:
Stochastik. Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2007
 Stochastik Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2007 1 1. Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Wahrscheinlichkeit / Länge / Fläche / Volumen
Stochastik Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2007 1 1. Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Wahrscheinlichkeit / Länge / Fläche / Volumen
Kapitel 19. Das Lebesgue Maß σ Algebren und Maße
 Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
Funktionalanalysis und Integrationstheorie
 Funktionalanalysis und Integrationstheorie Vorlesungsnotizen Johannes Kepler Universität Linz Technisch-Naturwissenschaftliche Fakultät Institut für Analysis Prof. Dr. Aicke Hinrichs Wintersemester 2015/16
Funktionalanalysis und Integrationstheorie Vorlesungsnotizen Johannes Kepler Universität Linz Technisch-Naturwissenschaftliche Fakultät Institut für Analysis Prof. Dr. Aicke Hinrichs Wintersemester 2015/16
10 Der Satz von Radon-Nikodym
 uch im Sinne einer Vorabinformation vor der Stochastik-Vorlesung wollen wir abschließend kurz absolut stetige Maße und den Satz von Radon-Nikodym streifen. Definition 10.1. Seien (, M) ein messbarer Raum
uch im Sinne einer Vorabinformation vor der Stochastik-Vorlesung wollen wir abschließend kurz absolut stetige Maße und den Satz von Radon-Nikodym streifen. Definition 10.1. Seien (, M) ein messbarer Raum
Maß & Integral de Gruyter Lehrbuch, Berlin 2015 ISBN:
 Maß & Integral de Gruyter Lehrbuch, Berlin 205 ISBN: 978 3 03484 9 Lösungshandbuch René L. Schilling & Franziska Kühn Dresden, Januar 205 Diese Version: Februar 206 R.L. Schilling: Maß & Integral Dank.
Maß & Integral de Gruyter Lehrbuch, Berlin 205 ISBN: 978 3 03484 9 Lösungshandbuch René L. Schilling & Franziska Kühn Dresden, Januar 205 Diese Version: Februar 206 R.L. Schilling: Maß & Integral Dank.
Meßbare Funktionen. Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen.
 Meßbare Funktionen Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen. Definition. Seien (X, Ω 1 ) und (Y, Ω 2 ) Meßräume. Eine Abbildung f : X Y heißt Ω 1 -Ω 2 -meßbar oder kurz
Meßbare Funktionen Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen. Definition. Seien (X, Ω 1 ) und (Y, Ω 2 ) Meßräume. Eine Abbildung f : X Y heißt Ω 1 -Ω 2 -meßbar oder kurz
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
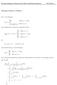 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Maße auf Produkträumen
 Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Maßtheorie. Wie interpretiert man Volumenmessung? Ziel :
 23 Maßtheorie Ziel : Entwicklung allgemeiner Konzepte, die es gestatten, z.b. Volumina und Oberflächen von Körpern R 3 sinnvoll zu definieren und zu berechnen; sinnvoll soll heißen : für den Einheitswürfel
23 Maßtheorie Ziel : Entwicklung allgemeiner Konzepte, die es gestatten, z.b. Volumina und Oberflächen von Körpern R 3 sinnvoll zu definieren und zu berechnen; sinnvoll soll heißen : für den Einheitswürfel
01145 Maß- und Integrationstheorie
 01145 Maß- und Integrationstheorie Eine Einführung Prof. Dr. Werner Kirsch Wissenschaftliche Mitarbeit: Dr. Tobias Mühlenbruch Lehrgebiet Stochastik FernUniversität in Hagen [email protected]
01145 Maß- und Integrationstheorie Eine Einführung Prof. Dr. Werner Kirsch Wissenschaftliche Mitarbeit: Dr. Tobias Mühlenbruch Lehrgebiet Stochastik FernUniversität in Hagen [email protected]
Stochastik I. Vorlesungsmitschrift
 Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Analysis 3. Stand 12. April Alle Rechte beim Autor.
 Analysis 3 Steffen Börm Stand 12. April 2011 Alle Rechte beim Autor. Inhaltsverzeichnis 1 Einleitung 5 2 Grundlagen der Maßtheorie 7 2.1 Motivation................................... 7 2.2 Systeme von
Analysis 3 Steffen Börm Stand 12. April 2011 Alle Rechte beim Autor. Inhaltsverzeichnis 1 Einleitung 5 2 Grundlagen der Maßtheorie 7 2.1 Motivation................................... 7 2.2 Systeme von
Maß- und Integrationstheorie
 Prof. Dr. László Székelyhidi Maß- und Integrationstheorie Vorlesungsskript WS2013/14 4. Februar 2014 Inhaltsverzeichnis 1 Maße und σ-algebren.......................................... 1 1.1 Einführung:
Prof. Dr. László Székelyhidi Maß- und Integrationstheorie Vorlesungsskript WS2013/14 4. Februar 2014 Inhaltsverzeichnis 1 Maße und σ-algebren.......................................... 1 1.1 Einführung:
Analysis III - Bachelorversion
 Analysis III - Bachelorversion Die Mitarbeiter von http://mitschriebwiki.nomeata.de/ 28. September 217 Inhaltsverzeichnis Inhaltsverzeichnis 2 I. Vorwort 5 I.1. Über dieses Skriptum..................................
Analysis III - Bachelorversion Die Mitarbeiter von http://mitschriebwiki.nomeata.de/ 28. September 217 Inhaltsverzeichnis Inhaltsverzeichnis 2 I. Vorwort 5 I.1. Über dieses Skriptum..................................
1 Grundlagen der Maßtheorie
 1 Grundlagen der Maßtheorie In diesem Kapitel führen wir die Mengensysteme ein, die eine systematische Betrachtung von Ereignissen und zufälligen Beobachtungen in der Wahrscheinlichkeitstheorie erlauben.
1 Grundlagen der Maßtheorie In diesem Kapitel führen wir die Mengensysteme ein, die eine systematische Betrachtung von Ereignissen und zufälligen Beobachtungen in der Wahrscheinlichkeitstheorie erlauben.
Darstellungssatz von Riesz in vollständig regulären Räumen. Carina Pöll Wintersemester 2012
 Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Zufallsvariable, Verteilung, Verteilungsfunktion
 Kapitel 5 Zufallsvariable, Verteilung, Verteilungsfunktion 5.1 Zufallsvariable Sei (Ω, A, P ) ein beliebiger Wahrscheinlichkeitsraum. Häufig interessiert nicht ω selbst, sondern eine Kennzahl X(ω), d.h.
Kapitel 5 Zufallsvariable, Verteilung, Verteilungsfunktion 5.1 Zufallsvariable Sei (Ω, A, P ) ein beliebiger Wahrscheinlichkeitsraum. Häufig interessiert nicht ω selbst, sondern eine Kennzahl X(ω), d.h.
I Grundbegriffe 1 1 Wahrscheinlichkeitsräume Bedingte Wahrscheinlichkeiten und Unabhängigkeit Reellwertige Zufallsvariablen...
 Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
Mathematik III. Henri Léon Lebesgue ( ) Das Borel-Lebesgue-Maß auf R.
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 67 Wir haben jetzt alle Hilfsmittel zusammen, um auf den Borel-Mengen des R n ein Maß zu definieren, dass für einen Quader, dessen Seiten
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 67 Wir haben jetzt alle Hilfsmittel zusammen, um auf den Borel-Mengen des R n ein Maß zu definieren, dass für einen Quader, dessen Seiten
Analysis 3. Vorlesungsskript Wintersemester 2011/12. Bernd Schmidt. Version vom 16. Februar 2012
 Analysis 3 Vorlesungsskript Wintersemester 2011/12 Bernd Schmidt Version vom 16. Februar 2012 Institut für Mathematik, Universität Augsburg, Universitätsstr. 14, 86135 Augsburg, [email protected]
Analysis 3 Vorlesungsskript Wintersemester 2011/12 Bernd Schmidt Version vom 16. Februar 2012 Institut für Mathematik, Universität Augsburg, Universitätsstr. 14, 86135 Augsburg, [email protected]
Kapitel II Kontinuierliche Wahrscheinlichkeitsräume
 Kapitel II Kontinuierliche Wahrscheinlichkeitsräume 1. Einführung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 211/476 Beispiel 85 Wir betrachten
Kapitel II Kontinuierliche Wahrscheinlichkeitsräume 1. Einführung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 211/476 Beispiel 85 Wir betrachten
Multiplikationsoperatoren
 Multiplikationsoperatoren Dennis Dyck 07.04.2014 1 Einleitung In dem ersten Vortrag des eminars soll es um die Untersuchung von Multiplikationsoperatoren gehen. Es werden grundlegende Eigenschaften hergeleitet
Multiplikationsoperatoren Dennis Dyck 07.04.2014 1 Einleitung In dem ersten Vortrag des eminars soll es um die Untersuchung von Multiplikationsoperatoren gehen. Es werden grundlegende Eigenschaften hergeleitet
Teil I: Maß- und Integrationstheorie
 Skript zur Vorlesung Maß- und Wahrscheinlichkeitstheorie Teil I: Maß- und Integrationstheorie Robert Hable Wintersemester 2009/2010 Institut für Statistik LMU München Korrigierte und erweiterte Fassung
Skript zur Vorlesung Maß- und Wahrscheinlichkeitstheorie Teil I: Maß- und Integrationstheorie Robert Hable Wintersemester 2009/2010 Institut für Statistik LMU München Korrigierte und erweiterte Fassung
3 Bedingte Erwartungswerte
 3 Bedingte Erwartungswerte 3.3 Existenz und Eindeutigkeit des bedingten Erwartungswertes E A 0(X) 3.6 Konvexitätsungleichung für bedingte Erwartungswerte 3.9 Konvergenzsätze von Levi, Fatou und Lebesgue
3 Bedingte Erwartungswerte 3.3 Existenz und Eindeutigkeit des bedingten Erwartungswertes E A 0(X) 3.6 Konvexitätsungleichung für bedingte Erwartungswerte 3.9 Konvergenzsätze von Levi, Fatou und Lebesgue
Wahrscheinlichkeitsrechnung
 Grundstudium Mathematik Wahrscheinlichkeitsrechnung Bearbeitet von Dominique Foata, Aime Fuchs 1. Auflage 1999. Taschenbuch. xv, 383 S. Paperback ISBN 978 3 7643 6169 3 Format (B x L): 17 x 24,4 cm Gewicht:
Grundstudium Mathematik Wahrscheinlichkeitsrechnung Bearbeitet von Dominique Foata, Aime Fuchs 1. Auflage 1999. Taschenbuch. xv, 383 S. Paperback ISBN 978 3 7643 6169 3 Format (B x L): 17 x 24,4 cm Gewicht:
Serie 5 Lösungsvorschläge
 D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 5 Lösungsvorschläge 1. Finden Sie eine stetige Funktion f : [, ) R, so dass f nicht Lebesgue-integrierbar T ist, jedoch der Grenzwert lim f(t)
D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 5 Lösungsvorschläge 1. Finden Sie eine stetige Funktion f : [, ) R, so dass f nicht Lebesgue-integrierbar T ist, jedoch der Grenzwert lim f(t)
Definitionen und Aussagen zur Maßtheorie
 Definitionen und Aussagen zur Maßtheorie Man möchte den Teilmengen eines Raumes ein Gewicht zuordnen. Wir werden sehen, daß dies in sinnvoller Weise häufig nicht für alle Teilmengen möglich ist, sondern
Definitionen und Aussagen zur Maßtheorie Man möchte den Teilmengen eines Raumes ein Gewicht zuordnen. Wir werden sehen, daß dies in sinnvoller Weise häufig nicht für alle Teilmengen möglich ist, sondern
Scheinklausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Wahrscheinlichkeitstheorie. von Peter Pfaffelhuber Version: 21. Oktober 2013
 Wahrscheinlichkeitstheorie von Peter Pfaffelhuber Version: 21. Oktober 2013 2 Vorbemerkung Dieses Manuskript ist parallel zu Vorlesungen entstanden, die ich im Wintersemester 2010 (Wahrscheinlichkeitstheorie),
Wahrscheinlichkeitstheorie von Peter Pfaffelhuber Version: 21. Oktober 2013 2 Vorbemerkung Dieses Manuskript ist parallel zu Vorlesungen entstanden, die ich im Wintersemester 2010 (Wahrscheinlichkeitstheorie),
Fraktale Geometrie. 9: Metrische äußere Maße II. Universität Regensburg Sommersemester Daniel Heiß:
 Universität Regensburg Sommersemester 013 Daniel Heiß: 9: Metrische äußere Maße II I Das mehrdimensionale Lebesguemaß 1.1 Definition (i) Für reelle Zahlen a b, c d ist ein Rechteck im R die Menge R = a,
Universität Regensburg Sommersemester 013 Daniel Heiß: 9: Metrische äußere Maße II I Das mehrdimensionale Lebesguemaß 1.1 Definition (i) Für reelle Zahlen a b, c d ist ein Rechteck im R die Menge R = a,
Höhere Analysis. dω = Reiner Lauterbach. Vorlesung. Universität Hamburg, WS 2015/2016
 Höhere Analysis Vorlesung Reiner Lauterbach M dω = M ω Universität Hamburg, WS 2015/2016 ii Inhaltsverzeichnis 12 Integration im R n 5 12.1 Mengenalgebren............................ 6 12.2 Inhalt und
Höhere Analysis Vorlesung Reiner Lauterbach M dω = M ω Universität Hamburg, WS 2015/2016 ii Inhaltsverzeichnis 12 Integration im R n 5 12.1 Mengenalgebren............................ 6 12.2 Inhalt und
8. Formelsammlung. Pr[ ] = 0. 0 Pr[A] 1. Pr[Ā] = 1 Pr[A] A B = Pr[A] Pr[B] DWT 8.1 Gesetze zum Rechnen mit Ereignissen 203/467 Ernst W.
![8. Formelsammlung. Pr[ ] = 0. 0 Pr[A] 1. Pr[Ā] = 1 Pr[A] A B = Pr[A] Pr[B] DWT 8.1 Gesetze zum Rechnen mit Ereignissen 203/467 Ernst W. 8. Formelsammlung. Pr[ ] = 0. 0 Pr[A] 1. Pr[Ā] = 1 Pr[A] A B = Pr[A] Pr[B] DWT 8.1 Gesetze zum Rechnen mit Ereignissen 203/467 Ernst W.](/thumbs/69/59978031.jpg) 8. Formelsammlung 8.1 Gesetze zum Rechnen mit Ereignissen Im Folgenden seien A und B, sowie A 1,..., A n Ereignisse. Die Notation A B steht für A B und zugleich A B = (disjunkte Vereinigung). A 1... A
8. Formelsammlung 8.1 Gesetze zum Rechnen mit Ereignissen Im Folgenden seien A und B, sowie A 1,..., A n Ereignisse. Die Notation A B steht für A B und zugleich A B = (disjunkte Vereinigung). A 1... A
Inhaltsfunktion für beliebige Mengen aus? 1, falls x Ω 0, falls x 6 Ω. Beispielsweise ermitteln wir für das kompakte Intervall [a,b] R
![Inhaltsfunktion für beliebige Mengen aus? 1, falls x Ω 0, falls x 6 Ω. Beispielsweise ermitteln wir für das kompakte Intervall [a,b] R Inhaltsfunktion für beliebige Mengen aus? 1, falls x Ω 0, falls x 6 Ω. Beispielsweise ermitteln wir für das kompakte Intervall [a,b] R](/thumbs/75/72889263.jpg) Kaitel 10 Das Lebesguesche Maß 10.1 Das Maßroblem Das ursrüngliche Problem der Geometrie ist das sogenannten Maßroblem, dessen Behandlung im Zentrum der folgenden Kaitel steht. Worum geht es? Ebenen, linear
Kaitel 10 Das Lebesguesche Maß 10.1 Das Maßroblem Das ursrüngliche Problem der Geometrie ist das sogenannten Maßroblem, dessen Behandlung im Zentrum der folgenden Kaitel steht. Worum geht es? Ebenen, linear
1. Masstheorie Mengensysteme 1. MASSTHEORIE 1
 1. MASSTHEORIE 1 1. Masstheorie In der Wahrscheinlichkeitstheorie betrachten wir Situationen, die wir nicht exakt vorhersagen können. Zum einen kann dies sein, da der Ausgang zufällig ist. Zum anderen
1. MASSTHEORIE 1 1. Masstheorie In der Wahrscheinlichkeitstheorie betrachten wir Situationen, die wir nicht exakt vorhersagen können. Zum einen kann dies sein, da der Ausgang zufällig ist. Zum anderen
Maß- und Integrationstheorie
 Maß- und Integrationstheorie Vorlesung an der Universität des Saarlandes Version 5.0 Klaus Schindler Version 5.0 c K. Schindler 2011 Für A... Inhaltsverzeichnis I Inhaltsverzeichnis Inhaltsverzeichnis
Maß- und Integrationstheorie Vorlesung an der Universität des Saarlandes Version 5.0 Klaus Schindler Version 5.0 c K. Schindler 2011 Für A... Inhaltsverzeichnis I Inhaltsverzeichnis Inhaltsverzeichnis
Serie 2 Lösungsvorschläge
 D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 2 Lösungsvorschläge 1. Seien folgende Mengen gegeben: und für a, b R R := [, ] := R {, }, (a, ] := (a, ) { }, [, b) := (, b) { }. Wir nennen
D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 2 Lösungsvorschläge 1. Seien folgende Mengen gegeben: und für a, b R R := [, ] := R {, }, (a, ] := (a, ) { }, [, b) := (, b) { }. Wir nennen
Das Lebesgue-Integral
 Das Lebesgue-Integral Bei der Einführung des Integralbegriffs gehen wir schrittweise vor. Zunächst erklären wir das Integral von charakteristischen Funktionen, danach von positiven einfachen Funktionen
Das Lebesgue-Integral Bei der Einführung des Integralbegriffs gehen wir schrittweise vor. Zunächst erklären wir das Integral von charakteristischen Funktionen, danach von positiven einfachen Funktionen
Maß- und Integrationstheorie
 Maß- und Integrationstheorie Klaus Ritter Kaiserslautern, SS 2014 Literatur Insbesondere J. Elstrodt, Maß- und Integrationstheorie, Springer, Berlin, 1. Auflage 1996, 7. Auflage 2011. Vorkenntnisse Grundlagen
Maß- und Integrationstheorie Klaus Ritter Kaiserslautern, SS 2014 Literatur Insbesondere J. Elstrodt, Maß- und Integrationstheorie, Springer, Berlin, 1. Auflage 1996, 7. Auflage 2011. Vorkenntnisse Grundlagen
A n a l y s i s. Wintersemester 16/17. Ernst Kuwert. Mathematisches Institut Universität Freiburg
 A n a l y s i s III Wintersemester 16/17 Ernst Kuwert Mathematisches Institut Universität Freiburg Vorbemerkung Dieses Skript ist aus meinen Vorlesungen im WS 07 und WS 16/17 entstanden, es entspricht
A n a l y s i s III Wintersemester 16/17 Ernst Kuwert Mathematisches Institut Universität Freiburg Vorbemerkung Dieses Skript ist aus meinen Vorlesungen im WS 07 und WS 16/17 entstanden, es entspricht
Analysis III. Inhaltsverzeichnis. Martin Brokate. 1 Maße 1. 2 Das Lebesgue-Integral Normierte und metrische Räume 38
 Analysis III Martin Brokate Inhaltsverzeichnis 1 Maße 1 2 Das Lebesgue-Integral 26 3 Normierte und metrische Räume 38 4 Konvergenzsätze und L p -Räume 48 5 Mehrfachintegrale, Satz von Fubini 63 6 Metrische
Analysis III Martin Brokate Inhaltsverzeichnis 1 Maße 1 2 Das Lebesgue-Integral 26 3 Normierte und metrische Räume 38 4 Konvergenzsätze und L p -Räume 48 5 Mehrfachintegrale, Satz von Fubini 63 6 Metrische
Maß- und Wahrscheinlichkeitstheorie
 Skript zur Vorlesung Maß- und Wahrscheinlichkeitstheorie Robert Hable Christina Schneider Paul Fink * Wintersemester 2014/15 LMU München Institut für Statistik * Originalfassung Kapitel 1-10: Robert Hable
Skript zur Vorlesung Maß- und Wahrscheinlichkeitstheorie Robert Hable Christina Schneider Paul Fink * Wintersemester 2014/15 LMU München Institut für Statistik * Originalfassung Kapitel 1-10: Robert Hable
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie. Tobias Ried
 Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Maß-, Integrationstheorie- und Wahrscheinlichkeitstheorie
 Maß-, Integrationstheorie- und Wahrscheinlichkeitstheorie Vorlesung an der Universität des Saarlandes Version 7.0 Klaus Schindler c K. Schindler 2014 Für A... Inhaltsverzeichnis Inhaltsverzeichnis Vorwort
Maß-, Integrationstheorie- und Wahrscheinlichkeitstheorie Vorlesung an der Universität des Saarlandes Version 7.0 Klaus Schindler c K. Schindler 2014 Für A... Inhaltsverzeichnis Inhaltsverzeichnis Vorwort
Grundlagen der Maßtheorie
 Kapitel 4 Grundlagen der Maßtheorie 4.1 Das Maßproblem Das vielleicht ursprünglichste Problem der Geometrie ist das sogenannten Maßproblem. Dessen Behandlung steht im Zentrum dieses vierten Kapitels. Unsere
Kapitel 4 Grundlagen der Maßtheorie 4.1 Das Maßproblem Das vielleicht ursprünglichste Problem der Geometrie ist das sogenannten Maßproblem. Dessen Behandlung steht im Zentrum dieses vierten Kapitels. Unsere
Skript zur Vorlesung. Mass und Integral. Urs Lang. Sommersemester 2005 ETH Zürich
 Skript zur Vorlesung Mass und Integral Urs Lang Sommersemester 2005 ETH Zürich Version vom 12. September 2006 Literatur [Rudin] W. Rudin, Real and Complex Analysis, Third Edition. McGraw-Hill Book Co.,
Skript zur Vorlesung Mass und Integral Urs Lang Sommersemester 2005 ETH Zürich Version vom 12. September 2006 Literatur [Rudin] W. Rudin, Real and Complex Analysis, Third Edition. McGraw-Hill Book Co.,
Zusammenfassung der Vorlesung. Analysis 3. Stefan Müller Universität Bonn Wintersemester
 Zusammenfassung der Vorlesung Analysis 3 Stefan Müller Universität Bonn Wintersemester 2016-2017 Dies ist eine gekürzte Zusammenfassung und kein vollständiges Skript der Vorlesung. Deshalb kann diese Zusammenfassung
Zusammenfassung der Vorlesung Analysis 3 Stefan Müller Universität Bonn Wintersemester 2016-2017 Dies ist eine gekürzte Zusammenfassung und kein vollständiges Skript der Vorlesung. Deshalb kann diese Zusammenfassung
Stochastik Wiederholung von Teil 1
 Stochastik Wiederholung von Teil 1 Andrej Depperschmidt Sommersemester 2016 Wahrscheinlichkeitsraum Definition Das Tripple (Ω, A, P) heißt Wahrscheinlichkeitsraum, falls gilt: (i) A ist eine σ-algebra,
Stochastik Wiederholung von Teil 1 Andrej Depperschmidt Sommersemester 2016 Wahrscheinlichkeitsraum Definition Das Tripple (Ω, A, P) heißt Wahrscheinlichkeitsraum, falls gilt: (i) A ist eine σ-algebra,
Im gesamten Kapitel sei Ω eine nichtleere Menge. Wir bezeichnen die Potenzmenge
 1 Mengensysteme Ein Mengensystem ist eine Familie von Teilmengen einer Grundmenge und damit eine Teilmenge der Potenzmenge der Grundmenge. In diesem Kapitel untersuchen wir Mengensysteme, die unter bestimmten
1 Mengensysteme Ein Mengensystem ist eine Familie von Teilmengen einer Grundmenge und damit eine Teilmenge der Potenzmenge der Grundmenge. In diesem Kapitel untersuchen wir Mengensysteme, die unter bestimmten
Beispielsammlung Prof. Kusolitsch
 Beispielsammlung Prof. Kusolitsch Inhaltsverzeichnis Maße und Mengensysteme. Lebesgue-Borel-Maß........................ Sigma(X)-meßbar......................... 3.3 Äusseres Maß & Maßfunktionen................
Beispielsammlung Prof. Kusolitsch Inhaltsverzeichnis Maße und Mengensysteme. Lebesgue-Borel-Maß........................ Sigma(X)-meßbar......................... 3.3 Äusseres Maß & Maßfunktionen................
Mengensysteme, Wahrscheinlichkeitsmaße
 Kapitel 1 Mengensysteme, Wahrscheinlichkeitsmaße Der Großteil der folgenden fundamentalen Begriffe sind schon aus der Vorlesung Stochastische Modellbildung bekannt: Definition 1.1 Eine Familie A von Teilmengen
Kapitel 1 Mengensysteme, Wahrscheinlichkeitsmaße Der Großteil der folgenden fundamentalen Begriffe sind schon aus der Vorlesung Stochastische Modellbildung bekannt: Definition 1.1 Eine Familie A von Teilmengen
Maßtheorie und Integralrechnung mehrerer Variablen
 Maßtheorie und Integralrechnung mehrerer Variablen Jan Swoboda 29. März 2014 Inhaltsverzeichnis Einleitung 1 1 Maßtheorie 3 1.1 Messbare Räume und messbare Abbildungen.................. 3 1.2 Maße und
Maßtheorie und Integralrechnung mehrerer Variablen Jan Swoboda 29. März 2014 Inhaltsverzeichnis Einleitung 1 1 Maßtheorie 3 1.1 Messbare Räume und messbare Abbildungen.................. 3 1.2 Maße und
1 Grundlagen der Maßtheorie
 1 Grundlagen der Maßtheorie In diesem Kapitel führen wir die Mengensysteme ein, die eine systematische Betrachtung von Ereignissen und zufälligen Beobachtungen in der Wahrscheinlichkeitstheorie erlauben.
1 Grundlagen der Maßtheorie In diesem Kapitel führen wir die Mengensysteme ein, die eine systematische Betrachtung von Ereignissen und zufälligen Beobachtungen in der Wahrscheinlichkeitstheorie erlauben.
DIFFERENTIATION PARAMETERABHÄNGIGER INTEGRALE
 DIFFERENTIATION PARAMETERABHÄNGIGER INTEGRALE Zusammenfassung. Ergänzend zur Übung vom 06.06.203 soll hier die Leibnizregel für die Differentiation parameterabhängiger Integrale formuliert und bewiesen
DIFFERENTIATION PARAMETERABHÄNGIGER INTEGRALE Zusammenfassung. Ergänzend zur Übung vom 06.06.203 soll hier die Leibnizregel für die Differentiation parameterabhängiger Integrale formuliert und bewiesen
Lösungsvorschläge für das 5. Übungsblatt
 Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Einführung in die Maß- und Integrationstheorie
 Kapitel 11 Einführung in die Maß- und Integrationstheorie Dozentin: Prof. Dr. Helga Baum Nach Vorlesungen im Sommersemester 2002 (1. Teil von Analysis IV) und im Sommersemester 2008 (1. Teil von Analysis
Kapitel 11 Einführung in die Maß- und Integrationstheorie Dozentin: Prof. Dr. Helga Baum Nach Vorlesungen im Sommersemester 2002 (1. Teil von Analysis IV) und im Sommersemester 2008 (1. Teil von Analysis
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
( ) ( ) < b k, 1 k n} (2) < x k
 Technische Universität Dortmund Fakultät für Mathematik Proseminar Analysis Prof. Dr. Röger Benjamin Czyszczon Satz von Heine Borel Gliederung 1. Zellen und offene Überdeckungen 2. Satz von Heine Borel
Technische Universität Dortmund Fakultät für Mathematik Proseminar Analysis Prof. Dr. Röger Benjamin Czyszczon Satz von Heine Borel Gliederung 1. Zellen und offene Überdeckungen 2. Satz von Heine Borel
