Behandlung der Kegelschnitte im virtuellen Raum mit Cabri 3D
|
|
|
- Hilke Linda Althaus
- vor 7 Jahren
- Abrufe
Transkript
1 Heinz Schumann mit Cabri 3D Zusammenfassung: In diesem Artikel wird eine Einführung in die Kegelschnitte dem dynamischen Raumgeometriesystem Cabri 3D gegeben, die traditionelle Inhalte auf neue Art und Weise behandelt und visualisiert. Im Zentrum steht die namensgebende Behandlung der Kegelschnitte mit einer Bweisführung nach Dandelin. Eine Betrachtung der Kegelschnitte als zentralprojektive Kreisbilder bzw. als Bilder bei axialer Projektivität schließt sich an. Die vorgestellte Einführung eignet sich für den Mathematikunterricht im Rahmen von mathematischen Schulcurricula der oberen Sekundarstufe. 1 Einleitung Die Geschichte der Integration der Kegelschnitte in den Mathematikunterricht ist eine sehr wechselhafte (vgl. u. a. Schupp 1988). Jetzt droht den Kegelschnitten eine weitere curricularen Vernachlässigung wegen des zu beobachteten mathematischen Substanzverlustes in den mathematischen Lehrplänen aufgrund anderer Schwerpunktsetzungen (e.g. mathematics literacy PISA). Obwohl der Unterrichtsgegenstand Kegelschnitte ein hervorragendes Beispiel für das Zusammenspiel von Geometrie und Algebra ist, für dessen Behandlung sich weitere Argumente in s Feld führen lassen: Anwendungsbezogenheit (Satellitenbahnen, Kugelstoß, Lithotriptor,...), innermathematische Relevanz, Problemhaftigkeit, Methodenvielfalt usw. Neue Medien, z. B. Dynamische Raumgeometriesysteme, eröffnen neue Methoden der Kegelschnitt-Behandlung, die auch im Rahmen des Schulcurriculum ihre Anwendung finden können. Während sich die fundierte didaktische Monographie über Kegelschnitte von Schupp (1988) sich noch ganz auf die Programmierung der grafischen Darstellung bezieht, werden bei Schumann (1991) erstmals die Behandlungsmöglichkeiten mit den Mitteln der Dynamischen Geometrie aufgezeigt. Allen bisherigen Beiträge zum Thema Kegelschnitte beschränken sich aber im wesentlichen auf die Behandlung der Kegelschnitte in der Ebene, was schon hinsichtlich der Namensgebung paradox ist. Diese Beschränkung dürfte vor allem an den Defiziten herkömmlicher Medien liegen, mit denen keine geignete Lernumgebung zur räumlichen Behandlung der Kegelschnitte gestaltet werden kann. Mit Cabri 3D (2004) steht erstmals ein schon sehr leistungsfähiges raumgeometrisches Dynamisches Geometriesystem zur Verfügung für diesen Zweck zur Verfügung. Im folgenden skizzieren wir eine adäquate Einführung in die räumlichen Kegelschnitte. 2 Einführung der Kegelschnitte im Raum Für eine dem Namen der Kegelschnitte adäquate dynamische Einführung als ebene Schnittfiguren eines (Doppel-)Kegels benötigen wir ein entsprechendes 3-dimensionales dynamisches Geometriesystem, das dem Nutzer eine gute Wahrnehmbarkeit bzw. Visualisierung räumlicher Objekte, die Konstruktion, die direkte Manipulation und Variation derselben bietet. Mit Cabri Géomètre 3D (Laborde, J. M.; Bainville, E., Cabri Géomètre 3D, Beta-Version 1.0, 2004) steht erstmals ein dreidimensionales dynamisches Geometriesystem zur Verfügung, das in der Version 1.0 bereits viele der Wünsche an ein Werkzeug erfüllt, mit dem man wie mit den zweidimensionale dynamischen Geometriesystemen im Raum dynamische Geometrie treiben kann.
2 76 Mit Cabri 3D können wir uns nun die ebenen Schnitte eines Kegels und die Begründung der phänotypischen Formen der Schnittkurven besser zugänglich machen als das mit traditionellen Medien im Unterricht möglich wäre. Die folgenden Abbildungen können nur sehr beschränkt die dynamischen Arbeitsmöglicheiten mit Cabri 3D und die dabei gemachten visuellen Wahrnehmungen und Erfahrungen wiedergeben. Wir konstruieren in Cabri 3D einen Kegel aus einem Kreis in einer Ebene und einem Punkt auf der Normalen zu dieser Ebene im Kreismittelpunkt (Abb. 1, Fächenmodell eines geraden Kreiskegels). Seine Form kann durch Verziehen des betreffenden Kreispunktes bzw. seiner Spitze variiert werden (Abb. 2, Ergebnis einer Formänderung). Den Kegel kann man von allen Seiten mittels des in Cabri 3D implementierten so genannten Virtual-Sphere-Device betrachten. Abb. 1 Abb. 2 Jetzt legen wir eine Ebene in den Kegel und lassen das Schnittkurve erzeugen, die in unserem Fall von Cabri 3D als Ellipse identifiziert wird (Abb. 3). Eine Formänderung des Kegels ändert nichts an diesem Ergebnis. Die Schnittkurve können wir auch von unten anschauen (Abb. 4). Wir drehen jetzt die Schnittszene so, dass die Ebene als Gerade zu sehen ist und erkennen, dass die Standebene mit der Schnittebene einen kleineren Winkel als mit dem Kegelmantel bildet (Abb. 5). Für einen Parabelschnitt konstruieren wir eine Ebene, die exakt parallel zu einer Mantellinie im Kegel liegt; die Abbildung 6 zeigt die Spurgerade dieser Ebene. Cabri 3D erkennt die mit dieser Ebene erzeugte Schnittkurve als Parabel (Abb. 7). Abb. 3 Abb. 4
3 77 Abb. 5 Abb. 6 Abb. 7 Abb. 8 Abb. 9
4 78 Variiert man die Lage der Schnittebene so, dass deren Winkel mit der Standebene größer ist als der Winkel des Kegelmantels, so erhält man eine Hyperbel. Der zweite Ast der Hyperbel befindet sich auf dem Kegel, den man durch Spiegelung an der Spitze des ursprünglichen Kegels erzeugt (Abb. 8 Spurgerade der Schnittebene im Doppelkegel; Abb. 9 Hyperbel als Schnittkurve im Doppelkegel). Die Schnittszene können wir uns von allen Seiten betrachten (Abb. 10, z. B. von unten). Geht die Schnittebene durch die Kegelspitze(n), so bekommt man eine Doppelgerade (Abb. 11) usw. Abb. 10 Abb. 11 Wir wollen nun begründen, warum beispielsweise die Schnittkurve in Abbildung 12 die Ortslinieneigenschaft einer Ellipse erfüllt, d. h., dass ihre Punkte von zwei festen Punkten konstante Entfernungssumme besitzen. Dafür wählen wir die elegante Methode von Dandelin ( ) aus (vgl. u. a. Handbuch der Schulmathematik, Band 4, S. 116/117). Zuerst konstruieren wir die so genannten Dandelinschen Kugeln, d. h. die Kugeln, die dem Kegel einbeschrieben sind und die die Schnittebene berühren. Für eine übersichtliche Konstruktion wählen wir für den Kegel die Umrissdarstellung (Abb. 13, Konstruktionsergebnis mit den Kugeln, den Berührpunkten, mit Spuren der Schnittebene und der Berührkreise; die Konstruktionslinien sind wegen der besseren Anschauung ausgeblendet; Abb. 14 Ergebnis in anderer Lage; Abb. 15 Dandelin- Kugeln von unten). Die beiden Kugelmittelpunkte werden in einer Ebene konstruiert, die die Kegelachse enthält, indem man analog zur Konstruktion eines Kreismittelpunkts aus zwei sich schneidenden Tangenten und einer Durchmessergeraden vorgeht. Die Kugelradien erhalten wir über Lote von den Kugelmittelpunkten auf Matellinien. Die Durchstoßpunkte der Lote von den Kugelmittelpunkten auf die Schnittebene sind die Berührpunkte (die späteren Brennpunkte der Ellipse). Auf die Schnittkurve legen wir einen beweglichen Punkt P. Zum Zwecke der Beweisführung nehmen wir nun weitere Objektbezeichnungen vor und stellen die Kugeln wegen der besseren Anschauung im Umriss dar (Abb. 16, Ausschnittsvergrößerung in Abb. 17): F 1,F 2 bezeichnen die Berührpunkte; k 1,k 2 die Berührkreise; B 1,B 2 die Schnittpunkte der Mantellinie durch P mit den Berührkreisen k 1,k 2 ; A 1,A 2 sind die Endpunkte einer Mantellinie des Kegelstumpfs, den k 1,k 2 bilden.
5 79 Abb. 12 Abb. 13 Abb. 14 Abb. 15 Abb. 16 Abb. 17
6 80 Abb. 18 Durch Verziehen von P beschreibt B 1 B 2 den Mantel dieses Kegelstumpfs; B 1 B 2 kann so mit A 1 A 2 zur Deckung gebracht werden. B 1,F 1 bzw. B 2,F 2 sind nach Konstruktion Berührpunkte an die 1. bzw. 2. Dandelin- Kugel, sie bilden mit P Tangentenabschnitte, die auf dem jeweiligen Berührkegel mit P als Spitze liegen (Abb. 18, beispielsweise für die 1. Kugel; Konstruktion dieses Kegels mit dem Dreipunktekreis durch B 1,F 1 und F 1 ; F 1 erhält man mittels Spiegelung von F 1 an der Ebene durch P und die Kegelachse). PB 1 und PF 1 sind also gleichlang und ebenso PB 2 und PF 2. Somit ist PF 1 + PF 2 = PB 1 + PB 2 = A 1 A 2 = konst. und die Schnittkurve ist eine Ellipse. Die Mantellinien des aus den Berührkreisen k 1,k 2 gebildeten Kegelstumpfs sind als so lang wie die noch einzuzeichnende Ellipsenhauptachse. Auf ähnliche Weise kann der Nachweis für den Parabel- und den Hyperbelschnitt geführt werden. 3 Ausblick: Zentralprojektive Kreisbilder Cabri 3D ist natürlich auch geeignet für die räumliche Konstruktion und Visualisierung von Kegelschnitten als zentralprojektive Kreisbilder in der üblichen zentralprojektiven Abbildungsvorrichtung mit dem Zentralpunkt Z (auch Augpunkt genannt), der Objektebene, der Bildebene (die die Objektebene in der Achse a schneidet) und der Verschwindungsebene (mit der Verschwindungsgeraden v). Die Abbildung 19 zeigt, wie der Kegel, gebildet aus einem einem Kreis in der Objektebene mit Z als Spitze die Bildebene in einer Ellipse schneidet; für einen, die Verschwindungsgerade berührenden Kreis erhält man als Schnittkurve eine Parabel. Das kann von allen Seiten betrachtet werden (Abb. 20, von unten mit transparenter Objektebene). Der Fall des Hyperbelschnitts ist in Abbildung 21 und 22 zu sehen. In der Abbildung 23 ist die Konfiguration für die punktweise zentralprojektive Konstruktion eines Kreisbildes am Beispiel der Ellipse dargestellt (k: Original, k : Bild; dabei ist der Lotfußpunkt des Lotes von Z auf die Bildebene der Hauptpunkt H und die Parallelebene zur Objektebene durch Z schneidet die Bildebene im Horizont h). Um das Bild k des Kreises k zu konstruieren, fällen wir vom Kreispunkt P das Lot auf die Achse a, Lotfußpunkt: A,... ; ZHAV ist ein Rechteck nach Konstruktion. Der Schnittpunkt des Projektionsstrahls ZP mit der Geraden AH ist der Bildpunkt P, der
7 81 das Kreisbild erzeugt, wenn P auf dem Kreis umläuft. Der Projektionsstrahl ZP beschreibt dabei als Kegelmantellinie den aus Z und k gebildeten schiefen Kegel. Nach Ausblendung der Bildebene und des Kegels bietet sich uns eine Szene wie in Abbildung 24. Abb. 19 Abb. 20
8 82 Abb. 21 Abb. 22
9 83 Abb. 23 Abb. 24
10 84 Abb. 25 Abb. 26 Klappt bzw. dreht man nun Bild- und Verschwindungsebene in die Objektebene (Abb. 25), so gewinnt man eine verebnete Konstruktion zentralprojektiver Kreisbilder als Sonderfall der Abbildung bei axialer Projektivität (Abb. 26). Jetzt wechseln wir wieder zu Cabri II Plus über, um diese verebnete Abbildung mit entsprechenden Fallunterscheidungen auf Kreise zur Erzeugung von Kegelschnitten anzuwenden:
11 85 Kreis meidet Verschwindungsgerade (Ellipse: Abbildung 27), berührt sie (Parabel: Abbildung 28) und schneidet sie (Hyperbel: Abbildung 29). Abb. 27 Abb. 28
12 86 Abb. 29 Kegelschnitte kann man sich auch als Schnitte eines Lichtkegels mit einer Ebene vorstellen. Die Kurven, die der Lichtkegel von einer punktförmigen Lichtquelle Z aus mit Ebenen bildet (Abb. 30), sind auch als zentralprojektive Bilder eines Kreises k interpretierbar; die Kreisebene steht dabei senkrecht zur Kegelachse, auf der auch der Kreismittelpunkt liegt. Mit Cabri 3D lässt sich mittels einer drehenden Ebene die Veränderung der Kurvenform von der Ellipse bis zur Hyperbel gut beobachten. Abb. 30
13 4 Literatur 87 Laborde, J. M. (2004): 20 Years of Cabri! Perspective of Geometry Based Computing Means of Tomorrow. (Vortrag), Third Cabri Geometry International Conference, Rome 9 th -12 th September 2004, Universitá La Sapienza Laborde, J. M.; Bellemain, F. ( ): Cabri Géomètre II Plus. Grenoble: Cabrilog (Deutsche Anpassung als Cabri-Geometrie II Plus von H. Schumann. Bezug u. a. bei Laborde, J. M.; Bainville, E. (2004) : Cabri Géomètre 3D (Version 1.0). Grenoble: Cabrilog Schumann, H. (1991): Schulgeometrisches Konstruieren mit dem Computer. Stuttgart: Metzler und Teubner (auch im Archiv von Schupp, H. (1988): Kegelschnitte. Mannheim: BI-Wissenschaftsverlag Wolff. G. (Hrsg.) (1966 ): Handbuch der Schulmathematik, Band 4, Geometrie der Oberstufe, 2. Auflage. Hannover: Schroedel
14 88
Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D
 Heinz Schumann Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet Das dynamische Raumgeometrie-System Cabri 3D eignet sich nicht nur für die
Heinz Schumann Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet Das dynamische Raumgeometrie-System Cabri 3D eignet sich nicht nur für die
Sätze über Kreise raumgeometrisch beweisen
 Sätze über Kreise raumgeometrisch beweisen Heinz Schumann Erschienen als Online-Ergänzung zu Praxis der Mathematik in der Schule 47 (2005) 6 Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet. Das
Sätze über Kreise raumgeometrisch beweisen Heinz Schumann Erschienen als Online-Ergänzung zu Praxis der Mathematik in der Schule 47 (2005) 6 Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet. Das
Parallelprojektive Schattenbilder von Körpern mit Cabri 3D
 Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Im folgenden sollen einige ausgewählte konstruktive Analogiebildungen aufgelistet werden.
 Heinz Schumann Materialien für die konstruktive Analogisierung ebener Geometrie im virtuellen Raum Analoge Dinge stimmen in gewissen Beziehungen zwischen ihren entsprechenden Teilen miteinander überein.
Heinz Schumann Materialien für die konstruktive Analogisierung ebener Geometrie im virtuellen Raum Analoge Dinge stimmen in gewissen Beziehungen zwischen ihren entsprechenden Teilen miteinander überein.
Abb.1. Falls die Spitze des Kegels (bzw. Doppelkegels) nicht in der jeweiligen Schnittebene liegt, können die folgende Kurven entstehen:
 Kegelschnitte Ein Kegelschnitt ist eine ebene Kurve, die entsteht, wenn man die Oberfläche eines Kreiskegels bzw. Doppelkreiskegels mit einer Ebene schneidet (vgl.abb.1). Der Doppelkreiskegel seinerseits
Kegelschnitte Ein Kegelschnitt ist eine ebene Kurve, die entsteht, wenn man die Oberfläche eines Kreiskegels bzw. Doppelkreiskegels mit einer Ebene schneidet (vgl.abb.1). Der Doppelkreiskegel seinerseits
Inhaltsverzeichnis. geometrischer Objekte auszufüllen. Die Liste der Lösungen kann auch eine ABC Liste zu diesen Themen sein.
 Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
6.4.3 Frontalperspektive
 102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
6.T³ - Regionaltagung an der Universität Mainz
 6.T³ - Regionaltagung an der Universität Mainz Samstag, 14. März 00 WorkshopII. Kegelschnitte sind Kegel-Schnitte! Plädoyer für die Renaissance eines interessanten Themas Ein Workshop mit CAS (Derive)
6.T³ - Regionaltagung an der Universität Mainz Samstag, 14. März 00 WorkshopII. Kegelschnitte sind Kegel-Schnitte! Plädoyer für die Renaissance eines interessanten Themas Ein Workshop mit CAS (Derive)
Entdeckung von Analogien mit Cabri 3D am Beispiel Dreieck Tetraeder
 Heinz Schumann am Beispiel Dreieck Tetraeder Erschienen in: math. did. 27 (2004) Bd. 1, 82-100 (Wiedergabe hier auszugsweise, insbesondere nur die Abbildungen) Nicht alles ist analog. Zusammenfassung:
Heinz Schumann am Beispiel Dreieck Tetraeder Erschienen in: math. did. 27 (2004) Bd. 1, 82-100 (Wiedergabe hier auszugsweise, insbesondere nur die Abbildungen) Nicht alles ist analog. Zusammenfassung:
Jürgen Roth Didaktik der Linearen Algebra und Analytischen Geometrie
 Jürgen Roth Didaktik der Linearen Algebra und Analytischen Geometrie Modul 12a: Fachdidaktische Bereiche juergen-roth.de/lehre/did_linalg_anageo/ Kapitel 4: Kegelschnitte 4.1 Inhalte Didaktik der Linearen
Jürgen Roth Didaktik der Linearen Algebra und Analytischen Geometrie Modul 12a: Fachdidaktische Bereiche juergen-roth.de/lehre/did_linalg_anageo/ Kapitel 4: Kegelschnitte 4.1 Inhalte Didaktik der Linearen
Inhalt. Erster Abschnitt. Parallelprojektion und Zentralprojektion ebener Mguren.
 Inhalt. Erster Abschnitt. Parallelprojektion und Zentralprojektion ebener Mguren. 1 6. Die Affinität. Definition und Eigenschaften. 1 7. Die Ellipse als affines Bild (Parallelprojektion) des Kreises. 5
Inhalt. Erster Abschnitt. Parallelprojektion und Zentralprojektion ebener Mguren. 1 6. Die Affinität. Definition und Eigenschaften. 1 7. Die Ellipse als affines Bild (Parallelprojektion) des Kreises. 5
Zentralprojektion im virtuellen Raum eine Einführung mit Cabri 3D
 Heinz Schumann Zentralprojektion im virtuellen Raum eine Einführung mit Cabri 3D 1. Einleitung Traditionelle Aufgabe der darstellenden Geometrie ist die Entwicklung und Anwendung zweckgebundener Abbildungsverfahren
Heinz Schumann Zentralprojektion im virtuellen Raum eine Einführung mit Cabri 3D 1. Einleitung Traditionelle Aufgabe der darstellenden Geometrie ist die Entwicklung und Anwendung zweckgebundener Abbildungsverfahren
Eine Projektionsaufgabe und eine Kugelaufgabe.
 Eine Projektionsaufgabe und eine Kugelaufgabe. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 1. September 1921.) I. Gesucht im Raum der Ort eines Punktes 0, von dem aus die Zentralprojektion eines
Eine Projektionsaufgabe und eine Kugelaufgabe. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 1. September 1921.) I. Gesucht im Raum der Ort eines Punktes 0, von dem aus die Zentralprojektion eines
Materialien für die konstruktive Analogisierung ebener Geometrie im virtuellen Raum (2)
 Heinz Schumann Materialien für die konstruktive Analogisierung ebener Geometrie im virtuellen Raum (2) Analoge Dinge stimmen in gewissen Beziehungen zwischen ihren entsprechenden Teilen miteinander überein.
Heinz Schumann Materialien für die konstruktive Analogisierung ebener Geometrie im virtuellen Raum (2) Analoge Dinge stimmen in gewissen Beziehungen zwischen ihren entsprechenden Teilen miteinander überein.
Polyedrische Approximation von Körpern mit Cabri 3D
 Heinz Schumann Polyedrische Approximation von Körpern mit Cabri 3D Die Approximation von konvexen Körpern, deren Oberfläche nicht aus Polygonen besteht, mittels einbeschriebener konvexer Polyeder ist notwendig,
Heinz Schumann Polyedrische Approximation von Körpern mit Cabri 3D Die Approximation von konvexen Körpern, deren Oberfläche nicht aus Polygonen besteht, mittels einbeschriebener konvexer Polyeder ist notwendig,
Name und des Einsenders
 Titel der Einheit Stoffgebiet Name und Email des Einsenders Ziel der Einheit Inhalt Voraussetzungen Konstruktion von Kegelschnitten Geometrie Andreas Ulovec Andreas.Ulovec@univie.ac.at Verwenden von Dynamischer
Titel der Einheit Stoffgebiet Name und Email des Einsenders Ziel der Einheit Inhalt Voraussetzungen Konstruktion von Kegelschnitten Geometrie Andreas Ulovec Andreas.Ulovec@univie.ac.at Verwenden von Dynamischer
Zentral- und parallelprojektive Darstellungen in Cabri 3D
 Heinz Schumann Zentral- und parallelprojektive Darstellungen in Cabri 3D 1. Einleitung Cabri 3D repräsentiert nicht nur geometrisches Wissen über raumgeometrische Objekte und ihre Generierung, sondern
Heinz Schumann Zentral- und parallelprojektive Darstellungen in Cabri 3D 1. Einleitung Cabri 3D repräsentiert nicht nur geometrisches Wissen über raumgeometrische Objekte und ihre Generierung, sondern
Schwerpunktfach AM/PH, 2011 KEGELSCHNITTE
 Schwerpunktfach AM/PH, 011 KEGELSCHNITTE 5. Kreis und Ellipse 5.1. Grundkonstruktionen am Kreis Konstruktion 1: Konstruiere einen Kreis, welcher durch die gegebenen 3 Punkte A,B und C verläuft: C B A Konstruktionsbericht:
Schwerpunktfach AM/PH, 011 KEGELSCHNITTE 5. Kreis und Ellipse 5.1. Grundkonstruktionen am Kreis Konstruktion 1: Konstruiere einen Kreis, welcher durch die gegebenen 3 Punkte A,B und C verläuft: C B A Konstruktionsbericht:
Dipl, ng (FH) Darstellende
 Kamprath-Reihe Technik Dipl, ng (FH) Darstellende Josef Vogelmann Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 6. Auflage Vogel Buchverlag Inhaltsverzeichnis 1. Einleitung
Kamprath-Reihe Technik Dipl, ng (FH) Darstellende Josef Vogelmann Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 6. Auflage Vogel Buchverlag Inhaltsverzeichnis 1. Einleitung
Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel.
 1 3 Die Parabel 3.1 Die Parabel als Kegelschnitt Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel. Sei SP
1 3 Die Parabel 3.1 Die Parabel als Kegelschnitt Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel. Sei SP
a) b) Abb. 1: Die klassische Aufgabe a) b) Abb. 2: Umkehrung
 Hans Walser, [20180528] Sehwinkel bei Kegelschnitten Anregung: N. Th.-Sch., V. 1 Wie das Problem entstand Eine klassische Aufgabe im Abiturtraining geht so: Gegeben sind eine Punkt und eine Parabel (Abb.
Hans Walser, [20180528] Sehwinkel bei Kegelschnitten Anregung: N. Th.-Sch., V. 1 Wie das Problem entstand Eine klassische Aufgabe im Abiturtraining geht so: Gegeben sind eine Punkt und eine Parabel (Abb.
Herleitung der Formel für die Krümmung von Funktionsgraphen
 Herleitung der Formel für die Krümmung von Funktionsgraphen mit Hilfe der Beispiele f(x) = x 2 und f(x) = x 4 Jens Weitendorf Kurzfassung des Inhalts: In dem Artikel wird in einer kurzen Einheit dargestellt,
Herleitung der Formel für die Krümmung von Funktionsgraphen mit Hilfe der Beispiele f(x) = x 2 und f(x) = x 4 Jens Weitendorf Kurzfassung des Inhalts: In dem Artikel wird in einer kurzen Einheit dargestellt,
Tutorium Mathematik in der gymnasialen Oberstufe 9. Veranstaltung: Kreis und Kugel 30. Januar 2013
 Tutorium Mathematik in der gymnasialen Oberstufe 9. Veranstaltung: Kreis und Kugel 30. Januar 013 1. Kreisgleichungen Kreisgleichung in Vektorschreibweise Sei k ein Kreis mit dem Radius r in der Koordinatenebene.
Tutorium Mathematik in der gymnasialen Oberstufe 9. Veranstaltung: Kreis und Kugel 30. Januar 013 1. Kreisgleichungen Kreisgleichung in Vektorschreibweise Sei k ein Kreis mit dem Radius r in der Koordinatenebene.
Konstruktion von Kreistangenten
 Konstruktion von Kreistangenten 1 Gegeben sind die Punkte A und B mit AB = 5cm Konstruiere die Geraden durch B, die von A den Abstand 3cm haben! 2 Eine Ecke einer Rasenfläche, an der die geraden Ränder
Konstruktion von Kreistangenten 1 Gegeben sind die Punkte A und B mit AB = 5cm Konstruiere die Geraden durch B, die von A den Abstand 3cm haben! 2 Eine Ecke einer Rasenfläche, an der die geraden Ränder
Mathematisches Kaleidoskop WS15/16 Materialien Teil 1
 Mathematisches Kaleidoskop WS15/16 Materialien Teil 1 Dr. Hermann Duerkop E-Mail: hd@nabla.de 1 1 Kegelschnitte 1.1 Kopernikus, Kepler und Newton: Planetenbewegungen Kopernikus (1473-1543) Kepler (1571-1630)
Mathematisches Kaleidoskop WS15/16 Materialien Teil 1 Dr. Hermann Duerkop E-Mail: hd@nabla.de 1 1 Kegelschnitte 1.1 Kopernikus, Kepler und Newton: Planetenbewegungen Kopernikus (1473-1543) Kepler (1571-1630)
Die interaktive Konstruktion von Durchdringungsobjekten mit Cabri 3D
 Heinz Schumann Die interaktive Konstruktion von Durchdringungsobjekten mit Cabri 3D 1. Einleitung Die Konstruktion neuer geometrischer Raumobjekte aus gegebenen räumlichen Objekten ist eine herausfordernde
Heinz Schumann Die interaktive Konstruktion von Durchdringungsobjekten mit Cabri 3D 1. Einleitung Die Konstruktion neuer geometrischer Raumobjekte aus gegebenen räumlichen Objekten ist eine herausfordernde
1. Semesterschularbeit
 1. Semesterschularbeit 3.2.2000 (100 Minuten) 1) Die Punkte A=[3,0,-1], B=[1,4,-1] und C=[-2,0,4] liegen auf einer Kugel, deren Mittelpunkt in der Ebene ε: 2x+3y-8z=4 liegt. a) Stelle die Kugelgleichung
1. Semesterschularbeit 3.2.2000 (100 Minuten) 1) Die Punkte A=[3,0,-1], B=[1,4,-1] und C=[-2,0,4] liegen auf einer Kugel, deren Mittelpunkt in der Ebene ε: 2x+3y-8z=4 liegt. a) Stelle die Kugelgleichung
Automatisierte. algebraische Berechnungen an geometrischen Figuren. Inhalt. 1. Einleitung. 2. DGS mit algebraischer Berechnungskomponente
 Wer um die Behauptung weiß, muss noch führen den Beweis. Automatisierte algebraische Berechnungen an geometrischen Figuren Prof. Dr. Heinz Schumann PH Weingarten Fak. II, Mathematik schumann@ph-weingarten.de
Wer um die Behauptung weiß, muss noch führen den Beweis. Automatisierte algebraische Berechnungen an geometrischen Figuren Prof. Dr. Heinz Schumann PH Weingarten Fak. II, Mathematik schumann@ph-weingarten.de
Einführung in die Dynamische Geometrie-Software GeoGebra
 Einführung in die Dynamische Geometrie-Software GeoGebra Aufgabe In der Lernumgebung 5 des mathbuch 1 geht es um Messen und Zeichnen. Für die Aufgabe 7 im Buch steht zwar bereits eine fertige Geogebra-Anwendung
Einführung in die Dynamische Geometrie-Software GeoGebra Aufgabe In der Lernumgebung 5 des mathbuch 1 geht es um Messen und Zeichnen. Für die Aufgabe 7 im Buch steht zwar bereits eine fertige Geogebra-Anwendung
Einige Aufgaben über extreme Werte.
 Einige Aufgaben über extreme Werte. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 5. August 1926.) I. Gesucht auf einer Regelfläche zweiten Grades von der einen Regelschar diejenigen Erzeugenden,
Einige Aufgaben über extreme Werte. Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 5. August 1926.) I. Gesucht auf einer Regelfläche zweiten Grades von der einen Regelschar diejenigen Erzeugenden,
2 Das Bild In Schulbüchern und Arbeitsblättern sieht man oft Würfel -Darstellungen wie etwa in der Abbildung 1. Abb. 1: Was ist denn das?
 Hans Walser, [20131013], [20160331], [20160401] Quetschwürfel 1 Worum geht es? Es wird auf die Problematik der in Schulen weitverbreiteten Schrägbilder eingegangen. 2 Das Bild In Schulbüchern und Arbeitsblättern
Hans Walser, [20131013], [20160331], [20160401] Quetschwürfel 1 Worum geht es? Es wird auf die Problematik der in Schulen weitverbreiteten Schrägbilder eingegangen. 2 Das Bild In Schulbüchern und Arbeitsblättern
8.Kreisdarstellung in Perspektive
 8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
Kugel - Tangentialebene und Tangentialkegel
 6. Tangentialebene an einem Punkt 7. Tangentialkegel von einem Punkt (Pol) aus Kugel - Tangentialebene und Tangentialkegel 6. Tangentialebene an einem Punkt, "Tangente" 6. Berührungspunkt gegeben Die Tangentialebene
6. Tangentialebene an einem Punkt 7. Tangentialkegel von einem Punkt (Pol) aus Kugel - Tangentialebene und Tangentialkegel 6. Tangentialebene an einem Punkt, "Tangente" 6. Berührungspunkt gegeben Die Tangentialebene
DG für Kunstpädagogik
 DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
Über Regelflächen zweiten Grades. Von. (Als Manuskript eingegangen ans 14. Oktober 1922.)
 Über Regelflächen zweiten Grades. Von A. KIEFER (Zürich). (Als Manuskript eingegangen ans 14. Oktober 1922.) I. Welches ist der Ort des Durchschnittspunktes derjenigen Erzeugenden eines Hyperboloids, welche
Über Regelflächen zweiten Grades. Von A. KIEFER (Zürich). (Als Manuskript eingegangen ans 14. Oktober 1922.) I. Welches ist der Ort des Durchschnittspunktes derjenigen Erzeugenden eines Hyperboloids, welche
Abb.1 Kegelschnitte [2]
![Abb.1 Kegelschnitte [2] Abb.1 Kegelschnitte [2]](/thumbs/91/106636815.jpg) und Kegelschnitte DGC-Mitteilungen Nr.106, 2006: "Jede Deklinationslinie der ist ein Stück eines echten Kegelschnittes" Bemerkung von heute, 2008 Im ursprünglichen Aufsatz machte ich auf Fehler in einer
und Kegelschnitte DGC-Mitteilungen Nr.106, 2006: "Jede Deklinationslinie der ist ein Stück eines echten Kegelschnittes" Bemerkung von heute, 2008 Im ursprünglichen Aufsatz machte ich auf Fehler in einer
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover
 Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Übung 1. Man nde die gesuchten Funktionswerte. (ii) f(x, y) = sin(xy)
 Man nde die gesuchten Funktionswerte. Übung (i) f(, ) = + 3 f(, ) f(, ) f(, 3) f( 3, ) f(, ) = sin() f(, π/6) f( 3, π/) f(π, /) f( π/, 7) Übung Man nde und skizziere den enitionsbereich und nde den Wertebereich
Man nde die gesuchten Funktionswerte. Übung (i) f(, ) = + 3 f(, ) f(, ) f(, 3) f( 3, ) f(, ) = sin() f(, π/6) f( 3, π/) f(π, /) f( π/, 7) Übung Man nde und skizziere den enitionsbereich und nde den Wertebereich
kommt zur Kreisinversion eine Spiegelung des Punktes an der reellen Achse dazu. Die folgenden vier Eigenschaften gelten auch für diese Abbildung
 1 3. Die Kreisinversion 3.1. Definition Die Abbildung 1 ordnet der Zahl das folgende Bild zu 1 1 1 1 1 Die Konstruktion des Bildpunkts besteht also aus zwei Schritten: Der Punkt wird in den Bildpunkt abgebildet,
1 3. Die Kreisinversion 3.1. Definition Die Abbildung 1 ordnet der Zahl das folgende Bild zu 1 1 1 1 1 Die Konstruktion des Bildpunkts besteht also aus zwei Schritten: Der Punkt wird in den Bildpunkt abgebildet,
Zu den Kegelschnitten
 Zum Skizzenverständnis: In der nebenstehenden Figur 1 sieht man die den Kegel schneidende Ebene in Projektionsdarstellung als Gerade durch die Punkte P und F. Mit eingezeichnet ist die obere Dandelinsche
Zum Skizzenverständnis: In der nebenstehenden Figur 1 sieht man die den Kegel schneidende Ebene in Projektionsdarstellung als Gerade durch die Punkte P und F. Mit eingezeichnet ist die obere Dandelinsche
Josef Vogelmann Darstellende Geometrie
 Josef Vogelmann Darstellende Geometrie Kamprath-Reihe Technik Dipl.-Ing. (FH) Josef Vogelmann Darstellende Geometrie Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 5. Auflage
Josef Vogelmann Darstellende Geometrie Kamprath-Reihe Technik Dipl.-Ing. (FH) Josef Vogelmann Darstellende Geometrie Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 5. Auflage
Stereometrie. Rainer Hauser. Dezember 2010
 Stereometrie Rainer Hauser Dezember 2010 1 Einleitung 1.1 Beziehungen im Raum Im dreidimensionalen Euklid schen Raum sind Punkte nulldimensionale, Geraden eindimensionale und Ebenen zweidimensionale Unterräume.
Stereometrie Rainer Hauser Dezember 2010 1 Einleitung 1.1 Beziehungen im Raum Im dreidimensionalen Euklid schen Raum sind Punkte nulldimensionale, Geraden eindimensionale und Ebenen zweidimensionale Unterräume.
WS 2010/ Januar Mathematisches Institut der Universität München Prof. Dr. Rudolf Fritsch
 Mathematisches Institut der Universität München Prof. Dr. Rudolf Fritsch WS 2010/2011 14. Januar 2011 Geometrie mit Übungen Übungsblatt 9, Musterlösungen Aufgabe 33. Es werden Kreise in der Euklidischen
Mathematisches Institut der Universität München Prof. Dr. Rudolf Fritsch WS 2010/2011 14. Januar 2011 Geometrie mit Übungen Übungsblatt 9, Musterlösungen Aufgabe 33. Es werden Kreise in der Euklidischen
Abbildung eines Punkts
 x 3 (bzw. z) - Höhe Abbildung eines Punkts Höhenmaßstab A A x 2 (bzw. y) - Breite 1 B 0 C A B (-5) C=C B C=C (0) A (3,5) B x 1 (bzw. x) - Tiefe In Klammern erfolgt jeweils die Angabe der Kote. Zusammenhang
x 3 (bzw. z) - Höhe Abbildung eines Punkts Höhenmaßstab A A x 2 (bzw. y) - Breite 1 B 0 C A B (-5) C=C B C=C (0) A (3,5) B x 1 (bzw. x) - Tiefe In Klammern erfolgt jeweils die Angabe der Kote. Zusammenhang
Inhaltsverzeichnis INHALTSVERZEICHNIS 1
 INHALTSVERZEICHNIS 1 Inhaltsverzeichnis 1 Die Parabel 2 1.1 Definition................................ 2 1.2 Bemerkung............................... 3 1.3 Tangenten................................ 3 1.4
INHALTSVERZEICHNIS 1 Inhaltsverzeichnis 1 Die Parabel 2 1.1 Definition................................ 2 1.2 Bemerkung............................... 3 1.3 Tangenten................................ 3 1.4
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen
 Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Grundregeln der Perspektive und ihre elementargeometrische Herleitung
 Vortrag zu Mathematik, Geometrie und Perspektive von Prof. Dr. Bodo Pareigis am 15.10.2007 im Vorlesungszyklus Naturwissenschaften und Mathematische Wissenschaften im Rahmen des Seniorenstudiums der LMU.
Vortrag zu Mathematik, Geometrie und Perspektive von Prof. Dr. Bodo Pareigis am 15.10.2007 im Vorlesungszyklus Naturwissenschaften und Mathematische Wissenschaften im Rahmen des Seniorenstudiums der LMU.
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Strophoiden. Eckart Schmidt
 Strophoiden Eckart Schmidt Strophoiden sind als anallagmatische Kurven invariant gegenüber einer Kreisspiegelung; sie sind weiterhin das Inverse einer gleichseitigen Hyperbel, die Fußpunktkurve einer Parabel
Strophoiden Eckart Schmidt Strophoiden sind als anallagmatische Kurven invariant gegenüber einer Kreisspiegelung; sie sind weiterhin das Inverse einer gleichseitigen Hyperbel, die Fußpunktkurve einer Parabel
Mathematisches Denken. Übungsserie 1. γ : [0, 2] IR 2,t r(t) := 2t 1
![Mathematisches Denken. Übungsserie 1. γ : [0, 2] IR 2,t r(t) := 2t 1 Mathematisches Denken. Übungsserie 1. γ : [0, 2] IR 2,t r(t) := 2t 1](/thumbs/97/134129340.jpg) Studiengang Architektur Mathematisches Denken Übungsserie 1 HS 2007 Abgabe der (z.t. mit dem TR) gelösten Aufgaben: Freitag 26. Oktober 2007 in der Vorlesung 1. Durch die folgende Parameterdarstellung
Studiengang Architektur Mathematisches Denken Übungsserie 1 HS 2007 Abgabe der (z.t. mit dem TR) gelösten Aufgaben: Freitag 26. Oktober 2007 in der Vorlesung 1. Durch die folgende Parameterdarstellung
Thema: Ein Ausblick auf die Möglichkeiten durch den Software-Einsatz im Mathematikunterricht.
 Vorlesung 2 : Do. 10.04.08 Thema: Ein Ausblick auf die Möglichkeiten durch den Software-Einsatz im Mathematikunterricht. Einführung in GeoGebra: Zunächst eine kleine Einführung in die Benutzeroberfläche
Vorlesung 2 : Do. 10.04.08 Thema: Ein Ausblick auf die Möglichkeiten durch den Software-Einsatz im Mathematikunterricht. Einführung in GeoGebra: Zunächst eine kleine Einführung in die Benutzeroberfläche
Über die Lösung des apollonischen Berührungsproblems auf der Kugel und im Raum mittels geometrischer Transformationen
 Über die Lösung des apollonischen Berührungsproblems auf der Kugel und im Raum mittels geometrischer Transformationen Klaus Holländer (FH Giessen-Friedberg) Abstract The problem of Apollonius on the sphere
Über die Lösung des apollonischen Berührungsproblems auf der Kugel und im Raum mittels geometrischer Transformationen Klaus Holländer (FH Giessen-Friedberg) Abstract The problem of Apollonius on the sphere
Die Abbildung (x 1 ;x 2 ) 7! (x 1 ;x 2 ; 1) ist eine Einbettung von R 2 in P 2 (als Mengen). Punkte mit z 6= 0 sind endliche" Punkte mit inhomogenen K
 Kapitel IV Projektive Geometrie In diesem Kapitel wird eine kurze Einführung in die projektive Geometrie gegeben. Es sollen unendlich ferne Punkte mit Hilfe von homogene Koordinaten eingeführt werden und
Kapitel IV Projektive Geometrie In diesem Kapitel wird eine kurze Einführung in die projektive Geometrie gegeben. Es sollen unendlich ferne Punkte mit Hilfe von homogene Koordinaten eingeführt werden und
Jahresplanung Vorschlag 1
 Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
Seminar für LAGym/LAB: Analytische Geometrie
 Seminar für LAGym/LAB: Analytische Geometrie Ingo Runkel und Peter Stender Euklidische Vektorräume und Geometrie E1: Lineare Gleichungssysteme - Affiner Unterraum eines Vektorraumes. Lineare Gleichungssysteme
Seminar für LAGym/LAB: Analytische Geometrie Ingo Runkel und Peter Stender Euklidische Vektorräume und Geometrie E1: Lineare Gleichungssysteme - Affiner Unterraum eines Vektorraumes. Lineare Gleichungssysteme
Einige Bemerkungen zu den verallgemeinerten Kegelschnitten von Zvonimir Durčević
 Definition 1. Es seien B, D Punkte und c eine Gerade oder ein Kreis in einer Ebene ε siehe Abb. 1 bzw.. Lässt man einen Punkt auf c laufen, dann durchläuft der Schnittpunkt X der Geraden g : D mit der
Definition 1. Es seien B, D Punkte und c eine Gerade oder ein Kreis in einer Ebene ε siehe Abb. 1 bzw.. Lässt man einen Punkt auf c laufen, dann durchläuft der Schnittpunkt X der Geraden g : D mit der
4. Mathematik Olympiade 3. Stufe (Bezirksolympiade) Klasse 12 Saison 1964/1965 Aufgaben und Lösungen
 4. Mathematik Olympiade 3. Stufe (Bezirksolympiade) Klasse 1 Saison 1964/1965 Aufgaben und Lösungen 1 OJM 4. Mathematik-Olympiade 3. Stufe (Bezirksolympiade) Klasse 1 Aufgaben Hinweis: Der Lösungsweg mit
4. Mathematik Olympiade 3. Stufe (Bezirksolympiade) Klasse 1 Saison 1964/1965 Aufgaben und Lösungen 1 OJM 4. Mathematik-Olympiade 3. Stufe (Bezirksolympiade) Klasse 1 Aufgaben Hinweis: Der Lösungsweg mit
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
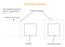 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung
 Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
Gert Bär. Geometrie. Eine Einführung für Ingenieure und Naturwissenschaftler. 2., überarbeitete und erweiterte Auflage
 Gert Bär Geometrie Eine Einführung für Ingenieure und Naturwissenschaftler 2., überarbeitete und erweiterte Auflage Teubner B.G.Teubner Stuttgart Leipzig Wiesbaden Inhalt 1 Aus der analytischen Geometrie
Gert Bär Geometrie Eine Einführung für Ingenieure und Naturwissenschaftler 2., überarbeitete und erweiterte Auflage Teubner B.G.Teubner Stuttgart Leipzig Wiesbaden Inhalt 1 Aus der analytischen Geometrie
Dem Höhenschnittpunkt auf der Spur Hans-Jürgen Elschenbroich
 Dem Höhenschnittpunkt auf der Spur Hans-Jürgen Elschenbroich 1. Parabállein Ein typisches Beispiel für Ortskurven ist die Höhenschnittpunktskurve. Dabei wandert die Ecke C eines Dreiecks ABC auf einer
Dem Höhenschnittpunkt auf der Spur Hans-Jürgen Elschenbroich 1. Parabállein Ein typisches Beispiel für Ortskurven ist die Höhenschnittpunktskurve. Dabei wandert die Ecke C eines Dreiecks ABC auf einer
Klausurenkurs zum Staatsexamen (SS 2014): Lineare Algebra und analytische Geometrie 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 204): Lineare Algebra und analytische Geometrie 8 8. (Herbst 202, Thema 3, Aufgabe 4) Bestimmen Sie die euklidische Normalform der Quadrik Q, gegeben
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 204): Lineare Algebra und analytische Geometrie 8 8. (Herbst 202, Thema 3, Aufgabe 4) Bestimmen Sie die euklidische Normalform der Quadrik Q, gegeben
EINFÜHRUNG IN DIE GEOMETRIE
 Dr. Michael Gieding EINFÜHRUNG IN DIE GEOMETRIE MATERIAL FÜR DAS SELBSTSTUDIUM WICHTIGE GRUNDBEGRIFFE DER MATHEMATIK: MENGEN UND RELATIONEN MENGEN 0. Mengen 0.0 Ziel der Ausführungen Die Mengenlehre bildet
Dr. Michael Gieding EINFÜHRUNG IN DIE GEOMETRIE MATERIAL FÜR DAS SELBSTSTUDIUM WICHTIGE GRUNDBEGRIFFE DER MATHEMATIK: MENGEN UND RELATIONEN MENGEN 0. Mengen 0.0 Ziel der Ausführungen Die Mengenlehre bildet
Übersicht 2.1 Polyeder Schrägbilder Abwicklungen und Auffaltungen Zylinder und Kegel Kugeln...
 2 Geometrie im Raum Übersicht 21 Polyeder 59 22 Schrägbilder 64 23 Abwicklungen und Auffaltungen 70 24 Zylinder und Kegel 72 25 Kugeln 76 21 Polyeder Eine begrenzte (beschränkte, endliche) Fläche nennt
2 Geometrie im Raum Übersicht 21 Polyeder 59 22 Schrägbilder 64 23 Abwicklungen und Auffaltungen 70 24 Zylinder und Kegel 72 25 Kugeln 76 21 Polyeder Eine begrenzte (beschränkte, endliche) Fläche nennt
1 Rund um die Kugel. a) Mathematische Beschreibung
 Rund um die Kugel a) Mathematische Beschreibung Die Punkte der Oberfläche haben vom Mittelpunkt M alle die Entfernung r. Oder, mit den Mitteln der analytischen Geometrie: Für alle Punkte der Kugeloberfläche
Rund um die Kugel a) Mathematische Beschreibung Die Punkte der Oberfläche haben vom Mittelpunkt M alle die Entfernung r. Oder, mit den Mitteln der analytischen Geometrie: Für alle Punkte der Kugeloberfläche
Liber Kegelflächen. A. KIEFER (Zürich),
 Liber Kegelflächen. Von A. KIEFER (Zürich), (Als Manuskript eingegangen am 13. November 1923.) Die Durchdringungskurve vierten Grades von zwei Kegelflächen zweiten Grades bekommt bekanntlich einen Doppelpunkt,
Liber Kegelflächen. Von A. KIEFER (Zürich), (Als Manuskript eingegangen am 13. November 1923.) Die Durchdringungskurve vierten Grades von zwei Kegelflächen zweiten Grades bekommt bekanntlich einen Doppelpunkt,
Mathematisches Kaleidoskop WS15/16 Materialien Teil 2
 Mathematisches Kaleidoskop WS15/16 Materialien Teil 2 Dr. Hermann Duerkop E-Mail: hd@nabla.de 1 1.2.7 Papierstreifenmethode zur Zeichnung einer Ellipse Die Gärtnermethode zum Zeichnen einer Ellipse war
Mathematisches Kaleidoskop WS15/16 Materialien Teil 2 Dr. Hermann Duerkop E-Mail: hd@nabla.de 1 1.2.7 Papierstreifenmethode zur Zeichnung einer Ellipse Die Gärtnermethode zum Zeichnen einer Ellipse war
DEMO für Abbildungen. Streckungen INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. 2. Teil: von Punkten und Kurven
 Abbildungen 2. Teil: Streckungen von Punkten und Kurven Datei Nr. 21020 Stand: 8. August 2012 FRIEDRICH W. UCKEL INTERNETILIOTHEK FÜR SCHULMATHEMATIK DEMO für 21020 Streckung von Punkten und Kurven 2 Vorwort
Abbildungen 2. Teil: Streckungen von Punkten und Kurven Datei Nr. 21020 Stand: 8. August 2012 FRIEDRICH W. UCKEL INTERNETILIOTHEK FÜR SCHULMATHEMATIK DEMO für 21020 Streckung von Punkten und Kurven 2 Vorwort
Die Kraft der Geometrie oder Eine geometrische Lösung zum Baseler Problem
 Die Kraft der Geometrie oder Eine geometrische Lösung zum Baseler roblem von Reimund Albers, Bremen Im Baseler roblem geht es um die Summe der reziproken Quadrate, also + + 2 3 + 2 4 + +..., und ein exaktes
Die Kraft der Geometrie oder Eine geometrische Lösung zum Baseler roblem von Reimund Albers, Bremen Im Baseler roblem geht es um die Summe der reziproken Quadrate, also + + 2 3 + 2 4 + +..., und ein exaktes
Aufgaben zur Übung der Anwendung von GeoGebra
 Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Dynamische Funktionen mit GeoGebra
 Markus HOHENWARTER, Salzburg Dynamische Funktionen mit GeoGebra GeoGebra ist ein Softwaresystem für den Unterricht, das dynamische Geometrie, Algebra und Analysis verbindet (http://www.geogebra.at). Insbesondere
Markus HOHENWARTER, Salzburg Dynamische Funktionen mit GeoGebra GeoGebra ist ein Softwaresystem für den Unterricht, das dynamische Geometrie, Algebra und Analysis verbindet (http://www.geogebra.at). Insbesondere
DARSTELLENDE GEOMETRIE I
 DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
Übungsaufgaben Geometrie und lineare Algebra - Serie 1
 Übungsaufgaben Geometrie und lineare Algebra - Serie. Bei einer geraden Pyramide mit einer quadratischen Grundfläche von 00 cm beträgt die Seitenkante 3 cm. a) Welche Höhe hat die Pyramide? b) Wie groß
Übungsaufgaben Geometrie und lineare Algebra - Serie. Bei einer geraden Pyramide mit einer quadratischen Grundfläche von 00 cm beträgt die Seitenkante 3 cm. a) Welche Höhe hat die Pyramide? b) Wie groß
1.2 Sonderfälle a) Für b = 0 wird die Ellipse zu einer Strecke und wir erhalten den gewöhnlichen Thaleskreis.
 Hans Walser, [0180604], [018077] Thaleskreis an Ellipse und Hyperbel 1 Ellipse 1.1 Thaleskreis Die Menge der Punkte, von denen aus eine Ellipse unter einem rechten Winkel gesehen wird, ist ein Kreis (Abb.
Hans Walser, [0180604], [018077] Thaleskreis an Ellipse und Hyperbel 1 Ellipse 1.1 Thaleskreis Die Menge der Punkte, von denen aus eine Ellipse unter einem rechten Winkel gesehen wird, ist ein Kreis (Abb.
Gymnasium Muttenz Maturitätsprüfung 2016 Mathematik Profile A und B
 Gymnasium Muttenz Maturitätsprüfung 2016 Mathematik Profile A und B Name, Vorname:... Hinweise: Klasse:... Die Prüfung dauert 4 Stunden. Es können maximal 48 Punkte erreicht werden. Es werden alle Aufgaben
Gymnasium Muttenz Maturitätsprüfung 2016 Mathematik Profile A und B Name, Vorname:... Hinweise: Klasse:... Die Prüfung dauert 4 Stunden. Es können maximal 48 Punkte erreicht werden. Es werden alle Aufgaben
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Geometrische Grundlagen der. Architekturdarstellung
 Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Gymnasium Oberwil / Maturitätsprüfung Mathematik
 Mathematik Verwenden Sie bitte für jede Aufgabe eine neue Seite. Dauer: Hilfsmittel: Bewertung: Vier Stunden Formeln, Tabellen, Begriffe (DMK), Taschenrechner TI-83, TI-83+, TI-84, TI-84+, TI-84+ Silver
Mathematik Verwenden Sie bitte für jede Aufgabe eine neue Seite. Dauer: Hilfsmittel: Bewertung: Vier Stunden Formeln, Tabellen, Begriffe (DMK), Taschenrechner TI-83, TI-83+, TI-84, TI-84+, TI-84+ Silver
Drei Kreise im Dreieck
 Ein Problem von, 171-1807 9. Juli 006 Gegeben sei das Dreieck ABC. Zeichne drei Kreise k 1, k, k im nneren von ABC, von denen jeder zwei Dreieckseiten und mindestens einen der übrigen zwei Kreise berührt
Ein Problem von, 171-1807 9. Juli 006 Gegeben sei das Dreieck ABC. Zeichne drei Kreise k 1, k, k im nneren von ABC, von denen jeder zwei Dreieckseiten und mindestens einen der übrigen zwei Kreise berührt
3 Abbildungen in der Ebene
 18 3 Abbildungen in der Ebene Wir behandeln in diesem Kapitel Abbildungen von Punkten der Ebene auf Punkte. Ziel dieser Betrachtung ist, Funktionsgraphen mit diesen Abbildungen (punktweise) abzubilden
18 3 Abbildungen in der Ebene Wir behandeln in diesem Kapitel Abbildungen von Punkten der Ebene auf Punkte. Ziel dieser Betrachtung ist, Funktionsgraphen mit diesen Abbildungen (punktweise) abzubilden
Seite 1 Einleitung Elemente der Darstellenden Geometrie 13. Lernkontrolle A 1 15
 Inhaltsverzeichnis Seite 1 Einleitung 13 2 Elemente der Darstellenden Geometrie 13 Lernkontrolle A 1 15 3 Projektionsarten und Verfahren 15 3.1 Projektionsvorgang 15 3.2 Projektionsarten 16 3.2.1 Zentralprojektion
Inhaltsverzeichnis Seite 1 Einleitung 13 2 Elemente der Darstellenden Geometrie 13 Lernkontrolle A 1 15 3 Projektionsarten und Verfahren 15 3.1 Projektionsvorgang 15 3.2 Projektionsarten 16 3.2.1 Zentralprojektion
Mathematische Probleme, SS 2015 Montag $Id: quadratisch.tex,v /06/22 12:08:41 hk Exp $
 Mathematische Probleme, SS 15 Montag 6 $Id: quadratischtex,v 111 15/06/ 1:08:41 hk Exp $ 4 Kegelschnitte 41 Quadratische Gleichungen In der letzten Sitzung hatten wir die Normalform (1 ɛ )x + y pɛx p =
Mathematische Probleme, SS 15 Montag 6 $Id: quadratischtex,v 111 15/06/ 1:08:41 hk Exp $ 4 Kegelschnitte 41 Quadratische Gleichungen In der letzten Sitzung hatten wir die Normalform (1 ɛ )x + y pɛx p =
Geometrische Grundkonstruktionen
 Geometrische Grundkonstruktionen Strecken...2 Halbierung einer Strecke und Mittelsenkrechte...2 Teilung einer Strecke in eine bestimmte Anzahl gleicher Teile...2 Halbierung eines Winkels...3 Tangente an
Geometrische Grundkonstruktionen Strecken...2 Halbierung einer Strecke und Mittelsenkrechte...2 Teilung einer Strecke in eine bestimmte Anzahl gleicher Teile...2 Halbierung eines Winkels...3 Tangente an
4 Ein wenig analytische Geometrie. 4.1 Einige Grundgebilde der projektiven Geometrie Geraden in homogenen Koordinaten
 4 Ein wenig analytische Geometrie 4.1 Einige Grundgebilde der projektiven Geometrie 4.1.1 Geraden in homogenen Koordinaten (a) Im Raum/Ebene in Parameterform Siehe Figur-4-1-1-a (ohne X g = P Q) P ( p),
4 Ein wenig analytische Geometrie 4.1 Einige Grundgebilde der projektiven Geometrie 4.1.1 Geraden in homogenen Koordinaten (a) Im Raum/Ebene in Parameterform Siehe Figur-4-1-1-a (ohne X g = P Q) P ( p),
8.Perspektive (oder Zentralprojektion)
 8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
Die stereografische Projektion. Hans Walser
 Die stereografische rojektion Hans Walser Die stereografische rojektion ii Inhalt 1 Worum geht es?...1 2 Die stereografische rojektion ist winkeltreu...3 3 Die stereografische rojektion ist kreistreu...5
Die stereografische rojektion Hans Walser Die stereografische rojektion ii Inhalt 1 Worum geht es?...1 2 Die stereografische rojektion ist winkeltreu...3 3 Die stereografische rojektion ist kreistreu...5
Proseminar über multimediale Lineare Algebra und Analytische Geometrie
 Proseminar über multimediale Lineare Algebra und Analytische Geometrie Aufgabensteller: Dr. M. Kaplan Josef Lichtinger Montag, 1. Dezember 008 Proseminar WS0809 Inhaltsverzeichnis 1 Aufgabenstellung 3
Proseminar über multimediale Lineare Algebra und Analytische Geometrie Aufgabensteller: Dr. M. Kaplan Josef Lichtinger Montag, 1. Dezember 008 Proseminar WS0809 Inhaltsverzeichnis 1 Aufgabenstellung 3
Klassische Lehrsätze der ebenen Geometrie: Verschiedene Zugänge zu Begründen und Beweisen
 Klassische Lehrsätze der ebenen Geometrie: Verschiedene Zugänge zu Begründen und Beweisen Mag. Walter Wegscheider BG/BRG Klosterneuburg, PI-Hollabrunn Ausgangslage Stellung der Geometrie in der M-Oberstufe
Klassische Lehrsätze der ebenen Geometrie: Verschiedene Zugänge zu Begründen und Beweisen Mag. Walter Wegscheider BG/BRG Klosterneuburg, PI-Hollabrunn Ausgangslage Stellung der Geometrie in der M-Oberstufe
Geometrie-Dossier Kreis 2
 Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
DEMO für Verkettung von Kongruenzabbildungen INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. FRIEDRICH W. BUCKEL.
 Abbildungen Verkettung von Kongruenzabbildungen Für Interessenten. Datei Nr. 11059 Stand: 3. Oktober 2013 DEMO für FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 11059 Verkettung von Kongruenzabbildungen
Abbildungen Verkettung von Kongruenzabbildungen Für Interessenten. Datei Nr. 11059 Stand: 3. Oktober 2013 DEMO für FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 11059 Verkettung von Kongruenzabbildungen
a, b, c bezeichnen nicht mehr Halbachsen von Ellipsen oder Hyperbeln. Für Hyperbeln und Ellipsen wurden spezielle Koordinatensysteme benutzt!
 5 Kegelschnitte und Hauptachsentransformation 5.1 Allgemeine Kegelschnittgleichung ax + by + cxy + dx + ey + f = 0 ) Die Buchstaben a, b, c sind relle Zahlen, die nicht gleichzeitig Null sind: a, b, c)
5 Kegelschnitte und Hauptachsentransformation 5.1 Allgemeine Kegelschnittgleichung ax + by + cxy + dx + ey + f = 0 ) Die Buchstaben a, b, c sind relle Zahlen, die nicht gleichzeitig Null sind: a, b, c)
4^ Springer Vieweg. Geometrische Grundlagen der Architekturdarstellung. Cornelie Leopold. 5V überarbeitete und erweiterte Auflage.
 Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 5V überarbeitete und erweiterte Auflage Unter Mitwirkung von Andreas Matievits 4^ Springer Vieweg Affinität INHALTSVERZEICHNIS Vorwort
Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 5V überarbeitete und erweiterte Auflage Unter Mitwirkung von Andreas Matievits 4^ Springer Vieweg Affinität INHALTSVERZEICHNIS Vorwort
Inversion an Kegelschnitten mit CINDERELLA
 Inversion an Kegelschnitten mit CINDERELLA Hermann Vogel, TU-München In diesem Vortrag wird aufgezeigt, wie man mit Hilfe des Programms CINDERELLA die bekannte Inversion am Kreis auf die Inversion an Kegelschnitten
Inversion an Kegelschnitten mit CINDERELLA Hermann Vogel, TU-München In diesem Vortrag wird aufgezeigt, wie man mit Hilfe des Programms CINDERELLA die bekannte Inversion am Kreis auf die Inversion an Kegelschnitten
Aufgabenstellung zur Wahlfachübung 2
 Darstellende Geometrie für Architekten III Institut für Geometrie und Prakt. Mathematik RWTH Aachen 5.2 Kegel Geometrie der Formen Übung 2 Seite 1 Aufgabenstellung zur Wahlfachübung 2 Hausübung zum Thema
Darstellende Geometrie für Architekten III Institut für Geometrie und Prakt. Mathematik RWTH Aachen 5.2 Kegel Geometrie der Formen Übung 2 Seite 1 Aufgabenstellung zur Wahlfachübung 2 Hausübung zum Thema
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 8
 Dr. Erwin Schörner Klausurenkurs zum Staatseamen (SS 205): Lineare Algebra und analtische Geometrie 8 8. (Herbst 202, Thema 3, Aufgabe 4) Bestimmen Sie die euklidische Normalform der Quadrik Q, gegeben
Dr. Erwin Schörner Klausurenkurs zum Staatseamen (SS 205): Lineare Algebra und analtische Geometrie 8 8. (Herbst 202, Thema 3, Aufgabe 4) Bestimmen Sie die euklidische Normalform der Quadrik Q, gegeben
1 + λ 0, die Geraden h : x =
 Amnalytische Geometrie. In einem kartesischen Koordinatensystem des R sind die Gerade g : x 7 + λ, die Geraden h : x 8 5 + µ, λ, µ, a R sowie die Ebene E durch die Punkte A 5, und gegeben. B 6 C 5 a) K
Amnalytische Geometrie. In einem kartesischen Koordinatensystem des R sind die Gerade g : x 7 + λ, die Geraden h : x 8 5 + µ, λ, µ, a R sowie die Ebene E durch die Punkte A 5, und gegeben. B 6 C 5 a) K
Demo-Text für Inversion (Spiegelung am Kreis) Ein Spezialthema INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 Inversion (Spiegelung am Kreis) Ein Spezialthema Teil 1 Grundlagen Text Nr. 1400 Stand: 4. Februar 016 FIEDICH W. BUCKEL INTENETBIBLIOTHEK FÜ SCHULMATHEMATIK 1400 Inversion 1 Vorwort Die Inversion, die
Inversion (Spiegelung am Kreis) Ein Spezialthema Teil 1 Grundlagen Text Nr. 1400 Stand: 4. Februar 016 FIEDICH W. BUCKEL INTENETBIBLIOTHEK FÜ SCHULMATHEMATIK 1400 Inversion 1 Vorwort Die Inversion, die
