Stefan A. Funken Numerische Mathematik IV
|
|
|
- Matthias Lorenz
- vor 7 Jahren
- Abrufe
Transkript
1 Stefan A. Funken Numerische Mathematik IV SKRIPT, UNIVERSITÄT ULM, SOMMERSEMESTER 200
2
3 i Vorbemerkung. Copyright. Alle Rechte, insbesondere das Recht auf Vervielfältigung und Verbreitung sowie der Übersetzung, vorbehalten. Kein Teil des Werkes darf in irgendeiner Form ohne schriftliche Genehmigung des Autors reproduziert oder unter Verwendung elektronischer Systeme oder auf anderen Wegen verarbeitet, vervielfältigt oder verbreitet werden. Stand. Ulm, April 200.
4
5 Inhaltsverzeichnis Symbolverzeichnis v Gewöhnliche Differentialgleichungen. Existenz- und Eindeutigkeitssätze.2 Theorie der Einschrittverfahren 3 Das explizite Euler-Verfahren und die Methode der Taylorreihe 3.3 Diskretisierungsfehler, Fehlerordnung 9.4 Verbesserte Polygonzugmethode, implizites Euler-Verfahren, Prädiktor-Korrektor-Verfahren 2.5 Runge-Kutta-Verfahren 5.6 Schrittweitensteuerung 8.7 Implizite Runge-Kutta-Verfahren 22.8 Mehrschrittverfahren 22.9 Konvergenz von Mehrschrittverfahren 34.0 Konvergenz- und Stabilitätsbedingungen für Mehrschrittverfahren 37. Prädiktor-Korrektor-Verfahren 42.2 Stabilitätsbegriffe, Stabilitätsbereiche 45.3 Steife Differentialgleichungen 53 2 Partielle Differentialgleichungen Beispiele und Motivation 59 Kollokation 59 Finite Differenzenmethode (FDM) 59 Finite Elemente Methode (FEM) 59 Randelementemethode (BEM) 59 Nyström-Methode Kollokation Finite Differenzenmethode (FDM) Finite Elemente Methode (FEM) Randelementemethode (BEM) 59
6 iv INHALTSVERZEICHNIS Literaturverzeichnis 6 Stichwortverzeichnis 6
7 Symbolverzeichnis Bemerkung. Mathematische Symbole sind auch (sofern möglich) alphabetisch im Stichwortverzeichnis aufgeführt. N natürliche Zahlen (ohne 0) N 0 R d natürliche Zahlen vereinigt mit0 Euklidischer Raum von (Spalten-) Vektoren indkomponenten Bemerkung: Diese Seite ändert sich noch während der Vorlesung, d.h. weitere, den Studenten unbekannte Notationen, werden laufend ergänzt.
8
9 GEWÖHNLICHE DIFFERENTIALGLEICHUNGEN Viele Anwendungen in Natur- und Ingenieurwissenschaften führen auf Differentialgleichungen oder Differentialgleichungssysteme, welche die zeitliche Änderung einer oder mehrerer Zustandsgrößen beschreiben. Exemplarisch seien hier die Berechnung der Flugbahn eines Raumfahrzeugs beim Wiedereintritt in die Erdatmosphäre, Räuber-Beute-Modelle oder chemische Reaktionen genannt, deren Modellierungen im Anhang hergeleitet werden. Wir betrachten im folgenden das System von N gewöhnlichen Differentialgleichungen erster Ordnung y (t) = f(t,y(t)) (t [a,b]) (.) für die gesuchte Lösungsfunktion y unter der Anfangsbedingung mit einem gegebenen endlichen Intervall [a, b] und einer Funktion y(a) = y 0 R N (.2) f : [a,b] R N R N. (.3) Das Problem (.), (.2) bezeichnen wir als Anfangswertproblem. Die Notation y = f(t,y) verwenden wir als Kurzform; dabei bedeute Differenzierbarkeit hier komponentenweise Differenzierbarkeit und es sei y (t) = (y (t),...,y N (t))t.. EXISTENZ- UND EINDEUTIGKEITSSÄTZE Wir wollen hier kurz auf die Existenz und Eindeutigkeit der Lösung bei Anfangswertproblemen für gewöhnliche Differentialgleichungen eingehen, auch wenn wir später stillschweigend voraussetzen, daß die betreffenden Voraussetzungen erfüllt sind und das Anfangswertproblem (.), (.2) jeweils eine eindeutig bestimmte Lösung besitzt. Bei der Eindeutigkeit einer Lösung spielt die folgende Lipschitzbedingung für Funktionen f von der Form (.3) eine wesentliche Rolle, f(t,u) f(t,v) L u v (t [a,b], u,v R N ), (.4) mit einer Konstanten L > 0 und einer beliebigen Vektornorm. Da Stetigkeit der Funktion f die Existenz einer Lösung liefert, erhält man aus dem Satz (Existenzsatz von Peano) Ist f(x,y) in einem Gebiet D stetig, so geht durch jeden Punkt (ξ,η) D mindestens eine Lösung der Differentialgleichung (.). Jede Lösung läßt sich bis zum Rand von D fortsetzen. Beispiele 2 i. Bevökerungswachstum. Sei p(t) die Größe der Bevölkerung zur Zeit t, bzw. p 0 die Größe der Bevölkerung zur Zeitt 0. Die Geburtenrate sei mitg(t,p bezeichnet und s(t,p) sei die Sterberate. Die Funktion p löst die Anfangswertaufgabe d dt p(t) = (g(t,p) s(t,p))p(t), p(t 0) = p 0.
10 2 Kapitel : Gewöhnliche Differentialgleichungen ii. Glatte rechte Seite f. Das Anfangswertproblem d dt y = +y2, y(0) = 0 hat die Lösung y = tan(x). Als stetig differenzierbare Funktion existiert diese nur für x < π, obwohl f(x,y) = +y 2 in C (R 2 ) ist. Wie verträgt sich das mit dem Satz von Piano? iii. Mathematisches Pendel. Ein mathematisches Pendel ist die Idealisierung eines realen Pendels. Hierbei herrscht keinerlei Reibung und die gesamte Masse des Pendels (inklusive Faden) ist in einem Punkt konzentriert. Die Bewegungsgleichung für den Auslenkungswinkel (bezüglich der Ruhelage) des Pendels lautet ϕ(t)+ g sin(ϕ(t)) = 0, l wobei g die Erdbeschleunigung und l die Fadenlänge ist. Die gewöhnliche Differentialgleichung 2. Ordnung ÿ = f(t,y,ẏ) wird durch den Ansatz y = y, ẏ = y 2 in das System einer gewöhnlichen Differentialgleichung. Ordnung überführt, nämlich ( ) ( ) d y y = 2. dt f(t,y,y 2 ) y 2 Im Falle des mathematischen Pendels ergibt sich also das folgende System einer gewöhnlichen Differentialgleichung. Ordnung, ( ) ( ) d ϕ ϕ = 2. dt g/l sin(ϕ ) ϕ 2 Der Ort des Pendels zum Zeitpunkt t ist dann (lsinϕ(t),lcosϕ(t)), wobei die y Achse nach unten zeigt. iv. Doppelpendel. Hängt man an den Arm eines Pendels ein weiteres Pendel, so spricht man vom Doppelpendel. Dies ist ein beliebtes Modell zur Demonstration chaotischer Prozesse. Die Bewegungsgleichungen für die Auslenkungswinkel ϕ und ϕ 2 i, welche die Fäden mit der Länge l und l 2 mit der Vertikalen einschließen, lautet (m +m 2 )l ϕ +m 2 l 2 ϕ 2 cos(ϕ ϕ 2 )+m 2 l 2 ϕ 2 sin(ϕ ϕ 2 )+g(m +m 2 )sin(ϕ 2 ) = 0 m 2 l 2 ϕ 2 +m 2 l ϕ cos(ϕ ϕ 2 ) m 2 l ϕ 2 sin(ϕ ϕ 2 )+gm 2 sin(ϕ 2 ) = 0 Die kartesischen Koordinaten (x 2,y 2 ) des zweiten Massepunktes kann man mittels ϕ und ϕ 2 ausdrücken, nämlich x 2 = l sinϕ +l 2 sinϕ 2, y 2 = l cosϕ +l 2 cosϕ 2. Hierbei liegt der Aufhängungspunkt im Ursprung und die y-achse zeigt nach unten. Mit dem Ansatz u = ϕ,u 2 = ϕ,u 3 = ϕ 2 und u 4 = ϕ 2 erhält man wie im Beispiel zuvor ein System einer gewöhnlichen Differentialgleichung. Ordnung. Nun jedoch von der Dimension vier. v. Anfangswertproblem mit unendlich vielen Lösungen. Durch die rein formale Trennung der Veränderlichen und formales Integrieren erhalten wir zu der Differentialgleichung y = y, (.5)
11 Abschnitt.2: Theorie der Einschrittverfahren 3 sofern wir nichtnegative Lösungen unterstellen, 2 y = t + c mit einer frei wählbaren Integrationskonstanten c. Dies motiviert die mit dem Parameter c R behaftete Funktion y = (t+c)2 4 als mögliche Lösung von (.5) zu testen. Tatsächlich ist (.6) differenzierbar und es gilt y = (t+c)/2 = y. Untersuchen wir nun z. B. die Anfangsbedingung (.6) y(0) = 0, (.7) so erhalten wir y(t) = 0 als offensichtliche Lösung des Anfangswertproblems (.5) und (.7). Es können jedoch überall weitere Funktionen der Form (.6) abzweigen. Betrachten wir dazu folgende Funktion y(,d) mit d > 0, { 0 für 0 t d, y(t,d) := (t d) 2 4 für d t. Diese Funktion ist offensichtlich überall stetig und differenzierbar mit stetiger Ableitung. Sowohl für t < d also auch für t > d erfüllt (.8) die Differentialgleichung (.5) und (.7). Da y(d) = 0 = y (d) ist, gilt (.5) für alle t und (.8) ist somit Lösung des Anfangswertproblems (.5) und (.7). Es liegen also unendlich viele Lösungen vor. Neben der Existenz und Eindeutigkeit einer Lösung für Anfangswertprobleme (.), (.2) liefert der folgende Satz auch ein wichtiges Resultat zur stetigen Abhängigkeit von den Anfangswerten. Satz 3 (Picard-Lindelöf) Es bezeichne 2 die euklidische Norm. Die Funktionf(x,y) sei stetig auf dem kompakten Rechteck D := {(x,y) x a α, y y 0 2 β} (α,β > 0) und genüge dort einer Lipschitzbedingung (.4) bezüglich y mit der Lipschitzkonstanten L. a) Dann besitzt das Anfangswertproblem (.), (.2) genau eine Lösung auf einem Intervall I := [a γ,a+γ] mit γ = min(α,β/max (x,y) D f(x,y)) b) Für differenzierbare Funktionen y,y : [a,b] R N mit gilt die Abschätzung y (t) = f(t,y) (t [a,b]), y(a) = y 0 y (t) = f(t,y) (t [a,b]), y(a) = y 0 (.8) y(t) y(t) 2 e L(t a) y 0 y 0 2 (t I)..2 THEORIE DER EINSCHRITTVERFAHREN Das explizite Euler-Verfahren und die Methode der Taylorreihe Beschränken wir uns zuerst auf die Situation N =. Aus geometrischen Anschauungen läßt sich recht einfach das explizite Euler-Verfahren motivieren, da die Differentialgleichung (.) im Punkt (t 0,y 0 ) mit dem Wert y (t 0 ) = f(t 0,y 0 ) die Steigung der gesuchten Funktion festlegt, d.h. es ergibt sich zu der Schrittweite h folgende Approximation y(t 0 +h) y(t 0 )+hf(t 0,y 0 ). (.9)
12 4 Kapitel : Gewöhnliche Differentialgleichungen Definieren wir nun Punkte t k = t 0 +kh (k = 0,,2,...) so ergibt sich durch sukzessives Anwenden von (.9) das explizite Euler-Verfahren y k+ = y k +hf(t k,y k ) (k = 0,,2,...), (.) wobei y k eine Approximation an y(t k ) (k = 0,,2,...) bezeichne. Man erhält somit eine stückweise lineare Approximation der gesuchten Funktion y(t), weswegen man dieses Verfahren auch Polygonzugverfahren nennt. Es treten nun folgende Fragen auf, mit denen wir uns im weiteren beschäftigen werden: Wird die Approximation besser, wenn man die Schrittweite h verkleinert? Wenn ja, in welchem Sinne und von welcher Größenordnung ist sie? In jedem Schritt des expliziten Euler-Verfahrens wird im allgemeinen ein Fehler y(t k ) y k (k = 0,,2,...) gemacht. Wie setzen sich solche Fehler in weiteren Schritten fort? Beispiel 4 (zum expliziten Euler-Verfahren) Betrachten wir die Anfangswertaufgabe y (t) = tsin(πy(t)), y(0) = 2. (.2) Die exakte Lösung lautet y(t) = 2 π arc tan(e πt2 /2 ). Mit dem expliziten Euler-Verfahren erhalten wir die in Tabelle 4 aufgelisteten Näherungswerte für verschieden Schrittweiten h an gleichen Stellen t k und die zugehörigen Fehler e k = y(t k ) y k. Man beachte, daß bei Zehntelung der Schrittweite sich auch der entsprechende Fehler zehntelt. Der Fehler nimmt proportional zur Schrittweite ab. Tab..: Numerische Ergebnisse des expl. Euler-Verfahrens für das Anfangswertproblem (.2) zu verschiedenen Schrittweiten h. Schrittweite h = 0. Schrittweite h = 0.0 Schrittweite h = 0.00 t k y(t k ) y k e k y k e k y k e k Die numerischen Ergebnisse wurden mit dem folgenden Matlab-Programm erstellt. % explizites Euler-Verfahren mit glm. Schrittweite function expl_euler(t,n,a,y0)
13 Abschnitt.2: Theorie der Einschrittverfahren 5 y=zeros(length(y0),n+); y(:,)=y0(:) ; h = (T-a)/N; for k=:n y(:,k+)=y(:,k) + h*f(a+(k-)*h,y(:,k)); end plot(linspace(a,t,n+),y, o- ); title( Approximation mit explizitem Euler-Verfahren ); % problemabhaengige Funktion f function wert = f(t,y) wert = -t*sin(pi*y); Für h = 0, ist die mit dem expliziten Eulerverfahren bestimmte Näherungslösung zum Anfangswertproblem in Abbildung (??) graphisch dargestellt. Eine bedeutend bessere Approximation der gesuchten Funktion y(t) in der Umgebung des Startpunktes (t 0,y 0 ) kann man mit der Taylorreihe mit Restglied, erhalten. y(t) = y(t 0 )+ (t t 0)! y (t 0 )+ (t t 0) 2 2! y (t 0 ) (t t 0) p y (p) (t 0 )+R p+ p! Bemerkung 5 (verschiedene Restglieder) Besitzt y auf dem kompakten Intervall I := [t 0,t] eine stetige Ableitung p-ter Ordnung, während y (p+) wenigstens im Innern o I von I vorhanden sei. Dann gibt es nach dem Satz von Taylor mindestens eine Zahlξ o I, so daß R p+ = (t t 0) p+ y (p+) (ξ) (Lagrangesches-Restglied) (p+)! gelte. Es sei q N. Dann gibt es ein ϑ (0,) mit R p+ = (t t 0) p+ p! ( ϑ) p+ q q y (p+) (t 0 +ϑ(t t 0 )) (Schlömilches-Restglied). Fürq = geht das Schlömilche Restglied in das Cauchysche-Restglied über. Isty (p+) aufi auch noch stetig, so gilt R p+ = p! t t 0 (t s) p y (p+) (s)ds. Durch Vernachlässigen des Restglieds R p+ erhält man mit der Schrittweite h = t t 0 die Rechenvorschrift für das explizite Euler-Verfahren höherer Ordnung y k+ = y k + h! y k + h2 2! y hp k p! y(p) k. (.3) Das Vorgehen erfordert höhere Ableitungen von y, welche sich durch sukzessives Differenzieren vony nachtgewinnen lassen. Die Terme werden dabei jedoch so kompliziert, daß diese Methode nur in sehr einfachen Fällen angewendet wird. Ein weiterer Punkt ist die vorausgesetzte hohe Regularität, die im allgemeinen nicht gewährleistet werden kann.
14 6 Kapitel : Gewöhnliche Differentialgleichungen Beispiel 6 (zum expliziten Euler-Verfahren höherer Ordnung) Untersuchen wir das explizite Euler-Verfahren höherer Ordnung exemplarisch anhand der Anfangswertaufgabe (.2). Aus y (t) = tsin(πy(t)) ergibt sich und y (t) = sin(πy(t))+ πt2 2 sin(2πy(t)) y (t) = 3tπ 2 sin(2πy(t))+ t3 π 2 2 (sin(πy(t)) sin(3πy(t))) Numerische Ergebnisse zu verschiedenen Schrittweiten sind in Tabelle 6 wiedergegeben. Eine Tab..2: Numerische Ergebnisse des expliziten Euler-Verfahrens höherer Ordnung für das Anfangswertproblem (.2) zu verschiedenen Schrittweiten h. Schrittweite h = 0. Schrittweite h = 0.0 Schrittweite h = 0.00 t k y(t k ) y k e k y k e k y k e k e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e-2 Matlab-Realisierung zur Berechnung einer Approximation mit dem expliziten Euler-Verfahren höherer Ordnung sieht etwa folgendermaßen aus. % Verfahren mit Taylorreihe und glm. Schrittweite function taylor(t,n,a,y0) y=zeros(length(y0),n+); y(:,)=y0(:) ; h = (T-a)/N; for k=:n diff = f(a+(k-)*h,y(:,k)); coeff = (h.ˆ[:size(diff,2)])./cumprod(:size(diff,2)); y(:,k+)=y(:,k) + diff*coeff ; end plot(linspace(a,t,n+),y, - ); title( Approximation mit explizitem Euler-Verfahren ); % problemabhaengige Funktion f=y und hoehere Ableitungen function wert = f(t,y) wert(:,) = -t*sin(pi*y); wert(:,2) = -sin(pi*y)+pi*t.ˆ2.*sin(2*pi*y)/2; wert(:,3) = 3 * pi * t.* sin(2*pi*y) / piˆ2 * t.ˆ3.* ( sin(3*pi*y) - sin(pi*y) ) / 2 ;
15 Abschnitt.2: Theorie der Einschrittverfahren 7 Sowohl bei dem klassischen expliziten Euler-Verfahren als auch bei dem expliziten Euler- Verfahren höherer Ordnung haben wir eine Approximation eines Differentialoperators vorgenommen, der beschreibt, wie sich eine Funktion unter den gegebenen Daten fortsetzen läßt. Betrachten wir zum Vergleich nun eine Methode, in der die gesuchte Funktion approximiert wird. Bemerkung 7 Die Idee, zum einen den Differentialoperator zu approximieren oder die Funktion anzunähern, wird uns bei den partiellen Differentialgleichungen z.b. in der Form der Finite- Differenzen-Methode (FDM) im Vergleich zur Finite-Elemente-Methode (FEM) wieder begegnen. Verfahren mit polynomialem Ansatz In einem allgemeinen Näherungspunkt (t k,y k ) lautet der gewählte Ansatz y(t) = y k +c (t t k )+c 2 (t t k ) c p (t t k ) p. (.4) Dieser wird in die Differentialgleichung y (t) = f(t,y(t)) eingesetzt. Ein Koeffizientenvergleich bezüglich der Potenzen von (t t k ) =: h liefert c,...,c p. Beispiel 8 Betrachten wir wieder die Anfangswertaufgabe y (t) = tsin(πy(t)), y(0) = 2. Die zu erfüllende Identität lautet für p = 3, wobei wir sin(x) = x x3 3! + x5 5!..., cos(x) = x2 2! + x4 4!... berücksichtigen. c +2c 2 h+3c 3 h 2 = (t k +h)sin(π(y k +c h+c 2 h 2 +c 3 h 3 )) = (t k +h)[sin(πy k )cos(π(c h+c 2 h 2 +c 3 h 3 )+cos(πy k )sin(π(c h+c 2 h 2 +c 3 h 3 ))] = (t k +h)sin(πy k )[ π 2 (c 2 h 2 +2c c 2 h 3 +(c c c 3 )h 4 +2c 2 c 3 h 5 +c 2 3h 6 )+O(h 4 )] t k cos(πy k )[π(c h+c 2 h 2 +c 3 h 3 )+O(h 3 )] = t k sin(πy k ) h(c t k πcos(πy k )+sin(πy k ))+h 2 ( t k ( c2 π2 2 sin(πy k)+πc 2 cos(πy k )) πc cos(πy k ))+O(h 3 ). (.5) Daraus folgt: c = c (t k,y k ) = t k sin(πy k ) c 2 = c 2 (t k,y k ) = c 2 t kcos(πy k ) c 3 = c 3 (t k,y k ) = t 3 3 [c2 π2 sin(πy k ) c 2 cos(πy k ). Die aufwendige Rechnung der rechten Seite in (.5) läßt sich mit Maple durch den Befehl taylor(-(t+h)*sin(pi*(y+c*h+c2*hˆ2+c3*hˆ3)),h=0,3); leicht verifizieren.
16 8 Kapitel : Gewöhnliche Differentialgleichungen Die numerischen Ergebnisse zu verschiedenen Schrittweiten und der oben genannten Methode finden sich in der folgenden Tabelle: Tab..3: Numerische Ergebnisse zum Verfahren mit polynomialem Ansatz (.4) für das Anfangswertproblem (.2) zu verschiedenen Schrittweiten h. Schrittweite h = 0. Schrittweite h = 0.0 Schrittweite h = 0.00 t y(t k ) y k e k y k e k y k e k e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e-2 Diskussion der Ergebnisse! Wie sieht man Konvergenz der FormO(h 3 ) Fehler Eine Matlab-Realisierung zur Berechnung einer Approximation mit polynomialem Ansatz sieht etwa folgendermaßen aus. % Verfahren mit stkw. poly. Approximation der Ftkn. % und glm. Schrittweite function stkw_approx(t,n,a,y0) y=zeros(length(y0),n+); y(:,)=y0(:) ; h = (T-a)/N; for k=:n cs = coeff(a+(k-)*h,y(:,k)); hs = (h.ˆ[:size(cs,2)]); y(:,k+) = y(:,k) + cs*hs ; end plot(linspace(a,t,n+),y, >- ); title( Approximation durch stkw. poly. Funktion ); % problemabh"angige Koeffizientenfunktionen function wert = coeff(t,y) wert(:,) = -t*sin(pi*y); wert(:,2) = -(wert(:,).*pi.*t.*cos(pi*y)+sin(pi*y))/2; wert(:,3) = (-t*(-wert(:,).ˆ2.*piˆ2.*sin(pi*y)/2+... pi*wert(:,2).*cos(pi*y))-pi*wert(:,).*cos(pi*y))/3; Vor- und Nachteile der letzten beiden Verfahren, welche auf der Entwicklung in eine Taylorreihe basieren, sind offensichtlich: Anzahl der Glieder der Taylorreihe läßt sich im Prinzip beliebig erhöhen (Regularität der gesuchten Funktion beachten!)
17 Abschnitt.3: Diskretisierungsfehler, Fehlerordnung 9 großer analytischer Aufwand um höhere Ableitungen in (.3) oder Koeffizientenc,...,c p zu erstellen. Um letzt genannten Nachteil zu vermeiden, werden wir später weitere Methoden motivieren und analysieren, welche direkt auf die Differentialgleichung anwendbar sind..3 DISKRETISIERUNGSFEHLER, FEHLERORDNUNG Die bisher betrachteten Verfahren zur numerischen Lösung von Anfangswertproblemen bezeichnet man als Einschrittverfahren, da vorherige Schritte des numerischen Verfahrens unberücksichtigt bleiben. Für eine Analyse solcher Einschrittverfahren stellen wir einige Aussagen in verallgemeinerter Form über Fehlerabschätzungen zusammen. Betrachten wir dazu die Rechenvorschrift y k+ = y k +hφ(t k,y k,h) (k = 0,,2,...). (.6) Dabei beschreibt φ(t k,y k,h) die zugrundeliegende Methode, z.b. im Falle des expliziten Euler- Verfahrens φ(t k,y k,h) = f(t k,y k ) oder in der Situation des Euler-Verfahrens höherer Ordnung φ(t k,y k,h) =! f(t k,y k )+ h 2! t f(t k,y k )+...+ hp p p! t pf(t k,y k ). Eine natürliche Voraussetzung an die Funktion φ ist sicherlich y k+ y k lim h 0 h = y (t k ) = φ(t k,y k,0). Definition 9 Ein Einschrittverfahren (.6) heißt mit einer Differentialgleichung y (t) = f(t,y) konsistent, falls φ(t,y,0) = f(t,y) gilt. Aufgabe Man zeige, daß die Konsistenzbedingung sowohl für das explizite Euler-Verfahren als auch für die auf der Taylorreihe basierenden Ansätze (.3) und (.4) erfüllt ist. Für die weitere Analyse setzen wir eine konstante Schrittweite (t k = a+kh,k = 0,,2,...) und exakte Arithmetik (keine Rundungsfehler!) Notiz voraus. Neben der Konsistenz ist eine wichtige Größe der Diskretisierungsfehler, der lokale wie der globale (totale). Definition 0 Unter dem lokalen Diskretisierungsfehler d k+ an der Stellet k+ versteht man den Wert d k+ := y(t k+ ) y(t k ) hφ(t k,y(t k ),h), wobei man beachte, daß auf der rechten Seite die exakten Werte y(t k ) und y(t k+ ) verwendet werden.
18 0 Kapitel : Gewöhnliche Differentialgleichungen Der lokale Diskretisierungsfehler beschreibt den Fehler, den die verwendete Rechenvorschrift in einem einzelnen Schritt macht. Da man im allgemeinen mehrere Schritte eines Verfahrens durchführt, um eine Anfangswertaufgabe zu lösen, ist für die Rechenpraxis der globale Fehler von Interesse. Sprich der Fehler, den die Näherung nach mehreren Integrationsschritten gegenüber der exakten Lösung aufweist.! Definition Als globalen Diskretisierungsfehler e k an der Stelle t k bezeichnet man die Differenz e k := y(t k ) y k. Für weitere Analysen setzen wir voraus, daß die Funktion φ in einem geeignet gewählten Bereich B bzgl. der Variablen y eine Lipschitz-Bedingung φ(x,y,h) φ(x,y,h) L y y ((x,y,y,h) B) (.7) erfüllt mit 0 < L <. Desweiteren setzen wir voraus, daß man eine Schranke D angeben kann mit max d k D. (.8) k Nach all diesen Definitionen, Voraussetzungen und Annahmen sind wir nun in der Lage, einen Satz über den globalen Diskretisierungsfehler zu formulieren. Satz 2 Für den globalen Diskretisierungsfehler e n an der festen Stelle t n = t 0 + nh gilt die Abschätzung e n D hl enhl D hl enhl Bemerkung 3 Für das explizite Euler-Verfahren läßt sich e n h 2L max t 0 ξ t n y (ξ) e L(tn t 0) (.9) zeigen. Bei konstantem (t n t 0 ) konvergiert folglich der Wert y n an der festgehaltenen Stelle t n proportional zu h 0. Bevor wir obigen Satz 2 zeigen, beweisen wir folgendes Lemma: Lemma 4 Erfüllen die Werte e k die Ungleichung so gilt e k+ (+C ) e k +D (k = 0,,2,...), (.20) e n (+C ) n C D +(+C ) n e 0 (.2) D C (e nc )+e nc e 0 (.22) Beweis. Sukzessive Anwendung von (.20) liefert Ungleichung (.2) e n (+C ) e n +D (+C )(+C ) e n 2 +((+C )+)D (+C ) 3 e n 3 +((+C ) 2 +(+C )+)D (+C ) n e 0 + (+C ) n (+C ) D
19 Abschnitt.3: Diskretisierungsfehler, Fehlerordnung Aus der Konvexität von e t und e t = +t für t = 0 folgt +t e t Mit dieser Ungleichung zusammen mit (.2) ergibt sich (.22), womit das Lemma bewiesen wäre. Beweis von Satz 2. Aus der Definition des lokalen Diskretisierungsfehlers ergibt sich nach Subtraktion der allgemeinen Rechenvorschrift (.6) e k+ = e k +h(φ(t k,y(t k ),h) φ(t k,y k,h))+d k+. Ausnutzen der Lipschitzbedingung (.7) und der oberen Schranke (.8) liefert e k+ e k +h φ(t k,y(t k ),h) φ(t k,y k,h) + d k+ e k +hl y(t k ) y k + d k+ (+hl) e k +D. Da der globale Diskretisierungsfehler an der Stellet 0 gleich null (e 0 = y(t 0 ) y 0 = 0) ist, ergibt sich unmittelbar mit Lemma 4 (setze C = hl) e n D hl (enhl )+e nhl e 0 = D hl (enhl ) D hl enhl Definition 5 Ein Einschrittverfahren (.6) zur Lösung des Anfangswertproblems y = f(t,y), y(t 0 ) = y 0 besitzt die Konvergenzordnung p, falls sich der globale Diskretisierungsfehler abschätzen läßt in der Form max k 0,...,n y(t k) y k 2 Ch p mit einer von der Schrittweite h unabhängigen Konstanten C > 0. Aus Satz 2 erhält man nun leicht Lemma 6 Gilt für die lokalen Diskretisierungsfehler d k eines Einschrittverfahren (.6) die Abschätzung max k n d k D = Ch p+ = O(h p+ ) (p ), so besitzt es die Konvergenzordnung p. Zusammenfassung: Im letzten Kapitel wurden einfache Einschrittverfahren vorgestellt. Die Unterschiede der Verfahren wurden durch die Art und Weise von Approximationen motiviert. Elementare Resultate zur Fehlerakkumulation wurden vorgestellt und numerische Beispiele haben die theoretischen Aussagen illustriert. Der Studierende sollte die Ideen hinter den Verfahren nachvollziehen können und den Inhalt der Fehleranalyse verstanden haben.
20 2 Kapitel : Gewöhnliche Differentialgleichungen.4 VERBESSERTE POLYGONZUGMETHODE, IMPLIZITES EULER-VERFAHREN, PRÄDIKTOR-KORREKTOR-VERFAHREN Nehmen wir an, mit der expliziten Euler-Methode seien zwei Integrationsschritte von einer gegebenen Stelle t aus gemacht worden. Zum einen mit der Schrittweite h, zum andern mit der Schrittweite h 2, dann gilt näherungsweise Bemerkung 7 Motivation ergibt sich aus (.9) y h = y(t)+c h+o(h 2 ) (.23) h yh = y(t)+c 2 2 +O(h2 ) (.24) Durch Linearkombination von (.23) und (.24) ergibt sich ein extrapolierter Wert y = 2yh 2 y h y(t+h)+o(h 2 ), dessen Fehler gegenüber der exakten Lösung von zweiter Ordnung ist, was wir später auch noch genauer beweisen werden. Wie wird diese verbesserte Polygonzugmethode nun numerisch realisiert? Ein Schritt mit der expliziten Methode von Euler mithvon t k nach t k+ liefert y () k+ = y k +hf(t k,y k ) (.25) und ein Doppelschritt mit h 2 liefert mit dem Zwischenschritt bei t k+ 2 = t k + h 2 y (2) k+ 2 = y k + h 2 f(t k,y k ) (.26) und die gesuchte Approximation lautet nun y (2) k+ = y (2) + h k+ 2 2 f(t k+,y (2) ) (.27) 2 k+ 2 y k+ = 2y(2) k+ y() k+ (.28) Zur Berechnung von yk+ benötigen wir somit 2 Auswertungen von f, 4 Multiplikationen und 5 Additionen (=Subtraktionen). Setzen wir jedoch (.25) - (.27) geschickt in (.28) ein, so erhalten wir y k+ = 2y(2) k+ y() k+ = 2y(2) k+ 2 +hf(t k+,y (2) ) y 2 k+ k hf(t k,y k ) 2 = 2y k +hf(t k,y k )+hf(t k+,y k + h 2 2 f(t k,y k )) y k hf(t k,y k ) = y k +hf(t k + h 2,y k + h 2 f(t k,y k )). Dies läßt sich algorithmisch schreiben in der Form k = y k + h 2 f(t k,y k ) k 2 = f(t k + h 2,y k + h 2 k ) y k+ = y k +hk 2.
21 Abschnitt.4: Verbesserte Polygonzugmethode, implizites Euler-Verfahren, Prädiktor-Korrektor-Verfahren 3 Nun benötigen wir 2 Funktionsauswertungen von f, 4 Multiplikationen und 4 Additionen, desweiteren ist diese Formulierung stabiler. Dieses Verfahren nennt man verbessertes Polygonzugverfahren von Euler. Man beachte, daß auch dieses Verfahren, trotz des Zwischenschrittes, als Einschrittverfahren bezeichnet wird. Um die lokale Konvergenzordnung bestimmen zu können, bereiten wir einige Aussagen vor, welche sich durch Differentiation der gegebenen Differentialgleichung ergeben. y = f(t,y) y = f t +f y y = f t +ff y =: G y = (f t ) +(f y y ) = f tt +f ty y +f y (f t +ff y )+f(f ty +f yy f) = (f tt +2f ty f +f 2 f yy ) +(f t +ff y )f y }{{} =:H = H +Gf y Damit erhalten wir für den lokalen Diskretisierungsfehler des verbesserten Polygonzugverfahrens nach einer Entwicklung in Taylorreihen d k+ = y(t k+ ) y(t k ) hf(t k + h 2,y(t k)+ h 2 f(t k,y(t k ))) = y(t k )+hy (t k )+ h2 2 y (t k )+ h3 6 y (t k )+O(h 4 ) y(t k ) h{f(t k,y(t k ))+ h 2 f t(t k,y(t k ))+ h 2 f(t k,y(t k ))f y (t k,y(t k )) + ( ) h 2 ( ) h 2 f tt + ff ty + ( ) h 2 f 2 f yy +O(h 3 )} Somit gilt = 6 { 4 H +Gf y}h 3 +O(h 4 ) = ( 24 (H +Gf y) Gf y)h 3 +O(h 4 ) d k+ 6 ( 4 y y f y )h 3 +O(h 4 ). Sind nun y,y und f y beschränkt, so gilt d k+ = O(h 3 ). Damit ist die Fehlerordnung der verbesserten Polygonzugmethode 2. Durch näherungsweise Integration der Differentialgleichung y = f(t,y) bezüglich der Variablen t über das Intervall [t k,t k+ ](k = 0,,2,...) erhalten wir nun weitere Einschrittmethoden. Betrachten wir dazu y(t k+ ) y(t k ) = tk+ t k f(t,y(t))dt. Verwenden wir zur Integration der rechten Seite die Trapezmethode, so erhalten wir y(t k+ ) y(t k ) h 2 [f(t k,y(t k ))+f(t k+,y(t k+ ))]. Dies motiviert das implizite Euler-Verfahren, welches man erhält, indem man y(t k ) durch y k ersetzt. Das implizite Euler-Verfahren lautet nun y k+ = y k + h 2 (f(t k,y k )+f(t k+,y k+ )). (.29)
22 4 Kapitel : Gewöhnliche Differentialgleichungen Da für eine allgemeine nichtlineare Differentialgleichung (.29) nur eine implizite Gleichung für den approximierten Funktionswert y k+ darstellt, spricht man hier von einer impliziten Integrationsmethode. Aufgabe 2 Man zeige, daß im Spezialfall einer linearen Differentialgleichung erster Ordnung y (x) = a(x)y(x)+b(x) mit gegebenen Funktionen a(x) und b(x) das implizite Euler-Verfahren auf eine lineare Gleichung für y k+ führt, aus der sich eine explizite Rekursionsformel für y k+ (k = 0,,2,...) ergibt. Erfüllt f(x,y) die übliche Lipschitzbedingung bzgl. y mit der Konstanten L und gilt 2hL <, so sind die Voraussetzungen für den lokalen Fixpunktsatz von Banach für die Fixpunktiteration y (n+) k+ = y k + h 2 (f(t k,y k )+f(t k+,y (n) k+ )) (n = 0,,2,...), (.30) y (0) k+ = y k erfüllt und diese ist somit konvergent. Untersuchen wir nun den lokalen Diskretisierungsfehler, aus dem mit Lemma 6 sofort auch eine Abschätzung für den globalen Diskretisierungsfehler folgt. Somit gilt d k+ = y(t k+ ) y k+ = y(t k+ ) y(t k ) h 2 (f(t k,y(t k ))+f(t k+,y k+ )) y(t k+ ) y(t k ) h 2 (y (t k )+y (t k+ )) + Lh 2 y(t k+) y k+ y(t k )+hy (t k )+ h2 2 y (t k )+ h3 6 y (t k )+O(h 4 ) y(t k ) h 2 y (t k ) h 2 (y (t k )+hy (t k )+ h2 2 y (t k )+O(h 3 )) + Lh 2 y(t k+) y k+ h3 2 y (t k )+O(h 4 ) + Lh 2 d k+. ( Lh 2 ) d k+ h3 2 y (t k )+O(h 4 ). Somit ist der lokale Diskretisierungsfehler von der Ordnung 3 und der globale Diskretisierungsfehler von der Ordnung 2. Wenn das implizite Euler-Verfahren jedoch die gleiche Konvergenzordnung wie das verbesserte Polygonzugverfahren hat, welches eine explizite Methode ist, was spricht dann für das aufwendigere Verfahren, d.h. das implizite Euler-Verfahren. Der entscheidende Begriff ist hier die Stabilität, auf welche wir aber erst später eingehen werden. Ein weiteres Einschrittverfahren erhält man, indem man die Fixpunktiteration (.30) nach der zweiten Iteration beendet. Man erhält dann das Verfahren von Heun, welches mit modifizierter Notation wie folgt lautet. Verfahren von Heun y (p) k+ = y k +hf(t k,y k ) y k+ = y k + h 2 (f(t k,y k )+f(t k+,y (p) k+ )). (.3)
23 Abschnitt.5: Runge-Kutta-Verfahren 5 Man bezeichnet diese Methode als Prädiktor-Korrektor-Methode, da zuerst ein Wert in einem Prädiktor-Schritt grob vorhergesagt wird und dieser dann in einem folgenden Korrektor-Schritt nachkorrigiert wird. Aufgabe 3 Man zeige, daß die Fehlerordnung des Verfahrens von Heun gleich 2 ist. Hinweis: Beweis ähnlich wie im Fall der verbesserten Polygonzugmethode. Algorithmisch schreiben wir das Verfahren von Heun k = f(t k,y k ) k 2 = f(t k +h,y k +hk ) y k+ = y k + 2 h(k +k 2 ) Bemerkung 8 Hängt f(t,y) nicht von y ab, so ist die Lösung des Anfangswertproblems y = f(t,y),y(t 0 ) = y 0 durch das Integral y(t) = y 0 + t t 0 f(τ)dτ gegeben. Das Verfahren von Heun entspricht dann der Approximation von y(t) mittels Trapezsummen, die verbesserte Polygonzugmethode der Mittelpunktsregel. Bemerkung 9 Sowohl die verbesserte Polygonzugmethode als auch die Methode von Heun sind Beispiele von expliziten zweistufigen Runge-Kutta-Verfahren mit der Fehlerordnung 2, welche wir in verallgemeinerter Form im nächsten Kapitel vorstellen werden..5 RUNGE-KUTTA-VERFAHREN Wir wollen nun die Herleitung von Einschrittverfahren höherer Ordnung beschreiben, welche keine Ableitungen von y benötigen (d.h. keine Methoden ähnlich zum expliziten Eulerverfahren höherer Ordnung oder zur Methode der Taylorreihe). (Da die Herleitung recht schnell kompliziert wird, beschränken wir uns hier zuerst auf dreistufige Runge-Kutta-Verfahren.) Das Prinzip der Runge-Kutta-Verfahren ist das folgende: Die zur Differentialgleichung äquivalente Integralgleichung lautet y(t k+ ) y(t k ) = tk+ t k f(t,y(t))dt. Analog zur Gauß-Quadratur approximieren wir das Integral durch eine allgemeine Quadraturformel n Q [t k,t k+ ] n (f) = w i f(ξ i ) mit Stützstellent k ξ... ξ n t k+ und Gewichtenw,...,w n so, daß wir eine möglichst hohe Konvergenzordnung erhalten. Für n = 3 gelangen wir zu dem allgemeinen Ansatz i= y k+ = y k +h{c f(ξ,y(ξ ))+c 2 f(ξ 2,y(ξ 2 ))+c 3 f(ξ 3,y(ξ 3 ))}. (.32) Desweiteren schränken wir die Wahl der Stützstellen bedingt durch die Zielsetzung eines einfachen und expliziten Verfahrens ein auf ξ = t k,ξ 2 = t k +a 2 h,ξ 3 = t k +a 3 h,(0 < a 2,a 3 ). (.33) Um nun ein explizites Verfahren herzuleiten, verwenden wir die Prädiktor-Methode und ersetzen y(ξ ),y(ξ 2 ),y(ξ 3 ) durch gute, explizit berechenbare Näherungen.
24 6 Kapitel : Gewöhnliche Differentialgleichungen Für die erste Stützstelle gilt y(ξ ) = y k (.34) und für die verbleibenden Stützstellen erhalten wir durch Einsetzen von Prädiktorwerten die allgemeinen Gleichungen y (p) (ξ 2 ) = y k +hb 2 f(t k,y k ), (.35) y (p) (ξ 3 ) = y k +hb 3 f(t k,y k )+hb 32 f(t k +a 2 h,y (p) (ξ 2 )). (.36) In algorithmischer Form schreibt sich das Verfahren (.32) - (.36) k = f(t k,y k ) k 2 = f(t k +a 2 h,y k +hb 2 k ) k 3 = f(t k +a 3 h,y k +h(b 3 k +b 32 k 2 )) y k+ = y k +h(c k +c 2 k 2 +c 3 k 3 ). (.37) Da die Funktion f pro Integrationsschritt hier dreimal ausgewertet werden muß, spricht man hier von einem dreistufigen Runge-Kutta-Verfahren. Bemerkung 20 Häufig findet man eine kürzere Schreibweise, bei der für mehrstufige Einschrittverfahren die Koeffizientena 2,a 3,b 2,b 3,b 32 undc,c 2,c 3 in Tabellenform festgehalten werden, d.h. z.b. für Verfahren (.37) 0 a 2 b 2 a 3 b 3 b 32 c c 2 c 3 Wir fordern von unserem gesuchten dreistufigen Runge-Kutta-Verfahren, daß es die spezielle Differentialgleichung y = exakt löst. Damit folgt für die Parameter a 2 = b 2 und a 3 = b 3 +b 32. Der lokale Diskretisierungsfehler des Verfahrens (.37) ist gegeben durch d k+ = y(t k+ ) y(t k ) h(c k +c 2 k 2 +c 3 k 3 ), (.38) wobei k i sich aus k i dadurch ergeben, daß y k durch y(t k ) ersetzt wird. Sukzessives Entwickeln der Termek,k 2,k 3 an der Stelle t k liefert k = f(t k,y(t k )) (.39) k 2 = f(t k +a 2 h,y(t k )+a 2 hf(t k,y(t k ))) (.40) = f +a 2 hf t +a 2 hff y + 2 a2 2 h2 f tt +a 2 2 h2 ff ty + 2 a2 2 h2 f 2 f yy +O(h 3 ) = f +a 2 hf + 2 a2 2h 2 G+O(h 3 ) k 3 = f(t k +a 3 h,y(t k )+h(b 3 k +b 32 k 2 )) (.4) = f +a 3 hf t +h(b 3 k +b 32 k 2 )f y + 2 a2 3h 2 f tt +a 3 (b 3 k +b 32 k 2 )h 2 f ty + 2 (b 3k +b 32 k 2 ) 2 h 2 f yy +O(h 3 ) = f +h{a 3 f t +(b 3 +b 32 )ff y } +h 2 {a 2 b 32 Ff y + 2 a2 3 f tt +a 3 (b 3 +b 32 )ff ty + 2 (b 3 +b 32 ) 2 f 2 f yy }+O(h 3 ) = f +a 3 hf +h 2 {a 2 b 32 Ff y + 2 a2 3G}+O(h 3 )
25 Abschnitt.5: Runge-Kutta-Verfahren 7 Einsetzen von (.39) - (.4) in (.38) liefert nun d k+ = hf( c c 2 c 3 )+h 2 F{ 2 a 2c 2 a 3 c 3 } +h 3 {Ff y [ 6 a 2c 3 b 32 ]+G[ 6 2 a2 2c 2 2 a2 3c 3 ]}+O(h 4 ) Damit das Verfahren mindestens die Konvergenzordnung 3 hat, müssen die Faktoren vorh,h 2,h 3 verschwinden. D.h. die sechs Parameter c,c 2,c 3,a 2,a 3 und b 32 müssen Lösung des folgenden nichtlinearen Gleichungssystem sein: c +c 2 +c 3 = a 2 c 2 +a 3 c 3 = 2 a 2 c 3 b 32 = 6 a 2 2c 2 +a 2 3c 3 = 3. Unter der Einschränkung a 2 a 3 und a ergibt sich die zweiparametrige Lösungsmenge c = 6 2a (a 2 +a 3 ) 6a 2 a 3 c 2 = 3a 3 2 6a 2 (a 3 a 2 ) c 3 = 2 3a 2 6a 3 (a 3 a 2 ) b 32 = a 3(a 3 a 2 ) a 2 (2 3a 2 ). Kriterien für die Festlegung der Parameter können sein: einfache bzw. einprägsame Zahlwerte, die bei Handrechnung auch bzgl. der Rundung günstig sind, für spezielle Klassen von Differentialgleichungen soll der Hauptteil von d k+ klein sein, simple Methoden der Schrittweitensteuerung sollen daraus herleitbar sein (siehe Kapitel.6) Ein erstes Runge-Kutta-Verfahren dritter Ordnung erhält man nun durch die Wahl a 2 = 3 und a 3 = 2 3. Das resultierende Verfahren von Heun dritter Ordnung in algorithmischer bzw. tabellarischer Form lautet: k = f(t k,y k ) k 2 = f(t k + 3 h,y k + 3 hk ) k 3 = f(t k h,y k hk 2) y k+ = y k + h 4 (k +3k 3 )
26 8 Kapitel : Gewöhnliche Differentialgleichungen Eine weitere Methode erhält man nun durch die ebenso ausgezeichnete Wahl der Konstanten zu a 2 = 2 und a 3 =. Dies liefert die Methode von Kutta dritter Ordnung k = f(t k,y k ) k 2 = f(t k + 2 h,y k + 2 hk ) k 3 = f(t k +h,y k hk +2hk 2 ) (.42) y k+ = y k + h 6 (k +4k 2 +k 3 ) Übungsaufgabe: In welchem Zusammenhang steht die Simpsonregel zur Methode (.42)? SCHRITTWEITENSTEUERUNG Da zur Zahldarstellung in einem Rechner nur endlich viele Ziffern verwendet werden können, ist es offensichtlich, daß h wegen der auftretenden Rundungsfehler nicht beliebig klein gemacht werden kann. Andererseits ist aber auch eine beliebige Erhöhung der Konvergenzordnung p, da dann der Rechenaufwand stark ansteigt. In vielen Fällen ist es aber auch gar nicht notwendig, für alle Schritte ein kleines h bzw. ein großes p zu verwenden, da die Lösung y(t) für verschiedene t unterschiedliches Verhalten zeigt. Das Ziel der adaptiven Schrittweitensteuerung ist es, die Schrittweite der Eigenschaft der Lösung anzupassen. Das Prinzip sieht dabei wie folgt aus. Es wird versucht, den lokalen Diskretisierungsfehler zu schätzen und dementsprechend die Schrittweite für den nächsten Schritt so zu wählen, daß er in einem kleinen Toleranzbereich bleibt. Somit ergibt sich bei geschätzten großen lokalen Diskretisierungsfehlern eine kleine Schrittweite und vice versa. Wie erhält man aber nun die wichtige Information über den lokalen Diskretisierungsfehler? Man verwendet dazu einfach zwei Verfahren unterschiedlicher Ordnung. Um den Mehraufwand zu minimieren, ist man daran interessiert, Paare von Einschrittverfahren zu finden, bei denen keine oder nur wenige zusätzliche Auswertungen der Funktion f notwendig sind, die grobe Information mit geringem Aufwand als Nebenprodukt des gewählten Verfahrens anfällt. Die verbesserte Polygonzugmethode und das Verfahren von Kutta erfüllen diese Forderung. Die Näherung des lokalen Diskretisierungsfehler ergibt sich mit d (K) k+ = y(t k+) y (K) k+ = O(h4 ) y(t k+ ) = y (K) k+ +O(h4 ) zu und somit (V P) d k+ = y(k) k+ y(vp) k+ +O(h4 ) d (VP) k+ h 6 (k +4k 2 +k 3 ) hk 2 = h 6 (k 2k 2 +k 3 ). Mit einer zusätzlichen Funktionsauswertung fürk 3 liefert der Term h 6 (k 2k 2 +k 3 ) eine Näherung an den lokalen Diskretisierungsfehler, welche um eine Ordnung größer ist als der lokale Diskretisierungsfehler selbst. Ein Algorithmus mit Schrittweitensteuerung basierend auf der Approximation des lokalen Diskretisierungsfehlers könnte wie folgt aussehen.
27 Abschnitt.6: Schrittweitensteuerung 9 function adaptiv_np(tn,t0,y0,h,tol) % % Adaptiv_VP(3.6,0,[.2;0;0; ],0.,0.002) % y(:,)=y0(:); t=t0; T=t; H=[]; while t<tn flag = ; while flag k = f(t,y(:,end)); k2 = f(t+h,y(:,end)+h*k); k3 = f(t+h/2,y(:,end)+h*(k+k2)/4); dk = norm(h*(k-2*k2+k3)/6); if dk >.2 * tol h = 0.9 * h; elseif dk < 0.8 *tol h =. * h; else flag = 0; end end y = [y,y(:,end)+h*k2]; t=t+h; T=[T,t]; H=[H,h]; subplot(,2,); plot(y(,:),y(3,:), r- ); title( Phasendiagramm ); subplot(,2,2); plot([t(:end-);t(2:end)],[h;h], g- ); title( Schrittweite ); drawnow end subplot(,2,) % plot(t,y, r- ); plot(y(,:),y(3,:), r- ); subplot(,2,2) plot([t(:end-);t(2:end)],[h;h], g- ); % problemabhaengige Funktion f function wert = f(t,y) mu = /82.45; z = ((y()+mu)ˆ2+y(3)ˆ2)ˆ(3/2); z2 = ((y()-+mu)ˆ2+y(3)ˆ2)ˆ(3/2); wert = [y(2); y()+2*y(4)-(-mu)*(y()+mu)/z-mu*(y()-+mu)/z2; y(4); y(3)-2*y(2)-(-mu)*y(3)/z-mu*y(3)/z2]; Beispiel 2 (R. D. Grigorieff) An einem Beispiel aus der Ingenieur-Wissenschaft wollen wir den obigen Algorithmus anwenden. Die folgende Differentialgleichung beschreibt eine periodische
28 20 Kapitel : Gewöhnliche Differentialgleichungen Satellitenbahn im Erde-Mond-System, wobei µ = (82.45) die relative Mondmasse ist: u+v ü = u+2 v ( µ) [(u+µ) 2 +v 2 ] 3 2 v v = v 2 u ( µ) [(u+µ) 2 +v 2 ] 3 2 u ( µ) µ [(u +µ) 2 +v 2 ] 3 2 v µ [(u +µ) 2 +v 2 ] 3 2 u(0) =.2 v(0) = 0 u (0) = 0 v (0) = Ersetzt man im Algorithmus den ersten plot -Befehl durch plot(y(,:),y(2,:),-); so erhält man für eine verwendete Toleranz tol = 0.0 (Anfangsschrittweite h = 0.) die folgende graphische Ausgabe: GRAPHIK Die historisch älteste, und deshalb oft als klassische Runge-Kutta-Methode vierter Ordnung bezeichnet, lautet Das Verfahren hat simple Parameterwerte und hat die Eigenschaft, daß für die sukzessive Bestimmung der Werte k i (i 2) nur die unmittelbar vorangehenden Werte k i benötigt werden, und der Algorithmus somit äußerst Speicherplatz sparend ist. Neben diesem Runge-Kutta- Verfahren vierter Ordnung existieren zahlreiche Varianten mit verschiedenen Zielsetzungen. Eine zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme keine Lösungen zulassen, so daß k,k 2 und k 3 in beiden Verfahren identisch sind. Die erreichbare Fehlerordnung p einer expliziten m-stufigen Runge-Kutta-Methode ist für p 9 gemäß der folgenden Tabelle gegeben. Tab..4: Maximale Fehlerordnung von expliziten Runge-Kutta-Verfahren m = p = Von Fehlberg stammt eine geschickte Kombination von Runge-Kutta-Verfahren 4. und 5. Ordnung, in welcher die Runge-Kutta-Methode 4. Ordnung fünf der ohnehin sechs der erforderlichen Auswertungen verwendet.
29 Abschnitt.6: Schrittweitensteuerung y k d k
30 22 Kapitel : Gewöhnliche Differentialgleichungen.7 IMPLIZITE RUNGE-KUTTA-VERFAHREN Zur numerischen Lösung von steifen Differentialgleichungen (siehe späteres Kapitel) sind spezielle Methoden erforderlich. Zu diesen gehören die impliziten Runge-Kutta-Verfahren, welche dadurch charakterisiert sind, daß die Steigungen k,k 2,... durch ein implizites Gleichungssystem definiert werden. Da die Herleitung von mehrstufigen impliziten Runge-Kutta-Methoden sehr aufwendig ist, wollen wir solche Verfahren hier definieren. Ein zweistufiges, implizites Runge-Kutta-Verfahren vierter Ordnung ist in algorithmischer Form k = f(t k k 2 = f(t k y k+ = y k + h 2 (k +k 2 ) h,y k + 4 hk hk 2 ) 2 h,y k + 3+s 3 hk hk 2) (.43) oder in tabellarischer Form s s Allgemein gilt, daß ein m-stufiges implizites Runge-Kutta-Verfahren durch geeignete Wahl der m(m + ) freien Parameter die maximal erreichbare Fehlerordnung 2m besitzt. Die Fixpunktiteration zum Lösen von (.43) ist konvergent für alle Schrittweiten h, die der Bedingung hbl < mit B := max i b ij genügen und L die Lipschitz-Konstante der Funktion f(x, y) darstellt. j Bemerkung 22 Die impliziten Runge-Kutta-Verfahren besitzen eine Stabilitätseigenschaft, die bei der Integration von steifen Differentialgleichungssystemen entscheidend ist. Für allgemeine Differentialgleichungssysteme sind die impliziten Runge-Kutta-Methoden trotz ihrer hohen Fehlerordnung wenig attraktiv, weil in jedem Integrationsschritt ein im allgemeinen nichtlineares Gleichungssystem für die m Unbekannten k i ( i m) zu lösen ist..8 MEHRSCHRITTVERFAHREN Ein Nachteil der Einschrittverfahren ist die hohe Anzahl der Funktionsauswertungen, die für eine hohe Konsistenzordnung und somit für eine hohe Konvergenzordnung nötig sind. Dieser Nachteil tritt bei den folgenden Mehrschrittverfahren nicht auf. Es bleibt im allgemeinen jedoch nur ein deutlicher Vorteil, solange die Schrittweite fest gewählt wird. Für Einschrittverfahren haben wir schon in Kapitel.6 gesehen, daß adaptive Schrittweitensteuerung dort recht einfach durchzuführen ist. Dies läßt sich für Mehrschrittverfahren nicht so einfach realisieren. Es sei t j = t 0 +jh (j = 0,,2,...).
31 Abschnitt.8: Mehrschrittverfahren 23 Ein k-schrittverfahren zur Lösung des AWP y (t) = f(t,y(t)), y(t 0 ) = y 0 ist ein Verfahren zur Berechnung von Näherungswerteny j+k zuy(t j+k ) ausy j,...,y j+k durch Lösen der Gleichung α l y j+l = hφ(t j,y j,...,y j+k,h,f) (.44) l=0 für j = 0,,2,... mit geeigneten Startwerten y 0,...,y k. Dabei ist h k l=0 α ly j+l als eine Näherung an die Ableitungy (bisher h (y j+ y j )) undφ(t j,y j,...,y j+k,h,f) als Näherung an f(t, y(t)) aufzufassen. Ein lineares k-schrittverfahren ist von der Form α l y j+l = h l=0 β l f(t j+l,y j+l ) (j = 0,,2,...) (.45) l=0 mit geeigneten Startwerteny 0,...,y k. Giltβ k = 0 so spricht man von einem expliziten Verfahren, ansonsten von einem impliziten. Die im allgemeinen nichtlineare Gleichung iny j+k im impliziten linearenk-schrittverfahren kann aus (.45) iterativ berechnet werden. Es sei f Lipschitz-stetig iny mit einer Lipschitz-Konstanten L. Dann gilt für die Iteration nach dem Banachschen Fixpunktsatz y (r+) j+k = h β k f(t j+k,y (r) α j+k ) k (h β l f(t j+l,y j+l ) k α k =: ψ(y (r) j+k ), l=0 k α l y j+l ) daß diese konvergent ist, falls β k α k hl < gilt. Untersuchen wir nun zuerst, ob die Diskretisierung der Differentialgleichung lokal vernünftig ist. Definition 23 Der lokale Diskretisierungsfehler des Mehrschrittverfahrens (.44) ist d j+k (t j,h,f) = l=0 α l y(t j+l ) hφ(t j,y(t j ),...,y(t j+k ),y j+k,h,f). l=0 Das Mehrschrittverfahren heißt mit einer Differentialgleichung y = f(t,y) konsistent, falls gilt. Es heißt konsistent von der Ordnung p, falls gilt. d j+k (t j,h,f) lim = 0 h 0 h d j+k (t j,h,f) = O(h p+ ) Beispiel 24 (eines Mehrschrittverfahrens) Man betrachte die Taylor-Entwicklungen Subtraktion beider Gleichungen liefert y(t+h) = y(t)+hy (t)+ h2 2 y (t)+o(h 3 ) y(t h) = y(t) hy (t)+ h2 2 y (t)+o(h 3 ) y(t+h) y(t h) = 2hy (t)+o(h 3 ) = 2hf(t,y(t))+O(h 3 ).
32 24 Kapitel : Gewöhnliche Differentialgleichungen Dies motiviert das lineare 2-Schrittverfahren y k+ = 2hf(t k,y k )+y k, k =,2,3,..., welches als Quadratur der Mittelpunktsregel entspricht. Die Konsistenzordnung ist 2, was sich aus der Herleitung sofort ergibt. Im Gegensatz zu Einschrittverfahren impliziert Konsistenz nicht immer Konvergenz, welches wir später untersuchen werden. Betrachten wir nun zuerst die Entwicklung der wichtigsten Mehrschrittverfahren, die man über numerische Integration herleiten kann, ähnlich wie Runge-Kutta-Verfahren. Es gilt y(t j+k ) y(t j+r l ) = tj+k t j+r l f(t,y(t))dt. (.46) Dabei sei y(t j+k ) der Wert, welcher approximiert werden soll. Es ist nun eine naheliegende Idee, den Integranden f durch ein Interpolationspolynom P r,j (s) = P f (s t j,...,t j+r ) vom Graderzu ersetzen, welches an den Stellen t j,...,t j+r interpoliert. Dabei betrachtet man das Integral über(t j+r l,t j+k ), während nur auf[t j,t j+r ] interpoliert wird. Dieses Vorgehen ist graphisch in Abbildung. dargestellt. P r f Interpolationsintervall Integrationsintervall t j t j+r l t j+r t j+k Abb..: Exemplarische Darstellung von Interpolations- und Integrationsintervall Die Lagrangesche Darstellungsform für das Interpolationspolynom P r,j (s) sieht folgendermaßen aus: P r,j (s) = = r f(t j+i,y j+i ) r f(t j+i,y j+i ) r p=0 p i r p=0 p i s t j+p t j+i t j+p s t j+p (i p)h Also erhalten wir, falls P r,j (s) in (.46) für f eingesetzt wird: y j+k y j+r l h r f(t j+i,y j+i )β (r,l) i, (.47)
33 Abschnitt.8: Mehrschrittverfahren 25 wobei tj+k hβ (r,l) i = t j+r l k r = h l r p=0 p i r p=0 p i s t j+p (i p) ds r p+ s i p ist. Dabei erhält man den letzten Schritt durch Substitution s = t j +(r + s)h. Die Rechenvorschrift lautet somit Übliche Wahlen für r und l: u j+k = u j+r l +h r d s β (r,l) i f(t j+i,y j+i ). r l Name Art k 0 Adams-Bashforth Extrapolation, explizites Verfahren k Nyström Extrapolation, explizites Verfahren k Adams-Moulton Interpolation, implizites Verfahren k 2 Milne-Simpson Interpolation, implizites Verfahren
34 26 Kapitel : Gewöhnliche Differentialgleichungen Interpolation Integration t j t j+k t j+k Abb..2: Allgemeine Darstellung des Adams-Bashforth Interpolation Integration t j t j+k 2 t j+k t j+k Abb..3: Allgemeine Darstellung des Nyström Interpolation Integration t j t j+k t j+k Abb..4: Allgemeine Darstellung des Adams-Moulton Interpolation Integration t j t j+k 2 t j+k t j+k Abb..5: Allgemeine Darstellung des Milne-Simpson
35 Abschnitt.8: Mehrschrittverfahren 27 Beispiel 25 Adams-Bashforth: Nyström: k y j+k = y j+k +h β (k,0) i f j+i r = k = 0: Hiermit ergibt sich: y j+ = y j +hf j (explizites Euler-Verfahren) r = k = : Hiermit ergibt sich: y j+2 = y j+ +h( 3 2 f j+ 2 f j) Adams-Moulton: Milne-Simpson: k y j+k = y j+k 2 +h β (k,) i f j+i r = k = 0: Hiermit ergibt sich: y j+ = y j +2hf j (Mittelpunktsregel) y j+k = y j+k +h β (k,) i f j+i r = k = 0: Hiermit ergibt sich: y j = y j +hf j (implizites Euler-Verfahren) r = k = : Hiermit ergibt sich: y j+ = y j + h 2 (f j+ f j ) r = k = 2: Hiermit ergibt sich: y j+2 = y j+ + h 2 (5f j+2 +8f j+ f j ) y j+k = y j+k 2 +h β (k,2) i f j+i Zusätzlich zu der Langrangschen Darstellungsformel für das Interpolationspolynom P r,j (s) gibt es die Newtonsche Interpolationsformel, welche für die paarweise verschiedenen (r + ) Stützstellen t j,t j+,...,t j+r lautet P r,j (s) = c 0 +c (s t j )+c 2 (s t j )(s t j+ )+...+c n (s t j )...(s t j+r ). (.48) Die unbekannten Koeffizienten c 0,...,c n lassen sich zu den (r + ) Stützpunkten (t j+l,f j+l ), (l = 0,..., r) prinzipiell aus den Interpolationsbedingungen P r,j (t j ) = c 0 = f j P r,j (t j+ ) = c 0 +c (t j+ t j ) = f j+ P r,j (t j+2 ) = c 0 +c (t j+2 t j )+c 2 (t j+2 t j )(t j+2 t j+ ) = f j+2 etc. (.49) sukzessive berechnen, da das lineare Gleichungssystem (.49) Linksdreiecksgestalt besitzt. Definition 26 Die eindeutig durch (r + ) Stützpunkte (t j+l,f j+l ) (l = 0,...,r) festgelegten Werte c l in (.48) bezeichnen wir durch c l := f[t j,t j+,...,t j+l ], (l = 0,,...,r). Unter Verwendung der Startwerte f k = f[t k ] (k = j,j +,...,j +r) lautet das Bildungsgesetz für die Koeffizienten c l im Prinzip f[t i0,t i,...,t ik ] = f[t i,...,t ik ] f[t i0,t i,...,t ik ] t ik t i0. (.50)
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Stefan A. Funken Angewandte Numerik II
 Stefan A. Funken Angewandte Numerik II ẏ(t) = t 2 +y(t) 2.5.5 y y.5.5.5.5 t.5.5 t SKRIPT, UNIVERSITÄT ULM, WINTERSEMESTER 23/4 i Vorbemerkung. Copyright. Alle Rechte, insbesondere das Recht auf Vervielfältigung
Stefan A. Funken Angewandte Numerik II ẏ(t) = t 2 +y(t) 2.5.5 y y.5.5.5.5 t.5.5 t SKRIPT, UNIVERSITÄT ULM, WINTERSEMESTER 23/4 i Vorbemerkung. Copyright. Alle Rechte, insbesondere das Recht auf Vervielfältigung
Stefan A. Funken Angewandte Numerik II
 Stefan A. Funken Angewandte Numerik II ẏ(t) = t +y(t).5.5 y y.5.5.5.5 t.5.5 t SKRIPT, UNIVERSITÄT ULM, WINTERSEMESTER 3/4 i Vorbemerkung. Copyright. Alle Rechte, insbesondere das Recht auf Vervielfältigung
Stefan A. Funken Angewandte Numerik II ẏ(t) = t +y(t).5.5 y y.5.5.5.5 t.5.5 t SKRIPT, UNIVERSITÄT ULM, WINTERSEMESTER 3/4 i Vorbemerkung. Copyright. Alle Rechte, insbesondere das Recht auf Vervielfältigung
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
3. Lineare Mehrschrittverfahren 3.1 Begriffe
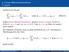 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren
 Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
KAPITEL 10. Numerische Integration
 KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
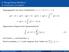 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
Diplom VP Numerik 28. August 2006
 Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
Gewöhnliche Differentialgleichungen Woche 6. Existenz nach Picard-Lindelöf
 d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler. (a) Bestimmen Sie die kartesische Form von Wintersemester 7/8 (..8) z = ( + i)( i) + ( + i). (b) Bestimmen Sie sämtliche komplexen Lösungen
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler. (a) Bestimmen Sie die kartesische Form von Wintersemester 7/8 (..8) z = ( + i)( i) + ( + i). (b) Bestimmen Sie sämtliche komplexen Lösungen
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Lösung Semesterendprüfung
 MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 23
 Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel;
 Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Numerik gewöhnlicher Differentialgleichungen. Übung 8 - Lösungsvorschlag
 Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Satz von Peano. Sei f stetig und beschränkt auf
 Satz von Peano Sei f stetig und beschränkt auf { } Q ab := (t,y) R n+1 : t t 0 a; y y 0 b mit f(t,y) M und α := min(a, b M ). Dann besitzt das Anfangswertproblem y = f(t,y), y(t 0 ) = y 0 Giuseppe Peano
Satz von Peano Sei f stetig und beschränkt auf { } Q ab := (t,y) R n+1 : t t 0 a; y y 0 b mit f(t,y) M und α := min(a, b M ). Dann besitzt das Anfangswertproblem y = f(t,y), y(t 0 ) = y 0 Giuseppe Peano
Übungsblatt 1 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
Kapitel 6. Nichtlineare Gleichungen. 6.1 Einführung. Problem: Idee: Beispiel:
 Kapitel 6 Nichtlineare Gleichungen 6. Einführung Problem: Gesucht sind Lösungen nichtlinearer Gleichungen bzw. Systeme, das heißt es geht beispielsweise um die Bestimmung der Nullstellen eines Polynoms
Kapitel 6 Nichtlineare Gleichungen 6. Einführung Problem: Gesucht sind Lösungen nichtlinearer Gleichungen bzw. Systeme, das heißt es geht beispielsweise um die Bestimmung der Nullstellen eines Polynoms
Musterlösung Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung (
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung (
8.1 Begriffsbestimmung
 8 Gewöhnliche Differentialgleichungen 8 Gewöhnliche Differentialgleichungen 8.1 Begriffsbestimmung Wir betrachten nur Differentialgleichungen für Funktionen einer (reellen) Variablen. Definition: Für eine
8 Gewöhnliche Differentialgleichungen 8 Gewöhnliche Differentialgleichungen 8.1 Begriffsbestimmung Wir betrachten nur Differentialgleichungen für Funktionen einer (reellen) Variablen. Definition: Für eine
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge
 Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Mathematische Grundlagen für die Vorlesung. Differentialgeometrie
 Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung (
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung (
Mathematische Grundlagen
 G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
Serie 13: Online Test
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
eps für alle x D. 4. Die Zahl 256 ist in M(2, 4, 6, 6) exakt darstellbar.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Nichtlineare Gleichungssysteme
 Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
Begleitmaterial zur Vorlesung Numerik II
 Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Rheinisch-Westfälische Technische Hochschule. Gegeben seien eine gewöhnliche Dierentialgleichung (DGL) und ein Anfangswert. γ l K l.
 Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Klassische Polynom Interpolation.
 Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
11. Einschrittverfahren
 H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
1 Einführung, Terminologie und Einteilung
 Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Klausurenkurs zum Staatsexamen (SS 2015): Differential und Integralrechnung 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2015): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung ( y
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2015): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung ( y
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Übungsblatt 4 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Übungsblatt 4 Musterlösung Aufgabe 7 (Nullstellen als Eigenwerte) Die Polynome {S n } n=0,,2,, S n P n, mit führem Koeffizienten eins, heißen Orthogonalpolynome
Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Übungsblatt 4 Musterlösung Aufgabe 7 (Nullstellen als Eigenwerte) Die Polynome {S n } n=0,,2,, S n P n, mit führem Koeffizienten eins, heißen Orthogonalpolynome
Nichtlineare Gleichungssysteme
 Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
ZWEITE KLAUSUR zur Numerik I mit Lösungen. Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
 MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Zweite Prüfung zur Vorlesung
 Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
Übungen zu Differentialgleichungen (WiSe 12/13)
 Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
ANALYSIS 2 VERSION 26. Juni 2018
 ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
5 Numerische Iterationsverfahren
 In diesem Kapitel besprechen wir numerische Iterationsverfahren (insbesondere Fixpunktverfahren) als eine weitere Lösungsmethode zur Lösung von linearen Gleichungssystemen (Kapitel 4) sowie zur Lösung
In diesem Kapitel besprechen wir numerische Iterationsverfahren (insbesondere Fixpunktverfahren) als eine weitere Lösungsmethode zur Lösung von linearen Gleichungssystemen (Kapitel 4) sowie zur Lösung
Newton-Verfahren für ein Skalarfunktion
 Newton-Verfahren für ein Skalarfunktion Für eine Näherungsberechnung von Nullstellen einer reellen Funktion f(x) : R R benutzt man das Newton-Verfahren: x (n+1) = x (n) f(x (n) )/f (x (n) ). Das Newton-Verfahren
Newton-Verfahren für ein Skalarfunktion Für eine Näherungsberechnung von Nullstellen einer reellen Funktion f(x) : R R benutzt man das Newton-Verfahren: x (n+1) = x (n) f(x (n) )/f (x (n) ). Das Newton-Verfahren
Adaptive Mehrschrittverfahren
 Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Parareal. Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen. Johannes Reinhardt. Parareal 1 Johannes Reinhardt
 Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
Gewöhnliche Differentialgleichungen Woche 7. Nicht-lineare und linearisierte Systeme
 Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
1 Die direkte Methode der Variationsrechnung
 Die direkte Methode der Variationsrechnung Betrachte inf I(u) = f(x, u(x), u(x)) dx : u u + W,p () wobei R n, u W,p mit I(u ) < und f : R R n R. (P) Um die Existenz eines Minimierers direkt zu zeigen,
Die direkte Methode der Variationsrechnung Betrachte inf I(u) = f(x, u(x), u(x)) dx : u u + W,p () wobei R n, u W,p mit I(u ) < und f : R R n R. (P) Um die Existenz eines Minimierers direkt zu zeigen,
Dr. R. Käppeli D-ITET, D-MATL Sommer Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Wie in der reellen Analysis üblich notiert man Folgen f in der Form
 2.1.3 Folgen und Konvergenz Viele aus der Analysisvorlesung bekannte Begriffe lassen sich in den Bereich der metrischen Räume verallgemeinern. Diese Verallgemeinerung hat sich als sehr nützliches mathematisches
2.1.3 Folgen und Konvergenz Viele aus der Analysisvorlesung bekannte Begriffe lassen sich in den Bereich der metrischen Räume verallgemeinern. Diese Verallgemeinerung hat sich als sehr nützliches mathematisches
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan :00-14:00 (120 min)
 Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Lösungsmenge L I = {x R 3x + 5 = 9} = L II = {x R 3x = 4} = L III = { }
 Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler Wintersemester 26/7 (2.3.27). (a) Bestimmen Sie die kartesische Form von z = 5i 2i und z 2 = ( ) 9 3 2 2 i. (b) Bestimmen Sie sämtliche
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler Wintersemester 26/7 (2.3.27). (a) Bestimmen Sie die kartesische Form von z = 5i 2i und z 2 = ( ) 9 3 2 2 i. (b) Bestimmen Sie sämtliche
Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8 8.1 (Herbst 2002, Thema 1, Aufgabe 6) y = 3y +2x x 8.2 (Frühjahr 2005, Thema 1, Aufgabe 6) (x > 0) y(1)
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8 8.1 (Herbst 2002, Thema 1, Aufgabe 6) y = 3y +2x x 8.2 (Frühjahr 2005, Thema 1, Aufgabe 6) (x > 0) y(1)
18.4 Das Newton-Verfahren
 18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
10 Der Satz über implizite Funktionen und Umkehrfunktionen
 Vorlesung SS 9 Analsis Prof. Dr. Siegfried Echterhoff SATZ ÜBER IMPLIZITE FKT UND UMKEHRFKT Der Satz über implizite Funktionen und Umkehrfunktionen Motivation: Sei F : U R R eine differenzierbare Funktion
Vorlesung SS 9 Analsis Prof. Dr. Siegfried Echterhoff SATZ ÜBER IMPLIZITE FKT UND UMKEHRFKT Der Satz über implizite Funktionen und Umkehrfunktionen Motivation: Sei F : U R R eine differenzierbare Funktion
6 Gewöhnliche Differentialgleichungen
 6 Gewöhnliche Differentialgleichungen Differentialgleichungen sind Gleichungen in denen nicht nur eine Funktion selbst sondern auch ihre Ableitungen vorkommen. Im einfachsten Fall gibt es eine unabhängige
6 Gewöhnliche Differentialgleichungen Differentialgleichungen sind Gleichungen in denen nicht nur eine Funktion selbst sondern auch ihre Ableitungen vorkommen. Im einfachsten Fall gibt es eine unabhängige
Numerische Mathematik
 ».- Numerische Mathematik Von Dr. sc. math. Hans Rudolf Schwarz o. Professor an der Universität Zürich Mit einem Beitrag von Dr. sc. math. Jörg Waldvogel Titularprofessor an der Eidg. Technischen Hochschule
».- Numerische Mathematik Von Dr. sc. math. Hans Rudolf Schwarz o. Professor an der Universität Zürich Mit einem Beitrag von Dr. sc. math. Jörg Waldvogel Titularprofessor an der Eidg. Technischen Hochschule
