Kryptographische Algorithmen
|
|
|
- Greta Solberg
- vor 6 Jahren
- Abrufe
Transkript
1 Kryptographische Algorithmen Lerneinheit 4: Advanced Encryption Standard (AES) Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2017/
2 Einleitung Bei der Standardisierung von DES wurde vorgeschrieben, daß DES alle 5 Jahre bezüglich seiner Sicherheit evaluiert wird. Ende der 1990er Jahre ergab die Überprüfung, daß DES nicht mehr als sicher einzustufen ist. Um einen neuen Standard für symmetrische Verschlüsselung zu schaffen, schrieb das NIST im Jahre 1997 einen Wettbewerb zur Bestimmung des Advanced Encryption Standard (AES) aus. Anforderungen an den Kryptoalgorithmus waren: Erfüllung aller heutigen Sicherheitsanforderungen Öffentlich zugängliche Dokumentation der Spezifikation und Designkriterien Weltweite kostenlose Nutzung Prof. Dr. C. Karg: Kryptographische Algorithmen 2/40
3 Die 15 AES Kandidaten Name Entwickler Typ CAST-256 Entrust (CA) Industrie Crypton Future Systems (KR) Industrie DEAL Outbridge, Knudsen (USA/DK) Forschung DFC ENS-CNRS (FR) Forschung E2 NTT (JP) Industrie Frog TecApro (CR) Industrie HPC Schroeppel (USA) Forschung LOKI97 Brown et al. (AU) Forschung Magenta Deutsche Telekom (DE) Industrie Mars IBM (USA) Industrie RC6 RSA (USA) Industrie Rijndael Daemen and Rijmen (BE) Forschung SAFER++ Cyling (USA) Industrie Serpent Anderson, Bihan, Knudson (UK/IL/DK) Forschung Twofish Counterpane (USA) Industrie Prof. Dr. C. Karg: Kryptographische Algorithmen 3/40
4 Auswahlkriterien Bei der Auswahl des Standards wurden folgende Kriterien angewandt: Sicherheit: Dies ist das wichtigste aber auch das am schwierigsten zu bewertende Kriterium. Kosten: Man unterscheidet zwei Arten von Kosten: Geistiges Eigentum: Freie Verfügbarkeit des Algorithmus, aber auch Verzicht auf Patentansprüche auf Ideen in Vorschlägen der Konkurrenten Resourcenverbrauch: Rechenzeit, Speicherplatzbedarf, Größe des Programms, etc. Prof. Dr. C. Karg: Kryptographische Algorithmen 4/40
5 Auswahlkriterien (Forts.) Implementierungsaspekte: Folgende Punkte wurden beurteilt: Flexibilität: Ist der Algorithmus vielseitig einsetzbar? Schlüsselagilität: Wie effizient ist die Schlüsselkonfiguration? Einfachheit: Wie hoch ist der Aufwand zur Implementierung des Algorithmus? Man beachte, daß diese Punkte schwer quantifizierbar sind. In einem ersten Auswahlverfahren wurden aus den Kandidanten folgende fünf Finalisten ausgewählt: RC6, Rijndael, Twofish, MARS und Crypton. Prof. Dr. C. Karg: Kryptographische Algorithmen 5/40
6 Und der Sieger ist Rijndael Die fünf Finalisten wurden nochmals genau untersucht. Am 2. Oktober 2000 gab die NIST bekannt, daß Rijndael der Gewinner des Wettbewerbs und somit der zukünftige AES ist. Die Gründe für diese Entscheidung sind: Sicherheit: Rijndael erfüllt alle Sicherheitsanforderungen. Geschwindigkeit: Die Implementierung von Rijndael war die schnellste aller Kandidaten mit gleichmässig guten Performanz auf allen betrachteten Plattformen. Speicherbedarf: Rijndael benötigt wenig RAM- und ROM-Speicher. Implementierung in Hardware: Rijndael liefert die beste Performanz in Hardware-Implementierung. Prof. Dr. C. Karg: Kryptographische Algorithmen 6/40
7 Wiederholung: Endliche Körper Ein Körper ist eine algebraische Struktur (A,, ) mit folgenden Eigenschaften: (A, ) und (A \ {0}, ) sind kommutative Gruppen. Es gilt das Distributivgesetz, d.h., für alle a, b, c gilt: (a b) c = a c b c c (a b) = c a c b Falls A <, dann nennt man (A,, ) einen endlichen Körper oder auch Galois-Feld. Fakt: Es gibt einen endlichen Körper mit A = n genau dann, wenn n eine Primzahlpotenz ist, d.h., n = p k für eine Primzahl p. Prof. Dr. C. Karg: Kryptographische Algorithmen 7/40
8 Rechnen mit endlichen Körpern Um über einem endlichen Körper GF(p k ) rechnen zu können, muß zunächst die Addition und Multiplikation definiert werden. Idee: Man stellt die Elemente als k-tupel über Z p dar und interpretiert diese als Polynome mit Grad k 1 mit Koeffizienten in Z p. Das Element (a k 1,..., a 1,, a 0 ) (Z p ) k steht für das Polynom a k 1 x k 1 + a k 2 x k a 1 x + a 0 Beispiel: Das Element (4, 0, 3, 2) aus GF(5 4 ) steht für das Polynom 4x 3 + 3x + 2. Prof. Dr. C. Karg: Kryptographische Algorithmen 8/40
9 Die Addition über GF(p k ) Die Addition über GF(p k ) ist die Polynomaddition. Für a(x) = a k 1 x k 1 + a k 2 x k a 1 x + a 0 und b(x) = b k 1 x k 1 + b k 2 x k b 1 x + b 0 ist a(x) b(x) = c(x) wobei c(x) = c k 1 x k 1 + c k 2 x k c 1 x + c 0 und c i = (a i + b i ) mod p. Prof. Dr. C. Karg: Kryptographische Algorithmen 9/40
10 Die Multiplikation über GF(p k ) Will man die Multiplikation über GF(p k ) auf analoge Weise, sprich als Polynommultiplikation, realisieren, dann trifft man auf das folgende Problem: Das Produkt zweier Polynome mit Grad k 1 ist ein Polynom vom Grad 2(k 1) und somit kein Element von GF(p k ). Lösung: Man reduziert das Ergebnis der Multiplikation indem man modulo einem irreduziblem Polynom mit Grad k rechnet. Man setzt hierzu die Polynomdivision mit Rest ein. Ein Polynom ist irreduzibel, falls es nur durch 1 und sich selbst ohne Rest teilbar ist. Prof. Dr. C. Karg: Kryptographische Algorithmen 10/40
11 Beispiel GF(2 3 ) (Teil 1) Die Elemente in GF(2 3 ) sind: Tupel Polynom Zahl (0, 0, 0) 0 0 (0, 0, 1) 1 1 (0, 1, 0) x 2 (0, 1, 1) x (1, 0, 0) x 2 4 (1, 0, 1) x (1, 1, 0) x 2 + x 6 (1, 1, 1) x 2 + x Prof. Dr. C. Karg: Kryptographische Algorithmen 11/40
12 Beispiel GF(2 3 ) (Teil 2) Die Addition von x 2 + x + 1 und x liefert das Ergebnis 2x 2 + x + 2 = x. Um obige Werte zu multiplizieren, berechnet man zunächst (x 2 + x + 1)(x 2 + 1) = x 4 + x 3 + 2x 2 + x + 1 = x 4 + x 3 + x + 1 Anschließend dividiert man das Ergebnis mit dem irreduziblen Polynom m(x) = x 3 + x + 1. Prof. Dr. C. Karg: Kryptographische Algorithmen 12/40
13 Beispiel GF(2 3 ) (Teil 3) Polynomdivision: (x 4 + x 3 + x + 1) : (x 3 + x + 1) = x + 1 x 4 + x 2 + x x 3 + x x 3 + x + 1 x 2 + x Rest Das Ergebnis des Produkts (x 2 + x + 1) (x 2 + 1) ist also x 2 + x. Somit ist (1, 1, 1) (1, 0, 1) = (1, 1, 0). Prof. Dr. C. Karg: Kryptographische Algorithmen 13/40
14 Algorithmen für Polynomarithmetik Um endliche Körper in der Praxis einsetzen zu können, benötigt man effiziente Algorithmen zur Berechnung der Polynomarithmetik. Die Addition ist einfach zu implementieren. Sie ist die komponentenweise Addition modulo der Primzahlbasis p. Die Multiplikation ist mittels Polynommultiplikation und Polynomdivision berechenbar. Der Aufwand ist quadratisch im Grad der Polynome. Eine weitere wichtige Operation ist die Bestimmung von multiplikativen Inversen. Sie kann mittels des Extended Euklid Algorithmus berechnet werden. Prof. Dr. C. Karg: Kryptographische Algorithmen 14/40
15 Verbesserung der Effizienz Ist bei einer Anwendung der endliche Körper GF(m) fest gewählt, dann läßt sich die Multiplikation und Inversenberechnung deutlich effizienter gestalten. Bekanntlich ist (GF(m) \ {0}, ) eine Gruppe und besitzt somit ein erzeugendes Element g. D.h., für jedes a GF(p n ) \ {0} existiert eine Zahl i so daß g i = a. Um das Produkt a b berechnen, verwendet man den Generator g. Falls a = g i und b = g j, dann ist a b = g i g j i+j mod (m 1) = g Das Inverse von a = g i ist a 1 = g m 1 i. Prof. Dr. C. Karg: Kryptographische Algorithmen 15/40
16 Verbesserung der Effizienz (Forts.) Die Berechnung der Multiplikation wurde also reduziert auf die Kombination der Funktion exp(i) = g i und deren inversen Funktion log g (x). Liegen diese Funktionen in tabellarischer Form vor, dann beschränkt sich die Berechnung auf ganzzahlige Arithmetik und Suche von Tabelleneinträgen. Berechnung der Multiplikation a b: 1. Finde in der log g -Tabelle die Indizes i und j so daß g i = a und g j = b 2. Berechne l = i + j mod (m 1) 3. a b ist der l-te Eintrag in der exp g -Tabelle. Analog: Berechnung von multiplikativen Inversen. Prof. Dr. C. Karg: Kryptographische Algorithmen 16/40
17 Beispiel GF(2 3 ) Das Element (0, 1, 0) = x ist ein erzeugendes Element der Gruppe GF(2 3 ) \ {0}. exp g -Tabelle i x i a 0 1 (0, 0, 1) 1 x (0, 1, 0) 2 x 2 (1, 0, 0) 3 x + 1 (0, 1, 1) 4 x 2 + x (1, 1, 0) 5 x 2 + x + 1 (1, 1, 1) 6 x (1, 0, 1) log g -Tabelle a Polynom i (0, 0, 1) 1 0 (0, 1, 1) x (0, 1, 0) x 1 (1, 0, 0) x 2 2 (1, 1, 0) x 2 + x 4 (1, 0, 1) x (1, 1, 1) x 2 + x Prof. Dr. C. Karg: Kryptographische Algorithmen 17/40
18 Beispiel GF(2 3 ) (Forts.) Zur Berechnung von (1, 1, 1) (1, 0, 1) = (x 2 + x + 1)(x 2 + 1) bestimmt man i = log x [(1, 1, 1)] = 5 und j = log x [(1, 0, 1)] = 6. Somit ist l = (5 + 6) mod 7 = 4 und obiges Produkt gleich exp x [4] = (1, 1, 0) = x 2 + x. Um (0, 1, 1) 1 bestimmen, setze i = log x [(0, 1, 1)] = 3 und berechne l = 7 3 = 4. (0, 1, 1) 1 ist gleich exp x [4] = (1, 1, 0). Prof. Dr. C. Karg: Kryptographische Algorithmen 18/40
19 Einsatz von endlichen Körpern in Rijndael Viele der in Rijndael eingesetzten Transformationen basieren auf arithmetischen Operationen über GF(2 8 ). Der Grund für die Wahl von GF(2 8 ) ist, daß man damit Operationen auf Byte-Ebene definieren kann. Das irreduzible Polynom ist m(x) = x 8 + x 4 + x 3 + x + 1. Multiplikation und Berechnung der multiplikativen Inversen werden mittels Exp- und Log-Tabellen implementiert. Jede dieser Tabellen hat eine Größe von 256 Byte. Prof. Dr. C. Karg: Kryptographische Algorithmen 19/40
20 Das Rijndael Kryptosystem Rijndael ist ein symmetrisches Kryptosystem mit folgenden Parametern: P = C = {0, 1} 32 n B, wobei nb = {4, 6, 8} K = {0, 1} 32 n K, wobei nk {4, 6, 8} Sowohl die Block- als auch die Schlüssellänge ist demnach variabel mit einer Länge von 128, 192 oder 256 Bit. Im AES Standard wurde die Blocklänge auf 128 Bit, d.h. n B = 4 festgelegt. Die Bezeichnung Rijndael wurde von den Namen seiner Erfinder Vincent Rijmen und Joan Daemen abgeleitet. Prof. Dr. C. Karg: Kryptographische Algorithmen 20/40
21 Der interne Zustand von Rijndael Der interne Zustand von Rijndael ist ein Bytefeld, dessen Länge mit der Blocklänge übereinstimmt. Das Feld wird entweder als Array der Länge 4n B oder als Matrix der Dimension 4 n B angesprochen. Die Konvertierung zwischen Arrayposition n und Matrixindex (i, j) erfolgt gemäß den folgenden Formeln: n i = n mod 4, j =, bzw. n = i + 4 j. 4 Der Schlüsselblock wird auf analoge Weise interpretiert. Prof. Dr. C. Karg: Kryptographische Algorithmen 21/40
22 Der Verschlüsselungsalgorithmus Rijndael(x, k) Input: Klartext x (4 n B Byte), Schlüssel k (4 n K Byte) Output: Geheimtext y (4 n B Byte) 1 s := x; 2 KeyExpansion(k, k R [0, n R ]); 3 AddRoundKey(s, k R [0]); 4 for i := 1 to n R 1 do Round(i, s, k R [i]); 5 FinalRound(n R, s, k R [n R ]); 6 return s; Prof. Dr. C. Karg: Kryptographische Algorithmen 22/40
23 Anzahl der Runden Die Anzahl der Runden n R ist abhängig von der Blocklänge n B und Schlüssellänge n K. n R n B = 4 n B = 6 n B = 8 n K = n K = n K = Für n B = 4 und n K = 6 ist beispielsweise n R = 12. Prof. Dr. C. Karg: Kryptographische Algorithmen 23/40
24 Aufbau einer Rundentransformation Bei einer Verschlüsselsrunde von Rijndael kommen die folgenden Funktionen zum Einsatz: ByteSub(s): Diese Operation ist eine nicht-lineare Substitution, die jedes Byte des Zustands unabhängig von den anderen verändert. ShiftRow(s): Bei dieser Operation wird zeilenweise eine Linksverschiebung durchgeführt. MixColumns(s): Diese Operation bearbeitet den Zustand spaltenweise. AddRoundKey(s, k R ): Hier wird der Rundenschlüssel auf den Zustand bitweise addiert. Jede dieser Funktionen ist für sich invertierbar. Prof. Dr. C. Karg: Kryptographische Algorithmen 24/40
25 Round() und FinalRound() Round(s, k R ) Input: Zustand s, Rundenschlüssel k R (jeweils 4 n B Byte) Output: Zustand s (4 n B Byte) 1 ByteSub(s); 2 ShiftRow(s); 3 MixColumn(s); 4 AddRoundKey(s, k R ); FinalRound(s, k R ) Input: Zustand s, Rundenschlüssel k R (jeweils 4 n B Byte) Output: Zustand s (4 n B Byte) 1 ByteSub(s); 2 ShiftRow(s); 3 AddRoundKey(s, k R ); Prof. Dr. C. Karg: Kryptographische Algorithmen 25/40
26 Die ByteSub Transformation S Box a i,j b i,j Die S-Box wird auf jedes Byte des Zustands angewandt. Sie ist eine Komposition aus zwei biijektiven Abbildungen. 1. Zuerst wird das zu berechnende Byte als Element von GF(2 8 ) interpretiert und auf sein multiplikatives Inverses abgebildet. Das Element 0 wird auf sich selbst abgebildet. 2. Der zweite Schritt besteht in der Berechnung einer affinen Abbildung, wobei über GF(2) gerechnet wird. Prof. Dr. C. Karg: Kryptographische Algorithmen 26/40
27 Die ByteSub Transformation (Forts.) Die affine Funktion f : {0, 1} 8 {0, 1} 8 ist wie folgt definiert: y x 0 1 y x 1 1 y x 2 0 y 3 y 4 = x x y x 5 1 y x 6 1 y x 7 0 Das zu transformierende Byte wird als Element in (Z 2 ) 8 interpretiert. Prof. Dr. C. Karg: Kryptographische Algorithmen 27/40
28 Die ByteSub Transformation (Forts.) Die zu f inverse Abbildung f 1 : {0, 1} 8 {0, 1} 8 ist ebenfalls eine affine Funktion und wie folgt definiert: x y 0 0 x y 1 0 x y 2 0 x 3 x 4 = y y x y 5 1 x y 6 0 x y 7 1 Prof. Dr. C. Karg: Kryptographische Algorithmen 28/40
29 Die ShiftRow Transformation Kein Links-Shift Links-Shift um c 1 Positionen Links-Shift um c 2 Positionen Links-Shift um c 3 Positionen Die ShiftRow-Operation ist eine zeilenweise Links-Verschiebung. Die Offsetwerte der Verschiebung sind abhängig von der Blocklänge: n B c 1 c 2 c Prof. Dr. C. Karg: Kryptographische Algorithmen 29/40
30 Die MixColumn Transformation a 0,j a 1,j M b 0,j a 2,j b 1,j b 2,j a 3,j b 3,j Die MixColumn Transformation bearbeitet den Zustand spaltenweise. Eine Spalte wird als Vektor interpretiert und mit einer 4 4 Matrix multipliziert. Die Berechnungen erfolgen über GF(2 8 ). Prof. Dr. C. Karg: Kryptographische Algorithmen 30/40
31 Die MixColumn Transformation (Forts.) b a 0 b 1 b 2 = a 1 a 2 b a 3 Die hierzu inverse Transformation ist: a b 0 a 1 a 2 = b 1 b 2 a b 3 Beachte: Man rechnet über dem Körper GF(2 8 ). Prof. Dr. C. Karg: Kryptographische Algorithmen 31/40
32 AddRoundKey Transformation a i,j k i,j XOR b i,j In der AddRoundKey Transformation wird der Rundenschlüssel auf den Zustand addiert. Hierzu wird jedes Byte des Zustand mit dem entsprechenden Byte des Rundenschlüssels via XOR verknüpft. Prof. Dr. C. Karg: Kryptographische Algorithmen 32/40
33 Entschlüsselungsalgorithmus Da jede der Basisoperationen für sich invertierbar ist, besteht die Entschlüsselung in der Anwendung der inversen Transformationen in umgekehrter Reihenfolge. Die Umkehrung von Round() ist beispielsweise: InvRound(s, k R ) Input: Zustand s, Rundenschlüssel k R (jeweils 4 n B Byte) Output: Zustand s (4 n B Byte) 1 AddRoundKey(s, k R ); 2 InvMixColumn(s); 3 InvShiftRow(s); 4 InvByteSub(s); Prof. Dr. C. Karg: Kryptographische Algorithmen 33/40
34 Erzeugen der Rundenschlüssel Für eine komplette Ver- bzw. Entschlüsselung werden n R + 1 Rundenschlüssel mit jeweils 4n B Byte benötigt. Mit anderen Worten: Aus den 4n K Byte des Schlüssels müssen also 4n B (n R + 1) Byte für die Rundenschlüssel genereriert werden. Notation: K[i] und W[i] bezeichnen 4 i-matrizen über GF(2 8 ). Die Spalten der Matrizen werden als Vektoren interpretiert. Ziel: Berechne aus K[n K ] die Matrix W[n B (n R + 1)] und zerlege diese in die Rundenschlüssel. Prof. Dr. C. Karg: Kryptographische Algorithmen 34/40
35 Schlüsselexpansion (Idee) f 1 f 2 f 3 Schlüssel Schlüsselexpansion Rundenschlüssel Prof. Dr. C. Karg: Kryptographische Algorithmen 35/40
36 Hilfsfunktionen Die Abbildung S : GF(2 8 ) GF(2 8 ) ist identisch mit der S-Box der ByteSub-Transformation. Die Funktion RC : GF(2 8 ) GF(2 8 ) ist rekursiv definiert: RC(0) = x 0 (= 1) RC(1) = x 1 (= 2) RC(i) = x i 1 für i 2 x 0 y 0 x 0 y 0 Vektoraddition: x 1 x 2 y 1 = x 1 y 1 x 3 y 2 y 3 x 2 y 2 x 3 y 3 Prof. Dr. C. Karg: Kryptographische Algorithmen 36/40
37 Hilfsfunktionen (Forts.) Abbildung f: x 0 S(y 1 ) RC(i) f(i, x, y) = x 1 x 2 S(y 2 ) S(y 3 ) 0 0 x 3 S(y 0 ) 0 Abbildung g: x 0 S(y 0 ) g( x, y) = x 1 x 2 S(y 1 ) S(y 2 ) x 3 S(y 3 ) Prof. Dr. C. Karg: Kryptographische Algorithmen 37/40
38 Schlüsselexpansion für n K 6 KeyExpansion(K[n K ], W[n B (n R + 1)]) Input: Schlüssel K (4n K Byte) wobei n K 6 Output: Rundenschlüssel (4n B (n R + 1) Byte) 1 for j := 0 to n K 1 do 2 W[j] := K[j]; 3 for (j := n K to n B (n R + 1) 1) do 4 if j mod n K = 0 then 5 W[j] := f(j/n K, W[j n K ], W[j 1]) 6 else 7 W[j] := W[j n K ] W[j 1]; Prof. Dr. C. Karg: Kryptographische Algorithmen 38/40
39 Schlüsselexpansion für n K > 6 KeyExpansion(K[n K ], W[n B (n R + 1)]) Input: Schlüssel K (4n K Byte) wobei n K > 6 Output: Rundenschlüssel (4n B (n R + 1) Byte) 1 for j := 0 to n K 1 do 2 W[j] := K[j]; 3 for j := n K to n B (n R + 1) 1 do 4 if (j mod n K = 0) then 5 W[j] := f(j/n K, W[j n K ], W[j 1]) 6 elseif (j mod n K = 4) then 7 W[j] := g(w[j n K ], W[j 1]); 8 else 9 W[j] := W[j n K ] W[j 1]; Prof. Dr. C. Karg: Kryptographische Algorithmen 39/40
40 Abschließende Bemerkungen Weitere Details zur Spezifikation und Implementierung von Rijndael sowie Quellcode in C, C++ und Java findet man unter rijmen/rijndael/ Zusätzliche Informationen zum AES und den Standardisierungsprozess findet man bei der NIST: Prof. Dr. C. Karg: Kryptographische Algorithmen 40/40
4.6.1 Mathematische Grundlagen
 4.6.1 Mathematische Grundlagen Die Basiseinheit für Berechnungen im AES stellt das Byte dar, daher sind viele Operationen im AES im GF(2 8 ) definiert. Um den Wert eines Byte darzustellen benutzen wir
4.6.1 Mathematische Grundlagen Die Basiseinheit für Berechnungen im AES stellt das Byte dar, daher sind viele Operationen im AES im GF(2 8 ) definiert. Um den Wert eines Byte darzustellen benutzen wir
Kryptographie. Vorlesung 7: Der AES Algorithmus. Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca
 Kryptographie Vorlesung 7: Der AES Algorithmus Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 1/48 KONSTRUKTION ENDLICHER KÖRPER Wir beschreiben, wie man zu jeder
Kryptographie Vorlesung 7: Der AES Algorithmus Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 1/48 KONSTRUKTION ENDLICHER KÖRPER Wir beschreiben, wie man zu jeder
Die (Un-)Sicherheit von DES
 Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997
Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997
6. Lösungsblatt
 TECHNISCHE UNIVERSITÄT DARMSTADT FACHGEBIET THEORETISCHE INFORMATIK PROF. JOHANNES BUCHMANN DR. JULIANE KRÄMER Einführung in die Kryptographie WS 205/ 206 6. Lösungsblatt 9..205 Ankündigung Es besteht
TECHNISCHE UNIVERSITÄT DARMSTADT FACHGEBIET THEORETISCHE INFORMATIK PROF. JOHANNES BUCHMANN DR. JULIANE KRÄMER Einführung in die Kryptographie WS 205/ 206 6. Lösungsblatt 9..205 Ankündigung Es besteht
Übersicht. Geschichte Mathematische Grundlagen Algorithmus. ISM WS 2017/18 Teil 6/AES
 Übersicht Geschichte Mathematische Grundlagen Algorithmus 2 Literatur [6-1] http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf [6-2] http://csrc.nist.gov/groups/stm/cavp/documents/aes/aesavs.pdf
Übersicht Geschichte Mathematische Grundlagen Algorithmus 2 Literatur [6-1] http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf [6-2] http://csrc.nist.gov/groups/stm/cavp/documents/aes/aesavs.pdf
Wiederholung. Symmetrische Verschlüsselung klassische Verfahren: moderne Verfahren: DES (Feistel-Chiffre) mehrfache Wiederholung einer Kombination aus
 Wiederholung Symmetrische Verschlüsselung klassische Verfahren: Substitutionschiffren Transpositionschiffren Vigenère-Chiffre One-Time-Pad moderne Verfahren: DES (Feistel-Chiffre) mehrfache Wiederholung
Wiederholung Symmetrische Verschlüsselung klassische Verfahren: Substitutionschiffren Transpositionschiffren Vigenère-Chiffre One-Time-Pad moderne Verfahren: DES (Feistel-Chiffre) mehrfache Wiederholung
6 Der Advanced Encryption Standard (AES)
 Stand: 9..25 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger Dieser Abschnitt lehnt sich an die Beschreibung im Buch Kryptographische Systeme von Baumann, Franz und Ptzmann an. 6 Der
Stand: 9..25 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger Dieser Abschnitt lehnt sich an die Beschreibung im Buch Kryptographische Systeme von Baumann, Franz und Ptzmann an. 6 Der
Die (Un-)Sicherheit von DES
 Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997
Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997
Erinnerung Blockchiffre
 Erinnerung Blockchiffre Definition schlüsselabhängige Permutation Seien F, F 1 pt Algorithmen. F heißt schlüsselabhängige Permutation auf l Bits falls 1 F berechnet eine Funktion {0, 1} n {0, 1} l {0,
Erinnerung Blockchiffre Definition schlüsselabhängige Permutation Seien F, F 1 pt Algorithmen. F heißt schlüsselabhängige Permutation auf l Bits falls 1 F berechnet eine Funktion {0, 1} n {0, 1} l {0,
IT-Sicherheit - Sicherheit vernetzter Systeme -
 IT-Sicherheit - Sicherheit vernetzter Systeme - Kapitel 5: Symmetrische Kryptosysteme Helmut Reiser, LRZ, WS 10/11 IT-Sicherheit 1 Inhalt Symmetrische Kryptosysteme Data Encryption Standard (DES) Advanced
IT-Sicherheit - Sicherheit vernetzter Systeme - Kapitel 5: Symmetrische Kryptosysteme Helmut Reiser, LRZ, WS 10/11 IT-Sicherheit 1 Inhalt Symmetrische Kryptosysteme Data Encryption Standard (DES) Advanced
Kryptographie. Vorlesung 5 und 6: Der AES Algorithmus. Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca
 Kryptographie Vorlesung 5 und 6: Der AES Algorithmus Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 1/68 AES Im September 1997 veröffentlichte das NIST eine Ausschreibung
Kryptographie Vorlesung 5 und 6: Der AES Algorithmus Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 1/68 AES Im September 1997 veröffentlichte das NIST eine Ausschreibung
Advanced Encryption Standard
 1 of 5 04.11.2005 14:36 Advanced Encryption Standard aus Wikipedia, der freien Enzyklopädie Der Advanced Encryption Standard (AES) ist ein symmetrisches Kryptosystem, welches als Nachfolger für DES bzw.
1 of 5 04.11.2005 14:36 Advanced Encryption Standard aus Wikipedia, der freien Enzyklopädie Der Advanced Encryption Standard (AES) ist ein symmetrisches Kryptosystem, welches als Nachfolger für DES bzw.
Betriebssysteme und Sicherheit Sicherheit. Florian Kerschbaum TU Dresden Wintersemester 2011/12
 Betriebssysteme und Sicherheit Sicherheit Florian Kerschbaum TU Dresden Wintersemester 2011/12 Begriffe Kryptographie: Geheimschrift Nachrichten schreiben ohne das sie von einem Anderen gelesen (verändert)
Betriebssysteme und Sicherheit Sicherheit Florian Kerschbaum TU Dresden Wintersemester 2011/12 Begriffe Kryptographie: Geheimschrift Nachrichten schreiben ohne das sie von einem Anderen gelesen (verändert)
AES und Public-Key-Kryptographie
 Jens Kubieziel jens@kubieziel.de Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik 22. Juni 2009 Beschreibung des Algorithmus Angriffe gegen AES Wichtige Algorithmen im 20. Jahrhundert
Jens Kubieziel jens@kubieziel.de Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik 22. Juni 2009 Beschreibung des Algorithmus Angriffe gegen AES Wichtige Algorithmen im 20. Jahrhundert
Pseudozufallsfunktionen (PRF) Kapitel 3
 Pseudozufallsfunktionen (PRF) Kapitel 3 Motivation Verschlüsselung eines Dateisystems durch PRG: PRG G(x) Entschlüsselung: berechne aus x entsprechende Generator-Ausgabe Aber: Entschlüsselung der letzten
Pseudozufallsfunktionen (PRF) Kapitel 3 Motivation Verschlüsselung eines Dateisystems durch PRG: PRG G(x) Entschlüsselung: berechne aus x entsprechende Generator-Ausgabe Aber: Entschlüsselung der letzten
AES. Jens Kubieziel jens@kubieziel.de. 07. Dezember 2009. Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik
 Angriffe gegen Jens Kubieziel jens@kubieziel.de Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik 07. Dezember 2009 Angriffe gegen Outline 1 Zur Geschichte 2 3 Angriffe gegen
Angriffe gegen Jens Kubieziel jens@kubieziel.de Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik 07. Dezember 2009 Angriffe gegen Outline 1 Zur Geschichte 2 3 Angriffe gegen
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Praktikum Algorithmische Anwendungen WS 2006/07
 Praktikum Algorithmische Anwendungen WS 2006/07 Thema Der Advanced Encryption Standard (AES) als symmetrisches Kryptosystem Gruppe B_gelb_Ala0607 Teilnehmer Florian Zaefferer, 04207, florian.zaefferer@gmx.de
Praktikum Algorithmische Anwendungen WS 2006/07 Thema Der Advanced Encryption Standard (AES) als symmetrisches Kryptosystem Gruppe B_gelb_Ala0607 Teilnehmer Florian Zaefferer, 04207, florian.zaefferer@gmx.de
Der Advanced Encryption Standard (AES)
 Der Advanced Encryption Standard (AES) Prof. Dr. Rüdiger Weis TFH Berlin Sommersemester 2008 Geschichte des AES Die Struktur des AES Angriffe auf den AES Aktuelle Ergebnisse DerAdvanced Encryption Standard
Der Advanced Encryption Standard (AES) Prof. Dr. Rüdiger Weis TFH Berlin Sommersemester 2008 Geschichte des AES Die Struktur des AES Angriffe auf den AES Aktuelle Ergebnisse DerAdvanced Encryption Standard
Diskrete Strukturen Kapitel 5: Algebraische Strukturen (Gruppen)
 WS 2015/16 Diskrete Strukturen Kapitel 5: Algebraische Strukturen (Gruppen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
WS 2015/16 Diskrete Strukturen Kapitel 5: Algebraische Strukturen (Gruppen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
IT-Sicherheit - Sicherheit vernetzter Systeme -
 IT-Sicherheit - Sicherheit vernetzter Systeme - Kapitel 5: Symmetrische Kryptosysteme Wolfgang Hommel, Helmut Reiser, LRZ, WS 12/13 IT-Sicherheit 1 Inhalt Symmetrische Kryptosysteme Data Encryption Standard
IT-Sicherheit - Sicherheit vernetzter Systeme - Kapitel 5: Symmetrische Kryptosysteme Wolfgang Hommel, Helmut Reiser, LRZ, WS 12/13 IT-Sicherheit 1 Inhalt Symmetrische Kryptosysteme Data Encryption Standard
Kapitel III Ringe und Körper
 Kapitel III Ringe und Körper 1. Definitionen und Beispiele Definition 117 Eine Algebra A = S,,, 0, 1 mit zwei zweistelligen Operatoren und heißt ein Ring, falls R1. S,, 0 eine abelsche Gruppe mit neutralem
Kapitel III Ringe und Körper 1. Definitionen und Beispiele Definition 117 Eine Algebra A = S,,, 0, 1 mit zwei zweistelligen Operatoren und heißt ein Ring, falls R1. S,, 0 eine abelsche Gruppe mit neutralem
Analyse Kryptographischer Algorithmen: KRYPTON & TWOFISH
 Analyse Kryptographischer Algorithmen: KRYPTON & TWOFISH Martin Lötzsch loetzsch@informatik.hu-berlin.de Einleitung. Das Seminar Analyse Kryptographischer Algorithmen beschäftigte sich mit interessanten,
Analyse Kryptographischer Algorithmen: KRYPTON & TWOFISH Martin Lötzsch loetzsch@informatik.hu-berlin.de Einleitung. Das Seminar Analyse Kryptographischer Algorithmen beschäftigte sich mit interessanten,
Vorlesung IT-Sicherheit FH Frankfurt Sommersemester 2007
 Vorlesung IT-Sicherheit FH Frankfurt Sommersemester 2007 Dr. Volker Scheidemann Standards für symmetrische Verschlüsselung DES, 3DES, AES DES Seite: 3 DES Data Encryption Standard 1974 von IBM unter Beteiligung
Vorlesung IT-Sicherheit FH Frankfurt Sommersemester 2007 Dr. Volker Scheidemann Standards für symmetrische Verschlüsselung DES, 3DES, AES DES Seite: 3 DES Data Encryption Standard 1974 von IBM unter Beteiligung
Kryptographische Protokolle
 Kryptographische Protokolle Lerneinheit 2: Generierung von Primzahlen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2018/2019 15.11.2018 Einleitung Einleitung Diese Lerneinheit
Kryptographische Protokolle Lerneinheit 2: Generierung von Primzahlen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2018/2019 15.11.2018 Einleitung Einleitung Diese Lerneinheit
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16
 Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16 21. Januar 2016 Definition 8.1 Eine Menge R zusammen mit zwei binären Operationen
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16 21. Januar 2016 Definition 8.1 Eine Menge R zusammen mit zwei binären Operationen
Betriebssysteme und Sicherheit
 Betriebssysteme und Sicherheit Symmetrische Kryptographie WS 2012/2012 Dr.-Ing. Elke Franz Elke.Franz@tu-dresden.de 1 Überblick 1 Einführung 2 Erreichbare Schutzziele 3 Prinzip symmetrischer Systeme 4
Betriebssysteme und Sicherheit Symmetrische Kryptographie WS 2012/2012 Dr.-Ing. Elke Franz Elke.Franz@tu-dresden.de 1 Überblick 1 Einführung 2 Erreichbare Schutzziele 3 Prinzip symmetrischer Systeme 4
Algorithmische Anwendungen Prof. Dr. Heinrich Klocke
 Algorithmische Anwendungen Prof. Dr. Heinrich Klocke Algorithmisches Projekt im Wintersemester 2005/06 Advanced Encryption Standard (AES) Rijndael Algorithmus Gruppe: C_gelb Thomas Boddenberg 11032925
Algorithmische Anwendungen Prof. Dr. Heinrich Klocke Algorithmisches Projekt im Wintersemester 2005/06 Advanced Encryption Standard (AES) Rijndael Algorithmus Gruppe: C_gelb Thomas Boddenberg 11032925
Bernd Borchert. Univ. Tübingen WS 13/14. Vorlesung. Kryptographie. Teil
 Bernd Borchert Univ. Tübingen WS 13/14 Vorlesung Kryptographie Teil 4 22.11.13 AES AES ist eine Blockchiffre in drei Varianten AES128, AES196 und AES256. Wichtigste Kennzahlen: Blocklänge bei allen drei
Bernd Borchert Univ. Tübingen WS 13/14 Vorlesung Kryptographie Teil 4 22.11.13 AES AES ist eine Blockchiffre in drei Varianten AES128, AES196 und AES256. Wichtigste Kennzahlen: Blocklänge bei allen drei
Algebra für Informationssystemtechniker
 Algebra für Informationssystemtechniker Prof. Dr. Ulrike Baumann Fachrichtung Mathematik Institut für Algebra www.math.tu-dresden.de/ baumann Ulrike.Baumann@tu-dresden.de 16.07.2018 14. Vorlesung irreduzible
Algebra für Informationssystemtechniker Prof. Dr. Ulrike Baumann Fachrichtung Mathematik Institut für Algebra www.math.tu-dresden.de/ baumann Ulrike.Baumann@tu-dresden.de 16.07.2018 14. Vorlesung irreduzible
10 Der Advanced Encryption Standard (AES)
 D3kjd3Di38lk323nnm 137 Das momentan bedeutendste symmetrische Verschlüsselungsverfahren ist der Advanced Encryption Standard (AES). Unter dem Namen Rijndael hat dieses Verfahren den Wettbewerb um die Nachfolge
D3kjd3Di38lk323nnm 137 Das momentan bedeutendste symmetrische Verschlüsselungsverfahren ist der Advanced Encryption Standard (AES). Unter dem Namen Rijndael hat dieses Verfahren den Wettbewerb um die Nachfolge
74 5 DES und AES. 5.1 Der Data Encryption Standard (DES)
 74 5 DES und AES 5 DES und AES 5.1 Der Data Encryption Standard (DES) Der DES wurde von IBM im Zuge einer im Mai 1973 veröffentlichten Ausschreibung des NBS (National Bureau of Standards; heute National
74 5 DES und AES 5 DES und AES 5.1 Der Data Encryption Standard (DES) Der DES wurde von IBM im Zuge einer im Mai 1973 veröffentlichten Ausschreibung des NBS (National Bureau of Standards; heute National
Teil I. Lineare Algebra I Vorlesung Sommersemester Olga Holtz. MA 378 Sprechstunde Fr und n.v.
 Teil I Lineare Algebra I Vorlesung Sommersemester 2011 Olga Holtz MA 378 Sprechstunde Fr 14-16 und nv holtz@mathtu-berlinde Sadegh Jokar MA 373 Sprechstunde, Do 12-14 und nv jokar@mathtu-berlinde Kapitel
Teil I Lineare Algebra I Vorlesung Sommersemester 2011 Olga Holtz MA 378 Sprechstunde Fr 14-16 und nv holtz@mathtu-berlinde Sadegh Jokar MA 373 Sprechstunde, Do 12-14 und nv jokar@mathtu-berlinde Kapitel
Algorithmische Kryptographie
 Algorithmische Kryptographie Walter Unger Lehrstuhl für Informatik I 16. Februar 2007 Public-Key-Systeme: Rabin 1 Das System nach Rabin 2 Grundlagen Körper Endliche Körper F(q) Definitionen Quadratwurzel
Algorithmische Kryptographie Walter Unger Lehrstuhl für Informatik I 16. Februar 2007 Public-Key-Systeme: Rabin 1 Das System nach Rabin 2 Grundlagen Körper Endliche Körper F(q) Definitionen Quadratwurzel
Diskreter Logarithmus und Primkörper
 Diskreter Logarithmus und Primkörper Neben dem RSA-Verfahren ist die ElGamal-Verschlüsselung 8 ein weiteres klassische Public-Key-Verfahren, welches von Taher ElGamal auf der Konferenz CRYPTO 84 vorgestellt
Diskreter Logarithmus und Primkörper Neben dem RSA-Verfahren ist die ElGamal-Verschlüsselung 8 ein weiteres klassische Public-Key-Verfahren, welches von Taher ElGamal auf der Konferenz CRYPTO 84 vorgestellt
Algebraische Strukturen. Idee. Gruppen, Ringe, Körper... (Teschl/Teschl Abschnitt 3.2, siehe auch Kap. 4)
 Algebraische Strukturen Gruppen, Ringe, Körper... (Teschl/Teschl Abschnitt 3.2, siehe auch Kap. 4) Idee Formalisierung von Strukturen, die in verschiedenen Bereichen der Mathematik und ihrer Anwendungen
Algebraische Strukturen Gruppen, Ringe, Körper... (Teschl/Teschl Abschnitt 3.2, siehe auch Kap. 4) Idee Formalisierung von Strukturen, die in verschiedenen Bereichen der Mathematik und ihrer Anwendungen
4: Blockchiffren. Klartexte (n bit) Chiffretexte. VERschlüsseln. ENTschlüsseln. Stefan Lucks Kryptographie und Mediensicherheit (2017)
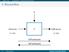 96 4: Blockchiffren 4: Blockchiffren K Klartexte (n bit) E Chiffretexte (n bit) VERschlüsseln ENTschlüsseln 97 4: Blockchiffren 4.1: Abstrakte Blockchiffren 4.1: Abstrakte Blockchiffren Familie von Paaren
96 4: Blockchiffren 4: Blockchiffren K Klartexte (n bit) E Chiffretexte (n bit) VERschlüsseln ENTschlüsseln 97 4: Blockchiffren 4.1: Abstrakte Blockchiffren 4.1: Abstrakte Blockchiffren Familie von Paaren
Galoiskörper GF(2 n ) (Teschl/Teschl 4)
 Galoiskörper GF(2 n ) (Teschl/Teschl 4) auch Galois-Felder (englisch Galois elds), benannt nach Evariste Galois (18111832). Körper (in der Mathematik) allgemein: Zahlenbereich, in dem die vier Grundrechenarten
Galoiskörper GF(2 n ) (Teschl/Teschl 4) auch Galois-Felder (englisch Galois elds), benannt nach Evariste Galois (18111832). Körper (in der Mathematik) allgemein: Zahlenbereich, in dem die vier Grundrechenarten
Advanced Encryption Standard. Copyright Stefan Dahler 20. Februar 2010 Version 2.0
 Advanced Encryption Standard Copyright Stefan Dahler 20. Februar 2010 Version 2.0 Vorwort Diese Präsentation erläutert den Algorithmus AES auf einfachste Art. Mit Hilfe des Wissenschaftlichen Rechners
Advanced Encryption Standard Copyright Stefan Dahler 20. Februar 2010 Version 2.0 Vorwort Diese Präsentation erläutert den Algorithmus AES auf einfachste Art. Mit Hilfe des Wissenschaftlichen Rechners
Systeme II 3. Die Datensicherungsschicht
 Systeme II 3. Die Datensicherungsschicht Christian Schindelhauer Technische Fakultät Rechnernetze und Telematik Albert-Ludwigs-Universität Freiburg Version 12.05.2016 1 Fehlererkennung: CRC Effiziente
Systeme II 3. Die Datensicherungsschicht Christian Schindelhauer Technische Fakultät Rechnernetze und Telematik Albert-Ludwigs-Universität Freiburg Version 12.05.2016 1 Fehlererkennung: CRC Effiziente
Galoiskörper GF(2 n ) (Teschl/Teschl 4)
 Galoiskörper GF(2 n ) (Teschl/Teschl 4) auch Galois-Felder (englisch Galois elds), benannt nach Evariste Galois (18111832). Körper (in der Mathematik) allgemein: Zahlenbereich, in dem die vier Grundrechenarten
Galoiskörper GF(2 n ) (Teschl/Teschl 4) auch Galois-Felder (englisch Galois elds), benannt nach Evariste Galois (18111832). Körper (in der Mathematik) allgemein: Zahlenbereich, in dem die vier Grundrechenarten
Kapitel 7: Symmetrische Kryptosysteme. Helmut Reiser, LRZ, WS 2016/17 IT-Sicherheit
 Kapitel 7: Symmetrische Kryptosysteme Helmut Reiser, LRZ, WS 2016/17 IT-Sicherheit 1 Inhalt Symmetrische Verschlüsselungsverfahren Data Encryption Standard (DES) Advanced Encryption Standard (AES) Kryptoregulierung
Kapitel 7: Symmetrische Kryptosysteme Helmut Reiser, LRZ, WS 2016/17 IT-Sicherheit 1 Inhalt Symmetrische Verschlüsselungsverfahren Data Encryption Standard (DES) Advanced Encryption Standard (AES) Kryptoregulierung
Die inverse Diskrete Fourier Transformation
 Die inverse Diskrete Fourier Transformation Konvertierung von der Point-value Form in Koeffizientenform. Dazu stellen wir die DFT als Matrix-Vektor Produkt dar 1 1 1... 1 1 ω n ωn 2... ωn n 1 a 0 y 0 1
Die inverse Diskrete Fourier Transformation Konvertierung von der Point-value Form in Koeffizientenform. Dazu stellen wir die DFT als Matrix-Vektor Produkt dar 1 1 1... 1 1 ω n ωn 2... ωn n 1 a 0 y 0 1
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen Lerneinheit : Dynamisches Programmieren Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester.. Einleitung Diese Lerneinheit widmet sich einer
Algorithmen und Datenstrukturen Lerneinheit : Dynamisches Programmieren Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester.. Einleitung Diese Lerneinheit widmet sich einer
Kapitel 7: Symmetrische Kryptosysteme. Wolfgang Hommel, Helmut Reiser, LRZ, WS 2015/16 IT-Sicherheit
 Kapitel 7: Symmetrische Kryptosysteme Wolfgang Hommel, Helmut Reiser, LRZ, WS 2015/16 IT-Sicherheit 1 Inhalt Symmetrische Verschlüsselungsverfahren Data Encryption Standard (DES) Advanced Encryption Standard
Kapitel 7: Symmetrische Kryptosysteme Wolfgang Hommel, Helmut Reiser, LRZ, WS 2015/16 IT-Sicherheit 1 Inhalt Symmetrische Verschlüsselungsverfahren Data Encryption Standard (DES) Advanced Encryption Standard
4 Diskrete Logarithmen und Anwendungen
 Stand: 05.11.2013 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 4 Diskrete Logarithmen und Anwendungen 4.1 Diskrete Logarithmen Wir betrachten eine endliche zyklische Gruppe (G,, e)
Stand: 05.11.2013 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 4 Diskrete Logarithmen und Anwendungen 4.1 Diskrete Logarithmen Wir betrachten eine endliche zyklische Gruppe (G,, e)
RSA Parameter öffentlich: N = pq mit p, q prim und e Z RSA Parameter geheim: d Z φ(n)
 RSA Parameter { öffentlich: N = pq mit p, q prim und e Z RSA Parameter φ(n) geheim: d Z φ(n) mit ed = 1 mod φ(n). Satz RSA Parameter Generierung RSA-Parameter (N, e, d) können in Zeit O(log 4 N) generiert
RSA Parameter { öffentlich: N = pq mit p, q prim und e Z RSA Parameter φ(n) geheim: d Z φ(n) mit ed = 1 mod φ(n). Satz RSA Parameter Generierung RSA-Parameter (N, e, d) können in Zeit O(log 4 N) generiert
Kapitel 7: Symmetrische Kryptosysteme. Prof. Dr. Helmut Reiser, LRZ, WS 2017/18 IT-Sicherheit
 Kapitel 7: Symmetrische Kryptosysteme Prof. Dr. Helmut Reiser, LRZ, WS 2017/18 IT-Sicherheit 1 Frauen MINT-Award BA und MA zu den Themen, dürfen 1,5 Jahre zurückliegen Preisgeld: 3.000 Euro Info: https://www.frauen-mint-award.de/#info
Kapitel 7: Symmetrische Kryptosysteme Prof. Dr. Helmut Reiser, LRZ, WS 2017/18 IT-Sicherheit 1 Frauen MINT-Award BA und MA zu den Themen, dürfen 1,5 Jahre zurückliegen Preisgeld: 3.000 Euro Info: https://www.frauen-mint-award.de/#info
Inhaltsverzeichnis. Wolfgang Ertel. Angewandte Kryptographie. ISBN (Buch): ISBN (E-Book):
 Inhaltsverzeichnis Wolfgang Ertel Angewandte Kryptographie ISBN (Buch): 978-3-446-42756-3 ISBN (E-Book): 978-3-446-43196-6 Weitere Informationen oder Bestellungen unter http://www.hanser-fachbuch.de/978-3-446-42756-3
Inhaltsverzeichnis Wolfgang Ertel Angewandte Kryptographie ISBN (Buch): 978-3-446-42756-3 ISBN (E-Book): 978-3-446-43196-6 Weitere Informationen oder Bestellungen unter http://www.hanser-fachbuch.de/978-3-446-42756-3
Definition 153 Sei n eine fest gewählte ganze Zahl 0. Für jedes l Z heißt die Menge
 3.6 Restklassen in Polynomringen 3.6.1 Einführung und Definitionen Der Begriff der Restklasse stammt ursprünglich aus der Teilbarkeitslehre in Z; (Z = Z, +, ist ein kommutativer Ring). Definition 153 Sei
3.6 Restklassen in Polynomringen 3.6.1 Einführung und Definitionen Der Begriff der Restklasse stammt ursprünglich aus der Teilbarkeitslehre in Z; (Z = Z, +, ist ein kommutativer Ring). Definition 153 Sei
Bemerkungen. Gilt m [l] n, so schreibt man auch m l mod n oder m = l mod n und spricht. m kongruent l modulo n.
![Bemerkungen. Gilt m [l] n, so schreibt man auch m l mod n oder m = l mod n und spricht. m kongruent l modulo n. Bemerkungen. Gilt m [l] n, so schreibt man auch m l mod n oder m = l mod n und spricht. m kongruent l modulo n.](/thumbs/69/61067953.jpg) 3.6 Restklassen in Polynomringen 3.6.1 Einführung und Definitionen Der Begriff der Restklasse stammt ursprünglich aus der Teilbarkeitslehre in Z; (Z = Z, +, ist ein kommutativer Ring). Definition 153 Sei
3.6 Restklassen in Polynomringen 3.6.1 Einführung und Definitionen Der Begriff der Restklasse stammt ursprünglich aus der Teilbarkeitslehre in Z; (Z = Z, +, ist ein kommutativer Ring). Definition 153 Sei
Kongruenz modulo g definiert auf K[x] eine Äquivalenzrelation g : h g f h f ist durch g teilbar, und [f] g ist die Äquivalenzklasse von f.
![Kongruenz modulo g definiert auf K[x] eine Äquivalenzrelation g : h g f h f ist durch g teilbar, und [f] g ist die Äquivalenzklasse von f. Kongruenz modulo g definiert auf K[x] eine Äquivalenzrelation g : h g f h f ist durch g teilbar, und [f] g ist die Äquivalenzklasse von f.](/thumbs/57/40324422.jpg) 3 Kongruenz modulo g definiert auf K[x] eine Äquivalenzrelation g : h g f h f ist durch g teilbar, und [f] g ist die Äquivalenzklasse von f 4 Auf der Menge aller Restklassen [f] g kann man Addition und
3 Kongruenz modulo g definiert auf K[x] eine Äquivalenzrelation g : h g f h f ist durch g teilbar, und [f] g ist die Äquivalenzklasse von f 4 Auf der Menge aller Restklassen [f] g kann man Addition und
Diskrete Mathematik. Sebastian Iwanowski FH Wedel. Kap. 4: Zahlentheorie
 Prof. Dr. Sebastian Iwanowski DM4 Folie 1 Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 4: Zahlentheorie Beutelspacher 5 Lang 7, Biggs 20, 22, 23 (jeweils teilweise,
Prof. Dr. Sebastian Iwanowski DM4 Folie 1 Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 4: Zahlentheorie Beutelspacher 5 Lang 7, Biggs 20, 22, 23 (jeweils teilweise,
Unterlagen zu Polynomringen. Erhard Aichinger
 Unterlagen zu Polynomringen Erhard Aichinger Linz, im November 2005 Alle Rechte vorbehalten 1 KAPITEL 1 Polynome und Körper 1. Körper DEFINITION 1.1. Ein kommutativer Ring mit Eins R R,,,, 0, 1 ist ein
Unterlagen zu Polynomringen Erhard Aichinger Linz, im November 2005 Alle Rechte vorbehalten 1 KAPITEL 1 Polynome und Körper 1. Körper DEFINITION 1.1. Ein kommutativer Ring mit Eins R R,,,, 0, 1 ist ein
4 Diskrete Logarithmen und Anwendungen
 Stand: 19.1.2015 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 4 Diskrete Logarithmen und Anwendungen 4.1 Diskrete Logarithmen Wir betrachten eine endliche zyklische Gruppe (G,, e)
Stand: 19.1.2015 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 4 Diskrete Logarithmen und Anwendungen 4.1 Diskrete Logarithmen Wir betrachten eine endliche zyklische Gruppe (G,, e)
31 Polynomringe Motivation Definition: Polynomringe
 31 Polynomringe 31.1 Motivation Polynome spielen eine wichtige Rolle in vielen Berechnungen, einerseits weil oftmals funktionale Zusammenhänge durch Polynome beschrieben werden, andererseits weil Polynome
31 Polynomringe 31.1 Motivation Polynome spielen eine wichtige Rolle in vielen Berechnungen, einerseits weil oftmals funktionale Zusammenhänge durch Polynome beschrieben werden, andererseits weil Polynome
Algebraische und arithmetische Algorithmen
 Kapitel 1 Algebraische und arithmetische Algorithmen 1.1 Das algebraische Berechnungsmodell Struktur: Körper (oder Ring) mit den Operationen +,,, (/) Eingabe: endliche Folge von Zahlen Ausgabe: endliche
Kapitel 1 Algebraische und arithmetische Algorithmen 1.1 Das algebraische Berechnungsmodell Struktur: Körper (oder Ring) mit den Operationen +,,, (/) Eingabe: endliche Folge von Zahlen Ausgabe: endliche
6.2. Ringe und Körper
 62 RINGE UND K ÖRPER 62 Ringe und Körper Wir betrachten nun Mengen (endlich oder unendlich) mit zwei Operationen Diese werden meist als Addition und Multiplikation geschrieben Meist ist dabei die additiv
62 RINGE UND K ÖRPER 62 Ringe und Körper Wir betrachten nun Mengen (endlich oder unendlich) mit zwei Operationen Diese werden meist als Addition und Multiplikation geschrieben Meist ist dabei die additiv
Analyse kryptographischer Algorithmen: Serpent
 Analyse kryptographischer Algorithmen: Serpent Michael Ueckerdt mailto://ueckerdt@informatik.hu-berlin.de 23. August 2002 1 Einleitung Dieses Seminar beschäftigt sich mit modernen aber etwas weniger bekannten
Analyse kryptographischer Algorithmen: Serpent Michael Ueckerdt mailto://ueckerdt@informatik.hu-berlin.de 23. August 2002 1 Einleitung Dieses Seminar beschäftigt sich mit modernen aber etwas weniger bekannten
Literatur und Videos. ISM WS 2017/18 Teil 4/Algebren
 Literatur und Videos [4-1] http://www.iti.fh-flensburg.de/lang/krypto [4-2] Forster, Otto: Algorithmische Zahlentheorie. 2. Auflage, Springer, 2015 [4-3] Teschl, Gerald; Teschl, Susanne: Mathematik für
Literatur und Videos [4-1] http://www.iti.fh-flensburg.de/lang/krypto [4-2] Forster, Otto: Algorithmische Zahlentheorie. 2. Auflage, Springer, 2015 [4-3] Teschl, Gerald; Teschl, Susanne: Mathematik für
2: Restklassen 2.1: Modulare Arithmetik
 2: Restklassen 2.1: Modulare Arithmetik Uhr: Stunden mod 24, Minuten mod 60, Sekunden mod 60,... Rechnerarithmetik: mod 2 w, w {8, 16, 32, 64} Prüfziffern mod 10 oder mod 11... 71 S. Lucks Diskr Strukt.
2: Restklassen 2.1: Modulare Arithmetik Uhr: Stunden mod 24, Minuten mod 60, Sekunden mod 60,... Rechnerarithmetik: mod 2 w, w {8, 16, 32, 64} Prüfziffern mod 10 oder mod 11... 71 S. Lucks Diskr Strukt.
II. Lineare Gleichungssysteme. 10 Matrizen und Vektoren. 52 II. Lineare Gleichungssysteme
 52 II Lineare Gleichungssysteme II Lineare Gleichungssysteme 10 Matrizen und Vektoren 52 11 Der Gaußsche Algorithmus 58 12 Basen, Dimension und Rang 62 13 Reguläre Matrizen 66 14 Determinanten 69 15 Skalarprodukte
52 II Lineare Gleichungssysteme II Lineare Gleichungssysteme 10 Matrizen und Vektoren 52 11 Der Gaußsche Algorithmus 58 12 Basen, Dimension und Rang 62 13 Reguläre Matrizen 66 14 Determinanten 69 15 Skalarprodukte
Blockverschlüsselung und AES
 Blockverschlüsselung und AES Proseminar/Seminar Kryptographie und Datensicherheit SoSe 2009 Universität Potsdam ein Vortrag von Linda Tschepe Übersicht Allgemeines SPNs (Substitutions- Permutations- Netzwerke)
Blockverschlüsselung und AES Proseminar/Seminar Kryptographie und Datensicherheit SoSe 2009 Universität Potsdam ein Vortrag von Linda Tschepe Übersicht Allgemeines SPNs (Substitutions- Permutations- Netzwerke)
Kryptographische Algorithmen
 Kryptographische Algorithmen Lerneinheit 3: Data Encryption Standard (DES) Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2018/2019 4.11.2018 Entstehungsgeschichte Anfang
Kryptographische Algorithmen Lerneinheit 3: Data Encryption Standard (DES) Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2018/2019 4.11.2018 Entstehungsgeschichte Anfang
IT-Sicherheit - Sicherheit vernetzter Systeme -
 IT-Sicherheit - Sicherheit vernetzter Systeme - Kapitel 5: Symmetrische Kryptosysteme Helmut Reiser, LRZ, WS 09/10 IT-Sicherheit 1 Inhalt Symmetrische Kryptosysteme Data Encryption Standard (DES) Advanced
IT-Sicherheit - Sicherheit vernetzter Systeme - Kapitel 5: Symmetrische Kryptosysteme Helmut Reiser, LRZ, WS 09/10 IT-Sicherheit 1 Inhalt Symmetrische Kryptosysteme Data Encryption Standard (DES) Advanced
9 Rechnergestütze Blockchiffren
 9 Rechnergestütze n 9.1 ata Encryption Standard (ES) 1977 von National Bureau of Standards (heute National Institute of Standards and Technology) genormt arbeitet auf bit-blöcken Schlüssel 5 bit + 8 bit
9 Rechnergestütze n 9.1 ata Encryption Standard (ES) 1977 von National Bureau of Standards (heute National Institute of Standards and Technology) genormt arbeitet auf bit-blöcken Schlüssel 5 bit + 8 bit
IT-Sicherheitsmanagement. Teil 4: Einführung in algebraische Strukturen
 IT-Sicherheitsmanagement Teil 4: Einführung in algebraische Strukturen 19.09.18 1 Literatur und Videos [4-1] http://www.iti.fh-flensburg.de/lang/krypto [4-2] Forster, Otto: Algorithmische Zahlentheorie.
IT-Sicherheitsmanagement Teil 4: Einführung in algebraische Strukturen 19.09.18 1 Literatur und Videos [4-1] http://www.iti.fh-flensburg.de/lang/krypto [4-2] Forster, Otto: Algorithmische Zahlentheorie.
Lineare Algebra I 5. Tutorium Die Restklassenringe /n
 Lineare Algebra I 5. Tutorium Die Restklassenringe /n Fachbereich Mathematik WS 2010/2011 Prof. Dr. Kollross 19. November 2010 Dr. Le Roux Dipl.-Math. Susanne Kürsten Aufgaben In diesem Tutrorium soll
Lineare Algebra I 5. Tutorium Die Restklassenringe /n Fachbereich Mathematik WS 2010/2011 Prof. Dr. Kollross 19. November 2010 Dr. Le Roux Dipl.-Math. Susanne Kürsten Aufgaben In diesem Tutrorium soll
Das Verschlüsseln verstehen
 Das Verschlüsseln verstehen Kurz-Vorlesung Security Day 2014 Prof. (FH) Univ.-Doz. DI. Dr. Ernst Piller Kurzvorlesung "Das Verschlüsseln verstehen", Security Day 2014, Ernst Piller 1 Warum eigentlich Verschlüsselung
Das Verschlüsseln verstehen Kurz-Vorlesung Security Day 2014 Prof. (FH) Univ.-Doz. DI. Dr. Ernst Piller Kurzvorlesung "Das Verschlüsseln verstehen", Security Day 2014, Ernst Piller 1 Warum eigentlich Verschlüsselung
Von den ganzen Zahlen zu GF(p)
 Endliche Körper p. 1 Von den ganzen Zahlen zu GF(p) Aus dem Ring aller ganzen Zahlen gewinnt man endliche Körper wie folgt: Man führt das Rechnen modulo n ein (modulare Arithmetik) und erhält so endliche
Endliche Körper p. 1 Von den ganzen Zahlen zu GF(p) Aus dem Ring aller ganzen Zahlen gewinnt man endliche Körper wie folgt: Man führt das Rechnen modulo n ein (modulare Arithmetik) und erhält so endliche
Prüfungsfragen zur Vorlesung Algebra und Diskrete Mathematik. Sommersemester 2018
 Prüfungsfragen zur Vorlesung Algebra und Diskrete Mathematik Sommersemester 2018 Erläutern Sie die Sätze über die Division mit Rest für ganze Zahlen und für Polynome (mit Koeffizienten in einem Körper).
Prüfungsfragen zur Vorlesung Algebra und Diskrete Mathematik Sommersemester 2018 Erläutern Sie die Sätze über die Division mit Rest für ganze Zahlen und für Polynome (mit Koeffizienten in einem Körper).
Kapitel 2. Elementare Zahlentheorie Primfaktorzerlegung
 Kapitel 2. Elementare Zahlentheorie 2.1. Primfaktorzerlegung Menge der ganzen Zahlen Z = {..., 3, 2, 1, 0, 1, 2, 3,...} Addition Inverse Multiplikation Z Z Z, Z Z, Z Z Z, (a, b) a + b a a (a, b) a b Ausgezeichnete
Kapitel 2. Elementare Zahlentheorie 2.1. Primfaktorzerlegung Menge der ganzen Zahlen Z = {..., 3, 2, 1, 0, 1, 2, 3,...} Addition Inverse Multiplikation Z Z Z, Z Z, Z Z Z, (a, b) a + b a a (a, b) a b Ausgezeichnete
Algebraische und arithmetische Algorithmen
 Kapitel 1 Algebraische und arithmetische Algorithmen 1.1 Das algebraische Berechnungsmodell Struktur: Körper (oder Ring) mit den Operationen +,,, (/) Eingabe: endliche Folge von Zahlen Ausgabe: endliche
Kapitel 1 Algebraische und arithmetische Algorithmen 1.1 Das algebraische Berechnungsmodell Struktur: Körper (oder Ring) mit den Operationen +,,, (/) Eingabe: endliche Folge von Zahlen Ausgabe: endliche
IT-Security. Teil 9: Einführung in algebraische Strukturen
 IT-Security Teil 9: Einführung in algebraische Strukturen 08.05.17 1 Literatur und Videos [9-1] http://www.iti.fh-flensburg.de/lang/krypto [9-2] Forster, Otto: Algorithmische Zahlentheorie. 2. Auflage,
IT-Security Teil 9: Einführung in algebraische Strukturen 08.05.17 1 Literatur und Videos [9-1] http://www.iti.fh-flensburg.de/lang/krypto [9-2] Forster, Otto: Algorithmische Zahlentheorie. 2. Auflage,
Kryptografische Algorithmen
 Kryptografische Algorithmen Lerneinheit 5: Weitere symmetrische Kryptosysteme Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2015/2016 21.9.2015 Einleitung Einleitung Diese
Kryptografische Algorithmen Lerneinheit 5: Weitere symmetrische Kryptosysteme Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2015/2016 21.9.2015 Einleitung Einleitung Diese
Kryptographische Protokolle
 Kryptographische Protokolle Lerneinheit 4: Schlüsselvereinbarung Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2017 8.5.2017 Einleitung Einleitung In dieser Lerneinheit
Kryptographische Protokolle Lerneinheit 4: Schlüsselvereinbarung Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2017 8.5.2017 Einleitung Einleitung In dieser Lerneinheit
Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt 12
 Dipl.Inf. Malte Isberner Dr. Oliver Rüthing Dipl.Inf. Melanie Schmidt Dr. Hubert Wagner Übungen zur Vorlesung Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt 12 Die Lösungshinweise dienen
Dipl.Inf. Malte Isberner Dr. Oliver Rüthing Dipl.Inf. Melanie Schmidt Dr. Hubert Wagner Übungen zur Vorlesung Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt 12 Die Lösungshinweise dienen
Endliche Körper Seminar: Diskrete Mathematik Leitung: Prof. Dr. Rainer Lang Von: Steffen Lohrke (ii5105) SS2005
 Endliche Körper Seminar: Diskrete Mathematik Leitung: Prof. Dr. Rainer Lang Von: Steffen Lohrke (ii5105) SS2005 Inhaltsverzeichnis Abelsche Gruppe 3 Kommutativer Ring 5 Körper 6 Endliche Körper 7 Endliche
Endliche Körper Seminar: Diskrete Mathematik Leitung: Prof. Dr. Rainer Lang Von: Steffen Lohrke (ii5105) SS2005 Inhaltsverzeichnis Abelsche Gruppe 3 Kommutativer Ring 5 Körper 6 Endliche Körper 7 Endliche
Euklidische Algorithmus, Restklassenringe (Z m,, )
 Euklidische Algorithmus, Restklassenringe (Z m,, ) Manfred Gruber http://www.cs.hm.edu/~gruber SS 2008, KW 14 Gröÿter gemeinsamer Teiler Denition 1. [Teiler] Eine Zahl m N ist Teiler von n Z, wenn der
Euklidische Algorithmus, Restklassenringe (Z m,, ) Manfred Gruber http://www.cs.hm.edu/~gruber SS 2008, KW 14 Gröÿter gemeinsamer Teiler Denition 1. [Teiler] Eine Zahl m N ist Teiler von n Z, wenn der
Kanonische Primfaktorzerlegung
 Kanonische Primfaktorzerlegung Jede natürliche Zahl Form kann auf eindeutige Weise in der geschrieben werden, wobei, für und Primzahlen sind. Dies ist die kanonische Primfaktorzerlegung von. Mathematik
Kanonische Primfaktorzerlegung Jede natürliche Zahl Form kann auf eindeutige Weise in der geschrieben werden, wobei, für und Primzahlen sind. Dies ist die kanonische Primfaktorzerlegung von. Mathematik
Vorlesung Mathematik 2 für Informatik
 Vorlesung Mathematik 2 für Informatik Inhalt: Modulare Arithmetik Lineare Algebra Vektoren und Matrizen Lineare Gleichungssysteme Vektorräume, lineare Abbildungen Orthogonalität Eigenwerte und Eigenvektoren
Vorlesung Mathematik 2 für Informatik Inhalt: Modulare Arithmetik Lineare Algebra Vektoren und Matrizen Lineare Gleichungssysteme Vektorräume, lineare Abbildungen Orthogonalität Eigenwerte und Eigenvektoren
35 Matrixschreibweise für lineare Abbildungen
 35 Matrixschreibweise für lineare Abbildungen 35 Motivation Wir haben gesehen, dass lineare Abbildungen sich durch ihre Wirkung auf die Basisvektoren ausdrücken lassen Mithilfe von Matrizen können wir
35 Matrixschreibweise für lineare Abbildungen 35 Motivation Wir haben gesehen, dass lineare Abbildungen sich durch ihre Wirkung auf die Basisvektoren ausdrücken lassen Mithilfe von Matrizen können wir
Übungen zu Einführung in die Lineare Algebra und Geometrie
 Übungen zu Einführung in die Lineare Algebra und Geometrie Andreas Cap Wintersemester 2014/15 Kapitel 1: Einleitung (1) Für a, b Z diskutiere analog zur Vorlesung das Lösungsverhalten der Gleichung ax
Übungen zu Einführung in die Lineare Algebra und Geometrie Andreas Cap Wintersemester 2014/15 Kapitel 1: Einleitung (1) Für a, b Z diskutiere analog zur Vorlesung das Lösungsverhalten der Gleichung ax
15. Vorlesung. Primitive Polynome (Beispiel) Beispiel zur Konstruktion von GF(p)[x]/f (x) mit einem primitiven Polynom f (x) (Logarithmentafel)
![15. Vorlesung. Primitive Polynome (Beispiel) Beispiel zur Konstruktion von GF(p)[x]/f (x) mit einem primitiven Polynom f (x) (Logarithmentafel) 15. Vorlesung. Primitive Polynome (Beispiel) Beispiel zur Konstruktion von GF(p)[x]/f (x) mit einem primitiven Polynom f (x) (Logarithmentafel)](/thumbs/95/122944635.jpg) 15. Vorlesung Primitive Polynome (Beispiel) Beispiel zur Konstruktion von GF(p)[x]/f (x) mit einem primitiven Polynom f (x) (Logarithmentafel) Struktur endlicher Körper Rechnen in endlichen Körpern Isomorphie
15. Vorlesung Primitive Polynome (Beispiel) Beispiel zur Konstruktion von GF(p)[x]/f (x) mit einem primitiven Polynom f (x) (Logarithmentafel) Struktur endlicher Körper Rechnen in endlichen Körpern Isomorphie
3 Public-Key-Kryptosysteme
 Stand: 05.11.2013 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 3 Public-Key-Kryptosysteme 3.1 Verschlüsselung von Nachrichten Wir betrachten ganz einfache Kommunikationsszenarien.
Stand: 05.11.2013 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 3 Public-Key-Kryptosysteme 3.1 Verschlüsselung von Nachrichten Wir betrachten ganz einfache Kommunikationsszenarien.
A2.3: Reduzible und irreduzible Polynome
 A2.3: Reduzible und irreduzible Polynome Wichtige Voraussetzungen für das Verständnis der Kanalcodierung sind Kenntnisse der Polynomeigenschaften. Wir betrachten in dieser Aufgabe Polynome der Form wobei
A2.3: Reduzible und irreduzible Polynome Wichtige Voraussetzungen für das Verständnis der Kanalcodierung sind Kenntnisse der Polynomeigenschaften. Wir betrachten in dieser Aufgabe Polynome der Form wobei
Mathematik IT 2 (Lineare Algebra)
 Lehrstuhl Mathematik, insbesondere Numerische und Angewandte Mathematik Prof Dr L Cromme Mathematik IT (Lineare Algebra für die Studiengänge Informatik, IMT und ebusiness im Sommersemester 3 Lineare Gleichungssysteme
Lehrstuhl Mathematik, insbesondere Numerische und Angewandte Mathematik Prof Dr L Cromme Mathematik IT (Lineare Algebra für die Studiengänge Informatik, IMT und ebusiness im Sommersemester 3 Lineare Gleichungssysteme
Algorithmen für die Speicherhierarchie
 Lineare Algebra: untere Schranken Lehrstuhl für Effiziente Algorithmen Fakultät für Informatik Technische Universität München Vorlesung Sommersemester 2009 Gliederung 1 2 Zusätzliche Überlegungen Erinnerung
Lineare Algebra: untere Schranken Lehrstuhl für Effiziente Algorithmen Fakultät für Informatik Technische Universität München Vorlesung Sommersemester 2009 Gliederung 1 2 Zusätzliche Überlegungen Erinnerung
Isomorphismus. Definition Gruppen-Isomorphismus. Seien (G, +) und (G, ) Gruppen. Die Abbildung f : G G heißt Gruppen-Isomorphismus, falls gilt
 Isomorphismus Definition Gruppen-Isomorphismus Seien (G, +) und (G, ) Gruppen. Die Abbildung f : G G heißt Gruppen-Isomorphismus, falls gilt 1 f ist bijektiv f (u + v) = f (u) f (v) für alle u, v G, die
Isomorphismus Definition Gruppen-Isomorphismus Seien (G, +) und (G, ) Gruppen. Die Abbildung f : G G heißt Gruppen-Isomorphismus, falls gilt 1 f ist bijektiv f (u + v) = f (u) f (v) für alle u, v G, die
Lösung zur Klausur zu Krypographie Sommersemester 2005
 Lösung zur Klausur zu Krypographie Sommersemester 2005 1. Bestimmen Sie die zwei letzten Ziffern der Dezimaldarstellung von 12 34 Es gilt: 12 34 = 12 32+2 = 12 32 12 2 = 12 (25) 12 2 = ((((12 2 ) 2 ) 2
Lösung zur Klausur zu Krypographie Sommersemester 2005 1. Bestimmen Sie die zwei letzten Ziffern der Dezimaldarstellung von 12 34 Es gilt: 12 34 = 12 32+2 = 12 32 12 2 = 12 (25) 12 2 = ((((12 2 ) 2 ) 2
Alice (A) und Bob (B) wollen sicher kommunizieren (vgl. Schutzziele) Oskar (O) versucht, die Schutzziele zu durchbrechen
 Vorlesung am 21.04.2015 3 Symmetrische Verschlüsselung Alice (A) und Bob (B) wollen sicher kommunizieren (vgl. Schutzziele) Oskar (O) versucht, die Schutzziele zu durchbrechen Passiver Angri : Abhören
Vorlesung am 21.04.2015 3 Symmetrische Verschlüsselung Alice (A) und Bob (B) wollen sicher kommunizieren (vgl. Schutzziele) Oskar (O) versucht, die Schutzziele zu durchbrechen Passiver Angri : Abhören
Algebra und Diskrete Mathematik, PS3. Sommersemester Prüfungsfragen
 Algebra und Diskrete Mathematik, PS3 Sommersemester 2016 Prüfungsfragen Erläutern Sie die Sätze über die Division mit Rest für ganze Zahlen und für Polynome (mit Koeffizienten in einem Körper). Wodurch
Algebra und Diskrete Mathematik, PS3 Sommersemester 2016 Prüfungsfragen Erläutern Sie die Sätze über die Division mit Rest für ganze Zahlen und für Polynome (mit Koeffizienten in einem Körper). Wodurch
Exponentiation: das Problem Gegeben: (multiplikative) Halbgruppe (H, ), Element a H, n N Aufgabe: berechne das Element
 Problemstellung Banale smethode : das Problem Gegeben: (multiplikative) Halbgruppe (H, ), Element a H, n N Aufgabe: berechne das Element a n = } a a a {{ a } H n (schreiben ab jetzt a n statt a n ) Hinweis:
Problemstellung Banale smethode : das Problem Gegeben: (multiplikative) Halbgruppe (H, ), Element a H, n N Aufgabe: berechne das Element a n = } a a a {{ a } H n (schreiben ab jetzt a n statt a n ) Hinweis:
a 11 a 12 a 1(m 1) a 1m a n1 a n2 a n(m 1) a nm Matrizen Betrachten wir das nachfolgende Rechteckschema:
 Matrizen Betrachten wir das nachfolgende Rechteckschema: a 12 a 1(m 1 a 1m a n1 a n2 a n(m 1 a nm Ein solches Schema nennt man (n m-matrix, da es aus n Zeilen und m Spalten besteht Jeder einzelne Eintrag
Matrizen Betrachten wir das nachfolgende Rechteckschema: a 12 a 1(m 1 a 1m a n1 a n2 a n(m 1 a nm Ein solches Schema nennt man (n m-matrix, da es aus n Zeilen und m Spalten besteht Jeder einzelne Eintrag
ist (oder besser Abspalten von Linearfaktoren beschäftigen. Zu einem beliebigen Körper K betrachten wir die Menge (j,k) N N j+k=n
 8. Polynomringe Das Umgehen mit Polynomen, d.h. mit Ausdrücken der Form a 0 + a 1 x + a 2 x 2 +... + a n x n ist aus der Schule vertraut, falls die Koeffizienten a 0,..., a n ganze oder rationale oder
8. Polynomringe Das Umgehen mit Polynomen, d.h. mit Ausdrücken der Form a 0 + a 1 x + a 2 x 2 +... + a n x n ist aus der Schule vertraut, falls die Koeffizienten a 0,..., a n ganze oder rationale oder
IT-Security. Teil 8b: Rechnen mit beliebiger Genauigkeit Algorithmen
 IT-Security Teil 8b: Rechnen mit beliebiger Genauigkeit Algorithmen 06.06.17 1 Überblick Potenzieren Quadrieren Euklid'scher Algorithmus In den meisten Fällen wird nur mit positiven Werten gerechnet. Bei
IT-Security Teil 8b: Rechnen mit beliebiger Genauigkeit Algorithmen 06.06.17 1 Überblick Potenzieren Quadrieren Euklid'scher Algorithmus In den meisten Fällen wird nur mit positiven Werten gerechnet. Bei
