Der Advanced Encryption Standard (AES)
|
|
|
- Gertrud Schenck
- vor 8 Jahren
- Abrufe
Transkript
1 Der Advanced Encryption Standard (AES) Prof. Dr. Rüdiger Weis TFH Berlin Sommersemester 2008
2 Geschichte des AES Die Struktur des AES Angriffe auf den AES Aktuelle Ergebnisse
3 DerAdvanced Encryption Standard (AES) AES = Advanced Encryption Standard : 128-bit Blockchiffre. 3 Varianten: 128-bit, 192-bit und 256-bit Schlüssel. Ziele: Sicherer als Triple-DES Effizienter als Triple-DES
4 Geschichte des AES, 1. Teil 1997 Ausschreibung des AES AES-Konferenz; Präsentation von 15 Kandidaten. The Demolition Derby begins AES-Konferenz; danach Auswahl der 5 Finalisten.
5 15 Kandidaten Feistel-Netzwerk S.-P. Netzerk Sonstige (wie DES) (erweitert) allgemein Square-artig DEAL DFC Cast-256 SAFER+ Crypton Frog Loki97 E2 MARS Serpent Rijndael HPC Magenta RC6 Twofish Major Attacks : DEAL, Frog, HPC, Loki97, Magenta Finalisten: MARS, RC6, Rijndael, Serpent, Twofish
6 Geschichte des AES 2. Teil April AES-Konferenz, Diskussion der Finalisten Mars, RC6, Rijndael, Twofish und Serpent. Oktober 2000 Rijndael wird ( draft ) Standard. 6 Monate später AES wird endgültig als Standard bestätigt.
7 Die Struktur des AES Vier Basis-Operationen Eine AES-Runde als Kombination der vier Basis-Operationen Der Key Schedule : Aus einem kurzen Chiffrier-Schlüssel (128 bit 256 bit) werden Rundenschlüssel (jeweils 128 bit). Anzahl Rundenschlüssel = 1 + Anzahl Runden
8 Die Basis-Operationen Byte Substitution (BS) Shift Row (SR) S Mix Column (MC) Key Addition (KA)
9 Die Byte Substitution Anwendung einer invertierbaren S-Box S : {0, 1} 8 {0, 1} 8 mit einer sehr einfachen algebraischen Struktur.
10 Algebraische Struktur Man kann z = S(x) in zwei Schritten berechnen: 1. Berechnung des Inversen: Wenn x = 0, dann y := 0. Sonst y = x 1 (in GF(2 8 )). 2. Affine Transformation: z := Ay + b Dabei sind die Matrix A {0, 1} 8 8 und der Vektor b {0, 1} 8 definierte Konstanten; y und z werden (wie b) als Bit-Vektoren aus {0, 1} 8 betrachtet. Sinn dieser speziellen Konstruktion für die S-Box: Optimale Widerstandsfähigkeit gegen differentielle und lineare Kryptanalyse.
11 Die Mix Column Operation y = x { }} { { }} { (y 1, y 2, y 3, y 4 ) := MC (x 1, x 2, x 3, x 4 ) Die Spalten x und y fassen wir als Vektoren auf: x, y GF(2 8 ) 4. Die Mix-Column-Operation ist eine Matrix-Operation über GF(2 8 ): y := A x: y := x.
12 Eigenschaften von Mix Column Invertierbarkeit: Die Matrix A ist invertierbar über GF(2 8 ). Deshalb ist die Mix Column Operation invertierbar. Ausbreitung von Differenzen: Eine Differenz in genau einem der Eingabe-Werte x i führt zu einer Differenz in allen vier Ausgabewerten y 1, y 2, y 3, y 4.
13 Die Rundenstruktur Plaintext Next Round Ciphertext Key Addition Byte Substitution Shift Row Mix Column Key Addition S
14 Der Key Schedule (für 128-bit Schlüssel): Es bez. W [ ] einen 32-bit Wert (= 1 Spalte in der Matrix). Aus dem 128-bit Chiffrierschlüssel W [0],..., W [3] sollen die Rundenschlüssel W [4j + 0],..., W [4j + 3] berechnet werden. If (i mod 4) = 0 then W [i] := W [i 4] f (W [i 1]) const(i) else W [i] := W [i 4] W [i 1] Kennt man i und zwei der Werte W [i 4], W [i 1] und W [i], kann man den dritten leicht berechnen.
15 Angriffe auf den AES Der gegenwärtige Stand der Forschung erlaubt es nicht, für eine (praktikable) Blockchiffre nachzuweisen, dass sie sicher ist. Vertrauen in die Sicherheit einer Chiffre gewinnt man, wenn es trotz intensiver jahrelanger Analyse niemandem gelingt, einen durchschlagenden Angriff zu finden (bzw. zu publizieren). Deshalb: Man berücksichtige die besten bekannten Angriffe und halte möglichst einen Sicherheitsabstand von ihnen ein ( einige Runden mehr ).
16 3 Runden des AES
17 Angriff auf 6 Runden des AES (stammt von den AES-Autoren selbst) Wähle 2 32 Klartexte. Rate 9 Schlüsselbytes (2 72 Einheiten Rechenzeit) 2 8 partielle Verschlüsselungen pro Einheit (jede Einheit entspricht etwa einer AES-Verschlüsselung) Rechenzeit 2 72 Verschlüsselungs-Operationen
18 Verbesserter Angriff (6 Runden) Wähle 2 32 Klartexte. Rate 5 Schlüsselbytes (2 40 Einheiten Rechenzeit, jede entspricht 1 Verschl.) 2 24 Rechenzeit 2 40 Verschlüsselungs-Operationen
19 Erweiterung des Angriffs auf 7 Runden Möglich mit Klartexten (= Codebuch). Rechenzeit entspricht etwa Verschlüsselungsoperationen (nicht mitgerechnet die Zeit zur Erstellung des Code-Buchs). Theoretischer Angriff (für 128-bit Schlüssel), aber besser als Brute Force (Suche über den gesamten Schlüsselraum).
20 Wieviele Runden werden gebraucht? Angriffe, die noch knapp effizienter sind als Brute Force: Chiffre (Schl.-Länge) # Runden definiert Angriff Rijndael/AES (128) 10 7 Rijndael/AES (192) 12 (8) 7 Rijndael/AES (256) 14 9 Twofish ( ) 16 (8) 6 Serpent ( ) 32 (10 11) 9 Stand: Ende Werte in Klammern stellen Verbesserungen gegenüber den dem NIST im Sommer 2000 bekannten Werten dar.
21 Wie relevant sind akademische Angriffe? Die besten Angriffe sind total unpraktikabel (da sie z.b Klartext-Chiffretext-Paare erfordern): Angriffe können nur besser werden. Let us destroy all the useless planets in our solar system, to get room for storage. Andere Sichtweise (Bsp. AES, 128-bit Schlüssel): Angriffe auf 5 Runden sind einfach. Angriffe auf 6 Runden sind vorstellbar (2 32 Paare). Angriffe auf 7 Runden sind bisher nur theoretisch möglich.
22 Darf es etwas mehr sein? Manchen erscheint der Sicherheitsspielraum des AES als zu gering. Einige Vorschläge zur Abhilfe: 1. Variable Anzahl an Runden. 2. Triple AES. 3. Nur die Variante mit 256-bit Schlüsseln einsetzen (14 Runden), kürzere Schlüssel ggf. strecken. 4. Andere Chiffren einsetzen, z.b. Twofish oder Serpent.
23 Risiken und Nebenwirkungen: Variable Anzahl an Runden. Gefährlich! Beispiel: 24 Runden AES und 25 Runden AES unter dem gleichenschlüssel... Triple AES. OK, aber vielleich Overkill. Nur die Variante mit 256-bit Schlüsseln einsetzen... Guter Ansatz, aber Vorsicht: Beim Strecken kann man sich auch in s Knie schiessen! Andere Chiffren einsetzen, z.b. Twofish oder Serpent. Nachteil: Andere Chiffren werden weniger genau untersucht werden wie der AES.
24 Aktuelle Ergebnisse Nutzen meistens die einfache algebraische Struktur der S-Box. Zwei interessante Ergebnisse: AES als geschlossene algebraische Formel Angriff auf den AES durch Lösen eines nichtlinearen Gleichungssystems
25 AES als geschlossene algebraische Formel Es existiert eine einfache geschlossene algebraische Formel für die Blockchiffre Rijndael. Die Größe der Formel hängt nur linear von der Anzahl der Runden ab. (Im Allgemeinen würde man von einer Blockchiffre erwarten, dass jede geschlossene algebraische Formel viel zu groß wäre, um jemals aufgeschrieben werden zu können.)
26 AES als geschlossene algebraische Formel (2) Eine Runde des AES verwendet den Rundenschlüssel k (r) und bildet die 128-bit Eingabe a (r) auf die Ausgabe a (r+1) ab: a (r+1) i,j = k (r) i,j e r =0 d r =0 (Berechnungen im Körper GF(2 8 ).) w i,er,d r ) 2 dr ( a (r) e r,e r +j
27 AES als geschlossene algebraische Formel (3) 2 Runden: a (r+1) i,j = k (r) i,j e r =0 d r =0 w i,er,d r ( k (r 1) i,j w... (a... (r 1) ) 2... ) 2 dr Allgemein: Bei r Runden enthält man eine Art Kettenbruch mit r Bruchstrichen...
28 Zusammenfassung AES: 128-bit Blockchiffe, sehr effizient einige Kritik an geringem Sicherheitsspielraum noch relativ jung, aber in einigen Jahren ebenso gut untersucht wie der DES heute Triple DES wird, trotz AES, noch lange Zeit weiter genutzt werden
29 Danksagungen Danksagungen Aus einer Vorlesung von Stefan Lucks Erstellt mit Freier Software
Stefan Lucks Krypto und Mediensicherheit (2009) 5: Blockchiffren. 5: Blockchiffren. (n bit) (n bit) VERschlüsseln ENTschlüsseln
 5: Blockchiffren Klartexte 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 Chiffretexte (n bit) (n bit) VERschlüsseln ENTschlüsseln 74 5.1: Abstrakte Blockchiffren Familie
5: Blockchiffren Klartexte 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 Chiffretexte (n bit) (n bit) VERschlüsseln ENTschlüsseln 74 5.1: Abstrakte Blockchiffren Familie
4: Blockchiffren. Klartexte (n bit) Chiffretexte. VERschlüsseln. ENTschlüsseln. Stefan Lucks Kryptographie und Mediensicherheit (2017)
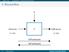 96 4: Blockchiffren 4: Blockchiffren K Klartexte (n bit) E Chiffretexte (n bit) VERschlüsseln ENTschlüsseln 97 4: Blockchiffren 4.1: Abstrakte Blockchiffren 4.1: Abstrakte Blockchiffren Familie von Paaren
96 4: Blockchiffren 4: Blockchiffren K Klartexte (n bit) E Chiffretexte (n bit) VERschlüsseln ENTschlüsseln 97 4: Blockchiffren 4.1: Abstrakte Blockchiffren 4.1: Abstrakte Blockchiffren Familie von Paaren
Sicherer Datenaustausch mit EurOwiG AG
 Sicherer Datenaustausch mit EurOwiG AG Inhalt AxCrypt... 2 Verschlüsselung mit Passwort... 2 Verschlüsseln mit Schlüsseldatei... 2 Entschlüsselung mit Passwort... 4 Entschlüsseln mit Schlüsseldatei...
Sicherer Datenaustausch mit EurOwiG AG Inhalt AxCrypt... 2 Verschlüsselung mit Passwort... 2 Verschlüsseln mit Schlüsseldatei... 2 Entschlüsselung mit Passwort... 4 Entschlüsseln mit Schlüsseldatei...
10. Public-Key Kryptographie
 Stefan Lucks 10. PK-Krypto 274 orlesung Kryptographie (SS06) 10. Public-Key Kryptographie Analyse der Sicherheit von PK Kryptosystemen: Angreifer kennt öffentlichen Schlüssel Chosen Plaintext Angriffe
Stefan Lucks 10. PK-Krypto 274 orlesung Kryptographie (SS06) 10. Public-Key Kryptographie Analyse der Sicherheit von PK Kryptosystemen: Angreifer kennt öffentlichen Schlüssel Chosen Plaintext Angriffe
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Musterlösungen zur Linearen Algebra II Blatt 5
 Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Ein Scan basierter Seitenangriff auf DES
 Ein Scan basierter Seitenangriff auf DES Seminar Codes & Kryptographie SS04 Tobias Witteler 29.06.2004 Struktur des Vortrags 1. Einführung / Motivation 2. Struktur von DES 3. Die Attacke Begriffsklärung:
Ein Scan basierter Seitenangriff auf DES Seminar Codes & Kryptographie SS04 Tobias Witteler 29.06.2004 Struktur des Vortrags 1. Einführung / Motivation 2. Struktur von DES 3. Die Attacke Begriffsklärung:
AES. Jens Kubieziel jens@kubieziel.de. 07. Dezember 2009. Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik
 Angriffe gegen Jens Kubieziel jens@kubieziel.de Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik 07. Dezember 2009 Angriffe gegen Outline 1 Zur Geschichte 2 3 Angriffe gegen
Angriffe gegen Jens Kubieziel jens@kubieziel.de Friedrich-Schiller-Universität Jena Fakultät für Mathem atik und Informatik 07. Dezember 2009 Angriffe gegen Outline 1 Zur Geschichte 2 3 Angriffe gegen
Die Post hat eine Umfrage gemacht
 Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
2. Negative Dualzahlen darstellen
 2.1 Subtraktion von Dualzahlen 2.1.1 Direkte Subtraktion (Tafelrechnung) siehe ARCOR T0IF Nachteil dieser Methode: Diese Form der Subtraktion kann nur sehr schwer von einer Elektronik (CPU) durchgeführt
2.1 Subtraktion von Dualzahlen 2.1.1 Direkte Subtraktion (Tafelrechnung) siehe ARCOR T0IF Nachteil dieser Methode: Diese Form der Subtraktion kann nur sehr schwer von einer Elektronik (CPU) durchgeführt
Wir machen neue Politik für Baden-Württemberg
 Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Kapitel 3: Etwas Informationstheorie
 Stefan Lucks 3: Informationstheorie 28 orlesung Kryptographie (SS06) Kapitel 3: Etwas Informationstheorie Komplexitätstheoretische Sicherheit: Der schnellste Algorithmus, K zu knacken erfordert mindestens
Stefan Lucks 3: Informationstheorie 28 orlesung Kryptographie (SS06) Kapitel 3: Etwas Informationstheorie Komplexitätstheoretische Sicherheit: Der schnellste Algorithmus, K zu knacken erfordert mindestens
Lineare Gleichungssysteme I (Matrixgleichungen)
 Lineare Gleichungssysteme I (Matrigleichungen) Eine lineare Gleichung mit einer Variable hat bei Zahlen a, b, die Form a b. Falls hierbei der Kehrwert von a gebildet werden darf (a 0), kann eindeutig aufgelöst
Lineare Gleichungssysteme I (Matrigleichungen) Eine lineare Gleichung mit einer Variable hat bei Zahlen a, b, die Form a b. Falls hierbei der Kehrwert von a gebildet werden darf (a 0), kann eindeutig aufgelöst
Verschlüsselung. Kirchstraße 18 Steinfelderstraße 53 76831 Birkweiler 76887 Bad Bergzabern. 12.10.2011 Fabian Simon Bfit09
 Verschlüsselung Fabian Simon BBS Südliche Weinstraße Kirchstraße 18 Steinfelderstraße 53 76831 Birkweiler 76887 Bad Bergzabern 12.10.2011 Fabian Simon Bfit09 Inhaltsverzeichnis 1 Warum verschlüsselt man?...3
Verschlüsselung Fabian Simon BBS Südliche Weinstraße Kirchstraße 18 Steinfelderstraße 53 76831 Birkweiler 76887 Bad Bergzabern 12.10.2011 Fabian Simon Bfit09 Inhaltsverzeichnis 1 Warum verschlüsselt man?...3
So gehts Schritt-für-Schritt-Anleitung
 So gehts Schritt-für-Schritt-Anleitung Software WISO Mein Büro Thema Eigene Auswertungen, Tabellenauswertungen Version/Datum V 13.00.05.101 Über die Tabellen-Auswertungen ist es möglich eigene Auswertungen
So gehts Schritt-für-Schritt-Anleitung Software WISO Mein Büro Thema Eigene Auswertungen, Tabellenauswertungen Version/Datum V 13.00.05.101 Über die Tabellen-Auswertungen ist es möglich eigene Auswertungen
6.2 Scan-Konvertierung (Scan Conversion)
 6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
Data Encryption Standard
 Sommersemester 2008 1 Blockchiffren 2 Der DES 3 Differentielle Kryptanalyse 4 Lineare Kryptanalyse 5 Triple DES Blockchiffren Klartext Arbeits richtung Schlüssel Chiffretext Wichtige Parameter: Blockgröße,
Sommersemester 2008 1 Blockchiffren 2 Der DES 3 Differentielle Kryptanalyse 4 Lineare Kryptanalyse 5 Triple DES Blockchiffren Klartext Arbeits richtung Schlüssel Chiffretext Wichtige Parameter: Blockgröße,
Digitale Unterschriften Grundlagen der digitalen Unterschriften Hash-Then-Sign Unterschriften Public-Key Infrastrukturen (PKI) Digitale Signaturen
 Sommersemester 2008 Digitale Unterschriften Unterschrift von Hand : Physikalische Verbindung mit dem unterschriebenen Dokument (beides steht auf dem gleichen Blatt). Fälschen erfordert einiges Geschick
Sommersemester 2008 Digitale Unterschriften Unterschrift von Hand : Physikalische Verbindung mit dem unterschriebenen Dokument (beides steht auf dem gleichen Blatt). Fälschen erfordert einiges Geschick
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
 9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
Digitale Magazine ohne eigenen Speicher
 Stefan Lucks Digitale Magazine ohne eigenen Speicher 1 Digitale Magazine ohne eigenen Speicher Wie man die Integrität fremdgespeicherter Archivalien sicherstellen kann Stefan Lucks Professur für Mediensicherheit
Stefan Lucks Digitale Magazine ohne eigenen Speicher 1 Digitale Magazine ohne eigenen Speicher Wie man die Integrität fremdgespeicherter Archivalien sicherstellen kann Stefan Lucks Professur für Mediensicherheit
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Erweiterung der Aufgabe. Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen:
 VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
Einrichtung des Cisco VPN Clients (IPSEC) in Windows7
 Einrichtung des Cisco VPN Clients (IPSEC) in Windows7 Diese Verbindung muss einmalig eingerichtet werden und wird benötigt, um den Zugriff vom privaten Rechner oder der Workstation im Home Office über
Einrichtung des Cisco VPN Clients (IPSEC) in Windows7 Diese Verbindung muss einmalig eingerichtet werden und wird benötigt, um den Zugriff vom privaten Rechner oder der Workstation im Home Office über
Excel Funktionen durch eigene Funktionen erweitern.
 Excel Funktionen durch eigene Funktionen erweitern. Excel bietet eine große Anzahl an Funktionen für viele Anwendungsbereiche an. Doch es kommt hin und wieder vor, dass man die eine oder andere Funktion
Excel Funktionen durch eigene Funktionen erweitern. Excel bietet eine große Anzahl an Funktionen für viele Anwendungsbereiche an. Doch es kommt hin und wieder vor, dass man die eine oder andere Funktion
11. Das RSA Verfahren und andere Verfahren
 Chr.Nelius: Kryptographie (SS 2011) 31 11. Das RSA Verfahren und andere Verfahren Eine konkrete Realisierung eines Public Key Kryptosystems ist das sog. RSA Verfahren, das im Jahre 1978 von den drei Wissenschaftlern
Chr.Nelius: Kryptographie (SS 2011) 31 11. Das RSA Verfahren und andere Verfahren Eine konkrete Realisierung eines Public Key Kryptosystems ist das sog. RSA Verfahren, das im Jahre 1978 von den drei Wissenschaftlern
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer
 Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Was bisher geschah Kryptographische Systeme (M, C, K, e, d) Verfahren: symmetrisch klassisch: Verschiebechiffren (Spezialfall Caesar-Code)
 Was bisher geschah Kryptographische Systeme (M, C, K, e, d) Verfahren: symmetrisch klassisch: Verschiebechiffren (Spezialfall Caesar-Code) Multiplikative Chiffren monoalphabetische Substitutions-Chiffren:
Was bisher geschah Kryptographische Systeme (M, C, K, e, d) Verfahren: symmetrisch klassisch: Verschiebechiffren (Spezialfall Caesar-Code) Multiplikative Chiffren monoalphabetische Substitutions-Chiffren:
Informatik für Ökonomen II HS 09
 Informatik für Ökonomen II HS 09 Übung 5 Ausgabe: 03. Dezember 2009 Abgabe: 10. Dezember 2009 Die Lösungen zu den Aufgabe sind direkt auf das Blatt zu schreiben. Bitte verwenden Sie keinen Bleistift und
Informatik für Ökonomen II HS 09 Übung 5 Ausgabe: 03. Dezember 2009 Abgabe: 10. Dezember 2009 Die Lösungen zu den Aufgabe sind direkt auf das Blatt zu schreiben. Bitte verwenden Sie keinen Bleistift und
Leitfaden zur ersten Nutzung der R FOM Portable-Version für Windows (Version 1.0)
 Leitfaden zur ersten Nutzung der R FOM Portable-Version für Windows (Version 1.0) Peter Koos 03. Dezember 2015 0 Inhaltsverzeichnis 1 Voraussetzung... 3 2 Hintergrundinformationen... 3 2.1 Installationsarten...
Leitfaden zur ersten Nutzung der R FOM Portable-Version für Windows (Version 1.0) Peter Koos 03. Dezember 2015 0 Inhaltsverzeichnis 1 Voraussetzung... 3 2 Hintergrundinformationen... 3 2.1 Installationsarten...
11.3 Komplexe Potenzreihen und weitere komplexe Funktionen
 .3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
.3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
1 Kryptosysteme 1 KRYPTOSYSTEME. Definition 1.1 Eine Kryptosystem (P(A), C(B), K, E, D) besteht aus
 1 RYPTOSYSTEME 1 ryptosysteme Definition 1.1 Eine ryptosystem (P(A), C(B),, E, D) besteht aus einer Menge P von lartexten (plaintext) über einem lartextalphabet A, einer Menge C von Geheimtexten (ciphertext)
1 RYPTOSYSTEME 1 ryptosysteme Definition 1.1 Eine ryptosystem (P(A), C(B),, E, D) besteht aus einer Menge P von lartexten (plaintext) über einem lartextalphabet A, einer Menge C von Geheimtexten (ciphertext)
Was heißt Kryptographie I? Understanding Cryptography Christof Paar und Jan Pelzl
 Was heißt Kryptographie I? Understanding Cryptography Christof Paar und Jan Pelzl Die Autoren Dr.-Ing. Jan Pelzl Prof. Dr.-Ing. Christof Paar Gliederung Historischer Überblick Begrifflichkeiten Symmetrische
Was heißt Kryptographie I? Understanding Cryptography Christof Paar und Jan Pelzl Die Autoren Dr.-Ing. Jan Pelzl Prof. Dr.-Ing. Christof Paar Gliederung Historischer Überblick Begrifflichkeiten Symmetrische
Klassenarbeit zu linearen Gleichungssystemen
 Klassenarbeit zu linearen Gleichungssystemen Aufgabe : Bestimme die Lösungsmenge der Gleichungssysteme mit Hilfe des Additionsverfahrens: x + 4y = 8 5x y = x y = x y = Aufgabe : Bestimme die Lösungsmenge
Klassenarbeit zu linearen Gleichungssystemen Aufgabe : Bestimme die Lösungsmenge der Gleichungssysteme mit Hilfe des Additionsverfahrens: x + 4y = 8 5x y = x y = x y = Aufgabe : Bestimme die Lösungsmenge
Summenbildung in Bauteiltabellen mit If Then Abfrage
 Summenbildung in Bauteiltabellen mit If Then Abfrage Die in Bauteiltabellen ausgelesenen Werte lassen sich in jeder Spalte als Summe berechnen. So können selbstverständlich die Flächen der in der Tabelle
Summenbildung in Bauteiltabellen mit If Then Abfrage Die in Bauteiltabellen ausgelesenen Werte lassen sich in jeder Spalte als Summe berechnen. So können selbstverständlich die Flächen der in der Tabelle
Serienbrieferstellung in Word mit Kunden-Datenimport aus Excel
 Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus:
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: If-clauses - conditional sentences - Nie mehr Probleme mit Satzbau im Englischen! Das komplette Material finden Sie hier: School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: If-clauses - conditional sentences - Nie mehr Probleme mit Satzbau im Englischen! Das komplette Material finden Sie hier: School-Scout.de
Betriebsarten für Blockchiffren
 Betriebsarten für Blockchiffren Prof. Dr. Rüdiger Weis TFH Berlin Sommersemester 2008 Betriebsarten für Blockchiffren Was ist eine Betriebsart (engl. Mode of Operation )? Blockchiffre wird genutzt, um
Betriebsarten für Blockchiffren Prof. Dr. Rüdiger Weis TFH Berlin Sommersemester 2008 Betriebsarten für Blockchiffren Was ist eine Betriebsart (engl. Mode of Operation )? Blockchiffre wird genutzt, um
Print2CAD 2017, 8th Generation. Netzwerkversionen
 Installation der Netzwerkversion Kazmierczak Software Print2CAD 2017, 8th Generation Print2CAD 2017, 8th Generation Netzwerkversionen Einführung Installationshinweise Die Programme von Kazmierczak Software
Installation der Netzwerkversion Kazmierczak Software Print2CAD 2017, 8th Generation Print2CAD 2017, 8th Generation Netzwerkversionen Einführung Installationshinweise Die Programme von Kazmierczak Software
Informationssicherheit - Lösung Blatt 2
 Informationssicherheit - Lösung Blatt 2 Adam Glodek adam.glodek@gmail.com 13.04.2010 1 1 Aufgabe 1: One Time Pad 1.1 Aufgabenstellung Gegeben ist der folgende Klartext 12Uhr (ASCII). Verschlüsseln Sie
Informationssicherheit - Lösung Blatt 2 Adam Glodek adam.glodek@gmail.com 13.04.2010 1 1 Aufgabe 1: One Time Pad 1.1 Aufgabenstellung Gegeben ist der folgende Klartext 12Uhr (ASCII). Verschlüsseln Sie
ALEMÃO. Text 1. Lernen, lernen, lernen
 ALEMÃO Text 1 Lernen, lernen, lernen Der Mai ist für viele deutsche Jugendliche keine schöne Zeit. Denn dann müssen sie in vielen Bundesländern die Abiturprüfungen schreiben. Das heiβt: lernen, lernen,
ALEMÃO Text 1 Lernen, lernen, lernen Der Mai ist für viele deutsche Jugendliche keine schöne Zeit. Denn dann müssen sie in vielen Bundesländern die Abiturprüfungen schreiben. Das heiβt: lernen, lernen,
Erklärung zu den Internet-Seiten von www.bmas.de
 Erklärung zu den Internet-Seiten von www.bmas.de Herzlich willkommen! Sie sind auf der Internet-Seite vom Bundes-Ministerium für Arbeit und Soziales. Die Abkürzung ist: BMAS. Darum heißt die Seite auch
Erklärung zu den Internet-Seiten von www.bmas.de Herzlich willkommen! Sie sind auf der Internet-Seite vom Bundes-Ministerium für Arbeit und Soziales. Die Abkürzung ist: BMAS. Darum heißt die Seite auch
Mediumwechsel - VR-NetWorld Software
 Mediumwechsel - VR-NetWorld Software Die personalisierte VR-NetWorld-Card wird mit einem festen Laufzeitende ausgeliefert. Am Ende der Laufzeit müssen Sie die bestehende VR-NetWorld-Card gegen eine neue
Mediumwechsel - VR-NetWorld Software Die personalisierte VR-NetWorld-Card wird mit einem festen Laufzeitende ausgeliefert. Am Ende der Laufzeit müssen Sie die bestehende VR-NetWorld-Card gegen eine neue
Asymmetrische. Verschlüsselungsverfahren. erarbeitet von: Emilia Winkler Christian-Weise-Gymnasium Zittau
 Asymmetrische Verschlü erarbeitet von: Emilia Winkler Christian-Weise-Gymnasium Zittau Gliederung 1) Prinzip der asymmetrischen Verschlü 2) Vergleich mit den symmetrischen Verschlü (Vor- und Nachteile)
Asymmetrische Verschlü erarbeitet von: Emilia Winkler Christian-Weise-Gymnasium Zittau Gliederung 1) Prinzip der asymmetrischen Verschlü 2) Vergleich mit den symmetrischen Verschlü (Vor- und Nachteile)
Was ist Sozial-Raum-Orientierung?
 Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Kryptografische Algorithmen
 Kryptografische Algorithmen Lerneinheit 5: Weitere symmetrische Kryptosysteme Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2015/2016 21.9.2015 Einleitung Einleitung Diese
Kryptografische Algorithmen Lerneinheit 5: Weitere symmetrische Kryptosysteme Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2015/2016 21.9.2015 Einleitung Einleitung Diese
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
EDV-Fortbildung Kombi-Schulung Word-Excel 2010. Modul Excel. Informationen zum Programm. Die Programmoberfläche von Excel
 EDV-Fortbildung Kombi-Schulung Word-Excel 2010 Modul Excel Informationen zum Programm Microsoft Excel ist das meistverbreitete Programm zur Tabellenkalkulation. Excel bietet sich für umfangreiche, aber
EDV-Fortbildung Kombi-Schulung Word-Excel 2010 Modul Excel Informationen zum Programm Microsoft Excel ist das meistverbreitete Programm zur Tabellenkalkulation. Excel bietet sich für umfangreiche, aber
Die Invaliden-Versicherung ändert sich
 Die Invaliden-Versicherung ändert sich 1 Erklärung Die Invaliden-Versicherung ist für invalide Personen. Invalid bedeutet: Eine Person kann einige Sachen nicht machen. Wegen einer Krankheit. Wegen einem
Die Invaliden-Versicherung ändert sich 1 Erklärung Die Invaliden-Versicherung ist für invalide Personen. Invalid bedeutet: Eine Person kann einige Sachen nicht machen. Wegen einer Krankheit. Wegen einem
Mikroökonomik 9. Vorlesungswoche
 Mikroökonomik 9. Vorlesungswoche Tone Arnold Universität des Saarlandes 18. Dezember 2007 Tone Arnold (Universität des Saarlandes) 9. Vorlesungswoche 18. Dezember 2007 1 / 31 Volkswirtschaftliche Rente
Mikroökonomik 9. Vorlesungswoche Tone Arnold Universität des Saarlandes 18. Dezember 2007 Tone Arnold (Universität des Saarlandes) 9. Vorlesungswoche 18. Dezember 2007 1 / 31 Volkswirtschaftliche Rente
Installation des Add-Ins für Lineare Algebra in Microsoft Excel
 Installation des Add-Ins für Lineare Algebra in Microsoft Excel Matrix 2.2 by The Foxes Team http://digilander.libero.it/foxes/ Download der Matrix 2.2 Im Browser die Seite http://digilander.libero.it/foxes/download.htm
Installation des Add-Ins für Lineare Algebra in Microsoft Excel Matrix 2.2 by The Foxes Team http://digilander.libero.it/foxes/ Download der Matrix 2.2 Im Browser die Seite http://digilander.libero.it/foxes/download.htm
12 Kryptologie. ... immer wichtiger. Militär (Geheimhaltung) Telebanking, Elektronisches Geld E-Commerce WWW...
 12 Kryptologie... immer wichtiger Militär (Geheimhaltung) Telebanking, Elektronisches Geld E-Commerce WWW... Kryptologie = Kryptographie + Kryptoanalyse 12.1 Grundlagen 12-2 es gibt keine einfachen Verfahren,
12 Kryptologie... immer wichtiger Militär (Geheimhaltung) Telebanking, Elektronisches Geld E-Commerce WWW... Kryptologie = Kryptographie + Kryptoanalyse 12.1 Grundlagen 12-2 es gibt keine einfachen Verfahren,
ESecuremail Die einfache Email verschlüsselung
 Wie Sie derzeit den Medien entnehmen können, erfassen und speichern die Geheimdienste aller Länder Emails ab, egal ob Sie verdächtig sind oder nicht. Die Inhalte von EMails werden dabei an Knotenpunkten
Wie Sie derzeit den Medien entnehmen können, erfassen und speichern die Geheimdienste aller Länder Emails ab, egal ob Sie verdächtig sind oder nicht. Die Inhalte von EMails werden dabei an Knotenpunkten
Erfahrungen mit Hartz IV- Empfängern
 Erfahrungen mit Hartz IV- Empfängern Ausgewählte Ergebnisse einer Befragung von Unternehmen aus den Branchen Gastronomie, Pflege und Handwerk Pressegespräch der Bundesagentur für Arbeit am 12. November
Erfahrungen mit Hartz IV- Empfängern Ausgewählte Ergebnisse einer Befragung von Unternehmen aus den Branchen Gastronomie, Pflege und Handwerk Pressegespräch der Bundesagentur für Arbeit am 12. November
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009)
 Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009) Probleme unseres Alltags E-Mails lesen: Niemand außer mir soll meine Mails lesen! Geld abheben mit der EC-Karte: Niemand außer mir soll
Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009) Probleme unseres Alltags E-Mails lesen: Niemand außer mir soll meine Mails lesen! Geld abheben mit der EC-Karte: Niemand außer mir soll
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Info zum Zusammenhang von Auflösung und Genauigkeit
 Da es oft Nachfragen und Verständnisprobleme mit den oben genannten Begriffen gibt, möchten wir hier versuchen etwas Licht ins Dunkel zu bringen. Nehmen wir mal an, Sie haben ein Stück Wasserrohr mit der
Da es oft Nachfragen und Verständnisprobleme mit den oben genannten Begriffen gibt, möchten wir hier versuchen etwas Licht ins Dunkel zu bringen. Nehmen wir mal an, Sie haben ein Stück Wasserrohr mit der
Diese Anleitung enthält Anweisungen, die nur durch erfahrene Anwender durchgeführt werden sollten!
 Anmeldung über SSH Diese Anleitung enthält Anweisungen, die nur durch erfahrene Anwender durchgeführt werden sollten! Besitzer der Homepage Advanced und Homepage Professional haben die Möglichkeit, direkt
Anmeldung über SSH Diese Anleitung enthält Anweisungen, die nur durch erfahrene Anwender durchgeführt werden sollten! Besitzer der Homepage Advanced und Homepage Professional haben die Möglichkeit, direkt
1. Einführung. 2. Alternativen zu eigenen Auswertungen. 3. Erstellen eigener Tabellen-Auswertungen
 1. Einführung Über die Tabellen-Auswertungen können Sie eigene Auswertungen nach Ihren Wünschen erstellen. Diese Auswertungen werden immer anhand der aktuellen Daten aus orgamax ermittelt, Sie können also
1. Einführung Über die Tabellen-Auswertungen können Sie eigene Auswertungen nach Ihren Wünschen erstellen. Diese Auswertungen werden immer anhand der aktuellen Daten aus orgamax ermittelt, Sie können also
Planen mit mathematischen Modellen 00844: Computergestützte Optimierung. Autor: Dr. Heinz Peter Reidmacher
 Planen mit mathematischen Modellen 00844: Computergestützte Optimierung Leseprobe Autor: Dr. Heinz Peter Reidmacher 11 - Portefeuilleanalyse 61 11 Portefeuilleanalyse 11.1 Das Markowitz Modell Die Portefeuilleanalyse
Planen mit mathematischen Modellen 00844: Computergestützte Optimierung Leseprobe Autor: Dr. Heinz Peter Reidmacher 11 - Portefeuilleanalyse 61 11 Portefeuilleanalyse 11.1 Das Markowitz Modell Die Portefeuilleanalyse
Diese Unterlage bezieht sich auf Excel 2010 (auf Deutsch). Die Benutzeroberfläche kann in anderen Versionen der Software erheblich anders aussehen.
 Vorbemerkung Diese Unterlage bezieht sich auf Excel 2010 (auf Deutsch). Die Benutzeroberfläche kann in anderen Versionen der Software erheblich anders aussehen. Einiges, das bei der Bearbeitung der Übung
Vorbemerkung Diese Unterlage bezieht sich auf Excel 2010 (auf Deutsch). Die Benutzeroberfläche kann in anderen Versionen der Software erheblich anders aussehen. Einiges, das bei der Bearbeitung der Übung
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Blumen-bienen-Bären Academy. Kurzanleitung für Google Keyword Planer + Google Trends
 Kurzanleitung für Google Keyword Planer + Google Trends Der Google Keyword Planer Mit dem Keyword Planer kann man sehen, wieviele Leute, in welchen Regionen und Orten nach welchen Begriffen bei Google
Kurzanleitung für Google Keyword Planer + Google Trends Der Google Keyword Planer Mit dem Keyword Planer kann man sehen, wieviele Leute, in welchen Regionen und Orten nach welchen Begriffen bei Google
Windows XP Jugendschutz einrichten. Monika Pross Molberger PC-Kurse
 Windows XP Jugendschutz einrichten Monika Pross Molberger PC-Kurse Um ein Benutzerkonto mit Jugendschutzeinstellungen zu verwenden, braucht man ein Eltern- Konto (Administrator) und eine Kinderkonto (Standard).
Windows XP Jugendschutz einrichten Monika Pross Molberger PC-Kurse Um ein Benutzerkonto mit Jugendschutzeinstellungen zu verwenden, braucht man ein Eltern- Konto (Administrator) und eine Kinderkonto (Standard).
Wie Google Webseiten bewertet. François Bry
 Wie Google Webseiten bewertet François Bry Heu6ge Vorlesung 1. Einleitung 2. Graphen und Matrizen 3. Erste Idee: Ranking als Eigenvektor 4. Fragen: Exisi6ert der Eigenvektor? Usw. 5. Zweite Idee: Die Google
Wie Google Webseiten bewertet François Bry Heu6ge Vorlesung 1. Einleitung 2. Graphen und Matrizen 3. Erste Idee: Ranking als Eigenvektor 4. Fragen: Exisi6ert der Eigenvektor? Usw. 5. Zweite Idee: Die Google
Die neue Aufgabe von der Monitoring-Stelle. Das ist die Monitoring-Stelle:
 Die neue Aufgabe von der Monitoring-Stelle Das ist die Monitoring-Stelle: Am Deutschen Institut für Menschen-Rechte in Berlin gibt es ein besonderes Büro. Dieses Büro heißt Monitoring-Stelle. Mo-ni-to-ring
Die neue Aufgabe von der Monitoring-Stelle Das ist die Monitoring-Stelle: Am Deutschen Institut für Menschen-Rechte in Berlin gibt es ein besonderes Büro. Dieses Büro heißt Monitoring-Stelle. Mo-ni-to-ring
8: Zufallsorakel. Wir suchen: Einfache mathematische Abstraktion für Hashfunktionen
 Stefan Lucks 8: Zufallsorakel 139 Kryptogr. Hashfunkt. (WS 08/09) 8: Zufallsorakel Unser Problem: Exakte Eigenschaften von effizienten Hashfunktionen nur schwer erfassbar (z.b. MD5, Tiger, RipeMD, SHA-1,...)
Stefan Lucks 8: Zufallsorakel 139 Kryptogr. Hashfunkt. (WS 08/09) 8: Zufallsorakel Unser Problem: Exakte Eigenschaften von effizienten Hashfunktionen nur schwer erfassbar (z.b. MD5, Tiger, RipeMD, SHA-1,...)
Tipp III: Leiten Sie eine immer direkt anwendbare Formel her zur Berechnung der sogenannten "bedingten Wahrscheinlichkeit".
 Mathematik- Unterrichts- Einheiten- Datei e. V. Klasse 9 12 04/2015 Diabetes-Test Infos: www.mued.de Blutspenden werden auf Diabetes untersucht, das mit 8 % in der Bevölkerung verbreitet ist. Dabei werden
Mathematik- Unterrichts- Einheiten- Datei e. V. Klasse 9 12 04/2015 Diabetes-Test Infos: www.mued.de Blutspenden werden auf Diabetes untersucht, das mit 8 % in der Bevölkerung verbreitet ist. Dabei werden
(λ Ri I A+BR)v Ri = 0. Lässt sich umstellen zu
 Herleitung der oppenecker-formel (Wiederholung) Für ein System ẋ Ax + Bu (B habe Höchstrang) wird eine Zustandsregelung u x angesetzt. Der geschlossene egelkreis gehorcht der Zustands-Dgl. ẋ (A B)x. Die
Herleitung der oppenecker-formel (Wiederholung) Für ein System ẋ Ax + Bu (B habe Höchstrang) wird eine Zustandsregelung u x angesetzt. Der geschlossene egelkreis gehorcht der Zustands-Dgl. ẋ (A B)x. Die
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen?
 Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Kryptographische Verfahren auf Basis des Diskreten Logarithmus
 Kryptographische Verfahren auf Basis des Diskreten Logarithmus -Vorlesung Public-Key-Kryptographie SS2010- Sascha Grau ITI, TU Ilmenau, Germany Seite 1 / 18 Unser Fahrplan heute 1 Der Diskrete Logarithmus
Kryptographische Verfahren auf Basis des Diskreten Logarithmus -Vorlesung Public-Key-Kryptographie SS2010- Sascha Grau ITI, TU Ilmenau, Germany Seite 1 / 18 Unser Fahrplan heute 1 Der Diskrete Logarithmus
10. Kryptographie. Was ist Kryptographie?
 Chr.Nelius: Zahlentheorie (SoSe 2015) 39 10. Kryptographie Was ist Kryptographie? Die Kryptographie handelt von der Verschlüsselung (Chiffrierung) von Nachrichten zum Zwecke der Geheimhaltung und von dem
Chr.Nelius: Zahlentheorie (SoSe 2015) 39 10. Kryptographie Was ist Kryptographie? Die Kryptographie handelt von der Verschlüsselung (Chiffrierung) von Nachrichten zum Zwecke der Geheimhaltung und von dem
Bearbeiten elektronische Rechnungen (Invoices)
 Bearbeiten elektronische Rechnungen (Invoices) 1. Zweck des Programms: Die elektronischen Rechnungen können zur Zeit für folgenden Bereiche genutzt werden:.. Anzeige der Rechnungen mit den relevanten Werten..
Bearbeiten elektronische Rechnungen (Invoices) 1. Zweck des Programms: Die elektronischen Rechnungen können zur Zeit für folgenden Bereiche genutzt werden:.. Anzeige der Rechnungen mit den relevanten Werten..
Hilfe zur Urlaubsplanung und Zeiterfassung
 Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Anleitung zum Computercheck Windows Firewall aktivieren oder eine kostenlose Firewall installieren
 Anleitung zum Computercheck Windows Firewall aktivieren oder eine kostenlose Firewall installieren Ziel der Anleitung Sie möchten ein modernes Firewallprogramm für Ihren Computer installieren, um gegen
Anleitung zum Computercheck Windows Firewall aktivieren oder eine kostenlose Firewall installieren Ziel der Anleitung Sie möchten ein modernes Firewallprogramm für Ihren Computer installieren, um gegen
Gratis Excel SVERWEIS Funktions-Anleitung, Tutorial, ebook, PDF-E-Book
 Gratis Excel SVERWEIS Funktions-Anleitung, Tutorial, ebook, PDF-E-Book Wir wollen wissen wieviel Umsatz Vertreter Müller im Juni gemacht hat? Dazu klicken wir irgendwo in ein Feld und geben ein: =SVERWEIS
Gratis Excel SVERWEIS Funktions-Anleitung, Tutorial, ebook, PDF-E-Book Wir wollen wissen wieviel Umsatz Vertreter Müller im Juni gemacht hat? Dazu klicken wir irgendwo in ein Feld und geben ein: =SVERWEIS
Nachrichten- Verschlüsselung Mit S/MIME
 Nachrichten- Verschlüsselung Mit S/MIME Höma, watt is S/MIME?! S/MIME ist eine Methode zum signieren und verschlüsseln von Nachrichten, ähnlich wie das in der Öffentlichkeit vielleicht bekanntere PGP oder
Nachrichten- Verschlüsselung Mit S/MIME Höma, watt is S/MIME?! S/MIME ist eine Methode zum signieren und verschlüsseln von Nachrichten, ähnlich wie das in der Öffentlichkeit vielleicht bekanntere PGP oder
2. Einrichtung der ODBC-Schnittstelle aus orgamax (für 32-bit-Anwendungen)
 1. Einführung: Über den ODBC-Zugriff können Sie bestimmte Daten aus Ihren orgamax-mandanten in anderen Anwendungen (beispielsweise Microsoft Excel oder Microsoft Access) einlesen. Dies bietet sich beispielsweise
1. Einführung: Über den ODBC-Zugriff können Sie bestimmte Daten aus Ihren orgamax-mandanten in anderen Anwendungen (beispielsweise Microsoft Excel oder Microsoft Access) einlesen. Dies bietet sich beispielsweise
Die integrierte Zeiterfassung. Das innovative Softwarekonzept
 Die integrierte Zeiterfassung Das innovative Softwarekonzept projekt - ein komplexes Programm mit Zusatzmodulen, die einzeln oder in ihrer individuellen Zusammenstellung, die gesamte Abwicklung in Ihrem
Die integrierte Zeiterfassung Das innovative Softwarekonzept projekt - ein komplexes Programm mit Zusatzmodulen, die einzeln oder in ihrer individuellen Zusammenstellung, die gesamte Abwicklung in Ihrem
Schritt für Schritt zur Krankenstandsstatistik
 Schritt für Schritt zur Krankenstandsstatistik Eine Anleitung zur Nutzung der Excel-Tabellen zur Erhebung des Krankenstands. Entwickelt durch: Kooperationsprojekt Arbeitsschutz in der ambulanten Pflege
Schritt für Schritt zur Krankenstandsstatistik Eine Anleitung zur Nutzung der Excel-Tabellen zur Erhebung des Krankenstands. Entwickelt durch: Kooperationsprojekt Arbeitsschutz in der ambulanten Pflege
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
6.2 Perfekte Sicherheit
 04 6.2 Perfekte Sicherheit Beweis. H(B AC) + H(A C) = H(ABC) H(AC) + H(AC) H(C) Wegen gilt Einsetzen in die Definition gibt = H(AB C). H(A BC) = H(AB C) H(B C). I(A; B C) = H(A C) H(AB C) + H(B C). Da
04 6.2 Perfekte Sicherheit Beweis. H(B AC) + H(A C) = H(ABC) H(AC) + H(AC) H(C) Wegen gilt Einsetzen in die Definition gibt = H(AB C). H(A BC) = H(AB C) H(B C). I(A; B C) = H(A C) H(AB C) + H(B C). Da
Netzwerkversion PVG.view
 Netzwerkversion PVG.view Installationshinweise Einführung Die Programm PVG.view kann zur Netzwerkversion erweitert werden. Die Erweiterung ermöglicht, bestehende oder neu erworbene Programmlizenzen im
Netzwerkversion PVG.view Installationshinweise Einführung Die Programm PVG.view kann zur Netzwerkversion erweitert werden. Die Erweiterung ermöglicht, bestehende oder neu erworbene Programmlizenzen im
SFirm32 Umstellung FTAM EBICS
 SFirm32 Umstellung FTAM EBICS Für die Umstellung des Übertragungsverfahrens FTAM auf EBICS sind folgende Voraussetzungen erforderlich: + Gültige FTAM-Freischaltung bei der Naspa ist vorhanden + Elektronische
SFirm32 Umstellung FTAM EBICS Für die Umstellung des Übertragungsverfahrens FTAM auf EBICS sind folgende Voraussetzungen erforderlich: + Gültige FTAM-Freischaltung bei der Naspa ist vorhanden + Elektronische
ESecure Vault Die verschlüsselte CloudFESTplatte
 Sie möchten von überall aus auf Ihre Daten zugreifen, aber niemand anderes soll Ihre Daten einsehen können? Mit dem Secure Vault von Evolution Hosting stellen wir Ihnen ein sicheres System vor. Sie müssen
Sie möchten von überall aus auf Ihre Daten zugreifen, aber niemand anderes soll Ihre Daten einsehen können? Mit dem Secure Vault von Evolution Hosting stellen wir Ihnen ein sicheres System vor. Sie müssen
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen
 Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Kevin Caldwell. 18.April 2012
 im Rahmen des Proseminars Numerische Lineare Algebra von Prof.Dr.Sven Beuchler 18.April 2012 Gliederung 1 2 3 Mathematische Beschreibung von naturwissenschaftlich-technischen Problemstellungen führt häufig
im Rahmen des Proseminars Numerische Lineare Algebra von Prof.Dr.Sven Beuchler 18.April 2012 Gliederung 1 2 3 Mathematische Beschreibung von naturwissenschaftlich-technischen Problemstellungen führt häufig
GRS SIGNUM Product-Lifecycle-Management
 GRS SIGNUM Product-Lifecycle-Management Das optionale Modul Product-Lifecycle-Management stellt eine mächtige Ergänzung zum Modul Forschung & Entwicklung dar. Folgende Punkte werden dabei abgedeckt: Definition
GRS SIGNUM Product-Lifecycle-Management Das optionale Modul Product-Lifecycle-Management stellt eine mächtige Ergänzung zum Modul Forschung & Entwicklung dar. Folgende Punkte werden dabei abgedeckt: Definition
Die Subnetzmaske/Netzwerkmaske
 Die Subnetzmaske/Netzwerkmaske Die Subnetzmaske (auch Netzwerkmaske genannt) ist eine mehrstellige Binärzahl (Bitmaske), die in einem Netzwerk eine IP-Adresse in eine Netzadresse und eine Geräteadresse
Die Subnetzmaske/Netzwerkmaske Die Subnetzmaske (auch Netzwerkmaske genannt) ist eine mehrstellige Binärzahl (Bitmaske), die in einem Netzwerk eine IP-Adresse in eine Netzadresse und eine Geräteadresse
Berechnungen in Access Teil I
 in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
Impulse Inklusion 2015. Selbst-bestimmtes Wohnen und Nachbarschaft
 Impulse Inklusion 2015 Selbst-bestimmtes Wohnen und Nachbarschaft Impulse sind Ideen und Vorschläge. Inklusion bedeutet: Alle Menschen können selbst-bestimmt und gleich-berechtigt am Leben teilnehmen.
Impulse Inklusion 2015 Selbst-bestimmtes Wohnen und Nachbarschaft Impulse sind Ideen und Vorschläge. Inklusion bedeutet: Alle Menschen können selbst-bestimmt und gleich-berechtigt am Leben teilnehmen.
Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit
 Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit Frau Dr. Eva Douma ist Organisations-Beraterin in Frankfurt am Main Das ist eine Zusammen-Fassung des Vortrages: Busines
Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit Frau Dr. Eva Douma ist Organisations-Beraterin in Frankfurt am Main Das ist eine Zusammen-Fassung des Vortrages: Busines
Die (Un-)Sicherheit von DES
 Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997
Die (Un-)Sicherheit von DES Sicherheit von DES: Bester praktischer Angriff ist noch immer die Brute-Force Suche. Die folgende Tabelle gibt eine Übersicht über DES Kryptanalysen. Jahr Projekt Zeit 1997
V 2 B, C, D Drinks. Möglicher Lösungsweg a) Gleichungssystem: 300x + 400 y = 520 300x + 500y = 597,5 2x3 Matrix: Energydrink 0,7 Mineralwasser 0,775,
 Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
10.1 Auflösung, Drucken und Scannen
 Um einige technische Erläuterungen kommen wir auch in diesem Buch nicht herum. Für Ihre Bildergebnisse sind diese technischen Zusammenhänge sehr wichtig, nehmen Sie sich also etwas Zeit und lesen Sie dieses
Um einige technische Erläuterungen kommen wir auch in diesem Buch nicht herum. Für Ihre Bildergebnisse sind diese technischen Zusammenhänge sehr wichtig, nehmen Sie sich also etwas Zeit und lesen Sie dieses
