Grundlegende Datentypen
|
|
|
- Andrea Brandt
- vor 10 Jahren
- Abrufe
Transkript
1 Foliensatz 4 Michael Brinkmeier Technische Universität Ilmenau Institut für Theoretische Informatik Sommersemester 2009 TU Ilmenau Seite 1 / 50 Grundlegende Datentypen TU Ilmenau Seite 2 / 50
2 Atomare Datentypen Die meisten höheren Programmiersprachen, kennen verschiedene atomare 1 Datentypen. Für uns sind das im Wesentlichen die folgenden: boolean Wahrheitswert, zwei mögliche Werte: true/false, 0/1 integer ganze Zahlen, Z real Reelle Zahlen, R char ASCII oder Unicode Zeichen pointer Zeiger auf Speicherbereiche Auf realen Rechnern sind die Typen in der Regel mit Größen- oder Genauigkeitsbesschränkungen versehen ( z.b. short/int/long, float/double ). 1 griech.: atomos unteilbar TU Ilmenau Seite 3 / 50 Zusammengesetzte Datentypen Mittels verschiedener Operationen können weitere Datentypen konstruiert werden. Zu ihnen gehören: Verbünde struct; Kombinationen von mehreren Daten Felder oder Arrays int[5]; Listen fester Länge, in denen jeder Eintrag denselben Typ hat Diese Arten von Datentypen und der Umgang mit ihnen wird als bekannt vorausgesetzt. TU Ilmenau Seite 4 / 50
3 Grundlegende Datenstrukturen Im Folgenden wollen wir uns mit einigen grundlegenden Datenstrukturen beschäftigen: Stacks Listen Queues Dynamische Mengen Bäumen Hashtabellen TU Ilmenau Seite 5 / 50 Die informale Beschreibung Die natürliche Sprache ist mit Sicherheit die einfachste Methode einen Datentyp zu beschreiben. Beispiel (Stack in natürlicher Sprache) Ein Stack (oder Stapel, Keller, LIFO last-in-first-out) ist wie ein Stapel von Gegenständen organisiert. Man kann immer nur einen neuen Gegenstand auf den Stapel drauf legen (push), den obersten Gegenstand vom Stapel betrachten (top) oder den obersten Gegenstand entfernen (pop). TU Ilmenau Seite 6 / 50
4 Die informale Beschreibung Alternativ kann man versuchen die Datenstruktur grafisch oder mit Hilfe von Beispielen zu beschreiben. Beispiel (Beschreibung eines Stacks mittels einer Graphik) TU Ilmenau Seite 7 / 50 Die informelle Beschreibung von Datentypen Die informale Beschreibung erweist sich im Allgemeinen als zu unpräzise. Eine Verbesserung stellt die informelle Beschreibung dar, bei der der Datentyp mittels einer konkreten Implementation in einer beliebigen Programmiersprache beschrieben wird. Vorteile: einfach und direkt Nachteile: verschleiert die wesentliche Funktionalität (eine Operation wird über den auszuführenden Quelltext definiert) erschwert Korrektheitsbeweise die gegebene Implementierung ist nicht universell nutzbar (Programmiersprache ist fixiert) fixiert bestimmte technische Entscheidungen (Eine andere Implementation könnte für die gegebene Aufgabe deutlich geeigneter sein) TU Ilmenau Seite 8 / 50
5 Abstrakte Datentypen Die Verwendung von Abstrakten Datentypen (ADT) erlaubt die Definition des Datentyps von seiner Implementierung zu trennen. Ein Abstrakter Datentyp besteht im Wesentlichen aus zwei Komponenten: einer Signatur und einer Semantik. Für beide Teile spielt die Implementierung keine Rolle. TU Ilmenau Seite 9 / 50 Signaturen Die Signatur eines ADT entspricht im Wesentlichen dem klassischen C-Header, bzw. den Deklaratoren. Sie beschreibt, welche Operationen im Zusammenhang mit dem ADT ausgeführt werden können. Definition (Signatur) Eine Signatur Σ = (S, O, domain, codomain) besteht aus einer Menge S von Sorten, die im Zusammenhang mit der ADT benötigt werden, einer Menge O von Operationen, zwei Abbildungen domain: O Seq(S) und codomain: O S wobei Seq(S) = {(S 1,...,S n ) n N, S 1,...,S n D} die Menge aller endlichen Tupel über S ist. TU Ilmenau Seite 10 / 50
6 Signaturen Ist Σ = (S, O, domain, codomain) eine Signatur, dann kann man eine Operation op O als Abbildung von ihrem Definitionsbereich (Domain, Domäne) domain(op) in ihren Wertebereich (Codomain) codomain(op) interpretieren. Notation Operationen beschreibt man häufig in der Form op: domain(op) codomain(op) Wenn domain(op) = (I 1,..., I n ) und codomain(op) = O schreibt man auch op: I 1 I n O. Die Forderung, dass jede Operation genau einen Ausgabetyp hat, ist auf technische Gründe zurück zu führen. TU Ilmenau Seite 11 / 50 Die Signatur eines Stacks Beispiel (Die Signatur eines Stacks) Sorten: Operationen: Elements Stacks Boolean empty : () Stacks push : Stacks Elements Stacks pop : Stacks Stacks top : Stacks Elements isempty : Stacks Boolean Bemerkung Der Definitionsbereich () von ist explizit erlaubt. Man spricht dann von Konstanten oder auch von Konstruktoren. TU Ilmenau Seite 12 / 50
7 Signaturen Bemerkung Wenn eine Operation den Inhalt eines Objektes verändert, muss das Objekt das Ergebnis der Operation sein! Bei den Signaturen handelt es sich um eine funktionale (applikative) Herangehesweise. Beispiel verändern beide den Stack. push: Stacks Elements Stacks pop: Stacks Stacks TU Ilmenau Seite 13 / 50 Algebren Eine Signatur Σ = (S, O, domain, codomain) ist lediglich eine Hülle, die die Syntax der Datenstruktur beschreibt. Es fehlt noch der Inhalt. Definition (Algebra) Sei Σ = (S, O, domain, codomain) eine Signatur. Eine Σ-Algebra A = (T, F) besteht aus einer Familie T = {T S S S} von Mengen und einer Familie F = { f op op O und f : T domain(op) T codomain(op) } von Abbildungen. Dabei ist T (S1,...,S n ) = T S1 T Sn. TU Ilmenau Seite 14 / 50
8 Algebren Anders gesagt: Eine Σ-Algebra A = (T, F) mit Σ = (S, T, domain, codomain) weist jeder Sorte S S eine Menge T S von Objekten dieser Sorte zu und jeder Operation op: I 1 I n O eine Abbildung f op : T I1 T In T O. TU Ilmenau Seite 15 / 50 Eine Algebra für Stacks Beispiel (Eine Algebra für Stacks) Elements = (nicht-leere) Menge D Boolean = {true, false} Stacks = Seq(D) Das leere Tupel () stellt den leeren Stack dar. TU Ilmenau Seite 16 / 50
9 Eine Algebra für Stacks Beispiel (Eine Algebra für Stacks Fortsetzung) empty() := () push((a 1,..., a n ),x) := (a 1,..., a n,x) ( steht für einen Fehler oder einen undefi- ((a 1,..., a n 1 ),a n ) falls n 1 pop((a 1,..., a n )) := nierten falls Wert. n = 0 ( (a 1,..., a n 1 ) falls n 1 pop((a 1,..., a n )) := falls n = 0 ( a n falls n 1 top((a 1,..., a n )) := falls n = 0 ( false falls n 1 isempty((a 1,..., a n )) := true falls n = 0 TU Ilmenau Seite 17 / 50 Axiome Um die Semantik einer Signatur festzulegen genügt es in der Regel nicht eine Algebra anzugeben. Häufig müssen zusätzlich bestimmte Gleichungen oder Axiome erfüllt werden. Beispiel (Die Axiomatik eines Stacks) s Stacks, x Elements: top(push(s, x)) = pop(push(s, x)) = isempty(empty()) = true isempty(push(s, x)) =false x s top(empty()) = pop(empty()) = TU Ilmenau Seite 18 / 50
10 Die Algebra und die Axiome Beispiel (Die Axiome und unsere Stack-Algebra) top(push((a 1,..., a n ), x)) = top((a 1,..., a n, x)) = x pop(push((a 1,..., a n ), x)) = pop((a 1,..., a n, x)) = (a 1,...,a n ) isempty(empty()) = isempty(()) = true isempty(push((a 1,..., a n ), x)) = isempty((a 1,...,a n, x)) = false TU Ilmenau Seite 19 / 50 Die Modellalgebra Hat man eine Signatur Σ und dazugehörige Axiome gegeben, so spricht man von einer algebraischen Spezifikation. Aus einer solchen algebraischen Spezifikation läßt sich eine Modellalgebra (oder auch mathematisches Modell) konstruieren (Stichwort: Quotiententermalgebra, AuP). Diese Modellalgebra hat einige sehr wichtige Eigenschaften, die bei dem Beweis der Korrekheit einer Implementierung helfen können. Unter Umständen lässt sich diese Modellalgebra auf elegante und einfach Weise beschreiben. Beispiel Die beschriebene Algebra für Stacks ist eine Modellalgebra für die gegebene algebraische Spezifikation. TU Ilmenau Seite 20 / 50
11 Algebraische Spezifikation eines ADT Vorteile: Universelle und vollständige Beschreibung Die axiomatische Darstellung ermöglicht automatisiere Beweise von Eigenschaften der Datenstruktur Nachteile: Das Finden eines geeigneten und vollständigen Axiomensystems ist in der Regel nicht einfach. Umsetzung in eine Implementation erfordert in der Regel einen weiteren Zwischenschritt über die Modellalgebra. Diese explizit zu beschreiben ist in der Regel ebenfalls sehr schwer. TU Ilmenau Seite 21 / 50 Implementierungen von Abstrakten Datentypen Das Konzept von Abstrakten Datentypen lässt sich in gewisser Weise in der Objektorientierung wiederfinden. Im Wesentlichen entspricht die Signatur der Definition der Klassen (z.b. in C++ und Java) und Interfaces. Abstrakte Klassen entsprechen direkt einer Signatur. Eine Implementierung entspricht einer Algebra. Sogar die abstrakte Definition von Signaturen mit nicht näher spezifizierten Sorten wie z.b. die Sorte Elements eines Stacks findet sich in modernen objektorientierten Sprachen in Templates wieder. TU Ilmenau Seite 22 / 50
12 Implementierungen eines Stacks Zur Realisierung eines Stacks über eine Menge D von Elementen, ergeben sich im wesentlichen zwei mögliche Implementierungen: Die Listenimplementierung Die Arrayimplementierung TU Ilmenau Seite 23 / 50 Die Listenimplementierung von Stacks TU Ilmenau Seite 24 / 50
13 Die Listenimplementierung eines Stacks Listen haben Sie schon in AuP kennengelernt. Nullzeiger S : a 1 a 2 a n empty LI : Erzeuge eine leere Liste. S : push LI (s, x): Füge am Anfang der Liste einen neues Element ein. S : x a 1 a 2 a n TU Ilmenau Seite 25 / 50 Die Listenimplementierung eines Stacks top LI (s): Gebe den Inhalt des ersten Listenknotens zurück, falls vorhanden S : a 1 a 2 a n pop LI (s): Entferne das erste Element der Liste. S : a 1 a 2 a 3 a n isempty LI (s): Gibt true zurück, falls die Liste leer ist, sonst false. TU Ilmenau Seite 26 / 50
14 Korrektheit der Listenimplementierung Da eine Modellalgebra für Stacks bekannt ist, kann die Korrektheit einer Implementierung auf einfache Art bewiesen werden. Dabei nutzt man das folgende Resultat: Sei A = (T, F) eine Modellalgebra von Σ = (S, O, domain, codomain) und I = (T I, F I ) eine Implementierung (interpretiert als Algebra). T S und f op seien die Mengen und Abbildungen in A und TS I und f op I die in I. I ist eine korrekte Implementierung von Σ oder A, wenn für jede Sorte S S eine Bijektion ϕ S : T S T I S existiert und für jede Operation op: I 1 I n O Folgendes gilt: ϕ O ( fop (x 1,..., x n ) ) = f I op (ϕ I1 (x 1 ),..., ϕ In (x n )). TU Ilmenau Seite 27 / 50 Korrektheit der Listenimplementierung Anders formuliert: Wir benötigen für jede Sorte S eine Bijektion ϕ S : T S TS I zwischen den Elementen der Sorte in der Modellalgebra und den Objekten der Sorte in der Implementation. Weiter müssen diese Bijektionen mit den Operationen kompatibel sein, d.h. im folgenden Diagramm ist es egal welchen der beiden Wege wir von der linken oberen Ecke zur rechten unteren Ecke nehmen. Beide führen zum selben Ergebnis. I 1 I n f op O ϕ I1 ϕ In ϕ O I I 1 II n f I op O I TU Ilmenau Seite 28 / 50
15 Korrektheit der Listenimplementierung Wie sieht nun die Bijektion zwischen Seq(D) und den Listen aus? Notation S : a 1 a 2 a n Das oben dargestellte Array notieren wir zur Abkürzung in der Form [a 1 a 2 a n ] Damit definieren wir ϕ((a 1,...,a n )) := [a n a n 1 a 2 a 1 ]. (Beachten Sie, dass die Reihenfolge umgekehrt wurde). Für Elements und Boolean gehen wir einfach von den Identitäten aus. TU Ilmenau Seite 29 / 50 Korrektheit der Listenimplementierung ((a 1,..., a n ), x) (a 1,...,a n, x) Seq(D) D push Seq(D) ϕ ϕ List < D > D List < D > push LI ([a n a 1 ], x) [x a n a 1 ] TU Ilmenau Seite 30 / 50
16 Korrektheit der Listenimplementierung (a 1,..., a n ) (a 1,...,a n 1 ) pop Seq(D) Seq(D) ϕ ϕ List < D > List < D > pop LI [a n a 1 ] [a n 1 a 1 ] TU Ilmenau Seite 31 / 50 Korrektheit der Listenimplementierung Auf ähnliche Weise kann man die übrigen Operationen auf Kompatibilität mit ϕ überprüfen. Satz Die beschriebene Listenimplementierung ist eine korrekte Implementierung des abstrakten Datentyps Stack. TU Ilmenau Seite 32 / 50
17 Zeitaufwand der Listenimplementierung Behauptung Jede Operation der Listenimplementierung hat Kosten O(1). Die Behauptung ist offensichlich korrekt. Allerdings erfordert push das Anlegen eines neuen Listeneintrages. Diese Operation (malloc in C, new in C++ und Java) ist auf realen Maschinen in der Regel deutlich teurer als der Zugriff auf einen Listeneintrag. Noch ein Problem Auf realen Maschinen kann push zu einem Speicherüberlauf führen. Im Beweis sind wir stillschweigend von einem unendlich großem Speicher ausgegangen. Die Korrektheit gilt also nur bis auf Speicherüberläufe. TU Ilmenau Seite 33 / 50 Die Arrayimplementierung von Stacks TU Ilmenau Seite 34 / 50
18 Die Arrayimplementierung von Stacks In der Arrayimplementierung besteht ein Stack s aus zwei Komponenten: einem Array A[1...m] der festen Größe m und einer Integervariablen p, genannt Pegel. s: p : n A : 1 a 1 a 2 n m a n TU Ilmenau Seite 35 / 50 Die Arrayimplementierung von Stacks empty(): A = new Elements[1...m] p = 0. push(s, x): if p == m then return else p = p + 1 ; A[p] = x pop(s): if p == 0 then return else p = p 1 ; return A[p + 1] top(s): if p == 0 then return else return A[p] isempty(s): if p == 0 then return true else return false TU Ilmenau Seite 36 / 50
19 Korrektheit der Arrayimplementierung Diesmal gehen wir einen anderen Weg für den Korrektheitsbeweis. Wir betrachten eine Folge (op 0 = empty,op 1,...,op N ) von Operationen auf demselben Stack mit op 1,...,op N empty. Im mathematischen Modell erzeugt diese Operationsfolge eine Folge von Tupeln mit s 0 = () und eine Folge (s 0, s 1,...,s N ) (z 0, z 1,..., z N ) von Ausgaben aus Elements {true, false} {, }, wobei die Ausgabe von empty und push ist und, falls ein Fehler auftritt (pop oder top auf leeren Stack). pop und top liefern das entsprechende Element als Ausgabe. TU Ilmenau Seite 37 / 50 Korrektheit der Arrayimplementierung Behauptung Die Arrayimplementierung erzeugt genau dieselbe Ausgabefolge wie das mathematische Modell, solange weder im mathematischen Modell ein Fehler auftritt (top ode pop auf leeren Stack), noch die Höhe des Stacks s i die Arraygröße m überschreitet. Beweis Man beweist per Induktion über i = 0, 1,..., N, dass nach Ausführen von op i die folgende Invariante gilt, sofern kein Fehler aufgetreten ist: p enthält die Länge n i von s i und s i = (A[1],...,A[n i ]). D.h. das Array A[1...n i ] stellt genau s i dar.... TU Ilmenau Seite 38 / 50
20 Korrektheit der Arrayimplementierung Beweis (Fortsetzung) Induktionsanfang (i = 0) : Nach op 0 = empty() hat p den Inhalt 0 und somit ist das Array A[1...p] leer, also gleich s 0 = (). Induktionsvoraussetzung: Die Behauptung gilt für i 1. Induktionsschritt: Wir müssen verschiedene Fälle unterscheiden: Falls s i 1 = d.h. im mathematischen Modell ist vorher ein Fehler aufgetreten ist nichts zu zeigen, da dieser Fall ausgeschlossen wurde. Falls in den Schritten 1,...,i 1 in der Implementierung ein Fehler aufgetreten ist, ist ebenfalls nichts zu zeigen. Wir können also s i 1 = (a 1,...,a ni 1 ) annehmen und p hat den Inhalt n i 1 und a j = A[j] für 1 j n i TU Ilmenau Seite 39 / 50 Korrektheit der Arrayimplementierung Beweis (Fortsetzung) Falls op i = push(s,x), ist s i = (a 1..., a ni 1, x). Wenn n i 1 < m, wird von der Prozedur push(s, x) das Objekt x an die Stelle A[n i 1 + 1] gesetzt und p auf den Wert n i erhöht. Das impliziert die Induktionsbehauptung in diesem Fall. Wenn n i 1 = m ist, tritt in der Implementierung ein Fehler auf und die Behauptung ist trivialerweise erfüllt. Die anderen Operationen können analog behandelt werden (Übungsaufgabe). TU Ilmenau Seite 40 / 50
21 Die Laufzeit der Arrayimplementierung Behauptung Bei der Arrayimplementierung hat jede Operation die Kosten O(1). Die Behauptung ist wahr, falls bei empty() das Array lediglich angelegt, nicht aber initialisiert wird. Im letzten Fall, wäre die Laufzeit für empty gerade O(m). Da der Inhalt in A[p m] aber unerheblich ist, beeinflusst diese Einschränkung die Korrektheit jedoch nicht. TU Ilmenau Seite 41 / 50 Arrayimplementierung ohne Platzprobleme Frage Ist es möglich, die Begrenzung auf ein Array fester Länge zu beheben? Antwort Ja! Mittels der Verdoppelungsstrategie! Sobald während push(s, x) ein Überlauf eintritt d.h. das m + 1-te Element würde hinzugefügt werden verdoppeln wir die Größe des Arrays. Genauer: Legen ein neues Array B der Größe 2m an. Kopieren das alte Array A in die ersten m Felder des neuen Arrays B. Gebe A frei. Setze A = B, d.h. setze die Referenz um. TU Ilmenau Seite 42 / 50
22 Die Verdoppelungsstrategie s: p: m A: 1 a 1 a 2 m a m B : 1 a 1 a 2 m 2m a m TU Ilmenau Seite 43 / 50 Kostenanalyse der Verdoppelungsstrategie Frage Wieviele Verdoppelungen können auftreten? k sei die Anzahl der push-opertationen in unserer Folge und j die Anzahl der Verdoppelungen. Damit enthält der Stack stets k Elemente. Also gilt vor der letzten Verdoppelung m 0 2 j 1 < k denn sonst, müsste nicht verdoppelt werden, und somit j 1 < log k m 0 = log k log m 0. TU Ilmenau Seite 44 / 50
23 Kostenanalyse der Verdoppelungsstrategie Sei L = log k log m 0. Dann lassen sich die Gesamtkosten für die Verdoppelungen nach oben abschätzen: L O ( ( m 0 2 i 1) = O m 0 i=1 = O = O(k) L 1 i=0 2 i ) (m 0 2 log k m 0 ) = O = O ( m 0 2 L) ( m 0 k m 0 ) Gesamtkosten mit k push-operationen N O(1) + O(k) = O(N) TU Ilmenau Seite 45 / 50 Kostenanalyse der Verdoppelungsstrategie Satz Wenn ein Stack mit Arrays und der Verdoppelungsstrategie implementiert wird, sind die Gesamtkosten für N Operationen in O(N). Der gesamte Platzbedarf ist O(k), wenn k die maximale je erreichte Stackgröße ist. Selbst wenn unbenutzte Arrays nie freigegeben werden, tritt ein Speicherüberlauf erst dann ein, wenn die Zahl der Stackeinträge zu einem bestimmten Zeitpunkt mehr als 1 4 des zur Verfügung stehenden Speichers beansprucht (Übungsaufgabe). TU Ilmenau Seite 46 / 50
24 Amortisierte Analyse Eine Analyse der Kosten, wie wir sie gerade durchgeführt haben, nennt man Amortisierte Analyse. Idee hinter der amortisierten Analyse Eine Datenstruktur wird häufig nicht für eine Operation, sondern für eine Reihe von insgesamt N Operationen genutzt. Betrachtet man die Kosten der einzelnen Operationen, so ergeben sich unter Umständen sehr hohe Worst-Case Kosten, wie z.b. die Kosten von push bei einem Stack mit Verdoppelungsstrategie. Betrachtet man jedoch die gesamte Folge, so könnte es sein, das diese relativ hohen Kosten nur in bestimmten Situationen eintreten (z.b. wenn besonders viele billige push Operationen seit der letzten teuren durchgeführt wurden). Dadurch ergeben sich insgesamt niedrigere Kosten, als bei der Verwendung der Worst-Case Laufzeit. TU Ilmenau Seite 47 / 50 Amortisierte Analyse Amortisierte Kosten Benötigt man im schlechtesten Fall T(N) Zeit für N Operationen auf einer Datenstruktur, so benötigt jede Operation die amortisierten Kosten T(N) N. Wichtig! Amortisierte Kosten müssen klar von Average-Case Kosten unterschieden werden! Bei letzteren geht eine Wahrscheinlichkeitsverteilung ein, und man betrachtet die erwartete Laufzeit. Bei den amortisiertern Kosten handelt es sich um eine tatsächliche obere Schranke, d.h. N beliebige Operationen auf der Datenstruktur benötigen höchstens T(N) Zeit. Die amortisierten Kosten für jede einzelne Operation sind dann die entstandenen durchschnittlichen Kosten für jede Operation. TU Ilmenau Seite 48 / 50
25 Vergleich von Listen- und Arrayimplementierung Arrayimplementierung: O(1) Kosten pro Operation, amortisiert d.h. im Mittel über alle Operationen. Sequentieller, indexbasierter Zugriff auf den Speicher (cachefreundlich) Höchstens die Hälfte des allozierten Speichers ist ungenutzt Listenimplementierung: O(1) Kosten pro Operation im schlechtesten Fall Hohe Allokationskosten, da jedes Listenelement einzeln angelegt wird Zusätzlicher Platz für Zeiger benötigt TU Ilmenau Seite 49 / 50
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Lernziele: Ausgleichstechniken für binäre Bäume verstehen und einsetzen können.
 6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
6. Bäume Lernziele 6. Bäume Lernziele: Definition und Eigenschaften binärer Bäume kennen, Traversierungsalgorithmen für binäre Bäume implementieren können, die Bedeutung von Suchbäumen für die effiziente
Semantik von Formeln und Sequenzen
 Semantik von Formeln und Sequenzen 33 Grundidee der Verwendung von Logik im Software Entwurf Syntax: Menge von Formeln = Axiome Ax K ist beweisbar Formel ϕ beschreiben Korrektkeit Vollständigkeit beschreibt
Semantik von Formeln und Sequenzen 33 Grundidee der Verwendung von Logik im Software Entwurf Syntax: Menge von Formeln = Axiome Ax K ist beweisbar Formel ϕ beschreiben Korrektkeit Vollständigkeit beschreibt
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Grundlagen der Informatik. Prof. Dr. Stefan Enderle NTA Isny
 Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 2 Datenstrukturen 2.1 Einführung Syntax: Definition einer formalen Grammatik, um Regeln einer formalen Sprache (Programmiersprache) festzulegen.
Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 2 Datenstrukturen 2.1 Einführung Syntax: Definition einer formalen Grammatik, um Regeln einer formalen Sprache (Programmiersprache) festzulegen.
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Folge 19 - Bäume. 19.1 Binärbäume - Allgemeines. Grundlagen: Ulrich Helmich: Informatik 2 mit BlueJ - Ein Kurs für die Stufe 12
 Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Objektorientierte Programmierung
 Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Objektorientierte Programmierung. Kapitel 12: Interfaces
 12. Interfaces 1/14 Objektorientierte Programmierung Kapitel 12: Interfaces Stefan Brass Martin-Luther-Universität Halle-Wittenberg Wintersemester 2012/13 http://www.informatik.uni-halle.de/ brass/oop12/
12. Interfaces 1/14 Objektorientierte Programmierung Kapitel 12: Interfaces Stefan Brass Martin-Luther-Universität Halle-Wittenberg Wintersemester 2012/13 http://www.informatik.uni-halle.de/ brass/oop12/
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
SEP 114. Design by Contract
 Design by Contract SEP 114 Design by Contract Teile das zu entwickelnde Programm in kleine Einheiten (Klassen, Methoden), die unabhängig voneinander entwickelt und überprüft werden können. Einheiten mit
Design by Contract SEP 114 Design by Contract Teile das zu entwickelnde Programm in kleine Einheiten (Klassen, Methoden), die unabhängig voneinander entwickelt und überprüft werden können. Einheiten mit
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Software Engineering Klassendiagramme Assoziationen
 Software Engineering Klassendiagramme Assoziationen Prof. Adrian A. Müller, PMP, PSM 1, CSM Fachbereich Informatik und Mikrosystemtechnik 1 Lesen von Multiplizitäten (1) Multiplizitäten werden folgendermaßen
Software Engineering Klassendiagramme Assoziationen Prof. Adrian A. Müller, PMP, PSM 1, CSM Fachbereich Informatik und Mikrosystemtechnik 1 Lesen von Multiplizitäten (1) Multiplizitäten werden folgendermaßen
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Also kann nur A ist roter Südler und B ist grüner Nordler gelten.
 Aufgabe 1.1: (4 Punkte) Der Planet Og wird von zwei verschiedenen Rassen bewohnt - dem grünen und dem roten Volk. Desweiteren sind die Leute, die auf der nördlichen Halbkugel geboren wurden von denen auf
Aufgabe 1.1: (4 Punkte) Der Planet Og wird von zwei verschiedenen Rassen bewohnt - dem grünen und dem roten Volk. Desweiteren sind die Leute, die auf der nördlichen Halbkugel geboren wurden von denen auf
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Beweisbar sichere Verschlüsselung
 Beweisbar sichere Verschlüsselung ITS-Wahlpflichtvorlesung Dr. Bodo Möller Ruhr-Universität Bochum Horst-Görtz-Institut für IT-Sicherheit Lehrstuhl für Kommunikationssicherheit [email protected] 6
Beweisbar sichere Verschlüsselung ITS-Wahlpflichtvorlesung Dr. Bodo Möller Ruhr-Universität Bochum Horst-Görtz-Institut für IT-Sicherheit Lehrstuhl für Kommunikationssicherheit [email protected] 6
Einführung in die Programmierung
 Technische Universität München WS 2003/2004 Institut für Informatik Prof. Dr. Christoph Zenger Testklausur Einführung in die Programmierung Probeklausur Java (Lösungsvorschlag) 1 Die Klasse ArrayList In
Technische Universität München WS 2003/2004 Institut für Informatik Prof. Dr. Christoph Zenger Testklausur Einführung in die Programmierung Probeklausur Java (Lösungsvorschlag) 1 Die Klasse ArrayList In
Kapitel 6. Komplexität von Algorithmen. Xiaoyi Jiang Informatik I Grundlagen der Programmierung
 Kapitel 6 Komplexität von Algorithmen 1 6.1 Beurteilung von Algorithmen I.d.R. existieren viele Algorithmen, um dieselbe Funktion zu realisieren. Welche Algorithmen sind die besseren? Betrachtung nicht-funktionaler
Kapitel 6 Komplexität von Algorithmen 1 6.1 Beurteilung von Algorithmen I.d.R. existieren viele Algorithmen, um dieselbe Funktion zu realisieren. Welche Algorithmen sind die besseren? Betrachtung nicht-funktionaler
Systeme 1. Kapitel 6. Nebenläufigkeit und wechselseitiger Ausschluss
 Systeme 1 Kapitel 6 Nebenläufigkeit und wechselseitiger Ausschluss Threads Die Adressräume verschiedener Prozesse sind getrennt und geschützt gegen den Zugriff anderer Prozesse. Threads sind leichtgewichtige
Systeme 1 Kapitel 6 Nebenläufigkeit und wechselseitiger Ausschluss Threads Die Adressräume verschiedener Prozesse sind getrennt und geschützt gegen den Zugriff anderer Prozesse. Threads sind leichtgewichtige
Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer
 Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer Klassendiagramme Ein Klassendiagramm dient in der objektorientierten Softwareentwicklung zur Darstellung von Klassen und den Beziehungen,
Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer Klassendiagramme Ein Klassendiagramm dient in der objektorientierten Softwareentwicklung zur Darstellung von Klassen und den Beziehungen,
Data Mining: Einige Grundlagen aus der Stochastik
 Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Verhindert, dass eine Methode überschrieben wird. public final int holekontostand() {...} public final class Girokonto extends Konto {...
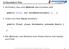 PIWIN I Kap. 8 Objektorientierte Programmierung - Vererbung 31 Schlüsselwort: final Verhindert, dass eine Methode überschrieben wird public final int holekontostand() {... Erben von einer Klasse verbieten:
PIWIN I Kap. 8 Objektorientierte Programmierung - Vererbung 31 Schlüsselwort: final Verhindert, dass eine Methode überschrieben wird public final int holekontostand() {... Erben von einer Klasse verbieten:
Beispiel 48. 4.3.2 Zusammengesetzte Zufallsvariablen
 4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
Einführung in die Java- Programmierung
 Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger [email protected] WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger [email protected] WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume?
 Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden [email protected] WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden [email protected] WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Objektorientierte Programmierung für Anfänger am Beispiel PHP
 Objektorientierte Programmierung für Anfänger am Beispiel PHP Johannes Mittendorfer http://jmittendorfer.hostingsociety.com 19. August 2012 Abstract Dieses Dokument soll die Vorteile der objektorientierten
Objektorientierte Programmierung für Anfänger am Beispiel PHP Johannes Mittendorfer http://jmittendorfer.hostingsociety.com 19. August 2012 Abstract Dieses Dokument soll die Vorteile der objektorientierten
Grammatiken. Einführung
 Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Einführung. Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Vorlesungen zur Komplexitätstheorie. K-Vollständigkeit (1/5)
 Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
a n + 2 1 auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert:
 Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
15 Optimales Kodieren
 15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
Einrichten eines Postfachs mit Outlook Express / Outlook bis Version 2000
 Folgende Anleitung beschreibt, wie Sie ein bestehendes Postfach in Outlook Express, bzw. Microsoft Outlook bis Version 2000 einrichten können. 1. Öffnen Sie im Menü die Punkte Extras und anschließend Konten
Folgende Anleitung beschreibt, wie Sie ein bestehendes Postfach in Outlook Express, bzw. Microsoft Outlook bis Version 2000 einrichten können. 1. Öffnen Sie im Menü die Punkte Extras und anschließend Konten
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann [email protected]
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann [email protected]
In diesem Thema lernen wir die Grundlagen der Datenbanken kennen und werden diese lernen einzusetzen. Access. Die Grundlagen der Datenbanken.
 In diesem Thema lernen wir die Grundlagen der Datenbanken kennen und werden diese lernen einzusetzen. Access Die Grundlagen der Datenbanken kurspc15 Inhaltsverzeichnis Access... Fehler! Textmarke nicht
In diesem Thema lernen wir die Grundlagen der Datenbanken kennen und werden diese lernen einzusetzen. Access Die Grundlagen der Datenbanken kurspc15 Inhaltsverzeichnis Access... Fehler! Textmarke nicht
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
Die Beschreibung bezieht sich auf die Version Dreamweaver 4.0. In der Version MX ist die Sitedefinition leicht geändert worden.
 In einer Website haben Seiten oft das gleiche Layout. Speziell beim Einsatz von Tabellen, in denen die Navigation auf der linken oder rechten Seite, oben oder unten eingesetzt wird. Diese Anteile der Website
In einer Website haben Seiten oft das gleiche Layout. Speziell beim Einsatz von Tabellen, in denen die Navigation auf der linken oder rechten Seite, oben oder unten eingesetzt wird. Diese Anteile der Website
Fachschaft Mathematik und Informatik (FIM) LA I VORKURS. Herbstsemester 2015. gehalten von Harald Baum
 Fachschaft Mathematik und Informatik (FIM) LA I VORKURS Herbstsemester 2015 gehalten von Harald Baum 2. September 2015 Inhaltsverzeichnis 1. Stichpunkte zur Linearen Algebra I 2. Körper 3. Vektorräume
Fachschaft Mathematik und Informatik (FIM) LA I VORKURS Herbstsemester 2015 gehalten von Harald Baum 2. September 2015 Inhaltsverzeichnis 1. Stichpunkte zur Linearen Algebra I 2. Körper 3. Vektorräume
Erstellen einer digitalen Signatur für Adobe-Formulare
 Erstellen einer digitalen Signatur für Adobe-Formulare (Hubert Straub 24.07.13) Die beiden Probleme beim Versenden digitaler Dokumente sind einmal die Prüfung der Authentizität des Absenders (was meist
Erstellen einer digitalen Signatur für Adobe-Formulare (Hubert Straub 24.07.13) Die beiden Probleme beim Versenden digitaler Dokumente sind einmal die Prüfung der Authentizität des Absenders (was meist
Verwendung des IDS Backup Systems unter Windows 2000
 Verwendung des IDS Backup Systems unter Windows 2000 1. Download der Software Netbackup2000 Unter der Adresse http://www.ids-mannheim.de/zdv/lokal/dienste/backup finden Sie die Software Netbackup2000.
Verwendung des IDS Backup Systems unter Windows 2000 1. Download der Software Netbackup2000 Unter der Adresse http://www.ids-mannheim.de/zdv/lokal/dienste/backup finden Sie die Software Netbackup2000.
Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER
 Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER Abamsoft Finos in Verbindung mit der Webshopanbindung wurde speziell auf die Shop-Software shop to date von DATA BECKER abgestimmt. Mit
Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER Abamsoft Finos in Verbindung mit der Webshopanbindung wurde speziell auf die Shop-Software shop to date von DATA BECKER abgestimmt. Mit
Wollen Sie einen mühelosen Direkteinstieg zum Online Shop der ÖAG? Sie sind nur einen Klick davon entfernt!
 Wollen Sie einen mühelosen Direkteinstieg zum Online Shop der ÖAG? Sie sind nur einen Klick davon entfernt! Sehr geehrte(r) Geschäftspartner(in), Um Ihre Transaktionen schneller durchzuführen, bieten wir
Wollen Sie einen mühelosen Direkteinstieg zum Online Shop der ÖAG? Sie sind nur einen Klick davon entfernt! Sehr geehrte(r) Geschäftspartner(in), Um Ihre Transaktionen schneller durchzuführen, bieten wir
Theoretische Informatik SS 04 Übung 1
 Theoretische Informatik SS 04 Übung 1 Aufgabe 1 Es gibt verschiedene Möglichkeiten, eine natürliche Zahl n zu codieren. In der unären Codierung hat man nur ein Alphabet mit einem Zeichen - sagen wir die
Theoretische Informatik SS 04 Übung 1 Aufgabe 1 Es gibt verschiedene Möglichkeiten, eine natürliche Zahl n zu codieren. In der unären Codierung hat man nur ein Alphabet mit einem Zeichen - sagen wir die
Kurzanleitung zur Bereitstellung von Sachverhalten und Lösungen zum Universitätsrepetitorium auf dem Server unirep.rewi.hu-berlin.
 Humboldt-Universität zu Berlin Juristische Fakultät Kurzanleitung zur Bereitstellung von Sachverhalten und Lösungen zum Universitätsrepetitorium auf dem Server unirep.rewi.hu-berlin.de Stand: 1. Juni 2010
Humboldt-Universität zu Berlin Juristische Fakultät Kurzanleitung zur Bereitstellung von Sachverhalten und Lösungen zum Universitätsrepetitorium auf dem Server unirep.rewi.hu-berlin.de Stand: 1. Juni 2010
Analysis I für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 2015/16 Prof. Dr. M. Hinze Dr. P. Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungshinweise zu Blatt 2 Aufgabe 1: (12 Punkte) a) Beweisen
Fachbereich Mathematik der Universität Hamburg WiSe 2015/16 Prof. Dr. M. Hinze Dr. P. Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungshinweise zu Blatt 2 Aufgabe 1: (12 Punkte) a) Beweisen
So die eigene WEB-Seite von Pinterest verifizieren lassen!
 So die eigene WEB-Seite von Pinterest verifizieren lassen! Quelle: www.rohinie.eu Die eigene Seite auf Pinterest verifizieren Es ist offiziell. Vielleicht haben auch Sie in den vergangenen Wochen die Informationen
So die eigene WEB-Seite von Pinterest verifizieren lassen! Quelle: www.rohinie.eu Die eigene Seite auf Pinterest verifizieren Es ist offiziell. Vielleicht haben auch Sie in den vergangenen Wochen die Informationen
Übungen 19.01.2012 Programmieren 1 Felix Rohrer. Übungen
 Übungen if / else / else if... 2... 2 Aufgabe 2:... 2 Aufgabe 3:... 2 Aufgabe 4:... 2 Aufgabe 5:... 2 Aufgabe 6:... 2 Aufgabe 7:... 3 Aufgabe 8:... 3 Aufgabe 9:... 3 Aufgabe 10:... 3 switch... 4... 4 Aufgabe
Übungen if / else / else if... 2... 2 Aufgabe 2:... 2 Aufgabe 3:... 2 Aufgabe 4:... 2 Aufgabe 5:... 2 Aufgabe 6:... 2 Aufgabe 7:... 3 Aufgabe 8:... 3 Aufgabe 9:... 3 Aufgabe 10:... 3 switch... 4... 4 Aufgabe
WS 2008/09. Diskrete Strukturen
 WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
Über Arrays und verkettete Listen Listen in Delphi
 Über Arrays und verkettete Listen Listen in Delphi Michael Puff [email protected] 2010-03-26 Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung 3 2 Arrays 4 3 Einfach verkettete Listen 7 4 Doppelt verkettete
Über Arrays und verkettete Listen Listen in Delphi Michael Puff [email protected] 2010-03-26 Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung 3 2 Arrays 4 3 Einfach verkettete Listen 7 4 Doppelt verkettete
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung: Lösungsvorschlag
 Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 9 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 9 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Individuelle Formulare
 Individuelle Formulare Die Vorlagen ermöglichen die Definition von Schnellerfassungen für die Kontenanlage sowie für den Im- und Export von Stammdaten. Dabei kann frei entschieden werden, welche Felder
Individuelle Formulare Die Vorlagen ermöglichen die Definition von Schnellerfassungen für die Kontenanlage sowie für den Im- und Export von Stammdaten. Dabei kann frei entschieden werden, welche Felder
Einrichtung des Cisco VPN Clients (IPSEC) in Windows7
 Einrichtung des Cisco VPN Clients (IPSEC) in Windows7 Diese Verbindung muss einmalig eingerichtet werden und wird benötigt, um den Zugriff vom privaten Rechner oder der Workstation im Home Office über
Einrichtung des Cisco VPN Clients (IPSEC) in Windows7 Diese Verbindung muss einmalig eingerichtet werden und wird benötigt, um den Zugriff vom privaten Rechner oder der Workstation im Home Office über
Folge 18 - Vererbung
 Workshop Folge 18 - Vererbung 18.1 Ein einfacher Fall der Vererbung Schritt 1 - Vorbereitungen Besorgen Sie sich - vielleicht aus einer der Übungen der Folge 17 - ein fertiges und lauffähiges Listenprojekt,
Workshop Folge 18 - Vererbung 18.1 Ein einfacher Fall der Vererbung Schritt 1 - Vorbereitungen Besorgen Sie sich - vielleicht aus einer der Übungen der Folge 17 - ein fertiges und lauffähiges Listenprojekt,
Fakultät Angewandte Informatik Lehrprofessur für Informatik 23.01.2012
 WS 2011/2012 Fakultät Angewandte Informatik Lehrprofessur für Informatik 23.01.2012 Prof. Dr. Robert Lorenz Musterlösung zur Vorlesung Informatik I, Extrablatt zu komplexen Datenstrukturen Aufgabe 45 **
WS 2011/2012 Fakultät Angewandte Informatik Lehrprofessur für Informatik 23.01.2012 Prof. Dr. Robert Lorenz Musterlösung zur Vorlesung Informatik I, Extrablatt zu komplexen Datenstrukturen Aufgabe 45 **
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
Grundbegriffe der Informatik Kapitel 6: Induktives Vorgehen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische
Second Steps in eport 2.0 So ordern Sie Credits und Berichte
 Second Steps in eport 2.0 So ordern Sie Credits und Berichte Schritt 1: Credits kaufen, um Zugangscodes generieren zu können Wählen Sie Credits verwalten und klicken Sie auf Credits kaufen. Geben Sie nun
Second Steps in eport 2.0 So ordern Sie Credits und Berichte Schritt 1: Credits kaufen, um Zugangscodes generieren zu können Wählen Sie Credits verwalten und klicken Sie auf Credits kaufen. Geben Sie nun
5.2 Neue Projekte erstellen
 5.2 Neue Projekte erstellen Das Bearbeiten von bestehenden Projekten und Objekten ist ja nicht schlecht wie aber können Sie neue Objekte hinzufügen oder gar völlig neue Projekte erstellen? Die Antwort
5.2 Neue Projekte erstellen Das Bearbeiten von bestehenden Projekten und Objekten ist ja nicht schlecht wie aber können Sie neue Objekte hinzufügen oder gar völlig neue Projekte erstellen? Die Antwort
Terme stehen für Namen von Objekten des Diskursbereichs (Subjekte, Objekte des natürlichsprachlichen Satzes)
 Prädikatenlogik Man kann den natürlichsprachlichen Satz Die Sonne scheint. in der Prädikatenlogik beispielsweise als logisches Atom scheint(sonne) darstellen. In der Sprache der Prädikatenlogik werden
Prädikatenlogik Man kann den natürlichsprachlichen Satz Die Sonne scheint. in der Prädikatenlogik beispielsweise als logisches Atom scheint(sonne) darstellen. In der Sprache der Prädikatenlogik werden
Virtueller Seminarordner Anleitung für die Dozentinnen und Dozenten
 Virtueller Seminarordner Anleitung für die Dozentinnen und Dozenten In dem Virtuellen Seminarordner werden für die Teilnehmerinnen und Teilnehmer des Seminars alle für das Seminar wichtigen Informationen,
Virtueller Seminarordner Anleitung für die Dozentinnen und Dozenten In dem Virtuellen Seminarordner werden für die Teilnehmerinnen und Teilnehmer des Seminars alle für das Seminar wichtigen Informationen,
Algorithmen & Datenstrukturen 1. Klausur
 Algorithmen & Datenstrukturen 1. Klausur 7. Juli 2010 Name Matrikelnummer Aufgabe mögliche Punkte erreichte Punkte 1 35 2 30 3 30 4 15 5 40 6 30 Gesamt 180 1 Seite 2 von 14 Aufgabe 1) Programm Analyse
Algorithmen & Datenstrukturen 1. Klausur 7. Juli 2010 Name Matrikelnummer Aufgabe mögliche Punkte erreichte Punkte 1 35 2 30 3 30 4 15 5 40 6 30 Gesamt 180 1 Seite 2 von 14 Aufgabe 1) Programm Analyse
Praktische Mathematik: Lineare und Netzwerk-Optimierung (SS 2015) Praktikumsaufgaben
 Technische Universität Kaiserslautern Prof Dr Sven O Krumke Dr Sabine Büttner MSc Marco Natale Praktische Mathematik: Lineare und Netzwerk-Optimierung (SS 2015) Praktikumsaufgaben Aufgabe 1 (Konvertieren
Technische Universität Kaiserslautern Prof Dr Sven O Krumke Dr Sabine Büttner MSc Marco Natale Praktische Mathematik: Lineare und Netzwerk-Optimierung (SS 2015) Praktikumsaufgaben Aufgabe 1 (Konvertieren
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Modellierung und Programmierung 1
 Modellierung und Programmierung 1 Prof. Dr. Sonja Prohaska Computational EvoDevo Group Institut für Informatik Universität Leipzig 19. November 2015 Gültigkeitsbereich (Scope) von Variablen { int m; {
Modellierung und Programmierung 1 Prof. Dr. Sonja Prohaska Computational EvoDevo Group Institut für Informatik Universität Leipzig 19. November 2015 Gültigkeitsbereich (Scope) von Variablen { int m; {
Einführung in. Logische Schaltungen
 Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Theoretische Grundlagen des Software Engineering
 Theoretische Grundlagen des Software Engineering 11: Abstrakte Reduktionssysteme [email protected] Reduktionssysteme Definition: Reduktionssystem Ein Reduktionssystem ist ein Tupel (A, ) Dabei gilt: A
Theoretische Grundlagen des Software Engineering 11: Abstrakte Reduktionssysteme [email protected] Reduktionssysteme Definition: Reduktionssystem Ein Reduktionssystem ist ein Tupel (A, ) Dabei gilt: A
Klausur WS 2006/07 Programmiersprache Java Objektorientierte Programmierung II 15. März 2007
 Fachhochschule Bonn-Rhein-Sieg University of Applied Sciences Fachbereich Informatik Prof. Dr. Peter Becker Klausur WS 2006/07 Programmiersprache Java Objektorientierte Programmierung II 15. März 2007
Fachhochschule Bonn-Rhein-Sieg University of Applied Sciences Fachbereich Informatik Prof. Dr. Peter Becker Klausur WS 2006/07 Programmiersprache Java Objektorientierte Programmierung II 15. März 2007
Berechnungen in Access Teil I
 in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
 Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
3. Zusammenhang. 22 Andreas Gathmann
 22 Andreas Gathmann 3. Zusammenhang Eine der anschaulichsten Eigenschaften eines topologischen Raumes ist wahrscheinlich, ob er zusammenhängend ist oder aus mehreren Teilen besteht. Wir wollen dieses Konzept
22 Andreas Gathmann 3. Zusammenhang Eine der anschaulichsten Eigenschaften eines topologischen Raumes ist wahrscheinlich, ob er zusammenhängend ist oder aus mehreren Teilen besteht. Wir wollen dieses Konzept
8: Zufallsorakel. Wir suchen: Einfache mathematische Abstraktion für Hashfunktionen
 Stefan Lucks 8: Zufallsorakel 139 Kryptogr. Hashfunkt. (WS 08/09) 8: Zufallsorakel Unser Problem: Exakte Eigenschaften von effizienten Hashfunktionen nur schwer erfassbar (z.b. MD5, Tiger, RipeMD, SHA-1,...)
Stefan Lucks 8: Zufallsorakel 139 Kryptogr. Hashfunkt. (WS 08/09) 8: Zufallsorakel Unser Problem: Exakte Eigenschaften von effizienten Hashfunktionen nur schwer erfassbar (z.b. MD5, Tiger, RipeMD, SHA-1,...)
Vorkurs Informatik WiSe 15/16
 Konzepte der Informatik Dr. Werner Struckmann / Stephan Mielke, Jakob Garbe, 16.10.2015 Technische Universität Braunschweig, IPS Inhaltsverzeichnis Suchen Binärsuche Binäre Suchbäume 16.10.2015 Dr. Werner
Konzepte der Informatik Dr. Werner Struckmann / Stephan Mielke, Jakob Garbe, 16.10.2015 Technische Universität Braunschweig, IPS Inhaltsverzeichnis Suchen Binärsuche Binäre Suchbäume 16.10.2015 Dr. Werner
10 Erweiterung und Portierung
 10.1 Überblick In vielen Fällen werden Compiler nicht vollständig neu geschrieben, sondern von einem Rechnersystem auf ein anderes portiert. Das spart viel Arbeit, ist aber immer noch eine sehr anspruchsvolle
10.1 Überblick In vielen Fällen werden Compiler nicht vollständig neu geschrieben, sondern von einem Rechnersystem auf ein anderes portiert. Das spart viel Arbeit, ist aber immer noch eine sehr anspruchsvolle
OUTLOOK (EXPRESS) KONFIGURATION POP3
 Seite 1 von 12 OUTLOOK (EXPRESS) KONFIGURATION POP3 Eine Anleitung zum Konfigurieren von Outlook (Express) zum Verwalten des Emailkontos am Mozarteum zur Verfügung gestellt durch: ZID Dezentrale Systeme
Seite 1 von 12 OUTLOOK (EXPRESS) KONFIGURATION POP3 Eine Anleitung zum Konfigurieren von Outlook (Express) zum Verwalten des Emailkontos am Mozarteum zur Verfügung gestellt durch: ZID Dezentrale Systeme
Datensicherung. Beschreibung der Datensicherung
 Datensicherung Mit dem Datensicherungsprogramm können Sie Ihre persönlichen Daten problemlos Sichern. Es ist möglich eine komplette Datensicherung durchzuführen, aber auch nur die neuen und geänderten
Datensicherung Mit dem Datensicherungsprogramm können Sie Ihre persönlichen Daten problemlos Sichern. Es ist möglich eine komplette Datensicherung durchzuführen, aber auch nur die neuen und geänderten
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können.
 Tutorial: Wie erfasse ich einen Termin? In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können. Neben den allgemeinen Angaben zu einem
Tutorial: Wie erfasse ich einen Termin? In diesem Tutorial lernen Sie, wie Sie einen Termin erfassen und verschiedene Einstellungen zu einem Termin vornehmen können. Neben den allgemeinen Angaben zu einem
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Rekursionen (Teschl/Teschl 8.1-8.2)
 Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Fallbeispiel: Eintragen einer Behandlung
 Fallbeispiel: Eintragen einer Behandlung Im ersten Beispiel gelernt, wie man einen Patienten aus der Datenbank aussucht oder falls er noch nicht in der Datenbank ist neu anlegt. Im dritten Beispiel haben
Fallbeispiel: Eintragen einer Behandlung Im ersten Beispiel gelernt, wie man einen Patienten aus der Datenbank aussucht oder falls er noch nicht in der Datenbank ist neu anlegt. Im dritten Beispiel haben
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier [email protected]
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier [email protected] 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier [email protected] 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ecaros2 - Accountmanager
 ecaros2 - Accountmanager procar informatik AG 1 Stand: FS 09/2012 Inhaltsverzeichnis 1 Aufruf des ecaros2-accountmanager...3 2 Bedienung Accountmanager...4 procar informatik AG 2 Stand: FS 09/2012 1 Aufruf
ecaros2 - Accountmanager procar informatik AG 1 Stand: FS 09/2012 Inhaltsverzeichnis 1 Aufruf des ecaros2-accountmanager...3 2 Bedienung Accountmanager...4 procar informatik AG 2 Stand: FS 09/2012 1 Aufruf
Cookies. Krishna Tateneni Jost Schenck Übersetzer: Jürgen Nagel
 Krishna Tateneni Jost Schenck Übersetzer: Jürgen Nagel 2 Inhaltsverzeichnis 1 Cookies 4 1.1 Regelungen......................................... 4 1.2 Verwaltung..........................................
Krishna Tateneni Jost Schenck Übersetzer: Jürgen Nagel 2 Inhaltsverzeichnis 1 Cookies 4 1.1 Regelungen......................................... 4 1.2 Verwaltung..........................................
3.2 Binäre Suche. Usr/local/www/ifi/fk/menschen/schmid/folien/infovk.ppt 1
 3.2 Binäre Suche Beispiel 6.5.1: Intervallschachtelung (oder binäre Suche) (Hier ist n die Anzahl der Elemente im Feld!) Ein Feld A: array (1..n) of Integer sei gegeben. Das Feld sei sortiert, d.h.: A(i)
3.2 Binäre Suche Beispiel 6.5.1: Intervallschachtelung (oder binäre Suche) (Hier ist n die Anzahl der Elemente im Feld!) Ein Feld A: array (1..n) of Integer sei gegeben. Das Feld sei sortiert, d.h.: A(i)
Musterlösungen zur Linearen Algebra II Blatt 5
 Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
