Formelsammlung Finanzmathematik

Regressionsverfahren haben viele praktische Anwendungen. Die meisten Anwendungen fallen in eine der folgenden beiden Kategorien:

Regressoslse De Regressoslse st ee Slug vo sttstshe Alseverfhre. Zel e de häufgste egesetzte Alseverfhre st es Bezehuge zwshe eer hägge ud eer oder ehrere uhägge rle festzustelle. Se wrd sesodere verwedet

Wärmedurchgang durch Rohrwände

ämeuchgng uch Rohwäne δ - L Rohlänge Bl: Sonäe ämeleung uch ene enschchge zylnsche n Fü e ämeleung gl llgemen: λ x Fü ene ünne konzensche Schch es Rohes von e Dcke gl: &Q λ Fläche: f(): 2 π L (Mnelfläche)

Formelsammlung Finanzmanagement

UNIERSIÄ REGENSBURG Lehsuhl fü Beebswschafslehe, sbesodee Fazdeslesuge UNI.-PROF. R. LUS RÖER Uvesässaße 3, 9353 Regesbug, el. (94) 943-73 Fomelsammlug Fazmaageme e Symbol espch de de jewelge easalug vewedee

Übungsaufgaben zur Finanzmathematik - Lösungen

Wshfsmhemk II Übugsufgbe zu Fzmhemk - Lösuge. Ee Bk lok m dem Agebo " W vedoppel h pl Jhe!! ". ) Welhe Vezsug bee Ihe de Bk? ( ) Edkpl od. Ede : Lufze od. Läge des Algezeumes Zse " Zseszsehug" z. B.: (

1.1. Jährliche Rentenzahlungen 1.1.1. Vorschüssige Rentenzahlungen. 1.1. Jährliche Rentenzahlungen 1.1.1. Vorschüssige Rentenzahlungen

.. Jährlche Retezahluge... Vorschüssge Retezahluge Ausgagspukt: Über ee edlche Zetraum wrd aus eem Kaptal (Retebarwert v, ), das zseszslch agelegt st, jewels zu Beg ees Jahres ee bestmmte Reterate ř gezahlt

Versicherungsmathematische Formeln und Sätze WS 2001/02

Pof. D. Detma Pfefe Vescheugsmathematsche Fomel ud Stze WS 200/02 Zsechug effete Zssatz: totale Zsetag aus dem fagsaptal "" ehalb ees Jahes Bawet des ach eem Jah fllge Kaptals "" Edwet des ach eem Jah

Analysis I Probeklausur 2

WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch

Festverzinsliche Wertpapiere. Kurse und Renditen bei ganzzahligen Restlaufzeiten

Festverzslche Wertaere Kurse ud Redte be gazzahlge Restlaufzete Glederug. Rückblck: Grudlage der Kursrechug ud Redteermttlug 2. Ausgagsstuato 3. Herletug der Formel 4. Abhäggket vom Marktzsveau 5. Übugsaufgabe

x mit Hilfe eines linearen, zeitinvarianten

Übug &Prktiku zu Digitle Sigle ud Systee The: Fltug Diskrete Fltug Wird ei zeitdiskretes Sigl ( T ) x it Hile eies liere, zeitivrite Siglverrbeitugssystes verrbeitet, so lässt sich ds Verhlte des verrbeitede

2. Arbeitsgemeinschaft (11.11.2002)

Mat T. Kocbk G Fazeugs- & Ivesttostheoe Veastaltug m WS / Studet d. Wtschatswsseschat. betsgemeschat (..). Fshe-Sepaato Das Fshe-Sepaatostheoem sagt aus, daß ute bestmmte ahme heutge ud mogge Kosum substtueba

Die Lagrangepunkte im System Erde-Mond

Die Lgngepunkte i Syste Ede-ond tthis Bochdt Tnnenbusch-ynsiu Bonn [email protected] Einleitung: Welche Käfte spüt eine Rusonde, die sich ntiebslos in de Nähe von Ede und ond ufhält? Zunächst sind

Formelsammlung zur Zuverlässigkeitsberechnung

Formelsmmlug zur Zuverlässgetsberechug zusmmegestellt vo Tt Lge Fchhochschule Merseburg Fchberech Eletrotech Ihlt:. Zuverlässget vo Betrchtugsehete.... Zuverlässget elemetrer, chtreprerbrer ysteme... 3.

(Markowitz-Portfoliotheorie)

Thema : ortfolo-selekto ud m-s-rzp (Markowtz-ortfolotheore) Beurtelugskrtere be quadratscher Nutzefukto: Beroull-rzp + quadratsche Nutzefukto Thema Höhekompoete: Erwartugswert µ Rskokompoete: Stadardabwechug

Finanzmathematik II: Barwert- und Endwertrechnung

D. habl. Bukhad Uech Beufsakademe Thüge Saalche Sudeakademe Sudeabelug Eseach Sudebeech Wschaf Wschafsmahemak Wesemese 004/0 Fazmahemak II: Bawe- ud Edweechug. Bawee ud Edwee vo Zahlugsehe. Effekve Jaheszssaz

( 3) k ) = 3) k 2 3 für k gerade

Aufgbe : ( Pute Zeige Sie mithilfe des Biomische Lehrstzes: ( 3 ( 3 ist für lle N eie türliche Zhl Lösug : Nch dem biomische Lehrstz gilt: ( 3 Somit ergibt sich ( 3 ( 3 ( ( 3 bzw ( 3 ( ( 3 ( ( 3 ( ( 3

F ORMELSKRIPT. Spektraler Transmissionsgrad einer planparallelen Platte aus isotropem homogenen

ORMESRI Zuammehäge zwche de etale Stoffezahle etale Reflexogad ( ( geamt ( ( fü läche etale Retamogad ( a ( b a b Setale amogad ee laaallele latte au otoem homogee Medum ( ( mt

von Prof. Dr. Ing. Dirk Rabe FH Emden/Leer

vo Prof. Dr. Ig. Dirk Rbe FH Emde/Leer Überblick: Folge ud Reihe Folge: Zhlefolge ( ) ; ; ; ist eie geordete Liste vo Zhle ( IN) : Glieder der Folge f(): Bildugsgesetz (eplizit i oder rekursiv) z.b.: (

Quantitative BWL 2. Teil: Finanzwirtschaft

Quattatve BWL. el: Fazwtschaft Mag. oáš Sedlačk Lehstuhl fü Fazdestlestuge Uvestät We Quattatve BWL: Fazwtschaft Ogasatosches Isgesat wd es 6 ee gebe (5 Ehete + Klausu Klausu fdet a D 7. Jaua 009 statt

Das Verfahren von Godunov. Seminar Numerik 25.11.2010 Anja Bettendorf

Das Verfahre vo Goduov Semar Numerk 5..00 Aja Beedorf Das Verfahre vo Goduov Übersch Goduov - Goduovs Verfahre für Leare Syseme Aweduge & Folgeruge aus Goduovs Verfahre - De Numersche Fluss-Fuko m Goduov

Lineare Algebra Formelsammlung

ee Algeb Fomelsmmlug vo Gábo Zogg Fomelsmmlug ee Algeb Gábo Zogg. ee Glechugsssteme. Ds Guss'sche Elmtosvefhe Defto: Σ Sstem vo m Glechuge ud Ubekte Opetoe: - Vetusche vo Glechuge - Addee/Subthee ees Velfche

Prof. Dr. Johann Graf Lambsdorff Universität Passau. Pflichtlektüre: WS 2007/08

y, s. y Pof. D. Johann Gaf Lambsdoff Unvestät Passau y* VI. Investton und Zns c* WS 2007/08 f(k) (n+δ)k Pflchtlektüe: Mankw, N. G. (2003), Macoeconomcs. 5. Aufl. S. 267-271. Wohltmann, H.-W. (2000), Gundzüge

Analytische Geometrie

Pives Gymsim Mies J Mhemik Alyishe Geomeie Ueihsfzeihe de Mhemikleisskse / i de Shljhe / d / Noe Mez Am Solz He Ihlsvezeihis LÄNG BTRAG) INS VKTORS INHITSVKTOR SKALARPRODUKT WINKL ZWISCHN ZWI VKTORN NORMALNFORM

Investmentfonds. Kennzahlenberechnung. Performance Risiko- und Ertragsanalyse, Risikokennzahlen

Ivestmetfods Kezahleberechug erformace Rsko- ud Ertragsaalyse, Rskokezahle Gültg ab 01.01.2007 Ihalt 1 erformace 4 1.1 Berechug der erformace über de gesamte Beobachtugzetraum (absolut)... 4 1.2 Aualserug

Übungen zur Analysis 1 für Informatiker und Statistiker. Lösung zu Blatt 12

Mthemtisches Istitut der Uiversität Müche Prof. Dr. Peter Otte WiSe 203/4 Lösug 2 2.0.204 Aufgbe 2. [8 Pute] Übuge zur Alysis für Iformtier ud Sttistier Lösug zu Bltt 2 Für eie Teilmege Ω R, sei {, flls

Im Wöhlerdiagramm wird die Lebensdauer (Lastwechsel oder Laufzeit) eines Bauteils in Abhängigkeit von der Belastung dargestellt.

Webull & Wöhler 0 CRGRAPH Wöhlerdagramm Im Wöhlerdagramm wrd de Lebesdauer ( oder Laufzet) ees Bautels Abhägget vo der Belastug dargestellt. Kurzetfestget Beaspruchug Zetfestget auerfestget 0 5 3 4 6 0

F 6-2 π. Seitenumbruch

6 trebsauslegug Für dese ckelprozess üsse de otore so ausgelegt werde, dass dese Fahrbetreb cht überlastet werde. Herfür üsse de ezele asseträghetsoete [7] der Bautele (otor, etrebe, ckler ud Ulekrolle)

Aufgaben zur Festigkeitslehre - ausführlich gelöst

ufge ur Festgketslere - usfürlc gelöst Mt Grudegrffe, Formel, Frge, tworte vo Gerrd Kppste üerretet ufge ur Festgketslere - usfürlc gelöst Kppste scell ud portofre erältlc e eck-sop.de DE FCHBUCHHNDLUNG

1 s. 1 s. 1 k. n j. j = Wärmedurchgang durch eine mehrschichtige, ebene Wand:

Wärmeurchgg urch ee mehrchchtge, ebee W: ugehe vo er Löug er Fourer'che Dfferetlglechug für e Wärmetrport urch ee ebee Wfläche : A T ergbt ch ru für ee mehrchchtge, ebee Wfläche: A ru wr e Wärmeurchggwertzhl

Ein Kredit von 350.000 soll mit 10% p.a. verzinst werden. Folgende Tilgungen sind vereinbart:

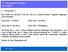E. Tlgugsechuge Aufgabe E Ked vo 350.000 soll 0% p.a. vezs wede. Folgede Tlguge sd veeba: Ede Jah : 70.000 Ede Jah : 63.000 Ede Jah 6:.500 Ede Jah 7: Reslgug. A Ede des 3. ud 5. Jahes efolge keele Zahluge

D-MATH, D-PHYS, D-CHAB Analysis II FS 2018 Prof. Manfred Einsiedler. Lösung 2

D-MATH, D-PHYS, D-CHAB Alysis II FS 28 Prof. Mfred Eisiedler Lösug 2 Hiweise. Gehe Sie log zum Kochrezept zur Treug der Vrible i liere Differetilgleichuge vor (siehe Abschitt 7.5.3 im Skript). 2. Bemerke

Rekurrenz. Algorithmen rufen sich selbst (rekursiv) auf.

Rekurrez Rekurso: Algorthme rue sch selst rekursv u. Rekurrez: Ds Luzetverhlte zw. der Specherpltzedr vo rekursve Algorthme k der Regel durch ee Rekursosormel recurrece, RF eschree werde. Rekurrez Bespel:

Sitzplatzreservierungsproblem

tzplatzreserverugsproblem Be vele Zugsysteme Europa müsse Passagere mt hrem Zugtcet ee tzplatzreserverug aufe. Da das Tcetsystem Kude ee ezele Platz zuwese muss, we dese e Tcet aufe, ohe zu wsse, welche

4 Deckungsrückstellung

eckugsrückstellug 33 4 eckugsrückstellug iel: erfhre zur Erittlug des Wertes eies ersicherugsvertrgs ud der zur eckug der Risike ötige Rückstelluge des ersicherugsuterehes. Proble: Präie werde kostt gezhlt,

Tao De / Pan JiaWei. Ihrig/Pflaumer Finanzmathematik Oldenburg Verlag 1999 =7.173,55 DM. ges: A m, A v

Tao De / Pa JiaWei Ihrig/Pflaumer Fiazmathematik Oldeburg Verlag 1999 1..Ei Darlehe vo. DM soll moatlich mit 1% verzist ud i Jahre durch kostate Auitäte getilgt werde. Wie hoch sid a) die Moatsrate? b)

Klasse 10 Graphen von ganzrationalen Funktionen skizzieren

Klsse 0 Grphe vo grtiole Fuktioe skiiere Nr.3-4.4.06 Ausggslge Vorwisse Die SuS kee Grudfuktioe ud ihre Grphe: f() = ²; ³; ⁴ f() = ; f() = Die SuS kee bei Grudfuktioe folgede Veräderuge: g() = f() Der

2. Mittelwerte (Lageparameter)

2. Mttelwerte (Lageparameter) Bespele aus dem täglche Lebe Pro Hemspel hatte Borussa Dortmud der letzte Saso durchschttlch 7.2 Zuschauer. De deutsche Akte sd m Durchschtt um 0 Zähler gefalle. I Ide wurde

Ausgangspunkt: Über einen endlichen Zeitraum wird aus einem Kapital (Rentenbarwert RBW v n,i

D. Reterechug 1.1. Jährliche Retezahluge 1.1.1. Vorschüssige Retezahluge Ausgagspukt: Über eie edliche Zeitraum wird aus eiem Kapital (Retebarwert RBW v,i ), das ziseszislich agelegt ist, jeweils zu Begi

Formelsammlung Elektrische Maschinen V EMA 1 245K. Der Motor hat durch seine Isolierklasse F eine Bezugstemperatur von ϑ B =115 C

Foellu lee e V.8 9..3 ) We Leeweoe. S See.9 ue: luu: 3 3,9 55 De oo u ee olele F ee ezueeu vo ϑ 5 uϑ uϑ u 5,94Ω [ ( ϑ ) ] 4,36Ω,39 ( 5 ) 3 4, 45 ϑ ϑ Gezeeu be le: Gezeeu: eu vo u ϑ Luze e ooe: Y 9 F H

1.1 Berechnung des Endwerts einer Einmalanlage bei linearer ganzjähriger Verzinsung nach n Verzinsungsjahren

Forelsalug zur Fiazatheatik 1. Eifache Zisrechug (lieare Verzisug) 1.1 Berechug des Edwerts eier Eialalage bei liearer gazjähriger Verzisug ach Verzisugsjahre p = 1 + = ( 1+ i ) 1 1.2 Berechug des Gegewartswerts

Die relevanten Cash Flows in der Unternehmensbewertung aus der Sicht des Rechnungswesens

De relevnen Csh Flows n der Unernehmensbewerun us der Sch des Rechnunswesens Edwn O Fscher rl-frnzens-unversä rz Oober 26 DCF-Bssmodelle Percen of Sles-Mehode Fllsude Übersch o onsner Verschuldunsrd o

3 Allgemeine lineare Gleichungssysteme über R. Superposition

Fole 3 Allgeee lere Glechugssystee üer R. Superposto (3.) Defto: E leres Glechugssyste Uestte ud Glechuge st: De sd de Koeffzete us R. De sd wetere Zhle, uch de Kostte get, ud de sd de Uestte, zw. de Uekte,

Finanzmathematik Folien zur Vorlesung

Fazmahemak Fole zu Volesug FINANZMAHEMAI. Zsechug.. Gudbegffe de Zsechug.. De ve Fageselluge de Zsechug.3. Beechug des Edkapals.4. Beechug vo Afagskapal, Zssaz ud Laufze.5. Uejähge Vezsug.6. Sege Vezsug.

(zur deiterleitimg an das RIGA)

Atg de Beuf sshulispektoekofeez die DK (zu deiteleitig ds GA) i. dei? geeblihidustielle Beufsshule besteht de Ffi Lhtuteiht fü lle Lehlige US Teile: d2heiid. de beuf skudlihe Jteiht luf ed i t de ElFs

Logarithmus - Übungsaufgaben. I. Allgemeines

Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht

Entdecke die Welt! Australien USA

Entdecke die Welt! Die Feien sind zu Ende endlich sieht Leon seine Feunde wiede! Jede von ihnen w im Ulub in einem ndeen Lnd. Sie hben lle Postkten geschieben und etws mitgebcht. Die blonde Nicole w in

Æ A BC A DC C C C C C A A BCBDECFE C F A C C F A A F C AC D A F C A F A AC F C C C C A C C AC C C C F F F C C F A C F F A C A C C F C F F C C A D F F C C C D F B A C C F C C F B C C F A A B A A A F A

Kennlinienaufnahme des Transistors BC170

Kennlnenufnhme des Trnsstors 170 Enletung polre Trnsstoren werden us zwe eng benchbrten pn-übergängen gebldet. Vorrusetzung für ds Funktonsprnzp st de gegensetge eenflussung beder pn-übergänge, de nur

Polynomprodukt und Fast Fourier Transformation

Polomrodut ud Fst Fourer Trsformto Polome Reelles Polom eer Vrble...... R : oeffzete vo Grd vo : höchste Potez Besel: 3 3 5 8 Mege ller reelle Polome: R[] 3 Oertoe uf Polome. Addto b b b q b b b b b q

STUDIUM. Mathematische Grundlagen für Betriebswirte

STUDIUM Mthetische Grudlge für Betrieswirte Mit de folgede Aufge köe Sie i eie Selsttest üerprüfe, o Sie och eiigerße die Grudlge der Alger eherrsche. Diese hdwerkliche Fertigkeite sid wesetlich, we es

Banken und Börsen, Kurs 41520 (Inhaltlicher Bezug: KE 4)

Lösugshiweise zu Eiseeabeit 2 zum Kus 452, ake u öse, WS 2/2 Lösugshiweise zu Eiseeabeit 2: WS 2/2 ake u öse, Kus 452 (Ihaltliche ezug: KE 4) alyse festvezisliche Wetpapiee 5 Pukte Vo Ihe ak wee Ihe ie

Konfliktpotential Wasser Versuch einer globalen Analyse als Grundlage zur Entwicklung eines thematischen Atlasses

Kflktpttl Wss Vsuch glbl Alys ls Gudlg zu Etwcklug s thmtsch Atlsss Pästt d stbt m Studfch Gdtfssug ud -vsulsug - Fchchtug Ktgph v J Schulz 06. 2013 Gldug 1 EIltug 2 Bdutug v Wss 3 Ausgwählt Kflktg 4 Etlug

Finanzierung: Übungsserie IV Aussenfinanzierung

Them Dokumetrt Fizierug: Übugsserie IV Aussefizierug Lösuge Theorie im Buch "Itegrle Betriebswirtschftslehre" Teil: pitel: D Fizmgemet 2.4 Aussefizierug Fizierug: Übugsserie IV Aussefizierug Aufgbe Eie

Mittelwerte und Zahlenfolgen Beat Jaggi, [email protected]

vsmp sspmp ssimf Mittelwete ud Zhlefolge Bet Jggi, [email protected] Eileitug Ds Bilde vo Mittelwete ist ei zetles Kozept i de Mthemtik: Lgemsse i de Sttistik (Mittelwet, Medi, Modus); Mitte, Mittelliie

Auf den Flügeln der Liebe

Auf de Flügel der Liebe für gemischte Chor ud Klavier Text: Floria Bald Musik ud Satz: Berd Stallma Klavierpartitur PG78 397 Korbach Tel: 05631/9370105 www.arragemetverlag.de Auf de Flügel der Liebe Text:

UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009

UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis

Marek Kubica, Diskrete Strukturen Übungsblatt 13 Gruppe 11

Mrek Kubic, [email protected] Diskrete Strukture Übugsbltt Gruppe Pukteverteilug: Σ Aufgbe () 8 () 7 Der Grph B ht de Prüfer-Code,,,,, der zustde kommt, we m de kleiste Kote vom Grd streicht ud de dere, übrig

Thema 8 Konvergenz von Funktionen-Folgen und - Reihen

Them 8 Kovergez vo Fuktioe-Folge ud - Reihe Defiitio Sei (f ) eie Folge vo Fuktioe vo D R i R. Wir sge, dß f puktweise gege eie Fuktio f kovergiert, flls gilt: f () f() für jedes D. Dies ist der türliche

Der Satz von Cavalieri: Zwei Körper gleicher Höhe sind volumengleich, wenn sie in jeweils gleicher Höhe flächengleiche Querschnitte haben.

Pof. D. Jüge Rot Didati de eometie alte Pizip d Satz vo Cavaliei dlage des olmebegiffs (eiscließlic Satz vo De) olme de d des stmpfs Kgelvolme d Kgelobefläce Pizip vo Cavaliei Boaveta Cavaliei (598 47;

Potenzen, Wurzeln und ihre Rechengesetze

R. Brik http://rik-du.de Seite 9.0.00 Poteze, Wurzel ud ihre Rechegesetze Der Potezegriff Defiitio: Eie Potez ist eie Multipliktio gleicher Fktore (Bsis), ei der der Epoet die Azhl der Fktore git. : =...

NvKG Bernkastel-Kues Mathematik Daten/Zufall Fachlehrer : W.Zimmer Mehrstufige Zufallsversuche - Baumdiagramme. b g. b g. b g

Kefe 6 Fee:. Ze NvK BekeKe Mek De/Zf Fee :.Ze Mefe Zfvee Bde I ee Ue d oe, e d üe Ke. E w zwe eede ee Ke ezoe d de Fe feee. N jede Z wd de ezoee Ke wede de Ue zükee. S={( ); ( ); ( ); ( ); ( ); ( ); (

7 Ungleichungen und Intervalle

Mthemtik. Klsse 7 Ugleichuge ud Itervlle Aufgbe 0 Löse Sie folgede Ugleichuge > + 8 < 5 + + 7. Itervlle Um gze Bereiche vo reelle Zhle zugebe, wird die Schreibweise mit Itervlle verwedet. Beispiele [,

Aufgabe 1 Ordnen Sie die folgenden vier Funktionen gemäß ihrem asymptotischen Wachstums ( ) ( ) log( n) ( ) ( ) ( log ( n)

Dtestrukture ud Agorthme: Btt Berhrd Detrh (656800 Lrs Ferhomberg (65600 Sebst Kesburges (65710 Mrus Köthebürger (658550 Übugsgruppe 11 Mttwoh, 11:00-1:00 Uhr D1.0 Mtths Erst Aufgbe 1 Orde Se de fogede

ALGEBRA. Potenzen und Wurzeln. Grundlagen. Manuskript zur Wiederholung. Datei Nr Dezember Friedrich W. Buckel

ALGEBRA Poteze ud Wurzel Grudlge Muskript zur Wiederholug Dtei Nr. Dezember 00 Friedrich W. Buckel Itertsgymsium Schloß Torgelow Ihlt Poteze mit türliche Expoete Potezgesetze Poteze mit egtive gze Expoete