Bedingte Wahrscheinlichkeit. G.Roolfs
|
|
|
- Curt Rothbauer
- vor 9 Jahren
- Abrufe
Transkript
1 Bedingte Wahrscheinlichkeit G.Roolfs
2 In einem Laden ist eine larmanlage eingebaut. Bei inbruch gibt sie mit 99%-iger Wahrscheinlichkeit larm. Wenn in einer bestimmten Nacht kein inbruch stattfindet, gibt sie mit der Wahrscheinlichkeit 0,005 falschen larm (ine Maus berührt die nlage oder Ähnliches). Die inbruchswahrscheinlichkeit für eine Nacht sei 0,002. Wie groß ist die Wahrscheinlichkeit, dass ein inbruch vorliegt, wenn larm ausgelöst wurde?
3 In einem Laden ist eine larmanlage eingebaut. Bei inbruch gibt sie mit 99%-iger Wahrscheinlichkeit larm. Wenn in einer bestimmten Nacht kein inbruch stattfindet, gibt sie mit der Wahrscheinlichkeit 0,005 falschen larm (ine Maus berührt die nlage oder Ähnliches). Die inbruchswahrscheinlichkeit für eine Nacht sei 0,002. Wie groß ist die Wahrscheinlichkeit, dass ein inbruch vorliegt, wenn larm ausgelöst wurde? Die Zusammenhänge werden in einem Pfaddiagramm dargestellt.
4 In einem Laden ist eine larmanlage eingebaut. Bei inbruch gibt sie mit 99%-iger Wahrscheinlichkeit larm. Wenn in einer bestimmten Nacht kein inbruch stattfindet, gibt sie mit der Wahrscheinlichkeit 0,005 falschen larm (ine Maus berührt die nlage oder Ähnliches). Die inbruchswahrscheinlichkeit für eine Nacht sei 0,002. Wie groß ist die Wahrscheinlichkeit, dass ein inbruch vorliegt, wenn larm ausgelöst wurde? Die Zusammenhänge werden in einem Pfaddiagramm dargestellt. s bedeuten: inbruch
5 In einem Laden ist eine larmanlage eingebaut. Bei inbruch gibt sie mit 99%-iger Wahrscheinlichkeit larm. Wenn in einer bestimmten Nacht kein inbruch stattfindet, gibt sie mit der Wahrscheinlichkeit 0,005 falschen larm (ine Maus berührt die nlage oder Ähnliches). Die inbruchswahrscheinlichkeit für eine Nacht sei 0,002. Wie groß ist die Wahrscheinlichkeit, dass ein inbruch vorliegt, wenn larm ausgelöst wurde? Die Zusammenhänge werden in einem Pfaddiagramm dargestellt. s bedeuten: inbruch kein inbruch
6 In einem Laden ist eine larmanlage eingebaut. Bei inbruch gibt sie mit 99%-iger Wahrscheinlichkeit larm. Wenn in einer bestimmten Nacht kein inbruch stattfindet, gibt sie mit der Wahrscheinlichkeit 0,005 falschen larm (ine Maus berührt die nlage oder Ähnliches). Die inbruchswahrscheinlichkeit für eine Nacht sei 0,002. Wie groß ist die Wahrscheinlichkeit, dass ein inbruch vorliegt, wenn larm ausgelöst wurde? Die Zusammenhänge werden in einem Pfaddiagramm dargestellt. s bedeuten: inbruch kein inbruch larm
7 In einem Laden ist eine larmanlage eingebaut. Bei inbruch gibt sie mit 99%-iger Wahrscheinlichkeit larm. Wenn in einer bestimmten Nacht kein inbruch stattfindet, gibt sie mit der Wahrscheinlichkeit 0,005 falschen larm (ine Maus berührt die nlage oder Ähnliches). Die inbruchswahrscheinlichkeit für eine Nacht sei 0,002. Wie groß ist die Wahrscheinlichkeit, dass ein inbruch vorliegt, wenn larm ausgelöst wurde? Die Zusammenhänge werden in einem Pfaddiagramm dargestellt. s bedeuten: inbruch kein inbruch larm kein larm
8
9 0,99
10 0,99 0,005
11 0,002 0,99 0,005
12 0,99 0,005
13 0,99 0,01 0,005
14
15 s wurde larm ausgelöst.
16 s wurde larm ausgelöst.
17 s wurde larm ausgelöst.
18 s wurde larm ausgelöst und es liegt ein inbruch vor.
19 s wurde larm ausgelöst und es liegt ein inbruch vor. P( ) =
20 s wurde larm ausgelöst und es liegt ein inbruch vor. P( ) = 0,002 0,99
21 s wurde larm ausgelöst und es liegt ein inbruch vor. P( ) = 0,002 0,99+0,998 0,005
22 s wurde larm ausgelöst und es liegt ein inbruch vor. P( ) = 0,002 0,99 0,002 0,99+0,998 0,005
23 s wurde larm ausgelöst und es liegt ein inbruch vor. P( ) = 0,002 0,99 0,002 0,99+0,998 0,005 =
24 s wurde larm ausgelöst und es liegt ein inbruch vor. P( ) = 0,002 0,99 0,002 0,99+0,998 0,005 = 0,284
25 Fülle die Vier-Felder-Tafel aus
26 Fülle die Vier-Felder-Tafel aus
27 Fülle die Vier-Felder-Tafel aus
28 Fülle die Vier-Felder-Tafel aus
29 Fülle die Vier-Felder-Tafel aus
30 Fülle die Vier-Felder-Tafel aus
31 Fülle die Vier-Felder-Tafel aus
32 Fülle die Vier-Felder-Tafel aus
33 Fülle die Vier-Felder-Tafel aus
34 Fülle die Vier-Felder-Tafel aus P( ) =
35 Fülle die Vier-Felder-Tafel aus P( ) = 279
36 Fülle die Vier-Felder-Tafel aus P( ) =
37 Fülle die Vier-Felder-Tafel aus P( ) = = 0,283
Vier-Felder-Tafel und bedingte Wahrscheinlichkeit
 Vier-Felder-Tafel und bedingte Wahrscheinlichkeit erkrankt nicht erkrankt geimpft 47 125 nicht geimpft 21 Summe 201 Ergänze die Vier-Felder-Tafel und stelle die Zusammenhänge in einem Pfaddiagramm dar,
Vier-Felder-Tafel und bedingte Wahrscheinlichkeit erkrankt nicht erkrankt geimpft 47 125 nicht geimpft 21 Summe 201 Ergänze die Vier-Felder-Tafel und stelle die Zusammenhänge in einem Pfaddiagramm dar,
Grundwasserschutzprogramm Graz bis Bad Radkersburg
 I36 658/2 147 0 100 155 152/1 150 151/2 153/2 152/2 149 148 211/1 566 210 200 300 Meter nlage 2-50 Karte 1 von 10 J13 378/1 344/6 390/7 343/5 376 482/3 377 343/7 344/5 343/12 495 344/7 353/4 353/1 505
I36 658/2 147 0 100 155 152/1 150 151/2 153/2 152/2 149 148 211/1 566 210 200 300 Meter nlage 2-50 Karte 1 von 10 J13 378/1 344/6 390/7 343/5 376 482/3 377 343/7 344/5 343/12 495 344/7 353/4 353/1 505
Bedingte Wahrscheinlichkeit
 Bedingte Wahrscheinlichkeit In einem Laden ist eine larmanlage eingebaut. Bei Einbruch gibt sie mit 99%-iger Wahrscheinlichkeit larm. Wenn in einer bestimmten Nacht kein Einbruch stattfindet, gibt sie
Bedingte Wahrscheinlichkeit In einem Laden ist eine larmanlage eingebaut. Bei Einbruch gibt sie mit 99%-iger Wahrscheinlichkeit larm. Wenn in einer bestimmten Nacht kein Einbruch stattfindet, gibt sie
Bedingte Wahrscheinlichkeit
 Bedingte Wahrscheinlichkeit In einem Laden ist eine Alarmanlage eingebaut. Bei Einbruch gibt sie mit 99%-iger Wahrscheinlichkeit Alarm. Wenn in einer bestimmten Nacht kein Einbruch stattfindet, gibt sie
Bedingte Wahrscheinlichkeit In einem Laden ist eine Alarmanlage eingebaut. Bei Einbruch gibt sie mit 99%-iger Wahrscheinlichkeit Alarm. Wenn in einer bestimmten Nacht kein Einbruch stattfindet, gibt sie
Vier-Felder-Tafel. Medizinische Tests sind grundsätzlich mit zwei Fehlern behaftet: 1. Erkrankte werden als gesund, 2. Gesunde als krank eingestuft.
 Vier-Felder-Tafel Mediziniche Tet ind grundätzlich mit zwei Fehlern behaftet:. Erkrankte werden al geund, 2. Geunde al krank eingetuft. Der. Fehler wird üblicherweie (nicht nur von Tet-Entwicklern) in
Vier-Felder-Tafel Mediziniche Tet ind grundätzlich mit zwei Fehlern behaftet:. Erkrankte werden al geund, 2. Geunde al krank eingetuft. Der. Fehler wird üblicherweie (nicht nur von Tet-Entwicklern) in
Mathematik EP - Stochastik VIERFELDERTAFEL UND BEDINGTE WKT.
 Mathematik EP - Stochastik VIERFELDERTAFEL UND BEDINGTE WKT. HIV - SCHNELLTEST Die Immunschwächekrankheit AIDS wird durch das HI-Virus, welches 1993 entdeckt wurde, verursacht. Die Krankheit gilt bis heute
Mathematik EP - Stochastik VIERFELDERTAFEL UND BEDINGTE WKT. HIV - SCHNELLTEST Die Immunschwächekrankheit AIDS wird durch das HI-Virus, welches 1993 entdeckt wurde, verursacht. Die Krankheit gilt bis heute
Für die Wahrscheinlichkeit P A (B) des Eintretens von B unter der Bedingung, dass das Ereignis A eingetreten ist, ist dann gegeben durch P(A B) P(A)
 3. Bedingte Wahrscheinlichkeit ================================================================== 3.1 Vierfeldertafel und Baumdiagramm Sind A und B zwei Ereignisse, dann nennt man das Schema B B A A P
3. Bedingte Wahrscheinlichkeit ================================================================== 3.1 Vierfeldertafel und Baumdiagramm Sind A und B zwei Ereignisse, dann nennt man das Schema B B A A P
Mathematik EP - Stochastik VIERFELDERTAFEL UND BAUMDIAGRAMM
 Mathematik EP - Stochastik VIERFELDERTAFEL UND BAUMDIAGRAMM HIV - SCHNELLTEST Die Immunschwächekrankheit AIDS wird durch das HI-Virus, welches 1993 entdeckt wurde, verursacht. Die Krankheit gilt bis heute
Mathematik EP - Stochastik VIERFELDERTAFEL UND BAUMDIAGRAMM HIV - SCHNELLTEST Die Immunschwächekrankheit AIDS wird durch das HI-Virus, welches 1993 entdeckt wurde, verursacht. Die Krankheit gilt bis heute
Bayern Aufgabe 1. Abitur Mathematik: Musterlösung
 Abitur Mathematik: Bayern 2013 Aufgabe 1 a) 1. SCHRITT: SITUATION MODELLIEREN Es handelt sich näherungsweise um eine Bernoullikette der Länge n = 25 mit Erfolgswahrscheinlichkeit p = 0,37 + 0,06 = 0,43.
Abitur Mathematik: Bayern 2013 Aufgabe 1 a) 1. SCHRITT: SITUATION MODELLIEREN Es handelt sich näherungsweise um eine Bernoullikette der Länge n = 25 mit Erfolgswahrscheinlichkeit p = 0,37 + 0,06 = 0,43.
Zu jeder Aufgabe darf nur eine Lösung eingereicht werden. Mehrfache Lösungen für eine Aufgabe werden nicht bewertet.
 Kantonsschule Zürcher Oberland Wetzikon Mathematik M6b Maturitätsprüfungen 2012 schriftlich Dauer: 4 Stunden Name: Punkte (max 58): Note: Die Aufgaben dürfen in beliebiger Reihenfolge gelöst werden. Beginnen
Kantonsschule Zürcher Oberland Wetzikon Mathematik M6b Maturitätsprüfungen 2012 schriftlich Dauer: 4 Stunden Name: Punkte (max 58): Note: Die Aufgaben dürfen in beliebiger Reihenfolge gelöst werden. Beginnen
Sobald bei einem Zufallsexperiment zusätzliche Bedingungen zutreffen ändern sich i.a. die Wahrscheinlichkeiten.
 26 6. Bedingte Wahrscheinlichkeit Sobald bei einem Zufallsexperiment zusätzliche Bedingungen zutreffen ändern sich i.a. die Wahrscheinlichkeiten. Alarmanlage Tritt bei einer Sicherungsanlage ein Alarm
26 6. Bedingte Wahrscheinlichkeit Sobald bei einem Zufallsexperiment zusätzliche Bedingungen zutreffen ändern sich i.a. die Wahrscheinlichkeiten. Alarmanlage Tritt bei einer Sicherungsanlage ein Alarm
(d) 1,5 1, 02 2x 1 = x x = 2
 KLASSENARBEIT MATHEMATIK G9A 14.03.013 Aufgabe 1 3 4 5 Punkte (max) 11 4 4 4 3 Punkte (1) Löse folgende Gleichungen. (a) x 3 5x + x = 0 (b) 4x 4 + 11x 3 = 0 (c) 1 x = 1 7 (e) (x + 17)(x 16) = 0 (f) (d)
KLASSENARBEIT MATHEMATIK G9A 14.03.013 Aufgabe 1 3 4 5 Punkte (max) 11 4 4 4 3 Punkte (1) Löse folgende Gleichungen. (a) x 3 5x + x = 0 (b) 4x 4 + 11x 3 = 0 (c) 1 x = 1 7 (e) (x + 17)(x 16) = 0 (f) (d)
K f. 3.4 Monotonie. I. Zusammenfassung der Analysis. Gilt im x-bereich:
 I. Zusammenfassung der Analysis 3.4 Monotonie Definition Gilt im x-bereich: f ( x )>0 f ( x)
I. Zusammenfassung der Analysis 3.4 Monotonie Definition Gilt im x-bereich: f ( x )>0 f ( x)
1 Du sollst auf diesem «Lottoschein» Zahlen ankreuzen.
 Roulette und Zahlenlotto 18 1 5 1 Du sollst auf diesem «Lottoschein» Zahlen ankreuzen. 1 2 3 4 5 6 7 8 9 Wie viele Möglichkeiten hast du, wenn du A zwei Zahlen ankreuzen darfst? = 9 8 2 1 B zwei gerade
Roulette und Zahlenlotto 18 1 5 1 Du sollst auf diesem «Lottoschein» Zahlen ankreuzen. 1 2 3 4 5 6 7 8 9 Wie viele Möglichkeiten hast du, wenn du A zwei Zahlen ankreuzen darfst? = 9 8 2 1 B zwei gerade
Stochastik in der Einführungsphase Bedingte Wahrscheinlichkeiten 1/6
 Stochastik in der Einführungsphase Bedingte Wahrscheinlichkeiten 1/6 Aufgabe 1 : In Köln findet man am Rosenmontag unter den Karnevalisten bzw. Narren entlang des Zugweges 7mal so viele Touristen wie Einheimische.
Stochastik in der Einführungsphase Bedingte Wahrscheinlichkeiten 1/6 Aufgabe 1 : In Köln findet man am Rosenmontag unter den Karnevalisten bzw. Narren entlang des Zugweges 7mal so viele Touristen wie Einheimische.
Abitur 2011 G8 Abitur Mathematik Stochastik IV
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2011 G8 Abitur Mathematik Stochastik IV Auf der Strecke München-Tokio bietet eine Fluggesellschaft ihren Passagieren verschiedene Menüs an, darunter
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2011 G8 Abitur Mathematik Stochastik IV Auf der Strecke München-Tokio bietet eine Fluggesellschaft ihren Passagieren verschiedene Menüs an, darunter
Mathematik Lösung Klassenarbeit Nr. 2 Klasse 10a
 Der GTR ist erlaubt, wird mitunter wirklich benötigt. Bitte lest die Lösungen in Ruhe durch. Ich hoffe sie sind so ausführlich, dass jeder alle Zwischenschritte versteht. Wenn nicht, meldet Euch bitte.
Der GTR ist erlaubt, wird mitunter wirklich benötigt. Bitte lest die Lösungen in Ruhe durch. Ich hoffe sie sind so ausführlich, dass jeder alle Zwischenschritte versteht. Wenn nicht, meldet Euch bitte.
Prüfung Prüfung nicht. Raucher 0,15 0,25 0,40 Nichtraucher 0,50 0,10 0,60 0,65 0,35 1,00
 7 Stochastische Unabhängigkeit Kommen wir noch einmal zu dem Beispiel der Studenten (Raucher/Nicht-Raucher), die eine Prüfung bestanden bzw. nicht bestanden haben zurück. s ist bekannt, dass 40% der Studenten
7 Stochastische Unabhängigkeit Kommen wir noch einmal zu dem Beispiel der Studenten (Raucher/Nicht-Raucher), die eine Prüfung bestanden bzw. nicht bestanden haben zurück. s ist bekannt, dass 40% der Studenten
Vorträge der Hochschulen der
 BUGA 2011 Vorträge der Hochschulen der Region Mittelrhein Prof. Dr. Albert Brühl Philosophisch Theologische Hochschule Vallendar Pflegewissenschaftliche Fakultät Lehrstuhl Statistik und standardisierte
BUGA 2011 Vorträge der Hochschulen der Region Mittelrhein Prof. Dr. Albert Brühl Philosophisch Theologische Hochschule Vallendar Pflegewissenschaftliche Fakultät Lehrstuhl Statistik und standardisierte
3 = 93% (a) Berechnen Sie den Anteil der weiblichen Raucher unter den Betriebsangehörigen.
 Übungsblatt Wahrscheinlichkeit 1. Neun von zehn Ungeborenen bevorzugen im Mutterleib den rechten Daumen zum Lutschen. Forscher fanden heraus, dass alle Kinder, die rechts genuckelt hatten, im Alter von
Übungsblatt Wahrscheinlichkeit 1. Neun von zehn Ungeborenen bevorzugen im Mutterleib den rechten Daumen zum Lutschen. Forscher fanden heraus, dass alle Kinder, die rechts genuckelt hatten, im Alter von
Modul 8: Vierfeldertafel und Baumdiagramm (bedingte Wahrscheinlichkeit)
 odul 8: Vierfeldertafel und Baumdiagramm (bedingte ahrscheinlichkeit) Beispiel: Baumdiagramm in Vierfeldertafel Ein ufallsexperiment mit zwei Stufen lässt sich in eine Vierfeldertafel überführen. weimaliges
odul 8: Vierfeldertafel und Baumdiagramm (bedingte ahrscheinlichkeit) Beispiel: Baumdiagramm in Vierfeldertafel Ein ufallsexperiment mit zwei Stufen lässt sich in eine Vierfeldertafel überführen. weimaliges
Programm Katze und Maus von Julia Gräml, 7. Klasse
 Programm Katze und Maus von Julia Gräml, 7. Klasse käse:dreieck käseloch1:kreis käseloch2:kreis käseloch3:kreis mauskörper:ellipse mauskopf:kreis mausbein1:ellipse mausbein2:ellipse mausmund:ellipse mausauge1:kreis
Programm Katze und Maus von Julia Gräml, 7. Klasse käse:dreieck käseloch1:kreis käseloch2:kreis käseloch3:kreis mauskörper:ellipse mauskopf:kreis mausbein1:ellipse mausbein2:ellipse mausmund:ellipse mausauge1:kreis
Inhalt. Lektion 13: Mini-Digitaltechnik 13. MINI-DIGITALTECHNIK 9
 Inhalt 13. MINI-DIGITLTECHNIK 9 13.1 Logische Verknüpfungen 9 13.1.1 ND-Verknüpfung 9 13.1.2 ufstellung einer Wahrheitstabelle 10 13.1.3 ND-Verknüpfung mit Schalter 11 13.1.4 OR-Verknüpfung 13 13.1.5 NOT-Verknüpfung
Inhalt 13. MINI-DIGITLTECHNIK 9 13.1 Logische Verknüpfungen 9 13.1.1 ND-Verknüpfung 9 13.1.2 ufstellung einer Wahrheitstabelle 10 13.1.3 ND-Verknüpfung mit Schalter 11 13.1.4 OR-Verknüpfung 13 13.1.5 NOT-Verknüpfung
Probearbeit 13.1 Schuljahr 2010/11 Kernfach Mathematik
 Aufgabe 3: Stochastik Vorbemerkung: Führen Sie stets geeignete Zufallsvariablen und Namen für Ereignisse ein. Machen Sie auch Angaben über die Verteilung der jeweiligen Zufallsvariablen. a) Das unten stehende
Aufgabe 3: Stochastik Vorbemerkung: Führen Sie stets geeignete Zufallsvariablen und Namen für Ereignisse ein. Machen Sie auch Angaben über die Verteilung der jeweiligen Zufallsvariablen. a) Das unten stehende
P A P( A B) Definition Wahrscheinlichkeit
 Unabhaengige Ereignisse edingte Wahrscheinlichkeit Definition Wahrscheinlichkeit Die Wahrscheinlichkeit eines Ereignisses ist das Verhältnis der günstigen Ergebnisse zur Gesamtmenge der Ergebnisse nzahl
Unabhaengige Ereignisse edingte Wahrscheinlichkeit Definition Wahrscheinlichkeit Die Wahrscheinlichkeit eines Ereignisses ist das Verhältnis der günstigen Ergebnisse zur Gesamtmenge der Ergebnisse nzahl
Vierfeldertafel und bedingte Wahrscheinlichkeit. 1 Ereignisse und Vierfeldertafel
 Seite 9 9 Lösungen vorläufig Vierfeldertafel und bedingte Wahrscheinlichkeit IV Vierfeldertafel und bedingte Wahrscheinlichkeit Ereignisse und Vierfeldertafel S. 9 a) 0 b) Zwei Personen aus der 0C sind
Seite 9 9 Lösungen vorläufig Vierfeldertafel und bedingte Wahrscheinlichkeit IV Vierfeldertafel und bedingte Wahrscheinlichkeit Ereignisse und Vierfeldertafel S. 9 a) 0 b) Zwei Personen aus der 0C sind
Grundlagen der Mathematik II Lösungsvorschlag zum 10. Tutoriumsblatt
 Mathematisches Institut der Universität München Sommersemester 204 Daniel Rost Lukas-Fabian Moser Grundlagen der Mathematik II Lösungsvorschlag zum 0. Tutoriumsblatt ufgabe. Wir betrachten in einem geeigneten
Mathematisches Institut der Universität München Sommersemester 204 Daniel Rost Lukas-Fabian Moser Grundlagen der Mathematik II Lösungsvorschlag zum 0. Tutoriumsblatt ufgabe. Wir betrachten in einem geeigneten
Wohnungen (2)* Aufgabennummer: B_424. Technologieeinsatz: möglich erforderlich T
 Wohnungen (2)* Aufgabennummer: B_424 Technologieeinsatz: möglich erforderlich T Der Fachverband der Immobilien- und Vermögenstreuhänder erstellt Statistiken zu den Trends auf dem Immobilienmarkt. Es werden
Wohnungen (2)* Aufgabennummer: B_424 Technologieeinsatz: möglich erforderlich T Der Fachverband der Immobilien- und Vermögenstreuhänder erstellt Statistiken zu den Trends auf dem Immobilienmarkt. Es werden
Modul 203: Stochastische Unabhängigkeit!
 Modul 203: Stochastische Unabhängigkeit! 1 Alarm und falscher Alarm 2 Alarm und falscher Alarm Feuer kein Feuer 3 Alarm und falscher Alarm Feuer p = 0.001 kein Feuer p = 0.999 4 Alarm und falscher Alarm
Modul 203: Stochastische Unabhängigkeit! 1 Alarm und falscher Alarm 2 Alarm und falscher Alarm Feuer kein Feuer 3 Alarm und falscher Alarm Feuer p = 0.001 kein Feuer p = 0.999 4 Alarm und falscher Alarm
Musterlösung. Abitur Mathematik Bayern G Bayern Aufgabe 1. Abitur Mathematik: Musterlösung. Stochastik II
 Abitur Mathematik: Bayern 2012 Aufgabe 1 a) VIERFELDERTAFEL P(R ) = 88 % und P(V) = 18 % stehen in der Aufgabenstellung. 60 % in der Angabe stehen für die bedingte Wahrscheinlichkeit P R (V). P(R V) =
Abitur Mathematik: Bayern 2012 Aufgabe 1 a) VIERFELDERTAFEL P(R ) = 88 % und P(V) = 18 % stehen in der Aufgabenstellung. 60 % in der Angabe stehen für die bedingte Wahrscheinlichkeit P R (V). P(R V) =
Stochastik Pfadregeln Erwartungswert einer Zufallsvariablen Vierfeldertafel Gymnasium
 Stochastik Pfadregeln Erwartungswert einer Zufallsvariablen Vierfeldertafel Gymnasium Alexander Schwarz www.mathe-aufgaben.com Oktober 205 Aufgabe : In einer Urne befinden sich drei gelbe, eine rote und
Stochastik Pfadregeln Erwartungswert einer Zufallsvariablen Vierfeldertafel Gymnasium Alexander Schwarz www.mathe-aufgaben.com Oktober 205 Aufgabe : In einer Urne befinden sich drei gelbe, eine rote und
Achtung: Aufgabe 1: Händischer Teil ( maximal 15 Minuten ) S. 1 / 4 Mathematik Einführungsphase 1. Klausur (18 Punkte)
 . 1 / 4 Mathematik Einführungsphase 1. Klausur 16.09.2015 chtung: Bitte für jede ufgabe ein eigenes Blatt verwenden! Die Bearbeitungen müssen einen Lösungsweg enthalten, eine reine Ergebnisangabe reicht
. 1 / 4 Mathematik Einführungsphase 1. Klausur 16.09.2015 chtung: Bitte für jede ufgabe ein eigenes Blatt verwenden! Die Bearbeitungen müssen einen Lösungsweg enthalten, eine reine Ergebnisangabe reicht
"gehört" Mein Ohr an Gottes Herz. Unser Auftrag und wie wir ihn erfüllen können
 "gehört" Mein Ohr an Gottes Herz Unser Auftrag und wie wir ihn erfüllen können Gottes Auftrag an uns in dieser Welt! Gottes Macht und Herrschaft sichtbar machen Unser Auftrag und wie wir ihn erfüllen können
"gehört" Mein Ohr an Gottes Herz Unser Auftrag und wie wir ihn erfüllen können Gottes Auftrag an uns in dieser Welt! Gottes Macht und Herrschaft sichtbar machen Unser Auftrag und wie wir ihn erfüllen können
R R M 0,0187 0,4957 0,514 M 0,0021 0,4839 0,486 0,0208 0,9792 1,00
 8 edingte Wahrscheinlichkeit 8 edingte Wahrscheinlichkeit 8.1 Einführung und Definition Der Zusammenhang zwischen dem Geschlecht einer beliebig ausgewählten erson und einer eventuellen Rotgrünblindheit
8 edingte Wahrscheinlichkeit 8 edingte Wahrscheinlichkeit 8.1 Einführung und Definition Der Zusammenhang zwischen dem Geschlecht einer beliebig ausgewählten erson und einer eventuellen Rotgrünblindheit
Erläutere die Entstehung von Geräuschen. Wie gelangen sie in das Ohr?
 Was ist Schall? 1 Erläutere die Entstehung von Geräuschen. Wie gelangen sie in das Ohr? Geräusche entstehen durch (unregelmäßige) Schwingungen einer Schallquelle, z. B. durch Vibration einer Gitarrensaite
Was ist Schall? 1 Erläutere die Entstehung von Geräuschen. Wie gelangen sie in das Ohr? Geräusche entstehen durch (unregelmäßige) Schwingungen einer Schallquelle, z. B. durch Vibration einer Gitarrensaite
WIE SICHER IST DIE DIAGNOSE?
 WIE SICHER IST DIE DIAGNOSE? ÜBER DEN UMGANG MIT UNSICHERHEIT IN DER MEDIZIN Mag. Andrea Fried Bundesgeschäftsführerin ARGE Selbsthilfe Österreich 2.10.2014 1 2.10.2014 2 Der Fluch der Statistik Medizinische
WIE SICHER IST DIE DIAGNOSE? ÜBER DEN UMGANG MIT UNSICHERHEIT IN DER MEDIZIN Mag. Andrea Fried Bundesgeschäftsführerin ARGE Selbsthilfe Österreich 2.10.2014 1 2.10.2014 2 Der Fluch der Statistik Medizinische
r Oberflächeninhalt 1 Berechnungen am Kreis O 4r 1.1 Bogenmaß Das Bogenmaß x ist das zu gehörende Verhältnis Bogenlänge, also die 1.
 Grundwissen Mathematik 0 Berechnungen am Kreis. Bogenmaß Das Bogenmaß ist das zu gehörende Verhältnis Bogenlänge, also die Radius Zahl / r Umrechnungen: r r 0 30 45 60 90 360 0. Kreisteile Sektorfläche:.3
Grundwissen Mathematik 0 Berechnungen am Kreis. Bogenmaß Das Bogenmaß ist das zu gehörende Verhältnis Bogenlänge, also die Radius Zahl / r Umrechnungen: r r 0 30 45 60 90 360 0. Kreisteile Sektorfläche:.3
Musterlösung zur Übungsklausur Statistik
 Musterlösung zur Übungsklausur Statistik WMS4A Oettinger 6/205 Aufgabe (a) Falsch: der Modus ist die am häufigsten auftretende Merkmalsausprägung in einer Stichprobe. (b) Richtig: ein ordinales Merkmal
Musterlösung zur Übungsklausur Statistik WMS4A Oettinger 6/205 Aufgabe (a) Falsch: der Modus ist die am häufigsten auftretende Merkmalsausprägung in einer Stichprobe. (b) Richtig: ein ordinales Merkmal
$ 8, ) 5 1 <, % 5 1 % ', & 0 ) 77 ' % ) % % 7
 ! " # $ %$ & ' ( )* #+ #, -- &.* / & /.0#1-2 3043045#)*# 6630450 + 5 7 %,& / / 5 ' 38 / 96 30 45 * #)# 92 30 45 + 4 ' %#8 / ' 3:;2 30 45 8 / 4%3 0 72;47 0 & ' (; )* * % 5, / & /.0#1 5#)*# 5 0 + 5 36 3
! " # $ %$ & ' ( )* #+ #, -- &.* / & /.0#1-2 3043045#)*# 6630450 + 5 7 %,& / / 5 ' 38 / 96 30 45 * #)# 92 30 45 + 4 ' %#8 / ' 3:;2 30 45 8 / 4%3 0 72;47 0 & ' (; )* * % 5, / & /.0#1 5#)*# 5 0 + 5 36 3
5. KLASSENARBEIT MATHEMATIK G9A
 5. KLASSENARBEIT MATHEMATIK G9A 11.04.2014 Aufgabe 1 2 3 4 5 6 Punkte (max) 2 4 4 8 4 2 Punkte (1) Eine Münze wird dreimal geworfen. Gib zu jedem der folgenden Ereignisse das Gegenereignis an! (a) Man
5. KLASSENARBEIT MATHEMATIK G9A 11.04.2014 Aufgabe 1 2 3 4 5 6 Punkte (max) 2 4 4 8 4 2 Punkte (1) Eine Münze wird dreimal geworfen. Gib zu jedem der folgenden Ereignisse das Gegenereignis an! (a) Man
13. Jgst. 1. Kursarbeit Datum:
 13. Jgst. 1. Kursarbeit Datum: 22.09.2017 Klasse: BGY LK 2 Fach: Mathematik (Leistungsfach) Thema: Grundlagen W keit; Baumdiagramm; Pfadregeln; Erwartungswert; Kombi- natorik; Bedingte W keit Name: Punkte:
13. Jgst. 1. Kursarbeit Datum: 22.09.2017 Klasse: BGY LK 2 Fach: Mathematik (Leistungsfach) Thema: Grundlagen W keit; Baumdiagramm; Pfadregeln; Erwartungswert; Kombi- natorik; Bedingte W keit Name: Punkte:
Klausur: Stochastik Stochastik
 Stochastik Klausur zu Pfadregeln, bedingte Wahrscheinlichkeit, Erwartungswert einer Zufallsvariablen Vierfeldertafel berufliche Gymnasien Oberstufe Alexander Schwarz www.mathe-aufgaben.com Oktober 0 Aufgabe
Stochastik Klausur zu Pfadregeln, bedingte Wahrscheinlichkeit, Erwartungswert einer Zufallsvariablen Vierfeldertafel berufliche Gymnasien Oberstufe Alexander Schwarz www.mathe-aufgaben.com Oktober 0 Aufgabe
Mathematik 2 für Naturwissenschaften
 Hans Walser Mathematik 2 für Naturwissenschaften Modul 203 Stochastische Unabhängigkeit Hans Walser: Modul 203, Stochastische Unabhängigkeit ii Inhalt 1 Bedingte Wahrscheinlichkeit... 1 1.1 Feuermeldeanlage,
Hans Walser Mathematik 2 für Naturwissenschaften Modul 203 Stochastische Unabhängigkeit Hans Walser: Modul 203, Stochastische Unabhängigkeit ii Inhalt 1 Bedingte Wahrscheinlichkeit... 1 1.1 Feuermeldeanlage,
Beispielaufgaben Mathematik Leistungskurs
 Beispielaufgaben Land Zentrale schriftliche Abiturprüfung Beispielaufgaben Leistungskurs Aufgabenvorschlag Teil 1 für Prüflinge Hilfsmittel: Nachschlagewerk zur Rechtschreibung der deutschen Sprache nicht
Beispielaufgaben Land Zentrale schriftliche Abiturprüfung Beispielaufgaben Leistungskurs Aufgabenvorschlag Teil 1 für Prüflinge Hilfsmittel: Nachschlagewerk zur Rechtschreibung der deutschen Sprache nicht
Richtigkeitskriterium vs. Entscheidungsverfahren, tatsächlicher vs. erwarteter Nutzen (Zu Timmons, S )
 Richtigkeitskriterium vs. Entscheidungsverfahren, tatsächlicher vs. erwarteter Nutzen (Zu Timmons, S. 121 26) Einwand gegen den klassischen Utilitarismus: Das Nutzenprinzip ist unbrauchbar. Gemäß dem Nutzenprinzip
Richtigkeitskriterium vs. Entscheidungsverfahren, tatsächlicher vs. erwarteter Nutzen (Zu Timmons, S. 121 26) Einwand gegen den klassischen Utilitarismus: Das Nutzenprinzip ist unbrauchbar. Gemäß dem Nutzenprinzip
M Kreissektoren und Bogenmaß. Kreissektor mit Mittelpunktswinkel? Kreissektors mit Mittelpunktswinkel? Was versteht man unter dem Bogenmaß?
 M 10.1 Kreissektoren und Bogenmaß Wie berechnet man in einem Kreis mit Radius Kreissektor mit Mittelpunktswinkel? die Länge des Kreisbogens für einen Wie berechnet man in einem Kreis mit Radius Kreissektors
M 10.1 Kreissektoren und Bogenmaß Wie berechnet man in einem Kreis mit Radius Kreissektor mit Mittelpunktswinkel? die Länge des Kreisbogens für einen Wie berechnet man in einem Kreis mit Radius Kreissektors
Spezifische Mathematik Lösung Serie 2: Wahrsch.-Rechnung
 Dr. Rudolf Riedi HT-FR, 2016-17 Spezifische Mathematik Lösung Serie 2: Wahrsch.-Rechnung 1. (3 Punkte) Ein System besteht aus zwei Bauteilen. Die Wahrscheinlichkeit p1, dass Bauteil 1 ausfällt ist 0.5;
Dr. Rudolf Riedi HT-FR, 2016-17 Spezifische Mathematik Lösung Serie 2: Wahrsch.-Rechnung 1. (3 Punkte) Ein System besteht aus zwei Bauteilen. Die Wahrscheinlichkeit p1, dass Bauteil 1 ausfällt ist 0.5;
Ich denk an Dich! mit der Angehörigen-App GutGepflegt
 Ich denk an Dich! mit der n-app GutGepflegt Jetzt herunterladen, ausprobieren und ab August produktiv nutzen. Wenn pflegebedürftiger Menschen an ihre Lieben denken, bedrückt so manchen die Frage, ob die
Ich denk an Dich! mit der n-app GutGepflegt Jetzt herunterladen, ausprobieren und ab August produktiv nutzen. Wenn pflegebedürftiger Menschen an ihre Lieben denken, bedrückt so manchen die Frage, ob die
htw saar 1 KAPITEL 4 BEDINGTE WAHRSCHEINLICHKEIT UND STOCHASTISCHE UNABHÄNGIGKEIT Hans-Peter Hafner WS 2016/2017
 htw saar 1 KAPITEL 4 BEDINGTE WAHRSCHEINLICHKEIT UND STOCHASTISCHE UNABHÄNGIGKEIT htw saar 2 Gliederung 25.01. Bedingte Wahrscheinlichkeit: Motivation und Definition Multiplikationssatz Stochastische Unabhängigkeit:
htw saar 1 KAPITEL 4 BEDINGTE WAHRSCHEINLICHKEIT UND STOCHASTISCHE UNABHÄNGIGKEIT htw saar 2 Gliederung 25.01. Bedingte Wahrscheinlichkeit: Motivation und Definition Multiplikationssatz Stochastische Unabhängigkeit:
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Stochastik am von 10:00 bis 11:00 Uhr
 Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Stochastik am 5..201 von 10:00 bis 11:00 Uhr Bearbeiten Sie zwei der drei folgenden Aufgaben! Sätze aus der Vorlesung und den Übungen dürfen Sie ohne
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Stochastik am 5..201 von 10:00 bis 11:00 Uhr Bearbeiten Sie zwei der drei folgenden Aufgaben! Sätze aus der Vorlesung und den Übungen dürfen Sie ohne
Bitte lesen Sie die folgende Musteraufgabe konzentriert durch. Musteraufgabe I
 Bitte lesen Sie die folgende Musteraufgabe konzentriert durch. Musteraufgabe I Mit dem Ziel der Früherkennung von Brustkrebs werden Frauen angehalten, ab einem bestimmten Alter regelmäßig eine Röntgenuntersuchung
Bitte lesen Sie die folgende Musteraufgabe konzentriert durch. Musteraufgabe I Mit dem Ziel der Früherkennung von Brustkrebs werden Frauen angehalten, ab einem bestimmten Alter regelmäßig eine Röntgenuntersuchung
Aufgabe 2 (Lange Nacht der Museen?, chi^2, Kontingenzkoeffizient) 13 Punkte
 Gedächtnisprotokoll Statistik 1 1. Termin 2018/19 Aufgabe 1 (Median, IQA) - 10 Punkte Aufgabenstellung: Ein Sozialpsychologe führt eine Studie mit 2 Gruppen durch. Gruppe 1 bekommt eine Rechenaufgabe,
Gedächtnisprotokoll Statistik 1 1. Termin 2018/19 Aufgabe 1 (Median, IQA) - 10 Punkte Aufgabenstellung: Ein Sozialpsychologe führt eine Studie mit 2 Gruppen durch. Gruppe 1 bekommt eine Rechenaufgabe,
DER BUCHSTABENVOGEL 1
 Vorname... Datum... DER BUCHSTABENVOGEL 1 Schreibe folgende Wörter an die richtige Stelle: der Autor die Eule der Titel der Rabe Der Buchstabenvogel: Eveline Hasler: Richtig oder falsch, kreise ein: Der
Vorname... Datum... DER BUCHSTABENVOGEL 1 Schreibe folgende Wörter an die richtige Stelle: der Autor die Eule der Titel der Rabe Der Buchstabenvogel: Eveline Hasler: Richtig oder falsch, kreise ein: Der
Flacher Universal-Akku mit Micro USB-Anschluss, Lightning und USB Ladekabel
 Flacher Universal-Akku mit Micro USB-Anschluss, Lightning und USB Ladekabel 01 SICHERHEITSHINWEISE Bitte lesen Sie sich die folgenden Sicherheitshinweise genau durch, bevor Sie den iwalk verwenden. Falsche
Flacher Universal-Akku mit Micro USB-Anschluss, Lightning und USB Ladekabel 01 SICHERHEITSHINWEISE Bitte lesen Sie sich die folgenden Sicherheitshinweise genau durch, bevor Sie den iwalk verwenden. Falsche
In einem kartesischen Koordinatensystem ist der Körper ABCDPQRS mit A(28 0 0),
 IQB-Aufgabe Analytische Geometrie I In einem kartesischen Koordinatensystem ist der Körper ABCDPQRS mit A(28 0 0), B(28 10 0), C(0 10 0), D(0 0 0) und P(20 0 6) gegeben. Der Körper ist ein schiefes Prisma,
IQB-Aufgabe Analytische Geometrie I In einem kartesischen Koordinatensystem ist der Körper ABCDPQRS mit A(28 0 0), B(28 10 0), C(0 10 0), D(0 0 0) und P(20 0 6) gegeben. Der Körper ist ein schiefes Prisma,
Musterlösung. Modulklausur Multivariate Verfahren
 Musterlösung Modulklausur 31821 Multivariate Verfahren 25. September 2015 Aufgabe 1 (15 Punkte) Kennzeichnen Sie die folgenden Aussagen zur Regressionsanalyse mit R für richtig oder F für falsch. F Wenn
Musterlösung Modulklausur 31821 Multivariate Verfahren 25. September 2015 Aufgabe 1 (15 Punkte) Kennzeichnen Sie die folgenden Aussagen zur Regressionsanalyse mit R für richtig oder F für falsch. F Wenn
Name: 3. MATHEMATIKKLAUSUR
 Name: 3. MTHEMTIKKLUSUR 03.04.2003 M3 Mathe 12 K () Bearbeitungszeit: 135 min Seite 1 ufgabe 1: rundlagen der Wahrscheinlichkeitsrechnung a) Seine und B zwei Ereignisse mit den Wahrscheinlichkeiten P()
Name: 3. MTHEMTIKKLUSUR 03.04.2003 M3 Mathe 12 K () Bearbeitungszeit: 135 min Seite 1 ufgabe 1: rundlagen der Wahrscheinlichkeitsrechnung a) Seine und B zwei Ereignisse mit den Wahrscheinlichkeiten P()
Aufgaben zur Wahrscheinlichkeit. Beispielsammlung 5. Thema: Bedingte Wahrscheinlichkeiten. gemischt mit anderen Fragestellungen. Datei Nummer 32112
 Wahrscheinlichkeitsrechnung ufgaben zur Wahrscheinlichkeit eispielsammlung 5 Thema: edingte Wahrscheinlichkeiten gemischt mit anderen Fragestellungen Datei Nummer 32112 Stand 24. Januar 2019 INTERNETILIOTHE
Wahrscheinlichkeitsrechnung ufgaben zur Wahrscheinlichkeit eispielsammlung 5 Thema: edingte Wahrscheinlichkeiten gemischt mit anderen Fragestellungen Datei Nummer 32112 Stand 24. Januar 2019 INTERNETILIOTHE
Sprünge und Schleifen
 Sprünge Sprünge und Schleifen Sprünge werden in einem SPS Programm ausgeführt, wenn Teile von Schrittketten Programmen übersprungen werden sollen, um bestimmte Funktionen des Programms nicht ausführen
Sprünge Sprünge und Schleifen Sprünge werden in einem SPS Programm ausgeführt, wenn Teile von Schrittketten Programmen übersprungen werden sollen, um bestimmte Funktionen des Programms nicht ausführen
Faire Spiele, bedingte Wahrscheinlichkeit und Unabhängigkeit
 Faire Spiele, bedingte Wahrscheinlichkeit und Unabhängigkeit Dr. Elke Warmuth Sommersemester 2018 1 / 66 Faires Spiel Bedingte Wahrscheinlichkeit Verstehen des Konzepts Definition und Multiplikationsformel
Faire Spiele, bedingte Wahrscheinlichkeit und Unabhängigkeit Dr. Elke Warmuth Sommersemester 2018 1 / 66 Faires Spiel Bedingte Wahrscheinlichkeit Verstehen des Konzepts Definition und Multiplikationsformel
Thema: Eigenschaften von Funktionen (Wiederholung und Symmetrie, Nullstellen, Transformation)
 1. Halbjahr EF 2. Halbjahr EF Einführungsphase (EF) Vektoren, ein Schlüsselkonzept (Punkte, Vektoren, Rechnen mit Vektoren, Betrag) Eigenschaften von Funktionen (Wiederholung und Symmetrie, Nullstellen,
1. Halbjahr EF 2. Halbjahr EF Einführungsphase (EF) Vektoren, ein Schlüsselkonzept (Punkte, Vektoren, Rechnen mit Vektoren, Betrag) Eigenschaften von Funktionen (Wiederholung und Symmetrie, Nullstellen,
STATISTISCHE KRANKHEITSTESTS. Simon Schimpf und Nico Schmitt
 1 STATISTISCHE KRANKHEITSTESTS 18.11.2008 Simon Schimpf und Nico Schmitt Gliederung 2 Hintergrund des Themas (worum geht es Voraussetzungen Lernziele Die intuitive Herangehensweise ohne Satz von Bayes
1 STATISTISCHE KRANKHEITSTESTS 18.11.2008 Simon Schimpf und Nico Schmitt Gliederung 2 Hintergrund des Themas (worum geht es Voraussetzungen Lernziele Die intuitive Herangehensweise ohne Satz von Bayes
Mathematik Übersichtsraster Unterrichtsvorhaben EF bis Q2
 Mathematik Übersichtsraster Unterrichtsvorhaben EF bis Q2 Die Reihenfolge der Unterrichtsvorhaben hängt von den Vorgaben der Zentralklausuren ab und wird zu Beginn des Schuljahres von den in dieser Stufe
Mathematik Übersichtsraster Unterrichtsvorhaben EF bis Q2 Die Reihenfolge der Unterrichtsvorhaben hängt von den Vorgaben der Zentralklausuren ab und wird zu Beginn des Schuljahres von den in dieser Stufe
Diagnostische Verfahren
 6. Diagnostische s Jede Registrierung oder Auswertung einer Information mit dem Ziel der Erkennung einer Erung oder eines speziellen Zustandes wird diagnostischer genannt. Beispiele Reaktion auf Ansprechen
6. Diagnostische s Jede Registrierung oder Auswertung einer Information mit dem Ziel der Erkennung einer Erung oder eines speziellen Zustandes wird diagnostischer genannt. Beispiele Reaktion auf Ansprechen
13. Jgst. 2. Kursarbeit Datum:
 13. Jgst. 2. Kursarbeit Datum: 23.11.2017 Klasse: GY LK 2 Fach: Mathematik (Leistungsfach) Thema: edingte W keit & Vierfeldertafel; inomial- & Normalverteilung; Sigma-Intervalle Name: Punkte: Note: Aufgabe
13. Jgst. 2. Kursarbeit Datum: 23.11.2017 Klasse: GY LK 2 Fach: Mathematik (Leistungsfach) Thema: edingte W keit & Vierfeldertafel; inomial- & Normalverteilung; Sigma-Intervalle Name: Punkte: Note: Aufgabe
Illustrierende Aufgaben zum LehrplanPLUS. Kandidatensuche für ein Fernsehquiz
 Kandidatensuche für ein Fernsehquiz Stand: 29.09.2017 Jahrgangsstufen Fach/Fächer FOS 11 (NT), BOS 12 (NT), FOS/BOS 13 (T) Mathematik Übergreifende Bildungs- und Erziehungsziele Zeitrahmen Benötigtes Material
Kandidatensuche für ein Fernsehquiz Stand: 29.09.2017 Jahrgangsstufen Fach/Fächer FOS 11 (NT), BOS 12 (NT), FOS/BOS 13 (T) Mathematik Übergreifende Bildungs- und Erziehungsziele Zeitrahmen Benötigtes Material
Primer: Inferenzstatistik 1.0
 : 1.0 Dr. Malte Persike [email protected] methodenlehre.com twitter.com/methodenlehre methodenlehre.com/g+ iversity.org/schoolinger Inhalte der nächsten Minuten Die Frage aller Fragen: Ist etwas groß?
: 1.0 Dr. Malte Persike [email protected] methodenlehre.com twitter.com/methodenlehre methodenlehre.com/g+ iversity.org/schoolinger Inhalte der nächsten Minuten Die Frage aller Fragen: Ist etwas groß?
Mathematik. Abiturprüfung Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten
 Mathematik Abiturprüfung 2018 Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
Mathematik Abiturprüfung 2018 Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
Das Bandtagebuch mit EINSHOCH6 Folge 35: IN DER BÄCKEREI
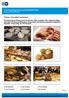 Übung 1: Was gehört zusammen? Bearbeite diese Übung, bevor du dir das Video ansiehst. Hier siehst du Bilder aus einer Bäckerei in München. Ordne ihnen jeweils den passenden Begriff zu. Benutze, wenn nötig,
Übung 1: Was gehört zusammen? Bearbeite diese Übung, bevor du dir das Video ansiehst. Hier siehst du Bilder aus einer Bäckerei in München. Ordne ihnen jeweils den passenden Begriff zu. Benutze, wenn nötig,
Seminar. Nur gucken nicht anfassen!
 Seminar Nur gucken nicht anfassen! vom 19. bis 21. Oktober 2018 im Jugendhotel Ostel Bremervörde Informationen Das Seminar ist für Männer und Frauen jeden Alters Inhalt: Ein kleiner Flirt, die große Liebe
Seminar Nur gucken nicht anfassen! vom 19. bis 21. Oktober 2018 im Jugendhotel Ostel Bremervörde Informationen Das Seminar ist für Männer und Frauen jeden Alters Inhalt: Ein kleiner Flirt, die große Liebe
Stochastik Musterlösung 2
 ETH Zürich HS 2018 RW, D-MATL, D-MAVT Prof. Marloes H. Maathuis Koordinator Dr. Marvin S. Müller Stochastik Musterlösung 2 1. Wir betrachten folgende vier Wettersituationen. Es regnet nur am Morgen; Es
ETH Zürich HS 2018 RW, D-MATL, D-MAVT Prof. Marloes H. Maathuis Koordinator Dr. Marvin S. Müller Stochastik Musterlösung 2 1. Wir betrachten folgende vier Wettersituationen. Es regnet nur am Morgen; Es
M 10.1. Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß Wie berechnet man in einem Kreis mit Radius die Länge des Kreisbogens für einen Kreissektor mit Mittelpunktswinkel? Wie berechnet man in einem Kreis mit Radius den Flächeninhalt
M 10.1 Kreissektoren und Bogenmaß Wie berechnet man in einem Kreis mit Radius die Länge des Kreisbogens für einen Kreissektor mit Mittelpunktswinkel? Wie berechnet man in einem Kreis mit Radius den Flächeninhalt
M 10.1. Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß Wie berechnet man in einem Kreis mit Radius die Länge des Kreisbogens für einen Kreissektor mit Mittelpunktswinkel? Wie berechnet man in einem Kreis mit Radius den Flächeninhalt
M 10.1 Kreissektoren und Bogenmaß Wie berechnet man in einem Kreis mit Radius die Länge des Kreisbogens für einen Kreissektor mit Mittelpunktswinkel? Wie berechnet man in einem Kreis mit Radius den Flächeninhalt
Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 10
 RMG Haßfurt Grundwissen Mathematik Jahrgangsstufe 0 Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 0 Wissen und Können. Berechnungen am Kreis Bogenmaß Das Bogenmaß ist das zu
RMG Haßfurt Grundwissen Mathematik Jahrgangsstufe 0 Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 0 Wissen und Können. Berechnungen am Kreis Bogenmaß Das Bogenmaß ist das zu
Wahrscheinlichkeitsrechnung
 Kapitel 3 Wahrscheinlichkeitsrechnung Beispiele Beispiel 3.1 Im Lotto aus 45 besteht ein Tipp aus dem Setzen von Zahlen zwischen 1 und 45. Wie groß ist die Wahrscheinlichkeit für den Gewinn in den folgenden
Kapitel 3 Wahrscheinlichkeitsrechnung Beispiele Beispiel 3.1 Im Lotto aus 45 besteht ein Tipp aus dem Setzen von Zahlen zwischen 1 und 45. Wie groß ist die Wahrscheinlichkeit für den Gewinn in den folgenden
Wiederholung der 2. Schularbeit aus. Mathematik und Angewandte Mathematik
 Wiederholung der. Schularbeit aus Mathematik und Angewandte Mathematik Montag,. April 06 5. Jahrgänge NAME: Punkte:. von 40 Note:.. Notenschlüssel Sehr Gut Gut Befriedigend Genügend Nicht Genügend 40 35
Wiederholung der. Schularbeit aus Mathematik und Angewandte Mathematik Montag,. April 06 5. Jahrgänge NAME: Punkte:. von 40 Note:.. Notenschlüssel Sehr Gut Gut Befriedigend Genügend Nicht Genügend 40 35
Pädagogische Arbeitsblätter zu Band 272 : von Saskia Hula Eine Maus kommt groß heraus Seite 23-30
 ine Maus kommt groß heraus Seite 23-30 Bei den folgenden Sätzen ist bei jeder Nummer eine falsche Antwort dabei. * Suche sie heraus und streiche sie durch! 1. Löwe fühlte sich sehr krank und Maus meinte:
ine Maus kommt groß heraus Seite 23-30 Bei den folgenden Sätzen ist bei jeder Nummer eine falsche Antwort dabei. * Suche sie heraus und streiche sie durch! 1. Löwe fühlte sich sehr krank und Maus meinte:
1. Grundbegri e der Stochastik
 Wiederholung von Grundwissen der Stochastik. Grundbegri e der Stochastik Menge der Ereignisse. Die Elemente! der Menge heißen Elementarereignisse und sind unzerlegbare Ereignisse. Das Ereignis A tritt
Wiederholung von Grundwissen der Stochastik. Grundbegri e der Stochastik Menge der Ereignisse. Die Elemente! der Menge heißen Elementarereignisse und sind unzerlegbare Ereignisse. Das Ereignis A tritt
Schallschutz gegen Aussen ein Praxisbeispiel
 Schallschutz gegen Aussen ein Praxisbeispiel Markus Strobel, dipl. Arch. FH, dipl. Akustiker SGA Planteam GHS AG, Sempach-Station Inhalt: 1. Gesetzliche Anforderungen 2. Schallschutz-Nachweis 3. Praxisbeispiel
Schallschutz gegen Aussen ein Praxisbeispiel Markus Strobel, dipl. Arch. FH, dipl. Akustiker SGA Planteam GHS AG, Sempach-Station Inhalt: 1. Gesetzliche Anforderungen 2. Schallschutz-Nachweis 3. Praxisbeispiel
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Fit in Test und Klassenarbeit Mathematik 9./10. Klasse
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Fit in Test und Klassenarbeit Mathematik 9./10. Klasse Das komplette Material finden Sie hier: School-Scout.de Wolfgang Göbels Fit
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Fit in Test und Klassenarbeit Mathematik 9./10. Klasse Das komplette Material finden Sie hier: School-Scout.de Wolfgang Göbels Fit
Alles rund um das Shooting im Skript
 Alles rund um das Shooting im Skript Das Shooting im Skript ist sicherlich die wichtigste Skriptanwendung. Dabei sind einige Dinge zu beachten. Es gibt mehrere Methoden, per Skript eine Auslösung zu erzeugen.
Alles rund um das Shooting im Skript Das Shooting im Skript ist sicherlich die wichtigste Skriptanwendung. Dabei sind einige Dinge zu beachten. Es gibt mehrere Methoden, per Skript eine Auslösung zu erzeugen.
Ich-kann-Sätze für die 4. Klausur M EPh GK 4
 Ich-kann-Sätze für die 4. Klausur M EPh GK 4 Dies ist die Ich-kann-Satz-Liste (Checkliste) für die zentrale Mathematikklausur am 13.06.2019. Grundsätzlich können natürlich alle mathematischen Inhalte aus
Ich-kann-Sätze für die 4. Klausur M EPh GK 4 Dies ist die Ich-kann-Satz-Liste (Checkliste) für die zentrale Mathematikklausur am 13.06.2019. Grundsätzlich können natürlich alle mathematischen Inhalte aus
Notfall-Update beim ProfiLux 3 & 3.1
 Notfall-Update beim ProfiLux 3 & 3.1 Wenn das Update mit ProfiLuxControl fehlschlug dann ist es möglich mit einem speziellen Tool das Update durchzuführen. Erläuterungen zum Notfall-Update Wie in der Bedienungsanleitung
Notfall-Update beim ProfiLux 3 & 3.1 Wenn das Update mit ProfiLuxControl fehlschlug dann ist es möglich mit einem speziellen Tool das Update durchzuführen. Erläuterungen zum Notfall-Update Wie in der Bedienungsanleitung
Name: Klasse: Datum: Wie viele Kinder haben gelb als Lieblingsfarbe genannt? 7 Kinder 4 Kinder 6 Kinder 5 Kinder
 Nachtest Mathematik: Daten und Zufall 7/8 Name: Klasse: Datum: 1) In der Klasse 7a wurde eine Umfrage durchgeführt. Alle Kinder wurden nach ihrer Lieblingsfarbe befragt. Wie viele Kinder haben gelb als
Nachtest Mathematik: Daten und Zufall 7/8 Name: Klasse: Datum: 1) In der Klasse 7a wurde eine Umfrage durchgeführt. Alle Kinder wurden nach ihrer Lieblingsfarbe befragt. Wie viele Kinder haben gelb als
Stochastik. Grundwissenskatalog G8-Lehrplanstandard
 GRUNDWISSEN MATHEMATIK Stochastik Grundwissenskatalog G8-Lehrplanstandard Basierend auf den Grundwissenskatalogen des Rhöngymnasiums Bad Neustadt und des Kurt-Huber-Gymnasiums Gräfelfing J O H A N N E
GRUNDWISSEN MATHEMATIK Stochastik Grundwissenskatalog G8-Lehrplanstandard Basierend auf den Grundwissenskatalogen des Rhöngymnasiums Bad Neustadt und des Kurt-Huber-Gymnasiums Gräfelfing J O H A N N E
Binomialverteilung Poisson-Verteilung (Grenzfall der Binomialverteilung) Kontinuierliche Wahrscheinlichkeitsverteilung
 Grundlagen der Statistik Wahrscheinlichkeitsverteilungen Diskrete Wahrscheinlichkeitsverteilungen Binomialverteilung Poisson-Verteilung (Grenzfall der Binomialverteilung) Kontinuierliche Wahrscheinlichkeitsverteilung
Grundlagen der Statistik Wahrscheinlichkeitsverteilungen Diskrete Wahrscheinlichkeitsverteilungen Binomialverteilung Poisson-Verteilung (Grenzfall der Binomialverteilung) Kontinuierliche Wahrscheinlichkeitsverteilung
Abschlussprüfung Berufliche Oberschule 2012 Mathematik 12 Nichttechnik - S I - Lösung
 Abschlussprüfung Berufliche Oberschule 2012 Mathematik 12 Nichttechnik - S I - Lösung Bei den folgenden Aufgaben sollen relative Häufigkeiten als Wahrscheinlichkeiten interpretiert werden Teilaufgabe 10
Abschlussprüfung Berufliche Oberschule 2012 Mathematik 12 Nichttechnik - S I - Lösung Bei den folgenden Aufgaben sollen relative Häufigkeiten als Wahrscheinlichkeiten interpretiert werden Teilaufgabe 10
Dem Schimmel Keine Chance
 Dem Schimmel Keine Chance Die Einsparung von Heizenergie ist heute von größter Bedeutung. Allerdings heizen viele Menschen aus falsch verstandener Sparsamkeit zu wenig oder falsch. Die unangenehme Folge:
Dem Schimmel Keine Chance Die Einsparung von Heizenergie ist heute von größter Bedeutung. Allerdings heizen viele Menschen aus falsch verstandener Sparsamkeit zu wenig oder falsch. Die unangenehme Folge:
Bayes-Statistik F F F
 Bayes-Statistik In einem Gerichtsprozess mutmaßt ein Geschworener, dass der Angeklagte zu 40% schuldig ist. Nun werden jedoch Fingerabdrücke des Angeklagten am Tatort gefunden. Der Chefermittler behauptet,
Bayes-Statistik In einem Gerichtsprozess mutmaßt ein Geschworener, dass der Angeklagte zu 40% schuldig ist. Nun werden jedoch Fingerabdrücke des Angeklagten am Tatort gefunden. Der Chefermittler behauptet,

 Was bedeutet p
Was bedeutet p