Numerische Verfahren
|
|
|
- Elly Schubert
- vor 9 Jahren
- Abrufe
Transkript
1 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät 03 WS 13/14 Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 1 / 18
2 Inhalt Explizite Zeitschrittverfahren für DGL 1. Ordnung 1 Explizite Zeitschrittverfahren für DGL 1. Ordnung Einleitung Explizites Euler-Verfahren Runge-Kutta-Verfahren 4. Ordnung 2 3 DGL-Systeme 1. Ordnung 4 Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 2 / 18
3 Einleitung Einleitung Explizites Euler-Verfahren Runge-Kutta-Verfahren 4. Ordnung Gegeben sei das Anfangswertproblem: ẏ = f (t, y), y(t 0) = y 0 Aufgabe Berechnung eines Näherungswertes an der Stelle t n = b. y n y(b) mit der Diskretisierung: Zerlegung des Integrationsintervalles [a = t 0, b] in: a = t 0 < t 1 < < t n = b Feste Schrittweite: h = b a = t n i t i 1 Achtung: Der Stabilitätsbereich eines expliziten Einschrittverfahrens und damit die Schrittweite h sind beschränkt. Für zu große h divergiert das Verfahren. h ist auch nach unten beschränkt, da sonst die Rundungsfehler überwiegen! Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 3 / 18
4 Explizites Euler-Verfahren Einleitung Explizites Euler-Verfahren Runge-Kutta-Verfahren 4. Ordnung Fortschreiterichtung: Steigung in t i 1 Euler-Verfahren Gegeben: Anfangswert: (t 0, y 0 ), Schrittweite: h y i = y i 1 + h f (t i 1, y i 1 ), i = 1,..., n Globaler Diskretisierungsfehler: O(h). Verfahren 1. Ordnung (Konvergenz) Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 4 / 18
5 Runge-Kutta-Verfahren 4. Ordnung Einleitung Explizites Euler-Verfahren Runge-Kutta-Verfahren 4. Ordnung Fortschreiterichtung: mittlere Steigung: Berechnet aus den 4 Steigungen in t i 1, t i und 2 Punkten in der Mitte Runge-Kutta-Verfahren 4. Ordnung Gegeben: Anfangswert: (t 0, y 0), Schrittweite: h y i = y i (k1 + 2k2 + 2k3 + k4), 6 k 1 = h f (t i 1, y i 1) k 2 = h f (t i h, 2 yi k1) 2 k 3 = h f (t i h, 2 yi k2) 2 k 4 = h f (t i 1 + h, y i 1 + k 3) i = 1,..., n Globaler Diskretisierungsfehler: O(h 4 ). Verfahren 4. Ordnung (Konvergenz) Matlab: ode45(...). Dieses und entsprechende Verfahren sind mit automatischer Schrittweitensteuerung implementiert. Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 5 / 18
6 Implizites Euler-Verfahren Implizites Verfahren: Die Funktion f wird nicht an dem schon berechneten Punkt (t i 1, y i 1) ausgewertet, sondern an dem neuen Punkt (t i, y i) Implizites Euler-Verfahren Gegeben: Anfangswert: (t 0, y 0), Schrittweite: h y i = y i 1 + h f (t i, y i), i = 1,..., n Globaler Diskretisierungsfehler: O(h). Verfahren 1. Ordnung (Konvergenz) Das Verfahren ist unbeschränkt absolut stabil (A-stabil), d.h. h unterliegt aufgrund der Stabilität keiner Beschränkung nach oben. Es entsteht eine (nicht)-lineare Gleichung (bzw. System). Diese muss mit geeigneten (numerischen) Verfahren (z.b.) Newton-Verfahren, Fixpunktiteration) gelöst werden. Implizite Verfahren werden insbesondere zur Lösung von steifen DGL-Systemen genutzt. Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 6 / 18
7 DGL-Systeme 1. Ordnung DGL-Systeme 1. Ordnung Die numerischen Verfahren zur Lösung von DGLn 1. Ordnung lassen sich entsprechend auf Systeme 1. Ordnung übertragen. Die skalaren Operationen müssen als Vektoroperationen aufgefasst werden. DGL-System 1. Ordnung ẏ 1 = f 1 (t, y 1,..., y n ) ẏ 2 = f 2 (t, y 1,..., y n ). ẏ n = f n (t, y 1,..., y n ) : Vektorschreibweise: ẏ = F(t, y) mit den Anfangsbedingungen y 1 (t 0 ) = y (0) 1, y 2(t 0 ) = y (0) 2,..., y n(t 0 ) = y n (0) bzw. y(t 0 ) = y 0. Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 7 / 18
8 DGL-Systeme 1. Ordnung Explizites Euler-Verfahren für DGL-System 1. Ordnung Euler-Verfahren Gegeben: Anfangswerte: y 1 (t 0 ) = y (0) 1, y 2(t 0 ) = y (0) 2,..., y n(t 0 ) = y n (0) bzw. y(t 0 ) = y 0, Schrittweite: h y i = y i 1 + h F(t i 1, y i 1 ), i = 1,..., n Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 8 / 18
9 auf ein System 1. Ordnung () Die numerische Lösung von DGLn höherer Ordnung oder von Systemen, erfordert ein Umschreiben in die sogenannte (System 1. Ordnung). DGL n-ter Ordnung: y (n) = f (t, y, ẏ,..., y (n 1) ), Anfangsbedingungen: y(t 0), ẏ(t 0),..., y (n 1) (t 0) Zustandsgrößen: z 1 = y, z 2 = ẏ, z 3 = ÿ,... z n = y (n 1) Umformung in ein System 1. Ordnung: ż 1 = z 2, z 1(t 0) = y(t 0) ż 2 = z 3, z 2(t 0) = ẏ(t 0).,. ż n 1 = z n, z n 1(t 0) = y (n 2) (t 0) ż n = f (t, z 1,..., z n), z n(t 0) = y (n 1) (t 0) Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 9 / 18
10 für DGLn 2. Ordnung I DGL 2. Ordnung: ÿ = f (t, y, ẏ) mit AB: y(t 0 ) = y (0) 1, ẏ(t 0) = y (0) 2 lässt sich durch z 1 = y, z 2 = ẏ überführen in die : ż 1 = z 2, z 1 (t 0 ) = z (0) 1 = y (0) 1 ż 2 = f (t, z 1, z 2 ), z 2 (t 0 ) = z (0) 2 = y (0) 2 Vektorielle Schreibweise: ż = z 2 f (t, z) (1) Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 10 / 18
11 für DGLn 2. Ordnung II Euler-Verfahren für obiges System (1) Gegeben: Anfangswerte: (t 0, z (0) 1 ),(t 0, z (0) 2 ) Schrittweite: h, Schrittanzahl: m z (i) 1 = z (i 1) 1 + h z (i 1) 2 z (i) 2 = z (i 1) 2 + h f (t i 1, z (i 1) 1, z (i 1) 2 ) i = 1,..., m Vektorielle Schreibweise: z i = z i 1 + h ż i 1 Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 11 / 18
12 einer DGL 2. Ordnung: Punktpendel Nichtlineare DGL 2. Ordnung in ϕ: m l 2 ϕ(t) = m g l sin (ϕ(t)) ϕ(t) = g l sin (ϕ(t)) Anfangsbedingungen: Anfangswinkel: ϕ(0), Anfangswinkelgeschwindigkeit: ϕ(0) Zustandsgrößen: Lage: z 1(t) = ϕ(t), Geschwindigkeit: z 2(t) = ϕ(t) Umformung in ein System 1. Ordnung: ż 1 = z 2, z 1(0) = ϕ(0) ż 2 = g l sin (z 1(t)), z 2(0) = ϕ(0) Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 12 / 18
13 eines Systems 2. Ordnung: I System von DGL 2. Ordnung in y 1,..., y n: ÿ 1 = f 1(t, y 1,..., y n, ẏ 1..., ẏ n). ÿ n = f n(t, y 1,..., y n, ẏ 1..., ẏ n) Anfangsbedingungen: y 1(t 0),..., y n(t 0), ẏ 1(t 0),..., ẏ n(t 0) Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 13 / 18
14 eines Systems 2. Ordnung: II Zustandsgrößen: z 1 = y 1,..., z n = y n z n+1 = ẏ 1,..., z 2n = ẏ n Umformung in ein System 1. Ordnung: ż 1 = z n+1, z 1(t 0) = y(t 0).,. ż n = z 2n, z n(t 0) = y n(t 0) ż n+1 = f 1(t, z 1,..., z n, z n+1..., z 2n), z n+1(t 0) = ẏ 1(t 0).,. ż 2n = f n(t, z 1,..., z n, z n+1..., z 2n), z 2n(t 0) = ẏ n(t 0) Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 14 / 18
15 eines Systems 2. Ordnung: Federpendel I System von DGL 2. Ordnung in ϕ, l: m (l(t) ϕ(t) + 2 l(t) ϕ(t)) = mg sin(ϕ(t)) m ( l(t) l(t) ϕ 2 (t)) = c(l(t) l F ) + mg cos(ϕ(t)) ϕ(t) = 1 l ( g sin(ϕ(t)) 2 l(t) ϕ(t)) l(t) = c m (l(t) l F) + g cos(ϕ(t)) + l(t) ϕ 2 (t) Anfangsbedingungen: Anfangslage: ϕ(0), l(0) Anfangswinkelgeschwindigkeit: ϕ(0), l(0) Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 15 / 18
16 eines Systems 2. Ordnung: Federpendel II Zustandsgrößen: Lage: z 1(t) = ϕ(t), z 2(t) = l(t) Geschwindigkeit: z 3(t) = ϕ(t), z 4(t) = l(t) Umformung in ein System 1. Ordnung: ż 1 = z 3, z 1(0) = ϕ(0) ż 2 = z 4, z 2(0) = l(0) ż 3 = 1 z 2 (g sin(z 1) + 2z 4z 3), z 3(0) = ϕ(0) ż 4 = c m (z2 l F) + g cos(z 1) + z 2z3 2, z 4(0) = l(0) Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 16 / 18
17 eines Systems 2. Ordnung: Massenmatrix I Falls das DGL-System nicht in expliziter Form gegeben ist und sich nur schwer nach den 2. Ableitungen auflösen lässt (starke Kopplung), ist eine andere Vorgehensweise zu empfehlen. System von 2 DGL (linear in den 2. Ableitungen) a 11ÿ 1 + a 12ÿ 2 = f 1(t, y 1, y 2, ẏ 1, ẏ 2) a 21ÿ 1 + a 22ÿ 2 = f 2(t, y 1, y 2, ẏ 1, ẏ 2) a ij können von t, y 1, y 2, ẏ 1 und ẏ 2 aber nicht von ÿ 1 und ÿ 2 abhängen. Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 17 / 18
18 eines Systems 2. Ordnung: Massenmatrix II Zustandsgrößen: z 1 = y 1, z 2 = y 2, z 3 = ẏ 1, z 4 = ẏ 2 ż 1 = z 3, z 1 (t 0 ) = y 1 (t 0 ) ż 2 = z 4, z 2 (t 0 ) = y 2 (t 0 ) a 11 ż 3 + a 12 ż 4 = f 1 (t, z 1, z 2, z 3, z 4 ), z 3 (t 0 ) = ẏ 1 (t 0 ) a 21 ż 3 + a 22 ż 4 = f 2 (t, z 1, z 2, z 3, z 4 ), z 4 (t 0 ) = ẏ 2 (t 0 ) Matrix-Schreibweise: ż 1 z ż 2 = z a 11 a 12 ż 3 f 1 (t, z 1, z 2, z 3, z 4 ) 0 0 a 21 a 22 }{{} Massenmatrix: M=M(t, z) ż 4 }{{} ż f 2 (t, z 1, z 2, z 3, z 4 ) }{{} F(t, z) Matlab kann diese gekoppelten Differentialgleichungen lösen. Dazu muss M mit dem Befehl odeset( bekannt gemacht werden. Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14 18 / 18
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Dierentialgleichungen 2. Ordnung
 Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
Numerische Integration von Differential-Gleichungen Das klassische Runge-Kutta-Verfahren
 Numerische Integration von Differential-Gleichungen Das klassische Runge-Kutta-Verfahren Gegeben sei ein Anfangswertproblem erster Ordnung: y = f (x;y y(x 0 = y 0 Wie schon erörtert, beschreibt eine DGl
Numerische Integration von Differential-Gleichungen Das klassische Runge-Kutta-Verfahren Gegeben sei ein Anfangswertproblem erster Ordnung: y = f (x;y y(x 0 = y 0 Wie schon erörtert, beschreibt eine DGl
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan :00-14:00 (120 min)
 Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm
 Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm Numerik Parameterschätzprobleme INHALT 1. 1D Wärmeleitungsgleichung 1.1 Finite-Differenzen-Diskretisierung
Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm Numerik Parameterschätzprobleme INHALT 1. 1D Wärmeleitungsgleichung 1.1 Finite-Differenzen-Diskretisierung
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Differenzialgleichungen erster Ordnung
 Differenzialgleichungen erster Ordnung Fakultät Grundlagen Mai 2011 Fakultät Grundlagen Differenzialgleichungen erster Ordnung Übersicht Grundsätzliches 1 Grundsätzliches Geometrische Deutung Numerik 2
Differenzialgleichungen erster Ordnung Fakultät Grundlagen Mai 2011 Fakultät Grundlagen Differenzialgleichungen erster Ordnung Übersicht Grundsätzliches 1 Grundsätzliches Geometrische Deutung Numerik 2
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
Parareal. Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen. Johannes Reinhardt. Parareal 1 Johannes Reinhardt
 Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
4 Gewöhnliche Differentialgleichungen
 4 Gewöhnliche Differentialgleichungen 4.1 Einleitung Definition 4.1 Gewöhnliche Differentialgleichung n-ter Ordnung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten
4 Gewöhnliche Differentialgleichungen 4.1 Einleitung Definition 4.1 Gewöhnliche Differentialgleichung n-ter Ordnung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten
Differentialgleichungen
 Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
D-MATH Numerische Methoden FS 2018 Dr. Vasile Gradinaru Kjetil Olsen Lye. Serie 6
 D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. [email protected]
D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. [email protected]
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
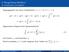 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Numerische Verfahren
 Numerische Verfahren Interpolation Prof Dr-Ing K Warendorf, Prof Dr-Ing P Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät 03 WS 13/14 Prof Dr-Ing K Warendorf (Fakultät 03) Numerische
Numerische Verfahren Interpolation Prof Dr-Ing K Warendorf, Prof Dr-Ing P Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät 03 WS 13/14 Prof Dr-Ing K Warendorf (Fakultät 03) Numerische
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
Ingenieurinformatik II Numerik für Ingenieure Teil 2
 Hochschule München, FK 03 MB SS 013 Name Vorname Matrikelnummer Sem.Gr. Hörsaal Platz Ingenieurinformatik II Numerik für Ingenieure Teil Bearbeitungszeit : 60 Minuten Aufgabensteller : Dr. Reichl Hilfsmittel
Hochschule München, FK 03 MB SS 013 Name Vorname Matrikelnummer Sem.Gr. Hörsaal Platz Ingenieurinformatik II Numerik für Ingenieure Teil Bearbeitungszeit : 60 Minuten Aufgabensteller : Dr. Reichl Hilfsmittel
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Übung zur Vorlesung Numerische Simulationsmethoden in der Geophysik
 Wenke Wilhelms, Julia Weißflog Institut für Geophysik und Geoinformatik Übung zur Vorlesung Numerische Simulationsmethoden in der Geophysik 04. Dezember 2013 Die Diffusionsgleichung 1D-Wärmeleitungsgleichung...
Wenke Wilhelms, Julia Weißflog Institut für Geophysik und Geoinformatik Übung zur Vorlesung Numerische Simulationsmethoden in der Geophysik 04. Dezember 2013 Die Diffusionsgleichung 1D-Wärmeleitungsgleichung...
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
11. Einschrittverfahren
 H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
Numerische Lösung von Differentialgleichungen
 Numerische Lösung von Differentialgleichungen Matheseminar 2017 Daniel Jodlbauer 9. Juni 2017 Überblick Motivation Voraussetzungen / Wiederholung Differentialgleichungen Lösungsverfahren Differentialgleichungen?
Numerische Lösung von Differentialgleichungen Matheseminar 2017 Daniel Jodlbauer 9. Juni 2017 Überblick Motivation Voraussetzungen / Wiederholung Differentialgleichungen Lösungsverfahren Differentialgleichungen?
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 2
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Euler-Verfahren. exakte Lösung. Euler-Streckenzüge. Folie 1
 exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
12 Gewöhnliche Differentialgleichungen
 12 Gewöhnliche Differentialgleichungen 121 Einführende Beispiele und Grundbegriffe Beispiel 1 ( senkrechter Wurf ) v 0 Ein Flugkörper werde zum Zeitpunkt t = 0 in der Höhe s = 0 t = 0 s = 0 mit der Startgeschwindigkeit
12 Gewöhnliche Differentialgleichungen 121 Einführende Beispiele und Grundbegriffe Beispiel 1 ( senkrechter Wurf ) v 0 Ein Flugkörper werde zum Zeitpunkt t = 0 in der Höhe s = 0 t = 0 s = 0 mit der Startgeschwindigkeit
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
4.3 Anwendungen auf Differentialgleichungen
 7 4.3 Anwendungen auf Differentialgleichungen Die Laplace-Transformation wird gerne benutzt, um lineare Differentialgleichungen mit konstanten Koeffizienten y n + a n y n +... + a y + a 0 y ft zu lösen,
7 4.3 Anwendungen auf Differentialgleichungen Die Laplace-Transformation wird gerne benutzt, um lineare Differentialgleichungen mit konstanten Koeffizienten y n + a n y n +... + a y + a 0 y ft zu lösen,
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
ETHZ, D-MATH. Numerische Methoden D-PHYS, WS 2015/16 Dr. V. Gradinaru
 ETHZ, D-MATH Prüfung Numerische Methoden D-PHYS, WS 5/6 Dr. V. Gradinaru..6 Prüfungsdauer: 8 Minuten Maximal erreichbare Punktzahl: 6. Der van-der-pol Oszillator ( Punkte) Der van-der-pol Oszillator kann
ETHZ, D-MATH Prüfung Numerische Methoden D-PHYS, WS 5/6 Dr. V. Gradinaru..6 Prüfungsdauer: 8 Minuten Maximal erreichbare Punktzahl: 6. Der van-der-pol Oszillator ( Punkte) Der van-der-pol Oszillator kann
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen
 Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Das Eulerverfahren zum numerischen Lösen von DGLen
 Das Eulerverfahren zum numerischen Lösen von DGLen Thomas Wassong FB17 Mathematik Universität Kassel 06.05.2008 Numerische Verfahren zur Berechnung von Differentialgleichungen Das Eulerverfahren: Programmierung
Das Eulerverfahren zum numerischen Lösen von DGLen Thomas Wassong FB17 Mathematik Universität Kassel 06.05.2008 Numerische Verfahren zur Berechnung von Differentialgleichungen Das Eulerverfahren: Programmierung
2. Quasilineare PDG erster Ordnung
 H.J. Oberle Differentialgleichungen II SoSe 2013 2. Quasilineare PDG erster Ordnung Eine skalare PDG erster Ordnung hat die allgemeine Form F (x, u(x), u x (x)) = 0. (2.1) Dabei ist u : R n G R die gesuchte
H.J. Oberle Differentialgleichungen II SoSe 2013 2. Quasilineare PDG erster Ordnung Eine skalare PDG erster Ordnung hat die allgemeine Form F (x, u(x), u x (x)) = 0. (2.1) Dabei ist u : R n G R die gesuchte
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik'
 Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Übungsaufgaben Mathematik III MST
 Übungsaufgaben Mathematik III MST Lösungen zu Blatt Differentialgleichungen Prof. Dr. B.Grabowski Zu Aufgabe ) Zu a) lassifizieren Sie folgende Differentialgleichungen nach folgenden riterien: -Ordnung
Übungsaufgaben Mathematik III MST Lösungen zu Blatt Differentialgleichungen Prof. Dr. B.Grabowski Zu Aufgabe ) Zu a) lassifizieren Sie folgende Differentialgleichungen nach folgenden riterien: -Ordnung
Lineare Differentialgleichungen erster und zweiter Ordnung
 Lineare Differentialgleichungen erster und zweiter Ordnung Jörn Loviscach Versionsstand: 11. Mai 2009, 18:13 1 DGLn erster Ordnung mit konstanten Koeffizienten Eine Differentialgleichung hat zwei Zutaten:
Lineare Differentialgleichungen erster und zweiter Ordnung Jörn Loviscach Versionsstand: 11. Mai 2009, 18:13 1 DGLn erster Ordnung mit konstanten Koeffizienten Eine Differentialgleichung hat zwei Zutaten:
Differentialgleichungen sind überall!
 Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
4 Runge-Kutta-Verfahren
 Numerik gewöhnlicher Differentialgleichungen 43 4 Runge-Kutta-Verfahren 4. Konstruktion Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0
Numerik gewöhnlicher Differentialgleichungen 43 4 Runge-Kutta-Verfahren 4. Konstruktion Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0
2. Übung: Lineare dynamische Systeme
 2. Übung: Lineare dynamische Systeme Aufgabe 2.. Gegeben sind die beiden autonomen Systeme und x (2.) {{ A 2 2 x. (2.2) {{ A 2 Berechnen Sie die regulären Zustandstransformationen x = V z und x = V 2 z,
2. Übung: Lineare dynamische Systeme Aufgabe 2.. Gegeben sind die beiden autonomen Systeme und x (2.) {{ A 2 2 x. (2.2) {{ A 2 Berechnen Sie die regulären Zustandstransformationen x = V z und x = V 2 z,
Numerische Verfahren
 Numerische Verfahren 1. Kapitel: Prof. Dr.-Ing. K. Warendorf Hochschule für Angewandte Wissenschaften München Fakultät 03 WS 13/14 Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14
Numerische Verfahren 1. Kapitel: Prof. Dr.-Ing. K. Warendorf Hochschule für Angewandte Wissenschaften München Fakultät 03 WS 13/14 Prof. Dr.-Ing. K. Warendorf (Fakultät 03) Numerische Verfahren WS 13/14
Dr. R. Käppeli D-ITET, D-MATL Sommer Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Kapitel 1 Gewöhnliche Differentialgleichungen
 Kapitel 1 Gewöhnliche Differentialgleichungen Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind Differentialgleichungen, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug
Kapitel 1 Gewöhnliche Differentialgleichungen Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind Differentialgleichungen, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug
2 Einschrittverfahren 2.1 Einführung
 Einschrittverfahren. Einführung Im folgenden werden wir uns bei der Beschreibung und Analyse von numerischen Verfahren für Anfangswertprobleme auf den Fall n = beschränken. Dies wird nur gemacht, um die
Einschrittverfahren. Einführung Im folgenden werden wir uns bei der Beschreibung und Analyse von numerischen Verfahren für Anfangswertprobleme auf den Fall n = beschränken. Dies wird nur gemacht, um die
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
8 Numerik gewöhnlicher Differentialgleichungen
 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 03 8 Numerik gewöhnlicher Differentialgleichungen 8. Grundlagen In der Numerik von gewöhnlichen Differentialgleichungen werden vorwiegend Aufgaben folgender
8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 03 8 Numerik gewöhnlicher Differentialgleichungen 8. Grundlagen In der Numerik von gewöhnlichen Differentialgleichungen werden vorwiegend Aufgaben folgender
BERGISCHE UNIVERSITÄT WUPPERTAL Fachbereich C Mathematik und Naturwissenschaften
 Musterl osung BERGISCHE UNIVERSITÄT WUPPERTAL Fachbereich C Mathematik und Naturwissenschaften Analysis II Klausur WS 211/212 Prof. Dr. Hartmut Pecher 3.2.212, 9:15 Uhr Name Matr.Nr. Studienfach Fachsemester
Musterl osung BERGISCHE UNIVERSITÄT WUPPERTAL Fachbereich C Mathematik und Naturwissenschaften Analysis II Klausur WS 211/212 Prof. Dr. Hartmut Pecher 3.2.212, 9:15 Uhr Name Matr.Nr. Studienfach Fachsemester
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
2. Übungsblatt zur Mathematik III für MB/MPE, LaB/WFM, VI, WI/MB
 Fachbereich Mathematik Prof. Dr. J. Lang Dipl.-Math. C. Schönberger Dipl.-Math. L. Kamenski WS 007/08 6.Oktober 007. Übungsblatt zur Mathematik III für MB/MPE, LaB/WFM, VI, WI/MB Gruppenübung Aufgabe G4
Fachbereich Mathematik Prof. Dr. J. Lang Dipl.-Math. C. Schönberger Dipl.-Math. L. Kamenski WS 007/08 6.Oktober 007. Übungsblatt zur Mathematik III für MB/MPE, LaB/WFM, VI, WI/MB Gruppenübung Aufgabe G4
Lösung Semesterendprüfung
 MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
T0: Rechenmethoden WiSe 2011/12. Lösungen: Ergänzungsaufgaben zur Klausurvorbereitung Differentialgleichungen
 T0: Rechenmethoden WiSe 20/2 Prof. Jan von Delft http://homepages.physik.uni-muenchen.de/~vondelft/lehre/2t0/ Lösungen: Ergänzungsaufgaben zur Klausurvorbereitung Differentialgleichungen Aufgabe. (**)
T0: Rechenmethoden WiSe 20/2 Prof. Jan von Delft http://homepages.physik.uni-muenchen.de/~vondelft/lehre/2t0/ Lösungen: Ergänzungsaufgaben zur Klausurvorbereitung Differentialgleichungen Aufgabe. (**)
Übungsaufgabe Numerische Lösung DGL
 Kallenrode, www.sotere.uos.de Übungsaufgabe Numerische Lösung DGL 1. Bestimmen Sie die Lösung der DGL ẋ = (t 2) 2 + t x mit x(0) = 1 im Bereich von t = 0 bis t = 5 mit Hilfe des Euler schen Streckenzugverfahrens,
Kallenrode, www.sotere.uos.de Übungsaufgabe Numerische Lösung DGL 1. Bestimmen Sie die Lösung der DGL ẋ = (t 2) 2 + t x mit x(0) = 1 im Bereich von t = 0 bis t = 5 mit Hilfe des Euler schen Streckenzugverfahrens,
Differentialgleichungen
 Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Differentialgleichungen
 Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
PVK Numerische Methoden Tag 1
 PVK Numerische Methoden Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G 23.8 8093 Zürich [email protected] June 19, 2017 Lucas Böttcher (ETH Zürich) PVK Numerik June 19,
PVK Numerische Methoden Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G 23.8 8093 Zürich [email protected] June 19, 2017 Lucas Böttcher (ETH Zürich) PVK Numerik June 19,
Kapitel L. Gewöhnliche Differentialgleichungen
 Kapitel L Gewöhnliche Differentialgleichungen Inhalt dieses Kapitels L000 1 Erste Beispiele von Differentialgleichungen 2 Exakte Differentialgleichungen 3 Fazit: Existenz, Eindeutigkeit, Lösungsmethoden
Kapitel L Gewöhnliche Differentialgleichungen Inhalt dieses Kapitels L000 1 Erste Beispiele von Differentialgleichungen 2 Exakte Differentialgleichungen 3 Fazit: Existenz, Eindeutigkeit, Lösungsmethoden
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 23
 Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure
 NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure Eine computerorientierte Einführung Von Prof. Dr. sc. nat. HUBERT SCHWETLICK Prof. Dr. sc. nat. HORST KRETZSCHMAR Mit 74 Bildern und 34 Tabellen
NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure Eine computerorientierte Einführung Von Prof. Dr. sc. nat. HUBERT SCHWETLICK Prof. Dr. sc. nat. HORST KRETZSCHMAR Mit 74 Bildern und 34 Tabellen
Numerische Mathematik I: Grundlagen
 Numerische Mathematik I: Grundlagen 09.10.2017 Inhalt der Lehrveranstaltung Inhaltlich sollen Sie in der Lehrveranstaltung Numerische Mathematik I insbesondere vertraut gemacht werden mit der Numerik linearer
Numerische Mathematik I: Grundlagen 09.10.2017 Inhalt der Lehrveranstaltung Inhaltlich sollen Sie in der Lehrveranstaltung Numerische Mathematik I insbesondere vertraut gemacht werden mit der Numerik linearer
Vorlesung, 26. Mai 2011, Inhalt. Eigenwerte und Eigenvektoren. Gewöhnliche Differentialgleichungen
 Vorlesung, 26. Mai 2011, Inhalt Eigenwerte und Eigenvektoren Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Es sei A eine n n-matrix, x ein vom Nullvektor verschiedener Vektor und λ
Vorlesung, 26. Mai 2011, Inhalt Eigenwerte und Eigenvektoren Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Es sei A eine n n-matrix, x ein vom Nullvektor verschiedener Vektor und λ
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
