PVK Numerische Methoden Tag 1
|
|
|
- Rainer Brandt
- vor 6 Jahren
- Abrufe
Transkript
1 PVK Numerische Methoden Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G Zürich lucasb@ethz.ch June 19, 2017 Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
2 Übersicht Daten und Zeiten: Kursdauer: von 08:00-12:30 Uhr Erste Lektion: 08:00-09:30 Uhr Pause: 09:30-09:45 Uhr Zweite Lektion: 09:45-11:15 Uhr Pause: 11:15-11:30 Uhr Dritte Lektion: 11:30-12:30 Uhr Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
3 Übersicht Ziel PVK: Vorbereitung auf die Prüfung (schriftlich, 180 min) am PC Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
4 Übersicht Ziel PVK: Vorbereitung auf die Prüfung (schriftlich, 180 min) am PC Erlaubte Hilfsmittel: 10 Seiten A4 eigenhändig verfasste Zusammenfassung, handgeschrieben, nicht ausgedruckt, nicht kopiert. Vorlesungsunterlagen stehen elektronisch während der Prüfung zur Verfügung. Sonst keine Hilfsmittel. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
5 Übersicht Kursziele laut VVZ: Studenten sind im Stande 1 zwischen verschiedenen numerischen Methoden zu differenzieren, um zu wissen, welche Methode ein bestimmtes mathematisches Problem löst. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
6 Übersicht Kursziele laut VVZ: Studenten sind im Stande 1 zwischen verschiedenen numerischen Methoden zu differenzieren, um zu wissen, welche Methode ein bestimmtes mathematisches Problem löst. 2 geeignete numerische Verfahren anzuwenden, um ein bestimmtes numerisches Problem der Physik zu lösen. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
7 Übersicht Kursziele laut VVZ: Studenten sind im Stande 1 zwischen verschiedenen numerischen Methoden zu differenzieren, um zu wissen, welche Methode ein bestimmtes mathematisches Problem löst. 2 geeignete numerische Verfahren anzuwenden, um ein bestimmtes numerisches Problem der Physik zu lösen. 3 geeignete Software Repositories anzuwenden, welche hilfreich sind, um ein gegebenes numerisches Problem zu lösen. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
8 Übersicht Kursziele laut VVZ: Studenten sind im Stande 1 zwischen verschiedenen numerischen Methoden zu differenzieren, um zu wissen, welche Methode ein bestimmtes mathematisches Problem löst. 2 geeignete numerische Verfahren anzuwenden, um ein bestimmtes numerisches Problem der Physik zu lösen. 3 geeignete Software Repositories anzuwenden, welche hilfreich sind, um ein gegebenes numerisches Problem zu lösen. 4 numerische Resultate, welche durch das numerische lösen mathematischer Probleme erhalten wurden, hinsichtlich Genauigkeit und Korrektheit zu interpretieren. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
9 Übersicht Kurstag Tag 1 Tag 2 Tag 3 Tag 4 Tag 5 Inhalt Differenzialgleichungen Quadratur, Nichtlineare algebraische Gleichungen Ausgleichsrechnung, Eigenwerte, Interpolation Lineare ODEs, Exponentielle Integratoren, Splitting-Verfahren Erweiterte Übungen Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
10 Lösen gewöhnlicher Differentialgleichungen Kapitel I Lösen gewöhnlicher Differentialgleichungen (Sektionen 8.2, 8.5, 8.6 im Skript) Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
11 Lösen gewöhnlicher Differentialgleichungen Lernziele: Numerische Lösung von Anfgangswertproblemen der Form ẏ = f (t, y) mit y(0) = y 0. Methoden: Eulerverfahren (explizit und implizit), implizite Mittelpunktsregel. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
12 Explizites Eulerverfahren Explizites Eulerverfahren Grundidee: Approximieren der ODE ẏ = f (t, y) durch y n+1 = y n + h n f (t n, y n ), n = 0,..., N 1. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
13 Explizites Eulerverfahren Explizites Eulerverfahren Grundidee: Approximieren der ODE ẏ = f (t, y) durch y n+1 = y n + h n f (t, y), n = 0,..., N 1. Denn der Vorwärts-Differenzen-Quotient ist f(t n, y(t n )) = ẏ(t n ) y(tn+hn) y(tn) h n. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
14 Explizites Eulerverfahren Explizites Eulerverfahren Grundidee: Approximieren der ODE ẏ = f (t, y) durch y n+1 = y n + h n f (t, y), n = 0,..., N 1. Denn der Vorwärts-Differenzen-Quotient ist f(t n, y(t n )) = ẏ(t n ) y(tn+hn) y(tn) h n. Keine Energieerhaltung, cf. p. 226 im Skript. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
15 Implizites Eulerverfahren Implizites Eulerverfahren Grundidee: Approximieren der ODE ẏ = f (t, y) durch y n+1 = y n + h n f (t n+1, y n+1 ), n = 0,..., N 1. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
16 Implizites Eulerverfahren Implizites Eulerverfahren Grundidee: Approximieren der ODE ẏ = f (t, y) durch y n+1 = y n + h n f (t n+1, y n+1 ), n = 0,..., N 1. Denn der Rückwärts-Differenzen-Quotient ist f(t n+1, y(t n+1 )) = ẏ(t n+1 ) y(t n+1 h n) y(t n+1 ) h n. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
17 Implizites Eulerverfahren Implizites Eulerverfahren Grundidee: Approximieren der ODE ẏ = f (t, y) durch y n+1 = y n + h n f (t n+1, y n+1 ), n = 0,..., N 1. Denn der Rückwärts-Differenzen-Quotient ist f(t n+1, y(t n+1 )) = ẏ(t n+1 ) y(t n+1 h n) y(t n+1 ) h n. Lösen eines nichtlinearen Systems notwendig. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
18 Implizites Eulerverfahren Implizites Eulerverfahren Grundidee: Approximieren der ODE ẏ = f (t, y) durch y n+1 = y n + h n f (t n+1, y n+1 ), n = 0,..., N 1. Denn der Rückwärts-Differenzen-Quotient ist f(t n+1, y(t n+1 )) = ẏ(t n+1 ) y(t n+1 h n) y(t n+1 ) h n. Lösen eines nichtlinearen Systems notwendig. Keine Energieerhaltung, cf. p. 226 im Skript. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
19 Implizite Mittelpunktsregel Implizite Mittelpunktsregel Grundidee: Approximieren ( der ODE ) ẏ = f (t, y) durch y n+1 = y n + h n f tn+tn+1 2, y n+1+y n 2, n = 0,..., N 1. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
20 Implizite Mittelpunktsregel Implizite Mittelpunktsregel Grundidee: Approximieren ( der ODE ) ẏ = f (t, y) durch y n+1 = y n + h n f tn+tn+1 2, y n+1+y n 2, n = 0,..., N 1. Lösen eines nichtlinearen Systems notwendig. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
21 Implizite Mittelpunktsregel Implizite Mittelpunktsregel Grundidee: Approximieren ( der ODE ) ẏ = f (t, y) durch y n+1 = y n + h n f tn+tn+1 2, y n+1+y n 2, n = 0,..., N 1. Lösen eines nichtlinearen Systems notwendig. Energieerhaltung gegeben, cf. p. 227 im Skript. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
22 Beispiel Mathematisches Pendel Beispiel Mathematisches Pendel Man schreibt die Differentialgleichung φ = g l sin (φ) um in ein System erster Ordnung: ( ) ( ) φ p = ṗ g. (1) l sin (φ) tananyag/mechatronikai modellezes angol/ch02.html Untersuche das zeitliche Verhalten der Gesamtenergie für das explizite und implizite Eulerverfahren sowie für die Mittelpunktsregel. Hinweis: Die Gesamtenergie ist (m = 1, l = 1) E tot = 1 2 φ 2 +g(1 cos (φ)). Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
23 Beispiel Mathematisches Pendel f = lambda alpha, p: array([p, 9.81 sin( alpha)]) def explicit euler(y0, dt, N): y ee = [] y ee.append(y0) for i in range(n): y ee. append( y ee[ 1] + dt f( y ee[ 1][0],y ee[ 1][1]) ) return asarray( y ee ) Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
24 Beispiel Mathematisches Pendel g impl = lambda x, y0, dt: y0+dt f(x[0], x[1]) x def implicit euler(y0, dt, N): y ie = [] y ie.append(y0) for i in range(n): y ie. append( fsolve( g impl, y ie[ 1], args=( y ie[ 1],dt)) ) return asarray( y ie ) Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
25 Beispiel Mathematisches Pendel g mid = lambda x, y0, dt: y0+ dt f(0.5 ( x[0]+ y0[0]),0.5 ( x[1]+ y0[1])) x def midpoint(y0, dt, N): y mp = [] y mp.append(y0) for i in range(n): y mp. append( fsolve( g mid, y mp[ 1], args=( y mp[ 1],dt)) ) return asarray( y mp ) Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
26 Beispiel Mathematisches Pendel Energy Energy Explicit Euler E tot E kin E pot Time E tot E kin Midpoint Energy Energy Implicit Euler E tot E kin E pot Time E pot E pot Time Time E tot E kin ODE 45 Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
27 Verletverfahren Lernziele: Integration von Differentialgleichungen der Form ÿ = f(t, y) (z.b.: Newtonsche Bewegungsgleichungen). Methoden: Velocity-Verlet- und Störmer-Verlet-Verfahren. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
28 Velocity-Verlet-Verfahren Velocity-Verlet-Verfahren Grundidee: Approximieren der ODE ÿ = f (t, y) mit Anfangsbedingungen y(0) = y 0 und ẏ = v 0. In diesem Verfahren ist: x n+1 = x n + hv n + h2 2 f (t n, x n ) und v n+1 = v n + h 2 (f (t n, x n ) + f (t n+1, x n+1 )). Energieerhaltung gegeben. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
29 Velocity-Verlet-Verfahren f = lambda phi: 9.81 sin( phi) def velocity verlet(x0, v0, dt, N): x vv = [] v vv = [] x vv.append(x0) v vv.append(v0) for i in range(n): x vv. append( x vv[ 1] + dt v vv[ 1] dt 2 f( x vv[ 1]) ) v vv. append( v vv[ 1] dt ( f( x vv[ 1]) + f( x vv[ 2]) )) return asarray( x vv ), asarray( v vv ) Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
30 Velocity-Verlet-Verfahren Velocity Velocity Verlet Position Energy Velocity Verlet E tot E kin E pot Time Das Velocity-Verlet-Verfahren erhält die Energie. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
31 Störmer-Verlet-Verfahren Störmer-Verlet-Verfahren Grundidee: Approximieren der ODE ÿ = f (t, y) durch y n+1 = y n 1 + 2y n + h 2 f (t n, y n ), n = 0,..., N 1. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
32 Störmer-Verlet-Verfahren Störmer-Verlet-Verfahren Grundidee: Approximieren der ODE ÿ = f (t, y) durch y n+1 = y n 1 + 2y n + h 2 f (t n, y n ), n = 0,..., N 1. Denn man kann die zweite Ableitung approximieren durch f (t, y) = ÿ y n+1 2y n+y n 1 h 2. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
33 Störmer-Verlet-Verfahren Störmer-Verlet-Verfahren Grundidee: Approximieren der ODE ÿ = f (t, y) durch y n+1 = y n 1 + 2y n + h 2 f (t n, y n ), n = 0,..., N 1. Denn man kann die zweite Ableitung approximieren durch f (t, y) = ÿ y n+1 2y n+y n 1 h 2. Typischerweise sind die Anfangswerte y(0) = y 0 und ẏ = v 0 gegeben. Dann ist y 1 = y 0 + hv 0 + h2 2 f(t 0, y 0 ), cf. p. 228 im Skript. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
34 Beispiel Streuung am Lennard-Jones Potential Beispiel Streuung am Lennard-Jones Potential Die Teilchenstreuung am Lennard-Jones ( Potential U(x, y) ist beschrieben ( durch r = U, wobei U(x, y) = 4 2 ) 12 ( r 1 ) ) 8 r. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
35 Beispiel Streuung am Lennard-Jones Potential Beispiel Streuung am Lennard-Jones Potential Die Teilchenstreuung am Lennard-Jones ( Potential U(x, y) ist beschrieben ( durch r = U, wobei U(x, y) = 4 2 ) 12 ( r 1 ) ) 8 r. Bestimme die Teilchentrajektorien für r 0 = ( 10, b) T mit b {0.15, 0.3,..., 3} und ṙ 0 = (1, 0) T. Der Zeitschritt ist t = 0.02 und T tot = 15. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
36 Beispiel Streuung am Lennard-Jones Potential f = lambda x: 24 (2./ sqrt(x[0] 2+x[1] 2) 14 1./sqrt(x[0] 2+x[1] 2) 8) x def stoermer verlet(x0, v0, dt, T): x sv = [] x sv.append(x0) x1 = x0 + dt v dt 2 f( x0) x sv.append(x1) for i in range( int(t/ dt)): x sv.append( x sv[ 2]+2 x sv[ 1] +dt 2 f( x sv[ 1]) ) return asarray( x sv ) Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
37 Beispiel Streuung am Lennard-Jones Potential 8 Stoermer-Verlet 6 4 y x Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
38 Runge-Kutta-Verfahren Lernziele: Integration von Differentialgleichungen der Form ẏ = f(t, y) mit Verfahren höherer Konvergenzordnung. Methoden: Runge-Kutta zweiter und vierter Ordnung, Kollokationsverfahren. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
39 Runge-Kutta-Verfahren Runge-Kutta-Verfahren Grundidee: Man nutzt eine Taylorentwicklung höherer Ordnung, um eine bessere Approximation der Differentialgleichung zu bekommen. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
40 Runge-Kutta-Verfahren Runge-Kutta-Verfahren Grundidee: Man nutzt eine Taylorentwicklung höherer Ordnung, um eine bessere Approximation der Differentialgleichung zu bekommen. Man behält alle Terme bis zur Ordnung h s : y n+1 = y n + h dy 1! dt + h2 d 2 y 2! + + hs d q y dt 2 s! dt + O ( h s+1). s Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
41 Runge-Kutta-Verfahren Runge-Kutta-Verfahren Grundidee: Man nutzt eine Taylorentwicklung höherer Ordnung, um eine bessere Approximation der Differentialgleichung zu bekommen. Man behält alle Terme bis zur Ordnung h s : y n+1 = y n + h dy 1! dt + h2 d 2 y 2! + + hs d s y dt 2 s! dt + O ( h s+1). s Allgemein schreibt man die Approximation als y n+1 = y n + h s ( i=1 b ik i, wobei k i = f t n + c i h, y n + s j=1 a ijk j ). c 1 a a 1s... c s a s1... a ss b 1... b s Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
42 Runge-Kutta-Verfahren Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
43 Beispiel Runge-Kutta-Verfahren 4. Ordnung Beispiel Runge-Kutta-Verfahren 4. Ordnung Butcher Tableau RK Definiere die 4 Koeffizienten: k 1 = f (t n, y n ) k 2 = f (t n + 0.5h, y n + 0.5hk 1 ) k 3 = f (t n + 0.5h, y n + 0.5hk 2 ) k 4 = f (t n + h, y n + hk 3 ) 2. Berechne den nächsten Schritt: y n+1 = y n + h ( 1 6 k k k k 4). Implementiere das RK Verfahren, um die Airy Gleichung ü(t) tu(t) = 0 für u(0) = und u(0) = im Zeitintervall [ 40, 0] zu lösen. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
44 Beispiel Runge-Kutta-Verfahren 4. Ordnung f = lambda t,y: array([ y[1], t y[0]]) def RK4(t0, y0, N, T): y RK4 = [] y RK4.append(y0) t RK4, h = linspace(t0, T, N+1, retstep =True) for i in range(n): k1 = f( t RK4 [i], y RK4[ 1]) k2 = f( t RK4 [i]+0.5 h, y RK4[ 1]+0.5 h k1) k3 = f( t RK4 [i]+0.5 h, y RK4[ 1]+0.5 h k2) k4 = f( t RK4 [i]+h, y RK4[ 1]+h k3) y RK4. append( y RK4[ 1]+h (1./6 k1+ 1./3 k2+1./3 k3+1./6 k4)) return t RK4, asarray( y RK4 ) Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
45 0.6 Airy function RK Ai(t) RK4 exact t Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
46 Runge-Kutta-Verfahren und Kollokation Runge-Kutta-Verfahren und Kollokation Grundidee: Kollokationsverfahren approximieren eine Differential, sodass Anfangsbedingung und die Differentialgleichung an Kollokationspunkten erfüllt ist Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
47 Runge-Kutta-Verfahren und Kollokation Runge-Kutta-Verfahren und Kollokation Grundidee: Kollokationsverfahren approximieren eine Differential, sodass Anfangsbedingung und die Differentialgleichung an Kollokationspunkten erfüllt ist Kollokationsmethoden erzeugen implizize Runge-Kutta-Verfahren. Für weitere Informationen: Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
48 Beispiel Gausskollokation 4. Ordnung Beispiel Gausskollokation 4. Ordnung Butcher Tableau Gausskollokationsmethoden haben die Ordnung p = 2s, also für das nebenstehende Verfahren findet man p = 4. Implementiere ein Gausskollokationsverfahren 4. Ordnung, um die Airy Gleichung ü(t) tu(t) = 0 für u(0) = und u(0) = im Zeitintervall [ 40, 0] zu lösen. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
49 Steife Differentialgleichungen Lernziele: Integration von steifen Differentialgleichungen, was für manche numerische Verfahren nur bei sehr kleiner Schrittweite möglich ist. Methoden: Beispiel explizites und implizites Eulerverfahren, Stabilitätsgebiet von Runge-Kutta-Verfahren, Radau-Verfahren und Rosenbrock-Wanner-Verfahren. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
50 Beispiel Dahlquist sche Testgleichung Beispiel Dahlquist sche Testgleichung Wir betrachten das Beispiel ẏ = λy mit y(0) = 1 und λ < 0. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
51 Beispiel Dahlquist sche Testgleichung Beispiel Dahlquist sche Testgleichung Wir betrachten das Beispiel ẏ = λy mit y(0) = 1 und λ < 0. Das explizite Eulerverfahren gibt y k = y k 1 + λhy k 1 = (1 λ h) k y 0, also 1 λ h < 1 und damit 0 < h < 2 λ. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
52 Beispiel Dahlquist sche Testgleichung Beispiel Dahlquist sche Testgleichung Wir betrachten das Beispiel ẏ = λy mit y(0) = 1 und λ < 0. Das explizite Eulerverfahren gibt y k = y k 1 + λhy k 1 = (1 λ h) k y 0, also 1 λ h < 1 und damit 0 < h < 2 λ. Für zu grosse Schrittweiten h > 2 λ wird das explizite Eulerverfahren instabil. Das passiert bei impliziten Methoden nicht. y(t) Stability Explicit Euler λ = 10, h = t y(t) Stability Explicit Euler λ = 10, h = t Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
53 Stabilitätsfunktionen für Runge-Kutta-Verfahren Stabilitätsfunktionen für Runge-Kutta-Verfahren Für ein Butcher-Tableau von Stufe s c U b T und die Differentialgleichung ẏ = λy mit λ C ist die Stabilitätsfunktion S(z) = 1 + zb T (1 zu) 1 1 = det(1 zu+z1bt ) det(1 zu), wobei z := λh und 1 = (1,..., 1) T R s, cf. p. 280 im Skript. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
54 Stabilitätsfunktionen für Runge-Kutta-Verfahren Stabilitätsfunktionen für Runge-Kutta-Verfahren Für ein Butcher-Tableau von Stufe s c U b T und die Differentialgleichung ẏ = λy mit λ C ist die Stabilitätsfunktion S(z) = 1 + zb T (1 zu) 1 1 = det(1 zu+z1bt ) det(1 zu), wobei z := λh und 1 = (1,..., 1) T R s, cf. p. 280 im Skript. Zum Beispiel ist für das explizite Eulerverfahren mit c = 0, U = 0 und b T = 1 die Stabilitätsfunktion S(z) = 1 + z. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
55 Radau-Verfahren Radau-Verfahren Im Gegensatz zur Gausskollokation, welche die maximale Ordnung p = 2s haben, erreichen Radau-Verfahren die Ordnung p = 2s 1. Es handelt sich ebenfalls um ein implizites Runge-Kutta-Verfahren. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
56 Radau-Verfahren Radau-Verfahren Im Gegensatz zur Gausskollokation, welche die maximale Ordnung p = 2s haben, erreichen Radau-Verfahren die Ordnung p = 2s 1. Es handelt sich ebenfalls um ein implizites Runge-Kutta-Verfahren. Beispiel Lösung der logistischen Gleichung Implementiere ein 2-stufiges Radau-Verfahren, um die logistische Gleichung ẏ = λy(1 y) mit y(0) = 0.1 und λ = 5 zu lösen. Das dazugehörige Butcher-Tableau ist, cf. p. 290 im Skript Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
57 Radau-Verfahren 1.0 Logistic Equation Radau y(t) Radau exact t Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
58 Rosenbrock-Wanner-Verfahren Rosenbrock-Wanner-Verfahren Grundidee: Implizite Runge-Kutta-Verfahren eignen sich gut zum Lösen steifer Anfangswertprobleme. Jedoch beinhaltet das die Lösung von Gleichungssystemen in jedem Iterationsschritt. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
59 Rosenbrock-Wanner-Verfahren Rosenbrock-Wanner-Verfahren Grundidee: Implizite Runge-Kutta-Verfahren eignen sich gut zum Lösen steifer Anfangswertprobleme. Jedoch beinhaltet dies die Lösung von Gleichungssystemen in jedem Iterationsschritt. Linear implizite Verfahren, wie das Rosenbrock-Wanner-Verfahren, nutzen approximierte lineare Gleichungssysteme. Beispiel Lösung der logistischen Gleichung Implementiere Rosenbrock-Wanner-Verfahren der Ordnung 2 und 3, um die logistische Gleichung ẏ = λy(1 y) mit y(0) = 0.1 und λ = 5 zu lösen. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
60 Rosenbrock-Wanner-Verfahren Rosenbrock-Wanner-Verfahren Grundidee: Implizite Runge-Kutta-Verfahren eignen sich gut zum Lösen steifer Anfangswertprobleme. Jedoch beinhaltet dies die Lösung von Gleichungssystemen in jedem Iterationsschritt. Linear implizite Verfahren, wie das Rosenbrock-Wanner-Verfahren, nutzen approximierte lineare Gleichungssysteme. Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
61 Rosenbrock-Wanner-Verfahren Rosenbrock-Wanner-Verfahren Grundidee: Implizite Runge-Kutta-Verfahren eignen sich gut zum Lösen steifer Anfangswertprobleme. Jedoch beinhaltet dies die Lösung von Gleichungssystemen in jedem Iterationsschritt. Linear implizite Verfahren, wie das Rosenbrock-Wanner-Verfahren, nutzen approximierte lineare Gleichungssysteme. Beispiel Lösung der logistischen Gleichung Implementiere Rosenbrock-Wanner-Verfahren der Ordnung 2 und 3 (p. 293 im Skript), um die logistische Gleichung ẏ = λy(1 y) mit y(0) = 0.1 und λ = 5 zu lösen. Weitere Informationen: ODEs/script_NumDGL_Tischendorf.pdf Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
62 Rosenbrock-Wanner-Verfahren 1.0 Logistic Equation ROW y(t) exact ROW 2 ROW t Lucas Böttcher (ETH Zürich) PVK Numerik June 19, / 62
PVK Probeprüfung FS 2017
PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
D-MATH Numerische Methoden FS 2018 Dr. Vasile Gradinaru Kjetil Olsen Lye. Serie 6
D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. kjetil.lye@sam.math.ethz.ch
1. Anfangswertprobleme 1. Ordnung
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. S. May D-ITET, D-MATL Sommer Numerische Methoden Bonuspunkte Punkte
Dr. S. May D-ITET, D-MATL Sommer 216 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
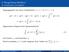4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski. Serie 1
D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski Serie 1 Best before: Di. 8.3 / Mi. 9.3, in den Übungsgruppen Koordinatoren: Alexander Dabrowski, HG G 52.1, alexander.dabrowski@sam.math.ethz.ch
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
ETHZ, D-MATH. Numerische Methoden D-PHYS, WS 2015/16 Dr. V. Gradinaru
ETHZ, D-MATH Prüfung Numerische Methoden D-PHYS, WS 5/6 Dr. V. Gradinaru..6 Prüfungsdauer: 8 Minuten Maximal erreichbare Punktzahl: 6. Der van-der-pol Oszillator ( Punkte) Der van-der-pol Oszillator kann
Differenzialgleichungen
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
10 Stabilität und steife Systeme
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerische Verfahren für gewöhnliche Differentialgleichungen
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Serie 2. D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Luc Grosheintz
D-MATH Numerische Methoden FS 206 Dr. Vasile Gradinaru Luc Grosheintz Serie 2 Abgabedatum: Di. 4.3 / Mi. 5.3 oder früher, in den Übungsgruppen Koordinatoren: Luc Grosheintz, HG J 46, luc.grosheintz@sam.math.ethz.ch
2.3.1 Explizite Runge-Kutta-Verfahren
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
2. Anfangswertprobleme 2. Ordnung
Zu einem Anfangswertproblem 2. Ordnung gehören folgende Daten: Eine Differenzialgleichung 2. Ordnung: ẍ t f [ x t, ẋ t,t ] Die Anfangsbedingungen: x 0 x 0, ẋ 0 ẋ 0 Das zu untersuchende Zeitintervall: t
Rheinisch-Westfälische Technische Hochschule. Gegeben seien eine gewöhnliche Dierentialgleichung (DGL) und ein Anfangswert. γ l K l.
Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Parareal. Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen. Johannes Reinhardt. Parareal 1 Johannes Reinhardt
Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz. Serie 10
D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz Serie 10 Abgabedatum: 23.5/24.5, in den Übungsgruppen Koordinatoren: Luc Grosheintz, HG G 46, luc.grosheintz@sam.math.ethz.ch Webpage:
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Dr. R. Käppeli D-ITET, D-MATL Sommer Numerische Methoden Punkte
Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Lösung Semesterendprüfung
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
Einführung und Beispiele
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
8 Gewöhnliche Differentialgleichungen
8 Gewöhnliche Differentialgleichungen Beispiel: Radioaktiver Zerfall Sei m(t) die Menge radioaktiven Materials zur Zeit t. Der Zerfall des Materials geschieht proportional zur vorhandenen Menge mit dem
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Differentialgleichungen
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Differentialgleichungen
Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
D-MAVT NUMERISCHE MATHEMATIK FS 14 K. Nipp, A. Hiltebrand Lösung vom Test 1
D-MAVT NUMERISCHE MATHEMATIK FS 4 K. Nipp, A. Hiltebrand Lösung vom Test. Sei eps die Maschinengenauigkeit in Matlab. Dann gilt: eps/4 = Richtig / Falsch + eps/2 = Richtig / Falsch 8 + eps = 8 Richtig
ZWEITE KLAUSUR zur Numerik I mit Lösungen. Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
Numerik gewöhnlicher Differentialgleichungen
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
5 Steife Differentialgleichungen
Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif,
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg "KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.")
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
5. Steife Differentialgleichungen 5.1 Was sind steife Differentialgleichungen?
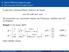5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG
Einführung in die Numerik strukturerhaltender Zeitintegratoren. Leonard Schlag 6. Dezember 2010
Einführung in die Numerik strukturerhaltender Zeitintegratoren Leonard Schlag 6. Dezember 2010 1 Inhaltsverzeichnis 1 Einführung in die Numerik strukturerhaltender Zeitintegratoren 3 1.1 Häuge Problemstellung:
Computersimulationen in der Astronomie
Computersimulationen in der Astronomie Fabian Heimann Universität Göttingen, Fabian.Heimann@stud.uni-goettingen.de Astronomisches Sommerlager 2013 Inhaltsverzeichnis 1 Differentialgleichungen 3 1.1 Beispiele.....................................
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Wir untersuchen die Bewegungsleichung des mathematischen (gedämpften) Fadenpendels in einer Dimension. = 0, ϕ (0)
3.1 Beispiel: mathematisches Pendel Wir untersuchen die Bewegungsleichung des mathematischen (gedämpften) Fadenpendels in einer Dimension ϕ+α ϕ+ω 2 0 sinϕ = 0, Ω2 0 = g/l (1) Das äquivalente System 1.
Öffnen Sie den Klausurbogen erst nach Aufforderung! Mathematische Grundlagen III (CES) SS 2017 Klausur
Prof. Dr. Martin Frank Prof. Dr. Martin Grepl Öffnen Sie den Klausurbogen erst nach Aufforderung! Zugelassene Hilfsmittel: Mathematische Grundlagen III (CES) SS 2017 Klausur 01.09.2017 Dokumentenechtes
Simulationstechnik V
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz. Serie 3
y D-MATH Numerische Methoden FS 17 Dr. Vasile Gradinaru Luc Grosheintz Serie 3 Abgabedatum: Di. 13.3 / Mi. 14.3, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Luc Grosheintz, HG J 46, luc.grosheintz@sam.math.ethz.ch
Computerphysik. Übungsblatt 6
Institut für Theoretische Physik der Universität zu Köln Computerphysik Übungsblatt 6 SS 2013 Prof. Dr. Simon Trebst Michael Becker, Peter Bröcker Website: http://www.thp.uni-koeln.de/trebst/lectures/2013-compphys.html
Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 13
Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Extrapolationsverfahren
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
u(x, 0) = g(x) : 0 x 1 u(0, t) = u(1, t) = 0 : 0 t T
8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
Öffnen Sie den Klausurbogen erst nach Aufforderung! Mathematische Grundlagen III (CES) WS 2017/2018 Klausur 23. März 2018
Prof. Dr. Manuel Torrilhon Prof. Dr. Sebastian Noelle Öffnen Sie den Klausurbogen erst nach Aufforderung! Zugelassene Hilfsmittel: Mathematische Grundlagen III (CES) WS 2017/2018 Klausur 23. März 2018
Numerik gewöhnlicher Differentialgleichungen
Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger. Lösung - Serie 26. ẋ 1 = x 1 + 2x ẋ 2 = 2x 1 + x 2
D-MAVT/D-MATL Analysis II FS 07 Dr. Andreas Steiger Lösung - Serie 6. Es ist das folgende autonome System ẋ = x + x + 3 ẋ = x + x von linearen Differenzialgleichungen. Ordung gegeben. Welche der folgenden
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
Simulationstechnik V
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Übungsblatt 13 Ausgabe: 11. Juli 2018
Universität Stuttgart 1. Institut für Theoretische Physik Prof. Dr. Jörg Main Übungen zur Vorlesung Physik auf dem Computer Sommersemester 218 Übungsgruppenleiter: Robin Bardakcioglu rhb@itp1.uni-stuttgart.de;
H. Achte Übungseinheit
H. Achte Übungseinheit Inhalt der achten Übungseinheit: Einschrittverfahren für gewöhnliche Differentialgleichungen erster Ordnung MATLAB-Löser Klassisches Euler-Verfahren und andere einfache explizite
Abschnitt 1.7: Schrittweitensteuerung 27
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
J Zehnte Übungseinheit
J Zehnte Übungseinheit Inhalt der zehnten Übungseinheit: Umformen von Differentialgleichungen 2. und höherer Ordnung auf Systeme 1. Ordnung Die Übungsaufgaben der zehnten Einheit werden nicht mehr angekreuzerlt.
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Strukturerhaltende Integratoren für Hamiltonsysteme
Strukturerhaltende Integratoren für Hamiltonsysteme Anna Schell 11. Dezember 2010 1 Inhaltsverzeichnis 1 Symplektizität 3 1.1 Symplektizität des Flusses eines Hamiltonsystems......... 3 1.2 Symplektizität
Numerische Verfahren
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Numerische Verfahren
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerisches Programmieren (IN0019)
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm
Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm Numerik Parameterschätzprobleme INHALT 1. 1D Wärmeleitungsgleichung 1.1 Finite-Differenzen-Diskretisierung
Lokaler Fehler y = y 2, y(0.2) = 5/9, Lösung: y = 1 Fehler nach dem 1. Schritt
Lokaler Fehler y = y, y(.) = /9, Lösung: y = Fehler nach dem. Schritt ( t) 4 Fehler 6 8 4 (I) Euler explizit (II) Euler implizit (IIIa) Crank Nicolson (IIIb) Heun (IVa) Euler modifiziert (IVb) Euler mod.
D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz. Serie 5
D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz Serie 5 Best Before: Di./ Mi. 28.3/29.3, in den Übungsgruppen oder im J 68 Koordinatoren: Luc Grosheintz, luc.grosheintz@sam.math.ethz.ch
Grundlagen der Numerischen Mathematik Sommersemester Kapitel 0. Jun.-Prof. Dr. Thorsten Raasch (JGU Mainz) 23. April 2014
Grundlagen der Numerischen Mathematik Sommersemester 2014 Kapitel 0 Jun.-Prof. Dr. Thorsten Raasch Johannes Gutenberg-Universität Mainz Institut für Mathematik 23. April 2014 Numerik Was ist das? Was ist
PVK Mathematik III Tag 1
PVK Mathematik III Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G 23.8 8093 Zürich lucasb@ethz.ch January 3, 2018 Lucas Böttcher (ETH Zürich) PVK Mathematik III January
Rückwärtsfehleranalyse und Langzeitenergieerhaltung
Rückwärtsfehleranalyse und Langzeitenergieerhaltung Henrike Köpke 9. Dezember 010 1 Inhaltsverzeichnis 1 Einleitung 3 Rückwärtsfehleranalyse 4.1 Idee der Vorwärts- und der Rückwärtsfehleranalyse..........
Numerik gewöhnlicher Differentialgleichungen. Übung 8 - Lösungsvorschlag
Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Numerische Methoden 7. Übungsblatt
Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Übungsblatt 6 Musterlösung
MSE SS6 Übungsblatt 6 Musterlösung Lösung (Fourierkoeffizienten) Eine Möglichkeit die Koeffizienten den Funktionen zuzuordnen, besteht darin, die Koeffizienten der Funktionen u i, i {,,3} zu berechnen
2. Anfangswertprobleme 2. Ordnung
2. Anfangswertprobleme 2. Ordnung 2.1 Grundlagen 2.2 Mathematisches Pendel 2.3 Selbstzentrierung Prof. Dr. Wandinger 7. Numerische Methoden Dynamik 2 7.2-1 2.1 Grundlagen Für ein Anfangswertproblem 2.
Differentialgleichungen
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Serie 9, Musterlösung. Klasse: 2Ub Semester: 2 Datum: 30. Mai z 3 = i z 4 = 15 Z 4 Z Re(z) z 4 = 1 e i 7π 4
anu donat.adams@fhnw.ch www.adams-science.com Serie 9, Musterlösung Klasse: Ub Semester: Datum: 3. Mai 17 1. Die komplee Zahlenebene Stelle die Zahlen als Punkte in der kompleen Zahlenebene dar. Berechne
14 Numerik hyperbolischer Differentialgleichungen
Numerik II 256 14 Numerik hyperbolischer Differentialgleichungen Während parabolische PDG Diffusionsvorgänge modellieren stellen hyperbolische PDG Modelle für Wellenphänomene dar. Wichtigste Anwendungsgebiete
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Numerische Lösung von Differentialgleichungen
Numerische Lösung von Differentialgleichungen Matheseminar 2017 Daniel Jodlbauer 9. Juni 2017 Überblick Motivation Voraussetzungen / Wiederholung Differentialgleichungen Lösungsverfahren Differentialgleichungen?
Gewöhnliche Differentialgleichungen
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
3. Berechnen Sie auch die Beschleunigung a als Funktion der Zeit t. 4. Erstellen Sie ein SIMULINK Modell, das x(t) numerisch berechnet.
unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
5 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen
Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 118 5 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Eine Differentialgleichung (DG) beschreibt eine Beziehung zwischen einer
Definition A-stabil. Wir betrachen das Modellproblem: y (t) = λy(t) y(0) = 1. für λ C, mit Re(λ) < 0
Wir betrachen das Modellproblem: { (t) = λ(t) () = Definition A-stabil für λ C, mit Re(λ) < Ein Verfahren heißt absolut stabil, falls lim i i =. Sei i+ = R(z) i, z = hλ, dann die R(z) heißt Stabilitätsfunktion.
Numerisches Programmieren
Technische Universität München WiSe 2015/16 Institut für Informatik Prof. Dr. Daniel Cremers Dr. Rudolph Triebel Nikola Tchipev Felix Dietrich Numerisches Programmieren 4. Programmieraufgabe: Freier Fall,
Für viele technische Anwendungen unverzichtbar!
Für viele technische Anwendungen unverzichtbar! Page 1 of 26 5.1. Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug zueinander
Musterlösung Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
Übungsaufgabe Numerische Lösung DGL
Kallenrode, www.sotere.uos.de Übungsaufgabe Numerische Lösung DGL 1. Bestimmen Sie die Lösung der DGL ẋ = (t 2) 2 + t x mit x(0) = 1 im Bereich von t = 0 bis t = 5 mit Hilfe des Euler schen Streckenzugverfahrens,
10 Gewöhnliche Differentialgleichungen
Gewöhnliche Differentialgleichungen. Aufgabenstellung, Beispiele.. Differentialgleichungen erster Ordnung Explizite gewöhnliche Differentialgleichung. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion
Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8 8.1 (Herbst 2002, Thema 1, Aufgabe 6) y = 3y +2x x 8.2 (Frühjahr 2005, Thema 1, Aufgabe 6) (x > 0) y(1)
Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren
Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren Manuel Hofmann 4..00 Einleitung Ziel dieser Arbeit ist es den Begriff der S-Stabilität einzuführen und im.
Diplom VP Numerik 28. August 2006
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
2 Einschrittverfahren 2.1 Einführung
Einschrittverfahren. Einführung Im folgenden werden wir uns bei der Beschreibung und Analyse von numerischen Verfahren für Anfangswertprobleme auf den Fall n = beschränken. Dies wird nur gemacht, um die
Dynamische Niedrigrang-Approximation an die Lösung von Wellengleichungen
Dynamische Niedrigrang-Approximation an die Lösung von Wellengleichungen J. Schweitzer M. Hochbruck Seminar für Angewandte Mathematik ETH Zürich Mathematisches Institut Heinrich Heine Universität Düsseldorf