14 Numerik hyperbolischer Differentialgleichungen
|
|
|
- Magdalena Stefanie Holtzer
- vor 5 Jahren
- Abrufe
Transkript
1 Numerik II Numerik hyperbolischer Differentialgleichungen Während parabolische PDG Diffusionsvorgänge modellieren stellen hyperbolische PDG Modelle für Wellenphänomene dar. Wichtigste Anwendungsgebiete sind hier Akustik Elektromagnetik Seismik Optik Strömungsmechanik. Handelt es sich um die Ausbreitung kleiner Störungen, so sind die Gleichungen meist linear. 14 Numerik hyperbolischer Differentialgleichungen TU Bergakademie Freiberg, SS 2010
2 Numerik II Die lineare Advektionsgleichung Wir betrachten hier das einfachste Modell einer hyperbolischen Gleichung, die lineare Wellengleichung erster Ordnung, und zwar zunächst das Cauchy-Problem mit einer Konstanten c. u t + cu x = 0, x R, t > 0, (14.1a) u(x, 0) = u 0 (x), (14.1b) Auch wenn die Lösung dieser Gleichung sicherlich keine Schwierigkeit darstellt, zumal die exakte Lösung u(x, t) = u 0 (x ct) bekannt ist, so lassen sich an dieser Gleichung einige typische Schwierigkeiten bei der numerischen Approximation hyperbolischer Gleichungen verdeutlichen Die lineare Advektionsgleichung TU Bergakademie Freiberg, SS 2010
3 Numerik II 258 Wir legen wieder ein Raum-Zeit-Gitter zugrunde. {(x j, t n ) : x j = j x, j Z; t n = n t, n N 0 } Naheliegendes explizites Schema: zentrale Differenz in x kombiniert mit explizitem Euler-Verfahren in t führt auf bzw. U n+1 j t U n j + c U n j+1 U n j 1 2 x = 0 U n+1 j = U n j c t 2 x (U n j+1 U n j 1). (14.2) Dieses Verfahren wird sich als unbrauchbar erweisen. Ersetzen von Uj n durch den Mittelwert 1 2 (U j 1 n + U j+1 n ) führt auf das Lax-Friedrichs-Verfahren U n+1 j = 1 2 (U n j 1 + U n j+1) c t 2 x (U n j+1 U n j 1). (14.3) 14.1 Die lineare Advektionsgleichung TU Bergakademie Freiberg, SS 2010
4 Numerik II 259 Wir werden sehen, dass (14.3) Lax-Richtmyer-stabil ist, sofern c t x 1. Dies gestattet insbesondere die Verwendung einer Zeitschrittweite t = O( x) Die lineare Advektionsgleichung TU Bergakademie Freiberg, SS 2010
5 Numerik II Diskretisierung durch die Linienmethode Zur Formulierung einer ARWA für (14.1a) auf dem Intervall x (0, 1) ist eine Randbedingung an einem der beiden Randpunkte erforderlich. Im Fall c > 0 ist diese bei x = 0 erforderlich, etwa u(0, t) = g 0 (t), t 0. Der linke Rand heißt in diesem Fall Einströmrand (inflow boundary), der rechte Ausströmrand (outflow boundary). Ist c < 0 vertauschen sich die Rollen. Bei den bisher genannten Schemata ist am Ausströmrand eine numerische Randbedingung erforderlich, was die Stabilitätsuntersuchung erschwert. Wir weichen daher zunächst auf periodische Randbedingungen aus, und gelangen zur ARWA u(0, t) = u(1, t) 14.2 Diskretisierung durch die Linienmethode TU Bergakademie Freiberg, SS 2010
6 Numerik II 261 u t + cu x = 0, x (0, 1), t > 0, (14.4a) u(0, t) = u(1, t), t 0, (14.4b) u(x, 0) = u 0 (x). Für den Vektor aus Approximationen U 1 (t) u(t) =., U j(t) u(x j, t) U J+1 (t) ergeben sich die GDG U j(t) = c ( Uj+1 (t) U j 1 (t) ), 2 j J, 2 x U 1(t) = c ( U2 (t) U J+1 (t) ), 2 x U J+1(t) = c ( U1 (t) U J (t) ). 2 x (14.4c) 14.2 Diskretisierung durch die Linienmethode TU Bergakademie Freiberg, SS 2010
7 Numerik II 262 In Matrixschreibweise: mit A = c t 2 x u (t) = Au(t) R (J+1) (J+1). (14.5) Diese Matrix ist schiefsymmetrisch (A T = A) mit Eigenwerten λ j = ic x und zugehörigen Eigenvektoren sin(2πj x), j = 1, 2,..., J + 1 [v j ] k = e 2πikj x, j = 1, 2,..., J Diskretisierung durch die Linienmethode TU Bergakademie Freiberg, SS 2010
8 Numerik II 263 Die Eigenwerte von A liegen somit in dem Intervall [ ic x, ic x] auf der imaginären Achse. Für absolute Stabilität ist bei der Linienmethode ein Verfahren für GDG erforderlich, dessen absolutes Stabilitätsgebiet ein solches Intervall umfasst. Dies ist beim expliziten Euler-Verfahren (14.2) für keinen Wert von t/ x der Fall, dieses Verfahren ist daher für keinen Wert dieses konstanten Gitterverhältnisses absolut stabil. Eine andere Wahl erfüllt jedoch die schwächere Variante (13.11) der Lax-Richtmyer- Stabilität: Für die Eigenwerte von B( t) = I + ta gilt dann nämlich 1 + tλ j 2 = 1 + ( c t x ) 2 sin 2 (2πj x) 1 + ( c t x ) 2, sodass die Wahl t = x 2 auf 1 + tλ j c 2 t führt und damit auf die Abschätzung B n = (I + ta) n (1 + c 2 t) n/2 e c2 T /2, n t T Diskretisierung durch die Linienmethode TU Bergakademie Freiberg, SS 2010
9 Numerik II Das Leapfrog-Verfahren Verwendet man in (14.1a) bzw. (14.4a) mit derselben zentralen Differenzenformel für x die Mittelpunktsregel y n+1 = y n tf(t n, y n ) anstelle des expliziten Euler-Verfahrens, so ergibt sich das sogenannte Leapfrog-Schema U n+1 j = U n 1 j c t x (U n j+1 U n j 1). (14.6) Da das absolute Stabilitätsgebiet der Mittelpunktsregel das Intervall {iy : 1 < y < 1} auf der imaginären Achse ist, ist das Leapfrog-Schema absolut stabil sofern c t/ x < Das Leapfrog-Verfahren TU Bergakademie Freiberg, SS 2010
10 Numerik II Das Lax-Friedrichs-Verfahren Durch die Ersetzung 1 2 (U n j 1 + U n j+1) = U n j (U n j 1 2U n j + U n j+1) geht das Lax-Friedrichs-Verfahren (14.3) über in U n+1 j = U n j c t 2 x (U n j+1 U n j 1) (U n j 1 2U n j und nach Umstellung der Terme in U n+1 j t U n j + c U n j+1 U n j 1 2 x = x2 2 t + U n j+1), U n j 1 2U n j + U n j+1 x 2. (14.7) Konsistenzanalyse zeigt, dass dieses Differenzenschema konsistent ist mit der PDG u t + cu x = 0, sieht aber eher aus wie eine Diskretisierung der Advektions- Diffusionsgleichung u t + cu x = ɛu xx, ɛ = x2 2 t Das Lax-Friedrichs-Verfahren TU Bergakademie Freiberg, SS 2010
11 Numerik II 266 Das Schema (14.7) entspricht somit dem expliziten Euler-Verfahren angewandt auf A ɛ = c 2 x u (t) = A ɛ u(t), mit der Matrix (14.8) ɛ x Die Matrix in (14.8) unterscheidet sich von der Matrix (14.5) durch die Addition eines kleinen Vielfaches eines symmetrisch negativ-definiten Differenzenoperators. Die Eigenwerte werden dadurch von der imaginären Achse weg in die linke Halbebene verschoben. Aufgrund der periodischen Randbedingung sind beide Matrizen zirkulant und haben daher dieselben (orthogonalen) Eigenvektoren. Die Eigenwerte lauten λ ɛ j = ic x sin(2πj x) 2ɛ (1 cos(2πj x), j = 1, 2,..., J. (14.9) x Das Lax-Friedrichs-Verfahren TU Bergakademie Freiberg, SS 2010
12 Numerik II Eigenwerte der Matrix ta ɛ für c = 1, x = 1/50 t = 0.8 x für verschieden Werte von ɛ. 1.5 expl. Euler (ɛ = 0) 1.5 ɛ = ɛ = Lax-Friedrichs (ɛ = ) 14.4 Das Lax-Friedrichs-Verfahren TU Bergakademie Freiberg, SS 2010
13 Numerik II Das Lax-Wendroff-Verfahren Möglichkeiten, die Konsistenzordnung bez. t zu erhöhen: Verfahren 2. Ordnung für Zeitdiskretisierung, z.b. Mittelpunktsregel/Leapfrog. Nachteile: beinhaltet drei aufeinanderfolgende Zeitschichten (Speicheraufwand, vor allem in 3D), RB schwieriger zu handhaben. Leapfrog nichtdissipativ (neutrale Stabilität), Probleme bei variablen Koeffizienten/nichtlinearen Termen. Trapezregel, diese ist aber implizit. Zweistufige Runge-Kutta-Verfahren Taylor-Ansatz angewandt auf u (t) = Au(t) unter Beachtung von u (t) = Au (t) = A 2 u(t): u n+1 = u n + tau n + t2 2 A2 u n Das Lax-Wendroff-Verfahren TU Bergakademie Freiberg, SS 2010
14 Numerik II 269 Ist A ist dabei die Matrix aus (14.5), so lautet dies ausgeschrieben U n+1 j = U n j c t 2 x (U n j+1 U n j 1) + c2 t 2 8 x 2 (U n j 2 2U n j Nachteil: 5-Punktestern in x, umständlich in Randnähe. + U n j+2). Ausweg: beachte, dass letzter Term Approximation darstellt an 1 2 c2 t 2 u xx. Ersetzen dieses Terms durch übliche 3-Punkteformel für u xx führt auf das Lax-Wendroff-Verfahren U n+1 j = U n j c t 2 x (U n j+1 U n j 1) + c2 t 2 2 x 2 (U n j 1 2U n j + U n j+1). (14.10) 14.5 Das Lax-Wendroff-Verfahren TU Bergakademie Freiberg, SS 2010
15 Numerik II Asymptotische Stabilität Beachte: Lax-Wendroff entspricht dem explizitem Euler-Verfahren angewandt auf u (t) = A ɛ u(t) mit A ɛ wie in (14.8) jedoch mit ɛ = c 2 t/2 anstelle von ɛ = x 2 /(2 t) wie im Lax-Friedrichs-Verfahren. Wie in (14.9) erhalten wir für die mit t durchmultiplizierten Eigenwerte von A ɛ tλ ɛ j = i c t x sin(jπ x) + ( ) 2 c t (cos(jπ x 1), j = 1, 2,..., J. x Diese liegen auf dem Rand einer Ellipse mit Mittelpunkt (c t/ x) 2 und Halbachsen der Länge (c c/ x) 2 und c t/ x. Diese Ellipse liegt im absoluten Stabilitätsgebiet des expliziten Euler- Verfahrens sofern c t/ x Das Lax-Wendroff-Verfahren TU Bergakademie Freiberg, SS 2010
16 Numerik II 271 Mit denselben Daten wie im vorigen Abschnitt zeigt das Bild die Eigenwerte des Lax-Wendroff-Verfahrens Lax-Wendroff (ɛ = 0.005) 14.5 Das Lax-Wendroff-Verfahren TU Bergakademie Freiberg, SS 2010
17 Numerik II Upwind-Verfahren Neben den bisher verwendeten zentralen Differenzenapproximationen an u x in der Advektionsgleichung (14.1a) sind auch die einseitigen Approximationen u x (x j, t) U j U j 1 x bzw. u x (x j, t) U j+1 U j x denkbar. Zusammen mit einer Vorwärtsdifferenz in der Zeit ergeben sich die Schemeta U n+1 j = U n j c t x (U j U j 1 ), U n+1 j = U n j c t x (U j+1 U j ). Beide besitzen Konsistenzordnung eins bezüglich x und t. (14.11a) (14.11b) 14.6 Upwind-Verfahren TU Bergakademie Freiberg, SS 2010
18 Numerik II 273 Niedrigere Approximationsordnung, aber Berücksichtigung einer qualitativen Eigenschaft der Lösung von (14.1a), nämlich der Ausbreitung von Information mit Geschwindigkeit c nach rechts (c > 0) bzw. links (c < 0). Für exakte Lösung: u(x j, t + t) = u(x j c t.t), d.h. Lösung im nächsten Zeitschritt gegeben durch Daten links von x j (c > 0) bzw. rechts von x j (c < 0) im aktuellen Zeitschritt. Naheliegend: Verwendung von (14.11a) falls c > 0 und von (14.11b), falls c < Upwind-Verfahren TU Bergakademie Freiberg, SS 2010
19 Numerik II 274 Zur Stabilitätsanalyse beachte man, dass (14.11a) umgeschrieben werden kann als U n+1 j = U n j c t 2 x (U n j+1 U n j 1) + c t 2 x (U n j+1 2U n j + U n j 1) (14.12) ein Schema von der Form (14.8) mit ɛ = c x/2. Bereits festgestellt: solche Schemata sind stabil, falls c t t x 1 und 2 < 2ɛ x 2 < Upwind-Verfahren TU Bergakademie Freiberg, SS 2010
20 Numerik II Numerisches Beispiel Wir betrachten die AWA (14.11a) mit c = 1 und Anfangsdaten u 0 (x) = e 20(x 2)2 + e (x 5)2 im Zeitraum t [0, 17] und vergleichen die exakte Lösung mit den durch das Upwind-, Lax-Wendroff- und Leapfrog-Schema gewonnenen Approximationen am Ende des Zeitintervalls. Die Anfangsfunktion besteht aus zwei Gaußsche Spitzen, einer etwas schlechter durch das gegebene räumliche Gitter aufgelöst als der andere. Dir räumliche Schrittweite beträgt x = 0.05, die Zeitschrittweite t = 0.8 x, als Randbedingung (echte und numerische) werden homogene Dirichlet-Bedingungen gestellt. Die schwarze durchgezogene Linie zeigt die exakte Lösung, die roten Punkte deren numerische Approximation an den Gitterpunkten an Numerisches Beispiel TU Bergakademie Freiberg, SS 2010
21 Numerik II Exakte Lösung t=0 1.5 Upwind, t= Numerisches Beispiel TU Bergakademie Freiberg, SS 2010
22 Numerik II Lax Wendroff, t= Leapfrog, t= Numerisches Beispiel TU Bergakademie Freiberg, SS 2010
23 Numerik II 278 Beobachtungen: Das Upwind-Verfahren ist stark diffusiv, approximiert aber die beiden Spitzen schlechter als die übrigen Schemata. Dies liegt an der niedrigeren Konsistenzordnung und kann durch Gitterverefeinerung verbessert werden. Bei Lax-Wendroff und Leapfrog ist die starke Dispersion, d.h., dass verschiedene Wellenanteile sich in der numerischen Approximation unterschiedlich schnell ausbreiten, deutlich zu erkennen Numerisches Beispiel TU Bergakademie Freiberg, SS 2010
24 Numerik II 279 Ziele von Kapitel 14. Sie sollten die Lösung der linearen Wellengleichung erster Ordnung hinschreiben und interpretieren können. Sie sollten die Konstruktionsprinzipien der Differenzenverfahren Leapfrog, Lax-Friedrichs, Lax-Wendroff und Upwind-Schema beschreiben können. Sie sollten den Unterschied zwischen asymptotischer und Lax-Richtmyer- Stabilität kennen. Sie sollten eine von-neumann-stabilitätsanalyse für Differenzenschemata für die lineare Wellengleichung erster Ordnung durchführen können. Sie sollten in der Lage sein, einfache Differenzenschema für die lineare Wellengleichung zu implementieren Numerisches Beispiel TU Bergakademie Freiberg, SS 2010
Numerik von Anfangswertaufgaben Teil II
 Institut für Numerische Mathematik und Optimierung Numerik von Anfangswertaufgaben Teil II Numerik partieller Differentialgleichungen Oliver Ernst Hörerkreis: 6. Mm, 8. Mm Sommersemester 2012 Inhalt 1.
Institut für Numerische Mathematik und Optimierung Numerik von Anfangswertaufgaben Teil II Numerik partieller Differentialgleichungen Oliver Ernst Hörerkreis: 6. Mm, 8. Mm Sommersemester 2012 Inhalt 1.
Numerik II Numerik Elliptischer Differentialgleichungen
 Numerik II 207 12 Numerik Elliptischer Differentialgleichungen 12 Numerik Elliptischer Differentialgleichungen TU Bergakademie Freiberg, SS 2010 Numerik II 208 12.1 Die Laplace-Gleichung in einem Quadrat
Numerik II 207 12 Numerik Elliptischer Differentialgleichungen 12 Numerik Elliptischer Differentialgleichungen TU Bergakademie Freiberg, SS 2010 Numerik II 208 12.1 Die Laplace-Gleichung in einem Quadrat
Dominik Desmaretz Universität Trier
 Dominik Desmaretz Universität Trier 25.11.2010 Inhaltsverzeichnis 1. Kurze Wiederholung/Einleitung 2. Die Lax-Friedrichs Methode 3. Die Richtmyer Zwei-Schritt Lax-Wendroff Methode 4. Upwind Methoden 5.
Dominik Desmaretz Universität Trier 25.11.2010 Inhaltsverzeichnis 1. Kurze Wiederholung/Einleitung 2. Die Lax-Friedrichs Methode 3. Die Richtmyer Zwei-Schritt Lax-Wendroff Methode 4. Upwind Methoden 5.
u(x, 0) = g(x) : 0 x 1 u(0, t) = u(1, t) = 0 : 0 t T
 8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerische Simulation mit finiten Elementen. O. Rheinbach
 Numerische Simulation mit finiten Elementen O. Rheinbach Numerische Simulation mit finiten Elementen INHALT 0.1 Finite Differenzen in 2D 1. Einleitung 1.1 Vorbemerkungen 1.2 Rand- und Anfangswertaufgaben
Numerische Simulation mit finiten Elementen O. Rheinbach Numerische Simulation mit finiten Elementen INHALT 0.1 Finite Differenzen in 2D 1. Einleitung 1.1 Vorbemerkungen 1.2 Rand- und Anfangswertaufgaben
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
Numerik partieller Differentialgleichungen für Ingenieure
 Numerik partieller Differentialgleichungen für Ingenieure Von ir. J. J.I.M. van Kan und ir. A. Segal Technische Universität Delft Aus dem Niederländischen übersetzt von Burkhard Lau, Technische Universität
Numerik partieller Differentialgleichungen für Ingenieure Von ir. J. J.I.M. van Kan und ir. A. Segal Technische Universität Delft Aus dem Niederländischen übersetzt von Burkhard Lau, Technische Universität
Wellen und wandernde Wellen Ähnlichkeitslösungen. Crashkurs PDG anhand von Beispielen. Wellen
 Wellen Crashkurs PDG anhand von Beispielen Eine Welle ist ein erkennbares Signal, welches innerhalb eines Mediums von einer Seite zur anderen übertragen wird, mit einer erkennbaren Ausbreitungsgeschwindigkeit.
Wellen Crashkurs PDG anhand von Beispielen Eine Welle ist ein erkennbares Signal, welches innerhalb eines Mediums von einer Seite zur anderen übertragen wird, mit einer erkennbaren Ausbreitungsgeschwindigkeit.
Übungsblatt 2 Musterlösung
 MSE SS17 Übungsblatt Musterlösung Lösung 5 (Transformation von Variablen) Zur Transformation gehen wir analog zur Vorlesung vor. Zunächst bestimmen wir die durch die PDGL definierte Matrix A und deren
MSE SS17 Übungsblatt Musterlösung Lösung 5 (Transformation von Variablen) Zur Transformation gehen wir analog zur Vorlesung vor. Zunächst bestimmen wir die durch die PDGL definierte Matrix A und deren
Randwertbedingungen und Ghost Cells
 Randwertbedingungen und Ghost Cells Olaf Kern Universität Trier 16.Dezember 2010 Olaf Kern (Universität Trier) Seminar Numerik 1/23 16.Dezember 2010 1 / 23 Inhaltsverzeichnis 1 Einführung 2 Periodische
Randwertbedingungen und Ghost Cells Olaf Kern Universität Trier 16.Dezember 2010 Olaf Kern (Universität Trier) Seminar Numerik 1/23 16.Dezember 2010 1 / 23 Inhaltsverzeichnis 1 Einführung 2 Periodische
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Übung zur Vorlesung Numerische Simulationsmethoden in der Geophysik
 Wenke Wilhelms, Julia Weißflog Institut für Geophysik und Geoinformatik Übung zur Vorlesung Numerische Simulationsmethoden in der Geophysik 04. Dezember 2013 Die Diffusionsgleichung 1D-Wärmeleitungsgleichung...
Wenke Wilhelms, Julia Weißflog Institut für Geophysik und Geoinformatik Übung zur Vorlesung Numerische Simulationsmethoden in der Geophysik 04. Dezember 2013 Die Diffusionsgleichung 1D-Wärmeleitungsgleichung...
Dr. S. May D-ITET, D-MATL Sommer Numerische Methoden Bonuspunkte Punkte
 Dr. S. May D-ITET, D-MATL Sommer 216 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Dr. S. May D-ITET, D-MATL Sommer 216 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Übungsblatt 6 Musterlösung
 MSE SS7 Übungsblatt 6 Musterlösung Lösung Methode der Charakteristiken) a) Hier ist c = x, d =. Also sind die Gleichungen für die Charakteristiken durch ẋt) = xt), żt) =, mit Anfangsbedingungen x) = x,
MSE SS7 Übungsblatt 6 Musterlösung Lösung Methode der Charakteristiken) a) Hier ist c = x, d =. Also sind die Gleichungen für die Charakteristiken durch ẋt) = xt), żt) =, mit Anfangsbedingungen x) = x,
Wir betrachten das Anfangsrandwertproblem auf dem Halbraum R + :
 Die Reflektionsmethode für den Halbraum R + = x > 0}: Wir betrachten das Anfangsrandwertproblem auf dem Halbraum R + : u tt u xx = 0 in R + (0, ) u = g, u t = h auf R + t = 0} u = 0 auf x = 0} (0, ) mit
Die Reflektionsmethode für den Halbraum R + = x > 0}: Wir betrachten das Anfangsrandwertproblem auf dem Halbraum R + : u tt u xx = 0 in R + (0, ) u = g, u t = h auf R + t = 0} u = 0 auf x = 0} (0, ) mit
Kapitel 3. Diskretisierungsverfahren. 3.1 Elliptische Differentialgleichung
 Kapitel 3 Diskretisierungsverfahren 3.1 Elliptische Differentialgleichung Wir beschränken uns auf elliptische Randwertaufgaben. Gesucht ist eine Funktion u (x, y) in R 2, welche die allgemeine partielle
Kapitel 3 Diskretisierungsverfahren 3.1 Elliptische Differentialgleichung Wir beschränken uns auf elliptische Randwertaufgaben. Gesucht ist eine Funktion u (x, y) in R 2, welche die allgemeine partielle
Übungsblatt 6 Musterlösung
 MSE SS6 Übungsblatt 6 Musterlösung Lösung (Fourierkoeffizienten) Eine Möglichkeit die Koeffizienten den Funktionen zuzuordnen, besteht darin, die Koeffizienten der Funktionen u i, i {,,3} zu berechnen
MSE SS6 Übungsblatt 6 Musterlösung Lösung (Fourierkoeffizienten) Eine Möglichkeit die Koeffizienten den Funktionen zuzuordnen, besteht darin, die Koeffizienten der Funktionen u i, i {,,3} zu berechnen
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Partielle Differentialgleichungen
 Partielle Differentialgleichungen Definition. Eine partielle Differentialgleichung ist eine Dgl., in der partielle Ableitungen einer gesuchten Funktion z = z(x 1, x 2,..., x n ) mehrerer unabhängiger Variabler
Partielle Differentialgleichungen Definition. Eine partielle Differentialgleichung ist eine Dgl., in der partielle Ableitungen einer gesuchten Funktion z = z(x 1, x 2,..., x n ) mehrerer unabhängiger Variabler
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
II. Elliptische Probleme
 II. Elliptische Probleme II.1 Finite Differenzen: Grundidee II.2 Konvergenzaussagen II.3 Allgemeine Randbedingungen II.4 Gekrümmte Ränder Kapitel II (0) 1 Dirichlet Randwerte mit finiten Differenzen Einfachster
II. Elliptische Probleme II.1 Finite Differenzen: Grundidee II.2 Konvergenzaussagen II.3 Allgemeine Randbedingungen II.4 Gekrümmte Ränder Kapitel II (0) 1 Dirichlet Randwerte mit finiten Differenzen Einfachster
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Heat Flow. Daniel Raß. 12. Juli
 d-rass@web.de 12. Juli 2007 Übersicht Einleitung Zuerst einige theoretische Grundlagen zur Diskretisierung der Wärmeleitungsgleichung und der Poissongleichung. Ausgangsgleichung Ausgehend von Masse-, Impuls-
d-rass@web.de 12. Juli 2007 Übersicht Einleitung Zuerst einige theoretische Grundlagen zur Diskretisierung der Wärmeleitungsgleichung und der Poissongleichung. Ausgangsgleichung Ausgehend von Masse-, Impuls-
Klassifikation von partiellen Differentialgleichungen
 Kapitel 2 Klassifikation von partiellen Differentialgleichungen Die meisten partiellen Differentialgleichungen sind von 3 Grundtypen: elliptisch, hyperbolisch, parabolisch. Betrachte die allgemeine Dgl.
Kapitel 2 Klassifikation von partiellen Differentialgleichungen Die meisten partiellen Differentialgleichungen sind von 3 Grundtypen: elliptisch, hyperbolisch, parabolisch. Betrachte die allgemeine Dgl.
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Inhaltsverzeichnis. 2 Numerische Methoden Dirichlet Problem der Poisson Gleichung RAWP der Wärmeleitungsgleichung...
 Inhaltsverzeichnis 1 Partielle Differentialgleichungen 1 1.1 Allgemeines und Klassifikation............................. 1 1.1.1 Grundbegriffe.................................. 1 1.1.2 Klassifikation der
Inhaltsverzeichnis 1 Partielle Differentialgleichungen 1 1.1 Allgemeines und Klassifikation............................. 1 1.1.1 Grundbegriffe.................................. 1 1.1.2 Klassifikation der
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 4. Teil Finite-Volumen-Methode
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 4. Teil Finite-Volumen-Methode
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 8 Partielle
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 8 Partielle
D-MATH Numerische Methoden FS 2018 Dr. Vasile Gradinaru Kjetil Olsen Lye. Serie 6
 D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. kjetil.lye@sam.math.ethz.ch
D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. kjetil.lye@sam.math.ethz.ch
Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm
 Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm Numerik Parameterschätzprobleme INHALT 1. 1D Wärmeleitungsgleichung 1.1 Finite-Differenzen-Diskretisierung
Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm Numerik Parameterschätzprobleme INHALT 1. 1D Wärmeleitungsgleichung 1.1 Finite-Differenzen-Diskretisierung
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
Rheinisch-Westfälische Technische Hochschule. Gegeben seien eine gewöhnliche Dierentialgleichung (DGL) und ein Anfangswert. γ l K l.
 Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Numerische Mathematik
 ».- Numerische Mathematik Von Dr. sc. math. Hans Rudolf Schwarz o. Professor an der Universität Zürich Mit einem Beitrag von Dr. sc. math. Jörg Waldvogel Titularprofessor an der Eidg. Technischen Hochschule
».- Numerische Mathematik Von Dr. sc. math. Hans Rudolf Schwarz o. Professor an der Universität Zürich Mit einem Beitrag von Dr. sc. math. Jörg Waldvogel Titularprofessor an der Eidg. Technischen Hochschule
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Hauptachsentransformation: Eigenwerte und Eigenvektoren
 Hauptachsentransformation: Eigenwerte und Eigenvektoren die bisherigen Betrachtungen beziehen sich im Wesentlichen auf die Standardbasis des R n Nun soll aufgezeigt werden, wie man sich von dieser Einschränkung
Hauptachsentransformation: Eigenwerte und Eigenvektoren die bisherigen Betrachtungen beziehen sich im Wesentlichen auf die Standardbasis des R n Nun soll aufgezeigt werden, wie man sich von dieser Einschränkung
4.8.1 Shortley Weller-Approximation Interpolation in randnahen Punkten... 81
 Inhaltsverzeichnis 1 Partielle Differentialgleichungen und ihre Typeneinteilung... 1 1.1 Beispiele... 1 1.2 Typeneinteilungen bei Gleichungen zweiter Ordnung.................. 5 1.3 Typeneinteilungen bei
Inhaltsverzeichnis 1 Partielle Differentialgleichungen und ihre Typeneinteilung... 1 1.1 Beispiele... 1 1.2 Typeneinteilungen bei Gleichungen zweiter Ordnung.................. 5 1.3 Typeneinteilungen bei
Lösungen der Aufgaben zu Kapitel 11
 Lösungen der Aufgaben zu Kapitel Vorbemerkung: Zur Bestimmung der Eigenwerte (bzw. des charakteristischen Polynoms) einer (, )-Matrix verwenden wir stets die Regel von Sarrus (Satz..) und zur Bestimmung
Lösungen der Aufgaben zu Kapitel Vorbemerkung: Zur Bestimmung der Eigenwerte (bzw. des charakteristischen Polynoms) einer (, )-Matrix verwenden wir stets die Regel von Sarrus (Satz..) und zur Bestimmung
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Unstetige Galerkin-Verfahren und die lineare Transportgleichung. Tobias G. Pfeiffer Freie Universität Berlin
 Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
PVK Probeprüfung FS 2017
 PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
5. Die eindimensionale Wellengleichung
 H.J. Oberle Differentialgleichungen II SoSe 2013 5. Die eindimensionale Wellengleichung Wir suchen Lösungen u(x, t) der eindimensionale Wellengleichung u t t c 2 u xx = 0, x R, t 0, (5.1) wobei die Wellengeschwindigkeit
H.J. Oberle Differentialgleichungen II SoSe 2013 5. Die eindimensionale Wellengleichung Wir suchen Lösungen u(x, t) der eindimensionale Wellengleichung u t t c 2 u xx = 0, x R, t 0, (5.1) wobei die Wellengeschwindigkeit
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
MODELLBILDUNG. Modellierung und Simulation von Strömen
 MODELLBILDUNG Modellierung und Simulation von Strömen Prof. Dr. Hans Babovsky Technische Universität Ilmenau, SS 2008 1 1 Konzept Wir wollen für ein Teilchensystem (Gasteilchen in der Luft, Rußteilchen
MODELLBILDUNG Modellierung und Simulation von Strömen Prof. Dr. Hans Babovsky Technische Universität Ilmenau, SS 2008 1 1 Konzept Wir wollen für ein Teilchensystem (Gasteilchen in der Luft, Rußteilchen
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Ein Blick über den Tellerrand... mit FreeFem++
 Ein Blick über den Tellerrand... mit FreeFem++ Eine Einführung und etwas Theorie Steffen Weißer Universität des Saarlandes 30. Oktober 2015 Gliederung 1 Zum Seminar 2 Was ist eine PDE? 3 Etwas Funktionalanalysis
Ein Blick über den Tellerrand... mit FreeFem++ Eine Einführung und etwas Theorie Steffen Weißer Universität des Saarlandes 30. Oktober 2015 Gliederung 1 Zum Seminar 2 Was ist eine PDE? 3 Etwas Funktionalanalysis
Transport Einführung
 Transport Einführung home/lehre/vl-mhs-1/inhalt/folien/vorlesung/8_transport/deckblatt.tex Seite 1 von 24. p.1/24 1. Einführung 2. Transportgleichung 3. Analytische Lösung Inhaltsverzeichnis 4. Diskretisierung
Transport Einführung home/lehre/vl-mhs-1/inhalt/folien/vorlesung/8_transport/deckblatt.tex Seite 1 von 24. p.1/24 1. Einführung 2. Transportgleichung 3. Analytische Lösung Inhaltsverzeichnis 4. Diskretisierung
D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz. Serie 10
 D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz Serie 10 Abgabedatum: 23.5/24.5, in den Übungsgruppen Koordinatoren: Luc Grosheintz, HG G 46, luc.grosheintz@sam.math.ethz.ch Webpage:
D-MATH Numerische Methoden FS 2017 Dr. Vasile Gradinaru Luc Grosheintz Serie 10 Abgabedatum: 23.5/24.5, in den Übungsgruppen Koordinatoren: Luc Grosheintz, HG G 46, luc.grosheintz@sam.math.ethz.ch Webpage:
Finite Elemente Methoden (aus der Sicht des Mathematikers) Alfred Schmidt
 Finite Elemente Methoden (aus der Sicht des Mathematikers) Alfred Schmidt Übersicht Partielle Differentialgleichungen, Approximation der Lösung Finite Elemente, lineare und höhere Ansatzfunktionen Dünn
Finite Elemente Methoden (aus der Sicht des Mathematikers) Alfred Schmidt Übersicht Partielle Differentialgleichungen, Approximation der Lösung Finite Elemente, lineare und höhere Ansatzfunktionen Dünn
ANALYSE NUMERISCHER VERFAHREN
 ANALYSE NUMERISCHER VERFAHREN von Eugene Isaacson Professor für Mathematik Leiter des Rechenzentrums Courant Institute of Mathematical Sciences New York University und Herbert Bishop Keller Professor für
ANALYSE NUMERISCHER VERFAHREN von Eugene Isaacson Professor für Mathematik Leiter des Rechenzentrums Courant Institute of Mathematical Sciences New York University und Herbert Bishop Keller Professor für
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Entwicklung von Differenzenschemata für geometrische Singularitäten
 Entwicklung von Differenzenschemata für geometrische Singularitäten Graz, Österreich herwig.grogger@fh-joanneum.at DGLR-Fachausschußsitzung T 2.3 Strömungsakustik / Fluglärm DLR Braunschweig 4. Februar
Entwicklung von Differenzenschemata für geometrische Singularitäten Graz, Österreich herwig.grogger@fh-joanneum.at DGLR-Fachausschußsitzung T 2.3 Strömungsakustik / Fluglärm DLR Braunschweig 4. Februar
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik'
 Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Lineare Gleichungssysteme Hierarchische Matrizen
 Kompaktkurs Lineare Gleichungssysteme Hierarchische Matrizen M. Bebendorf, O. Steinbach O. Steinbach Lineare Gleichungssysteme SIMNET Kurs 24. 27.4.26 / 6 Numerische Simulation stationäre und instationäre
Kompaktkurs Lineare Gleichungssysteme Hierarchische Matrizen M. Bebendorf, O. Steinbach O. Steinbach Lineare Gleichungssysteme SIMNET Kurs 24. 27.4.26 / 6 Numerische Simulation stationäre und instationäre
Finite Elemente I Konvergenzaussagen
 Finite Elemente I 195 5 onvergenzaussagen 5 onvergenzaussagen TU Bergakademie Freiberg, SoS 2006 Finite Elemente I 196 5.1 Interpolation in Sobolev-Räumen Wesentlicher Baustein der FE-onvergenzanalyse
Finite Elemente I 195 5 onvergenzaussagen 5 onvergenzaussagen TU Bergakademie Freiberg, SoS 2006 Finite Elemente I 196 5.1 Interpolation in Sobolev-Räumen Wesentlicher Baustein der FE-onvergenzanalyse
PRÜFUNG AUS MATHEMATIK 3
 (8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
(8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
3. Normalform linearer PDG zweiter Ordnung
 H.J. Oberle Differentialgleichungen II SoSe 2013 3. Normalform linearer PDG zweiter Ordnung Wir beschreiben in diesem Abschnitt Verfahren zur Transformation linearer oder auch halblinearer PDG zweiter
H.J. Oberle Differentialgleichungen II SoSe 2013 3. Normalform linearer PDG zweiter Ordnung Wir beschreiben in diesem Abschnitt Verfahren zur Transformation linearer oder auch halblinearer PDG zweiter
Modellierung elastischer Materialien Variationsformulierung Galerkin-Approximation FreeFem++ Ausblick: Lineare Thermoelastiz. Lineare Elastizität
 Lineare Elastizität Dominik Woznica Universität des Saarlandes 05.02.2016 Gliederung 1 Modellierung elastischer Materialien 2 Variationsformulierung 3 Galerkin-Approximation 4 FreeFem++ 5 Ausblick: Lineare
Lineare Elastizität Dominik Woznica Universität des Saarlandes 05.02.2016 Gliederung 1 Modellierung elastischer Materialien 2 Variationsformulierung 3 Galerkin-Approximation 4 FreeFem++ 5 Ausblick: Lineare
Grundlagen der Numerischen Mathematik II
 J Manfred Reimer Grundlagen der Numerischen Mathematik II Studienbuch für Studenten der Mathematik, Informatik, Statistik und aller Naturwissenschaften Mit 29 Abbildungen Akademische Verlagsgesellschaft
J Manfred Reimer Grundlagen der Numerischen Mathematik II Studienbuch für Studenten der Mathematik, Informatik, Statistik und aller Naturwissenschaften Mit 29 Abbildungen Akademische Verlagsgesellschaft
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Inhaltsverzeichnis Partielle Differentialgleichungen und ihre T ypeneinteilung B eispiele...
 Inhaltsverzeichnis 1 Partielle Differentialgleichungen und ihre Typeneinteilung... 1 1.1 Beispiele... 1 1.2 Typeneinteilungen bei Gleichungen zweiter Ordnung... 5 1.3 Typeneinteilungen bei Systemen erster
Inhaltsverzeichnis 1 Partielle Differentialgleichungen und ihre Typeneinteilung... 1 1.1 Beispiele... 1 1.2 Typeneinteilungen bei Gleichungen zweiter Ordnung... 5 1.3 Typeneinteilungen bei Systemen erster
Computerphysik. Übungsblatt 6
 Institut für Theoretische Physik der Universität zu Köln Computerphysik Übungsblatt 6 SS 2013 Prof. Dr. Simon Trebst Michael Becker, Peter Bröcker Website: http://www.thp.uni-koeln.de/trebst/lectures/2013-compphys.html
Institut für Theoretische Physik der Universität zu Köln Computerphysik Übungsblatt 6 SS 2013 Prof. Dr. Simon Trebst Michael Becker, Peter Bröcker Website: http://www.thp.uni-koeln.de/trebst/lectures/2013-compphys.html
I. Einführung in die PDGL
 I. Einführung in die PDGL I. Modellierungsbeispiele I.2 Wohlgestelltheit I.3 Klassifizierung I.4 Lösungskonzepte Kapitel I () Vorgehen bei der groben Einteilung von PDGL: ) System von PDGL (ja/nein) 2)
I. Einführung in die PDGL I. Modellierungsbeispiele I.2 Wohlgestelltheit I.3 Klassifizierung I.4 Lösungskonzepte Kapitel I () Vorgehen bei der groben Einteilung von PDGL: ) System von PDGL (ja/nein) 2)
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei die Matrix
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Rechenmethoden der Physik
 May-Britt Kallenrode Rechenmethoden der Physik Mathematischer Begleiter zur Experimentalphysik Mit 47 Abbildungen, 297 Aufgaben und Lösungen Springer Teil I Erste Schritte Rechnen in der Mechanik Rechnen
May-Britt Kallenrode Rechenmethoden der Physik Mathematischer Begleiter zur Experimentalphysik Mit 47 Abbildungen, 297 Aufgaben und Lösungen Springer Teil I Erste Schritte Rechnen in der Mechanik Rechnen
Numerische Mathematik I: Grundlagen
 Numerische Mathematik I: Grundlagen 09.10.2017 Inhalt der Lehrveranstaltung Inhaltlich sollen Sie in der Lehrveranstaltung Numerische Mathematik I insbesondere vertraut gemacht werden mit der Numerik linearer
Numerische Mathematik I: Grundlagen 09.10.2017 Inhalt der Lehrveranstaltung Inhaltlich sollen Sie in der Lehrveranstaltung Numerische Mathematik I insbesondere vertraut gemacht werden mit der Numerik linearer
Übungsaufgabe Numerische Lösung DGL
 Kallenrode, www.sotere.uos.de Übungsaufgabe Numerische Lösung DGL 1. Bestimmen Sie die Lösung der DGL ẋ = (t 2) 2 + t x mit x(0) = 1 im Bereich von t = 0 bis t = 5 mit Hilfe des Euler schen Streckenzugverfahrens,
Kallenrode, www.sotere.uos.de Übungsaufgabe Numerische Lösung DGL 1. Bestimmen Sie die Lösung der DGL ẋ = (t 2) 2 + t x mit x(0) = 1 im Bereich von t = 0 bis t = 5 mit Hilfe des Euler schen Streckenzugverfahrens,
Hyperbolische Erhaltungsgleichungen und die Wellengleichung
 Hyperbolische Erhaltungsgleichungen und die Wellengleichung Stefanie Günther Universität Trier 11.November 2010 Stefanie Günther (Universität Trier) Seminar Numerik 1/29 11.November 2010 1 / 29 Inhaltsverzeichnis
Hyperbolische Erhaltungsgleichungen und die Wellengleichung Stefanie Günther Universität Trier 11.November 2010 Stefanie Günther (Universität Trier) Seminar Numerik 1/29 11.November 2010 1 / 29 Inhaltsverzeichnis
Numerische Behandlung linearer und semilinearer partieller differentiell-algebraischer Systeme mit Runge-Kutta-Methoden.
 Numerische Behandlung linearer und semilinearer partieller differentiell-algebraischer Systeme mit Runge-Kutta-Methoden Dissertation zur Erlangung des akademischen Grades doctor rerum naturalium (Dr. rer.
Numerische Behandlung linearer und semilinearer partieller differentiell-algebraischer Systeme mit Runge-Kutta-Methoden Dissertation zur Erlangung des akademischen Grades doctor rerum naturalium (Dr. rer.
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Partielle Differentialgleichungen. Hofer Joachim/Panis Clemens
 9.11.2010 Contents 1 Allgemein 2 1.1 Definition................................................. 2 1.2 Klassifikation............................................... 2 1.3 Lösbarkeit.................................................
9.11.2010 Contents 1 Allgemein 2 1.1 Definition................................................. 2 1.2 Klassifikation............................................... 2 1.3 Lösbarkeit.................................................
METHODEN HÖHERER LÖSUNG Kapitel 6 Mareike Börsch Universität Trier
 METHODEN HÖHERER LÖSUNG Kapitel 6 Mareike Börsch Universität Trier 02.12.2010 Überblick 1. Wiederholung 2. Lineare Methoden 3. Limiter und Slope Limiter Methoden 4. Fluss Limiter Funktionen 5. Harten Theorem
METHODEN HÖHERER LÖSUNG Kapitel 6 Mareike Börsch Universität Trier 02.12.2010 Überblick 1. Wiederholung 2. Lineare Methoden 3. Limiter und Slope Limiter Methoden 4. Fluss Limiter Funktionen 5. Harten Theorem
Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
 Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Effiziente Diskretisierungs- und Lösungstechniken für die Lattice-Boltzmann Equation auf unstrukturierten Gittern
 Effiziente Diskretisierungs- und Lösungstechniken für die Lattice-Boltzmann Equation auf unstrukturierten Gittern Thomas Hübner, Stefan Turek (thomas.huebner@math.uni-dortmund.de, ture@featflow.de) LS
Effiziente Diskretisierungs- und Lösungstechniken für die Lattice-Boltzmann Equation auf unstrukturierten Gittern Thomas Hübner, Stefan Turek (thomas.huebner@math.uni-dortmund.de, ture@featflow.de) LS
PVK Numerische Methoden Tag 1
 PVK Numerische Methoden Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G 23.8 8093 Zürich lucasb@ethz.ch June 19, 2017 Lucas Böttcher (ETH Zürich) PVK Numerik June 19,
PVK Numerische Methoden Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G 23.8 8093 Zürich lucasb@ethz.ch June 19, 2017 Lucas Böttcher (ETH Zürich) PVK Numerik June 19,
Burgers Gleichung. Juri Chomé, Olaf Merkert. 2. Dezember J. Chomé, O. Merkert () Burgers Gleichung 2. Dezember / 25
 Burgers Gleichung Juri Chomé, Olaf Merkert 2. Dezember 2009 J. Chomé, O. Merkert () Burgers Gleichung 2. Dezember 2009 1 / 25 Gliederung 1 Geschichte 2 Herleitung 3 Charakteristiken 4 Numerische Lösung
Burgers Gleichung Juri Chomé, Olaf Merkert 2. Dezember 2009 J. Chomé, O. Merkert () Burgers Gleichung 2. Dezember 2009 1 / 25 Gliederung 1 Geschichte 2 Herleitung 3 Charakteristiken 4 Numerische Lösung
D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski. Serie 9
 D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski Serie 9 Best Before: 24.5/25.5, in den Übungsgruppen (2 wochen) Koordinatoren: Alexander Dabrowski, HG G 52.1, alexander.dabrowski@sam.math.ethz.ch
D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski Serie 9 Best Before: 24.5/25.5, in den Übungsgruppen (2 wochen) Koordinatoren: Alexander Dabrowski, HG G 52.1, alexander.dabrowski@sam.math.ethz.ch
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: f = 3N) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung:
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: f = 3N) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung:
Inhaltsverzeichnis. Kapitel 9. Gewöhnliche Differentialgleichungen... 1
 Inhaltsverzeichnis Kapitel 9. Gewöhnliche Differentialgleichungen... 1 1. Einführung... 1 1.1 Grundbegriffe 1.2 Anfangswertprobleme 1.3 Geometrische Bedeutung der DGL 1. Ordnung 2. Spezielle Differentialgleichungen
Inhaltsverzeichnis Kapitel 9. Gewöhnliche Differentialgleichungen... 1 1. Einführung... 1 1.1 Grundbegriffe 1.2 Anfangswertprobleme 1.3 Geometrische Bedeutung der DGL 1. Ordnung 2. Spezielle Differentialgleichungen
2. Quasilineare PDG erster Ordnung
 H.J. Oberle Differentialgleichungen II SoSe 2013 2. Quasilineare PDG erster Ordnung Eine skalare PDG erster Ordnung hat die allgemeine Form F (x, u(x), u x (x)) = 0. (2.1) Dabei ist u : R n G R die gesuchte
H.J. Oberle Differentialgleichungen II SoSe 2013 2. Quasilineare PDG erster Ordnung Eine skalare PDG erster Ordnung hat die allgemeine Form F (x, u(x), u x (x)) = 0. (2.1) Dabei ist u : R n G R die gesuchte
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
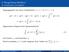 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Level Set Methods. Hamilton-Jacobi Equations Motion in the Normal Direction. Ralf Engbers
 Level Set Methods Motion in the Normal Direction Ralf Engbers ralf.engbers@gmx.de 26.04.2007 Ralf Engbers (ralf.engbers@gmx.de) Level Set Methods 26.04.2007 1 / 39 Inhalt des Vortrags Kapitel 5 - Introduction
Level Set Methods Motion in the Normal Direction Ralf Engbers ralf.engbers@gmx.de 26.04.2007 Ralf Engbers (ralf.engbers@gmx.de) Level Set Methods 26.04.2007 1 / 39 Inhalt des Vortrags Kapitel 5 - Introduction
D-MAVT NUMERISCHE MATHEMATIK FS 14 K. Nipp, A. Hiltebrand Lösung vom Test 1
 D-MAVT NUMERISCHE MATHEMATIK FS 4 K. Nipp, A. Hiltebrand Lösung vom Test. Sei eps die Maschinengenauigkeit in Matlab. Dann gilt: eps/4 = Richtig / Falsch + eps/2 = Richtig / Falsch 8 + eps = 8 Richtig
D-MAVT NUMERISCHE MATHEMATIK FS 4 K. Nipp, A. Hiltebrand Lösung vom Test. Sei eps die Maschinengenauigkeit in Matlab. Dann gilt: eps/4 = Richtig / Falsch + eps/2 = Richtig / Falsch 8 + eps = 8 Richtig
Übungen zu Partielle Differentialgleichungen, WS 2016
 Übungen zu Partielle Differentialgleichungen, WS 2016 Ulisse Stefanelli 16. Januar 2017 1 Beispiele 1. Betrachten Sie die Beispiele von nichtlinearen PDG und Systemen, die wir im Kurs diskutiert haben,
Übungen zu Partielle Differentialgleichungen, WS 2016 Ulisse Stefanelli 16. Januar 2017 1 Beispiele 1. Betrachten Sie die Beispiele von nichtlinearen PDG und Systemen, die wir im Kurs diskutiert haben,
Aufgabe 1 (12 Punkte)
 Aufgabe ( Punkte) Ein Medikament wirkt in drei Organen O, O, O 3. Seine Menge zur Zeit t im Organ O k wird mit x k (t) bezeichnet, und die Wechselwirkung wird durch folgendes System von Differentialgleichungen
Aufgabe ( Punkte) Ein Medikament wirkt in drei Organen O, O, O 3. Seine Menge zur Zeit t im Organ O k wird mit x k (t) bezeichnet, und die Wechselwirkung wird durch folgendes System von Differentialgleichungen
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Angewandte Strömungssimulation
 Angewandte Strömungssimulation 6. Vorlesung Stefan Hickel Finite - Volumen - Methode Finite - Volumen - Methode! Das Rechengebiet wird in nicht überlappende Bereiche (= finite Volumina) unterteilt.! Jedem
Angewandte Strömungssimulation 6. Vorlesung Stefan Hickel Finite - Volumen - Methode Finite - Volumen - Methode! Das Rechengebiet wird in nicht überlappende Bereiche (= finite Volumina) unterteilt.! Jedem
Multidimensionale Probleme. Johannes Engel
 Multidimensionale Probleme Johannes Engel 5..4 Zusammenfassung In diesem Vortrag wird es darum gehen, die im bisherigen Seminarverlauf gewonnenen Erkenntnisse über hyperbolische Differentialgleichungen
Multidimensionale Probleme Johannes Engel 5..4 Zusammenfassung In diesem Vortrag wird es darum gehen, die im bisherigen Seminarverlauf gewonnenen Erkenntnisse über hyperbolische Differentialgleichungen
Modellieren in der Angewandten Geologie II. Sebastian Bauer
 Modellieren in der Angewandten Geologie II Geohydromodellierung Institut für Geowissenschaften Christian-Albrechts-Universität zu Kiel CAU 3-1 Die Finite Elemente Method (FEM) ist eine sehr allgemeine
Modellieren in der Angewandten Geologie II Geohydromodellierung Institut für Geowissenschaften Christian-Albrechts-Universität zu Kiel CAU 3-1 Die Finite Elemente Method (FEM) ist eine sehr allgemeine
c i u i. (10.2) x = i
 Kapitel 0 Von Mises Wielandt Verfahren Im Folgenden wollen wir uns ausschließlich auf reelle, symmetrischen Matrizen der Ordnung n beschränken. Wie im letzten Kapitel diskutiert, sind für solche Matrizen
Kapitel 0 Von Mises Wielandt Verfahren Im Folgenden wollen wir uns ausschließlich auf reelle, symmetrischen Matrizen der Ordnung n beschränken. Wie im letzten Kapitel diskutiert, sind für solche Matrizen
Finite-Differenzen-Verfahren hoher Genauigkeit
 Universität Stuttgart, Fakultät Luft- und Raumfahrttechnik und Geodäsie - Vorlesung Finite-Differenzen-Verfahren Master-Studium, Spezialisierung 2 Semesterwochenstunden im SS, 3 LPs/ECTS Dr. Markus J.
Universität Stuttgart, Fakultät Luft- und Raumfahrttechnik und Geodäsie - Vorlesung Finite-Differenzen-Verfahren Master-Studium, Spezialisierung 2 Semesterwochenstunden im SS, 3 LPs/ECTS Dr. Markus J.
NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure
 NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure Eine computerorientierte Einführung Von Prof. Dr. sc. nat. HUBERT SCHWETLICK Prof. Dr. sc. nat. HORST KRETZSCHMAR Mit 74 Bildern und 34 Tabellen
NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure Eine computerorientierte Einführung Von Prof. Dr. sc. nat. HUBERT SCHWETLICK Prof. Dr. sc. nat. HORST KRETZSCHMAR Mit 74 Bildern und 34 Tabellen
3. Lineare Mehrschrittverfahren 3.1 Begriffe
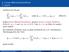 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
7. Die eindimensionale Wärmeleitungsgleichung
 H.J. Oberle Differentialgleichungen II SoSe 2013 7. Die eindimensionale Wärmeleitungsgleichung Als Beispiel für eine parabolische PDG betrachten wir die eindimensionale Wärmeleitungsgleichung u t (x, t)
H.J. Oberle Differentialgleichungen II SoSe 2013 7. Die eindimensionale Wärmeleitungsgleichung Als Beispiel für eine parabolische PDG betrachten wir die eindimensionale Wärmeleitungsgleichung u t (x, t)
Notizen zur Vorlesung Differentialgleichungen I
 Notizen zur Vorlesung Differentialgleichungen I Henrik Schumacher TUHH, 24 Januar 217 1 Randwertaufgaben für Differentialoperatoren zweiter Ordnung Zu Funktionen a, a 1 und a 2 C [a, b]) betrachten wir
Notizen zur Vorlesung Differentialgleichungen I Henrik Schumacher TUHH, 24 Januar 217 1 Randwertaufgaben für Differentialoperatoren zweiter Ordnung Zu Funktionen a, a 1 und a 2 C [a, b]) betrachten wir
