4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
|
|
|
- Jasmin Franke
- vor 5 Jahren
- Abrufe
Transkript
1 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel t+h t y (s) ds g(τ) dτ 0 j= m β j g(γ j ) ( ) mit Knoten γ j und Gewichten β j. Damit zumindest g exakt integriert wird, fordern wir m j= β j =. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 4
2 4. Konstruktion und Beispiele Daraus folgt m y(t + h) y(t) + h β j y (t + γ j h) = y(t) + h j= m β j f (t + γ j h, y(t + γ j h)). j= (RK-) Problem: y(t + γ j h) = y(t) + h γ j 0 y (t + τh) dτ sind unbekannt. Näherungen wieder durch Quadraturformeln, aber mit den alten Knoten γ j (j =,..., m) aus ( ) (sonst würden sich neue Unbekannte y(t + Knoten h) ergeben). γj 0 g(τ) dτ m α j,l g(γ l ) (j =,..., m). ( ) l= Damit zumindest g exakt integriert wird, fordern wir wie oben m l= α j,l = γ j j =,..., m. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 42
3 4. Konstruktion und Beispiele Damit ergibt sich y(t + γ j h) y(t) + h m l= α j,ly (t + γ l h) = y(t) + h m l= α j,lf (t + γ l h, y(t + γ l h)). (RK-2) Abkürzung: k j := ( f (t + γ j h, y(t + γ j h)) (j =,..., m). (RK-2): kj f t + γ j h, y(t) + h ) m l= α j,l k l (j =,..., m). (RK-): y(t + h) y(t) + h m j= β k j j. m-stufiges Runge-Kutta-Verfahren (RKV): m y n+ = y n + h β j k j mit j= ( ) m k j = f t n + γ j h, y n + h α j,l k l l= (j =,..., m). (RKV) Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 43
4 4. Konstruktion und Beispiele Butcher-Matrix (John Charles Butcher, 933) (auch Runge-Kutta-ABC): γ α, α,m... γ m α m, α m,m β β m Beispiele /2 /2 symbolisiert ein zweistufiges explizites RKV (ein RKV ist explizit, wenn α j,l = 0 j l gilt), nämlich das verbesserte Euler-Verfahren. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 44
5 4. Konstruktion und Beispiele 0 /4 /4 2/3 /4 5/2 /4 3/4 symbolisiert ein zweistufiges implizites RKV: k = f ( t n, y n + 4 hk 4 hk 2), k 2 = f ( t n h, y n + 4 hk hk 2), ( zwei i.a. nichtlineare Gleichungen für k und k 2 ) y n+ = y n + 4 h(k + 3k 2 ). (Beispiel 2 aus Abschnitt 2.2 ist ein weiteres implizites zweistufiges RKV.) Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 45
6 4. Konstruktion und Beispiele /2 / /6 4/6 /6 symbolisiert ein dreistufiges explizites RKV. Verfahren dritter Ordnung von Kutta: k = f (t n, y n ), k 2 = f ( t n + 2 h, y n + 2 hk ), k 3 = f (t n + h, y n hk + 2hk 2 ), y n+ = y n + 6 h(k + 4k 2 + k 3 ). Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 46
7 4. Konstruktion und Beispiele /3 / /3 0 2/3 0 /4 0 3/4 symbolisiert ein dreistufiges explizites RKV. Verfahren dritter Ordnung von Heun: k = f (t n, y n ), (Vgl. Beispiel aus Abschnitt 2.2.) k 2 = f ( t n + 3 h, y n + 3 hk ), k 3 = f ( t n h, y n hk 2), y n+ = y n + 4 h(k + 3k 3 ). Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 47
8 4. Konstruktion und Beispiele /2 / /2 0 / /6 2/6 2/6 /6 symbolisiert ein vierstufiges explizites RKV. Klassisches Runge-Kutta-Verfahren: k = f (t n, y n ), k 2 = f (t n + 2 h, y n + 2 hk ), k 3 = f (t n + 2 h, y n + 2 hk 2), k 4 = f (t n + h, y n + hk 3 ), y n+ = y n + 6 h(k + 2k 2 + 2k 3 + k 4 ). Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 48
9 4. Konstruktion und Beispiele Eine alternative Form von (RKV) ist m y n+ = y n + h β j f (t n + γ j h, ỹ j ) mit ỹ j = y n + h j= m α j,l f (t n + γ l h, ỹ l ) l= (j =,..., m). (RKV ) Setze k j = f (t n + γ j h, ỹ j ). Die ỹ j können als Approximationen an die Lösung y zur Zeit t n + γ j h interpretiert werden, die k j als Approximationen an y (t n + γ j h). Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 49
10 4.2 Konsistenzordnung Jedes RKV hat die Form y n+ = y n + hφ f (y n, t n ; h) mit Φ f (y n, t n ; h) = m β j k j. Es ist ein Einschrittverfahren (ρ(ζ) = ζ ), also stabil und (vgl. Abschnitt 2.3) genau dann konsistent, wenn Φ f (y(t n ), t n ; 0) = f (t n, y(t n ))ρ () erfüllt ist, was hier zu m j= β j = äquivalent ist. Ein RKV ist deshalb genau dann konvergent, wenn gilt. m β j = j= j= Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 50
11 4.2 Konsistenzordnung Um die Konsistenzordnung eines RKVs zu bestimmen (oder um m-stufige RKV mit möglichst hoher Konsistenzordnung zu konstruieren), sind wie im Fall der Taylor-Verfahren (siehe Abschnitt 2.5) komplizierte Rechnungen erforderlich. Wir untersuchen als Beispiel explizite dreistufige RKV, und entwickeln γ 2 γ 2 0 0, γ 3 γ 3 α 3,2 α 3,2 0 β β 2 β 3 h R n+ = y(t n+) y(t n ) Φ f (y(t n ), t n ; h) = y(t n+) y(t n ) h h 3 β j k j nach Potenzen von h (unter der Voraussetzung, dass y bzw. f genügend oft differenzierbar sind). j= Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 5
12 4.2 Konsistenzordnung Für skalare AWPe ergibt sich mit den Abkürzungen F := f t + f y f und G := f tt + 2f ty f + f yy f 2 (alle Ableitungen von f werden an der Stelle (t n, y(t n )) ausgewertet) die Beziehung Anderseits ist y(t n+ ) y(t n ) h k = f(t n, y(t n )) = f, = f + 2 F h + 6 (G + f yf )h 2 + O(h 3 ). k 2 = f(t n + hγ 2, y(t n ) + hγ 2 k ) = f + hγ 2 F + 2 h2 γ 2 2G + O(h 3 ), k 3 = f(t n + hγ 3, y(t n ) + h(γ 3 α 3,2 )k + hα 3,2 k 2 ) = f + hγ 3 F + h 2 (γ 2 α 3,2 F f y + 2 γ2 3G) + O(h 3 ). Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 52
13 4.2 Konsistenzordnung Das bedeutet: [ h R n+ = ] 3 j= β j f + [ 2 β ] 2γ 2 β 3 γ 3 F h Folgerungen. + [ ( 3 β 2γ 2 2 β 3 γ 2 3) 2 G + ( 6 β 3γ 2 α 3,2 )F f y ] h 2 + O(h 3 ).. Das Euler-Verfahren ist das einzige einstufige explizite RKV der Ordnung (β = ). Es gibt kein einstufiges explizites RKV höherer Ordnung. 2. Die zweistufigen expliziten RKV der Ordnung 2 sind durch β + β 2 = und β 2 γ 2 = 2 charakterisiert. Beispiele sind das modifizierte (β = 0, β 2 =, γ 2 = 2 ) und das verbesserte Euler-Verfahren (β = β 2 = 2, γ 2 = ). Kein explizites zweistufiges RKV besitzt die Ordnung 3. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 53
14 4.2 Konsistenzordnung 3. Explizite dreistufige RKV der Ordnung 3 sind durch die vier Gleichungen β + β 2 + β 3 =, β 2 γ β 3 γ 2 3 = 3, β 2 γ 2 + β 3 γ 3 = 2, β 3γ 2 α 3,2 = 6 charakterisiert. (Man kann zeigen, dass keine dieser Methoden die Ordnung 4 besitzt.) Beispiele sind das Verfahren von Heun (β = 4, β 2 = 0, β 3 = 3 4, γ 2 = 3, γ 3 = α 3,2 = 2 3 ) und das Verfahren von Kutta (β = 6, β 2 = 2 3, β 3 = 6, γ 2 = 2, γ 3 =, α 3,2 = 2). 4. Ähnliche (kompliziertere) Rechnungen zeigen, dass es eine zweiparametrige Familie expliziter vierstufiger RKV der Ordnung 4 gibt, von denen keines die Ordnung 5 besitzt. Ein Beispiel ist das klassische Runge-Kutta-Verfahren. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 54
15 4.2 Konsistenzordnung Weitere Beispiele sind (3/8-Regel) /3 / /3 / /8 3/8 3/8 /8 (Formel von Kuntzmann) /5 2/ /5 3/20 3/ /44 5/44 40/ /360 25/360 25/360 55/360 Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 55
16 4.2 Konsistenzordnung Die oben beschriebene Methode, die Ordnung eines RKVs zu bestimmen, wird für Verfahren höherer Stufenzahl schnell unübersichtlich: Die Koeffizienten eines expliziten dreistufigen Verfahrens müssen 4 Gleichungen erfüllen (s.o.), während bei einem achtstufigen Verfahren bereits 200 nichtlineare Gleichungen überprüft werden müssen. Die sog. Butcher-Theorie (vgl. J. C. Butcher, The Numerical Analysis of Ordinary Differential Equations. Runge-Kutta and General Linear Methods. John Wiley & Sons, Chichester 987) erleichtert mit Hilfe graphentheoretischer Bäume die Buchhaltung bei den partiellen Ableitungen von f und erlaubt eine elegante Berechnung der Ordnung eines gegebenen RKVs (sie liefert aber keine Methode, ein Verfahren mit gewünschter Ordnung zu konstruieren). Wir beschränken uns hier darauf, notwendige Ordnungsbedingungen abzuleiten, die sich aus den speziellen AWPen y = y + t l, y(0) = 0, (l N) ergeben. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 56
17 4.2 Konsistenzordnung Theorem 4. (Notwendige Ordnungsbedingungen für RKV) Das durch die Butcher-Matrix c A b T definierte RKV besitze die Ordnung p. Dann gelten Dabei sind b T A k C l e = (l )! (l + k)! = l(l + )... (l + k) für l =, 2,..., p und k = 0,,..., p l. b := [β, β 2,..., β m ] T, A := [α j,ν ] j,ν m, C := diag(γ, γ 2,..., γ m ) und e := [,,..., ] T R m. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 57
18 4.2 Konsistenzordnung Spezialfälle der notwendigen Bedingungen aus Satz 4. sind (für k = 0) b T C l e = m j= β j γ l j = l für l =, 2,..., p sowie (für l = mit k k + ) b T A k e = k! für k =, 2,..., p. Bemerkung. Ein explizites m-stufiges RKV besitzt höchstens die Konsistenzordnung m, denn hier ist A m = O (A ist echte untere Dreiecksmatrix). Für die optimale Ordnung p(m) eines expliziten m-stufigen RKVs gilt sogar p(m) m falls m 5, genauer: m p(m) Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 58
19 4.3 Absolute Stabilität Wir wenden ein m-stufiges RKV auf die Testgleichung y = λy an und erhalten mit ĥ = λh [ ] y n+ = + ĥbt (I m ĥa) e y n =: R(ĥ)y n, so dass (bei festem h) lim n y n = 0 (für alle y 0 ) genau dann gilt, wenn R(ĥ) < erfüllt ist. In Analogie zu Abschnitt 3.5 definieren wir den Stabilitätsbereich eines RKVs durch Für ein beliebiges m-stufiges RKV gilt R A := {ĥ C : R(ĥ) < }. R(ĥ) = + ĥbt (I m ĥa) e = + ĥ j b T A j e. j= Besitzt das Verfahren die Ordnung p, so folgt p R(ĥ) = j!ĥj + ĥ j b T A j e. j=0 j=p+ Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 59
20 4.3 Absolute Stabilität Ist das RKV explizit, so folgt m R(ĥ) = + ĥ j b T A j e. j= Insbesondere hängt der Stabilitätsbereich eines m-stufigen expliziten RKVs der Ordnung m ( m 4) wegen R(ĥ) = m j=0 j!ĥj nicht von den Koeffizienten des Verfahrens ab. Außerdem besitzt kein explizites RKV einen unbeschränkten Stabilitätsbereich (denn R ist ein Polynom). 3 Verfahren dritter Ordnung von Heun 3 klassisches Rung Kutta Verfahren Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 60
21 4.4 Eingebettete Runge-Kutta-Verfahren Kein Verfahren zur Lösung von AWPen arbeitet in der Praxis mit einer konstanten Schrittweite. Man wird vielmehr versuchen, die Schrittweite an das Verhalten der Lösung y anzupassen (ändert sich y in einem Bereich schnell, so ist dort eine kleine Schrittweite angebracht; in Bereichen, in denen y kaum variiert, ist eine größere Schrittweite ausreichend). Wir werden hier eine Schrittweitensteuerung vorstellen, die zum Ziel hat, den Konsistenzfehler K n+ := h R n+ (wird in der Literatur oft lokaler Diskretisierungsfehler genannt, vgl. Abschnitt 2.3) zu kontrollieren: K n tol, n =, 2,..., mit einer vorgebenen Toleranz tol. Bei Systemen von DGen (insbesondere dann, wenn die Lösungskomponenten von unterschiedlicher Größenordnung sind) wird man für jede Komponente eine eigene absolute Fehlertoleranz und global eine relative Fehlertoleranz festsetzen. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 6
22 4.4 Eingebettete Runge-Kutta-Verfahren Das folgende Lemma besagt, dass mit dem Konsistenzfehler auch der (eigentlich interessante) globale Diskretisierungsfehler kontrolliert wird. Lemma 4.2 Für den globalen Diskretisierungsfehler e n = y(t n ) y n eines Einschrittverfahrens gilt e n (t n t 0 ) κ n exp(m(t n t 0 )). Dabei ist κ n := max{ K j : j = 0,,..., n} und M die Lipschitzkonstante der Verfahrensfunktion (vgl. (V 2 ) aus Abschnitt 2.2). Um den Konsistenzfehler zu schätzen, verwendet man zwei Methoden unterschiedlicher Konsistenzordnungen (sagen wir p und q mit p < q), um y n aus y n zu berechnen: y n = y n + hφ f (y n, t n ; h) bzw. ŷ n = y n + hˆφ f (y n, t n ; h). Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 62
23 4.4 Eingebettete Runge-Kutta-Verfahren Für die zugehörigen Konsistenzfehler gelten: Daraus folgt K n = y(t n) y(t n ) h ˆK n = y(t n) y(t n ) h Φ(y n, t n ; h) = O(h p ), ˆΦ(y n, t n ; h) = O(h q ). K n ˆK n = ˆΦ(y n, t n ; h) Φ(y n, t n ; h) = h (ŷ n y n ). Wegen K n ˆK n = K n ( + O(h q p )) K n erhalten wir aus eine (grobe) Schätzung für K n. h y n ŷ n K n Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 63
24 4.4 Eingebettete Runge-Kutta-Verfahren Ist h y n ŷ n > tol, so wird die Schrittweite h verworfen und mit ( ) p h = α h tol h y n ŷ n ( ) eine neue Schrittweite h bestimmt (α ist hier ein Sicherheitsfaktor, etwa α = 0.9). Ausgehend von y n werden jetzt neue Näherungen y n und ŷ n (an der Stelle t n + h) berechnet. Diesen Prozess wiederholt man so lange, bis h y n ŷ n tol erfüllt ist. Dann wird ( ) verwendet, um eine neue (größere) Schrittweite für den nächsten Schritt (n n + ) vorzuschlagen. Die Wahl von h nach ( ) motiviert sich folgendermaßen: benutzte Schrittweite h: h y n ŷ n K n = ch p + O(h p+ ) ch p, erwünschte Schrittweite h: tol = K n = c h p + O( h p+ ) c h p. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 64
25 4.4 Eingebettete Runge-Kutta-Verfahren Um den Aufwand in Grenzen zu halten, verwendet man zur Berechnung von y n und ŷ n zwei RKV (verschiedener Ordnungen), deren Butcher-Matrizen sich nur im Vektor b unterscheiden (d.h. A und c sind für beide Verfahren gleich, so dass die Größen k j nur einmal berechnet werden müssen). Man spricht von eingebetteten RKV und schreibt c A b T, z.b. ˆb T /2 /2. Im Beispiel wird ein RKV der Ordnung (das Euler-Verfahren) in ein RKV der Ordnung 2 (das verbesserte Euler-Verfahren) eingebettet. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 65
26 4.4 Eingebettete Runge-Kutta-Verfahren Ein populäres Beispiel ist die Fehlberg 4(5)-Formel: Hier werden zwei sechsstufige RKV der Ordnungen 4 bzw. 5 kombiniert. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 66
27 4.5 Implizite und halb-implizite Verfahren Ist die Matrix A eines m-stufigen RKVs keine echte untere -Matrix (ist das RKV also implizit), so muss in jedem Zeitschritt ein nicht-lineares Gleichungssystem der Form k = f (t n + γ h, h m l= α,lk l ). k m. =. f (t n + γ m h, h m l= α m,lk l ) ( ) gelöst werden. Dieses System hat also mn Unbekannte, wenn y = f(t, y) aus n Gleichungen besteht. Mit Hilfe des Banachschen Fixpunktsatzes erkennt man, dass ( ) für genügend kleine h eindeutig lösbar ist. In der Praxis wird man dieses System aber nicht mit der Fixpunktiteration, sondern mit einem Newton- bzw. Quasi-Newton-Verfahren lösen. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 67
28 4.5 Implizite und halb-implizite Verfahren Ist A eine untere (aber keine echte untere) -Matrix, so nennt man das zugehörige RKV halb-implizit. Das System ( ) zerfällt dann in m Systeme mit jeweils n Unbekannten. Implizite RKV werden oft mit Hilfe von Gauß-Quadraturformeln konstruiert. Dies sind Formeln der Bauart b a g(τ)dτ = m β j g(γ j ) + R m (g). j= Hier werden die Gewichte β j und Knoten γ j so gewählt, dass R m (p) = 0 für Polynome p möglichst hohen Grads d erfüllt ist. Man kann zeigen (vgl. Numerik I), dass eine optimale Wahl auf d = 2m führt (man sagt die Quadraturformel hat den Exaktheitsgrad 2m). Die zugehörigen RKV (auch sie werden Gauß-Formeln genannt) haben die Ordnung 2m. Beachte, dass kein m-stufiges RKV eine höhere Ordnung besitzen kann. Warum? Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 68
29 4.5 Implizite und halb-implizite Verfahren Für m = ergibt sich die implizite Mittelpunktsregel 2 2, welche die Ordnung 2 besitzt. Für m = 2 und m = 3 ergeben sich die Gauß-Formeln bzw mit den Konsistenzordnungen 4 bzw. 6. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 69
30 4.5 Implizite und halb-implizite Verfahren Bei Gauß-Radau-Integrationsformeln wählt man einen Knoten als (entweder linken oder rechten) Endpunkt des Integrationsintervalls. Die übrigen Knoten und alle Gewichte werden so bestimmt, dass sich ein möglichst hoher Exaktheitsgrad ergibt. Man kann zeigen, dass eine Gauß-Radau-Formel mit m Knoten den Exaktheitsgrad 2m besitzt. Daher haben die zugehörigen impliziten RKV die Konsistenzordnung 2m. Zu dieser Klasse gehören die Verfahren und Schließlich kann man noch beide Enden des Integrationsintervalls als Knoten wählen und die übrigen Daten so bestimmen, dass die zugehörige Integrationsformel den Exaktheitsgrad 2m 2 (bzw. das zugehörige implizite RKV die Konsistenzordnung 2m 2) besitzt. Man spricht von Gauß-Lobatto-Formeln. Ein Beispiel ist die Trapezregel (für m = 2) Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 70
31 4.5 Implizite und halb-implizite Verfahren Ein Vorteil von impliziten gegenüber expliziten RKV ist ihr wesentlich größerer Stabilitätsbereich (wird im nächsten Kapitel diskutiert). Wir betrachten die Trapezregel 0 0 /2 /2 /2 /2 d.h. k = f (t n, y n ), k 2 = f (t n+, y n + h(k + k 2 )/2), y n+ = y n + h(k + k 2 )/2, oder kürzer: y n+ = y n + h(f (t n, y n ) + f (t n+, y n+ ))/2. Die zugehörige Stabilitätsfunktion ist R(ĥ) = ( + ĥ/2)/( ĥ/2) und es gilt: R(ĥ) < + ĥ/2 < ĥ/2 Real(ĥ) < 0. Die Trapezregel ist daher A-stabil. (Man nennt ein Verfahren A-stabil, wenn sein Stabilitätsbereich die (offene) linke Halbebene enthält.) Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 7
32 4.6 Kollokationsmethoden Kollokationsmethoden sind spezielle implizite RKV, die auf Grund ihrer Konstruktion sehr viel leichter zu analysieren sind als allgemeine RKV. Mit gegebenen setzen wir 0 γ < γ 2 < < γ m t (j) := t n + γ j h (j =, 2,..., m) und suchen ein Polynom p vom Grad m (bei Systemen von k DGen ist das ein Vektor p = [p, p 2,..., p k ] T aus k Polynomen vom Grad höchstens m), das die m + Interpolationsbedingungen p(t n ) = y n, p (t (j) ) = f (t (j), p(t (j) )) (j =, 2,..., m) erfüllt. Die Näherung y n+ an der Stelle t n+ wird dann definiert durch y n+ := p(t n+ ). Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 72
33 4.6 Kollokationsmethoden p ist ein Polynom vom Grad m, das durch die letzten m dieser Interpolationsbedingungen eindeutig bestimmt ist. In Lagrange-Form besitzt es die Darstellung p (t n + τh) = m j= l j(t n + τh)k j mit l j (t n + τh) = m τ γ i j i= und k j := p (t (j) ). γ j γ i Jetzt folgt für jedes i {, 2,..., m} Analog: p(t (i) ) p(t n ) = t (i) t n p (t n + sh) ds = t (i) m t n j= l j(t n + sh)k j ds = h m ( γi j= 0 l j(r) dr ) k j =: h m j= α i,jk j. p(t n+ ) p(t n ) = h ( m ) j= 0 l j(r) dr k j =: h m j= β jk j. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 73
34 4.6 Kollokationsmethoden Daraus folgt y n+ = p(t n+ ) = p(t n ) + h m j= β jk j = y n + h m j= β jk j mit k j = p (t (j) ) = f (t (j), p(t (j) )) = f (t n + γ j h, y n + m l= α j,lk l ). Mit anderen Worten: Jedes Kollokationsverfahren ist ein (implizites) RKV. Implementiert wird es in der Form (RKV) bzw. (RKV ), d.h. zu gegebenen γ j (j =, 2,..., m) bestimmt man zunächst (i, j =, 2..., m). α i,j = γ i 0 l j(r) dr und β j = 0 l j(r) dr Nicht jedes implizite RKV ist ein Kollokationsverfahren. Beispiel /3 /3 /3 /4 3/4 repräsentiert kein Kollokationsverfahren. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 74
35 4.6 Kollokationsmethoden Theorem 4.3 (Konsistenzordnung bei Kollokationsverfahren) Für ein m-stufiges Kollokationsverfahren mit der Butcher-Matrix c A b T sind die folgenden drei Aussagen äquivalent: Das Verfahren besitzt die Konsistenzordnung m + p. 0 τ j m j= (τ γ j) dτ = 0 für j = 0,,..., p. b T C l e = /l für l =, 2,..., m + p. Dabei sind C := diag(γ, γ 2,..., γ m ) und e := [,,..., ] T R m. Michael Eiermann (TU Freiberg) Numerik gewöhnlicher Differentialgleichungen Wintersemester 203/4 75
4 Runge-Kutta-Verfahren
 Numerik gewöhnlicher Differentialgleichungen 43 4 Runge-Kutta-Verfahren 4. Konstruktion Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0
Numerik gewöhnlicher Differentialgleichungen 43 4 Runge-Kutta-Verfahren 4. Konstruktion Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
3. Lineare Mehrschrittverfahren 3.1 Begriffe
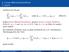 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
9 Numerische Verfahren für Anfangswertaufgaben
 Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
5. Steife Differentialgleichungen 5.1 Was sind steife Differentialgleichungen?
 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG
5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
5 Steife Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif,
Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif,
5 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen
 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 118 5 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Eine Differentialgleichung (DG) beschreibt eine Beziehung zwischen einer
Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 118 5 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Eine Differentialgleichung (DG) beschreibt eine Beziehung zwischen einer
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
KAPITEL 10. Numerische Integration
 KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
11. Einschrittverfahren
 H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren
 Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren Manuel Hofmann 4..00 Einleitung Ziel dieser Arbeit ist es den Begriff der S-Stabilität einzuführen und im.
Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren Manuel Hofmann 4..00 Einleitung Ziel dieser Arbeit ist es den Begriff der S-Stabilität einzuführen und im.
ZWEITE KLAUSUR zur Numerik I mit Lösungen. Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
 MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Zweite Prüfung zur Vorlesung
 Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Lokaler Fehler y = y 2, y(0.2) = 5/9, Lösung: y = 1 Fehler nach dem 1. Schritt
 Lokaler Fehler y = y, y(.) = /9, Lösung: y = Fehler nach dem. Schritt ( t) 4 Fehler 6 8 4 (I) Euler explizit (II) Euler implizit (IIIa) Crank Nicolson (IIIb) Heun (IVa) Euler modifiziert (IVb) Euler mod.
Lokaler Fehler y = y, y(.) = /9, Lösung: y = Fehler nach dem. Schritt ( t) 4 Fehler 6 8 4 (I) Euler explizit (II) Euler implizit (IIIa) Crank Nicolson (IIIb) Heun (IVa) Euler modifiziert (IVb) Euler mod.
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
eps für alle x D. 4. Die Zahl 256 ist in M(2, 4, 6, 6) exakt darstellbar.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Lösung Semesterendprüfung
 MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Dr. R. Käppeli D-ITET, D-MATL Sommer Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Musterlösungen zur Leistungsnachweisklausur vom Studiengang Informatik, Ingenieurinformatik, Lehramt
 TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra
TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra
Musterlösung. Modulprüfung MA2302. Numerik. 8. Oktober Prüfer: Prof. Dr. Bernd Simeon. Aufgabe 1 (ca. 12 P.) Sei f C (R). Das bestimmte Integral
 Modulprüfung MA2302 Numerik 8. Oktober 2009 Musterlösung Prüfer: Prof. Dr. Bernd Simeon Aufgabe 1 (ca. 12 P.) Sei f C (R). Das bestimmte Integral soll durch die Quadraturformel approximiert werden. I n
Modulprüfung MA2302 Numerik 8. Oktober 2009 Musterlösung Prüfer: Prof. Dr. Bernd Simeon Aufgabe 1 (ca. 12 P.) Sei f C (R). Das bestimmte Integral soll durch die Quadraturformel approximiert werden. I n
KAPITEL 9 Splinefunktionen
 KAPITEL 9 Splinefunktionen 9.1 Splineräume und Approximationsgüte Bei der Behandlung von Splines ist es bequemer, statt mit dem Grad von Polynomen, mit der Ordnung k := Grad + 1 zu arbeiten. Für eine Knotenmenge
KAPITEL 9 Splinefunktionen 9.1 Splineräume und Approximationsgüte Bei der Behandlung von Splines ist es bequemer, statt mit dem Grad von Polynomen, mit der Ordnung k := Grad + 1 zu arbeiten. Für eine Knotenmenge
Mathematische Grundlagen
 G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
Numerisches Programmieren (IN0019) 11. Gewöhnliche Differenzialgleichungen. Differenzialgleichungen. Differenzialgleichungen (Physik)
 umerisches Programmieren (I19) Frank R. Schmidt 11. Gewöhnliche Differenzialgleichungen Winter Semester 16/17 Differenzialgleichungen (Phsik) Differenzialgleichungen Phsikalische Prozesse lassen sich mit
umerisches Programmieren (I19) Frank R. Schmidt 11. Gewöhnliche Differenzialgleichungen Winter Semester 16/17 Differenzialgleichungen (Phsik) Differenzialgleichungen Phsikalische Prozesse lassen sich mit
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Unstetige Galerkin-Verfahren und die lineare Transportgleichung. Tobias G. Pfeiffer Freie Universität Berlin
 Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
PVK Numerische Methoden Tag 1
 PVK Numerische Methoden Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G 23.8 8093 Zürich lucasb@ethz.ch June 19, 2017 Lucas Böttcher (ETH Zürich) PVK Numerik June 19,
PVK Numerische Methoden Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G 23.8 8093 Zürich lucasb@ethz.ch June 19, 2017 Lucas Böttcher (ETH Zürich) PVK Numerik June 19,
Diplom VP Numerik 28. August 2006
 Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen
 Proseminar Lineare Algebra SS10 Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen Simon Strahlegger Heinrich-Heine-Universität Betreuung: Prof. Dr. Oleg Bogopolski Inhaltsverzeichnis:
Proseminar Lineare Algebra SS10 Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen Simon Strahlegger Heinrich-Heine-Universität Betreuung: Prof. Dr. Oleg Bogopolski Inhaltsverzeichnis:
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
Numerische Methoden 7. Übungsblatt
 Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Diplom VP Numerik 27. August 2007
 Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
8 Numerik gewöhnlicher Differentialgleichungen
 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 03 8 Numerik gewöhnlicher Differentialgleichungen 8. Grundlagen In der Numerik von gewöhnlichen Differentialgleichungen werden vorwiegend Aufgaben folgender
8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 03 8 Numerik gewöhnlicher Differentialgleichungen 8. Grundlagen In der Numerik von gewöhnlichen Differentialgleichungen werden vorwiegend Aufgaben folgender
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
u(x, 0) = g(x) : 0 x 1 u(0, t) = u(1, t) = 0 : 0 t T
 8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
Diplom VP Informatik / Numerik 2. September 2002
 Diplom VP Informatik / Numerik. September 00 Aufgabe Gegeben sei das lineare Gleichungssystem A x = b mit 0 4 0 0 0 0 A = 4 0 0 0 0 0 0 0 0 und b = 4 4 8 5. Punkte a Berechnen Sie die Cholesky Zerlegung
Diplom VP Informatik / Numerik. September 00 Aufgabe Gegeben sei das lineare Gleichungssystem A x = b mit 0 4 0 0 0 0 A = 4 0 0 0 0 0 0 0 0 und b = 4 4 8 5. Punkte a Berechnen Sie die Cholesky Zerlegung
(a), für i = 1,..., n.
 .4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
.4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Institut für Geometrie und Praktische Mathematik Multiple-Choice-Test NumaMB F08 (30 Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine
RWTH Aachen Institut für Geometrie und Praktische Mathematik Multiple-Choice-Test NumaMB F08 (30 Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine
Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
 Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Klassische Polynom Interpolation.
 Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
8 Extremwerte reellwertiger Funktionen
 8 Extremwerte reellwertiger Funktionen 34 8 Extremwerte reellwertiger Funktionen Wir wollen nun auch Extremwerte reellwertiger Funktionen untersuchen. Definition Es sei U R n eine offene Menge, f : U R
8 Extremwerte reellwertiger Funktionen 34 8 Extremwerte reellwertiger Funktionen Wir wollen nun auch Extremwerte reellwertiger Funktionen untersuchen. Definition Es sei U R n eine offene Menge, f : U R
Klausur Numerische Mathematik (für Elektrotechniker), 24. Februar 2016
 Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben. Eine kurze Einführung in Quasi Newton Verfahren
 Ergänzungen zu dem Buch Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben von Carl Geiger und Christian Kanzow (Springer Verlag, 1999) Eine kurze Einführung in Quasi Newton Verfahren
Ergänzungen zu dem Buch Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben von Carl Geiger und Christian Kanzow (Springer Verlag, 1999) Eine kurze Einführung in Quasi Newton Verfahren
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei die Matrix
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL)
 Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL) Problemstellung Beispiele Klassifizierung von DGLs, Existenz und Eindeutigkeit des AWPs Einschrittverfahren Stabilität & Schrittweitenkontrolle Mehrschrittverfahren
Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL) Problemstellung Beispiele Klassifizierung von DGLs, Existenz und Eindeutigkeit des AWPs Einschrittverfahren Stabilität & Schrittweitenkontrolle Mehrschrittverfahren
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge
 Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Kapitel 11 Gewöhnliche Differentialgleichungen
 Kapitel 11 Gewöhnliche Differentialgleichungen 11.1 Einführung Gesucht wird eine Funktion y = y(t) einer (Zeit-)Variablen t, die der Gleichung und der Anfangsbedingung genügen soll. y (t) = f(t, y(t)),
Kapitel 11 Gewöhnliche Differentialgleichungen 11.1 Einführung Gesucht wird eine Funktion y = y(t) einer (Zeit-)Variablen t, die der Gleichung und der Anfangsbedingung genügen soll. y (t) = f(t, y(t)),
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen
 Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Numerik für Ingenieure I Wintersemester 2008
 1 / 32 Numerik für Ingenieure I Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 23.1.2009 2 / 32 Wiederholung Stückweise Polynominterpolation Stückweise lineare Interpolierende
1 / 32 Numerik für Ingenieure I Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 23.1.2009 2 / 32 Wiederholung Stückweise Polynominterpolation Stückweise lineare Interpolierende
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen
 Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
Teil 6. Differentialrechnung mehrerer Veränderlicher
 Teil 6 Differentialrechnung mehrerer Veränderlicher 95 96 6.1 Topologie von Mengen Umgebung ε-umgebung eines Punktes x R n : B ε (x) = {y : y x < ε} Umgebung U von x: Menge, die eine ε-umgebung von x enthält
Teil 6 Differentialrechnung mehrerer Veränderlicher 95 96 6.1 Topologie von Mengen Umgebung ε-umgebung eines Punktes x R n : B ε (x) = {y : y x < ε} Umgebung U von x: Menge, die eine ε-umgebung von x enthält
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Numerik gewöhnlicher Differentialgleichungen. Prof. Dr. Guido Kanschat
 Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Ferienkurs Numerik Lösungsskizze. 1 Iterative Verfahren für lineare Gleichungssysteme
 Technische Universität München SoSe 1 Zentrum Mathematik Ferienkurse Dipl.-Math. Konrad Waldherr Ferienkurs Numerik Lösungsskizze 1 Iterative Verfahren für lineare Gleichungssysteme 1. Wir erhalten folgende
Technische Universität München SoSe 1 Zentrum Mathematik Ferienkurse Dipl.-Math. Konrad Waldherr Ferienkurs Numerik Lösungsskizze 1 Iterative Verfahren für lineare Gleichungssysteme 1. Wir erhalten folgende
Öffnen Sie den Klausurbogen erst nach Aufforderung! Mathematische Grundlagen III (CES) SS 2017 Klausur
 Prof. Dr. Martin Frank Prof. Dr. Martin Grepl Öffnen Sie den Klausurbogen erst nach Aufforderung! Zugelassene Hilfsmittel: Mathematische Grundlagen III (CES) SS 2017 Klausur 01.09.2017 Dokumentenechtes
Prof. Dr. Martin Frank Prof. Dr. Martin Grepl Öffnen Sie den Klausurbogen erst nach Aufforderung! Zugelassene Hilfsmittel: Mathematische Grundlagen III (CES) SS 2017 Klausur 01.09.2017 Dokumentenechtes
2 Einschrittverfahren 2.1 Einführung
 Einschrittverfahren. Einführung Im folgenden werden wir uns bei der Beschreibung und Analyse von numerischen Verfahren für Anfangswertprobleme auf den Fall n = beschränken. Dies wird nur gemacht, um die
Einschrittverfahren. Einführung Im folgenden werden wir uns bei der Beschreibung und Analyse von numerischen Verfahren für Anfangswertprobleme auf den Fall n = beschränken. Dies wird nur gemacht, um die
D-MATH Numerische Methoden FS 2018 Dr. Vasile Gradinaru Kjetil Olsen Lye. Serie 6
 D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. kjetil.lye@sam.math.ethz.ch
D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. kjetil.lye@sam.math.ethz.ch
18.2 Implizit definierte Funktionen
 18.2 Implizit definierte Funktionen Ziel: Untersuche Lösungsmengen von nichtlinearen Gleichungssystemen g(x) = 0 mit g : D R m, D R n, d.h. betrachte m Gleichungen für n Unbekannte mit m < n, d.h. wir
18.2 Implizit definierte Funktionen Ziel: Untersuche Lösungsmengen von nichtlinearen Gleichungssystemen g(x) = 0 mit g : D R m, D R n, d.h. betrachte m Gleichungen für n Unbekannte mit m < n, d.h. wir
Höhere Mathematik II für die Fachrichtung Physik. Übungs- und Scheinklausur
 Institut für Analysis SS17 PD Dr. Peer Christian Kunstmann 15.7.17 Dipl.-Math. Leonid Chaichenets, Johanna Richter, M.Sc., Tobias Ried, M.Sc., Tobias Schmid, M.Sc. Höhere Mathematik II für die Fachrichtung
Institut für Analysis SS17 PD Dr. Peer Christian Kunstmann 15.7.17 Dipl.-Math. Leonid Chaichenets, Johanna Richter, M.Sc., Tobias Ried, M.Sc., Tobias Schmid, M.Sc. Höhere Mathematik II für die Fachrichtung
Kapitel 4: Nichtlineare Nullstellenprobleme
 Vorlesung Höhere Mathematik: Numerik (für Ingenieure) Kapitel 4: Nichtlineare Nullstellenprobleme Jun.-Prof. Dr. Stephan Trenn AG Technomathematik, TU Kaiserslautern Sommersemester 2015 HM: Numerik (SS
Vorlesung Höhere Mathematik: Numerik (für Ingenieure) Kapitel 4: Nichtlineare Nullstellenprobleme Jun.-Prof. Dr. Stephan Trenn AG Technomathematik, TU Kaiserslautern Sommersemester 2015 HM: Numerik (SS
Einführung in die numerische Mathematik
 Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan :00-14:00 (120 min)
 Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Übungen zu Splines Lösungen zu Übung 20
 Übungen zu Splines Lösungen zu Übung 20 20.1 Gegeben seien in der (x, y)-ebene die 1 Punkte: x i 6 5 4 2 1 0 1 2 4 5 6 y i 1 1 1 1 1 + 5 1 + 8 4 1 + 8 1 + 5 1 1 1 1 (a) Skizzieren Sie diese Punkte. (b)
Übungen zu Splines Lösungen zu Übung 20 20.1 Gegeben seien in der (x, y)-ebene die 1 Punkte: x i 6 5 4 2 1 0 1 2 4 5 6 y i 1 1 1 1 1 + 5 1 + 8 4 1 + 8 1 + 5 1 1 1 1 (a) Skizzieren Sie diese Punkte. (b)
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1. Prof. Dr. Hans Babovsky. Technische Universität Ilmenau
 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
Numerik gewöhnlicher Differentialgleichungen. Übung 8 - Lösungsvorschlag
 Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
NUMERIK 1. Sommersemester 2016
 NUMERIK 1 Soerseester 2016 KLAUSUR LÖSUNGSVORSCHLAG Aufgabe 1 (Multiple Choice) (ca. 20 Minuten, 8 Punkte) Kreuzen Sie korrekte Aussagen an. Es können ehrere Antworten richtig sein, indestens eine ist
NUMERIK 1 Soerseester 2016 KLAUSUR LÖSUNGSVORSCHLAG Aufgabe 1 (Multiple Choice) (ca. 20 Minuten, 8 Punkte) Kreuzen Sie korrekte Aussagen an. Es können ehrere Antworten richtig sein, indestens eine ist
Nachklausur am Donnerstag, den 7. August 2008
 Nachklausur zur Vorlesung Numerische Mathematik (V2E2) Sommersemester 2008 Prof. Dr. Martin Rumpf Dr. Martin Lenz Dipl.-Math. Nadine Olischläger Nachklausur am Donnerstag, den 7. August 2008 Bearbeitungszeit:
Nachklausur zur Vorlesung Numerische Mathematik (V2E2) Sommersemester 2008 Prof. Dr. Martin Rumpf Dr. Martin Lenz Dipl.-Math. Nadine Olischläger Nachklausur am Donnerstag, den 7. August 2008 Bearbeitungszeit:
Nichtlineare Gleichungssysteme
 Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
