Explizite Runge-Kutta-Verfahren
|
|
|
- Felix Goldschmidt
- vor 6 Jahren
- Abrufe
Transkript
1 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit
2 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher Differentialgleichungen kennengelernt haben, befasse ich mich mit der Herleitung eines Einzelschrittverfahrens höherer Fehlerordnung, dem Runge-Kutta-Verfahren. Hierbei beschränke ich mich zunächst auf das dreistufige Runge-Kutta-Verfahren, d.h. in jedem Schritt des Verfahrens werden drei Funktionsauswertungen vorgenommen. Später werden wir auch vierstufige Runge-Kutta-Verfahren kennenlernen, allerdings wird mit wachsender Stufe die Herleitung der Verfahren immer komplizierter, weshalb ich die grundlegenden Überlegungen an den dreistufigen Verfahren erläutern werde. 2 Herleitung 2.1 Allgemeine Form Ausgangspunkt ist wie schon bei den vorherigen Verfahren die Integraldarstellung: xk+1 y(x k+1 ) = y(x k ) + f(x, y(x))dx (1) x k Anstatt jedoch eine bekannte Quadraturfomel zur Auswertung des Integrals zu benutzen, wollen wir das Integral mit Hilfe einer allgemein gehaltenen Quadraturformel bestimmen. Unter Verwendung von drei beliebigen Stützstellen ξ 1, ξ 2, ξ 3 im Intervall [x k, x k+1 und beliebigen Integrationsgewichten c 1, c 2, c 3 erhält die Quadraturformel folgende Gestalt: xk+1 x k [ f(x, y(x))dx = h c 1 f(ξ 1, y(ξ 1 )) + c 2 f(ξ 2, y(ξ 2 )) + c 3 f(ξ 3, y(ξ 3 )) Nach Einsetzen in (1) ergibt sich für das Verfahren: [ y(x k+1 ) = y(x k ) + h c 1 f(ξ 1, y(ξ 1 )) + c 2 f(ξ 2, y(ξ 2 )) + c 3 f(ξ 3, y(ξ 3 )) (2) Die zunächst beliebig gwählten Stützstellen ξ 1, ξ 2, ξ 3 und Integrationsgewichte c 1, c 2, c 3 sollen später so gewählt werden, dass ein Verfahren möglichst hoher Fehlerordnung entsteht. Zunächst beschäftigen wir uns mit der Wahl der Unbekannten ξ i bzw. y(ξ i ) in Gleichung (2). Die Stützstellen ξ 1, ξ 2, ξ 3 im Intervall [x k, x k+1 legen wir allgemein fest. Hierbei wird ξ 1 = x k gesetzt, da später y(ξ 1 ) = y(x k ) = y k gelten soll. Zur Bestimmung von y(ξ 1 ) und y(ξ 2 ) wenden wir die schon bekannte Prädiktormethode an. Damit erhalten wir: ξ 1 = x k ξ 2 = x k + a 2 h ξ 3 = x k + a 3 h, 0 < a 2, a 3 1 2
3 y(ξ 1 ) = y k y(ξ 2 ) := y 2 = y k + hb 21 f(x k, y k ) y(ξ 3 ) := y 3 = y k + hb 31 f(x k, y k ) + hb 32 f(ξ 2, y 2) Nach Einsetzen dieser Ergebnisse in (2) erhält man die allgemeine Form des Einzelschrittverfahrens: k 2 = f(ξ 2, y(ξ 2 )) = f(x k + a 2 h, y k + hb 21 k 1 ) k 3 = f(ξ 3, y(ξ 3 )) = f(x k + a 3 h, y k + h(b 31 k 1 + b 32 k 2 )) y k+1 = y k + h [c 1 k 1 + c 2 k 2 + c 3 k Bestimmung der Parameter Unser System hat demnach 8 Parameter a 2, a 3, b 21, b 31, b 32, c 1, c 2 und c 3, die wir beliebig bestimmen können. Allerdings stellt man einige Anforderungen an das Verfahren, so dass man zusätzliche Gleichungen zur Bestimmung der Parameter erhält. Eine Anforderung ist, dass die Prädiktorwerte y 2 und y 3 für die Differentialgleichung y = f(x, y(x)) = 1 exakt sein sollen. Da die Lösung der Differentialgleichung y(x) = x ist, erhält man folgende Gleichungen: y(ξ 2 ) = ξ 2 y k + hb 21 f(x k, y k ) = x k + a 2 h hb 21 = a 2 h a 2 = b 21 y(ξ 3 = ξ ( ) 3 y k + h b 31 f(x k, y k ) + b 32 f(ξ 2, y(ξ 2 )) = x k + a 3 h h(b 31 + b 32 ) = a 3 h a 3 = b 31 + b 32 Ausgangspunkt unserer Überlegungen war ein Einzelschrittverfahren möglichst hoher Fehlerordnung zu konstruieren. Daher werden die restlichen Parameter so bestimmt, dass die Fehlerordnung maximal ist. Dafür betrachten wir zunächst den lokalen Diskretisationsfehler: d k+1 = y(x k+1 ) y(x k ) h [c 1 k1 + c 2 k2 + c 3 k3, (3) 3
4 wobei k i die ungerundeten Werte der k i sind. Um die Fehlerordnung des Verfahrens zu bestimmen entwickeln wir die Ausdrücke y(x k+1 ) und k i aus (3) in Taylorreihen an der Stelle x k. Unter Verwendung der bereits im letzten Vortrag benutzten Abkürzungen F, G, f y, f x, f xx, f xy und f yy erhält man: y(x k+1 ) = y(x k + h) = y(x k ) + hy h2 y h3 y + O(h 4 ) = y(x k ) + hf h2 F h3 (F f y + G) + O(h 4 ) k 1 k 2 k 3 = f(x k, y(x k )) = f ( ) = f x k + a 2 h, y(x k ) + a 2 hf(x k, y(x k )) = f + a 2 hf x + a 2 hff y a2 2h 2 f xx + a 2 2h 2 ff xy a2 2h 2 f 2 f yy + O(h 3 ) = f + a 2 hf a2 2h 2 G + O(h 3 ) ( ) = f x k + a 3 h, y(x k ) + h(b 31 k1 + b 32 k2 ) = f + a 3 hf x + h(b 31 k1 + b 32 k2 )f y a2 3h 2 f xx + a 3 (b 31 k1 + b 32 k2 )h 2 f xy (b k b 32 k2 ) 2 h 2 f yy + O(h 3 ) = f + a 3 hf x + hb 31 ff y + hb 32 ff y + h 2 b 32 a 2 F f y h2 a 2 3f xx + a 3 h 2 (b 31 + b 32 )ff xy h2 (b 31 + b 32 ) 2 f 2 f yy + O(h 3 ) = f + h(a 3 f x + (b 31 + b 32 )ff y ) + h [a 2 2 b 32 F f y a2 3f xx + a 3 (b 31 + b 32 )ff xy (b 31 + b 32 ) 2 f 2 f yy + O(h 3 ) = f + a 3 hf + h 2 (a 2 b 32 F f y a2 3G) + O(h 3 ) Für den lokalen Diskretisationsfehler (3) ergibt sich damit: d k+1 = y(x k ) + hf h2 F h3 (F f y + G) + O(h 4 ) y(x k ) hc 1 f [hc 2 f + h 2 c 2 a 2 F h3 c 2 a 2 2G + O(h 4 ) [hc 3 f + h 2 c 3 a 3 F + h 3 c 3 (a 2 b 32 F f y a2 3G) + O(h 4 ) = hf(1 c 1 c 2 c 3 ) + h 2 F ( 1 2 a 2c 2 a 3 c 3 ) (4) ) +h (F 3 f y ( 1 6 a 2c 3 b 32 ) + G( a2 2c a2 3c 3 ) + O(h 4 ) 4
5 Damit wir ein Verfahren 3.Ordnung erhalten, müssen alle Terme in (4) bis auf O(h 4 ) verschwinden. Mit dieser Bedingung erhält man folgendes Gleichungssystem: c 1 + c 2 + c 3 = 1 a 2 c 2 + a 3 c 3 = 1 2 a 2 c 3 b 32 = 1 6 a 2 2c 2 + a 2 3c 3 = 1 3 Da das System 6 Unbekannte und 4 Gleichungen aufweist, erhält man eine zweiparametrige Lösungsmenge. Wir wählen (beliebig) a 2 und a 3 als Parameter und erhalten durch einfache Umformungen, unter der Voraussetzung a 2 a 3 und a 2 2 3, eine Darstellung der 6 Variablen in Abhängigkeit von a 2 und a 3 : c 1 = 6a 2a (a 2 + a 3 ) 6a 2 a 3 c 2 = 3a 3 2 6a 2 (a 3 a 2 ) c 3 = 2 3a 2 6a 3 (a 3 a 2 ) b 21 = a 2 b 32 = a 3(a 3 a 2 ) a 2 (2 3a 2 ) b 31 = a 3 b 32 (5) Wie die beiden freien Parameter gewählt werden ist im Grunde völlig beliebig, so dass die Parameter je nach Anforderung gewählt werden können. Beispielsweise war man anfänglich daran interessiert einfache Zahlenwerte für die Handrechnung oder Werte, die gegenüber der Rundung unanfällig sind, zu erhalten. Heutzutage werden die Werte jedoch eher abhängig von einer Schrittweitensteuerung gewählt oder auch so, dass der Hauptanteil des lokalen Diskretisationsfehler für eine spezielle Klasse von Differentialgleichungen möglichst klein ausfällt. 3 Runge-Kutta-Verfahren dritter Ordnung Zur Veranschaulichung werde ich 2 bekannte Runge-Kutta-Verfahren dritter Ordnung angeben, so dass ersichtlich wird, wie das Verfahren aus den zwei zu wählenden Parametern a 2 und a 3 entsteht. 5
6 3.1 Die Methode von Heun dritter Ordnung: Mit den Koeffizienten a 2 = 1 3 und a 3 = 2 3 erhält man aus (5): c 1 = 1 4, c 2 = 0, c 3 = 3 4, b 21 = 1 3, b 32 = 2 3, b 31 = 0 und damit hat die Methode von Heun dritter Ordnung folgende Form: k 2 = f(x k h, y k hk 1) k 3 = f(x k h, y k hk 2) y k+1 = y k + h 4 (k 1 + 3k 3 ) Bei dem so konstruierten Verfahren wird der Wert von k 2 also nur zur Berechnung von k 3 benötigt, denn für die Berechnung von y k+1 werden nur die Steigungen von k 1 und k 3 berücksichtigt. 3.2 Methode von Kutta dritter Ordnung: Mit den Koeffizienten a 2 = 1 2 und a 3 = 1 erhält man aus (5): c 1 = 1 6, c 2 = 2 3, c 3 = 1 6, b 21 = 1 2, b 32 = 2, b 31 = 1 und damit hat die Methode von Kutta dritter Ordnung folgende Form: k 2 = f(x k h, y k hk 1) k 3 = f(x k + h, y k hk 1 + 2hk 2 ) y k+1 = y k + h 6 (k 1 + 4k 2 + k 3 ) Nachdem wir zu Beginn eine allgemeine Quadraturformel zur Herleitung benutzt haben, erhalten wir bei obiger Wahl der Koeffizienten die uns bereits bekannte Simpsonregel als Quadraturformel. 4 Schrittweitenanpassung Ähnlich wie beim adaptiven Simpsonverfahren ist auch bei der numerischen Lösung von gewöhnlichen Differentialgleichungen mit dem Runge-Kutta-Verfahren eine Schrittweitenanpassung möglich und sinnvoll. Hierbei wird der lokale Diskretisationsfehler mit Hilfe eines Verfahrens höherer Ordnung abgeschätzt. Um den Aufwand möglichst gering zu halten, benutzt man für diese Abschätzung Runge-Kutta-Verfahren, in denen die gleichen k i verwendet werden, wie in dem Ausgangsverfahren. Mit dieser Abschätzung wird dann nach jedem Schritt der 6
7 Fehler berechnet und die Schrittweite je nach vorgegebener Fehlerschranke angepasst. 4.1 Die verbesserte Polygonzugmethode Die verbesserte Polygonzugmethode (VP) ist ein Runge-Kutta-Verfahren 2. Ordnung in folgender Form: k 2 = f(x k h, y k hk 1) y k+1 = y k + hk 2 Zur Abschätzung der verbesserten Polygonzugmethode eignet sich die gerade vorgestellte Methode von Kutta (K), ein Runge-Kutta-Verfahren 3. Ordnung, denn es gilt: k V P 1 = f(x k, y k ) = k K 1 und k V P 2 = f(x k h, y k hk 1) = k K 2 Die lokalen Diskretisationsfehler der beiden Verfahren sind: d V P k+1 = y(x k+1 ) y(x k ) h k 2 d K k+1 = y(x k+1 ) y(x k ) h 6 ( k k 2 + k 3 ) Durch Subtraktion der beiden Gleichungen erhält man für den lokalen Diskretisationsfehler: d V P k+1 = h 6 ( k k 2 + k 3 ) h k 2 + d K k+1 Nach Ersetzen der exakten Werte k i durch die bekannte Näherungen k i und mit dem Wissen, dass d K k+1 = O(h4 ) erhält man schließlich folgenden Ausdruck: d V P k+1 h 6 (k 1 + 4k 2 + k 3 ) hk 2 + O(h 4 ) = h 6 (k 1 2k 2 + k 3 ) + O(h 4 ) (6) Somit kann der lokale Diskretisationsfehler der Verbesserten Polygonzugmethode mit einer einzigen zusätzlichen Auswertung von k 3 abgeschätzt und je nach Größe des Fehlers, die Schrittweite angepasst werden. 7
8 4.2 Methode von Heun zweiter Ordnung Es ist auch möglich ein Runge-Kutta-Verfahren höherer Ordnung zur Abschätzung eines Verfahrens einfach zu konstruieren. Als Beispiel sei hier die Methode von Heun zweiter Ordnung angegeben: k 2 = f(x k + h, y k + hk 1 ) y k+1 = y k h(k 1 + k 2 ) Diese kann in ein Runge-Kutta-Verfahren 3.Ordnung eingebettet werden. Ein Parameter ist schon durch das Verfahren vorgegeben: a 2 = 1. Wir wählen zusätzlich a 3 = 1 2 und erhalten mit (5) die restlichen Parameter: c 1 = 1 6, c 2 = 1 6, c 3 = 2 3, b 32 = 1 4, b 31 = 1 4 Zur Abschätzung der Methode von Heun 2.Ordnung erhält man somit ein Runge- Kutta-Verfahren 3.Ordnung der folgeden Gestalt: k 2 = f(x k + h, y k + hk 1 ) k 3 = f(x k h, y k + h 4 (k 1 + k 2 )) y k+1 = y k + h 6 (k 1 + k 2 + 4k 3 ) Als Fehlerabschätzung erhalten wir in diesem Fall: d H k+1 h 6 (k 1 + k 2 + 4k 3 ) h 2 (k 1 + k 2 )O(h 4 ) = h 3 ( k 1 k 2 + 2k 3 ) + O(h 4 ) Literatur: H.R. Schwarz: Numerische Mathematik (1997 Stuttgart, Teubner),
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 23
 Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Musterlösung. Modulprüfung MA2302. Numerik. 8. Oktober Prüfer: Prof. Dr. Bernd Simeon. Aufgabe 1 (ca. 12 P.) Sei f C (R). Das bestimmte Integral
 Modulprüfung MA2302 Numerik 8. Oktober 2009 Musterlösung Prüfer: Prof. Dr. Bernd Simeon Aufgabe 1 (ca. 12 P.) Sei f C (R). Das bestimmte Integral soll durch die Quadraturformel approximiert werden. I n
Modulprüfung MA2302 Numerik 8. Oktober 2009 Musterlösung Prüfer: Prof. Dr. Bernd Simeon Aufgabe 1 (ca. 12 P.) Sei f C (R). Das bestimmte Integral soll durch die Quadraturformel approximiert werden. I n
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge
 Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Polynominterpolation
 Polynominterpolation In der numerischen Mathematik versteht man unter Polynominterpolation die Suche nach einem Polynom, welches exakt durch vorgegebene Punkte (z. B. aus einer Messreihe) verläuft. Dieses
Polynominterpolation In der numerischen Mathematik versteht man unter Polynominterpolation die Suche nach einem Polynom, welches exakt durch vorgegebene Punkte (z. B. aus einer Messreihe) verläuft. Dieses
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Numerische Methoden 7. Übungsblatt
 Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Numerische Mathematik
 ».- Numerische Mathematik Von Dr. sc. math. Hans Rudolf Schwarz o. Professor an der Universität Zürich Mit einem Beitrag von Dr. sc. math. Jörg Waldvogel Titularprofessor an der Eidg. Technischen Hochschule
».- Numerische Mathematik Von Dr. sc. math. Hans Rudolf Schwarz o. Professor an der Universität Zürich Mit einem Beitrag von Dr. sc. math. Jörg Waldvogel Titularprofessor an der Eidg. Technischen Hochschule
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
Numerische Integration von Differential-Gleichungen Das klassische Runge-Kutta-Verfahren
 Numerische Integration von Differential-Gleichungen Das klassische Runge-Kutta-Verfahren Gegeben sei ein Anfangswertproblem erster Ordnung: y = f (x;y y(x 0 = y 0 Wie schon erörtert, beschreibt eine DGl
Numerische Integration von Differential-Gleichungen Das klassische Runge-Kutta-Verfahren Gegeben sei ein Anfangswertproblem erster Ordnung: y = f (x;y y(x 0 = y 0 Wie schon erörtert, beschreibt eine DGl
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 21 Quadraturverfahren R. Steuding
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 21 Quadraturverfahren R. Steuding
Differentialgleichungen
 Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Übungsblatt 4 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Übungsblatt 4 Musterlösung Aufgabe 7 (Nullstellen als Eigenwerte) Die Polynome {S n } n=0,,2,, S n P n, mit führem Koeffizienten eins, heißen Orthogonalpolynome
Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Übungsblatt 4 Musterlösung Aufgabe 7 (Nullstellen als Eigenwerte) Die Polynome {S n } n=0,,2,, S n P n, mit führem Koeffizienten eins, heißen Orthogonalpolynome
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
a) Die Householder-Transformation, welche den ersten Spaltenvektor a 1 = der Matrix A auf , a 1 αe A = QR, A k =: Q k R k, A k+1 := R k Q k.
 Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. W. Reichel Sommersemester 00 7.07.00 MODULPRÜFUNG Numerische Methoden (Höhere Mathematik IV für die Fachrichtung Meteorologie bzw.
Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. W. Reichel Sommersemester 00 7.07.00 MODULPRÜFUNG Numerische Methoden (Höhere Mathematik IV für die Fachrichtung Meteorologie bzw.
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei die Matrix
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Dr. R. Käppeli D-ITET, D-MATL Sommer Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Wa
 103 Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Was bedeutet das für die Ableitungen? Was ist eine
103 Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Was bedeutet das für die Ableitungen? Was ist eine
Kapitel 3: Differentialgleichungen
 Kapitel 3: Differentialgleichungen Einführung: Vergleich zur Integration Zwischen der Integration und der Lösung von Differentialgleichungen besteht ein enger Zusammenhang: Das Aufsuchen der Lösung y(b)
Kapitel 3: Differentialgleichungen Einführung: Vergleich zur Integration Zwischen der Integration und der Lösung von Differentialgleichungen besteht ein enger Zusammenhang: Das Aufsuchen der Lösung y(b)
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
ZWEITE KLAUSUR zur Numerik I mit Lösungen. Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
 MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
Klassische Polynom Interpolation.
 Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Numerisches Programmieren, Übungen
 Technische Universität München WiSe 07 / 08 Institut für Informatik Univ-Prof Dr Hans-Joachim Bungartz Michael Obersteiner Philipp Samfass Numerisches Programmieren, Übungen Musterlösung 3 Übungsblatt:
Technische Universität München WiSe 07 / 08 Institut für Informatik Univ-Prof Dr Hans-Joachim Bungartz Michael Obersteiner Philipp Samfass Numerisches Programmieren, Übungen Musterlösung 3 Übungsblatt:
4 Gewöhnliche Differentialgleichungen
 4 Gewöhnliche Differentialgleichungen 4.1 Einleitung Definition 4.1 Gewöhnliche Differentialgleichung n-ter Ordnung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten
4 Gewöhnliche Differentialgleichungen 4.1 Einleitung Definition 4.1 Gewöhnliche Differentialgleichung n-ter Ordnung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten
18.2 Implizit definierte Funktionen
 18.2 Implizit definierte Funktionen Ziel: Untersuche Lösungsmengen von nichtlinearen Gleichungssystemen g(x) = 0 mit g : D R m, D R n, d.h. betrachte m Gleichungen für n Unbekannte mit m < n, d.h. wir
18.2 Implizit definierte Funktionen Ziel: Untersuche Lösungsmengen von nichtlinearen Gleichungssystemen g(x) = 0 mit g : D R m, D R n, d.h. betrachte m Gleichungen für n Unbekannte mit m < n, d.h. wir
KAPITEL 10. Numerische Integration
 KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
A 1 A 2 A 3 A 4 A 5 A 6 A 7
 Institut für Geometrie und Praktische Mathematik Numerisches Rechnen für Informatiker WS 7/8 Prof. Dr. H. Esser J. Grande, Dr. M. Larin Klausur Numerisches Rechnen für Informatiker Hilfsmittel: keine (außer
Institut für Geometrie und Praktische Mathematik Numerisches Rechnen für Informatiker WS 7/8 Prof. Dr. H. Esser J. Grande, Dr. M. Larin Klausur Numerisches Rechnen für Informatiker Hilfsmittel: keine (außer
Diplom VP Numerik 27. August 2007
 Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
Numerische Mathematik
 Numerische Mathematik Von Prof. Dr. sc. math. Hans Rudolf Schwarz Universität Zürich Mit einem Beitrag von Prof. Dr. sc. math. Jörg Waldvogel Eidg. Technische Hochschule Zürich 4., überarbeitete und erweiterte
Numerische Mathematik Von Prof. Dr. sc. math. Hans Rudolf Schwarz Universität Zürich Mit einem Beitrag von Prof. Dr. sc. math. Jörg Waldvogel Eidg. Technische Hochschule Zürich 4., überarbeitete und erweiterte
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Numerische Verfahren
 Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 15.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren Numerische
Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 15.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren Numerische
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
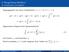 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Der Taylorsche Satz Herleitung und Anwendungen
 Der Taylorsche Satz Herleitung und Anwendungen Joachim Schneider Juni 2004 Zusammenfassung Es wird ein enfacher Beweis des Taylorsche Satz über die lokale Approximierbarkeit hinreichend glatter Funktionen
Der Taylorsche Satz Herleitung und Anwendungen Joachim Schneider Juni 2004 Zusammenfassung Es wird ein enfacher Beweis des Taylorsche Satz über die lokale Approximierbarkeit hinreichend glatter Funktionen
8 Numerik gewöhnlicher Differentialgleichungen
 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 03 8 Numerik gewöhnlicher Differentialgleichungen 8. Grundlagen In der Numerik von gewöhnlichen Differentialgleichungen werden vorwiegend Aufgaben folgender
8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 03 8 Numerik gewöhnlicher Differentialgleichungen 8. Grundlagen In der Numerik von gewöhnlichen Differentialgleichungen werden vorwiegend Aufgaben folgender
Mathematik für Wirtschaftswissenschaftler im WS 12/13 Lösungen zu den Übungsaufgaben Blatt 12
 Mathematik für Wirtschaftswissenschaftler im WS /3 Lösungen zu den Übungsaufgaben Blatt Aufgabe 5 Welche der folgenden Matrizen sind positiv bzw negativ definit? A 8, B 3 7 7 8 9 3, C 7 4 3 3 8 3 3 π 3
Mathematik für Wirtschaftswissenschaftler im WS /3 Lösungen zu den Übungsaufgaben Blatt Aufgabe 5 Welche der folgenden Matrizen sind positiv bzw negativ definit? A 8, B 3 7 7 8 9 3, C 7 4 3 3 8 3 3 π 3
Numerik gewöhnlicher Differentialgleichungen. Übung 8 - Lösungsvorschlag
 Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
y(x) ist die gesuchte Lsg.-Funktion der unabhängigen Variablen x Anfangswertproblem: Lsg. heißt Integralkurve
 Kapitel 8 Gewöhnliche Differentialgleichungen 8.1 Vorbemerkungen Betrachte skalare Gleichung y = dy dx = f(x, y(x)) (8.1) y(x) ist die gesuchte Lsg.-Funktion der unabhängigen Variablen x Mit der Anfangsbed.
Kapitel 8 Gewöhnliche Differentialgleichungen 8.1 Vorbemerkungen Betrachte skalare Gleichung y = dy dx = f(x, y(x)) (8.1) y(x) ist die gesuchte Lsg.-Funktion der unabhängigen Variablen x Mit der Anfangsbed.
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
Euler-Verfahren. exakte Lösung. Euler-Streckenzüge. Folie 1
 exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, August BIOL-B GES+T PHARM Lösungen zu Mathematik I/II. ( Punkte) a) Wir führen Polynomdivision durch und erhalten (x 3 5) : (x ) = x +x+ 4 x. Also ist g(x) die Asymptote von f(x)
Dr. A. Caspar ETH Zürich, August BIOL-B GES+T PHARM Lösungen zu Mathematik I/II. ( Punkte) a) Wir führen Polynomdivision durch und erhalten (x 3 5) : (x ) = x +x+ 4 x. Also ist g(x) die Asymptote von f(x)
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
Lösung Semesterendprüfung
 MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2012/13 DGL Grundlage Klassifikation Anwendung von lin. Ggln. M. konst.
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2012/13 DGL Grundlage Klassifikation Anwendung von lin. Ggln. M. konst.
Lösungen der Aufgaben zu Kapitel 10
 Lösungen der Aufgaben zu Kapitel 10 Abschnitt 10.2 Aufgabe 1 (a) Die beiden Funktionen f(x) = 1 und g(y) = y sind auf R definiert und stetig. 1 + x2 Der Definitionsbereich der Differentialgleichung ist
Lösungen der Aufgaben zu Kapitel 10 Abschnitt 10.2 Aufgabe 1 (a) Die beiden Funktionen f(x) = 1 und g(y) = y sind auf R definiert und stetig. 1 + x2 Der Definitionsbereich der Differentialgleichung ist
Einführung in die numerische Mathematik
 Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 014 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 014 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Exakte Differentialgleichungen
 Kapitel 4 Exakte Differentialgleichungen 4.1 Kurvenscharen Sei D R 2 ein offenes und zusammenhängendes Gebiet. Dann kann man zu jeder D einfach überdeckenden Kurvenschar eine Differentialgleichung erster
Kapitel 4 Exakte Differentialgleichungen 4.1 Kurvenscharen Sei D R 2 ein offenes und zusammenhängendes Gebiet. Dann kann man zu jeder D einfach überdeckenden Kurvenschar eine Differentialgleichung erster
Klausur im Fach Numerische Methoden II Universität Siegen; Fachbereich Maschinenbau,
 Aufgabe 1 (Polynominterpolation) Abb. 1: Roboter für Positionierungsaufgaben Industrieroboter erledigen oft Positionierungsaufgaben, indem sie einen vorgegebenen Pfad abfahren. Diese Trajektorie entspricht
Aufgabe 1 (Polynominterpolation) Abb. 1: Roboter für Positionierungsaufgaben Industrieroboter erledigen oft Positionierungsaufgaben, indem sie einen vorgegebenen Pfad abfahren. Diese Trajektorie entspricht
Rheinisch-Westfälische Technische Hochschule. Gegeben seien eine gewöhnliche Dierentialgleichung (DGL) und ein Anfangswert. γ l K l.
 Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Diplom VP Informatik / Numerik 2. September 2002
 Diplom VP Informatik / Numerik. September 00 Aufgabe Gegeben sei das lineare Gleichungssystem A x = b mit 0 4 0 0 0 0 A = 4 0 0 0 0 0 0 0 0 und b = 4 4 8 5. Punkte a Berechnen Sie die Cholesky Zerlegung
Diplom VP Informatik / Numerik. September 00 Aufgabe Gegeben sei das lineare Gleichungssystem A x = b mit 0 4 0 0 0 0 A = 4 0 0 0 0 0 0 0 0 und b = 4 4 8 5. Punkte a Berechnen Sie die Cholesky Zerlegung
Lineare Algebra und Numerische Mathematik für D-BAUG
 R Käppeli L Herrmann W Wu Herbstsemester 26 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 2 Aufgabe 2 Welche der folgenden Aussagen sind korrekt? (i) Jedes
R Käppeli L Herrmann W Wu Herbstsemester 26 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 2 Aufgabe 2 Welche der folgenden Aussagen sind korrekt? (i) Jedes
Analysis I. 14. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I 4. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching June 6, 207 Erinnerung Die Reihe a k konvergiert falls, lim S n = lim n n n a k =: a k existiert. Satz (Majoranten/Minorantenkriterium)
Analysis I 4. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching June 6, 207 Erinnerung Die Reihe a k konvergiert falls, lim S n = lim n n n a k =: a k existiert. Satz (Majoranten/Minorantenkriterium)
19. Januar Universität Erlangen-Nürnberg Department Mathematik PD Dr. Markus Bause. . Danach liefert die Gauss-Elinination. .
 Universität Erlangen-Nürnberg Department Mathematik PD Dr Markus Bause Numerik I 9 Januar A Gegeben sei die Matrix A = a Führen Sie eine Zeilenskalierung der Matrix durch Klausur b Bestimmen Sie mit Hilfe
Universität Erlangen-Nürnberg Department Mathematik PD Dr Markus Bause Numerik I 9 Januar A Gegeben sei die Matrix A = a Führen Sie eine Zeilenskalierung der Matrix durch Klausur b Bestimmen Sie mit Hilfe
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Lineare Algebra und Numerische Mathematik D-BAUG. Sommer 2012 Prof. H.-R. Künsch
 b Prüfung Lineare Algebra und Numerische Mathematik D-BAUG. Multiple Choice: Sommer Prof. H.-R. Künsch Gegeben sei die folgende Matrix A = 4. 4 (a) x AA T ist eine 4 4 Matrix mit ( AA T) = 4. AA T ist
b Prüfung Lineare Algebra und Numerische Mathematik D-BAUG. Multiple Choice: Sommer Prof. H.-R. Künsch Gegeben sei die folgende Matrix A = 4. 4 (a) x AA T ist eine 4 4 Matrix mit ( AA T) = 4. AA T ist
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, Januar 0 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 3 6 Total Vollständigkeit Bitte
Dr. A. Caspar ETH Zürich, Januar 0 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 3 6 Total Vollständigkeit Bitte
Mathematik III für MB, MPE, LaB, WI(MB) Übung 1, Lösungsvorschlag
 Gruppenübung Mathematik III für MB, MPE, LaB, WI(MB) Übung 1, Lösungsvorschlag G 11 (Klassifikation von Differentialgleichungen) Klassifizieren Sie die folgenden Differentialgleichungen: x 2 y + x y +
Gruppenübung Mathematik III für MB, MPE, LaB, WI(MB) Übung 1, Lösungsvorschlag G 11 (Klassifikation von Differentialgleichungen) Klassifizieren Sie die folgenden Differentialgleichungen: x 2 y + x y +
Diplom VP Numerik 21. März 2005
 Diplom VP Numerik. März 5 Aufgabe Gegeben sei das lineare Gleichungssystem Ax = b mit A = 3 3 4 8 und b = 4 5.5 6. ( Punkte) a) Berechnen Sie die LR-Zerlegung von A mit Spaltenpivotisierung. Geben Sie
Diplom VP Numerik. März 5 Aufgabe Gegeben sei das lineare Gleichungssystem Ax = b mit A = 3 3 4 8 und b = 4 5.5 6. ( Punkte) a) Berechnen Sie die LR-Zerlegung von A mit Spaltenpivotisierung. Geben Sie
KAPITEL 5. Damit wird F n (B) selbst zu einer Booleschen Algebra und es gilt f(x) := f(x) 0(x) := 0 B 1(x) := 1 B
 KAPITEL 5 Boolesche Polynome Polynome über R, d.h. reelle Funktionen der Form p(x) = a 0 + a 1 x + + a n x n, x R, sind schon aus der Schulmathematik bekannt. Wir beschäftigen uns nun mit Booleschen Polynomen,
KAPITEL 5 Boolesche Polynome Polynome über R, d.h. reelle Funktionen der Form p(x) = a 0 + a 1 x + + a n x n, x R, sind schon aus der Schulmathematik bekannt. Wir beschäftigen uns nun mit Booleschen Polynomen,
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
HTL Saalfelden Taylorreihen Seite 1 von 13. Wilfried Rohm
 HTL Saalfelden Taylorreihen Seite von 3 Wilfried Rohm wrohm@aon.at Taylorreihen Mathematische / Fachliche Inhalte in Stichworten: Approximation von Funktionen durch Taylorpolynome, Integration durch Reihentwicklung,
HTL Saalfelden Taylorreihen Seite von 3 Wilfried Rohm wrohm@aon.at Taylorreihen Mathematische / Fachliche Inhalte in Stichworten: Approximation von Funktionen durch Taylorpolynome, Integration durch Reihentwicklung,
Interpolation und Integration mit Polynomen
 Interpolation und Integration mit Polynomen Philipp Andrea Zardo Universität Kassel 23. Februar 2006 / Kassel Outline 1 Einleitung Was ist numerische Mathematik? Die eulersche e-funktion Ein Wurzelalgorithmus
Interpolation und Integration mit Polynomen Philipp Andrea Zardo Universität Kassel 23. Februar 2006 / Kassel Outline 1 Einleitung Was ist numerische Mathematik? Die eulersche e-funktion Ein Wurzelalgorithmus
1 Einführung, Terminologie und Einteilung
 Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Klausur Mathematik 2
 Mathematik für Ökonomen WS 2009/10 Campus Duisburg U. Herkenrath/H. Hoch, Fachbereich Mathematik Klausur Mathematik 2 09. Febr. 2010, 16:00 18:00 Uhr (120 Minuten) Erlaubte Hilfsmittel: Nur reine Schreib-
Mathematik für Ökonomen WS 2009/10 Campus Duisburg U. Herkenrath/H. Hoch, Fachbereich Mathematik Klausur Mathematik 2 09. Febr. 2010, 16:00 18:00 Uhr (120 Minuten) Erlaubte Hilfsmittel: Nur reine Schreib-
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
(3D-)Extrema unter Nebenbedingungen. Problemstellung (lokale Optimierung)
 (3D-)Extrema unter Nebenbedingungen Wir beschränken uns wieder (meistens) auf Funktionen von zwei Variablen x, y. Bei drei oder mehr Variablen x 1,..., x n sind die gleichen Techniken analog anwendbar,
(3D-)Extrema unter Nebenbedingungen Wir beschränken uns wieder (meistens) auf Funktionen von zwei Variablen x, y. Bei drei oder mehr Variablen x 1,..., x n sind die gleichen Techniken analog anwendbar,
Mathematische Methoden für Informatiker
 Prof. Dr. www.math.tu-dresden.de/ baumann 8.12.2016 20. Vorlesung Differentialgleichungen n-ter Ordnung Lösung einer Differentialgleichung Veranschaulichung der Lösungsmenge Anfangswertprobleme Differentialgleichungen
Prof. Dr. www.math.tu-dresden.de/ baumann 8.12.2016 20. Vorlesung Differentialgleichungen n-ter Ordnung Lösung einer Differentialgleichung Veranschaulichung der Lösungsmenge Anfangswertprobleme Differentialgleichungen
z 2 + 2z + 10 = 0 = 2 ± 36 2 Aufgabe 2 (Lineares Gleichungssystem) Sei die reelle 3 4 Matrix
 Mathematik für Wirtschaftswissenschaftler im WS 03/04 Lösungsvorschläge zur Klausur im WS 03/04 Aufgabe (Komplexe Zahlen (4 Punkte a Berechnen Sie das Produkt der beiden komplexen Zahlen + i und 3 + 4i
Mathematik für Wirtschaftswissenschaftler im WS 03/04 Lösungsvorschläge zur Klausur im WS 03/04 Aufgabe (Komplexe Zahlen (4 Punkte a Berechnen Sie das Produkt der beiden komplexen Zahlen + i und 3 + 4i
Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik II für biw/ciw/mach/mage/vt
 Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
ANALYSIS 2 VERSION 26. Juni 2018
 ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
ANALYSIS VERSION 6 Juni 018 LISIBACH ANDRÉ 6 Potenzreihenentwicklung 61 Einleitung Die Linearisierung einer Funktion f(x an der Stelle x ist die Funktion L(x f( + df dx ((x Die Linearisierung ist ein Polynom
NUMERIK 1. Sommersemester 2016
 NUMERIK 1 Soerseester 2016 KLAUSUR LÖSUNGSVORSCHLAG Aufgabe 1 (Multiple Choice) (ca. 20 Minuten, 8 Punkte) Kreuzen Sie korrekte Aussagen an. Es können ehrere Antworten richtig sein, indestens eine ist
NUMERIK 1 Soerseester 2016 KLAUSUR LÖSUNGSVORSCHLAG Aufgabe 1 (Multiple Choice) (ca. 20 Minuten, 8 Punkte) Kreuzen Sie korrekte Aussagen an. Es können ehrere Antworten richtig sein, indestens eine ist
Numerische Mathematik
 Numerische Mathematik SS 999 Augabe 6 Punkte Das Integral I ln d soll numerisch bis au eine Genauigkeit von mindestens - approimiert werden. a Wie groß muss die Anzahl N der Teilintervalle sein damit mit
Numerische Mathematik SS 999 Augabe 6 Punkte Das Integral I ln d soll numerisch bis au eine Genauigkeit von mindestens - approimiert werden. a Wie groß muss die Anzahl N der Teilintervalle sein damit mit
Prüfungsvorbereitungskurs Höhere Mathematik 3
 Prüfungsvorbereitungskurs Höhere Mathematik 3 Gewöhnliche Differentialgleichungen Marco Boßle Jörg Hörner Mathematik Online Frühjahr 2011 PV-Kurs HM 3 Gew. DGl 1-1 Zusammenfassung y (x) = F (x, y) Allgemeine
Prüfungsvorbereitungskurs Höhere Mathematik 3 Gewöhnliche Differentialgleichungen Marco Boßle Jörg Hörner Mathematik Online Frühjahr 2011 PV-Kurs HM 3 Gew. DGl 1-1 Zusammenfassung y (x) = F (x, y) Allgemeine
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
Klausurlösung Einführung in Numerische Methoden und FEM Universität Siegen, Department Maschinenbau,
 Universität Siegen, Department Maschinenbau, 7.7. Aufgabe y 3 l 3 3 F l l x Das dargestellte Fachwerk soll statisch mit Hilfe der FEM untersucht werden. Die Knoten und Elemente sind in der Abbildung nummeriert.
Universität Siegen, Department Maschinenbau, 7.7. Aufgabe y 3 l 3 3 F l l x Das dargestellte Fachwerk soll statisch mit Hilfe der FEM untersucht werden. Die Knoten und Elemente sind in der Abbildung nummeriert.
PRÜFUNG AUS MATHEMATIK 3
 (8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
(8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel;
 Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Der exakte Schnittpunkt ist aus der Grafik nur schwer heraus zu lesen. Es ist daher erfordelich, Gleichungssysteme auch rechnerisch lösen zu können!
 Das Problem des grafischen Lösungsverfahrens Die Lösungsmenge eines linearen Gleichungssystems in 2 Variablen lässt sich mit der grafischen Lösungsmethode nicht immer genau bestimmen. Die folgende Grafik
Das Problem des grafischen Lösungsverfahrens Die Lösungsmenge eines linearen Gleichungssystems in 2 Variablen lässt sich mit der grafischen Lösungsmethode nicht immer genau bestimmen. Die folgende Grafik
