7 Das Eulersche Polygonzugverfahren
|
|
|
- Insa Goldschmidt
- vor 5 Jahren
- Abrufe
Transkript
1 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem Abschnitt wird zunächst das einfachste Verfahren zur Berechnung solcher Approximationen, das Eulersche Polygonzugverfahren, vorgestellt. Dieses liefert auch einen neuen Beweis des Satzes von Picard-Lindelöf. Anschließend wird kurz auf schneller konvergente numerische Verfahren eingegangen. 7.1 Approximative Lösungen. a) Wie in der Situation des Satzes von Picard- Lindelöf seien τ R, ξ K n, d, b > 0, R = [τ, τ + d] K b (ξ) und f C(R, K n ) gegeben; es wird allerdings (zunächst) keine Lipschitz-Bedingung (1.1) vorausgesetzt. Mit M := f R definiert man δ := min {d, b } und I := [τ, τ + δ]. Für m N M und Schrittweiten h = h m = δ > 0 konstruiert man nun in den Punkten der m äquidistanten Zerlegungen I h := {t j = τ + jh j = 0...m} (1) von I Näherungen an eine Lösung des Anfangswertproblems ẋ = f(t, x), x(τ) = ξ : (2) b) Für eine Lösung ϕ C 1 (I, K n ) von (2) gilt natürlich ϕ(τ) = ξ und ϕ(t + h) ϕ(t) = t f(s, ϕ(s)) ds für t, t + h I h. (3) Man ersetzt nun das Integral einfach durch h f(t, ϕ(t)) und (3) durch das Anfangswertproblem für ein System von Differenzengleichungen y 0 = ξ, y j+1 y j = h f(t j, y j ) für j = 0...m 1. (4) Es ist (4) wohldefiniert und besitzt eindeutige Lösungen y0 h,...,yh m : Zunächst gilt y1 h ξ hm b, also (t 1, y1 h) R. Sind für 1 k m 1 bereits yh 1,...,yh k mit (4) und yj h ξ jhm b, insbesondere also (t j, yj h ) R, konstruiert, so liefert (4) genau ein yk+1 h Kn mit yk+1 h ξ yh k+1 yh k + yh k ξ hm + khm = (k + 1)hM b, insbesondere also auch (t k+1, y h k+1) R. c) Der Polygonzug durch die Punkte (τ, ξ), (t 1, y1 h),...,(τ +δ, yh m ) ist der Graph der Funktion y h : I K n, y h (t) := y h j + (t t j ) f(t j, y h j ) für t j t t j+1. (5) Es ist y h stückweise affin, und aus b) ergibt sich y h (t) y h (s) M (t s) für alle s t I. (6) d) Da f gleichmäßig stetig ist, gibt es zu ε > 0 ein α > 0 mit f(t 1, x 1 ) f(t 2, x 2 ) ε für (t 1, x 1 ), (t 2, x 2 ) R (7) mit t 1 t 2 α und x 1 x 2 α.
2 36 Gewöhnliche Differentialgleichungen / Sommersemester 2008 Für Schrittweiten h < γ := min {α, α M } und t (t j, t j+1 ) gilt nun ẏ h (t) = f(t j, y h j ) und y h (t) y h j M (t t j) < Mγ α, und aus (7) folgt ẏ h (t) f(t, y h (t)) = f(t j, y h j ) f(t, y h (t)) ε. Setzt man noch ẏ h (t j ) := f(t j, yj h ), so gilt also sup t I ẏ h (t) f(t, y h (t)) 0 für h 0 ; (8) die C 1 st -Funktionen yh sind also approximative Lösungen von (2). Mittels des Eulerschen Polygonzugverfahrens und des Lemmas von Gronwall ergibt sich ein neuer Beweis des Satzes von Picard-Lindelöf: 7.2 Theorem (Picard-Lindelöf). Für τ R, ξ K n, d, b > 0 sei J = [τ, τ +d] und R = J K b (ξ). Für f C(R, K n ) gelte eine Lipschitz-Bedingung (1.1) f(t, x 1 ) f(t, x 2 ) L x 1 x 2 für t J, x 1, x 2 K b (ξ). Mit M := f R, δ := min {d, b } und I = [τ, τ + δ] besitzt dann das Anfangswertproblem M (2) ẋ = f(t, x), x(τ) = ξ genau eine Lösung ϕ C 1 (I, K n ). Beweis. a) Für h k = δ k seien ϕ k = y h k C 1 st (I, K n ) die in 7.1 konstruierten approximativen Lösungen von (2); dann gilt also nach (8) Man hat ε k := sup t I ϕ k (t) f(t, ϕ k (t)) 0 für k. (9) ϕ k (t) = ϕ k (τ) + t τ ϕ k(s) ds = ξ + t τ f(s, ϕ k(s)) ds + t τ d k(s) ds (10) mit d k (s) := ϕ k (s) f(s, ϕ k (s)), also d k sup ε k. b) Für k, l N und ψ := ϕ k ϕ l ergibt sich aus (10) und (1.1) ψ(t) = t τ (f(s, ϕ k(s)) f(s, ϕ l (s))) ds + t τ (d k(s) d l (s)) ds, ψ(t) L t τ ϕ k(s) ϕ l (s) ds + δ (ε k + ε l ) für t I. Das Lemma von Gronwall liefert dann ψ(t) δ (ε k + ε l ) e L(t τ), also also ϕ k ϕ l I δ e Lδ (ε k + ε l ). (11) Folglich ist (ϕ k ) eine Cauchy-Folge in C(I), und somit existiert der gleichmäßige Limes ϕ = lim k ϕ k C(I). c) Nach (7) (oder auch (1.1)) gilt auch f(s, ϕ k (s)) f(s, ϕ(s)) gleichmäßig auf I ; wegen d k 0 folgt daher ϕ(t) = ξ + t τ f(s, ϕ(s)) ds für t I, und somit ist ϕ eine Lösung des Anfangswertproblems (2). d) Die Eindeutigkeit folgt sofort aus dem Argument in b): Sind ϕ k und ϕ l Lösungen von (2), so gilt (11) mit ε k = ε l = 0, und man hat ϕ k = ϕ l.
3 7 Das Eulersche Polygonzugverfahren Konvergenzgeschwindigkeit. a) In der Situation des Satzes von Picard- Lindelöf sei ϕ C 1 (I, K n ) die Lösung des Anfangswertproblems (2). Für die lokalen Abschneidefehler T h (t) := 1 h t f(s, ϕ(s)) ds f(t, ϕ(t)) für t I h := I h\{τ + δ} (12) gilt aufgrund der gleichmäßigen Stetigkeit von f offenbar T h := t I h T h (t) 0 für h 0. (13) b) Für die in (5) definierten Funktionen y h gilt die Abschätzung y h (t) ϕ(t) (t τ) T h e L(t τ) für t I h. (14) Denn: Nach (3), (4) und (12) erfüllen die Fehler r j := r h j := y h (t j ) ϕ(t j ) (15) in den Punkten t j I h die Differenzengleichung r j+1 r j = y h (t j+1 ) ϕ(t j+1 ) (y h (t j ) ϕ(t j )) = h f(t j, y h (t j )) t j +h t j f(s, ϕ(s)) ds = h (f(t j, y h (t j )) f(t j, ϕ(t j )) h T h (t j ) ; aus der Lipschitz-Bedingung (1.1) folgt also r j+1 r j + h L r j + h T h. Für t = t 0 ist (14) klar. Gilt nun (14) für t = t j, so folgt wegen 1 + hl e hl und h h e L(t j+1 τ) auch r j+1 e hl (t j τ) T h e L(t j τ) + h T h also (14) für t = t j+1. (t j+1 τ) T h e L(t j+1 τ), c) Gilt nun f C 1 (R, K n ), so folgt ϕ C 2 (I, K n ), und für die lokalen Abschneidefehler liefert die Taylor-Formel mit Integral-Restglied und somit T h (t) = 1 h (ϕ(t + h) ϕ(t)) ϕ (t) = h 1 0 ϕ (t + sh) (1 s) ds T h = t I h T h (t) 1 2 ϕ h. (16) Aus Satz (14) ergibt sich dann sofort die O(h) -Abschätzung y h (t) ϕ(t) δ 2 elδ ϕ h (17) für die Konvergenzgeschwindigkeit des Eulerschen Polygonzugverfahrens.
4 38 Gewöhnliche Differentialgleichungen / Sommersemester Einschrittverfahren. a) Man erhält schneller konvergente Verfahren, wenn man das Integral in (3) durch eine bessere Approximation als h f(t, ϕ(t)) ersetzt; statt (4) löst man dann Systeme y 0 = ξ, y j+1 y j = h Φ h (t j, y j ) für j = 0...m 1 (18) von Differenzengleichungen mit geeigneten Funktionen Φ h (t, x). Durch (18) wird ein Einschrittverfahren zur Lösung von (2) definiert; auf Mehrschrittverfahren, bei denen yj+1 h aus mehreren vorhergehenden Werten yh j,..., yh j s berechnet wird, kann hier nicht eingegangen werden. b) Das Verfahren (18) heißt konsistent, wenn für die lokalen Abschneidefehler T h (t) := 1 h t f(s, ϕ(s)) ds Φ h (t, ϕ(t)) für t I h := I h\{a + δ} (19) bei Einsetzen der Lösung ϕ C 1 (I, K n ) von (2) wieder T h 0 für h 0 gilt (vgl. (13)); es besitzt die Konsistenzordnung p N, wenn T h = O(h p ) für h 0 (20) ist. Gilt nun eine in 0 < h h 0 gleichmäßige Lipschitz-Bedingung Φ h (t, x 1 ) Φ h (t, x 2 ) L x 1 x 2 (21) in einer Umgebung {(t, x) τ t τ +δ, x ϕ(t) β} der Lösung ϕ, so folgt wie in 7.3 y h (t) ϕ(t) 0 (22) für konsistente Verfahren und y h (t) ϕ(t) = O(h p ) für h 0 (23) für Verfahren der Konsistenzordnung p N. Die Lipschitz-Bedingung (21) impliziert auch die Stabilität des Verfahrens (gegen kleine Störungen der Daten, insbesondere gegen Rundungsfehler). 7.5 Beispiele. a) Approximation des Integrals in (3) durch die Sehnentrapezregel liefert t f(s, ϕ(s)) ds h (f(t, ϕ(t)) + f(t + h, ϕ(t + h))) 2 und mit ϕ(t + h) ϕ(t) + h f(t, ϕ(t)) dann das modifizierte Polygonzugverfahren (18) mit Φ h (t, x) := 1 (f(t, x) + f(t + h, x + h f(t, x))). (24) 2 b) Approximation des Integrals in (3) durch die Keplersche Faßregel liefert t f(s, ϕ(s)) ds h (f(t, ϕ(t)) + 4f(t + h, ϕ(t + h )) + f(t + h, ϕ(t + h))) ; 6 2 2
5 7 Das Eulersche Polygonzugverfahren 39 mit den Hilfsfunktionen k 0 (h, t, x) : = f(t, x), k 1 (h, t, x) : = f(t + h 2, x + h 2 k 0(t, x)), k 2 (h, t, x) : = f(t + h 2, x + h 2 k 1(t, x)), k 3 (h, t, x) : = f(t + h, x + h k 2 (t, x)) konstruiert man dann das Runge-Kutta-Verfahren (18) mit Φ h (t, x) := 1 6 (k 0 + 2k 1 + 2k 2 + k 3 )(h, t, x). (25) c) Das modifizierte Polygonzugverfahren und das Runge-Kutta-Verfahren sind konsistent mit den Konsistenzordnungen 2 und 4 (für f C 2 (R, K n ) bzw. f C 4 (R, K n ) ); aus der Lipschitz-Bedingung (1.1) für f folgt die Lipschitz-Bedingung (21) für Φ h (für Beweise dieser Aussagen sei auf Lehrbücher über numerische Mathematik verwiesen). Nach 7.4 b) sind die beiden Verfahren also konvergent und besitzen die Konvergenzordnungen 2 und 4 für f C 2 (R, K n ) bzw. f C 4 (R, K n ).
Übungen zu Differentialgleichungen (WiSe 12/13)
 Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Gewöhnliche Differentialgleichungen Woche 6. Existenz nach Picard-Lindelöf
 d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
14 Ljapunov-Funktionen
 14 Ljapunov-Funktionen 67 14 Ljapunov-Funktionen 14.1 Gradientenfelder. a Ein Vektorfeld v C 1 D, R n besitze ein Potential U C 2 D, R, d.h. es sei v = gradu. Dann ist Dvx = HUx symmetrisch, und man hat
14 Ljapunov-Funktionen 67 14 Ljapunov-Funktionen 14.1 Gradientenfelder. a Ein Vektorfeld v C 1 D, R n besitze ein Potential U C 2 D, R, d.h. es sei v = gradu. Dann ist Dvx = HUx symmetrisch, und man hat
Gewöhnliche Differentialgleichungen Woche 7. Globale Existenz einer Lösung
 Gewöhnliche Differentialgleichungen Woche 7 Globale Existenz einer Lösung 7.1 Von lokal zu global Wir betrachten wiederum das Anfangswertproblem { y (x = f (x, y(x, y( = y 0. (7.1 Eine erste Erweiterung
Gewöhnliche Differentialgleichungen Woche 7 Globale Existenz einer Lösung 7.1 Von lokal zu global Wir betrachten wiederum das Anfangswertproblem { y (x = f (x, y(x, y( = y 0. (7.1 Eine erste Erweiterung
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 Einschrittverfahren 2.1 Einführung
 Einschrittverfahren. Einführung Im folgenden werden wir uns bei der Beschreibung und Analyse von numerischen Verfahren für Anfangswertprobleme auf den Fall n = beschränken. Dies wird nur gemacht, um die
Einschrittverfahren. Einführung Im folgenden werden wir uns bei der Beschreibung und Analyse von numerischen Verfahren für Anfangswertprobleme auf den Fall n = beschränken. Dies wird nur gemacht, um die
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Skript zur Vorlesung Analysis 3
 Skript zur Vorlesung Analysis 3 Herbstsemester 204 Prof. Benjamin Schlein Inhaltsverzeichnis Gewöhnliche Differentialgleichungen 2. Differentialgleichungen erster Ordnung, elementare Lösungsmethoden..
Skript zur Vorlesung Analysis 3 Herbstsemester 204 Prof. Benjamin Schlein Inhaltsverzeichnis Gewöhnliche Differentialgleichungen 2. Differentialgleichungen erster Ordnung, elementare Lösungsmethoden..
Analysis II (FS 2015): Vektorfelder und Flüsse
 Analysis II (FS 215): Vektorfelder und Flüsse Dietmar A. Salamon ETH-Zürich 7. April 215 1 Der Fluss eines Vektorfeldes Sei U R n eine offene Menge und sei f : U R n eine lokal Lipschitz-stetige Abbildung.
Analysis II (FS 215): Vektorfelder und Flüsse Dietmar A. Salamon ETH-Zürich 7. April 215 1 Der Fluss eines Vektorfeldes Sei U R n eine offene Menge und sei f : U R n eine lokal Lipschitz-stetige Abbildung.
Theorie der Anfangswertaufgaben
 34 KAPITEL 3 Theorie der Anfangswertaufgaben In diesem Abschnitt geht es um eine allgemeine theoretische Untersuchung von Anfangswertaufgaben der Form: Anfangswertproblem: Dabei ist y (x) = f(x, y(x)),
34 KAPITEL 3 Theorie der Anfangswertaufgaben In diesem Abschnitt geht es um eine allgemeine theoretische Untersuchung von Anfangswertaufgaben der Form: Anfangswertproblem: Dabei ist y (x) = f(x, y(x)),
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Existenz- und Eindeutigkeitssätze für Anfangswertprobleme
 Kapitel 2 Existenz- und Eindeutigkeitssätze für Anfangswertprobleme In diesem Kapitel sei K = R oder K = C. Satz 2.1 (Existenzsatz von Peano) Sei D R K N offen, f : D K N eine stetige Funktion, (, y 0
Kapitel 2 Existenz- und Eindeutigkeitssätze für Anfangswertprobleme In diesem Kapitel sei K = R oder K = C. Satz 2.1 (Existenzsatz von Peano) Sei D R K N offen, f : D K N eine stetige Funktion, (, y 0
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky. Institut für Mathematik
 NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
Satz von Peano. Sei f stetig und beschränkt auf
 Satz von Peano Sei f stetig und beschränkt auf { } Q ab := (t,y) R n+1 : t t 0 a; y y 0 b mit f(t,y) M und α := min(a, b M ). Dann besitzt das Anfangswertproblem y = f(t,y), y(t 0 ) = y 0 Giuseppe Peano
Satz von Peano Sei f stetig und beschränkt auf { } Q ab := (t,y) R n+1 : t t 0 a; y y 0 b mit f(t,y) M und α := min(a, b M ). Dann besitzt das Anfangswertproblem y = f(t,y), y(t 0 ) = y 0 Giuseppe Peano
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Gewöhnliche Dierentialgleichungen
 Prof. Dr. Guido Sweers WS 28/29 Jan Gerdung, M.Sc. Gewöhnliche Dierentialgleichungen Übungsblatt 6 Die Lösungen müssen in den Übungsbriefkasten Gewöhnliche Dierentialgleichungen Raum 3 im MI) geworfen
Prof. Dr. Guido Sweers WS 28/29 Jan Gerdung, M.Sc. Gewöhnliche Dierentialgleichungen Übungsblatt 6 Die Lösungen müssen in den Übungsbriefkasten Gewöhnliche Dierentialgleichungen Raum 3 im MI) geworfen
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1. Prof. Dr. Hans Babovsky. Technische Universität Ilmenau
 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
11. Einschrittverfahren
 H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
Maximalität und Globalität von Lösungen
 Gewöhnliche Differentialgleichungen Florian Wörz SoSe 205 Maximalität und Globalität von Lösungen Maximale Lösungen Sei Ω : T U R R n ein Gebiet, f : Ω R n stetig und (t 0, u 0 ) Ω. Im Folgenden betrachten
Gewöhnliche Differentialgleichungen Florian Wörz SoSe 205 Maximalität und Globalität von Lösungen Maximale Lösungen Sei Ω : T U R R n ein Gebiet, f : Ω R n stetig und (t 0, u 0 ) Ω. Im Folgenden betrachten
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Formelsammlung Analysis I & II
 Formelsammlung Analysis I & II Wichtige eindimensionale Integrale: { x s dx = s+ xs+ + C falls s log x + C falls s = exp(x dx = exp(x + C cos(x dx = sin(x + C sin(x dx = cos(x + C sinh(x dx = cosh(x +
Formelsammlung Analysis I & II Wichtige eindimensionale Integrale: { x s dx = s+ xs+ + C falls s log x + C falls s = exp(x dx = exp(x + C cos(x dx = sin(x + C sin(x dx = cos(x + C sinh(x dx = cosh(x +
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 2
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
Differentialgleichungen
 Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Ana-2 1. Ss n + 1 < t 1 n, 1. eine Treppenfunktion, eine Regelfunktion, oder keins von beidem?
 Ana-2 1 Ss 218 11.4.18 Votieraufgaben 1 Ist f : [a,b] R eine Regelfunktion und φ : R R stetig, so ist auch φ f eine Regelfunktion. 2 Sei f : [a,b] R stetig. Dann existiert zu jedem ε > ein δ >, so dass
Ana-2 1 Ss 218 11.4.18 Votieraufgaben 1 Ist f : [a,b] R eine Regelfunktion und φ : R R stetig, so ist auch φ f eine Regelfunktion. 2 Sei f : [a,b] R stetig. Dann existiert zu jedem ε > ein δ >, so dass
Differentialgeometrie I (Kurventheorie) SS 2013
 Differentialgeometrie I (Kurventheorie) SS 2013 Lektion 6 5. Juni 2013 c Daria Apushkinskaya 2013 () Kurventheorie: Lektion 6 5. Juni 2013 1 / 23 8. Fundamentalsatz der lokalen Kurventheorie (Fortsetzung)
Differentialgeometrie I (Kurventheorie) SS 2013 Lektion 6 5. Juni 2013 c Daria Apushkinskaya 2013 () Kurventheorie: Lektion 6 5. Juni 2013 1 / 23 8. Fundamentalsatz der lokalen Kurventheorie (Fortsetzung)
Institut für Analysis WS 2014/15 PD Dr. Peer Christian Kunstmann Dipl.-Math. Leonid Chaichenets
 Institut für Analysis WS 4/5 PD Dr. Peer Christian Kunstmann 9..4 Dipl.-Math. Leonid Chaichenets Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zum 5. Übungsblatt Aufgabe : (a) Sei
Institut für Analysis WS 4/5 PD Dr. Peer Christian Kunstmann 9..4 Dipl.-Math. Leonid Chaichenets Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zum 5. Übungsblatt Aufgabe : (a) Sei
Der Satz von Arzelà-Ascoli und der Satz von Peano. Anna Katharina Zentgraf Studiengang: Master GyGe Matrikelnummer:
 Der Satz von Arzelà-Ascoli und der Satz von Peano Anna Katharina Zentgraf Studiengang: Master GyGe Matrikelnummer: 134156 9. Mai 2013 Betreuer: JP Dr. Tomas Dohnal Fakultät für Mathematik Analysis (Ls1)
Der Satz von Arzelà-Ascoli und der Satz von Peano Anna Katharina Zentgraf Studiengang: Master GyGe Matrikelnummer: 134156 9. Mai 2013 Betreuer: JP Dr. Tomas Dohnal Fakultät für Mathematik Analysis (Ls1)
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
Höhere Mathematik III für die Fachrichtung Physik Wintersemester 2016/17. Lösungsvorschlag zu Übungsblatt 5
 Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Numerik und Simulation in der Geoökologie
 1/49 Rekapitulation Das Euler-Verfahren für ODE-IVP Eigenschaften von Einschrittverfahren Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 2 WS 2007/2008 2/49 Rekapitulation Das Euler-Verfahren
1/49 Rekapitulation Das Euler-Verfahren für ODE-IVP Eigenschaften von Einschrittverfahren Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 2 WS 2007/2008 2/49 Rekapitulation Das Euler-Verfahren
4 Autonome Systeme und Erste Integrale
 4 Autonome Systeme und Erste Integrale 17 4 Autonome Systeme und Erste Integrale 4.1 Autonome Systeme haben die Form ẋ = v(x) (1) mit lokal Lipschitz-stetigen Vektorfeldern v C(D, K n ). a) Man kann v
4 Autonome Systeme und Erste Integrale 17 4 Autonome Systeme und Erste Integrale 4.1 Autonome Systeme haben die Form ẋ = v(x) (1) mit lokal Lipschitz-stetigen Vektorfeldern v C(D, K n ). a) Man kann v
3. Lineare Mehrschrittverfahren 3.1 Begriffe
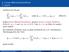 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
Analysis II. 8. Klausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis II 8. Klausur mit en 1 2 Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Eine Metrik auf einer Menge M. 2) Die Kurvenlänge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis II 8. Klausur mit en 1 2 Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Eine Metrik auf einer Menge M. 2) Die Kurvenlänge
Caputo fraktionale Differentialgleichungen. 1 Riemann Liouville fraktionale Differentialgleichungen
 Seminar Fraktionale Differentialgleichungen Prof. Dr. P.E. Kloeden, WS1000/2001 Caputo fraktionale Differentialgleichungen Lars Grüne, 25.1.2001 Basierend auf Fractional Differential Equations, Theory
Seminar Fraktionale Differentialgleichungen Prof. Dr. P.E. Kloeden, WS1000/2001 Caputo fraktionale Differentialgleichungen Lars Grüne, 25.1.2001 Basierend auf Fractional Differential Equations, Theory
4 Numerik von Anfangswertaufgaben
 4 Numerik von Anfangswertaufgaben Diese Einführung behandelt numerische Lösungsverfahren für gewöhnliche, explizite Differentialgleichungen. Ordnung. Im Folgenden wird die Variable t R die Zeit und x R
4 Numerik von Anfangswertaufgaben Diese Einführung behandelt numerische Lösungsverfahren für gewöhnliche, explizite Differentialgleichungen. Ordnung. Im Folgenden wird die Variable t R die Zeit und x R
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
mathematik und informatik
 Prof. Dr. Torsten Linß Kurs 037 Numerische Mathematik II LESEPROBE mathematik und informatik Das Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere das Recht der Vervielfältigung
Prof. Dr. Torsten Linß Kurs 037 Numerische Mathematik II LESEPROBE mathematik und informatik Das Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere das Recht der Vervielfältigung
4 Numerik von Anfangswertaufgaben
 4 Numerik von Anfangswertaufgaben Diese Einführung behandelt numerische Lösungsverfahren für gewöhnliche, explizite Differentialgleichungen. Ordnung. Im Folgenden wird die Variable t R die Zeit und x R
4 Numerik von Anfangswertaufgaben Diese Einführung behandelt numerische Lösungsverfahren für gewöhnliche, explizite Differentialgleichungen. Ordnung. Im Folgenden wird die Variable t R die Zeit und x R
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Gewöhnliche Differentialgleichungen Woche 7. Nicht-lineare und linearisierte Systeme
 Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
Numerische Methoden für gewöhnliche Differentialgleichungen
 Numerische Methoden für gewöhnliche Differentialgleichungen Lars Grüne Lehrstuhl für Angewandte Mathematik Mathematisches Institut Universität Bayreuth 9544 Bayreuth lars.gruene@uni-bayreuth.de www.math.uni-bayreuth.de/
Numerische Methoden für gewöhnliche Differentialgleichungen Lars Grüne Lehrstuhl für Angewandte Mathematik Mathematisches Institut Universität Bayreuth 9544 Bayreuth lars.gruene@uni-bayreuth.de www.math.uni-bayreuth.de/
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
6 Iterationsverfahren für lineare und nichtlineare Gleichungssysteme
 6 Iterationsverfahren für lineare und nichtlineare Gleichungssysteme 6.1 Nullstellen reeller Funktionen Bemerkung 6.1 (Problemstellung) geg.: f C[a, b] ges.: x [a, b] mit f(x ) = 0 Lösungstheorie f linear
6 Iterationsverfahren für lineare und nichtlineare Gleichungssysteme 6.1 Nullstellen reeller Funktionen Bemerkung 6.1 (Problemstellung) geg.: f C[a, b] ges.: x [a, b] mit f(x ) = 0 Lösungstheorie f linear
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
74 Gewöhnliche Differentialgleichungen / Sommersemester 2008
 74 Gewöhnliche Differentialgleichungen / Sommersemester 2008 15 Flüsse Bisher wurde im wesentlichen die Abhängigkeit der Lösungen autonomer Systeme von der Zeit bei festem Anfangswert untersucht. Nun wird
74 Gewöhnliche Differentialgleichungen / Sommersemester 2008 15 Flüsse Bisher wurde im wesentlichen die Abhängigkeit der Lösungen autonomer Systeme von der Zeit bei festem Anfangswert untersucht. Nun wird
MIA Analysis einer reellen Veränderlichen WS 06/07. Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen
 Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
TECHNISCHE UNIVERSITÄT BERLIN BACHELORARBEIT. Theorie und Simulation einer zweidimensionalen stochastischen Differentialgleichung.
 TECHNISCHE UNIVERSITÄT BERLIN Fakultät II Institut für Mathematik BACHELORARBEIT im Studiengang Mathematik über das Thema Theorie und Simulation einer zweidimensionalen stochastischen Differentialgleichung
TECHNISCHE UNIVERSITÄT BERLIN Fakultät II Institut für Mathematik BACHELORARBEIT im Studiengang Mathematik über das Thema Theorie und Simulation einer zweidimensionalen stochastischen Differentialgleichung
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
 Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
Seminar Gewöhnliche Dierentialgleichungen
 Seminar Gewöhnliche Dierentialgleichungen Dynamische Systeme II Valentin Jonas 8. 6. 215 1 Einleitung In dem letzten Kapitel "Dynamische Systeme I" ging es vor allem um in t glatte, autonome, dynamische
Seminar Gewöhnliche Dierentialgleichungen Dynamische Systeme II Valentin Jonas 8. 6. 215 1 Einleitung In dem letzten Kapitel "Dynamische Systeme I" ging es vor allem um in t glatte, autonome, dynamische
12.1 Kurven und Parametertransformationen. Wir untersuchen in diesem Abschnitt so genannte Kurven, die in der nachstehenden Definition
 Kapitel 1 Kurven im R n 1.1 Kurven und Parametertransformationen 1. Funktionen von beschränkter Schwankung 1.3 Die Bogenlänge von Kurven 1.4 Parametrisierung nach der Bogenlänge 1.1 Kurven und Parametertransformationen
Kapitel 1 Kurven im R n 1.1 Kurven und Parametertransformationen 1. Funktionen von beschränkter Schwankung 1.3 Die Bogenlänge von Kurven 1.4 Parametrisierung nach der Bogenlänge 1.1 Kurven und Parametertransformationen
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
ist ein n-dimensionaler, reeller Vektorraum (vgl. Lineare Algebra). Wir definieren auf diesem VR ein Skalarprodukt durch i y i i=1
 24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung. Lösungen zur Probeklausur 2.
 Adµ Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung Blatt Probeklausur 2 Lösungen zur Probeklausur 2 Aufgabe 1 1. Formulieren Sie den Satz von Taylor
Adµ Universität Stuttgart Fakultät Mathematik und Physik Institut für Analysis, Dynamik und Modellierung Blatt Probeklausur 2 Lösungen zur Probeklausur 2 Aufgabe 1 1. Formulieren Sie den Satz von Taylor
x= f(x) p= U (x). (b) Zeigen Sie, dass auf jeder auf einem Intervall existierenden Lösung t x(t) die Energie E(t) := 1 2 p(t)2 + U(x(t)) x 1
 Blatt 1 03042006 H-Ch Grunau Aufgabe 1 Betrachten Sie die Differentialgleichung x= f(x) mit f = U und U C 2 ((α, β), R) und schreiben Sie diese in der Form x= p, p= U (x) (a) Skizzieren Sie die Phasenportraits
Blatt 1 03042006 H-Ch Grunau Aufgabe 1 Betrachten Sie die Differentialgleichung x= f(x) mit f = U und U C 2 ((α, β), R) und schreiben Sie diese in der Form x= p, p= U (x) (a) Skizzieren Sie die Phasenportraits
Anfangswertprobleme bei differential-algebraischen Gleichungen (DAEs)
 Anfangswertprobleme bei differential-algebraischen Gleichungen (DAEs) Elgersburg, 13. Februar 2006 Gliederung 1 Differential-algebraische Gleichungen 2 Distributionen 3 Anfangswertprobleme 4 Zusammenfassung
Anfangswertprobleme bei differential-algebraischen Gleichungen (DAEs) Elgersburg, 13. Februar 2006 Gliederung 1 Differential-algebraische Gleichungen 2 Distributionen 3 Anfangswertprobleme 4 Zusammenfassung
Numerische Mathematik II: Differentialgleichungen
 Numerische Mathematik II: Differentialgleichungen Lars Grüne Mathematisches Institut Fakultät für Mathematik und Physik Universität Bayreuth 95440 Bayreuth lars.gruene@uni-bayreuth.de www.uni-bayreuth.de/departments/math/
Numerische Mathematik II: Differentialgleichungen Lars Grüne Mathematisches Institut Fakultät für Mathematik und Physik Universität Bayreuth 95440 Bayreuth lars.gruene@uni-bayreuth.de www.uni-bayreuth.de/departments/math/
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
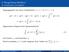 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
D-MATH, D-PHYS, D-CHAB Analysis II FS 2017 Prof. Manfred Einsiedler. Übungsblatt 5 A := u = Au, u(0) = 1. 1
 D-MATH, D-PHYS, D-CHAB Analysis II FS 2017 Prof. Manfred Einsiedler Übungsblatt 5 1. Gegeben sei die Matrix 1 1 0 A := 0 1 0 0 0 2 a) Bestimmen Sie ein Fundamentalsystem (das heisst eine Basis des Lösungsraums)
D-MATH, D-PHYS, D-CHAB Analysis II FS 2017 Prof. Manfred Einsiedler Übungsblatt 5 1. Gegeben sei die Matrix 1 1 0 A := 0 1 0 0 0 2 a) Bestimmen Sie ein Fundamentalsystem (das heisst eine Basis des Lösungsraums)
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Der Satz von Arzelà-Ascoli und der Satz von Peano
 Der Satz von Arzelà-Ascoli und der Satz von Peano Judith Vorwerk 13.05.2013 Inhaltsverzeichnis 1 Der Satz von Arzelà-Ascoli 5 2 Der Satz von Peano 10 2 Einleitung Diese Ausarbeitung beschäftigt sich mit
Der Satz von Arzelà-Ascoli und der Satz von Peano Judith Vorwerk 13.05.2013 Inhaltsverzeichnis 1 Der Satz von Arzelà-Ascoli 5 2 Der Satz von Peano 10 2 Einleitung Diese Ausarbeitung beschäftigt sich mit
Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi
![Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi](/thumbs/92/110521610.jpg) Funktionentheorie, Woche 7 Eigenschaften holomorpher Funktionen 7.1 Ganze Funktionen Definition 7.1 Eine Funktion f : C C, die holomorph ist auf C, nennt man eine ganze Funktion. Bemerkung 7.1.1 Als Folge
Funktionentheorie, Woche 7 Eigenschaften holomorpher Funktionen 7.1 Ganze Funktionen Definition 7.1 Eine Funktion f : C C, die holomorph ist auf C, nennt man eine ganze Funktion. Bemerkung 7.1.1 Als Folge
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 1
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Numerik gewöhnlicher Differentialgleichungen. Prof. Dr. Guido Kanschat
 Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Nachklausur am Donnerstag, den 7. August 2008
 Nachklausur zur Vorlesung Numerische Mathematik (V2E2) Sommersemester 2008 Prof. Dr. Martin Rumpf Dr. Martin Lenz Dipl.-Math. Nadine Olischläger Nachklausur am Donnerstag, den 7. August 2008 Bearbeitungszeit:
Nachklausur zur Vorlesung Numerische Mathematik (V2E2) Sommersemester 2008 Prof. Dr. Martin Rumpf Dr. Martin Lenz Dipl.-Math. Nadine Olischläger Nachklausur am Donnerstag, den 7. August 2008 Bearbeitungszeit:
Zweite Prüfung zur Vorlesung
 Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Darstellungsformeln für die Lösung von parabolischen Differentialgleichungen
 Kapitel 8 Darstellungsformeln für die Lösung von parabolischen Differentialgleichungen Wir hatten im Beispiel 5. gesehen, dass die Wärmeleitungsgleichung t u u = f auf Ω (0, ) (8.1) eine parabolische Differentialgleichung
Kapitel 8 Darstellungsformeln für die Lösung von parabolischen Differentialgleichungen Wir hatten im Beispiel 5. gesehen, dass die Wärmeleitungsgleichung t u u = f auf Ω (0, ) (8.1) eine parabolische Differentialgleichung
Numerische Mathematik II: Differentialgleichungen
 Numerische Mathematik II: Differentialgleichungen Lars Grüne Mathematisches Institut Fakultät für Mathematik und Physik Universität Bayreuth 95440 Bayreuth lars.gruene@uni-bayreuth.de www.uni-bayreuth.de/departments/math/
Numerische Mathematik II: Differentialgleichungen Lars Grüne Mathematisches Institut Fakultät für Mathematik und Physik Universität Bayreuth 95440 Bayreuth lars.gruene@uni-bayreuth.de www.uni-bayreuth.de/departments/math/
Numerik gewöhnlicher Differentialgleichungen
 Skript zur Vorlesung im WS 4/5 Numerik gewöhnlicher Differentialgleichungen Thorsten Raasch. Februar 5 Inhaltsverzeichnis Einleitung 5 Anfangswertprobleme gewöhnlicher Differentialgleichungen 7. Grundbegriffe
Skript zur Vorlesung im WS 4/5 Numerik gewöhnlicher Differentialgleichungen Thorsten Raasch. Februar 5 Inhaltsverzeichnis Einleitung 5 Anfangswertprobleme gewöhnlicher Differentialgleichungen 7. Grundbegriffe
Universität Ulm Abgabe: Mittwoch,
 Universität Ulm Abgabe: Mittwoch, 8.5.23 Prof. Dr. W. Arendt Jochen Glück Sommersemester 23 Punktzahl: 36+4* Lösungen Halbgruppen und Evolutionsgleichungen: Blatt 2. Sei X ein Banachraum und (T (t)) t
Universität Ulm Abgabe: Mittwoch, 8.5.23 Prof. Dr. W. Arendt Jochen Glück Sommersemester 23 Punktzahl: 36+4* Lösungen Halbgruppen und Evolutionsgleichungen: Blatt 2. Sei X ein Banachraum und (T (t)) t
S k r i p t Analysis III. Herbstsemester Prof. Dr. Camillo de Lellis
 S k r i p t Analysis III Herbstsemester 2011 Prof. Dr. Camillo de Lellis Stand: 26. Dezember 2012 INHALTSVRZICHNIS i Inhaltsverzeichnis 1 Gewöhnliche Differentialgleichungen 2 1.1 Systeme von gewöhnlichen
S k r i p t Analysis III Herbstsemester 2011 Prof. Dr. Camillo de Lellis Stand: 26. Dezember 2012 INHALTSVRZICHNIS i Inhaltsverzeichnis 1 Gewöhnliche Differentialgleichungen 2 1.1 Systeme von gewöhnlichen
9 Numerische Verfahren für Anfangswertaufgaben
 Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik Partieller Differentialgleichungen
 Numerik Partieller Differentialgleichungen Martin Neumüller, Institute of Computational Mathematics, JKU Linz martin.neumueller@jku.at www.numa.uni-linz.ac.at Inhaltsverzeichnis 2 Parabolische Differentialgleichungen
Numerik Partieller Differentialgleichungen Martin Neumüller, Institute of Computational Mathematics, JKU Linz martin.neumueller@jku.at www.numa.uni-linz.ac.at Inhaltsverzeichnis 2 Parabolische Differentialgleichungen
8. Die Nullstellen der Zeta-Funktion
 8.. Wie vorher sei ( s ξ(s = π s/ Γ ζ(s. ξ ist meromorph in ganz C, hat Pole (erster Ordnung nur bei s = und s = und genügt der Funktionalgleichung ξ(s = ξ( s. Daraus folgt: Für Re s < hat die Zeta-Funktion
8.. Wie vorher sei ( s ξ(s = π s/ Γ ζ(s. ξ ist meromorph in ganz C, hat Pole (erster Ordnung nur bei s = und s = und genügt der Funktionalgleichung ξ(s = ξ( s. Daraus folgt: Für Re s < hat die Zeta-Funktion
Nichtlineare Gleichungssysteme
 Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Öffnen Sie den Klausurbogen erst nach Aufforderung! Mathematische Grundlagen III (CES) WS 2017/2018 Klausur 23. März 2018
 Prof. Dr. Manuel Torrilhon Prof. Dr. Sebastian Noelle Öffnen Sie den Klausurbogen erst nach Aufforderung! Zugelassene Hilfsmittel: Mathematische Grundlagen III (CES) WS 2017/2018 Klausur 23. März 2018
Prof. Dr. Manuel Torrilhon Prof. Dr. Sebastian Noelle Öffnen Sie den Klausurbogen erst nach Aufforderung! Zugelassene Hilfsmittel: Mathematische Grundlagen III (CES) WS 2017/2018 Klausur 23. März 2018
4 Kurven im R n. Sei I R ein beliebiges Intervall (offen, halboffen, abgeschlossen, beschränkt oder unbeschränkt), das mindestens einen Punkt enthält.
 4 Kurven im R n Sei I R ein beliebiges Intervall (offen, halboffen, abgeschlossen, beschränkt oder unbeschränkt), das mindestens einen Punkt enthält. Definition 4.1. (a) Unter einer Kurve im R n versteht
4 Kurven im R n Sei I R ein beliebiges Intervall (offen, halboffen, abgeschlossen, beschränkt oder unbeschränkt), das mindestens einen Punkt enthält. Definition 4.1. (a) Unter einer Kurve im R n versteht
