Numerik gewöhnlicher Differentialgleichungen
|
|
|
- Ina Holst
- vor 5 Jahren
- Abrufe
Transkript
1 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17
2 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3 Lineare Differenzengleichungen 1.4 Matrixfunktionen 1.5 Systeme linearer Differentialgleichungen erster Ordnung 1.6 Die Fälschungen des Han van Meegeren 1.7 Weitere Beispiele Das Euler-Verfahren 2.2 Eine Sammlung von Beispielverfahren 2.3 Konvergenz, Konsistenz und Stabilität 2.4 Der Hauptsatz 2.5 Einschrittverfahren 2.6 Numerische Experimente 3 Lineare Mehrschrittverfahren 3.1 Begriffe 3.2 Konsistenzordnung linearer Mehrschrittverfahren Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 6 / 294
3 Inhalt II 3.3 Die erste Dahlquist-Barriere 3.4 Die Verfahren von Adams-Bashforth und Adams-Moulton 3.5 Prädiktor-Korrektor-Verfahren 3.6 Absolute Stabilität 3.7 BDF-Verfahren 4 Runge-Kutta-Verfahren 4.1 Konstruktion 4.2 Konsistenzordnung 4.3 Absolute Stabilität 4.4 Eingebettete Runge-Kutta-Verfahren 4.5 Implizite und halb-implizite Verfahren 4.6 Kollokationsmethoden 5 Steife Differentialgleichungen 5.1 Was sind steife Differentialgleichungen? 5.2 Stabilitätsbegriffe 5.3 Ordnungssterne 5.4 Lineare MSV für steife Probleme Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 7 / 294
4 Inhalt III 5.5 RKV für steife Probleme 5.6 Nichtlineare Stabilitätstheorie 6 Ausblick Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 8 / 294
5 Inhalt 1 Einleitung 2 3 Lineare Mehrschrittverfahren 4 Runge-Kutta-Verfahren 5 Steife Differentialgleichungen 6 Ausblick Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 91 / 294
6 6 Ausblick Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 92 / 294 Inhalt 1 Einleitung Das Euler-Verfahren 2.2 Eine Sammlung von Beispielverfahren 2.3 Konvergenz, Konsistenz und Stabilität 2.4 Der Hauptsatz 2.5 Einschrittverfahren 2.6 Numerische Experimente 3 Lineare Mehrschrittverfahren 4 Runge-Kutta-Verfahren 5 Steife Differentialgleichungen
7 Das Euler-Verfahren Wir betrachten das AWP y 1 f pt, yq, ypt 0 q y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese Lösung yptq für t P rt 0, t end s Ď I durch das Euler-Verfahren 14, auch Euler-Cauchy-Verfahren 15 oder Polygonzug-Verfahren, den Prototyp eines numerischen Verfahrens zur Lösung von AWPen, approximieren. Wie alle numerischen Methoden, die hier besprochen werden, basiert das Euler-Verfahren auf der Idee der Diskretisierung: Statt (AWP) über rt 0, t end s zu lösen, geben wir uns damit zufrieden, Näherungswerte für die Lösung auf einer diskreten Teilmenge zu bestimmen. 14 Leonhard Euler ( ) 15 Augustin Louis Cauchy ( ) tt n : n 0, 1,..., Nu Ă rt 0, t end s Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 93 / 294
8 Das Euler-Verfahren Wähle N P N, h pt end t 0 q{n und definiere t n : t 0 ` nh, n 0, 1,..., N, d.h. t 0 ă t 1 ă t n 1 ă t N t end. Die Zahl h ą 0 heißt Schrittweite. (Nur der Bequemlichkeit wählen wir die Schrittweite h zunächst konstant.) Bezeichnet nun y n einen Näherungswert für ypt n q, n 0, 1,..., N 1, dann ist (falls y P C 2 rt 0, t end s) ypt n`1 q ypt n ` hq ypt n q ` hy 1 pt n q ` 1 2 h2 y 2 pξq «ypt n q ` hy 1 pt n q ypt n q ` hf pt n, ypt n qq «y n ` hf pt n, y n q. Euler-Verfahren y 0 gegeben, y n`1 : y n ` hf pt n, y n q, n 0, 1,..., N 1. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 94 / 294
9 Das Euler-Verfahren Zur Veranschaulichung einer GDG 1. Ordnung y 1 fpt, yq wird oft das assoziierte Richtungsfeld herangezogen: In jedem Punkt pt, yq wird ein Pfeil gezeichnet, der von dort aus in Richtung der Steigung y 1 fpt, yq weist. Der Graph der Lösung des AWPs y 1 fpt, yq, ypt 0 q y 0, muss einerseits das Richtungsfeld respektieren (d.h. die Tangenten an den Graphen sind Elemente des Richtungsfelds), andererseits den Punkt pt 0, y 0 q enthalten. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 95 / 294
10 Das Euler-Verfahren 4 Richtungsfeld von y =t(y 2) und Loesungen mit Anfangswerten y(0) = 1:0.5:3 Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 96 / 294
11 Das Euler-Verfahren Die nächste Abbildung zeigt, wie das Euler-Verfahren die logistische Gleichung y 1 yp1 yq, yp0q 1 10, löst. Statt der exakten Trajektorie zu folgen (was natürlich unmöglich ist), produziert das Euler-Verfahren eine stückweise lineare Lösung (einen Polygonzug). An der Stelle t 0 0 arbeitet das Euler-Verfahren mit der richtigen Steigung fpt 0, y 0 q 9{100, bereits an der Stelle t 1 ist die Steigung falsch. In späteren Schritten entfernt man sich (potentiell) immer weiter von der exakten Lösung. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 97 / 294
12 Das Euler-Verfahren 0.9 Euler Verfahren y =y(1 y), y(0)=1/10 Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 98 / 294
13 Das Euler-Verfahren Konvergiert das Euler-Verfahren, d.h. strebt die Näherungslösung für h Ñ 0 gegen die exakte Lösung yptq? Formal: Zu jedem Wert von h ą 0 gehört eine Folge von Näherungen y n y n phq, n 0, 1,..., Nphq : floorppt end t 0 q{hq. Das Verfahren heißt konvergent (in rt 0, t end sq, wenn gilt lim hñ0` max }y nphq ypt n q} 0. 0ďnďNphq (Konv) Satz 2.1 Unter den Voraussetzungen von Satz 1.1 konvergiert das Euler-Verfahren. Genauer: max 0ďnďNphq }y nphq ypt n q} Ophq für h Ñ 0. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/17 99 / 294
14 Das Euler-Verfahren exakte Loesung Schrittweite h 0 Schrittweite h 1 Schrittweite h 2 t_0 t Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
15 Modifiziertes und verbessertes Euler-Verfahren Die Idee dieser beiden Verfahren macht man sich leicht im Richtungsfeld klar. Modifiziertes Euler-Verfahren y 0 gegeben, y n`1 : y n ` hf `t n ` 1 2 h, y n ` 1 2 hf pt n, y n q pn 0, 1,..., N 1q. Verbessertes Euler-Verfahren (Verfahren von Heun) y 0 gegeben, y n`1 : y n ` 1 2 hrf pt n, y n q ` f pt n ` h, y n ` hf pt n, y n qqs pn 0, 1,..., N 1q. Auch das modifizierte und das verbesserte Euler-Verfahren konvergieren: Eine triviale Modifikation des Beweises von Satz 2.1 zeigt, dass für diese Verfahren sogar max 0ďnďNphq }y n phq ypt n q} Oph 2 q gilt. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
16 Das Euler-Verfahren exakte Loesung Euler Verfahren modifiziertes Euler Verf. verbessertes Euler Verf Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
17 6 Ausblick Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294 Inhalt 1 Einleitung Das Euler-Verfahren 2.2 Eine Sammlung von Beispielverfahren 2.3 Konvergenz, Konsistenz und Stabilität 2.4 Der Hauptsatz 2.5 Einschrittverfahren 2.6 Numerische Experimente 3 Lineare Mehrschrittverfahren 4 Runge-Kutta-Verfahren 5 Steife Differentialgleichungen
18 Eine Sammlung von Beispielverfahren Wir werden nun eine Reihe numerischer Verfahren zur Lösung von AWPen angeben (nicht alle davon sind für einen praktischen Einsatz geeignet), um später auf eine gewisse Anzahl von Beispielen zurückgreifen zu können. Beispiel 1 y n`1 y n 1 4 hpk 1 ` 3k 3 q mit k 1 f pt n, y n q, k 2 f pt n ` 1 3 h, y n ` 1 3 hk 1q, k 3 f pt n ` 2 3 h, y n ` 2 3 hk 2q. (2.1) Dieses Verfahren ist ein Einschrittverfahren (zur Berechnung von y n`1 ist nur die Kenntnis von y n erforderlich). Es ist explizit, d.h. nach y n`1 aufgelöst. Es gehört zur Klasse der Runge-Kutta-Verfahren Carl Runge ( ), Martin Kutta ( ) Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
19 Eine Sammlung von Beispielverfahren Beispiel 2 y n`1 y n 1 2 hpk 1 ` k 2 q mit k 1 f pt n, y n q, k 2 f pt n ` h, y n ` 1 2 hk 1 ` 1 2 hk 2q (2.2) ist ebenfalls ein Einschrittverfahren der Runge-Kutta-Klasse. Im Gegensatz zu (2.1) ist es aber implizit, d.h. um y n`1 zu bestimmen, muss ein (im Allgemeinen nichtlineares) Gleichungssystem gelöst werden. Beispiel 3 y n`2 y n`1 1 3 h r3f pt n`1, y n`1 q 2f pt n, y n qs (2.3) ist ein explizites Zweischrittverfahren: Man benötigt y n und y n`1, um y n`2 zu bestimmen. Es gehört zur Familie der linearen Mehrschrittverfahren. Neben y 0 ist hier zusätzlich y 1 (ein sog. Anlaufstück) erforderlich, was man sich üblicherweise mit Hilfe eines Einschrittverfahrens beschafft. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
20 Eine Sammlung von Beispielverfahren Auch Beispiel 4 y n`2 ` y n`1 2y n 1 4 h rf pt n`2, y n`2 q ` 8f pt n`1, y n`1 q ` 3fpt n, y n qs (2.4) ist ein lineares Mehr- (genauer: Zwei-) Schrittverfahren. Es ist implizit. Beispiel 5 y n`3 ` 1 4 y n`2 1 2 y n`1 3 4 y n 1 8 hr19f pt n`2, y n`2 q ` 5f pt n, y n qs (2.5) stellt ein explizites lineares Dreischrittverfahren dar. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
21 Eine Sammlung von Beispielverfahren Beispiel 6 y n`2 y n hrf pt n`2, y n`2q ` f pt n, y n qs mit y n`2 3y n`1 ` 2y n 1 2 hrf pt n`1, y n`1 q 3f pt n, y n qs (2.6) ist ein Prädiktor-Korrektor-Verfahren, bei dem ein implizites Zweischrittverfahren (der Korrektor) mit einem expliziten Zweischrittverfahren (dem Prädiktor) kombiniert wird. Das zusammengesetzte Verfahren ist explizit. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
22 Eine Sammlung von Beispielverfahren Alle Verfahrensbeispiele haben die Struktur kÿ α j y n`j hφ f py n`k, y n`k 1,..., y n, t n ; hq j 0 (V) (wir normieren im Folgenden durch α k : 1) mit und Φ f 0 py n`k, y n`k 1,..., y n, t n ; hq 0 (V 1 ) }Φ f py n`k,..., y n, t n ; hq Φ f py n`k,..., y n, t n ; hq} ď M kÿ }y n`j y n`j}. (V 2 ) Die Eigenschaft (V 2 ) ist eine Folge der Lipschitz-Stetigkeit von f (vgl. Satz 1.1), die immer vorausgesetzt wird. Wir werden ausschließlich numerische Verfahren untersuchen, die die Struktur (V) besitzen und dabei den Bedingungen (V 1 ) und (V 2 ) genügen. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294 j 0
23 6 Ausblick Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294 Inhalt 1 Einleitung Das Euler-Verfahren 2.2 Eine Sammlung von Beispielverfahren 2.3 Konvergenz, Konsistenz und Stabilität 2.4 Der Hauptsatz 2.5 Einschrittverfahren 2.6 Numerische Experimente 3 Lineare Mehrschrittverfahren 4 Runge-Kutta-Verfahren 5 Steife Differentialgleichungen
24 Konvergenz Definition 2.2 (Konvergenz) Das Verfahren (V) heißt konvergent, wenn gilt, und zwar lim y n lim y n phq yptq hñ0 hñ0 t t 0`nh t t 0`nh für alle AWPe, die den Voraussetzungen von Satz 1.1 genügen (y ptq bezeichnet die Lösung eines solchen AWPs), gleichmäßig für alle t P rt 0, t end s, für alle Lösungen ty n phqu ty n u von (V) mit Anfangswerten y 0 phq,..., y k 1 phq, die lim hñ0 y j phq y 0, j 0,..., k 1, erfüllen. Äquivalent: lim hñ0 max }ypt nq y n phq} 0. 0ďnďN Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
25 Lokaler Diskretisierungsfehler, Residuum Setzt man die exakte Lösung in (V) ein, so werden linke und rechte Seite nicht übereinstimmen. Es ergibt sich ein Residuum kÿ R n`k : α j ypt n`j q hφ f pypt n`k q, ypt n`k 1 q,..., ypt n q, t n ; hq. j 0 R n`k ist eng verknüpft mit dem lokalen Diskretisierungsfehler T n`k. Unter der Lokalisierungsannahme liefert (V) in Schritt n ` k: y n`j ypt n`j q für j 0, 1,..., k 1 k 1 ÿ ŷ n`k ` α j ypt n`j q hφ f pŷ n`k, ypt n`k 1 q,..., ypt n q, t n ; hq. j 0 Für die exakte Lösung gilt hingegen k 1 ÿ ypt n`k q ` α j ypt n`j q hφ f pypt n`k q,..., ypt n q, t n ; hq ` R n`k. j 0 Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
26 Lokaler Diskretisierungsfehler, Residuum Definiert man nun T n`k : ypt n`k q ŷ n`k (Vorsicht: die Definition ist nicht einheitlich in der Literatur), so folgt T n`k h rφ f pypt n`k q,..., ypt n q, t n ; hq Φ f pŷ n`k, ypt n`k 1 q,..., ypt n q, t n ; hs ` R n`k. In speziellen Fällen (lineare Mehrschrittverfahren) kann man die rechte Seite mit dem Mittelwertsatz weiter bearbeiten. Immer folgt aus (V 2 ) }T n`k } ď hm}t n`k } ` }R n`k } und damit p1 hmq}t n`k } ď }R n`k }. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
27 Lokaler Diskretisierungsfehler, Residuum y(t n+1 ) globaler DF y(t n ) z(t n+1 ) lokaler DF y n+1 y n t n t n+1 Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
28 Konsistenz Definition 2.3 (Konsistenz) Das Verfahren (V) heißt konsistent [mit (AWP)], wenn 1 h R n`k 0 lim hñ0 t t 0`nh für alle AWPe gilt, die den Voraussetzungen von Satz 1.1 genügen. Satz 2.4 (Konsistenzbedingung) Das Verfahren (V) ist genau dann konsistent, wenn gilt und kÿ α j 0 (K 1 ) j 0 ÿ k jα j jf pt n, ypt n qq Φ f pypt n q,..., ypt n q, t n ; 0q. (K 2 ) j 0 Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
29 Konsistenz Das zum Verfahren (V) gehörende erste charakteristische Polynom ist durch ρpζq α k ζ k ` α k 1 ζ k 1 ` ` α 1 ζ ` α 0 definiert. Hiermit läßt sich Satz 2.4 kompakter formulieren: Satz 2.5 (Konsistenzbedingung ) Das Verfahren (V) ist genau dann konsistent, wenn gilt und ρp1q 0 (K 1 1) f pt n, ypt n qq Φ f pypt n q,..., ypt n q, t n ; 0q ρ 1. (K 1 p1q 2) Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
30 Beispiel zu Konsistenz Wir betrachten als Beispiel das AWP y 1 y, yp0q 1 mit Lösung yptq expp tq. Das implizite Zweischrittverfahren y n`2 p1 ` αqy n`1`αy n ist konsistent (für jedes α P Rq: 1 2 hrfpt n`2, y n`2 q ` p1 αqfpt n`1, y n`1 q αfpt n, y n qs ρp1q 1 p1 ` αq ` α 0, Φ f pypt n q, ypt n q, ypt n q, t n ; 0q{ρ 1 p1q 1 2 p2 2αqfpt n, ypt n qq{p2 p1 ` αqq Lösung mit Anfangswerten y 0 y 1 1: fpt n, ypt n qq. p1 ` 1 2 hqy n`2 r1 ` α 1 2 p1 αqhsy n`1 ` αp1 1 2 hqy n 0 ( ) (Differenzengleichung zweiter Ordnung mit konstanten Koeffizienten). Allgemeine Lösung: y n c 1 ξ n 1 ` c 2 ξ n 2, ξ 1 α und ξ 2 p1 1 2 hq{p1 ` 1 2 hq. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
31 Beispiel zu Konsistenz Störe nun ( ) (Rundungsfehler, δ ą 0): p1 ` 1 2 hqz n`2 r1 ` α 1 2 p1 αqhsz n`1 ` αp1 1 2 hqz n hδ z 0 1 ` δ, z 1 1 ` δ. ( 1) Allgemeine Lösung: z n c 1 ξ n 1 ` c 2 ξ n 2 ` # δ{p1 αq, falls α 1, nδ, falls α 1. Fall 1: α 1 mit z n 1 γ rµpδqξn 1 ` νpδqξ n 2 s ` δ 1 α γ 1 α hp1 ` αq{2, µpδq hrαδ{p1 αq 1s, νpδq r1 αp1 ` δqsp1 ` h{2q. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
32 Beispiel zu Konsistenz Ersetze δ durch δ, ergibt Lösung tz nu statt tz n u. Fall 1a: 1 ď α ă 1, z n z n ď für alle h ď h 0 2p1 αq{p1 ` αq. h{p1 αq ` 1 ` h{2 1 α hp1 ` αq{2 ` 1 j δ δ 1 α Fall 1b: α ą 1 tz n z nu ist unbeschränkt für h Ñ 0. Fall 2: α 1 z n 1 ` h 2 2h δ ` h ` 2 2h δ und tz n z nu ist unbeschränkt für h Ñ 0. n ˆ1 h{2 ` nδ 1 ` h{2 Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
33 Beispiel zu Konsistenz 1 α = α = h= h=0.05 h=0.02 h= exakt α = α = Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
34 Stabilität Definition 2.6 (Stabilität) Seien tδ plq n u n 0,1,...,N, l 1, 2, zwei beliebige Störungen der Differenzengleichung (V) und seien tzn plq u, l 1, 2, die Lösungen von kÿ j 0 α j y n`j hrφ f py n`k, y n`k 1,..., y n, t n ; hq ` δ plq n`k s, y plq j y j phq ` δ plq j pj 0, 1,..., k 1q. (V δ ) Die Methode (V) heißt stabil, wenn es positive Konstanten S und h 0 gibt mit p1q max }zn 0ďnďN für alle h P p0, h 0 s und alle zulässigen f. zn p2q } ď S max 0ďnďN }δp1q n δ p2q n } Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
35 Stabilität Bemerkungen. (1) Stabilität bedeutet, dass die Differenzengleichung sachgemäß gestellt ist (vgl. Satz 1.1 und 1.2, wo gezeigt wird, dass die Bedingung (Lip) garantiert, dass das (AWP) sachgemäß gestellt ist). (2) Stabilität ist ein Muss für Rechnungen in Gleitpunktarithmetik. Das Verfahren (V) erfüllt die Wurzelbedingung, wenn sämtliche Nullstellen ξ seines ersten charakteristischen Polynoms betragsmäßig kleiner oder gleich 1 sind, und zusätzlich aus ξ 1 stets folgt, dass ξ eine einfache Nullstelle ist. Satz 2.7 (Stabilität ô Wurzelbedingung) Das Verfahren (V) ist genau dann stabil, wenn es die Wurzelbedingung erfüllt. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
36 6 Ausblick Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294 Inhalt 1 Einleitung Das Euler-Verfahren 2.2 Eine Sammlung von Beispielverfahren 2.3 Konvergenz, Konsistenz und Stabilität 2.4 Der Hauptsatz 2.5 Einschrittverfahren 2.6 Numerische Experimente 3 Lineare Mehrschrittverfahren 4 Runge-Kutta-Verfahren 5 Steife Differentialgleichungen
37 Der Hauptsatz Satz 2.8 (Dahlquist) Das Verfahren (V) ist genau dann konvergent, wenn es konsistent und stabil ist. Oder kürzer: Konsistenz & Stabilität ô Konvergenz. Bemerkungen. (1) Der Beweis zeigt, dass der globale Diskretisierungsfehler max 0ďnďN }ypt n q y n phq} bei stabilen Verfahren von der Ordnung p ist, wenn max R n`k{h Oph p q 0ďnďN k max }ypt nq y n phq} Oph p q 0ďnďk 1 (Konsistenzordnung p) und (Anfangswerte) gelten. (2) Ob ein Verfahren konvergent ist, kann jetzt rein algebraisch nachgeprüft werden (i.w. über die Nullstellen des ersten charakteristischen Polynoms). Germund Dahlquist ( ) Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
38 6 Ausblick Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294 Inhalt 1 Einleitung Das Euler-Verfahren 2.2 Eine Sammlung von Beispielverfahren 2.3 Konvergenz, Konsistenz und Stabilität 2.4 Der Hauptsatz 2.5 Einschrittverfahren 2.6 Numerische Experimente 3 Lineare Mehrschrittverfahren 4 Runge-Kutta-Verfahren 5 Steife Differentialgleichungen
39 Einschrittverfahren Ein Einschrittverfahren hat die Form y n`1 y n ` hφ f py n`1, y n, t n ; hq. (ESV) Es ist immer stabil, also genau dann konvergent, wenn es konsistent ist. Ist 1 h R n`1 ypt n`1q ypt n q Φ f pypt n`1 q, ypt n q, t n ; hq Oph p q ph Ñ 0q, h so besitzt es (mindestens) die Konsistenzordnung p. Das Euler-Verfahren besitzt die Konsistenzordnung 1, denn: ypt n`1 q ypt n q h f pt n, ypt n qq hy 1 pt n q ` 1 2 h2 y 2 pξ n q y 1 pt n q 1 h 2 hy 2 pξ n q. Ist f p-mal stetig differenzierbar, so kann man Einschrittverfahren der Konsistenzordnung p mit der Methode des Taylor-Abgleichs konstruieren: Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
40 Einschrittverfahren Man entwickelt die (unbekannte) Lösung ypt n ` hq formal nach Potenzen von h, ypt n ` hq ypt n q ` hy 1 pt n q ` 1 2 h2 y 2 pt n q `, und nutzt aus, dass y 1 ptq f pt, yptqq gilt, z.b. y 1 pt n q f pt n, ypt n qq, y 2 pt n q f t pt, yptqq t tn ` f y pt, yptqqy 1 ptq t tn f t pt n, ypt n qq ` f y pt n, ypt n qqf pt n, ypt n qq. Bricht man etwa nach dem zweiten Term ab, so ergibt sich mit y n`1 y n ` h f pt n, y n q ` 1 2 h pf tpt n, y n q ` f y pt n, y n qf pt n, y n qq ein Verfahren zweiter Ordnung. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
41 Einschrittverfahren Es ist klar, dass man dieses Verfahren (oder entsprechende Verfahren für p ą 2) nur dann verwenden kann, wenn f einfach zu differenzieren ist (oder mittels automatische Differentiation). Für die skalare GDG y 1 ptq typtq ergibt sich z.b. y n`1 y n 1 ` 1 2 h2 ` ht n ` 1 2 h2 t 2 n im Fall von p 2 und y n`1 y n 1 ` 1 2 h2 ` ht n ` 1 2 h2 t 2 n ` 1 2 h3 t n ` 1 6 h3 t 3 n im Fall von p 3. Für p 1 erhält man stets das Euler-Verfahren. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
42 Einschrittverfahren Für dieses Beispiel ergibt sich mit Anfangsbedingung yp0q 1, d.h. mit exakter Lösung yptq exppt 2 {2q als (normalisierter) globaler Diskretisierungsfehler h p max ypt nq y n 0ďnďN für die Taylor-Verfahren der Ordnung p P t1, 2, 3u: N h p 1 p 2 p e e e e e e e e e e e e e e e e-1 Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
43 6 Ausblick Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294 Inhalt 1 Einleitung Das Euler-Verfahren 2.2 Eine Sammlung von Beispielverfahren 2.3 Konvergenz, Konsistenz und Stabilität 2.4 Der Hauptsatz 2.5 Einschrittverfahren 2.6 Numerische Experimente 3 Lineare Mehrschrittverfahren 4 Runge-Kutta-Verfahren 5 Steife Differentialgleichungen
44 Numerische Experimente Wir werden jetzt die Verfahren aus Abschnitt 2 (ab Seite 104) an folgendem AWP testen: y 1 1 y 2 y 1 2 y 2py 2 1q y 1 mit den Anfangsbedingungen y 1 p0q 1 2, y 2 p0q 3. Die Lösung wird für t P r0, 1s gesucht. Die exakte Lösung lautet y 1 ptq r1 ` 3 expp 8tqs{8, y 2 ptq 3 expp 8tq. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
45 Numerische Experimente 0.5 Numerische Experimente: Exakte Loesung y 1 (t)=(1+3exp( 8t))/8 y 2 (t)= 3exp( 8t) Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
46 Numerische Experimente zu Beispiel 4: Für ρpζq ζ 2 ` ζ 2 pζ 1qpζ ` 2q gelten ρp1q 0 und Φ f pypt n q, ypt n q, ypt n q, t n ; 0q ρ 1 p1q Die Methode ist also konsistent, aber instabil. 3f pt n, ypt n qq 3 t h 0.1 h 0.05 h h e e e e e e e e e e e e e e e+05 Inf e e e+10 f pt n, ypt n qq. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
47 Numerische Experimente zu Beispiel 3: Für ρpζq ζ 2 ζ pζ 1qζ gelten ρp1q 0 und Φ f pypt n q, ypt n q, ypt n q, t n ; 0q ρ 1 p1q Die Methode ist also stabil, aber inkonsistent. f pt n, ypt n qq{3 1 t h 10 1 h 10 2 h 10 3 h e e e e e e e e e e e e e e e e e e e e 01 f pt n, ypt n qq. 3 Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
48 Numerische Experimente Die Methode ist aber konsistent mit dem AWP y 1 f pt, yq{3, yp0q y 0. Für den Abstand zu dessen exakter Lösung ỹptq rp1 ` 3 expp 8t{3qq{8, 3 expp 8t{3qs J ergibt sich: t h 10 1 h 10 2 h 10 3 h e e e e e e e e e e e e e e e e e e e e 04. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
49 Numerische Experimente zu Beispiel 5: Für ρpζq ζ 3 ` ζ 2 {4 ζ{2 3{4 pζ 1qpζ ` 5{8?23i{8qpζ ` 5{8 `?23i{8q gelten ρp1q 0 und Φ f pypt n q, ypt n q, ypt n q, t n ; 0q ρ 1 p1q 3f pt n, ypt n qq 3 Die Methode ist also konsistent und stabil, damit konvergent. t h 0.1 Ò h 0.05 Ò h Ó h Ó e e e e e e e e e e e e e e e e e e e 07 f pt n, ypt n qq. Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
50 Numerische Experimente zu Beispiel 6: Die Methode ist konsistent und stabil, also konvergent. t h 10 1 h 10 2 h e e e e e e e e e e e e e e e e e e e e e e Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
51 Numerische Experimente zu Beispiel 1: Die Methode ist konsistent und stabil, also konvergent. t h 0.4 Ò h 0.2 Ó h 0.1 Ó h 0.05 Ó e e e e e e e e e e e e e e e e e e+01 Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
52 Numerische Experimente zu Beispiel 2: Die Methode ist konsistent und stabil, also konvergent. t h 0.8 Ó h 0.4 Ó h 0.2 Ó h 0.1 Ó e e e e e e e e e e e e e e e e e 04 Oliver Ernst (Numerische Mathematik) ODE Wintersemester 2016/ / 294
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
3. Lineare Mehrschrittverfahren 3.1 Begriffe
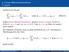 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
9 Numerische Verfahren für Anfangswertaufgaben
 Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren
 Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
Numerisches Programmieren (IN0019) 11. Gewöhnliche Differenzialgleichungen. Differenzialgleichungen. Differenzialgleichungen (Physik)
 umerisches Programmieren (I19) Frank R. Schmidt 11. Gewöhnliche Differenzialgleichungen Winter Semester 16/17 Differenzialgleichungen (Phsik) Differenzialgleichungen Phsikalische Prozesse lassen sich mit
umerisches Programmieren (I19) Frank R. Schmidt 11. Gewöhnliche Differenzialgleichungen Winter Semester 16/17 Differenzialgleichungen (Phsik) Differenzialgleichungen Phsikalische Prozesse lassen sich mit
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen
 Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik'
 Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
5. Steife Differentialgleichungen 5.1 Was sind steife Differentialgleichungen?
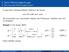 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG
5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
5 Steife Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif,
Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif,
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1. Prof. Dr. Hans Babovsky. Technische Universität Ilmenau
 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky. Institut für Mathematik
 NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
Nichtlineare Gleichungssysteme
 Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan :00-14:00 (120 min)
 Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
Mathematische Grundlagen
 G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
Analysis I. 1. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
5 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen
 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 118 5 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Eine Differentialgleichung (DG) beschreibt eine Beziehung zwischen einer
Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 118 5 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Eine Differentialgleichung (DG) beschreibt eine Beziehung zwischen einer
Nichtlineare Gleichungssysteme
 Kapitel 2 Nichtlineare Gleichungssysteme Problem: Für vorgegebene Abbildung f : D R n R n finde R n mit oder ausführlicher f() = 0 (21) f 1 ( 1,, n ) = 0, f n ( 1,, n ) = 0 Einerseits führt die mathematische
Kapitel 2 Nichtlineare Gleichungssysteme Problem: Für vorgegebene Abbildung f : D R n R n finde R n mit oder ausführlicher f() = 0 (21) f 1 ( 1,, n ) = 0, f n ( 1,, n ) = 0 Einerseits führt die mathematische
Analysis I. 7. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 1
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Kapitel 1 Gewöhnliche Differentialgleichungen
 Kapitel 1 Gewöhnliche Differentialgleichungen Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind Differentialgleichungen, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug
Kapitel 1 Gewöhnliche Differentialgleichungen Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind Differentialgleichungen, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug
Numerik gewöhnlicher Differentialgleichungen. Prof. Dr. Guido Kanschat
 Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Adaptive Mehrschrittverfahren
 Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Reihenentwicklungen von Lösungen (I) 1 Einleitung
 Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 22.11.2011 Carmen Freuen Ziel dieses Vortrages ist es, die Reihenentwicklung von Lösungen linearer Differentialgleichungen vorzustellen und zu untersuchen.
Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 22.11.2011 Carmen Freuen Ziel dieses Vortrages ist es, die Reihenentwicklung von Lösungen linearer Differentialgleichungen vorzustellen und zu untersuchen.
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Übungen zu Differentialgleichungen (WiSe 12/13)
 Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge
 Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript
 Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik für Anwender I. Klausur
 Fachbereich Mathematik/Informatik 27. März 2012 Prof. Dr. H. Brenner Mathematik für Anwender I Klausur Dauer: Zwei volle Stunden + 10 Minuten Orientierung, in denen noch nicht geschrieben werden darf.
Fachbereich Mathematik/Informatik 27. März 2012 Prof. Dr. H. Brenner Mathematik für Anwender I Klausur Dauer: Zwei volle Stunden + 10 Minuten Orientierung, in denen noch nicht geschrieben werden darf.
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Mathematik für Anwender I. Beispielklausur 3 mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Mathematik für Anwender I Beispielklausur mit en Dauer: Zwei volle Stunden + 0 Minuten Orientierung, in denen noch nicht geschrieben werden darf.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Mathematik für Anwender I Beispielklausur mit en Dauer: Zwei volle Stunden + 0 Minuten Orientierung, in denen noch nicht geschrieben werden darf.
u(x, 0) = g(x) : 0 x 1 u(0, t) = u(1, t) = 0 : 0 t T
 8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Rückwärtsfehleranalyse und Langzeitenergieerhaltung
 Rückwärtsfehleranalyse und Langzeitenergieerhaltung Henrike Köpke 9. Dezember 010 1 Inhaltsverzeichnis 1 Einleitung 3 Rückwärtsfehleranalyse 4.1 Idee der Vorwärts- und der Rückwärtsfehleranalyse..........
Rückwärtsfehleranalyse und Langzeitenergieerhaltung Henrike Köpke 9. Dezember 010 1 Inhaltsverzeichnis 1 Einleitung 3 Rückwärtsfehleranalyse 4.1 Idee der Vorwärts- und der Rückwärtsfehleranalyse..........
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Lösungen der Übungsaufgaben von Kapitel 3
 Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL)
 Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL) Problemstellung Beispiele Klassifizierung von DGLs, Existenz und Eindeutigkeit des AWPs Einschrittverfahren Stabilität & Schrittweitenkontrolle Mehrschrittverfahren
Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL) Problemstellung Beispiele Klassifizierung von DGLs, Existenz und Eindeutigkeit des AWPs Einschrittverfahren Stabilität & Schrittweitenkontrolle Mehrschrittverfahren
Differentialgleichungen
 Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Differentialgleichungen
 Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 23
 Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Skript zur Vorlesung Analysis 3
 Skript zur Vorlesung Analysis 3 Herbstsemester 204 Prof. Benjamin Schlein Inhaltsverzeichnis Gewöhnliche Differentialgleichungen 2. Differentialgleichungen erster Ordnung, elementare Lösungsmethoden..
Skript zur Vorlesung Analysis 3 Herbstsemester 204 Prof. Benjamin Schlein Inhaltsverzeichnis Gewöhnliche Differentialgleichungen 2. Differentialgleichungen erster Ordnung, elementare Lösungsmethoden..
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
3 Nichtlineare Gleichungssysteme
 3 Nichtlineare Gleichungsssteme 3.1 Eine Gleichung in einer Unbekannten Problemstellung: Gegeben sei die stetige Funktion f(). Gesucht ist die Lösung der Gleichung f() = 0. f() f() a) f ( ) 0 b) f ( )
3 Nichtlineare Gleichungsssteme 3.1 Eine Gleichung in einer Unbekannten Problemstellung: Gegeben sei die stetige Funktion f(). Gesucht ist die Lösung der Gleichung f() = 0. f() f() a) f ( ) 0 b) f ( )
Systemanalyse und Modellbildung
 Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 26 1. Folgen R. Steuding (HS-RM)
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 26 1. Folgen R. Steuding (HS-RM)
Analysis I. 6. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Analysis I. 3. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
8.1 Begriffsbestimmung
 8 Gewöhnliche Differentialgleichungen 8 Gewöhnliche Differentialgleichungen 8.1 Begriffsbestimmung Wir betrachten nur Differentialgleichungen für Funktionen einer (reellen) Variablen. Definition: Für eine
8 Gewöhnliche Differentialgleichungen 8 Gewöhnliche Differentialgleichungen 8.1 Begriffsbestimmung Wir betrachten nur Differentialgleichungen für Funktionen einer (reellen) Variablen. Definition: Für eine
Merkblatt zur Funktionalanalysis
 Merkblatt zur Funktionalanalysis Literatur: Hackbusch, W.: Theorie und Numerik elliptischer Differentialgleichungen. Teubner, 986. Knabner, P., Angermann, L.: Numerik partieller Differentialgleichungen.
Merkblatt zur Funktionalanalysis Literatur: Hackbusch, W.: Theorie und Numerik elliptischer Differentialgleichungen. Teubner, 986. Knabner, P., Angermann, L.: Numerik partieller Differentialgleichungen.
2 Einschrittverfahren 2.1 Einführung
 Einschrittverfahren. Einführung Im folgenden werden wir uns bei der Beschreibung und Analyse von numerischen Verfahren für Anfangswertprobleme auf den Fall n = beschränken. Dies wird nur gemacht, um die
Einschrittverfahren. Einführung Im folgenden werden wir uns bei der Beschreibung und Analyse von numerischen Verfahren für Anfangswertprobleme auf den Fall n = beschränken. Dies wird nur gemacht, um die
ist ein n-dimensionaler, reeller Vektorraum (vgl. Lineare Algebra). Wir definieren auf diesem VR ein Skalarprodukt durch i y i i=1
 24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
Stetige Funktionen. Definition. Seien (X, d) und (Y, D) metrische Räume und f : X Y eine Abbildung. i) f heißt stetig in x 0 (x 0 D(f)), wenn
 Stetige Funktionen Eine zentrale Rolle in der Analysis spielen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume). Dabei sind i.a. nicht beliebige
Stetige Funktionen Eine zentrale Rolle in der Analysis spielen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume). Dabei sind i.a. nicht beliebige
18.4 Das Newton-Verfahren
 18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
Einführung in die numerische Mathematik
 Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Kapitel 6. Nichtlineare Gleichungen. 6.1 Einführung. Problem: Idee: Beispiel:
 Kapitel 6 Nichtlineare Gleichungen 6. Einführung Problem: Gesucht sind Lösungen nichtlinearer Gleichungen bzw. Systeme, das heißt es geht beispielsweise um die Bestimmung der Nullstellen eines Polynoms
Kapitel 6 Nichtlineare Gleichungen 6. Einführung Problem: Gesucht sind Lösungen nichtlinearer Gleichungen bzw. Systeme, das heißt es geht beispielsweise um die Bestimmung der Nullstellen eines Polynoms
Numerik gewöhnlicher Differentialgleichungen. Übung 8 - Lösungsvorschlag
 Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Analysis I Lösung von Serie 14. Um die Inhomogene DGl zu lösen, müssen wir partikuläre Lösungen finden. (a) Wir machen den Ansatz:
 d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
mathematik und informatik
 Prof. Dr. Torsten Linß Kurs 037 Numerische Mathematik II LESEPROBE mathematik und informatik Das Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere das Recht der Vervielfältigung
Prof. Dr. Torsten Linß Kurs 037 Numerische Mathematik II LESEPROBE mathematik und informatik Das Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere das Recht der Vervielfältigung
Definition 3.1: Ein Differentialgleichungssystem 1. Ordnung
 Kapitel 3 Dynamische Systeme Definition 31: Ein Differentialgleichungssystem 1 Ordnung = f(t, y) ; y R N ; f : R R N R N heißt namisches System auf dem Phasenraum R N Der Parameter t wird die Zeit genannt
Kapitel 3 Dynamische Systeme Definition 31: Ein Differentialgleichungssystem 1 Ordnung = f(t, y) ; y R N ; f : R R N R N heißt namisches System auf dem Phasenraum R N Der Parameter t wird die Zeit genannt
Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Mayr)
 WS 2011/12 Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Mayr) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2011ws/ds/uebung/ 18. Januar 2012 ZÜ DS ZÜ XII
WS 2011/12 Zentralübung zur Vorlesung Diskrete Strukturen (Prof. Mayr) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2011ws/ds/uebung/ 18. Januar 2012 ZÜ DS ZÜ XII
Wiederholungsklausur zur Analysis I
 Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
4 Runge-Kutta-Verfahren
 Numerik gewöhnlicher Differentialgleichungen 43 4 Runge-Kutta-Verfahren 4. Konstruktion Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0
Numerik gewöhnlicher Differentialgleichungen 43 4 Runge-Kutta-Verfahren 4. Konstruktion Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen Aufgaben für das Seminar und zum selbständigen Üben 22. Januar 2018 Vorbereitende Übungen Aufgabe 1: Bestimmen Sie die Isoklinen zu den folgenden Differentialgleichungen
Gewöhnliche Differentialgleichungen Aufgaben für das Seminar und zum selbständigen Üben 22. Januar 2018 Vorbereitende Übungen Aufgabe 1: Bestimmen Sie die Isoklinen zu den folgenden Differentialgleichungen
Höhere Mathematik III
 Universität Stuttgart Fachbereich Mathematik Prof. Dr. J. Pöschel Dr. D. Zimmermann Dipl.-Math. K. Sanei Kashani Blatt 5 Höhere Mathematik III el, kb, mecha, phs Vortragsübungen (Musterlösungen) 7..4 Aufgabe
Universität Stuttgart Fachbereich Mathematik Prof. Dr. J. Pöschel Dr. D. Zimmermann Dipl.-Math. K. Sanei Kashani Blatt 5 Höhere Mathematik III el, kb, mecha, phs Vortragsübungen (Musterlösungen) 7..4 Aufgabe
Kap. 10: Folgen und Reihen. Eine Funktion a : N Ñ R
 Definition: Zahlenfolge Kap. 10: Folgen und Reihen 10.1 Definition: Zahlenfolge Eine Funktion a : N Ñ R poder Cq heißt reelle (oder komplexe) Zahlenfolge. Man nennt a n apnq das n-te Folgenglied und schreibt
Definition: Zahlenfolge Kap. 10: Folgen und Reihen 10.1 Definition: Zahlenfolge Eine Funktion a : N Ñ R poder Cq heißt reelle (oder komplexe) Zahlenfolge. Man nennt a n apnq das n-te Folgenglied und schreibt
5 Potenzreihenansatz und spezielle Funktionen
 5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
4 Gewöhnliche Differentialgleichungen
 4 Gewöhnliche Differentialgleichungen 4.1 Einleitung Definition 4.1 Gewöhnliche Differentialgleichung n-ter Ordnung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten
4 Gewöhnliche Differentialgleichungen 4.1 Einleitung Definition 4.1 Gewöhnliche Differentialgleichung n-ter Ordnung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten
