Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen
|
|
|
- Ingrid Gundi Baum
- vor 6 Jahren
- Abrufe
Transkript
1 Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
2 Einschrittverfahren Allgemeiner Näherungsverlauf y x y 3 y y y Abbildung: Richtungsfeld zur Dgl y (x) = y(x) und Näherungsverlauf des Euler-Verfahrens Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
3 Einschrittverfahren Lokaler Diskretisierungsfehler y x y x x Η 3 y 3 Η Η y y y Abbildung: Lokaler Diskretisierungsfehler des Euler-Verfahrens zur Dgl y (x) = y(x) Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 3 / 3
4 Einschrittverfahren Globaler Diskretisierungsfehler y x y x x e 3 y 3 e e y y y Abbildung: Globaler Diskretisierungsfehler des Euler-Verfahrens zur Dgl y (x) = y(x) Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
5 Einschrittverfahren Runge-Verfahren Abbildung: Auswertungsstellen zum Runge-Verfahren Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 5 / 3
6 Einschrittverfahren Klassisches Runge-Kutta-Verfahren Abbildung: Auswertungsstellen zum klassischen Runge-Kutta-Verfahren Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
7 Einschrittverfahren Heun-Verfahren Abbildung: Auswertungsstellen zum Prädiktor-Korrektor-Verfahren Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 7 / 3
8 Einschrittverfahren im Vergleich Konvergenzordnung t Euler-Verf. Runge-Verf. Runge-Kutta Runge-Kutta Verfahren Verfahren. Ord.. Ord. 3. Ord. (.7). Ord...95e 5 5.5e 5.355e 5.55e e 5.e.3e 7.5e..3e 5.55e 7.573e.9e..55e.3e 7 3.3e 9 3.3e.5.533e.95e 3.73e.5e..9e 7.573e 9.35e 5.53e. 9.59e e 9.939e.9959e Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
9 Einschrittverfahren Konvergenzordnung Abbildung: Konvergenzverhalten unterschiedlicher Runge-Kutta-Verfahren Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 9 / 3
10 Mehrschrittverfahren Stabilität Näherungen y i für Exakte Werte t i t =. t =.5 t =.5 y(t i ) Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
11 Ein- und Mehrschrittverfahren im Vergleich Modellproblem mit k =.3 und c =. Lösung y (t) = k(c y(t)), t R + y() = y(t) = c ( e kt ) Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
12 Ein- und Mehrschrittverfahren im Vergleich Gruppe A: Explizite Einschrittverfahren Verfahrensname Ordnung p Abkürzung Explizites Euler-Verfahren EE Runge-Verfahren Runge Heun-Verfahren Heun 3-stufiges Runge-Kutta-Verfahren 3 ERK3 Klassisches Runge-Kutta-Verfahren ERK Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
13 Ein- und Mehrschrittverfahren im Vergleich Gruppe B: Implizite Einschrittverfahren Verfahrensname Ordnung p Abkürzung Implizites Euler-Verfahren IE Implizite Mittelpunktregel IM Implizite Trapezregel IT SDIRK-Verfahren 3 SDIRK Implizites Verfahren nach Hammer und Hollingsworth IHH Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 3 / 3
14 Ein- und Mehrschrittverfahren im Vergleich Gruppe C: Explizite Mehrschrittverfahren Verfahrensname Ordnung p Abkürzung Adams-Bashfort-Verfahren m = AB Adams-Bashfort-Verfahren m = 3 3 AB3 Nyström-Verfahren m = NYS Nyström-Verfahren m = 3 3 NYS3 Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
15 Ein- und Mehrschrittverfahren im Vergleich Gruppe D: Implizite Mehrschrittverfahren Verfahrensname Ordnung p Abkürzung Adams-Moulton-Verfahren m = 3 AM Adams-Moulton-Verfahren m = 3 AM3 Milne-Simpson-Verfahren m = MS BDF()-Verfahren m = BDF BDF(3)-Verfahren m = 3 3 BDF3 Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 5 / 3
16 Ein- und Mehrschrittverfahren im Vergleich Fehlerverläufe für e(5, t) = y(5) y num (5, t) Gruppe A: Explizite Einschrittverfahren t EE Runge/Heun ERK3 ERK Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
17 Ein- und Mehrschrittverfahren im Vergleich Fehlerverläufe für e(5, t) = y(5) y num (5, t) Gruppe B: Implizite Einschrittverfahren t IE IM/IT SDIRK IHH Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 7 / 3
18 Ein- und Mehrschrittverfahren im Vergleich Fehlerverläufe für e(5, t) = y(5) y num (5, t) Gruppe C: Explizite Mehrschrittverfahren t AB AB3 NYS NYS Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
19 Ein- und Mehrschrittverfahren im Vergleich Fehlerverläufe für e(5, t) = y(5) y num (5, t) Gruppe D: Implizite Mehrschrittverfahren t AM AM3 MS BDF BDF Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 9 / 3
20 Einschrittverfahren Stabilität beim expliziten Euler-Verfahren t =.,.5,., Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
21 Einschrittverfahren Stabilität beim expliziten Euler-Verfahren t =.9,.,., Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
22 Einschrittverfahren Stabilität beim expliziten Runge-Verfahren t =.,.5,., Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
23 Einschrittverfahren Stabilität beim expliziten Runge-Verfahren t =.9,.,., Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 3 / 3
24 Einschrittverfahren Stabilität beim klassischen Runge-Kutta-Verfahren t =.,.5,., Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
25 Einschrittverfahren Stabilität beim klassischen Runge-Kutta-Verfahren t =.9,.,., Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 5 / 3
26 Einschrittverfahren Stabilität beim klassischen Runge-Kutta-Verfahren t =.7,., Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
27 Positivitätserhaltende, konservative Verfahren Analytische Lösung des linearen Testproblems T.. Y.. L L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 7 / 3
28 Positivitätserhaltende, konservative Verfahren Hochauflösende Lösung des nichtlinearen Testproblems T Y L L L3 L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
29 Positivitätserhaltende, konservative Verfahren Hochauflösende Lösung des Robertson Testfalls T. Y.. L L L3 L. e-.. e+ e+ e+ X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 9 / 3
30 Positivitätserhaltende, konservative Verfahren Lösung des linearen Testproblems mittels Euler-Verfahren bei t =.5 T.5 Y.5 L -.5 L L3 L L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 3 / 3
31 Positivitätserhaltende, konservative Verfahren Lösung des nichtlinearen Testproblems mittels Euler-Verfahren bei t =.5 T Y L L L3 L L5 L L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 3 / 3
32 Positivitätserhaltende, konservative Verfahren Lösung des linearen Testproblems mittels Patankar-Verfahren bei t =.5 T.5 Y.5 L -.5 L L3 L L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 3 / 3
33 Positivitätserhaltende, konservative Verfahren Lösung des nichtlinearen Testproblems mittels Patankar-Verfahren bei t =.5 T Y L L L3 L L5 L L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 33 / 3
34 Positivitätserhaltende, konservative Verfahren Lösung des linearen Testproblems mittels modifiziertem Patankar-Verfahren bei t =.5 T.5 Y.5 L -.5 L L3 L L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 3 / 3
35 Positivitätserhaltende, konservative Verfahren Lösung des linearen Testproblems mittels modifiziertem Patankar-Runge-Kutta-Verfahren bei t =.5 T.5 Y.5 L -.5 L L3 L L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 35 / 3
36 Positivitätserhaltende, konservative Verfahren Lösung des nichtlinearen Testproblems mittels modifiziertem Patankar-Verfahren bei t =.5 T Y L L L3 L L5 L L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 3 / 3
37 Positivitätserhaltende, konservative Verfahren Lösung des nichtlinearen Testproblems mittels modifiziertem Patankar-Runge-Kutta-Verfahren bei t =.5 T Y L L L3 L L5 L L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 37 / 3
38 Positivitätserhaltende, konservative Verfahren Lösung des nichtlinearen Testproblems mittels hybriden modifiziertem Patankar-Runge-Kutta-Verfahren bei t =.5 T Y L L L3 L L5 L L X Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 3 / 3
39 Positivitätserhaltende, konservative Verfahren Lösung des Robertson Problems mittels Patankar-Verfahren.5 PE Ci.5 L L L3 L L5 L L e+ e+ e+ time / s Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 39 / 3
40 Positivitätserhaltende, konservative Verfahren Lösung des Robertson Problems mittels modifiziertem Patankar-Verfahren.5 MPE Ci.5 L L L3 L L5 L L e+ e+ e+ time / s Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
41 Positivitätserhaltende, konservative Verfahren Lösung des Robertson Problems mittels modifiziertem Patankar-Runge-Kutta-Verfahren.5 MPRK Ci.5 L L L3 L L5 L L e+ e+ e+ time / s Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
42 Schießverfahren Lösung des RWPs y (x) = y 3 mit y() = und y() = / n s n F(s n ).e + 3.e +.e +.7e + 9.7e 3.3e e.9e e.e 5.3e +.e.39e + 3.9e 7.7e +.e 3.e + 7.e 9.e +.53e 9 Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln / 3
43 Schießverfahren Lösung des RWPs y (x) = y 3 mit y() = und y() = / Andreas Meister (Universität Kassel) Begleitmaterial Numerik von Dgln 3 / 3
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
Gewöhnliche Differentialgleichungen
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Numerische Verfahren
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Angewandte Mathematik und Programmierung
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2012/13 DGL Grundlage Klassifikation Anwendung von lin. Ggln. M. konst.
Grundlagen der Numerischen Mathematik II
J Manfred Reimer Grundlagen der Numerischen Mathematik II Studienbuch für Studenten der Mathematik, Informatik, Statistik und aller Naturwissenschaften Mit 29 Abbildungen Akademische Verlagsgesellschaft
Abschnitt 1.7: Schrittweitensteuerung 27
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
3. Lineare Mehrschrittverfahren 3.1 Begriffe
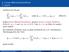3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
10 Stabilität und steife Systeme
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
9 Numerische Verfahren für Anfangswertaufgaben
Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik gewöhnlicher Differentialgleichungen
Numerik gewöhnlicher Differentialgleichungen Band 2 Mehrschrittverfahren Von Dr. phil. nat. Rolf Dieter Grigorieff o. Professor an der Technischen Universität Berlin unter Mitwirkung von Dr. phil. nat.
Numerik gewöhnlicher Differentialgleichungen
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Differentialgleichungen
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Einführung und Beispiele
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Numerik gewöhnlicher Differentialgleichungen
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Extrapolationsverfahren
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Numerische Verfahren
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Numerische Mathematik
».- Numerische Mathematik Von Dr. sc. math. Hans Rudolf Schwarz o. Professor an der Universität Zürich Mit einem Beitrag von Dr. sc. math. Jörg Waldvogel Titularprofessor an der Eidg. Technischen Hochschule
Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan :00-14:00 (120 min)
Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky. Institut für Mathematik
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
Numerik I. Gewöhnliche Differentialgleichungen und Differenzenverfahren für partielle Differentialgleichungen
Numerik I Gewöhnliche Differentialgleichungen und Differenzenverfahren für partielle Differentialgleichungen Vorlesungsskriptum Wintersemester 08/9 R. Verfürth Fakultät für Mathematik, Ruhr-Universität
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1. Prof. Dr. Hans Babovsky. Technische Universität Ilmenau
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
Musterlösung Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
Numerische Mathematik
Numerische Mathematik Von Prof. Dr. sc. math. Hans Rudolf Schwarz Universität Zürich Mit einem Beitrag von Prof. Dr. sc. math. Jörg Waldvogel Eidg. Technische Hochschule Zürich 4., überarbeitete und erweiterte
7 Das Eulersche Polygonzugverfahren
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
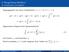4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
8 Numerik gewöhnlicher Differentialgleichungen
8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 03 8 Numerik gewöhnlicher Differentialgleichungen 8. Grundlagen In der Numerik von gewöhnlichen Differentialgleichungen werden vorwiegend Aufgaben folgender
Numerische Verfahren für gewöhnliche Differentialgleichungen
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Differenzialgleichungen
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
1. Anfangswertprobleme 1. Ordnung
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Numerik gewöhnlicher Differentialgleichungen
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL)
Kapitel 6 Gewöhnliche Differenzialgleichungen (DGL) Problemstellung Beispiele Klassifizierung von DGLs, Existenz und Eindeutigkeit des AWPs Einschrittverfahren Stabilität & Schrittweitenkontrolle Mehrschrittverfahren
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik'
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Nebenfach Mathematik im Informatik-Studium. Martin Gugat FAU: Friedrich-Alexander-Universität Erlangen-Nürnberg 25.
Nebenfach Mathematik im Informatik-Studium Martin Gugat martin.gugat@fau.de FAU: Friedrich-Alexander-Universität Erlangen-Nürnberg 25. Oktober 2017 Motivation Die rigorose Analyse von Algorithmen erfordert
NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure
NUMERISCHE VERFAHREN für Naturwissenschaftler und Ingenieure Eine computerorientierte Einführung Von Prof. Dr. sc. nat. HUBERT SCHWETLICK Prof. Dr. sc. nat. HORST KRETZSCHMAR Mit 74 Bildern und 34 Tabellen
D-MATH Numerische Methoden FS 2018 Dr. Vasile Gradinaru Kjetil Olsen Lye. Serie 6
D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. kjetil.lye@sam.math.ethz.ch
Nebenfach Mathematik im Informatik-Studium. Martin Gugat FAU: Friedrich-Alexander-Universität Erlangen-Nürnberg 26.
Nebenfach Mathematik im Informatik-Studium Martin Gugat martin.gugat@fau.de FAU: Friedrich-Alexander-Universität Erlangen-Nürnberg 26. Oktober 2016 Motivation Die rigorose Analyse von Algorithmen erfordert
Kapitel 11 Gewöhnliche Differentialgleichungen
Kapitel 11 Gewöhnliche Differentialgleichungen 11.1 Einführung Gesucht wird eine Funktion y = y(t) einer (Zeit-)Variablen t, die der Gleichung und der Anfangsbedingung genügen soll. y (t) = f(t, y(t)),
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Das Eulerverfahren zum numerischen Lösen von DGLen
Das Eulerverfahren zum numerischen Lösen von DGLen Thomas Wassong FB17 Mathematik Universität Kassel 06.05.2008 Numerische Verfahren zur Berechnung von Differentialgleichungen Das Eulerverfahren: Programmierung
Numerische Mathematik
Hans Rudolf Schwarz I Norbert Köckler Numerische Mathematik 8., aktualisierte Auflage STUDIUM VIEWEG+, TEUBNER / Iahalt Einleitung 13 1 Fehlertheorie 15 1.1 Fehlerarten 15 1.2 Zahldarstellung 16 1.3 Rundungsfehler
Übungsblatt 10 Musterlösung
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 23
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Numerische Mathematik
Hans Rudolf Schwarz I Norbert Köckler Numerische Mathematik 8., aktualisierte Auflage STUDIUM 11 VIEWEG+ TEUBNER Inhalt Einleitung 13 1 1.1 1.2 1.3 1.4 1..5 1.6 1.7 2 2.1 2.1.1 2.1.2 2.1.3 2.2 2.2.1 2.2.2
8 Gewöhnliche Differentialgleichungen
8 Gewöhnliche Differentialgleichungen Beispiel: Radioaktiver Zerfall Sei m(t) die Menge radioaktiven Materials zur Zeit t. Der Zerfall des Materials geschieht proportional zur vorhandenen Menge mit dem
H. Achte Übungseinheit
H. Achte Übungseinheit Inhalt der achten Übungseinheit: Einschrittverfahren für gewöhnliche Differentialgleichungen erster Ordnung MATLAB-Löser Klassisches Euler-Verfahren und andere einfache explizite
Numerik gewöhnlicher Differentialgleichungen. Übung 8 - Lösungsvorschlag
Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Kapitel 1 Gewöhnliche Differentialgleichungen
Kapitel 1 Gewöhnliche Differentialgleichungen Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind Differentialgleichungen, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug
Lösung Semesterendprüfung
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
Parareal. Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen. Johannes Reinhardt. Parareal 1 Johannes Reinhardt
Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
2.3.1 Explizite Runge-Kutta-Verfahren
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
PVK Numerische Methoden Tag 1
PVK Numerische Methoden Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G 23.8 8093 Zürich lucasb@ethz.ch June 19, 2017 Lucas Böttcher (ETH Zürich) PVK Numerik June 19,
Tutorial Differentialgleichungen Band I
Tutorial Differentialgleichungen Band I mit einem kurzen Repetitorium der Differentialrechnung und einem ausführlichen Tutorial über unbestimmte Integrale und numerische Verfahren P. Schneider, Herborn,
Hohere Mathematik. fur Ingenieure, Physiker und Mathematiker von Dr. Dr. h.c. Norbert Herrmann Leibniz Universitat Hannover 2., uberarbeitete Auflage
Hohere Mathematik fur Ingenieure, Physiker und Mathematiker von Dr. Dr. h.c. Norbert Herrmann Leibniz Universitat Hannover 2., uberarbeitete Auflage Oldenbourg Verlag MunchenWien Inhaltsverzeichnis Einleitung
Numerik gewöhnlicher Differentialgleichungen. Prof. Dr. Guido Kanschat
Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Formelsammlung zur Numerischen Mathematik mitturbo-pascal- Programmen
Formelsammlung zur Numerischen Mathematik mitturbo-pascal- Programmen von PROF. DR. GISELA ENGELN-MÜLLGES Fachhochschule Aachen und 0. PROF. EM. DR. FRITZ REUTTER Rheinisch-Westfälische Technische Hochschule
Mathematische Grundlagen
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
Kapitel 3: Differentialgleichungen
Kapitel 3: Differentialgleichungen Einführung: Vergleich zur Integration Zwischen der Integration und der Lösung von Differentialgleichungen besteht ein enger Zusammenhang: Das Aufsuchen der Lösung y(b)
10 Gewöhnliche Differentialgleichungen
Gewöhnliche Differentialgleichungen. Aufgabenstellung, Beispiele.. Differentialgleichungen erster Ordnung Explizite gewöhnliche Differentialgleichung. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion
Numerik gewöhnlicher Differentialgleichungen
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Inhaltsverzeichnis. Kapitel 9. Gewöhnliche Differentialgleichungen... 1
Inhaltsverzeichnis Kapitel 9. Gewöhnliche Differentialgleichungen... 1 1. Einführung... 1 1.1 Grundbegriffe 1.2 Anfangswertprobleme 1.3 Geometrische Bedeutung der DGL 1. Ordnung 2. Spezielle Differentialgleichungen
Numerische Lösungsverfahren im Maschinenbau
I, 73 (04) c 04 Numerische Lösungsverfahren im Maschinenbau Dr. Jürgen Bolik Technische Hochschule Nürnberg f (x) n= x 3 x a n= b x TH Nürnberg Inhaltsverzeichnis Näherungsverfahren zur Lösung nichtlinearer
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Vorlesung, 26. Mai 2011, Inhalt. Eigenwerte und Eigenvektoren. Gewöhnliche Differentialgleichungen
Vorlesung, 26. Mai 2011, Inhalt Eigenwerte und Eigenvektoren Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Es sei A eine n n-matrix, x ein vom Nullvektor verschiedener Vektor und λ
Adaptive Mehrschrittverfahren
Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Inhaltsverzeichnis. 1 Einleitung... 1
Inhaltsverzeichnis 1 Einleitung................................................. 1 2 Fehleranalyse: Kondition, Rundungsfehler, Stabilität...... 11 2.1 Kondition eines Problems................................
5 Steife Differentialgleichungen
Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif,
mathematik und informatik
Prof. Dr. Torsten Linß Kurs 037 Numerische Mathematik II LESEPROBE mathematik und informatik Das Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere das Recht der Vervielfältigung
(45 Min) als auch schriftlich im Rahmen einer Ausarbeitung zu präsentieren. 1. Gusfield: Algorithms on strings, trees and sequences.
1. Thema: Dynamische Programmierung Das Prinzip des dynamischen Programmierens wird bei der Lösung kombinatorischer Optimierungsprobleme eingesetzt. Grundidee ist, das Problem auf kleinere Teilprobleme
5. Steife Differentialgleichungen 5.1 Was sind steife Differentialgleichungen?
5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG
Numerik Grundpraktikum: Numerische Verfahren für gewöhnliche Differentialgleichungen
Numerik Grundpraktikum: Numerische Verfahren für gewöhnliche Differentialgleichungen Roland Pulch Vorlesung im Wintersemester 205/6 Institut für Mathematik und Informatik Ernst-Moritz-Arndt-Universität
Grundlagen der Numerischen Mathematik Sommersemester Kapitel 0. Jun.-Prof. Dr. Thorsten Raasch (JGU Mainz) 23. April 2014
Grundlagen der Numerischen Mathematik Sommersemester 2014 Kapitel 0 Jun.-Prof. Dr. Thorsten Raasch Johannes Gutenberg-Universität Mainz Institut für Mathematik 23. April 2014 Numerik Was ist das? Was ist
Uberblick Kapitel 1. Kapitel 2.
Überblick Das Buch gliedert sich in acht Kapitel, ein Softwareverzeichnis, ein Literaturverzeichnis und einen Index. Die ersten drei Kapitel legen die Grundlagen der Modellierung, der Analysis und der
Explizite Runge-Kutta-Verfahren
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Lokaler Fehler y = y 2, y(0.2) = 5/9, Lösung: y = 1 Fehler nach dem 1. Schritt
Lokaler Fehler y = y, y(.) = /9, Lösung: y = Fehler nach dem. Schritt ( t) 4 Fehler 6 8 4 (I) Euler explizit (II) Euler implizit (IIIa) Crank Nicolson (IIIb) Heun (IVa) Euler modifiziert (IVb) Euler mod.
Simulation of planets and satellites
Simulation of planets and satellites Präsentation im Fach Computervisualistik von Roman Pethe Virtuelles Labor Einführung Grundlagen Probleme & Lösungen Anwendungen Zusammenfassung Einführung Grundlagen
y(x) ist die gesuchte Lsg.-Funktion der unabhängigen Variablen x Anfangswertproblem: Lsg. heißt Integralkurve
Kapitel 8 Gewöhnliche Differentialgleichungen 8.1 Vorbemerkungen Betrachte skalare Gleichung y = dy dx = f(x, y(x)) (8.1) y(x) ist die gesuchte Lsg.-Funktion der unabhängigen Variablen x Mit der Anfangsbed.
Einführung in die Numerik strukturerhaltender Zeitintegratoren. Leonard Schlag 6. Dezember 2010
Einführung in die Numerik strukturerhaltender Zeitintegratoren Leonard Schlag 6. Dezember 2010 1 Inhaltsverzeichnis 1 Einführung in die Numerik strukturerhaltender Zeitintegratoren 3 1.1 Häuge Problemstellung:
Vorlesung Mathematik 2 für Ingenieure (A)
1 Vorlesung Mathematik 2 für Ingenieure (A) Sommersemester 2017 Kapitel 8: Gewöhnliche Differenzialgleichungen Prof. Dr. Gerald Warnecke Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke
Für viele technische Anwendungen unverzichtbar!
Für viele technische Anwendungen unverzichtbar! Page 1 of 26 5.1. Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug zueinander
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
MATHEMATIK. Numerische Mathematik. Hans-Görg Roos/Hubert Schwetlick. Das Grundwissen für jedermann. B. G. Teubner Stuttgart Leipzig
MATHEMATIK FÜR INGENIEURE UND NATURWISSENSCHAFTLER Hans-Görg Roos/Hubert Schwetlick Numerische Mathematik Das Grundwissen für jedermann B. G. Teubner Stuttgart Leipzig Begründer dieses Lehrwerkes: Prof.
Parameterschätzung an einem Anfangswertproblem aus der Physiologie
Parameterschätzung an einem Anfangswertproblem aus der Physiologie Erkki Silde und Horatio Cuesdeanu 13. Juli 2010 Erkki Silde und Horatio Cuesdeanu () Parameterschätzung 13. Juli 2010 1 / 7 Gegeben sei
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere