Numerische Lösungsverfahren im Maschinenbau

Transkript

1 I, 73 (04) c 04 Numerische Lösungsverfahren im Maschinenbau Dr. Jürgen Bolik Technische Hochschule Nürnberg f (x) n= x 3 x a n= b x

2 TH Nürnberg Inhaltsverzeichnis Näherungsverfahren zur Lösung nichtlinearer Gleichungen und Gleichungssysteme 3. Das Newtonsche Verfahren zur Lösung nichtlinearer Gleichungen Das Newtonsche Verfahren zur Lösung nichtlinearer Gleichungssysteme Das Gauß-Newton-Verfahren zur Lösung nichtlinearer Gleichungssysteme Übungsaufgaben Numerische Integration von Funktionen 7. Newton-Cotes-Formeln und Gaußsche Integrationsmethode Lagrangesche Interpolationsformel Newton-Cotes-Formeln Die Gaußsche Integrationsmethode Adaptive Integration: Fehlerschätzung und Schrittweitensteuerung Anwendung einer Extrapolation auf Integrationsverfahren Übungsaufgaben Anfangswertprobleme für gewöhnliche Differentialgleichungen Reduktion der Ordnung Einschrittverfahren mit Schrittweitensteuerung Die Verfahren von Euler-Cauchy und Heun Explizite Runge-Kutta-Verfahren Numerische Stabilität Fehlerschätzung und Schrittweitensteuerung Systeme von Differentialgleichungen erster Ordnung und Differentialgleichungen höherer Ordnung MATLAB-Routinen zu Differentialgleichungen Übungsaufgaben

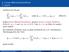
3 TH Nürnberg 3 Näherungsverfahren zur Lösung nichtlinearer Gleichungen und Gleichungssysteme. Das Newtonsche Verfahren zur Lösung nichtlinearer Gleichungen Bei dem Newtonschen Verfahren zur Lösung von f(x) = 0 für eine Funktion f : D R, mit D R, handelt es sich um ein Iterationsverfahren mit x i+ := x i f(x i) f (x i ), i N 0. y f (x) x x x 0 Abbildung. Newtonsches Verfahren x Satz: Ist f : [a, b] R eine zweimal differenzierbare konvexe Funktion mit f(a) < 0 und f(b) > 0, so gilt: Es gibt genau ein ξ (a, b) mit f(ξ) = 0. Ist x 0 [a, b] ein Punkt mit f(x 0 ) 0, so existiert die Folge (x i ) i N0, mit x i+ := x i f(x i) f (x i ), i N 0, die monoton fallend gegen ξ konvergiert.

4 TH Nürnberg 4 Beispiel Gesucht ist die Lösung der impliziten Gleichung Lösung Mit und erhalten wir x = sin x. f(x) := x sin x f (x) = cos x x i+ = x i x i sin x i cos x i, i N 0. und mit 3 Iterationen: i x i f(x i )

5 TH Nürnberg 5 Weitere Beispiele Tritt in der Iterationsfolge für die Nullstellenbestimmung von f(x) = x x der Iterationswert x i = auf, so bricht das Verfahren ab. Warum? Wir betrachten f(x) = x + tanh(x 5) mit x 0 = 3.9. y x 0 x Abbildung. Nicht-konvexe Funktion x

6 TH Nürnberg 6. Das Newtonsche Verfahren zur Lösung nichtlinearer Gleichungssysteme Sei U R n offen und f : U R m eine Abbildung, die im Punkt x 0 U differenzierbar sei. Dann lässt sich f durch affin-lineare Funktionen f(x) = f(x 0 ) + Df(x 0 ) (x x 0 ) approximieren, wobei für die Matrixelemente (Df(x 0 )) kl mit k n und l n gilt (Df(x 0 )) kl = f k x l (x 0 ). Anmerkung: Die Variable x und der Punkt x 0 sind Elemente des R n. Die Matrix f x (x 0 ) f x (x 0 )... f x n (x 0 ) f x (x 0 ) f x (x 0 )... f x n (x 0 ) Df(x 0 ) =.... f n x (x 0 ) fn x (x 0 )... fn x n (x 0 ) wird als das Differential oder die Jacobi- oder Funktional-Matrix von f im Punkte x 0 bezeichnet. Sei x Nullstelle von f. Ist die Funktionalmatrix Df(x 0 ) nichtsingulär, so lässt sich die Gleichung f(x 0 ) + Df(x 0 )(x x 0 ) = 0 nach x auflösen und es gilt x = x 0 (Df(x 0 )) f(x 0 ). Das Newton-Verfahren zur Lösung von f(x) = 0 ist durch die Folge (x i ) i N0, mit gegeben. x i+ = x i (Df(x i )) f(x i ), Wir betrachten Ds i = f(x i ),

7 TH Nürnberg 7 mit s i := x i+ x i. Beispiel Bestimmung des Arbeitspunktes eines Gebläses, das einen Volumenstrom V (t) in einem vertikalen Rohr erzeugen soll. Gebläsekennlinie Sei V (t) (in m3 ) der Volumenstrom und H (in m) die Förderhöhe. Ferner gelte s H = V. Kennlinie der Rohrleitung Sei H (in m) die Verlusthöhe. Ferner gelte H = 4 V +. V.75. H m 500 Gebläse Rohrleitung Abbildung.3 Kennlinie Gebläse-Rohrleitung 8 m 3 s V ' Wir setzen f := x x und f := x 4 x. x.75.

8 TH Nürnberg 8 Es gilt f x =, f x = 6 x und f x =, f x = 8 x. x Wir wählen als Startwerte x,0 = 00, x,0 = 7, d. h. x 0 = (00, 7) und erhalten ( ) Df(x 0 ) =. 64 Mit f(x 0 ) = ( , ) = ( 8, 3) ergibt sich ( ) ( ) 8 s 0 = 64 3 und demnach s,0 = 86.4 s,0 = 0.7. Demnach gilt x, = H = = 86.4, x, = V = = 6.3

9 TH Nürnberg 9 und f(x ) = ( , ) = (3.9,.4). Während f(x 0 ) = = 7488 erhalten wir nun f(x ) =

10 TH Nürnberg 0.3 Das Gauß-Newton-Verfahren zur Lösung nichtlinearer Gleichungssysteme Hier nehmen wir an, dass eine Näherung x i vorliegt und betrachten das in x i linearisierte Ausgleichsproblem mit min E(x) x R n E(x) := f(x i ) + Df(x i )(x x i ). Hierzu werden folgende Iterationsschritte durchgeführt: mit Df(x i ) T Df(x i )s i = Df(x i ) T f(x i ) x i+ = x i + s i. Dieses Verfahren wird auch in ähnlicher Form im Rahmen der Ausgleichsrechnung verwendet. Es bietet sich daher an, es hier im Zusammenhang mit der linearen Regression vorzustellen. Lineare Regression Lassen sich die Daten der Ausprägungen zweier Merkmale X und Y näherungsweise in Form eines linearen Zusammenhangs darstellen, so verhilft die lineare Regressionsrechnung zu einer genaueren Analyse der funktionalen Abhängigkeit beider Merkmalsausprägungen. Dabei liegen die Daten in Form von Wertepaaren (x, y ),..., (x n, y n ), mit x i, y i R, vor. Es wird davon ausgegangen, dass y i = α + βx i + c i für i =,..., n gilt. Hier sind α, β, c i R, wobei die Größen c i zufällige Fehler darstellen. Die Methode der kleinsten Quadrate Die Parameter α und β sollen so bestimmt werden, dass durch die Regressionsgerade ŷ = a + bx eine möglichst gute Schätzung ŷ für die Ausprägung y des Merkmals Y bietet.

11 TH Nürnberg Ein geeignetes Maß für die Güte dieser Schätzung stellt die Summe der Abweichungsquadrate S = dar, wobei (y i ŷ i ) i= ŷ i := a + bx i sei. Nun sollen die Schätzgrößen a und b für α und β so bestimmt werden, dass S minimal wird. y 6 5 (x i, y i ) 4 ŷ=a+b x 3 (x i, ŷ i ) x Abbildung.4 Methode der kleinsten Quadrate Die Parameter a und b ergeben sich dann als Lösungen des Normalengleichungssystems S a = (y i a bx i ) = 0 i= und S b = x i (y i a bx i ) = 0. i= Nach der ersten der beiden Gleichungen ist der Schätzwert für α a = ȳ b x, wobei x = n i= x i und ȳ = n i= y i

12 TH Nürnberg die Mittelwerte der Größen x i bzw. y i sind. Die zweite Gleichung impliziert x i y i ȳ x + b x b n n i= x i = 0. i= Nach dieser Gleichung und mit Hilfe der Identitäten (x i x)(y i ȳ) = x i y i n xȳ und i= (x i x) = i= i= x i x n i= erhalten wir schließlich (x i x)(y i ȳ) i= b =, (x i x) i= den Schätzwert für β. Beispiel Gesucht ist die Regressionsgerade für folgende Daten (x i, y i ): ( 4, 3), (, ), (, 0), (0, ), (4, 5). Die Schätzwerte a und b lassen sich mittels 5 5 x i = = 3, y i = = 4, i= i= 5 x i = = 37 i= und 5 x i y i = ( 4) ( 3) + ( ) + ( ) = 30 i= bestimmen. Demnach gilt b(9 5 37) = 0 und 5a = 4 + 3b.

13 TH Nürnberg 3 Die Parameter der Regressionsgerade y = a + bx sind daher a, 35, b 0, 9. y x Abbildung.5 Datenpunkte und die zugehörige Regressionsgerade Treten nicht nur zwei, sondern allgemein m unabhängige Merkmale auf, so verwenden wir bei einem linearen Ansatz als Schätzfunktion ŷ i = a 0 + a x i + a x i a m x mi. Mit und x x... x m x x... x m X = x n x n... x mn y a 0 y a y =.., a =.... y n a m

14 TH Nürnberg 4 folgt a = (X t X) X t y Beweis Es gilt ŷ = Xa. Gemäß der Methode der kleinsten Quadrate wird S = (y i ŷ i ) i= minimiert. Differenzieren wir S nach a 0, a,..., a m und beachten, dass grad S = 0 eine notwendige Bedingung für das Vorliegen eines kritischen Punktes ist, so erhalten wir y i = a 0 n + a x i + a x i a m x mi i= i= i= i= y i x i = a 0 x i + a x i + a x i x i a m x mi x i i= y i x i = a 0 i= x i + a i= i= i= i= i= i= i= x i x i + a x i a m i= x mi x i. y i x mi = a 0 i= Demnach gilt. x mi + a i=. x i x mi + a i=.. x i x mi a m x mi. i= i= X t Xa = X t y und daher a = (X t X) X t y. Anmerkung: Mit Hilfe der euklidischen Norm. können wir auch S = y Xa = (y Xa) t (y Xa) = y t y y t Xa (Xa) t y + (Xa) t Xa = a t X t Xa y t Xa + y t y schreiben.

15 TH Nürnberg 5.4 Übungsaufgaben Aufgabe Lösen Sie die Gleichung cos(x) = x mit dem Newton-Verfahren. Aufgabe Berechnen Sie die Nullstellen und die Stellen mit waagrechter Tangente der Funktion f : R R, x f(x) = x x mit Hilfe des Newton-Verfahrens. Aufgabe 3 Leiten Sie aus dem Planckschen Strahlungsgesetz ρ(ν, T ) = 4πh c 3 ν 3 e hν kt den Wert ν m her, an dem das Maximum der Strahlungsdichte ρ(., T ) eines Hohlraumstahlers liegt. Aufgabe 4 Bestimmen Sie die Regressionsgerade für folgende Daten (t i, s i ): (, ), (3, 6 5 ), (, 3 ), (7, 3 0 ). Aufgabe 5 Bestimmen Sie die Koeffizienten a 0, a, a für eine linearen Regression zu folgenden Daten: x x y

16 TH Nürnberg 6 Aufgabe 6 Sei mit f : R R, (x, y) f = (f, f ) f := x + y 3 und f := 5x y. a) Die Werte x 0 := 0. und y 0 := sind Näherungswerte für eine Nullstelle von f. Bestimmen Sie die Fehlerquadratsumme für diese Näherung. b) Wie lauten die Näherungswerte x, y und die Fehlerquadratsumme der. Iteration nach dem Newton-Verfahren? c) Wie lauten die Näherungswerte x, y und die Fehlerquadratsumme der. Iteration nach dem Gauß-Newton-Verfahren?

17 TH Nürnberg 7 Numerische Integration von Funktionen. Newton-Cotes-Formeln und Gaußsche Integrationsmethode Beispielsweise lässt sich ein Anfangswertproblem für eine Differentialgleichung erster Ordnung, wie y (x) = f(x) mit y(x 0 ) = y 0, mittels Integration lösen. Dabei setzen wir voraus, dass f eine stetige Funktion ist. Eine Integration dieser Differentialgleichung führt dann zu x x 0 y (x) dx = und somit zu x x 0 y(x ) = y(x 0 ) + f(x) dx x x 0 f(x) dx. Ist f : I R eine stetige Funktion und x 0 I, dann ist F : I R, x F (x) := differenzierbar und es gilt F = f. x x 0 f(t) dt Allerdings kann F (x) nicht immer explizit angeben werden, so dass dann nach einer numerischen Lösung gesucht wird.

18 TH Nürnberg 8.. Lagrangesche Interpolationsformel Hierbei wird eine beliebige stetigen Funktion f durch Polynom n-ten Grades, P, interpoliert. Ein solches Interpolationspolynom P n (x) = c i x i i=0 soll an den Stützstellen t k, k = 0,..., n, mit den Funktionswerten f(t k ) übereinstimmen, d. h. P n (x k ) = c i x i k = f(x k ) := f k, k = 0,,..., n. i=0 Hierbei werden die n + Koeffizienten c i durch n + Gleichungen bestimmt. Zu beliebigen n + Punkten (x i, f i ) mit x i, f i R, i = 0,..., n, und x i x k für i k gibt es genau ein Polynom m-ten Grades mit m n und Durch P (x i ) = f i, i = 0,,..., n. L i (x) := (x x 0)... (x x i )(x x i+ )... (x x n ) (x i x 0 )... (x i x i )(x i x i+ )... (x i x n ) = ω(x) (x x i )ω (x i ), wobei ω(x) := n (x x i ), i=0 ist ein Interpolationspolynom gegeben, das die Eigenschaft { für i = k L i (x k ) = δ ik = 0 für i k besitzt. Weiterhin gilt P (x) = f i L i (x) = i=0 i=0 f i n k=0,k i x x k x i x k.

19 TH Nürnberg 9 Beispiele Für (i) Für n = gilt und (ii) Für n = gilt L 0 (x) = x x x 0 x, L (x) = x x 0 x x 0 P (x) = f 0 L 0 (x) + f L (x). L 0 (x) = (x x )(x x ) (x 0 x )(x 0 x ), L (x) = (x x 0)(x x ) (x x 0 )(x x ), L (x) = (x x 0)(x x ) (x x 0 )(x x ) und P (x) = f 0 L 0 (x) + f L (x) + f L (x). f : R R, x f(x) = x 3 x erhalten wir folgende graphische Darstellung der Interpolationspolynome für n = und n = : f (x) n= x 3 x a n= b x Abbildung. Graphen von Interpolationspolynomen

20 TH Nürnberg 0.. Newton-Cotes-Formeln Isaac Newton (643-77), Roger Cotes (68-76) Nun betrachten wir eine äquidistante Unterteilung des Intervalls [a, b] mit x i := a + ih, i = 0,,..., n, wobei die Schrittweite h := b a n, mit n N := {,, 3,...}, sei. Ferner sei P n das interpolierende Polynom vom Grad n mit und P n (x i ) = f i := f(x i ) P n (x) := f i L i (x). i=0 Aus der Interpolationsformel von Lagrange folgen die Newton-Cotes-Formeln b a P n (x) dx = f i b L i (x) dx = h i=0 a i=0 0 i=0 f i n ϕ i (t) dt = h f i α i wobei x = a + ht und ϕ i (t) = n k=0,k i t k i k und die Gewichte α i gegeben sind durch α i := n 0 ϕ i (t) dt. Die Gewichte sind rationale Zahlen mit der Eigenschaft α i = n, i=0 was, wegen der Eindeutigkeit der Polynominterpolation, mit f(x) :=, und daher P n (x) :=, folgt.

21 TH Nürnberg Ist q ein Hauptnenner der rationalen Zahlen α i, so sind die Zahlen σ i := qα i, i = 0,,..., n ganzzahlig und wir erhalten b a P n (x) dx = h i=0 f i α i = b a qn σ i f i, i=0 wobei σ i, q und n vom verwendeten Interpolationsverfahren abhängige Parameter sind. Die hier hergeleiteten Integrationsformeln heißen Newton-Cotes-Formeln vom geschlossenen Typ, da die Intervallgrenzen als Stützstellen verwendet werden. Da die Newton-Cotes-Formeln von höherem Grad instabil sind, werden die Formeln mit geringeren Polynomgraden genutzt. Beispiele (i) Für n = 0 erhalten wir die Mittelpunktregel (mittlere Rechteckregel) bzw. rechte Rechteckregel, da b a P 0 (x) dx = (b a) f(ξ), mit ξ = (a + b) für erstere und ξ = b für letztere. (ii) Für n = erhalten wir die Trapezregel, da mit b a a 0 := P (x) dx = f 0 a 0 + f a b a L 0 (x) dx = a b b a (x b) dx = (b a), oder a := b a L (x) dx = b a b a (x a) dx = (b a) ϕ 0 (t) = t,

22 TH Nürnberg ϕ (t) = t, somit α 0 = ϕ 0 (t) dt =, 0 α = ϕ (t) dt = und daher 0 b a P (x) dx = (b a) (f 0 + f ). (iii) Für n = erhalten wir die Simpsonregel (Thomas Simpson (70-76), Johannes Kepler (57-630)), da somit ϕ 0 (t) = t 0 t 0, ϕ (t) = t 0 0 t, ϕ (t) = t 0 0 t, α 0 = α = 0 0 (t 3t + ) dt = ( ) = 3, (t t) dt = ( 8 3 4) = 4 3, α = (t t) dt = (8 3 4 ) = 3 und demnach 0 b a P (x) dx = 6 (b a) (f 0 + 4f + f ) = h 3 (f 0 + 4f + f ).

23 TH Nürnberg 3 Anmerkung und A = b a 3 ( (f(a) + y(a )) + (y(a ) + y(a )) + (y(a ) + f(b))) f( a + b ) = (y(a ) + y(a ))

24 TH Nürnberg 4 Der Quadraturfehler Ein Approximationsverfahren heißt von Ordnung p, wenn p N die größte ganze Zahl ist, für die das Verfahren alle Polynome kleineren Grades als p exakt integriert. Dann wird p als dessen Exaktheitsgrad bezeichnet. Beispiele (i) Trapezregel: p = (ii) Simpsonregel: p = 4 Ein Maß für die Abweichung des approximierten Integrationswertes für b a f(x) dx von dem exakten Wert bietet der sogenannten Quadraturfehler (Approximations-, Abschneideoder Verfahrensfehler) E n (f) := b a (P n (x) f(x)) dx. Für den Quadraturfehler der Newton-Cotes-Quadraturformel gilt: Es existiert ein ξ (a, b), ein p = p(n) N und eine Konstante K = K(n), so dass E n (f) = h p+ Kf (p) (ξ). Ist f ein Polynom mit einem Grad kleiner als p, so gilt demnach E n (f) = 0.

25 TH Nürnberg 5 Newton-Cotes-Formeln im Überblick Neben der Trapez- und der Simpsonregel gibt es eine Reihe weiterer elementarer Integrationsformeln, beispielsweise von Edward Arthur Milne ( ) oder von Thomas Weddle (87-858). Zusammengefasst lassen sich die Newton-Cotes-Formeln für n =,,..., 6 folgendermaßen beschreiben: n σ i qn Fehler Name h3 f () (ξ) Trapezregel h5 f (4) (ξ) Simpson-Regel h5 f (4) (ξ) 3 8 -Regel h7 f (6) (ξ) Milne-Regel h7 f (6) (ξ) h9 f (8) (ξ) Weddle-Regel

26 TH Nürnberg 6 Wiederholte Anwendung der Newton-Cotes-Formeln Mit äquidistanten Teilintervallen von [a, b] erhalten wir (i) im Falle n = im Intervall [x i, x i+ ], i = 0,,..., N, den Näherungswert I i := h (f(x i) + f(x i+ )) (ii) im Falle n = für gerades N im Intervall [x i, x i+ ], i = 0,,..., N, den Näherungswert I i := h 3 (f(x i) + 4f(x i+ ) + f(x i+ )). Somit ergeben sich für das Intervall [a, b] (i) die Trapezsumme (zusammengesetzte Trapezregel) zur Schrittweite h und T (h) := N i=0 I i = h( f(a) (ii) die (zusammengesetzte) Simpsonregel zur Schrittweite h + f(a + h) + f(a + h) f(b h) + f(b) ), S(h) := h 3 (f(a)+4f(a+h)+f(a+h)+4f(a+3h)+...+f(b h)+4f(b h)+f(b)),

27 TH Nürnberg 7 Lemma. Sei f C ([a, b]). Für die Trapezregel gilt x i+ x i f(x) dx = mit x i ξ x i+, und T (h) = N i=0 h (f(x i) + f(x i + h)) h3 f (ξ), h (f(x i) + f(x i+ )) = h (f(a) + f(a + h) f(b h) + f(b)). Die globale Fehlerordnung der Trapezregel wird durch O(h ) charakterisiert, da T (h) b a f(x) dx = h N (b a) N f () (ξ i ) i=0 = b a h f () (ξ) für ein ξ (a, b). Beweis: Mit Hilfe der Taylor-Entwicklung erhalten wir und f(x i + h) = f(x i ) + hf (x i ) + h! f (x i ) +... x i +h Daher gilt x i f(x) dx = hf(x i ) + h! f (x i ) + h3 3! f (x i ) h (f(x i) + f(x i + h)) = hf(x i ) + h f (x i ) + h3 4 f (x i ) Das Landau-Symbol O(h k ) bedeutet, dass eine Konstante C existiert, so dass f(h) h k C für h 0.

28 TH Nürnberg 8 Somit folgt x i +h x i f(x) dx h (f(x i) + f(x i + h)) = h3 f (x i ).... Daher existiert ein ξ [x i, x i + h], so dass für den lokalen Diskretisierungsfehler E (f) = h 3 f () (ξ) gilt. Für die Abschätzung des globalen Diskretisierungsfehlers nutzen wir die Eigenschaft min f () (ξ i ) N f () (ξ i ) max f () (ξ i ). i N 0 N i N 0 i=0 Da f C ([a, b]) existiert demnach ein ξ (min i ξ i, max ξ i ) (a, b), so dass i f () (ξ) = N N i=0 f () (ξ i ). Lemma. Sei f C ([a, b]). Für die Simpson-Regel gilt x i+ x i f(x) dx = mit x i ξ x i+, und, falls N gerade, S(h) = N i=0 h 3 (f(x i) + 4f(x i+ ) + f(x i+ )) h5 90 f (4) (ξ), h 3 (f(x i) + 4f(x i+ ) + f(x i+ )) = h (f(a) + 4f(a + h) + f(a + h) + 4f(a + 3h) f(b h) + 4f(b h) + f(b)). Die globale Fehlerordnung der Simpson-Regel wird durch O(h 4 ) charakterisiert, da S(h) b a f(x) dx = b a 80 h4 f (4) (ξ) für ein ξ (a, b).

29 TH Nürnberg 9 Beweis: Mit Hilfe der Taylor-Entwicklung der Funktion f(x) in x [x j, x j + h] erhalten wir f(x) = f(x j+ ) + (x x j+ )f (x j+ ) + (x x j+) f (x j+ ) +...,! wobei x j+ = x j + h. Es gilt x j +h x j f(x) dx = h(f(x j+ ) + und nach der Simpson-Regel x j +h x j P (x) dx = h 3! f (x j+ ) + h 4 5 4! f (4) (x j+ ) +...) h 3 (f(x j) + 4f(x j+ ) + f(x j+ )) = h 3 ((f(x j+) hf (x j+ )+ h! f (x j+ )...)+4f(x j+ )+(f(x j+ )+hf (x j+ )+ h! f (x j+ )+...)) = h(f(x j+ ) + h 3! f (x j+ ) + h 4 3 4! f (4) (x j+ ) +...). Somit erhalten wir für den lokalen Diskretisierungsfehler E (f) = h( 5 3 )h4 4! f (4) (ξ) = h5 90 f (4) (ξ). Den globalen Diskretisierungsfehler erhalten wir wie im Beweis des Lemmas (.), wobei hier f () (ξ) = N N f () (ξ i ) i=0 ist.

30 TH Nürnberg 30 Anmerkung: Die Simpsonregel läßt sich, für N gerade, folgendermaßen schreiben: N i=0 x i+ x i 6 (f(x i ) + 4 f( x i+ + x i ) + f(x i+ )) = h N (f(a + i h) + 4 f(a + i h + h) + f(a + (i + ) h)) 3 i=0 = h N 3 (f(a) + 4 i=0 N f(a + i h + h) + i= f(a + i h) + f(b)). Bezeichnet I(f) den exakten Integralwert von f und Q(h) den Wert, der sich durch das jeweilige numerische Integrationsverfahren ergibt, so sagen wir, das Verfahren hat die Konsistenzoder Genauigkeitsordnung k, falls I(f) Q(h) = O(h k ) für h 0. Beispiele Es gilt e t dt = e = Summierte Trapezregel h T (h) Fehler Hier führt eine Halbierung der Schrittweite zu einem des bisherigen Fehlerwerts. 4

31 TH Nürnberg 3 Summierte Simpson-Regel h S(h) Fehler Hier führt eine Halbierung der Schrittweite zu einem des bisherigen Fehlerwerts. 6

32 TH Nürnberg 3..3 Die Gaußsche Integrationsmethode Karl Friedrich Gauß ( ) Hierbei lassen sich Integrale der Form I(f) = b a ω(x)f(x) dx numerisch auswerten. Dabei ist ω : [a, b] R gegeben und genüge einigen Voraussetzungen, wie beispielsweise ω 0. Hier beschränken wir uns auf ω =. Wie bei den Newton-Cotes-Formeln werden Integrationsregeln der Form Ĩ(f) := w i f(x i ) i= verwendet. Allerdings ist die Schrittweite bei den Newton-Cotes-Verfahren konstant. Die Gaußsche Integrationsmethode zielt hingegen darauf ab, die Gewichte w i und Stützstellen x i so zu wählen, dass der Integrationsfehler Ĩ(f) I(f) von Ĩ(f) für Polynome möglichst hohen Grades verschwindet. Theorem.3 Sind x, x,..., x n die Nullstellen des Legendre-Polynoms p n, wobei d n p n (x) = n n! dx n (x ) n, n N 0, dann gilt w i > 0, i =,,..., n, und b a p(x) dx = w i p(x i ). i= Die Gauß-Quadraturformeln für ω = lassen sich in (i) Gauß-Legendre-Formeln, wobei alle Stützstellen optimal bestimmt werden, und (ii) Gauß-Lobatto-Formeln, wobei die Stützstellen fest vorgegeben werden und nur die inneren Stützstellen optimal bestimmt werden, unterteilen. Da das Intervall [, ] mittels t x = b a t + a + b bijektiv auf [a, b] abgebildet werden kann, beschränken wir uns hier auf das Intervall [, ]. siehe Anhang

33 TH Nürnberg 33 Die Gauß-Legendre-Formeln Um ein Polynom mit n = Stützstellen zu interpolieren, suchen wir Gewichte w und w, so dass x 3 dx = 0 = w x 3 + w x 3 x dx = 3 = w x + w x x dx = 0 = w x + w x dx = = w + w gilt. Als Lösung dieses Gleichungssystems für w, w, x, x ergibt sich w = w =, x = x = 3. Die Gauß-Legendre-Formel für n = zur Integration einer Funktion f lautet Q = f( 3 ) + f( 3 ). Beispiel Es gilt 3 e x 3 dx = 3 (e3 e ) 4.3. Mit der genannten Gauß-Quadraturformel für n = erhalten wir Q = 3 (exp(5 3 ) + exp(5 + )) Die Trapezregel (mit zwei Stützstellen) ergibt T = 3 (e3 + e )

34 TH Nürnberg 34 Für das Intervall [, ] sind die Werte w i und x i der Gauß-Legendre-Formel in folgender Tabelle angegeben: n w i x i w = x = 0 w = w = x = x = w = w 3 = 5 9 x 3 = x = w = 8 9 x = 0 4 w = w 4 = x 4 = x = w = w 3 = x 3 = x = w = w 5 = x 5 = x = w = w 4 = x 4 = x = w 3 = 8 5 x 3 = 0 Bei f C n ([a, b]) und Verwendung von n Stützstellen beträgt der Exaktheitsgrad n und es existiert ein ξ (a, b), so dass b a f(x) dx i= w i f(x i ) = b (n)! f (n) (ξ) a p n(x) dx gilt. Wenden wir die Gauß-Formel auf Teilintervalle an und summieren die Resultate, so gehört der globale Diskretisierungsfehler zu O(h n ) (Konsistenzordnung n). Beispiel Vergleich der Fehler zusammengesetzter Gauß-Legendre-Formeln, mit verschiedener Teil-Intervalllängen h des Intervalls [0, ] und n Stützstellen auf jedem Teilintervall, bei der Berechnung von I = 0 e t dt = e.

35 TH Nürnberg 35 h n = n = n = 3 n = 4 Ordnung Ordnung 4 Ordnung 6 Ordnung e e e e e e e e e e e e e e e e e e e e e e e e 06 3

36 TH Nürnberg 36 Die Gauß-Lobatto-Formeln Hierbei sind zwei Stütztellen durch die Randpunkte des Intervalls vorgegeben. Für n + Stützstellen sind die inneren Stützstellen die Nullstellen von M n+ (x) = (x )p n(x), wobei p n die erste Ableitung des Legendre-Polynoms p n, mit p n (x) = d n n n! dx n (x ) n, n N 0, ist. Der Exaktheitsgrad des Verfahrens ist (n + ) 3 = n. Beispiele (i) Sei n =. Dann erhalten wir für das Intervall [, ] Q = f( ) + f() und für [0, ] Q = (f(0) + f()), was der Trapezregel entspricht. (ii) Sei n =, x = und x 3 =. Die Bestimmungsgleichungen für w, w, w 3 und x lauten x 3 dx = 0 = w + w x 3 + w 3 x dx = 3 = w + w x + w 3 x dx = 0 = w + w x + w 3 dx = = w + w + w 3. Demnach gilt w = w 3 = 3, w = 4 3 und x = 0. Der Exaktheitsgrad ist 3. Für das Intervall [, ] gilt Q = (f( ) + 4f(0) + f()) 3

37 TH Nürnberg 37 und für [0, ] Q = 6 (f(0) + 4f( ) + f()), was der Simpson-Regel entspricht. (iii) Für n = 3 erhalten wir x =, x = 5, x 3 = 5, x 4 =, w = w 4 = 6, w = w 3 = 5 6. Der Exaktheitsgrad ist 5. Für das Intervall [, ] gilt Q = (f( ) + 5f( ) + 5f( ) + f()) und für [0, ] Q = (f(0) + 5f( 5 ) + 5f( + 5 ) + f()), Wenden wir das Gauß-Lobatto-Verfahren auf Teilintervalle an, so erhalten wir wieder summierte Formeln.

38 TH Nürnberg Adaptive Integration: Fehlerschätzung und Schrittweitensteuerung Geben wir eine Fehlertoleranz ɛ mit ɛ max(e abs, e rel Q(h) ) vor, wobei e abs eine obere Schranke für den absoluten Fehler und e rel eine solche für den relativen Fehler bezeichnet, so lässt sich der absolute Fehler beschränken, wenn Q(h) klein, bzw. der relative Fehler, wenn Q(h) groß ist. Ein Verfahren zur Fehlerschätzung mit unterschiedlichen Schrittweiten Die Schätzwerte eines Verfahrens werden für unterschiedliche Schrittweite verglichen. Beispiel Wird das Integral b I(f) = f(x) dx a mit der zusammengesetzten Trapezregel T (h) zur Schrittweite h und h für den absoluten globalen Diskretisierungfehler bestimmt, erhalten wir e abs (h) = I(f) T (h) = α h, mit einer Konstanten α. Außerdem folgt e abs ( h ) = I(f) T (h ) = α h 4, mit einer Konstanten α. Demnach gilt e abs (h) 4 3 (T (h ) T (h)). Entsprechend erhalten wir für ein Verfahren der Konsistenzordnung k e abs (h) = I(f) Q(h) O(h k ), e abs ( h ) = I(f) Q(h ) k e abs(h) und demnach e abs (h) k k (Q(h ) Q(h)).

39 TH Nürnberg 39 Beispiel Vergleich der geschätzen Fehler bei der Berechnung von I = e t dt = e. 0 h T (h) absoluter Fehler geschätzter Fehler e e e e e e e e e e e e e e Ein Verfahren zur Fehlerschätzung für unterschiedliche Approximationsmethoden Beispiel Sei f C 4 ([a, b]). Wird das Integral I(f) = b a f(x) dx mit der einfachen Trapezregel T ( Stütztellen) und der einfachen Simpson-Regel S (3 Stützstellen) bestimmt, dann erhalten wir I(f) T = (b a)3 f (ξ ) und I(f) S = 880 (b a)5 f (4) (ξ ).

40 TH Nürnberg 40 Demnach gilt für b a S T (b a)3 f (ξ ) = I(f) T und S T lässt sich als Fehlerschätzung für die Trapezregel verwenden. Schrittweitensteuerung Hierbei wird das Integrationsintervall in Teilintervalle unterteilt und die Unterteilung dort verfeinert, wo der Integrationsfehler am größten ist. Beispiele: MATLAB-Routinen quad für die adaptive Simpson-Regel und quadl für die adaptive Gauß-Lobatto-Regel

41 TH Nürnberg 4. Anwendung einer Extrapolation auf Integrationsverfahren Beispiel Wird das Integral I(f) = b a f(x) dx mit der zusammengesetzten Trapezregel T (h) bestimmt, so gilt e(h) = T (h) I(f) = c h + c h c m h m + O(h m+ ). Bei der Richardson-Extrapolation wird in jedem Schritt die Ordnung des Verfahrens um erhöht. Damit erhalten wir T (h) = I(f) + c h + c h c m h m +..., T ( h ) = I(f) + c ( h ) + c ( h ) c m ( h )m +... und die Approximation T := 3 (4T (h ) T (h)) = I(f) + 3 ( 4 )c h ( 6 )c 3h ist von der Ordnung 4. Allgemeiner können wir folgendermaßen vorgehen: Seien Q := Q(h ) und Q := Q(h ) Quadraturformeln der Konsistenzordnung k, d. h. e i = I(f) Q(h i ) = α h k i, i =,, mit Konstanten α i. Wir nehmen an, dass α α und schreiben für diese Konstanten α. Demnach gilt e e = Q Q α(h k h k ) und folglich erhalten wir mit I(f) = Q + e Q + αh k einen neuen Schätzwert für I(f). h k h k Q Q h k h k

42 TH Nürnberg 4 Q(h) Q(h ) Q(h ) Q(0) 0 h h h Abbildung. Anwendung einer Extrapolation Gehen wir davon aus, dass Q(h) = a + bh k gilt, so lässt sich, mit lim Q(h) = I(f) h 0 wieder obige Näherungsformel herleiten. Das Romberg-Verfahren Sei h 0 := b a n 0, h := h 0 n,..., h m := h 0 n m, mit n i N und 0 < n 0 < n <... < n m. Bestimmen wir die Trapezsummen T i0 := T (h i ), i = 0,,..., m, und dasjenige Polynom T mm höchstens m-ten Grades in h, für welches T mm (h i ) = T (h i ), i = 0,,..., m, gilt, so wird der Wert T mm (0) das Integral I(f) in der Regel gut approximieren.

43 TH Nürnberg 43 Mit Hilfe des Algorithmus von Neville-Aitken lässt sich T mm (0) folgendermaßen bestimmen: (i) Sei T ik (h) das Polynom vom Grad k in h mit T ik (h ν ) = T (h ν ), ν = i k, i k +,..., i. (ii) Für die extrapolierten Werte T i,k := T ik (0) gilt T i,k = T i,k + T i,k T i,k ( h i k h i ), k i m. Beispiel Berechnung von 0 e t dt = e. i h i T i,0 T i, T i, T i, i h i F ehler i,0 F ehler i, F ehler i, F ehler i,3.4086e e e e e e e e e e 00

44 TH Nürnberg 44.3 Übungsaufgaben Aufgabe a) Die Mittelpunktregel integriert konstante Polynome exakt. Zeigen Sie, dass auch Polynome vom Grad exakt integriert werden, indem Sie die Quadraturformel und das Integral für b a vergleichen. f(x) dx f(x) = x (a + b) b) Die Simpsonregel integriert Polynome vom Grad exakt. Zeigen Sie, dass auch Polynome vom Grad 3 exakt integriert werden, indem Sie die Quadraturformel und das Integral für b a f(x) dx vergleichen. f(x) = (x (a + b))3 Aufgabe Geben Sie eine Herleitung für den Näherungswert V a, mit V a = (d + D )πh, für das Volumen eines kreisförmigen Fasses an. Dabei bezeichnet h den Abstand der Böden, D den Durchmesser in halber Höhe und d den Durchmesser der Böden.

45 TH Nürnberg 45 Aufgabe 3 Es soll e x dx bis auf einen absoluten Fehler von maximal 0 5 mit der summierten Trapezregel berechnet werden. Bestimmen Sie eine geeignete Schrittweite h und berechnen Sie den Wert des Integrals nach der summierten Trapezregel. Aufgabe 4 Schätzen Sie den Fehler der summierten mittleren Rechteckregel ab, wenn Sie das Intervall in in N Teilintervalle der Länge h unterteilen. Aufgabe 5 Berechnen Sie 4 x dx für h = 0.5 mit der summierten Mittelpunktregel und der summierten Trapezregel und geben Sie eine Fehlerabschätzung an. Vergleichen Sie das Resultat mit dem tatsächlichen Fehler. Was lässt sich feststellen? Aufgabe 6 Das Integral I = cos t t dt 0 soll berechnet werden. Benutzen die summierte Mittelpunktregel und vergleichen Sie die Ergebnisse, indem Sie zum einen das Integral direkt berechnen und zum anderen das Integral I = bestimmen. 0 ( cos t t t + ) dt

46 TH Nürnberg 46 Aufgabe 7 Vergleichen Sie die Verfahren von Gauß-Lobatto und Gauß-Legendre am Beispiel des Integrals 0 sin(πx) dx für 3 Stützstellen pro (Teil-)Intervall. Unterteilen Sie hierzu das Intervall in ein und zwei Teilintervalle. Aufgabe 8 Es gilt und I = I = 0 π 4 + x = π x cos x dx = + π. 0 Vergleichen Sie die Quadraturformeln nach Newton-Cotes, Gauss-Legendre und Gauss-Lobatto für Integrale mit zwei, drei und vier Stützstellen. Was lässt sich über den jeweiligen Fehler aussagen? Aufgabe 9 Gesucht ist eine Integrationsformel, die mit einer möglichst geringen Anzahl von Stützstellen ein Polynom fünften Grades exakt integriert. Benutzen Sie diese Formel und berechnen Sie damit I = 0 (x 6 x3 + 0 x5 ) dx. Aufgabe 0 Es soll 4 x dx mit der Gauß-Legendre-Formel mit zwei Stützstellen berechnet und der Fehler abgeschätzt werden.

47 TH Nürnberg 47 Aufgabe Berechnen Sie x + dx exakt und numerisch. Benutzen Sie die Trapezregel, Simpsonregel und Gauß-Legendre-Formel (3 Stützstellen). Vergleichen Sie den Fehler und die Anzahl der Funktionsauswertungen. Aufgabe Berechnen Sie 3 0 (e x + sin 3 (x)) dx. Benutzen Sie dazu die summierte Simpsonregel mit h = Geben Sie eine Fehlerabschätzung an und wählen Sie die Schrittweiten so, dass der Fehler kleiner als 0.0 bzw. 0 5 ist. Aufgabe 3 Berechnen Sie das Integral x + dx nach dem Romberg-Verfahren. Dabei sei h = b a. Führen Sie dazu 4 Schritte durch. Berechnen Sie die Fehlerwerte und diskutieren Sie diese. Aufgabe 4 Berechnen Sie 0 e t dt mit Hilfe der Gauß-Legendre-Formeln für und 3 Stützstellen und den Gauß-Lobatto-Formeln für, 3 und 4 Stützstellen. Vergleichen Sie die Fehler.

48 TH Nürnberg 48 Aufgabe 5 Berechnen Sie 0 e t dt mit den zusammengesetzten Gauß-Legendre-Formeln ( Stützstellen) mit Teilintervallen der Länge h i, wobei h i = ( )i, i = 0,,, und diskutieren Sie den Fehler. Aufgabe 6 Es soll 4 x dx näherungsweise mit der summierten Trapezregel und Extrapolation bestimmt werden, wobei von den Schrittweiten h i = 4 i, i = 0,,, 3, ausgegangen werden soll.

49 TH Nürnberg 49 3 Anfangswertprobleme für gewöhnliche Differentialgleichungen 3. Reduktion der Ordnung Sei Ω R R n und f : Ω R n, (x, y) f(x, y) eine stetige Funktion. Dann heißt y = f(x, y) ein System von n Differentialgleichungen erster Ordnung, und für n = eine Differentialgleichung erster Ordnung. Methode der Reduktion der Ordnung Eine Differentialgleichung n-ter Ordnung y (n) = f(x, y, y,..., y (n ) ) lässt sich mittels y 0 := y y := y... y n := y n y n := f(x, y 0, y,..., y n ) auf ein System. Ordnung abbilden.

50 TH Nürnberg Einschrittverfahren mit Schrittweitensteuerung Das Anfangswertproblem für y C ([a, b]) mit y (x) = f(x, y(x)) und y(a) = y 0 lässt sich als schreiben. y(x) = y 0 + x a f(t, y(t)) dt Sei x 0 := a. Gesucht ist eine gute Näherungslösung für y(x) an den Stellen x i+ = x i + h für i = 0,,,... Sei φ(x, y, h) eine noch zu bestimmende Näherungsfunktion. η i seien Näherungswerte für die Größen y i := y(x i ). Dann setzen wir η 0 := y 0 und η i+ := η i + hφ(x i, η i, h) Sei a, b R. Unter F ([a, b]) verstehen wir die Menge jener Funktionen f : [a, b] R R, deren partielle Ableitungen erster Ordnung existieren, stetig und beschränkt sind. Diskretisierungsfehler Es bezeichnen y(x + h) y(x) für h 0 (x, y, h) := h f(x, y) für h = 0 Differenzenquotienten hinsichtlich der exakten Lösung y(x) und entsprechend η Differenzenquotienten hinsichtlich der Näherungslösung η(x). Der lokale Diskretisierungsfehler ist durch erklärt. τ(x, y, h) := η (x, y, h) (x, y, h)

51 TH Nürnberg 5 Da und somit lim τ(x, y, h) = 0, für alle x [a, b], y R, f F ([a, b]), h 0 lim φ(x, y, h) = f(x, y) h 0 gilt, wird das Verfahren als konsistent bezeichnet. Gilt τ(x, y, h) = O(h p ), so sprechen wir von einem Verfahren der Ordnung p. Der globale Diskretisierungsfehler ist durch erklärt. Sei e(x, h) := η(x, h) y(x) Gilt h n := x x 0 n. lim e(x, h n) = 0, für alle x [a, b], f F ([a, b]), h 0 so nennen wir ein Einschrittverfahren konvergent. Ist p > 0, so ist das Verfahren konvergent und es gilt e(x, h n ) = O(h p n). Demnach stimmt die Ordnung des globalen Diskretisierungsfehler mit dem lokalen Diskretisierungsfehler überein.

52 TH Nürnberg Die Verfahren von Euler-Cauchy und Heun Ist U x R eine Umgebung von x mit x + h U x und y C p (U x ), so gilt Mit erhalten wir y(x + h) = y(x) + hy (x) + h y (x) hp p! y(p) (x + ϑh), 0 < ϑ <. y = f(x, y(x)) y (x) = d dt f(t, y(t)) t=x = x f(t, y(t)) t=x + y f(t, y(t))y (t) t=x und demnach (x, y, h) = f(x, y) + h ( f(x, y) + x ) f(x, y) f(x, y) +... y a) Methode von Euler-Cauchy Leonhard Euler ( ), Augustin-Louis Cauchy ( ) Hier wird φ(x, y, h) = f(x, y) gesetzt. Es handelt sich um ein Verfahren. Ordnung, da τ(x, y, h) = (x, y, h) φ(x, y, h) = h ( f(x, y) + x = O(h). ) f(x, y) f(x, y) +... y

53 TH Nürnberg 53 b) Methode von Karl Heun (900) Karl Heun (859-99) Hier wird φ(x, y, h) = (f(x, y) + f(x + h, y + hf(x, y))) gesetzt. Es handelt sich um ein Verfahren. Ordnung (O(h )). c) Modifiziertes Euler-Verfahren (960) Lothar Collatz (90-990) Hier wird φ(x, y, h) = f(x + h, y + h f(x, y))) gesetzt. Es handelt sich um ein Verfahren. Ordnung. Beispiele zum Euler-Cauchy-Verfahren (i) Sei y = xy mit y(0) = Die exakte Lösung lautet y(x) = exp( x 4 ). Selbstverständlich können wir auch andere Anfangsbedingungen wählen, ohne die Lösung zu ändern. So ergibt beispielsweise die Anfangsbedingung y( 3 ) = exp( 9 6 ) das gleiche Ergebnis.

54 TH Nürnberg 54 y g(x)=exp( x 4 ) x Abbildung 3. Der Graph von exp( x 4 ) Wählen wir x 0 =.5, so erhalten wir folgende Approximationswerte η und η dieses Polygonzug-Verfahrens: y η g(x)=exp( x 4 ) η h f (x, η ) h f (x 0, η 0 )=h g ' (x 0 ) h η x 0 x x x x Abbildung 3. Das Euler-Cauchy-Verfahren (ii) Die Geschwindigkeit der Bewegung eines geradlinig bewegten Objekts unter dem Einfluss einer konstanten Beschleunigungskraft und einer Reibungskraft F r v wird beschrieben durch dv dt = α βv.

55 TH Nürnberg 55 Als exakte Lösung erhalten wir α v(t) = β tanh( βα t). Für Näherungslösungen mit dem Euler-Verfahren sei auf [9] verwiesen. Beispiel zum Verfahren von Heun Für das Anfangswertwertproblem der Schwingungsgleichung mit periodischer Anregung, y + ω y = A sin(ωt) mit y(0) = y (0) = 0, ist in [9] ein Programmierbeispiel angegeben.

56 TH Nürnberg 56 Mit A =, ω = ω 0 = erhalten wir y(t) Abbildung 3.3 Oszillation mit periodischer Anregung t In Hinblick auf den Rechenaufwand einfache Verfahren erhalten wir mit dem Ansatz φ(x, y, h) := a f(x, y) + a f(x + p h, y + p hf(x, y)). Wir erhalten die Taylorentwicklung φ(x, y, h) = (a + a )f(x, y) + a h So ergeben sich die Bedingungen ( p f(x, y) x ) f(x, y) + p f(x, y) + O(h ). y a + a =, a p =, a p = für Verfahren. Ordnung. Im Falle a = a =, p = p = wählen wir das Verfahren von Heun, im Falle a = 0, a =, p = p = das modifizierte Euler-Verfahren.

57 TH Nürnberg Explizite Runge-Kutta-Verfahren Methode von Runge-Kutta (895) (Carl Runge (856-97), Martin Wilhelm Kutta ( )) Hier wird mit gesetzt. φ(x, y, h) = 6 (k + k + k 3 + k 4 ) k := f(x, y) k := f(x + h, y + hk ) k 3 := f(x + h, y + hk ) k 4 := f(x + h, y + hk 3 ) Es handelt sich um ein Verfahren 4. Ordnung. Das Verfahren von Heun und das Verfahren von Runge-Kutta entsprechen bekannten Methoden zur numerischen Integration. So lässt sich dem Heun-Verfahren die Trapezregel und dem Runge-Kutta-Verfahren die Simpson-Regel zuordnen. Beispiel y = xy mit y( 3 ) = exp( 9 6 ) Die exakte Lösung lautet y(x) = c exp( x 4 ). Mit x 0 =.5, y 0 = y(x 0 ) = exp( 9 ) und h = erhalten wir 6 i x i exakt Euler-Cauchy Heun Runge-Kutta

58 TH Nürnberg 58 Verfeinern wir die Schrittweite so, dass h =, dann erhalten wir 0 i x i exakt Euler-Cauchy Heun Runge-Kutta

59 TH Nürnberg 59 Unter einem expliziten Runge-Kutta-Verfahren verstehen wir ein Verfahren mit φ(x, y, h) := s b l k l. l= Hierzu zählen beispielsweise Verfahren mit s = und k = f(x, y), k = f(x + p h, y + p hk ). Notation der expliziten Runge-Kutta-Verfahren Dabei gilt Schema k = f(x, y) k = f(x + c h, y + ha k ) k 3 = f(x + c 3 h, y + h(a 3 k + a 3 k )). =. s k s = f(x + c s h, y + h a sl k l ) η i+ = η i + h s b l k l. l= b + b b s =. 0 c a c 3 a 3 a 3... c s a s a s a s,s b b... b s b s l=

60 TH Nürnberg 60 Beispiele (i) Euler-Verfahren 0 (ii) modifiziertes Euler-Verfahren 0 0 (iii) Heun-Verfahren 0 (iv) 3-stufiges Verfahren 3. Ordnung (v) 3-stufiges Verfahren 3. Ordnung (vi) 4-stufiges Verfahren 4. Ordnung

61 TH Nürnberg 6 (vii) klassisches Runge-Kutta-Verfahren (viii) Blutcher-Verfahren (5. Ordnung, 6-stufig) Beispiel: Dreikörperproblem Die Beschreibung des Problems, die Bewegung dreier Körper unter dem Einfluss der Schwerkraft zu bestimmen, und ein entsprechendes Scilab-Programm lassen sich dem Übungsblatt unter ftp://ftp.hof-university.de/lehre/rhonke/alt/ws0/dynsimmechsys/uebungen/uebungen 0.pdf entnehmen. Als Anfangsbedingungen der Orte der drei Körper zur Zeit t = 0 wurden (0., 0, 0), ( 0., 0, 0), (, 0.4, 0.) gewählt. Zusätzlich sind die Geschwindigkeiten der Körper zur Zeit t = 0 vorgegeben.

62 TH Nürnberg 6 Abbildung 3.4 Ortskoordinaten der Bewegung dreier Objekte unter dem Einfluss der Schwerkraft 3..3 Numerische Stabilität Eine Differentialgleichung wird als sachgemäß gestellt bezeichnet, wenn die Lösung eindeutig bestimmt ist und stetig von den Daten abhängt. Beispiel zur inhärenten Instabilität Das Anfangswertproblem y = y 3e x mit y(0) = y 0 hat die Lösung y(x) = e x + (y 0 )e x. Demnach gilt lim y(x) = x falls y 0 < 0 falls y 0 = falls y 0 >. Somit können kleine Rundungsfehler bei y 0 = zu großen Abweichungen bei der Bestimmung von y führen. Ist y eine Lösung von y (x) = f(x, y(x)),

63 TH Nürnberg 63 mit x R +, so soll, für ɛ, auch ỹ(x) := y(x) + ɛ(x) eine Lösung dieser Differentialgleichung sein. Demnach soll gelten und somit ỹ (x) = f(x, ỹ(x)) ɛ (x) = ỹ (x) y (x) = f(x, y + ɛ) f(x, y) = ɛ f y (x, y) + ɛ f y Ist ɛ hinreichend klein, dann gilt ɛ (x) ɛ f y und ɛ stimmt näherungsweise mit ɛ(0) exp( f y x) überein. Ist f y gilt. lim ɛ(x) = 0 x < 0, so ist die Stabiltät gewährleistet, da dann Amerkung: Gilt für das Euler-Cauchy-Verfahren + h f y <, so ist das Verfahren numerisch stabil.

64 TH Nürnberg Fehlerschätzung und Schrittweitensteuerung Beispiel: Fehlerschätzung für das Euler-Verfahren Sei y die exakte Lösung des Anfangswertproblems und Es gilt y = f(x, y) mit y(x i ) = η i η i+ = η i + hf(x i, η i ). y(x) = y(x) + hf(x, y) + h y (x) + O(h 3 ) und demnach ɛ i+ (h) := y(x i+ ) η i+ ch mit c := y (x i ). Seien η h und η h die numerischen Lösungen bei Schrittweite h bzw. h x = x i+. Dann gilt jeweils an der Stelle η h y(x i + h) ch und η h Somit erhalten wir y(x i + h) c( h ). ɛ i+ (h) ch = (η h η h ). Für ein Verfahren der Ordnung p erhalten wir ɛ i+ (h) := y(x i+ ) η i+ ch p+ = p p (η η h h ).

65 TH Nürnberg Systeme von Differentialgleichungen erster Ordnung und Differentialgleichungen höherer Ordnung Eine Differentialgleichung. Ordnung y = f(x, y, y ) lässt sich mittels y 0 = y y := f(x, y 0, y ) auf ein System. Ordnung abbilden. Wir schreiben ( ) ( ) y y = 0 y y =. f(x, y 0, y ) Beispiel: Oszillation einer Radaufhängung bei kurzfristiger Anregung y A Auto d A Dämpfer k A y R Rad k R u(x) Straße Abbildung 3.5 Modell für die Schwingungen einer Radaufhängung

66 TH Nürnberg 66 Die Differentialgleichungen m A y A = k A (y A y R ) d A (y A y R), m R y R = k A (y A y R ) + d A (y A y R) + k R (u y R ) schreiben wir um in y A = z y R = z y A = z 3 y R = z 4 z 3 = m A ( k A (z z ) d A (z 3 z 4 )) z 4 = m R (k A (z z ) + d A (z 3 z 4 ) + k R (u z )), und für u(x) nehmen wir an, dass u(x) = Somit gilt wobei d dx z z z 3 z 4 { 0.0 sin( π x ) 0. falls 0 < x < falls x > 0.. = f(x, z, z, z 3, z 4 ), f(x, z, z, z 3, z 4 ) = z 3 z 4 m A ( k A (z z ) d A (z 3 z 4 )) m R (k A (z z ) + d A (z 3 z 4 ) + k R (u z )).

67 TH Nürnberg 67 Anmerkung Sind λ k, k N, Eigenwerte der Jacobi-Matrix ( ) fi, z j ij der hinsichtlich z j linearen Funktion f, so muss für ein numerisch stabiles Euler-Verfahren und damit gelten. + λ k h < h < Re(λ k) λ k Beispiel: Das Runge-Kutta-Verfahren für eine Differentialgleichung. Ordnung Die Iterationsfolge (η i ) mit η 0 := (y 0 (x 0 ), y (x 0 )) und η i+ := η i + hφ(x i, η i ; h) ist Teilmenge des R. Auch die Funktion φ(x, y; h) = 6 (k + k + k 3 + k 4 ) und k := f(x, y) k := f(x + h, y + hk ) k 3 := f(x + h, y + hk ) k 4 := f(x + h, y + hk 3 ) sind Elemente des R. Schreiben wir y = (y 0, y ), so lassen sich die Größen k i folgendermaßen ausdrücken: ( ) ( ) k,0 y k = = k, f(x, y 0, y ) ( ) ( k,0 y k = = + hk ), k, f(x + h, y 0 + hk,0, y + hk,) ( ) ( k3,0 y k 3 = = + hk ), k 3, f(x + h, y 0 + hk,0, y + hk,) ( ) ( ) k4,0 y k 4 = = + hk 3,. f(x + h, y 0 + hk 3,0, y + hk 3, ) k 4,

68 TH Nürnberg 68 Linearisierung nicht-linearer Differentialgleichungssysteme Beispiel y (x) = y (x) =: f (y, y ), y = a y (x) + a sin(y (x)) =: f (y, y ). Die Linearisierung in der Umgebung von (ỹ, ỹ ) ergibt und somit f (y, y ) = y, f (y, y ) f (ỹ, ỹ ) + f y (y ỹ ) + f y (y ỹ ), d dx ( y y a sin(ỹ ) + a cos(ỹ ) (y ỹ ) + a y ) ( ) ( ) ( ) 0 y 0 = +. a cos(ỹ ) a y a (sin(ỹ ) cos(ỹ ) ỹ )

69 TH Nürnberg MATLAB-Routinen zu Differentialgleichungen Solver Problem Verfahren ode45 nicht-steife Dgl. Runge-Kutta-Paar der Ordnung 4 und 5 Schrittweitensteuerung ode3 nicht-steife Dgl. Runge-Kutta-Paar der Ordnung und 3 Schrittweitensteuerung ode3 nicht-steife Dgl. Adams-Bashforth-Moulton variable Schrittweite ode5s steife Dgl. BDF ode3s steife Dgl. Alternative zu ode5s Einschrittverfahren ode3t mäßig steife Dgl. Trapezregel ode3tb steife Dgl. Prädiktor-Korrektor-Trapezregel. Ordnung ode5i implizite Dgl. BDF bvp4c Randwertproblem bei Dgl. Lobatto-Verfahren vgl. auch MATLAB Help

70 TH Nürnberg Übungsaufgaben Aufgabe Sei y = y + mit y(0) =. Berechnen Sie y() für h = mit dem Euler- und dem Runge-Kutta-Verfahren. Aufgabe Gegeben ist das Anfangswertproblem y = 00 y mit y(0) =. (i) Begründen Sie, dass für die exakte Lösung gilt. lim y(x) = 0 x (ii) Formulieren Sie das Euler-Verfahren mit Schrittweite h. (iii) Welche Bedingung muss h erfüllen, damit auch für die durch das Euler-Verfahren erzeugten Näherungen y i gilt. lim y i = 0 i Aufgabe 3 Sei λ eine negative reelle Zahl und y = λ y mit y(0) = y 0. Geben Sie das einfache explizite Euler-Cauchy-Verfahren an und zeigen Sie, dass y i = C i, mit einer Konstanten C = C(λ, h), gilt. Wie muss die Schrittweite h gewählt werden, damit dieses Problem numerisch stabil gelöst werden kann?

71 TH Nürnberg 7 Aufgabe 4 Berechnen Sie mit dem klassischen Runge-Kutta-Verfahren einen Näherungswert für y(0.), wobei y(x) die Lösung des Anfangswertproblems y (x) = + y(x) e x mit y(0) = ist. Verwenden Sie die Schrittweiten h = 0. und h = 0. und geben Sie eine Fehlerschätzung an. Aufgabe 5 Wenden Sie das Euler-Verfahren auf das Anfangswertproblem y (x) = 5 mit y(0) = mit den Schrittweiten h = 0.5 und h = 0.5 an, um einen Näherungswert für y() zu bestimmen. Vergleichen Sie diese Näherung mit der exakten Lösung und erklären Sie Ihre Beobachtung. Aufgabe 6 Sei f : R R eine stetige Funktion. Gegeben ist das Anfangswertproblem y (x) = f(x) mit y(a) = 0. Wie lautet die exakte Lösung von y(b) für b > a? Formulieren Sie die Mittelpunktregel und das Verfahren von Heun. Aufgabe 7 Die Mittelpunktregel soll benutzt werden, um ein Anfangswertproblem zu lösen. Dabei soll der lokale Fehler mittels eines Verfahrens 3. Ordnung geschätzt werden. Aufgabe 8 Gegeben ist das Anfangswertproblem y + ω sin y = 0, y(0) = π, y (0) = 0, wobei ω = 30 s. Berechnen Sie y(0.) für h = 0. mit dem dem Runge-Kutta-Verfahren.

72 TH Nürnberg 7 Aufgabe 9 Gegeben ist das Anfangswertproblem y (x) = Ay(x) mit A = ( ) 0 0 und y(0) = ( ) 5. 5 Berechnen Sie die exakte Lösung und y(4π) mit h = impliziten Euler-Verfahren. 00 4π mit dem expliziten und dem Aufgabe 0 Gegeben ist das Anfangswertproblem y (x) = y(x) cos x mit y(0) =. Berechnen Sie y() näherungsweise mit der Schrittweite h =. Benutzen Sie dazu ein Prädiktor- Korrektorverfahren, wobei für den Prädiktor das Euler-Verfahren und für den Korrektor ein Verfahren. Ordnung verwendet werden soll. Wie oft sollte der Korrektorschritt ausgeführt werden?

73 TH Nürnberg 73 Literatur [] I. N. Bronstein, K. A. Semendjajew, Taschenbuch der Mathematik, B. G. Teubner, Nauka [] O. Forster, Analysis,, Vieweg-Verlag [3] H. Heuser, Gewöhnliche Differentialgleichungen, B. G. Teubner [4] C. Rademacher, Vorlesungsskript Master Maschinenbau, Mathematische Methoden und Numerische Simulation im Maschinenbau, TH Nürnberg, 0 [5] F. Reinhardt, H. Soeder, dtv-atlas zur Mathematik, Deutscher Taschenbuch Verlag [6] Th. Sandner, Vorlesungsskript Numerische Lösungsverfahren im Maschinenbau, TH Nürnberg, 008 [7] SMART, Mathematik- und Physikaufgabensammlung, Universität Bayreuth, [8] J. Stoer, R. Bulirsch, Numerische Mathematik,, Springer-Verlag [9] A. Stoffel, Materialien zur Vorlesung Programmierung numerischer Verfahren, FH Köln, 0 ( zu Scilab