Numerik I. Gewöhnliche Differentialgleichungen und Differenzenverfahren für partielle Differentialgleichungen
|
|
|
- Chantal Gehrig
- vor 5 Jahren
- Abrufe
Transkript
1 Numerik I Gewöhnliche Differentialgleichungen und Differenzenverfahren für partielle Differentialgleichungen Vorlesungsskriptum Wintersemester 08/9 R. Verfürth Fakultät für Mathematik, Ruhr-Universität Bochum
2
3 Inhaltsverzeichnis Kapitel I. Anfangswertprobleme für gewöhnliche Differentialgleichungen 5 I.. Einige theoretische Ergebnisse 6 I.. Einschrittverfahren 5 I.3. Konvergenz von Einschrittverfahren 7 I.4. Implementierung von Einschrittverfahren 9 I.5. Lineare Mehrschrittverfahren 35 I.6. Konvergenz von linearen Mehrschrittverfahren 4 I.7. Implementierung linearer Mehrschrittverfahren 50 I.8. Stabilität von Ein- und Mehrschrittverfahren 5 I.9. Algebro-Differentialgleichungen 59 Kapitel II. Randwertprobleme für gewöhnliche Differentialgleichungen 63 II.. Einige theoretische Ergebnisse 64 II.. Das Schießverfahren 67 II.3. Die Mehrzielmethode 69 II.4. Differenzenverfahren 7 Kapitel III. Differenzenverfahren für partielle Differentialgleichungen 8 III.. Beispiele partieller Differentialgleichungen 8 III.. Konvergenz von Diskretisierungsverfahren 9 III.3. Elliptische Differentialgleichungen 96 III.4. Parabolische Differentialgleichungen 09 III.5. Hyperbolische Differentialgleichungen 6 III.6. Numerische Lösung der diskreten Probleme Index 4 Literaturverzeichnis 45 3
4
5 KAPITEL I Anfangswertprobleme für gewöhnliche Differentialgleichungen In diesem Kapitel betrachten wir numerische Verfahren zur Lösung von Anfangswertproblemen für gewöhnliche Differentialgleichungen, d.h. von Problemen der Form: Finde eine differenzierbare Funktion y einer reellen Veränderlichen t mit y (t) = f(t, y(t)) und y(t 0 ) = y 0. Zuerst stellen wir in I. einige theoretische Ergebnisse für derartige Probleme bereit und zeigen unter anderem die eindeutige Lösbarkeit dieses Problems und die stetige und differenzierbare Abhängigkeit der Lösung von dem Anfangswert y 0. In den I. I.4 untersuchen wir dann Einschrittverfahren, die ausgehend von einer Näherung η i für y(t i ) eine neue Näherung η i+ für y(t i + h) berechnen. Wichtigste Vertreter dieser Verfahrensklasse sind das explizite und das implizite Euler-Verfahren, die Trapezregel und die Runge-Kutta-Verfahren. In I.3 zeigen wir, dass diese Verfahren unter geeigneten Annahmen an die Funktion f gegen die Lösung y des Anfangswertproblemes konvergieren und dass der Fehler bestimmt wird von demjenigen eines einzelnen Schrittes. In I.4 betrachten wir dann einige Aspekte zur praktischen Durchführung dieser Verfahren. In den I.5 I.7 betrachten wir lineare Mehrschrittverfahren. Bei diesen Verfahren werden zur Berechnung der Näherung η i+ für y(t i +h) mehrere alte Näherungen η i,..., η i k für y(t i ),..., y(t i kh) herangezogen. Wichtigste Vertreter dieser Verfahrensklasse sind die Adams- Bashforth-, Adams-Moulton-, Nyström- und BDF-Verfahren. Wir zeigen in I.6 die Konvergenz der Verfahren und untersuchen in I.7 Aspekte ihrer praktischen Implementierung. Die Konvergenzresultate der I.3 und I.6 sind asymptotischer Natur, d.h. sie treffen eine Aussage über das Verhalten des Fehlers im Grenzfall h 0. Tatsächlich rechnet man aber natürlich mit einer festen endlichen Schrittweite. Verfahren, die sich im Grenzfall h 0 gleich verhalten, können für endliches h völlig unterschiedliches Verhalten aufweisen. Die genaue Analyse dieses Effektes ist Gegenstand des I.8. Im abschließenden I.9 betrachten wir kurz Algebro-Differentialgleichungen, bei denen Differentialgleichungen mit algebraischen Zwangsbedingungen gekoppelt sind. Viele der in diesem und den folgenden Kapiteln vorgestellten Algorithmen sind in der Scilab-Funktionsbibliothek Numerics realisiert, 5
6 6 I. ANFANGSWERTPROBLEME die man zusammen mit einer kurzen englischen Bedienungsanleitung unter der Adresse findet. I.. Einige theoretische Ergebnisse In diesem Paragraphen stellen wir einige für die Numerik wichtige theoretische Ergebnisse über Anfangswertprobleme für gewöhnliche Differentialgleichungen zusammen. Die Ergebnisse werden in der Regel nicht bewiesen. Stattdessen verweisen wir auf [, Kapitel II] und [8, Kapitel XI]. Im Folgenden bezeichnen stets I R ein nicht leeres offenes Intervall und U R n, n N, eine nicht leere offene Menge; ist eine beliebige Norm auf R n. Definition I.. (Gewöhnliche Differentialgleichungen, Anfangswertprobleme). () Seien k N, V R kn eine nicht leere offene Menge und f : I V R n eine Funktion. Dann heißt das Problem: Finde y C k (I, R n ) mit (I..) y (k) (t) = f(t, y(t),..., y (k ) (t)) in I eine gewöhnliche Differentialgleichung k-ter Ordnung auf I. Ist speziell k =, so sprechen wir einfach von einer gewöhnlichen Differentialgleichung (gdgl). () Seien t 0 I und v 0 = (v 0,0,..., v 0,k ) V. Dann heißt (I..) zusammen mit den Bedingungen y(t 0 ) = v 0,0,..., y (k ) (t 0 ) = v 0,k ein Anfangswertproblem (AWP). (3) Eine gdgl bzw. ein AWP heißen autonom, wenn die Funktion f nicht von der Variablen t abhängt. Bemerkung I.. (Ordnungsreduktion, Autonomisierung). () Eine gdgl k-ter Ordnung, k, kann stets in eine äquivalente gdgl erster Ordnung auf R nk umformuliert werden. Um dies einzusehen, setze und z(t) = (z 0 (t),..., z k (t)) = (y(t), y (t),..., y (k ) (t)) R nk F (t, z(t)) = (z (t),..., z k (t), f(t, z 0 (t),..., z k (t))) R nk. Dann ist offensichtlich y genau dann eine Lösung von (I..), wenn z eine Lösung von z (t) = F (t, z(t)) ist. Aus diesem Grunde betrachten wir im Folgenden nur gewöhnliche Differentialgleichungen erster Ordnung.
7 I.. EINIGE THEORETISCHE ERGEBNISSE 7 () Eine gdgl kann stets in eine äquivalente autonome gdgl umformuliert werden. Um dies einzusehen, setze z(s) = (y(s), s) R n+ und F (z) = F ((y(s), s)) = (f(s, y(s)), ) R n+. Dann ist y genau dann eine Lösung von (I..), wenn z eine Lösung von z (s) = F (z(s)) ist. Beispiel I..3 (Populationsdynamik). Die Funktion y(t) beschreibe die Größe einer Population zur Zeit t > 0. Die relative zeitliche Änderung der Populationsgröße sei eine bekannte Funktion r der Zeit und der aktuellen Populationsgröße. Diese Annahmen führen auf die gdgl y (t) = r(t, y(t))y(t). Wichtige Spezialfälle sind die des unbeschränkten Wachstums und des beschränkten Wachstums r(t, y(t)) = α > 0 r(t, y(t)) = α(y y(t)) mit α > 0, y > 0. Die Zahl y spielt die Rolle einer Grenzpopulation, deren Überschreiten zum Absterben der Population führt. Beispiel I..4 (Federschwingung). Die vertikale Schwingung z(t) einer Feder mit Masse m > 0 wird nach den Newtonschen Kraftgesetzen durch die gdgl. Ordnung mz (t) = kz(t) rz (t) beschrieben. Dabei ist kz(t), k > 0, die Rückstellkraft der Feder und rz (t), r 0, die Reibungskraft. Die äquivalente gdgl. Ordnung lautet z (t) = v(t) v (t) = k m z(t) r m v(t). Dabei ist v(t) die Geschwindigkeit der Auslenkung. Wir stellen uns zunächst die Frage nach der Existenz und Eindeutigkeit von Lösungen von AWPen. Dazu benötigen wir einige Vorbereitungen. Definition I..5 (Lipschitz-Stetigkeit). Die Funktion f C(I U, R n ) heißt gleichmäßig Lipschitz-stetig auf I U bzgl. U wenn es ein L R +, die sog. Lipschitz-Konstante, gibt mit f(t, x) f(t, y) L x y
8 8 I. ANFANGSWERTPROBLEME für alle t I, x, y U. Die Funktion f heißt Lipschitz-stetig auf I U bzgl. U, wenn es zu jedem (t 0, x 0 ) I U eine Umgebung J V U((t 0, x 0 )) gibt, derart dass f auf J V gleichmäßig Lipschitzstetig ist bzgl. V. Bemerkung I..6 (Lipschitz-Stetigkeit und Differenzierbarkeit). () Ist f C(I U, R n ) bzgl. der Variablen y differenzierbar und D y f C(I U, L(R n, R n )), so ist f auf I U bzgl. U Lipschitz-stetig. () Ist f C(I U, R n ) Lipschitz-stetig auf I U bzgl. U und J K I U kompakt, so ist f auf J K gleichmäßig Lipschitz-stetig bzgl. K. (3) Ist f C (U, R n ), so ist f Lipschitz-stetig (auf U bzgl. U). Ist f C(U, R n ) Lipschitz-stetig und K U kompakt, so ist f gleichmäßig Lipschitz-stetig auf K. Satz I..7 (Lemma von Gronwall). Seien α, β, u C(I, R + ) und t 0 I mit t u(t) α(t) + β(s)u(s)ds t 0 für alle t I. Dann gilt für alle t I t u(t) α(t) + α(s)β(s)e t β(σ)dσ) s ds. t 0 Beweis. [, Lemma 6.] und [8, Satz XI..6]. Beweisidee: Betrachte t I mit t > t 0 und setze Dann folgt v(t) = t t 0 β(s)u(s)ds, γ(t) = e t t β(s)ds 0. (γv) (t) = γ (t)v(t) + γ(t)v (t) = β(t)γ(t)v(t) + γ(t)β(t)u(t) γ(t)β(t)α(t) und somit t t 0 β(s)u(s)ds = v(t) γ(t) t t t 0 α(s)β(s)γ(s)ds = α(s)β(s)e t s β(σ)dσ ds. t 0 Hieraus folgt die Behauptung für t > t 0. Der Fall t < t 0 wird analog behandelt. Satz I..8 (Satz von Picard-Lindelöf). Sei f C(I U, R n ) auf I U bzgl. U Lipschitz-stetig. Dann gibt es zu jedem (t 0, y 0 ) I U ein ε > 0, so dass das AWP y = f(t, y) auf (t 0 ε, t 0 + ε), y(t 0 ) = y 0 eine eindeutige Lösung y C ((t 0 ε, t 0 + ε), R n ) hat.
9 I.. EINIGE THEORETISCHE ERGEBNISSE 9 Beweis. [, Satz 7.4] und [8, Satz XI..7]. Beweisidee: Wähle ε 0 > 0 und R > 0 so, dass [t 0 ε 0, t 0 + ε 0 ] B(y 0, R) I U ist und f auf [t 0 ε 0, t 0 + ε 0 ] B(y 0, R) gleichmäßig Lipschitz-stetig ist bzgl. B(y 0, R). Bezeichne die Lipschitz-Konstante mit L. Sei M das Maximum von f auf [t 0 ε 0, t 0 + ε 0 ] B(y 0, R) und setze ε = min{ε 0, R }. Sei X = C([t M 0 ε, t 0 + ε], R n ) und K = B (y 0, R). Dabei bezeichnet die Maximumsnorm auf X und y 0 die konstante Funktion mit Wert y 0. Definiere die Abbildung Φ : X X durch t Φy(t) = y 0 + f(s, y(s))ds t 0 für alle t t 0 < ε. Dann ist y X genau dann ein Fixpunkt von Φ, wenn es das AWP löst. Mit Hilfe der Definition von Φ und der Lipschitz-Stetigkeit von f zeigt man, dass Φ eine Kontraktion auf K ist mit Kontraktionsrate κ = e Lε. Dabei wird X versehen mit der Norm y L = max e L t t 0 y(t). t t 0 ε Dann folgt die Behauptung aus dem Banachschen Fixpunktsatz. Bemerkung I..9 (Nicht eindeutige und nicht globale Lösbarkeit, Autonomisierung). () Auf die Lipschitz-Bedingung kann man in Satz I..8 nicht verzichten. Betrachte dazu das autonome AWP y = y, y(0) = 0. Die Funktion y ist in keiner Umgebung von 0 Lipschitz-stetig. Dieses AWP hat offensichtlich die Lösungen y(t) = 0 und y(t) = 4 t. Für beliebiges a, b R + {+ } sind weitere Lösungen gegeben durch (t + a) für t a, 4 y a,b (t) = 0 für a < t < b, (t 4 b) für b t. () Unter den Voraussetzungen von Satz I..8 kann man i.a. nur die lokale Existenz der Lösung des AWP erwarten. Betrachte z.b. das autonome AWP y = y, y(0) =. Die eindeutige Lösung lautet y(t) = t für alle t <. Sie explodiert für t. (3) Satz I..8 zeigt, dass es nicht immer ratsam ist, eine nicht autonome gdgl in die äquivalente autonome gdgl umzuformen. Für die nicht
10 0 I. ANFANGSWERTPROBLEME autonome gdgl benötigen wir nämlich nur Lipschitz-Stetigkeit bzgl. y, für die äquivalente autonome gdgl dagegen Lipschitz-Stetigkeit bzgl. y und t. Satz I..0 (Globaler Existenz- und Eindeutigkeitssatz). Sei f C(I U, R n ) auf I U bzgl. U Lipschitz-stetig. Dann existiert für jedes (t 0, y 0 ) I U genau eine nicht fortsetzbare Lösung y( ; t 0, y 0 ) C (I(t 0, y 0 ), U) des AWP (I..) y = f(t, y), y(t 0 ) = y 0. Das maximale Existenzintervall I(t 0, y 0 ) ist offen, d.h. und es gilt entweder oder I(t 0, y 0 ) = (t (t 0, y 0 ), t + (t 0, y 0 )), t = t (t 0, y 0 ) = inf I bzw. t + = t + (t 0, y 0 ) = sup I lim min { dist(y(t; t 0, y 0 ), U), y(t; t 0, y 0 ) } = 0. t t ± 0 Dabei ist dist(z, ) = + und dist(z, A) = inf{ z y : y A} für eine nicht leere abgeschlossene Menge A. Beweis. [, Satz 7.6] und [8, Satz XI..9 ]. Beweisidee: Sei (t 0, y 0 ) I U beliebig. Wegen Satz I..8 gibt es ein ε > 0, so dass (I..) eine eindeutige Lösung u auf I = [t 0 ε, t 0 +ε ] besitzt. Wegen Satz I..8 gibt es weiter ein ε > 0, so dass das AWP y = f(t, y), y(t 0 + ε ) = u(t 0 + ε ) eine eindeutige Lösung v auf I, = [t 0 + ε ε, t 0 + ε + ε ] besitzt. Wegen der Eindeutigkeit der Lösung gilt u = v auf I I,. Folglich ist u mit { u auf I u = v auf I, eine Lösung von (I..), die u echt fortsetzt. Wegen dieses Fortsetzungsargumentes ist folgende Definition sinnvoll t + =t + (t 0, y 0 ) = sup{β I : (I..) besitzt eine Lösung auf [t 0, β]}, t =t (t 0, y 0 ) = inf{β I : (I..) besitzt eine Lösung auf [β, t 0 ]}. Dann existert genau eine nicht fortsetzbare Lösung u C ((t, t + ), U) von (I..). Das maximale Existenzintervall ist offen, da wir sonst das obige Fortsetzungsargument anwenden können. Nehme nun an, dass t + < sup I und lim min { dist(u(t), U), u(t) } > 0 t t + 0
11 I.. EINIGE THEORETISCHE ERGEBNISSE ist. Dann kann man zeigen, dass es eine Folge (t n ) n N I mit lim n t n = t + und t n < t + für alle n N und Zahlen ε > 0, δ > 0 gibt, so dass für alle n N und alle s [0, min{δ, t + t n }] gilt u(t n + s) < ε und dist(u(t n + s), U) > ε. Hieraus folgt dann, dass es eine Konstante M > 0 gibt mit u(t) u(s) M t s für alle s, t [t + δ, t + ). Daher ist (u(t n)) n N eine Cauchy-Folge, wenn (t n) n N eine beliebige Folge mit t n < t + für alle n N und lim t n = t + n bezeichnet. Hieraus folgt aber, dass die maximale Lösung u von (I..) auf [t 0, t + ] fortgesetzt werden kann im Widerspruch zur Definition von t +. Ganz analog beweist man die Aussage für t. Bemerkung I.. (Maximale Trajektorien). Die Bezeichnungen und Voraussetzungen seien wie in Satz I..0. Definiere γ + (t 0, y 0 ) = { u(t; t 0, y 0 ) : t [t 0, t + (t 0, y 0 )) }, γ (t 0, y 0 ) = { u(t; t 0, y 0 ) : t (t (t 0, y 0 ), t 0 ] }. Dann gilt: () Ist γ ± beschränkt, so ist t + = sup I bzw. t = inf I oder es gilt dist(u(t; t 0, y 0 ), U) 0 für t t ± 0. D.h., die Lösung existiert entweder für alle Zeiten oder sie läuft gegen den Rand von U. () Ist γ ± in einer kompakten Menge enthalten, so ist t + = sup I bzw. t = inf I. Bemerkung I.. (Linear beschränkte Differentialgleichungen). Die Funktion f sei linear beschränkt, d.h. es gebe α, β C(I, R + ) mit f(t, y) α(t) y + β(t) für alle (t, y) I U. Dann folgt aus dem Lemma von Gronwall, Satz I..7, dass jede Lösung von y = f(t, y) beschränkt ist auf beschränkten Intervallen. Ist insbesondere U = R n, so besitzt das AWP y = f(t, y), y(t 0 ) = y 0 für alle t 0 I, y 0 R n eine eindeutige globale Lösung. Insbesondere für die Behandlung von Randwertproblemen in Kapitel II ist die stetige und differenzierbare Abhängigkeit der Lösungen von AWPen von den Anfangswerten von fundamentaler Bedeutung. Sei hierzu f C(I U, R n ) auf I U Lipschitz-stetig bzgl. U. Wegen Satz I..8 wissen wir, dass das AWP (I..) für jedes (t 0, y 0 ) I U in einer Umgebung von t 0 eine eindeutige Lösung y = y( ; t 0, y 0 ) besitzt. Wir wollen zeigen, dass y( ; t 0, y 0 ) stetig und unter zusätzlichen Voraussetzungen an f differenzierbar von y 0 abhängt. Dazu benutzen wir zunächst, dass aus dem Beweis von Satz I..8 folgt, dass es
12 I. ANFANGSWERTPROBLEME zu jedem (t 0, y 0 ) I U zwei Umgebungen J = J(t 0 ) U(t 0 ) und V = V (y 0 ) U(y 0 ) mit den folgenden Eigenschaften gibt: () f ist gleichmäßig Lipschitz-stetig auf J V bzgl. V. () Zu jedem y V besitzt das AWP y = f(t, y(t)), y(t 0 ) = y eine eindeutige Lösung y( ; t 0, y ) C (J, V ) auf J. Daher können wir durch ϕ(z) = y( ; t 0, z) eine Abbildung ϕ : V C (J, V ) definieren. Damit können wir unser Ziel wie folgt formulieren: ϕ C(V, C(J, V )) bzw. unter zusätzlichen Bedingungen an f ϕ C (V, C(J, V )). Dazu nehmen wir zur Vereinfachung an, dass J beschränkt ist. Satz I..3 (Stetige Abhängigkeit von den Anfangswerten). Die Funktion ϕ ist gleichmäßig Lipschitz-stetig auf V : ϕ(z ) ϕ(z ) C(J,V ) e Ld z z R n für alle z, z V. Dabei ist d = sup{ s t : s, t J} die Länge von J und L die Lipschitz-Konstante von f. Beweis. [, Satz 8.3] und [8, Satz XI.3.]. Beweisidee: Aus der Darstellung folgt ϕ(z)(t) = y(t; t 0, z) = z + ϕ(z )(t) ϕ(z )(t) = z z + t t und somit wegen der Lipschitz-Stetigkeit von f t 0 f(s, y(s; t 0, z))ds t 0 [f(s, y(s; t 0, z )) f(s, y(s; t 0, z ))] ds ϕ(z )(t) ϕ(z )(t) t z z + L y(s; t 0, z )) y(s; t 0, z )) ds t 0 t = z z + L ϕ(z )(s) ϕ(z )(s) ds. t 0 Damit folgt die Behauptung aus dem Lemma von Gronwall, Satz I..7. Satz I..4 (Differenzierbare Abhängigkeit von den Anfangswerten). Die Funktion f(t, y) sei zusätzlich auf J V stetig differenzierbar bzgl. der Variablen y und D y f sei Lipschitz-stetig bzgl. V. Dann ist ϕ stetig differenzierbar: (Dϕ(z)w)(t) = Z(t; t 0, z)w
13 I.. EINIGE THEORETISCHE ERGEBNISSE 3 für alle t J, z V, w R n. Dabei ist Z( ; t 0, z) C (J, R n n ) die eindeutige Lösung des linearen AWP Z = D y f(t, y(t; t 0, z))z, Z(t 0 ) = Id R n. Beweis. [, Satz 9.] und [8, Satz XI.3.]. Beweisidee: Aus der Definition von ϕ und Z und dem Hauptsatz der Differential- und Integralrechnung folgt ϕ(z )(t) ϕ(z )(t) Z(t; t 0, z )(z z ) = y(t; t 0, z ) y(t; t 0, z ) Z(t; t 0, z )(z z ) = = t t 0 [y (s; t 0, z ) y (s; t 0, z ) Z (s; t 0, z )(z z )] ds t t 0 [f(s, y(s; t 0, z )) f(s, y(s; t 0, z )) D y f(s, y(s; t 0, z ))Z(s; t 0, z )(z z )] ds. Erneute Anwendung des Hauptsatzes der Differential- und Integralrechnung ergibt f(s, y(s; t 0, z )) f(s, y(s; t 0, z )) = = 0 D y f(s, y(s; t 0, z ))Z(s; t 0, z )(z z ) + 0 [D y f(s, y(s; t 0, z ) + θ(y(s; t 0, z ) y(s; t 0, z ))) [y(s; t 0, z ) y(s; t 0, z )] D y f(s, y(s; t 0, z ))Z(s; t 0, z )(z z )] dθ D y f(s, y(s; t 0, z ) + θ(y(s; t 0, z ) y(s; t 0, z ))) 0 [y(s; t 0, z ) y(s; t 0, z ) Z(s; t 0, z )(z z )] dθ [D y f(s, y(s; t 0, z ) + θ(y(s; t 0, z ) y(s; t 0, z ))) D y f(s, y(s; t 0, z ))] Z(s; t 0, z )(z z )dθ. Aus diesen Gleichungen und der Lipschitz-Stetigkeit von D y f folgt mit dem Lemma von Gronwall, Satz I..7, lim z z 0 z z ϕ(z ) ϕ(z ) Z( ; t 0, z )(z z ) C(J,V ) = 0 und damit die Behauptung. Für die Anwendungen in Kapitel II ist es wichtig, eine Abschätzung über das Wachstum der Funktion Z aus Satz I..4 zu haben. Hierzu bezeichne L eine beliebige Matrixnorm auf R n n.
14 4 I. ANFANGSWERTPROBLEME Satz I..5 (Wachstum von Lösungen linearer Differentialgleichungen). Sei T C([a, b], R n n ) und k(t) = T (t) L. Dann gilt für die Lösung Y des AWP Y = T (t)y (t), Y (a) = I die Abschätzung { t } Y (t) I L exp k(s)ds. a Beweis. Offensichtlich gilt für alle t [a, b] Y (t) = I + Mit u(t) = Y (t) I L, folgt u(t) t a t T (s) L Y (s) L ds a T (s)y (s)ds. t a k(s)[u(s) + ]ds. Diese Abschätzung und das Lemma von Gronwall, Satz I..7, mit α(t) = t k(s)ds und β(t) = k(t) beweisen die Behauptung. a Die Sätze I..3 I..5 liefern sinnvolle Aussagen über das Kurzzeitverhalten von Lösungen des AWP (I..) bei Störungen des Anfangswertes. Für Aussagen über das Langzeitverhalten, d.h. t t 0, sind sie unbrauchbar, da ihre Abschätzungen Faktoren enthalten, die exponentiell mit t t 0 wachsen. Andererseits zeigt das Beispiel f(y) = y mit der Lösung y(t; t 0, y 0 ) = y 0 e (t t 0), dass u.u. für alle Anfangswerte y, y gilt lim y(t; t 0, y ) y(t; t 0, y ) = 0. t Derartige Aussagen über das Langzeitverhalten von Lösungen von Anfangswertproblemen sind mit den Begriffen Ljapunov-Stabilität bzw. asymptotische Stabilität verbunden. Aus Zeitgründen können wir hier auf diesen Problemkreis nicht näher eingehen und verweisen stattdessen auf [, 3, 5] und [8, XI.4]. Wir schließen diesen einführenden, theoretischen Paragraphen mit einem Regularitätssatz für Lösungen von gdglen, der mit der Kettenregel durch vollständige Induktion folgt. Aufgrund dieses Regularitätssatzes unterscheiden sich gdglen grundsätzlich von partiellen Differentialgleichungen. Satz I..6 (Regularitätssatz). Sei f C k (I U, R n ). Dann gilt für jede Lösung y der gdgl y = f(t, y) auf ihrem Definitionsbereich J die Regularitätsaussage y C k+ (J, R n ).
15 I.. EINSCHRITTVERFAHREN 5 I.. Einschrittverfahren Im Folgenden wollen wir die Lösung des AWP (I..) (S. 0) mit Lipschitz-stetigem f numerisch approximieren. Dazu betrachten wir Gitterpunkte t 0 < t <... und bezeichnen die numerische Approximation mit η i oder η(t i, h i ). Dabei bezeichnet h i = t i t i die Schrittweite. Häufig ist sie konstant, d.h., die Gitterpunkte sind äquidistant. Für gegebenes t > t 0 sind wir an der Konvergenz(-geschwindigkeit) von η(t, (t t 0 )/n) für n gegen die exakte Lösung y(t) interessiert. Dazu bezeichnet eine beliebige Norm auf R n und L die zugehörige Matrixnorm. Bevor wir eine allgemeine Definition von Einschrittverfahren geben, wollen wir drei der gebräuchlichsten Verfahren, an denen sich die prinzipiellen Strukturen besonders gut studieren lassen, aus geometrischen und analytischen Überlegungen herleiten. Angenommen wir kennen die Lösung y des AWP (I..) (S. 0) im Punkte t. Wegen y (t) = f(t, y(t)) gibt f(t, y(t)) die Steigung der Tangente an die Lösungskurve im Punkt t an. Daher sollte y(t)+hf(t, y(t)) eine passable Näherung an y(t + h) sein. Diese Überlegung führt auf: Definition I.. (Explizites Euler-Verfahren; explicit euler fs in Numerics). Das explizite Euler-Verfahren ist gegeben durch: η 0 = y 0 η i+ = η i + hf(t i, η i ) t i+ = t i + h. Genauso gut hätten wir eine Näherung η i+ für y(t + h) aus der Bedingung herleiten können, dass die Tangente durch die Lösungskurve im Punkte t i+ = t i + h durch den Punkt (t i, y i ) gehen soll, d.h. Dies führt auf: y i = η i+ hf(t i + h, η i+ ). Definition I.. (Implizites Euler-Verfahren; implicit euler fs in Numerics). Das implizite Euler-Verfahren ist gegeben durch: η 0 = y 0 η i+ = η i + hf(t i+, η i+ ) t i+ = t i + h. Im Gegensatz zu I.. muss man in I.. in jedem Schritt ein nichtlineares Gleichungssystem der Form u = z + hf(t, u) mit bekannten Größen z und t lösen. Falls f stetig differenzierbar ist, folgt aus dem Satz über implizite Funktionen, dass dieses Gleichungssystem für hinreichend kleines h eine Lösung in der Nähe von z hat. Auf die praktische Berechnung dieser Lösung gehen wir in I.4 (S. 9) ein.
16 6 I. ANFANGSWERTPROBLEME Das dritte Verfahren erhalten wir durch folgende Überlegung. Für die exakte Lösung von (I..) (S. 0) gilt (I..) y(t + h) = y(t) + t+h t f(s, y(s))ds. Das Integral in (I..) wird beim expliziten Euler-Verfahren durch t+h t f(s, y(s))ds hf(t, y(t)) approximiert und beim impliziten Euler-Verfahren durch t+h t f(s, y(s))ds hf(t + h, y(t + h)). Ebenso könnten wir es aber auch durch die Trapezregel t+h t annähern. Dies führt zu: f(s, y(s))ds h [f(t, y(t)) + f(t + h, y(t + h))] Definition I..3 (Trapezregel, Crank-Nicolson-Verfahren; Funktion crank nicolson fs in Numerics). Die Trapezregel bzw. das Verfahren von Crank-Nicolson ist gegeben durch: η 0 = y 0 η i+ = η i + h [f(t i, η i ) + f(t i+, η i+ )] t i+ = t i + h. Bei den drei vorgestellten Verfahren wird die Näherung η i+ für y(t i+ ) ausschließlich durch die letzte Näherung η i für y(t i ) bestimmt. Daher spricht man von einem Einschrittverfahren kurz ESV. Die allgemeine Definition lautet: Definition I..4 (Einschrittverfahren, Verfahrensfunktion). Ein allgemeines Einschrittverfahren kurz ESV zur Lösung des AWP (I..) (S. 0) hat die Form η 0 = y 0 η i+ = η i + hφ(t i, η i, h; f) t i+ = t i + h. Die Funktion Φ heißt die Verfahrensfunktion des ESV. Der Einfachheit halber lassen wir im Folgenden stets das Argument f bei der Verfahrensfunktion fort. Für das explizite Euler-Verfahren ist offensichtlich Φ(t, y, h) = f(t, y). Die Verfahrensfunktionen für das implizite Euler-Verfahren und die Trapezregel sind komplizierter. Aus der Definition der Verfahren und
17 I.. EINSCHRITTVERFAHREN 7 dem Satz über implizite Funktionen erhalten wir für hinreichend kleines h für das implizite Euler-Verfahren Φ(t, y, h) = [ [Id hf(t + h, )] y y ] h und für die Trapezregel [ [ Φ(t, y, h) = Id h ] f(t + h, ) [y + h ] ] h f(t, y) y, wobei g die Umkehrfunktion der Funktion g bezeichnet. An dieser Stelle sei betont, dass die Verfahrensfunktion der theoretischen Analyse der Verfahren dient. Für praktische Rechnungen arbeitet man mit den Definitionen I.. I..3. Die Verfahrensfunktion eines ESV ist gleich dem Differenzenquotienten der Näherungslösung. Für vernünftige Verfahren sollte sie den Differenzenquotienten der exakten Lösung möglichst gut approximieren. Dies führt auf: Definition I..5 (Lokaler Verfahrensfehler, Konsistenz, Ordnung). Bezeichne für x [a, b] und y R n mit z die Lösung des AWP Dann heißt die Funktion z = f(t, z(t)), z(x) = y. τ(x, y, h) = {z(x + h) y} Φ(x, y, h), h > 0, h der lokale Verfahrensfehler des ESV mit Verfahrensfunktion Φ. Das Verfahren heißt konsistent, falls gilt lim τ(x, y, h) = 0 h 0 für alle x [a, b], y R n und f C ((a, b) R n, R n ). Es hat die Ordnung p, falls gilt lim sup h p τ(x, y, h) < h 0 für alle x [a, b], y R n und f C [p] ((a, b) R n, R n ). Bemerkung I..6 (Fehler eines Schrittes und lokaler Verfahrensfehler). Setzen wir η 0 = y, ist τ(x, y, h) = h [z(x + h) η ], d.h., der lokale Verfahrensfehler ist der durch die Schrittweite dividierte Fehler eines Schrittes des ESV. Die Division durch die Schrittweite wird durch folgende heuristische Überlegung motiviert: Wir wollen ein AWP auf dem Intervall [t 0, t ] lösen und führen hierzu n Schritte des ESV mit Schrittweite h = t t 0 aus. Dann erwarten wir, dass der Fehler zur n Endzeit t das n-fache des Fehlers eines einzelnen Schrittes ist. Der
18 8 I. ANFANGSWERTPROBLEME Einzelfehler wird also mit dem Faktor n = h t t 0 verstärkt. Satz I.3. (S. 7) zeigt, dass diese heuristische Überlegung korrekt ist. Für das explizite Euler-Verfahren erhalten wir durch Taylor-Entwicklung wegen f(x, y) = z (x) τ(x, y, h) = {z(x + h) y} f(x, y) h = z (x) + hz (x) + O(h ) f(x, y) = hz (x) + O(h ). Also hat das explizite Euler-Verfahren die Ordnung. Für das implizite Euler-Verfahren und die Trapezregel bestimmen wir die Ordnung am besten durch die Analyse des Fehlers eines einzelnen Schrittes. Für das implizite Euler-Verfahren erhalten wir wegen η 0 = y = z(x) z(x + h) η = z(x + h) η 0 (η η 0 ) = = = x+h x x+h x x+h x z (t)dt hf(x + h, η ) f(t, z(t))dt hf(x + h, η ) [f(t, z(t)) f(x + h, z(x + h))] dt + h [f(x + h, z(x + h)) f(x + h, η )]. Bezeichnet L die Lipschitz-Konstante von f und K eine Schranke für D y f L, so folgt hieraus z(x + h) η Kh + hl z(x + h) η. Also ist für hinreichend kleines h z(x + h) η Kh hl. Also hat das implizite Euler-Verfahren ebenfalls die Ordnung. Für die Trapezregel erhalten wir analog z(x + h) η = z(x + h) η 0 h [f(x, η 0) + f(x + h, η )] = x+h x f(t, z(t))dt h [f(x, z(x)) + f(x + h, z(x + h))] + h [f(x + h, z(x + h)) f(x + h, η )].
19 I.. EINSCHRITTVERFAHREN 9 Bezeichnet p(t) das lineare Interpolationspolynom von f(t, z(t)) in den Punkten x und x + h, ist und daher x = h [f(x, z(x)) + f(x + h, z(x + h))] = x+h x+h x p(t)dt f(t, z(t))dt h [f(x, z(x)) + f(x + h, z(x + h))] x+h x Mh3, [f(t, z(t)) p(t)] dt wobei M eine obere Schranke für D f L ist. Hieraus folgt wie beim impliziten Euler-Verfahren z(x + h) η Also hat die Trapezregel die Ordnung. Mh3 hl. Beispiel I..7 (Schwingung). Wir führen jeweils 00 Schritte der beiden Euler-Verfahren und der Trapezregel für das AWP ( ) ( 0 y = y, y(0) = 0 0) mit h = 0.3 aus. Die exakte Lösung lautet y(t) = (cos t, sin t) mit 0 t 3. Abbildung I.. zeigt die entsprechenden Lösungskurven. Das explizite Euler-Verfahren explodiert. Dies ist eine Folge seiner fehlenden Stabilität (s. I.8). Das implizite Euler-Verfahren dagegen dämpft die Lösung zu stark. Die Trapezregel schließlich liefert eine Lösungskurve, die auf der exakten Lösungskurve, dem Kreis um den Ursprung mit Radius, liegt. Beispiel I..8 (Räuber-Beute-Modell). Wir führen jeweils 000 Schritte der Euler-Verfahren und der Trapezregel für das AWP ( ) ( ) ( ) ( ) x 4x 8xy x(0) 0.9 y =, = 0.3y + 0.6xy y(0) 0. mit h = 0.0 aus. Dieses AWP beschreibt ein Räuber-Beute-Modell. Die exakte Lösung ist eine geschlossene Kurve [8, Beispiel XI..]. Abbildung I.. zeigt die Lösungskurven der drei Verfahren. Das explizite Euler-Verfahren explodiert. Das implizite Euler-Verfahren dämpft die Lösung zu stark. Die Trapezregel dagegen liefert qualitativ gute Ergebnisse.
20 0 I. ANFANGSWERTPROBLEME steps of several single- or multi- step methods ee ie cn x_ x_ Abbildung I... Lösungskurven der beiden Euler- Verfahren und der Trapezregel für das AWP aus Beispiel I steps of several single- or multi- step methods ee ie cn.5 x_ x_ Abbildung I... Lösungskurven der beiden Euler- Verfahren und der Trapezregel für das AWP aus Beispiel I..8 Die bisher betrachteten Verfahren sind Spezialfälle einer größeren Verfahrensklasse, den sog. Runge-Kutta-Verfahren. Um diese Verfahren zu motivieren betrachten wir die beiden Euler Verfahren unter einem anderen Blickwinkel. Seien dazu ηi EE und ηi IE die mit dem expliziten und dem impliziten Euler-Verfahren berechneten Näherungen für die
21 I.. EINSCHRITTVERFAHREN Lösung des AWP (I..) (S. 0). Sei u P das lineare Polynom, das in den Punkten t i und t i+ die Werte ηi EE und ηi+ EE annimmt. Dann gilt offensichtlich η EE i = u(t i ) η EE i+ = u(t i + h) { η EE i+ ηi EE u (t i ) = h = f(t i, u(t i )). } = f(ti, η EE i ) Analog sei v P das lineare Polynom, das in den Punkten t i und t i+, die Werte ηi IE und ηi+ IE annimmt. Dann gilt offensichtlich η IE i = v(t i ) η IE i+ = v(t i + h) v (t i + h) = { } η IE h i+ ηi IE = f(ti + h, ηi+) IE = f(t i + h, v(t i + h)). Die beiden Euler-Verfahren haben also folgende allgemeine Struktur: Wähle r Punkte 0 c <... < c r, bestimme das Polynom w P r mit () w(t i ) = η i, () w (t i + c l h) = f(t i + c l h, w(t i + c l h)), l r, und setze η i+ = w(t i + h). Die Bedingung () heißt auch Kollokationsbedingung. Bei den beiden Euler-Verfahren ist r =. Beim expliziten Euler-Verfahren ist c = 0; beim impliziten Euler-Verfahren ist c =. Um aus den Bedingungen () und () das Polynom w zu bestimmen, setzen wir k i,j = w (t i + c j h), j r und bezeichnen mit λ,..., λ r die Lagrangeschen Grundpolynome zu den Knoten c,..., c r mit λ i P r und λ i (c j ) = δ ij für i, j r. Dann gilt w (t i + θh) = r k i,j λ j (θ). j=
22 I. ANFANGSWERTPROBLEME Durch Integration folgt für l r mit a lj = und mit b j = cl w(t i + c l h) = w(t i ) + h 0 λ j (θ)dθ = η i + h = η i + h 0 cl 0 w (t i + θh)dθ r cl k i,j λ j (θ)dθ j= 0 r k i,j a lj j= η i+ = w(t i + h) = w(t i ) + h = η i + h = η i + h r k i,j λ j (θ)dθ j= 0 r k i,j b j. j= 0 λ j (θ)dθ w (t i + θh)dθ Einsetzen der Darstellung von w(t i + c l h) in die Kollokationsbedingungen () liefert schließlich die äquivalenten Bedingungen k i,l = w (t i + c l h) = f(t i + c l h, w(t i + c l h)) ( ) r = f t i + c l h, η i + h k i,j a lj. Insgesamt erhalten wir somit die folgende Verfahrensvorschrift: Definition I..9 (Runge-Kutta-Verfahren). Ein r-stufiges Runge- Kutta-Verfahren ist gegeben durch: η 0 = y 0 ( k i,l = f η i+ = η i + h t i+ = t i + h t i + c l h, η i + h r b j k i,j j= j= ) r a lj k i,j, l r, mit 0 c <... < c r. Der Übersichtlichkeit halber fasst man die Zahlen c k, a lj, b k in einem j=
23 I.. EINSCHRITTVERFAHREN 3 Schema der Form c a a... a r c r a r a r... a rr b b... b r zusammen. Außerdem definiert man die r r Matrizen A und C und die r-vektoren b und e durch a... a r c 0 A =.., C =..., a r... a rr 0 c r b b =., e =.. b r Ein Runge-Kutta-Verfahren heißt: explizit, wenn A eine strikte untere Dreiecksmatrix ist, diagonal-implizit, wenn A eine untere Dreiecksmatrix mit nicht verschwindender Diagonale ist, implizit, wenn A eine allgemeine Matrix ist, linear-implizit oder stark diagonal-implizit, wenn es diagonal implizit ist und die Diagonalelemente von A alle gleich sind. Bei einem diagonal-impliziten Verfahren müssen in jedem Schritt r nichtlineare Gleichungssysteme mit n Unbekannten gelöst werden; bei einem impliziten Verfahren ist es ein nichtlineares Gleichungssystem mit rn Unbekannten pro Schritt. Eine besonders effiziente numerische Lösung der nichtlinearen Gleichungssysteme erlauben die linearimpliziten Runge-Kutta-Verfahren. Bemerkung I..0 (Alternative Darstellung, Invarianz unter Autonomisierung). () Eine äquivalente Darstellung von Runge-Kutta- Verfahren erhält man durch Einführen der Größen r η i,l = η i + h a lj k i,j Damit lautet das Verfahren η 0 = y 0 r η i,l = η i + h a lj f(t i + c j h, η i,j ), l r, η i+ = η i + h t i+ = t i + h j= j= r b j f(t i + c j h, η i,j ) j=
24 4 I. ANFANGSWERTPROBLEME Diese Darstellung ist für die Ordnungsberechnung von Vorteil. () Eine wünschenswerte Eigenschaft eines Runge-Kutta-Verfahrens ist seine Invarianz unter Autonomisierung: Das Verfahren angewandt auf das äquivalente autonome AWP sollte das gleiche Ergebnis liefern wie das Verfahren angewandt auf das ursprüngliche AWP. Wie man leicht nachrechnet ist dies der Fall, falls für alle k r gilt r Ae = Ce oder äquivalent c k = a kj. Die Verfahrensfunktion eines r-stufigen Runge-Kutta-Verfahren ist gegeben durch r (I..) Φ(t, y, h) = b j f(t + c j h, u j (h)) mit (I..3) u l (h) = y + h j= j= r a lj f(t + c j h, u j (h)), l r. j= Alle bisher betrachteten Verfahren sind Runge-Kutta-Verfahren. Dem expliziten Euler-Verfahren entspricht das Schema 0 0 r =. Dem impliziten Euler-Verfahren entspricht das Schema r =. Der Trapezregel entspricht schließlich das Schema Für r = und das Schema r =. erhalten wir das sog. modifizierte Euler-Verfahren: η 0 = y 0 η i+ = η i + hf t i+ = t i + h. ( t i + h, η i + ) hf(t i, η i )
25 I.. EINSCHRITTVERFAHREN 5 Für r = und das Schema erhalten wir das Verfahren von Heun, auch modifizierte Trapezregel genannt: η 0 = y 0 η i+ = η i + h f(t i, η i ) + h f (t i + h, η i + hf(t i, η i )) t i+ = t i + h. Das sog. klassische Runge-Kutta-Verfahren (rk fs in Numerics) ist schließlich gegeben durch das Schema r = 4. Die entsprechende Verfahrensvorschrift lautet: η 0 = y 0 η i, = η i η i, = η i + h f(t i, η i, ) ) η i,3 = η i + h (t f i + h, η i, ( η i,4 = η i + hf t i + h ), η i,3 η i+ = η i + h { ( f (t i, η i, ) + f t i + h ) 6, η i, ( +f t i + h ) }, η i,3 + f (t i + h, η i,4 ) t i+ = t i + h. Die Bestimmung der Ordnung eines Runge-Kutta-Verfahrens erfolgt durch Taylor-Entwicklung von (I..), (I..3). So folgt z. B. aus (I..), (I..3): mit u l (h) = u l + h u l + O(h ), u l = y, l r l r
26 6 I. ANFANGSWERTPROBLEME und sowie mit und r u l = a lj f(t, y), l r, j= Φ(t, y, h) = Φ 0 (t, y) + Φ (t, y)h + O(h ) r Φ 0 (t, y) = b j f(t, y) = b T ez (t) j= } r r Φ (t, y) = b j {c j f t (t, y) + f y (t, y)f(t, y) a jl j= l= = b T Cef t (t, y) + b T Aef y (t, y)f(t, y). Hieraus folgt für den lokalen Verfahrensfehler: τ(x, y, h) = ( b T e)z (x) [ ] + h z (x) b T Cef x (x, y) b T Aef y (x, y)f(x, y) + O(h ) = ( b T e)z (x) [( ) + h bt Ce f x (x, y) + + O(h ). Also hat das Verfahren die Ordnung, falls gilt b T e = und die Ordnung, falls zusätzlich gilt b T Ce = b T Ae =. ( ) ] bt Ae f y (x, y)f(x, y) Ganz analog beweist man den folgenden Satz [, Lemme 5.0, 5.]. Satz I.. (Ordnung eines Runge-Kutta-Verfahrens). Ein r-stufiges Runge-Kutta-Verfahren hat die Ordnung: b T e =, Ordnung plus b T Ce = b T Ae =.
27 I.3. KONVERGENZ VON EINSCHRITTVERFAHREN 7 Falls Ae = Ce ist, hat es die Ordnung 3 Ordnung plus b T C e = 3, bt ACe = 6, 4 Ordnung 3 plus b T C 3 e = 4, bt AC e =, bt A Ce = 4, bt CACe = 8. Aus Satz I.. folgt zusammenfassend: Korollar I.. (Ordnung einiger wichtiger Runge-Kutta-Verfahren). () Das explizite und das implizite Euler-Verfahren haben die Ordnung. () Die Trapezregel, das modifizierte Euler-Verfahren und die modifizierte Trapezregel haben die Ordnung. (3) Das klassische Runge-Kutta-Verfahren hat die Ordnung 4. I.3. Konvergenz von Einschrittverfahren In diesem Paragraphen sei stets f Lipschitz-stetig auf (a, b) R n bzgl. R n, t 0 (a, b), y 0 R n und y = y( ; t 0, y 0 ) die nicht fortsetzbare Lösung des AWP (I..) (S. 0). Wir wollen die Konvergenz eines allgemeinen ESV mit Verfahrensfunktion Φ untersuchen. Dazu bezeichnen wir für t t 0 mit η(t; h) = η i falls t = t 0 + ih die numerische Näherungslösung und mit e(t; h) = η(t; h) y(t) den globalen Diskretisierungsfehler. Der folgende Satz zeigt, dass Verfahren der Ordnung p, p > 0, konvergent sind und dass für t t 0 die Fehlerabschätzung e(t; h n ) = O(h p n) mit h n = t t 0 gilt. n Satz I.3. (Globale Fehlerbschätzung für Einschrittverfahren). Die Funktion f sei gleichmäßig Lipschitz-stetig mit Lipschitz-Konstante L. Weiter gebe es ein h 0 > 0, so dass die Verfahrensfunktion Φ des ESV für alle t [a, b], alle z R n und alle 0 < h h 0 die Ordnungsbedingung τ(t, z, h) Kh p erfüllt. Dann gilt für den globalen Diskretisierungsfehler des ESV für alle t t 0 und alle n mit h n h 0 die Abschätzung e(t; h n ) h p nk el(t t 0). L Beweis. Offensichtlich ist e(t 0 ) = 0. Für i 0 bezeichne z i die Lösung des AWP z = f(t, z(t)), z(t i ) = η i. Dann ist e(t i+ ) = η i+ y(t i+ ) η i+ z i (t i+ ) + z i (t i+ ) y(t i+ ).
28 8 I. ANFANGSWERTPROBLEME Da η i+ z i (t i+ ) = hτ(t i, η i, h) ist, folgt aus der Ordnungsbedingung Da y auch das AWP löst, folgt aus Satz I..3 (S. ) η i+ z i (t i+ ) Kh p+. x = f(t, x(t)), x(t i ) = y(t i ) z i (t i+ ) y(t i+ ) e Lh η i y(t i ) = e Lh e(t i ). Also gilt für alle i 0 e(t i+ ) e Lh e(t i ) + Kh p+. Hieraus folgt durch Induktion für alle i 0 i e(t i ) e ilh e(t 0 ) + Kh p+ e jlh = Kh p+ eilh e Lh. Wegen e Lh Lh und e ilh = e (t i t 0 )L folgt hieraus die Behauptung. Bemerkung I.3.. () Die Einschränkung der Schrittweite ist für implizite Verfahren erforderlich, da die Lösbarkeit der auftretenden nichtlinearen Probleme nur für hinreichend kleine Schrittweiten gewährleistet ist. () Die Voraussetzungen von Satz I.3. können dahin gehend abgeschwächt werden, dass die Funktion f nur Lipschitz-stetig sein muss in einem Streifen um die Lösung von (I..) (S. 0) und dass die Ordnungsbedingung für die Verfahrensfunktion Φ auch nur in einem solchen Streifen gelten muss. Der folgende Satz ist für eine effiziente Implementierung der ESV von Bedeutung. Wir verzichten hier auf den sehr technischen Beweis und verweisen stattdessen auf [5, S. 76 ff]. Satz I.3.3 (Asymptotische Fehlerentwicklung für Einschrittverfahren). Sei f C K+ ((a, b) R n, R n ) und η(t; h) eine mit einem ESV der Ordnung p K gewonnene Näherung für die Lösung y(t) des AWP (I..) (S. 0). Dann besitzt η(t; h) die asymptotische Entwicklung j=0 η(t; h) = y(t) + e p (t)h p + e p+ (t)h p e K (t)h K + E K+ (t; h)h K+ für alle t [x 0, b), h = t t 0 mit e n k (t 0 ) = 0, p k K. Die Funktionen e k, k p K, sind stetig und von h unabhängig. Die Funktion E K+ (t,.) ist für jedes t beschränkt.
29 I.4. IMPLEMENTIERUNG VON EINSCHRITTVERFAHREN 9 I.4. Implementierung von Einschrittverfahren In diesem Paragraphen befassen wir uns mit zwei Aspekten der praktischen Implementierung von ESV: dem Lösen der nichtlinearen Gleichungssysteme, der Schrittweitensteuerung. Bei impliziten ESV wie dem impliziten Euler-Verfahren oder der Trapezregel müssen in jedem Schritt ein (oder mehrere) nichtlineare Gleichungssysteme gelöst werden. Dies kann mit Hilfe des Newton- Verfahrens geschehen. Die Näherungslösung η i am Punkt t i ist dabei ein guter Startwert für das Newton-Verfahren zur Berechnung von η i+. Wegen der quadratischen Konvergenz des Newton-Verfahrens reichen in der Regel wenige Iterationen aus. Bei der praktischen Implementierung beschränkt man sich häufig sogar auf eine Newton-Iteration pro Schritt. Beim Newton-Verfahren muss in jeder Iteration eine Jacobi-Matrix berechnet und ein lineares Gleichungssystem mit N Unbekannten gelöst werden. Da dies häufig recht aufwändig ist, benutzt man in der Praxis als Alternative sog. Prädiktor-Korrektor-Verfahren. Dabei berechnet man ausgehend von η i zunächst mit einem expliziten Verfahren eine und benutzt diese dann als Startwert für eine Fixpunktiteration angewandt auf das implizite Verfahren, wobei man häufig nur einen Iterationsschritt durchführt. Damit das Gesamtverfahren die gleiche Ordnung hat wie das benutzte implizite Verfahren, sollte das explizite Verfahren die gleiche Ordnung haben wie das implizite. Dieses Vorgehen wird an folgenden zwei Beispielen deutlich. Näherung η (0) i+ Beispiel I.4. (Implizites Euler-Verfahren mit Prädiktor-Korrektor). Wir betrachten das explizite Euler-Verfahren als Prädiktor und das implizite Euler-Verfahren als Korrektor. Dies liefert oder direkt η (0) i+ = η i + hf(t i, η i ) η i+ = η i + hf(t i + h, η (0) i+ ) η i+ = η i + hf (t i + h, η i + hf(t i, η i )). Dies ist ein explizites zweistufiges Runge-Kutta-Verfahren mit dem Schema Aus Satz I.. (S. 6) folgt, dass es die Ordnung hat..
30 30 I. ANFANGSWERTPROBLEME Beispiel I.4. (Trapezregel mit Prädiktor-Korrektor). Wir nehmen wieder das explizite Euler-Verfahren als Prädiktor, aber die Trapezregel als Korrektor. Dies liefert oder direkt η (0) i+ = η i + hf(t i, η i ) η i+ = η i + h f(t i, η i ) + h f(t i + h, η (0) i+ ) η i+ = η i + h f(t i, η i ) + h f (t i + h, η i + hf(t i, η i )). Wir erhalten also die modifizierte Trapezregel, die die Ordnung hat. Wir wenden uns nun dem Problem der Schrittweitensteuerung zu. Ziel ist es, ausgehend vom Punkt t 0 in möglichst wenigen Schritten eine Näherung der Lösung y(t) im Punkt t mit einer gegebenen Genauigkeit ε zu berechnen. Typischerweise ist ε = K eps, wobei eps die Maschinengenauigkeit und K eine obere Schranke für y(t) ist. Es gibt zwei Strategien zur Schrittweitensteuerung: Vergleich verschiedener Schrittweiten, Vergleich verschiedener Verfahren. Zur Darstellung der ersten Strategie bezeichne mit η(t; h) die mit einem ESV der Ordnung p und Schrittweite h gewonnene Näherung für y(t). Dann ist unter Vernachlässigung von Termen höherer Ordnung gemäß Satz I.3.3 (S. 8) und somit e p (t) = η(t; h) = y(t) + e p (t)h p ( η t; h ) ( h = y(t) + e p (t) ) p { ( η(t; h) η t; h )}. h p ( p ) Also gilt bei Fortführen des Verfahrens mit der neuen Schrittweite H unter Vernachlässigung von Termen höherer Ordnung e(t + H; H) = η(t + H; H) y(t + H) = e p (t + H)H p = e p (t)h p = p { ( η(t; h) η t; h )} ( ) p H. h Mithin erhalten wir als optimale Schrittweite { } p H = h ( p ε ) ( ) η(t; h) η t; h. Dies führt auf Algorithmus I.4. zur Schrittweitensteuerung.
31 I.4. IMPLEMENTIERUNG VON EINSCHRITTVERFAHREN 3 Algorithmus I.4. Schrittweitensteuerung durch Halbieren; Funktionen explicit euler vs, implicit euler vs, crank nicolson vs, rk vs, sdirk vs in Numerics Gegeben: Gegeben t 0, y 0, Startschrittweite h und Toleranz ε Gesucht: Neue Werte t 0, y 0 ( und h für nächsten Zeitschritt t 0 + h; h ). : Berechne η(t 0 + h; h), η { : H h ( p ε ) η(t0 + h; h) η ( t 0 + h; h 3: if H h then 4 4: h H 5: Gehe zu zurück. 6: end if 7: t 0 t 0 + h, y 0 η ( t 0 + h; h ), h H ) } p Bei der Durchführung von Algorithmus I.4. muss man im Normalfall drei Schritte des ESV pro Iteration durchführen: einen mit Schrittweite h und zwei mit Schrittweite h. Aus Satz I.3.3 (S. 8) folgt außerdem, dass { ( p η t p 0 + h; h ) } η(t 0 + h; h) eine Näherung der Ordnung h p+ für y(t 0 +h) ist. Dies ist das einfachste Beispiel für ein Extrapolationsverfahren. Beispiel I.4.3 (Schwingung). Wir wenden die beiden Euler-Verfahren und die Trapezregel mit der Schrittweitensteuerung von Algorithmus I.4. auf das AWP aus Beispiel I..7 (S. 9) an. Alle Verfahren liefern die exakte Lösungskurve, den Kreis um den Ursprung mit Radius. Wie aus Tabelle I.4. ersichtlich ist, unterscheiden sie sich aber deutlich bei der erreichten Endzeit T, der maximalen Schrittweite h max und der Rechenzeit. Die Anfangszeit und die zu erreichende Endzeit ist jeweils 0 bzw. 3, die erste Schrittweite ist immer 0.03 und die Toleranz ist stets ε = 0 6. Beispiel I.4.4 (Räuber-Beute-Modell). Wir wenden die beiden Euler-Verfahren und die Trapezregel mit der Schrittweitensteuerung von Algorithmus I.4. auf das Räuber-Beute-Modell aus Beispiel I..8 an. Anfangs- und Endzeit sind jeweils 0 bzw. 00, die erste Schrittweite ist immer 0. und die Toleranz ist stets ε = 0 6. Alle Verfahren liefern die gleiche Lösungskurve. Die erreichten Endzeiten, benötigten Schritte, minimalen Schrittweiten und benötigten Rechenzeiten sind in Tabelle I.4. angegeben.
32 3 I. ANFANGSWERTPROBLEME Tabelle I.4.. Euler-Verfahren und Trapezregel mit Schrittweitensteuerung durch Halbieren für die Schwingungsgleichung aus Beispiel I..7; angegeben sind die erreichte Endzeit T, die Zahl der Schritte N, die maximale Schrittweite h max und die Rechenzeit in Millisekunden auf einem MacBook Pro T N h max msec expliziter Euler impliziter Euler Trapezregel Tabelle I.4.. Euler-Verfahren und Trapezregel mit Schrittweitensteuerung durch Halbieren für das Räuber- Beute-Modell aus Beispiel I..8; angegeben sind die erreichte Endzeit T, die Zahl der Schritte N, die maximale Schrittweite h max und die Rechenzeit in Millisekunden auf einem MacBook Pro T N h max msec expliziter Euler impliziter Euler Trapezregel Zur Darstellung der zweiten Strategie bezeichnen wir mit η(t; h) die mit einem Verfahren der Ordnung q, q > p, gewonnenen Näherungen. Dann ist bis auf Terme höherer Ordnung und somit η(t; h) = y(t) + e p (t)h p η(t; h) = y(t) + ẽ q (t)h q e p (t) = h p {η(t; h) η(t; h)}. Mithin ist für das Verfahren der Ordnung p die optimale Schrittweite gegeben durch { H = h ε η(t; h) η(t; h) } p. Dies führt zu Algorithmus I.4. zur Schrittweitensteuerung:
33 I.4. IMPLEMENTIERUNG VON EINSCHRITTVERFAHREN 33 Algorithmus I.4. Schrittweitensteuerung durch Ordnungsvergleich; rkf vs in Numerics Gegeben: Gegeben t 0, y 0, Startschrittweite h und Toleranz ε Gesucht: Neue Werte t 0, y 0 und h für nächsten Zeitschritt : Berechne η(t 0 + h; h), η(t 0 + h; h). { } ε p : H h. η(t 0 + h; h) η(t 0 + h; h) 3: if H h then 4: h H 5: Gehe zu zurück. 6: end if 7: t 0 t 0 + h, y 0 η (t 0 + h; h), h H Bei den Runge-Kutta-Fehlberg-Verfahren kann man die Näherung η ohne großen zusätzlichen Aufwand berechnen. Beispiel I.4.5 (Runge-Kutta-Fehlberg-Verfahren). () Das Schema beschreibt ein Runge-Kutta-Fehlberg-Verfahren (RKF) der Ordnung. Dann ist η = η hf(t 0, η 0, ) + 33 hf ( 89 hf t ) 40 h, η 0,3 ( t 0 + ) 4 h, η 0, eine Näherung der Ordnung p = und η = η hf(t 0, η 0, ) ( 053 hf t ) 40 h, η 0,3 78 hf(t 0 + h, η )
34 34 I. ANFANGSWERTPROBLEME eine Näherung der Ordnung q = 3. () Das Schema beschreibt ein Runge-Kutta-Fehlberg-Verfahren (RKF3) der Ordnung 3. Dann ist η = η hf(t 0, η 0, ) + (t 3 hf 0 + ) h, η 0, + (t 3 hf 0 + ) h, η 0,3 + 6 hf(t 0 + h, η 0,4 ) eine Näherung der Ordnung p = 3 und ) η = η hf(t 0, η 0, ) + (t 3 hf 0 + h, η 0, + (t 3 hf 0 + ) h, η 0,3 + 6 hf(t 0 + h, η ) eine Näherung der Ordnung q = 4. (3) Das Schema beschreibt ein Runge-Kutta-Fehlberg-Verfahren (RKF4) der Ordnung 4. Dann ist η = η hf(t 0, η 0, ) ( 3 hf t ) 0 h, η 0,3 + 5 ( 9 hf t ) 0 h, η 0,4 87 ( 6784 hf t ) 9 h, η 0, hf(t 0 + h, η 0,6 ) 40
35 I.5. LINEARE MEHRSCHRITTVERFAHREN 35 eine Näherung der Ordnung p = 4 und η = η hf(t 0, η 0, ) ( 6695 hf t ) 0 h, η 0, ( 640 hf t ) 0 h, η 0, ( hf t ) 9 h, η 0, hf(t 0 + h, η 0,6 ) + 40 hf(t 0 + h, η ) eine Näherung der Ordnung q = 5. Beispiel I.4.6 (Schwingung). Wir wenden die Runge-Kutta-Fehlberg-Verfahren aus Beispiel I.4.5 mit der Schrittweitensteuerung von Algorithmus I.4. auf das AWP aus Beispiel I..7 (S. 9) an. Alle Verfahren liefern die exakte Lösungskurve, den Kreis um den Ursprung mit Radius. Die entsprechenden Ergebnisse sind in Tabelle I.4.3 angegeben. Dabei sind die Bezeichnungen wie in Beispiel I.4.3. Tabelle I.4.3. Runge-Kutta-Fehlberg-Verfahren mit Schrittweitensteuerung durch Ordnungsvergleich für die Schwingungsgleichung aus Beispiel I..7; angegeben sind die erreichte Endzeit T, die Zahl der Schritte N, die maximale Schrittweite h max und die Rechenzeit in Millisekunden auf einem MacBook Pro T N h max msec RKF RKF RKF Beispiel I.4.7 (Räuber-Beute-Modell). Wir wenden die Runge- Kutta-Fehlberg-Verfahren aus Beispiel I.4.5 mit der Schrittweitensteuerung von Algorithmus I.4. auf das Räuber-Beute-Modell aus Beispiel I..8 (S. 9) an. Alle Verfahren liefern die gleiche Lösungskurve. Die entsprechenden Ergebnisse sind in der folgenden Tabelle angegeben. Dabei sind die Bezeichnungen wie in Beispiel I.4.4. I.5. Lineare Mehrschrittverfahren Bei den bisher betrachteten ESV wird die neue Näherung η j+ direkt aus der alten Näherung η j berechnet. In diesem und den nächsten Paragraphen wollen wir lineare Mehrschrittverfahren (MSV) betrachten, bei denen zur Berechnung von η j+ alte Näherungen η j, η j,..., η j k benötigt werden. Bevor wir eine allgemeine Definition geben, betrachten wir einige Beispiele.
36 36 I. ANFANGSWERTPROBLEME Tabelle I.4.4. Runge-Kutta-Fehlberg-Verfahren mit Schrittweitensteuerung durch Ordnungsvergleich für das Räuber-Beute-Modell aus Beispiel I..8, angegeben sind die erreichte Endzeit T, die Zahl der Schritte N, die maximale Schrittweite h max und die Rechenzeit in Millisekunden auf einem MacBook Pro T N h max msec RKF RKF RKF Beispiel I.5. (Formeln von Adams-Bashforth, Adams-Moulton und Nyström; Funktionen adams bashforth fs, adams moulton fs und nystroem fs in Numerics). Wir wählen äquidistante Punkte t i = t 0 + ih, i N. Sei p > 0. Wir nehmen an, dass wir die Lösung y des AWP (I..) (S. 0) in den Punkten t 0,..., t p kennen. Sei 0 s p. Dann folgt (I.5.) y(t p+ ) y(t p s ) = = tp+ t p s tp+ t p s y (τ)dτ f(t, y(τ))dτ. Sei nun k {0, } und q 0 so, dass p + k q 0 ist. Dann approximieren wir den Integranden in (I.5.) durch das Interpolationspolynom in den Punkten t p+k, t p+k,..., t p+k q und erhalten y(t p+ ) y(t p s ) tp+ q f(t p+k i, y(t p+k i )) = h = h t p s q i=0 i=0 f(t p+k i, y(t p+k i )) s q f(t p+k i, y(t p+k i ))β qi. i=0 Dies liefert das MSV η p+ = η p s + h q j=0 j i q j=0 j i τ t p+k j t p+k i t p+k j dτ z k + j dz j i q β qi f(t p+k i, η p+k i ). i=0 Je nach Wahl von s und k erhalten wir drei häufig benutzte Klassen von Verfahren:
37 I.5. LINEARE MEHRSCHRITTVERFAHREN 37 Adams-Bashforth-Formeln: s = 0, k = 0 η p+ = η p + h q i=0 β AB qi f(t p i, η p i ). Die Koeffizienten sind in folgender Tabelle zusammengefasst: q β AB qi Für q = 0 erhalten wir also das explizite Euler-Verfahren zurück. Adams-Moulton-Formeln: s = 0, k = η p+ = η p + h q i=0 β AM qi f(t p+ i, η p+ i ). Die Koeffizienten sind in folgender Tabelle zusammengefasst: q β AM qi Die Formeln von Adams-Moulton sind also implizit. Für q = 0 erhalten wir das implizite Euler-Verfahren, und für q = erhalten wir die Trapezregel. Nyström-Formeln: s =, k = 0 η p+ = η p + h q βqi N f(t p i, η p i ). i=0
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Gewöhnliche Differentialgleichungen Woche 6. Existenz nach Picard-Lindelöf
 d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Übungen zu Differentialgleichungen (WiSe 12/13)
 Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Gewöhnliche Differentialgleichungen Woche 7. Globale Existenz einer Lösung
 Gewöhnliche Differentialgleichungen Woche 7 Globale Existenz einer Lösung 7.1 Von lokal zu global Wir betrachten wiederum das Anfangswertproblem { y (x = f (x, y(x, y( = y 0. (7.1 Eine erste Erweiterung
Gewöhnliche Differentialgleichungen Woche 7 Globale Existenz einer Lösung 7.1 Von lokal zu global Wir betrachten wiederum das Anfangswertproblem { y (x = f (x, y(x, y( = y 0. (7.1 Eine erste Erweiterung
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Skript zur Vorlesung Analysis 3
 Skript zur Vorlesung Analysis 3 Herbstsemester 204 Prof. Benjamin Schlein Inhaltsverzeichnis Gewöhnliche Differentialgleichungen 2. Differentialgleichungen erster Ordnung, elementare Lösungsmethoden..
Skript zur Vorlesung Analysis 3 Herbstsemester 204 Prof. Benjamin Schlein Inhaltsverzeichnis Gewöhnliche Differentialgleichungen 2. Differentialgleichungen erster Ordnung, elementare Lösungsmethoden..
3. Lineare Mehrschrittverfahren 3.1 Begriffe
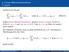 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
Analysis II. 8. Klausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis II 8. Klausur mit en 1 2 Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Eine Metrik auf einer Menge M. 2) Die Kurvenlänge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis II 8. Klausur mit en 1 2 Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Eine Metrik auf einer Menge M. 2) Die Kurvenlänge
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Nichtlineare Gleichungssysteme
 Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Gewöhnliche Differentialgleichungen Woche 7. Nicht-lineare und linearisierte Systeme
 Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Diplom VP Numerik 28. August 2006
 Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Institut für Analysis WS 2014/15 PD Dr. Peer Christian Kunstmann Dipl.-Math. Leonid Chaichenets
 Institut für Analysis WS 4/5 PD Dr. Peer Christian Kunstmann 9..4 Dipl.-Math. Leonid Chaichenets Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zum 5. Übungsblatt Aufgabe : (a) Sei
Institut für Analysis WS 4/5 PD Dr. Peer Christian Kunstmann 9..4 Dipl.-Math. Leonid Chaichenets Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zum 5. Übungsblatt Aufgabe : (a) Sei
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: b a 2 3a 1
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Teil 6. Differentialrechnung mehrerer Veränderlicher
 Teil 6 Differentialrechnung mehrerer Veränderlicher 95 96 6.1 Topologie von Mengen Umgebung ε-umgebung eines Punktes x R n : B ε (x) = {y : y x < ε} Umgebung U von x: Menge, die eine ε-umgebung von x enthält
Teil 6 Differentialrechnung mehrerer Veränderlicher 95 96 6.1 Topologie von Mengen Umgebung ε-umgebung eines Punktes x R n : B ε (x) = {y : y x < ε} Umgebung U von x: Menge, die eine ε-umgebung von x enthält
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei die Matrix
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
Adaptive Mehrschrittverfahren
 Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
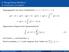 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Höhere Mathematik III für die Fachrichtung Physik Wintersemester 2016/17. Lösungsvorschlag zu Übungsblatt 5
 Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
18.4 Das Newton-Verfahren
 18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen
 Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Numerik gewöhnlicher Differentialgleichungen. Prof. Dr. Guido Kanschat
 Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV Aufgabe N1 (LR-Zerlegung mit Pivotisierung) Gegeben seien R 3.
 Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV 7.7.6 Aufgabe N (LR-Zerlegung mit Pivotisierung) Gegeben seien 6 8 A = 8 6 R und b = 6 R. a) Berechnen Sie die LR-Zerlegung von A mit Spaltenpivotisierung.
Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV 7.7.6 Aufgabe N (LR-Zerlegung mit Pivotisierung) Gegeben seien 6 8 A = 8 6 R und b = 6 R. a) Berechnen Sie die LR-Zerlegung von A mit Spaltenpivotisierung.
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen
 Kapitel XII Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen 53 Implizite Funktionen und allgemeine partielle Differenzierbarkeit 54 Der Umkehrsatz 55 Lokale Extrema unter Nebenbedingungen,
Kapitel XII Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen 53 Implizite Funktionen und allgemeine partielle Differenzierbarkeit 54 Der Umkehrsatz 55 Lokale Extrema unter Nebenbedingungen,
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Musterlösung Klausur zu Analysis II. Verständnisteil
 Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Gewöhnliche Dierentialgleichungen
 Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1. Prof. Dr. Hans Babovsky. Technische Universität Ilmenau
 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
Inexakte Newton Verfahren
 Kapitel 3 Inexakte Newton Verfahren 3.1 Idee inexakter Newton Verfahren Wir betrachten weiterhin das nichtlineare Gleichungssystem F (x) = mit einer zumindest stetig differenzierbaren Funktion F : R n
Kapitel 3 Inexakte Newton Verfahren 3.1 Idee inexakter Newton Verfahren Wir betrachten weiterhin das nichtlineare Gleichungssystem F (x) = mit einer zumindest stetig differenzierbaren Funktion F : R n
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky. Institut für Mathematik
 NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
KAPITEL 5. Nichtlineare Gleichungssysteme
 KAPITEL 5. Nichtlineare Gleichungssysteme Beispiel 5.1. Gravitationskraft zwischen zwei Punktmassen m 1 und m 2 mit gegenseitigem Abstand r: F = G m 1m 2 r 2, wobei G = 6.67 10 11 Nm 2 /kg. Gravitationsfeld
KAPITEL 5. Nichtlineare Gleichungssysteme Beispiel 5.1. Gravitationskraft zwischen zwei Punktmassen m 1 und m 2 mit gegenseitigem Abstand r: F = G m 1m 2 r 2, wobei G = 6.67 10 11 Nm 2 /kg. Gravitationsfeld
6 Iterationsverfahren für lineare und nichtlineare Gleichungssysteme
 6 Iterationsverfahren für lineare und nichtlineare Gleichungssysteme 6.1 Nullstellen reeller Funktionen Bemerkung 6.1 (Problemstellung) geg.: f C[a, b] ges.: x [a, b] mit f(x ) = 0 Lösungstheorie f linear
6 Iterationsverfahren für lineare und nichtlineare Gleichungssysteme 6.1 Nullstellen reeller Funktionen Bemerkung 6.1 (Problemstellung) geg.: f C[a, b] ges.: x [a, b] mit f(x ) = 0 Lösungstheorie f linear
Probeklausur zur Analysis II
 Probeklausur zur Analysis II Prof. Dr. C. Löh/M. Blank 3. Februar 2012 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Probeklausur zur Analysis II Prof. Dr. C. Löh/M. Blank 3. Februar 2012 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Diplom VP Numerik 27. August 2007
 Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
Parareal. Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen. Johannes Reinhardt. Parareal 1 Johannes Reinhardt
 Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Lösung Semesterendprüfung
 MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen
 Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
Klausur Numerische Mathematik (für Elektrotechniker), 24. Februar 2016
 Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
A 1 A 2 A 3 A 4 A 5 A 6 A 7
 Institut für Geometrie und Praktische Mathematik Numerisches Rechnen für Informatiker WS 7/8 Prof. Dr. H. Esser J. Grande, Dr. M. Larin Klausur Numerisches Rechnen für Informatiker Hilfsmittel: keine (außer
Institut für Geometrie und Praktische Mathematik Numerisches Rechnen für Informatiker WS 7/8 Prof. Dr. H. Esser J. Grande, Dr. M. Larin Klausur Numerisches Rechnen für Informatiker Hilfsmittel: keine (außer
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 1
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
5 Numerische Iterationsverfahren
 In diesem Kapitel besprechen wir numerische Iterationsverfahren (insbesondere Fixpunktverfahren) als eine weitere Lösungsmethode zur Lösung von linearen Gleichungssystemen (Kapitel 4) sowie zur Lösung
In diesem Kapitel besprechen wir numerische Iterationsverfahren (insbesondere Fixpunktverfahren) als eine weitere Lösungsmethode zur Lösung von linearen Gleichungssystemen (Kapitel 4) sowie zur Lösung
Karlsruher Institut für Technologie (KIT) SS 2013 Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning
 Karlsruher Institut für Technologie KIT SS 2013 Institut für Analysis 06.05.2013 Prof. Dr. Tobias Lamm Dr. Patrick Breuning Höhere Mathematik II für die Fachrichtung Physik 4. Übungsblatt Aufgabe 1 Bestimmen
Karlsruher Institut für Technologie KIT SS 2013 Institut für Analysis 06.05.2013 Prof. Dr. Tobias Lamm Dr. Patrick Breuning Höhere Mathematik II für die Fachrichtung Physik 4. Übungsblatt Aufgabe 1 Bestimmen
Newton-Verfahren für ein Skalarfunktion
 Newton-Verfahren für ein Skalarfunktion Für eine Näherungsberechnung von Nullstellen einer reellen Funktion f(x) : R R benutzt man das Newton-Verfahren: x (n+1) = x (n) f(x (n) )/f (x (n) ). Das Newton-Verfahren
Newton-Verfahren für ein Skalarfunktion Für eine Näherungsberechnung von Nullstellen einer reellen Funktion f(x) : R R benutzt man das Newton-Verfahren: x (n+1) = x (n) f(x (n) )/f (x (n) ). Das Newton-Verfahren
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Maximalität und Globalität von Lösungen
 Gewöhnliche Differentialgleichungen Florian Wörz SoSe 205 Maximalität und Globalität von Lösungen Maximale Lösungen Sei Ω : T U R R n ein Gebiet, f : Ω R n stetig und (t 0, u 0 ) Ω. Im Folgenden betrachten
Gewöhnliche Differentialgleichungen Florian Wörz SoSe 205 Maximalität und Globalität von Lösungen Maximale Lösungen Sei Ω : T U R R n ein Gebiet, f : Ω R n stetig und (t 0, u 0 ) Ω. Im Folgenden betrachten
Aufgabe 1. Berechnen Sie die absolute und die relative Kondition des Problems x f(x) für die Abbildung. x = x 2 e x 1.
 Name: Matrikel-Nr.: 1 Aufgabe 1. Berechnen Sie die absolute und die relative Kondition des Problems x f(x) für die Abbildung R 3 R 2, x 1 f : x 1 + e x2 2 sin(x3 ) x = x 2 e x 1 (1 + x 2 1 + x, 2x 3 )
Name: Matrikel-Nr.: 1 Aufgabe 1. Berechnen Sie die absolute und die relative Kondition des Problems x f(x) für die Abbildung R 3 R 2, x 1 f : x 1 + e x2 2 sin(x3 ) x = x 2 e x 1 (1 + x 2 1 + x, 2x 3 )
Einführung in die numerische Mathematik
 Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Wiederholungsklausur zur Analysis II
 Wiederholungsklausur zur Analysis II Prof. Dr. C. Löh/M. Blank 11. April 2012 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Wiederholungsklausur zur Analysis II Prof. Dr. C. Löh/M. Blank 11. April 2012 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Begleitmaterial zur Vorlesung Numerik II
 Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel;
 Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Gewöhnliche Dierentialgleichungen
 Prof. Dr. Guido Sweers WS 28/29 Jan Gerdung, M.Sc. Gewöhnliche Dierentialgleichungen Übungsblatt 6 Die Lösungen müssen in den Übungsbriefkasten Gewöhnliche Dierentialgleichungen Raum 3 im MI) geworfen
Prof. Dr. Guido Sweers WS 28/29 Jan Gerdung, M.Sc. Gewöhnliche Dierentialgleichungen Übungsblatt 6 Die Lösungen müssen in den Übungsbriefkasten Gewöhnliche Dierentialgleichungen Raum 3 im MI) geworfen
Analysis 2, Woche 9. Mehrdimensionale Differentialrechnung I. 9.1 Differenzierbarkeit
 A Analysis, Woche 9 Mehrdimensionale Differentialrechnung I A 9. Differenzierbarkeit A3 =. (9.) Definition 9. Sei U R m offen, f : U R n eine Funktion und a R m. Die Funktion f heißt differenzierbar in
A Analysis, Woche 9 Mehrdimensionale Differentialrechnung I A 9. Differenzierbarkeit A3 =. (9.) Definition 9. Sei U R m offen, f : U R n eine Funktion und a R m. Die Funktion f heißt differenzierbar in
Lösungen der Übungsaufgaben von Kapitel 3
 Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 2
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
11. Einschrittverfahren
 H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
Wie in der reellen Analysis üblich notiert man Folgen f in der Form
 2.1.3 Folgen und Konvergenz Viele aus der Analysisvorlesung bekannte Begriffe lassen sich in den Bereich der metrischen Räume verallgemeinern. Diese Verallgemeinerung hat sich als sehr nützliches mathematisches
2.1.3 Folgen und Konvergenz Viele aus der Analysisvorlesung bekannte Begriffe lassen sich in den Bereich der metrischen Räume verallgemeinern. Diese Verallgemeinerung hat sich als sehr nützliches mathematisches
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Steffen Börm Stand 16. April 2010 Alle Rechte beim Autor. Inhaltsverzeichnis 1 Einleitung 4 1.1 Federpendel................................... 4 1.2 Mehrkörperprobleme..............................
Numerik gewöhnlicher Differentialgleichungen Steffen Börm Stand 16. April 2010 Alle Rechte beim Autor. Inhaltsverzeichnis 1 Einleitung 4 1.1 Federpendel................................... 4 1.2 Mehrkörperprobleme..............................
Banach scher Fixpunktsatz. 1) D ist abgeschlossen und konvex; 2) f ist selbstabbildend, d.h. f(d) D;
 Institut für Geometrie und Praktische Mathematik Höhere Mathematik IV (für Elektrotechniker und Technische Informatiker) - Numerik - SS 2007 Dr. S. Börm, Dr. M. Larin Banach scher Fixpunktsatz Gegeben
Institut für Geometrie und Praktische Mathematik Höhere Mathematik IV (für Elektrotechniker und Technische Informatiker) - Numerik - SS 2007 Dr. S. Börm, Dr. M. Larin Banach scher Fixpunktsatz Gegeben
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
(a), für i = 1,..., n.
 .4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
.4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
eps für alle x D. 4. Die Zahl 256 ist in M(2, 4, 6, 6) exakt darstellbar.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Lösung - Serie 25. D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger
 D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
Musterlösung Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
Analysis 4. Lösungsvorschlag zum 12. Übungsblatt
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Andreas Geyer-Schulz SS 208. Juli 208 Analysis 4 Lösungsvorschlag zum 2. Übungsblatt Aufgabe 42 Wir untersuchen
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Andreas Geyer-Schulz SS 208. Juli 208 Analysis 4 Lösungsvorschlag zum 2. Übungsblatt Aufgabe 42 Wir untersuchen
Dierentialgleichungen 2. Ordnung
 Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Fachbereich Mathematik/Informatik 16. Juni 2012 Prof. Dr. H. Brenner. Mathematik für Anwender II. Testklausur mit Lösungen
 Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
