5 Steife Differentialgleichungen

Transkript

1 Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn.... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG an Beispielen. Beispiel. Die beiden AWPe [ ] [ ] [ ] y sin t = y +, y() =, (AWP ) (cos t sin t) 3 [ ] [ ] [ ] y sin t = y +, y() =, (AWP ) (cos t sin t) 3 haben dieselbe Lösung. 5 Steife Differentialgleichungen Technische Universität Bergakademie Freiberg

2 Numerik gewöhnlicher Differentialgleichungen 8 [ ] y(t) = exp( t) + [ ] sin t. cos t 3.5 y.5 y Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

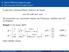
3 Numerik gewöhnlicher Differentialgleichungen 8 Wir lösen beide Probleme für t [, ] mit der Matlab-Routine ode45 (die ein eingebettetes RKV, das Verfahren von Dormand-Prince, verwendet, bei dem zwei RKV der Ordnungen 4 bzw. 5 kombiniert werden), wobei wir eine relative Toleranz von. vorgeben. 3 System : 64 Schritte (ode45) 3 System : 44 Schritte (ode45).5.5 y y.5.5 y y Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

4 Numerik gewöhnlicher Differentialgleichungen 8 Obwohl die exakte Lösung in beiden Fällen dieselbe ist, erfordert die Lösung von (AWP ) etwa -mal mehr Aufwand als die von (AWP ): AWP h min h max h Schritte (AWP ).7e-.3e-.56e- 64 (AWP ) 5.98e-4.88e-3 8.3e Lösen wir die beiden Probleme mit der Matlab-Routine ode3tb (die die Trapezregel mit der Gear-Formel der Ordnung kombiniert), so ergibt sich (relative Toleranz wie oben =.): AWP h min h max h Schritte (AWP ).3e- 5.8e- 5.6e- 9 (AWP ).3e- 7.36e- 5.e-. Beide Probleme werden ohne Schwierigkeiten gelöst. 5. Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

5 Numerik gewöhnlicher Differentialgleichungen 83 3 System : 9 Schritte (ode3tb) 3 System : Schritte (ode3tb).5.5 y y.5.5 y y Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

6 Numerik gewöhnlicher Differentialgleichungen 84 Die Unterschiede zwischen den beiden AWPen werden sichtbar, wenn wir alle Lösungen der zugehörigen Systeme betrachten. Im ersten Fall ergibt sich [ ] [ ] [ ] sin t y = κ exp( t) + κ exp( 3t) +, cos t während im zweiten Fall [ ] [ ] [ ] sin t y = κ exp( t) + κ exp( t) cos t die allgemeine Lösung ist. (Beide Systeme sind inhomogene lineare Systeme mit konstanten Koeffizienten, wobei die Eigenwerte der Koeffizientenmatrix im ersten Fall λ =, λ = 3 und im zweiten Fall λ =, λ = sind.) Die Lösungen der konkreten AWPe sind jeweils durch κ = und κ = (!) gegeben. 5. Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

7 Numerik gewöhnlicher Differentialgleichungen 85 In beiden Fällen ist die Lösung aus einem Gleichgewichtsanteil, nämlich [sin t, cos t], und einem transienten Anteil der Form exp(λ t)a + exp(λ t)a zusammengesetzt. Die Unterschiede liegen in der Geschwindigkeit, mit der der transiente Teil (für t ) verschwindet. Obwohl in der exakten Lösung der AWPe gar nicht erkennbar ist, wie schnell der abklingende Anteil verschwindet (κ = ), bestimmt er die erforderliche Schrittweite. Würde man in (AWP ) die AB in y() = [, ] ändern, so würde κ = κ = folgen, d.h. der transiente Teil ist in der Lösung y(t) = [sin t, cos t] vollständig unsichtbar. Selbst dann wäre ode45 nur mit extrem kleiner Schrittweite in der Lage, die Aufgabe zu lösen. Wir betrachten die Stabilitätsbereiche R A : Für ode45 kann man zeigen, dass R A R [ 3, ] (Stabilitätsintervall). Will man für (AWP ) also λh R A (für alle Eigenwerte λ) garantieren, genügt es, h < zu fordern (die durchschnittliche Schrittweite von h.56 resultiert aus der geforderten Genauigkeit!). 5. Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

8 Numerik gewöhnlicher Differentialgleichungen 86 Dagegen muss für (AWP ) h <.3 gefordert werden, damit λh R A für alle λ folgt und es sind Stabilitätsprobleme, die zu der kleinen durchschnittlichen Schrittweite von h.8 führen. Das Verfahren ode3tb ist absolut stabil, so dass hier λ h für alle h > (in jedem der beiden Fälle (AWP ) und (AWP )) im Stabilitätsbereich liegt. Für y = Ay + b(t) heißt max Re λ / min Re λ λ Λ(A) λ Λ(A) Steifigkeitsquotient des linearen DG-Systems. Ein lineares DG-System mit konstanten Koeffizienten heißt steif, wenn seine Eigenwerte alle negativen Realteil besitzen und sein Steifigkeitsquotient groß ist. 5. Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

9 Numerik gewöhnlicher Differentialgleichungen 87 Um die Problematik dieser gebräuchlichen Definition zu erläutern, betrachten wir ein weiteres AWP (mit derselben Lösung): [ ] [ ] [ ] y sin t = y +, y() =. (AWP 3 ) (cos t sin t) 3 Die Matrix dieses Systems besitzt die Eigenwerte λ =, λ =. und sein Steifigkeitsquotient beträgt (wie bei (AWP )). Trotzdem hat ode45 keine ernsten Probleme: AWP h min h max h Schritte (AWP 3 ).9e-.5e-.7e- 44 (ode45) (AWP 3 ).5e- 4.9e- 4.55e- (ode3tb) 5. Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

10 Numerik gewöhnlicher Differentialgleichungen 88 Ob ein System steif ist oder nicht kann also nicht immer aus dem Steifigkeitsquotienten abgelesen werden. Auch Definitionen wie ein System ist steif, wenn max Re λ groß ist (etwa max Re λ ) sind natürlich wenig hilfreich (die Variablentransformation t.t macht aus (AWP ) ein Problem, das dieselbe Steifigkeit besitzt, bei dem aber max Re λ = gilt). Pragmatische Definitionen für Steifigkeit sind: Ein System ist steif, wenn Stabilitätsanforderungen und nicht Genauigkeitsanforderungen die Größe der Schrittweite bestimmen. Ein System heißt steif, wenn gewisse Komponenten der Lösung sehr viel schneller abklingen als andere. 5. Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

11 Numerik gewöhnlicher Differentialgleichungen 89 Beispiel. Die Differentialgleichung y (t) = λ(y(t) g(t)) + g (t) ( ) besitzt die allgemeine Lösung y(t) = γ exp(λt) + g(t) (γ R). Wir wählen g als glatte Funktion, z.b. g(t) = arctan t und λ =. Auch hier setzt sich die Lösung aus einem glatten (g(t) = Gleichgewichtsanteil) und einem schnell abklingenden Teil (γ exp(λt) = transienter Anteil) zusammen. Wir wählen die AB y() = und approximieren die exakte Lösung y(t) = arctan t für t [, 5] mit dem expliziten Euler-Verfahren (R A = {ĥ : ĥ + < }) und dem impliziten Euler-Verfahren (R A = C \ {ĥ : ĥ }). 5. Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

12 Numerik gewöhnlicher Differentialgleichungen Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

13 Numerik gewöhnlicher Differentialgleichungen 9 Explizit: h= h= h= Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

14 Numerik gewöhnlicher Differentialgleichungen 9 Implizit: h= h= h= Was sind steife Differentialgleichungen? Technische Universität Bergakademie Freiberg

15 Numerik gewöhnlicher Differentialgleichungen Stabilitätsbegriffe Erinnerung. Ein numerisches Verfahren zur Lösung von y = f (t, y), y() = y, heißt A-stabil, wenn folgendes gilt: Wendet man das Verfahren auf ein lineares Problem y = Ay (t [, )) an und liegen die Eigenwerte von A alle in der linken Halbebene {ζ : Real ζ < }, dann soll für die Näherungslösung stets lim n y n = gelten (die exakte Lösung erfüllt lim t y(t) = ). In konkreten Fällen wird die äquivalente Bedingung R A {ĥ : Real ĥ < } überprüft. Zur Definition des Stabilitätsbereichs R A vergleiche Abschnitt 3.5 für lineare Mehrschrittverfahren und Abschnitt 4.3 für RKV (oder allgemeine Einschrittverfahren). 5. Stabilitätsbegriffe Technische Universität Bergakademie Freiberg

16 Numerik gewöhnlicher Differentialgleichungen 94 Abgeschwächte Stabilitätsbegriffe sind A(α)-stabil für α (, π/) R A {ĥ : α < π arg ĥ < α}, A -stabil R A (, ), steif-stabil R A R (β) R (β, γ) für positive β und γ, wobei R (β) := {ĥ : Real ĥ < β} und R (β, γ) := {ĥ : β Real ĥ <, Imag ĥ γ}. Außerdem heißt ein Einschrittverfahren L-stabil, wenn es A-stabil ist und zusätzlich gilt: Bei Anwendung auf die Testgleichung y = λy, Real λ <, resultiert eine Näherung y n+ = R(hλ)y n mit lim hλ R(hλ) =. 5. Stabilitätsbegriffe Technische Universität Bergakademie Freiberg

17 Numerik gewöhnlicher Differentialgleichungen 95 A stabil A(α) stabil steif stabil Imag ζ Imag ζ Imag ζ γ Real ζ α Real ζ β Real ζ α γ 5. Stabilitätsbegriffe Technische Universität Bergakademie Freiberg

18 Numerik gewöhnlicher Differentialgleichungen 96 Offensichtlich gilt ( < α arg(β + iγ)) L-stabil A-stabil steif-stabil A(α)-stabil A -stabil. Die Trapezregel y n+ = y n + h(f n+ + f n ), d.h. R(ĥ) = ( + ĥ/)/( ĥ/), ist A-stabil, aber nicht L-stabil. Das implizite Euler-Verfahren y n+ = y n + hf n+, d.h. R(ĥ) = /( ĥ), ist dagegen L-stabil. Wir illustrieren den Unterschied, indem wir mit beiden Verfahren die Lösung von (AWP ) aus Abschnitt 5. approximieren. Um den transienten Anteil der Lösung besser sichtbar zu machen, werden die ABen y() = [, ] vorgeschrieben. Die exakte Lösung ist dann [ ] [ ] [ ] sin t y(t) = 999 exp( t) exp( t) cos t Die folgende Abbildung zeigt die zweite Komponente der (Näherungs)lösung für h =.. 5. Stabilitätsbegriffe Technische Universität Bergakademie Freiberg

19 Numerik gewöhnlicher Differentialgleichungen 97.5 h=. exakte Loesung Trapezregel implizites Euler Verfahren Stabilitätsbegriffe Technische Universität Bergakademie Freiberg

20 Numerik gewöhnlicher Differentialgleichungen 98 Das Beispiel y = y, y() = , mit der exakten Lösung y(t) = exp(.8t) sin(8t) + exp( 5t) exp(.t) cos(8t) exp( 5t) exp(.t) (sin(8t) + cos(8t)) + exp( 5t) zeigt, dass L-stabile Verfahren nicht immer besser sind als A-stabile (die folgende Abbildung zeigt die erste Komponente der (Näherungs)lösung für h =.4 und t [,.5]). Beim impliziten Euler-Verfahren müsste man h <.3... wählen, um eine akzeptable Näherung zu erhalten (warum?). 5. Stabilitätsbegriffe Technische Universität Bergakademie Freiberg

21 Numerik gewöhnlicher Differentialgleichungen 99 h= exakte Loesung Trapezregel implizites Euler Verfahren Stabilitätsbegriffe Technische Universität Bergakademie Freiberg

22 Numerik gewöhnlicher Differentialgleichungen 5.3 Ordnungssterne Wendet man ein Einschrittverfahren (ESV) auf die Testgleichung y = λy an, so gilt y n+ = R(λh)y n. Dabei ist R ein Polynom (bei expliziten Verfahren) oder eine (gebrochen) rationale Funktion in ĥ = λh. Besitzt das ESV die Konsistenzordnung p, so ist R(ĥ) exp(ĥ) = O(ĥp+ ) (ĥ ). Natürlicher Ansatz: Bestimme eine rationale Funktion R vom Typ (k, l) (k = Zählergrad, l = Nennergrad), so dass der Exponent µ in R(ĥ) exp(ĥ) = O(ĥµ ) maximal wird. Es zeigt sich, dass das Maximum µ = k + l + durch die in Abschnitt.4 eingeführten Padé-Approximationen (k, l) exp realisiert wird. 5.3 Ordnungssterne Technische Universität Bergakademie Freiberg

23 Numerik gewöhnlicher Differentialgleichungen (k, l) exp (ζ) für k, l 3: k, l 3 ζ ζ+ ζ ζ+ ζ 6 ζ3 +ζ + ζ + 3 ζ + ζ 3 ζ+ 4 ζ 6 ζ 3 4 ζ+ 4 ζ 4 ζ3 +ζ+ + 3 ζ+ 6 ζ + ζ ζ+ ζ + 3 ζ ζ+ 5 ζ+ ζ ζ 3 5 ζ+ 3 ζ 6 ζ3 3 +ζ+ ζ ζ+ 4 ζ ζ3 + 6 ζ3 5 ζ+ 3 ζ + 6 ζ3 + 4 ζ 5 ζ+ ζ+ ζ + ζ3 ζ ζ+ ζ ζ3 5.3 Ordnungssterne Technische Universität Bergakademie Freiberg

24 Numerik gewöhnlicher Differentialgleichungen Eine rationale Approximation R(ζ) an exp(ζ) heißt A-akzeptabel, wenn R(ζ) < für alle ζ C mit Re ζ <, A -akzeptabel, wenn R(ζ) < für alle ζ R mit ζ <, L-akzeptabel, wenn R A-akzeptabel ist und R(ζ) für ζ gilt. Satz 5. Es gilt. (k, k) exp ist A-akzeptabel (G. Birkhoff, R.S. Varga 96).. (k, l) exp ist A -akzeptabel für k l (R.S. Varga 96). 3. (k, l) exp ist L-akzeptabel für k {l, l } (B.L. Ehle, 969). 4. (k, l) exp ist genau dann A-akzeptabel, wenn k {l, l, l } (Ehle-Vermutung; G. Wanner, E. Hairer, S.P. Nørsett 978). 5.3 Ordnungssterne Technische Universität Bergakademie Freiberg

25 Numerik gewöhnlicher Differentialgleichungen 3 Der Beweis der vierten Aussage basiert auf der Theorie der Ordnungssterne. Ist R(ζ) eine rationale Funktion, so heißt S R := {ζ C : R(ζ) > exp(ζ) } der zugehörige Ordnungsstern. Sei T R := C \ S R sein Komplement. Vier Eigenschaften.. R ist genau dann eine Approximation der Ordnung p an die Exponentialfunktion (d.h. R(ζ) exp(ζ) = O(ζ p+ ) für ζ ), wenn Folgendes gilt: Für ζ besteht sowohl S R als auch T R aus genau p + Sektoren mit Winkel jeweils π/(p+). Die Sektoren von S R und T R trennen sich. (p = 5) 5.3 Ordnungssterne Technische Universität Bergakademie Freiberg

26 Numerik gewöhnlicher Differentialgleichungen 4. Der Rand von S R enthält genau zwei unbeschränkte Zweige. 3. Komponenten von S R, die k Sektoren enthalten, nennt man Finger der Ordnung k. Komponenten von T R, die k Sektoren enthalten, heißen duale Finger der Ordnung k. Es gilt: Jeder beschränkte Finger der Ordnung k enthält mindestens k Pole von R (Vielfachheiten mitzählen). Jeder beschränkte duale Finger der Ordnung k enthält mindestens k Nullstellen von R (Vielfachheiten mitzählen). 4. R ist genau dann A-akzeptabel, wenn S R keine Punkte der imaginären Achse enthält und R keine Pole in der linken Halbebene Real ζ < besitzt. 5.3 Ordnungssterne Technische Universität Bergakademie Freiberg

27 Numerik gewöhnlicher Differentialgleichungen o: Pole, +: Nullstellen o: Pole, +: Nullstellen Ordnungssterne der Padé-Approximationen (, 3) exp (links) und (, 4) exp (rechts). 5.3 Ordnungssterne Technische Universität Bergakademie Freiberg

28 Numerik gewöhnlicher Differentialgleichungen o: Pole, +: Nullstellen o: Pole, +: Nullstellen Ordnungssterne der Padé-Approximation (, 5) exp (links) und einer (nicht A-akzeptablen) (4, 5)-Approximation R der Ordnung 5 (rechts) (R(ζ) = [ 4 4 ζ ζ3 9ζ + 4ζ 5]/[ζ ζ4 + 8ζ 3 5 ζ + 9ζ 5]). 5.3 Ordnungssterne Technische Universität Bergakademie Freiberg

29 Numerik gewöhnlicher Differentialgleichungen Lineare MSV für steife Probleme Satz 5. (Zweite Dahlquist Barriere) Es gilt: Kein explizites lineares MSV ist A-stabil. Ein A-stabiles lineares MSV besitzt höchstens die Ordnung. Das A-stabile lineare MSV mit Konsistenzordnung und kleinster Fehlerkonstante ist die Trapezregel. Satz 5.3 (C.W. Cryer, 73) Es gilt: Kein explizites lineares MSV ist A -stabil. Es gibt A -stabile lineare MSV beliebig hoher Konsistenzordnung. Beispielsweise sind die Gear-Verfahren aus Abschnitt 3.6 alle A -stabil. 5.4 Lineare MSV für steife Probleme Technische Universität Bergakademie Freiberg

30 Numerik gewöhnlicher Differentialgleichungen RKV für steife Probleme Entscheidend (vgl. Abschnitt 4.3) R(ĥ) = + ĥb (I ĥa) e = det(i ĥ(a ebt )) det(i ĥa). Ordnung Typ von R Stabilität Gauß m (m, m) A-stabil Gauß-Radau m (m, m) L-stabil Gauß-Lobatto m (m, m ) A-stabil 5.5 RKV für steife Probleme Technische Universität Bergakademie Freiberg

31 Numerik gewöhnlicher Differentialgleichungen Bemerkungen Alle bisher getroffenen Stabilitätsaussagen basieren auf der Untersuchung linearer Systeme mit konstanten Koeffizienten (lineare Stabilitätstheorie). Oft wird versucht, diese Aussagen mit folgender Argumentation zu verallgemeinern: Die Lösung y des AWPs y = f (t, y), y(t ) = y kann durch die Lösung der linearen Variationsgleichung y = f (t, y (t)) + f y(t, y (t))[y y (t)] ( ) approximiert werden. Lokal ist f y(t, y ) nahezu zeitunabhängig, so dass ( ) näherungsweise die Form y = Ay + g(t) besitzt. Zwei Beispiele sollen zeigen, dass Skepsis gegenüber diesem frozen Jacobian argument angebracht ist. 5.6 Bemerkungen Technische Universität Bergakademie Freiberg

32 Numerik gewöhnlicher Differentialgleichungen Beispiel. [ ] 9 cos y (6t) + 6 sin(t) cos (6t) sin(t) = y. sin (6t) sin(t) 9 sin (6t) 6 sin(t) Die Systemmatrix A(t) besitzt die (t-unabhängigen!) Eigenwerte λ =, λ =. Obwohl die Eigenwerte negativ sind, ist die allgemeine Lösung [ ] [ ] cos(6t) + sin(6t) sin(6t) cos(6t) y(t) = κ exp(t) + κ exp( 3t) cos(6t) sin(6t) sin(6t) + cos(6t) sicher nicht monoton fallend für t. 5.6 Bemerkungen Technische Universität Bergakademie Freiberg

33 Numerik gewöhnlicher Differentialgleichungen Beispiel. y = [ t t t 3 t ] y, t. ( ) Die Systemmatrix A(t) besitzt die Eigenwerte λ, = ( ± i)/(t), die für t negativen Realteil besitzen. Die allgemeine Lösung ist [ ] [ ] t 3/ t 3/ ln(t) y(t) = κ + κ. t / ( ln(t)) Für κ =, κ = ist t/ y = t t streng monoton wachsend (für t /4 = ). 5.6 Bemerkungen Technische Universität Bergakademie Freiberg

34 Numerik gewöhnlicher Differentialgleichungen Definition [dissipativ]. Das System y = f (t, y) heißt dissipativ in [t, t end ], wenn f (t, y) f (t, ỹ), y ỹ für alle t [t, t end ] und alle y, ỹ aus dem Definitionsbereich von f gilt., bezeichnet ein (z.b. das Euklidische) Innenprodukt im R n. Satz 5.4 Ist das System y = f (t, y) dissipativ in [t, t end ], dann ist es auch kontraktiv in [t, t end ]. Bedeutet: Für je zwei Lösungen y, ỹ von y = f (t, y) mit Anfangsbedingungen y(t ) = y, ỹ(t ) = ỹ, y ỹ, gilt y(t ) ỹ(t ) y(t ) ỹ(t ) für alle t, t mit t t t t end. ( :=, / ) 5.6 Bemerkungen Technische Universität Bergakademie Freiberg

35 Numerik gewöhnlicher Differentialgleichungen 3 Ob ein System dissipativ (kontraktiv) ist, kann mit Hilfe logarithmischer Normen entschieden werden. Sei eine (von einer Vektornorm induzierte) Matrixnorm im R n n. Dann heißt I n + ha µ(a) = µ (A) := lim (A R n n ) h + h die zu gehörige logarithmische Norm. Ist = p, so schreibt man µ p ( ) für die zugehörige logarithmische Norm. Eigenschaften.. Die logarithmische Norm ist trotz ihres Namens keine Norm.. Wird von einem Innenprodukt, induziert, so gilt µ(a) = max x = Ax, x. 3. µ (A) = ρ( (A + A )) (ρ = Spektralradius). 4. Ist f (t, y) = A(t)y, so ist f (t, y) f (t, ỹ), y ỹ = A(y ỹ), y ỹ µ(a) y ỹ. 5.6 Bemerkungen Technische Universität Bergakademie Freiberg

36 Numerik gewöhnlicher Differentialgleichungen 4 Satz 5.5 Seien eine Norm im R n und ν(t) : R R eine stückweise stetige Funktion mit µ(f y(t, y)) ν(t) für alle t [t, t end ] und alle y aus dem Definitionsbereich von f. Dann gilt für je zwei Lösungen y, ỹ von y = f (t, y) mit Anfangsbedingungen y(t ) = y, ỹ(t ) = ỹ, y ỹ, ( t ) y(t ) ỹ(t ) exp ν(s) ds y(t ) ỹ(t ) für alle t, t mit t t t t end. t 5.6 Bemerkungen Technische Universität Bergakademie Freiberg

37 Numerik gewöhnlicher Differentialgleichungen 5 Beispiel. Für das System ( ) von Seite gilt: Es folgt f y(t, y) = A(t) = [ t t µ (A(t)) = ρ( (A(t) + A(t) )) = max { t ± ( ) } t t 3 4 und damit µ (A(t)) genau dann, wenn t [t, t ] [.,.8] mit t, = ( 5 ) /. Das System ist daher in [t, t ] dissipativ (und kontraktiv). Folglich ist y(t) für jede Lösung y in [t, t ] monoton fallend. t 3 t ]. 5.6 Bemerkungen Technische Universität Bergakademie Freiberg

38 Numerik gewöhnlicher Differentialgleichungen 6 y(t) / y() als Funktion von t κ =, κ =.5 κ =, κ =.54 κ =, κ = t_ t_ 5.6 Bemerkungen Technische Universität Bergakademie Freiberg

39 Numerik gewöhnlicher Differentialgleichungen 7 Definition [algebraische Stabilität]. Ein Runge-Kutta-Verfahren gegeben durch die Butcher-Matrix c A heißt algebraisch stabil, wenn die symmetrischen Matrizen B := diag(β, β,..., β m ) und M := BA + A B bb beide positiv semidefinit sind. Satz 5.6 Seien y = f (t, y) ein dissipatives System und {y n }, {ỹ n }, y ỹ, Näherungslösungen, die aus der Anwendung eines Runge-Kutta-Verfahrens resultieren. Dann gilt: Ist das Verfahren algebraisch stabil, so sind die Näherungen kontraktiv, d.h. y n+ ỹ n+ y n ỹ n (n =,,...). b 5.6 Bemerkungen Technische Universität Bergakademie Freiberg

40 Numerik gewöhnlicher Differentialgleichungen 8 Beispiele. Die m-stufigen Gauß-Formeln (m {,, 3}) aus Abschnitt 4.5 sind alle algebraisch stabil (hier ist M die Nullmatrix!). Die Gauß-Radau-Formel ist algebraisch stabil, denn: [ ] M =, d.h. Λ(M) = {, /8}. 6 Die Trapez-Regel (aufgefasst als implizites zweistufiges RKV) ist nicht algebraisch stabil (Λ(M) = {±/}) Bemerkungen Technische Universität Bergakademie Freiberg