4 Runge-Kutta-Verfahren
|
|
|
- Astrid Bruhn
- vor 10 Jahren
- Abrufe
Transkript
1 Numerik gewöhnlicher Differentialgleichungen 43 4 Runge-Kutta-Verfahren 4. Konstruktion Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. t+h t y (s) ds Approximiere durch Quadraturformel 0 g(τ) dτ m β j g(γ j ). j= ( ) Damit zumindest g exakt integriert wird, fordern wir m j= β j =. 4 Runge-Kutta-Verfahren Technische Universität Bergakademie Freiberg
2 Numerik gewöhnlicher Differentialgleichungen 44 Daraus folgt y(t + h) y(t) + h = y(t) + h m β j y (t + γ j h) j= m β j f (t + γ j h, y(t + γ j h)). j= (RK-) Problem: y(t + γ j h) = y(t) + h γ j 0 y (t + τh) dτ sind unbekannt. Näherungen wieder durch Quadraturformeln, aber mit den alten Knoten γ j (j =,..., m) aus ( ) (sonst würden sich neue Unbekannte y(t + Knoten h) ergeben). γj 0 g(τ) dτ m α j,l g(γ l ) (j =,..., m). ( ) l= Damit zumindest g exakt integriert wird, fordern wir m l= α j,l = γ j j =,..., m. 4. Konstruktion Technische Universität Bergakademie Freiberg
3 Numerik gewöhnlicher Differentialgleichungen 45 Damit ergibt sich y(t + γ j h) y(t) + h m l= α j,ly (t + γ l h) = y(t) + h m l= α j,lf (t + γ l h, y(t + γ l h)). (RK-2) Abkürzung: k j := ( f (t + γ j h, y(t + γ j h)) (j =,..., m). (RK-2): kj f t + γ j h, y(t) + h ) m l= α j,l k l (j =,..., m). (RK-): y(t + h) y(t) + h m j= β j k j. m-stufiges Runge-Kutta-Verfahren (RKV): y n+ = y n + h m β j k j mit k j = f ( j= t n + γ j h, y n + h ) m α j,l k l (j =,..., m). (RKV) l= 4. Konstruktion Technische Universität Bergakademie Freiberg
4 Numerik gewöhnlicher Differentialgleichungen 46 Butcher-Matrix (John Charles Butcher, 933) (auch Runge-Kutta-ABC): γ α, α,m... γ m α m, α m,m β β m Beispiele /2 /2 symbolisiert ein zweistufiges explizites RKV (ein RKV ist explizit, wenn α j,l = 0 j l gilt), nämlich das verbesserte Euler-Verfahren. 4. Konstruktion Technische Universität Bergakademie Freiberg
5 Numerik gewöhnlicher Differentialgleichungen 47 0 /4 /4 2/3 /4 5/2 /4 3/4 symbolisiert ein zweistufiges implizites RKV: k = f ( t n, y n + 4 hk 4 hk 2), k 2 = f ( t n h, y n + 4 hk hk 2), ( zwei i.a. nichtlineare Gleichungen für k und k 2 ) y n+ = y n + 4 h(k + 3k 2 ). (Beispiel 2 aus Abschnitt 2.2 ist ein weiteres implizites zweistufiges RKV.) 4. Konstruktion Technische Universität Bergakademie Freiberg
6 Numerik gewöhnlicher Differentialgleichungen /2 / /6 4/6 /6 symbolisiert ein dreistufiges explizites RKV. Verfahren dritter Ordnung von Kutta: k = f (t n, y n ), k 2 = f ( t n + 2 h, y n + 2 hk ), k 3 = f (t n + h, y n hk + 2hk 2 ), y n+ = y n + 6 h(k + 4k 2 + k 3 ). 4. Konstruktion Technische Universität Bergakademie Freiberg
7 Numerik gewöhnlicher Differentialgleichungen /3 / /3 0 2/3 0 /4 0 3/4 symbolisiert ein dreistufiges explizites RKV. Verfahren dritter Ordnung von Heun: k = f (t n, y n ), k 2 = f ( t n + 3 h, y n + 3 hk ), k 3 = f ( t n h, y n hk 2), y n+ = y n + 4 h(k + 3k 3 ). (Vgl. Beispiel aus Abschnitt 2.2.) 4. Konstruktion Technische Universität Bergakademie Freiberg
8 Numerik gewöhnlicher Differentialgleichungen /2 / /2 0 / /6 2/6 2/6 /6 symbolisiert ein vierstufiges explizites RKV. Klassisches Runge-Kutta-Verfahren: k = f (t n, y n ), k 2 = f (t n + 2 h, y n + 2 hk ), k 3 = f (t n + 2 h, y n + 2 hk 2), k 4 = f (t n + h, y n + hk 3 ), y n+ = y n + 6 h(k + 2k 2 + 2k 3 + k 4 ). 4. Konstruktion Technische Universität Bergakademie Freiberg
9 Numerik gewöhnlicher Differentialgleichungen 5 Eine alternative Form von (RKV) ist y n+ = y n + h m β j f (t n + γ j h, ỹ j ) mit ỹ j = y n + h j= m α j,l f (t n + γ l h, ỹ l ) (j =,..., m). (RKV ) l= Setze k j = f (t n + γ j h, ỹ j ). Die ỹ j können als Approximationen an die Lösung y zur Zeit t n + γ j h interpretiert werden, die k j als Approximationen an y (t n + γ j h). 4. Konstruktion Technische Universität Bergakademie Freiberg
10 Numerik gewöhnlicher Differentialgleichungen Konsistenzordnung Jedes RKV hat die Form y n+ = y n + hφ f (y n, t n ; h) mit Φ f (y n, t n ; h) = m β j k j. j= Es ist ein Einschrittverfahren (ρ(ζ) = ζ ), also stabil und (vgl. Abschnitt 2.3) genau dann konsistent, wenn Φ f (y(t n ), t n ; 0) = f (t n, y(t n ))ρ () erfüllt ist, was hier zu m j= β j = äquivalent ist. Ein RKV ist deshalb genau dann konvergent, wenn gilt. m β j = j= 4.2 Konsistenzordnung Technische Universität Bergakademie Freiberg
11 Numerik gewöhnlicher Differentialgleichungen 53 Um die Konsistenzordnung eines RKVs zu bestimmen (oder um m-stufige RKV mit möglichst hoher Konsistenzordnung zu konstruieren), sind wie im Fall der Taylor-Verfahren (siehe Abschnitt 2.5) komplizierte Rechnungen erforderlich. Wir untersuchen als Beispiel explizite dreistufige RKV, γ 2 γ γ 3 γ 3 α 3,2 α 3,2 0, β β 2 β 3 und entwickeln h R n+ = y(t n+) y(t n ) h Φ f (y(t n ), t n ; h) = y(t n+) y(t n ) h 3 β j k j j= nach Potenzen von h (unter der Voraussetzung, dass y bzw. f genügend oft differenzierbar sind). 4.2 Konsistenzordnung Technische Universität Bergakademie Freiberg
12 Numerik gewöhnlicher Differentialgleichungen 54 Für skalare AWPe ergibt sich mit den Abkürzungen F := f t + f y f und G := f tt + 2f ty f + f yy f 2 (alle Ableitungen von f werden an der Stelle (t n, y(t n )) ausgewertet) die Beziehung Anderseits ist y(t n+ ) y(t n ) h k = f(t n, y(t n )) = f, = f + 2 F h + 6 (G + f yf )h 2 + O(h 3 ). k 2 = f(t n + hγ 2, y(t n ) + hγ 2 k ) = f + hγ 2 F + 2 h2 γ 2 2G + O(h 3 ), k 3 = f(t n + hγ 3, y(t n ) + h(γ 3 α 3,2 )k + hα 3,2 k 2 ) = f + hγ 3 F + h 2 (γ 2 α 3,2 F f y + 2 γ2 3G) + O(h 3 ). 4.2 Konsistenzordnung Technische Universität Bergakademie Freiberg
13 Numerik gewöhnlicher Differentialgleichungen 55 Das bedeutet: h R n+ = Folgerungen. [ 3 j= β j ] f + [ 2 β 2γ 2 β 3 γ 3 ] F h + [ ( 3 β 2γ 2 2 β 3 γ 2 3) 2 G + ( 6 β 3γ 2 α 3,2 )F f y ] h 2 + O(h 3 ).. Das Euler-Verfahren ist das einzige einstufige explizite RKV der Ordnung (β = ). Es gibt kein einstufiges explizites RKV höherer Ordnung. 2. Die zweistufigen expliziten RKV der Ordnung 2 sind durch β + β 2 = und β 2 γ 2 = 2 charakterisiert. Beispiele sind das modifizierte (β = 0, β 2 =, γ 2 = 2 ) und das verbesserte Euler-Verfahren (β = β 2 = 2, γ 2 = ). Kein explizites zweistufiges RKV besitzt die Ordnung Konsistenzordnung Technische Universität Bergakademie Freiberg
14 Numerik gewöhnlicher Differentialgleichungen Explizite dreistufige RKV der Ordnung 3 sind durch die vier Gleichungen β + β 2 + β 3 =, β 2 γ β 3 γ 2 3 = 3, β 2 γ 2 + β 3 γ 3 = 2, β 3γ 2 α 3,2 = 6 charakterisiert. (Man kann zeigen, dass keine dieser Methoden die Ordnung 4 besitzt.) Beispiele sind das Verfahren von Heun (β = 4, β 2 = 0, β 3 = 3 4, γ 2 = 3, γ 3 = α 3,2 = 2 3 ) und das Verfahren von Kutta (β = 6, β 2 = 2 3, β 3 = 6, γ 2 = 2, γ 3 =, α 3,2 = 2). 4. Ähnliche (kompliziertere) Rechnungen zeigen, dass es eine zweiparametrige Familie expliziter vierstufiger RKV der Ordnung 4 gibt, von denen keines die Ordnung 5 besitzt. Ein Beispiel ist das klassische Runge-Kutta-Verfahren. Weitere Beispiele sind 4.2 Konsistenzordnung Technische Universität Bergakademie Freiberg
15 Numerik gewöhnlicher Differentialgleichungen /3 / /3 / /8 3/8 3/8 /8 (3/8-Regel) /5 2/ /5 3/20 3/ /44 5/44 40/ /360 25/360 25/360 55/360 (Formel von Kuntzmann). 4.2 Konsistenzordnung Technische Universität Bergakademie Freiberg
16 Numerik gewöhnlicher Differentialgleichungen 58 Die oben beschriebene Methode, die Ordnung eines RKVs zu bestimmen, wird für Verfahren höherer Ordnung schnell unübersichtlich: Die Koeffizienten eines expliziten Verfahrens der Ordnung 3 müssen 4 Gleichungen erfüllen (s.o.), während bei einem Verfahren der Ordnung 8 bereits 200 nicht-lineare Gleichungen überprüft werden müssen. Die sog. Butcher-Theorie (vgl. J. C. Butcher, The Numerical Analysis of Ordinary Differential Equations. Runge-Kutta and General Linear Methods. John Wiley & Sons, Chichester 987) erleichtert mit Hilfe graphentheoretischer Bäume die Buchhaltung bei den partiellen Ableitungen von f und erlaubt eine elegante Berechnung der Ordnung eines gegebenen RKVs (sie liefert aber keine Methode, ein Verfahren mit gewünschter Ordnung zu konstruieren). Wir beschränken uns hier darauf, notwendige Ordnungsbedingungen abzuleiten, die sich aus den speziellen AWPen y = y + t l, y(0) = 0, (l N) ergeben. 4.2 Konsistenzordnung Technische Universität Bergakademie Freiberg
17 Numerik gewöhnlicher Differentialgleichungen 59 Satz 4. (Notwendige Ordnungsbedingungen für RKV) Das durch die Butcher-Matrix c A b definierte RKV besitze die Ordnung p. Dann gelten b A k C l (l )! e = (l + k)! = l(l + )... (l + k) für l =, 2,..., p und k = 0,,..., p l. Dabei sind b := [β, β 2,..., β m ], A := [α j,ν ] j,ν m, C := diag(γ, γ 2,..., γ m ) und e := [,,..., ] R m. 4.2 Konsistenzordnung Technische Universität Bergakademie Freiberg
18 Numerik gewöhnlicher Differentialgleichungen 60 Spezialfälle der notwendigen Bedingungen aus Satz 4. sind (für k = 0) b C l e = m j= β j γ l j = l für l =, 2,..., p sowie (für l = mit k k + ) b A k e = k! für k =, 2,..., p. Bemerkung. Ein explizites m-stufiges RKV besitzt höchstens die Konsistenzordnung m, denn hier ist A m = O (A ist echte untere Dreiecksmatrix). Für die optimale Ordnung p(m) eines expliziten m-stufigen RKVs gilt sogar p(m) m falls m 5, genauer: m p(m) Konsistenzordnung Technische Universität Bergakademie Freiberg
19 Numerik gewöhnlicher Differentialgleichungen Absolute Stabilität Wir wenden ein m-stufiges RKV auf die Testgleichung y = λy an und erhalten mit ĥ = λh [ ] y n+ = + ĥb (I m ĥa) e y n =: R(ĥ)y n, so dass (bei festem h) lim n y n = 0 (für alle y 0 ) genau dann gilt, wenn R(ĥ) < erfüllt ist. In Analogie zu Abschnitt 3.5 definieren wir den Stabilitätsbereich eines RKVs durch R A := {ĥ C : R(ĥ) < }. Für ein beliebiges m-stufiges RKV gilt R(ĥ) = + ĥb (I m ĥa) e = + ĥ j b T A j e. j= 4.3 Absolute Stabilität Technische Universität Bergakademie Freiberg
20 Numerik gewöhnlicher Differentialgleichungen 62 Besitzt das Verfahren die Ordnung p, so folgt R(ĥ) = p j=0 j!ĥj + j=p+ ĥ j b A j e. Ist das RKV explizit, so folgt m R(ĥ) = + ĥ j b T A j e. j= Insbesondere hängt der Stabilitätsbereich eines m-stufigen expliziten RKVs der Ordnung m ( m 4) wegen R(ĥ) = m j=0 j!ĥj nicht von den Koeffizienten des Verfahrens ab. Außerdem besitzt kein explizites RKV einen unbeschränkten Stabilitätsbereich (denn R ist ein Polynom). 4.3 Absolute Stabilität Technische Universität Bergakademie Freiberg
21 Numerik gewöhnlicher Differentialgleichungen 63 3 Verfahren dritter Ordnung von Heun 3 klassisches Rung Kutta Verfahren Absolute Stabilität Technische Universität Bergakademie Freiberg
22 Numerik gewöhnlicher Differentialgleichungen Eingebettete Runge-Kutta-Verfahren Kein Verfahren zur Lösung von AWPen arbeitet in der Praxis mit einer konstanten Schrittweite. Man wird vielmehr versuchen, die Schrittweite an das Verhalten der Lösung y anzupassen (ändert sich y in einem Bereich schnell, so ist dort eine kleine Schrittweite angebracht; in Bereichen, in denen y kaum variiert, ist eine größere Schrittweite ausreichend). Wir werden hier eine Schrittweitensteuerung vorstellen, die zum Ziel hat, den Konsistenzfehler K n+ := h R n+ (wird in der Literatur oft lokaler Diskretisierungsfehler genannt, vgl. Abschnitt 2.3) zu kontrollieren: K n tol, n =, 2,..., mit einer vorgebenen Toleranz tol. Bei Systemen von DGen (insbesondere dann, wenn die Lösungskomponenten von unterschiedlicher Größenordnung sind) wird man für jede Komponente eine eigene absolute Fehlertoleranz und global eine relative Fehlertoleranz festsetzen. 4.4 Eingebettete Runge-Kutta-Verfahren Technische Universität Bergakademie Freiberg
23 Numerik gewöhnlicher Differentialgleichungen 65 Das folgende Lemma besagt, dass mit dem Konsistenzfehler auch der (eigentlich interessante) globale Diskretisierungsfehler kontrolliert wird. Lemma 4.2 Für den globalen Diskretisierungsfehler e n = y(t n ) y n eines Einschrittverfahrens gilt e n (t n t 0 ) κ n exp(m(t n t 0 )). Dabei ist κ n := max{ K j : j = 0,,..., n} und M die Lipschitzkonstante der Verfahrensfunktion (vgl. (V 2 ) aus Abschnitt 2.2). Um den Konsistenzfehler zu schätzen, verwendet man zwei Methoden unterschiedlicher Konsistenzordnungen (sagen wir p und q mit p < q), um y n aus y n zu berechnen: y n = y n + hφ f (y n, t n ; h) bzw. ŷ n = y n + h Φ f (y n, t n ; h). 4.4 Eingebettete Runge-Kutta-Verfahren Technische Universität Bergakademie Freiberg
24 Numerik gewöhnlicher Differentialgleichungen 66 Für die zugehörigen Konsistenzfehler gelten: Daraus folgt K n = y(t n) y(t n ) h K n = y(t n) y(t n ) h Φ(y n, t n ; h) = O(h p ), Φ(y n, t n ; h) = O(h q ). K n K n = Φ(y n, t n ; h) Φ(y n, t n ; h) = h (ŷ n y n ). Wegen K n K n = K n ( + O(h q p )) K n erhalten wir aus eine (grobe) Schätzung für K n. h y n ŷ n K n 4.4 Eingebettete Runge-Kutta-Verfahren Technische Universität Bergakademie Freiberg
25 Numerik gewöhnlicher Differentialgleichungen 67 Ist h y n ŷ n > tol, so wird die Schrittweite h verworfen und mit ( h h ) p = α h tol y n ŷ n ( ) eine neue Schrittweite h bestimmt (α ist hier ein Sicherheitsfaktor, etwa α = 0.9). Ausgehend von y n werden jetzt neue Näherungen y n und ŷ n (an der Stelle t n + h) berechnet. Diesen Prozess wiederholt man so lange, bis h y n ŷ n tol erfüllt ist. Dann wird ( ) verwendet, um eine neue (größere) Schrittweite für den nächsten Schritt (n n + ) vorzuschlagen. Die Wahl von h nach ( ) motiviert sich folgendermaßen: benutzte Schrittweite h: h y n ŷ n K n = ch p + O(h p+ ) ch p, erwünschte Schrittweite h: tol = K n = c h p + O( h p+ ) c h p. 4.4 Eingebettete Runge-Kutta-Verfahren Technische Universität Bergakademie Freiberg
26 Numerik gewöhnlicher Differentialgleichungen 68 Um den Aufwand in Grenzen zu halten, verwendet man zur Berechnung von y n und ŷ n zwei RKV (verschiedener Ordnungen), deren Butcher-Matrizen sich nur im Vektor b unterscheiden (d.h. A und c sind für beide Verfahren gleich, so dass die Größen k j nur einmal berechnet werden müssen). Man spricht von eingebetteten RKV und schreibt c A b, z.b. b /2 /2. Im Beispiel wird ein RKV der Ordnung (das Euler-Verfahren) in ein RKV der Ordnung 2 (das verbesserte Euler-Verfahren) eingebettet. 4.4 Eingebettete Runge-Kutta-Verfahren Technische Universität Bergakademie Freiberg
27 Numerik gewöhnlicher Differentialgleichungen 69 Ein populäres Beispiel ist die Fehlberg 4(5)-Formel: Hier werden zwei sechsstufige RKV der Ordnungen 4 bzw. 5 kombiniert Eingebettete Runge-Kutta-Verfahren Technische Universität Bergakademie Freiberg
28 Numerik gewöhnlicher Differentialgleichungen Implizite und halb-implizite Verfahren Ist die Matrix A eines m-stufigen RKVs keine echte untere -Matrix (ist das RKV also implizit), so muss in jedem Zeitschritt ein nicht-lineares Gleichungssystem der Form k = f (t n + γ h, h m l= α,lk l ).. k m = f (t n + γ m h, h m l= α m,lk l ). ( ) gelöst werden. Dieses System hat also mn Unbekannte, wenn y = f(t, y) aus n Gleichungen besteht. Mit Hilfe des Banachschen Fixpunktsatzes erkennt man, dass ( ) für genügend kleine h eindeutig lösbar ist. In der Praxis wird man dieses System aber nicht mit der Fixpunktiteration, sondern mit einem Newton- bzw. Quasi-Newton-Verfahren lösen. 4.5 Implizite und halb-implizite Verfahren Technische Universität Bergakademie Freiberg
29 Numerik gewöhnlicher Differentialgleichungen 7 Ist A eine untere (aber keine echte untere) -Matrix, so nennt man das zugehörige RKV halb-implizit. Das System ( ) zerfällt dann in m Systeme mit jeweils n Unbekannten. Implizite RKV werden oft mit Hilfe von Gauß-Quadraturformeln konstruiert. Dies sind Formeln der Bauart b m g(τ)dτ = β j g(γ j ) + R m (g). a j= Hier werden die Gewichte β j und Knoten γ j so gewählt, dass R m (p) = 0 für Polynome p möglichst hohen Grades d erfüllt ist. Man kann zeigen (vgl. Numerik I), dass eine optimale Wahl auf d = 2m führt (man sagt die Quadraturformel hat Exaktheitsgrad 2m). Die zugehörigen RKV (auch sie werden Gauß-Formeln genannt) haben die Ordnung 2m. Beachte, dass kein m-stufiges RKV eine höhere Ordnung besitzen kann. Warum? 4.5 Implizite und halb-implizite Verfahren Technische Universität Bergakademie Freiberg
30 Numerik gewöhnlicher Differentialgleichungen 72 Für m = ergibt sich die implizite Mittelpunktsregel welche die Ordnung 2 besitzt. /2 /2, Für m = 2 und m = 3 ergeben sich die Gauß-Formeln bzw mit den Konsistenzordnungen 4 bzw. 6. Bei Gauß-Radau-Integrationsformeln wählt man einen Knoten als (entweder linken oder rechten) Endpunkt des Integrationsintervalls. 4.5 Implizite und halb-implizite Verfahren Technische Universität Bergakademie Freiberg
31 Numerik gewöhnlicher Differentialgleichungen 73 Die übrigen Knoten und alle Gewichte werden so bestimmt, dass sich ein möglichst hoher Exaktheitsgrad ergibt. Man kann zeigen, dass eine Gauß-Radau-Formel mit m Knoten den Exaktheitsgrad 2m besitzt. Daher haben die zugehörigen impliziten RKV die Konsistenzordnung 2m. Zu dieser Klasse gehören die Verfahren und Schließlich kann man noch beide Enden des Integrationsintervalls als Knoten wählen und die übrigen Daten so bestimmen, dass die zugehörige Integrationsformel den Exaktheitsgrad 2m 2 (bzw. das zugehörige implizite RKV die Konsistenzordnung 2m 2) besitzt. Man spricht von Gauß-Lobatto-Formeln. Ein Beispiel ist die Trapezregel (für m = 2). 4.5 Implizite und halb-implizite Verfahren Technische Universität Bergakademie Freiberg
32 Numerik gewöhnlicher Differentialgleichungen 74 Ein Vorteil von impliziten gegenüber expliziten RKV ist ihr wesentlich größerer Stabilitätsbereich (wird ausführlicher im nächsten Kapitel diskutiert). Wir betrachten die Trapezregel 0 0 /2 /2 /2 /2 d.h. k = f (t n, y n ), k 2 = f (t n+, y n + h(k + k 2 )/2), y n+ = y n + h(k + k 2 )/2, oder kürzer: y n+ = y n + h(f (t n, y n ) + f (t n+, y n+ ))/2. Die zugehörige Stabilitätsfunktion ist R(ĥ) = ( + ĥ/2)/( ĥ/2) und es gilt: R(ĥ) < + ĥ/2 < ĥ/2 Real(ĥ) < 0. Die Trapezregel ist daher A-stabil. (Man nennt ein Verfahren A-stabil, wenn sein Stabilitätsbereich die (offene) linke Halbebene enthält.) 4.5 Implizite und halb-implizite Verfahren Technische Universität Bergakademie Freiberg
33 Numerik gewöhnlicher Differentialgleichungen Kollokationsmethoden Kollokationsmethoden sind spezielle implizite RKV, die auf Grund ihrer Konstruktion sehr viel leichter zu analysieren sind als allgemeine RKV. Mit gegebenen 0 γ < γ 2 < < γ m setzen wir t (j) := t n + γ j h (j =, 2,..., m) und suchen ein Polynom p vom Grad m (bei Systemen von k DGen ist das ein Vektor p = [p, p 2,..., p k ] aus k Polynomen vom Grad höchstens m), das die Interpolationsbedingungen p(t n ) = y n, p (t (j) ) = f (t (j), p(t (j) )) (j =, 2,..., m) erfüllt. Die Näherung y n+ an der Stelle t n+ wird dann definiert durch y n+ := p(t n+ ). 4.6 Kollokationsmethoden Technische Universität Bergakademie Freiberg
34 Numerik gewöhnlicher Differentialgleichungen 76 p ist ein Polynom vom Grad m, das durch die letzten m dieser Interpolationsbedingungen eindeutig bestimmt ist. In Lagrange-Form besitzt es die Darstellung p (t n + τh) = m j= l j(t n + τh)k j mit l j (t n + τh) = m j i= Jetzt folgt für jedes i {, 2,..., m} Analog: τ γ i γ j γ i und k j := p (t (j) ). p(t (i) ) p(t n ) = t (i) t n p (t n + sh) ds = t (i) m t n j= l j(t n + sh)k j ds = h m ( γi j= 0 l j(r) dr ) k j =: h m j= α i,jk j. p(t n+ ) p(t n ) = h ( m ) j= 0 l j(r) dr k j =: h m j= β jk j. 4.6 Kollokationsmethoden Technische Universität Bergakademie Freiberg
35 Numerik gewöhnlicher Differentialgleichungen 77 Daraus folgt y n+ = p(t n+ ) = p(t n ) + h m j= β jk j = y n + h m j= β jk j mit k j = p (t (j) ) = f (t (j), p(t (j) )) = f (t n + γ j h, y n + m l= α j,lk l ). Mit anderen Worten: Jedes Kollokationsverfahren ist ein (implizites) RKV. Implementiert wird es in der Form (RKV) bzw. (RKV ), d.h. zu gegebenen γ j (j =, 2,..., m) bestimmt man zunächst (i, j =, 2..., m). α i,j = γ i 0 l j(r) dr und β j = 0 l j(r) dr Nicht jedes implizite RKV ist ein Kollokationsverfahren. Beispiel /3 /3 /3 /4 3/4 repräsentiert kein Kollokationsverfahren. 4.6 Kollokationsmethoden Technische Universität Bergakademie Freiberg
36 Numerik gewöhnlicher Differentialgleichungen 78 Satz 4.3 (Konsistenzordnung bei Kollokationsverfahren) Für ein m-stufiges Kollokationsverfahren mit der Butcher-Matrix c A b sind die folgenden drei Aussagen äquivalent: Das Verfahren besitzt die Konsistenzordnung m + p. 0 τ j m j= (τ γ j) dτ = 0 für j = 0,,..., p. b C l e = /l für l =, 2,..., m + p. Dabei sind C := diag(γ, γ 2,..., γ m ) und e := [,,..., ] R m. 4.6 Kollokationsmethoden Technische Universität Bergakademie Freiberg
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
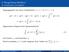 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Definition 3.1: Ein Differentialgleichungssystem 1. Ordnung
 Kapitel 3 Dynamische Systeme Definition 31: Ein Differentialgleichungssystem 1 Ordnung = f(t, y) ; y R N ; f : R R N R N heißt namisches System auf dem Phasenraum R N Der Parameter t wird die Zeit genannt
Kapitel 3 Dynamische Systeme Definition 31: Ein Differentialgleichungssystem 1 Ordnung = f(t, y) ; y R N ; f : R R N R N heißt namisches System auf dem Phasenraum R N Der Parameter t wird die Zeit genannt
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Tangentengleichung. Wie lautet die Geradengleichung für die Tangente, y T =? Antwort:
 Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Charakteristikenmethode im Beispiel
 Charakteristikenmethode im Wir betrachten die PDE in drei Variablen xu x + yu y + (x + y )u z = 0. Das charakteristische System lautet dann ẋ = x ẏ = y ż = x + y und besitzt die allgemeine Lösung x(t)
Charakteristikenmethode im Wir betrachten die PDE in drei Variablen xu x + yu y + (x + y )u z = 0. Das charakteristische System lautet dann ẋ = x ẏ = y ż = x + y und besitzt die allgemeine Lösung x(t)
Rekursionen. Georg Anegg 25. November 2009. Methoden und Techniken an Beispielen erklärt
 Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
 9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
Musterlösungen zur Linearen Algebra II Blatt 5
 Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Kevin Caldwell. 18.April 2012
 im Rahmen des Proseminars Numerische Lineare Algebra von Prof.Dr.Sven Beuchler 18.April 2012 Gliederung 1 2 3 Mathematische Beschreibung von naturwissenschaftlich-technischen Problemstellungen führt häufig
im Rahmen des Proseminars Numerische Lineare Algebra von Prof.Dr.Sven Beuchler 18.April 2012 Gliederung 1 2 3 Mathematische Beschreibung von naturwissenschaftlich-technischen Problemstellungen führt häufig
Lösungsmethoden gewöhnlicher Differentialgleichungen (Dgl.)
 Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen.
 13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
DIFFERENTIALGLEICHUNGEN
 DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
!(0) + o 1("). Es ist damit möglich, dass mehrere Familien geschlossener Orbits gleichzeitig abzweigen.
 Bifurkationen an geschlossenen Orbits 5.4 167 der Schnittabbldung konstruiert. Die Periode T (") der zugehörigen periodischen Lösungen ergibt sich aus =! + o 1 (") beziehungsweise Es ist also t 0 = T (")
Bifurkationen an geschlossenen Orbits 5.4 167 der Schnittabbldung konstruiert. Die Periode T (") der zugehörigen periodischen Lösungen ergibt sich aus =! + o 1 (") beziehungsweise Es ist also t 0 = T (")
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Universität Bonn, Institut für Angewandte Mathematik. WS 2012/2013 Prüfung Angewandte Mathematik und Statistik - Agrarwiss. /ELW
 Universität Bonn, Institut für Angewandte Mathematik Dr. Antje Kiesel WS 2012/2013 Prüfung Angewandte Mathematik und Statistik - Agrarwiss. /ELW 08.03.2013 Matrikelnummer Platz Name Vorname 1 2 3 4 5 6
Universität Bonn, Institut für Angewandte Mathematik Dr. Antje Kiesel WS 2012/2013 Prüfung Angewandte Mathematik und Statistik - Agrarwiss. /ELW 08.03.2013 Matrikelnummer Platz Name Vorname 1 2 3 4 5 6
Approximation durch Taylorpolynome
 TU Berlin Fakultät II - Mathematik und Naturwissenschaften Sekretariat MA 4-1 Straße des 17. Juni 10623 Berlin Hochschultag Approximation durch Taylorpolynome Im Rahmen der Schülerinnen- und Schüler-Uni
TU Berlin Fakultät II - Mathematik und Naturwissenschaften Sekretariat MA 4-1 Straße des 17. Juni 10623 Berlin Hochschultag Approximation durch Taylorpolynome Im Rahmen der Schülerinnen- und Schüler-Uni
11.3 Komplexe Potenzreihen und weitere komplexe Funktionen
 .3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
.3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
 Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand
 Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Modulabschlussklausur Analysis II
 Modulabschlussklausur Analysis II. Juli 015 Bearbeitungszeit: 150 min Aufgabe 1 [5/10 Punkte] Es sei a R und f a : R 3 R mit f a (x, y, z) = x cos(y) + z 3 sin(y) + a 3 + (z + ay a y) cos(x) a) Bestimmen
Modulabschlussklausur Analysis II. Juli 015 Bearbeitungszeit: 150 min Aufgabe 1 [5/10 Punkte] Es sei a R und f a : R 3 R mit f a (x, y, z) = x cos(y) + z 3 sin(y) + a 3 + (z + ay a y) cos(x) a) Bestimmen
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Eigenwerte und Eigenvektoren von Matrizen
 Eigenwerte und Eigenvektoren von Matrizen Das Eigenwertproblem Sei A eine quadratische Matrix vom Typ m,m. Die Aufgabe, eine Zahl λ und einen dazugehörigen Vektor x zu finden, damit Ax = λx ist, nennt
Eigenwerte und Eigenvektoren von Matrizen Das Eigenwertproblem Sei A eine quadratische Matrix vom Typ m,m. Die Aufgabe, eine Zahl λ und einen dazugehörigen Vektor x zu finden, damit Ax = λx ist, nennt
Abschlussprüfung Realschule Bayern II / III: 2009 Haupttermin B 1.0 B 1.1
 B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Modellbildungssysteme: Pädagogische und didaktische Ziele
 Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
6 Allgemeine Theorie des elektromagnetischen Feldes im Vakuum
 6 ALLGEMEINE THEORIE DES ELEKTROMAGNETISCHEN FELDES IM VAKUUM 25 Vorlesung 060503 6 Allgemeine Theorie des elektromagnetischen Feldes im Vakuum 6.1 Grundaufgabe der Elektrodynamik Gegeben: Ladungsdichte
6 ALLGEMEINE THEORIE DES ELEKTROMAGNETISCHEN FELDES IM VAKUUM 25 Vorlesung 060503 6 Allgemeine Theorie des elektromagnetischen Feldes im Vakuum 6.1 Grundaufgabe der Elektrodynamik Gegeben: Ladungsdichte
Konzepte der Informatik
 Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
3.1. Die komplexen Zahlen
 3.1. Die komplexen Zahlen Es gibt viele Wege, um komplexe Zahlen einzuführen. Wir gehen hier den wohl einfachsten, indem wir C R als komplexe Zahlenebene und die Punkte dieser Ebene als komplexe Zahlen
3.1. Die komplexen Zahlen Es gibt viele Wege, um komplexe Zahlen einzuführen. Wir gehen hier den wohl einfachsten, indem wir C R als komplexe Zahlenebene und die Punkte dieser Ebene als komplexe Zahlen
Anmerkungen zur Übergangsprüfung
 DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
3. LINEARE GLEICHUNGSSYSTEME
 176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
Optimale Steuerung. Sequentielle Quadratische Programmierung. Kevin Sieg. 14. Juli 2010. Fachbereich für Mathematik und Statistik Universität Konstanz
 Optimale Steuerung Kevin Sieg Fachbereich für Mathematik und Statistik Universität Konstanz 14. Juli 2010 1 / 29 Aufgabenstellung 1 Aufgabenstellung Aufgabenstellung 2 Die zusammengesetzte Trapezregel
Optimale Steuerung Kevin Sieg Fachbereich für Mathematik und Statistik Universität Konstanz 14. Juli 2010 1 / 29 Aufgabenstellung 1 Aufgabenstellung Aufgabenstellung 2 Die zusammengesetzte Trapezregel
Stabilität mittels Ljapunov Funktion
 Stabilität mittels Ljapunov Funktion Definition Eine C 1 Funktion V : D R, D R, heißt eine Ljapunov Funktion auf K r (0) D für f(y), falls gilt: 1) V(0) = 0, V(y) > 0 für y 0 2) V,f(y) 0 ( y, y r) Gilt
Stabilität mittels Ljapunov Funktion Definition Eine C 1 Funktion V : D R, D R, heißt eine Ljapunov Funktion auf K r (0) D für f(y), falls gilt: 1) V(0) = 0, V(y) > 0 für y 0 2) V,f(y) 0 ( y, y r) Gilt
6.2 Perfekte Sicherheit
 04 6.2 Perfekte Sicherheit Beweis. H(B AC) + H(A C) = H(ABC) H(AC) + H(AC) H(C) Wegen gilt Einsetzen in die Definition gibt = H(AB C). H(A BC) = H(AB C) H(B C). I(A; B C) = H(A C) H(AB C) + H(B C). Da
04 6.2 Perfekte Sicherheit Beweis. H(B AC) + H(A C) = H(ABC) H(AC) + H(AC) H(C) Wegen gilt Einsetzen in die Definition gibt = H(AB C). H(A BC) = H(AB C) H(B C). I(A; B C) = H(A C) H(AB C) + H(B C). Da
2.4 Adaptive Verfahren mit Schrittweitensteuerung
 0 0 0 Euler und RK4 fuer f(t,y) = t 0. Euler RK4 /N 0 0 f(t,y) =. t 0., graduiertes Gitter RK4 /N 4 Fehler bei T = 0 3 0 4 0 5 Fehler bei T = 0 5 0 0 0 6 0 7 0 0 0 0 2 0 3 0 4 0 5 Anzahl Schritte N 0 5
0 0 0 Euler und RK4 fuer f(t,y) = t 0. Euler RK4 /N 0 0 f(t,y) =. t 0., graduiertes Gitter RK4 /N 4 Fehler bei T = 0 3 0 4 0 5 Fehler bei T = 0 5 0 0 0 6 0 7 0 0 0 0 2 0 3 0 4 0 5 Anzahl Schritte N 0 5
Vorkurs Mathematik Übungen zu Polynomgleichungen
 Vorkurs Mathematik Übungen zu en 1 Aufgaben Lineare Gleichungen Aufgabe 1.1 Ein Freund von Ihnen möchte einen neuen Mobilfunkvertrag abschließen. Es gibt zwei verschiedene Angebote: Anbieter 1: monatl.
Vorkurs Mathematik Übungen zu en 1 Aufgaben Lineare Gleichungen Aufgabe 1.1 Ein Freund von Ihnen möchte einen neuen Mobilfunkvertrag abschließen. Es gibt zwei verschiedene Angebote: Anbieter 1: monatl.
Optimierung für Nichtmathematiker
 Optimierung für Nichtmathematiker Typische Prüfungsfragen Die folgenden Fragen dienen lediglich der Orientierung und müssen nicht den tatsächlichen Prüfungsfragen entsprechen. Auch Erkenntnisse aus den
Optimierung für Nichtmathematiker Typische Prüfungsfragen Die folgenden Fragen dienen lediglich der Orientierung und müssen nicht den tatsächlichen Prüfungsfragen entsprechen. Auch Erkenntnisse aus den
Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. z(t) = at + b
 Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
1. Weniger Steuern zahlen
 1. Weniger Steuern zahlen Wenn man arbeitet, zahlt man Geld an den Staat. Dieses Geld heißt Steuern. Viele Menschen zahlen zu viel Steuern. Sie haben daher wenig Geld für Wohnung, Gewand oder Essen. Wenn
1. Weniger Steuern zahlen Wenn man arbeitet, zahlt man Geld an den Staat. Dieses Geld heißt Steuern. Viele Menschen zahlen zu viel Steuern. Sie haben daher wenig Geld für Wohnung, Gewand oder Essen. Wenn
Codierungstheorie Rudolf Scharlau, SoSe 2006 9
 Codierungstheorie Rudolf Scharlau, SoSe 2006 9 2 Optimale Codes Optimalität bezieht sich auf eine gegebene Quelle, d.h. eine Wahrscheinlichkeitsverteilung auf den Symbolen s 1,..., s q des Quellalphabets
Codierungstheorie Rudolf Scharlau, SoSe 2006 9 2 Optimale Codes Optimalität bezieht sich auf eine gegebene Quelle, d.h. eine Wahrscheinlichkeitsverteilung auf den Symbolen s 1,..., s q des Quellalphabets
0, v 6 = 2 2. 1, v 4 = 1. 2. span(v 1, v 5, v 6 ) = span(v 1, v 2, v 3, v 4, v 5, v 6 ) 4. span(v 1, v 2, v 4 ) = span(v 2, v 3, v 5, v 6 )
 Aufgabe 65. Ganz schön span(n)end. Gegeben sei folgende Menge M von 6 Vektoren v, v,..., v 6 R 4 aus Aufgabe P 6: M = v =, v =, v =, v 4 =, v 5 =, v 6 = Welche der folgenden Aussagen sind wahr? span(v,
Aufgabe 65. Ganz schön span(n)end. Gegeben sei folgende Menge M von 6 Vektoren v, v,..., v 6 R 4 aus Aufgabe P 6: M = v =, v =, v =, v 4 =, v 5 =, v 6 = Welche der folgenden Aussagen sind wahr? span(v,
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen
 Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
Prozentrechnung. Klaus : = Karin : =
 Prozentrechnung Klaus erzählt, dass bei der letzten Mathe-Arbeit 6 seiner Mitschüler die Note gut erhalten hätten. Seine Schwester Karin hat auch eine Arbeit zurück bekommen. In ihrer Klasse haben sogar
Prozentrechnung Klaus erzählt, dass bei der letzten Mathe-Arbeit 6 seiner Mitschüler die Note gut erhalten hätten. Seine Schwester Karin hat auch eine Arbeit zurück bekommen. In ihrer Klasse haben sogar
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen?
 Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Rekursionen (Teschl/Teschl 8.1-8.2)
 Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Taylorentwicklung der k ten Dimension
 Taylorentwicklung der k ten Dimension 1.) Taylorentwicklung... 2 1.1.) Vorgehenesweise... 2 1.2.) Beispiel: f ((x, y)) = e x2 +y 2 8x 2 4y 4... 3 2.) Realisierung des Algorithmus im CAS Sage Math... 5
Taylorentwicklung der k ten Dimension 1.) Taylorentwicklung... 2 1.1.) Vorgehenesweise... 2 1.2.) Beispiel: f ((x, y)) = e x2 +y 2 8x 2 4y 4... 3 2.) Realisierung des Algorithmus im CAS Sage Math... 5
Bestimmung einer ersten
 Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Fachschaft Mathematik und Informatik (FIM) LA I VORKURS. Herbstsemester 2015. gehalten von Harald Baum
 Fachschaft Mathematik und Informatik (FIM) LA I VORKURS Herbstsemester 2015 gehalten von Harald Baum 2. September 2015 Inhaltsverzeichnis 1. Stichpunkte zur Linearen Algebra I 2. Körper 3. Vektorräume
Fachschaft Mathematik und Informatik (FIM) LA I VORKURS Herbstsemester 2015 gehalten von Harald Baum 2. September 2015 Inhaltsverzeichnis 1. Stichpunkte zur Linearen Algebra I 2. Körper 3. Vektorräume
a n + 2 1 auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert:
 Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
3.3 Eigenwerte und Eigenräume, Diagonalisierung
 3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
x 2 2x + = 3 + Es gibt genau ein x R mit ax + b = 0, denn es gilt
 - 17 - Die Frage ist hier also: Für welche x R gilt x = x + 1? Das ist eine quadratische Gleichung für x. Es gilt x = x + 1 x x 3 = 0, und man kann quadratische Ergänzung machen:... ( ) ( ) x x + = 3 +
- 17 - Die Frage ist hier also: Für welche x R gilt x = x + 1? Das ist eine quadratische Gleichung für x. Es gilt x = x + 1 x x 3 = 0, und man kann quadratische Ergänzung machen:... ( ) ( ) x x + = 3 +
Kapitel 15. Lösung linearer Gleichungssysteme
 Kapitel 15. Lösung linearer Gleichungssysteme Lineare Gleichungssysteme Wir befassen uns nun mit der Lösung im allgemeinen nichthomogener linearer Gleichungssysteme in zweifacher Hinsicht. Wir studieren
Kapitel 15. Lösung linearer Gleichungssysteme Lineare Gleichungssysteme Wir befassen uns nun mit der Lösung im allgemeinen nichthomogener linearer Gleichungssysteme in zweifacher Hinsicht. Wir studieren
Auswertung des Jahresabschlusses Bilanzanalyse 2
 KA11 Unternehmensergebnisse aufbereiten, bewerten und nutzen Auswertung des Jahresabschlusses Bilanzanalyse 2 Kennzahlen zur Bilanzanalyse Die aufbereitete Bilanz kann mit Hilfe unterschiedlicher Kennzahlen
KA11 Unternehmensergebnisse aufbereiten, bewerten und nutzen Auswertung des Jahresabschlusses Bilanzanalyse 2 Kennzahlen zur Bilanzanalyse Die aufbereitete Bilanz kann mit Hilfe unterschiedlicher Kennzahlen
Umgekehrte Kurvendiskussion
 Umgekehrte Kurvendiskussion Bei einer Kurvendiskussion haben wir eine Funktionsgleichung vorgegeben und versuchen ihre 'Besonderheiten' herauszufinden: Nullstellen, Extremwerte, Wendepunkte, Polstellen
Umgekehrte Kurvendiskussion Bei einer Kurvendiskussion haben wir eine Funktionsgleichung vorgegeben und versuchen ihre 'Besonderheiten' herauszufinden: Nullstellen, Extremwerte, Wendepunkte, Polstellen
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer
 Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
5 Eigenwerte und die Jordansche Normalform
 Mathematik für Physiker II, SS Mittwoch 8.6 $Id: jordan.tex,v.6 /6/7 8:5:3 hk Exp hk $ 5 Eigenwerte und die Jordansche Normalform 5.4 Die Jordansche Normalform Wir hatten bereits erwähnt, dass eine n n
Mathematik für Physiker II, SS Mittwoch 8.6 $Id: jordan.tex,v.6 /6/7 8:5:3 hk Exp hk $ 5 Eigenwerte und die Jordansche Normalform 5.4 Die Jordansche Normalform Wir hatten bereits erwähnt, dass eine n n
5. Bildauflösung ICT-Komp 10
 5. Bildauflösung ICT-Komp 10 Was sind dpi? Das Maß für die Bildauflösung eines Bildes sind dpi. Jeder spricht davon, aber oft weiß man gar nicht genau was das ist. Die Bezeichnung "dpi" ist ein Maß, mit
5. Bildauflösung ICT-Komp 10 Was sind dpi? Das Maß für die Bildauflösung eines Bildes sind dpi. Jeder spricht davon, aber oft weiß man gar nicht genau was das ist. Die Bezeichnung "dpi" ist ein Maß, mit
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Wurzeln als Potenzen mit gebrochenen Exponenten. Vorkurs, Mathematik
 Wurzeln als Potenzen mit gebrochenen Exponenten Zur Einstimmung Wir haben die Formel benutzt x m n = x m n nach der eine Exponentialzahl potenziert wird, indem man die Exponenten multipliziert. Dann sollte
Wurzeln als Potenzen mit gebrochenen Exponenten Zur Einstimmung Wir haben die Formel benutzt x m n = x m n nach der eine Exponentialzahl potenziert wird, indem man die Exponenten multipliziert. Dann sollte
Lösungsvorschlag für die Probeklausuren und Klausuren zu Algebra für Informations- und Kommunikationstechniker bei Prof. Dr.
 Lösungsvorschlag für die Probeklausuren und Klausuren zu Algebra für Informations- und Kommunikationstechniker bei Prof. Dr. Kurzweil Florian Franzmann André Diehl Kompiliert am 10. April 2006 um 18:33
Lösungsvorschlag für die Probeklausuren und Klausuren zu Algebra für Informations- und Kommunikationstechniker bei Prof. Dr. Kurzweil Florian Franzmann André Diehl Kompiliert am 10. April 2006 um 18:33
W-Rechnung und Statistik für Ingenieure Übung 11
 W-Rechnung und Statistik für Ingenieure Übung 11 Christoph Kustosz ([email protected]) Mathematikgebäude Raum 715 Christoph Kustosz ([email protected]) W-Rechnung und Statistik
W-Rechnung und Statistik für Ingenieure Übung 11 Christoph Kustosz ([email protected]) Mathematikgebäude Raum 715 Christoph Kustosz ([email protected]) W-Rechnung und Statistik
Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme
 Übung Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme Diese Übung beschäftigt sich mit Grundbegriffen der linearen Algebra. Im Speziellen werden lineare Abbildungen, sowie
Übung Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme Diese Übung beschäftigt sich mit Grundbegriffen der linearen Algebra. Im Speziellen werden lineare Abbildungen, sowie
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Behörde für Bildung und Sport Abitur 2008 Lehrermaterialien zum Leistungskurs Mathematik
 Abitur 8 II. Insektenpopulation LA/AG In den Tropen legen die Weibchen einer in Deutschland unbekannten Insektenpopulation jedes Jahr kurz vor Beginn der Regenzeit jeweils 9 Eier und sterben bald darauf.
Abitur 8 II. Insektenpopulation LA/AG In den Tropen legen die Weibchen einer in Deutschland unbekannten Insektenpopulation jedes Jahr kurz vor Beginn der Regenzeit jeweils 9 Eier und sterben bald darauf.
Abituraufgabe zur Analysis, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Analysis, Hessen 2009, Grundkurs (TR) Gegeben ist die trigonometrische Funktion f mit f(x) = 2 sin(2x) 1 (vgl. Material 1). 1.) Geben Sie für die Funktion f den Schnittpunkt mit der y
Abituraufgabe zur Analysis, Hessen 2009, Grundkurs (TR) Gegeben ist die trigonometrische Funktion f mit f(x) = 2 sin(2x) 1 (vgl. Material 1). 1.) Geben Sie für die Funktion f den Schnittpunkt mit der y
Theoretische Grundlagen der Informatik WS 09/10
 Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
Theoretische Grundlagen der Informatik WS 09/10 - Tutorium 6 - Michael Kirsten und Kai Wallisch Sitzung 13 02.02.2010 Inhaltsverzeichnis 1 Formeln zur Berechnung Aufgabe 1 2 Hamming-Distanz Aufgabe 2 3
14 Schmiegeparabel und Freunde, Taylor-Reihe
 14 Schmiegeparabel und Freunde, Taylor-Reihe Jörn Loviscach Versionsstand: 20. März 2012, 16:01 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.j3l7h.de/videos.html
14 Schmiegeparabel und Freunde, Taylor-Reihe Jörn Loviscach Versionsstand: 20. März 2012, 16:01 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.j3l7h.de/videos.html
Wir machen neue Politik für Baden-Württemberg
 Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Codierungsverfahren SS 2011. Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur
 Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur Wie die zyklischen BCH-Codes zur Mehrbitfehler-Korrektur eignen sich auch die sehr verwandten Reed-Solomon-Codes (= RS-Codes) zur Mehrbitfehler-Korrektur.
Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur Wie die zyklischen BCH-Codes zur Mehrbitfehler-Korrektur eignen sich auch die sehr verwandten Reed-Solomon-Codes (= RS-Codes) zur Mehrbitfehler-Korrektur.
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
6.2 Scan-Konvertierung (Scan Conversion)
 6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
der Eingabe! Haben Sie das Ergebnis? Auf diesen schwarzen Punkt kommen wir noch zu sprechen.
 Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
BONUS MALUS SYSTEME UND MARKOV KETTEN
 Fakultät Mathematik und Naturwissenschaften, Fachrichtung Mathematik, Institut für Mathematische Stochastik BONUS MALUS SYSTEME UND MARKOV KETTEN Klaus D. Schmidt Ringvorlesung TU Dresden Fakultät MN,
Fakultät Mathematik und Naturwissenschaften, Fachrichtung Mathematik, Institut für Mathematische Stochastik BONUS MALUS SYSTEME UND MARKOV KETTEN Klaus D. Schmidt Ringvorlesung TU Dresden Fakultät MN,
Definition:Eine meromorphe Modulform vom Gewicht k Z ist eine meromorphe. f : H C. (ii) C > 0, so daß f(z) im Bereich Im z > C keine Singularität hat.
 Die k/2 - Formel von Renate Vistorin Zentrales Thema dieses Vortrages ist die k/2 - Formel für meromorphe Modulformen als eine Konsequenz des Residuensatzes. Als Folgerungen werden danach einige Eigenschaften
Die k/2 - Formel von Renate Vistorin Zentrales Thema dieses Vortrages ist die k/2 - Formel für meromorphe Modulformen als eine Konsequenz des Residuensatzes. Als Folgerungen werden danach einige Eigenschaften
Skript und Aufgabensammlung Terme und Gleichungen Mathefritz Verlag Jörg Christmann Nur zum Privaten Gebrauch! Alle Rechte vorbehalten!
 Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Wichtig ist die Originalsatzung. Nur was in der Originalsatzung steht, gilt. Denn nur die Originalsatzung wurde vom Gericht geprüft.
 Das ist ein Text in leichter Sprache. Hier finden Sie die wichtigsten Regeln für den Verein zur Förderung der Autonomie Behinderter e. V.. Das hier ist die Übersetzung der Originalsatzung. Es wurden nur
Das ist ein Text in leichter Sprache. Hier finden Sie die wichtigsten Regeln für den Verein zur Förderung der Autonomie Behinderter e. V.. Das hier ist die Übersetzung der Originalsatzung. Es wurden nur
Die Übereckperspektive mit zwei Fluchtpunkten
 Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
