8 Numerik gewöhnlicher Differentialgleichungen
|
|
|
- Hedwig Beckenbauer
- vor 6 Jahren
- Abrufe
Transkript
1 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 03 8 Numerik gewöhnlicher Differentialgleichungen 8. Grundlagen In der Numerik von gewöhnlichen Differentialgleichungen werden vorwiegend Aufgaben folgender Art behandelt: Definition 8.. (Aufgabenstellung) gegeben ist eine Anfangswertaufgabe: explizites Differentialgleichungssystem Ordnung: Anfangswert: y = f(x, y ) mit f : R R n R n y(x 0 ) = y 0 = ( y 0,.. ) T.,y0 n R n gesucht ist der Funktionswert ( Vektor) y(b) an der rechts von x 0 liegenden Stelle b. Es ist also nicht die Lösungsfunktion als solche gesucht, sondern der Funktionswert der Lösung an einer bestimmten Stelle b > x 0. Bemerkung 8.. Unter vernünftigen Voraussetzungen an die Funktion f etwa: f ist auf [x0, b] R n stetig bzgl. y gleichmäßig lipschitzstetig, d.h. es gibt eine Konstante L > 0 mit für alle x [x 0, b] und y, y R n f(x, y ) f(x, y ) L y y ist die Anfangswertaufgabe 8.. eindeutig lösbar. In vielen Anwendungen gilt n =, d.h. es handelt sich um eine explizite Differentialgleichung. Ordnung. Bemerkung 8..3 Differentialgleichungen (oder auch Differentialgleichungssysteme) höherer Ordnung können immer auf ein äquivalentes Differentialgleichungssystem. Ordnung zurückgeführt werden: Die DGL z (n) = f(x, z, z, z,...,z (n ) ) (6) n ter Ordnung. Fachhochschule Aachen. Januar 008
2 04 8. Grundlagen wird durch: y = z y = z y n y n. = z (n ) = z (n ) überführt in das Differentialgleichungssystem. Ordnung: y = y y = y 3. = y n y n = f(x, y, y,...,y n ) y n Eine Lösung z der Differentialgleichung 6 der Ordnung n führt zur Lösung (7) y = (z, z,..., z (n ) ) T des Differentialgleichungssystems 7 und umgekehrt eine Lösung y = (y, y,...,y n ) T des Differentialgleichungssystems 7 führt zu der Lösung der Differentialgleichung 6 der Ordnung n. Beispiel 8..4 ( Körper Problem) z = y Befindet sich im Punkt P (t) im Raum eine Masse M und bewegt sich mit der Geschwindigkeit P (t), sowie in Punkt P (t) eine Masse M mit Geschwindigkeit P (t), so beeinflussen sich die Massen gegenseitig aufgrund der Gravitation. Es gilt: P = γ M P = γ M ( P P ) P P 3 ( P P ) P P 3 (Ableitungen nach der Zeit t) wobei γ = m 3 Mit für i =, und P i (t) = P ix (t) P iy (t) P iz (t), P i(t) = P ix (t) P iy(t) P iz (t) die Gravitationskonstante ist. Kg s und P i (t) = P P P ix (t) iy(t) iz (t) y (t) = P x (t), y (t) = P y (t), y 3 (t) = P z (t), y 4 (t) = P x (t), y 5(t) = P y (t), y 6(t) = P z (t) Mathematik III/Numerik Fachbereich 8
3 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 05 y 7 (t) = P x (t), y 8 (t) = P y (t), y 9 (t) = P z (t), y 0 (t) = P x (t), y (t) = P y (t), y (t) = P z (t) führt das auf das Differentialgleichungssystem. Ordnung: y = y 4 y = y 5 y 3 = y 6 y 4 = γ M y 5 = γ M y 6 = γ M y 7 y ( (y7 y ) + (y 8 y ) + (y 9 y 3 ) ) 3 y 8 y ( (y7 y ) + (y 8 y ) + (y 9 y 3 ) ) 3 y 9 y 3 ( (y7 y ) + (y 8 y ) + (y 9 y 3 ) ) 3 y 7 = y 0 y 8 = y y 9 = y y 0 = γ M y = γ M y = γ M y y 7 ( (y7 y ) + (y 8 y ) + (y 9 y 3 ) ) 3 y y 8 ( (y7 y ) + (y 8 y ) + (y 9 y 3 ) ) 3 y 3 y 9 ( (y7 y ) + (y 8 y ) + (y 9 y 3 ) ) 3 Satz 8..5 (Rückführung der Anfangswertaufgabe auf eine Integralgleichung) Es sei eine Anfangswertaufgabe y = f(x, y), y(x 0 ) = y 0 gegeben. Integriert man die Gleichung y = f(x, y), unter der Voraussetzung, dass y und y eine Funktion von x ist, über dem Intervall [x 0, x] (d.h. linker Randpunkt ist das feste x 0 und der rechte Randpunkt das variable x), so erhält man (wegen der oberen Grenze x wird hier t als Integrationsvariable eingeführt, es wird komponentenweise integriert): x x 0 y (t) dt = y(x) y(x 0 ) = x x 0 x y(x) = y(x 0 ) + x 0 y(x) = y 0 + f(t, y(t)) dt f(t, y(t)) dt x x 0 x x 0 f(t, y(t)) dt mit y(x0 ) = y 0 f(t, y(t)) dt Fachhochschule Aachen. Januar 008
4 06 8. Grundlagen Die Anfangswertaufgabe ist also äquivalent zur Integralgleichung y(x) = y 0 + x x 0 f(t, y(t)) dt (8) Diese Integralgleichung ist mathematisch gesehen genauso kompliziert wie die Anfangswertaufgabe, denn die Anfangswertaufgabe besteht (im Wesentlichen) aus einer Gleichung, in der eine unbekannte Funktion y und deren Ableitung y vorkommen in der Integralgleichung taucht dieselbe unbekannte Funktion y und ein Integral über diese Funktion auf. Bemerkung 8..6 (Ansatz für numerische Verfahren) Intervallaufteilung: x 0 < x <... < x k < x k+ <... < x n = b unter der Voraussetzung, dass man y k = y(x k ) schon kennt, die Integralgleichung 8 lokal für das Intervall von x k bis x k+ anwenden: y(x k+ ) = y k+ = y k + x k+ x k f(t, y(t)) dt das in dieser Gleichung stehende Integral x k+ f(t, y(t)) dt x k näherungsweise mit einer (interpolatorischen) Quadraturformel berechnen. f(x, y(x)) x k x k x k x k+ Mathematik III/Numerik Fachbereich 8
5 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 07 Beispiel 8..7 (explizites Euler Verfahren) Nimmt man zur näherungsweisen Berechnung des Integrals die (linksseitige) Rechteckregel: x k+ x k f(t, y(t)) dt f(xk, y k ) (x k+ x k ) Skizze: bekannt f(x k, y k ) f(x, y(x)) x k x k x k x k+ so erhält man die Formel: y k+ y k + h k f(x k, y k ) mit h k = x k+ x k Das auf dieser Formel beruhende Verfahren heißt explizites Euler Cauchy Polygonzugverfahren. Algorithmus 8..8 (explizites Euler Verfahren) Gegeben: Anfangswertaufgabe y = f(x, y), y(x 0 ) = y 0. Gesucht: Funktionswert (eigentlich: Vektor) y(b) mit b > x 0. Vorgehen: Unterteile das Intervall [x 0, b] in viele kleine Teilintervalle x 0 < x < x <... < x n = b und setze h k = x k+ x k (Teilintervalllänge des k-ten Intervalls). Ausgehend vom Anfangswert (x 0, y 0 ) berechne iterativ für k = 0,,,..., n : Dann gilt: y k+ = y k + h k f(x k, y k ) y n y(x n ) = y(b) Man kann zeigen: Sei h = max{ h k 0 k < n } die größte der beteiligten Teilintervalllängen, so gilt für den Fehler: y n y(b) O(h) d.h. das Euler Cauchy Verfahren hat die Ordnung. Fachhochschule Aachen. Januar 008
6 08 8. Grundlagen Beispiel 8..9 gegeben: Anfangswertaufgabe y = x + y, y(0) =.0 }{{} f(x,y) gesucht: y(.0) Es soll das Euler Cauchy Polygonzugverfahren mit konstanter Schrittweite h = 0. durchgeführt werden. Anfangswert: x 0 = 0.0, y 0 =.0 x = 0., y = y 0 + h f(x 0, y 0 ) = x = 0., y = y + h f(x, y ) = x 3 = 0.3, y 3 = y + h f(x, y ) = x 4 = 0.4, y 4 = y 3 + h f(x 3, y 3 ) = x 5 = 0.5, y 5 = y 4 + h f(x 4, y 4 ) = x 6 = 0.6, y 6 = y 5 + h f(x 5, y 5 ) = x 7 = 0.7, y 7 = y 6 + h f(x 6, y 6 ) = x 8 = 0.8, y 8 = y 7 + h f(x 7, y 7 ) = x 9 = 0.9, y 9 = y 8 + h f(x 8, y 8 ) = x 0 =.0, y 0 = y 9 + h f(x 9, y 9 ) = Ein Näherungswert für den gesuchten Funktionswert y(.0) ist y 0 = Bemerkung 8..0 (geometrische Beschreibung des Euler Cauchy Verfahrens) Im eindimensionalen Fall kann das explizite Euler Cauchy-Polygonzugverfahren geometrisch anhand des Richtungsfeldes der Differentialgleichung y = f(x, y) hergeletitet werden: Zur Anfangswertaufgabe y = f(x, y), y(x 0 ) = y 0 sei der Funktionswert der Lösung y(x) an der Stelle b > x 0 gesucht. Hierzu wird auf der x Achse die Strecke von x 0 nach b in kleine Teilintervalle unterteilt: x 0 < x < x <... < x n = b Aufgrund des Anfangswertes kennen wir den Funktionswert y 0 der Lösung y(x) an der Stelle x 0 die Lösung y(x) soll ja durch den Punkt (x 0, y 0 ) gehen. Ausgehend von diesem Anfangswert (x 0, y 0 ) wird jetzt wie folgt ein Näherungswert y für den Funktionswert y(x ) der Lösung y(x) an der Stelle x ermittelt:. Man setzt den Punkt (x 0, y 0 ) in die rechte Seite der Differentialgleichung ein und erhält die Steigung y 0 = f(x 0, y 0 ) der (ansonsten unbekannten) Lösungskurve y(x) im Punkt (x 0, y 0 ).. Hiermit ist die Tangente der Lösungskurve im Punkt (x 0, y 0 ) bekannt: diese geht durch den Punkt (x 0, y 0 ) und hat die Steigung y 0 = f(x 0, y 0 ). Mathematik III/Numerik Fachbereich 8
7 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 09 Skizzen: 3. In einer (kleinen) Umgebung von x 0 wird die Lösung y(x) ganz gut durch ihre Tangente angenähert: Es gilt nach Taylor: y(x) y(x 0 ) + y (x 0 ) (x x 0 ) }{{} Tangente von y(x) in (x 0,y 0 ) Durch Einsetzen von x für x folgt mit y(x 0 ) = y 0 und y (x 0 ) = y 0 = f(x 0, y 0 ): y(x ) y := y 0 + f(x 0, y 0 ) (x x 0 ) Mit dieser Formel kann also anhand des Anfangswertes (x 0, y 0 ) ein Näherungswert y für den Funktionswert der (unbekannten) Lösung y(x) an der Stelle x ermittelt werden! a.) Anfangswert: b.) Linienelement mit Steigung f(x 0, y 0 ) ermitteln: y 0 (x0, y 0 ) y 0 (x0, y 0 ) x 0 x x 0 x c.) Linienelement zu Tangente vervollständigen: d.) Tangente an der Stelle x auswerten: y 0 (x 0, y 0 ) x 0 x Mit diesem Verfahren bzw. der Formel y (x, y ) y 0 (x 0, y 0 ) x 0 x y = y 0 + (x x 0 ) f(x 0, y 0 ) ist es also gelungen, ausgehend vom Anfangspunkt (x 0, y 0 ) einen weiter rechts liegenden Punkt (x, y ) zu ermitteln mit y y(x ). Dies kann nun iterativ fortgesetzt werden: y = y + (x x ) f(x, y ), y y(x ) y 3 = y + (x 3 x ) f(x, y ), y 3 y(x 3 ). y n = y n + (x n x n ) f(x n, y n ), y n y(x n ) = y(b) Fachhochschule Aachen. Januar 008
8 0 8. Grundlagen Die Linienelemente in den Punkten (x k, y k ) legen die Geradenstücke von (x k, y k ) nach (x k+, y k+ ) fest und man gelangt mit diesen Geradenstücken von einem Punkt zum nächsten: Skizze: y 0 y y y y 3 0 y 4 y 5 y 6 y 7 y 9 y(b) y 8 x 0 x x x 3 x 4 x 5 x 6 x 7 x 8 x 9 = b Diese Skizze motiviert auch den Namen Polygonzugverfahren, der in der Literatur ebenfalls für dieses Euler Cauchy Verfahren verwendet wird. Beispiel 8.. (implizites Euler Verfahren) Nimmt man zur näherungsweisen Berechnung des Integrals die (rechtsseitige) Rechteckregel: x k+ x k f(t, y(t)) dt f(xk+, y k+ ) (x k+ x k ) Skizze: unbekannt f(x k+, y k+ ) f(x, y(x)) x k x k x k x k+ so erhält man die Formel: y k+ y k + h k f(x k+, y k+ ) mit h k = x k+ x k In dieser Formel taucht der zu berechnende Wert (Vektor) y k+ sowohl auf der linken Seite, als auch auf der rechten Seite als zweites Argument der Funktion f auf es handelt sich somit um eine implizite Gleichung für y k+. Diese implizite Gleichung muss dann gelöst werden im Allgemeinen iterativ. Das auf dieser Formel beruhende Verfahren heißt implizites Euler Verfahren. Mathematik III/Numerik Fachbereich 8
9 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN Algorithmus 8.. (implizites Euler Verfahren) Gegeben: Anfangswertaufgabe y = f(x, y), y(x 0 ) = y 0. Gesucht: Funktionswert (eigentlich: Vektor) y(b) mit b > x 0. Vorgehen: Unterteile das Intervall [x 0, b] in viele kleine Teilintervalle x 0 < x < x <... < x n = b und setze h k = x k+ x k (Teilintervalllänge des k-ten Intervalls). Ausgehend vom Anfangswert (x 0, y 0 ) berechne iterativ für k = 0,,,..., n : y k+ = y k + h k f(x k+, y k+ ) Diese (für jeden Schritt von x k nach x k+ anfallende) implizite Gleichung muss iterativ ausgehend von einem geeigneten Startvektor gelöst werden. Dann gilt: y n y(x n ) = y(b) Auch dieses Verfahren hat die Ordnung, d.h. mit h = max{ h k 0 k < n } gilt für den Fehler: y n y(b) O(h) Bemerkung 8..3 (Durchführung der Fixpunktiteration in jedem Schritt) Die in jedem Schritt des impliziten Euler Verfahrens (iterativ) zu lösende Fixpunktgleichung: kann umgeschrieben werden zu also zu y k+ = y k + h k f(x k+, y k+ ) y k+ y }{{} k = h k f(x k+, y k + y k+ y k ) }{{} =: z =: z z = h k f(x k+, y k + z) wobei z = 0 ein vernünftiger Startvektor für die Fixpunktiteration ist. Hierbei kann die Gleichung z = h k f(x k+, y k + z) selbst als Fixpunktgleichung verwendet und mit dieser Gleichung die Fixpunktiteration durchgeführt werden. die Gleichung umgeformt werden zu einer Nullstellengleichung: g( z) = z h k f(x k+, y k + z) = 0 für welche dann das (ggf. mehrdimensionale) Newton Verfahren zur Nullstellenbestimmung (mit Startvektor 0) durchgeführt werden kann. Fachhochschule Aachen. Januar 008
10 8. Grundlagen Beispiel 8..4 gegeben: Anfangswertaufgabe y = x + y, y(0) =.0 }{{} f(x,y) gesucht: y(.0) Es soll das implizite Euler Verfahren mit konstanter Schrittweite h = 0. durchgeführt werden. Die in jedem Schritt zu lösende implizite Gleichung lautet: z = h f(x k+, y k + z) = h x k+ + y k + z a.) Jeweilige Berechnung der impliziten Gleichung mit dem allgemeinen Iterationsverfahren b.) Jeweilige Berechnung der impliziten Gleichung mit dem Newton Verfahren Startwert jeweils 0 (die Iteration wird abgebrochen, sobald sich zwei iterierte Werte um weniger als 0 0 unterscheiden): k x k y k Anzahl Iterationen a.) b.) Beispiel 8..5 (Trapezregel) Die Berechnung des Integrals mit der Trapezregel: x k+ x k f(t, y(t)) dt (x k+ x k ) ( f(xk, y k ) + ) f(x k+, y k+ ) Skizze: Mathematik III/Numerik Fachbereich 8
11 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 3 bekannt unbekannt f(x k, y k ) f(x k+, y k+ ) f(x, y(x)) x k x k x k x k+ führt mit h k = x k+ x k auf die ebenfalls implizite Gleichung: y i+k = y k + h k f(x k, y k ) + h k f(x k+, y k+ ) für den zu berechnenden Wert y k+. Das auf dieser Formel beruhende (implizite) Verfahren für Differentialgleichungsn heißt Trapezregel. Algorithmus 8..6 (Trapezregel) Gegeben: Anfangswertaufgabe y = f(x, y), y(x 0 ) = y 0. Gesucht: Funktionswert (eigentlich: Vektor) y(b) mit b > x 0. Vorgehen: Unterteile das Intervall [x 0, b] in viele kleine Teilintervalle x 0 < x < x <... < x n = b und setze h k = x k+ x k (Teilintervalllänge des k-ten Intervalls). Ausgehend vom Anfangswert (x 0, y 0 ) berechne iterativ für k = 0,,,..., n : y k+ = y k + h k f(x k, y k ) + h k f(x k+, y k+ ) Diese (für jeden Schritt von x k nach x k+ anfallende) implizite Gleichung muss iterativ ausgehend von einem geeigneten Startvektor gelöst werden. Dann gilt: y n y(x n ) = y(b) Dieses Verfahren hat die Ordnung, d.h. mit h = max{ h k 0 k < n } gilt für den Fehler: y n y(b) O(h ) Bemerkung 8..7 Mit z = y k+ y k kann diese implizite Gleichung umgeschrieben werden zu z = h f(x k, y k ) + h f(x k+, y k + z) und diese Gleichung kann (ausgehend vom Startvektor 0) Fachhochschule Aachen. Januar 008
12 4 8. Grundlagen entweder direkt zur Iteration verwendet werden, oder (nach Umformung in eine Nullstellengleichung) mit dem Newton Verfahren gelöst werden. Beispiel 8..8 gegeben: Anfangswertaufgabe y = x + y, y(0) =.0 }{{} f(x,y) gesucht: y(.0) Es soll die Trapezregel mit konstanter Schrittweite h = 0. durchgeführt werden. Die in jedem Schritt zu lösende implizite Gleichung lautet: z = h f(x k, y k ) + h f(x k+, y k + z) = h x k + y k + h x k+ + y k + z a.) Jeweilige Berechnung der impliziten Gleichung mit dem allgemeinen Iterationsverfahren b.) Jeweilige Berechnung der impliziten Gleichung mit dem Newton Verfahren Startwert jeweils 0 (die Iteration wird abgebrochen, sobald sich zwei iterierte Werte um weniger als 0 0 unterscheiden): Definition und Bemerkung 8..9 k x k y k Anzahl Iterationen a.) b.) Zur Berechnung des neuen Wertes y k+ wird in allen Verfahren das Integral x k+ f(t, y(t)) dt x k über ein Interpolationspolynom ϕ(t) für die unbekannte Funktion f(t, y(t)) näherungsweise berechnet. Je nachdem, wo die Stützstellen dieses Interpolationspolynoms liegen, unterscheidet man die Verfahrenstypen: Mathematik III/Numerik Fachbereich 8
13 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 5 Einschrittverfahren: Bei den Einschrittverfahren liegen alle Stützstellen des Interpolationspolynoms ϕ im aktuellen Integrationsintervall [x k, x k+ ]: f(x, y) ϕ(x) x k x k t k t k... t km x k+ Mehrschrittverfahren Bei den Mehrschrittverfahren sind die Stützstellen des Interpolationspolynoms ausschließlich unter den bereits durch die Intervallaufteilung gegebenen x Werten: bekannt unbekannt ϕ(x) f(x k, y k ) f(x k, y k ) f(x k, y k ) f(x, y(x)) f(x k+, y k+ ) x k x k x k x k+ Je nachdem, ob x k+ zu den Stützstellen des Interpolations dazugehört oder nicht, spricht man von einem expliziten (gehört nicht dazu) oder einem impliziten (gehört dazu) Mehrschrittverfahren. 8. Einschrittverfahren Definition und Bemerkung 8.. (Runge Kutta Verfahren) Zur Berechnung des nächsten Näherungswertes y k+ für y(x k+ ) ausgehend vom aktuellen Wert y k werden im Intervall [x k, x k+ ] die Länge des Interalls sei h = x k+ x k die m Stützstellen x kj = x k + a j h für das Interpolationspolynom zugrunde gelegt. Die systematische Berechnung des Interpolationspolynoms ϕ(x) (mit zum Teil noch unbekann- Fachhochschule Aachen. Januar 008
14 6 8. Einschrittverfahren ten Stützwerten) und die anschließende näherungsweise Berechnung des Integrals x k+ f(t, y(t)) dt über dieses Interpolatinspolynom ϕ(x) führt auf Gleichungen folgender Form: K = f (x k + a h, y k + h m ) b j K j j= = f (x k + a h, y k + h m ) b j K j und K K m x k j=. = f (x k + a m h, y k + h m ) b mj K j y k+ = y k + h j= m c j K j mit fest vorgegebenen, von den konkreten Stützstellen (und vom Verfahren) abhängenden Konstanten a i, c i und b ij, i, j m. Das auf diesen Formeln beruhende Verfahren heißt m stufiges Runge Kutta Verfahren. Die Koeffizienten, welche dieses Verfahren vollständig beschreiben, werden häufig in einer Tabelle, dem sogenannten Butcher Diagramm, angegeben: Bemerkung 8.. j= a b b... b m a b b... b m a m b m b m... b mm c c... c m Die bislang kennengelernten Verfahren sind von diesem Typ:. explizites Euler Verfahren: Stufenzahl m ist. und y k+ = y k + h f(x k, y k ) }{{} =: K K = f(x k + 0 h, y k + h 0 K ) y k+ = y k + h K Butcher Diagramm für das explizite Euler Verfahren: 0 0 (9) Mathematik III/Numerik Fachbereich 8
15 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 7. implizites Euler Verfahren: y k+ = y k + h f(x k+, y k+ ) }{{} =: K Stufenzahl m ist. und K = f(x k + h, y k + h K ) y k+ = y k + h K Butcher Diagramm für das implizite Euler Verfahren: 3. Trapezregel: Stufenzahl m ist. und ( y k+ = y k + h f(x k, y k ) + }{{} f(x ) k+, y k+ ) }{{} =: K =: K K K = ( ) f x k + 0 h, y k + h (0 K + 0 K ) = ( ) f x k + h, y k + h ( K + K ) y k+ = y k + h ( K + K ) Butcher Diagramm für die Trapezregel: Definition Ein Runge Kutta Verfahren, bei dem die Matrix der Koeffizienten b ij eine strikte untere Dreiecksmatrix ist: a a b a 3 b 3 b a m b m b m... b m(m ) 0 c c... c m c m Fachhochschule Aachen. Januar 008
16 8 8. Einschrittverfahren heißt (m stufiges) explizites Runge Kutta Verfahren. Bei den meisten expliziten Runge Kutta Verfahren gilt darüber hinaus, dass a 0 = 0 gilt. In diesem Fall werden die Einträge gleich 0 im Butcher Diagramm fortgelassen, so dass ein solches explizites Runge Kutta Verfahren dann durch das Schema beschrieben wird. a b a 3 b 3 b a m b m b m... b m(m ) c c... c m c m. Ein Runge Kutta Verfahren, bei dem die Matrix der Koeffizienten b ij eine untere Dreiecksmatrix ist: a b a b b a m b m b m... b mm c c... c m heißt (m stufiges) diagonal implizites Runge Kutta Verfahren. Sind darüberhinaus alls Diagonalelemente b jj gleich, so spricht man von einem einfach diagonal impliziten Runge Kutta Verfahren. 3. Ist die Matrix b ij keine untere Dreiecksmatrix, so spricht man von einem (m stufigen) voll impliziten Runge Kutta Verfahren. Bemerkung 8..4 Bei einem expliziten Runge Kutta Verfahren ist das System 9 zur Bestimmung der K s ein explizites Gleichungssystem, d.h.. zuerst kann K ausgerechnet werden,. anschließend kann K mit Hilfe von K berechnet werden, 3. dann kann K 3 mit Hilfe von K und K berechnet werden 4. usw. Nach der Berechnung aller K s wird y k+ mit Hilfe der K s berechnet. Bei einem impliziten Runge Kutta Verfahren ist das Gleichungssystem 9 zur Bestimmung der K s ein implizites Gleichungssystem, welches iterativ zu lösen ist. Hierbei kann Mathematik III/Numerik Fachbereich 8
17 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 9 entweder das System 9 selbst zur Fixpunktiteration verwendet, oder (nach Umformung in eine Nullstellengleichung) ein Newton Verfahren angewendet werden. Als Startwert kann man jeweils K j = f(x k, y k ) für alle j verwenden. Es kann gezeigt werden, dass bei vernünftigen Aufgabenstellungen und hinreichend kleinen Schrittweiten h das System 9 für die K s eine eindeutige Lösung hat. Definition 8..5 (Konsistenzordnung eines Einschrittverfahrens) Sei y k+ der mittels des Einschrittverfahrens ausgehend von der Stelle x k und exaktem Anfangswert y k = y(x k ) berechnete Näherungswert für die exakte Lösung y(x k+ ) an der Stelle x k+ = x k + h und gilt: y(x k+ ) y k+ h O(h p ) so heißt p die Konsistenzordnung des Verfahrens und das Verfahren heißt konsistent, falls p gilt. (Der Bruch in obiger Gleichung ist der durch h geteilte lokale Fehler, also der Fehler, der im Punkt x k+ vorliegt, falls y k im Punkt x k noch fehlerfrei war.) Definition und Bemerkung 8..6 Sei y n der mittels Intervallaufteilung (Konvergenzordnung eines Einschrittverfahrens) x 0 < x <... < x n = b ausgehend von dem Anfangswert y(x 0 ) = y 0 bestimmte Näherungswert für die Lösung y(x n ) = y(b), so heißt p die Konvergenzordnung des Verfahrens, wenn ( y(x n ) y n ) O(h p ) gilt (globaler Fehler). Man kann zeigen, dass bei einem Einzelschrittverfahren die Konvergenzordnung und die Konsitenzordnung gleich sind! Algorithmus 8..7 Butcher Diagramm: (verbessertes Euler Verfahren) (es handelt sich somit um ein stufiges explizites Verfahren!) In Formeln: K = f(x k, y k ) K = f(x k + h, y k + hk ) Fachhochschule Aachen. Januar 008
18 0 8. Einschrittverfahren und oder kürzer in einer Formel: y k+ = y k + h K y k+ = y k + h f(x k + h, y k + h f(x k, y k )) Die Konvergenzordnung des verbesserten Euler Verfahrens ist. Algorithmus 8..8 Butcher Diagramm: (Verfahren von Heun) (es handelt sich somit um ein explizites Verfahren, die Stufenzahl m ist!) In Formeln: K = f(x k, y k ) K = f(x k + h, y k + h K ) und y k+ = y k + h (K + K ) Die Ordnung des Verfahrens ist. Algorithmus 8..9 Butcher Diagramm: (Klassisches Runge Kutta Verfahren) (Wiederum ein explizites Verfahren, die Stufenzahl m ist 4!) In Formeln: K = f(x k, y k ) K = f(x k + h, y k + h K ) K 3 = f(x k + h, y k + h K ) K 4 = f(x k + h, y k + h K 3 ) und 6 3 y k+ = y k + h ( 6 K + 3 K + 3 K K 4) Das klassische Runge Kutta Verfahren hat die Ordnung Mathematik III/Numerik Fachbereich 8
19 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN Beispiel 8..0 gegeben: Anfangswertaufgabe y = x + y, y(0) =.0 }{{} f(x,y) gesucht: y(.0) Es soll das klassische Runge Kutta Verfahren mit konstanter Schrittweite h = 0. durchgeführt werden. k x k y k K s K = K = K 3 = K 4 = K = K = K 3 = K 4 = K = K = K 3 = K 4 = K = K = K 3 = K 4 = K = K = K 3 = K 4 = Der mit dem klassischen Runge Kutta Verfahren berechnete Näherungswert lautet: y(.0) Algorithmus 8.. (Gauß Verfahren der Ordnung 4) Butcher Diagramm: Es handelt sich somit um ein stufiges implitzites Verfahren. In Formeln: K = f(x k K = f(x k h, y k + h ( 4 K h, y k + h ( K )) K + 4 K )) Fachhochschule Aachen. Januar 008
20 8.3 Schrittweitensteuerung und y k+ = y k + h (K + K ) Algorithmus 8.. (Gauß Verfahren der Ordnung 6) Butcher Diagramm: Es handelt sich somit um ein 3 stufiges implitzites Verfahren. (Auf eine explizite Angabe der Formelm wird hier verzichtet!) 8.3 Schrittweitensteuerung Ist eine Anfangswertaufgabe y = f(x, y), y(x 0 ) = y 0 gegeben und ist der Funktionswert y(b) der Lösung y(x) an der Stelle b > x 0 gesucht, so muss man, um mit einem numerischen Verfahren die Lösung einigermaßen genau zu bestimmen, das Intervall in Teilintervalle aufteilen: x 0 < x < x <... < x n = b um dann ausgehend vom Funktionswert y 0 an der Anfangsstelle x 0 schrittweise über y y(x ), y y(x ),... zum gewünschten Näherungswert y n y(x n ) = y(b) zu gelangen. Wählt man (zu) viele kleine Teilintervalle, so ist das Ergebnis zwar sehr genau, dafür ist der Rechenaufwand aber sehr hoch. Wählt man (zu) wenige große Teilintervalle, ist der Rechenaufwand sehr gering, dafür dürfte das Ergebnis aber zu ungenau sein. Wie bei der numerischen Integration (Adaptive Quadratur) ist es anzustreben, bei einer vorgegebenen Genauigkeitsschranke (b x 0 ) ε > 0 die Schrittweiten der Intervallaufteilung jeweils so groß zu wählen, dass die vorgegebene Genauigkeitsschranke gerade noch unterboten wird. Tunlichst sollte die Wahl der passenden Schrittweiten dem numerischen Verfahren selbst überlassen werden, so dass das Verfahren selbständig die lokalen Schrittweiten den lokalen Bedürfnissen anpasst. Bei den adaptiven Verfahren ist es in jedem Berechnungsschritt (Berechnung von y k+ ausgehend von x k und y k ) erforderlich, den hierbei gemachten lokalen Fehler zu schätzen, um entscheiden zu können, ob das Ergebnis genau genug ist und zum nächsten Teilintervall übergegangen werden kann Mathematik III/Numerik Fachbereich 8
21 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 3 oder ob das Ergebnis zu ungenau ist und ausgehend von x k mit einer kleineren Schrittweite neu gerechnet werden muss. Es gibt unterschiedliche Möglichkeiten, den lokalen Fehler zu schätzen: Bemerkung 8.3. (Schätzung des lokalen Fehlers). Rechnung mit einem Verfahren und unterschiedlichen Schrittweiten: Sei V ein Verfahren mit Konsistenzordnung (=Konvergenzordnung) q, weiter sei Ỹ der mittels dieses Verfahrens und Schrittweite h = x k+ x k in einem Schritt mit Schrittweite h ausgehend von (x k, y k ) berechnete Näherungswert für y(x k+ ), Y der mittels dieses Verfahrens mit Schrittweite h in zwei Schritten ausgehend von (x k, y k ) berechnete Näherungswert für y(x k+ ) so ist (Y Ỹ) q eine Schätzung für den lokalen Fehler der (besseren) Näherung Y und F = (Y Ỹ) q ist ein Schätzwert für den Betrag eben dieses (lokalen) Fehlers.. Rechnung mit zwei unterschiedlichen Verfahren und gleicher Schrittweite: Sei V ein Verfahren der Konsistenzordnung (=Konvergenzordnung) q und Ṽ ein Verfahren mit Konsistenzordnung mindestens q +, weiter sei Y der ausgehend von (x k, y k ) mit dem Verfahren V und Schrittweite h = x k+ x k berechnete Näherungswert für y(x k+ ), und Ỹ der ausgehend von (x k, y k ) mit dem Verfahren Ṽ und derselben Schrittweite h berechnete Näherungswert für y(x k+ ), so ist die Differenz Y Ỹ eine Schätzung für den lokalen Fehler der (schlechteren) Näherung Y und F = Y Ỹ ist ein Schätzwert für den Betrag eben dieses (lokalen) Fehlers. Ein möglicher Ansatz zur Schrittweitensteuerung ist dann (nach dem Buch Numerik Algorithmen von Frau Prof. Dr. G. Engeln Müllges) der folgende: Fachhochschule Aachen. Januar 008
22 4 8.3 Schrittweitensteuerung Algorithmus 8.3. (Schrittweitensteuerung) Es sei eine Fehlerschranke (b x 0 ) ε > 0 vorgegeben. In folgendem Algorithmus wird sichergestellt, dass in jedem Integrationsschritt der Intervalllänge h der lokale Fehler ungefähr gleich h ε ist. Ausgehend vom aktuellen Punkt (x k, y k ) und Schrittweite h = x k+ x k werden zwei Näherungswerte Y bzw. Ỹ für den nächsten Wert y(x k+) berechnet, entweder mit ein und demselben Verfahren V der Ordnung q und den beiden Schrittweiten h (Näherung Ỹ und h (Näherung Y) oder mit zwei Verfahren V der Ordnung q (Näherung Y) und Ṽ der Ordnung mindestens q + (Näherung Ỹ) und der Betrag des hierbei gemachten Fehlers F nach Bemerkung 8.3. geschätzt. Mit dieser Fehlerschätzung F wird die folgende Steuergröße berechnet: S = q h ε F Ist S, so wird der Fehler als klein genug angesehen, der Wert Y wird als Näherungswert für y(x k+ ) akzeptiert, man geht zum nächsten x Wert x k+ über und wählt als neue Schrittweite: h = min{, S } h d.h. die Schrittweite wird nächsten Schritt geringfügig vergrößert, Ist S <, so wird der Fehler als zu groß angesehen, der Schritt ausgehend von x k muss mit der kleineren Schrittweite: h = max{, S } h und neuem x k+ = x k + h wiederholt werden Einbettungsformeln erleichtern die Schrittweitensteuerung, wenn pro Schritt mit zwei unterschiedlichen Verfahren Näherungen berechnet werden. Hierbei ist es hilfreich, wenn die beiden verwendeten Verfahren V und Ṽ so in einem Zusammenhang stehen, dass etwa die Zwischen und Hilfswerte, welche zur Ausführung eines Schrittes mit dem Verfahren V berechnet werden, bei der Durchführung des Schrittes mit Verfahren Ṽ wiederverwendet werden können, so dass für Ṽ nicht alles neu berechnet werden muss. Solche Paare zusammenhängender Verfahren V und Ṽ heißen Einbettungsformeln. Einbettungsformeln sind vor allem bei expliziten Runge Kutta Verfahren weit verbreitet. Mathematik III/Numerik Fachbereich 8
23 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 5 Beispiele hierzu sind das verbesserte Polygonzugverfahren (Ordnung, übernimmt die Rolle von Verfahren V) mit dem Koeffizientenschema: ausgeschrieben: und 0 K = f(x i, y i ) K = f(x i + h, y i + h ) Y = y i + h (0 K + K ) und folgendes Runge Kutta Verfahren der Ornung 3 (übernimmt die Rolle von Verfahren Ṽ), Koeffizientenschema: ausgeschrieben: und K = f(x i, y i ) 6 K = f(x i + h, y i + h ) K 3 = f(x i + h, y i + h ( K + K )) Ỹ = y i + h ( 6 K + 3 K + 6 K 3) Wie man sieht, werden in beiden Verfahren V und Ṽ die Größen K und K gleich berechnet und verwendet bei Verfahren Ṽ kommt zusätzlich ein K 3 hinzu. Bei den Formeln für die Näherungswerte Y bzw. Ỹ treten dann unterschiedliche Koeffizienten auf. Man kann die Koeffizienten beider Verfahren in ein Schema hineinschreiben: 3 V 0 Ṽ Bemerkung (Koeffizientenschema für Einbettungsformeln) Das Koeffizientenschema einer allgemeinen (expliziten) Einbettungsformel lautet: a b a 3 b 3 b a m b m b m,m V c c... c m c m Ṽ c c... c m c m (i. Allg. sind die letzten Koeffizienten c m, c m,... gleich 0) Fachhochschule Aachen. Januar 008
24 6 8.3 Schrittweitensteuerung In jedem Schritt mit diesen Verfahren werden die Hilfsgrößen wie folgt berechnet: K = f(x i, y i ) K = f(x i + a h, y i + h b K )... m K m = f(x i + a m h, y i + h b ml K l ) und anschließend mit denselben Hilfsgrößen die beiden Näherungen: l= Y = y i + h m c i K i i= und Ỹ = y i + h m c i K i i= berechnet. Bemerkung (Einbettungsformel von England) Eine bekanntes Formelpaar von diesem Typ sind die England Formeln mit Ordnung q = 4 für V und 5 für Ṽ. Sie haben folgendes Koeffizientenschema: V Ṽ Beispiel (Beispiel zur Schrittweitensteuerung) Beute Räuber Differentialgleichungssystem (Lotka Volterra): y (t) = a y (t) ( y (t)) y (t) = y (t) (y (t) ) y (t) = Beute und y (t) = Räuber. Zeitliche Entwicklung der Populationen, berechnet mit der Formel von England (a = 0.0, y (0) = 3.0, y (0) =.0): Mathematik III/Numerik Fachbereich 8
25 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 7 4 "beute" "raeuber" Entwicklung der Schrittweiten: 0. "schrittweite" Fachhochschule Aachen. Januar 008
26 8 8.4 Stabilität, steife Differentialgleichungen 8.4 Stabilität, steife Differentialgleichungen In der Praxis auftretende Differentialgleichungssysteme haben häufig die Eigenschaft, dass sich die Lösungen aus abklingenden e Funktionen e λt zusammensetzen mit λ C und negativem Realteil Re(λ) < 0. Beachte: ist λ = a + b i mit a, b R und a > 0, so ist: e λt = e at (cos(bt) + i sin(bt)) eine oszillierende, aber wegen a > 0 betragsmäßig abklingende (komplexe) Funktion. Man möchte natürlich, dass auch eine numerisch bestimmte Näherungslösung für das Differentialgleichungssystem genauso abklingende Bestandteile hat. Hierzu sind je nach Verfahren an die zu verwendende Schrittweite h Bedingungen zu knüpfen! Definition 8.4. Das Anfangswertproblem (Testproblem) (λ C, Re(λ) < 0) heißt Testproblem. y (x) = λ y(x), y(0) = Die exakte Lösung des Testproblems lautet bekanntlich y(x) = e λx Da Re(λ) < 0 handelt es sich bei der Lösung um eine betragsmäßig monoton fallende Funktion. Ist x k+ = x k + h, so gilt für die exakte Lösung: y(x k+ ) = e λx k+ = e λ(x k + h) = e λh e λx k = e λh y(x k ) d.h. die exakte Lösung y(x k+ ) an der Stelle x k+ erhält man aus der exakten Lösung y(x k ) an der Stelle x k durch Multiplikation mit dem Faktor e λh. Wegen Re(λ) < 0 ist der Betrag dieses Faktors e λh kleiner als. Bemerkung 8.4. (numerische Verfahren für die Testaufgabe) Wendet man ein Runge Kutta Verfahren auf die Testdifferentialgleichung y = λy an, so geht ebenfalls der Näherungswert y k+ für y(x k+ ) durch Multiplikation mit einem Faktor F(λh) aus dem Näherungswert y k für y(x k ) hervor, d.h. es gibt eine (komplexe) Funktion F(z), so dass dieser Faktor gleich F(λh) ist: y k+ = F(λh) y k Diese (komplexe) Funktion F(z) heißt Stabilitätsfunktion des numerischen Verfahrens. Bemerkung (Explizites Euler-Verfahren für das Testproblem) Wendet man das explizite Euler Verfahren mit Schrittweite h auf das Testproblem an, so erhält man y(x k+ ) y k+ = y k + h f(x k, y k ) = y k + hλ y k = ( + λh) y k Mathematik III/Numerik Fachbereich 8
27 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 9 d.h. die Stabilitätsfunktion des expliziten Euler Verfahrens ist F(z) = + z. Damit das qualitative Verhalten der exakten Lösung (betragsmäßig abklingend) auch für die numerisch bestimmte Näherungslösung gilt, ist zu fordern, dass auch der beim Euler Verfahren verwendete Faktor F(λh) = ( + λh) betragsmäßig kleiner als ist, es ist also zu fordern: F(λh) < mit F(z) = + z Ist diese (vom Wert λ abhängende) Bedingung für die verwendete Schrittweite h verletzt, so kommt mit dem Euler Verfahren ein unsinniges Ergebnis heraus! Beispiel Es wird das Testproblem mit λ = 00 und das explizite Euler Verfahren zugrundegelegt. Die exakte Lösung y(x) = e 00x ist eine extrem schnell abklingende e Funktion. Die Stailitätsbedingung für das Euler Verfahren + λh < führt mit λ = 00 auf h < 0.0 Wählt man die Schrittweite h = 0.005, so ist diese Bedingung erfüllt und die für das Intervall [0, ] mit dem Euler Verfahren berechneten Lösung sieht wie folgt aus: "h=0.005.txt" Wie man sieht, stimmt die Lösung mit der exakten Lösung sehr gut überein. Wählt man als Schrittweite h = 0.05, so ist diese Bedingung verletzt und die für das Intervall [0, ] mit dem Euler Verfahren berechnete Näherungslösung Fachhochschule Aachen. Januar 008
28 Stabilität, steife Differentialgleichungen.e+07 "h=0.05.txt" e+07 8e+06 6e+06 4e+06 e e+06-4e+06-6e+06-8e hat mit der exakten Lösung nicht viel zu tun. Bemerkung (Klassisches Runge Kutta Verfahren für das Testproblem) Wendet man das klassische Runge Kutta Verfahren auf die Testdifferentialgleichung y = λy an, so erhält man die Formel: ) y k+ = ( + (λh) + (λh) + (λh)3 + (λh)4 y k 3! 4! D.h. die Stabilitätsfunktion für das klassiche Runge Kutta Verfahren lautet: F(z) = + z + z + z3 3! + z4 4! Um auch hier abklingendes Verhalten der Näherungslösung zu bekommen, muss für die zu verwendende Schrittweite h gefordert werden. F(λh) < Beispiel Es wird das Testproblem mit λ = 00 und das explizite klassiche Runge Kutta Verfahren zugrundegelegt. Die exakte Lösung y(x) = e 00x ist eine extrem schnell abklingende e Funktion. Die Stailitätsbedingung für das klassiche Runge Kutta Verfahren führt mit λ = 00 auf h < Wählt man die Schrittweite h = 0.0, so ist diese Bedingung erfüllt und die für das Intervall [0, ] mit dem klassichen Runge Kutta Verfahren berechnete Lösung sieht wie folgt aus: Mathematik III/Numerik Fachbereich 8
29 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 3 "rk_0_0.txt" Wie man sieht, stimmt die Lösung mit der exakten Lösung sehr gut überein. Wählt man als Schrittweite h = 0.03, so ist diese Bedingung verletzt und die für das Intervall [0, ] mit dem klassichen Runge Kutta Verfahren berechnete Näherungslösung "rk_0_03.txt" hat mit der exakten Lösung nicht viel zu tun. Bemerkung In den Anwendungen bei Differentialgleichungsen ist das Problem, dass sich die Lösungen häufig aus abklingenden e Funktionen mit unterschiedlichen Abklingkonstanten λ und λ zusammensetzen, etwa: hier hat man λ = und λ = 000. y(t) = c e} {{ } t +c e} 00 {{ } t +... y (t) y (t) Fachhochschule Aachen. Januar 008
30 3 8.4 Stabilität, steife Differentialgleichungen Im Vergleich zu y (t) ist der Bestandteil y (t) extrem schnell abklingend und schon für kleine Werte für t spielt y (t) in der Lösung y(t) keinerlei Rolle mehr. Damit der von λ = 000 herrührende Bestandteil auch in der numerischen Lösung keine Rolle spielt, muss dennoch für dass gewählte Verfahren mit Stabilitätsfunktion F(z): F(λ h) < gelten, ansonsten sind die Ergebnisse unbrauchbar. Definition (steifes Differentialgleichungssystem) Ein Differentialgleichungssystem heißt steif, falls in der Lösung abklingende e Funktionen mit stark unterschiedlichen Abklingkonstanten λ k, k =,,... beteiligt sind. Quantitativ: die Zahl St = max{ Re(λ k) } min{ Re(λ k ) } heißt Steifheitsmaß. Das System heißt steif, falls das Steifheitsmaß St größer als 000 ist. Beispiel In der Lösung des Differentialgleichungssystems: ( ) ( ) ( ) ( y y 50 sin(00t) = y 3 y ) mit Anfangswerten y (0) = und y (0) = tauchen die e Funktionen e t (also λ = ) und e 000 t (also λ = 000) auf. Löst man dieses System mit dem Euler Cauchy Polygonzugverfahren, so muss für den Hauptbestandteil e t der Lösung gelten. F(λ h) < also h < also h < Damit also der Hauptbestandteil e t der Lösung qualitativ richtig erfasst wird, reicht eine Schrittweite h < aus. für den (eigentlich in der Lösung keine große Rolle spielenden) Bestandteil e 000t muss gelten. F(λ h) < also 000h < also h < 0.00 Obwohl dieser Bestandteil e 000t in der exakten Lösung keine große Rolle spielt, muss im numerischen Verfahren dennoch eine winzig kleine Schrittweite zugrunde gelegt werden, damit dieser auch in der numerischen Lösung keine Rolle spielt! Je nachdem, ob und wie diese Bedingung eingehalten wird, sehen die berechneten Lösungen (etwa für y (t)) aus: Mathematik III/Numerik Fachbereich 8
31 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 33. Rechnung mit h = 0.000, die Stabilitätsbedingung ist bei weitem erfüllt: 5 "h_000.txt" so in etwa sieht die exakte Lösung für y (t) aus!. Rechnung mit h = 0.009, die Stabilitätsbedingung ist so gerade noch erfüllt: 5 "h_009.txt" "h_000.txt" erst nach einiger Zeit klingt der von λ = 000 herrührende, stark oszilierende Bestandteil der numerischen Lösung ab die berechnete Lösung nähert sich mehr und mehr der exakten Lösung. 3. Berechnung mit h = 0.000, die Stabilitätsbedingung ist knapp nicht mehr erfüllt: Fachhochschule Aachen. Januar 008
32 Stabilität, steife Differentialgleichungen 5 "h_000.txt" "h_000.txt" der von λ = 000 herrührende, stark oszilierende Bestandteil der numerischen Lösung schaukelt sich auf! Die ermittelte Lösung stimmt immer weniger mit der exakten Lösung überein. Definition (Stabilitätsgebiet, Stabilitätsintervall) Sei V ein numerisches Einschrittverfahren mit Stabilitätsfunktion F(z), d.h. bei Anwendung auf die Testdifferentialgleichung y = λy erhält man die Iterationsvorschrift: Die Menge komplexer Zahlen: y k+ = F(λh) y k S := {z C F(z) < } heißt das Stabilitätsgebiet des Verfahrens V. Ist bei der Lösung eines Differentialgleichungssystems eine (abklingende) e Funktion mit Abklingkonstante λ C (Re(λ) < 0) beteiligt, muss die Schrittweite so bemessen sein, dass λ h im Stabilitätsgebiet liegt! Die Menge reeller Zahlen I := {x R F(x) < } heißt das Stabilitätsintervall des Verfahrens V (es handelt sich meißt wirklich um ein Intervall!). Bemerkung 8.4. (Stabilitätsgebiet/Stabilitätsindervall einfacher Verfahren). das Stabilitätsgebiet des Euler Cauchy Polygonzugverfahrens ist das Innere des Kreises um mit Radius : Mathematik III/Numerik Fachbereich 8
33 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 35 Skizze: i 3 Das Stabilitätsintervall ist (, 0).. Skizze des Stabilitätsgebietes des klassischen Runge Kutta Verfahrens: i 3 Das Stabilitätsintervall ist (.78, 0). Man kann zeigen: Bemerkung 8.4. Für alle expliziten Runge Kutta Verfahren ist die Stabilitätsfunktion F(z) ein Polynom in z, das Stabilitätsgebiet ist ein (links des Nullpunktes) liegendes beschränktes Gebiet und das Stabilitätsintervall ist ein endliches Intervall der Form ( a, 0) mit a > 0. Bemerkung (Stabilitätsfunktion/ Gebiet/ Interval des impliziten Euler Verfahrens) Die Anwendung des impliziten Euler Verfahrens auf die Testdifferentialgleichung y = λy führt auf die explizite Gleichung y k+ = λh y k Die Stabilitätsfunktion lautet somit: F(z) = z Das Stabilitätsgebiet ist das Äußere des Kreises um mit Radius : Fachhochschule Aachen. Januar 008
34 Stabilität, steife Differentialgleichungen i 3 Definition (A Stabilität) Ein Runge Kutta Verfahren mit Stabilitätsgebiet S heißt A stabil oder absolut stabil, falls C = {z C Re(z) < 0 } S gilt. Bei einem absolut stabilen Verfahren werden ohne Einschränkung für die Schrittweite alle abklingenden e Funktionen qualitativ richtig berechnet. Das implizite Euler Verfahren ist absolut stabil. Beispiel Es wird das Testproblem mit λ = 00 und das implizite Euler Verfahren zugrundegelegt. Die exakte Lösung y(x) = e 00x ist eine extrem schnell abklingende e Funktion. Bereits mit der recht großen Schrittweite h = 0. erhählt man qualitativ die richtige Lösung: "ime_0_.txt" Es liegt λ h = = 0 im Stabilitätsgebiet. Für jede positive Schrittweite liegt λ h im Stabilitätsgebiet! Bemerkung Wird die (eindimensionale) Trapezregel (Stabilitätsfunktion/ Gebiet/ Intervall der Trapezregel) Mathematik III/Numerik Fachbereich 8
35 8 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 37 y k+ = y k + h f(x k, y k ) + h f(x k+, y k+ ) auf die Testdifferentialgleichung y = λy angewendet, so erhält man also die (explizite) Gleichung: Die Stabilitätsfunktion ist somit Die Bedingung ist für alle z mit Re(z) < erfüllt, y k+ = y k + λh y k + λh y k+ y k+ = + λh λh F(z) = + z z Skizze des Stabilitätsgebietes der Trapezregel: F(z) < y k = + z z i 3 Somit folgt: auch die (ebenfalls implizite) Trapezregel ist absolut stabil. Man kann zeigen: Bemerkung (Stabilität von Runge Kutta Verfahren) Alle impliziten Runge Kutta Verfahren sind absolut stabil. Ein explizites Runge Kutta Verfahren kann nicht absolut stabil sein! Bemerkung Für steife Differentialgleichungssysteme darf man kein explizites Runge Kutta Verfahren verwenden! Fachhochschule Aachen. Januar 008
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 23
 Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Musterlösungen zur Leistungsnachweisklausur vom Studiengang Informatik, Ingenieurinformatik, Lehramt
 TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra
TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Differentialgleichungen
 Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Euler-Verfahren. exakte Lösung. Euler-Streckenzüge. Folie 1
 exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
Diplom VP Informatik / Numerik 2. September 2002
 Diplom VP Informatik / Numerik. September 00 Aufgabe Gegeben sei das lineare Gleichungssystem A x = b mit 0 4 0 0 0 0 A = 4 0 0 0 0 0 0 0 0 und b = 4 4 8 5. Punkte a Berechnen Sie die Cholesky Zerlegung
Diplom VP Informatik / Numerik. September 00 Aufgabe Gegeben sei das lineare Gleichungssystem A x = b mit 0 4 0 0 0 0 A = 4 0 0 0 0 0 0 0 0 und b = 4 4 8 5. Punkte a Berechnen Sie die Cholesky Zerlegung
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
eps für alle x D. 4. Die Zahl 256 ist in M(2, 4, 6, 6) exakt darstellbar.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Institut für Geometrie und Praktische Mathematik Diplom VP Numerik 13. September 004 Aufgabe 1 10 0 40 Gegeben sei die Matrix A = 80 10 10. 10 5 5 (6 Punkte) a) Skalieren (Zeilenäquilibrierung)
RWTH Aachen Institut für Geometrie und Praktische Mathematik Diplom VP Numerik 13. September 004 Aufgabe 1 10 0 40 Gegeben sei die Matrix A = 80 10 10. 10 5 5 (6 Punkte) a) Skalieren (Zeilenäquilibrierung)
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Diplom VP Numerik 28. August 2006
 Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei die Matrix
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Dr. R. Käppeli D-ITET, D-MATL Sommer Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Musterlösung Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Institut für Geometrie und Praktische Mathematik Multiple-Choice-Test NumaMB F08 (30 Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine
RWTH Aachen Institut für Geometrie und Praktische Mathematik Multiple-Choice-Test NumaMB F08 (30 Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine
Mathematische Grundlagen
 G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
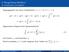 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Einführung in die numerische Mathematik
 Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Übungsaufgabe Numerische Lösung DGL
 Kallenrode, www.sotere.uos.de Übungsaufgabe Numerische Lösung DGL 1. Bestimmen Sie die Lösung der DGL ẋ = (t 2) 2 + t x mit x(0) = 1 im Bereich von t = 0 bis t = 5 mit Hilfe des Euler schen Streckenzugverfahrens,
Kallenrode, www.sotere.uos.de Übungsaufgabe Numerische Lösung DGL 1. Bestimmen Sie die Lösung der DGL ẋ = (t 2) 2 + t x mit x(0) = 1 im Bereich von t = 0 bis t = 5 mit Hilfe des Euler schen Streckenzugverfahrens,
5 Numerische Mathematik
 6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Lösung Semesterendprüfung
 MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).
Übungen zu Splines Lösungen zu Übung 20
 Übungen zu Splines Lösungen zu Übung 20 20.1 Gegeben seien in der (x, y)-ebene die 1 Punkte: x i 6 5 4 2 1 0 1 2 4 5 6 y i 1 1 1 1 1 + 5 1 + 8 4 1 + 8 1 + 5 1 1 1 1 (a) Skizzieren Sie diese Punkte. (b)
Übungen zu Splines Lösungen zu Übung 20 20.1 Gegeben seien in der (x, y)-ebene die 1 Punkte: x i 6 5 4 2 1 0 1 2 4 5 6 y i 1 1 1 1 1 + 5 1 + 8 4 1 + 8 1 + 5 1 1 1 1 (a) Skizzieren Sie diese Punkte. (b)
Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan :00-14:00 (120 min)
 Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
8 Gewöhnliche Differentialgleichungen
 8 Gewöhnliche Differentialgleichungen Beispiel: Radioaktiver Zerfall Sei m(t) die Menge radioaktiven Materials zur Zeit t. Der Zerfall des Materials geschieht proportional zur vorhandenen Menge mit dem
8 Gewöhnliche Differentialgleichungen Beispiel: Radioaktiver Zerfall Sei m(t) die Menge radioaktiven Materials zur Zeit t. Der Zerfall des Materials geschieht proportional zur vorhandenen Menge mit dem
Ausgleichsproblem. Definition (1.0.3)
 Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen
 Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
ZWEITE KLAUSUR zur Numerik I mit Lösungen. Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
 MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
D-MAVT NUMERISCHE MATHEMATIK FS 14 K. Nipp, A. Hiltebrand Lösung vom Test 1
 D-MAVT NUMERISCHE MATHEMATIK FS 4 K. Nipp, A. Hiltebrand Lösung vom Test. Sei eps die Maschinengenauigkeit in Matlab. Dann gilt: eps/4 = Richtig / Falsch + eps/2 = Richtig / Falsch 8 + eps = 8 Richtig
D-MAVT NUMERISCHE MATHEMATIK FS 4 K. Nipp, A. Hiltebrand Lösung vom Test. Sei eps die Maschinengenauigkeit in Matlab. Dann gilt: eps/4 = Richtig / Falsch + eps/2 = Richtig / Falsch 8 + eps = 8 Richtig
Gleichungsbasierte Modellierung
 1 Gleichungsbasierte Modellierung Die Benutzung von Gleichungen zur Geometrischen Modellierung wurde bereits von Sutherland eingeführt. Fortgeführt wurde sie durch die Arbeiten von Light und Gossard. Wie
1 Gleichungsbasierte Modellierung Die Benutzung von Gleichungen zur Geometrischen Modellierung wurde bereits von Sutherland eingeführt. Fortgeführt wurde sie durch die Arbeiten von Light und Gossard. Wie
a) Die Householder-Transformation, welche den ersten Spaltenvektor a 1 = der Matrix A auf , a 1 αe A = QR, A k =: Q k R k, A k+1 := R k Q k.
 Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. W. Reichel Sommersemester 00 7.07.00 MODULPRÜFUNG Numerische Methoden (Höhere Mathematik IV für die Fachrichtung Meteorologie bzw.
Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. W. Reichel Sommersemester 00 7.07.00 MODULPRÜFUNG Numerische Methoden (Höhere Mathematik IV für die Fachrichtung Meteorologie bzw.
Nichtlineare Gleichungssysteme
 Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Klausur Numerische Mathematik (für Elektrotechniker), 24. Februar 2016
 Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
18.4 Das Newton-Verfahren
 18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Parareal. Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen. Johannes Reinhardt. Parareal 1 Johannes Reinhardt
 Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
D-MATH Numerische Methoden FS 2018 Dr. Vasile Gradinaru Kjetil Olsen Lye. Serie 6
 D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. kjetil.lye@sam.math.ethz.ch
D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. kjetil.lye@sam.math.ethz.ch
2. Geben Sie für das Jacobi-Verfahren eine scharfe a-priori Abschätzung für den Fehler. x (10) x p
 Wiederholungsaufgaben Algorithmische Mathematik Sommersemester Prof. Dr. Beuchler Markus Burkow Übungsaufgaben Aufgabe. (Jacobi-Verfahren) Gegeben sei das lineare Gleichungssystem Ax b = für A =, b = 3.
Wiederholungsaufgaben Algorithmische Mathematik Sommersemester Prof. Dr. Beuchler Markus Burkow Übungsaufgaben Aufgabe. (Jacobi-Verfahren) Gegeben sei das lineare Gleichungssystem Ax b = für A =, b = 3.
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: b a 2 3a 1
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Begleitmaterial zur Vorlesung Numerik II
 Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Nichtlineare Gleichungen in einer und mehreren Unbekannten
 Gleichungen in einer und mehreren Unbekannten 2. Vorlesung 170004 Numerische Methoden I Clemens Brand 26. Februar 2009, Gliederung,, Gleichungen in einer Variablen Was ist... Wie geht... eine lineare (nichtlineare,
Gleichungen in einer und mehreren Unbekannten 2. Vorlesung 170004 Numerische Methoden I Clemens Brand 26. Februar 2009, Gliederung,, Gleichungen in einer Variablen Was ist... Wie geht... eine lineare (nichtlineare,
(x x j ) x [a,b] n! j=0
![(x x j ) x [a,b] n! j=0 (x x j ) x [a,b] n! j=0](/thumbs/88/115477375.jpg) IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (4 Punkte Es gibt zu jeder der 1 Aufgaben vier Aussagen. Diese sind mit bzw. zu kennzeichnen (hinschreiben. Es müssen alle Fragen mit oder gekennzeichnet
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (4 Punkte Es gibt zu jeder der 1 Aufgaben vier Aussagen. Diese sind mit bzw. zu kennzeichnen (hinschreiben. Es müssen alle Fragen mit oder gekennzeichnet
PVK Probeprüfung FS 2017
 PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
y(x) ist die gesuchte Lsg.-Funktion der unabhängigen Variablen x Anfangswertproblem: Lsg. heißt Integralkurve
 Kapitel 8 Gewöhnliche Differentialgleichungen 8.1 Vorbemerkungen Betrachte skalare Gleichung y = dy dx = f(x, y(x)) (8.1) y(x) ist die gesuchte Lsg.-Funktion der unabhängigen Variablen x Mit der Anfangsbed.
Kapitel 8 Gewöhnliche Differentialgleichungen 8.1 Vorbemerkungen Betrachte skalare Gleichung y = dy dx = f(x, y(x)) (8.1) y(x) ist die gesuchte Lsg.-Funktion der unabhängigen Variablen x Mit der Anfangsbed.
Diplom VP Numerik 27. August 2007
 Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
KAPITEL 10. Numerische Integration
 KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
 Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
KLAUSUR. Mathematik IV Wolfram Koepf. Name: Vorname: Matr. Nr.:
 KLAUSUR Mathematik IV 5. 3. 2007 Wolfram Koepf Name: Vorname: Matr. Nr.: Bitte lassen Sie genügend Platz zwischen den Aufgaben und beschreiben Sie nur die Vorderseite der Blätter! Zum Bestehen der Klausur
KLAUSUR Mathematik IV 5. 3. 2007 Wolfram Koepf Name: Vorname: Matr. Nr.: Bitte lassen Sie genügend Platz zwischen den Aufgaben und beschreiben Sie nur die Vorderseite der Blätter! Zum Bestehen der Klausur
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
H. Achte Übungseinheit
 H. Achte Übungseinheit Inhalt der achten Übungseinheit: Einschrittverfahren für gewöhnliche Differentialgleichungen erster Ordnung MATLAB-Löser Klassisches Euler-Verfahren und andere einfache explizite
H. Achte Übungseinheit Inhalt der achten Übungseinheit: Einschrittverfahren für gewöhnliche Differentialgleichungen erster Ordnung MATLAB-Löser Klassisches Euler-Verfahren und andere einfache explizite
Differentialgleichungen
 Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Differentialgleichungen
 Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
Numerische Mathematik
 Numerische Mathematik SS 999 Augabe 6 Punkte Das Integral I ln d soll numerisch bis au eine Genauigkeit von mindestens - approimiert werden. a Wie groß muss die Anzahl N der Teilintervalle sein damit mit
Numerische Mathematik SS 999 Augabe 6 Punkte Das Integral I ln d soll numerisch bis au eine Genauigkeit von mindestens - approimiert werden. a Wie groß muss die Anzahl N der Teilintervalle sein damit mit
y hom (x) = C e p(x) dx
 Gewöhnliche Differentialgleichungen F (x, y, y,..., y n ) = 0 Gleichung, die die Veränderliche x sowie die Funktion y = y(x) und ihre Ableitungen y,..., y n beinhaltet. Klassifiaktion: implizit F (...)
Gewöhnliche Differentialgleichungen F (x, y, y,..., y n ) = 0 Gleichung, die die Veränderliche x sowie die Funktion y = y(x) und ihre Ableitungen y,..., y n beinhaltet. Klassifiaktion: implizit F (...)
6. Polynom-Interpolation
 6. Polynom-Interpolation 1 6.1. Klassische Polynom-Interpolation 2 6.2. Lösung mit Hilfe Lagrange scher Basisfunktionen 3 6.3. Lösung mit Hilfe Newton scher Basisfunktionen 4 6.4. Fehlerabschätzung für
6. Polynom-Interpolation 1 6.1. Klassische Polynom-Interpolation 2 6.2. Lösung mit Hilfe Lagrange scher Basisfunktionen 3 6.3. Lösung mit Hilfe Newton scher Basisfunktionen 4 6.4. Fehlerabschätzung für
Fachbereich Mathematik/Informatik 16. Juni 2012 Prof. Dr. H. Brenner. Mathematik für Anwender II. Testklausur mit Lösungen
 Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2012/13 DGL Grundlage Klassifikation Anwendung von lin. Ggln. M. konst.
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2012/13 DGL Grundlage Klassifikation Anwendung von lin. Ggln. M. konst.
Numerische Methoden 7. Übungsblatt
 Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Rheinisch-Westfälische Technische Hochschule. Gegeben seien eine gewöhnliche Dierentialgleichung (DGL) und ein Anfangswert. γ l K l.
 Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
Iterative Verfahren, Splittingmethoden
 Iterative Verfahren, Splittingmethoden Theodor Müller 19. April 2005 Sei ein lineares Gleichungssystem der Form Ax = b b C n, A C n n ( ) gegeben. Es sind direkte Verfahren bekannt, die ein solches Gleichungssystem
Iterative Verfahren, Splittingmethoden Theodor Müller 19. April 2005 Sei ein lineares Gleichungssystem der Form Ax = b b C n, A C n n ( ) gegeben. Es sind direkte Verfahren bekannt, die ein solches Gleichungssystem
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
19. Januar Universität Erlangen-Nürnberg Department Mathematik PD Dr. Markus Bause. . Danach liefert die Gauss-Elinination. .
 Universität Erlangen-Nürnberg Department Mathematik PD Dr Markus Bause Numerik I 9 Januar A Gegeben sei die Matrix A = a Führen Sie eine Zeilenskalierung der Matrix durch Klausur b Bestimmen Sie mit Hilfe
Universität Erlangen-Nürnberg Department Mathematik PD Dr Markus Bause Numerik I 9 Januar A Gegeben sei die Matrix A = a Führen Sie eine Zeilenskalierung der Matrix durch Klausur b Bestimmen Sie mit Hilfe
