Numerisches Programmieren (IN0019)
|
|
|
- Kai Auttenberg
- vor 5 Jahren
- Abrufe
Transkript
1 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/ Gewöhnliche Differenzialgleichungen Differenzialgleichungen 3 Differenzialgleichungen (Physik) Differenzialgleichungen (Biologie) Anfangswertproblem AWP m-ter Ordnung Spezialfall: Integration Picard-Lindelöf 9 Iteratives Verfahren Iterative Funktionenfolge (Bsp.) Zusammenfassung Einschritt-Verfahren 13 Einschritt-Verfahren Euler-Verfahren Implizite Verfahren Verbessertes Euler-Verfahren Euler-Verfahren (Exp. Wachstum)
2 Euler-Verfahren (Bsp.) Klassisches Runge-Kutta-Verfahren Runge-Kutta (Exp. Wachstum) Einschritt-Verfahren (Exp.) Fehleranalyse 23 Diskretisierungsfehler Konsistenz Konsistenzordnung (Bsp.) Konvergenz Stabilität Expl. Euler (Stabilität) Impl. Euler (Stabilität) Stabilität in der Praxis Logistisches Wachstum Logistisches Wachstum (Bsp.) Logistisches Wachstum (Bsp.)
3 11. Gewöhnliche Differenzialgleichungen 2 / 34 Differenzialgleichungen 3 / 34 Differenzialgleichungen (Physik) Physikalische Prozesse lassen sich mit Differenzialgleichungen beschreiben. Das 2. Newtonsche Gesetz F m 0 a geht davon aus, dass auf einen Körper der Ruhemasse m 0 eine konstante Kraft F ausgeübt wird. Da die Beschleunigung aptq die Zeit-Ableitung der Geschwindigkeit vptq ist, erhält man folgende Beschreibung v 1 ptq F m 0 vp0q 0 Modelliert man außerdem noch, dass sich die Masse mit der Geschwindigkeit verändert (Spezielle Relativität), so erhält man v 1 ptq F a c2 vptq m 0 c 2 vp0q 0 Man erhält also eine Gleichung, die von einer Funktion und ihren Ableitungen (Differenzialen) abhängt. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 4 / 34 3
4 Differenzialgleichungen (Biologie) Auch Wachstumsprozesse lassen sich mit Differenzialgleichungen darstellen. Setzt man eine Bakterienkultur auf einem Nährboden aus, so kann man mit pptq die Population zum Zeitpunkt t angeben. Da die Reproduktionsrate p 1 ptq von der aktuellen Population abhängt, erhält man p 1 ptq α pptq pp0q 1 Modelliert man außerdem, dass die Petrischale nur Platz für eine Population p ď K zulässt, kann man das wie folgt modellieren ˆ p 1 ptq α pptq 1 pptq pp0q 1 K Es ist oft schwer, diese Probleme analytisch zu lösen. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 5 / 34 4
5 Anfangswertproblem Wir suchen eine Funktion y: R Ñ R, die folgende Differenzialgleichung erfüllt: y 1 pxq F px,ypxqq ypx 0 q y 0, wobei F : R ˆR Ñ R stetig ist. Wir nennen dieses Problem ein Anfangswertproblem (AWP), da neben der Differenzialgleichung auch der Anfangswert y 0 an der Stelle x 0 gegeben ist. Man kann zeigen, dass das AWP eindeutig lösbar ist, wenn F px,yq in y differenzierbar ist und diese Ableitungen durch eine Zahl L beschränkt sind. Ein AWP kann auch für Funktionen y: R Ñ R n beschrieben werden: y 1 pxq F px,ypxqq ypx 0 q y 0 P R n, wobei F : R ˆR n Ñ R n stetig ist. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 6 / 34 5
6 AWP m-ter Ordnung Weiter kann man Differenzialgleichungen auch für höhere Ableitungen beschreiben. Wir erhalten dann das AWP m-ter Ordnung y pmq pxq F px,y p0q pxq,...,y pm 1q pxqq y pkq px 0 q y ă m mit F : R ˆR n Ñ R n. Ein AWP m-ter Ordnung kann in ein vektorwertiges AWP erster Ordnung transformiert werden: zk 1 z k`1 k ă m 1 zm 1 1 F px,z 0 pxq,...,z m 1 pxqq zpx 0 q py 0,0,...,y 0,m 1 q J Es reicht also, Lösungen für das AWP erster Ordnung zu finden. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 7 / 34 6
7 Spezialfall: Integration Hängt F nicht von ypxq ab, so erhalten wir das AWP Dieses Problem lässt sich mit Hilfe der Integration eindeutig lösen y 1 pxq F pxq ypx 0 q y 0, fpxq y 0 ` Hierzu gehört z.b. das Bewegungsgesetz von Newton und wir erhalten für gerade die eindeutige Lösung ż x x 0 F ptqdt v 1 pxq F m 0 vp0q 0 ż x F vpxq 0 ` dt F x 0 m 0 m 0 IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 8 / 34 7
8 Picard-Lindelöf 9 / 34 Iteratives Verfahren Wir wollen nun mit der Integration eine Fixpunkt-Gleichung formulieren. Ist z.b. y die Lösung, die wir suchen, so gilt für dieses y gerade ypxq y 0 ` ż x ż x y 1 ptqdt y 0 ` F pt,yptqqdt : Φpyq x 0 x 0 Das Theorem von Picard-Lindelöf sagt aus, dass die Iterationsvorschrift Φ die Voraussetzung des Banachschen Fixpunktsatzes erfüllt. Damit wissen wir zum Einen, dass die Lösung y des AWP eindeutig ist. Außerdem erhalten wir durch wiederholtes Anwenden von Φ eine Funktionsfolge y rks die gegen die eindeutige Lösung y des AWP konvergiert. Für den Spezialfall des Integrationsproblem haben wir bereits gesehen, dass eine einmalige Anwendung von Φ zur Lösung y führt. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 10 / 34 8
9 Iterative Funktionenfolge (Bsp.) Betrachten wir nun das AWP Wir erhalten die folgende Iterationsfolge y rk`1s pxq 1 ` şx 0 yrks ptqdt. Starten wir mit der Einsfunktion, y r0s : 1, so erhalten wir y 1 pxq ypxq yp0q 1. y r1s pxq 1 ` y r2s pxq 1 ` ż x ż x y rk`1s pxq 1 ` d.h. die Funktionsfolge konvergiert zur eindeutigen Lösung y pxq exppxq. 0 0 ż x 0 1dt 1 `x 1 `tdt 1 `x` 1 kÿ n 0 t n k`1 n! dt ÿ IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 11 / 34 n 0 x n n!, 2 x2 Zusammenfassung Viele naturwissenschaftliche Probleme lasses sich als Lösungen von Differenzialgleichungen y 1 pxq F px,ypxqq darstellen. Das AWP mit ypx 0 q y 0 lässt sich immer eindeutig lösen, wenn F in y differenzierbar ist und diese Ableitung beschränkt ist. Die eindeutige Lösung lässt sich mit Hilfe eines iterativen Verfahrens lösen, das in jedem Schritt ein Integral berechnet. Ist F von der Gestalt F pxq, lässt sich das Problem auf ein Integrationsproblem zurückführen, das von dem iterativen Verfahren in einem Schritt gelöst wird. Anstelle der Iterationsvorschrift werden wir im Folgenden die Fixpunktgleichung y Φpyq direkt benutzen. Die Integralberechung wird mit Hilfe von Quadratur-Formeln durchgeführt. Unterschiedliche Quadratur-Formeln führen zu unterschiedlichen Verfahren. 9
10 IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 12 / 34 10
11 Einschritt-Verfahren 13 / 34 Einschritt-Verfahren Wir sind an dem Verlauf der Funktion y: rx 0 ;x 0 `T s Ñ R interessiert. Dazu zerlegen wir das Intervall rx 0 ;x 0 `T s in N äquidistante Abschnitte x k x 0 `h k h : T N k 0,...,N Jedes Verfahren brechnet y k «ypx k q nachdem alle y j mit j ă k bereits berechnet wurden. Wir starten mit der exakten Lösung des Anfangswertes y 0 ypx 0 q und berechnen zuerst y 1, y 2, etc. bis y N «ypx 0 `T q berechnet ist. Hängt y k`1 nur von y k ab, sprechen wir von einem Einschritt-Verfahren. Andernfalls von einem Mehrschritt-Verfahren. Alle Verfahren basieren üblicherweise auf Quadratur-Formeln. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 14 / 34 Euler-Verfahren Die einfachste Quadratur-Formel geht davon aus, dass der Integrand konstant ist. Wir erhalten damit das explizite Euler-Verfahren ypx 0 `hq y 0 ` ż h 0 F px 0 `t,ypx 0 `tqqdt «y 0 ` ż h 0 F px 0,y 0 qdt y 0 `h F px 0,y 0 q : y 1 Approximieren wir den Integranden mit dem konstanten Wert F px 0,ypx 0 `hqq, erhalten wir das implizite Euler-Verfahren ypx 0 `hq y 0 `h F px 0,ypx 0 `hqq Während im expliziten Verfahren, der neue Wert y 1 explizit gegeben ist, muss beim impliziten Verfahren die folgende Gleichung gelöst werden: y 1 y 0 `h F px 0,y 1 q 11
12 IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 15 / 34 12
13 Implizite Verfahren Um y 1 zu erhalten, ist die Nullstelle der Funktion fpy 1 q py 0 y 1 q `h F px 0,y 1 q zu finden. Hier kann man z.b. das Newton-Verfahren benutzen. Da implizite Verfahren oft exaktere Werte als explizite Verfahren liefern, ist es sinnvoll, das Newton-Verfahren mit dem Wert zu initialisieren, der das Ergebnis des expliziten Verfahrens ist. Man spricht dann von dem expliziten Euler-Schritt als Predictor und von dem Newton-Verfahren als Corrector. Nach der Berechnung von y 1 kann man y 2 «ypx 1 `hq berechnen, etc. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 16 / 34 13
14 Verbessertes Euler-Verfahren Die einfachste Gauß-Quadratur-Formel ist die Mittelpunktsregel. Mit ihr erhält man das verbesserte Euler-Verfahren ż h ypx 0 `hq y 0 ` F px 0 `t,ypx 0 `tqqdt «y 0 ` 0 ˆ y 0 `h F x 0 ` h 2,y 0.5 ż h 0 F ˆ x 0 ` h 2,y 0.5 dt Da y 0.5 nicht bekannt ist, wird hierfür das explizite Euler-Verfahren benutzt, d.h. wir erhalten insgesamt folgende Vorschrift: y 0.5 y 0 ` h 2 F px 0,y 0 q ˆ y 1 y 0 `h F x 0 ` h 2,y 0.5 Da die benutzte Quadratur eine Gauß-Quadratur ist, erwarten wir eine bessere Konvergenz als bei dem expliziten Euler-Verfahren mit halber Schrittweite. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 17 / 34 14
15 Euler-Verfahren (Exp. Wachstum) Betrachten wir die drei Euler-Verfahren für das folgende AWP y 1 pxq ypxq y 0 1 Das explizite Euler-Verfahren berechnet y 1 y 0 `h y 0 y 0 p1 `hq Das implizite Euler-Verfahren berechnet Das verbesserte Euler-Verfahren berechnet y 0.5 y 0 ˆ 1 ` h 2 y 1 y 0 `h y 1 y h ˆ y 1 y 0 1 `h 1 ` h j 2 IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 18 / 34 15
16 Euler-Verfahren (Bsp.) y y y x x x Euler (explizit) Euler (implizit) Euler (verbessert) Lösungen der drei Euler-Verfahren für x 0 0, T 1 und N 2,3,4. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 19 / 34 16
17 Klassisches Runge-Kutta-Verfahren Das klassische Runge-Kutta-Verfahren benutzt die Simpson-Regel als Quadratur-Formel: y 1 y 0 ` ż h 0 F px 0 `t,ypx 0 `tqqdt «y 0 ` h ˆ k 1 `4 k 2 `k 3 `k 4, 6 2 wobei k 1,k 4 den Integrand an den Rändern approximiert und k 2 sowie k 3 den zentralen Punkt des Integranden approximiert. Runge schlug 1895 folgende Werte für k 1 bis k 4 vor: k 1 F px 0,y 0 q k 2 F px 0 `0.5h,y 0 `0.5h k 1 q k 3 F px 0 `0.5h,y 0 `0.5h k 2 q k 4 F px 0 `h,y 0 `h k 3 q (Exakte Berechnung) ( Expliziter Euler-Schritt) ( Impliziter Euler-Schritt) ( Verbesserter Euler-Schritt) IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 20 / 34 17
18 Runge-Kutta (Exp. Wachstum) Betrachten wir erneut das AWP y 1 pxq ypxq y 0 1 Dann gilt für k 1 bis k 4 sowie y 1 gerade k 1 F px 0,y 0 q y 0 ˆ k 2 y 0 `0.5h k 1 y 0 1 ` 1 k 3 y 0 `0.5h k 2 y 0 k 4 y 0 `h k 3 y 0 2 h ˆ 1 ` 1 2 h ` 1 4 h2 ˆ 1 `h` 1 2 h2 ` 1 y 1 y 0 ` h 6 pk 1 `2k 2 `2k 3 `k 4 q y 0 4 h3 ˆ 1 `h` 1 2 h2 ` 1 6 h3 ` 1 24 h4 IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 21 / 34 18
19 Einschritt-Verfahren (Exp.) y y y y x x x x Euler (explizit) Euler (implizit) Euler (verbessert) Runge-Kutta (klassisch) Lösungen von Einschritt-Verfahren für x 0 0, T 1 und N 2,3,4. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 22 / 34 19
20 Fehleranalyse 23 / 34 Diskretisierungsfehler Bei der Definition des lokalen Diskretisierungsfehlers ε k beschreiben wir nur den Fehler, der entsteht, wenn wir den Übergang von px k,ypx k qq nach px k`1,ŷ k`1 q berechnen. ypx k q ist also der exakte Wert von y und nicht die Approximation y k. Der lokale Diskretisierungsfehler ist somit: e k : ŷ k`1 ypx k`1 q. Als globalen Diskretisierungsfehler bezeichnen wir: ε k : y k ypx k q. Dieser Fehler berücksichtigt alle Fehler bei der Berechnung von y k. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 24 / 34 20
21 Konsistenz Bei Einschritt-Verfahren wollen wir also erreichen, dass in jedem Schritt ein möglichst kleiner Fehler entsteht. Wir sagen, dass ein Verfahren die Konsistenzordnung p P N besitzt, falls Für den globalen Diskretisierungsfehler gilt nun bzgl. einer Konstanten L ą L: Wir nennen ein Verfahren konsistent, wenn p ě 1 gilt. y 1 y 0 Oph 1`p q. ε N ypx N q ŷ N ` ŷ N y N ď e N 1 ` p1 `Lhq ε N 1 N 1 ÿ ď... ď e LT k 0 e k Oph p q Dann verbessert sich der globale Diskretisierungsfehler bei jeder Verfeinerung. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 25 / 34 21
22 Konsistenzordnung (Bsp.) Die Konsistenzordnung des expliziten Euler-Verfahrens ist p 1. Die Konsistenzordnung des impliziten Euler-Verfahrens ist p 1. Die Konsistenzordnung des verbesserten Euler-Verfahrens ist p 2. Hierdurch ist der Name des verbesserten Euler-Verfahrens gerechtfertigt. Die Konsistenzordnung des klassischen Runge-Kutta-Verfahrens ist p 4. Wir haben das bereits am Beispiel des exponentiellen Wachstums gesehen: (expl. Euler:) (verb. Euler:) y 1 y 0 y 1 y 0 1ÿ k 0 2ÿ k 0 h k k! h k k! (impl. Euler:) (Runge-Kutta:) y 1 y 0 y 1 y 0 1ÿ k 0 4ÿ k 0 h k k! `Oph2 q h k k! IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 26 / 34 22
23 Konvergenz Ein konsistentes Verfahren stellt sicher, dass wir für h Ñ 0 die korrekte Lösung berechnen, d.h. wir betrachten folgende Folgen y 0 y phq 1... y phq N für h T N Dann ist y phq N eine Approximation von ypx 0 `T q und es gilt lim yp T N q NÑ8 N ypx 0 `T q Dieses Verhalten nennen wir Konvergenz des Verfahrens. Man kann zeigen, dass ein Verfahren mit der Konsistenzordnung p auch mit der Ordnung p konvergiert, d.h. eine höhere Konsistenzordnung ist grundsätzlich besser, um eine Differenzialgleichung approximativ zu lösen. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 27 / 34 Stabilität Die Konsistenz beantwortet die Frage nach der Konvergenz für h Ñ 0. Nun beschäftigen wir uns mit der Frage, welche h sinnvolle Ergebnisse liefern. Betrachten wir hierzu erneut das AWP y 1 pxq λ ypxq yp0q 1 Wir sagen, dass ein Verfahren bzgl. h ą 0 stabil ist, wenn die Folge y 1,...,y n,... folgende Eigenschaften hat lim n 8 nñ8 (λ ą 0) lim n 0 nñ8 (λ ă 0) Wir definieren die Stabilität nur bzgl. des exponentiellen Wachstums, da man hierfür die exakte Lösung der Differenzialgleichung kennt. 23
24 IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 28 / 34 24
25 Expl. Euler (Stabilität) Das explizite Euler-Verfahren berechnet die folgende Folge y k`1 y k `hλy k y k p1 `hλq y k p1 `hλq k Für λ ą 0 erhalten wir die Stabilitätsbedingung 1 `hλ ą 1, die wegen h ą 0 immer erfüllt ist. Für λ ă 0 erhalten wir die Stabilitätsbedingung 1 `hλ ă 1, die nur für h ă 2 λ erfüllt ist. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 29 / 34 25
26 Impl. Euler (Stabilität) Das implizite Euler-Verfahren berechnet die folgende Folge y k y k`1 1 hλ 1 y k p1 hλq k Für λ ą 0 erhalten wir die Stabilitätsbedingung 1 hλ ă 1, die nur für h ă 2 λ erfüllt ist. Für λ ă 0 erhalten wir die Stabilitätsbedingung 1 hλ ą 1, die wegen h ą 0 immer erfüllt ist. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 30 / 34 26
27 Stabilität in der Praxis Das explizite Euler-Verfahren ist stabil für alle Schrittweiten, falls λ ą 0 gilt. Das implizite Euler-Verfahren ist stabil für alle Schrittweiten, falls λ ă 0 gilt. In der Praxis ist der Fall λ ă 0 wichtiger als λ ą 0, da λ ă 0 eine Dämpfung beschreibt. Wenn man z.b. bei statischen Problemen, Spannungen korrekt beschreiben möchte, sollte auf jeden Fall die Situation λ ă 0 korrekt dargestellt werden. Aus diesen Gründen wird das implizite Euler-Verfahren oft dem expliziten Euler-Verfahren vorgezogen. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 31 / 34 Logistisches Wachstum Im Folgenden betrachten wir das AWP des logistischen Wachstums ˆ p 1 ptq pptq 1 pptq 5 pp0q 1. Der explizite Euler-Schritt ist p 1 p 0 p1 `hq h 5 p2 0 Der implizite Euler-Schritt ist p 1 a r2.5p1 hqs2 `5hp 0 2.5p1 hq Der verbesserte Euler-Schritt ist ein Polynom 4. Grades in y 0 und h. Das klassische Runge-Kutta-Verfahren benutzt ein Polynom 16. Grades in y 0 und 15. Grades in h. IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 32 / 34 h 27
28 Logistisches Wachstum (Bsp.) y y x x Euler (explizit) Euler (implizit) IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 33 / 34 28
29 Logistisches Wachstum (Bsp.) y y x x Euler (verbessert) Runge-Kutta (klassisch) IN Numerisches Programmieren 11. Gewöhnliche Differenzialgleichungen 34 / 34 29
Numerisches Programmieren (IN0019) 11. Gewöhnliche Differenzialgleichungen. Differenzialgleichungen. Differenzialgleichungen (Physik)
 umerisches Programmieren (I19) Frank R. Schmidt 11. Gewöhnliche Differenzialgleichungen Winter Semester 16/17 Differenzialgleichungen (Phsik) Differenzialgleichungen Phsikalische Prozesse lassen sich mit
umerisches Programmieren (I19) Frank R. Schmidt 11. Gewöhnliche Differenzialgleichungen Winter Semester 16/17 Differenzialgleichungen (Phsik) Differenzialgleichungen Phsikalische Prozesse lassen sich mit
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Mathematische Grundlagen
 G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 9. Symmetrisches Eigenwertproblem.................................................................................... 2 Eigenwert-Problem
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 9. Symmetrisches Eigenwertproblem.................................................................................... 2 Eigenwert-Problem
Dr. R. Käppeli D-ITET, D-MATL Sommer Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Diplom VP Numerik 28. August 2006
 Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
Lösung Semesterendprüfung
 MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Newton-Verfahren für ein Skalarfunktion
 Newton-Verfahren für ein Skalarfunktion Für eine Näherungsberechnung von Nullstellen einer reellen Funktion f(x) : R R benutzt man das Newton-Verfahren: x (n+1) = x (n) f(x (n) )/f (x (n) ). Das Newton-Verfahren
Newton-Verfahren für ein Skalarfunktion Für eine Näherungsberechnung von Nullstellen einer reellen Funktion f(x) : R R benutzt man das Newton-Verfahren: x (n+1) = x (n) f(x (n) )/f (x (n) ). Das Newton-Verfahren
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen Aufgaben für das Seminar und zum selbständigen Üben 22. Januar 2018 Vorbereitende Übungen Aufgabe 1: Bestimmen Sie die Isoklinen zu den folgenden Differentialgleichungen
Gewöhnliche Differentialgleichungen Aufgaben für das Seminar und zum selbständigen Üben 22. Januar 2018 Vorbereitende Übungen Aufgabe 1: Bestimmen Sie die Isoklinen zu den folgenden Differentialgleichungen
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
eps für alle x D. 4. Die Zahl 256 ist in M(2, 4, 6, 6) exakt darstellbar.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
3. Lineare Mehrschrittverfahren 3.1 Begriffe
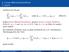 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Höhere Mathematik III für die Fachrichtung Physik Wintersemester 2016/17. Lösungsvorschlag zu Übungsblatt 5
 Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Folgen und Reihen Folgen
 Folgen und Reihen 30307 Folgen Einstieg: Wir beginnen mit einigen Beispielen für reelle Folgen: (i),, 4, 8, 6, (ii) 4,, 6, 3, 7, (iii) 0,,,, 3,, (iv), 3, 7,,, Aufgabe : Setzt die Zahlenfolgen logisch fort
Folgen und Reihen 30307 Folgen Einstieg: Wir beginnen mit einigen Beispielen für reelle Folgen: (i),, 4, 8, 6, (ii) 4,, 6, 3, 7, (iii) 0,,,, 3,, (iv), 3, 7,,, Aufgabe : Setzt die Zahlenfolgen logisch fort
Differentialgleichungen
 Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
(c) Gegeben sei der zweidimensionale Raum L mit den Basisfunktionen. [ φ i, φ j ] 3 i,j=1 =
![(c) Gegeben sei der zweidimensionale Raum L mit den Basisfunktionen. [ φ i, φ j ] 3 i,j=1 = (c) Gegeben sei der zweidimensionale Raum L mit den Basisfunktionen. [ φ i, φ j ] 3 i,j=1 =](/thumbs/88/117470920.jpg) 1. (a) i. Wann besitzt A R n n eine eindeutige LR-Zerlegung mit R invertierbar? ii. Definieren Sie die Konditionszahl κ(a) einer Matrix A bzgl. einer Norm.! iii. Welche Eigenschaften benötigt eine Matrix
1. (a) i. Wann besitzt A R n n eine eindeutige LR-Zerlegung mit R invertierbar? ii. Definieren Sie die Konditionszahl κ(a) einer Matrix A bzgl. einer Norm.! iii. Welche Eigenschaften benötigt eine Matrix
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
PVK Probeprüfung FS 2017
 PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
Klausur Numerische Mathematik (für Elektrotechniker), 24. Februar 2016
 Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
A 1 A 2 A 3 A 4 A 5 A 6 A 7
 Institut für Geometrie und Praktische Mathematik Numerisches Rechnen für Informatiker WS 7/8 Prof. Dr. H. Esser J. Grande, Dr. M. Larin Klausur Numerisches Rechnen für Informatiker Hilfsmittel: keine (außer
Institut für Geometrie und Praktische Mathematik Numerisches Rechnen für Informatiker WS 7/8 Prof. Dr. H. Esser J. Grande, Dr. M. Larin Klausur Numerisches Rechnen für Informatiker Hilfsmittel: keine (außer
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
Skript zur Vorlesung Analysis 3
 Skript zur Vorlesung Analysis 3 Herbstsemester 204 Prof. Benjamin Schlein Inhaltsverzeichnis Gewöhnliche Differentialgleichungen 2. Differentialgleichungen erster Ordnung, elementare Lösungsmethoden..
Skript zur Vorlesung Analysis 3 Herbstsemester 204 Prof. Benjamin Schlein Inhaltsverzeichnis Gewöhnliche Differentialgleichungen 2. Differentialgleichungen erster Ordnung, elementare Lösungsmethoden..
Numerische Methoden 7. Übungsblatt
 Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 10. Minimieren von Funktionen....................................................................................... 2 Gradienten-Abstieg
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 10. Minimieren von Funktionen....................................................................................... 2 Gradienten-Abstieg
1/26. Integration. Numerische Mathematik 1 WS 2011/12
 1/26 Integration Numerische Mathematik 1 WS 2011/12 Notation 2/26 Die Abbildung I b a : C([a, b]) R gegeben durch Ia b (f ) := beschreibt die Integration. b a f (x)dx, Um das Integral I(f ) zu approximieren
1/26 Integration Numerische Mathematik 1 WS 2011/12 Notation 2/26 Die Abbildung I b a : C([a, b]) R gegeben durch Ia b (f ) := beschreibt die Integration. b a f (x)dx, Um das Integral I(f ) zu approximieren
Musterlösung Klausur zu Analysis II. Verständnisteil
 Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 2
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Gewöhnliche Differentialgleichungen Woche 7. Nicht-lineare und linearisierte Systeme
 Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Gewöhnliche Differentialgleichungen Woche 6. Existenz nach Picard-Lindelöf
 d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei die Matrix
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 5. Interpolation.................................................................................................. 2 Interpolation
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 5. Interpolation.................................................................................................. 2 Interpolation
1 Einführung, Terminologie und Einteilung
 Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Kapitel 16 : Differentialrechnung
 Kapitel 16 : Differentialrechnung 16.1 Die Ableitung einer Funktion 16.2 Ableitungsregeln 16.3 Mittelwertsätze und Extrema 16.4 Approximation durch Taylor-Polynome 16.5 Zur iterativen Lösung von Gleichungen
Kapitel 16 : Differentialrechnung 16.1 Die Ableitung einer Funktion 16.2 Ableitungsregeln 16.3 Mittelwertsätze und Extrema 16.4 Approximation durch Taylor-Polynome 16.5 Zur iterativen Lösung von Gleichungen
Dierentialgleichungen 2. Ordnung
 Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Übungen zu Differentialgleichungen (WiSe 12/13)
 Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
NUMERIK 1. Sommersemester 2016
 NUMERIK 1 Soerseester 2016 KLAUSUR LÖSUNGSVORSCHLAG Aufgabe 1 (Multiple Choice) (ca. 20 Minuten, 8 Punkte) Kreuzen Sie korrekte Aussagen an. Es können ehrere Antworten richtig sein, indestens eine ist
NUMERIK 1 Soerseester 2016 KLAUSUR LÖSUNGSVORSCHLAG Aufgabe 1 (Multiple Choice) (ca. 20 Minuten, 8 Punkte) Kreuzen Sie korrekte Aussagen an. Es können ehrere Antworten richtig sein, indestens eine ist
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
Numerische Verfahren
 Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 15.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren Numerische
Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 15.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren Numerische
Kapitel 4: Nichtlineare Nullstellenprobleme
 Vorlesung Höhere Mathematik: Numerik (für Ingenieure) Kapitel 4: Nichtlineare Nullstellenprobleme Jun.-Prof. Dr. Stephan Trenn AG Technomathematik, TU Kaiserslautern Sommersemester 2015 HM: Numerik (SS
Vorlesung Höhere Mathematik: Numerik (für Ingenieure) Kapitel 4: Nichtlineare Nullstellenprobleme Jun.-Prof. Dr. Stephan Trenn AG Technomathematik, TU Kaiserslautern Sommersemester 2015 HM: Numerik (SS
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Serie 13: Online Test
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
Computersimulationen in der Astronomie
 Computersimulationen in der Astronomie Fabian Heimann Universität Göttingen, Fabian.Heimann@stud.uni-goettingen.de Astronomisches Sommerlager 2013 Inhaltsverzeichnis 1 Differentialgleichungen 3 1.1 Beispiele.....................................
Computersimulationen in der Astronomie Fabian Heimann Universität Göttingen, Fabian.Heimann@stud.uni-goettingen.de Astronomisches Sommerlager 2013 Inhaltsverzeichnis 1 Differentialgleichungen 3 1.1 Beispiele.....................................
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
 Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Numerische Ableitung
 Numerische Ableitung Die Ableitung kann angenähert werden durch den Differentenquotient: f (x) f(x + h) f(x) h oder f(x + h) f(x h) 2h für h > 0, aber h 0. Beim numerischen Rechnen ist folgendes zu beachten:
Numerische Ableitung Die Ableitung kann angenähert werden durch den Differentenquotient: f (x) f(x + h) f(x) h oder f(x + h) f(x h) 2h für h > 0, aber h 0. Beim numerischen Rechnen ist folgendes zu beachten:
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
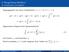 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Prüfer: Dr. M. Lenz, Prof. Dr. M. Rumpf. Klausurdauer: 180 Minuten. Bitte Namen, Vornamen und Matrikel-Nr. einsetzen. Name:... Vorname:...
 Klausur zum Modul Ingenieurmathematik II (B22) 20. März 2014 für den Bachelorstudiengang Geodäsie und Geoinformation In der Klausur können 10 Punkte pro Aufgabe, also insgesamt 100 Punkte erreicht werden.
Klausur zum Modul Ingenieurmathematik II (B22) 20. März 2014 für den Bachelorstudiengang Geodäsie und Geoinformation In der Klausur können 10 Punkte pro Aufgabe, also insgesamt 100 Punkte erreicht werden.
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Kapitel 3. Konvergenz von Folgen und Reihen
 Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
Analysis I. 14. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I 4. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching June 6, 207 Erinnerung Die Reihe a k konvergiert falls, lim S n = lim n n n a k =: a k existiert. Satz (Majoranten/Minorantenkriterium)
Analysis I 4. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching June 6, 207 Erinnerung Die Reihe a k konvergiert falls, lim S n = lim n n n a k =: a k existiert. Satz (Majoranten/Minorantenkriterium)
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Differenzialgleichungen
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 30. Januar 2008 (System von) Differenzialgleichung(en) Schwingungsgleichung Newtonsche Mechanik Populationsdynamik...DGLn höherer Ordnung auf
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 30. Januar 2008 (System von) Differenzialgleichung(en) Schwingungsgleichung Newtonsche Mechanik Populationsdynamik...DGLn höherer Ordnung auf
Lösungen zur Übungsserie 9
 Analysis 1 Herbstsemester 2018 Prof. Peter Jossen Montag,? November Lösungen zur Übungsserie 9 Aufgaben 1,2,3,5,6,8,9,11 Aufgabe 1. Sei a R. Berechnen Sie die folgenden Grenzwerte, falls sie existieren.
Analysis 1 Herbstsemester 2018 Prof. Peter Jossen Montag,? November Lösungen zur Übungsserie 9 Aufgaben 1,2,3,5,6,8,9,11 Aufgabe 1. Sei a R. Berechnen Sie die folgenden Grenzwerte, falls sie existieren.
Numerik und Simulation in der Geoökologie
 1/49 Rekapitulation Das Euler-Verfahren für ODE-IVP Eigenschaften von Einschrittverfahren Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 2 WS 2007/2008 2/49 Rekapitulation Das Euler-Verfahren
1/49 Rekapitulation Das Euler-Verfahren für ODE-IVP Eigenschaften von Einschrittverfahren Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 2 WS 2007/2008 2/49 Rekapitulation Das Euler-Verfahren
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
7. Nichtlineare Gleichngssysteme. Problem 7: Sei f : R n R n stetig. Löse f(x) = 0.
 7. Nichtlineare Gleichngssysteme Problem 7: Sei f : R n R n stetig. Löse f(x) = 0. Das Gleichungssystem f(x) = 0 lässt sich in die Fixpunktgleichung x = φ(x) umschreiben, wobei φ : D R n R n. Beispielsweise
7. Nichtlineare Gleichngssysteme Problem 7: Sei f : R n R n stetig. Löse f(x) = 0. Das Gleichungssystem f(x) = 0 lässt sich in die Fixpunktgleichung x = φ(x) umschreiben, wobei φ : D R n R n. Beispielsweise
Kapitel L. Gewöhnliche Differentialgleichungen
 Kapitel L Gewöhnliche Differentialgleichungen Inhalt dieses Kapitels L000 1 Erste Beispiele von Differentialgleichungen 2 Exakte Differentialgleichungen 3 Fazit: Existenz, Eindeutigkeit, Lösungsmethoden
Kapitel L Gewöhnliche Differentialgleichungen Inhalt dieses Kapitels L000 1 Erste Beispiele von Differentialgleichungen 2 Exakte Differentialgleichungen 3 Fazit: Existenz, Eindeutigkeit, Lösungsmethoden
Klausur,,Algorithmische Mathematik II
 Institut für angewandte Mathematik Sommersemester 017 Andreas Eberle, Matthias Erbar / Behrend Heeren Klausur,,Algorithmische Mathematik II Musterlösung 1 (Unabhängige Zufallsvariablen) a) Wir bezeichnen
Institut für angewandte Mathematik Sommersemester 017 Andreas Eberle, Matthias Erbar / Behrend Heeren Klausur,,Algorithmische Mathematik II Musterlösung 1 (Unabhängige Zufallsvariablen) a) Wir bezeichnen
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
(Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
4 Gewöhnliche Differentialgleichungen
 4 Gewöhnliche Differentialgleichungen 4.1 Einleitung Definition 4.1 Gewöhnliche Differentialgleichung n-ter Ordnung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten
4 Gewöhnliche Differentialgleichungen 4.1 Einleitung Definition 4.1 Gewöhnliche Differentialgleichung n-ter Ordnung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten
C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: Ort: Geschwindigkeit:
 C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel
C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel
Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben. Eine kurze Einführung in Quasi Newton Verfahren
 Ergänzungen zu dem Buch Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben von Carl Geiger und Christian Kanzow (Springer Verlag, 1999) Eine kurze Einführung in Quasi Newton Verfahren
Ergänzungen zu dem Buch Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben von Carl Geiger und Christian Kanzow (Springer Verlag, 1999) Eine kurze Einführung in Quasi Newton Verfahren
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Die Differentialgleichung :
 Die Differentialgleichung : Erstellt von Judith Ackermann 1.) Definition, Zweck 1.1) verschiedene Arten von Differentialgleichungen 2.) Beispiele und Lösungswege 2.1) gewöhnliche Differentialgleichungen
Die Differentialgleichung : Erstellt von Judith Ackermann 1.) Definition, Zweck 1.1) verschiedene Arten von Differentialgleichungen 2.) Beispiele und Lösungswege 2.1) gewöhnliche Differentialgleichungen
Nichtlineare Gleichungssysteme
 Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
PRÜFUNG AUS MATHEMATIK 3
 (8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
(8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
Teil 6. Differentialrechnung mehrerer Veränderlicher
 Teil 6 Differentialrechnung mehrerer Veränderlicher 95 96 6.1 Topologie von Mengen Umgebung ε-umgebung eines Punktes x R n : B ε (x) = {y : y x < ε} Umgebung U von x: Menge, die eine ε-umgebung von x enthält
Teil 6 Differentialrechnung mehrerer Veränderlicher 95 96 6.1 Topologie von Mengen Umgebung ε-umgebung eines Punktes x R n : B ε (x) = {y : y x < ε} Umgebung U von x: Menge, die eine ε-umgebung von x enthält
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
