Numerik Grundpraktikum: Numerische Verfahren für gewöhnliche Differentialgleichungen
|
|
|
- Rudolf Frei
- vor 5 Jahren
- Abrufe
Transkript
1 Numerik Grundpraktikum: Numerische Verfahren für gewöhnliche Differentialgleichungen Roland Pulch Vorlesung im Wintersemester 205/6 Institut für Mathematik und Informatik Ernst-Moritz-Arndt-Universität Greifswald Inhalt:. Problemstellung und Beispiele 2. Einschrittverfahren 3. Mehrschrittverfahren 4. Methoden für steife Differentialgleichungen Literatur: J. Stoer, R. Bulirsch: Numerische Mathematik 2. (5. Aufl.) Springer, (Kapitel 7) P. Deuflhard, F. Bornemann: Numerische Mathematik 2. Gewöhnliche Differentialgleichungen. (3. Aufl.) de Gruyter, K. Strehmel, R. Weiner, H. Podhaisky: Numerik gewöhnlicher Differentialgleichungen. (2. Aufl.) Springer Spektrum, 202. H.R. Schwarz, N. Köckler: Numerische Mathematik. (8. Aufl.) Vieweg+Teubner, 20. (Kapitel 8)
2 Inhaltsverzeichnis Problemstellung und Beispiele. Existenz und Eindeutigkeit Chemische Reaktionskinetik Elektrische Schaltungen Mehrkörpersysteme Einschrittverfahren 2. Vorbereitungen Elementare Integrationsverfahren Konsistenz und Konvergenz Runge-Kutta-Verfahren Schrittweitensteuerung Mehrschrittverfahren Methoden über numerischer Quadratur Methoden über numerische Differentiation Konsistenz, Stabilität und Konvergenz Prädiktor-Korrektor-Verfahren Ordnungssteuerung ii
3 4 Methoden für steife Differentialgleichungen Beispiele Testgleichungen A-Stabilität für Einschrittverfahren A-Stabilität für Mehrschrittverfahren Vergleich der Verfahrensklassen Literaturverzeichnis 85 iii
4 Kapitel Problemstellung und Beispiele Diese Veranstaltung behandelt die numerische Lösung von Anfangswertproblemen zu gewöhnlichen Differentialgleichungen. Systeme aus gewöhnlichen Differentialgleichungen (gew. Dgln.) erster Ordnung besitzen die Gestalt oder komponentenweise geschrieben y (x) = f(x, y(x)), y (x) = f (x, y (x),..., y n (x)) y 2(x) = f 2 (x, y (x),..., y n (x)). y n(x) = f n (x, y (x),..., y n (x)). Ein solches System besitzt im allgemeinen unendlich viele Lösungen. Daher sind zusätzliche Bedingungen notwendig, um eine eindeutige Lösung zu identifizieren. Ein Anfangswertproblem (AWP) ergibt sich durch Vorgabe eines Anfangswerts y(x 0 ) = y 0 zu einem bestimmten Anfangspunkt x 0 R zusammen mit einem vorgegebenem Wert y 0 R n. Abb. verdeutlicht diese Problemstellung. Demgegenüber liegt bei einem Randwertproblem (RWP) eine Bedingung vor, die sowohl einen Anfangszustand als auch einen Endzustand einbezieht,
5 y y 0 x 0 x d.h. Abbildung : Anfangswertproblem einer gewöhnlichen Differentialgleichung. r(y(a), y(b)) = 0 mit gegebener Funktion r : R n R n R n zu einem Intervall [a, b]. Beispielsweise ergibt sich ein periodisches RWP durch die Forderung y(a) y(b) = 0. Eine gew. Dgl. n-ter Ordnung lautet z (n) (x) = g(x, z(x), z (x), z (x),..., z (n ) (x)). Wir erhalten ein äquivalentes System erster Ordnung durch die Definition Es folgt das System y := z, y 2 := z, y 3 := z,..., y n := z (n ). y = y 2, y 2 = y 3,..., y n = y n, y n = g(x, y,..., y n ). Daher betrachten wir in dieser Veranstaltung o.e.d.a. nur Systeme erster Ordnung. Desweiteren gibt es die Klasse der partiellen Differentialgleichungen (part. Dgln.), wobei die Lösung nicht mehr nur von einer unabhängigen Veränderlichen sondern mehreren unabhängigen Veränderlichen abhängt. Hier können AWPe, RWPe oder Kombinationen aus beiden vorliegen. In den meisten Fällen können AWPe oder RWPe von Dgln. nicht analytisch gelöst werden, d.h. es existiert keine geschlossene Formel für die Lösung. 2
6 Auch wenn ein analytischer Lösungsweg möglich ist, so möchte man diesen meist vermeiden wegen des hohen Aufwands. Daher sind numerische Verfahren für diese Probleme erforderlich. Wir präsentieren später Beispiele von Modellen aus gew. Dgln., die in verschiedenen Anwendungsgebieten auftreten: in der Chemie (Reaktionskinetik), in der Elektrotechnik (elektrische Schaltung) und in der Mechanik (Mehrkörperproblem). In allen Fällen werden diese mathematischen Modelle zur (näherungsweisen) Beschreibung von realen Prozessen eingesetzt. Wegen vereinfachender Modellannahmen stellt die Lösung der Dgln. eine Approximation der realen Zustände dar.. Existenz und Eindeutigkeit Gegeben sei das AWP y (x) = f(x, y(x)), y(x 0 ) = y 0 (.) mit der rechten Seite f : G R n auf einer offenen Menge G R R n. Es gilt (x 0, y 0 ) G für den Anfangswert. Wir benötigen als Voraussetzung die Existenz und Eindeutigkeit der Lösung y. Der Satz von Peano liefert eine Existenzaussage für eine stetige rechte Seite, jedoch keine Eindeutigkeitsaussage. Für die Eindeutigkeit wird eine stärkere Eigenschaft benötigt. Definition. Die rechte Seite f genügt auf der offenen Menge G einer globalen Lipschitz-Bedingung, wenn eine Konstante L > 0 existiert mit f(x, y) f(x, z) L y z (.2) für alle (x, y), (x, z) G. Die rechte Seite f erfüllt eine lokale Lipschitz- Bedingung, wenn zu jedem (ˆx, ŷ) G eine Umgebung U G exisitert, so dass f auf U eine Lipschitz-Bedingung mit einer von U abhängigen Konstanten L > 0 erfüllt. In dieser Definition wird eine beliebige Vektornorm auf dem R n verwendet. Hinreichend für die lokale Lipschitz-Bedingung ist, dass f auf G 3
7 bezüglich der Variablen y stetig differenzierbar ist. Der Satz von Picard- Lindelöf gibt nun eine Existenz- und Eindeutigkeitsaussage. Satz. (Picard-Lindelöf) Sei G R R n offen und f : G R n eine stetige Funktion, die eine lokale Lipschitz-Bedingung erfüllt. Dann gibt es zu jedem Anfangswert (x 0, y 0 ) G ein ε > 0 und eine eindeutige Lösung y : [x 0 ε, x 0 + ε] R n des AWPs (.). Beweis: siehe Satz 4 in Kapitel 2 aus [3]..2 Chemische Reaktionskinetik Chemische Prozesse enthalten typischerweise bimolekulare Reaktionen der Gestalt A + B C + D. Sei c S die Konzentration der Substanz S, welche von der Zeit t abhängt. Das zugehörige System gew. Dgln. lautet c A (t) = k c A(t)c B (t) c B (t) = k c A(t)c B (t) c C (t) = +k c A(t)c B (t) c D (t) = +k c A(t)c B (t). (.3) Die Reaktionsrate k > 0 charakterisiert die Wahrscheinlichkeit der chemischen Reaktion im Fall einer Kollision der Moleküle A und B. Der Koeffizient k kann daher Geschwindigkeit der Reaktion interpretiert werden. Die physikalische Einheit des Parameters k ist liter/(s mol). Anfangswerte sind für das System (.3) vorzugeben. Nun betrachten wir eine Menge aus m allgemeinen chemischen Reaktionen zwischen n verschiedenen Stoffen A,..., A n (Moleküle/Atome), d.h. α j A + α 2j A α nj A n k j γj A + γ 2j A γ nj A n 4
8 für j =,..., m oder äquivalent n k j n α ij A i γ ij A i für j =,..., m. (.4) i= i= Die Parameter α ij, γ ij N 0 stellen die stoichiometrischen Konstanten dar. Die j-te Reaktion besitzt die Geschwindigkeit k j R +. Es entsteht als mathematisches Modell dc Ai m n α = (γ ij α ij )k j c lj Al für i =,..., n, dt j= l= welches ein System aus n gew. Dgln. für die unbekannten Konzentrationen darstellt. Die Auswertung der rechten Seite kann automatisch erfolgen, wenn die Reaktionsgleichungen (.4) spezifiziert sind. Die Hydrolyse von Harnstoff ist ein Beispiel für ein chemisches Reaktionssystem. Dabei reagiert Harnstoff (Urea) zusammen mit Wasser zu Ammoniumcarbonat. Für eine genügende Schnelligkeit der Reaktion ist die Hilfe des Enzyms Urease erforderlich, da es die Aktivierungsenergie verringert, d.h. das Enzym fungiert als Katalysator. Das gesamte Reaktion lautet (NH 2 ) 2 CO + 2 H 2 O + Urease (NH 4 ) 2 CO 3 + Urease. (.5) Dieser Prozess ergibt sich aus drei einfacheren Reaktionen. Mit den Abkürzungen U: Urea, E: Urease, UE: Kombination aus Urea and Urease, A: Ammoniumcarbonat besteht die Reaktion (.5) aus den drei Anteilen U + E UE UE + 2 H 2 O k k 2 UE U + E (.6) k 3 A + E. Die Parameter k, k 2, k 3 spezifizieren die Reaktionsgeschwindigkeiten. Wir konstruieren ein mathematisches Modell für dieses Reaktionssystem. Sei wieder c S die Konzentration der Substanz S in der Einheit mol/liter (mol/l). Die zeitliche Änderung der Konzentrationen soll bestimmt werden. Da alle Reaktionen in Wasser stattfinden und die anderen Konzentrationen 5
9 Konzentrationen [mol/l] [U] [E] [UE] [A] Zeit [s] Abbildung 2: Simulation der Hydrolyse von Harnstoff. demgegenüber relativ klein sind, nehmen wir eine konstante Wasserkonzentration (55.56 mol/l) an. Die Reaktionsgeschwindigkeiten sind k = 3.0 l mol s, k 2 = 0.02 s, k 3 = 0. s. (.7) Es folgt ein System aus vier gew. Dgln. für die unbekannten Konzentrationen c U = k c U c E + k 2 c UE c E = k c U c E + k 2 c UE + k 3 c UE c UE = k c U c E k 2 c UE k 3 c UE c A = k 3 c UE. (.8) Dieses System besitzt eine eindeutige Lösung für vorgegebene Anfangswerte. Wir verwenden die Anfangsbedingungen c U = 0. mol l, c E = 0.02 mol, c l UE = c A = 0. (.9) Wie bei vielen anderen Anwendungen ist eine analytische Lösung des Systems aus gew. Dgln. nicht möglich, d.h. wir können keine explizite Formel 6
10 für die unbekannte Lösung erhalten. Daher verwenden wir eine numerisches Verfahren um eine Näherungslösung zu erhalten. Abb. 2 zeigt das Ergebnis. Zum einen verringert sich die Konzentration von Harnstoff mit der Zeit bis auf null, da die Substanz in der Hydrolyse abgebaut wird. Zum anderen erhöht sich die Konzentration des Reaktionsprodukts Ammoniumcarbonat bis kein Harnstoff mehr vorhanden ist. Die Konzentration des Enzyms verringert sich zwar anfangs, jedoch liegt am Ende wieder genau soviel Enzym vor wie zu Beginn..3 Elektrische Schaltungen Als ein einfaches Beispiel einer elektrischen Schaltung betrachten wir den elektromagnetischen Schwingkreis. Dieser besteht aus einer Kapazität C, einer Induktivität L und einem Widerstand R, siehe Abb. 3 (links). Die Kirchhoffsche Knotenregel liefert die Gleichung I C + I L + I R = 0. Die Kirchhoffsche Maschenregel impliziert U := U C = U L = U R. Jedes Element der Schaltung ist durch eine Strom-Spannungs-Relation gekennzeichnet, nämlich CU C = I C, LI L = U L, R = U R I R. Es folgt ein lineares System aus zwei gew. Dgln. U = C I L RC U I L = L U (.0) für die unbekannten Funktionen U und I L. Weitere Umformungen liefern eine gew. Dgl. zweiter Ordnung für die unbekannte Spannung U + RC U + LC U = 0. Wenn der Widerstand hinreichend klein ist, dann entsteht als Lösung eine gedämpfte Schwingung U(t) = e 2RC t [A sin (ωt) + B cos (ωt)] mit ω = LC 4R 2 C. 2 7
11 U U I I I R L C I I I R L C I S Abbildung 3: Elektromagnetischer Schwingkreis ohne (links) und mit (rechts) Stromquelle. Die Konstanten A und B bestimmen sich aus Anfangsbedingungen. Das System (.0) aus gew. Dgln. ist autonom. Wir erhalten eine zeitabhängiges System durch Hinzufügen einer unabhängigen Stromquelle, siehe Abb. 3 (rechts). Als Eingabe verwenden wir Es folgen dann die Dgln. I in (t) = I 0 sin (ω 0 t). U = C I L RC U C I in(t) I L = L U. (.) In diesem Fall entstehen als Spannungen und Ströme dann erzwungene Schwingungen. Abb. 4 zeigt Beispiele zu Lösungen von Anfangswertproblemen der Systeme (.0) und (.)..4 Mehrkörpersysteme Wir betrachten ein Zwei-Körper-Problem bestehend aus Partikeln mit den Massen m, m 2. Sei Xi = (x i, y i, z i ) die Position der i-ten Masse. Die Positionen und die Geschwindigkeiten der Körper hängen von der Zeit ab. Die Gravitation bewirkt Kräfte zwischen den Massen. Das Newtonsche Bewegungsgesetz liefert ein System aus gew. Dgln. zweiter Ordnung m X (t) = G m m 2 X (t) X 2 (t) 3( X 2 (t) X (t)) m 2 X 2 (t) = G m m 2 X (t) X 2 (t) 3( X (t) X 2 (t)) 8
12 Spannung [V] Spannung [V] Zeit [ms] Zeit [ms] Abbildung 4: Lösung U der Dgl. (.0) (links) und der Dgl. (.) (rechts). mit der Gravitationskonstanten G > 0. Setzen wir V i := X i für die Geschwindigkeiten, so folgt ein System erster Ordnung X = V V = G m 2 X X 2 3( X 2 X ) X 2 = V 2 V 2 = G m X X 2 3( X X 2 ) bestehend aus zwölf Gleichungen. Dieses System ist autonom. Anfangsbedingungen X i (0), V i (0) müssen vorgegeben werden. Abb. 5 zeigt die Trajektorien eines Zwei-Körper-Problems mit unterschiedlichen Massen m > m 2. Die Bewegung erfolgt hier typischerweise ungefähr entlang von Ellipsen. Wir leiten nun das N-Körper-Problem für Massen m,..., m N her. Sei F ij die Gravitationskraft auf die i-te Masse verursacht von der j-ten Masse. Das Newtonsche Bewegungsgesetz impliziert m i X i = N j=,j i N F ij = j=,j i G m im j X j X i 3( X j X i ) 9
13 z z y x y x Abbildung 5: Trajektorien (Positionen) eines Zwei-Körper-Problems mit Massen m > m 2 aus zwei unterschiedlichen Blickwinkeln (Linie: erster Körper, Punkte: zweiter Körper). für i =,..., N. Es folgt ein System erster Ordnung aus 6N gew. Dgln. X i = V i V i = G N j=,j i m j X j X i 3( X j X i ) für i =,..., N. Das Zwei-Körper-Problem kann noch analytisch gelöst werden, während dies nicht mehr für das N-Körper-Problem mit N > 2 gilt. Daher benötigen wir numerische Verfahren für diese Aufgabenstellung. Weitere Modelle In den vorangehenden Abschnitten wurden Probleme aus dem Bereich der Chemie, der Elektrotechnik und der Mechanik besprochen. Systeme aus gew. Dgln. treten ebenfalls in den folgenden Anwendungen auf: Biologie (z.b. Räuber-Beute-Modelle, Epidemie-Modelle), Simulation von Kriegsgefechten (Lanchester Modelle), Diskretisierung von partiellen Differentialgleichungen, und andere. Weitere Literatur zu Modellen mit gew. Dgln. ist beispielsweise [, 2]. 0
14 Kapitel 2 Einschrittverfahren 2 Wir besprechen jetzt numerische Methoden für die Anfangswertprobleme, die im vorhergehenden Kapitel eingeführt wurden. Dabei wird mit Einschrittverfahren begonnen, während Mehrschrittverfahren im nächsten Kapitel behandelt werden. 2. Vorbereitungen Wir möchten ein AWP (.) eines Systems gew. Dgln. in einem Intervall [x 0, x end ] (x 0 < x end ) numerisch lösen. Alle Verfahren für AWPe, die in dieser Veranstaltung betrachtet werden, verwenden eine endliche Anzahl von Gitterpunkten x 0 < x < x 2 < x 3 < < x N < x N = x end. Eine mögliche Wahl sind äquidistante Gitterpunkte x i := x 0 + ih mit h := x end x 0 N für i = 0,,..., N. Numerische Lösungen y i y(x i ) werden sukzessive berechnet. In einem Einschrittverfahren ist die Abhängigkeit der Werte einfach y 0 y y 2 y N y N.
15 Im Gegensatz dazu liegt bei einem Mehrschrittverfahren mit k Schritten eine Abhängigkeit vor der Gestalt y i k, y i k+,..., y i 2, y i y i für i = k, k +,..., N. Dabei müssen die ersten Werte y,..., y k durch eine andere Methode bestimmt werden im Fall k >. Ein Einschrittverfahren liegt auch in einer Mehrschrittmethode im Spezialfall k = vor. Ein allgemeines Einschrittverfahren kann in der Form y i+ = y i + h i Φ(x i, y i, h i ), (2.) geschrieben werden mit einer Inkrementfunktion Φ, die von sowohl dem Verfahren als auch der rechten Seite f abhängt. 2.2 Elementare Integrationsverfahren Die meisten Methoden für AWP (.) basieren auf einer Approximation der äquivalenten Integralgleichung y(x) = y(x 0 ) + Im Intervall [x 0, x 0 + h] erhalten wir y(x 0 + h) = y 0 + = y 0 + h x0 +h x 0 0 x x 0 f(s, y(s)) ds. (2.2) f(s, y(s)) ds f(x 0 + sh, y(x 0 + sh)) ds. (2.3) Nun wird das Integral auf der rechten Seite durch eine Quadraturformel ersetzt. Die Schwierigkeit besteht darin, dass die Funktion y, welche im Integranden auftritt, a priori unbekannt ist. Da die Schrittweite h klein ist, verwenden wir einfache Quadraturformeln und keine zusammengesetzten Quadraturformeln. Wir diskutieren die folgenden Beispiele, siehe Abb. 6: 2
16 (a) (b) (c) (d) Abbildung 6: Elementare Quadraturregeln: (a) Rechteck (linksseitig), (b) Rechteck (rechtsseitig), (c) Trapezregel, (d) Mittelpunktregel. (a) Rechteckregel (linksseitig): Als Näherung ergibt sich y = y 0 + hf(x 0, y 0 ). Diese Methode wird (explizites) Euler-Verfahren genannt. Es ist die einfachste Methode, die durchführbar ist. Ist der Anfangswert y(x 0 ) = y 0 gegeben, dann kann die Näherung y direkt über eine Funktionsauswertung von f berechnet werden. (b) Rechteckregel (rechtsseitig): Nun folgt als Methode y = y 0 + hf(x 0 + h, y ). (2.4) Diese Technik wird implizites Euler-Verfahren genannt. Der unbekannte Wert y tritt auf beiden Seiten der Gleichung auf. Im allgemeinen kann hier keine explizite Formel für y bestimmt werden. Die Vorschrift (2.4) stellt ein nichtlineares Gleichungssystem (aus algebraischen Gleichungen) für die Unbekannte y dar, d.h. der Wert y ist implizit definiert. Beispielsweise kann mit einer Newton-Iteration eine Näherungslösung erhalten werden. Der Rechenaufwand für einen Integrationsschritt ist somit aber deutlich höher als im expliziten Euler-Verfahren. 3
17 (c) Trapezregel: Wird das Integral mit der Trapezregel approximiert, dann folgt die Vorschrift y = y 0 + h 2 (f(x 0, y 0 ) + f(x 0 + h, y )). Dieser Ansatz führt daher wieder auf eine implizite Methode. Der Rechenaufwand für einen Integrationsschritt ist ungefähr so hoch wir im impliziten Euler-Verfahren. Jedoch kann man eine deutlich besser Näherung erwarten, da die Trapeze besser approximieren als die Rechtecke in der Quadratur. (d) Mittelpunktregel: Die Mittelpunktregel verwendet ein bestimmtes Rechteck. Es folgt y = y 0 + hf(x h, y(x 0 + 2h)). (2.5) Diese Vorschrift ist noch nicht durchführbar, denn Unbekannte sind sowohl y als auch y(x 0 + 2h). Daher benötigen wir eine weitere Gleichung, um den Zwischenwert y(x 0 + 2h) zu bestimmen. Beispielsweise kann das explizite Euler-Verfahren diesen Wert liefern, wodurch folgt { y/2 = y 0 + h 2 f(x 0, y 0 ) oder äquivalent y = y 0 + hf(x h, y /2) y = y 0 + hf(x 0 + h 2, y 0 + h 2 f(x 0, y 0 )). (2.6) Diese Methode ist explizit, denn man kann sukzessive y /2 und y berechnen ohne nichtlineare Gleichungssysteme zu lösen. Es werden nur zwei Funktionsauswertungen von f benötigt. Die Vorschrift (2.6) wird modifiziertes Euler-Verfahren oder Collatz-Verfahren genannt. Alternativ entsteht eine implizite Methode, wenn der Zwischenwert linear durch y 0 und y interpoliert wird, d.h. y = y 0 + hf(x 0 + h 2, 2 (y 0 + y )) ergibt sich als Verfahrensvorschrift. Man nennt dies auch die implizite Mittelpunktregel. 4
18 Die Genauigkeit dieser Methoden wird später untersucht. Explizites Euler-Verfahren Wir betrachten das explizite Euler-Verfahren jetzt genauer. Diese Formel kann auch durch zwei andere Ansätze erhalten werden. Zum einen ersetzen wir die Ableitung in der Dgl. y = f(x, y) durch den Differenzenquotienten (erster Ordnung), wodurch folgt y(x 0 + h) y(x 0 ) h. = f(x 0, y(x 0 )) y = y 0 + hf(x 0, y 0 ). Zum anderen verwenden wir die Tangente zu y(x) im Anfangspunkt (x 0, y 0 ) zur Approximation der Lösung. Die Tangentengleichung lautet Es folgt t(x) = y(x 0 ) + (x x 0 )y (x 0 ) = y(x 0 ) + (x x 0 )f(x 0, y(x 0 )). y := t(x 0 + h) = y 0 + hf(x 0, y 0 ), d.h. wir erhalten das explizite Euler-Verfahren. Die sukzessive Anwendung dieser Methode liefert daher Tangentenstücke, wodurch diese Technik auch Polygonzugverfahren genannt wird. Als Beispiel lösen wir das AWP y = 2y, y( 4 ) = 2, x [ 4, 2]. Die exakte Lösung ist y(x) = x. Abb. 7 zeigt die Näherungslösungen aus dem expliziten Euler-Verfahren. Wir erkennen, dass die Näherungen mit steigender Schrittzahl N bzw. kleinerer Schrittweite h genauer werden. 5
19 .6 N = y(x) x.6 N = y(x) x.6 N = y(x) x Abbildung 7: Lösung von y =, y( ) = (Linie) und Näherungslösung (Punkte) aus 2y 4 2 dem expliziten Euler-Verfahren mit N Schritten. 6
20 2.3 Konsistenz und Konvergenz Wir betrachten ein allgemeines Einschrittverfahren der Gestalt (2.) mit der Inkrementfunktion Φ. Es existieren unterschiedliche Notationen, um die Genauigkeit der Näherung y i+ mit der exakten Lösung y(x i+ ) zu vergleichen. Zu einem lokalen Bereich formulieren wir die folgende Definition. Definition 2. (lokaler Diskretisierungsfehler) Sei y(x) die exakte Lösung des AWPs y = f(x, y), y(x 0 ) = y 0 und y = y 0 + hφ(x 0, y 0, h) die Näherung aus einem Einschrittverfahren mit Schrittweite h > 0. Dann lautet der lokale Diskretisierungsfehler τ(h) := y(x 0 + h) y. (2.7) h Der lokale Diskretisierungsfehler hängt auch von der Wahl des Anfangswerts (x 0, y 0 ) ab, welches in der Notation jedoch nicht extra aufgezeigt wird. Die Definition (2.7) des lokalen Diskretisierungsfehlers kann auf drei Arten interpretiert werden: die Differenz zwischen der exakten Lösung und der Näherungslösung (Diskretisierungsfehler nach einem Schritt ausgehend von der exakten Lösung) skaliert mit der Schrittweite h. die Differenz zwischen den Steigungen der entsprechenden Sekanten τ(h) = y(x 0 + h) y 0 h } {{ } exakte Lösung y y 0. }{{ h } Näherungslösung Die Sekanten sind in Abb. 8 dargestellt. Für τ(h) 0 werden beide Sekanten zur Tangente t(x) = y(x 0 ) + (x x 0 )y (x 0 ) im Grenzfall. der Defekt τ(h) = y(x 0 + h) y 0 h 7 Φ(x 0, y 0, h), (2.8)
21 y y Sekante an exakter Lösung Sekante an Näherung y(x) y 0 x 0 x 0+h x Abbildung 8: Sekanten an die exakte Lösung und an die Näherungslösung. welcher sich durch Einsetzen der exakten Lösung in die Formel der Näherung ergibt. Mit Definition der stetigen Funktion (x 0, y 0, h) := { y(x0 +h) y 0 h für h > 0 f(x 0, y 0 ) für h = 0 (2.9) kann man genauer schreiben τ(x 0, y 0, h) = (x 0, y 0, h) Φ(x 0, y 0, h) für h 0. Beispiel : Lokaler Diskretisierungsfehler im expliziten Euler-Verfahren Taylor-Entwicklung liefert unter der Annahme y C 2 y(x 0 + h) = y(x 0 ) + hy (x 0 ) + 2 h2 y (x 0 + ϑ(h)h) = y 0 + hf(x 0, y 0 ) + 2 h2 y (x 0 + ϑ(h)h) mit 0 < ϑ(h) <. Der lokale Diskretisierungsfehler ergibt sich zu τ(h) = h (y(x 0 + h) y ) = h (y(x 0 + h) y 0 hf(x 0, y 0 )) = 2 hy (x 0 + ϑ(h)h). Es folgt τ(h) = O(h). 8
22 Beispiel 2: Lokaler Diskretisierungsfehler im impliziten Euler-Verfahren Zur Vereinfachung setzen wir eine beschränkte rechte Seite voraus, d.h. f M. Zum einen liefert das implizite Euler-Verfahren y = y 0 + hf(x 0 + h, y ) = y 0 + hf(x 0 + h, y 0 + hf(x 0 + h, y )). Mehrdimensionale Taylor-Entwicklung der Funktion f C 2 zeigt uns [ ] y = y 0 + h f(x 0, y 0 ) + f x (x 0, y 0 )h + f y (x 0, y 0 )hf(x 0 + h, y ) + O(h 2 ) = y 0 + hf(x 0, y 0 ) + O(h 2 ). Zum anderen liefert eine Taylor-Entwicklung der exakten Lösung τ(h) = h (y(x 0 + h) y ) = h (y 0 + hf(x 0, y 0 ) + O(h 2 ) (y 0 + hf(x 0, y 0 ) + O(h 2 ))) = O(h). Wieder folgt τ(h) = O(h). Aufbauend auf den Eigenschaften des lokalen Diskretisierungsfehlers definieren wir die Konsistenz. Definition 2.2 (Konsistenz) Ein Einschrittverfahren (oder dessen Inkrementfunktion Φ) heißt konsistent, wenn der lokale Diskretisierungsfehler bei allen Anfangswerten (x 0, y 0 ) G (G: Definitionsbereich von f) gegen null konvergiert für kleine Schrittweiten: τ(h) σ(h) mit lim h 0 σ(h) = 0. Das Verfahren heißt konsistent von (mindestens) Ordnung p, wenn τ(h) = O(h p ). Die Konsistenz eines Einschrittverfahrens kann leicht mit der folgenden Eigenschaft charakterisiert werden. Lemma 2. Sei die rechte Seite f der Dgl. y = f(x, y) stetig in x und erfülle die Lipschitz-Bedingung (.2) bezüglich y. Dann gilt die Äquivalenz Φ ist konsistent lim h 0 Φ(x, y, h) = f(x, y). 9
23 Beweis: Sei z die Lösung des AWPs z (x) = f(x, z(x)), z(x 0 ) = y 0 mit (x 0, y 0 ) G. Wegen der Definition von τ und dem Mittelwertsatz der Differentialrechnung gilt komponentenweise τ j (x 0, y 0, h) = z j(x 0 + h) y 0 h Φ j (x 0, y 0, h) = z j(x 0 + θ j h) Φ j (x 0, y 0, h) mit Zwischenwerten θ j (0, ) für j =,..., n. Mit der Stetigkeit von z folgt lim h 0 z j(x 0 + θ j h) = z j(x 0 ) = f j (x 0, y 0 ) für j =,..., n. Somit gilt lim τ(x 0, y 0, h) = f(x 0, y 0 ) lim Φ(x 0, y 0, h) h 0 h 0 falls die Grenzwerte existieren. Diese Gleichung liefert die Behauptung. Die Konsistenzordnung beschreibt die Qualität der Näherung nach einem einzelnen Schritt. Jedoch sind wir an der Qualität der Approximation nach N Schritten interessiert, wo der Endpunkt x end erreicht wird. Dies motiviert die nächste Definition. Definition 2.3 (globaler Diskretisierungsfehler und Konvergenz) Der globale Diskretisierungsfehler einer Methode auf einem Gitter x 0 < x < < x N ist definiert durch die Differenz e N := y(x N ) y N. (2.0) Für N nehmen wir h max 0 mit h max := max x i+ x i an. Das i=0,...,n Verfahren heißt konvergent, wenn für festes x end = x N gilt lim e N = 0. N Das Verfahren ist konvergent von (mindestens) Ordnung p, falls e N = O(h p max). 20
24 Bezüglich des Zusammenhangs zwischen Konsistenz und Konvergenz beweisen wir einen Satz. O.E.d.A. verwenden wir dabei die Maximumnorm als Vektornorm. Desweiteren benötigen wir noch eine Hilfsaussage. Lemma 2.2 Erfüllt eine Folge (r i ) i N R n die Abschätzung r i+ ( + δ) r i + β für i = 0,, 2,... mit Konstanten β 0 und δ > 0, dann gilt für k N 0 wobei die Vektornorm beliebig ist. r k e kδ r 0 + ekδ δ β, Beweis: Verwendet wird Induktion über k. Der Induktionsanfang mit k = lautet r ( + δ) r 0 + β e δ r 0 + eδ δ wegen + δ e δ und somit auch (e δ )/δ. Zum Induktionsschluss sei die Aussage für ein k erfüllt. Es folgt wieder mit + δ e δ β r k+ ( + δ) r k + β ( + δ)e kδ r 0 + ( + δ) ekδ δ e δ e kδ r 0 + (+δ)ekδ (+δ)+δ δ e (k+)δ r 0 + e(k+)δ δ und damit ist die Aussage für k + gezeigt. β β β + β Nun ergibt sich das Hauptresultat dieses Unterabschnitts. Satz 2. (Konvergenz von Einschrittverfahren) Gegeben sei ein AWP y = f(x, y), y(x 0 ) = y 0 mit der exakten Lösung y(x) für x [x 0, x end ]. Die Inkrementfunktion Φ sei stetig auf G := { (x, y, h) : x [x 0, x end ], y y(x) γ, 0 < h h } 2
25 mit Konstanten γ, h > 0 und es gelte die Lipschitz-Bedingung Φ(x, y, h) Φ(x, y 2, h) K y y 2 (2.) für alle (x, y i, h) G, i =, 2 mit einer Konstanten K > 0. Das Einschrittverfahren sei konsistent von Ordnung p im Sinne von τ(x, y(x), h) = (x, y(x), h) Φ(x, y(x), h) C h p (2.2) für alle x [x 0, x end ] und 0 < h h mit einer Konstanten C > 0. Verwendet wird konstante Schrittweite h N := x end x 0 N, d.h. Gitterpunkte sind x i := x 0 + ih N für i = 0,,..., N. Dann gibt es ein ĥ (0, h], so dass die globalen Diskretisierungsfehler beschränkt sind durch e i h p N C exp(k(x end x 0 )) K und für alle h N ĥ. für i =,..., N (2.3) Beweis: Zu y, z R n definieren wir für γ > 0 die Hilfsgröße ỹ(y, z) R n komponentenweise für j =,..., n (ỹ = (ỹ,..., ỹ n ) ) durch z j + γ falls y j z j + γ, ỹ j := z j γ falls y j z j γ, y j sonst. Damit konstruieren wir die Hilfsfunktion Offensichtlich ist Φ stetig auf Φ(x, y, h) := Φ(x, ỹ(y, y(x)), h). G := { (x, y, h) : x [x 0, x end ], y R n, h h } und erfüllt wegen (2.) die Bedingung Φ(x, y, h) Φ(x, y 2, h) K y y 2 (2.4) 22
26 für alle (x, y i, h) G, i =, 2. Wegen Φ(x, y(x), h) = Φ(x, y(x), h) für alle x [x 0, x end ] sowie 0 < h h und (2.2) gilt auch (x, y(x), h) Φ(x, y(x), h) C h p (2.5) für x [x 0, x end ] und 0 < h h. Das zu Φ gehörige Einschrittverfahren liefert die Näherungslösungen ũ i über die Formel ũ i+ = ũ i + h N Φ(xi, ũ i, h N ) mit Anfangswert ũ 0 = y 0. Mit der Funktion (2.9) folgt direkt y i+ = y i + h N (x i, y i, h N ) für die exakten Lösungswerte y i = y(x i ). Durch Subtraktion erhalten wir für die Fehler ẽ i := ũ i y i die Rekursionsformel ] ẽ i+ = ẽ i + h N [ Φ(xi, ũ i, h N ) (x i, y i, h N ) = ẽ i + h N [ Φ(xi, ũ i, h N ) Φ(x ] i, y i, h N ) ] + h N [ Φ(xi, y i, h N ) (x i, y i, h N ). Es ergibt sich aus (2.4) und (2.5) Φ(x i, ũ i, h N ) Φ(x i, y i, h N ) K ũ i y i = K ẽ i, (x i, y i, h N ) Φ(x i, y i, h N ) C h p N. Wir erhalten die Abschätzung ẽ i+ ( + h N K) ẽ i + C h p+ N für i = 0,,..., N. Lemma 2.2 liefert nun mit ẽ 0 = ũ 0 y 0 = 0 die Abschätzung ẽ i C h p N exp(kih N) K für alle i = 0,,..., N. 23
27 Damit folgt auch ẽ i C h p N exp(k(x end x 0 )) für alle i = 0,,..., N K wegen ih N x end x 0. Wir erkennen, dass ein ĥ h existiert, so dass ẽ i γ für alle i = 0,,..., N gilt, falls h N ĥ. Damit erhalten wir Φ i (x i, ũ i, h N ) = Φ(x i, ũ i, h N ) für h N ĥ aus der Definition der Hilfsfunktion Φ. In diesem Fall sind die Näherungen ũ i aus dem von Φ erzeugten Einschrittverfahren identisch mit den Näherungen u i aus dem von Φ festgelegten Einschrittverfahren. Somit gilt ẽ i = e i für i = 0,,..., N mit e i := u i y i. Dadurch folgt die Abschätzung (2.3). Bemerkungen: Die Lipschitz-Bedingung (2.) ist bei den üblichen Verfahren erfüllt, falls die rechte Seite f der Dgl. lokal Lipschitz-stetig in y auf G ist. Die Konsistenzbedingung (2.2) stellt eine leichte Verschärfung der Bedingung aus Def. 2.2 dar und ist bei allen gängigen Verfahren gegeben. Die Konvergenzaussage (2.3) in Satz 2. betrifft nicht nur den Endwert bei x = x end sondern alle Gitterpunkte x,..., x N. Die Konvergenzaussage gilt auch bei nichtkonstanten Schrittweiten, d.h. einem Gitter x 0 < x < x 2 < < x N < x N = x end und h i := x i+ x i. Im Grenzfall muss dann h max 0 gelten mit der maximalen Schrittweite h max := max{h 0, h,..., h N }. In die Konvergenzanalyse können auch Fehler e 0 = u 0 y 0 0 in den Anfangswerten sowie Rundungsfehler einbezogen werden. Satz 2. zeigt, dass die Konsistenz hinreichend für die Konvergenz ist. Zudem stimmt die Konsistenzordnung mit der Konvergenzordnung überein. Die Konsistenz kann durch eine Untersuchung der Inkrementfunktion Φ des Einschrittverfahrens nachgewiesen werden. Umgekehrt gibt es konvergente Methoden, die nicht konsistent sind. Konsistenz ist somit nicht notwendig für Konvergenz. Jedoch werden inkonsistente Verfahren nicht in der Praxis eingesetzt. 24
28 2.4 Runge-Kutta-Verfahren Der wichtigste Typ von Einschrittverfahren sind die Runge-Kutta-Verfahren. Die Idee besteht darin, das Integral in (2.3) durch eine Quadraturformel mit den Knoten c,..., c s [0, ] und (äußeren) Gewichten b,..., b s R zu ersetzen. O.E.d.A. sei c c 2 c s. Es folgt eine endliche Summe s y = y 0 + h b i f(x 0 + c i h, y(x 0 + c i h)). i= Das Problem dabei ist, dass die Zwischenwerte y(x 0 + c i h) a priori unbekannt sind. Wir erhalten Näherungen für die Zwischenwerte wieder aus der Integralgleichung (2.2), d.h. y(x 0 + c i h) = y 0 + h ci 0 f(x 0 + sh, y(x 0 + sh)) ds. Die beteiligten Integrale werden durch Quadraturformeln ersetzt. Um die Einführung neuer Unbekannten zu vermeiden, dürfen nur die gleichen Knoten c,..., c s wie zuvor verwendet werden. Jedoch entstehen neue (innere) Gewichte. Es folgen die Näherungen s z i = y 0 + h a ij f(x 0 + c j h, z j ) (2.6) für i =,..., s. Die letztlich gesuchte Näherung wird zu s y = y 0 + h b i f(x 0 + c i h, z i ). j= i= Die Gleichungen (2.6) stellen ein nichtlineares Gleichungssystem (aus algebraischen Gleichungen) für die Unbekannten z,..., z s dar. Wenn die Zwischenwerte bestimmt wurden, dann können wir die Näherung y direkt aus s Auswertungen der Funktion f erhalten. Man nennt s auch die Stufenzahl des Verfahrens. Betreffend (2.6) ist eine natürliche Forderung, dass eine konstante Funktion f (y(x 0 + c i h) = y 0 + c i h) exakt reproduziert. Wir erhalten die 25
29 Bedingungen c i = s a ij für jedes i =,..., s. (2.7) j= Diese Gleichung bedeutet, dass die Summe der Gewichte gleich der (relativen) Länge des Teilintervalls sein muss. Eine Runge-Kutta-Methode ist eindeutig durch seine Koeffizienten festgelegt. Die Koeffizienten können in einem sogenannten Butcher-Tableau angeordnet werden: c a a 2 a s c 2 a 2 a 22 a 2s c s a s a s2 a ss b b 2 b s oder kurz c A b mit c R s, b R s, A R s s. Beispiele: Verfahren aus Abschnitt 2.2 (a): expl. Euler-Verfahren, (b): impl. Euler-Verfahren, (c): Trapezregel, (d): Collatz-Verfahren: (a) 0 0 (b) (c) (d)
30 Beispiel: Gauß-Runge-Kutta-Verfahren Wir verwenden die Gauß-Legendre-Quadratur für die Knoten c i und die Gewichte b i. Diese Quadraturformel besitzt die Ordnung 2s, d.h. es gilt s b i p(c i ) = i= 0 p(x) dx für alle p P 2s (P m : Polynome bis Grad m). Die Gewichte a ij bestimmen wir für jedes i =,..., s derart, dass s a ij p(c j ) = j= ci 0 p(x) dx für alle p P s. Im einfachen Fall s = folgt direkt c = 2, b = und a = 2. Es entsteht das Runge-Kutta-Verfahren z = y 0 + h 2 f(x 0 + h 2, z ), y = y 0 + hf(x 0 + h 2, z ). (2.8) Dieser Ansatz entspricht der Mittelpunktregel (2.5), wobei die Näherung. z = y(x0 + 2h) durch das implizite Euler-Verfahren bestimmt wird. Das Butcher-Tableau schreibt sich im Fall s = 2: Wenn die Matrix A = (a ij ) vollbesetzt ist, dann ist das Runge-Kutta- Verfahren implizit. Ein nichtlineares Gleichungssystem (2.6) aus s n algebraischen Gleichungen muss dann gelöst werden. Im Gegensatz dazu möchten wir nun explizite Methoden erhalten. Die entsprechende Bedingung lautet a ij = 0 für i j. Dadurch wir A zu einer strikten unteren Dreiecksmatrix. Das Butcher-Tableau besitz dann die Gestalt: 27
31 c 2 a c s a s a s,s 0 b b 2 b s b s Insbesondere folgt c = 0 aus der Bedingung (2.7) und damit z = y 0. Nun ergeben sich die Zwischenwerte sukzessive aus i z i = y 0 + h a ij f(x 0 + c j h, z j ) für i =,..., s. j= Der Rechenaufwand einer expliziten Runge-Kutta-Methode besteht somit nur in s Auswertungen der rechten Seite f. Man kann ein explizites Verfahren daher als eine sukzessive Extrapolation mit den gegebenen Zwischenwerten interpretieren. Implizite Verfahren entsprechen dann einer Interpolation mit den Zwischenwerten. Beispiele: Einige bekannte explizite Runge-Kutta-Verfahren Heun-Verfahren (links), Kutta-Simpson-Verfahren (mitte) und klassisches Runge-Kutta-Verfahren (rechts): Eine äquivalente Notation für Runge-Kutta-Schemata entsteht durch die Definition von Inkrementen k i mittels ( ) s k i = f(x 0 + c i h, z i ) = f x 0 + c i h, y 0 + h a ij k j (2.9) 28 j=
32 für i =,..., s. Ein Runge-Kutta-Verfahren besitzt dann die Gestalt ( ) s = f x 0 + c i h, y 0 + h a ij k j, i =,..., s, k i y = y 0 + h s b i k i. i= j= Die Inkremente k i sind nun a priori unbekannt. Ordnungsbedingungen (2.20) Ein Runge-Kutta-Methode ist durch ihre Koeffizienten c i, b i, a ij eindeutig bestimmt. Wir leiten Bedingungen an diese Koeffizienten her, welche die Konsistenz des Einschrittverfahrens mit Ordnung p liefern. Wir betrachten eine autonome skalare Dgl. y = f(y). Es folgt y = f y = f f, y = f y f + f f y = f f 2 + (f ) 2 f. Taylor-Entwicklung der exakten Lösung führt auf y(x 0 + h) = y(x 0 ) + hy (x 0 ) + h2 2 y (x 0 ) + h3 6 y (x 0 ) + O(h 4 ) = y 0 + hf(y 0 ) + h2 2 f (y 0 )f(y 0 ) [ f (y 0 )f(y 0 ) 2 + f (y 0 ) 2 f(y 0 ) ] + O(h 4 ). + h3 6 Im folgenden benutzen wir die Abkürzungen f = f(y 0 ), f = f (y 0 ), etc. Die Inkremente k i aus (2.20) hängen von der Wahl der Schrittweite h ab. Wir nehmen an, dass diese Inkremente beschränkt sind in einer Umgebung von h = 0. Dies ist beispielsweise gesichert, wenn eine beschränkte rechte Seite f auftritt. Die Runge-Kutta-Methode erfülle die fundamentale Bedingung (2.7). Eine Taylor-Entwicklung der Funktion f bezüglich der Inkremente (2.9) liefert 29
33 für i =,..., s ( s ) ( s ) 2 = f + f h a ij k j + 2 f h 2 ij k j + O(h j=a 3 ) k i ( j= s ( s ) )) = f + f h a ij (f + f h a jl k l + O(h 2 ) j= l= ( s f h 2 ij (f + O(h))) + O(h j=a 3 ) ( s ( s ) )) = f + f h a ij (f + f h a jl (f + O(h)) + O(h 2 ) j= l= + 2 f h 2 (fc i + O(h)) 2 + O(h 3 ) ( s ( = f + f h a ij f + f fhc j + O(h 2 ) )) + 2 f f 2 h 2 c 2 i + O(h3 ) j= ( s ) = f + hf fc i + h 2 (f ) 2 f a ij c j + 2 h2 f f 2 c 2 i + O(h3 ). Die Näherung aus dem Runge-Kutta-Verfahren resultiert zu y s = y 0 + h b i k i i= j= ( s ) ( s ) ( s ) = y 0 + hf b i + h 2 f f b i c i + h 3 (f ) 2 f b i a ij c j i= ) ( s + 2 h3 f f 2 b i c 2 i + O(h 4 ). i= i= i,j= Ein Vergleich mit der Taylor-Entwicklung der exakten Lösung zeigt die Bedingungen für Konsistenz bis Ordnung p = 3. Die Konsistenzbedingungen bis Ordnung p = 4 sind ebenfalls dargestellt: 30
34 p = : p = 2 : p = 3 : s b i = i= s b i c i = 2 i= s b i c 2 i = 3 i= s b i a ij c j = 6 i,j= p = 4 : s b i c 3 i = 4 i= s b i a ij c i c j = 8 i,j= s b i a ij c 2 j = i,j= 2 s b i a ij a jl c l = i,j,l= 24 Die Konsistenzbedingungen können mit dem Ansatz über Taylor-Entwicklungen bis zu einer beliebigen Ordnung p hergeleitet werden. Im Fall von expliziten Runge-Kutta-Verfahren brauchen in den Summen nur die Koeffizienten ungleich null aufgeführt zu werden. Zu einer gewünschten Konsistenzordnung p möchten wir ein Runge-Kutta-Verfahren mit möglichst kleiner Stufenzahl s erhalten. Bei impliziten Methoden kann mit s Stufen die maximale Ordnung p = 2s erreicht werden, welche dann bei den Gauß- Runge-Kutta-Schemata auftritt. Bei den explizten Methoden gibt Tabelle eine Information. Stufenzahl s maximale Ordnung p Ordnung p minimale Stufenzahl s Anzahl Ordnungsbedingungen Tabelle : Ordnung und Stufenzahl bei expliziten Runge-Kutta-Verfahren. 2.5 Schrittweitensteuerung. In einer numerischen Integration werden die Näherungen y k = y(xk ) sukzessive durch eine numerische Methode berechnet. Wir möchten, dass die 3
35 Schrittweiten h k := x k+ x k automatisch bestimmt werden, so dass der entstehende Fehler in der Methode hinreichend klein bleibt. Seien y = (y,..., y n ) die Komponenten der Lösung. Wir nehmen an, dass das numerische Verfahren die Konsistenzordnung p besitzt, d.h. die Näherung y h. = y(x0 + h) erfüllt die Bedingung y h i y i (x 0 + h) = O(h p+ ) = C i h p+ + O(h p+2 ) (2.2) mit Konstanten C i 0 für jede Komponente. Ein ähnliches numerisches Verfahren wird zur Berechnung der Näherung ŷ h mit einer Ordnung höher eingesetzt, d.h. ŷ h i y i (x 0 + h) = O(h p+2 ). (2.22) Bei Runge-Kutta-Methoden werden typischerweise eingebettete Verfahren eingesetzt. Bei Mehrschrittverfahren existieren verschiedene Möglichkeiten. Desweiteren kann Richardson-Extrapolation sowohl bei Einschritt- als auch Mehrschrittverfahren eingesetzt werden. Wir möchten den Fehler y h y(x 0 +h) im Verfahren der niedrigeren Ordnung schätzen. Die Bedingungen (2.2) und (2.22) liefern y h i y i (x 0 + h) = y h i ŷ h i (y i (x 0 + h) ŷ h i ) = y h i ŷ h i + O(h p+2 ). (2.23) Daher stellt ŷ h y h einen Schätzer für den lokalen Fehler, welcher Größenordnung p + hat, dar. Aus (2.2) und (2.23) folgt y h i ŷ h i = C i h p+ + O(h p+2 ). (2.24) Wir nehmen an, dass wir bereits einen Integrationsschritt mit der Schrittweite h used durchgeführt haben. Nun möchten wir eine geeignete Schrittweite h opt schätzen, um den Integrationsschritt zu wiederholen. Die Eigenschaften (2.2) und (2.24) implizieren ungefähr y h used i ŷ h used i y h opt i y i (x 0 + h opt ) Elimination der Konstanten C i liefert y h opt i y i (x 0 + h opt ) y h used i ŷ h used i 32 =. = C i h p+ used,. = C i h p+ opt. ( hopt h used ) p+. (2.25)
36 Der Fehlerschätzer zum durchgeführten Schritt lautet η i := y h used i für i =,..., n. Der Fehler zum neuen Schritt soll ŷ h used i (2.26) y h opt i y i (x 0 + h opt ) = TOL (2.27) erfüllen mit einer absoluten Toleranz TOL > 0 in allen Komponenten. Wir möchten nicht, dass der Fehler kleiner als TOL ist, denn ein kleinerer Fehler bedeutet eine kleinere Schrittweite und dadurch einen höheren Rechenaufwand aufgrund eine größeren Schrittanzahl. Einsetzen von (2.26),(2.27) in Gleichung (2.25) führt auf TOL h opt,i = h used p+, η i wobei jede Kompomente eine eigene Schrittweite erzeugt. Die Länge des nächsten Schritts wird daher gewählt als h new = δ min i=,...,n h opt,i mit einem Sicherheitsfaktor δ, z.b. δ = 0.9. Um oszillierende Schrittweiten zu verhindern, wird desweiteren gefordert mit 0 < σ < < θ, z.b. σ = 5, θ = 5. σ h used h new θ h used Falls h new < h used gilt, dann wurde unsere Genauigkeitsforderung (2.27) verfehlt, da der Fehler größer ist. Somit wiederholen wir den Schritt mit h new anstelle von h used. Daraufhin wird jedoch wieder der Fehler geschätzt. Falls h new h used erfüllt ist, dann akzeptieren wir den Schritt, da der Fehler kleiner oder gleich der Genauigkeitsforderung (2.27) ist. Der nächste Schritt wird dann mit h new als vorgeschlagene Schrittweite durchgeführt. Oft wird die Toleranz relativ bezüglich der Größenordnung der Lösung vorgegeben. Sei RTOL > 0 eine relative Toleranz und ATOL > 0 eine absolute Toleranz, dann definieren wir TOL = ATOL + RTOL y h used i. 33
37 Der absolute Teil ATOL wird benötigt für den Fall y h used i 0. Typische Werte sind z.b. RTOL = 0 3 und ATOL = 0 6. Die obige Verwendung des Betrags entspricht der Maximumnorm als Vektornorm. Jedoch besitzt die Maximumnorm ein Defizit an Glattheit und verursacht dadurch manchmal Probleme in der Integration. Daher wir in der Praxis häufig die skalierte Norm ERR = n ( n i= ŷ h used i y h used i ATOL + RTOL y h used i ) 2 (2.28) eingesetzt, die man als gewichtete Euklidische Norm interpretieren kann. Man beachte, dass der Nenner in (2.28) immer positiv ist. Die Bedingung (2.27) entspricht nun ERR =. Die neue Schrittweite wird definiert als mit einem Sicherheitsfaktor δ. h new = δ h used p+ ERR Die Schätzung des lokalen Fehlers erfolgt für das Verfahren mit Ordnung p, während das Ergebnis aus dem Verfahren der Ordnung p + nur zur Berechnung des Fehlerschätzers eingesetzt wird. Jedoch ist die Näherung aus der Methode mit Ordnung p + in den meisten Fällen genauer. Daher wird häufig die Näherung höherer Ordnung als Ausgabe des Integrationsschritts festgesetzt. Der obige Ansatz kontrolliert den lokalen Fehler in jedem Integrationsschritt. Jedoch hätten wir gerne eine Schrittweitenbestimmung derart, dass der globale Fehler (2.0) eine Genauigkeitsschranke erfüllt. Leider existieren keine erfolgreichen Strategien zur Kontrolle des globalen Fehlers. Daher verwenden numerische Integrationsverfahren aus üblichen Softwarepaketen (z.b. MATLAB) nur Schrittweitensteuerungen auf Basis der lokalen Fehler. Eingebettete Verfahren Es verbleibt zwei numerische Verfahren zur Schätzung des lokalen Fehlers festzulegen. Im Fall von Runge-Kutta-Methoden werden eingebettete Ver- 34
38 fahren angewendet, da der zusätzliche Rechenaufwand für die zweite Näherung relativ klein ausfällt. Das Butcher-Tableau eines eingebetteten Verfahrens lautet c a a 2 a s c 2 a 2 a 22 a 2s c s a s a s2 a ss b b 2 b s ˆb ˆb2 ˆbs mit zwei Mengen b i und ˆb i von Gewichten. Die entstehenden Näherungen sind y h = y 0 + h(b k + + b s k s ), ŷ h = y 0 + h(ˆb k + + ˆb s k s ). Wenn die Inkremente k,..., k s zur Berechnung der Näherung y h verfügbar sind, dann kann die zweite Näherung ŷ h ohne wesentlichen Mehraufwand bestimmt werden. Im Fall von expliziten Runge-Kutta-Verfahren stellen die Runge-Kutta- Fehlberg Methoden eine Klasse eingebetteter Verfahren dar. Beispiel: Runge-Kutta-Fehlberg 2(3)
39 Kapitel 3 Mehrschrittverfahren 3 In diesem Kapitel untersuchen wir Mehrschrittmethoden, d.h. mehrere alte Näherungen werden eingesetzt um eine neue Näherung zu konstruieren. Betrachtet wird wieder ein AWP y = f(x, y), y(x 0 ) = y 0, siehe (.). Sind die Approximationen (x i k+, y i k+ ), (x i k+2, y i k+2 ),..., (x i, y i ), (x i, y i ) (3.) für ein k gegeben, dann wird daraus eine neue Näherung (x i+, y i+ ) bestimmt. Im Gegensatz zu Einschrittverfahren reicht hier die Konsistenz alleine für die Konvergenz der Methoden nicht aus. 3. Methoden über numerischer Quadratur Wir führen eine wichtige Klasse von Mehrschrittverfahren ein, deren Konstruktionsprinzip auf der Integralgleichung (2.2) beruht. Eine Polynominterpolation wird aufgestellt und das exakte Integral wird mit dem Integral des Polynoms approximiert. Wir wählen eine ganze Zahl l und erhalten für die exakte Lösung des AWPs (.) die Integralgleichung y(x i+ ) = y(x i l+ ) + = y(x i l+ ) + xi+ x i l+ y (s) ds xi+ x i l+ f(s, y(s)) ds. (3.2) 36
40 Nun approximieren wir den Integranden f(x, y(x)). Wir stellen das Polynom p k,i P k auf, welches die Stützpunkte (x j, f(x j, y j )) für j = i k +, i k + 2,..., i, i interpoliert. Dementsprechend gilt p k,i (x j ) = f(x j, y j ) für j = i k +, i k + 2,..., i, i. Dieses Interpolationspolynom existiert und ist eindeutig. Mit der Lagrange- Basis k x x i ν+ L i,j (x) = für j =,..., k, x i j+ x i ν+ ν=,ν j und f i := f(x i, y i ) lautet das Polynom p k,i (x) = k f i j+ L i,j (x). j= Die Erwartung ist p k,i (x) f(x, y(x)) im betrachteten Gebiet. Daher ergibt sich als neue Näherung wegen (3.2) y i+ = y i l+ + k xi+ f i j+ j= x i l+ L i,j (s) ds. Da die Lagrange-Polynome gegeben sind, kann das Integral exakt ausgewertet werden. In den meisten Fällen gilt l k, d.h. das Intervall der Interpolation enthält das Intervall der Integration (zur linken Seite hin). Abb. 9 verdeutlicht diese Konstruktion. Wir erhalten ein explizites k-schritt-verfahren. Im Fall von äquidistanten Gitterpunkten x i = x 0 + ih sind die Lagrange- 37
41 f p(x) x x i k+ i l+ i i+ x x x Abbildung 9: Konstruktion von Mehrschrittverfahren mittels Quadratur. Polynome unabhängig vom Index i xi+ x i l+ L i,j (s) ds = = h Es folgt die Methode xi+ x i l+ ν j = h l l ν j ν j y i+ = y i l+ + h l ν=,ν j s x i ν+ x i j+ x i ν+ ds x 0 + (i + u)h (x 0 + (i ν + )h) x 0 + (i j + )h (x 0 + (i ν + )h) du u + ν ν j du. k β j f(x i j+, y i j+ ) mit den konstanten Koeffizienten k u + ν β j := du für j =,..., k. ν j j= Ein implizites Mehrschrittverfahren entsteht, wenn die unbekannte neue Näherung (x i+, y i+ ) in die Interpolation einbezogen wird. Sei q k,i P k das Interpolationspolynom zu den Stützpunkten (x j, f(x j, y j )) für j = i k +, i k + 2,..., i, i, i +. 38
42 Es folgt q k,i (x j ) = f(x j, y j ) fürr j = i k +, i k + 2,..., i, i, i +. Die zugehörigen Lagrange-Polynome lauten L i,j(x) = k ν=0,ν j x x i ν+ x i j+ x i ν+ für j = 0,,..., k und somit q k,i (x) = k f i j+ L i,j(x). j=0 Wir schreiben q k,i (x; y i+ ) um zu betonen, dass dieses Polynom noch von der neuen Näherung abhängt, welche a priori unbekannt ist. Es ergibt sich y i+ = y i l+ + xi+ x i l+ q k,i (s; y i+ ) ds. Diese Formel stellt ein nichtlineares Gleichungssystem für die Unbekannten y i+ dar. Daher liefert dieser Ansatz eine implizite Methode mit k Schritten. Im Fall von äquidistanten Schrittweiten lautet das Verfahren y i+ = y i l+ + h k βj f(x i j+, y i j+ ) (3.3) j=0 mit den konstanten Koeffizienten β j := k l ν=0,ν j u + ν ν j du für j = 0,,..., k. Äquivalent können wir schreiben y i+ hβ 0f(x i+, y i+ ) = y i l+ + h k βj f(x i j+, y i j+ ), j= 39
43 β β 2 β 3 β 4 k = 3 k = k = k = β0 β β2 β3 β4 k = k = k = k = Tabelle 2: Koeffizienten in Adams-Bashforth (links) und Adams-Moulton (rechts). wobei die rechte Seite die bekannten Daten und die linke Seite die unbekannte neue Näherung enthält. Adams-Methoden Eine beliebte Klasse von Mehrschrittverfahren sind die Adams-Methoden, die aus der Wahl l = in (3.2) entstehen. Daher wird die Integration nur im Teilintervall [x i, x i+ ] durchgeführt. Die expliziten Methoden heißen Adams-Bashforth-Verfahren. Das k-schritt- Verfahren lautet k y i+ = y i + h β j f(x i j+, y i j+ ) (3.4) j= im Fall von äquidistanten Schrittweiten. Die impliziten Methoden heißen Adams-Moulton-Verfahren. Das k-schritt-verfahren besitzt die Formel k y i+ = y i + h βj f(x i j+, y i j+ ). (3.5) j=0 Tabelle 2 zeigt die Koeffizienten dieser Methode für k =, 2, 3, 4. Die Einschritt-Adams-Bashforth-Methode ist gerade das explizite Euler-Verfahren, während die Einschritt-Adams-Moulton-Methode die Trapezregel ergibt. Nyström-Verfahren und Milne-Verfahren Wir erhalten eine weitere bedeutende Klasse von Mehrschrittverfahren aus der Wahl l = 2 in (3.2). Die zugehörigen expliziten Verfahren heißen dann 40
44 Nyström-Methoden. Beispielsweise führt die Wahl k = (jetzt ausnahmsweise k < l) auf die explizite Mittelpunktregel y i+ = y i + 2hf(x i, y i ), (3.6) welche ein Zweischrittverfahren darstellt. Die entsprechenden impliziten Verfahren heißen Milne-Methoden. Für äquidistante Schrittweiten liefert der Fall k = wieder die explizite Mittelpunktregel, da der Term mit f i+ herausfällt. Die Wahl k = 2 ergibt die Milne-Simpson-Regel y i+ = y i + h 3 (f(x i, y i ) + 4f(x i, y i ) + f(x i+, y i+ )), d.h. ein implizites Verfahren. Diese Methode entspricht der Simpson-Regel in der numerischen Quadratur. Die Fälle l 3 in (3.2) sind für die Praxis irrelevant. Zudem ist die Anzahl der Schritte (d.h. max{k, l}) üblicherweise kleiner 5 und häufig nicht größer als 5 in Softwarebibliotheken. 3.2 Methoden über numerische Differentiation Wir führen einen anderen Typ von impliziten Mehrschrittverfahren ein, welcher durch numerische Differentiation entsteht. Ist eine Differentialgleichung y = f(x, y) gegeben, dann können wir die Ableitung auf der linken Seite durch eine Differenzenformel ersetzen, was einer numerischen Differentiation entspricht. Der übliche Differenzenquotient lautet y (x 0 + h) = h [y(x 0 + h) y(x 0 )] + O(h). Zusammen mit y (x 0 + h) = f(x 0 + h, y(x 0 + h)) erhalten wir als numerische Methode y = y 0 + hf(x 0 + h, y ), d.h. das implizite Euler-Verfahren Dieser Ansatz kann zu einem k-schritt-verfahren verallgemeinert werden wie folgt: Mit den gegebenen Daten (x i k+l, y i k+l ) für l =,..., k stellen wir das Interpolationspolynom p P k mit p(x i k+l ) = y i k+l für l =,..., k, k + 4
45 y p(x) x i k+ i i+ x x x Abbildung 0: Konstruktion von Mehrschrittverfahren durch numerische Differentiation. auf. Darin ist der unbekannte Wert y i+ eingeschlossen, wodurch die Methode implizit ist. Die Strategie ist in Abb. 0 dargestellt. Die Ableitung p kann man als Approximation der Ableitung y interpretieren. Der unbekannte Wert wird bestimmt durch die Bedingung p (x i+ ) = f(x i+, y i+ ), (3.7) d.h. man verlangt, dass das Interpolationspolynom nur an der Stelle x i+ die Differentialgleichung erfüllt. Die entstehenden Schemata nennt man BDF- Methoden (backward differentiation formulas). Das Interpolationspolynom besitzt die Darstellung p(x) = mit den Lagrange-Polynomen k y i+ j L j (x) j=0 Wir erhalten p (x i+ ) = L j (x) = k ν=0,ν j x x i+ ν x i+ j x i+ ν. k y i+ j L j(x i+ ) = f(x i+, y i+ ). j=0 42
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
3. Lineare Mehrschrittverfahren 3.1 Begriffe
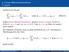 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
11. Einschrittverfahren
 H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel;
 Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Gewöhnliche Differentialgleichungen Woche 6. Existenz nach Picard-Lindelöf
 d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
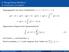 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
Nichtlineare Gleichungssysteme
 Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Numerik gewöhnlicher Differentialgleichungen. Übung 8 - Lösungsvorschlag
 Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Systeme von Differentialgleichungen. Beispiel 1: Chemische Reaktionssysteme. Beispiel 2. System aus n Differentialgleichungen 1. Ordnung: y 1.
 Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Diplom VP Numerik 28. August 2006
 Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
ZWEITE KLAUSUR zur Numerik I mit Lösungen. Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
 MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
KAPITEL 10. Numerische Integration
 KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen
 Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
1 Einführung, Terminologie und Einteilung
 Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Numerische Verfahren
 Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 15.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren Numerische
Numerische Verfahren Jens-Peter M. Zemke zemke@tu-harburg.de Institut für Numerische Simulation Technische Universität Hamburg-Harburg 15.04.2008 TUHH Jens-Peter M. Zemke Numerische Verfahren Numerische
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen
 Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Einführung in die numerische Mathematik
 Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Begleitmaterial zur Vorlesung Numerik II
 Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
(c) Gegeben sei der zweidimensionale Raum L mit den Basisfunktionen. [ φ i, φ j ] 3 i,j=1 =
![(c) Gegeben sei der zweidimensionale Raum L mit den Basisfunktionen. [ φ i, φ j ] 3 i,j=1 = (c) Gegeben sei der zweidimensionale Raum L mit den Basisfunktionen. [ φ i, φ j ] 3 i,j=1 =](/thumbs/88/117470920.jpg) 1. (a) i. Wann besitzt A R n n eine eindeutige LR-Zerlegung mit R invertierbar? ii. Definieren Sie die Konditionszahl κ(a) einer Matrix A bzgl. einer Norm.! iii. Welche Eigenschaften benötigt eine Matrix
1. (a) i. Wann besitzt A R n n eine eindeutige LR-Zerlegung mit R invertierbar? ii. Definieren Sie die Konditionszahl κ(a) einer Matrix A bzgl. einer Norm.! iii. Welche Eigenschaften benötigt eine Matrix
Differentialgleichungen
 Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
eps für alle x D. 4. Die Zahl 256 ist in M(2, 4, 6, 6) exakt darstellbar.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Gewöhnliche Differentialgleichungen Woche 7. Globale Existenz einer Lösung
 Gewöhnliche Differentialgleichungen Woche 7 Globale Existenz einer Lösung 7.1 Von lokal zu global Wir betrachten wiederum das Anfangswertproblem { y (x = f (x, y(x, y( = y 0. (7.1 Eine erste Erweiterung
Gewöhnliche Differentialgleichungen Woche 7 Globale Existenz einer Lösung 7.1 Von lokal zu global Wir betrachten wiederum das Anfangswertproblem { y (x = f (x, y(x, y( = y 0. (7.1 Eine erste Erweiterung
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Klassische Polynom Interpolation.
 Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Klassische Polynom Interpolation. Bestimme ein Polynom (höchstens) n ten Grades p n (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n, das die gegebenen Daten interpoliert, d.h. p n (x i ) = f i, 0 i n. Erster
Klausur Numerische Mathematik (für Elektrotechniker), 24. Februar 2016
 Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
ε δ Definition der Stetigkeit.
 ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Numerische Mathematik
 6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
Zweite Prüfung zur Vorlesung
 Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Gewöhnliche Dierentialgleichungen
 Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Formelsammlung Numerik
 Formelsammlung Numerik Fachbereich Design und Informatik Fachhochschule Trier University of Applied Sciences - 1-1 Grundlagen 1. Festlegungen: x - exakter Wert x - Näherungswert 2. Wahrer Fehler: 3. Absoluter
Formelsammlung Numerik Fachbereich Design und Informatik Fachhochschule Trier University of Applied Sciences - 1-1 Grundlagen 1. Festlegungen: x - exakter Wert x - Näherungswert 2. Wahrer Fehler: 3. Absoluter
Diplom VP Numerik 27. August 2007
 Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
Diplom VP Numerik 27. August 2007 Multiple-Choice-Test 30 Punkte Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 1
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Übungsblatt 4 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Übungsblatt 4 Musterlösung Aufgabe 7 (Nullstellen als Eigenwerte) Die Polynome {S n } n=0,,2,, S n P n, mit führem Koeffizienten eins, heißen Orthogonalpolynome
Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Übungsblatt 4 Musterlösung Aufgabe 7 (Nullstellen als Eigenwerte) Die Polynome {S n } n=0,,2,, S n P n, mit führem Koeffizienten eins, heißen Orthogonalpolynome
(a), für i = 1,..., n.
 .4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
.4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
Skalare Differenzialgleichungen
 3 Skalare Differenzialgleichungen Differenzialgleichungen stellen eine Beziehung her zwischen einer oder mehreren Funktionen und ihren Ableitungen. Da Ableitungen Veränderungen beschreiben, modellieren
3 Skalare Differenzialgleichungen Differenzialgleichungen stellen eine Beziehung her zwischen einer oder mehreren Funktionen und ihren Ableitungen. Da Ableitungen Veränderungen beschreiben, modellieren
Dierentialgleichungen 2. Ordnung
 Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
9 Numerische Verfahren für Anfangswertaufgaben
 Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerische Methoden 7. Übungsblatt
 Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Karlsruher Institut für Technologie (KIT) SS 01 Institut für Analysis Prof Dr Michael Plum Dipl-Mathtechn Rainer Mandel Numerische Methoden 7 Übungsblatt Aufgabe 17: Quadratur II Die Menge aller Polynome
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Einführung in die numerische Mathematik
 Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 014 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 014 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei die Matrix
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
2. Quasilineare PDG erster Ordnung
 H.J. Oberle Differentialgleichungen II SoSe 2013 2. Quasilineare PDG erster Ordnung Eine skalare PDG erster Ordnung hat die allgemeine Form F (x, u(x), u x (x)) = 0. (2.1) Dabei ist u : R n G R die gesuchte
H.J. Oberle Differentialgleichungen II SoSe 2013 2. Quasilineare PDG erster Ordnung Eine skalare PDG erster Ordnung hat die allgemeine Form F (x, u(x), u x (x)) = 0. (2.1) Dabei ist u : R n G R die gesuchte
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
KAPITEL 5. Nichtlineare Gleichungssysteme
 KAPITEL 5. Nichtlineare Gleichungssysteme Beispiel 5.1. Gravitationskraft zwischen zwei Punktmassen m 1 und m 2 mit gegenseitigem Abstand r: F = G m 1m 2 r 2, wobei G = 6.67 10 11 Nm 2 /kg. Gravitationsfeld
KAPITEL 5. Nichtlineare Gleichungssysteme Beispiel 5.1. Gravitationskraft zwischen zwei Punktmassen m 1 und m 2 mit gegenseitigem Abstand r: F = G m 1m 2 r 2, wobei G = 6.67 10 11 Nm 2 /kg. Gravitationsfeld
C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: Ort: Geschwindigkeit:
 C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel
C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2.
 Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHE- MIE UND LEBENSMITTELCHEMIE
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHE- MIE UND LEBENSMITTELCHEMIE Differentialrechnung für Funktionen mehrerer
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHE- MIE UND LEBENSMITTELCHEMIE Differentialrechnung für Funktionen mehrerer
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Institut für Geometrie und Praktische Mathematik Multiple-Choice-Test NumaMB F08 (30 Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine
RWTH Aachen Institut für Geometrie und Praktische Mathematik Multiple-Choice-Test NumaMB F08 (30 Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine
Numerik für Ingenieure I Wintersemester 2008
 1 / 32 Numerik für Ingenieure I Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 23.1.2009 2 / 32 Wiederholung Stückweise Polynominterpolation Stückweise lineare Interpolierende
1 / 32 Numerik für Ingenieure I Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 23.1.2009 2 / 32 Wiederholung Stückweise Polynominterpolation Stückweise lineare Interpolierende
Differenzialgleichungen
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 30. Januar 2008 (System von) Differenzialgleichung(en) Schwingungsgleichung Newtonsche Mechanik Populationsdynamik...DGLn höherer Ordnung auf
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 30. Januar 2008 (System von) Differenzialgleichung(en) Schwingungsgleichung Newtonsche Mechanik Populationsdynamik...DGLn höherer Ordnung auf
Mathematische Grundlagen
 G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
Höhere Mathematik III für die Fachrichtung Physik Wintersemester 2016/17. Lösungsvorschlag zu Übungsblatt 5
 Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Adaptive Mehrschrittverfahren
 Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Nichtlineare Gleichungssysteme
 Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren
 Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan :00-14:00 (120 min)
 Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Kapitel 3: Differentialgleichungen
 Kapitel 3: Differentialgleichungen Einführung: Vergleich zur Integration Zwischen der Integration und der Lösung von Differentialgleichungen besteht ein enger Zusammenhang: Das Aufsuchen der Lösung y(b)
Kapitel 3: Differentialgleichungen Einführung: Vergleich zur Integration Zwischen der Integration und der Lösung von Differentialgleichungen besteht ein enger Zusammenhang: Das Aufsuchen der Lösung y(b)
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
6. Polynom-Interpolation
 6. Polynom-Interpolation 1 6.1. Klassische Polynom-Interpolation 2 6.2. Lösung mit Hilfe Lagrange scher Basisfunktionen 3 6.3. Lösung mit Hilfe Newton scher Basisfunktionen 4 6.4. Fehlerabschätzung für
6. Polynom-Interpolation 1 6.1. Klassische Polynom-Interpolation 2 6.2. Lösung mit Hilfe Lagrange scher Basisfunktionen 3 6.3. Lösung mit Hilfe Newton scher Basisfunktionen 4 6.4. Fehlerabschätzung für
MATHEMATISCHE METHODEN DER PHYSIK 1
 MATHEMATISCHE METHODEN DER PHYSIK 1 Helmuth Hüffel Fakultät für Physik der Universität Wien Vorlesungsskriptum Sommersemester 2012 Version vom 08-03-2012 Inhaltsverzeichnis 1 Lineare gewöhnliche Differentialgleichungen
MATHEMATISCHE METHODEN DER PHYSIK 1 Helmuth Hüffel Fakultät für Physik der Universität Wien Vorlesungsskriptum Sommersemester 2012 Version vom 08-03-2012 Inhaltsverzeichnis 1 Lineare gewöhnliche Differentialgleichungen
