5 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen
|
|
|
- Heinz Böhme
- vor 5 Jahren
- Abrufe
Transkript
1 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Eine Differentialgleichung (DG) beschreibt eine Beziehung zwischen einer gesuchten Funktion y und ihren Ableitungen. Ist dabei y = y(t) eine Funktion, die nur von einer Variablen hier t abhängt, so spricht man von einer gewöhnlichen Differentialgleichung (gdg). Da explizite Lösungen nur in wenigen Ausnahmefällen zur Verfügung stehen, ist der Einsatz numerischer Methoden zur Lösung von DGen unvermeidbar. Wir befassen uns hier ausschließlich mit numerischen Verfahren zur Lösung gewöhnlicher DGen: Zum Einen wegen der überragenden Rolle, die sie in vielen Anwendungen spielen, zum Zweiten aber auch wegen ihrer Bedeutung für die Entwicklung und Analyse von numerischen Methoden zur Lösung partieller DGen (das sind DGen für Funktionen mehrerer Variablen), die sehr viel schwieriger zu lösen sind und hier leider nur an einem Beispiel behandelt werden können. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen TU Bergakademie Freiberg, SS 2010
2 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Ein Beispiel Wir betrachten einen Satellit im Kraftfeld von Erde und Mond unter den Annahmen, dass die drei Körper sich in einer festen Ebene bewegen und die beiden großen Körper mit konstanter Winkelgeschwindigkeit und konstantem Abstand um ihren gemeinsamen Schwerpunkt rotieren. Der Satellit hat also keinerlei Einfluss auf die Bahnen von Erde und Mond. In einem mitrotierenden Koordinatensystem (bezüglich dem Erde und Mond ruhend sind) mit dem gemeinsamen Schwerpunkt von Erde und Mond als Ursprung wird die Bahn (x, y) = (x(t), y(t)) des Satelliten durch ein System von DGen zweiter Ordnung beschrieben: Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Ein Beispiel TU Bergakademie Freiberg, SS 2010
3 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 120 x = x + 2y µ x + µ [(x + µ) 2 + y 2 ] µ x µ 3/2 [(x µ ) 2 + y 2 ], 3/2 y = y 2x µ y [(x + µ) 2 + y 2 ] µ y 3/2 [(x µ ) 2 + y 2 ]. 3/2 Hier ist µ = 1/82.45 das Verhältnis zwischen der Masse des Mondes zur Gesamtmasse von Erde und Mond und µ = 1 µ. Die Längeneinheit ist so gewählt, dass der Abstand zwischen Erde und Mond 1 ist, wobei der Mond auf der positiven reellen Achse und die Erde auf der negativen reellen Achse plaziert werden. Die Zeiteinheit ist so gewählt, dass die Winkelgeschwindigkeit der Rotation ebenfalls 1 beträgt, d.h. der Mond die Erde in 2π Zeiteinheiten umrundet. Man spricht von einem restringierten Dreikörperproblem ( restringiert, weil der dritte Körper die beiden anderen nicht beeinflusst). Außerdem sind Anfangsbedingungen erforderlich: Der Satellit möge sich zur Zeit t = 0 in der Position (x(0), y(0)) = (1.2, 0) befinden und die Geschwindigkeit (x (0), y (0)) = (0, 1.05) besitzen. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Ein Beispiel TU Bergakademie Freiberg, SS 2010
4 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 121 Wir transformieren dieses System in ein System erster Ordnung und setzen dazu y 1 = x, y 2 = y, y 3 = x, y 4 = y. Damit ergibt sich y 1 = y 3, y 2 = y 4, y 3 = y 1 + 2y 4 µ y 1 + µ [(y 1 + µ) 2 + y 2 2 ]3/2 µ y 1 µ [(y 1 µ ) 2 + y 2 2 ]3/2, y 4 = y 2 + 2y 3 µ y 2 [(y 1 + µ) 2 + y 2 2 ]3/2 µ y 2 [(y 1 µ ) 2 + y 2 2 ]3/2 mit den Anfangsbedingungen y 1 (0) = 1.2, y 2 (0) = y 3 (0) = 0 und y 4 (0) = Die Lösung (x(t), y(t)) = (y 1 (t), y 2 (t)) ist eine geschlossene Bahn mit Periode T = Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Ein Beispiel TU Bergakademie Freiberg, SS 2010
5 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge E M Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Ein Beispiel TU Bergakademie Freiberg, SS 2010
6 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Geschwindigkeit in x Richtung Geschwindigkeit in y Richtung t Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Ein Beispiel TU Bergakademie Freiberg, SS 2010
7 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Definitionen und theoretischer Hintergrund Ein Gleichungssystem der Form y 1 = f 1 (x, y 1, y 2,..., y n ) y 2 = f 2 (x, y 1, y 2,..., y n ). =. y n = f n (x, y 1, y 2,..., y n ) (DG) heißt explizites System gewöhnlicher Differentialgleichungen (gdg) erster Ordnung in den n unbekannten Funktionen y 1, y 2,..., y n. Jedes System von n Funktionen y 1 = y 1 (x),..., y n = y n (x) C 1 [a, b], das (DG) für alle x [a, b] erfüllt, heißt Lösung von (DG) über [a, b]. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Definitionen TU Bergakademie Freiberg, SS 2010
8 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 125 Beispiel. Das System { y 1 = 1 y 2 = 2y 1 } besitzt die Lösungen über (, ). y 1 (x) = x + α, y 2 (x) = x 2 + 2αx + β (α, β R) Für eine eindeutige Lösung: Zusatzbedingungen, etwa Anfangsbedingungen, z.b. y 1 (0) = 1, y 2 (0) = 2. Dann ist y 1 (x) = x + 1, y 2 (x) = x 2 + 2x + 2 die einzige Lösung. Allgemein: Das Problem, eine Lösung von (DG) zu finden, die die Anfangsbedingung y 1 (x 0 ) = y 0,1,..., y n (x 0 ) = y 0,n (AB) erfüllt, heißt Anfangswertproblem (AWP) für die gdg (DG). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Definitionen TU Bergakademie Freiberg, SS 2010
9 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 126 Mit y := y 1., f := f 1., y 0 := y 0,1., y n f n y 0,n Kurzschreibweise: y = f (x, y), (DG ) y(x 0 ) = y 0. (AB ) Bemerkung. gdgen höhere Ordnung lassen sich auf Systeme von gdgen erster Ordnung umschreiben: Aus y + 3y + y = sin(x) wird etwa y 3 3y 3 y 2 + sin(x) y 2 = y 3 y 1 (y 1 = y, y 2 = y 1 = y, y 3 = y 2 = y ). y 2 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Definitionen TU Bergakademie Freiberg, SS 2010
10 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 127 Existenz und Eindeutigkeit der Lösung: Satz 5.1 (Satz von Picard-Lindelöf) Gegeben ist das AWP y = f (x, y), y(x 0 ) = y 0. (AWP) f sei stetig im Quader Q := {(x, y) : x x 0 a, y y 0 b} R n+1 und es sei M := max{ f (x, y) : (x, y) Q}. Außerdem erfülle f in Q die Lipschitzbedingung f (x, y) f (x, ỹ) L y ỹ (x, y), (x, ỹ) Q. (Lip) Dann besitzt das Problem (AWP) genau eine Lösung über I := [x 0 α, x 0 + α], wobei α = min{a, b/m}. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Definitionen TU Bergakademie Freiberg, SS 2010
11 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 128 Stetige Abhängigkeit von den Daten: Die Voraussetzungen von Satz 1 seien erfüllt. Sind y, z Lösungen der AWPe y = f (x, y), y(x 0 ) = y 0 bzw. z = g(x, z ), z (x 0 ) = z 0 über I (g sei stetig in Q) und gilt sowie y 0 z 0 γ f (x, y) g(x, y) δ ( (x, y) Q), dann folgt für x I y(x) z (x) γ e L(x x 0) + δ L ( ) e L(x x0) 1. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Definitionen TU Bergakademie Freiberg, SS 2010
12 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Euler-Verfahren Gesucht: Lösung eines AWP im Intervall I = [x 0, x end ]: y = f (x, y), y(x 0 ) = y 0. Diskretisiere I durch (der Einfachheit halber) äquidistantes Gitter mit Schrittweite h = (x end x 0 )/m, Ω h = {x 0 < x 1 <... < x m = x end } mit x j := x 0 + jh (j = 0,..., m) Es bezeichne y j einen Näherungswert für y(x j ), j = 1,..., m. Dann y j+1 y(x j+1 ) = y(x j + h) = y(x j ) + hy (x j ) h2 y (ξ) y(x j ) + hy (x j ) = y(x j ) + hf (x j, y(x j )) y j + hf (x j, y j ). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Euler-Verfahren TU Bergakademie Freiberg, SS 2010
13 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 130 Eulersches Polygonzugverfahren oder explizites Euler-Verfahren: y 0 ist gegeben, y j+1 = y j + hf (x j, y j ) (j = 0, 1,...) Aufwand pro Schritt: Eine Auswertung von f. Beispiel. AWP: [ ] y 1 (x) [ ].5 y2 (x) y 1 (x)y 2 (x) [ ] y1 (.5) [ ] 1 y 2(x) =.5 y 1 (x) 2 + 5x, y 2 (.5) = 2. Rechenvorschrift des Eulerschen Polygonzugverfahrens (x j =.5 + jh): [ ] [ ] [ ] [ ] [ ] (1) (1) (1) (2) y 0 1 y j+1 y j.5 y j y (1) j y (2) j y (2) =, 0 2 y (2) = j+1 y (2) + h j.5 [y (1) (j = 0, 1,...). j ] 2 + 5x j Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Euler-Verfahren TU Bergakademie Freiberg, SS 2010
14 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Richtungsfeld von y =t(y 2) und Loesungen mit Anfangswerten y(0) = 1:0.5:1 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Euler-Verfahren TU Bergakademie Freiberg, SS 2010
15 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 132 Zur Veranschaulichung einer GDG 1. Ordnung y = f(t, y) wird oft das assoziierte Richtungsfeld herangezogen: In jedem Punkt von (t, y) wird ein Pfeil gezeichnet, der in die Richtung y = f(t, y) weist. Der Graph der Lösung des AWPs y = f(t, y), y(t 0 ) = y 0, muss einerseits das Richtungsfeld respektieren (d.h. die Tangenten an den Graphen sind Elemente des Richtungsfelds), andererseits den Punkt (t 0, y 0 ) enthalten. Die nächste Abbildung zeigt, wie das Euler-Verfahren die logistische Gleichung y = y(1 y) mit AB y(0) = 1/10 löst. Statt der exakten Trajektorie zu folgen (was natürlich unmöglich ist), produziert das Euler-Verfahren eine stückweise lineare Lösung (einen Polygonzug). An der Stelle t 0 = 0 arbeitet das Euler-Verfahren mit der richtigen Steigung f(t 0, y 0 ) = 9/100, bereits an der Stelle t = 1 ist die Steigung falsch. In späteren Schritten entfernt man sich (potentiell) immer weiter von der exakten Lösung. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Euler-Verfahren TU Bergakademie Freiberg, SS 2010
16 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Euler Verfahren y =y(1 y), y(0)=1/10 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Euler-Verfahren TU Bergakademie Freiberg, SS 2010
17 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 134 Varianten des Polygonzugverfahrens Modifiziertes Polygonzugverfahren: y 0 ist gegeben, y j+1 = y j + hf (x j + h 2, y j + h 2 f (x j, y j )) (j = 0, 1,...). Aufwand pro Schritt: Zwei Auswertungen von f. Verbessertes Polygonzug-Verfahren: y 0 ist gegeben, y j+1 = y j + h 2 [f (x j, y j ) + f (x j + h, y j + hf (x j, y j ))] (j = 0, 1,...). Aufwand pro Schritt: Zwei Auswertungen von f. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Euler-Verfahren TU Bergakademie Freiberg, SS 2010
18 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 135 Beispiel. AWP y (x) = y(x) 2, y(0) = 4 besitzt in I = [0, ) die Lösung y(x) = 1/(x +.25). Polygonzugverfahren: y 0 = 4, y j+1 = y j + hyj 2 (j = 0, 1,...). Modifiziertes Polygonzugverfahren: y 0 = 4, y j+1 = y j + h(y j +.5 hyj 2 ) 2 (j = 0, 1,...). Verbessertes Polygonzugverfahren: y 0 = 4, y j+1 = y j +.5 h[yj 2 + (y j + hyj 2 ) 2 ] (j = 0, 1,...). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Euler-Verfahren TU Bergakademie Freiberg, SS 2010
19 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 136 Eine weitere wichtige Variante ist das implizite Euler-Verfahren: y 0 ist gegeben, y j+1 = y j + hf (x j+1, y j+1 ) (j = 0, 1,...). Aufwand pro Schritt: Eine Auswertung von f sowie Lösung eines i.a. nichtlinearen Gleichungssystems. Im Beispiel: y 0 = 4, y j+1 löst y j+1 = y j + hy 2 j+1 (j = 0, 1,...). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Euler-Verfahren TU Bergakademie Freiberg, SS 2010
20 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 137 h = 10 1 : x j exakt E-Euler modifiziert verbessert I-Euler Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Euler-Verfahren TU Bergakademie Freiberg, SS 2010
21 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 138 h = 10 2 : x j exakt E-Euler modifiziert verbessert I-Euler Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Euler-Verfahren TU Bergakademie Freiberg, SS 2010
22 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Runge-Kutta-Verfahren Konstruktion. Es bezeichne y(x) die Lösung von (AWP) an der Stelle x I. Gesucht: Näherung für y(x + h). y(x + h) = y(x) + [y(x + h) y(x)] = y(x) + (Substitution: s = x + th, 0 t 1) x+h x y (s) ds = y(x) + h 1 0 y (x + th) dt. Approximiere durch Quadraturformel 1 0 g(t) dt m γ i g(α i ). i=1 ( ) Damit zumindest g 1 exakt integriert wird, fordern wir m i=1 γ i = 1. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Runge-Kutta-Verfahren TU Bergakademie Freiberg, SS 2010
23 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 140 Damit ergibt sich y(x + h) y(x) + h = y(x) + h m γ i y (x + α i h) i=1 m γ i f (x + α i h, y(x + α i h)) i=1 (RK-1) Problem: y(x + α i h) = y(x) + h α i 0 y (x + th) dt sind unbekannt. Näherungen wieder durch Quadraturformeln, aber mit den alten Knoten α j (j = 1,..., m) aus ( ) (sonst würden sich neue Unbekannte der Form y(x + Knoten h) ergeben). αi 0 g(t) dt m β i,l g(α l ) (i = 1,..., m). ( ) l=1 Damit zumindest g 1 exakt integriert wird, fordern wir m l=1 β i,l = α i i = 1,..., m. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Runge-Kutta-Verfahren TU Bergakademie Freiberg, SS 2010
24 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 141 Damit ergibt sich m y(x + α i h) y(x) + h β i,l y (x + α l h) = y(x) + h l=1 m β i,l f (x + α l h, y(x + α l h)) Abkürzung: k i := f (x + α i h, y(x + α i h)) (i = 1,..., m). (RK-1): y(x + h) y(x) + h m i=1 γ ik i. (RK-2): k i f (x + α i h, y(x) + h m l=1 β i,lk l ) (i = 1,..., m). m-stufiges Runge-Kutta-Verfahren (RKV): m y j+1 = y j + h γ i k i (j = 0, 1,...) mit i=1 l=1 k i = f (x j + α i h, y j + h m β i,l k l ) (i = 1,..., m). l=1 (RK-2) (RK) Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Runge-Kutta-Verfahren TU Bergakademie Freiberg, SS 2010
25 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 142 α 1 β 1,1 β 1,m Butcher-Tableau:... α m β m,1 β m,m γ 1 γ m Beispiele /2 1/2 0 1/2 1/2 symbolisiert ein zweistufiges explizites RKV (ein R-K-V heißt explizit, wenn β i,l = 0 i l gilt), nämlich eine Variante des verbesserten Euler-Verfahrens. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Runge-Kutta-Verfahren TU Bergakademie Freiberg, SS 2010
26 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge /4 1/4 2/3 1/4 5/12 1/4 3/4 symbolisiert ein zweistufiges implizites RKV: k 1 = f (x j, y j + hk 1 /4 hk 2 /4), k 2 = f (x j + 2h/3, y j + hk 1 /4 + 5hk 2 /12) ( zwei i.a. nichtlineare Gleichungen für k 1 und k 2 ), y j+1 = y j + h(k 1 /4 + 3k 2 /4). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Runge-Kutta-Verfahren TU Bergakademie Freiberg, SS 2010
27 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge /2 1/ /6 2/3 1/6 symbolisiert ein dreistufiges explizites RKV, das Verfahren von Heun: k 1 = f (x j, y j ), k 2 = f (x j + h/2, y j + hk 1 /2), k 3 = f (x j + h, y j hk 1 + 2hk 2 ), y j+1 = y j + h(k 1 + 4k 2 + k 3 )/6. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Runge-Kutta-Verfahren TU Bergakademie Freiberg, SS 2010
28 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge /2 1/ /2 0 1/ /6 1/3 1/3 1/6 symbolisiert ein vierstufiges explizites RKV, das klassische Runge-Kutta-Verfahren: k 1 = f (x j, y j ), k 2 = f (x j + h/2, y j + hk 1 /2), k 3 = f (x j + h/2, y j + hk 2 /2), k 4 = f (x j + h, y j + hk 3 ), y j+1 = y j + h(k 1 + 2k 2 + 2k 3 + k 4 )/6. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Runge-Kutta-Verfahren TU Bergakademie Freiberg, SS 2010
29 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 146 Beispiel. AWP y (x) = y(x) 2, y(0) = 4 besitzt in I = [0, ) die Lösung y(x) = 1/(x +.25). Verfahren von Heun: y 0 = 4, k 1 = yj 2, k 2 = (y j +.5 hk 1 ) 2, k 3 = (y j + h( k 1 + 2k 2 )) 2, y j+1 = y j + h(k 1 + 4k 2 + k 3 )/6 (j = 0, 1,...). Klassisches Runge-Kutta-Verfahren: y 0 = 4, k 1 = yj 2, k 2 = (y j +.5 hk 1 ) 2, k 3 = (y j +.5 hk 2 ) 2, k 4 = (y j + hk 3 ) 2, y j+1 = y j + h(k 1 + 2k 2 + 2k 3 + k 4 )/6 (j = 0, 1,...). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Runge-Kutta-Verfahren TU Bergakademie Freiberg, SS 2010
30 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 147 h = 10 1 : x j exakt verb. Euler Heun klass. RKV Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Runge-Kutta-Verfahren TU Bergakademie Freiberg, SS 2010
31 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Einschrittverfahren Ein Einschrittverfahren (ESV) hat die Form y n+1 = y n + hφ f (y n+1, y n, t n ; h). (ESV) Wir werden ausschließlich Verfahren untersuchen, bei denen die Verfahrensfunktion Φ f die folgenden beiden Eigenschaften besitzt: und Φ f 0 (y n+1, y n, t n ; h) 0 (V 1 ) Φ f (y n+1, y n, t n ; h) Φ f (y n+1, y n, t n ; h) M 1 y n+j yn+j. (V 2 ) j=0 Bei vernünftigen ESV ist (V 2 ) eine Folge der Lipschitz-Stetigkeit von f (vgl. Satz 5.1), die immer vorausgesetzt wird. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
32 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 149 Beispiele für etwas kompliziertere ESV: y n+1 y n = 1 4 h(k 1 + 3k 3 ) mit k 1 = f (t n, y n ), k 2 = f (t n h, y n hk 1), k 3 = f (t n h, y n hk 2), (Beispiel 1) ein explizites ESV, das zur Klasse der Runge-Kutta-Verfahren gehört, und ein implizites ESV der Runge-Kutta-Klasse, die sog. Trapezregel y n+1 y n = 1 2 h(k 1 + k 2 ) mit k 1 = f (t n, y n ), k 2 = f (t n + h, y n hk hk (Beispiel 2) 2). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
33 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 150 Das Verfahren (ESV) heißt konvergent, wenn lim h 0 t=t 0 +nh y n = lim h 0 t=t 0 +nh y n (h) = y(t) gilt und zwar für alle AWPe, die den Voraussetzungen von Satz 5.1 genügen (y(t) bezeichnet die Lösung eines solchen AWPs), gleichmäßig für alle t [t 0, t end ], für alle Lösungen {y n (h)} = {y n } von (ESV) mit Anfangswert y 0 (h), der lim h 0 y 0 (h) = y 0 erfüllt. Äquivalent: Der globale Diskretisierungsfehler e n = e n (h) := y(t n ) y n (h) strebt gleichmäßig gegen 0 (für h 0): lim h 0 max e n(h) = lim 0 n N h 0 max y(t n) y n (h) = 0. 0 n N Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
34 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 151 exakte Loesung Schrittweite h 0 Schrittweite h 1 Schrittweite h 2 t_0 t Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
35 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 152 Setzt man die exakte Lösung in (ESV) ein, so werden linke und rechte Seite nicht übereinstimmen. Es ergibt sich ein Residuum R n+1 (h) = R n+1 := y(t n+1 ) y(t n ) hφ f (y(t n+1 ), y(t n ), t n ; h). R n+1 ist eng verknüpft mit dem Schrittfehler S n+1. Gilt y n = y(t n ) (Lokalisierungsannahme), so liefert (ESV) in Schritt n + 1: ŷ n+1 (h) = y(t n ) + hφ f (ŷ n+1, y(t n ), t n ; h). Gleichzeitig gilt für die exakte Lösung y(t n+1 ) = y(t n ) + hφ f (y(t n+1 ), y(t n ), t n ; h) + R n+1. Wir definieren nun den Schrittfehler durch S n+1 (h) = S n+1 := y(t n+1 ) ŷ n+1 (h) Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
36 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 153 Es folgt S n+1 = h [Φ f (y(t n+1 ), y(t n ), t n ; h) Φ f (ŷ n+1, y(t n ), t n ; h)] + R n+1 und, mit (V 2 ), S n+1 hm S n+1 + R n+1, d.h. (1 hm) S n+1 R n+1. Man kann zeigen, dass Schrittfehler und Residuum für h 0 dasselbe Verhalten aufweisen. Wir definieren nun den lokalen Diskretisierungsfehler T n = T n (h) (lokaler Abbruchfehler) eines Verfahrens im n-ten Schritt als T n (h) := R n(h), h das heißt als Differenz von linker Seite und rechter Seite der Verfahrensgleichung (so skaliert, dass für h 0 die Differentialgleichung approximiert wird) wenn anstelle der Näherungslösung die exakte Lösung eingesetzt wird. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
37 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 154 Das Verfahren (ESV) heißt konsistent, wenn lim h 0 t=t 0 +nh T n (h) = 0 gilt für alle AWPe, die den Voraussetzungen von Satz 5.1 genügen, und für alle t [t 0, t end ]. Entsprechend heißt das Verfahren (ESV) konsistent von der Ordnung p, falls T n (h) = O(h p ) für h 0 gilt für alle AWPe mit genügend glattem f und alle t = t 0 + nh [t 0, t end ]. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
38 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 155 y(t n+1 ) globaler DF y(t n ) Schrittfehler y n+1 y n = ^y(t n ) t n t n+1 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
39 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 156 Die anschauliche Bedeutung der Konsistenz ergibt sich aus der offensichtlichen Identität T n+1 (h) = 1 h (y(t n+1) y(t n )) }{{} Sekantensteigung der Lösung Φ f (y(t n+1 ), y(t n ), t n ; h). }{{} Näherung dieser Steigung Wir wollen eine Beziehung zwischen lokalem und globalem Diskretisierungsfehler beweisen. Dazu ein Hilfssatz Satz 5.2 (Wachstumsverhalten rekursiv definierter Folgen) Es gelte y n+1 (1 + K n ) y n + M n (n = 0, 1,..., n 0 ) mit M n, K n 0. Dann gilt auch die Abschätzung n n y n+1 y 0 + exp (n = 0, 1,..., n 0 ). j=1 M j j=1 K j Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
40 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 157 Satz 5.3 (Beziehung zwischen lokalem und globalem Dis.-Fehler) Unter den gebenen Voraussetzungen (vgl. Satz 5.1 sowie (V 2 )) gilt ( ) e n ( e 0 + (t n t 0 ) max T j exp(m(t n t 0 )). 1 j n Insbesondere ist ein ESV genau dann konvergent, wenn es konsistent ist. Satz 5.3 besagt, dass bei ESV der Konsistenzordnung p der globale Diskretisierungsfehler wie h p gegen 0 strebt (für h 0). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
41 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 158 Ist f p-mal stetig differenzierbar, so kann man sich Einschrittverfahren der Konsistenzordnung p mit der Methode des Taylor-Abgleichs konstruieren: Man entwickelt die (unbekannte) Lösung y(t n + h) formal nach Potenzen von h, y(t n + h) = y(t n ) + hy (t n ) h2 y (t n ) +, und nutzt aus, daß y (t) = f (t, y(t)) gilt, z.b. y (t n ) = f (t n, y(t n )), y (t n ) = f t (t, y(t)) t=tn + f y (t, y(t))y (t) t=tn = f t (t n, y(t n )) + f y (t n, y(t n ))f (t n, y(t n )). Bricht man etwa nach dem zweiten Term ab, so ergibt sich mit y n+1 = y n + h [ f (t n, y n ) h (f t(t n, y n ) + f y (t n, y n )f (t n, y n )) ] ein Verfahren zweiter Ordnung. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
42 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 159 Es ist klar, daß man dieses Verfahren (oder gar die analogen Verfahren für p > 2) nur dann verwenden kann, wenn f einfach zu differenzieren ist (automatische Differentiation). Für die skalare GDG y (t) = ty(t) ergibt sich z.b. [ y n+1 = y n h2 + ht n h2 t 2 ] n im Fall von p = 2 und [ y n+1 = y n h2 + ht n h2 t 2 n h3 t n h3 t 3 ] n im Fall von p = 3. Für p = 1 erhält man stets das Euler-Verfahren. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
43 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 160 In diesem Beispiel (mit AB y(0) = 1, dh. mit exakter Lösung y(t) = exp(0.5t 2 )) ergibt sich als (normalisierter) globaler Diskretisierungsfehler h p max y(t n) y n 0 n N für die Taylor-Verfahren der Ordnung p {1, 2, 3}: N h p = 1 p = 2 p = e e e e e e e e e e e e e e e e-1 Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
44 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 161 Satz 5.4 (Gesamtfehler bei expliziten ESV) Das explizite ESV (ESV) werde auf einem Rechner durch ỹ n+1 = ỹ n + hφ f (ỹ n, t n ; h) + ɛ n+1, ỹ 0 = y 0 + ɛ 0, realisiert. Ist ɛ n ε und T n T für alle n = 0, 1,..., so folgt y(t n ) ỹ n ( ɛ 0 + (t n t 0 )(T + ε h )) exp(m(t n t 0 )). Dilemma: Bei großer Schrittweite h ist (üblicherweise) T groß; wählt man h sehr klein, so ist zwar T klein, aber ε h groß, dh. der Anteil der Rundungsfehler dominiert den Gesamtfehler. Wichtig sind also Verfahren hoher Ordnung, weil bei dort T schon bei moderater Größe von h klein wird. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Einschrittverfahren TU Bergakademie Freiberg, SS 2010
45 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Schrittweitensteuerung Kein Verfahren zur Lösung von AWPen arbeitet in der Praxis mit einer konstanten Schrittweite. Man wird vielmehr versuchen, die Schrittweite an das Verhalten der Lösung y anzupassen (ändert sich y in einem Bereich schnell, so ist dort eine kleine Schrittweite angebracht; in Bereichen, in den y kaum variiert, ist eine größere Schrittweite ausreichend). Wir werden hier eine Schrittweitensteuerung vorstellen, die zum Ziel hat, den lokalen Diskretisierungsfehler T n+1 (und damit den globalen Diskretisierungsfehler) zu kontrollieren: T n tol, n = 1, 2,..., mit einer vorgebenen Toleranz tol. Bei Systemen von DGen (insbesondere dann, wenn die Lösungskomponenten von unterschiedlicher Größenordnung sind) wird man für jede Kopmponente eine eigene absolute Fehlertoleranz und global eine relative Fehlertoleranz festsetzen, Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Schrittweitensteuerung TU Bergakademie Freiberg, SS 2010
46 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 163 Um den lokalen Diskretisierungsfehler zu schätzen, verwendet man zwei Methoden unterschiedlicher Konsistenzordnungen (sagen wir p und q mit p < q), um y n aus y n 1 zu berechnen: y n = y n 1 + hφ f (y n 1, t n 1 ; h) bzw. ŷ n = y n 1 + h Φ f (y n 1, t n 1 ; h) Für die zugehörigen lokalen Diskretisierungsfehler gelten: Daraus folgt T n = y(t n) y(t n 1 ) h T n = y(t n) y(t n 1 ) h Φ f (y n 1, t n 1 ; h) = O(h p ), Φ f (y n 1, t n 1 ; h) = O(h q ). T n T n = Φ f (y n 1, t n 1 ; h) Φ f (y n 1, t n 1 ; h) = 1 h (ŷ n y n ). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Schrittweitensteuerung TU Bergakademie Freiberg, SS 2010
47 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 164 Wegen T n T n = T n (1 + O(h q p )) T n erhalten wir aus eine (grobe) Schätzung für T n. 1 h y n ŷ n K n Ist 1 h y n ŷ n > tol, so wird die Schrittweite h verworfen und mit ) p ( h = α h tol h y n ŷ n ( ) eine neue Schrittweite h bestimnmt (α ist hier ein Sicherheitsfaktor, etwa α = 0.9). Ausgehend von y n 1 werden jetzt neue Näherungen y n und ŷ n (an der Stelle t n 1 + h) berechnet. Diesen Prozess wiederholt man solange bis 1 h y n ŷ n tol erfüllt ist. Dann wird ( ) verwendet, um eine neue (größere) Schrittweite für den nächsten Schritt (n n + 1) vorzuschlagen. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Schrittweitensteuerung TU Bergakademie Freiberg, SS 2010
48 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 165 Die Wahl von h nach ( ) motiviert sich folgendermaßen: benutzte Schrittweite h: 1 h y n ŷ n T n = ch p + O(h p+1 ) ch p, erwünschte Schrittweite h: tol = T n = c h p + O( h p+1 ) c h p. Um den Aufwand in Grenzen zu halten, verwendet man zur Berechnung von y n und ŷ n zwei RKV (verschiedener Ordnungen), deren Butcher-Matrizen sich nur in b unterscheiden (d.h. A und c sind gleich, so daß die k j nur einmal berechnet werden müssen). Man spricht von eingebetteten RKV und schreibt c A b b z.b /2 1/2 Hier wird das Euler-Verfahren (p = 1) in das verbesserte Euler-Verfahren (p = 2) eingebettet.. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Schrittweitensteuerung TU Bergakademie Freiberg, SS 2010
49 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 166 Ein populäres Beispiel ist die Fehlberg 4(5)-Formel: Hier werden zwei sechsstufige RKV der Ordnungen 4 bzw. 5 kombiniert Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Schrittweitensteuerung TU Bergakademie Freiberg, SS 2010
50 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 167 Ein weiteres Beispiel ist die Dormand-Prince 4(5)-Formel: Hier wird ein sechsstufiges RKV der Ordnung 4 in ein siebenstufiges der Ordnung 5 eingebettet Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Schrittweitensteuerung TU Bergakademie Freiberg, SS 2010
51 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Absolute Stabilität Bekanntlich streben die Lösungen y(t) von y = Ay, A R n n (konstant) gegen 0 (für t ), wenn Re(λ) < 0 für alle Eigenwerte λ von A gilt. Wir suchen Bedingungen an ein ESV, so dass die Näherungslösungen dasselbe asymptotische Verhalten besitzen. Wir wenden z.b. ein m-stufiges RKV auf die Testgleichung y = λy an und erhalten mit ĥ = λh [ ] y n+1 = 1 + ĥb (I m ĥa) 1 e y n =: R(ĥ)y n, so dass (bei festem h) lim n y n = 0 (für alle y 0 ) genau dann gilt, wenn R(ĥ) < 1 erfüllt ist. Allgemein gilt für jedes ESV (angewandt auf die Testgleichung) y n+1 = R(ĥ)y n mit einer verfahrensspezifischen Funktion R von ĥ = λh. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Absolute Stabilität TU Bergakademie Freiberg, SS 2010
52 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 169 Wir definieren den Stabilitätsbereich eines ESVs durch R A := {ĥ C : R(ĥ) < 1}. Ein ESV heißt absolut stabil, wenn R A {ĥ : Re ĥ < 0} gilt. Für ein beliebiges m-stufiges RKV gilt R(ĥ) = 1 + ĥb (I m ĥa) 1 e = 1 + j=1 ĥj b T A j 1 e. Besitzt das Verfahren die Ordnung p, so folgt R(ĥ) = p j=0 1 j!ĥj + j=p+1 ĥj b A j 1 e. Ist das RKV explizit, so folgt R(ĥ) = 1 + m j=1 ĥj b T A j 1 e. Insbesondere hängt der Stabilitätsbereich eines m-stufigen expliziten RKVs der Ordnung m (1 m 4) wegen R(ĥ) = m j=0 1 j!ĥj nicht von den Koeffizienten des Verfahrens ab. Außerdem besitzt kein explizites RKV einen unbeschränkten Stabilitätsbereich (denn R ist ein Polynom). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Absolute Stabilität TU Bergakademie Freiberg, SS 2010
53 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Verfahren dritter Ordnung von Heun 3 klassisches Rung Kutta Verfahren Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Absolute Stabilität TU Bergakademie Freiberg, SS 2010
54 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 171 Beim impliziten Euler-Verfahren ist R(ĥ) = 1 1 ĥ } so dass hier R A = {ĥ : 1 ĥ > 1 (Außengebiets des Kreises um 1 mit Radius 1) gilt. Bei der Trapezregel ist 1 + ĥ/2 R(ĥ) = 1 ĥ/2 so dass hier R A = {ĥ : Re ĥ < 0} (linke Halbebene) gilt. Beide Verfahren sind damit absolut stabil. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Absolute Stabilität TU Bergakademie Freiberg, SS 2010
55 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben verschiedene Aspekte des Phänomens Steifheit einer DG an Beispielen: Beispiel 1. Die beiden AWPe [ ] [ ] 2 1 y 2 sin t = y +, y(0) = 1 2 2(cos t sin t) [ ] [ ] 2 1 y 2 sin t = y +, y(0) = (cos t sin t) [ ] 2, (AWP 1 ) 3 [ ] 2, (AWP 2 ) 3 haben dieselbe Lösung Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
56 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 173 [ ] 2 y(t) = exp( t) 2 + [ ] sin t. cos t y y Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
57 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 174 Wir lösen beide Probleme für t [0, 10] mit der MATLAB-Routine ode45 (die ein eingebettetes RKV, das Verfahren von Dormand-Prince, verwendet, bei dem zwei RKV der Ordnungen 4 bzw. 5 kombiniert werden), wobei wir eine relative Toleranz von 0.01 vorgeben. 3 System 1: 64 Schritte (ode45) 3 System 2: Schritte (ode45) y 2 y y 1 y Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
58 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 175 Obwohl die exakte Lösung in beiden Fällen dieselbe ist, erfordert die Lösung von (AWP 2 ) etwa 200-mal mehr Aufwand als die von (AWP 1 ): AWP h min h max h Schritte (AWP 1 ) 2.27e e e-1 64 (AWP 2 ) 5.98e e e Lösen wir die beiden Probleme mit der MATLAB-Routine ode23tb (die die Trapezregel mit der Gear-Formel der Ordnung 2 kombiniert), so ergibt sich (relative Toleranz wie oben = 0.01): AWP h min h max h Schritte (AWP 1 ) 2.13e e e-1 19 (AWP 2 ) 2.13e e e-1 20 Beide Probleme werden ohne Schwierigkeiten gelöst. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
59 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge System 1: 19 Schritte (ode23tb) 3 System 2: 20 Schritte (ode23tb) y 2 y y 1 y Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
60 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 177 Die Unterschiede zwischen den beiden AWPen werden sichtbar, wenn wir alle Lösungen der zugehörigen Systeme betrachten. Im ersten Fall ergibt sich [ ] [ ] [ ] 1 1 sin t y = κ 1 exp( t) + κ 2 exp( 3t) +, 1 1 cos t während im zweiten Fall [ ] [ ] [ ] 1 1 sin t y = κ 1 exp( t) + κ 2 exp( 1000t) cos t die allgemeine Lösung ist. (Beide Systeme sind inhomogene lineare Systeme mit konstanten Koeffizienten, wobei die Eigenwerte der Koeffizientenmatrix im ersten Fall λ 1 = 1, λ 2 = 3 und im zweiten Fall λ 1 = 1, λ 2 = 1000 sind.) Die Lösungen der konkreten AWPe sind jeweils durch κ 1 = 2 und κ 2 = 0 (!) gegeben. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
61 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 178 In beiden Fällen ist die Lösung aus einem Gleichgewichtsanteil, nämlich [sin t, cos t], und einem transienten Anteil der Form exp(λ 1 t)a 1 + exp(λ 2 t)a 2 zusammengesetzt. Die Unterschiede liegen in der Geschwindigkeit, mit der der transiente Teil (für t ) verschwindet. Obwohl in der exakten Lösung der AWPe gar nicht erkennbar ist, wie schnell der abklingende Anteil verschwindet (κ 2 = 0), bestimmt sie die erforderliche Schrittweite. Würde man in (AWP 2 ) die AB in y(0) = [0, 1] ändern, so würde κ 1 = κ 2 = 0 folgen, d.h. der transiente Teil ist in der Lösung y(t) = [sin t, cos t] vollständig unsichtbar. Selbst dann wäre ode45 nur mit extrem kleiner Schrittweite in der Lage, die Aufgabe zu lösen. Wir betrachten die Stabilitätsbereiche R A : Für ode45 kann man zeigen, dass R A R [ 3, 0] (Stabilitätsintervall). Will man für (AWP 1 ) also λh R A (für alle Eigenwerte λ) garantieren, genügt es, h < 1 zu fordern (die durchschnittliche Schrittweite von h resultiert aus der geforderten Genauigkeit!). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
62 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 179 Dagegen muss für (AWP 2 ) h < gefordert werden, damit λh R A für alle λ folgt und es sind Stabilitätsprobleme, die zu der kleinen durchschnittlichen Schrittweite von h führen. Das Verfahren ode23tb ist absolut stabil, so dass hier λ h für alle h > 0 (in jedem der beiden Fälle (AWP 1 ) und (AWP 2 )) im Stabilitätsbereich liegt. Für y = Ay + b(t) heißt max Re λ / min Re λ λ Λ(A) λ Λ(A) Steifigkeitsquotient des linearen DG Systems. Ein lineares DG System mit konstanten Koeffizienten heißt steif, wenn seine Eigenwerte alle negativen Realteil besitzen und sein Steifigkeitsquotient groß ist. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
63 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 180 Um die Problematik dieser gebräuchlichen Definition zu erläutern, betrachten wir ein weiteres AWP (mit derselben Lösung): [ ] [ ] [ ] 2 1 y 2 sin t 2 = y +, y(0) =. (AWP 3 ) (cos t sin t) 3 Die Matrix dieses Systems besitzt die Eigenwerte λ 1 = 1, λ 2 = und sein Steifigkeitsquotient beträgt 1000 (wie bei (AWP 2 )). Trotzdem hat ode45 keine ernsten Probleme: AWP h min h max h Schritte (AWP 3 ) 1.19e e e-1 44 (ode45) (AWP 3 ) 1.25e e e-1 22 (ode23tb) Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
64 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 181 Ob ein System steif ist oder nicht kann also nicht immer aus dem Steifigkeitsquotienten abgelesen werden. Auch Definitionen wie ein System ist steif, wenn max Re λ groß ist (etwa max Re λ 1) sind natürlich wenig hilfreich (die Variablentransformation t 0.001t macht aus (AWP 2 ) ein Problem, das dieselbe Steifigkeit besitzt, bei dem aber max Re λ = 1 gilt). Pragmatische Definitionen für Steifigkeit sind: Ein System ist steif, wenn Stabilitätsanforderungen und nicht Genauigkeitsanforderungen die Größe der Schrittweite bestimmen. Ein System heißt steif, wenn gewisse Komponenten der Lösung sehr viel schneller abklingen als andere. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
65 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 182 Beispiel 2. Die Differentialgleichung y (t) = λ(y(t) g(t)) + g (t) ( ) besitzt die allgemeinen Lösung y(t) = γ exp(λt) + g(t) (γ R). Wir wählen g als glatte Funktion, z.b. g(t) = arctan t und λ = 10. Auch hier setzt sich die Lösung aus einem glatten (g(t) = Gleichgewichtsanteil) und einem schnell abklingenden Teil (γ exp(λt) = transienter Anteil) zusammen. Wir wählen die AB y(0) = 0 und approximieren die exakten Lösung y(t) = arctan t für t [0, 5] mit dem expliziten Euler-Verfahren (R A = {ĥ : ĥ + 1 < 1}) und dem impliziten Euler-Verfahren (R A = C \ {ĥ : ĥ 1 1}). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
66 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
67 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge h= h= h= Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
68 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge h= h= h= Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Steife Differentialgleichungen TU Bergakademie Freiberg, SS 2010
69 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Die Wärmeleitungsgleichung Problem. Die Temperatur u(x, t), 0 x π, in einem homogenen Stab mit konstantem Querschnitt habe zur Zeit t = 0 den Wert u(x, 0) = f(x). Der Stab sei wärmeisoliert außer an den Rändern x = 0 und x = π, wo die Temperatur konstant auf u(0, t) = u(π, t) = 0 gehalten wird (t > 0). Bestimme die Wärmeverteilung u(x, t ), 0 x π, im Stab zur Zeit t > 0. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
70 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 187 Mathematisches Modell. Energieerhaltungssatz und Fouriersches Gesetz (Jean-Baptiste-Joseph Fourier, ), Wärme fließt in Richtung abfallender Temperatur und zwar umso intensiver, je größer die Temperaturdifferenzen sind, führen auf die Aufgabe: Gesucht ist eine Funktion u : [0, π] [0, ) R, (x, t) u(x, t), die die folgenden Eigenschaften besitzt: u t (x, t) = γ2 2 u (x, t), x2 0 < x < π, t > 0 (WLG) mit einer Materialkonstanten γ( 1). Außerdem u(x, 0) = f(x), 0 x π, (Anfangsbedingung) (AB) Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
71 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 188 z.b. f(x) = 3 sin(x) sin(2x) + sin(3x), u(0, t) = u(π, t) = 0, t 0, (Randbedingungen). (RB) Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
72 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge Waerme Zeit Ort Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
73 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 190 (WLG) heißt Wärmeleitungsgleichung. Für komplizierte Anfangs- und Randbedingungen oder ortsabhängige Materialkonstanten kann man die Lösung solcher Probleme nicht explizit angeben. Es lässt sich jedoch beweisen, dass (WLG), (AB), (RB) auch dann ein sachgemäß gestelltes Problem (im Sinne von Jacques Salomon Hadamard ( )) ist: 1. Es besitzt eine Lösung. 2. Diese Lösung ist eindeutig. 3. Sie hängt stetig von den Daten (den Anfangs- und Randbedingungen) ab! Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
74 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 191 Diskretisierung durch finite Differenzen: Bestimme u nur noch auf den Linien (Linienmethode) Ω i = {(x i, t) : x i = ih und t 0}, i = 1, 2,..., n. Dabei ist h := π/(n + 1) die Schrittweite (Gitterweite) in x-richtung. Unsere Näherungen für u(x i, t) werden wir mit u i (t) : [0, ) R bezeichnen (wir wissen: u i (0) = f(x i )). Dazu müssen wir die partiellen Ableitungen 2 u/ x 2 aus (WLG) durch Ausdrücke annähern, die wir auf den Gitterlinien bestimmen können. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
75 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 192 Dazu betrachten wir zuerst eine Funktion in einer Variablen, f : R I = [α, β] R, x f(x), und nehmen an, dass f in x 0 I differenzierbar ist. Weil f (x 0 ) = lim h 0 f(x 0 + h) f(x 0 ) h gilt, liegt es nahe, f (x 0 ) etwa durch eine der drei Formeln f(x 0 + h) f(x 0 ) h (Vorwärtsdifferenz) (Vorw-Diff) f(x 0 ) f(x 0 h) h (Rückwärtsdifferenz) f(x 0 + h) f(x 0 h) (zentrale Differenz) 2h anzunähern. Dabei soll die Schrittweite h natürlich klein sein. (Rück-Diff) (Zent-Diff) Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
76 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 193 Die zweite Ableitung f (x 0 ) approximieren wir durch eine zentrale Differenz zweiter Ordnung f (x 0 ) f (x 0 + h) f (x 0 ) h f(x 0 +h) f(x 0 ) h f(x 0) f(x 0 h) h h = f(x 0 + h) 2f(x 0 ) + f(x 0 h) h 2. (Zent-Diff-2) Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
77 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 194 Diskretisierungsfehler: a) Ist f in I zweimal stetig differenzierbar, so gilt f(x 0 + h) f(x 0 ) h = f (x 0 ) + C 1 h mit C max x I f (x) (analog für Rückwärtsdifferenz). b) Ist f in I dreimal stetig differenzierbar, so gilt mit C max x I f (x). f(x 0 + h) f(x 0 h) 2h c) Ist f in I viermal stetig differenzierbar, so gilt = f (x 0 ) + C 3 h 2 f(x 0 + h) 2f(x 0 ) + f(x 0 h) h 2 = f (x 0 ) + C 4 h 2 mit C max x I f (4) (x). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
78 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 195 Analog bei partiellen Ableitungen, z.b.: und u u(x + h, t) u(x, t) (x, t) = x h + O(h) für h 0 2 u u(x + h, t) 2u(x, t) + u(x h, t) (x, t) = x2 h 2 + O ( h 2) für h 0. O (h p ) für h 0 (sprich: Groß O von h p ) ist eines der Landau-Symbole (Edmund Georg Hermann Landau, ) und wie folgt definiert: f(y) = O(g(y)) für y a : f(y)/g(y) ist beschränkt für y a. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
79 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 196 Also: Approximiere u 2 / x 2 (x, t 0 ) durch eine zentrale Differenz zweiter Ordnung. Für n = 4 ergibt sich dann (mit u 0 (t) = u 5 (t) 0). u 1(t) = u 0(t) 2u 1 (t) + u 2 (t) h 2, u 2(t) = u 1(t) 2u 2 (t) + u 3 (t) h 2, u 3(t) = u 2(t) 2u 3 (t) + u 4 (t) h 2, u 4(t) = u 3(t) 2u 4 (t) + u 5 (t) h 2. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
80 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 197 Alternativ: u (t) = 1 h 2 A 4u(t) mit A 4 = Bekannt sind die Anfangsbedingungen f(h) u(0) = f(2h) f(3h) f(4h). Es handelt sich also um ein AWP für ein System gdgn (semi-diskrete Form der Wärmeleitungsgleichung). Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
81 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 198 Explizites Euler-Verfahren (Leonhard Euler, ): Ziel: Berechne Näherungen u i,j für die Lösung u(ih, jk) von (WLG), (AB), (RB), wobei 1 i n, 1 j m. Bestimme u (0) := [u 1,0, u 2,0,..., u n,0 ] T = [f(x 1 ), f(x 2 ),..., f(x n )] T aus der gegebenen Anfangsbedingung. Für j = 1, 2,..., m berechne u (j) = [u 1,j, u 2,j,..., u n,j ] T durch u (j) = [I + τa n ] u (j 1). (5.6) Dabei bezeichnen I die (n n)-einheitsmatrix, τ = k/h 2, A n die Tridiagonalmatrix A n = tridiag(1, 2, 1) R n n (s.o.) und u (j) den Vektor, der die Näherungen für die Temperatur zur Zeit t = jk enthält. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
82 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 199 Für k = 1/11, h = π/30: 10 8 Temperatur Zeit Ort Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
83 Numerische Mathematik für ingenieurwissenschaftliche Studiengänge 200 Die folgende Tabelle zeigt, dass man für kleinere Werte von k sogar noch unsinnigere Werte erhält. Erst wenn die Zeitschrittweite k winzig ist, ergeben sich brauchbare Näherungen. k u(7h, 1) u(14h, 1) u(21h, 1) u(28h, 1) 1/ / / / / / (h = π/30, k = 0 bedeutet hier, dass es sich bei den zugehörigigen u-werten um die Funktionswerte der exakten Lösung handelt.) Anfangswertprobleme bei gewöhnlichen Differentialgleichungen Die Wärmeleitungsgleichung TU Bergakademie Freiberg, SS 2010
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
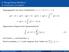 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
5 Steife Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif,
Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif,
5. Steife Differentialgleichungen 5.1 Was sind steife Differentialgleichungen?
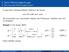 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG
5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
1 Einführung und Begriffe
 Numerische Mathematik 5 1 Einführung und Begriffe 1.1 Mathematische Modellbildung und numerische Simulation am Beispiel eines Wasserkreislaufs Simulation ist die Nachbildung eines dynamischen Prozesses
Numerische Mathematik 5 1 Einführung und Begriffe 1.1 Mathematische Modellbildung und numerische Simulation am Beispiel eines Wasserkreislaufs Simulation ist die Nachbildung eines dynamischen Prozesses
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
3. Lineare Mehrschrittverfahren 3.1 Begriffe
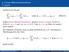 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
9 Numerische Verfahren für Anfangswertaufgaben
 Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
1 Einführung und Begriffe
 Numerik 4 1 Einführung und Begriffe 1.1 Mathematische Modellbildung und numerische Simulation am Beispiel eines Wasserkreislaufs 1.2 Linearisierung und Iterationsverfahren am Beispiel des Newton-Verfahrens
Numerik 4 1 Einführung und Begriffe 1.1 Mathematische Modellbildung und numerische Simulation am Beispiel eines Wasserkreislaufs 1.2 Linearisierung und Iterationsverfahren am Beispiel des Newton-Verfahrens
Gewöhnliche Differentialgleichungen Woche 7. Nicht-lineare und linearisierte Systeme
 Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Lösung - Schnellübung 13
 D-MAVT/D-MATL Analysis II FS 7 Dr. Andreas Steiger Lösung - Schnellübung 3. Gegeben sei die Differentialgleichung y + λ 4 y + λ y = 0. Für welche Werte des reellen Parameters λ gibt es eine von Null verschiedene
D-MAVT/D-MATL Analysis II FS 7 Dr. Andreas Steiger Lösung - Schnellübung 3. Gegeben sei die Differentialgleichung y + λ 4 y + λ y = 0. Für welche Werte des reellen Parameters λ gibt es eine von Null verschiedene
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
11. Einschrittverfahren
 H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 11. Einschrittverfahren Es geht in diesem Abschnitt um die numerische Lösung einer AWA y (t) = f(t, y(t)), y(t 0 ) = y 0. (11.1) Aufgabe
Serie 13: Online Test
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
4 Runge-Kutta-Verfahren
 Numerik gewöhnlicher Differentialgleichungen 43 4 Runge-Kutta-Verfahren 4. Konstruktion Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0
Numerik gewöhnlicher Differentialgleichungen 43 4 Runge-Kutta-Verfahren 4. Konstruktion Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Numerik II Numerik Elliptischer Differentialgleichungen
 Numerik II 207 12 Numerik Elliptischer Differentialgleichungen 12 Numerik Elliptischer Differentialgleichungen TU Bergakademie Freiberg, SS 2010 Numerik II 208 12.1 Die Laplace-Gleichung in einem Quadrat
Numerik II 207 12 Numerik Elliptischer Differentialgleichungen 12 Numerik Elliptischer Differentialgleichungen TU Bergakademie Freiberg, SS 2010 Numerik II 208 12.1 Die Laplace-Gleichung in einem Quadrat
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung (
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung (
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Klausurenkurs zum Staatsexamen (SS 2015): Differential und Integralrechnung 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2015): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung ( y
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2015): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung ( y
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Klausur: Differentialgleichungen Version mit Lösungen
 Universität Kassel Fachbereich 10/16 Dr. Sebastian Petersen 16.03.2016 Klausur: Differentialgleichungen Version mit Lösungen Name: Vorname: Matrikelnummer: Versuch: Unterschrift: Bitte fangen Sie für jede
Universität Kassel Fachbereich 10/16 Dr. Sebastian Petersen 16.03.2016 Klausur: Differentialgleichungen Version mit Lösungen Name: Vorname: Matrikelnummer: Versuch: Unterschrift: Bitte fangen Sie für jede
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Rheinisch-Westfälische Technische Hochschule. Gegeben seien eine gewöhnliche Dierentialgleichung (DGL) und ein Anfangswert. γ l K l.
 Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung (
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 8 8.1 (Herbst 2012, Thema 2, Aufgabe 5) Bestimmen Sie die allgemeine Lösung der Differentialgleichung (
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Analysis II. 8. Klausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis II 8. Klausur mit en 1 2 Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Eine Metrik auf einer Menge M. 2) Die Kurvenlänge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis II 8. Klausur mit en 1 2 Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Eine Metrik auf einer Menge M. 2) Die Kurvenlänge
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Übungen zu Differentialgleichungen (WiSe 12/13)
 Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
i j m f(y )h i h j h m
 10 HÖHERE ABLEITUNGEN UND ANWENDUNGEN 56 Speziell für k = 2 ist also f(x 0 + H) = f(x 0 ) + f(x 0 ), H + 1 2 i j f(x 0 )h i h j + R(X 0 ; H) mit R(X 0 ; H) = 1 6 i,j,m=1 i j m f(y )h i h j h m und passendem
10 HÖHERE ABLEITUNGEN UND ANWENDUNGEN 56 Speziell für k = 2 ist also f(x 0 + H) = f(x 0 ) + f(x 0 ), H + 1 2 i j f(x 0 )h i h j + R(X 0 ; H) mit R(X 0 ; H) = 1 6 i,j,m=1 i j m f(y )h i h j h m und passendem
Mathematische Grundlagen
 G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 23
 Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
Übungen zu gewöhnlichen Differentialgleichungen Lösungen zu Übung 3 3.1 Gegeben sei die Anfangswertaufgabe (AWA) Zeigen Sie, dass die Funktion y (x) = x y(x) mit y(0) = 1 die einzige Lösung dieser AWA
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
1 Einführung, Terminologie und Einteilung
 Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Zusammenfassung Kapitel V: Differentialgleichungen 1 Einführung, Terminologie und Einteilung Eine gewöhnliche Differentialgleichungen ist eine Bestimmungsgleichung um eine Funktion u(t) einer unabhängigen
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei die Matrix
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei die Matrix 1 1 1 A = 3 3 3 2 2 2 (a) Bestimmen Sie Rang(A), Kern(A) und Bild(A). Ist A invertierbar? Geben Sie zwei verschiedene rechte Seiten b 1, b 2 an, so
Lösung Semesterendprüfung
 MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
Fachbereich Mathematik/Informatik 16. Juni 2012 Prof. Dr. H. Brenner. Mathematik für Anwender II. Testklausur mit Lösungen
 Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Numerische Simulation mit finiten Elementen. O. Rheinbach
 Numerische Simulation mit finiten Elementen O. Rheinbach Numerische Simulation mit finiten Elementen INHALT 0.1 Finite Differenzen in 2D 1. Einleitung 1.1 Vorbemerkungen 1.2 Rand- und Anfangswertaufgaben
Numerische Simulation mit finiten Elementen O. Rheinbach Numerische Simulation mit finiten Elementen INHALT 0.1 Finite Differenzen in 2D 1. Einleitung 1.1 Vorbemerkungen 1.2 Rand- und Anfangswertaufgaben
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Lösungsvorschlag zur Nachklausur zur Analysis
 Prof Dr H Garcke, D Depner SS 09 NWF I - Mathematik 080009 Universität Regensburg Lösungsvorschlag zur Nachklausur zur Analysis Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz und berechnen Sie
Prof Dr H Garcke, D Depner SS 09 NWF I - Mathematik 080009 Universität Regensburg Lösungsvorschlag zur Nachklausur zur Analysis Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz und berechnen Sie
KARLSRUHER INSTITUT FÜR TECHNOLOGIE Institut für Analysis
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE Institut für Analysis Höhere Mathematik III für die Fachrichtung Elektro- und Informationstechnik D. A MR Frühjahr 2014 T R, M.S. 06.03.2014 Bachelor-Modulprüfung Aufgabe
KARLSRUHER INSTITUT FÜR TECHNOLOGIE Institut für Analysis Höhere Mathematik III für die Fachrichtung Elektro- und Informationstechnik D. A MR Frühjahr 2014 T R, M.S. 06.03.2014 Bachelor-Modulprüfung Aufgabe
Analysis II. Aufgaben zum Stoff der Analysis I und II Lösungsvorschlag
 Prof Dr H Garcke, D Depner SS 9 NWF I - Mathematik 1979 Universität Regensburg Aufgabe 1 Analysis II Aufgaben zum Stoff der Analysis I und II Lösungsvorschlag i Erinnern Sie sich an die Konvergenzkriterien
Prof Dr H Garcke, D Depner SS 9 NWF I - Mathematik 1979 Universität Regensburg Aufgabe 1 Analysis II Aufgaben zum Stoff der Analysis I und II Lösungsvorschlag i Erinnern Sie sich an die Konvergenzkriterien
12 Gewöhnliche Differentialgleichungen
 12 Gewöhnliche Differentialgleichungen 12.1 Der Satz von Picard-Lindelöf 12.1.1 Definition (Explizite Differentialgleichung erster Ordnung) Ω 1 R, Ω 2 R n seien offen und f : Ω 1 Ω 2 R n, (x,y) f (x,y)
12 Gewöhnliche Differentialgleichungen 12.1 Der Satz von Picard-Lindelöf 12.1.1 Definition (Explizite Differentialgleichung erster Ordnung) Ω 1 R, Ω 2 R n seien offen und f : Ω 1 Ω 2 R n, (x,y) f (x,y)
Gewöhnliche Differentialgleichungen Woche 6. Existenz nach Picard-Lindelöf
 d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen Aufgaben für das Seminar und zum selbständigen Üben 22. Januar 2018 Vorbereitende Übungen Aufgabe 1: Bestimmen Sie die Isoklinen zu den folgenden Differentialgleichungen
Gewöhnliche Differentialgleichungen Aufgaben für das Seminar und zum selbständigen Üben 22. Januar 2018 Vorbereitende Übungen Aufgabe 1: Bestimmen Sie die Isoklinen zu den folgenden Differentialgleichungen
7. Die eindimensionale Wärmeleitungsgleichung
 H.J. Oberle Differentialgleichungen II SoSe 2013 7. Die eindimensionale Wärmeleitungsgleichung Als Beispiel für eine parabolische PDG betrachten wir die eindimensionale Wärmeleitungsgleichung u t (x, t)
H.J. Oberle Differentialgleichungen II SoSe 2013 7. Die eindimensionale Wärmeleitungsgleichung Als Beispiel für eine parabolische PDG betrachten wir die eindimensionale Wärmeleitungsgleichung u t (x, t)
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Serie 13. Analysis D-BAUG Dr. Cornelia Busch FS 2016
 Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8 8.1 (Herbst 2002, Thema 1, Aufgabe 6) y = 3y +2x x 8.2 (Frühjahr 2005, Thema 1, Aufgabe 6) (x > 0) y(1)
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8 8.1 (Herbst 2002, Thema 1, Aufgabe 6) y = 3y +2x x 8.2 (Frühjahr 2005, Thema 1, Aufgabe 6) (x > 0) y(1)
u(x, 0) = g(x) : 0 x 1 u(0, t) = u(1, t) = 0 : 0 t T
 8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Kapitel L. Gewöhnliche Differentialgleichungen
 Kapitel L Gewöhnliche Differentialgleichungen Inhalt dieses Kapitels L000 1 Erste Beispiele von Differentialgleichungen 2 Exakte Differentialgleichungen 3 Fazit: Existenz, Eindeutigkeit, Lösungsmethoden
Kapitel L Gewöhnliche Differentialgleichungen Inhalt dieses Kapitels L000 1 Erste Beispiele von Differentialgleichungen 2 Exakte Differentialgleichungen 3 Fazit: Existenz, Eindeutigkeit, Lösungsmethoden
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
9 Lineare Differentialgleichungen
 $Id: lineartex,v 3 //8 ::37 hk Exp hk $ 9 Lineare Differentialgleichungen 9 Homogene lineare Differentialgleichungen Wir beschäftigen uns gerade mit den homogenen linearen Differentialgleichungen, also
$Id: lineartex,v 3 //8 ::37 hk Exp hk $ 9 Lineare Differentialgleichungen 9 Homogene lineare Differentialgleichungen Wir beschäftigen uns gerade mit den homogenen linearen Differentialgleichungen, also
Zweite Prüfung zur Vorlesung
 Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Skript zur Vorlesung Analysis 3
 Skript zur Vorlesung Analysis 3 Herbstsemester 204 Prof. Benjamin Schlein Inhaltsverzeichnis Gewöhnliche Differentialgleichungen 2. Differentialgleichungen erster Ordnung, elementare Lösungsmethoden..
Skript zur Vorlesung Analysis 3 Herbstsemester 204 Prof. Benjamin Schlein Inhaltsverzeichnis Gewöhnliche Differentialgleichungen 2. Differentialgleichungen erster Ordnung, elementare Lösungsmethoden..
Analysis 4. Lösungsvorschlag zum 12. Übungsblatt
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Andreas Geyer-Schulz SS 208. Juli 208 Analysis 4 Lösungsvorschlag zum 2. Übungsblatt Aufgabe 42 Wir untersuchen
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Andreas Geyer-Schulz SS 208. Juli 208 Analysis 4 Lösungsvorschlag zum 2. Übungsblatt Aufgabe 42 Wir untersuchen
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
(Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
Differentialgleichungen
 Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Differentialgleichungen
 Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: b a 2 3a 1
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Öffnen Sie den Klausurbogen erst nach Aufforderung! Mathematische Grundlagen III (CES) SS 2017 Klausur
 Prof. Dr. Martin Frank Prof. Dr. Martin Grepl Öffnen Sie den Klausurbogen erst nach Aufforderung! Zugelassene Hilfsmittel: Mathematische Grundlagen III (CES) SS 2017 Klausur 01.09.2017 Dokumentenechtes
Prof. Dr. Martin Frank Prof. Dr. Martin Grepl Öffnen Sie den Klausurbogen erst nach Aufforderung! Zugelassene Hilfsmittel: Mathematische Grundlagen III (CES) SS 2017 Klausur 01.09.2017 Dokumentenechtes
Analysis III. Teil I. Rückblick auf das letzte Semester. Themen aus dem SS Inhalt der letzten Vorlesung aus dem SS.
 Analysis III für Studierende der Ingenieurwissenschaften Technische Universität Hamburg-Harburg Reiner Lauterbach Teil I Rückblick auf das letzte Semester Fakultät für Mathematik, Informatik und Naturwissenschaften
Analysis III für Studierende der Ingenieurwissenschaften Technische Universität Hamburg-Harburg Reiner Lauterbach Teil I Rückblick auf das letzte Semester Fakultät für Mathematik, Informatik und Naturwissenschaften
(a), für i = 1,..., n.
 .4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
.4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
Höhere Mathematik III für die Fachrichtung Physik Wintersemester 2016/17. Lösungsvorschlag zu Übungsblatt 5
 Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Numerische Mathematik I: Grundlagen
 Numerische Mathematik I: Grundlagen 09.10.2017 Inhalt der Lehrveranstaltung Inhaltlich sollen Sie in der Lehrveranstaltung Numerische Mathematik I insbesondere vertraut gemacht werden mit der Numerik linearer
Numerische Mathematik I: Grundlagen 09.10.2017 Inhalt der Lehrveranstaltung Inhaltlich sollen Sie in der Lehrveranstaltung Numerische Mathematik I insbesondere vertraut gemacht werden mit der Numerik linearer
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
