4 Numerik von Anfangswertaufgaben

Transkript

1 4 Numerik von Anfangswertaufgaben Diese Einführung behandelt numerische Lösungsverfahren für gewöhnliche, explizite Differentialgleichungen. Ordnung. Im Folgenden wird die Variable t R die Zeit und x R n den Zustand der Dimension n N + bezeichnen. Eine gewöhnliches, implizites Differentialgleichungssystem m-ter Ordnung mit r Gleichungen lässt sich in der Form F t, y, ẏ,..., y m)) = 0, yt 0 ) = y 0, ẏt 0 ) = ẏ 0,..., y m ) t 0 ) = y m ) 0, 4.) mit y R r und den Anfangsbedingungen y 0, ẏ 0,..., y m ) 0 zum Startzeitpunkt t 0 angeben. Dabei ist F ) ) eine auf der Menge Θ R R r definierte Abbildung F ) : Θ R r. Ist F ) invertierbar, erhält man eine explizite Darstellung y m) Mit der Einführung des Zustandsvektors x T = y m) = F t, y, ẏ,..., y m )). 4.2) [ y T ẏ T... sich schlussendlich eine explizite Zustandsdarstellung. Ordnung y m )) T ] R n ergibt d dt x = ft, x), xt 0) = x ) Dabei ist die rechte Seite der Differentialgleichung ft, x) eine auf der Menge Ω R R n definierte Abbildung f ) : Ω R n mit n = mr. Die Menge Ω heißt erweiterter Zustandsraum. Darüber hinaus wird stets vorausgesetzt, dass t 0, x 0 ) Ω gilt. Beispiel 4.. Die Bewegungsgleichungen eines Starrkörpers, d. h. sind in der Form 4.) Dq) q + Cq, q) q + gq) = τt), 4.4) Ft, q, q, q) = 0 4.5) als Differentialgleichungssystem 2. Ordnung m = 2) bestehend ] aus r Gleichungen gegeben. Führt man den Zustandsvektor x T = [q T q T ein, und ist q ) ) F =

2 4 Numerik von Anfangswertaufgaben Seite 6 Dq) invertierbar für alle q, so ergibt sich die explizite Zustandsdarstellung d dt x = q D q) Cq, q) q + gq) τt) ). 4.6) Die Lösung von 4.3) kann allgemein wie folgt definiert werden: Definition 4.. Sei J R ein nicht leeres Intervall mit t 0 J. Eine Abbildung xt) C J) ) n heißt Lösung des Anfangswertproblems genau dann, wenn und xt 0 ) = x 0 gilt. d dt xt) = f t, xt) ) für alle t J 4.7) Für die spätere numerische Lösung ist folgendes Lemma von großer Bedeutung: Lemma 4.. Eine Funktion xt) ist genau dann eine stetig differenzierbare Lösung des Anfangswertproblems 4.3) mit der Anfangsbedingung x 0, wenn sie der Integralgleichung genügt. t xt) = x 0 + f τ, xτ) ) dτ 4.8) t 0 Für den Beweis sei auf die am Ende des Skriptes angeführte Literatur verwiesen. Das Lemma 4. ergibt sich als einfache Folgerung aus dem Hauptsatz der Differential- und Integralrechnung und liefert die Äquivalenz von Anfangswertproblem und Integralgleichung. Das numerische Lösen der Anfangswertaufgabe 4.3) kann damit auf eine numerische Integration zurückgeführt werden. Viele der im Folgenden angeführten numerischen Verfahren für Anfangswertprobleme können mit Verfahren zur numerischen Integration Quadraturformeln) in Verbindung gebracht werden. Zudem besagt das Lemma 4., dass wenn eine stetige Funktion xt) die Integralgleichung 4.8) mit stetigem f ) erfüllt, dieses xt) automatisch stetig differenzierbar ist. Autonome Systeme Ein Spezialfall von 4.3) tritt auf, wenn die rechte Seite der Differentialgleichung nicht explizit von der Zeit abhängt. Man spricht dann von einem autonomen Anfangswertproblem, andernfalls von einem nichtautonomen Anfangswertproblem. Nichtautonome Systeme der Form 4.3) können in ein autonomes System transformiert werden, indem für die Zeit ein neuer Zustand x n+ = t eingeführt wird und das System 4.3) um f n+ = erweitert wird.

3 4 Numerik von Anfangswertaufgaben Seite 62 Lösungseigenschaften Die Lösung einer nichtlinearen Differentialgleichung 4.3) kann formal in der Form xt) = Φ t0,tx 0 ) 4.9) angegeben werden. Die zweiparametrige Familie Φ t0,t ) von im Allgemeinen nichtlinearen Abbildungen heißt Evolution der Differentialgleichung d dt xt) = f t, xt) ), xt 0 ) = x 0. Die Evolution erfüllt für t 0, x 0 ) Ω offensichtlich folgende Eigenschaften: i.) Φ t,t x) = x 4.0a) ii.) Φ σ,t Φs,σ x) ) = Φ s,t x) 4.0b) ) iii.) h Φ ) ) t,t+h x = f t, x 4.0c) Für autonome Differentialgleichungen ist die Startzeit t 0 beliebig. Man schreibt daher kurz Φ t ) anstatt von Φ t0,t ) und bezeichnet Φ t ) als Fluss. Eine spezielle Lösungskurve nennt man dann Trajektorie. Taylorentwicklung und Landau-Symbol Im Folgenden wird mehrfach von der Taylorentwicklung einer analytischen Funktion Gebrauch gemacht werden. Satz 4.. Es gibt zu jeder vektorwertigen Funktion fx δ ) : Ω R n, die k-fach stetig differenzierbar in x δ ist, eine Taylorentwicklung in x der Form fx + δx) = k j=0 h=0 ) j j! x j f x)δx j + o δx ) für δx 0, 4.) δ wobei die Punkte x sowie x δ = x + δx mitsamt ihrer Verbindungsstrecke in Ω liegen. Für den Beweis sei auf die angeführte Literatur verwiesen. Das kleine Landau-Symbol o ) wird verwendet, ) um anzudeuten, dass das Restglied vernachlässigbar klein gegenüber f x)δx j ist. Äquivalent schreibt man auch z.b. für k = 2 kj=0 j! j x j δ ) fx + δx) = fx) + f x)δx + ) 2 x δ 2 xδ 2 f x)δx 2 + O δx 3 ) für δx ) Das große Landau-Symbol O ) wird hierbei verwendet, um das asymptotische Verhalten bei Annäherung an einen endlichen oder unendlichen Grenzwert zu beschreiben. Für die Norm des Approximationsfehlers r = O δx 3 ) gilt folglich r C δx 3 für ein hinreichend kleines δx > 0, wobei C eine Konstante ist. Mit der Konstanten C wird somit 6 3 x 3 δ ) f x) abgeschätzt.

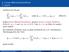
4 4 Numerik von Anfangswertaufgaben Seite 63 Newton-Verfahren Eine Möglichkeit, ein nichtlineares ] Gleichungssystem der Form γξ) = 0 r mit γξ) : R r R r und ξ T = [ξ... ξ r, zu lösen, besteht in der Anwendung des sogenannten Newton-Raphson-Simpson-)Verfahrens. Dazu wird angenommen, dass γξ) zumindest - fach stetig differenzierbar in ξ ist. Führt man für γξ) eine Taylorentwicklung im Punkt ξ l mit ξ = ξ l + δξ durch, so erhält man γξ) = γ ξ l) + Bricht man 4.3) nach dem linearen Glied ab und fordert γ ξ γ ) ξ l) ξ ξ l) + O δξ 2 ). 4.3) ξ l+) = 0 r, so ergibt sich ξ l+ = ξ l + d l, l = 0,, 2, a) mit der sogenannten Newton-Richtung d l, welche Lösung des linearen Gleichungssystems ) ξ γ ξ l) d l = γ ξ l) 4.4b) ist. Die Newton-Iteration 4.4) wird dabei solange ausgeführt, bis eine vorzugebende Toleranz TOL erreicht wird, d. h. ξ l+ ξ l TOL 4.5) gilt. Anhand des Newton-Verfahrens wird dementsprechend die numerische Lösung eines nichtlinearen Gleichungssystems auf eine iterative Lösung reduziert, für welche mehrere lineare Gleichungssysteme gelöst werden müssen. Das Newton-Verfahren gehört dabei zur Klasse der Fixpunktiterationen und man kann zeigen, dass das Verfahren für Startwerte ξ 0, die hinreichend ) nahe von ξ sind, mindestens quadratisch konvergent ist. Die Ableitung ξ γ ξ) kann auch anhand von finiten Differenzen approximiert werden. Mit dem zentralen Differenzenquotienten erhält man z.b. ) γ ξ) γξ + he i) γξ he i ), i =,..., r, 4.6) ξ i 2h wobei h eine geeignete Schrittweite und e i der i-te Einheitsvektor ist. Beim sogenannten vereinfachten Newton-Verfahren wird zudem die Newton-Richtung gemäß 4.4b) nur für l = 0 bestimmt und in allen Iterationen 4.4a) verwendet. Polynominterpolation Gegeben sind s + voneinander verschiedene Wertepaare t j, x j ), j = 0,,..., s, t j t i i j. Gesucht ist ein Polynom s-ten Grades p s t) mit der Basisdarstellung s p s t) = a j φ j, 4.7) j=0

5 4. Existenz und Eindeutigkeit Seite 64 den konstanten Koeffizienten a 0,..., a s und den Basisfunktionen φ 0,..., φ s, welche die Interpolationsbedingungen p s t j ) = x j, j = 0,,..., s 4.8) erfüllt. Für die Basis {φ 0 =, φ = t,..., φ s = t s } erhält man anhand von 4.8) ein lineares Gleichungssystem für die Koeffizienten a 0,..., a s. Lagrange-Interpolation Die Polynominterpolation lässt sich auch geschickt mithilfe sogenannter Lagrange-Polynome formulieren. Dazu verwendet man als Basisfunktionen s + Lagrange-Polynome der Form l j t) = s i=0 i j t t i t j t i = t t 0 t j t 0 t t j t j t j t t j+ t j t j+ t t s t j t s, 4.9a) 4.9b) womit sich das Interpolationspolynom direkt zu s p s t) = x j l j t) 4.20) j=0 ergibt. Das Interpolationspolynom p s t) erfüllt 4.8), da l j t k ) = { für j = k 0 für j k 4.2) gilt. 4. Existenz und Eindeutigkeit Dass die Lösung einer Differentialgleichung nicht eindeutig sein muss, zeigt folgendes Beispiel. Beispiel 4.2. Hierzu betrachte man die Differentialgleichung Man überzeugt sich leicht, dass d dt x = x/3, x0) = x 0 = ) xt) = a) ) 2t 3/2 xt) = b)

6 4.2 Einfluss von Störungen Seite 65 Lösungen von 4.22) sind. Obwohl die rechte Seite der Differentialgleichung stetig ist, ist die Lösung nicht eindeutig. Tatsächlich garantiert die Stetigkeit die Existenz einer Lösung, für die Eindeutigkeit werden jedoch weitere Bedingungen benötigt. Satz 4.2 Lokale Existenz und Eindeutigkeit). Es sei ft, x) stückweise stetig in t und genüge der Abschätzung Lipschitz-Bedingung) ft, x) ft, z) L x z, 0 < L < 4.24) für alle x, z B = {x R n x x 0 r} und alle t [t 0, t 0 + δ]. Dann existiert ein δ > 0 so, dass d dt x = ft, x), xt 0) = x ) genau eine Lösung für t [t 0, t 0 + δ] besitzt. Man sagt dann auch, die Funktion ft, x) ist lokal Lipschitz auf B R n. Gilt die Bedingung 4.24) sogar im gesamten R n, dann bezeichnet man die Funktion ft, x) als global Lipschitz. Für eine skalare Funktion fx) : R R, die nicht explizit von der Zeit t abhängt, kann die Bedingung 4.24) in der Form fx) fz) x z L 4.26) angeschrieben werden. Die Bedingung 4.26) erlaubt eine sehr einfache grafische Interpretation, nämlich die, dass die Funktion fx) keine Steigung besitzen darf, die größer als L ist. Daher sind Funktionen fx), die an einem Punkt eine unendliche Steigung aufweisen wie die Funktion x /3 von 4.22) am Punkt x = 0) sicher nicht lokal Lipschitz. Dies impliziert natürlich auch, dass unstetige Funktionen fx) am Punkt der Unstetigkeitsstelle die Lipschitz-Bedingung 4.26) nicht erfüllen. Dieser Zusammenhang zwischen der Lipschitz-Bedingung und der Beschränktheit von x )x) f wird im folgenden Satz ohne Beweis verallgemeinert: Satz 4.3 Lipschitz-Bedingung und Stetigkeit). Sind die Funktion ft, x) von 4.25) und x )t, f x) auf der Menge [t 0, t 0 + δ] B mit B R n stetig, dann erfüllt ft, x) lokal die Lipschitz-Bedingung von 4.24) mit einer Konstanten L, die gleich einer oberen Schranke für x )t, f x) auf B ist, d. h. es gilt L = sup x )t, f x). 4.27) x B 4.2 Einfluss von Störungen Wir werden uns zunächst mit der Frage beschäftigen, wie sich Störungen des Problems auf die Lösung auswirken. Prinzipiell können zwei Fehler unterschieden werden, nämlich

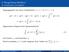
7 4.2 Einfluss von Störungen Seite 66 Eingabefehler und Fehler verursacht durch den Algorithmus. Die Wirkung von Eingabefehlern wird durch die Kondition des Problems beschrieben. Im folgenden Abschnitt steht daher die Kondition des Anfangswertproblems im Mittelpunkt. Es wird gezeigt, wie Störungen in den Anfangswerten, in der rechten Seite und in möglichen Parametern die Lösung beeinflussen. Satz 4.4 Störungen der Anfangsbedingungen). Falls die Funktion ft, x) von 4.3) der Lipschitz-Bedingung 4.24) genügt, gilt für zwei Lösungen xt) und zt) mit den Anfangsbedingungen xt 0 ) = x 0, zt 0 ) = z 0 die Abschätzung xt) zt) x 0 z 0 e L t t ) Beweis. Anhand von d dt x = ft, x) und d dtz = ft, z) folgt durch Integration und damit t xt) zt) = xt 0 ) zt 0 ) + fτ, x) fτ, z))dτ t ) xt) zt) }{{} mt) t xt 0 ) zt 0 ) +L }{{} m 0 Aufgrund der Stetigkeit von mt) folgt, dass die Hilfsgröße qt) = e Lt t stetig differenzierbar ist. Es gilt dementsprechend xτ) zτ) dτ. 4.30) t 0 }{{} mτ) t 0 mτ)dτ 4.3) mt) = d dt e Lt qt) ) = Le Lt qt) + e Lt qt) 4.32) und damit ergibt sich nach Einsetzen von 4.30) in Kombination mit 4.3) bzw. liefert die Integration über das Intervall [t 0, t] qt) m 0 e Lt 4.33) qt) m 0 e Lt 0 e Lt L. 4.34) Eingesetzt in 4.32) folgt schließlich mt) m 0 e Lt t 0). 4.35) Die Integration in die Vergangenheit liefert ein analoges Ergebnis, womit die Gültigkeit von 4.28) gezeigt ist.

8 4.3 Parameterabhängige Differentialgleichungen Seite 67 Dem Beweis von Satz 4.4 liegt eine vereinfachte Fassung des Lemmas von Gronwall zugrunde, das eine wichtige Rolle bei verschiedenen Abschätzungen spielt. In der vollständigen Fassung lautet es: Lemma 4.2 Gronwall). Sei J R ein nicht leeres Intervall mit t 0 J und ρ, ε, L [0, ). Ferner sei mt) : J [0, ) stetig und erfülle Dann gilt die Abschätzung t mt) ρ + εt t 0 ) + L mτ)dτ. t ) mt) ρ e L t t 0 + ε L Für den Beweis sei auf die angeführte Literatur verwiesen. ) e L t t ) Mit dem Lemma von Gronwall kann man die Abschätzung über die Auswirkung von Störungen in den Anfangswerten erweitern. Erfüllt ft, x) die Lipschitz-Bedingung 4.24) und sei x eine exakte Lösung und z eine approximative Lösung, die eine Störung δt) aufweist, d. h. es gilt d z = ft, z) + δt), δt) ε. 4.38) dt Mit mt) := xt) zt) und ρ := xt 0 ) zt 0 ) = x 0 z 0 sind die obigen Voraussetzungen erfüllt, denn es gilt und damit t t xt) zt) = xt 0 ) zt 0 ) δτ)dτ + t 0 fτ, x) fτ, z)dτ t ) t xt) zt) x 0 z 0 + εt t 0 ) + L xτ) zτ) dτ. t ) Anwendung des Gronwallschen Lemmas liefert nunmehr xt) zt) x 0 z 0 e L t t 0 + ε L ) e L t t0 4.4) als Verallgemeinerung von Satz 4.4. Hierbei beinhaltet der zweite Term die Auswirkungen der Störung. Für eine große Lipschitz-Konstante wächst e Lt t 0) sehr schnell und 4.4) stellt eine sehr konservative Abschätzung dar. Ein Anfangswertproblem ist also dann schlecht konditioniert, wenn die zugehörige Lipschitz-Konstante groß ist. 4.3 Parameterabhängige Differentialgleichungen Anfangswertprobleme beinhalten meist eine Reihe von Parametern. Es stellt sich dabei die Frage, wie sich Störungen in den Parametern auf die Lösung auswirken. Den Einfluss

9 4.3 Parameterabhängige Differentialgleichungen Seite 68 dieser Parameter auf die Lösung soll im Folgenden untersucht werden. Es wird dazu die parameterabhängige Differentialgleichung d dt x = ft, x, p), xt 0) = x ) ] mit dem Parametervektor p T = [p... p d R d betrachtet. Die partiellen Ableitungen x ) ) f sowie p ) ) f seien stetig in einer Umgebung der Lösungskurve von 4.42). Als Sensitivität bzw. Sensitivitätsmatrix) bezeichnet man die partielle Ableitung der Lösung nach dem Parametervektor, d. h. Sx) := mit den Matrixelementen S ij ) der Form p x ) t, p) 4.43) x j t, p i + δp i ) x j t, p i ) S ij x) = lim 4.44) δp i 0 δp i für i =,..., d und j =,..., n. Die Sensitivität kann als Lösung einer Differentialgleichung charakterisiert werden. Dazu betrachte man eine Lösung x δ = x + δx zum Parameter p δ = p + δp in der Form d dt x δ = ft, x δ, p δ ), x δ t 0 ) = x ) Eine Taylorentwicklung von ft, x, p) in p und x ergibt ) ) ft, x + δx, p + δp) = ft, x, p) + f t, x, p)δx + f t, x, p)δp x δ p δ + o δx ) + o δp ). Bildet man die Differenz aus 4.46) mit 4.42) und 4.45), so folgt ) ) d dt x δ x) = f t, x, p)δx + f t, x, p)δp x δ p δ + o δx ) + o δp ). 4.46) 4.47) Die Differenz der beiden Lösungen kann über die Differenz der Parametervariation δp = p δ p beliebig klein gemacht werden. Im Grenzfall δp 0 folgt aus 4.47) mithilfe von 4.43) die Sensitivitätsdifferentialgleichung ) ) d dt S = x f t, x, p)s + p f t, x, p), St 0, p) = )

10 4.3 Parameterabhängige Differentialgleichungen Seite 69 Anhand der Taylorentwicklung ist es nun möglich, für kleine Änderungen δp des Parametervektors vom nominellen Wert p die Lösung x δ t, p + δp) von 4.45) in folgender Form ) x δ t, p + δp) = xt, p) + x δ t, p)δp + o δp ) 4.49) p δ anzugeben und für δxt) = x δ t, p + δp) xt, p) gilt die Beziehung δxt) = St)δp. 4.50) Da St) offensichtlich den Einfluss von Parameterfehlern δp auf den Fehler δxt) der Lösung wiedergibt, wird St) auch als die zugehörige punktweise) Konditionszahl bezeichnet. Es kann nun einfach gezeigt werden, dass auch die Anfangsbedingungen als Parameter interpretiert werden können. Dazu führt man die Ersatzgröße zt) := xt) x 0 ein und betrachtet die Differentialgleichung d dt zt) = d dt xt) = f t, xt) ) = ft, zt) + x 0 ) := ft, zt), x 0 ), zt 0 ) = ) Offensichtlich hängt z vom Parametervektor x 0 ab und xt) = zt)+x 0 löst das Anfangswertproblem Definiert man die Sensitivitätsmatrizen ) Γt) := z t, x 0 ) und Λt) := x 0 d dt xt) = f t, xt) ), xt 0 ) = x ) ) x t, x 0 ) = Γt) + E n n, 4.53) x 0 so ergibt sich analog zu 4.48) die Sensitivitätsdifferentialgleichung da z f) ) = folgt: d dt Γt) = z f ) x 0 f ) = = ) ) t, z, x 0 )Γt) + t, z, x 0 ) x 0 f 4.54a) ) t, x f ) xt) Γt) + En n ), 4.54b) x ) ) f gilt. Wegen d dt Γt) = d dt Λt) sowie Γt 0) = 0 n n Satz 4.5 Abhängigkeit der Lösung von den Anfangsbedingungen). Sei f stetig mit partiellen Ableitungen x ) ). f Dann hängt die Lösung xt) stetig differenzierbar ) von der Anfangsbedingung x 0 ab und die Ableitung Λt) = x 0 x t, x 0 ) genügt der Anhand der Kettenregel folgt zum Beispiel f = f = f x = f. z z x z x

11 4.4 Diskretisierungsverfahren Seite 70 Sensitivitätsdifferentialgleichung Variationsgleichung) d dt Λt) = x f ) t, xt, x0 ) ) Λt), Λt 0 ) = E n n. 4.55) Eine Störung δx 0 in der Anfangsbedingung führt auf die Lösung x δ t, x 0 + δx 0 ). Für kleine Änderungen δxt) = x δ t, x 0 + δx 0 ) xt, x 0 ) gilt δxt) = Λt)δx ) und Λt) stellt die zugehörige Konditionszahl dar. Wie in 4.50) bestimmt also das linearisierte Differentialgleichungssystem die Kondition. Nachdem der Einfluss von Störungen charakterisiert wurde, werden nunmehr die numerischen Lösungsverfahren diskutiert. 4.4 Diskretisierungsverfahren Zur numerischen Lösung eines Anfangswertproblems 4.3) wird das kontinuierliche Zeitintervall [t 0, t f ] in m Teilintervalle, welche durch die m + diskreten Zeitpunkte t 0 < t <... < t m = t f 4.57) definiert sind, unterteilt. Die diskreten Zeitpunkte bilden ein Gitter = {t 0, t,..., t f } auf [t 0, t f ] und heißen Gitterpunkte. Die Anzahl der Gitterpunkte muss nicht a priori bekannt sein. Sie hängt damit von der Wahl des Gitters ab, weshalb im Folgenden m anstelle von m zur Charakterisierung der Anzahl der Gitterpunkte verwendet wird. Ferner bezeichnet h j = t j+ t j, j = 0,..., m 4.58) die Schrittweite, welche nicht äquidistant sein muss, und h max = max h j 4.59) 0 j m heißt maximale Schrittweite. Eine Funktion x : R n heißt Gitterfunktion. Eine Gitterfunktion x auf den Gittern mit maximaler Schrittweite h max heißt diskrete) Approximation der Lösung xt) falls ein M > 0 existiert, so dass max t j x t j ) xt j ) Mh pv max 4.60) gilt. Konvergente numerische Approximationen können als Folgen approximierender Vektoren x t j ) = x j xt j ), j = 0,..., m interpretiert werden, die umso genauere Näherungen darstellen, je feiner das zugrundeliegende Gitter ist. Je größer dabei die Konvergenzordnung p v ist, desto schneller konvergieren die Approximationen bei feiner werdendem Gitter gegen die exakte Lösung.

12 4.4 Diskretisierungsverfahren Seite 7 Die Aufgabe besteht nun darin, einen Algorithmus zur Konstruktion einer Gitterfunktion x zu finden, welcher die Lösung x an den Gitterpunkten möglichst gut approximiert, d. h. es soll x xt) für alle t erfüllt sein. Ausgehend von einer Anfangsbedingung x 0 soll der Algorithmus sukzessive eine Nährung x an den diskreten Gitterpunkten bestimmen. Diese Algorithmen zur Approximation nennt man Diskretisierungsverfahren oder kurz Diskretisierung und man unterscheidet: i.) Einschrittverfahren ESV): Nur die Daten t l, x t l ), h l für l = j aus dem aktuellen Zeitschritt t j gehen in die Berechnung von x t j+ ) ein, d. h. x t j ) x t j+ ) für j = 0,,..., m. 4.6) ii.) Mehrschrittverfahren MSV): Die Daten t l, x t l ), h l für l = j k +,..., j mit k N + aus dem aktuellen und aus vorangegangenen Zeitschritten gehen in die Berechnung von x t j+ ) ein, d. h. x t j k+ ),..., x t j ) x t j+ ) für j = k,..., m. 4.62) Mehrschrittverfahren werden auch k-schrittverfahren genannt. Sie benötigen eine Anlaufrechnung mit einem Einschrittverfahren zur Bestimmung der k Startwerte x t j ) für j =,..., k. xt) x x 2 x 0 x m x m t 0... t t 2 t m t m t h 0 h h m Abbildung 4.: Grundidee der Diskretisierungsverfahren.

13 4.5 Einschrittverfahren Seite Einschrittverfahren Mithilfe von expliziten Einschrittverfahren kann anhand der Rekursionsvorschrift x t 0 ) = x a) x t j+ ) = Ψ tj,t j+ x t j ) ) für j = 0,,..., m 4.63b) eine Approximation x, mit der von unabhängigen Funktion Ψ gewonnen werden. In Anlehnung an die Evolution Φ der Differentialgleichung siehe 4.9)) wird Ψ diskrete Evolution genannt. Ein Einschrittverfahren ordnet damit jeder Differentialgleichung, repräsentiert durch die rechte Seite f ), eine diskrete Evolution Ψ zu Konsistenz und Konvergenz Die diskrete Evolution Ψ t,t+h ) = Φ t,t+h ) würde für alle Gitter an den Gitterpunkten die exakte Lösung liefern. Diese spezielle diskrete Evolution ist jedoch nahezu nie auswertbar. Man sucht daher nach einer berechenbaren diskreten Evolution Ψ t,t+h ), die sich aus einer festen Anzahl von Auswertungen der rechten Seite f ) ergibt. Dabei werden im Allgemeinen nicht alle Eigenschaften 4.0) einer diskreten Evolution erfüllt, weshalb man den Begriff der Konsistenz einer diskreten Evolution einführt. Definition 4.2 Konsistenz). Die diskreten Evolutionen Ψ, die den Eigenschaften i.) und iii.) nach 4.0a) und 4.0c) genügen, bezeichnet man als konsistent mit der Differentialgleichung. Definition 4.3. Sei t, x) Ω. Die für hinreichend kleine Schrittweite h sich ergebende Differenz heißt Konsistenzfehler der diskreten Evolution Ψ. εt, x, h) = Φ t,t+h x) Ψ t,t+h x) 4.64) Lemma 4.3. Die diskrete Evolution Ψ t,t+h x) sei für festes t, x) Ω und hinreichend kleines h bezüglich h stetig differenzierbar. Dann sind folgende Eigenschaften äquivalent: i.) Die diskrete Evolution ist konsistent. ii.) Die diskrete Evolution besitzt die Darstellung Ψ t,t+h x) = x + hψt, x, h), ψt, x, 0) = ft, x) 4.65) mit einer bezüglich h stetigen Funktion ψ, der sogenannten Inkrementalfunktion.

14 4.5 Einschrittverfahren Seite 73 iii.) Der Konsistenzfehler erfüllt εt, x, h) = oh) für h 0. Beweis. Der Beweis beruht darauf, dass man die Taylorentwicklung von Φ t,t+h x) und Ψ t,t+h x) in t für h 0 vergleicht. Die dritte Eigenschaft 4.0c) der Evolution Φ ist äquivalent zur Taylorentwicklung ) Φ t,t+h x) = Φ t,t x) + h h Φ ) t,t+h x + oh) h=0 = x + hft, x) + oh) für h 0. Analog ist die Konsistenz der diskreten Evolution Ψ äquivalent zu 4.66) Ψ t,t+h x) = x + hft, x) + oh) für h ) Subtraktion von 4.67) und 4.66) zeigt die Äquivalenz von i) und iii). Eine leichte Umformung von 4.67) der Form Ψ t,t+h x) x h = ft, x) + o) für h ) zeigt die Äquivalenz der Konsistenz mit der Darstellung ii). Die diskrete Evolution ist dementsprechend automatisch konsistent, wenn sie in der Form 4.65) gegeben ist. Für die weiteren Betrachtungen wird noch die Konsistenzordung definiert. Definition 4.4 Konsistenzordnung). Eine diskrete Evolution Ψ besitzt die Konsistenzordnung p s, wenn der Konsistenzfehler die Beziehung lokal gleichmäßig in Ω erfüllt. εt, x, h) = Oh ps+ ) für h ) Es stellt sich nun die Frage, wie die Inkrementalfunktion ψ aussehen kann. Eine Antwort auf diese Frage findet man anhand der Integralgleichung 4.). Diese besagt, dass die exakte Lösung die Gleichung tj+ xt j+ ) = xt j ) + f τ, xτ) ) dτ 4.70) t j erfüllt. Die Idee besteht nun darin, das Integral durch einen Ausdruck zu ersetzen, der numerisch berechenbar ist, wenn xt) für τ > t j nicht bekannt ist.

15 4.5 Einschrittverfahren Seite 74 Explizites Euler-Verfahren Eine einfache numerische Approximation des Integrals ist mit der Rechteck-Regel in der Form tj+ f τ, xτ) ) dτ t j+ t j ) f tj, xt j ) ) 4.7) t j }{{} gegeben. Setzt man also eine Inkrementalfunktion in 4.65) der Form an, so ergibt sich die Iterationsvorschrift 4.63) zu h j ψt, x, h) = ft, x) 4.72) x t 0 ) = x a) x t j+ ) = x t j ) + h j f t j, x t j ) ) für j = 0,,..., m. 4.73b) Das durch 4.73) gegebene Verfahren ist das einfachste Einschrittverfahren und heißt Eulersche Polygonzugmethode oder explizites) Euler-Verfahren. Das Verfahren kann auch geometrisch interpretiert werden: In jedem Zeitschritt t j berechnet man die Steigung der exakten Lösung durch den Punkt t j, xt j ) ), d. h. f t j, xt j ) ), und folgt dann der dadurch definierten Geraden bis zum nächsten Zeitschritt t j+. Zudem kann 4.73) auch als numerische Approximation des Differentialquotienten dx/dt interpretiert werden, da sich anhand von 4.73b) d dt xt j) f t j, x t j ) ) = x t j+ ) x t j ) h j für j = 0,,..., m 4.74) ergibt. Die Approximationsvorschrift 4.74) stellt den sogenannten Vorwärtsdifferenzenquotienten dar, weshalb das explizite Euler-Verfahren auch als Vorwärts-Euler-Verfahren bezeichnet wird. Abbildung 4.2 verdeutlicht diesen Zusammenhang grafisch. Heun-Verfahren Bessere Verfahren kann man erhalten, wenn man anstatt 4.7) eine genauere Approximation verwendet. Eine bessere Möglichkeit ist durch die Verwendung von tj+ t j f τ, xτ) ) dτ h j f t j, xt j ) ) + f ) ) t j+, xt j ) + h j ft j, xt j )) 4.75) 2 }{{} xt j+ ) gegeben. Dabei entspricht 4.75) der expliziten) Trapez-Regel, wobei der unbekannte Wert xt j+ ) zur Approximation des Integrals mithilfe des expliziten Euler-Verfahrens xt j+ ) = xt j ) + h j f t j, xt j ) ) gewonnen wird. Setzt man also eine Inkrementalfunktion in 4.65) in der Form ψt, x, h) = 2 ft, xt)) + f t + h, xt) + hft, xt)) )) 4.76)

16 4.5 Einschrittverfahren Seite 75 ft, xt)) xt) ft j, x t j )) Fehler x t j ) h j f t j, xt j )) ft j, x t j )) t t j t j+ t j t j+ t Flächenapproximation Steigungsapproximation Abbildung 4.2: Grundidee des expliziten Euler-Verfahrens. an, so ergibt sich die Iterationsvorschrift 4.63) zu x t 0 ) = x 0 x t j+ ) = x t j ) + h j 2 ft j, x t j )) + f t j + h j, x t j ) + h j ft j, x t j )) )) 4.77a) 4.77b) für j = 0,,..., m. Die Approximationsvorschrift 4.77) wird auch als Heun-Verfahren bezeichnet. Explizite Runge-Kutta-Verfahren Bei der Konstruktion des Heun-Verfahrens wurde das Euler-Vorwärts-Verfahren verwendet, um einen Schätzwert für den unbekannten Wert xt j+ ) zu erhalten. Es liegt nun nahe, diese Methode systematisch rekursiv anzuwenden, um zu besseren Einschrittverfahren zu gelangen. Dies ist die Grundidee der Runge-Kutta-Verfahren. Um die dabei entstehenden Verfahren übersichtlich zu schreiben, benötigt man einen geeigneten Formalismus. Dieser wird im Folgenden anhand des Heun-Verfahrens erläutert. Schreibt man dieses nun in der Form k = ft, x) 4.78a) k 2 = ft + h, x + hk ) 4.78b) Ψ t,t+h x) = x + h 2 k + ) 2 k 2, 4.78c) so lässt sich eine günstige Schreibweise ableiten, um weitere k i -Terme hinzuzufügen. Die Verallgemeinerung dieser Vorgehensweise führt auf die s-stufigen expliziten Runge-Kutta- Verfahren.

17 4.5 Einschrittverfahren Seite 76 Definition 4.5. Ein s-stufiges explizites Runge-Kutta-Verfahren ist gegeben durch i k i = f t + c i h, x + h a i,j k j für i =, 2,..., s 4.79a) s Ψ t,t+h x) = x + h b i k i. i= j= Dabei wird k i = k i t, x, h) als i-te Stufe bezeichnet. 4.79b) Anzumerken ist, dass die Vektoren k i, i =, 2,..., s nach 4.79a) den Steigungen zu den Zwischenpunkten t + c i h entsprechen und 4.79) prinzipiell einer gewichteten Mitteilung dieser entspricht. Die Koeffizienten eines expliziten Runge-Kutta-Verfahrens können kompakt in der Form b c 0 0 b 2 c 2 a 2, 0 b = b 3, c = c 3, A = a 3, a 3, ) a s, a s,s 0 b s c s angeschrieben werden. Konkrete Verfahren werden verkürzt im Butcher-Schema c A b T angegeben und man spricht auch von Runge-Kutta-Verfahren b, c, A). In dieser Schreibweise ergibt sich das Butcher-Schema für das explizite Euler-Verfahren s = ) nach Tabelle 4., für das Heun-Verfahren s = 2) nach Tabelle 4.2 und für das klassische Runge-Kutta-Verfahren s = 4) nach Tabelle Tabelle 4.: Butcher-Schema des expliziten Euler-Verfahrens. Zufolge der Konstruktion des Runge-Kutta-Verfahrens benötigt man somit für die Berechnung des Schrittes Ψ t,t+h ) eines s-stufigen Verfahrens s Auswertungen der rechten Seite f ).

18 4.5 Einschrittverfahren Seite Tabelle 4.2: Butcher-Schema des Heun-Verfahrens Tabelle 4.3: Butcher-Schema des klassischen Runge-Kutta-Verfahrens vierter Ordnung. Beispiel 4.3 Berechnung der Konsistenzordnung). Zur Bestimmung der Konsistenzordnung vergleicht man die Taylorentwicklung der exakten Lösung xt) in t = t j, also xt j + h) = xt j+ ) ) d = xt j ) + h )t dt x j ) + h2 d 2 2 dt 2 x t j ) + Oh 3 ), 4.8) mit der diskreten Evolution Ψ. Für das Euler-Verfahren ergibt sich beispielsweise der Konsistenzfehler zu εt j, x, h) = xt j+ ) Ψ tj,t j +h xtj ) ) ) d = xt j ) + h )t dt x j ) + h2 d 2 2 dt 2 x t j ) + Oh 3 ) xt j ) + hf t j, xt j ) )) 4.82) = Oh 2 ) und damit gemäß Definition 4.4 die Konsistenzordnung p s =. Analog kann man vorgehen um zu zeigen, dass das Heun-Verfahren die Konsistenzordnung p s = 2 und das klassische Runge-Kutta-Verfahren die Konsistenzordnung p s = 4 besitzt. Um die Konvergenz dieser Approximationsvorschriften zu diskutieren, sind folgende Definitionen notwendig:

19 4.5 Einschrittverfahren Seite 78 Definition 4.6 Gitterfehler und Diskretisierungsfehler). Der Vektor der Approximationsfehler auf dem Gitter wird als Gitterfehler bezeichnet und seine Maximumnorm als globaler) Diskretisierungsfehler. ε t) = xt) x t) 4.83) ε t) = max t ε t) 4.84) Definition 4.7 Konvergenz und Konvergenzordnung). Zu jedem Gitter auf [t 0, t f ] mit hinreichend kleinem h max sei eine Gitterfunktion x gegeben. Die Gitterfunktionen konvergieren gegen x C [t 0, t f ]) n, wenn für den globalen Diskretisierungsfehler ε t) 0 für h max ) gilt. Sie konvergieren mit der Konvergenzordnung p v > 0, wenn gilt. ε t) = Oh pv max) für h max ) Der folgende Satz garantiert die Konvergenz der betrachteten Einschrittverfahren: Satz 4.6 Konvergenzsatz für Einschrittverfahren). Gegeben sei eine diskrete Evolution Ψ mit in der Zustandsvariablen x Lipschitz-stetiger Inkrementalfunktion ψ. Entlang einer Trajektorie x C [t 0, t f ]) n genügt der Konsistenzfehler der diskreten Evolution Ψ der Abschätzung εt, x, h) = xt + h) Ψ t,t+h xt) ) = Oh p s+ ). 4.87) Dann definiert die diskrete Evolution Ψ für alle Gitter mit hinreichend kleinem h max eine Gitterfunktion x zum Anfangswert x t 0 ) = xt 0 ). Die Gitterfunktionen konvergieren mit der Konvergenzordnung p v = p s gegen die Trajektorie x. Für den Beweis sei auf die angeführte Literatur verwiesen. Ein sehr wichtiges Ergebnis des Satzes 4.6 sind die Folgerungen: Korollar 4.. Ein konsistentes Einschrittverfahren ist konvergent. Korollar 4.2. Der Konvergenzsatz 4.6 liefert die asymptotische Genauigkeitsaussage ε t) Ch pv max + Oh pv+ max ), C > ) Beispiel 4.4. Das Euler-Verfahren besitzt die Konsistenzordnung p s =. Die Inkrementalfunktion ist Lipschitz-stetig und das Verfahren damit konvergent mit der

20 4.5 Einschrittverfahren Seite 79 Konvergenzordnung p v = p s =. Also führt das Euler-Verfahren für ein hinreichend kleines h max zu einem Konsistenzfehler, siehe Definition 4.4, εt, x, h) = Oh 2 ) 4.89) und einem globalen Diskretisierungsfehler, siehe Korollar 4.2, ε t) = Oh max ) Ch max + Oh 2 max). 4.90) Die Halbierung des Fehlers erfordert damit asymptotisch die Halbierung der maximalen Schrittweite Fehlerschätzung und Schrittweitensteuerung Im vorherigen Teil wurde versucht, die Lösung des Anfangswertproblems 4.3) durch eine Gitterfunktion x bei einem gegebenen Gitter t 0 < t <... < t m = t f zu approximieren. Die einfachste Wahl eines Gitters ist ein äquidistantes Gitter der Form { m = t 0 + j t f t 0 m } für j = 0,,..., m. 4.9) Diese Wahl ist in den meisten Anwendungen allerdings wenig effizient. Es stellt sich somit die Frage, wie ein problemangepasstes Gitter zu konstruieren ist. Ziel der Konstruktion sollte es sein, ein Gitter so zu wählen, dass i.) eine vorgegebene Genauigkeit der Approximation x erreicht wird, ii.) die Anzahl der Gitterpunkte m möglichst klein ist und iii.) damit der notwendige Rechenaufwand minimal wird. Im Folgenden werden die Grundlagen einer adaptiven Gittersteuerung vorgestellt. Dabei sind verschiedene Faktoren zu berücksichtigen. Der Aufwand einer numerischen Lösung verringert sich für größere Schrittweiten, möglicherweise steigt damit aber der Fehler an. Für kleine Schrittweiten nimmt der Aufwand zu und gleichzeitig vergrößert sich der Einfluss von Rundungsfehlern. Insbesondere gibt es eine untere Schranke, die die Schrittweite nicht unterschreiten sollte. Weiterhin verlangen starke Änderungen in der Lösung ein lokal feines Gitter, während annähernd konstante Lösungsabschnitte mit großen Schrittweiten durchlaufen werden können. Da das Lösungsverhalten aber a priori nicht bekannt ist, kann die Gitterstruktur nicht zu Beginn der numerischen Integration festgelegt werden. Vielmehr wird man die Gitterpunkte während des Lösungsprozesses schrittweise anpassen, d. h. ausgehend von t j, x t j ) ) wird eine neue Schrittweite h j bestimmt und damit t j+, x t j+ ) ) festgelegt. Man spricht deswegen von einer Schrittweitensteuerung. Für die Schrittweitensteuerung betrachtet man zunächst den Gitterfehler 4.83) ε t j+ ) = xt j+ ) x t j+ ) = xt j+ ) Ψ tj,t j+ x t j ) ) 4.92)

21 4.5 Einschrittverfahren Seite 80 und schreibt diesen in folgender Weise an ε t j+ ) = Φ tj,t j+ xtj ) ) Ψ tj,t j+ x t j ) )) + Φ tj,t j+ x t j ) ) Φ tj,t j+ x t j ) )). 4.93) Man erkennt, dass der Gitterfehler aus zwei Anteilen besteht: Dem sogenannten lokalen Gitterfehler und einen Anteil ε j+ = Φ tj,t j+ x t j ) ) Ψ tj,t j+ x t j ) ) 4.94) ε j+ = Φ tj,t j+ ε t j ) ), 4.95) der die Auswirkungen des vorherigen Gitterfehlers ε t j ) durch die Evolution des Anfangswertproblems darstellt. Dieser Fehleranteil wäre durch eine Verbesserung der Approximation x korrigierbar. Allerdings müsste dazu die gesamte Rechnung global wiederholt werden. Bei der Genauigkeitskontrolle beschränkt man sich daher in der Regel auf die Kontrolle des lokalen Gitterfehlers ε j+ nach 4.94) und führt den lokalen Diskretisierungsfehler ε j+ = Φ tj,t j+ x t j ) ) Ψ tj,t j+ x t j ) ) TOL 4.96) als Qualitätsanforderung ein, wobei TOL 2 eine vorzugebende lokale Toleranz ist. Im Allgemeinen kann der lokale Gitterfehler ε j+ nicht exakt bestimmt werden, weshalb man auf eine Schätzung des lokalen Gitterfehlers ˆε j+ angewiesen ist, so dass die implementierbare Ersatzforderung in der Form ˆε j+ TOL 4.97) gegeben ist. Die Fehlerschätzung ˆε j+ beschreibt somit die Qualität des Schrittes von t j zu t j+. Von der aktuellen optimalen Schrittweite h j verlangt man nun, dass der erzeugte geschätzte) Fehler ˆε j+ die vorgegebene Toleranz weder wesentlich unter- noch überschreitet, d. h. näherungsweise ε j+ TOL gilt. Zwischen dem lokalen Fehler besteht näherungsweise der Zusammenhang, vgl. 4.69), ˆε j+ ε j+ = ct j )h ps+ j und entsprechend gilt die Forderung + Oh ps+2 j ) ct j )h ps+ j 4.98) ps+ TOL ˆε j+ ct j ) hj). 4.99) 2 In der Regel wird die Qualitätsanforderung 4.97) als Kombination einer relativen Toleranz TOL rel und einer absoluten Toleranz TOL abs vorgegeben.

22 4.5 Einschrittverfahren Seite 8 Die Kombination von 4.98) und 4.99) liefert schließlich eine Schätzformel für die optimale Schrittweite h ps+ TOL j = h j ˆε j ) Für die Schrittweitensteuerung wird eine Schätzung des lokalen Diskretisierungsfehlers ˆε j+ benötigt. Eine Schätzung des lokalen Fehlers ˆε kann aus der Differenz der lokalen Konsistenzfehler und zu ε = Φ t,t+h x) Ψ t,t+h x) 4.0) ε = Φ t,t+h x) Ψ t,t+h x) 4.02) ˆε = ε ε = Ψ t,t+h x) Ψ t,t+h x) 4.03) gewonnen werden. Üblicherweise wird eine Approximation höherer Ordnung Ψ) mit einer niedrigeren Ordnung Ψ) verglichen. Es wird daher vorausgesetzt, dass Ψ genauer als Ψ ist, so dass θ = ε ε ˆε = < 4.04) ε ε gilt. Anhand der Dreiecksungleichung ε ˆε ε ˆε folgt damit ˆε ε ˆε. 4.05) + θ θ Gilt θ 0 für h 0, so nennt man den Schätzer asymptotisch exakt konsistent). In der Praxis wird die Fehlerschätzung von ˆε j+ nach 4.97) durch ε j+ = n x l t j+ ) x l t ) 2 j+) n x l t 4.06) j+) TOL rel + TOL abs l= ersetzt, wobei x l ) die l-te Komponente von x ), x l ) die l-te Komponente von x ) und TOL abs bzw. TOL rel die absolute und relative Toleranz bezeichnen. Für die optimale Schrittweite 4.00) ergibt sich damit h ps+ j = h j ε j+ 4.07) und man vergleicht den Fehler ε j+ gegen, d. h. für ε j+ wird die Schrittweite akzeptiert. In Tabelle ist ein Grundalgorithmus zur Schrittweitensteuerung dargestellt, wobei die Sicherheitsfaktoren q, q max und q min eingeführt wurden.

23 4.5 Einschrittverfahren Seite 82 Initialisierung: j 0 Iterationsindex) x t 0 ) x 0 Anfangsbedingung) {t 0 } Gitter) TOL rel, TOL abs > 0 relative und absolute Toleranz) h 0 > 0 initiale Schrittweite) q, q max, q min > 0 Sicherheitsfaktoren) repeat t t j + h j probiere Zeitschritt) x Ψ tj,t x t j ) ) erste Schätzung) x Ψ tj,t x t j ) ) zweite Schätzung) ε j+ Fehlerschätzung nach 4.06)) h h j ps+ ε j+ h min q max h j, maxq min h j, qh ) ) optimale Schrittweite) neue Schrittweite) if ε j+ ) do t j+ t {t j+ } x t j+ ) x h j+ minh, t f t j+ ) j j + else h j h Schrittweite wird akzeptiert) neuer Zeitschritt) aktualisiere Gitter) aktualisiere Gitterfunktion) neue Schrittweite) erhöhe Index) Schrittweite wird verworfen) end until t j > t f Tabelle 4.4: Basisalgorithmus zur Schrittweitensteuerung Eingebettete Runge-Kutta-Verfahren Die Einbettung eines zweiten Runge-Kutta-Verfahrens stellt die gängige Technik zur Schrittweitensteuerung dar. Mithilfe sogenannter eingebetteter Runge-Kutta-Verfahren ist es möglich, die Anzahl der Funktionsauswertungen der rechten Seite f ) für das Paar Ψ, Ψ) zu optimieren. Dabei wird Ψ durch das Butcher-Schema b, c, A) und Ψ durch das Butcher-Schema b, c, A) beschrieben, d. h. die diskreten Evolutionen verwenden

24 4.5 Einschrittverfahren Seite 83 aufgrund der selben Koeffizientenmatrix A dieselben Funktionsauswertungen der rechten Seite f ). Ein eingebettetes Verfahren wird im Butscher-Schema daher in der Form 4.5 dargestellt. c A b T Tabelle 4.5: Butcher-Schema der eingebetteten Runge-Kutta-Verfahren. Das zur Zeit wohl am weitesten verbreitete und für mittlere Genauigkeitsanforderungen effizienteste explizite Runge-Kutta-Verfahren geht auf Dormand und Prince 980) zurück. Das Verfahren hat die Konsistenzordnung 5 mit einem eingebetteten Verfahren der Konsistenzordnung 4, daher stammt die Namensgebung DOPRI54). Erreicht wird dies mit s = 6 und s = 7 Stufen. b T Ψ Ψ Tabelle 4.6: Butcher-Schema des Dormand-Prince-Verfahrens DOPRI54). In MATLAB steht das Dormand-Prince-Verfahren der Ordnung 5 als ode45 zur Verfügung. Daneben bietet MATLAB noch ein eingebettetes Runge-Kutta-Verfahren ode23 an, das aber nur bei geringen Genauigkeitsanforderungen oder nicht glatter rechter Seite f ) zu empfehlen ist. Beispiel 4.5. Abbildung 4.3 zeigt die numerische Lösung der sogenannten Van-der- Pol-Gleichung siehe 4.74)) mit ode45. Man erkennt deutlich, dass starke Änderungen in der Lösung ein lokal feines Gitter verlangen.

25 4.5 Einschrittverfahren Seite x x Abbildung 4.3: Phasendiagramm der numerischen Lösung der Van-der-Pol-Gleichung mit ode Implizite Runge-Kutta-Verfahren Durch Auffüllen der Koeffizientenmatrix A in der Definition 4.5 definiert man allgemeine s-stufige Runge-Kutta-Verfahren s k i = f t + c i h, x + h a i,j k j für i =, 2,..., s 4.08a) s Ψ t,t+h x) = x + h b i k i. i= j= 4.08b) Falls a i,j = 0 für i j gilt, so ist das Verfahren explizit, andernfalls ist es implizit. Im Vergleich zum expliziten Ansatz hat man durch die insgesamt 2s + s 2 Verfahrenskoeffizienten nun noch mehr Freiheitsgrade, um Ordnung, aber auch Stabilitätseigenschaften festzulegen. Für implizite Verfahren können die Koeffizienten k i in 4.08) nicht direkt bestimmt werden. Vielmehr definiert 4.08a) ein System von impliziten Gleichungen für die einzelnen Koeffizienten k i. Für hinreichend kleine Schrittweiten h kann man zeigen, dass die Stufen k i eindeutig bestimmt werden können, wenn f ) lokal Lipschitz-stetig in x ist. In der Regel wird zur Bestimmung der Koeffizienten k i das Newton-Verfahren, oder das vereinfachte Newton-Verfahren eingesetzt.

26 4.5 Einschrittverfahren Seite 85 Implizites Euler-Verfahren Beispielsweise ergibt sich für s = das implizite Euler-Verfahren in der Form x t 0 ) = x a) x t j+ ) = x t j ) + h j f t j+, x t j+ ) ) für j = 0,,..., m. 4.09b) In Tabelle 4.7 ist das zugehörige Butcher-Schema dargestellt. Tabelle 4.7: Butcher-Schema des impliziten Euler-Verfahrens. Implizite Trapez-Regel Für s = 2 erhält man die implizite Trapez-Regel x t 0 ) = x 0 x t j+ ) = x t j ) + h j 2 f t j, x t j ) ) + f t j+, x t j+ ) )) 4.0a) 4.0b) für j = 0,,..., m. Das zugehörige Butcher-Schema ist in Tabelle 4.8 dargestellt. In MATLAB steht die eingebettete, implizite Trapez-Regel als ode23t zur Verfügung Tabelle 4.8: Butcher-Schema der impliziten Trapez-Regel. Beispiel 4.6 Newton-Iteration für das explizite Euler-Verfahren). Wendet man das Newton-Verfahren 4.4) auf das nichtlineare Gleichungssystem γ x t j+ ) ) = x t j+ ) x t j ) h j f t j+, x t j+ ) ) = 0 n 4.) an, vgl. 4.09), so ergibt sich für l = 0,, 2,... die Iterationsvorschrift x l+ t j+) = x l t j+) + d l, x t 0 ) = x 0 4.2a)

27 4.6 Mehrschrittverfahren Seite 86 mit der Newton-Richtung d l = ) ) ) E n n h j x f x l t j+) x l t j+) x l t j) h j f t j+, x l t j+) )). 4.2b) Diagonal implizite Runge-Kutta-Verfahren Die sogenannten DIRK diagonal impliziten Runge-Kutta)-Verfahren weisen eine Koeffizientenmatrix A mit blockförmiger Struktur auf. Durch diese Vereinfachung kann zur Lösung des entstehenden linearen Gleichungssystems mit einer einfachen Block-Gauß- Elimination gearbeitet werden. Die Verfahren sind damit effizienter implementierbar. In MATLAB steht ein eingebettetes DIRK-Verfahren der Ordnung 2 als ode23tb zur Verfügung. Das Verfahren eignet sich bei sehr hohen Genauigkeitsanforderungen. 4.6 Mehrschrittverfahren Lineare k-schrittverfahren Mehrschrittverfahren MSV)) zur Bestimmung der Gitterfunktion x sind durch die Rekursionsvorschrift bzw. α k x t j+k ) + α k x t j+k ) α 0 x t j ) = h β k f t j+k ) + β k f t j+k ) β 0 f t j ) ) 4.3) k α k l x t j+k l ) = h l=0 k β k l f t j+k l ) 4.4) für j = 0,..., m k und k N + mit konstanten Koeffizienten α 0,..., α k, β 0,..., β k R gegeben, wobei die Gitterfunktion f : R n, t f t, x t) ) eingeführt wurde. Es wird ferner vorausgesetzt, dass α 0 + β 0 > 0 gilt, da es sich ansonsten um ein k )-Schrittverfahren handelt. Falls β k = 0, ist das Mehrschrittverfahren explizit, für β k 0 implizit. Zudem wird α k 0 vorausgesetzt, da explizite Verfahren sonst k )- Schrittverfahren wären. Es ist ersichtlich, dass ein Mehrschrittverfahren im Gegensatz zu einem Einschrittverfahren ältere Information zur Bestimmung einer Approximation verwendet. Ein k-schrittverfahren benötigt daher zum Start k zusätzliche Startwerte x t l ), l =,..., k. Diese müssen mit einer sogenannten Anlaufrechung mithilfe eines Einschrittverfahrens bestimmt werden. Im Folgenden wird, ähnlich wie bei den Einschrittverfahren, der Konsistenzfehler und die Konsistenzordnung für Mehrschrittverfahren eingeführt. Dabei wird von einer äquidistanten Schrittweite ausgegangen. Die Erweiterung der theoretischen Ergebnisse auf variable Schrittweiten ist möglich, aber mit großem Aufwand verbunden. l=0

28 4.6 Mehrschrittverfahren Seite 87 Definition 4.8 Konsistenzfehler MSV). Der Konsistenzfehler des MSV 4.4) mit konstanter Schrittweite h ist definiert als εt, x, h) = k α k l xt j+k l ) h l=0 k β k l f t j+k l, xt j+k l ) ). 4.5) l=0 Definition 4.9 Konsistenzordnung MSV). Ein lineares Mehrschrittverfahren besitzt die Konsistenzordnung p s, wenn der Konsistenzfehler die Beziehung gleichmäßig für alle t, h erfüllt. εt, x, h) = Oh ps+ ) 4.6) Beispiel 4.7 Berechnung der Konsistenzordnung). Zur Bestimmung der Konsistenzordnung geht man ähnlich wie bei den Runge-Kutta-Verfahren vor. Man vergleicht die Taylorentwicklung der exakten Lösung xt) und der rechten Seite ft, x), also ) d xt j + lh) = xt j ) + lh )t dt x j ) + lh)2 d 2 2 dt 2 x t j ) ) und f t j + lh, xt j + lh) ) = f t j, xt j ) ) ) d + lh dt f tj, xt j ) ) ) tj, xt j ) ) lh)2 2 d 2 dt 2 f 4.8) Sortiert man nach Potenzen in h und ersetzt d dtx = ft, x), so ergibt sich εt j, x, h) = xt j ) k l=0 ) d α k l + h dt x t j ) ) + h2 d 2 2 dt 2 x. + hps p s! d p s dt ps x ) t j ) + Oh ps+ ). k α k l l β k l l=0 k t j ) α k l l 2 2β k l l l=0 k α k l l ps p s β k l l ps l=0 4.9)

29 4.6 Mehrschrittverfahren Seite 88 Ein MSV ist demnach konsistent, falls k α k l = 0 l=0 und k α k l l β k l = ) l=0 gilt und besitzt damit die Konsistenzordnung p s =. Für die Ordnung p s > müssen auch die höheren Terme in 4.9) verschwinden, d. h. es muss gelten. k α k l l q qβ k l l q = 0 für q =,..., p s 4.2) l=0 Im Vergleich zu ESV reicht die Konsistenz eines MSV nicht aus um die Konvergenz sicherzustellen. Vielmehr muss zusätzlich die Stabilität des Verfahrens gewährleistet werden. Zur Analyse des Stabilitätsproblems wird die triviale Testgleichung ẋ = 0, xt 0 ) = betrachtet. Ein darauf angewandtes MSV liefert die Differenzengleichung k α k l x j+k l = ) l=0 mit den Startwerten x 0,..., x k. Die Differenzengleichung 4.22) ist stabil, falls das zugehörige charakteristische Polynom ein Einheitskreispolynom ist. Satz 4.7 Stabilitätsbedingung MSV). Ein MSV ist stabil, falls alle Nullstellen des charakteristischen Polynoms ρz) = k α k l z k l 4.23) l=0 mit der komplexen Variablen z im abgeschlossenen Einheitskreis von C liegen und diejenigen auf dem Rand nur einfach sind. Wie bereits bei den Einschrittverfahren setzt man voraus, dass die rechte Seite f ) der Differentialgleichung Lipschitz-stetig und zudem hinreichend glatt ist. Satz 4.8 Konvergenzsatz für Mehrschrittverfahren). Gegeben sei ein stabiles Mehrschrittverfahren 4.4). Entlang einer Trajektorie x C [t 0, t f ]) n genügt der Konsistenzfehler der Abschätzung k α k l xt j+k l ) h l=0 k β k l f t j+k l, xt j+k l ) ) = Oh ps+ ). 4.24) l=0 Dann definiert 4.4) für alle Gitter für ein festes h eine Gitterfunktion x zum Anfangswert x t 0 ) = xt 0 ). Die Gitterfunktionen konvergieren mit der Konvergenzordnung p v = p s gegen die Trajektorie x.

30 4.6 Mehrschrittverfahren Seite 89 Für den Beweis sei auf die angeführte Literatur verwiesen. Der Fundamentalsatz, der die Konvergenz von Mehrschrittverfahren sichert, lautet: Korollar 4.3. Ein stabiles und konsistentes Mehrschrittverfahren ist konvergent. Im Folgenden werden ohne detaillierte Herleitung einige der wichtigsten Mehrschrittverfahren angeführt. Adams-Verfahren Die Herleitung der Adams-Verfahren basiert auf der Integralgleichung 4.8), d. h. xt j+ ) = xt j ) + tj+ t j fτ, xτ))dτ. 4.25) Die Idee besteht darin, die rechte Seite ft, xt)) der Anfangswertaufgabe 4.3) durch ein Interpolationspolynom pt) Lagrange-Polynom) zu ersetzen, vgl. Abbildung 4.4. f f j k+ pt) f j fj f j+... t j k+ t j t j t j+ t Abbildung 4.4: Grundidee der Adams-Verfahren. Beim sogenannten k-adams-bashforth-verfahren interpoliert das Polynom pt) die rechte Seite f t l ) für l = j k +,..., j. Adams-Bashforth-Verfahren sind explizite Mehrschrittverfahren. Sie bilden eine wichtige Verfahrensklasse und sind allgemein in der Form k x t j+ ) = x t j ) + hc p l=0 β l f t j l ), j = k, k, ) gegeben. Es soll nun kurz skizziert werden, wie die Koeffizienten c p βl bestimmt werden können. Mit der Lagrange-Interpolation 4.20) findet man k pt) = f t j l )r l t) mit r l t) = l=0 k ν=0 ν l t t j ν t j l t j ν. 4.27)

31 4.6 Mehrschrittverfahren Seite 90 Eingesetzt in 4.25) ergibt sich tj+ xt j+ ) = xt j ) + pτ)dτ = xt j ) + t j k tj+ l=0 t j r l τ)dτ f t j l ). 4.28) } {{ } hc p βl Für ein äquidistantes Gitter = {t j t j = t 0 +hj} und unter Verwendung der Zeittransformation t = t j + hτ, die das Intervall t [t j, t j+ ] auf τ [0, ] transformiert, erhält man die Koeffizienten c p βl = h = 0 tj +h t j r l t)dt = k ν=0 ν l 0 r l t j + hτ)dτ t 0 + hj + hτ t 0 + hj ν)) t 0 + hj l)) t 0 + hj ν)) dτ = 0 k ν=0 ν l ν + τ 4.29) ν l dτ. Spezielle Verfahren ergeben sich damit mit 4.26) und den Koeffizienten nach 4.29). Die Koeffizienten sind für k =, 2, 3, 4, 5 in der Tabelle 4.9 angeführt. p s k c p β0 β β2 β3 β4 2 2 / / / / Tabelle 4.9: Koeffizienten der Adams-Bashforth-Verfahren. Beim sogenannten k-adams-moulton-verfahren interpoliert das Polynom pt) die rechte Seite f t l ) für l = j k +,..., j +. Die Adams-Moulton-Verfahren sind damit implizite Mehrschrittverfahren. Sie lassen sich in der Form x t j+ ) = x t j ) + hc p k β l f t j+ l ), j = k, k, ) l=0 angeben. Spezielle Verfahren ergeben sich mit 4.30) und den Koeffizienten nach Tabelle 4.0. Das Verfahren für k = 0 entspricht dem impliziten Euler-Verfahren und für k = ergibt sich die implizite Trapez-Regel.

32 4.6 Mehrschrittverfahren Seite 9 p s k c p β0 β β2 β3 β4 0 2 /2 3 2 / / / Tabelle 4.0: Koeffizienten der Adams-Moulton-Verfahren. Prädiktor-Korrektor-Verfahren Die Adams-Verfahren sind in der Praxis von großer Bedeutung und werden meist als Prädiktor-Korrektor-Verfahren PEK-Verfahren) implementiert. Dabei geht man wie folgt vor: P) Man führt einen Startschritt mit einem expliziten k-schritt-adams-verfahren 4.26) durch, um x 0 t j+) zu erhalten E) und wertet diesem bei f 0 t j+) = f t j+, x 0 t j+) ) aus. K) Anschließend kann dann die Fixpunktiteration x n+ t j+) = Λ x n t j+) ), n = 0,,... mit einem impliziten k-schritt-adams-verfahren 4.30) durchgeführt werden, d. h. mit Λ x n t j+) ) = x t j ) + hc p β 0 f n t j+) + ) k β l f t j+ l ). Die Kontraktion der Fixpunktiteration kann mithilfe des Banachschen Fixpunktsatzes gezeigt werden. Mit der Fixpunktiteration kann elegant die Verwendung eines aufwändigen Newton-Verfahrens zur Lösung der impliziten Gleichungen umgangen werden. In MATLAB ist das Adams-Verfahren ode3, mit der Ordnung k 3 implementiert. Für die Anlaufrechnung kommt das Euler-Verfahren zum Einsatz, anschließend wird sukzessiv die Ordnung erhöht. Das Verfahren eignet sich bei hohen Genauigkeitsanforderungen oder wenn die Berechnung der rechten Seite f ) sehr aufwändig ist. BDF-Verfahren Die Herleitung der BDF Backwards Difference Formulas)-Verfahren basiert im Gegensatz zu den Adams-Verfahren auf der Differentiation. Man konstruiert ein Polynom qt) durch die Punkte x t l ) für l = j k +,..., j ) l=