Thermodynamische Diagramme
|
|
|
- Catrin Simen
- vor 9 Jahren
- Abrufe
Transkript
1 Einführung in die Meteorologie Teil I Thermodynamische Diagramme Thermodynamischen Diagramme Mit thermodynamischen (aerologischen) Diagrammen lassen sich Zustandsänderungen von Luftpaketen bei Vertikalbewegungen graphisch untersuchen. Man trägt die Radiosondenmessungen (Druck, Temperatur, Feuchte) in diese Diagramme ein, um den Zustand der Atmosphäre zu bestimmen. Man kann ohne aufwendige Rechenarbeit die Stabilität der atmosphärischen Schichtung beurteilen und Aussagen über Thermik, Quellwolkenbildung, Schauer- und Gewitterwahrscheinlichkeit machen.
2 Graphische Darstellung von Zustandsänderungen Der thermodynamische Zustand eines Gases läßt sich durch einen Punkt im pv- oder pα-diagramm angeben. p p A (a,p) B a a Zustandsänderungen kann man durch Kurven in diesem Diagramm darstellen. Thermodynamischen Diagramme 2 Wir haben bereits das p-α Diagramm vorgestellt. Jeder Zustand eines trockenen Luftpakets läbt sich durch einen Punkt in diesem Diagramm angeben. Jedes feuchte Luftpaket wird mit zwei Punkten (Temperatur und Feuchtegröbe) bestimmt. Bei einer Zustandsänderung trockener Luft (z.b. isotherm oder adiabatisch) ergibt sich ein charakteristischer Kurvenverlauf. Zu jedem Wertepaar von p und α kann man die Temperatur, die potentielle Temperatur und das Sättigungsmischungsverhältnis ablesen, denn das Diagramm enthält die Kurvenscharen der Isothermen Adiabaten und Isolinien des Sättigungsmischungsverhältnis.
3 T = 200 K T = 400 K 500 p p = RT/α a m 3 /kg Adiabaten in einem p-a-diagramm Die potentielle Temperatur ist eine Funktion von Druck und Temperatur: θ = θ(p,t) = T(p*/p )κ. Mit T = pα/r: θ = θ(p,α) = (pα/r)(p * /p) κ. Löst man die Gleichung θ = (pα/r)(p * /p) κ ergibt sich: 1 κ Rθ p* α= p * p nach α auf, Für verschiedene Werte θ = Konstant können die Kurven α = α(p) in einem ( p)α-diagramm eingetragen werden. Wir nennen diese Kurven Trockenadiabaten. Entlang dieser Linien erfolgt die trockenadiabatische Zustandsänderung eines Luftpakets.
4 q = 280 K T = 280 K q = 400 K T = 400 K 800 p a m 3 /kg Das Sättigungsmischungsverhältnis Das Mischungsverhältnis ist definiert von εe(t s d) e(t s d) r = r(p,t) s d = ε p e(t ) p s d Das Sättigungsmischungsverhältnis r s ist definiert von r(p,t) s εe(t) e(t) s p e(t) p s = ε s Linien von konstantem Sättigungsmischungsverhältnis r s (p,t) können in einem p-α Diagramm eingetragen werden.
5 r s = 20 g/kg Thermodynamischen Diagramme 3 Wenn ein Luftvolumen einen Kreisprozeb durchläuft (d.h. nach mehreren Zustandsänderungen soll wieder der Anfangszustand erreicht werden), ergibt sich eine geschlossene Kurve. Eine vorteilhafte Eigenschaft von p-α Diagrammen ist, dab die von der Kurve eingeschlossene Fläche der verrichteten Arbeit proportional ist. -p C a
6 Thermodynamischen Diagramme 4 Da p und T leichter mebbar als p und α sind, transformiert man für meteorologische Anwendungen die Koordinaten des p-α Diagramms auf geeignete Weise. Ein thermodynamisches Diagramm ist einfach ein transformiertes p-α Diagramm. Die neuen Koordinaten wählt man unter folgenden Gesichtspunkten aus: Thermodynamischen Diagramme 5 Die von der Kurve eines Kreisprozesses eingeschlossene Fläche soll wie im p-α Diagramm der dabei verrichteten Arbeit proportional sein. Die wichtigsten Linien (Isobaren, Isothermen, Trockenadiabaten) sollen möglichst geradlinig verlaufen. Der Winkel zwischen Isothermen und Trockenadiabaten soll möglichst grob (90 o ) sein. -p C A C a B
7 Thermodynamischen Diagramme 5 -p C A C a B Die Forderung, daß auch nach der Transformation von den Koordinaten ( p, α) auf die Koordinaten (A, B) die von einer Kurve eingeschlossene Fläche gleich groß ist lautet in mathematischer Schreibweise: pd AdB C C C α= (pdα+ AdB) = 0 Thermodynamischen Diagramme 6 C (pdα+ AdB) = 0 Aus dieser Gleichung folgt, daß pdα + AdB ein vollständiges Differential sein muß, A p = α B B α Herleitung
8 C (pdα+ AdB) = 0 df= df( α,b) F = F( α,b) F F df= dα+ db α B B α p A F F = B α α B B α A p = α B B α Thermodynamischen Diagramme 7 C (pdα+ AdB) = 0 A p = α B B α Nach der Wahl der Koordinate B, wird die Koordinate A so festgelegt, daß die Transformation flächentreu ist. Für die Koordinatenwahl gibt es mehrere Möglichkeiten:
9 Emagramm: B = T Das Emagramm ermöglicht die Bestimmung des Energiebetrages pro Masseneinheit und somit quantitative Vorstellungen von der Stabilität bzw. Labilität der Atmosphäre. Mit B = T, pα = RT: A p = α B B α F AI p HG α K J F = H G I T K J = T α R α Integration ergibt: A= Rlnα+ F(T) pα = RT lnα= lnr+ lnt lnp A= Rlnp+ RlnR+ RlnT+ F(T) Wähle F(T) so, daß dieser Ausdruck Null wird. Emagramm: A = Rlnp, B= T Die Gleichung der Trockenadiabaten θ in diesem Diagramm läßt sich folgendermaßen ableiten: p T =θ p * κ lnt lnθ=κlnp κlnp * c p lnp= lnt+ const R A = c lnb+ const Die Trockenadiabaten sind im Emagramm logarithmische Kurven; für die in der Atmosphäre vorkommenden Werte A und B verlaufen die Trockenadiabaten (genauso wie die Sättigungsmischungsverhältnislinien) jedoch fast gerade. p
10 Emagramm Adiabate Sättigungsmischungsverhältnis A = Rlnp Isobare Isotherm Feuchtadiabate B = T Tephigramm: B = T Das Emagramm ist zwar eine flächentreue Transformation des pα-diagramms, hat aber den Nachteil, daß der Winkel zwischen den Isothermen und (Trocken-) Adiabaten nur 45 beträgt, d. h.. es ergeben sich kleine Flächen bei Energieberechnungen. Dieses Problem löst das von Sir Napier Shaw entwickelte Tephigramm. Wie vorher B= T, A= Rlnα+ F(T) lnα= lnr+ lnt lnp Wähle F(T) so, daß A = c p lnθ lnt lnθ=κlnp κlnp * A = cp ln θ, B= T
11 Tephigramm: A = cp ln θ, B= T Die Gleichung der Isobaren p = const. in diesem Diagramm: lnθ= lnt+κlnp κlnp * A = cp lnb+ const Die logarithmische Abhängigkeit äußert sich in einer Krümmung der Isobaren (im meteorologisch interessanten Bereich ist die Krümmung relativ schwach). Zu beachten ist, daß im Tephigramm der Winkel zwischen Isothermen und Adiabaten genau 90 beträgt. Änderungen im vertikalen Temperaturverlauf (z. B. Temperaturzunahme an einer Inversion) kann man deshalb besonders deutlich erkennen. Tephigramm Isotherm A = c p lnθ Adiabate Isobare B = T
12 Um 45 gedrehtes Tephigramm Feuchtadiabate Sättigungsmischungsverhältnis p Isobare Isotherm Adiabate Skew T, log p-diagramm (Schiefes T, log p) In diesem von Herlofson 1947 eingeführten Diagramm ist der Schnittwinkel zwischen Adiabaten und Isothermen fast so groß wie im Tephigramm. Die Isobaren horizontale sind Geraden zählt zu den gebräuchlichsten thermodynamischen Diagrammen. A = T +µ lnp, B= Rlnp µ = const. Isothermen: Adiabaten: R B= A+ const. µ µ A B Ce R B/c schräge (engl. skew) Geraden. p + = konkav gekrümmt.
13 Skew T, log p-diagramm Isobare B = Rlnp Feuchtadiabate Adiabate Isotherm A = T + µlnp Stüve-Diagramm: Ordinate p κ, Abszisse T (nicht flächentreu) A = p κ Feuchtadiabate Isotherm Isobare Sättigungsmischungsverhältnis Sättigungsmischungsverhältnis Adiabate B = T
14 Feuchtadiabaten Nun geht es um die Auswirkung der Wasserdampf- Kondensation auf die Vertikalbewegung von feuchter Luft (= trockene Luft + Wasserdampf). Wird ein Paket mit feuchter Luft adiabatisch gehoben, d. h. ohne Wärmezufuhr von außen, ohne Mischung mit der Umgebungsluft, bleibt das Wasserdampfmischungsverhältnis konstant: r = r s (p,t d ) T d = T d (p, r). Solange noch keine Sättigung erreicht ist, (r < r s ) für die Temperatur bzw. virtuelle Temperatur und den Druck in jeweiliger Höhe), wird keine Kondensationswärme frei. Das bedeutet, daß bei der Vertikalbewegung von feuchter, ungesättigter Luft die adiabatische Temperaturänderung so groß ist wie die eines trockenen Luftpakets, nämlich 1 K pro 100 m. Feuchtadiabaten 2 Wegen der Temperaturabnahme bei der Hebung erhöht die relativen Feuchte (r s wird immer kleiner, r bleibt konstant). In einer bestimmten Höhe erreicht die relative Feuchte 100% und das Luftpaket ist gesättigt (r = r s ). Diese Höhe bezeichnet man als Hebungskondensationsniveau (HKN) (engl. lifting condensation level, LCL). HKN Isotherme r, θ konst. Sättigungsmischungsverhältnis Adiabate
15 Feuchtadiabaten 3 Bei weiterer Hebung (über das HKN) kondensiert der überschüssige Wasserdampf zu Wolkentröpfchen. Dabei wird Kondensationswärme frei, die die Luft im Paket erwärmt Die feuchtadiabatische Temperaturabnahme (Temperaturabnahme in gesättigter Luft) ist kleiner als die trockenadiabatische. Bei der Berechnung der feuchtadiabatischen Temperaturabnahme vernachlässigt man normalerweise die (kleine) Wärmemenge, die vom Flüssigwasser aufgenommen wird (pseudoadiabatischer Prozeß). Es wird angenommen, daß der überschüssige Wasserdampf sofort als Regen ausfällt, die freiwerdende Wärme aber im Luftpaket verbleibt. Ein derartiger pseudoadiabatischer Prozeß ist irreversibel. Feuchtadiabaten 4 Bleibt dagegen das gesamte kondensierte Wasser im Luftpaket, handelt es sich um einen reversiblen Prozeß. Bei den in der Natur vorkommenden Hebungsvorgängen beobachtet man meistens eine Mischung zwischen den beiden Extremen. pseudoadiabatischer Prozeß (irreversibel) reversibler Prozeß
16 Feuchtadiabaten 5 p - dp, T - dt, r s (p,t) - dr s dq = Ldr s die Menge des kondensierten Wassers HKN p, T, r s (p,t) Wenn Kondensation eintritt, verringert sich der Wasserdampfanteil im Luftpaket, das Wasserdampf-mischungsverhältnis r (in gesättigter Luft). Feuchtadiabaten 6 Der 1. Hauptsatz der Thermodynamik in der Form dq = c p dt αdp RT Ldrs = cdt p dp p r(p,t) s εe(t) e(t) s p e(t) p s = ε s dt RT dr dp p dt s = L + c p 1 Dieser Gleichung kann numerisch integriert werden.
17 Feuchtadiabaten 7 dt RT dr dp p dt s = L + c p 1 Die Kurven, die die Abhängigkeit der Temperatur vom Druck bei der feuchtadiabatischen Vertikalbewegung eines Luftpakets wiedergeben, nennt man Feuchtadiabaten. Feuchtadiabaten 8 Jedes thermodynamische Diagramm enthält neben den Isobaren, Isothermen, Sättigungsmischungs-verhältnislinien und Trockenadiabaten auch die Feuchtadiabaten. Die Feuchtadiabaten nähern sich in großer Höhe (geringer Druck, tiefe Temperaturen) asymptotisch den Trockenadiabaten, denn bei der Hebung von kalter, wasserdampfarmer Luft mit niedrigem r s (p,t) ist auch Lr s klein, d. h. dem Luftpaket wird nur wenig latente Wärme zugeführt. Die feuchtadiabatische Temperaturabnahme beträgt in sehr warmer Luft 0,4 K pro 100 m, in mittleren Breiten in der unteren Troposphäre 0,6 K pro 100 m und nähert sich bei sehr tiefen Temperaturen 1 K pro 100 m.
18 Feuchtadiabaten 9 Feuchtadiabat r = r s (p,t), dθ/dz > 0. Isotherme r, θ konst. HKN Sättigungsmischungsverhältnis Adiabate Feuchtadiabaten 10 Die Feuchtadiabaten werden in thermodynamischen Diagrammen meist mit der pseudopotentiellen Temperatur gekennzeichnet. Die pseudopotentielle Temperatur θ e nimmt eine gesättigte Luftmenge an, wenn sie vom Kondensationsniveau solange feuchtadiabatisch aufsteigt, bis der gesamte Wasserdampf kondensiert und ausgefallen ist, und dann trockenadiabatisch auf einen Druck von 1000 mb absinkt. Manchmal gibt man zu den Feuchtadiabaten auch die zugehörige feuchtpotentielle Temperatur (auf Englisch, wetbulb potential temperature) θ w an. Diese Temperatur herrscht in gesättigter Luft, wenn sie feuchtadiabatisch auf das Druckniveau von 1000 mb gebracht wird. Es mub flüssiges Wasser vorhanden sein.
19 q e, q w feuchter Adiabat gesättigtes Luftpaket T = -3 o C trockener Adiabat 850 mb T = 5 o C θ w = 5 o C T = 20 o C θ e = 20 o C 1000 mb Feuchtadiabaten 11 Die pseudopotentielle Temperatur wird häufig zur Bestimmung der Luftmassen im Druckniveau p = 850 mb verwendet. Innerhalb einer Luftmasse variiert oft der Feuchtegehalt und damit die Differenz zwischen der Lufttemperatur T und dem Taupunkt T d (Taupunktdifferenz T T d ) (auf Englisch, Taupunktdifferenz = dew-point depression). Charakteristisch für eine Luftmasse ist also weniger ihre (Trocken-)Temperatur, sondern mehr ihr Energiegehalt. Die Werte T = T d = 3 C, T = 0 C/T d = 8 C, T = 2 C/T d = 14 C führen alle zur gleichen pseudopotentiellen Temperatur von 20 C.
20 Feuchtadiabaten 12 Auf einer θ e -Karte kann man Gebiete mit einheitlichen pseudopotentiellen Temperaturen (Luftmassen) und Gebiete mit großem θ e -Gradienten (Luftmassengrenzen) unterschieiden. Zur Bestimmung der pseudopotentiellen Temperatur von ungesättigter Luft werden T und T d z. B. in ein Tephigramm eingetragen. Die zum Taupunkt gehörende Sättigungsmischungsverhältnislinie (= Wasserdampfgehalt des Luftpakets) verfolgt man dann bis zum Schnittpunkt mit der durch T verlaufenden Trockenadiabaten. In der Höhe des Schnittpunktes ist das Lufpaket gesättigt. θ e läßt sich dann an der Feuchtadiabaten ablesen. Ende
Thermodynamische Diagramme
 Einführung in die Meteorologie eil I hermodynamische Diagramme q = 20 o C d r s = Konst. Abb 5.12 800 mb 900 mb 1000 mb d 10 o C 15 o C 20 o C Feuchtadiabaten 4 Feuchtadiabat r = r s (p,), dθ/dz > 0. Isotherme
Einführung in die Meteorologie eil I hermodynamische Diagramme q = 20 o C d r s = Konst. Abb 5.12 800 mb 900 mb 1000 mb d 10 o C 15 o C 20 o C Feuchtadiabaten 4 Feuchtadiabat r = r s (p,), dθ/dz > 0. Isotherme
Gleichgewichtszustand Beschreibung der Gleichgewichtslage Kugel kehrt in die Ruhelage zurück Kugel entfernt sich beschleunigt aus der Ruhelage
 Statische Stabilität oder thermische Schichtung der Troposphäre Die vertikale Temperatur-, Feuchte- und Druckverteilung der Atmosphäre wird im synoptisch-aerologischen-routinedienst täglich um 00 und 12
Statische Stabilität oder thermische Schichtung der Troposphäre Die vertikale Temperatur-, Feuchte- und Druckverteilung der Atmosphäre wird im synoptisch-aerologischen-routinedienst täglich um 00 und 12
Thermodynamik der Atmosphäre III
 Einführung in die Meteorologie Teil I Thermodynamik der Atmosphäre III Änderung der inneren Energie du dq = du + pdα Wärmezufuhr bewirkt nicht nur eine Ausdehnung sondern auch eine Temperaturerhöhung des
Einführung in die Meteorologie Teil I Thermodynamik der Atmosphäre III Änderung der inneren Energie du dq = du + pdα Wärmezufuhr bewirkt nicht nur eine Ausdehnung sondern auch eine Temperaturerhöhung des
Physik 2 (B.Sc. EIT) 2. Übungsblatt
 Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Umweltphysik / Atmosphäre V2: Struktur der Atmosphäre WS 2011/12
 Umweltphysik / Atmosphäre V2: Struktur der Atmosphäre WS 2011/12 - Temperaturgradient - Vertikales Temperaturprofil - Trockenadiabatischer T-Gradient, potentielle Temperatur Feuchtadiabatischer T-Gradient
Umweltphysik / Atmosphäre V2: Struktur der Atmosphäre WS 2011/12 - Temperaturgradient - Vertikales Temperaturprofil - Trockenadiabatischer T-Gradient, potentielle Temperatur Feuchtadiabatischer T-Gradient
Erklärungen zu den Radiosondendiagrammen Autor: Volker Ermert Institut für Geophysik und Meteorologie Universität zu Köln Stand:
 Erklärungen zu den Radiosondendiagrammen Autor: Volker Ermert Institut für Geophysik und Meteorologie Universität zu Köln Stand: 05.06.2007 Inhalt 1. Begriffserklärungen 2. Stabilitätsindizes 3. Thermische
Erklärungen zu den Radiosondendiagrammen Autor: Volker Ermert Institut für Geophysik und Meteorologie Universität zu Köln Stand: 05.06.2007 Inhalt 1. Begriffserklärungen 2. Stabilitätsindizes 3. Thermische
Die Atmosphäre der Erde (2)
 Die Atmosphäre der Erde (2) Wiederholung: Vertikaler Aufbau der Erdatmosphäre Für das Wetter- und Klimageschehen auf der Erde ist im Wesentlichen nur die Troposphäre verantwortlich Domäne der Meteorologie
Die Atmosphäre der Erde (2) Wiederholung: Vertikaler Aufbau der Erdatmosphäre Für das Wetter- und Klimageschehen auf der Erde ist im Wesentlichen nur die Troposphäre verantwortlich Domäne der Meteorologie
Thermodynamik der Atmosphäre II
 Einführung in die Meteorologie Teil I Thermodynamik der Atmosphäre II Der erste Hauptsatz der Thermodynamik Die Gesamtenergie in einem geschlossenen System bleibt erhalten. geschlossen steht hier für thermisch
Einführung in die Meteorologie Teil I Thermodynamik der Atmosphäre II Der erste Hauptsatz der Thermodynamik Die Gesamtenergie in einem geschlossenen System bleibt erhalten. geschlossen steht hier für thermisch
Das Emagramm Möglichkeiten und Grenzen der Thermikprognose für die Fluggebiete
 1 von 5 21.07.2006 17:26 Das Emagramm Möglichkeiten und Grenzen der Thermikprognose für die Fluggebiete Die Radiosonde Von vielen Punkten der Erdoberfläche aus steigen zweimal täglich Wetterballone in
1 von 5 21.07.2006 17:26 Das Emagramm Möglichkeiten und Grenzen der Thermikprognose für die Fluggebiete Die Radiosonde Von vielen Punkten der Erdoberfläche aus steigen zweimal täglich Wetterballone in
Wie kann man die thermischen Unterschiede zwischen Kalt- und Warmluft beim Segelflug am besten managen? Von Dr. Manfred Reiber
 Wie kann man die thermischen Unterschiede zwischen Kalt- und Warmluft beim Segelflug am besten managen? Von Dr. Manfred Reiber Wir wissen aus der Erfahrung, dass Thermik stark von der Luftmasse abhängt.
Wie kann man die thermischen Unterschiede zwischen Kalt- und Warmluft beim Segelflug am besten managen? Von Dr. Manfred Reiber Wir wissen aus der Erfahrung, dass Thermik stark von der Luftmasse abhängt.
Einführung in die Meteorologie Teil I. Thermodynamik der Atmosphäre IV
 Einführung in die Meteorologie Teil I Thermodynamik der Atmosphäre IV Feuchtemeßgrößen: das Mischungsverhältnis Die Luftfeuchtigkeit kann in verschiedene Feuchtemeßgrößen angegeben werden, je nachdem,
Einführung in die Meteorologie Teil I Thermodynamik der Atmosphäre IV Feuchtemeßgrößen: das Mischungsverhältnis Die Luftfeuchtigkeit kann in verschiedene Feuchtemeßgrößen angegeben werden, je nachdem,
1 Thermodynamik allgemein
 Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
10. Thermodynamik Der erste Hauptsatz Der zweite Hauptsatz Thermodynamischer Wirkungsgrad Der Carnotsche Kreisprozess
 Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Inversion/Isothermie:
 Emagramm Das Emagramm gehört zu den thermodynamischen Diagrammen, mit welchem bestimmte Vorgänge in der Atmosphäre graphisch nachvollzogen werden können. Das Emagramm wird in der Schweiz eingesetzt. In
Emagramm Das Emagramm gehört zu den thermodynamischen Diagrammen, mit welchem bestimmte Vorgänge in der Atmosphäre graphisch nachvollzogen werden können. Das Emagramm wird in der Schweiz eingesetzt. In
Wolfgang Gebhardt und Andreas Schäfer Ausbildungsseminar Wetter und Klima Vortrag Vertikale Luftbewegungen
 Universität Regensburg Fakultät Physik WS 09/10 Wolfgang Gebhardt und Andreas Schäfer Ausbildungsseminar Wetter und Klima Vortrag Vertikale Luftbewegungen Referentin: Johanna Kirschner 30.10.2009 1 Gliederung
Universität Regensburg Fakultät Physik WS 09/10 Wolfgang Gebhardt und Andreas Schäfer Ausbildungsseminar Wetter und Klima Vortrag Vertikale Luftbewegungen Referentin: Johanna Kirschner 30.10.2009 1 Gliederung
Inhaltsverzeichnis. 4. Register 79. 5. Formelgrößen und Symbole 85 -1-
 -1- Inhaltsverzeichnis Seite 1. Allgemeines 1 1.1 Trockenadiabaten 2 1.2 Linien gleichen Sättigungsmischungsverhältnis 3 1.3 Feuchtadiabaten 4 1.4 Das Stüvediagramm (FA 1/2A2 Z) 6 1.4.1 Koordinatensystem
-1- Inhaltsverzeichnis Seite 1. Allgemeines 1 1.1 Trockenadiabaten 2 1.2 Linien gleichen Sättigungsmischungsverhältnis 3 1.3 Feuchtadiabaten 4 1.4 Das Stüvediagramm (FA 1/2A2 Z) 6 1.4.1 Koordinatensystem
Musterlösung zu Übung 2: Thermodynamik
 Musterlösung zu Übung 2: Thermodynamik Wettersysteme, HS 2011 1 Thermodynamisches Diagramm 1 Die folgenden Messungen geben eine Mitternacht-Radiosondierung im Juni über Liverpool an. Druck (hpa) Temperatur
Musterlösung zu Übung 2: Thermodynamik Wettersysteme, HS 2011 1 Thermodynamisches Diagramm 1 Die folgenden Messungen geben eine Mitternacht-Radiosondierung im Juni über Liverpool an. Druck (hpa) Temperatur
Enthalpienullpunkt von Luft und Wasser am Tripelpunkt des siedenden Wassers T=T tr = 273,16 K:
 3.3.5 Energiebilanz bei der Mischung feuchter Luft Bezugsgröße: Masse der trockenen Luft m L Beladung: Auf die Masse der Luft bezogene Enthalpie Enthalpienullpunkt von Luft und Wasser am Tripelpunkt des
3.3.5 Energiebilanz bei der Mischung feuchter Luft Bezugsgröße: Masse der trockenen Luft m L Beladung: Auf die Masse der Luft bezogene Enthalpie Enthalpienullpunkt von Luft und Wasser am Tripelpunkt des
Die Atmosphäre der Erde
 Helmut Kraus Die Atmosphäre der Erde Eine Einführung in die Meteorologie Mit 196 Abbildungen, 184 Übungsaufgaben und einer farbigen Klimakarte der Erde Springer VII Vorwort I. Einige Grundlagen 1.1 Erster
Helmut Kraus Die Atmosphäre der Erde Eine Einführung in die Meteorologie Mit 196 Abbildungen, 184 Übungsaufgaben und einer farbigen Klimakarte der Erde Springer VII Vorwort I. Einige Grundlagen 1.1 Erster
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
Thermodynamik I. Sommersemester 2012 Kapitel 3, Teil 3. Prof. Dr.-Ing. Heinz Pitsch
 Thermodynamik I Sommersemester 2012 Kapitel 3, Teil 3 Prof. Dr.-Ing. Heinz Pitsch Kapitel 3, Teil 2: Übersicht 3 Energiebilanz 3.3 Bilanzgleichungen 3.3.1 Massebilanz 3.3.2 Energiebilanz und 1. Hauptsatz
Thermodynamik I Sommersemester 2012 Kapitel 3, Teil 3 Prof. Dr.-Ing. Heinz Pitsch Kapitel 3, Teil 2: Übersicht 3 Energiebilanz 3.3 Bilanzgleichungen 3.3.1 Massebilanz 3.3.2 Energiebilanz und 1. Hauptsatz
PCG Grundpraktikum Versuch 5 Lösungswärme Multiple Choice Test
 PCG Grundpraktikum Versuch 5 Lösungswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Lösungswärme wird dieses Vorgespräch durch einen Multiple Choice
PCG Grundpraktikum Versuch 5 Lösungswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Lösungswärme wird dieses Vorgespräch durch einen Multiple Choice
Thermodynamik I. Sommersemester 2012 Kapitel 3, Teil 2. Prof. Dr. Ing. Heinz Pitsch
 Thermodynamik I Sommersemester 2012 Kapitel 3, Teil 2 Prof. Dr. Ing. Heinz Pitsch Kapitel 3, Teil 2: Übersicht 3 Energiebilanz 3.3Bilanzgleichungen 3.3.1Massenbilanz 3.3.2 Energiebilanz und 1. Hauptsatz
Thermodynamik I Sommersemester 2012 Kapitel 3, Teil 2 Prof. Dr. Ing. Heinz Pitsch Kapitel 3, Teil 2: Übersicht 3 Energiebilanz 3.3Bilanzgleichungen 3.3.1Massenbilanz 3.3.2 Energiebilanz und 1. Hauptsatz
Absolute Luftfeuchtigkeit Ist die in einem bestimmten Luftvolumen V enthaltene Wasserdampfmasse m W. Übliche Einheit: g/m 3.
 Die Luftfeuchtigkeit Die Luftfeuchtigkeit oder kurz Luftfeuchte bezeichnet den Anteil des Wasserdampfs am Gasgemisch der Erdatmosphäre oder in Räumen. Flüssiges Wasser (zum Beispiel Regentropfen, Nebeltröpfchen)
Die Luftfeuchtigkeit Die Luftfeuchtigkeit oder kurz Luftfeuchte bezeichnet den Anteil des Wasserdampfs am Gasgemisch der Erdatmosphäre oder in Räumen. Flüssiges Wasser (zum Beispiel Regentropfen, Nebeltröpfchen)
Einführung in die Technische Thermodynamik
 Arnold Frohn Einführung in die Technische Thermodynamik 2., überarbeitete Auflage Mit 139 Abbildungen und Übungen AULA-Verlag Wiesbaden INHALT 1. Grundlagen 1 1.1 Aufgabe und Methoden der Thermodynamik
Arnold Frohn Einführung in die Technische Thermodynamik 2., überarbeitete Auflage Mit 139 Abbildungen und Übungen AULA-Verlag Wiesbaden INHALT 1. Grundlagen 1 1.1 Aufgabe und Methoden der Thermodynamik
d) Das ideale Gas makroskopisch
 d) Das ideale Gas makroskopisch Beschreibung mit Zustandsgrößen p, V, T Brauchen trotzdem n, R dazu Immer auch Mikroskopische Argumente dazunehmen Annahmen aus mikroskopischer Betrachtung: Moleküle sind
d) Das ideale Gas makroskopisch Beschreibung mit Zustandsgrößen p, V, T Brauchen trotzdem n, R dazu Immer auch Mikroskopische Argumente dazunehmen Annahmen aus mikroskopischer Betrachtung: Moleküle sind
PCG Grundpraktikum Versuch 4 Neutralisationswärme Multiple Choice Test
 PCG Grundpraktikum Versuch 4 Neutralisationswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Neutralisationswärme wird dieses Vorgespräch durch einen
PCG Grundpraktikum Versuch 4 Neutralisationswärme Multiple Choice Test 1. Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Neutralisationswärme wird dieses Vorgespräch durch einen
6.2 Zweiter HS der Thermodynamik
 Die Änderung des Energieinhaltes eines Systems ohne Stoffaustausch kann durch Zu-/Abfuhr von Wärme Q bzw. mechanischer Arbeit W erfolgen Wird die Arbeit reversibel geleistet (Volumenarbeit), so gilt W
Die Änderung des Energieinhaltes eines Systems ohne Stoffaustausch kann durch Zu-/Abfuhr von Wärme Q bzw. mechanischer Arbeit W erfolgen Wird die Arbeit reversibel geleistet (Volumenarbeit), so gilt W
T4p: Thermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 8 Lösungsvorschlag
 T4p: Thermodynamik und Statistische Physik Pro Dr H Ruhl Übungsblatt 8 Lösungsvorschlag 1 Adiabatengleichung Als adiabatische Zustandssänderung bezeichnet man einen thermodynamischen organg, bei dem ein
T4p: Thermodynamik und Statistische Physik Pro Dr H Ruhl Übungsblatt 8 Lösungsvorschlag 1 Adiabatengleichung Als adiabatische Zustandssänderung bezeichnet man einen thermodynamischen organg, bei dem ein
Aufgabe 1: Theorie Punkte
 Aufgabe 1: Theorie.......................................... 30 Punkte (a) (2 Punkte) In einen Mischer treten drei Ströme ein. Diese haben die Massenströme ṁ 1 = 1 kg/s, ṁ 2 = 2 kg/s und ṁ 3 = 2 kg/s.
Aufgabe 1: Theorie.......................................... 30 Punkte (a) (2 Punkte) In einen Mischer treten drei Ströme ein. Diese haben die Massenströme ṁ 1 = 1 kg/s, ṁ 2 = 2 kg/s und ṁ 3 = 2 kg/s.
Physik 2 ET, SoSe 2013 Aufgaben mit Lösung 2. Übung (KW 17/18)
 2. Übung (KW 17/18) Aufgabe 1 (T 3.1 Sauerstoffflasche ) Eine Sauerstoffflasche, die das Volumen hat, enthält ab Werk eine Füllung O 2, die bei Atmosphärendruck p 1 das Volumen V 1 einnähme. Die bis auf
2. Übung (KW 17/18) Aufgabe 1 (T 3.1 Sauerstoffflasche ) Eine Sauerstoffflasche, die das Volumen hat, enthält ab Werk eine Füllung O 2, die bei Atmosphärendruck p 1 das Volumen V 1 einnähme. Die bis auf
Physikalische Chemie: Kreisprozesse
 Physikalische Chemie: Kreisprozesse Version vom 29. Mai 2006 Inhaltsverzeichnis 1 Diesel Kreisprozess 2 1.1 Wärmemenge Q.................................. 2 1.2 Arbeit W.....................................
Physikalische Chemie: Kreisprozesse Version vom 29. Mai 2006 Inhaltsverzeichnis 1 Diesel Kreisprozess 2 1.1 Wärmemenge Q.................................. 2 1.2 Arbeit W.....................................
Grundlagen der Physik II
 Grundlagen der Physik II Othmar Marti 05. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 05. 07. 2007 Klausur Die Klausur
Grundlagen der Physik II Othmar Marti 05. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 05. 07. 2007 Klausur Die Klausur
Season Opener 2012 MET
 Season Opener 2012 MET Stabilität der Atmosphäre Thermodynamisches Diagrammpapier am Beispiel SHB Typische Wetterlagen und Ableitung von Gefahrenpotentialen DIESER TEXT DIENT DER NAVIGATION Inhalt Grundlagen,
Season Opener 2012 MET Stabilität der Atmosphäre Thermodynamisches Diagrammpapier am Beispiel SHB Typische Wetterlagen und Ableitung von Gefahrenpotentialen DIESER TEXT DIENT DER NAVIGATION Inhalt Grundlagen,
Aktuelle Vertikalprofile
 Vertikalprofile (TEMPs) Ein Vertikalprofil beschreibt den Verlauf von Temperatur, Taupunkt und Wind mit der Höhe. Man unterscheidet aktuelle Vertikalprofile, die auf tatsächlichen Radiosondierungen basieren,
Vertikalprofile (TEMPs) Ein Vertikalprofil beschreibt den Verlauf von Temperatur, Taupunkt und Wind mit der Höhe. Man unterscheidet aktuelle Vertikalprofile, die auf tatsächlichen Radiosondierungen basieren,
T 300K,p 1,00 10 Pa, V 0, m,t 1200K, Kontrolle Physik Leistungskurs Klasse Hauptsatz, Kreisprozesse
 Kontrolle Physik Leistungskurs Klasse 2 7.3.207. Hauptsatz, Kreisprozesse. Als man früh aus dem Haus gegangen ist, hat man doch versehentlich die Kühlschranktür offen gelassen. Man merkt es erst, als man
Kontrolle Physik Leistungskurs Klasse 2 7.3.207. Hauptsatz, Kreisprozesse. Als man früh aus dem Haus gegangen ist, hat man doch versehentlich die Kühlschranktür offen gelassen. Man merkt es erst, als man
Versuch: Sieden durch Abkühlen
 ersuch: Sieden durch Abkühlen Ein Rundkolben wird zur Hälfte mit Wasser gefüllt und auf ein Dreibein mit Netz gestellt. Mit dem Bunsenbrenner bringt man das Wasser zum Sieden, nimmt dann die Flamme weg
ersuch: Sieden durch Abkühlen Ein Rundkolben wird zur Hälfte mit Wasser gefüllt und auf ein Dreibein mit Netz gestellt. Mit dem Bunsenbrenner bringt man das Wasser zum Sieden, nimmt dann die Flamme weg
Aufgabe 1 (60 Punkte, TTS & TTD1) Bitte alles LESBAR verfassen!!!
 Aufgabe (60 Punkte, TTS & TTD) Bitte alles LESBAR verfassen!!!. In welcher Weise ändern sich intensive und extensive Zustandsgrößen bei der Zerlegung eines Systems in Teilsysteme?. Welche Werte hat der
Aufgabe (60 Punkte, TTS & TTD) Bitte alles LESBAR verfassen!!!. In welcher Weise ändern sich intensive und extensive Zustandsgrößen bei der Zerlegung eines Systems in Teilsysteme?. Welche Werte hat der
Institut für Thermodynamik Prof. Dr. rer. nat. M. Pfitzner Thermodynamik II - Lösung 04. Aufgabe 6: (1): p 1 = 1 bar, t 1 = 15 C.
 Aufgabe 6: 2) 3) ): p = bar, t = 5 C 2): p 2 = 5 bar ) 3): p 3 = p 2 = 5 bar, t 3 = 5 C Die skizzierte Druckluftanlage soll V3 = 80 m 3 /h Luft vom Zustand 3) liefern. Dazu wird Luft vom Zustand ) Umgebungszustand)
Aufgabe 6: 2) 3) ): p = bar, t = 5 C 2): p 2 = 5 bar ) 3): p 3 = p 2 = 5 bar, t 3 = 5 C Die skizzierte Druckluftanlage soll V3 = 80 m 3 /h Luft vom Zustand 3) liefern. Dazu wird Luft vom Zustand ) Umgebungszustand)
8.4.5 Wasser sieden bei Zimmertemperatur ******
 8.4.5 ****** 1 Motivation Durch Verminderung des Luftdrucks siedet Wasser bei Zimmertemperatur. 2 Experiment Abbildung 1: Ein druckfester Glaskolben ist zur Hälfte mit Wasser gefüllt, so dass die Flüsigkeit
8.4.5 ****** 1 Motivation Durch Verminderung des Luftdrucks siedet Wasser bei Zimmertemperatur. 2 Experiment Abbildung 1: Ein druckfester Glaskolben ist zur Hälfte mit Wasser gefüllt, so dass die Flüsigkeit
Hauptsatz der Thermodynamik
 0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
4 Hauptsätze der Thermodynamik
 I Wärmelehre -21-4 Hauptsätze der hermodynamik 4.1 Energieformen und Energieumwandlung Innere Energie U Die innere Energie U eines Körpers oder eines Systems ist die gesamte Energie die darin steckt. Es
I Wärmelehre -21-4 Hauptsätze der hermodynamik 4.1 Energieformen und Energieumwandlung Innere Energie U Die innere Energie U eines Körpers oder eines Systems ist die gesamte Energie die darin steckt. Es
Thermodynamische Hauptsätze, Kreisprozesse Übung
 Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Thermodynamik 1 Klausur 12. März Alle Unterlagen zu Vorlesung und Übung sowie Lehrbücher und Taschenrechner sind als Hilfsmittel zugelassen.
 Institut für Energie- und Verfahrenstechnik Thermodynamik und Energietechnik Prof. Dr.-Ing. habil. Jadran Vrabec ThEt Thermodynamik 1 Klausur 12. März 2014 Bearbeitungszeit: 150 Minuten Umfang der Aufgabenstellung:
Institut für Energie- und Verfahrenstechnik Thermodynamik und Energietechnik Prof. Dr.-Ing. habil. Jadran Vrabec ThEt Thermodynamik 1 Klausur 12. März 2014 Bearbeitungszeit: 150 Minuten Umfang der Aufgabenstellung:
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases. f=5 Translation + Rotation. f=7 Translation + Rotation +Vibration. Wiederholung
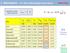 1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
Allgemeine Gasgleichung und technische Anwendungen
 Allgemeine Gasgleichung und technische Anwendungen Ziele i.allgemeine Gasgleichung: Darstellung in Diagrammen: Begriffsdefinitionen : Iso bar chor them Adiabatische Zustandsänderung Kreisprozess prinzipiell:
Allgemeine Gasgleichung und technische Anwendungen Ziele i.allgemeine Gasgleichung: Darstellung in Diagrammen: Begriffsdefinitionen : Iso bar chor them Adiabatische Zustandsänderung Kreisprozess prinzipiell:
Die Wirkung der Reibungskraft
 Die Wirkung der Reibungskraft T H Die Wirkung der Reibungskraft In einem Drucktrog (z.b. entlang einer Front) und in einem Tiefdruckzentrum konvergiert die Strömung. ----- Dabei wird die Luft gehoben.
Die Wirkung der Reibungskraft T H Die Wirkung der Reibungskraft In einem Drucktrog (z.b. entlang einer Front) und in einem Tiefdruckzentrum konvergiert die Strömung. ----- Dabei wird die Luft gehoben.
Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung.
 Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung. Nullter und Erster Hauptsatz der Thermodynamik. Thermodynamische
Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung. Nullter und Erster Hauptsatz der Thermodynamik. Thermodynamische
2. Thermodynamik Grundbegriffe Hauptsätze Thermodynamische Potentiale response -Funktionen
 2. Thermodynamik 1 2.1 Grundbegriffe 2 2.2 Hauptsätze 3 2.3 Thermodynamische Potentiale 4 2.4 response -Funktionen G. Kahl & F. Libisch (E136) Statistische Physik I Kapitel 2 5. April 2016 1 / 25 2.1 Grundbegriffe
2. Thermodynamik 1 2.1 Grundbegriffe 2 2.2 Hauptsätze 3 2.3 Thermodynamische Potentiale 4 2.4 response -Funktionen G. Kahl & F. Libisch (E136) Statistische Physik I Kapitel 2 5. April 2016 1 / 25 2.1 Grundbegriffe
Kapitel 8: Thermodynamik
 Kapitel 8: Thermodynamik 8.1 Der erste Hauptsatz der Thermodynamik 8.2 Mechanische Arbeit eines expandierenden Gases 8.3 Thermische Prozesse des idealen Gases 8.4 Wärmemaschine 8.5 Der zweite Hauptsatz
Kapitel 8: Thermodynamik 8.1 Der erste Hauptsatz der Thermodynamik 8.2 Mechanische Arbeit eines expandierenden Gases 8.3 Thermische Prozesse des idealen Gases 8.4 Wärmemaschine 8.5 Der zweite Hauptsatz
Thermodynamik I Formeln
 Thermodynamik I Formeln Tobi 4. September 2006 Inhaltsverzeichnis Thermodynamische Systeme 3. Auftriebskraft........................................ 3 2 Erster Hauptsatz der Thermodynamik 3 2. Systemenergie........................................
Thermodynamik I Formeln Tobi 4. September 2006 Inhaltsverzeichnis Thermodynamische Systeme 3. Auftriebskraft........................................ 3 2 Erster Hauptsatz der Thermodynamik 3 2. Systemenergie........................................
Vertikalprofile (TEMPs)
 Vertikalprofile (TEMPs) Inhalt 1. Einleitung... 1 2. Aktuelle Vertikalprofile... 2 3. Vertikalprofile als Prognosen... 3 4. Auswahl von Vertikalprofilen... 3 5. Interpretation der Vertikalprofile... 4
Vertikalprofile (TEMPs) Inhalt 1. Einleitung... 1 2. Aktuelle Vertikalprofile... 2 3. Vertikalprofile als Prognosen... 3 4. Auswahl von Vertikalprofilen... 3 5. Interpretation der Vertikalprofile... 4
Aufgabe 1: Kolben. Allgemeine Hinweise:
 Matrikelnummer Anzahl der bisherigen Antritte Familienname Vorname Allgemeine Hinweise: Alle Blätter sind mit Namen und Matrikelnummer zu versehen. Aus der Beschriftung muss deutlich ersichtlich sein,
Matrikelnummer Anzahl der bisherigen Antritte Familienname Vorname Allgemeine Hinweise: Alle Blätter sind mit Namen und Matrikelnummer zu versehen. Aus der Beschriftung muss deutlich ersichtlich sein,
Thermodynamik I. Sommersemester 2012 Kapitel 3, Teil 2. Prof. Dr.-Ing. Heinz Pitsch
 Thermodynamik I Sommersemester 2012 Kapitel 3, Teil 2 Prof. Dr.-Ing. Heinz Pitsch Kapitel 3, Teil 2: Übersicht 3 Energiebilanz 3.3 Bilanzgleichungen 3.3.1 Massebilanz 3.3.2 Energiebilanz und 1. Hauptsatz
Thermodynamik I Sommersemester 2012 Kapitel 3, Teil 2 Prof. Dr.-Ing. Heinz Pitsch Kapitel 3, Teil 2: Übersicht 3 Energiebilanz 3.3 Bilanzgleichungen 3.3.1 Massebilanz 3.3.2 Energiebilanz und 1. Hauptsatz
Thermodynamik I Klausur SS 2010
 Thermodynamik I Klausur 00 Prof. Dr. J. Kuck, Prof. Dr. G. Wilhelms Aufgabenteil / 00 Minuten/eite Name: Vorname: Matr.-Nr.: Das Aufgabenblatt muss unterschrieben und zusammen mit den (nummerierten und
Thermodynamik I Klausur 00 Prof. Dr. J. Kuck, Prof. Dr. G. Wilhelms Aufgabenteil / 00 Minuten/eite Name: Vorname: Matr.-Nr.: Das Aufgabenblatt muss unterschrieben und zusammen mit den (nummerierten und
Kapitel 9: Der Temperaturgradient, kurz Temp oder Emagramm, und was er bedeutet
 Kapitel 9: Der Temperaturgradient, kurz Temp oder Emagramm, und was er bedeutet Der Temperaturgradient gibt an, um wieviel C es pro 100 Meter nach oben hin kälter wird. Je schneller es nach oben hin kälter
Kapitel 9: Der Temperaturgradient, kurz Temp oder Emagramm, und was er bedeutet Der Temperaturgradient gibt an, um wieviel C es pro 100 Meter nach oben hin kälter wird. Je schneller es nach oben hin kälter
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Prof. Dr. U. Schollwöck Sommersemester 2013
 Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Winter-Semester 2017/18. Moderne Theoretische Physik IIIa. Statistische Physik
 Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
Thermodynamik Hauptsatz
 Thermodynamik. Hauptsatz Inhalt Wärmekraftmaschinen / Kälteprozesse. Hauptsatz der Thermodynamik Reversibilität Carnot Prozess Thermodynamische Temperatur Entropie Entropiebilanzen Anergie und Exergie
Thermodynamik. Hauptsatz Inhalt Wärmekraftmaschinen / Kälteprozesse. Hauptsatz der Thermodynamik Reversibilität Carnot Prozess Thermodynamische Temperatur Entropie Entropiebilanzen Anergie und Exergie
Institut für Thermodynamik Prof. Dr. rer. nat. M. Pfitzner Thermodynamik I - Lösung 8. Aufgabe kg Luft (perfektes Gas: κ = 1,4 ; R L = 287 J
 Aufgabe 3 0 kg Luft perfektes Gas: κ,4 ; R L 287 J von T 293 K und p 0,96 bar werden auf 0 bar verdichtet. Dies soll. isochor 2. isotherm 3. reversibel adiabat und 4. polytrop mit n,3 geschehen. a Skizzieren
Aufgabe 3 0 kg Luft perfektes Gas: κ,4 ; R L 287 J von T 293 K und p 0,96 bar werden auf 0 bar verdichtet. Dies soll. isochor 2. isotherm 3. reversibel adiabat und 4. polytrop mit n,3 geschehen. a Skizzieren
2. Thermodynamik Grundbegriffe Hauptsätze Thermodynamische Potentiale response -Funktionen
 2. Thermodynamik 1 2.1 Grundbegriffe 2 2.2 Hauptsätze 3 2.3 Thermodynamische Potentiale 4 2.4 response -Funktionen G. Kahl & B.M. Mladek (E136) Statistische Physik I Kapitel 2 5. März 2012 1 / 25 2.1 Grundbegriffe
2. Thermodynamik 1 2.1 Grundbegriffe 2 2.2 Hauptsätze 3 2.3 Thermodynamische Potentiale 4 2.4 response -Funktionen G. Kahl & B.M. Mladek (E136) Statistische Physik I Kapitel 2 5. März 2012 1 / 25 2.1 Grundbegriffe
Wärmelehre Wärme als Energie-Form
 Wärmelehre Wärme als Energie-Form Joule's Vorrichtung zur Messung des mechanischen Wärme-Äquivalents alte Einheit: 1 cal = 4.184 J 1 kcal Wärme erwärmt 1 kg H 2 O um 1 K Wird einem Körper mit der Masse
Wärmelehre Wärme als Energie-Form Joule's Vorrichtung zur Messung des mechanischen Wärme-Äquivalents alte Einheit: 1 cal = 4.184 J 1 kcal Wärme erwärmt 1 kg H 2 O um 1 K Wird einem Körper mit der Masse
Erinnerung an die Thermodynamik
 2 Erinnerung an die Thermodynamik 2.1 Erinnerung an die Thermodynamik Hauptsätze der Thermodynamik Thermodynamische Potentiale 14 2 Erinnerung an die Thermodynamik 2.1 Thermodynamik: phänomenologische
2 Erinnerung an die Thermodynamik 2.1 Erinnerung an die Thermodynamik Hauptsätze der Thermodynamik Thermodynamische Potentiale 14 2 Erinnerung an die Thermodynamik 2.1 Thermodynamik: phänomenologische
Grundlagen der Physik 2 Schwingungen und Wärmelehre
 Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti [email protected] Institut für Experimentelle Physik 21. 05. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 21. 05.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti [email protected] Institut für Experimentelle Physik 21. 05. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 21. 05.
Die zugeführte Wärmemenge bei isochorer Zustandsänderung berechnet sich aus
 Ü 9. Aufheizung einer Preßluftflasche Eine Preßluftflasche, in der sich.84 kg Luft bei einem Druck on.74 bar und einer Temeratur on T 0 C befinden, heizt sich durch Sonneneinstrahlung auf 98 C auf. Gesucht
Ü 9. Aufheizung einer Preßluftflasche Eine Preßluftflasche, in der sich.84 kg Luft bei einem Druck on.74 bar und einer Temeratur on T 0 C befinden, heizt sich durch Sonneneinstrahlung auf 98 C auf. Gesucht
U. Nickel Irreversible Volumenarbeit 91
 U. Nickel Irreversible Volumenarbeit 91 geben, wird die bei unterschiedlichem Innen- und Außendruck auftretende Arbeit als irreversible Volumenarbeit irr bezeichnet. Die nachfolgend angegebene Festlegung
U. Nickel Irreversible Volumenarbeit 91 geben, wird die bei unterschiedlichem Innen- und Außendruck auftretende Arbeit als irreversible Volumenarbeit irr bezeichnet. Die nachfolgend angegebene Festlegung
Mögliche Klausurfragen und aufgaben (Beispiele mit keinem Anspruch auf Vollständigkeit)
 LTT ERLANGEN 1 VON 5 FRAGENSAMMLUNG Mögliche Klausurfragen und aufgaben (Beispiele mit keinem Anspruch auf Vollständigkeit) Neben den Fragen können einfachste Rechenaufgaben gestellt werden. Bei einigen
LTT ERLANGEN 1 VON 5 FRAGENSAMMLUNG Mögliche Klausurfragen und aufgaben (Beispiele mit keinem Anspruch auf Vollständigkeit) Neben den Fragen können einfachste Rechenaufgaben gestellt werden. Bei einigen
Thermodynamik Prof. Dr.-Ing. Peter Hakenesch
 Thermodynamik Thermodynamik Prof. Dr.-Ing. Peter Hakenesch [email protected] www.lrz-muenchen.de/~hakenesch Thermodynamik Einleitung Grundbegriffe 3 Systembeschreibung 4 Zustandsgleichungen 5 Kinetische
Thermodynamik Thermodynamik Prof. Dr.-Ing. Peter Hakenesch [email protected] www.lrz-muenchen.de/~hakenesch Thermodynamik Einleitung Grundbegriffe 3 Systembeschreibung 4 Zustandsgleichungen 5 Kinetische
Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler
 TU München Reinhard Scholz Physik Department, T33 Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler http://www.wsi.tum.de/t33/teaching/teaching.htm Übung in Theoretischer Physik B (Thermodynamik)
TU München Reinhard Scholz Physik Department, T33 Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler http://www.wsi.tum.de/t33/teaching/teaching.htm Übung in Theoretischer Physik B (Thermodynamik)
Isotherme 3. 4 Adiabate 2 T 1. Adiabate Isotherme T 2. Arbeit nach außen = eingeschlossene Kurve
 Carnotscher Kreisprozess Carnot Maschine = idealisierte Maschine, experimentell nicht gut zu realisieren. Einfacher Kreisprozess aus zwei isothermen und zwei adiabatischen Zustandsänderungen. Arbeit nach
Carnotscher Kreisprozess Carnot Maschine = idealisierte Maschine, experimentell nicht gut zu realisieren. Einfacher Kreisprozess aus zwei isothermen und zwei adiabatischen Zustandsänderungen. Arbeit nach
Technische Universität Hamburg
 NAME, Vorname Studiengang Technische Universität Hamburg ÈÖÓ º Öº¹ÁÒ º Ö Ö Ë Ñ ØÞ Prüfung am 16. 08. 2016 im Fach Technische Thermodynamik II Fragenteil ohne Hilfsmittel erreichbare Punktzahl: 20 Dauer:
NAME, Vorname Studiengang Technische Universität Hamburg ÈÖÓ º Öº¹ÁÒ º Ö Ö Ë Ñ ØÞ Prüfung am 16. 08. 2016 im Fach Technische Thermodynamik II Fragenteil ohne Hilfsmittel erreichbare Punktzahl: 20 Dauer:
Phasenumwandlungsenthalpie
 Universität Potsdam Institut für Physik und Astronomie Grundpraktikum 7 Phasenumwandlungsenthalpie Die Enthalpieänderung beim Übergang eines Systems in einen anderen Aggregatzustand kann unter der Voraussetzung,
Universität Potsdam Institut für Physik und Astronomie Grundpraktikum 7 Phasenumwandlungsenthalpie Die Enthalpieänderung beim Übergang eines Systems in einen anderen Aggregatzustand kann unter der Voraussetzung,
Änderungen der kinetischen Energien sind ausschließlich in der Düse zu berücksichtigen.
 Thermodynamik II - Lösung 3 Aufgabe 5: Auf den windreichen Kanarischen Inseln ist eine Kühlanlage geplant, die Kaltwasser (Massenstrom ṁ w = 5 kg/s) von t aus = 18 C liefern soll. Das Wasser wird der Umgebung
Thermodynamik II - Lösung 3 Aufgabe 5: Auf den windreichen Kanarischen Inseln ist eine Kühlanlage geplant, die Kaltwasser (Massenstrom ṁ w = 5 kg/s) von t aus = 18 C liefern soll. Das Wasser wird der Umgebung
II. Wärmelehre. II.2. Die Hauptsätze der Wärmelehre. Physik für Mediziner 1
 II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
Dampfdruck von Flüssigkeiten (Clausius-Clapeyron' sche Gleichung)
 Versuch Nr. 57 Dampfdruck von Flüssigkeiten (Clausius-Clapeyron' sche Gleichung) Stichworte: Dampf, Dampfdruck von Flüssigkeiten, dynamisches Gleichgewicht, gesättigter Dampf, Verdampfungsenthalpie, Dampfdruckkurve,
Versuch Nr. 57 Dampfdruck von Flüssigkeiten (Clausius-Clapeyron' sche Gleichung) Stichworte: Dampf, Dampfdruck von Flüssigkeiten, dynamisches Gleichgewicht, gesättigter Dampf, Verdampfungsenthalpie, Dampfdruckkurve,
Klausur zur Vorlesung Thermodynamik
 Institut für Thermodynamik 23. August 2013 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
Institut für Thermodynamik 23. August 2013 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
Die innere Energie and die Entropie
 Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
5. Die Thermodynamischen Potentiale
 5. Die hermodynamischen Potentiale 5.1. Einführung der Potentiale Gibbs'sche Fundamentalgleichung. d = du + d, du + d δ Q d = = Ist die Entroie als Funktion von U und bekannt, = ( U, ) dann lassen sich
5. Die hermodynamischen Potentiale 5.1. Einführung der Potentiale Gibbs'sche Fundamentalgleichung. d = du + d, du + d δ Q d = = Ist die Entroie als Funktion von U und bekannt, = ( U, ) dann lassen sich
! #!! % & ( )! ! +, +,# # !.. +, ) + + /) # %
 ! #! #!! % & ( )!! +, +,# #!.. +, ) + + /)!!.0. #+,)!## 2 +, ) + + 3 4 # )!#!! ), 5 # 6! # &!). ) # )!#! #, () # # ) #!# #. # ) 6 # ) )0 4 )) #, 7) 6!!. )0 +,!# +, 4 / 4, )!#!! ))# 0.(! & ( )!! 8 # ) #+,
! #! #!! % & ( )!! +, +,# #!.. +, ) + + /)!!.0. #+,)!## 2 +, ) + + 3 4 # )!#!! ), 5 # 6! # &!). ) # )!#! #, () # # ) #!# #. # ) 6 # ) )0 4 )) #, 7) 6!!. )0 +,!# +, 4 / 4, )!#!! ))# 0.(! & ( )!! 8 # ) #+,
Kapitel IV Wärmelehre und Thermodynamik
 Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
Klausur zur Vorlesung Thermodynamik
 Institut für Thermodynamik 8. September 2015 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
Institut für Thermodynamik 8. September 2015 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
Probeklausur STATISTISCHE PHYSIK PLUS
 DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
4.6 Hauptsätze der Thermodynamik
 Thermodynamik.6 Hautsätze der Thermodynamik.6. Erster Hautsatz: Energieerhaltungssatz In einem abgeschlossenen System bleibt der gesamte Energievorrat, also die Summe aus Wärmeenergie, mechanischer Energie
Thermodynamik.6 Hautsätze der Thermodynamik.6. Erster Hautsatz: Energieerhaltungssatz In einem abgeschlossenen System bleibt der gesamte Energievorrat, also die Summe aus Wärmeenergie, mechanischer Energie
Thermodynamik. Thermodynamics. Markus Arndt. Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008
 Thermodynamik Thermodynamics Markus Arndt Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008 Die Hauptsätze der Thermodynamik & Anwendungen in Wärmekraft und Kältemaschinen
Thermodynamik Thermodynamics Markus Arndt Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008 Die Hauptsätze der Thermodynamik & Anwendungen in Wärmekraft und Kältemaschinen
6 Thermodynamische Potentiale und Gleichgewichtsbedingungen
 6 hermodynamische Potentiale und Gleichgewichtsbedingungen 6.1 Einführung Wir haben bereits folgende thermodynamische Potentiale untersucht: U(S,V ) S(U,V ) hermodynamische Potentiale sind Zustandsfunktionen
6 hermodynamische Potentiale und Gleichgewichtsbedingungen 6.1 Einführung Wir haben bereits folgende thermodynamische Potentiale untersucht: U(S,V ) S(U,V ) hermodynamische Potentiale sind Zustandsfunktionen
Einführung in die Meteorologie
 Zusammenfassung des Skripts Einführung in die Meteorologie gehalten von Prof. Roger Smith LMU München 22. Juni 2005 geschrieben von Christoph Moder http://www.skriptweb.de Hinweise (z.b. auf Fehler) bitte
Zusammenfassung des Skripts Einführung in die Meteorologie gehalten von Prof. Roger Smith LMU München 22. Juni 2005 geschrieben von Christoph Moder http://www.skriptweb.de Hinweise (z.b. auf Fehler) bitte
Becker: Thermodynamik (WS14/15) Zammefassung von Thomas Welter Stand:
 Becker: Thermdynamik (WS4/5 Zammefassung vn Thmas Welter Stand: 9.0.5 Arten vn thermdynamischen Systemen ffen Austausch vn Masse und Wärme/Arbeit geschlssen Austausch vn Wärme/Arbeit, kein Masseaustausch
Becker: Thermdynamik (WS4/5 Zammefassung vn Thmas Welter Stand: 9.0.5 Arten vn thermdynamischen Systemen ffen Austausch vn Masse und Wärme/Arbeit geschlssen Austausch vn Wärme/Arbeit, kein Masseaustausch
Einführung in die Meteorologie Teil II
 Einführung in die Meteorologie Teil II Roger K. Smith Einführung in die Meteorologie I Kinetische Gastheorie Struktur und Zusammensetzung der Atmosphäre Thermodynamik der Atmosphäre Feuchtigkeit die ützung
Einführung in die Meteorologie Teil II Roger K. Smith Einführung in die Meteorologie I Kinetische Gastheorie Struktur und Zusammensetzung der Atmosphäre Thermodynamik der Atmosphäre Feuchtigkeit die ützung
Physik III - Anfängerpraktikum- Versuch 203
 Physik III - Anfängerpraktikum- Versuch 203 Sebastian Rollke (103095) und Daniel Brenner (105292) 1. Februar 2005 Inhaltsverzeichnis 1 Vorbetrachtung 2 2 Theorie 2 2.1 Die mikroskopischen Vorgänge bei
Physik III - Anfängerpraktikum- Versuch 203 Sebastian Rollke (103095) und Daniel Brenner (105292) 1. Februar 2005 Inhaltsverzeichnis 1 Vorbetrachtung 2 2 Theorie 2 2.1 Die mikroskopischen Vorgänge bei
7. Übung: Analyse von Wetterlagen I. Nächste Übung: Donnerstag, , 14:00 MEZ. Listen Anwesenheitsliste
 7. Übung: Analyse von Wetterlagen I Nächste Übung: Donnerstag, 05.12.2013, 14:00 MEZ Listen Anwesenheitsliste Rossby-Wellen Die großräumigen, atmosphärischen Wellen auf der synoptischen bzw. planetarischen
7. Übung: Analyse von Wetterlagen I Nächste Übung: Donnerstag, 05.12.2013, 14:00 MEZ Listen Anwesenheitsliste Rossby-Wellen Die großräumigen, atmosphärischen Wellen auf der synoptischen bzw. planetarischen
Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke)
 Freie Universität Berlin W 006/007 Fachbereich Physik 8..006 tatistische Physik - heorie der Wärme (PD Dr. M. Falcke) Übungsblatt 9: hermodynamische Identitäten, hermische/kalorische Zustandsgleichung,
Freie Universität Berlin W 006/007 Fachbereich Physik 8..006 tatistische Physik - heorie der Wärme (PD Dr. M. Falcke) Übungsblatt 9: hermodynamische Identitäten, hermische/kalorische Zustandsgleichung,
Sieben Hauptsünden konservativer Auffassung der Wetterkunde
 Wie stellt man sich die Wetterkunde richtig vor, wie unterrichtet man sie korrekt? Gewisse Meteorologen, darunter auch Profis, bleiben einer Auffassung treu, die bereits 30 Jahre alt ist. Und exakt diese
Wie stellt man sich die Wetterkunde richtig vor, wie unterrichtet man sie korrekt? Gewisse Meteorologen, darunter auch Profis, bleiben einer Auffassung treu, die bereits 30 Jahre alt ist. Und exakt diese
Klausur zur Vorlesung Thermodynamik
 Institut für Thermodynamik 27. August 2012 Technische Universität Braunschweig Prof. Dr. ürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
Institut für Thermodynamik 27. August 2012 Technische Universität Braunschweig Prof. Dr. ürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
