Proseminar Datensicherheit & Versicherungsmathematik ElGamal-Verfahren
|
|
|
- Insa Melsbach
- vor 5 Jahren
- Abrufe
Transkript
1 Proseminar Datensicherheit & Versicherungsmathematik ElGamal-Verfahren Markus Kröll 14. Jänner 2009 Inhaltsverzeichnis 1 Einführung 2 2 Das ElGamal-Verfahren Schlüsselerzeugung Ver- und Entschlüsselung Effizienz des Verfahrens Beispiel Verallgemeinerung Mögliche Verallgemeinerungen Allgemeines Verfahren Elliptische Kurven Ausblick elliptische Kurven ElGamal Grundlagen über elliptischen Kurven ElGamal-Verfahren über elliptischen Kurven Beispiel Vorteile
2 1 Einführung Das ElGamal-Verfahren ist ein Public-Key Verschlüsselungssystem. Es wurde 1985 vom Kryptographen Taher Elgamal entwickelt, woher auch der Name des Kryptosystems kommt. Das Verfahren, ähnlich wie das sogenannte Diffie-Hellman-Verfahren zum Schlüsselaustausch, beruht auf der Schwierigkeit, den diskreten Logarithmus über einer primen Restklassengruppe zu lösen. Der diskrete Logarithmus ist dabei wie folgt definiert: A g a mod p A {1,..., p 1}, g Primitivwurzel, a {0,..., p 2} Der Exponent a heißt diskreter Logarithmus von A zur Basis g. Wie bei der Faktorisierung großer Zahlen oder bei einer kryptographischen Hashfunktion wird bei der Berechnung des diskreten Logarithmus angenommen, dass es sich um eine Einwegfunktion handelt. Das heißt, die bijektive Funktion selbst (potenzieren) kann ohne großen Aufwand durchgeführt werden, die dazugehörige Umkehrfunktion (logarithmieren) aber kann nicht in vertretbarer Zeit gefunden werden. Die daraus resultierende Schwierigkeit den diskreten Logarithmus in Z/pZ zu berechnen wird auch als das Diffi-Hellman Problem genannt. Bis heute kennt man keine Funktion, bei der man die Eigenschaft Einwegfunktion beweisen könnte. Auch hier, bei der Schwierigkeit des Lösens des diskreten Logarithmus, kann man also nicht absolute Sicherheit garantieren. Gerade deswegen ist ein wichtiger Vorteil des ElGamal-Verfahrens, verallgemeinert werden zu können. So können Ver- und Entschlüsselung zum Beispiel über elliptischen Kurven stattfinden. 2 Das ElGamal-Verfahren 2.1 Schlüsselerzeugung Alice wählt als erstes eine zufällige und ausreichend große Primzahl p. Desweiteren wählt Alice eine Primitivwurzel g mod p und einen Exponenten a N mit 2 a p 2, zufällig und gleichverteilt. Sie berechnet A = g a mod p. Als öffentlichen Schlüssel kann Alice nun das Tripel (p, g, A) bekannt geben, den Exponenten a hält sie geheim. 2.2 Ver- und Entschlüsselung Der Klartextraum ist die Menge {0, 1,..., p 1}. Damit Bob einen Klartext m {0, 1,..., p 1} verschlüsseln kann, wählt er zunächst eine Zufallszahl b {1,..., p 2} und berechnet und auch B = g b mod p c = A b m mod p. Der Schlüsseltext ist nun das Paar (B, c). Alice erhält von Bob diesen Schlüsseltext. Um den Klartext m wiederherzustellen, bestimmt Alice einen neuen Exponenten x = p 1 a, für den x {1,..., p 2} gilt. Durch Berechnung von B x c mod p kann der Klartext erhalten werden: 2
3 B x c g b(p 1 a) A b m (g p 1 ) b (g a ) b A b m A b A b m m mod p Dies beweist auch die Korrektheit des Verfahrens. (Von Zeile zwei auf drei wurde der kleine Satz von Fermat verwendet.) Hier nochmal das Verfahren in einer Tabelle übersichtlich zusammengefasst: Alice Bob Schlüsselerzeugung Wählt große Primzahl p, Primitvwurzel g mod p und Exponent a {2,..., p 2}. Berechnet A = g a mod p und veröffentlicht (p, g, A) Verschlüsselung Wählt zufällig b {1,..., p 2}, berechnet B = g b mod p und mit Klartext m c = A b m mod p. (B, c) ist Schlüsseltext. Entschlüsselung Berechnet mit x = p 1 a den Klartext B x c m mod p 2.3 Effizienz des Verfahrens Ein möglicher Angreifer an einer unsicheren Leitung erfährt die Zahlen p, g, A, B und c. Er erfährt aber nicht die diskreten Logarithmen a von A oder b von B zur Basis g. Zur Entschlüsselung der Nachricht würde ebendieser Angreifer aber den geheimen Schlüssel von Alice kennen. Da es keine bekannten Algorithmen gibt, die a oder b in vertretbarer Zeit berechnen können, ist das ElGamal-Verfahren sicher. Die Verschlüsselung benötigt zwei modulare Exponentationen, die Berechnung von A b mod p und g b mod p. Beide sind von der zu verschlüsselnden Nachricht unabhängig, können also vorher berechnet und in einer sicheren Umgebung abgespeichert werden. Die Verschlüsselung der aktuellen Nachricht benötigt dann nur noch eine Multiplikation modulo p. Die gewählte Primzahl p ist von derselben Größenordnung wie die des RSA-Verfahrens. Ein Effizienznachteil besteht in der sogenannten Nachtichtenexpansion: Der Schlüsseltext ist doppelt so lang wie der Klartext. Die Entschlüsselung benötigt eine einzige modulare Exponentation. Diese kann aber aber nicht durch den chinesischen Restsatz beschleunigt werden. Auch wenn theoretisch bei jeder Verschlüsselung derselbe Exponent b gewählt werden könnte, sollte dies aufgrund der Sicherheit nicht gemacht werden. Um dies zu zeigen, nehmen wir an, dass Bob zweimal dasselbe b wählt und damit zwei Nachrichten m und m verschlüsselt: c = A b m mod p c = A b m mod p = c c 1 m m 1 mod p 3
4 Wenn ein möglicher Angreifer den Klartext m kennt, dann kann er m (und auch jeden anderen Klartext) mit m c c 1 m mod p berechnen. 2.4 Beispiel Nehmen wir, an Alice will die Nachricht m = 2132 via ElGamal an Bob senden. Bob wählt p = 3359, g = 11 und a = 5 als geheimen Schlüssel. Er berechnet g a (mod 3359) und somit ist der public key das Tripel (p, g, A) = (3359, 11, 3178). Alice kennt nun diese Zahlen und wählt b = 69 um und auch g b (mod 3359) A b m (mod 3359) zu berechnen. Alice kann so den Schlüsseltext (193, 2719) an Bob senden. Dieser benutzt seinen private key und berechnet: und schließlich was der zu verschlüsselnde Wert von m war. 3 Verallgemeinerung 3.1 Mögliche Verallgemeinerungen B p 1 a (mod 3359) (mod 3359), Ein wichtiger Vorteil des ElGamal-Verfahrens ist die gewisse Flexibilität. Das Verfahren selbst funktioniert nämlich nicht nur über der primen Restklassengruppe, sondern kann auch in jeder anderen zyklischen Gruppe verwendet werden. Einzig wichtige Voraussetzungen für diese Gruppen: Die Schlüsselerzeugung, Verschlüsselung als auch die Entschlüsselung müssen innerhalb der Gruppe und mit den dort zur Verfügung stehenden Operationen effizient durchzuführen sein. Ein sicheres Verschlüsselungsystem muss auch gut und effektiv implementiert werden können, was mit ineffizienten Gruppenoperationen nicht möglich ist. Desweiteren muss natürlich das Lösen des diskreten Logarithmus innerhalb der Gruppe schwer sein, was die Grundlage des Verschlüsselungsverfahrens darstellt. Es ist vor allem dann wichtig, das ElGamal-Verfahren zu verallgemeinern, wenn ein effizienter Algorithmus zum Lösen des diskreten Algorithmus in Z/pZ bekannt werden sollte, wodurch das Verschlüsseln dort unsicher wäre. Folgende Gruppen wären zum Beispiel für ElGamal geeignet: Die Punktgruppe einer elliptischen Kurve über einem endlichen Körper (siehe 4.2). Die Jakobische Varietät hyperelliptischer Kurven über endlichen Körpern. Die Klassengruppe imaginär-quadratischer Ordnung. 4
5 3.2 Allgemeines Verfahren Alice wählt eine endliche Gruppe (G, ), ein g G und erhält die davon erzeugte zyklische Gruppe H =< g >. Sie wählt einen Exponenten a {1,..., H 1} zufällig und berechnet A = g a. (Es werden alle Berechnungen in (G, ) durchgeführt.) Das Tripel ((G, ), g, A) ist nun der public key, den Exponenten a hält Alice geheim. Bob will nun seine Nachricht m, die er zuerst in (G, ) darstellen muss, verschlüsseln. Dazu wählt er ein b {1,..., H 1} zufällig und berechnet B = g b und c = m A b. Sein Schlüsseltext lautet (B, c). Alice kann nun durch c (B a ) 1 dechiffrieren: c (B a ) 1 = m A b ((g b ) a ) 1 = m (g a ) b ((g b ) a ) 1 = m Was die ursprüngliche Nachricht ergibt. 4 Elliptische Kurven 4.1 Ausblick elliptische Kurven Als elliptische Kurve wird die Menge aller Lösungen von einer Gleichung der Form Y 2 = X 3 + AX + B bezeichnet. Diese Gleichung wird auch Weierstraßsche Normalform genannt. Für A und B muss 4A B 2 0 gelten, da sonst die Kurve mehrfache Nullstellen hätte und manche der folgenden Aussagen nicht zutreffen würden. Punkte auf einer elliptischen Kurve werden als Paare (X 1, Y 1 ) gesehen. Definiert man ein neutrales Element O mit der Eigenschaft P + O = O + P = P und setzt man für einen von O verschiedenen Punkt P = (x, y) die Regeln P = (x, y) und P + ( P ) = O, so kann man folgende wohldefinierte Addition beschreiben: Seien P 1 = (x 1, y 1 ),P 2 = (x 2, y 2 ) Punkte einer elliptischen Kurve, die beide von O verschieden sind, und für die P 1 P 2 gilt. Man berechnet P 1 + P 2 = (x 3, y 3 ) durch x 3 = λ 2 x 1 x 2 y 3 = λ(x 1 x 3 ) y 1, 5
6 wobei y 2 y 1 falls P 1 P 2 x 2 x 1 λ = 3x A falls P 1 = P 2 2y 1 Man kann zeigen, dass die Punkte einer elliptischen Kurve mit dieser Addition eine abelsche Gruppe bilden. Es ist auch möglich die Addition von Punkten einer Elliptischen Kurve rein geometrisch zu betrachten. Wollen wir auf diese Art zwei Punkte P und Q addieren, so gehen wir wie folgt vor: Gegeben sei eine elliptische Kurve E und darauf liegende Punkte P und Q. Als erstes werden die Punkte P und Q durch eine Gerade verbunden. Diese Gerade schneidet (mit einer Ausnahme auf die hier nicht weiter eingegangen wird) im endlichen ein weiteres mal die elliptische Kurve. Der erhaltene Schnittpunkt wird danach mithilfe einer vertikalen Gerade bezüglich der X-Achse gespiegelt, und man erhält den Punkt P + Q. Für diese Art der Addition gelten auch oben genannte Regeln. Leider stößt man aber bei der kryptographischen Anwendung elliptischer Kurven auf das Problem, die Grafik nicht über R, sondern über F p zu betrachten. Dies kann man nur mit fundiertem Wissen in algebraischer Geometrie bewerkstelligen. 4.2 ElGamal Grundlagen über elliptischen Kurven Wir betrachten elliptische Kurven auf endlichen Körpern F p. Dort können wir wieder wie zuvor elliptische Kurven definieren: E : Y 2 = X 3 + AX + B A, B F p, 4A B 2 0 Die Punktemenge ist nun die folgende: E(F p ) = {(x, y) : x, y F p, wobei y 2 = x 3 + Ax + b} {O} Schließlich ist der diskrete Logarithmus in E(F p ) recht analog zu Z/pZ zu betrachten. Seien P und Q Punkte in E(F p ). Das Problem des diskreten Logarithmus in elliptischen Kurven ist, eine natürliche Zahl n zu finden, so dass die Gleichung 6
7 erfüllt ist. Wir können also auch schreiben: Q = } P + P + {{... + P } = np n Additionen auf E n = log P Q Wie bereits erwähnt, müssen gewisse Kriterien gegeben sein, damit die Gruppe für El- Gamal geeignet ist. Eine davon ist die Effektivität des eigentlichen Verfahrens, was natürlich auch auf der Effektivität der Operationen der Gruppe beruht. Um n P auf E zu berechnen, wäre es vor allem für große n zu aufwendig, P, 2P, 3P,... einzeln zu berechnen. Es gibt aber den sogenannten Double-and-Add Algorithmus. Dabei werden für n 2 r r Verdoppelungen von P vorgenommen, und höchstens r Glieder zu n P aufsummiert. Dieser Algorithmus braucht also höchstens 2 log 2 n Schritte um n P zu berechnen, was auch bei sehr großen n vertretbar umgesetzt werden kann. Das zweite Kriterium für ElGamal ist die Schwierigkeit das Problem des diskreten Algorithmus zu lösen. Auch das ist in E(F p ) gegeben: Der sogenannte Pohlig-Hellman Algorithmus ist der schnellste bekannte Algorithmus, der das Problem lösen kann. Er benötigt O( p) Schritte. 4.3 ElGamal-Verfahren über elliptischen Kurven Das Verfahren selbst verläuft folgendermaßen: Alice und Bob einigen sich auf eine (außreichend große) Primzahl p, eine elliptische Kurve E über F p und auf einen Punkt P E(F p ). Alice wählt nun als Faktor ein n A N und berechnet damit Q A = n A P. Dabei ist n A der private key von Alice, Q A wird veröffentlicht. Der Text, den Bob verschlüsseln will, ist ein M E(F p ). Er wählt zufällig ein k N und berechnet C 1 = kp und C 2 = M + kq A Diese beiden Punkte (C 1, C 2 ) sendet Bob an Alice, und diese kann jetzt mit ihrem geheimen Schlüssel und C 2 n A C 1 den ursprünglichen Text berechnen: C 2 n A C 1 = (M + kq A ) n A (kp ) = M + k(n A P ) n A (kp ) = M Hier das ElGamal-Verfahren über elliptischen Kurven in einer Übersicht: 7
8 Alice Bob Schlüsselerzeugung Beide einigen sich auf große Primzahl p, eine elliptische Kurve E über F p und auf einen Punkt P E(F p ). Wählt einen Faktor n A N und berechnet Q A = n A P. Q A wird veröffentlicht. Verschlüsselung Will ein M E(F p ) verschlüsseln. Wählt zufällig k N und berechnet C 1 = kp, C 2 = M + kq A. (C 1, C 2 ) ist Schlüsseltext. Entschlüsselung Berechnet durch C 2 n A C 1 = M den Klartext. 4.4 Beispiel Gegeben sei die elliptische Kurve E(Z 11 ) : Y 2 = X 3 + 3X + 9. Diese elliptische Kurve hat folgende Punkte: X Y 2 Y 1, Y 2 Punkte 0 9 3,8 (0,3), (0,8) 2 1 1,10 (2,1), (2,10) 3 1 1,10 (3,1), (3,10) 6 1 1,10 (6,1), (6,10) ,7 (10,4), (10,7) Wir erhalten für X = 1, 4, 5, 7, 8, 9 keine Punkte, da die zugehörigen Y 2 in Z 11 keine Quadratzahl ist. Der Punkt auf den sich Alice und Bob einigen sei P = (2, 1). Alice wählt nun den Faktor n A = 7, un berechnet Q A = 7(2, 1) = (3, 10). Diesen Punkt veröffentlicht sie. Bob möchte seine Nachricht M = (10, 4) vercshlüsseln. Er wählt dafür zufällig die Zahl k = 3 und berechnet kp = 2 (2, 1) = (10, 7) M + kq A = (10, 4) + 3 (3, 10) = (10, 4) + (2, 10) = (3, 10) Der Schlüsseltext den Bob an Alice sendet ist ((10, 7), (3, 10)) Alice kann nun die verschlüsselte Nachricht wie folgt berechnen: C 2 n A C 1 = (3, 10) t (10, 7) = (3, 10) (2, 10) = (10, 4) = M 8
9 4.5 Vorteile Wie schon erwähnt besteht ein ganz offensichtlicher Vorteil in der Möglichkeit, dass ein schneller Algorithmus zum Lösen des Problems des diskreten Logarithmus in Z/pZ gefunden werden könnte. Doch nicht nur dafür ist die sogenannte EC-Cryptography (EC = Elliptic Curves) gut. Auch als alternative zu RSA-basierten Verfahren ist sie sehr wichtig. Auch hier gilt: Niemand kann die Sicherheit von RSA garantieren. Doch EC-Cryptography ist mehr als nur eine gute Alternative. Zwar ist die modulare Arithmetik auf elliptischen Kurven aufwendiger als die in primen Restklassengruppen, was aber durch eine geringere Länge der verwendeten Zahlen kompensiert wird. Während RSA-Verfahren modulare Arithmetik mit 1024-Bit-Zahlen verwenden, reichen in der EC-Cryptography bereits 160-Bit-Zahlen. So werden aufgrund der kürzeren Schlüssellänge die EC-Cryptography-Verfahren besonders für den Einsatz von SmartCards verwendet. Die Schlüssel des ElGamal-Verfahrens können auf Vorrat berechnet und abgespeichert werden. Die reine Verschlüsselung von Daten kann so sehr effizient durchgeführt werden. Je nach Implementierung besteht der Klartext aus zweibis viermal mehr Bits als die urspürngliche Nachricht. Da aber keine effizienten Angriffe auf EC-Cryptography-Verfahren bekannt sind, ist der erhöhte Datentransfer aufgrund der Sicherheit durchaus akkzeptabel Das US National Institute for Standards and Technology hat vorhergesagt, dass die 1024-Bit- Zahlen, die auch von Diffie-Hellman-Verfahren verwendet werden, höchstens bis ins Jahr 2010 ausreichende Sicherheit versprechen. Danach, so das NIST, kann man entweder die Sicherheit durch Vergrößerung der Schlüssel erreichen oder durch Umstieg auf auf EC-Cryptography. Literatur [1] Johannes Buchmann, Einführung in die Kryptographie, Springer, 2003 [2] Richard Mollin, An Introduction to Cryptography, Chapman & Hall/CRC, 2006 [3] A. Menezes et al., Handbook of Applied Cryptography, CRC-Press, 1996 [4] A. Beutelspacher, J. Schwenk, K. Wolfenstetter, Moderene Verfahren der Kryptographie Vieweg
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 5.2 ElGamal Systeme 1. Verschlüsselungsverfahren 2. Korrektheit und Komplexität 3. Sicherheitsaspekte Das ElGamal Verschlüsselungsverfahren Public-Key Verfahren von
Kryptographie und Komplexität Einheit 5.2 ElGamal Systeme 1. Verschlüsselungsverfahren 2. Korrektheit und Komplexität 3. Sicherheitsaspekte Das ElGamal Verschlüsselungsverfahren Public-Key Verfahren von
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 5 Kryptosysteme auf der Basis diskreter Logarithmen 1. Diffie Hellman Schlüsselaustausch 2. El Gamal Systeme 3. Angriffe auf Diskrete Logarithmen 4. Elliptische Kurven
Kryptographie und Komplexität Einheit 5 Kryptosysteme auf der Basis diskreter Logarithmen 1. Diffie Hellman Schlüsselaustausch 2. El Gamal Systeme 3. Angriffe auf Diskrete Logarithmen 4. Elliptische Kurven
Public-Key-Verschlüsselung und Diskrete Logarithmen
 Public-Key-Verschlüsselung und Diskrete Logarithmen Carsten Baum Institut für Informatik Universität Potsdam 10. Juni 2009 1 / 30 Inhaltsverzeichnis 1 Mathematische Grundlagen Gruppen, Ordnung, Primitivwurzeln
Public-Key-Verschlüsselung und Diskrete Logarithmen Carsten Baum Institut für Informatik Universität Potsdam 10. Juni 2009 1 / 30 Inhaltsverzeichnis 1 Mathematische Grundlagen Gruppen, Ordnung, Primitivwurzeln
Elliptische Kurven und ihre Anwendung in der Kryptographie
 Elliptische Kurven und ihre Anwendung in der Kryptographie Carsten Baum Institut für Informatik Universität Potsdam 17. Juni 2009 1 / 29 Inhaltsverzeichnis 1 Mathematische Grundlagen Charakteristik eines
Elliptische Kurven und ihre Anwendung in der Kryptographie Carsten Baum Institut für Informatik Universität Potsdam 17. Juni 2009 1 / 29 Inhaltsverzeichnis 1 Mathematische Grundlagen Charakteristik eines
VI.4 Elgamal. - vorgestellt 1985 von Taher Elgamal. - nach RSA das wichtigste Public-Key Verfahren
 VI.4 Elgamal - vorgestellt 1985 von Taher Elgamal - nach RSA das wichtigste Public-Key Verfahren - besitzt viele unterschiedliche Varianten, abhängig von zugrunde liegender zyklischer Gruppe - Elgamal
VI.4 Elgamal - vorgestellt 1985 von Taher Elgamal - nach RSA das wichtigste Public-Key Verfahren - besitzt viele unterschiedliche Varianten, abhängig von zugrunde liegender zyklischer Gruppe - Elgamal
Elliptic Curve Cryptography
 Elliptic Curve Cryptography Institut für Informatik Humboldt-Universität zu Berlin 10. November 2013 ECC 1 Aufbau 1 Asymmetrische Verschlüsselung im Allgemeinen 2 Elliptische Kurven über den reellen Zahlen
Elliptic Curve Cryptography Institut für Informatik Humboldt-Universität zu Berlin 10. November 2013 ECC 1 Aufbau 1 Asymmetrische Verschlüsselung im Allgemeinen 2 Elliptische Kurven über den reellen Zahlen
Proseminar Schlüsselaustausch (Diffie - Hellman)
 Proseminar Schlüsselaustausch (Diffie - Hellman) Schlüsselaustausch Mathematische Grundlagen Das DH Protokoll Sicherheit Anwendung 23.06.2009 Proseminar Kryptographische Protokolle SS 2009 : Diffie Hellman
Proseminar Schlüsselaustausch (Diffie - Hellman) Schlüsselaustausch Mathematische Grundlagen Das DH Protokoll Sicherheit Anwendung 23.06.2009 Proseminar Kryptographische Protokolle SS 2009 : Diffie Hellman
6: Public-Key Kryptographie (Grundidee)
 6: Public-Key Kryptographie (Grundidee) Ein Teil des Schlüssels ist nur dem Empfänger bekannt. Der auch dem Sender bekannte Teil kann sogar veröffentlicht werden. Man spricht dann von einem Schlüsselpaar.
6: Public-Key Kryptographie (Grundidee) Ein Teil des Schlüssels ist nur dem Empfänger bekannt. Der auch dem Sender bekannte Teil kann sogar veröffentlicht werden. Man spricht dann von einem Schlüsselpaar.
IT-Sicherheit Kapitel 4 Public Key Algorithmen
 IT-Sicherheit Kapitel 4 Public Key Algorithmen Dr. Christian Rathgeb Sommersemester 2014 1 Einführung Der private Schlüssel kann nicht effizient aus dem öffentlichen Schlüssel bestimmt werden bzw. die
IT-Sicherheit Kapitel 4 Public Key Algorithmen Dr. Christian Rathgeb Sommersemester 2014 1 Einführung Der private Schlüssel kann nicht effizient aus dem öffentlichen Schlüssel bestimmt werden bzw. die
Kryptographie und elliptische Kurven - oder: Wie macht man Mathematikern das Leben schwer?
 Kryptographie und elliptische Kurven - oder: Wie macht man Mathematikern das Leben schwer? Harold Gutch logix@foobar.franken.de KNF Kongress 2007, 25. 11. 2007 Outline Worum geht es überhaupt? Zusammenhang
Kryptographie und elliptische Kurven - oder: Wie macht man Mathematikern das Leben schwer? Harold Gutch logix@foobar.franken.de KNF Kongress 2007, 25. 11. 2007 Outline Worum geht es überhaupt? Zusammenhang
Einführung in die asymmetrische Kryptographie
 !"#$$% Einführung in die asymmetrische Kryptographie Dipl.-Inform. Mel Wahl Prof. Dr. Christoph Ruland Universität Siegen Institut für digitale Kommunikationssysteme Grundlagen Verschlüsselung Digitale
!"#$$% Einführung in die asymmetrische Kryptographie Dipl.-Inform. Mel Wahl Prof. Dr. Christoph Ruland Universität Siegen Institut für digitale Kommunikationssysteme Grundlagen Verschlüsselung Digitale
4 Kryptologie. Übersicht
 4 Kryptologie Übersicht 4.1 Der erweiterte euklidische Algorithmus................................ 38 4.2 Rechnen mit Restklassen modulo p................................... 39 4.3 Der kleine Satz von
4 Kryptologie Übersicht 4.1 Der erweiterte euklidische Algorithmus................................ 38 4.2 Rechnen mit Restklassen modulo p................................... 39 4.3 Der kleine Satz von
Technikseminar SS2012
 Technikseminar SS2012 ECC - Elliptic Curve Cryptography Kryptosysteme basierend auf elliptischen Kurven 11.06.2012 Gliederung Was ist ECC? ECC und andere Verfahren Diffie-Hellman-Schlüsselaustausch Funktionsweise
Technikseminar SS2012 ECC - Elliptic Curve Cryptography Kryptosysteme basierend auf elliptischen Kurven 11.06.2012 Gliederung Was ist ECC? ECC und andere Verfahren Diffie-Hellman-Schlüsselaustausch Funktionsweise
Kryptographie - eine mathematische Einführung
 Kryptographie - eine mathematische Einführung Rosa Freund 28. Dezember 2004 Überblick Grundlegende Fragestellungen Symmetrische Verschlüsselung: Blockchiffren, Hashfunktionen
Kryptographie - eine mathematische Einführung Rosa Freund 28. Dezember 2004 Überblick Grundlegende Fragestellungen Symmetrische Verschlüsselung: Blockchiffren, Hashfunktionen
Abschnitt 5: Kryptographie. j (p j 1). 1 (p 1 1)p α 2
 Abschnitt 5: Kryptographie. Zunächst wollen wir die Struktur von (Z/mZ) untersuchen. 5.1 Definition: Die Eulersche ϕ-funktion: ϕ : N N; ϕ(m) := (Z/mZ) 5.2 Bemerkung: (Z/mZ) {a {1,..., m 1} ggt(a, m) =
Abschnitt 5: Kryptographie. Zunächst wollen wir die Struktur von (Z/mZ) untersuchen. 5.1 Definition: Die Eulersche ϕ-funktion: ϕ : N N; ϕ(m) := (Z/mZ) 5.2 Bemerkung: (Z/mZ) {a {1,..., m 1} ggt(a, m) =
Kurzskript MfI:AGS WS 2018/19 Teil II: Gruppen / Teil III: Ringe 34
 Kurzskript MfI:AGS WS 2018/19 Teil II: Gruppen / Teil III: Ringe 34 Satz 4.2.11 (Chinesischer Restsatz, Ring-Version) Sind N teilerfremd (d.h. ggt( ) =1), so ist die Abbildung ein Ring-Isomorphismus. :
Kurzskript MfI:AGS WS 2018/19 Teil II: Gruppen / Teil III: Ringe 34 Satz 4.2.11 (Chinesischer Restsatz, Ring-Version) Sind N teilerfremd (d.h. ggt( ) =1), so ist die Abbildung ein Ring-Isomorphismus. :
Literatur. ISM SS 2017 Teil 8/Asymmetrische Verschlüsselung
 Literatur [8-1] Beutelspacher, A.; Schwenk, J.; Wolfenstetter, K.-D.: Moderne Verfahren der Kryptographie. 4. Auflage, Vieweg 2001 [8-2] Schmeh, Klaus: Kryptografie. dpunkt, 4. Auflage, 2009 [8-3] Schneier,
Literatur [8-1] Beutelspacher, A.; Schwenk, J.; Wolfenstetter, K.-D.: Moderne Verfahren der Kryptographie. 4. Auflage, Vieweg 2001 [8-2] Schmeh, Klaus: Kryptografie. dpunkt, 4. Auflage, 2009 [8-3] Schneier,
Literatur. [8-9] ISM WS 2018/19 Teil 8/Asymmetrische Verschlüsselung
![Literatur. [8-9] ISM WS 2018/19 Teil 8/Asymmetrische Verschlüsselung Literatur. [8-9] ISM WS 2018/19 Teil 8/Asymmetrische Verschlüsselung](/thumbs/97/132476475.jpg) Literatur [8-1] Beutelspacher, A.; Schwenk, J.; Wolfenstetter, K.-D.: Moderne Verfahren der Kryptographie. 4. Auflage, Vieweg 2001 [8-2] Schmeh, Klaus: Kryptografie. dpunkt, 6. Auflage, 2017 [8-3] Schneier,
Literatur [8-1] Beutelspacher, A.; Schwenk, J.; Wolfenstetter, K.-D.: Moderne Verfahren der Kryptographie. 4. Auflage, Vieweg 2001 [8-2] Schmeh, Klaus: Kryptografie. dpunkt, 6. Auflage, 2017 [8-3] Schneier,
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 4.4 Semantische Sicherheit 1. Sicherheit partieller Informationen 2. Das Verfahren von Rabin 3. Sicherheit durch Randomisierung Semantische Sicherheit Mehr als nur
Kryptographie und Komplexität Einheit 4.4 Semantische Sicherheit 1. Sicherheit partieller Informationen 2. Das Verfahren von Rabin 3. Sicherheit durch Randomisierung Semantische Sicherheit Mehr als nur
Elliptische Kurven. Definition Elliptische Kurve nach Willems Sei K ein Körper der Charakteristik ungleich 2 und 3. Eine Polynomgleichung der Form
 Elliptische Kurven Einstieg: - Elliptische Kurven sind spezielle algebraische Kurven, auf denen geometrisch eine Addition definiert ist. - Diese Addition spielt in der Kryptographie eine wichtige Rolle,
Elliptische Kurven Einstieg: - Elliptische Kurven sind spezielle algebraische Kurven, auf denen geometrisch eine Addition definiert ist. - Diese Addition spielt in der Kryptographie eine wichtige Rolle,
El Gamal Verschlüsselung und seine Anwendungen
 El Gamal Verschlüsselung und seine Anwendungen Andrés Guevara July 11, 2005 1 Kurze Einführung in die Kryptographie Situation: Absender will Empfänger eine Nachricht schicken. Einige Ziele der Kryptographie
El Gamal Verschlüsselung und seine Anwendungen Andrés Guevara July 11, 2005 1 Kurze Einführung in die Kryptographie Situation: Absender will Empfänger eine Nachricht schicken. Einige Ziele der Kryptographie
IT-Sicherheitsmanagement. Teil 8: Asymmetrische Verschlüsselung
 IT-Sicherheitsmanagement Teil 8: Asymmetrische Verschlüsselung 02.01.18 1 Literatur [8-1] Beutelspacher, A.; Schwenk, J.; Wolfenstetter, K.-D.: Moderne Verfahren der Kryptographie. 4. Auflage, Vieweg 2001
IT-Sicherheitsmanagement Teil 8: Asymmetrische Verschlüsselung 02.01.18 1 Literatur [8-1] Beutelspacher, A.; Schwenk, J.; Wolfenstetter, K.-D.: Moderne Verfahren der Kryptographie. 4. Auflage, Vieweg 2001
Public-Key-Kryptographie
 Kapitel 2 Public-Key-Kryptographie In diesem Kapitel soll eine kurze Einführung in die Kryptographie des 20. Jahrhunderts und die damit verbundene Entstehung von Public-Key Verfahren gegeben werden. Es
Kapitel 2 Public-Key-Kryptographie In diesem Kapitel soll eine kurze Einführung in die Kryptographie des 20. Jahrhunderts und die damit verbundene Entstehung von Public-Key Verfahren gegeben werden. Es
Kryptograhie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik
 Kryptograhie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik Übersicht Zwecke der Krytographie Techniken Symmetrische Verschlüsselung( One-time Pad,
Kryptograhie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik Übersicht Zwecke der Krytographie Techniken Symmetrische Verschlüsselung( One-time Pad,
Public Key Kryptographie
 3. Juni 2006 1 Algorithmen für Langzahlen 1 RSA 1 Das Rabin-Kryptosystem 1 Diskrete Logarithmen Grundlagen der PK Kryptographie Bisher: Ein Schlüssel für Sender und Empfänger ( Secret-Key oder symmetrische
3. Juni 2006 1 Algorithmen für Langzahlen 1 RSA 1 Das Rabin-Kryptosystem 1 Diskrete Logarithmen Grundlagen der PK Kryptographie Bisher: Ein Schlüssel für Sender und Empfänger ( Secret-Key oder symmetrische
Digitale Unterschriften mit ElGamal
 Digitale Unterschriften mit ElGamal Seminar Kryptographie und Datensicherheit Institut für Informatik Andreas Havenstein Inhalt Einführung RSA Angriffe auf Signaturen und Verschlüsselung ElGamal Ausblick
Digitale Unterschriften mit ElGamal Seminar Kryptographie und Datensicherheit Institut für Informatik Andreas Havenstein Inhalt Einführung RSA Angriffe auf Signaturen und Verschlüsselung ElGamal Ausblick
Sicherheit: Fragen und Lösungsansätze
 Vorlesung (WS 2014/15) Sicherheit: Fragen und Lösungsansätze Dr. Thomas P. Ruhroth TU Dortmund, Fakultät Informatik, Lehrstuhl XIV 1 Asymmetrische Verschlüsselung [mit freundlicher Genehmigung basierend
Vorlesung (WS 2014/15) Sicherheit: Fragen und Lösungsansätze Dr. Thomas P. Ruhroth TU Dortmund, Fakultät Informatik, Lehrstuhl XIV 1 Asymmetrische Verschlüsselung [mit freundlicher Genehmigung basierend
VI.3 RSA. - RSA benannt nach seinen Erfindern R. Rivest, A. Shamir und L. Adleman. - vorgestellt erstes Public-Key Verschlüsselungsverfahren
 VI.3 RSA - RSA benannt nach seinen Erfindern R. Rivest, A. Shamir und L. Adleman - vorgestellt 1977 - erstes Public-Key Verschlüsselungsverfahren - auch heute noch das wichtigste Public-Key Verfahren 1
VI.3 RSA - RSA benannt nach seinen Erfindern R. Rivest, A. Shamir und L. Adleman - vorgestellt 1977 - erstes Public-Key Verschlüsselungsverfahren - auch heute noch das wichtigste Public-Key Verfahren 1
Anwendung der Zahlenthoerie in der Kryptograe
 Anwendung der Zahlenthoerie in der Kryptograe Jens Helge Micke Henning Schlautmann Erstellt am: 21. Januar 2008 FÜr alles erzeugte LATEX2e 1 INHALTSVERZEICHNIS 2 Inhaltsverzeichnis 1 RSA-Verschlüsselung
Anwendung der Zahlenthoerie in der Kryptograe Jens Helge Micke Henning Schlautmann Erstellt am: 21. Januar 2008 FÜr alles erzeugte LATEX2e 1 INHALTSVERZEICHNIS 2 Inhaltsverzeichnis 1 RSA-Verschlüsselung
4 Der diskrete Logarithmus mit Anwendungen
 4 Der diskrete Logarithmus mit Anwendungen 62 4.1 Der diskrete Logarithmus Für eine ganze Zahl a Z mit ggt(a, n) = 1 hat die Exponentialfunktion mod n zur Basis a exp a : Z M n, x a x mod n, die Periode
4 Der diskrete Logarithmus mit Anwendungen 62 4.1 Der diskrete Logarithmus Für eine ganze Zahl a Z mit ggt(a, n) = 1 hat die Exponentialfunktion mod n zur Basis a exp a : Z M n, x a x mod n, die Periode
3 Public-Key-Kryptosysteme
 Stand: 05.11.2013 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 3 Public-Key-Kryptosysteme 3.1 Verschlüsselung von Nachrichten Wir betrachten ganz einfache Kommunikationsszenarien.
Stand: 05.11.2013 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 3 Public-Key-Kryptosysteme 3.1 Verschlüsselung von Nachrichten Wir betrachten ganz einfache Kommunikationsszenarien.
Public Key Kryptographie
 Public Key Kryptographie Georg Stütz 4. Dezember 2007 Inhaltsverzeichnis 1 Einführung 2 1.1 Anwendungsbeispiel................................ 2 1.2 Unterschiede zwischen symmetrischen und asymmetrischen
Public Key Kryptographie Georg Stütz 4. Dezember 2007 Inhaltsverzeichnis 1 Einführung 2 1.1 Anwendungsbeispiel................................ 2 1.2 Unterschiede zwischen symmetrischen und asymmetrischen
Wiederholung. Symmetrische Verfahren: klassische Verfahren / grundlegende Prinzipien: Substitution, Transposition, One-Time-Pad DES AES
 Wiederholung Symmetrische Verfahren: klassische Verfahren / grundlegende Prinzipien: Substitution, Transposition, One-Time-Pad DES AES Mathematische Grundlagen: algebraische Strukturen: Halbgruppe, Monoid,
Wiederholung Symmetrische Verfahren: klassische Verfahren / grundlegende Prinzipien: Substitution, Transposition, One-Time-Pad DES AES Mathematische Grundlagen: algebraische Strukturen: Halbgruppe, Monoid,
Algorithmische Kryptographie
 Algorithmische Kryptographie Walter Unger Lehrstuhl für Informatik I 16. Februar 2007 Public-Key-Systeme: Rabin 1 Das System nach Rabin 2 Grundlagen Körper Endliche Körper F(q) Definitionen Quadratwurzel
Algorithmische Kryptographie Walter Unger Lehrstuhl für Informatik I 16. Februar 2007 Public-Key-Systeme: Rabin 1 Das System nach Rabin 2 Grundlagen Körper Endliche Körper F(q) Definitionen Quadratwurzel
4: Algebraische Strukturen / Gruppen
 Stefan Lucks Diskrete Strukturen (WS 2009/10) 120 4: Algebraische Strukturen / Gruppen Definition 46 Sei G eine nichtleere Menge. Eine Funktion : G G G bezeichnen wir als Verknüpfung auf G. Das Paar (G,
Stefan Lucks Diskrete Strukturen (WS 2009/10) 120 4: Algebraische Strukturen / Gruppen Definition 46 Sei G eine nichtleere Menge. Eine Funktion : G G G bezeichnen wir als Verknüpfung auf G. Das Paar (G,
Einführung in. Elliptische Kurven. Seminarvortrag im Rahmen des Proseminars. Public-Key Kryptographie. Björn Mühlenfeld
 Einführung in Elliptische Kurven Seminarvortrag im Rahmen des Proseminars Public-Key Kryptographie Björn Mühlenfeld 10.01.2006 Übersicht 1/15 Definition Addition auf elliptischen Kurven Elliptische Kurven
Einführung in Elliptische Kurven Seminarvortrag im Rahmen des Proseminars Public-Key Kryptographie Björn Mühlenfeld 10.01.2006 Übersicht 1/15 Definition Addition auf elliptischen Kurven Elliptische Kurven
Kryptographische Protokolle
 Kryptographische Protokolle Lerneinheit 4: Schlüsselvereinbarung Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2017 8.5.2017 Einleitung Einleitung In dieser Lerneinheit
Kryptographische Protokolle Lerneinheit 4: Schlüsselvereinbarung Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2017 8.5.2017 Einleitung Einleitung In dieser Lerneinheit
Elliptische Kurven in der Kryptographie. Prusoth Vijayakumar / 16
 1 / 16 06. 06. 2011 2 / 16 Übersicht Motivation Verfahren 3 / 16 Motivation Relativ sicher, da auf der Schwierigkeit mathematischer Probleme beruhend (z.b. Diskreter Logarithmus, Faktorisieren) Schnellere
1 / 16 06. 06. 2011 2 / 16 Übersicht Motivation Verfahren 3 / 16 Motivation Relativ sicher, da auf der Schwierigkeit mathematischer Probleme beruhend (z.b. Diskreter Logarithmus, Faktorisieren) Schnellere
Hintergründe zur Kryptographie
 3. Januar 2009 Creative Commons by 3.0 http://creativecommons.org/licenses/by/3.0/ CAESAR-Chiffre Vigenère CAESAR-Chiffre Vigenère Einfache Verschiebung des Alphabets Schlüsselraum: 26 Schlüssel Einfaches
3. Januar 2009 Creative Commons by 3.0 http://creativecommons.org/licenses/by/3.0/ CAESAR-Chiffre Vigenère CAESAR-Chiffre Vigenère Einfache Verschiebung des Alphabets Schlüsselraum: 26 Schlüssel Einfaches
Satz von Euler. Satz von Euler. Korollar 1. Korollar 2 Kleiner Fermat. Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G.
 Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Satz von Euler. Satz von Euler. Korollar 1. Korollar 2 Kleiner Fermat. Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G.
 Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Satz von Euler Satz von Euler Sei (G, ) eine endl. abelsche Gruppe. Dann gilt a G = 1 für alle a G. Beweis: Sei G = {g 1,..., g n } und a G. Betrachte die Abbildung f : G G, g ag. Da a G, besitzt a ein
Vorkurs für. Studierende in Mathematik und Physik. Einführung in Kryptographie Kurzskript 2015
 Vorkurs für Studierende in Mathematik und Physik Einführung in Kryptographie Kurzskript 2015 Felix Fontein Institut für Mathematik Universität Zürich Winterthurerstrasse 190 8057 Zürich 11. September 2015
Vorkurs für Studierende in Mathematik und Physik Einführung in Kryptographie Kurzskript 2015 Felix Fontein Institut für Mathematik Universität Zürich Winterthurerstrasse 190 8057 Zürich 11. September 2015
Kryptographie mit elliptischen Kurven
 Kryptographie mit elliptischen Kurven Dr. Dirk Feldhusen SRC Security Research & Consulting GmbH Bonn - Wiesbaden Inhalt Elliptische Kurven! Grafik! Punktaddition! Implementation Kryptographie! Asymmetrische
Kryptographie mit elliptischen Kurven Dr. Dirk Feldhusen SRC Security Research & Consulting GmbH Bonn - Wiesbaden Inhalt Elliptische Kurven! Grafik! Punktaddition! Implementation Kryptographie! Asymmetrische
Asymmetrische Kryptographie u
 Asymmetrische Kryptographie u23 2015 Simon, Florob e.v. https://koeln.ccc.de Cologne 2015-10-05 1 Zahlentheorie Modulare Arithmetik Algebraische Strukturen Referenzprobleme 2 Diffie-Hellman Diffie-Hellman-Schlüsselaustausch
Asymmetrische Kryptographie u23 2015 Simon, Florob e.v. https://koeln.ccc.de Cologne 2015-10-05 1 Zahlentheorie Modulare Arithmetik Algebraische Strukturen Referenzprobleme 2 Diffie-Hellman Diffie-Hellman-Schlüsselaustausch
Proseminar Bakkalaureat TM 2008/2009 Datensicherheit und Versicherungsmathematik Public-Key-Kryptosystem
 Proseminar Bakkalaureat TM 2008/2009 Datensicherheit und Versicherungsmathematik Technische Universität Graz 29. Dezember 2008 Überblick Unterschied zwischen symmetrischen und asymmetrischen Verschlüsselungsverfahren
Proseminar Bakkalaureat TM 2008/2009 Datensicherheit und Versicherungsmathematik Technische Universität Graz 29. Dezember 2008 Überblick Unterschied zwischen symmetrischen und asymmetrischen Verschlüsselungsverfahren
Aufgabe der Kryptografie
 Aufgabe der Kryptografie Eve möchte die Unterhaltung mithören und/oder ausgetauschte Informationen ändern. Alice & Bob kommunzieren über einen unsicheren Kanal. Alice & Bob nutzen Verschlüsselung und digitale
Aufgabe der Kryptografie Eve möchte die Unterhaltung mithören und/oder ausgetauschte Informationen ändern. Alice & Bob kommunzieren über einen unsicheren Kanal. Alice & Bob nutzen Verschlüsselung und digitale
Einführung in die Kryptographie
 Ä Johannes Buchmann Einführung in die Kryptographie Dritte, erweiterte Auflage Inhaltsverzeichnis 1. Einleitung 1 2. Ganze Zahlen 3 2.1 Grundlagen 3 2.2 Teilbarkeit 4 2.3 Darstellung ganzer Zahlen 5 2.4
Ä Johannes Buchmann Einführung in die Kryptographie Dritte, erweiterte Auflage Inhaltsverzeichnis 1. Einleitung 1 2. Ganze Zahlen 3 2.1 Grundlagen 3 2.2 Teilbarkeit 4 2.3 Darstellung ganzer Zahlen 5 2.4
Proseminar Datensicherheit & Versicherungsmathematik RSA-Verfahren
 Proseminar Datensicherheit & Versicherungsmathematik RSA-Verfahren Herwig Stütz 2007-11-23 1 Inhaltsverzeichnis 1 Einführung 2 2 Das RSA-Verfahren 2 2.1 Schlüsselerzeugung.................................
Proseminar Datensicherheit & Versicherungsmathematik RSA-Verfahren Herwig Stütz 2007-11-23 1 Inhaltsverzeichnis 1 Einführung 2 2 Das RSA-Verfahren 2 2.1 Schlüsselerzeugung.................................
Betriebssysteme und Sicherheit
 Betriebssysteme und Sicherheit Asymmetrische Kryptographie WS 2012/2012 Dr.-Ing. Elke Franz Elke.Franz@tu-dresden.de 1 Überblick 1 Prinzip asymmetrischer (Konzelations-)Systeme 2 Mathematische Grundlagen
Betriebssysteme und Sicherheit Asymmetrische Kryptographie WS 2012/2012 Dr.-Ing. Elke Franz Elke.Franz@tu-dresden.de 1 Überblick 1 Prinzip asymmetrischer (Konzelations-)Systeme 2 Mathematische Grundlagen
Diskreter Logarithmus und Primkörper
 Diskreter Logarithmus und Primkörper Neben dem RSA-Verfahren ist die ElGamal-Verschlüsselung 8 ein weiteres klassische Public-Key-Verfahren, welches von Taher ElGamal auf der Konferenz CRYPTO 84 vorgestellt
Diskreter Logarithmus und Primkörper Neben dem RSA-Verfahren ist die ElGamal-Verschlüsselung 8 ein weiteres klassische Public-Key-Verfahren, welches von Taher ElGamal auf der Konferenz CRYPTO 84 vorgestellt
$Id: ring.tex,v /05/03 15:13:26 hk Exp $
 $Id: ring.tex,v 1.13 2012/05/03 15:13:26 hk Exp $ 3 Ringe 3.1 Der Ring Z m In der letzten Sitzung hatten wir die sogenannten Ringe eingeführt, dies waren Mengen A versehen mit einer Addition + und einer
$Id: ring.tex,v 1.13 2012/05/03 15:13:26 hk Exp $ 3 Ringe 3.1 Der Ring Z m In der letzten Sitzung hatten wir die sogenannten Ringe eingeführt, dies waren Mengen A versehen mit einer Addition + und einer
Trim Size: 176mm x 240mm Lang ftoc.tex V1-5.Juli :54 P.M. Page 9
 Trim Size: 176mm x 240mm Lang ftoc.tex V1-5.Juli 2018 7:54 P.M. Page 9 Auf einen Blick Über den Autor... 7 Einleitung... 19 Teil I: Verschlüsseln... 25 Kapitel 1: Sicherheit in Zeiten des Internet... 27
Trim Size: 176mm x 240mm Lang ftoc.tex V1-5.Juli 2018 7:54 P.M. Page 9 Auf einen Blick Über den Autor... 7 Einleitung... 19 Teil I: Verschlüsseln... 25 Kapitel 1: Sicherheit in Zeiten des Internet... 27
4 Diskrete Logarithmen und Anwendungen
 Stand: 19.1.2015 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 4 Diskrete Logarithmen und Anwendungen 4.1 Diskrete Logarithmen Wir betrachten eine endliche zyklische Gruppe (G,, e)
Stand: 19.1.2015 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 4 Diskrete Logarithmen und Anwendungen 4.1 Diskrete Logarithmen Wir betrachten eine endliche zyklische Gruppe (G,, e)
3: Zahlentheorie / Primzahlen
 Stefan Lucks Diskrete Strukturen (WS 2009/10) 96 3: Zahlentheorie / Primzahlen 3: Zahlentheorie / Primzahlen Stefan Lucks Diskrete Strukturen (WS 2009/10) 97 Definition 37 (Teiler, Vielfache, Primzahlen,
Stefan Lucks Diskrete Strukturen (WS 2009/10) 96 3: Zahlentheorie / Primzahlen 3: Zahlentheorie / Primzahlen Stefan Lucks Diskrete Strukturen (WS 2009/10) 97 Definition 37 (Teiler, Vielfache, Primzahlen,
Einführung in die Kryptographie
 Johannes Buchmann Einführung in die Kryptographie Fünfte Auflage \ - ' '' "'-'"*' : ) ^ Springer Inhaltsverzeichnis 1. Einleitung, : 1 2. Ganze Zahlen 3 2.1 Grundlagen 3 2.2 Teilbarkeit 4 2.3 Darstellung
Johannes Buchmann Einführung in die Kryptographie Fünfte Auflage \ - ' '' "'-'"*' : ) ^ Springer Inhaltsverzeichnis 1. Einleitung, : 1 2. Ganze Zahlen 3 2.1 Grundlagen 3 2.2 Teilbarkeit 4 2.3 Darstellung
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 4 Public Key Kryptographie mit RSA 1. Ver- und Entschlüsselung 2. Schlüsselerzeugung und Primzahltests 3. Angriffe auf das RSA Verfahren 4. Sicherheit von RSA Probleme
Kryptographie und Komplexität Einheit 4 Public Key Kryptographie mit RSA 1. Ver- und Entschlüsselung 2. Schlüsselerzeugung und Primzahltests 3. Angriffe auf das RSA Verfahren 4. Sicherheit von RSA Probleme
6: Diskrete Wahrscheinlichkeit
 Stefan Lucks Diskrete Strukturen (WS 2009/10) 219 6: Diskrete Wahrscheinlichkeit 6: Diskrete Wahrscheinlichkeit Stefan Lucks Diskrete Strukturen (WS 2009/10) 220 Wahrscheinlichkeitsrechnung Eines der wichtigsten
Stefan Lucks Diskrete Strukturen (WS 2009/10) 219 6: Diskrete Wahrscheinlichkeit 6: Diskrete Wahrscheinlichkeit Stefan Lucks Diskrete Strukturen (WS 2009/10) 220 Wahrscheinlichkeitsrechnung Eines der wichtigsten
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
4 Diskrete Logarithmen und Anwendungen
 Stand: 05.11.2013 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 4 Diskrete Logarithmen und Anwendungen 4.1 Diskrete Logarithmen Wir betrachten eine endliche zyklische Gruppe (G,, e)
Stand: 05.11.2013 Vorlesung Grundlagen und Methoden der Kryptographie Dietzfelbinger 4 Diskrete Logarithmen und Anwendungen 4.1 Diskrete Logarithmen Wir betrachten eine endliche zyklische Gruppe (G,, e)
Diffie-Hellman, ElGamal und DSS. Vortrag von David Gümbel am 28.05.2002
 Diffie-Hellman, ElGamal und DSS Vortrag von David Gümbel am 28.05.2002 Übersicht Prinzipielle Probleme der sicheren Nachrichtenübermittlung 'Diskreter Logarithmus'-Problem Diffie-Hellman ElGamal DSS /
Diffie-Hellman, ElGamal und DSS Vortrag von David Gümbel am 28.05.2002 Übersicht Prinzipielle Probleme der sicheren Nachrichtenübermittlung 'Diskreter Logarithmus'-Problem Diffie-Hellman ElGamal DSS /
Public-Key Kryptographie mit dem RSA Schema. Torsten Büchner
 Public-Key Kryptographie mit dem RSA Schema Torsten Büchner 7.12.2004 1.Einleitung 1. symmetrische-, asymmetrische Verschlüsselung 2. RSA als asymmetrisches Verfahren 2.Definition von Begriffen 1. Einwegfunktionen
Public-Key Kryptographie mit dem RSA Schema Torsten Büchner 7.12.2004 1.Einleitung 1. symmetrische-, asymmetrische Verschlüsselung 2. RSA als asymmetrisches Verfahren 2.Definition von Begriffen 1. Einwegfunktionen
Mathematische Grundlagen der Kryptografie (1321) SoSe 06
 Mathematische Grundlagen der Kryptografie (1321) SoSe 06 Klausur am 19.08.2006: Lösungsvorschläge zu den Aufgaben zu Aufgabe I.1 (a) Das numerische Äquivalent zu KLAUSUR ist die Folge [10, 11, 0, 20, 18,
Mathematische Grundlagen der Kryptografie (1321) SoSe 06 Klausur am 19.08.2006: Lösungsvorschläge zu den Aufgaben zu Aufgabe I.1 (a) Das numerische Äquivalent zu KLAUSUR ist die Folge [10, 11, 0, 20, 18,
Kleiner Fermatscher Satz, Chinesischer Restsatz, Eulersche '-Funktion, RSA
 Kleiner Fermatscher Satz, Chinesischer Restsatz, Eulersche '-Funktion, RSA Manfred Gruber http://www.lrz-muenchen.de/~gruber SS 2009, KW 15 Kleiner Fermatscher Satz Satz 1. Sei p prim und a 2 Z p. Dann
Kleiner Fermatscher Satz, Chinesischer Restsatz, Eulersche '-Funktion, RSA Manfred Gruber http://www.lrz-muenchen.de/~gruber SS 2009, KW 15 Kleiner Fermatscher Satz Satz 1. Sei p prim und a 2 Z p. Dann
Der kleine Satz von Fermat
 Der kleine Satz von Fermat Luisa-Marie Hartmann 5. Mai 2017 Inhaltsverzeichnis 1 Einleitung 3 2 Hauptteil 4 2.1 Prime Restklassengruppen............................ 4 2.2 Ordnung von Gruppenelementen........................
Der kleine Satz von Fermat Luisa-Marie Hartmann 5. Mai 2017 Inhaltsverzeichnis 1 Einleitung 3 2 Hauptteil 4 2.1 Prime Restklassengruppen............................ 4 2.2 Ordnung von Gruppenelementen........................
Das RSA-Verfahren. Proseminar Kryptographische Protokolle SS Armin Litzel
 in der Praxis Proseminar Kryptographische Protokolle SS 2009 5.5.2009 in der Praxis Gliederung 1 Grundlegendes über RSA 2 in der Praxis Allgemeine Vorgehensweise zur Verschlüsselung Signieren mit RSA 3
in der Praxis Proseminar Kryptographische Protokolle SS 2009 5.5.2009 in der Praxis Gliederung 1 Grundlegendes über RSA 2 in der Praxis Allgemeine Vorgehensweise zur Verschlüsselung Signieren mit RSA 3
Volker Kaatz. Faktorisierung. Faktorisierung. Problem und Algorithmen. Relevanz in der Kryptographie
 Faktorisierung Problem und Algorithmen Relevanz in der Kryptographie Inhalt Begriff Faktorisierung Algorithmen (Übersicht) Strategie und Komplexität Pollard p-1 Algorithmus Pseudocode, mathematische Basis,
Faktorisierung Problem und Algorithmen Relevanz in der Kryptographie Inhalt Begriff Faktorisierung Algorithmen (Übersicht) Strategie und Komplexität Pollard p-1 Algorithmus Pseudocode, mathematische Basis,
Verschlüsselung durch Exponentiation (Pohlig, Hellman, 1976)
 Verschlüsselung durch Exponentiation (Pohlig, Hellman, 1976) p : eine (grosse) Primzahl e : Zahl 0 < e < p mit ggt(e, p 1) = 1 d Inverses von e in Z p 1, dh d e 1 mod p 1 (= φ(p)) M : numerisch codierter
Verschlüsselung durch Exponentiation (Pohlig, Hellman, 1976) p : eine (grosse) Primzahl e : Zahl 0 < e < p mit ggt(e, p 1) = 1 d Inverses von e in Z p 1, dh d e 1 mod p 1 (= φ(p)) M : numerisch codierter
3: Primzahlen. 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen
 3: Primzahlen 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen Definition 40 (Teiler, Vielfache, Primzahlen, zusammengesetzte Zahlen) Seien a, b N. a ist ein Teiler von b ( a b ), falls es ein k N gibt
3: Primzahlen 111 S. Lucks Diskr Strukt. (WS 18/19) 3: Primzahlen Definition 40 (Teiler, Vielfache, Primzahlen, zusammengesetzte Zahlen) Seien a, b N. a ist ein Teiler von b ( a b ), falls es ein k N gibt
Kryptographie. Nachricht
 Kryptographie Kryptographie Sender Nachricht Angreifer Empfänger Ziele: Vertraulichkeit Angreifer kann die Nachricht nicht lesen (Flüstern). Integrität Angreifer kann die Nachricht nicht ändern ohne dass
Kryptographie Kryptographie Sender Nachricht Angreifer Empfänger Ziele: Vertraulichkeit Angreifer kann die Nachricht nicht lesen (Flüstern). Integrität Angreifer kann die Nachricht nicht ändern ohne dass
4 Der diskrete Logarithmus mit Anwendungen
 4 Der diskrete Logarithmus mit Anwendungen 53 4.1 Der diskrete Logarithmus Sei G eine Gruppe (multiplikativ geschrieben) und a G ein Element der Ordnung s (die auch sein kann). Dann ist die Exponentialfunktion
4 Der diskrete Logarithmus mit Anwendungen 53 4.1 Der diskrete Logarithmus Sei G eine Gruppe (multiplikativ geschrieben) und a G ein Element der Ordnung s (die auch sein kann). Dann ist die Exponentialfunktion
Zahlentheorie und Geometrie: alltäglich?!
 Zahlentheorie und Geometrie: alltäglich?! Gabor Wiese Institut für Experimentelle Mathematik Universität Duisburg-Essen Zahlentheorie und Geometrie: alltäglich?! p.1/26 Dinge aus dem Alltag Zahlentheorie
Zahlentheorie und Geometrie: alltäglich?! Gabor Wiese Institut für Experimentelle Mathematik Universität Duisburg-Essen Zahlentheorie und Geometrie: alltäglich?! p.1/26 Dinge aus dem Alltag Zahlentheorie
RSA Verfahren. Kapitel 7 p. 103
 RSA Verfahren RSA benannt nach den Erfindern Ron Rivest, Adi Shamir und Leonard Adleman war das erste Public-Key Verschlüsselungsverfahren. Sicherheit hängt eng mit der Schwierigkeit zusammen, große Zahlen
RSA Verfahren RSA benannt nach den Erfindern Ron Rivest, Adi Shamir und Leonard Adleman war das erste Public-Key Verschlüsselungsverfahren. Sicherheit hängt eng mit der Schwierigkeit zusammen, große Zahlen
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 12.05.2014 1 / 26 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 12.05.2014 1 / 26 Überblick 1 Hashfunktionen Erinnerung Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel:
7: Grundlagen der Public-Key-Kryptographie
 7: Grundlagen der Public-Key-Kryptographie 214 7: Public-Key-Kryptographie 7: Grundlagen der Public-Key-Kryptographie Wiederholung: Symmetrische Kryptographie 1 Schlüssel für Sender und Empfänger Benötigt
7: Grundlagen der Public-Key-Kryptographie 214 7: Public-Key-Kryptographie 7: Grundlagen der Public-Key-Kryptographie Wiederholung: Symmetrische Kryptographie 1 Schlüssel für Sender und Empfänger Benötigt
Das Verschlüsseln verstehen
 Das Verschlüsseln verstehen Kurz-Vorlesung Security Day 2014 Prof. (FH) Univ.-Doz. DI. Dr. Ernst Piller Kurzvorlesung "Das Verschlüsseln verstehen", Security Day 2014, Ernst Piller 1 Warum eigentlich Verschlüsselung
Das Verschlüsseln verstehen Kurz-Vorlesung Security Day 2014 Prof. (FH) Univ.-Doz. DI. Dr. Ernst Piller Kurzvorlesung "Das Verschlüsseln verstehen", Security Day 2014, Ernst Piller 1 Warum eigentlich Verschlüsselung
Digitale Signaturen. Einführung und das Schnorr Signatur Schema. 1 Digitale Signaturen Einführung & das Schnorr Signatur Schema.
 Digitale Signaturen Einführung und das Schnorr Signatur Schema 1 Übersicht 1. Prinzip der digitalen Signatur 2. Grundlagen Hash Funktionen Diskreter Logarithmus 3. ElGamal Signatur Schema 4. Schnorr Signatur
Digitale Signaturen Einführung und das Schnorr Signatur Schema 1 Übersicht 1. Prinzip der digitalen Signatur 2. Grundlagen Hash Funktionen Diskreter Logarithmus 3. ElGamal Signatur Schema 4. Schnorr Signatur
Mathematische Methoden für Informatiker
 Prof. Dr. 29.11.2018 32. Vorlesung Homomorphiesatz für Ringe Chinesischer Restsatz, speziell für Ringe Z n Lösen von t simultanen linearen Kongruenzen Sonderfall t = 2 Anwendungen, z.b. schnelle Addition
Prof. Dr. 29.11.2018 32. Vorlesung Homomorphiesatz für Ringe Chinesischer Restsatz, speziell für Ringe Z n Lösen von t simultanen linearen Kongruenzen Sonderfall t = 2 Anwendungen, z.b. schnelle Addition
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 11 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
ADS: Algorithmen und Datenstrukturen 2 Teil 11 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
Zahlentheorieseminar: Einführung in die Public-Key-Kryptographie
 Dozent: Dr. Ralf Gerkmann Referenten: Jonathan Paulsteiner (10939570) und Roman Lämmel ( ) Zahlentheorieseminar: Einführung in die Public-Key-Kryptographie 0. Inhalt 1. Einführung in die Kryptographie
Dozent: Dr. Ralf Gerkmann Referenten: Jonathan Paulsteiner (10939570) und Roman Lämmel ( ) Zahlentheorieseminar: Einführung in die Public-Key-Kryptographie 0. Inhalt 1. Einführung in die Kryptographie
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 4 Public Key Kryptographie mit RSA 1. Ver- und Entschlüsselung 2. Schlüsselerzeugung und Primzahltests 3. Angriffe auf das RSA Verfahren 4. Sicherheit von RSA Probleme
Kryptographie und Komplexität Einheit 4 Public Key Kryptographie mit RSA 1. Ver- und Entschlüsselung 2. Schlüsselerzeugung und Primzahltests 3. Angriffe auf das RSA Verfahren 4. Sicherheit von RSA Probleme
Kryptographie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik
 Kryptographie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik Übersicht Zwecke der Kryptographie Techniken Symmetrische Verschlüsselung( One-time Pad,
Kryptographie Wie funktioniert Electronic Banking? Kurt Mehlhorn Adrian Neumann Max-Planck-Institut für Informatik Übersicht Zwecke der Kryptographie Techniken Symmetrische Verschlüsselung( One-time Pad,
Gruppenbasierte Kryptographie. ElGamal Sicherheit. Drei Probleme. ElGamal Verschlüsselung. Benutzt zyklische Gruppen von (fast) Primzahlordnung:
 Gruppenbasierte Kryptographie Benutzt zyklische Gruppen von (fast) Primzahlordnung: G = g und #G = l = cl 0 mit c klein und l 0 prim. b G : x Z : b = g x. Das Element x heißt diskreter Logarithmus von
Gruppenbasierte Kryptographie Benutzt zyklische Gruppen von (fast) Primzahlordnung: G = g und #G = l = cl 0 mit c klein und l 0 prim. b G : x Z : b = g x. Das Element x heißt diskreter Logarithmus von
Vorlesung Sicherheit
 Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 15.05.2017 1 / 25 Überblick 1 Hashfunktionen Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel: RSA
Vorlesung Sicherheit Dennis Hofheinz ITI, KIT 15.05.2017 1 / 25 Überblick 1 Hashfunktionen Angriffe auf Hashfunktionen Zusammenfassung Hashfunktionen 2 Asymmetrische Verschlüsselung Idee Beispiel: RSA
7.3 Unizitätslänge. 8 Schlüsselaustausch und öffentliche Schlüssel
 7.3 Unizitätslänge ein Chiffrierverfahren sei über Z verschiedene Schlüssel parametrierbar also könnte ein Geheimtext zu (höchstens) Z verschiedenen Klartexten entschlüsselt werden wie viele davon sind
7.3 Unizitätslänge ein Chiffrierverfahren sei über Z verschiedene Schlüssel parametrierbar also könnte ein Geheimtext zu (höchstens) Z verschiedenen Klartexten entschlüsselt werden wie viele davon sind
Kryptographie mit elliptischen Kurven
 Westfälische Wilhelms-Universität Münster Fachbereich Mathematik und Informatik Kryptographie mit elliptischen Kurven Ausarbeitung im Rahmen des Seminars Verschlüsselungs- und Codierungstheorie an der
Westfälische Wilhelms-Universität Münster Fachbereich Mathematik und Informatik Kryptographie mit elliptischen Kurven Ausarbeitung im Rahmen des Seminars Verschlüsselungs- und Codierungstheorie an der
Diskrete Strukturen Kapitel 5: Algebraische Strukturen (RSA-Verfahren)
 WS 2016/17 Diskrete Strukturen Kapitel 5: Algebraische Strukturen (RSA-Verfahren) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 5: Algebraische Strukturen (RSA-Verfahren) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
Übungen zur Vorlesung Systemsicherheit
 Übungen zur Vorlesung Systemsicherheit Asymmetrische Kryptographie Tilo Müller, Reinhard Tartler, Michael Gernoth Lehrstuhl Informatik 1 + 4 24. November 2010 c (Lehrstuhl Informatik 1 + 4) Übungen zur
Übungen zur Vorlesung Systemsicherheit Asymmetrische Kryptographie Tilo Müller, Reinhard Tartler, Michael Gernoth Lehrstuhl Informatik 1 + 4 24. November 2010 c (Lehrstuhl Informatik 1 + 4) Übungen zur
Regine Schreier
 Regine Schreier 20.04.2016 Kryptographie Verschlüsselungsverfahren Private-Key-Verfahren und Public-Key-Verfahren RSA-Verfahren Schlüsselerzeugung Verschlüsselung Entschlüsselung Digitale Signatur mit
Regine Schreier 20.04.2016 Kryptographie Verschlüsselungsverfahren Private-Key-Verfahren und Public-Key-Verfahren RSA-Verfahren Schlüsselerzeugung Verschlüsselung Entschlüsselung Digitale Signatur mit
Elliptische Kurven in der Kryptographie
 Elliptische Kurven in der Kryptographie Sandro Schugk und Günther Nieß 25. Januar 2007 Inhalt Motivation Elliptische Kurven über R Elliptische Kurven über Z p Elliptische Kurven über K Kryptoanalyse Fazit
Elliptische Kurven in der Kryptographie Sandro Schugk und Günther Nieß 25. Januar 2007 Inhalt Motivation Elliptische Kurven über R Elliptische Kurven über Z p Elliptische Kurven über K Kryptoanalyse Fazit
Public Key Kryptographie
 4. Dezember 2007 Outline 1 Einführung 2 3 4 Einführung 1976 Whitefield Diffie und Martin Hellman 2 Schlüsselprinzip Asymmetrische Verschlüsselungsverfahren public Key private Key Anwendung E-Mail PGP openpgp
4. Dezember 2007 Outline 1 Einführung 2 3 4 Einführung 1976 Whitefield Diffie und Martin Hellman 2 Schlüsselprinzip Asymmetrische Verschlüsselungsverfahren public Key private Key Anwendung E-Mail PGP openpgp
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 6.2 Digitale Signaturen 1. Sicherheitsanforderungen 2. RSA Signaturen 3. ElGamal Signaturen Wozu Unterschriften? Verbindliche Urheberschaft von Dokumenten Unterschrift
Kryptographie und Komplexität Einheit 6.2 Digitale Signaturen 1. Sicherheitsanforderungen 2. RSA Signaturen 3. ElGamal Signaturen Wozu Unterschriften? Verbindliche Urheberschaft von Dokumenten Unterschrift
Grundlagen der Elliptic Curve Cryptography
 Grundlagen der Elliptic Curve Crptograph Mathias Schmalisch Dirk Timmermann Institut für Angewandte Mikroelektronik und Datentechnik, Universität Rostock Richard-Wagner-Str., 89 Rostock Tel.: +49 (8) 498
Grundlagen der Elliptic Curve Crptograph Mathias Schmalisch Dirk Timmermann Institut für Angewandte Mikroelektronik und Datentechnik, Universität Rostock Richard-Wagner-Str., 89 Rostock Tel.: +49 (8) 498
RSA-Verfahren Schnelle Ver- / Entschlüsselung Zusammenhang mit dem Faktorisierungsproblem. RSA-Verfahren. Herwig Stütz
 2007-11-23 Überblick 1 2 Schnelle modulare Exponentiation Chinesischer Restsatz 3 Allgemeines Public-Key Methode Rivest, Shamir und Adleman 1977 Sicherheit des Verfahrens beruht auf Schwierigkeit der Primfaktorenzerlegung
2007-11-23 Überblick 1 2 Schnelle modulare Exponentiation Chinesischer Restsatz 3 Allgemeines Public-Key Methode Rivest, Shamir und Adleman 1977 Sicherheit des Verfahrens beruht auf Schwierigkeit der Primfaktorenzerlegung
Digitale Signaturen. Prinzipielle Verfahren und mathematische Hintergründe
 Digitale Signaturen Prinzipielle Verfahren und mathematische Hintergründe Seminar für Lehramtskandidaten SS2014 a1125227 - Roman Ledinsky Digitale Signaturen Was Euch heute erwartet: 1 2 3 4 5 Prinzip
Digitale Signaturen Prinzipielle Verfahren und mathematische Hintergründe Seminar für Lehramtskandidaten SS2014 a1125227 - Roman Ledinsky Digitale Signaturen Was Euch heute erwartet: 1 2 3 4 5 Prinzip
Kryptographie und Komplexität
 Kryptographie und Komplexität Einheit 5.4 Endliche Körper und Elliptische Kurven 1. Endliche Körper 2. Elliptische Kurven über R 3. Elliptische Kurven über Z p Schwächen von ElGamal Verfahren über Z p
Kryptographie und Komplexität Einheit 5.4 Endliche Körper und Elliptische Kurven 1. Endliche Körper 2. Elliptische Kurven über R 3. Elliptische Kurven über Z p Schwächen von ElGamal Verfahren über Z p
Kryptographische Algorithmen
 Kryptographische Algorithmen Lerneinheit 6: Public Key Kryptosysteme Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2016/2017 19.9.2016 Public Key Kryptosysteme Einleitung
Kryptographische Algorithmen Lerneinheit 6: Public Key Kryptosysteme Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Wintersemester 2016/2017 19.9.2016 Public Key Kryptosysteme Einleitung
VIII. Digitale Signaturen
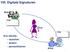 VIII. Digitale Signaturen Bob Eve Eve möchte - lauschen - ändern - personifizieren Alice 1 Aufgaben - Vertraulichkeit - Lauschen - Authentizität - Tauschen des Datenursprungs - Integrität - Änderung der
VIII. Digitale Signaturen Bob Eve Eve möchte - lauschen - ändern - personifizieren Alice 1 Aufgaben - Vertraulichkeit - Lauschen - Authentizität - Tauschen des Datenursprungs - Integrität - Änderung der
