Graphentheorie. Peter Becker Fachbereich Informatik, Hochschule Bonn-Rhein-Sieg Vorlesung Wintersemester 2014/15
|
|
|
- Frida Hummel
- vor 6 Jahren
- Abrufe
Transkript
1 Graphentheorie Peter Becker Fachbereich Informatik, Hochschule Bonn-Rhein-Sieg Vorlesung Wintersemester 2014/15
2 Allgemeines zur Vorlesung Es gibt eine Homepage zur Vorlesung: Die Vorlesung wird folienbasiert gehalten, aber die Folien enthalten nur die wichtigsten Aspekte (Definitionen, Sätze, knappe Beispiele, wichtige Bemerkung). Alles was sonst eine Vorlesung ausmacht (Erläuterungen, ausführliche Beispiele, Beweise von Sätzen, Anwendungen, Querverweise auf andere Gebiete der Informatik, etc.) gibt es nur in der Vorlesung selbst. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 1
3 Die Folien zur Vorlesung (Skript) stehen auf der Homepage vor der Vorlesung zur Verfügung. Format: PDF, einseitig Sie können also die ausgedruckten Folien mit in die Vorlesung bringen und dort mit schriftlichen Bemerkungen versehen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 2
4 Übungen Verfahrensweise für Übungen in Graphentheorie im WS 2014/15: Es gibt Hörsaalübungen (P) Homework (H) Es finden keine Übungen in Gruppen statt! Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 3
5 Hörsaalübungen (P) vierzehntäglich (ukw), jeweils Montags im HS 1/2 von 15:15 bis 16:45 Uhr (Wirtschaftsinformatik) bzw. 17:00 bis 18:30 Uhr (Informatik) Beginn der Hörsaalübungen: KW 41, 6. Oktober Ausgabe des P-Übungsblattes eine Woche vorher, zur Vorlesung in gkw. Übungsblatt 1P heute! P-Übungsblätter werden nicht bewertet. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 4
6 Primäre Ziele der P-Übungsblätter: Vorbereitung auf das kommende H-Übungsblatt Durchführung von Übungen, die nicht automatisiert überprüft werden können (insbesondere Beweise) Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 5
7 Homework (H) Mit der Hörsaalübung erscheint das H-Übungsblatt: selbständige Bearbeitung elektronische Abgabe automatisierte Bewertung keine Musterlösung Bearbeitungszeit: eine Woche Die Übungsblätter werden individuell generiert: Jeder hat andere (aber gleichartige) Aufgaben. Abgabe erfolgt Java-basiert, genauere Informationen folgen Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 6
8 Ab und zu auch Programmieraufgaben System ist Eigenentwicklung, kein Moodle, kein Praktomat Graphentheorie ist der Beta-Test für das System. Beginn von Homework erst mit dem 2. Übungsblatt. Es gibt also kein Übungsblatt 1H. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 7
9 Prüfung Gemeinsame Prüfung Graphentheorie/Stochastik 6 ECTS-Punkte für Graphentheorie/Stochastik Prüfungstermin: siehe Prüfungsplan Prüfungsform: schriftlich (Klausur) Hilfsmittel für die Gesamtprüfung: DIN A4 Blatt, zweiseitig beschrieben keine Zwischenklausur Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 8
10 Zulassungsvoraussetzung zur Klausur Insgesamt mindestens 50% der Punkte aus den H-Übungen zu Graphentheorie und Moodle-Übungen zu Statistik (wird gemeinsam gewertet)! Dies gilt für alle, auch Wiederholer! Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 9
11 Inhalt 1. Einführung 2. Repräsentation von Graphen in Computern 3. Durchsuchen von Graphen 4. Kreis- und Wegeprobleme 5. Bäume und Minimalgerüste 6. Planare Graphen und Färbungen 7. Flüsse und Zuordnungen Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 10
12 Literatur V. Turau Algorithmische Graphentheorie Oldenbourg 2009 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 11
13 S. O. Krumke, H. Noltemeier Graphentheoretische Konzepte und Algorithmen Vieweg und Teubner 2012 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 12
14 D. Jungnickel Graphen, Netzwerke und Algorithmen Spektrum Akademischer Verlag 1994 Im Buchhandel nicht mehr erhältlich Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 13
15 D. Jungnickel Graphs, Networks and Algorithms Springer 2013 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 14
16 1. Einführung Kapitelübersicht 1. Einführung Grundbegriffe und Bezeichnungen Beispiele Bäume gerichtete Graphen Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 15
17 1. Einführung Grundbegriffe und Bezeichungen Das Königsberger Brückenproblem Beispiel 1.1. [Euler, 1736] Gibt es einen Rundweg durch Königsberg, der jede der sieben Brücken genau einmal überquert? Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 16
18 1. Einführung Grundbegriffe und Bezeichungen Das Königsberger Brückenproblem (2) Die Abstraktion des Problems: Norden Insel Osten Süden Gibt es einen Rundweg, der jede Linie (Kante) genau einmal enthält? Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 17
19 1. Einführung Grundbegriffe und Bezeichungen Das Haus vom Nikolaus c b d a e Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 18
20 1. Einführung Grundbegriffe und Bezeichungen Labyrinth Beispiel 1.2. Finde einen Weg vom Start zum Ziel durch das Labyrinth! Start Ziel Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 19
21 1. Einführung Grundbegriffe und Bezeichungen Repräsentation als Graph: Start Ziel Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 20
22 1. Einführung Grundbegriffe und Bezeichungen Beispielgraph Beispiel 1.3. b Ein Graph besteht aus Knoten und Kanten. e 8 e 1 e 4 e 5 a,b,c,d sind Knoten. a e 2 c Diese Knoten werden durch die Kanten e 1 bis e 8 miteinander verbunden. e 3 e 6 e 7 d Ein Graph symbolisiert die max. zweistelligen Beziehungen zwischen Elementen einer Menge. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 21
23 1. Einführung Grundbegriffe und Bezeichungen Graph Definition 1.1. Ein Graph (graph) G = (V,E,γ) ist ein Tripel bestehend aus: V, einer nicht leeren Menge von Knoten (vertices), E, einer Menge von Kanten (edges) und γ, einer Inzidenzabbildung (incidence relation), mit γ : E {X X V,1 X 2} Zwei Knoten a,b V heißen adjazent (adjacent) gdw. e E : γ(e) = {a,b}. a V und e E heißen inzident (incident) gdw. a γ(e). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 22
24 1. Einführung Grundbegriffe und Bezeichungen Beispielgraph (2) b e 8 a e 1 e 2 e 4 e 5 c V = {a,b,c,d} E = {e 1,e 2,...,e 8 } γ = {(e 1,{a,b}),(e 2,{a,c}),(e 3,{a,d}), e 3 e 6 e 7 d (e 4,{b,c}),(e 5,{b,c}),(e 6,{c,d}), (e 7,{c,d}),(e 8,{a})} Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 23
25 1. Einführung Grundbegriffe und Bezeichungen Endliche Graphen Definition 1.2. Ein Graph G = (V,E,γ) heißt endlich (finite) gdw. die Knotenmenge V und die Kantenmenge E endlich sind. Bemerkung 1.1. Wir treffen folgende Vereinbarung: Im weiteren werden nur endliche Graphen betrachtet. Der Zusatz endlich wird dabei weggelassen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 24
26 1. Einführung Grundbegriffe und Bezeichungen Schlichte Graphen Definition 1.3. Eine Kante e heißt Schlinge (loop) gdw. e nur zu einem Knoten inzident ist. Zwei Kanten e 1,e 2 heißen parallel (parallel) gdw. sie zu den selben Knoten inzident sind. Ein Graph heißt schlicht (simple) gdw. G keine Schlingen und keine parallelen Kanten enthält. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 25
27 1. Einführung Grundbegriffe und Bezeichungen Schlichte Graphen (2) Beispiel 1.4. Der linke Graph ist schlicht, der rechte nicht. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 26
28 1. Einführung Grundbegriffe und Bezeichungen Schlichte Graphen (3) Bemerkung 1.2. Ein schlichter Graph G = (V, E) wird beschrieben durch eine Knotenmenge V und eine Kantenmenge E, wobei E eine Menge zweielementiger Teilmengen von V ist, also E {{v,w} v,w V,v w} Wir betrachten im folgenden fast ausschließlich schlichte Graphen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 27
29 1. Einführung Grundbegriffe und Bezeichungen Schlichte Graphen (4) Beispiel 1.5. c b d V = {a,b,c,d,e} E = {{a,b},{a,d},{a,e},{b,c}, {b,d},{b,e},{c,d},{d,e}} a e Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 28
30 1. Einführung Grundbegriffe und Bezeichungen Diagramme Graphen können durch Diagramme veranschaulicht werden. p q r Der selbe Graph kann viele verschiedene Diagramme haben. t s q Beispiel 1.6. G = (V,E) mit V = {p,q,r,s,t} p q t p s r E = {{p,q},{p,s},{p,t},{q,r}, r {q,s},{q,t},{r,s},{s,t}} t s Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 29
31 1. Einführung Grundbegriffe und Bezeichungen Grad Definition 1.4. Der Grad (degree) deg(v) eines Knotens v V ist die Zahl der zu v inzidenten Kanten. Hierbei zählen Schlingen doppelt. Der Maximalgrad (G) eines Graphen G ist definiert durch (G) = max{deg(v) v V} Der Minimalgrad δ(g) eines Graphen G ist definiert durch δ(g) = min{deg(v) v V} Ein Knoten v V mit deg(v) = 0 heißt isoliert. Ein Knoten v V mit deg(v) = 1 heißt Blatt. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 30
32 1. Einführung Grundbegriffe und Bezeichungen Grad (2) Beispiel 1.7. δ(g) = 0 (für Knoten h) (G) = 5 (für Knoten e) Knoten c ist ein Blatt. Knoten h ist ein isolierter Knoten. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 31
33 1. Einführung Grundbegriffe und Bezeichungen Handschlaglemma Jede Kante liefert genau zweimal einen Beitrag zu der Summe der Grade über alle Knoten. Dies gilt auch für Schlingen. Lemma 1.1. [Handschlaglemma] Für jeden Graphen G = (V,E,γ) gilt v V deg(v) = 2 E Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 32
34 1. Einführung Grundbegriffe und Bezeichungen Handschlaglemma (2) Korollar 1.2. Jeder Graph hat eine gerade Anzahl an Knoten mit ungeradem Grad. Beweis: V g := {v V deg(v) ist gerade} Definition V u := {v V deg(v) ist ungerade} Definition 2 E = v V deg(v) Handschlaglemma = v V g deg(v)+ v V u deg(v) weil V = V g +V u v V u deg(v) ist gerade V u ist gerade weil 2 E und v V g deg(v) gerade weil alle Summanden ungerade Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 33
35 1. Einführung Grundbegriffe und Bezeichungen Grad (3) Satz 1.3. Jeder Graph G = (V,E) mit mindestens zwei Knoten enthält zwei Knoten, die den gleichen Grad haben. Der Beweis dieses Satzes erfolgt mit Hilfe eines wichtigen kombinatorischen Prinzips, dem Schubfachprinzip. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 34
36 1. Einführung Grundbegriffe und Bezeichungen Schubfachprinzip Satz 1.4. [Schubfachprinzip] Es seien n Elemente auf m (paarweise disjunkte) Mengen verteilt und es gelte n > m. Dann gibt es mindestens eine Menge, die mindestens zwei Elemente enthält. Beweis: Wenn jede der m Mengen höchstens ein Element enthalten würde, dann gäbe es insgesamt höchstens m Elemente. Widerspruch zu n > m. Andere Bezeichnungen für das Schubfachprinzip: Taubenschlagprinzip, engl.: pigeonhole principle Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 35
37 1. Einführung Grundbegriffe und Bezeichungen Schubfachprinzip (2) Beispiel 1.8. Herr Müller hat in seiner Sockenkiste weiße, schwarze und grüne Socken. Wenn er vier Socken aus der Kiste nimmt, hat er mindestens zwei Socken mit der gleichen Farbe. n = 4 Elemente verteilt auf m = 3 Mengen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 36
38 1. Einführung Grundbegriffe und Bezeichungen Schubfachprinzip (3) Beispiel 1.9. Unter je fünf Punkten, die in einem Quadrat der Seitenlänge 2 liegen, gibt es stets zwei, die einen Abstand 2 haben. Wir unterteilen das Quadrat durch halbieren der Seitenlänge in vier Unterquadrate mit Seitenlänge 1. n = 5 Punkte verteilen sich auf m = 4 Unterquadrate. Dann muss mindestens ein Unterquadrat zwei Punkte enthalten Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 37
39 1. Einführung Grundbegriffe und Bezeichungen Beweis von Satz 1.3 n := V V i := {v V deg(v) = i} für i = 0,...,n 1 Definition Definition Damit haben wir aber genauso viele Knoten wie Mengen, das Schubfachprinzip ist noch nicht anwendbar. Deshalb Fallunterscheidung: G hat keinen isolierten Knoten Annahme für den 1. Fall V 0 = nach Ann. und Def. von V 0 n Knoten verteilen sich auf die m = n 1 Mengen V 1,...,V n 1 i : V i 2 weil V 0 = Schubfachprinzip Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 38
40 1. Einführung Grundbegriffe und Bezeichungen G hat einen isolierten Knoten 2. Fall, komplementär zum 1. Es existiert kein Knoten, der zu allen anderen Knoten adjazent ist V n 1 = n Knoten verteilen sich auf die m = n 1 Mengen V 0,...,V n 2 i : V i 2 kein Knoten kann zu einem isolierten Knoten adjazent sein ein Knoten v V n 1 wäre adjazent zu allen anderen Knoten weil V n 1 = Schubfachprinzip Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 39
41 1. Einführung Grundbegriffe und Bezeichungen Vollständiger Graph Definition 1.5. Sei G = (V,E) ein Graph. Gilt {v,w} E für alle v,w V,v w, dann heißt G vollständig (complete). Mit K n wird der vollständige Graph mit n Knoten bezeichnet. Bemerkung 1.3. In einem vollständigen Graphen sind je zwei Knoten adjazent. Der K n hat ( ) n 2 = n(n 1) 2 Kanten. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 40
42 1. Einführung Grundbegriffe und Bezeichungen Vollständiger Graph (2) Beispiel Die vollständigen Graphen K 4 und K 5. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 41
43 1. Einführung Grundbegriffe und Bezeichungen Komplementgraph Definition 1.6. Es sei G = (V,E) ein Graph. Dann heißt der Graph G = (V,E) mit E = {{v,w} v,w V,v w}\e Komplementgraph (complementary graph) von G. Beispiel Das Haus vom Nikolaus und sein Komplementgraph. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 42
44 1. Einführung Grundbegriffe und Bezeichungen Untergraph Definition 1.7. Sei G = (V,E) ein Graph. Ein Graph H = (W,F) mit W V und F E heißt Untergraph (subgraph) von G. Gilt W = V, dann heißt H aufspannender Untergraph (spanning subgraph) von G. Gilt F = {{v,w} {v,w} E,v,w W}, dann heißt H induzierter Untergraph (induced subgraph) von G. Für solch einen induzierten Untergraphen schreiben wir auch G(W). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 43
45 1. Einführung Grundbegriffe und Bezeichungen Untergraph (2) Beispiel Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 44
46 1. Einführung Grundbegriffe und Bezeichungen Clique Definition 1.8. Es sei G = (V,E) ein Graph. Eine Knotenmenge U V (bzw. der von U induzierte Untergraph G(U)) heißt Clique (clique) gdw. G(U) ein vollständiger Graph ist. Die maximale Größe einer Clique in G wird mit ω(g) bezeichnet, d.h. ω(g) := max{ U U ist Clique in G} Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 45
47 1. Einführung Grundbegriffe und Bezeichungen Clique (2) Beispiel {a,b,c,d} bildet eine Clique der Größe 4. {d,e,g} bildet eine Clique der Größe 3. {d,f} bildet eine Clique der Größe 2. ω(g) = 4 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 46
48 1. Einführung Grundbegriffe und Bezeichungen Wege Definition 1.9. Es sei G = (V,E) ein Graph. Eine Folge (v 0,v 1,...,v n ) von Knoten mit e i := {v i 1,v i } E für i = 1,2,...,n heißt Kantenzug (walk). Ein Kantenzug, bei dem die Kanten e i alle verschieden sind, heißt Weg (trail). Die Länge des Weges ist n. Ein Weg heißt einfacher Weg (path) gdw. die Knoten v j paarweise verschieden sind. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 47
49 1. Einführung Grundbegriffe und Bezeichungen Wege (2) Beispiel (a,b,c,a,b,f) ist ein Kantenzug, aber kein Weg. (c,b,f,c,d) ist ein Weg, aber kein einfacher Weg. (a,b,f,c,d) ist ein einfacher Weg. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 48
50 1. Einführung Grundbegriffe und Bezeichungen Kreise Definition Die folgenden Bezeichnungen beziehen sich auf Definition 1.9. Gilt in einem Kantenzug v 0 = v n, so sprechen wir von einem geschlossenen Kantenzug (closed walk). Ein Weg für den v 0 = v n gilt heißt Kreis (closed trail). Ein Kreis, bei dem die Knoten v j mit Ausnahme von v 0 = v n paarweise verschieden sind, heißt einfacher Kreis (cycle). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 49
51 1. Einführung Grundbegriffe und Bezeichungen Kreise (2) Beispiel (a,b,c,a,d,c,a) ist ein geschlossener Kantenzug, aber kein Kreis. (b,c,e,d,c,f,b) ist ein Kreis, aber kein einfacher Kreis. (a,b,f,c,a) ist ein einfacher Kreis. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 50
52 1. Einführung Grundbegriffe und Bezeichungen Bemerkungen zu Wegen und Kreisen Bemerkung 1.4. Ein Knoten alleine stellt einen Kreis der Länge 0 dar. Im folgenden ist mit Kreis immer ein nichttrivialer Kreis gemeint, d.h. ein Kreis mit Länge > 0. Nur in schlichten Graphen ist durch die Knotenfolge der Weg bzw. Kreis eindeutig bestimmt. In schlichten Graphen existieren keine Kreise der Länge 1 und 2. Die Begriffe werden in der Literatur nicht einheitlich verwendet. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 51
53 1. Einführung Grundbegriffe und Bezeichungen Hilfssätze für Wege und Kreise Lemma 1.5. Es sei G = (V,E) ein Graph und es seien a,b V,a b zwei verschiedene Knoten von G. Dann gilt: Wenn ein Kantenzug von a nach b existiert, dann existiert auch ein einfacher Weg von a nach b. Lemma 1.6. Wenn ein Graph G einen geschlossenen Kantenzug K enthält, in dem eine Kante von K nicht mehrfach vorkommt, dann enthält G auch einen einfachen Kreis. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 52
54 1. Einführung Grundbegriffe und Bezeichungen Zusammenhang Definition Es sei G = (V,E) ein Graph. Zwei Knoten v,w V heißen verbindbar gdw. ein Weg von v nach w existiert. G heißt zusammenhängend (connected) gdw. je zwei Knoten von G verbindbar sind. Eine Zusammenhangskomponente (connected component) von G ist ein durch eine Knotenmenge U V induzierter Untergraph G(U), der zusammenhängend und bezüglich der Knotenmenge maximal ist, d.h. G(W) ist nicht zusammenhängend für alle W U. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 53
55 1. Einführung Grundbegriffe und Bezeichungen Zusammenhang (2) Beispiel Ein nicht zusammenhängender Graph mit Zusammenhangskomponenten induziert durch {a,b,c} und {d,e} Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 54
56 1. Einführung Grundbegriffe und Bezeichungen Zusammenhang (3) Satz 1.7. Jeder zusammenhängende Graph mit n Knoten hat mindestens n 1 Kanten. Beweis: Mittels vollständiger Induktion über die Anzahl der Knoten, also über n. Induktionsanfang: n = 1: Ein Graph mit genau einem Knoten ist zusammenhängend und hat keine Kanten. Induktionsschritt: n n+1: Induktionsvoraussetzung: Jeder zusammenhängende Graph mit n n Knoten hat mindestens n 1 Kanten. Induktionsbehauptung: Jeder zusammenhängende Graph mit n + 1 Knoten hat mindestens n Kanten. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 55
57 1. Einführung Grundbegriffe und Bezeichungen Es sei G = (V,E) ein Graph mit n+1 Knoten. Wähle beliebigen Knoten v V. k := deg(v). k 1 Es sei G der Graph der entsteht, wenn wir aus G den Knoten v und alle mit v inzidenten Kanten entfernen. G besteht aus höchstens l k ZHKs, ZHK 1,...,ZHK l. Jede ZHK i enthält höchstens n Knoten. Wir können für jede ZHK i die Induktionsvoraussetzung anwenden. Es sei n i die Anzahl der Knoten in ZHK i. Jede ZHK i hat mindestens n i 1 Kanten. Definition weil G z.h. Definition wegen deg(v) = k weil G insgesamt nur n Knoten hat Definition Induktionsvoraussetzung Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 56
58 1. Einführung Grundbegriffe und Bezeichungen Weiterhin gilt n 1 +n 2 + +n l = n. AlleKnotenvon Gausgenommen v sind in den ZHKs von G. E (n 1 1)+ +(n l 1)+k Kanten in ZHKs von G plus die mit v inzidenten Kanten = n 1 + +n l l+k n k +k s.o., und weil l k = n q.e.d. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 57
59 1. Einführung Grundbegriffe und Bezeichungen Isomorphie Definition Zwei Graphen G 1 = (V 1,E 1 ) und G 2 = (V 2,E 2 ) heißen isomorph (isomorphic) gdw. es eine bijektive Abbildung ϕ : V 1 V 2 gibt, so dass folgendes gilt: v,w V 1 : {v,w} E 1 {ϕ(v),ϕ(w)} E 2 Wir nennen ϕ dann einen Isomorphismus von G 1 auf G 2 und schreiben G 1 = G2. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 58
60 1. Einführung Grundbegriffe und Bezeichungen Isomorphie (2) Bemerkung 1.5. Zwei Graphen sind genau dann isomorph, wenn der eine Graph aus dem anderen Graphen durch Umbennenung der Knoten hervorgeht. Isomorphe Graphen haben die gleichen graphentheoretischen Eigenschaften. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 59
61 1. Einführung Grundbegriffe und Bezeichungen Isomorphie (3) Beispiel Die Abbildung ϕ = {a w,b v,c y,d x,e z} ist ein Isomorphismus für die folgenden Graphen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 60
62 1. Einführung Grundbegriffe und Bezeichungen Isomorphie (4) Definition Wenn in Defintion 1.12 G 1 = G 2 gilt, dann ist ϕ ein Automorphismus. Bemerkung 1.6. Ein Automorphismus für einen Graphen G ist eine strukturerhaltende Abbildung von G auf sich selbst. Beispiel Für den linken Graphen aus Beispiel 1.17 ist ein Automorphismus. {a c,b b,c a,d e,e d} Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 61
63 1. Einführung Grundbegriffe und Bezeichungen Bäume Definition Es sei G = (V,E) ein Graph. G heißt Wald (forest) gdw. G keinen Kreis enthält. G heißt Baum (tree) gdw. G ein Wald und zusammenhängend ist. Beispiel Die (nichtisomorphen) Bäume mit fünf Knoten. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 62
64 1. Einführung Grundbegriffe und Bezeichungen Charakterisierung von Bäume Satz 1.8. Für einen Graphen G = (V,E) mit V = n sind die folgenden Aussagen äquivalent: 1. G ist ein Baum, 2. je zwei Knoten von G sind durch genau einen Weg verbunden, 3. G ist zusammenhängend, aber für jede Kante e E ist G = (V,E \{e}) nicht zusammenhängend, 4. G ist zusammenhängend und hat genau n 1 Kanten, Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 63
65 1. Einführung Grundbegriffe und Bezeichungen 5. G ist kreisfrei und hat genau n 1 Kanten, 6. G ist kreisfrei, aber für je zwei nicht adjazente Knoten v,w von G enthält G = (V,E {{v,w}}) genau einen Kreis. Beweis. Der Beweis zur Äquivalenz von (1) bis (3) ist Übungsaufgabe. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 64
66 1. Einführung Grundbegriffe und Bezeichungen Gerichtete Graphen Für viele Anwendungen ist es sinnvoll, die Kanten mit einer Richtung zu versehen. Definition Ein gerichteter Graph (directed graph) ist ein Paar G = (V, A) bestehend aus den Mengen V, der Menge der Knoten und A, der Menge der gerichteten Kanten (arcs), die aus geordneten Paaren (v,w) mit v,w V,v w besteht. Für eine gerichtete Kante a = (v, w) heißt v der Anfangsknoten (initial vertex) und w der Endknoten (terminal vertex) von a. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 65
67 1. Einführung Grundbegriffe und Bezeichungen Bemerkung 1.7. Man kann ungerichtete Graphen als gerichtete Graphen betrachten, bei denen die Relation A symmetrisch ist. Definition Es sei G = (V,A) ein gerichteter Graph. indeg(v) := {(x,v) (x,v) A} heißt der Eingangsgrad von v V. outdeg(v) := {(v,y) (v,y) A} heißt der Ausgangsgrad von v V. Ein gerichteter Kantenzug ist eine Folge (v 0,...,v n ) von Knoten mit e i := (v i 1,v i ) A für i = 1,...,n. Die Begriffe aus Definition 1.9 und Definition 1.10 werden analog auf gerichtete Graphen übertragen. Der einem gerichteten Graph G = (V, A) zugeordnete ungerichtete Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 66
68 1. Einführung Grundbegriffe und Bezeichungen Graph G = (V,A ) ist definiert durch: {v,w} A gdw. (v,w) A oder (w,v) A. G heißt zusammenhängend gdw. der zugeordnete ungerichtete Graph G zusammenhängend ist. G heißt stark zusammenhängend gdw. es für je zwei Knoten v,w V einen gerichteten Weg von v nach w gibt. Lemma 1.9. Für einen gerichteten Graphen G = (V,A) gilt: v V Beispiel Tafel. indeg(v) = v V outdeg(v) Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 67
69 1. Einführung Grundbegriffe und Bezeichungen DAGs Definition Ein gerichteter Graph G = (V,A) heißt DAG (dag, directed acyclic graph) gdw. G keinen einfachen gerichteten Kreis der Länge 2 enthält. Beispiel Der linke Graph ist ein DAG, der rechte nicht. c c b d b d a e a e Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 68
70 2. Repräsentationen von Graphen in Computern Kapitelinhalt 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Berechnung der Anzahl der verschiedenen Kantenzüge zwischen zwei Knoten Eigenwertprobleme und lineare Differenzengleichungen Anwendung von Differenzengleichungen für Graphen Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 69
71 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Adjazenzmatrix Definition 2.1. Gegeben sei ein Graph G = (V,E) mit V = {v 1,...,v n },n 1. Dann kann E in Form einer n n-matrix repräsentiert werden. Es sei { 1 falls {vi,v a ij = j } E 0 sonst A G = (a ij ) i,j {1,...,n} heißt die Adjazenzmatrix (adjacency matrix) von G. Bemerkung 2.1. A G ist symmetrisch und a ii = 0,1 i n. Analog kann die Adjazenzmatrix für die Darstellung gerichteter Graphen verwendet werden. Sie ist dann i.d.r. nicht symmetrisch. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 70
72 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Adjazenzmatrix (2) v 3 G = v 2 v 4 A G = v 1 v 5 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 71
73 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Adjazenzmatrix (3) Es kann in Zeit O(1) überprüft werden, ob zwei Knoten v i und v j adjazent sind. deg(v i ) ist gleich der Zeilensumme der i-ten Zeile (bzw. der Spaltensumme der i-spalte). Aufwand: O( V ) Ermittlung der Nachbarn zu einem Knoten v i : Suche in der i-ten Zeile/Spalte notwendiger Speicherplatz: O( V 2 ) Platzverbrauch ineffizient für bestimmte Graphklassen, z.b. Bäume, planare Graphen (siehe Kapitel 6) Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 72
74 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Beispiel: Adjazenzmatrix für gerichtete Graphen A = Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 73
75 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Adjazenzmatrix für nicht schlichte Graphen Für nicht schlichte Graphen gibt a ij die Anzahl der Kanten zwischen v i und v j an. Wenn Schlingen vorliegen, sind die Diagonalelemente der entsprechenden Knoten ungleich 0. Das Element a ii gibt dann die Anzahl der Schlingen am Knoten v i an. Bei der Gradermittlung müssen die Diagonalelemente doppelt gezählt werden: n deg(v i ) = 2 a ii + k=1,k i a ik Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 74
76 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Beispiel: Adjazenzmatrix für nicht schlichte Graphen A = Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 75
77 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Adjazenzmatrix: gerichtet und nicht schlicht Prinzipiell können natürlich auch gerichtete Graphen nicht schlicht sein, d.h. an Knoten existieren Schlingen oder zwischen zwei Knoten a und b gibt es mehrere Kanten mit der gleichen Richtung (von a nach b). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 76
78 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Beispiel: gerichtet und nicht schlicht A = Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 77
79 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Adjazenzliste Definition 2.2. Gegeben sei ein Graph G = (V,E) mit V = {v 1,...,v n },n 1. Dann kann E in Form einer Liste von n-listen A i repräsentiert werden. Für 1 i n seien v i1,v i2,...,v ni die mit v i V adjazenten Knoten. Die Liste heißt die Adjazenzliste von v i V. A i = (v i1,v i2,...,v ni ) Die Liste L G = (A 1,...,A n ) ist die Adjazenzlistendarstellung von G. Für einen gerichteten Graphen G = (V,A) enthält die Adjazenzliste A i die Knoten w V, für die (v i,w) A gilt. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 78
80 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Adjazenzliste (2) v 1 v 2 v 5 v 3 v 2 v 1 v 3 v 4 v 2 v 4 L G = v 3 v 2 v 4 G = v 4 v 2 v 3 v 5 v 5 v 1 v 4 v 1 v 5 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 79
81 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Adjazenzliste (3) Um zu überprüfen, ob zwei Knoten v i und v j adjazent sind, muss die Adjazenzliste von v i durchsucht werden. Dies ist nicht in O(1) möglich, der genaue Aufwand hängt von der Implementierung der Adjazenzliste ab. Der Knotengrad entspricht der Länge der Adjazenzliste. Die Nachbarn zu einem Knoten liegen direkt in der Adjazenzliste vor. notwendiger Speicherplatz: O( V + E ) Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 80
82 2. Repräsentationen von Graphen in Computern Anzahl der Kantenzüge zwischen zwei Knoten Beispiel: Anzahl Wege zwischen zwei Knoten (1) Wir betrachten als Beispiel den folgenden gerichteten Graphen G mit seiner Adjazenzmatrix: A = Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 81
83 2. Repräsentationen von Graphen in Computern Anzahl der Kantenzüge zwischen zwei Knoten Beispiel: Anzahl Wege zwischen zwei Knoten (2) Wir bilden die Potenzen der Adjazenzmatrix A: A 2 = A 3 = Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 82
84 2. Repräsentationen von Graphen in Computern Anzahl der Kantenzüge zwischen zwei Knoten A 4 = A k = für k 5 Das Element a i,j der Matrizen A k gibt hier die Anzahl der (einfachen) Wege der Länge k von i nach j an. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 83
85 2. Repräsentationen von Graphen in Computern Anzahl der Kantenzüge zwischen zwei Knoten Anzahl der Kantenzüge zwischen zwei Knoten Satz 2.1. Es sei G = (V,E) ein Graph mit der Adjazenzmatrix A = (a ij ). Dann gibt das Element a (r) ij der Matrix A r die Anzahl der Kantenzüge der Länge r von v i nach v j an. Beweis: Induktion über r. r = 1 : Damit gilt A r = A. Die Adjazenzmatrix gibt genau die Kantenzüge der Länge 1 an. r r +1: Jeder Kantenzug der Länge r+1 zwischen zwei Knoten v i und v j besteht Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 84
86 2. Repräsentationen von Graphen in Computern Anzahl der Kantenzüge zwischen zwei Knoten aus einem Kantenzug der Länge r zwischen v i und einem Knoten v k sowie der Kante {v k,v j }. Nach I.V. gibt A r die Anzahl der Kantenzüge der Länge r zwischen zwei Knoten an. Es gilt a (r+1) ij = V k=1 a (r) ik a kj Da a kj = 1 gdw. zwischen v i und v j eine Kante ist, beschreibt diese Formel die Anzahl der Möglichkeiten, einen Kantenzug der Länge r + 1 zwischen v i und v j aus einem Kantenzug der Länge r zwischen v i und einem Knoten v k sowie der Kante {v k,v j } zu bilden. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 85
87 2. Repräsentationen von Graphen in Computern Anzahl der Kantenzüge zwischen zwei Knoten Korollar 2.2. Es sei G = (V,E) ein Graph mit der Adjazenzmatrix A = (a ij ). Dann gibt das Element b ij der Matrix B = A+A 2 + +A p die Anzahl der Kantenzüge mit einer Länge p von v i nach v j an. Korollar 2.3. Es sei G = (V,E) ein Graph mit der Adjazenzmatrix A = (a ij ) und es sei B = A+A 2 + +A V 1 Dann gilt: G ist genau dann zusammenhängend, wenn b ij > 0 für alle i j gilt. Beweis: Wenn G zusammenhängend ist, Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 86
88 2. Repräsentationen von Graphen in Computern Anzahl der Kantenzüge zwischen zwei Knoten gibt es zwischen zwei beliebigen Knoten v i und v j mindestens einen Weg, damit auch mindestens einen einfachen Weg. Ein einfacher Weg hat eine Länge V 1. Damit liefert der einfache Weg (als Kantenzug) einen Beitrag zu b ij. Also folgt b ij > 0. Andererseits folgt aus b ij > 0, dass es mindestens einen Kantenzug und damit auch einen Weg von v i nach v j gibt. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 87
89 2. Repräsentationen von Graphen in Computern Anzahl der Kantenzüge zwischen zwei Knoten Somit folgt aus b ij > 0 für alle i j, dass es zwischen je zwei Knoten von G einen Weg gibt. Damit ist G zusammenhängend. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 88
90 2. Repräsentationen von Graphen in Computern Anzahl der Kantenzüge zwischen zwei Knoten Bemerkungen Weil in Dags jeder Kantenzug ein gerichteter einfacher Weg ist, liefert A r dort sogar die Anzahl der einfachen Wege der Länge r. Auch können wir mit diesem Ansatz prinzipiell testen, ob ein gerichteter Graph kreisfrei ist (für p = V müssen die b ii alle ungleich 0 sein). Sowohl für die Kreisfreiheit als auch für den Zusammenhang sind diese Berechnungsansätze aber ineffizient. Im nächsten Kapitel werden wir effizientere Algorithmen für diese Probleme kennenlernen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 89
91 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Eigenwerte und Eigenvektoren Siehe Analysis (von der Hude, Folie 20): Definition 2.3. Ein Vektor x R n heißt Eigenvektor der quadratischen n n-matrix A zum Eigenwert λ R, wenn gilt Ax = λx Die Eigenwerte der Matrix A sind alle Werte λ, für die ein Eigenvektor existiert. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 90
92 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Bemerkungen zu Eigenwerten und Eigenvektoren Da der Nullvektor natürlich immer auf sich selbst abgebildet wird, verlangen wir von einem Eigenvektor stets x 0. In der Ebene (2D) beschreiben Eigenwerte und Eigenvektoren Fixgeraden von linearen Abbildungen. ( ) 0 4 Beispiel: A =. 1 0 ( ) ( ) 2 2 A hat die Eigenvektoren u = und v = mit den Eigenwerte 1 1 λ = 2 und µ = 2. Die durch die Eigenvektoren definierten Geraden werden auf sich selbst abgebildet (als Menge, nicht punktweise). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 91
93 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Eine punktweise Abbildung wäre eine Fixpunktgerade. Dies sind Geraden definiert durch Eigenvektoren zum Eigenwert 1. Eigenwertprobleme betrachtet man üblicherweise nicht in R, sondern in C, weil für eine allgemeine reelle Matrix die Existenz von reellen Eigenwerten nicht garantiert ist. Beispiel: I.A. liefert eine Drehung keine Fixgeraden. So hat die Drehmatrix ( ) nur komplexe Eigenwerte (Drehung um 90 bzw. π 2 ). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 92
94 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Eigenwerte symmetrischer Matrizen Vgl. Analysis (von der Hude, Folie 28 und Aufgabe 4 von Aufgabenblatt 1P): Satz 2.4. Es sei A eine reelle symmetrische n n-matrix. Dann sind alle Eigenwerte von A reell. Es gibt n linear unabhängige Eigenvektoren von A. Linear unabhängige Eigenvektoren von A sind zueinander orthogonal (stehen senkrecht aufeinander). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 93
95 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Berechnung von Eigenwerten und -vektoren Die Eigenwerte ergeben sich aus den Nullstellen des charakteristischen Polynoms P(λ) = det(a λe) = A λe Hierbei ist E die n-dimensionale Einheitsmatrix. ( ) 1 6 Beispiel 2.1. Für A = ergibt sich 1 0 P(λ) = (1 λ)( λ) 6 = λ 2 λ 6! = 0 Mit der p-q-formel erhalten wir λ 1,2 = 1 2 ± = 1 2 ± 5 2 = 3 bzw. 2 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 94
96 2. Repräsentationen von Graphen in Computern Eigenwertprobleme ( ) u1 Für λ = 3 ergibt sich der Eigenvektor u = aus u u 1 = 3u 2 (zweite ( ) 2 3 Zeile von A). Somit ist u = ein Eigenvektor zum Eigenwert 3. 1 ( ) 2 Analog ergibt sich, dass v = ein Eigenvektor zum Eigenwert 2 1 ist. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 95
97 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Was bringen uns Eigenwerte? Wir können bspw. die Berechnung einer n-fachen Anwendung einer linearen Abbildung deutlich beschleunigen. Beispiel 2.2. Wo landet der Punkt p = (11, 3), wenn wir ihn n-mal mit der linearen Abbildung bzw. der Matrix A aus Beispiel 2.1 transformieren? Bei p = A n p Naive Berechnung: n-fach Multiplikation von A mit einem Vektor, beginnend mit dem Vektor p. p (0) = p p (i+1) = Ap (i) für i = 0,1,... Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 96
98 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Es gilt dann p = p (n). Aufwand: 4n Multiplikationen und 2n Additionen, also O(n). Angenommen wir könnten p als Linearkombination der Eigenvektoren u und v darstellen, also p = αu+βv Dann ergibt sich p = A n p = A n (αu+βv) = αa n u+βa n v = αλ n 1u+βλ n 2v = α3 n u+β( 2) n v Aufwand: 2 Exponentenberechnungen, 6 Multiplikationen, 2 Additionen, also O(1) Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 97
99 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Aber wie bestimmen wir α und β? Prinzipiell kein Problem, sie ergeben sich aus dem linearen GLS αu+βv = ( 11 3 ) also Lösung hier: α = 1,β = 4, also 3α 2β = 11 α + β = 3 p = A n p = ( ) 3 n+1 n+3 +( 1) n 2 3 n +( 1) n+1 2n+2 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 98
100 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Und für einen beliebigen Punkt p = ( x y )? Dann lautet das GLS 3α 2β = x α + β = y Allgemeine Lösung: α = x+2y,β = 5 Ebenfalls in O(1) berechenbar. 3y x 5 Fazit: Für jedes p R 2 können wir A n p in O(1) berechnen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 99
101 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Berechnung der Potenzen einer Adjazenzmatrix Zur Berechnung der Anzahl an Kantenzügen zwischen Knoten benötigen wir die Potenzen der Adjazenzmatrix. Können wir auch A k mit der Hilfe von Eigenwerten und -vektoren explizit berechnen? Ansatz: Wir betrachten die einzelnen Spaltenvektoren der Adjazenzmatrix. A = (a (1) a (2) a (n)) wobei a (i) der i-te Spaltenvektor von A ist. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 100
102 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Dann gilt: A k = A k 1( a (1) a (2) a (n)) = (A k 1 a (1) A k 1 a (2) A k 1 a (n)) Damit können wir A k mit Hilfe der Techniken aus Beispiel 2.2 berechnen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 101
103 2. Repräsentationen von Graphen in Computern Eigenwertprobleme Berechnungsbeispiel Beispiel 2.3. Graph zur Adjazenzmatrix aus Beispiel 2.1. ( 1 1 ) = 3 5 ( 3 1 ) ( 2 1 ) ( 6 0 ) = 6 5 ( 3 1 ) 6 5 ( 2 1 ) Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 102
104 2. Repräsentationen von Graphen in Computern Eigenwertprobleme ( ( ) ( )) A n = A n 1 1 A 1 n ( ) 3 3 = 5 3n 1( + 2 ( ) ) ( 2)n n 1( 6 ( ( 2)n 1 1 = 1 ( 3 n+1 +( 1) n 2 ) n n+1 n+1 3 ( 1) n n +( 1) n 1 2 n 2 3 n 3 ( 1) n 1 2n Damit haben wir für alle Kantenzüge der Länge n eine explizite Formel. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 103
105 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Lineare Differenzengleichungen Die Fibonacci-Zahlen F n sind definiert durch F 0 = 0 F 1 = 1 F n = F n 1 +F n 2 für n >= 2 Die letzte Zeile ist ein Beispiel für eine homogene lineare Differenzengleichung zweiter Ordnung. Allgemein k-ter Ordnung: F n = a 1 F n 1 + +a k F n k Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 104
106 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Lösungsansatz für homogene lineare Differenzengleichungen Wir stellen die homogene lineare Differenzengleichung in Matrixform dar. Beispiel für die Fibonnaci-Zahlen: ( Fn F n 1 ) = = = ( ( ( )( Fn 1 ) F n 2 )( ) n 1 ( ) F1 F 0 )( Fn 2 F n 3 ) Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 105
107 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Jetzt können wir vorgehen wie in Beispiel 2.2: Wir stellen das charakteristische Polynom von ( ) auf, berechnen die Eigenwerte der Matrix, anschließend die Eigenvektoren, stellen und ( F1 F 0 ) = ( 1 0 ) als Linearkombination der Eigenvektoren dar erhalten so eine explizite Formel für F n. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 106
108 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Fibonacci-Zahlen Formel von Moivre-Binet: F n = 1 5 [( Charakteristisches Polynom mit den Eigenwerten 1+ ) n 5 ( 2 P(λ) = λ 2 λ 1 1 ) n ] 5 2 λ = und µ = Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 107
109 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Homogene lineare Differenzengleichung Definition 2.4. Für a i R,i = 1,...,k heißt die Gleichung F n = a 1 F n 1 + +a k F n k homogene lineare Differenzengleichung k-ter Ordnung mit konstanten Koeffizienten. In Matrixdarstellung können wir solch eine Differenzengleichung schreiben als F n a 1 a 2 a k F n 1 F n 1.. = 1 0. F n F n k F n k Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 108
110 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Satz 2.5. Das charakteristische Polynom P(λ) einer homogenen linearen Differenzengleichung k-ter Ordnung mit konstanten Koeffizienten hat die Form P(λ) = ( 1) k( λ k a 1 λ k 1 a 2 λ k 2 a k ) Beweis: Vollständige Induktion und Entwicklung der Matrix A λe nach der (k +1)-ten Spalte. Bemerkung: Damit können wir das charakteristische Polynom direkt an der Gleichung ablesen, die Berechnung von det(a λe) ist nicht notwendig. Da wir nur an den Nullstellen von P(λ) interessiert sind, spielt der Faktor ( 1) k keine Rolle. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 109
111 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Satz 2.6. Es sei λ eine Nullstelle mit Vielfachheit m des charakteristischen Polynoms. Dann sind die Folgen F n = n i λ n füri = 0,...,m 1Lösungen der homogenenlinearendifferenzengleichung. Beispiel 2.4. Aus der Differenzengleichung F n = 7F n 1 16F n 2 +12F n 3 ergibt sich das charakteristische Polynom P(λ) = λ 3 7λ 2 +16λ 12 = (λ 3)(λ 2) 2 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 110
112 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Also ist 3 eine einfache Nullstelle und 2 ist eine zweifache Nullstelle. Damit sind F n = 3 n F n = 2 n F n = n2 n Lösungen der homogenen linearen Differenzengleichung. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 111
113 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Anfangswertprobleme In der Praxis hat man neben der Differenzengleichung häufig Anfangsbedingungen für die ersten k Folgenglieder. Dieses Problem nennt man Anfangswertproblem. Beispiel Fibonacci-Zahlen: Neben F n = F n 1 + F n 2 wird zusätzlich F 0 = 0 und F 1 = 1 verlangt. Zur Lösung des Anfangswertproblems müssen wir eine Linearkombination der homogenen Lösungen finden. Dies resultiert in einem linearen Gleichungssystem. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 112
114 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Beispiel 2.5. Zu der Differenzengleichung von Beispiel 2.4 wollen wir das Anfangswertproblem F 0 = 2,F 1 = 7,F 2 = 21 lösen. Es muss gelten Daraus ergibt sich das lineare GLS F n = α 3 n +β 2 n +γ n2 n für n = 0 : α + β = 2 für n = 1 : 3α + 2β + 2γ = 7 für n = 2 : 9α + 4β + 8γ = 21 mit der Lösung α = β = γ = 1. Also wird das Anfangswertproblem gelöst durch: F n = 3 n +2 n +n2 n Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 113
115 2. Repräsentationen von Graphen in Computern Lineare Differenzengleichungen Zusammenfassung Adjazenzmatrix und Adjazenzliste zur Repräsentation von Graphen Berechnung der Anzahl an Kantenfolgen zwischen Knoten mit Hilfe der Potenzen der Adjazenzmatrix Eigenwerte und Eigenvektoren zur expliziten Berechnung der Potenzen einer Adjazenzmatrix Eigenwerte zur Lösung von Anfangswertproblemen homogener linearer Differenzengleichungen mit konstanten Koeffizienten Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 114
116 3. Durchsuchen von Graphen Tiefensuche 3. Durchsuchen von Graphen Tiefensuche Breitensuche Topologisches Sortieren Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 115
117 3. Durchsuchen von Graphen Tiefensuche Tiefensuche Verallgemeinerung des preorder-durchlaufprinzips für binäre Bäume. Kanten werden ausgehend von dem zuletzt entdeckten Knoten v, der mit noch unerforschten Kanten inzident ist, erforscht. Erreicht man von v aus einen noch nicht erforschten Knoten w, so verfährt man mit w genauso wie mit v. Wenn alle mit w inzidenten Kanten erforscht sind, erfolgt ein Backtracking zu v. Die Knoten v V erhalten in der Reihenfolge ihres Erreichens eine DFS-Nummer t(v). Zu Beginn setzen wir t(v) = für alle v V. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 116
118 3. Durchsuchen von Graphen Tiefensuche Für einen Knoten v sei die Prozedur DFSEARCH(v) wie folgt definiert: i := i+1;t(v) := i;n(v) := {w {v,w} E}; while w N(v) mit t(w) = do N(v) := N(v)\{w}; B := B {{v,w}}; DFSEARCH(w); end Algorithmus 3.1. [Tiefensuche (Depth-First Search)] Es sei G = (V,E) ein Graph. B := ;i := 0; for all v V do t(v) := ; while v V mit t(v) = do DFSEARCH(v); Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 117
119 3. Durchsuchen von Graphen Tiefensuche Bemerkung 3.1. Das Ergebnis für t(v) und B hängt i.d.r. von der Repräsenation des Graphen (z.b. als Adjazenzliste) ab. Beispiel 3.1. Wir betrachten den folgenden Graphen: b a c d e f g h Adjazenzlisten: a b e b a c d c b d d b c e e a d f g h g f h h f g Durchlauf und weitere Beispiele: Tafel. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 118
120 3. Durchsuchen von Graphen Tiefensuche Eigenschaften der Tiefensuche Bemerkung 3.2. Durch DFS wird jeder Knoten besucht und jede Kante wird untersucht. Ist G nicht zusammenhängend, dann werden durch DFS nacheinander die Zusammenhangskomponenten ermittelt. DFS unterteilt die Kantenmenge E in die Menge der Baumkanten (die Menge B) und die Menge der Rückwärtskanten (E \B). (V, B) bildet einen aufspannenden Untergraphen von G, der ein Wald ist. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 119
121 3. Durchsuchen von Graphen Tiefensuche Ist G zusammenhängend, dann ist (V, B) ein sogenannter aufspannender Baum von G. Satz 3.1. Der Zeitaufwand für DFS ist O( V + E ). Beweis. Tafel. Definition 3.1. Es sei G = (V,E). Ein Knoten w V heißt Nachfolger von v V gdw. DFSEARCH(w) wird nach Eröffnung und vor Beendigung von DFSEARCH(v) aufgerufen. Lemma 3.2. Wenn {v,w} eine Rückwärtskante ist, dann ist v Vorfahr von w oder umgekehrt. Bemerkung 3.3. D.h., durch DFS werden keine sogenannten Querkanten konstruiert. Tafel. Beweis. Tafel. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 120
122 3. Durchsuchen von Graphen Breitensuche Breitensuche Man geht an einem Knoten nicht sofort in die Tiefe, sondern bearbeitet zunächst alle noch nicht erreichten Nachbarn dieses Knotens. Anschließend fügt man die Knoten in eine Warteschlange ein. Ein Knoten gilt als erreicht, wenn er in die Warteschlange aufgenommen wurde. Solange die Warteschlange nicht leer ist, selektiert man einen Knoten aus der Warteschlange und geht wie oben beschrieben vor. Die Knoten v V erhalten in der Reihenfolge ihres Herausnehmens aus der Warteschlange eine BFS-Nummer b(v). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 121
123 3. Durchsuchen von Graphen Breitensuche Für einen Knoten v sei die Prozedur BFSEARCH(v) wie folgt definiert: i := i+1;b(v) := i;n(v) := {w {v,w} E} while w N(v) mit r(w) = false do N(v) := N(v)\{w}; B := B {{v,w}}; füge w an W an; r(w) := true; end Diese Prozedur wird für den jeweils ersten Knoten der Warteschlange W ausgeführt. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 122
124 3. Durchsuchen von Graphen Breitensuche Algorithmus 3.2. [Breitensuche (Breadth-First Search)] Es sei G = (V,E) ein Graph. B := ;i := 0;W := (); for all v V do b(v) := ;r(v) := false; end while W = () and v V : b(v) = do W := (v); r(v) := true; while W () do wähle ersten Knoten w aus W; entferne w aus W; BFSEARCH(w); end end Beispiel 3.2. Tafel. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 123
125 3. Durchsuchen von Graphen Breitensuche Eigenschaften der Breitensuche Jeder Knoten wird besucht und jede Kante wird untersucht. Es werden nacheinander die Zusammenhangskomponenten ermittelt. (V, B) bildet einen aufspannenden Untergraphen, der ein Wald ist. Satz 3.3. Der Zeitaufwand für BFS ist O( V + E ). Beweis. Tafel. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 124
126 3. Durchsuchen von Graphen Topologisches Sortieren Halbordnung Definition 3.2. Eine binäre Relation R V V heißt Halbordnung auf V gdw. folgendes gilt: 1. v V : (v,v) R (Reflexivität) 2. v,w V : (v,w) R (w,v) R v = w (Antisymmetrie) 3. u,v,w V : (u,v) R (v,w) R (u,w) R (Transitivität) Beispiel 3.3. Die Teilbarkeitseigenschaft definiert eine Halbordnung auf den natürlichen Zahlen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 125
127 3. Durchsuchen von Graphen Topologisches Sortieren Topologische Ordnung Lemma 3.4. Es sei G = (V,A) ein DAG. Die Relation R V V mit (v,w) R gerichteter Weg von v nach w definiert eine Halbordnung auf V. Definition 3.3. Es sei G = (V,A) ein DAG mit V = {v 1,...,v n }. Eine Knotenreihenfolge L = (v i1,...,v in ) aller Knoten aus V heißt topologische Ordnung von G gdw. Beispiel 3.4. Tafel. (v ij,v ik ) A = i j < i k Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 126
128 3. Durchsuchen von Graphen Topologisches Sortieren Topologisches Sortieren Algorithmus 3.3. Gegeben sei ein DAG G = (V, A) beschrieben durch seine Adjazenzlisten. Berechnet wird eine topologische Sortierung, die durch die Numerierung t(v) gegeben ist. k := 0;Q := {v V indeg(v) = 0} while Q do wähle ein v aus Q; k := k +1; t(v) := k; Q := Q\{v}; for all (v,w) A do indeg(w) := indeg(w) 1; if indeg(w) = 0 then Q := Q {w}; end end Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 127
129 3. Durchsuchen von Graphen Topologisches Sortieren Beispiel 3.5. Tafel. Satz 3.5. Algorithmus 3.3 liefert in O( V + E ) eine topologische Sortierung L = (v i1,...,v in ), wobei v i der Knoten mit t(v) = i ist. Beweis. Tafel. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 128
130 3. Durchsuchen von Graphen Topologisches Sortieren Zusammenfassung des Kapitels Tiefensuche: Gehe in die Tiefe solange wie möglich Knotennumerierung und aufspannender, kreisfreier Untergraph Breitensuche: Prinzip der Warteschlange Anwendungen: systematisches Durchsuchen von Graphen, z.b. Labyrinth Ermittlung von Eigenschaften eines Graphen Berechnung von zulässigen Reihenfolgen durch topologische Sortierung der Knoten Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 129
131 4. Kreis- und Wegeprobleme Kapitelübersicht 4. Kreis- und Wegeprobleme Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Abstände in Graphen Berechnung kürzester Wege Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 130
132 4. Kreis- und Wegeprobleme Eulersche Graphen Das Königsberger Brückenproblem Norden Insel Osten Süden Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 131
133 4. Kreis- und Wegeprobleme Eulersche Graphen Eulerweg, Eulerkreis Definition 4.1. Es sei G = (V,E) ein Graph. Ein Weg, der jede Kante von G genau einmal enthält, heißt eulerscher Weg von G. Ein Kreis, der jede Kante von G genau einmal enthält, heißt eulerscher Kreis von G. G heißt eulersch gdw. G einen eulerschen Kreis enthält. Leonhard Euler Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 132
134 4. Kreis- und Wegeprobleme Eulersche Graphen Beispiel 4.1. Der Graph des Königsberger Brückenproblems scheint nicht eulersch zu sein, er scheint auch keinen eulerschen Weg zu enthalten. Das Haus des Nikolaus enthält einen eulerschen Weg. c b d Das Haus des Nikolaus mit Keller ist eulersch: a e f g Weitere Graphen:. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 133
135 4. Kreis- und Wegeprobleme Eulersche Graphen Charakterisierung von eulerschen Graphen Satz 4.1. [Euler 1736] Es sei G = (V,E) ein Graph. G hat einen eulerschen Weg gdw. G bis auf isolierte Knoten zusammenhängend ist und für die Zahl u der Knoten mit ungeradem Grad gilt: u = 0 oder u = 2. Die Existenz eines Eulerkreises ist äquivalent mit u = 0. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 134
136 4. Kreis- und Wegeprobleme Eulersche Graphen Beweis. 1. = : G habe einen eulerschen Kreis K = (v 0,v 1,...,v m 1,v 0 ). Dann ist G bis auf isolierte Knoten zusammenhängend und tritt der Knoten v in der Folge v 0,v 1,...,v m 1 genau t-mal auf, so gilt deg(v) = 2t, d.h. v hat geraden Grad. 2. = : Beweis durch vollständige Induktion über die Zahl der Knoten. Induktionsanfang: Der Graph G = ({v 0 },{}) ist eulersch, denn (v 0 ) ist ein eulerscher Kreis. Induktionsannahme: Für Graphen mit höchsten n Knoten gelte die Behauptung. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 135
137 4. Kreis- und Wegeprobleme Eulersche Graphen Induktionsschritt: Sei G = (V, E) ein zusammenhängender Graph mit n+1 Knoten und und alle Knoten haben geraden Grad. Wähle einen beliebigen Knoten v 0 V. v0 v1 Wähle solange dies möglich ist Knoten v 1,v 2,..., so dass (v 0,...,v i ) jeweils ein Weg in G ist. v0 v2 Unter den gegebenen Voraussetzungen entsteht so automatisch ein Kreis K. Sei E k die Menge der Kanten in K. v3 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 136
138 4. Kreis- und Wegeprobleme Eulersche Graphen Wenn K alle Kanten aus E enthält, so ist K ein Eulerkreis. Ansonsten bildet man den Restgraphen G = (V,E \E K ). v0 v1 v5 Für die Komponenten des Restgraphen gilt die Induktionsannahme. v4 v2 v7 v3 v6 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 137
139 4. Kreis- und Wegeprobleme Eulersche Graphen Nun fügt man die Kreise an Knoten zusammen, die in K und einer Komponente des Restgraphen enthalten sind. Man läuft entlang K bis zu solch einem Knoten, dann entlang des Kreises des Restgraphen und anschließend wieder entlang K. v0 v1 v9 v10 v5 v2 v6 v3 v8 v11 v4 v7 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 138
140 4. Kreis- und Wegeprobleme Eulersche Graphen Berechnung eines Eulerkreises Algorithmus 4.1. [Hierholzer 1873] Es sei G = (V,E) ein bis auf isolierte Knoten zusammenhängender Graph, der nur Knoten mit geradem Grad aufweist. 1. Wähle einen beliebigen Knoten v 0 V. Wähle solange dies möglich ist Knoten v 1,v 2,..., so daß (v 0,...,v i ) jeweils ein Weg in G ist. Unter den gegebenen Voraussetzungen entsteht so automatisch ein Kreis K. Setze w := v Prüfe, ob K ein eulerscher Kreis ist. Wenn ja, dann STOP, ansonsten gehe zu 3. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 139
141 4. Kreis- und Wegeprobleme Eulersche Graphen 3. Setze K := K. Laufe ab w entlang K und wähle einen in K enthaltenen Knoten w, der mit einer nicht in K enthaltenen Kante inzident ist. Konstruiere wie unter 1. ausgehend von w einen Kreis K, der keine Kanten von K enthält. Füge K in den Kreis K an der Stelle w ein. Setze w := w und K := K. Gehe zu 2. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 140
142 4. Kreis- und Wegeprobleme Eulersche Graphen Beispiel 4.2. Wir demonstrieren den Algorithmus von Hierholzer an dem folgenden Graphen: b c d a e h g f Tafel. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 141
143 4. Kreis- und Wegeprobleme Eulersche Graphen Eigenschaften des Algorithmus von Hierholzer Satz 4.2. Algorithmus 4.1 ist korrekt, d.h. bei erfüllten Voraussetzungen wird ein eulerscher Kreis konstruiert. Beweis. Tafel. Bemerkung 4.1. Wir können Algorithmus 4.1 auch zur Berechnung eines Eulerweges benutzen. Satz 4.3. Die Zeitkomplexität von Algorithmus 4.1 beträgt O( V + E ). Beweis. Siehe Übungen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 142
144 4. Kreis- und Wegeprobleme Eulersche Graphen Anwendung von Eulerwegen Dominospiel: Gegeben sind eine Menge S von Spielsteinen, die auf jeder Seite mit einem Symbol markiert sind. Einen Spielstein [A : B] kann man sowohl in dieser Form als auch als [B : A] verwenden. Man darf zwei Spielsteine aneinander legen, wenn die sich berührenden Hälften das gleiche Symbol aufweisen. Kann man die Steine einer Menge S zu einer ununterbrochenen Kette zusammenlegen? Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 143
145 4. Kreis- und Wegeprobleme Eulersche Graphen Beispiel 4.3. Gegeben ist die folgende Menge an Spielsteinen: [A : B] [A : D] [B : C] [C : D] [A : A] [D : D] [B : C] [A : C] [B : D] Zugehöriger Graph: B C Jede Kante entspricht einem Spielstein. Eulerweg entspricht einer ununterbrochenen Dominokette. A D Anwendung in der Praxis: Berechnung von Prozessketten mit möglichst wenigen Unterbrechungen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 144
146 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Hamiltonsche Graphen Definition 4.2. Es sei G = (V,E) ein Graph. Ein Weg, der jeden Knoten von G genau einmal enthält, heißt hamiltonscher Weg. Ein Kreis, der jeden Knoten von G genau einmal enthält, heißt hamiltonscher Kreis. G heißt hamiltonsch gdw. G einen hamiltonschen Kreis enthält. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 145
147 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Beispiel 4.4. Die Bezeichnung hamiltonsch geht auf Sir William Rowan Hamilton ( ) zurück, der 1859 das Spiel around the world erfand. Die Punkte eines Dodekaeders stellten Städte dar. Die Aufgabe des Spiels bestand darin, entlang der Kanten des Dodekaeders eine Rundreise zu unternehmen, bei der man jede Stadt genau einmal besucht. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 146
148 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Sir William Rowan Hamilton Around the World Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 147
149 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Charakterisierung von hamiltonschen Graphen Satz 4.4. Es sei G = (V,E) ein Graph mit n := V 3. Gilt: v V : deg(v) n/2, dann ist G hamiltonsch. Beweis. Wir erzeugen den Graph G aus G, indem wir k neue Knoten in G einfügen und jeden neuen Knoten mit allen Knoten von G über neue Kanten verbinden. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 148
150 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Wie viele solcher neuer Knoten brauchen wir mindestens, damit G hamiltonsch wird? Mit k = n gelingt es uns immer, G hamiltonsch werden zu lassen. Wir wählen k so klein wie möglich ist und nehmen an, dass k > 0 gilt. Hieraus konstruieren wir einen Widerspruch. Es sei K = (a,x,b,...,a) ein hamiltonscher Kreis von G, a,b seien Knoten von G, x sei ein neuer Knoten. Dann gilt: (i) a und b sind nicht benachbart, denn sonst wäre x für den hamiltonschen Kreis überflüssig. (ii) In K kann ein zu b benachbarter Knoten b nie direkt auf einen zu a benachbarten Knoten a folgen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 149
151 4. Kreis- und Wegeprobleme Hamiltonsche Graphen x x a b a b b a b a Beweisskizze zu (ii). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 150
152 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Wir definieren: A := Menge der Nachbarn von a in G B := Menge der Nachbarn von b in G F := Menge der Knoten von G, die in K direkt auf einen Knoten aus A folgen Wegen (i) und (ii) gilt: B F =. Weiterhin gilt: B n 2 +k und F = A = n 2 +k. Konsequenz: B F = B + F n+2k. Da G nur n+k Knoten hat, ist dies ein Widerspruch für k > 0. Bemerkung 4.2. Das Entscheidungsproblem, ob ein Gaph G hamiltonsch ist (HC), ist N P-vollständig. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 151
153 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Crashkurs N P-Vollständigkeit Die Klasse P: Ein Entscheidungsproblem heißt polynomiell lösbar, wenn es einen Algorithmus zur Lösung des Problems gibt, dessen Worst-Case-Laufzeit durch ein Polynom in der Länge der Eingabe beschränkt ist. Die Klasse P ist die Klasse der polynomiell lösbaren Probleme. Beispiele: Ist der Graph G zusammenhängend? Hat der Graph G einen eulerschen Kreis? Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 152
154 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Die Klasse NP Die Klasse N P ist die Klasse der Entscheidungsprobleme, für die ein Lösungsvorschlag in polynomieller Rechenzeit überprüft werden kann. Beispiel: Überprüfung, ob eine Knotenfolge eines Graphen einen hamiltonschen Kreis bildet. Beispiel: Überprüfung, ob eine TSP-Tour eine Länge l hat. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 153
155 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Beziehung zwischen P und NP Es gilt: P NP Gilt sogar P = NP? Man weiß es nicht! Man vermutet, dass dies nicht der Fall ist. Stand heute kann man beweisen. weder P = NP noch P NP Die Lösung des P = NP Problems gehört zu den wichtigsten offenen Problemen der Mathematik/Informatik. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 154
156 4. Kreis- und Wegeprobleme Hamiltonsche Graphen N P-Vollständigkeit Ein Problem Π aus NP ist NP-vollständig, wenn aus seiner polynomiellen Lösbarkeit P = N P folgt, d.h. alle Probleme in N P polynomiell lösbar wären. Die N P-vollständigen Probleme können anschaulich als die schwersten Probleme in der Klasse N P angesehen werden. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 155
157 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Wie kann man zeigen, dass ein Problem Π N P-vollständig ist? Man nimmt sich ein Problem Π, von dem man weiß, dass es NPvollständig ist und zeigt, dass Π nicht leichter ist. Genauer: Man reduziert Π auf Π, d.h. man zeigt, dass man Π in polynomieller Zeit lösen könnte, wenn man Π in polynomieller Zeit lösen könnte. Schreibweise: Π Π Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 156
158 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Welche N P-vollständigen Probleme kennt man denn? Satz von Cook [1971]: Das Erfüllbarkeitsproblem der Aussagenlogik(SAT) ist N P-vollständig. Das Erfüllbarkeitsproblem der Aussagenlogik fragt, ob eine aussagenlogische Formel erfüllbar ist. Karps 21 N P-vollständige Probleme [1972]: Richard Karp griff die Idee von Cook auf und zeigte für 21 verschiedene kombinatorische und graphentheoretische Probleme, dass sie N P-vollständig sind, darunter auch das Hamiltonkreisproblem (HC). Seitdem konnte für viele weitere Probleme gezeigt werden, dass sie N P- vollständig sind. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 157
159 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Was bringt einem das in der Praxis? Stellen Sie sich vor, Ihr Chef gibt Ihnen den Auftrag, für ein wichtiges Problem innerhalb eines Projekts einen effizienten Algorithmus zu programmieren, Ihnen gelingt die Konstruktion solch eines Algorithmus aber nicht. I can t find an efficient algorithm, I guess I m just too dumb. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 158
160 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Sie wären natürlich aus dem Schneider, wenn Sie zeigen könnten, dass solch ein Algorithmus nicht existiert. I can t find an efficient algorithm, because no such algorithm is possible. Unglücklicherweise gelingt Ihnen dies aber auch nicht. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 159
161 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Wenn Sie aber nachweisen, dass das betreffen Problem N P-vollständig ist, haben Sie gegenüber Ihrem Chef gute Argumente. I can t find an efficient algorithm, but neither can all these famous people. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 160
162 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Gelingt der Nachweis der N P-Vollständigkeit, so zeigt dies, dass man nicht zu dumm ist, ein polynomielles Lösungsverfahren zu finden. Vermutlich existiert keines. Zumindest hat noch nie jemand ein solches gefunden und es macht keinen Sinn, nach einem solchen zu suchen. Man kann für große Probleme keine (optimalen) Lösungen erwarten. Anwendung heuristischer statt exakter Verfahren Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 161
163 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Traveling Salesman Problem Definition 4.3. Gegeben sei ein vollständiger Graph G = (V,E) mit einer Kostenfunktion c : E IN auf den Kanten. Die Enscheidungsvariante des Traveling Salesman Problems (TSP) lautet: Existiert ein hamiltonscher Kreis (eine TSP-Tour) K in G, für den die Summe der Kantengewichte c(k) k ist. Bemerkung 4.3. Die Entscheidungsvariante des TSP ist N P-vollständig. Dies kann durch HC TSP bewiesen werden. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 162
164 4. Kreis- und Wegeprobleme Hamiltonsche Graphen Skizze für HC TSP Es sei G = (V,E) ein Graph. Wir wollen entscheiden, ob G hamiltonsch ist. Es sei G = (V,E ) ein vollständiger Graph für die Knotenmenge von G. Die Kostenfunktion c : E IN sei c(e) = { 1 für e E, also die Kanten aus G 2 sonst Dann hat G genau dann einen hamiltonschen Kreis, wenn in G eine TSP-Tour der Länge V existiert. Konsequenz: Würde es einen polynomiellen Algorithmus für das TSP- Problem geben, wäre auch das HC-Problem polynomiell lösbar. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 163
165 4. Kreis- und Wegeprobleme Hamiltonsche Graphen TSP als Optimierungsproblem Die Optimierungsvariante des TSP lautet: Finde einen hamiltonschen Kreis mit minimalem Gewicht. Durch die N P-Vollständigkeit des zugehörigen Entscheidungsproblems kann es optimal nur für kleine n gelöst werden. Für große n müssen Heuristiken zur Berechnung einer möglichst guten Lösung angewendet werden. Theoretisch interessant sind Heuristiken mit Gütegarantie (siehe folgendes Kapitel). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 164
166 4. Kreis- und Wegeprobleme Abstände in Graphen Abstände in Graphen Definition 4.4. Es sei G = (V,E) ein Graph. Der Abstand d(v,w) zweier Knoten v,w V ist die minimale Länge eines Weges von v nach w. Falls es keinen solchen Weg gibt, setzen wir d(v,w) =. Bemerkung 4.4. Die Länge eines Kantenzugs bzw. Weges ist definiert als die Anzahl der Kanten, die in diesem enthalten sind. Insbesondere gilt also d(v,v) = 0 für alle v V. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 165
167 4. Kreis- und Wegeprobleme Abstände in Graphen Berechnung von Abständen Algorithmus 4.2. Es sei G = (V,E) ein durch seine Adjazenzlisten A v gegebener Graph und v 0 sei ein Knoten von G. Es werden die Abstände d(v) von v 0 zu v für alle v V berechnet. d(v 0 ) := 0;V(0) := {v 0 };k := 1; for all v V,v v 0 do d(v) := ; while V(k 1) do V(k) := for all v {A u u V(k 1)} do if d(v) = then d(v) := k;v(k) := V(k) {v} end end k := k +1; Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 166
168 4. Kreis- und Wegeprobleme Abstände in Graphen end Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 167
169 4. Kreis- und Wegeprobleme Abstände in Graphen Erläuterungen zu Algorithmus 4.2: Ausgehend von V(0) = {v 0 } werden sukzessive die Mengen V(1),V(2),... berechnet. V(k) besteht aus den Knoten, die mit Knoten aus V(k 1) adjazent sind, aber nicht in V(0)... V(k 1) liegen. Mit Induktion zeigt man leicht, daß jedes V(k) genau aus den Knoten besteht, die von v 0 den Abstand k haben. Dieses Vorgehen entspricht einer Breitensuche. Die Zeitkomplexität beträgt O( V + E ). Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 168
170 4. Kreis- und Wegeprobleme Abstände in Netzwerken Abstände in Netzwerken Wir ordnen nun jeder Kante eines Graphen eine Länge zu. Typisches Beispiel sind Straßennetze mit Entfernungsangaben. Definition 4.5. Es sei G = (V,E) ein Graph sowie w : E IR eine Bewertung der Kanten mit reellen Zahlen. Das Paar (G,w) heißt Netzwerk. Für jede Kante e E heißt w(e) die Länge oder das Gewicht von e. Für einen Kantenzug K = (v 0,...,v k ) ist w(k) := k i=1 w({v i 1,v i }) die Länge von K. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 169
171 4. Kreis- und Wegeprobleme Abstände in Netzwerken Bei den Längen können auch negative Werte sinnvoll sein (z.b. Ertrag, Aufwand). Bei der Definition des Abstandes können solche negativen Längen aber zu Problemen führen. Wir setzen daher voraus, daß die Längen nicht negativ sind. Definition 4.6. Es sei (G,w) ein Netzwerk, G = (V,E) sowie w(e) 0 für alle e E. Der Abstand d(v,w) zweier Knoten v,w V in einem Netzwerk ist definiert alsdasminimumderlängenallerwegevonv nachw.fallseskeinensolchen Weg gibt, setzen wir d(v,w) =. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 170
172 4. Kreis- und Wegeprobleme Abstände in Netzwerken Beispiel 4.5. In einem Netzwerk sei jeder Kante e eine Ausfallwahrscheinlichkeit p(e) zugeordnet. Setzt man voraus, daß Fehler unabhängig voneinander auftreten, dann ist (1 p({v 0,v 1 })) (1 p({v k 1,v k })) die Wahrscheinlichkeitfür dasfunktionieren eineskantenzuges(v 0,...,v k ). Dieser Wert ist maximal, wenn k i=1 log(1 p({v i 1,v i })) maximal ist. Setzt man w(e) := log(1 p(e)), dann ist die zuverlässigste Verbindung zwischen zwei Knoten v und w äquivalent zu einem kürzesten Weg zwischen v und w. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 171
173 4. Kreis- und Wegeprobleme Abstände in Netzwerken Kürzeste Wege in Netzwerken Algorithmus 4.3. [Dijkstra] Es sei (G,w) ein Netzwerk mit G = (V,E) und einer nichtnegativen Längenfunktion w auf E sowie v 0 V. Es werden alle Abstände d(v) von v 0 zu einem Knoten v V berechnet. 1. Setze d(v 0 ) := 0,d(v) := für alle v V \{v 0 },U := V. 2. Falls U =, dann STOP. Sonst weiter mit Finde ein u U, für das d(u) minimal ist. 4. Fürallev U mit{u,v} E setzed(v) := min{d(v),d(u)+w({u,v})}. 5. Setze U := U \{u}. Gehe zu 2. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 172
174 4. Kreis- und Wegeprobleme Abstände in Netzwerken Bemerkung 4.5. Der Algorithmus von Dijkstra kann analog für gerichtete Graphen verwendet werden. Der Algorithmus kann leicht so erweitert werden, daß nicht nur die Abstände d(v 0,v) sondern auch die kürzesten Wege berechnet werden. Satz 4.5. Nach der Terminierung von Algorithmus 4.3 gilt d(v) = d(v 0,v) für alle v V. Die Zeitkomplexität des Algorithmus ist O( V 2 ). Beweis. Tafel. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 173
175 4. Kreis- und Wegeprobleme Abstände in Netzwerken Beispiel 4.6. Wir betrachten das folgende gerichtete Netzwerk: v0=a b 5 6 c d e 2 2 f g Algorithmus 4.3 liefert hierfür die folgenden Abstände: v a d f e g c b d(v) Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 174
176 4. Kreis- und Wegeprobleme Abstände in Netzwerken Beispiel 4.7. Wir betrachten das folgende nicht gerichtete Netzwerk: v0=a 9 b 4 c d e 13 1 f g 2 2 h i Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 175
177 4. Kreis- und Wegeprobleme Abstände in Netzwerken Bemerkung 4.6. In einem Netzwerk mit negativen Katenlängen werden durch den Dijkstra- Algorithmus u.u. falsche Abstände ermittelt und zwar selbst dann, wenn keine Kreise negativer Länge existieren. Durch die Wahl einer geeigneten Datenstruktur für die Selektion des Knotens u (Schritt 3) kann die Laufzeit erheblich verbessert werden. Für die Berechnung von Routen in Straßennetzen benötigt man optimierte Varianten des Dijkstra-Algorithmus. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 176
178 4. Kreis- und Wegeprobleme Abstände in Netzwerken Kürzeste Wege in DAGs Da in DAGs keine Kreise auftreten, sind negative Kantenlängen unproblematisch. Satz 4.6. Gegeben sei ein gerichtetes Netzwerk (G,w) mit G = (V,A). Wir lassen auch w(e) < 0 zu. L = (v 1,...,v n ) sei eine topologische Sortierung von V. Dann ergibt sich die Länge d(v 1,v i ) eines kürzesten Weges von v 1 zu einem Knoten v i durch die folgende Rekursion für d(v i ): 1. d(v 1 ) = 0 2. Für i > 1: d(v i ) = min w(v j,v i )+d(v j ) {1 j<i (v j,v i ) A} Beispiel 4.8. Tafel. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 177
179 4. Kreis- und Wegeprobleme Abstände in Netzwerken Bemerkung 4.7. Wenn man in Satz 4.6 min durch max ersetzt, dann erhält man die Länge eines längsten Weges. Das allgemeine Entscheidungsproblem, ob in einem(ungerichteten) Netzwerk ein (einfacher) Weg der Länge l existiert, ist dagegen N P- vollständig. Die in Satz 4.6 angewendete Vorgehensweise, eine optimale Lösung durch eine bestmögliche Kombination der Lösungen zu Subproblemen zu finden, nennt man dynamisches Programmieren. Satz 4.6 läßt sich in einen Algorithmus mit Zeitkomplexität O( V + A ) umsetzen. Beweis. Mit Induktion über i. Tafel. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 178
180 4. Kreis- und Wegeprobleme Abstände in Netzwerken Bemerkung 4.8. Mit dem Verfahren aus Satz 4.6 können nicht nur kürzeste und längste Wege sondern auch Anzahlen von Wegen berechnet werden. Z.B. die Anzahl #(v i ) der Wege von v 1 nach v i. Hierfür muss der Minimum-Operator durch die Summenbildung #(v i ) = {1 j<i (v j,v i ) A} #(v j ) ersetzt und die Initialisierung #(v 1 ) = 1 verwendet werden. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 179
181 4. Kreis- und Wegeprobleme Abstände in Netzwerken Anwendungen Für optimale Wege in DAGs gibt es eine Fülle von Anwendungen. Wir betrachten zwei: Optimale Einteilung in Blöcke (z.b. in der Textverarbeitung) Projektplanung Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 180
182 4. Kreis- und Wegeprobleme Abstände in Netzwerken Blocksatzbildung Beispiel 4.9. [Berechnung optimaler Blockungen] Gegeben ist eine Folge F = (1,...,n) von n Gegenständen. Jeder Gegenstand hat eine Länge l(i). Die Gegenstände sollen in Blöcke eingeteilt werden, wobei die Idealgröße eines Blockes B ist. Die Gesamtlänge der Gegenstände in einem Block darf B nicht übersteigen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 181
183 4. Kreis- und Wegeprobleme Abstände in Netzwerken Die Gegenstände dürfen nicht umsortiert werden. Ein Block B j ergibt sich also durch einen Index i j mit i j 1 +1 ist das erste Element im Block j und i j ist das letzte Element im Block B j. Für die Abweichung der Länge L j := i j r=i j 1 +1 l(r) eines Blockes B j von B wird eine Bewertung definiert, die monoton in der Größe der Abweichung ist, z.b. (B L j ) 2. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 182
184 4. Kreis- und Wegeprobleme Abstände in Netzwerken Gesucht ist eine Blockung, die eine möglichst kleine Bewertung hat, also eine Anzahlk an Blöcken und eine Folge 0 = i 0 < i 1 < i 2 < < i k = n mit k (B L j ) 2 min unter den Bedingungen j=1 L j = i j r=i j 1 +1 l(r) B für j = 1,...,k Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 183
185 4. Kreis- und Wegeprobleme Abstände in Netzwerken Beispielproblem: Länge der Gegenstände: 9,1,5,5,1,10 Blockgröße: 10 gierige Einteilung: [9, 1],[5, 5],[1],[10], Bewertung: 81 andere Einteilung: [9],[1, 5],[5, 1],[10], Bewertung: 33 Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 184
186 4. Kreis- und Wegeprobleme Abstände in Netzwerken Modellierung des Problems als Wegeproblem: V := {0,...,n} E := {(i,j) i < j und j r=i+1l(r) B} Gewichte: w(i,j) := (B j r=i+1 l(r))2 Jeder Weg von 0 nach n definiert dann eine zulässige Einteilung in Blöcke, wobei die Bewertung dieser Blockung gleich der Länge des Weges ist. Also: Finde einen Weg minimaler Länge von 0 nach n. Auf diesem Prinzip basiert die Formatierung in TeX. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 185
187 4. Kreis- und Wegeprobleme Abstände in Netzwerken Projektplanung mit Netzplantechnik Beispiel [Netzplantechnik mit CPM] Bei der Durchführung umfangreicher Projekte ist es erforderlich, dass einzelne Teilaufgaben (Jobs) zeitlich genau aufeinander abgestimmt werden. Hierfür werden häufig Methoden der Netzplantechnik eingesetzt. Die bekannteste Methode der Netzplantechnik heißt CPM (Critical Path Method). J sei die Menge der Jobs eines Projekts. Jeder Job j J hat eine zugeordnete Dauer t(j) sowie eine Menge P(j) J von Vorgängern. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 186
188 4. Kreis- und Wegeprobleme Abstände in Netzwerken Ein Job j kann erst dann gestartet werden, wenn alle Jobs aus P(j) beendet wurden. Wir gehen davon aus, dass Jobs parallel bearbeitet werden können. Man möchte z.b. wissen: Ab welchem Zeitpunkt kann mit einem Job begonnen werden? Wie lange wird ein Projekt dauern? Welche Jobs sind besonders kritisch in bezug auf die Gesamtdauer eines Projekts? Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 187
189 4. Kreis- und Wegeprobleme Abstände in Netzwerken Beispiel Zusammenbau eines Fahrrads: Job Beschreibung Dauer Vorg. a Rahmen vorbereiten (Gabel, Schutzbleche, usw.) 6 b Kettenführung anbringen 2 c Gangschaltung anbringen 3 b d Kettenblatt an Kurbel montieren 4 b e Vorderrad montieren und anpassen 6 a f Hinterrad montieren und anpassen 6 a,c g Kurbel am Rahmen anbringen 3 d h Endmontage (Lenker, Sattel, usw.) 12 e,f j Linkel Pedal anbringen 3 c,g k Rechtes Pedal anbringen 3 c,g Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 188
190 4. Kreis- und Wegeprobleme Abstände in Netzwerken Die Abhängigkeiten der Jobs untereinander können wir in Form eines DAGs repräsentieren. Die Knoten stellen hierbei die Jobs dar. Die Kanten stellen Vorgängerbeziehungen zwischen den Jobs dar. e a f h c j b d g k Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 189
191 4. Kreis- und Wegeprobleme Abstände in Netzwerken Die Jobs a und b können offensichtlich sofort begonnen werden. Der Job f kann begonnen werden, wenn a beendet ist und wenn c beendet ist. a ist nach einer Dauer von 6 beendet, c nach einer Dauer von 5, da c erst gestartet werden kann, wenn b beendet ist. Somit kann f frühestens zum Zeitpunkt 6 begonnen werden. Allgemein: Der frühste Starttermin eines Jobs ergibt sich durch einen Weg zu diesem Job mit maximaler Gesamtdauer. Hier liegen die Bewertungen aber auf den Knoten. Tafel: Frühste Starttermine für die Jobs des Beispiels. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 190
192 4. Kreis- und Wegeprobleme Abstände in Netzwerken Die Critical-Path-Method (CPM) stellt eine Modellierung dar, bei der die Jobs die Kanten eines DAGs sind. Die Knoten können als Fertigstellungsereignisse angesehen werden. Projektbeginn b 2 a 6 c 3 d e 6 f 6 j 3 g 3 k 3 h Projektende Die Kanten a, e, h stellen einen längsten Weg vom Projektbeginn zum -ende dar (kritische Pfad). Die Gesamtlaufzeit des Projekts ist also 24. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 191
193 4. Kreis- und Wegeprobleme Abstände in Netzwerken Für die Projektplanung sind u.a. die folgenden interessant: Projektdauer D: Länge eines längsten Weges (kritischer Pfad) vom Projektbeginn bis zum Projektende. Starttermin für Jobs j: Länge eines längsten Weges bis zum Startknoten von j. Zeitkritische Jobs: Alle Jobs, die auf einem kritischen Pfad liegen. Pufferzeit für Job j: D Länge eines längsten Weges, der Kante j enthält. Und warum verzögern sich Projekte trotz ausgefeilter Planungsmethoden? Siehe Übungen. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 192
194 4. Kreis- und Wegeprobleme Abstände in Netzwerken Die Routen der geringsten Videoüberwachung Aus der Rheinischen Post vom : New Yorker Webpage sucht kamerafreie Wege New York (rpo). Wer in einer Großstadt lebt, kann sich kaum noch bewegen, ohne von diversen Überwachungskameras aufgenommen zu werden. Da war es zwangsläufig nur eine Frage der Zeit, bis sich Widerstand regt. Ein Projekt von US-Bürgerrechtsaktivisten berechnet Usern jetzt die Route mit der geringsten Video- Überwachung durch New York. Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 193
Eigenwerte und Eigenvektoren
 Eigenwerte und Eigenvektoren Siehe Analysis (von der Hude, Folie 20: Definition 2.3. Ein Vektor x R n heißt Eigenvektor der quadratischen n n-matrix A zum Eigenwert λ R, wenn gilt Ax = λx Die Eigenwerte
Eigenwerte und Eigenvektoren Siehe Analysis (von der Hude, Folie 20: Definition 2.3. Ein Vektor x R n heißt Eigenvektor der quadratischen n n-matrix A zum Eigenwert λ R, wenn gilt Ax = λx Die Eigenwerte
1. Einführung. Grundbegriffe und Bezeichnungen. Beispiele. gerichtete Graphen. 1. Einführung Kapitelübersicht
 1. Einführung Kapitelübersicht 1. Einführung Grundbegriffe und Bezeichnungen Beispiele Bäume gerichtete Graphen Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 15 Das Königsberger Brückenproblem Beispiel
1. Einführung Kapitelübersicht 1. Einführung Grundbegriffe und Bezeichnungen Beispiele Bäume gerichtete Graphen Graphentheorie HS Bonn-Rhein-Sieg, WS 2014/15 15 Das Königsberger Brückenproblem Beispiel
Vollständiger Graph. Definition 1.5. Sei G =(V,E) ein Graph. Gilt {v, w} E für alle v, w V,v w, dann heißt G vollständig (complete).
 Vollständiger Graph Definition 1.5. Sei G =(V,E) ein Graph. Gilt {v, w} E für alle v, w V,v w, dann heißt G vollständig (complete). Mit K n wird der vollständige Graph mit n Knoten bezeichnet. Bemerkung
Vollständiger Graph Definition 1.5. Sei G =(V,E) ein Graph. Gilt {v, w} E für alle v, w V,v w, dann heißt G vollständig (complete). Mit K n wird der vollständige Graph mit n Knoten bezeichnet. Bemerkung
2. Repräsentationen von Graphen in Computern
 2. Repräsentationen von Graphen in Computern Kapitelinhalt 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Berechnung der Anzahl der verschiedenen Kantenzüge zwischen
2. Repräsentationen von Graphen in Computern Kapitelinhalt 2. Repräsentationen von Graphen in Computern Matrizen- und Listendarstellung von Graphen Berechnung der Anzahl der verschiedenen Kantenzüge zwischen
Lineare Differenzengleichungen
 Lineare Differenzengleichungen Die Fibonacci-Zahlen F n sind definiert durch F 0 = 0 F 1 = 1 F n = F n 1 +F n 2 für n >= 2 Die letzte Zeile ist ein Beispiel für eine homogene lineare Differenzengleichung
Lineare Differenzengleichungen Die Fibonacci-Zahlen F n sind definiert durch F 0 = 0 F 1 = 1 F n = F n 1 +F n 2 für n >= 2 Die letzte Zeile ist ein Beispiel für eine homogene lineare Differenzengleichung
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 3: Einführung in die Graphentheorie - Teil 3 Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 2. März 2018 1/72 ZUSAMMENHANG
Algorithmische Graphentheorie Vorlesung 3: Einführung in die Graphentheorie - Teil 3 Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 2. März 2018 1/72 ZUSAMMENHANG
Graphentheorie. für Wiederholer Bachelor Informatik und Wirtschaftsinformatik. Prof. Dr. Peter Becker
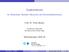 Graphentheorie für Wiederholer Bachelor Informatik und Wirtschaftsinformatik Prof. Dr. Peter Becker Fachbereich Informatik Hochschule Bonn-Rhein-Sieg Wintersemester 2018/19 Peter Becker (H-BRS) Graphentheorie
Graphentheorie für Wiederholer Bachelor Informatik und Wirtschaftsinformatik Prof. Dr. Peter Becker Fachbereich Informatik Hochschule Bonn-Rhein-Sieg Wintersemester 2018/19 Peter Becker (H-BRS) Graphentheorie
Einführung in die Graphentheorie (Mathematik IIIb)
 Einführung in die Graphentheorie (Mathematik IIIb) Peter Becker FH Bonn-Rhein-Sieg, FB Angewandte Informatik!" $# Vorlesung Wintersemester 2002/03 Allgemeines zur Vorlesung Es gibt eine Homepage zur Vorlesung:
Einführung in die Graphentheorie (Mathematik IIIb) Peter Becker FH Bonn-Rhein-Sieg, FB Angewandte Informatik!" $# Vorlesung Wintersemester 2002/03 Allgemeines zur Vorlesung Es gibt eine Homepage zur Vorlesung:
5. Bäume und Minimalgerüste
 5. Bäume und Minimalgerüste Charakterisierung von Minimalgerüsten 5. Bäume und Minimalgerüste Definition 5.1. Es ein G = (V, E) ein zusammenhängender Graph. H = (V,E ) heißt Gerüst von G gdw. wenn H ein
5. Bäume und Minimalgerüste Charakterisierung von Minimalgerüsten 5. Bäume und Minimalgerüste Definition 5.1. Es ein G = (V, E) ein zusammenhängender Graph. H = (V,E ) heißt Gerüst von G gdw. wenn H ein
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 2: Einführung in die Graphentheorie - Teil 2 Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 2. März 2018 1/48 OPERATIONEN
Algorithmische Graphentheorie Vorlesung 2: Einführung in die Graphentheorie - Teil 2 Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 2. März 2018 1/48 OPERATIONEN
5 Graphen. Repräsentationen endlicher Graphen. 5.1 Gerichtete Graphen. 5.2 Ungerichtete Graphen. Ordnung von Graphen
 Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 5 Graphen 5.1 Gerichtete Graphen Definition 5.1 (V, E) heißt gerichteter Graph (Digraph), wenn V Menge von Knoten
Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 5 Graphen 5.1 Gerichtete Graphen Definition 5.1 (V, E) heißt gerichteter Graph (Digraph), wenn V Menge von Knoten
4. Kreis- und Wegeprobleme
 4. Kreis- und Wegeprobleme Kapitelübersicht 4. Kreis- und Wegeprobleme Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Abstände in Graphen Berechnung
4. Kreis- und Wegeprobleme Kapitelübersicht 4. Kreis- und Wegeprobleme Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Abstände in Graphen Berechnung
6. Planare Graphen und Färbungen
 6. Planare Graphen und Färbungen Lernziele: Den Begriff der Planarität verstehen und erläutern können, wichtige Eigenschaften von planaren Graphen kennen und praktisch einsetzen können, die Anzahl von
6. Planare Graphen und Färbungen Lernziele: Den Begriff der Planarität verstehen und erläutern können, wichtige Eigenschaften von planaren Graphen kennen und praktisch einsetzen können, die Anzahl von
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 1: Grundlagen der algorithmischen Graphentheorie
 Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 1: Grundlagen der algorithmischen Graphentheorie Dipl-Math. Wolfgang Kinzner 2.4.2012 Kapitel 1: Grundlagen der algorithmischen Graphgentheorie
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 1: Grundlagen der algorithmischen Graphentheorie Dipl-Math. Wolfgang Kinzner 2.4.2012 Kapitel 1: Grundlagen der algorithmischen Graphgentheorie
8. Übung Algorithmen I
 INSTITUT FÜR THEORETISCHE INFORMATIK 1 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft Institut für Theoretische www.kit.edu Informatik Grundlagen
INSTITUT FÜR THEORETISCHE INFORMATIK 1 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft Institut für Theoretische www.kit.edu Informatik Grundlagen
Graphentheorie Graphentheorie. Grundlagen Bäume Eigenschaften von Graphen Graphen-Algorithmen Matchings und Netzwerke
 Graphen Graphentheorie Graphentheorie Grundlagen Bäume Eigenschaften von Graphen Graphen-Algorithmen Matchings und Netzwerke 2 Was ist ein Graph? Ein Graph ist in der Graphentheorie eine abstrakte Struktur,
Graphen Graphentheorie Graphentheorie Grundlagen Bäume Eigenschaften von Graphen Graphen-Algorithmen Matchings und Netzwerke 2 Was ist ein Graph? Ein Graph ist in der Graphentheorie eine abstrakte Struktur,
Nachbarschaft, Grad, regulär, Inzidenz
 Nachbarschaft, Grad, regulär, Inzidenz Definition Eigenschaften von Graphen Sei G = (V, E) ein ungerichteter Graph. 1 Die Nachbarschaftschaft Γ(u) eines Knoten u V ist Γ(u) := {v V {u, v} E}. 2 Der Grad
Nachbarschaft, Grad, regulär, Inzidenz Definition Eigenschaften von Graphen Sei G = (V, E) ein ungerichteter Graph. 1 Die Nachbarschaftschaft Γ(u) eines Knoten u V ist Γ(u) := {v V {u, v} E}. 2 Der Grad
Algorithmen und Datenstrukturen SS09. Foliensatz 16. Michael Brinkmeier. Technische Universität Ilmenau Institut für Theoretische Informatik
 Foliensatz 16 Michael Brinkmeier Technische Universität Ilmenau Institut für Theoretische Informatik Sommersemester 2009 TU Ilmenau Seite 1 / 45 Graphen TU Ilmenau Seite 2 / 45 Graphen 1 2 3 4 5 6 7 8
Foliensatz 16 Michael Brinkmeier Technische Universität Ilmenau Institut für Theoretische Informatik Sommersemester 2009 TU Ilmenau Seite 1 / 45 Graphen TU Ilmenau Seite 2 / 45 Graphen 1 2 3 4 5 6 7 8
Diskrete Strukturen. Hausaufgabe 1 (5 Punkte) Hausaufgabe 2 (5 Punkte) Wintersemester 2007/08 Lösungsblatt Januar 2008
 Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
Planare Graphen und Färbungen. Kapitel 7. Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/ / 296
 Kapitel 7 Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 256 / 296 Inhalt Inhalt 7 Färbungen Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 257 / 296 Jordankurve Zentrale Frage
Kapitel 7 Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 256 / 296 Inhalt Inhalt 7 Färbungen Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 257 / 296 Jordankurve Zentrale Frage
Lösungen zu Kapitel 5
 Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
Definition Gerichteter Pfad. gerichteter Pfad, wenn. Ein gerichteter Pfad heißt einfach, falls alle u i paarweise verschieden sind.
 3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
Übersicht. Bielefeld Hannover. Kamen Paderborn. Unna Wünnenberg Kassel. Ziffer wählen. abheben. auflegen. Gespräch führen
 Übersicht Graphen beschreiben Objekte und Beziehungen zwischen ihnen geeignet für Modellierung verschiedener Aufgaben betrachten endliche, ungerichtete und endliche, gerichtete Graphen Graphen bestehen
Übersicht Graphen beschreiben Objekte und Beziehungen zwischen ihnen geeignet für Modellierung verschiedener Aufgaben betrachten endliche, ungerichtete und endliche, gerichtete Graphen Graphen bestehen
Programmiertechnik II
 Graph-Algorithmen Anwendungsgebiete "Verbundene Dinge" oft Teilproblem/Abstraktion einer Aufgabenstellung Karten: Wie ist der kürzeste Weg von Sanssouci nach Kunnersdorf? Hypertext: Welche Seiten sind
Graph-Algorithmen Anwendungsgebiete "Verbundene Dinge" oft Teilproblem/Abstraktion einer Aufgabenstellung Karten: Wie ist der kürzeste Weg von Sanssouci nach Kunnersdorf? Hypertext: Welche Seiten sind
Definition Ein gerichteter Graph G = (V, E) ist ein Graph von geordneten Paaren (u, v) mit u V und v V.
 Kapitel 4 Graphenalgorithmen 4.1 Definitionen Definition 4.1.1. Der Graph G = (V, E) ist über die beiden Mengen V und E definiert, wobei V die Menge der Knoten und E die Menge der Kanten in dem Graph ist.
Kapitel 4 Graphenalgorithmen 4.1 Definitionen Definition 4.1.1. Der Graph G = (V, E) ist über die beiden Mengen V und E definiert, wobei V die Menge der Knoten und E die Menge der Kanten in dem Graph ist.
Programmiertechnik II
 Graph-Algorithmen Anwendungsgebiete "Verbundene Dinge" oft Teilproblem/Abstraktion einer Aufgabenstellung Karten: Wie ist der kürzeste Weg von Sanssouci nach Kunnersdorf? Hypertext: Welche Seiten sind
Graph-Algorithmen Anwendungsgebiete "Verbundene Dinge" oft Teilproblem/Abstraktion einer Aufgabenstellung Karten: Wie ist der kürzeste Weg von Sanssouci nach Kunnersdorf? Hypertext: Welche Seiten sind
Am Dienstag, den 15. Dezember, ist Eulenfest. 1/60
 Am Dienstag, den 15. Dezember, ist Eulenfest. 1/60 Grundbegriffe der Informatik Einheit 12: Erste Algorithmen in Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester
Am Dienstag, den 15. Dezember, ist Eulenfest. 1/60 Grundbegriffe der Informatik Einheit 12: Erste Algorithmen in Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester
Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen)
 WS 2015/16 Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
WS 2015/16 Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
15. Elementare Graphalgorithmen
 Graphen sind eine der wichtigste Modellierungskonzepte der Informatik Graphalgorithmen bilden die Grundlage vieler Algorithmen in der Praxis Zunächst kurze Wiederholung von Graphen. Dann Darstellungen
Graphen sind eine der wichtigste Modellierungskonzepte der Informatik Graphalgorithmen bilden die Grundlage vieler Algorithmen in der Praxis Zunächst kurze Wiederholung von Graphen. Dann Darstellungen
Eulerweg, Eulerkreis. Das Königsberger Brückenproblem. Definition 3.1. Ein Weg, der jede Kante von G genau einmal
 3. Kreis- und Wegeprobleme Kapitelübersicht 3. Kreis- und Wegeprobleme Eulerweg, Eulerkreis Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Definition
3. Kreis- und Wegeprobleme Kapitelübersicht 3. Kreis- und Wegeprobleme Eulerweg, Eulerkreis Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Definition
Diskrete Strukturen WS 2005/06. Ernst W. Mayr. 27. Januar Fakultät für Informatik TU München
 WS 2005/06 Ernst W. Mayr Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2005ws/ds/ 27. Januar 2006 Ernst W. Mayr 2.16 Inzidenzmatrix 3. Definitionen für gerichtete Graphen 3.1 Digraph
WS 2005/06 Ernst W. Mayr Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2005ws/ds/ 27. Januar 2006 Ernst W. Mayr 2.16 Inzidenzmatrix 3. Definitionen für gerichtete Graphen 3.1 Digraph
Ecken des Zuordnungsproblems
 Total unimodulare Matrizen Ecken des Zuordnungsproblems Definition.6 Ein Zuordnungsproblem mit den Vorzeichenbedingungen 0 apple x ij apple für i, j =,...,n statt x ij 2{0, } heißt relaxiertes Zuordnungproblem.
Total unimodulare Matrizen Ecken des Zuordnungsproblems Definition.6 Ein Zuordnungsproblem mit den Vorzeichenbedingungen 0 apple x ij apple für i, j =,...,n statt x ij 2{0, } heißt relaxiertes Zuordnungproblem.
Algorithmen und Datenstrukturen 2-1. Seminar -
 Algorithmen und Datenstrukturen 2-1. Seminar - Dominic Rose Bioinformatics Group, University of Leipzig Sommersemster 2010 Outline 1. Übungsserie: 3 Aufgaben, insgesamt 30 28 Punkte A1 Spannbäume (10 8
Algorithmen und Datenstrukturen 2-1. Seminar - Dominic Rose Bioinformatics Group, University of Leipzig Sommersemster 2010 Outline 1. Übungsserie: 3 Aufgaben, insgesamt 30 28 Punkte A1 Spannbäume (10 8
WS 2008/09. Diskrete Strukturen
 WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Programm heute. Algorithmen und Datenstrukturen (für ET/IT) Übersicht: Graphen. Definition: Ungerichteter Graph. Definition: Ungerichteter Graph
 Programm heute Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 07 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München 7 Fortgeschrittene Datenstrukturen Graphen
Programm heute Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 07 Dr. Stefanie Demirci Computer Aided Medical Procedures Technische Universität München 7 Fortgeschrittene Datenstrukturen Graphen
Graphen. Graphen und ihre Darstellungen
 Graphen Graphen und ihre Darstellungen Ein Graph beschreibt Beziehungen zwischen den Elementen einer Menge von Objekten. Die Objekte werden als Knoten des Graphen bezeichnet; besteht zwischen zwei Knoten
Graphen Graphen und ihre Darstellungen Ein Graph beschreibt Beziehungen zwischen den Elementen einer Menge von Objekten. Die Objekte werden als Knoten des Graphen bezeichnet; besteht zwischen zwei Knoten
Naiver Algorithmus für Hamiltonkreis
 Naiver Algorithmus für Hamiltonkreis Algorithmus HAMILTON EINGABE: G = ([n], E) in Adjazenzmatrixdarstellung 1 Für alle Permutationen π : [n] [n]. 1 Falls (π(1), π(2),..., π(n)) ein Kreis in G ist, AUSGABE
Naiver Algorithmus für Hamiltonkreis Algorithmus HAMILTON EINGABE: G = ([n], E) in Adjazenzmatrixdarstellung 1 Für alle Permutationen π : [n] [n]. 1 Falls (π(1), π(2),..., π(n)) ein Kreis in G ist, AUSGABE
Statistik und Graphentheorie
 Statistik und Graphentheorie Sommersemester 2014 24. März 2015 Teil Graphentheorie Matrikelnummer: 1 (12) 2 (12) 3 (12) 4 (12) 5 (12) (60) Aufgabe 1 (12 Punkte) Gegeben sei das folgende Netzwerk: (a) Berechnen
Statistik und Graphentheorie Sommersemester 2014 24. März 2015 Teil Graphentheorie Matrikelnummer: 1 (12) 2 (12) 3 (12) 4 (12) 5 (12) (60) Aufgabe 1 (12 Punkte) Gegeben sei das folgende Netzwerk: (a) Berechnen
Übung zur Vorlesung Diskrete Mathematik (MAT.107) Blatt Beispiellösungen Abgabefrist:
 Svenja Hüning, Michael Kerber, Hannah Schreiber WS 2016/2017 Übung zur Vorlesung Diskrete Mathematik (MAT.107) Blatt Beispiellösungen Abgabefrist: Hinweise: Dieses Blatt präsentiert Beispiellösungen zu
Svenja Hüning, Michael Kerber, Hannah Schreiber WS 2016/2017 Übung zur Vorlesung Diskrete Mathematik (MAT.107) Blatt Beispiellösungen Abgabefrist: Hinweise: Dieses Blatt präsentiert Beispiellösungen zu
Freie Bäume und Wälder
 (Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
(Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Prof. Martin Lercher Institut für Informatik Heinrich-Heine-Universität Düsseldorf Teil 10 Suche in Graphen Version vom 13. Dezember 2016 1 / 2 Vorlesung 2016 / 2017 2 /
Algorithmen und Datenstrukturen Prof. Martin Lercher Institut für Informatik Heinrich-Heine-Universität Düsseldorf Teil 10 Suche in Graphen Version vom 13. Dezember 2016 1 / 2 Vorlesung 2016 / 2017 2 /
3.6 Eigenwerte und Eigenvektoren
 3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
Berechnung von Abständen
 3. Kreis- und Wegeprobleme Abstände in Graphen Abstände in Graphen Definition 3.4. Es sei G = (V, E) ein Graph. Der Abstand d(v, w) zweier Knoten v, w V ist die minimale Länge eines Weges von v nach w.
3. Kreis- und Wegeprobleme Abstände in Graphen Abstände in Graphen Definition 3.4. Es sei G = (V, E) ein Graph. Der Abstand d(v, w) zweier Knoten v, w V ist die minimale Länge eines Weges von v nach w.
9. Übung Algorithmen I
 Timo Bingmann, Christian Schulz INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS 1 KIT Timo Universität Bingmann, des LandesChristian Baden-Württemberg Schulz und nationales Forschungszentrum in der
Timo Bingmann, Christian Schulz INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS 1 KIT Timo Universität Bingmann, des LandesChristian Baden-Württemberg Schulz und nationales Forschungszentrum in der
Übung zur Vorlesung Diskrete Strukturen I
 Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
(a, b)-bäume / 1. Datenmenge ist so groß, dass sie auf der Festplatte abgespeichert werden muss.
 (a, b)-bäume / 1. Szenario: Datenmenge ist so groß, dass sie auf der Festplatte abgespeichert werden muss. Konsequenz: Kommunikation zwischen Hauptspeicher und Festplatte - geschieht nicht Byte für Byte,
(a, b)-bäume / 1. Szenario: Datenmenge ist so groß, dass sie auf der Festplatte abgespeichert werden muss. Konsequenz: Kommunikation zwischen Hauptspeicher und Festplatte - geschieht nicht Byte für Byte,
1 Beispiele für Graphen
 Beispiele für Graphen 1 Beispiele für Graphen 1. Kreuzungsproblem : 3 Häuser sollen mit einem Wasser-, Gas- und Elektroanschluß verbunden werden, wobei keine Kreuzung entstehen darf. Abbildung 1: Kreuzungsproblem
Beispiele für Graphen 1 Beispiele für Graphen 1. Kreuzungsproblem : 3 Häuser sollen mit einem Wasser-, Gas- und Elektroanschluß verbunden werden, wobei keine Kreuzung entstehen darf. Abbildung 1: Kreuzungsproblem
Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume)
 WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
2. November Gradfolgen Zusammenhang Kürzeste Wege. H. Meyerhenke: Algorithmische Methoden zur Netzwerkanalyse 37
 2. November 2011 Gradfolgen Zusammenhang Kürzeste Wege H. Meyerhenke: Algorithmische Methoden zur Netzwerkanalyse 37 Satz von Erdős und Gallai Eine Partition einer natürlichen Zahl ist genau dann die Gradfolge
2. November 2011 Gradfolgen Zusammenhang Kürzeste Wege H. Meyerhenke: Algorithmische Methoden zur Netzwerkanalyse 37 Satz von Erdős und Gallai Eine Partition einer natürlichen Zahl ist genau dann die Gradfolge
Vier-Farben-Vermutung (1)
 Vier-Farben-Vermutung (1) Landkarten möchte man so färben, dass keine benachbarten Länder die gleiche Farbe erhalten. Wie viele Farben braucht man zur Färbung einer Landkarte? Vier-Farben-Vermutung: Jede
Vier-Farben-Vermutung (1) Landkarten möchte man so färben, dass keine benachbarten Länder die gleiche Farbe erhalten. Wie viele Farben braucht man zur Färbung einer Landkarte? Vier-Farben-Vermutung: Jede
Bemerkung: Der vollständige Graph K n hat n(n 1)
 Bemerkung: Der vollständige Graph K n hat n(n 1) 2 Kanten. Bew: Abzählen! Definition 111. Graphen mit n paarweise zyklisch verbundenen Kanten heißen Kreise (vom Grad n) und werden mit C n bezeichnet. Beispiel
Bemerkung: Der vollständige Graph K n hat n(n 1) 2 Kanten. Bew: Abzählen! Definition 111. Graphen mit n paarweise zyklisch verbundenen Kanten heißen Kreise (vom Grad n) und werden mit C n bezeichnet. Beispiel
Kapitel IV Minimale Spannbäume
 Kapitel IV Minimale Spannbäume. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten.
Kapitel IV Minimale Spannbäume. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten.
Motivation Kap. 6: Graphen
 Motivation Kap. 6: Graphen Warum soll ich heute hier bleiben? Graphen sind wichtig und machen Spaß! Professor Dr. Lehrstuhl für Algorithm Engineering, LS Fakultät für Informatik, TU Dortmund Was gibt es
Motivation Kap. 6: Graphen Warum soll ich heute hier bleiben? Graphen sind wichtig und machen Spaß! Professor Dr. Lehrstuhl für Algorithm Engineering, LS Fakultät für Informatik, TU Dortmund Was gibt es
12. Graphen. Notation, Repräsentation, Traversieren (DFS, BFS), Topologisches Sortieren, Ottman/Widmayer, Kap ,Cormen et al, Kap.
 254 12. Graphen Notation, Repräsentation, Traversieren (DFS, BFS), Topologisches Sortieren, Ottman/Widmayer, Kap. 9.1-9.4,Cormen et al, Kap. 22 Königsberg 1736 255 Königsberg 1736 255 Königsberg 1736 255
254 12. Graphen Notation, Repräsentation, Traversieren (DFS, BFS), Topologisches Sortieren, Ottman/Widmayer, Kap. 9.1-9.4,Cormen et al, Kap. 22 Königsberg 1736 255 Königsberg 1736 255 Königsberg 1736 255
Kapitel IV Minimale Spannbäume
 Kapitel IV Minimale Spannbäume 1. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten.
Kapitel IV Minimale Spannbäume 1. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten.
Dieser Graph hat 3 Zusammenhangskomponenten
 Vl 2, Informatik B, 19. 04. 02 1.1.3 Definitionen und wichtige Graphen Sei im folgenden G =(V;E) ein schlichter ungerichteter Graph. Definition: Der Grad eines Knoten v in einem ungerichteten Graphen ist
Vl 2, Informatik B, 19. 04. 02 1.1.3 Definitionen und wichtige Graphen Sei im folgenden G =(V;E) ein schlichter ungerichteter Graph. Definition: Der Grad eines Knoten v in einem ungerichteten Graphen ist
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 2014/15 17. Vorlesung Graphen: Repräsentation und Durchlaufstrategien Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Vorlesungsumfrage Nutzen Sie
1 Algorithmen und Datenstrukturen Wintersemester 2014/15 17. Vorlesung Graphen: Repräsentation und Durchlaufstrategien Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Vorlesungsumfrage Nutzen Sie
Graphen KAPITEL 3. Dieses Problem wird durch folgenden Graph modelliert:
 KAPITEL 3 Graphen Man kann als Ursprung der Graphentheorie ein Problem sehen, welches Euler 1736 von Studenten aus Königsberg gestellt bekam. Der Fluss Pregel wird von 7 Brücken überquert, und die Frage
KAPITEL 3 Graphen Man kann als Ursprung der Graphentheorie ein Problem sehen, welches Euler 1736 von Studenten aus Königsberg gestellt bekam. Der Fluss Pregel wird von 7 Brücken überquert, und die Frage
Ferienkurs Propädeutikum Diskrete Mathematik
 Ferienkurs Propädeutikum Diskrete Mathematik Teil 3: Grundlagen Graphentheorie Tina Janne Schmidt Technische Universität München April 2012 Tina Janne Schmidt (TU München) Ferienkurs Propädeutikum Diskrete
Ferienkurs Propädeutikum Diskrete Mathematik Teil 3: Grundlagen Graphentheorie Tina Janne Schmidt Technische Universität München April 2012 Tina Janne Schmidt (TU München) Ferienkurs Propädeutikum Diskrete
1. Einige Begriffe aus der Graphentheorie
 . Einige Begriffe aus der Graphentheorie Notation. Sei M eine Menge, n N 0. Dann bezeichnet P n (M) die Menge aller n- elementigen Teilmengen von M, und P(M) die Menge aller Teilmengen von M, d.h. die
. Einige Begriffe aus der Graphentheorie Notation. Sei M eine Menge, n N 0. Dann bezeichnet P n (M) die Menge aller n- elementigen Teilmengen von M, und P(M) die Menge aller Teilmengen von M, d.h. die
Diskrete Strukturen. Hausaufgabe 1 (5 Punkte) Wintersemester 2007/08 Lösungsblatt Januar 2008
 Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 8
Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 8
Kapitel 6. Elementare Kombinatorik und Abzählbarkeit. Elementare Kombinatorik und Abzählbarkeit
 und Abzählbarkeit Kapitel 6 und Abzählbarkeit Peter Becker (H-BRS) Mathematische Grundlagen Wintersemester 2016/17 253 / 288 und Abzählbarkeit Inhalt Inhalt 6 und Abzählbarkeit Abzählbarkeit Peter Becker
und Abzählbarkeit Kapitel 6 und Abzählbarkeit Peter Becker (H-BRS) Mathematische Grundlagen Wintersemester 2016/17 253 / 288 und Abzählbarkeit Inhalt Inhalt 6 und Abzählbarkeit Abzählbarkeit Peter Becker
Grundlagen der Theoretischen Informatik
 1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Notation für Wörter w a is die Anzahl der Vorkommen von
1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Notation für Wörter w a is die Anzahl der Vorkommen von
Seien u, v V, u v. Da G zusammenhängend ist, muss mindestens ein Pfad zwischen u und v existieren.
 Beweis: 1. 2. Seien u, v V, u v. Da G zusammenhängend ist, muss mindestens ein Pfad zwischen u und v existieren. Widerspruchsannahme: Es gibt zwei verschiedene Pfade zwischen u und v. Dann gibt es einen
Beweis: 1. 2. Seien u, v V, u v. Da G zusammenhängend ist, muss mindestens ein Pfad zwischen u und v existieren. Widerspruchsannahme: Es gibt zwei verschiedene Pfade zwischen u und v. Dann gibt es einen
Informatik II, SS 2018
 Informatik II - SS 2018 (Algorithmen & Datenstrukturen) Vorlesung 13 (6.6.2018) Graphenalgorithmen II Yannic Maus Algorithmen und Komplexität Repräsentation von Graphen Zwei klassische Arten, einen Graphen
Informatik II - SS 2018 (Algorithmen & Datenstrukturen) Vorlesung 13 (6.6.2018) Graphenalgorithmen II Yannic Maus Algorithmen und Komplexität Repräsentation von Graphen Zwei klassische Arten, einen Graphen
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 02. Mai 2017 [Letzte Aktualisierung: 10/07/2018,
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 02. Mai 2017 [Letzte Aktualisierung: 10/07/2018,
= n (n 1) 2 dies beruht auf der Auswahl einer zweielementigen Teilmenge aus V = n. Als Folge ergibt sich, dass ein einfacher Graph maximal ( n E = 2
 1 Graphen Definition: Ein Graph G = (V,E) setzt sich aus einer Knotenmenge V und einer (Multi)Menge E V V, die als Kantenmenge bezeichnet wird, zusammen. Falls E symmetrisch ist, d.h.( u,v V)[(u,v) E (v,u)
1 Graphen Definition: Ein Graph G = (V,E) setzt sich aus einer Knotenmenge V und einer (Multi)Menge E V V, die als Kantenmenge bezeichnet wird, zusammen. Falls E symmetrisch ist, d.h.( u,v V)[(u,v) E (v,u)
VL-14: Graphalgorithmen I. (Datenstrukturen und Algorithmen, SS 2017) Gerhard Woeginger
 VL-14: Graphalgorithmen I (Datenstrukturen und Algorithmen, SS 2017) Gerhard Woeginger SS 2017, RWTH DSAL/SS 2017 VL-14: Graphalgorithmen I 1/48 Organisatorisches Vorlesung: Gerhard Woeginger (Zimmer 4024
VL-14: Graphalgorithmen I (Datenstrukturen und Algorithmen, SS 2017) Gerhard Woeginger SS 2017, RWTH DSAL/SS 2017 VL-14: Graphalgorithmen I 1/48 Organisatorisches Vorlesung: Gerhard Woeginger (Zimmer 4024
4. Kreis- und Wegeprobleme Abstände in Graphen
 4. Kreis- und Wegeprobleme Abstände in Graphen Abstände in Graphen Definition 4.4. Es sei G = (V,E) ein Graph. Der Abstand d(v,w) zweier Knoten v,w V ist die minimale Länge eines Weges von v nach w. Falls
4. Kreis- und Wegeprobleme Abstände in Graphen Abstände in Graphen Definition 4.4. Es sei G = (V,E) ein Graph. Der Abstand d(v,w) zweier Knoten v,w V ist die minimale Länge eines Weges von v nach w. Falls
Lineare Algebra: Determinanten und Eigenwerte
 : und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
: und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 16: Erste Algorithmen in Graphen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für
Grundbegriffe der Informatik Kapitel 16: Erste Algorithmen in Graphen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Einheit 11 - Graphen
 Einheit - Graphen Bevor wir in medias res (eigentlich heißt es medias in res) gehen, eine Zusammenfassung der wichtigsten Definitionen und Notationen für Graphen. Graphen bestehen aus Knoten (vertex, vertices)
Einheit - Graphen Bevor wir in medias res (eigentlich heißt es medias in res) gehen, eine Zusammenfassung der wichtigsten Definitionen und Notationen für Graphen. Graphen bestehen aus Knoten (vertex, vertices)
Graphenalgorithmen I. Geschickt Programmieren für den ICPC- Wettbewerb. Felix Weissenberger
 Graphenalgorithmen I Geschickt Programmieren für den ICPC- Wettbewerb Felix Weissenberger Inhalt Grundlagen zu Graphen Begriffe Darstellung von Graphen Graphenalgorithmen Breitensuche Tiefensuche Topologisches
Graphenalgorithmen I Geschickt Programmieren für den ICPC- Wettbewerb Felix Weissenberger Inhalt Grundlagen zu Graphen Begriffe Darstellung von Graphen Graphenalgorithmen Breitensuche Tiefensuche Topologisches
Musterlösungen Blatt Mathematischer Vorkurs. Sommersemester Dr. O. Zobay. Matrizen
 Musterlösungen Blatt 8 34007 Mathematischer Vorkurs Sommersemester 007 Dr O Zobay Matrizen Welche Matrixprodukte können mit den folgenden Matrizen gebildet werden? ( 4 5 A, B ( 0 9 7, C 8 0 5 4 Wir können
Musterlösungen Blatt 8 34007 Mathematischer Vorkurs Sommersemester 007 Dr O Zobay Matrizen Welche Matrixprodukte können mit den folgenden Matrizen gebildet werden? ( 4 5 A, B ( 0 9 7, C 8 0 5 4 Wir können
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Prof. Martin Lercher Institut für Informatik Heinrich-Heine-Universität Düsseldorf Teil 9 Graphen Version vom 13. Dezember 2016 1 / 1 Vorlesung Fortsetzung 13. Dezember
Algorithmen und Datenstrukturen Prof. Martin Lercher Institut für Informatik Heinrich-Heine-Universität Düsseldorf Teil 9 Graphen Version vom 13. Dezember 2016 1 / 1 Vorlesung Fortsetzung 13. Dezember
Einführung in die Graphentheorie. Monika König
 Einführung in die Graphentheorie Monika König 8. 11. 2011 1 Vorwort Diese Seminararbeit basiert auf den Unterkapiteln 1.1-1.3 des Buches Algebraic Graph Theory von Chris Godsil und Gordon Royle (siehe
Einführung in die Graphentheorie Monika König 8. 11. 2011 1 Vorwort Diese Seminararbeit basiert auf den Unterkapiteln 1.1-1.3 des Buches Algebraic Graph Theory von Chris Godsil und Gordon Royle (siehe
2.4 Starke Zusammenhangskomponenten in Digraphen
 Starke Zusammenhangskomponenten Einleitung 2.4 Starke Zusammenhangskomponenten in Digraphen Definition 2.4.1 Zwei Knoten v und w in einem Digraphen G heißen äquivalent, wenn v w und w v gilt. Notation:
Starke Zusammenhangskomponenten Einleitung 2.4 Starke Zusammenhangskomponenten in Digraphen Definition 2.4.1 Zwei Knoten v und w in einem Digraphen G heißen äquivalent, wenn v w und w v gilt. Notation:
Algorithmen und Datenstrukturen (ESE) Entwurf, Analyse und Umsetzung von Algorithmen (IEMS) WS 2013 / 2014 Vorlesung 12, Donnerstag, 23.
 Algorithmen und Datenstrukturen (ESE) Entwurf, Analyse und Umsetzung von Algorithmen (IEMS) WS 0 / 04 Vorlesung, Donnerstag,. Januar 04 (Graphen, Breiten/Tiefensuche, Zusammenhangskomponenten) Junior-Prof.
Algorithmen und Datenstrukturen (ESE) Entwurf, Analyse und Umsetzung von Algorithmen (IEMS) WS 0 / 04 Vorlesung, Donnerstag,. Januar 04 (Graphen, Breiten/Tiefensuche, Zusammenhangskomponenten) Junior-Prof.
Graphentheorie. Yichuan Shen. 10. Oktober 2013
 Graphentheorie Yichuan Shen 0. Oktober 203 Was ist ein Graph? Ein Graph ist eine kombinatorische Struktur, die bei der Modellierung zahlreicher Probleme Verwendung findet. Er besteht ganz allgemein aus
Graphentheorie Yichuan Shen 0. Oktober 203 Was ist ein Graph? Ein Graph ist eine kombinatorische Struktur, die bei der Modellierung zahlreicher Probleme Verwendung findet. Er besteht ganz allgemein aus
Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od
 Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od Diskrete Strukturen 3.7 dag 473/556 3.8 Zusammenhang Definition
Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od Diskrete Strukturen 3.7 dag 473/556 3.8 Zusammenhang Definition
Kap. 5: Graphen. Carsten Gutwenger Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund. 17. VO DAP2 SS
 Kap. 5: Graphen Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 17. VO DAP2 SS 2009 23. Juni 2008 1 Motivation Warum soll ich heute hier bleiben? Graphen sind wichtig und
Kap. 5: Graphen Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 17. VO DAP2 SS 2009 23. Juni 2008 1 Motivation Warum soll ich heute hier bleiben? Graphen sind wichtig und
Vorlesungstermin 2: Graphentheorie II. Markus Püschel David Steurer. Algorithmen und Datenstrukturen, Herbstsemester 2018, ETH Zürich
 Vorlesungstermin 2: Graphentheorie II Markus Püschel David Steurer Algorithmen und Datenstrukturen, Herbstsemester 2018, ETH Zürich Wiederholung: Vollständige Induktion Ziel: zeige n N. A(n) für eine Aussage
Vorlesungstermin 2: Graphentheorie II Markus Püschel David Steurer Algorithmen und Datenstrukturen, Herbstsemester 2018, ETH Zürich Wiederholung: Vollständige Induktion Ziel: zeige n N. A(n) für eine Aussage
Graphen. Definitionen
 Graphen Graphen werden häufig als Modell für das Lösen eines Problems aus der Praxis verwendet, wie wir im Kapitel 1 gesehen haben. Der Schweizer Mathematiker Euler hat als erster Graphen verwendet, um
Graphen Graphen werden häufig als Modell für das Lösen eines Problems aus der Praxis verwendet, wie wir im Kapitel 1 gesehen haben. Der Schweizer Mathematiker Euler hat als erster Graphen verwendet, um
Am Dienstag, den 16. Dezember, ist Eulenfest. 1/45
 Am Dienstag, den 16. Dezember, ist Eulenfest. 1/45 Grundbegriffe der Informatik Einheit 12: Erste Algorithmen in Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009
Am Dienstag, den 16. Dezember, ist Eulenfest. 1/45 Grundbegriffe der Informatik Einheit 12: Erste Algorithmen in Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 4: Suchstrategien Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 14. April 2017 HALBORDNUNG TOPOLOGISCHE ORDNUNG TOPOLOGISCHES
Algorithmische Graphentheorie Vorlesung 4: Suchstrategien Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 14. April 2017 HALBORDNUNG TOPOLOGISCHE ORDNUNG TOPOLOGISCHES
12. Graphen. Königsberg Zyklen. [Multi]Graph
![12. Graphen. Königsberg Zyklen. [Multi]Graph 12. Graphen. Königsberg Zyklen. [Multi]Graph](/thumbs/94/119271554.jpg) Königsberg 76. Graphen, Repräsentation, Traversieren (DFS, BFS), Topologisches Sortieren, Ottman/Widmayer, Kap. 9. - 9.,Cormen et al, Kap. [Multi]Graph Zyklen C Kante Gibt es einen Rundweg durch die Stadt
Königsberg 76. Graphen, Repräsentation, Traversieren (DFS, BFS), Topologisches Sortieren, Ottman/Widmayer, Kap. 9. - 9.,Cormen et al, Kap. [Multi]Graph Zyklen C Kante Gibt es einen Rundweg durch die Stadt
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 15: Graphen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Grundbegriffe der Informatik Kapitel 15: Graphen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 7 und 8: Euler- und Hamilton-Graphen Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 17. April 2018 1/96 WIEDERHOLUNG Eulersche
Algorithmische Graphentheorie Vorlesung 7 und 8: Euler- und Hamilton-Graphen Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 17. April 2018 1/96 WIEDERHOLUNG Eulersche
Graphdurchmusterung, Breiten- und Tiefensuche
 Prof. Thomas Richter 18. Mai 2017 Institut für Analysis und Numerik Otto-von-Guericke-Universität Magdeburg thomas.richter@ovgu.de Material zur Vorlesung Algorithmische Mathematik II am 18.05.2017 Graphdurchmusterung,
Prof. Thomas Richter 18. Mai 2017 Institut für Analysis und Numerik Otto-von-Guericke-Universität Magdeburg thomas.richter@ovgu.de Material zur Vorlesung Algorithmische Mathematik II am 18.05.2017 Graphdurchmusterung,
Fortgeschrittene Netzwerk- und Graph-Algorithmen
 Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
7.3 Unitäre Operatoren
 Wir können jeden Operator T wie folgt schreiben: Dabei gilt T = 1 2 (T + T ) + i( 1 2 i (T T )) (T + T ) = T + T sowie ( 1 2 i (T T )) = 1 2 i (T T) = 1 2 i (T T ). Wir können T also in zwei lineare Operatoren
Wir können jeden Operator T wie folgt schreiben: Dabei gilt T = 1 2 (T + T ) + i( 1 2 i (T T )) (T + T ) = T + T sowie ( 1 2 i (T T )) = 1 2 i (T T) = 1 2 i (T T ). Wir können T also in zwei lineare Operatoren
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil II Peter F. Stadler & Konstantin Klemm Bioinformatics Group, Dept. of Computer Science & Interdisciplinary Center for Bioinformatics, University of Leipzig 07.
ADS: Algorithmen und Datenstrukturen 2 Teil II Peter F. Stadler & Konstantin Klemm Bioinformatics Group, Dept. of Computer Science & Interdisciplinary Center for Bioinformatics, University of Leipzig 07.
Übungsaufgaben Graphentheorie, Wintersemester 2011/12
 Übungsaufgaben Graphentheorie, Wintersemester 2011/12 Frank Göring 25. Januar 2012 Zusammenfassung Übungsaufgaben zur Graphentheorievorlesung. 1 Bis 19.10.2011 1. Wir hatten einen Graphen G als zusammenhängend
Übungsaufgaben Graphentheorie, Wintersemester 2011/12 Frank Göring 25. Januar 2012 Zusammenfassung Übungsaufgaben zur Graphentheorievorlesung. 1 Bis 19.10.2011 1. Wir hatten einen Graphen G als zusammenhängend
Diskrete Mathematik. Sebastian Iwanowski FH Wedel. Kap. 6: Graphentheorie
 Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
