Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern
|
|
|
- Erica Schuster
- vor 6 Jahren
- Abrufe
Transkript
1 Überblick Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern Thomas Schneider April Grundbegriffe 2 Anwendung: Textsuche 3 Abschlusseigenschaften 4 Reguläre Ausdrücke und Anwendungen 5 Charakterisierungen 6 Entscheidungsprobleme Thomas Schneider Automatentheorie 1: endliche Wörter 1 Und nun... Thomas Schneider Automatentheorie 1: endliche Wörter 2 Wörter, Sprachen,... 1 Grundbegriffe 2 Anwendung: Textsuche 3 Abschlusseigenschaften 4 Reguläre Ausdrücke und Anwendungen 5 Charakterisierungen 6 Entscheidungsprobleme Symbole a, b,... Alphabet Σ: endliche nichtleere Menge von Symbolen (endliches) Wort w über Σ: endliche Folge w = a 1 a 2... a n von Symbolen a i Σ leeres Wort ε Wortlänge a 1 a 2... a n = n, ε = 0 Menge aller Wörter über Σ: Σ Sprache L über Σ: Teilmenge L Σ von Wörtern Sprachklasse L: Menge von Sprachen Thomas Schneider Automatentheorie 1: endliche Wörter 3 Thomas Schneider Automatentheorie 1: endliche Wörter 4
2 Endliche Automaten Beispiel und graphische Repräsentation von NEAs Definition 1 Ein nichtdeterministischer endlicher Automat (NEA) über einem Alphabet Σ ist ein 5-Tupel A = (Q, Σ,, I, F ), wobei Q eine endliche nichtleere Zustandsmenge ist, Σ eine endliche nichtleere Menge von Zeichen ist, Q Σ Q die Überführungsrelation ist, (*) I Q die Menge der Anfangszustände ist, F Q die Menge der Endzustände ist. (*) bedeutet: besteht aus Tripeln (q, a, q ) mit q, q Q und a Σ (q, a, q ) bedeutet: ist A in Zustand q und liest ein a, geht er in Zustand q über. Betrachte A = ({q 0, q 1 }, {a, b}, {(q 0, a, q 0 ), (q 0, b, q 1 ), (q 1, b, q 1 )}, {q 0 }, {q 1 }) Zustände: q 0, q 1 Alphabet {a, b} Übergänge: von q 0 mittels a zu q 0,... q 0 Anfangszustand q 0 q 0 Endzustand q 1 q 1 a b b A: q 0 q 1 q i a Thomas Schneider Automatentheorie 1: endliche Wörter 5 Berechnungen und Akzeptanz Thomas Schneider Automatentheorie 1: endliche Wörter 6 Beispiele Definition 2 Sei A = (Q, Σ,, I, F ) ein NEA. Eine Berechnung (Run) von A auf w = a 1 a 2... a n ist eine Folge q 0 q 1 q 2... q n, so dass für alle i = 0,..., n gilt: (q i, a i+1, q i+1 ). Man sagt auch: w überführt q 0 in q n. A akzeptiert w = a 1 a 2... a n, wenn es eine Berechnung q 0 q 1 q 2... q n von A auf w gibt mit q 0 I und q n F. Die von A erkannte Sprache ist L(A) = {w Σ A akzeptiert w}. a b A 1 : q 0 q 1 b a a, b a b A 2 : q 0 q 1 q 2 b L(A 2 ) = {w {a, b} w enthält Teilwort ab} a, b a b A 3 : q 0 q 1 q 2 L(A 3 ) = {w {a, b} w endet auf ab} L(A 1 ) = {a n b m n 0, m 1} Thomas Schneider Automatentheorie 1: endliche Wörter 7 Thomas Schneider Automatentheorie 1: endliche Wörter 8
3 Erkennbare Sprache Determinismus Definition 3 Eine Sprache L Σ ist (NEA-)erkennbar, wenn es einen NEA A gibt mit L = L(A). Definition 4 Sei A = (Q, Σ,, I, F ) ein NEA. Enthält für jedes q Q u. jedes a Σ genau 1 Tripel (q, a, q ) und enthält I genau 1 Zustand, dann ist A ein deterministischer endlicher Automat (DEA). Nachfolgezustand für jedes Paar (q, a) eindeutig bestimmt Jeder DEA ist ein NEA, aber nicht umgekehrt (z. B. A 1, A 3 auf Folie 8). Auf Folie 8 ist nur A 2 ein DEA; A 1 kann mittels Papierkorbzustand zum DEA werden und A 3? Frage Sind DEAs schwächer als NEAs? Thomas Schneider Automatentheorie 1: endliche Wörter 9 Potenzmengenkonstruktion Thomas Schneider Automatentheorie 1: endliche Wörter 10 Und nun... Antwort Nein, DEAs und NEAs sind gleichstark. Satz 5 Sei A ein NEA. Dann gibt es einen DEA A d mit L(A d ) = L(A). 1 Grundbegriffe 2 Anwendung: Textsuche 3 Abschlusseigenschaften 4 Reguläre Ausdrücke und Anwendungen Beweis: siehe Tafel. Im schlimmsten Fall kann A d im Vergleich zu A exponentiell viele Zustände haben (s. Hopcroft et al. 2001, S. 65). 5 Charakterisierungen 6 Entscheidungsprobleme Thomas Schneider Automatentheorie 1: endliche Wörter 11 Thomas Schneider Automatentheorie 1: endliche Wörter 12
4 Stichwortsuche Stichwortsuche ohne invertierte Indizes? Typisches Problem aus dem Internetzeitalter Gegeben sind Stichwörter w 1,..., w n Σ und Dokumente D 1,..., D M Σ. Finde alle j, so dass D j mindestens ein (alle) w i als Teilwort hat. relevant z.b. für Suchmaschinen übliche Technologie: invertierter Index (II) speichert für jedes im Internet auftretende w i eine Liste aller Dokumente D j, die w i enthalten IIs sind zeitaufwändig zu erstellen und setzen voraus, dass die D i sich nur langsam ändern IIs versagen, wenn die (relevanten) Dokumente sich schnell ändern: Suche in tagesaktuellen Nachrichtenartikeln Einkaufshelfer sucht nach bestimmten Artikeln in aktuellen Seiten von Online-Shops die Dokumente nicht katalogisiert werden können: Online-Shops wie Amazon generieren oft Seiten für ihre Artikel nur auf Anfragen hin. Wie kann man dafür Stichwortsuche implementieren? Thomas Schneider Automatentheorie 1: endliche Wörter 13 Ein Fall für endliche Automaten! Thomas Schneider Automatentheorie 1: endliche Wörter 14 Implementation des NEAs A Wdhlg.: Typisches Problem aus dem Internetzeitalter Gegeben sind Stichwörter w 1,..., w n Σ und Dokumente D 1,..., D M Σ. Finde alle j, so dass D j mindestens ein w i als Teilwort hat. Ziel: konstruiere NEA A, der Eine Möglichkeit: 1 Determinisierung (Potenzmengenkonstruktion) 2 Simulation des resultierenden DEA A d Wird A d nicht zu groß? (2 27 > 134 Mio. Zustände bei Stichw. Binomialkoeffizient, Polynom ) ein D j zeichenweise liest und in einen Endzustand geht gdw. er eins der Stichwörter findet Beispiel 6 Seien w 1 = web und w 2 = ebay. Wie muss A aussehen? siehe Tafel. Nein, für unsere spezielle Form von A, mit unserer Version der Potenzmengenkonstruktion wird A d genauso viele Zustände haben wie A! Beispiel: siehe Tafel Thomas Schneider Automatentheorie 1: endliche Wörter 15 Thomas Schneider Automatentheorie 1: endliche Wörter 16
5 Zum Nachdenken Und nun... 1 Grundbegriffe Übung: Konstruiere den DEA A d für A von Folie 15. Beschreibe die Konstruktion von A d allgemein, wenn w 1,..., w n gegeben sind, mit w i = a i1... a ili für jedes i = 1,..., n. 2 Anwendung: Textsuche 3 Abschlusseigenschaften 4 Reguläre Ausdrücke und Anwendungen 5 Charakterisierungen 6 Entscheidungsprobleme Thomas Schneider Automatentheorie 1: endliche Wörter 17 Operationen auf Sprachen sind Operationen auf Mengen Thomas Schneider Automatentheorie 1: endliche Wörter 18 Abgeschlossenheit Wie können (NEA-erkennbare) Sprachen kombiniert werden? L 1 L 2 = {w w L 1 oder w L 2 } L 1 L 2 = {w w L 1 und w L 2 } L = {w Σ w / L} L 1 L 2 = {vw v L 1 und w L 2 } L = L i, (Kleene-Hülle) i 0 wobei L 0 = {ε} und L i+1 = L i L für alle i 0. Satz 7 Die Menge der NEA-erkennbaren Sprachen ist abgeschlossen unter den Operationen,,,,. Das heißt: Wenn L, L 1, L 2 NEA-erkennbar sind, dann sind auch L 1 L 2, L 1 L 2, L, L 1 L 2 und L NEA-erkennbar. Beweis: Direkte Konsequenz aus den folgenden Lemmata. Thomas Schneider Automatentheorie 1: endliche Wörter 19 Thomas Schneider Automatentheorie 1: endliche Wörter 20
6 Abgeschlossenheit unter Vereinigung Abgeschlossenheit unter Durchschnitt Lemma 8 Seien A 1, A 2 NEAs über Σ. Dann gibt es einen NEA A 3 mit L(A 3 ) = L(A 1 ) L(A 2 ). Lemma 9 Seien A 1, A 2 NEAs über Σ. Dann gibt es einen NEA A 3 mit L(A 3 ) = L(A 1 ) L(A 2 ). Beweis: Seien A i = (Q i, Σ, i, I i, F i ) für i = 1, 2. O. B. d. A. gelte Q 1 Q 2 =. Konstruieren A 3 = (Q 3, Σ, 3, I 3, F 3 ) wie folgt. Idee: vereinige A 1 und A 2. Q 3 = Q 1 Q 2 3 = 1 2 I 3 = I 1 I 2 F 3 = F 1 F 2 (Beispiel siehe Tafel) Dann gilt L(A 3 ) = L(A 1 ) L(A 2 ). (Übung) Thomas Schneider Automatentheorie 1: endliche Wörter 21 Abgeschlossenheit unter Komplement Beweis: Seien A i = (Q i, Σ, i, I i, F i ) für i = 1, 2. Konstruieren A 3 = (Q 3, Σ, 3, I 3, F 3 ) wie folgt. Idee: lasse A 1 und A 2 gleichzeitig auf Eingabewort laufen. Q 3 = Q 1 Q 2 3 = {((p, p ), a, (q, q )) (p, a, q) 1 & (p, a, q ) 2 } I 3 = I 1 I 2 F 3 = F 1 F 2 (Beispiel siehe Tafel) Dann gilt L(A 3 ) = L(A 1 ) L(A 2 ). (Übung) Thomas Schneider Automatentheorie 1: endliche Wörter 22 Abgeschlossenheit unter Verkettung Lemma 10 Sei A ein NEA über Σ. Dann gibt es einen NEA A c mit L(A c ) = L(A). Lemma 11 Seien A 1, A 2 NEAs über Σ. Dann gibt es einen NEA A 3 mit L(A 3 ) = L(A 1 ) L(A 2 ). Beweis: Idee: Umwandlung in DEA Vertauschen von End- und Nicht-Endzuständen O. B. d. A. sei A = (Q, Σ,, I, F ) ein DEA (Satz 5). Dann erkennt A = (Q, Σ,, I, Q \ F ) die Sprache L(A). ( ) Jetzt erhält man Abgeschlossenheit unter auch mittels L 1 L 2 = L 1 L 2 ). Thomas Schneider Automatentheorie 1: endliche Wörter 23 Beweis: Seien A i = (Q i, Σ, i, I i, F i ) für i = 1, 2. O. B. d. A. gelte Q 1 Q 2 = und I i = {q 0i }. Konstruieren A 3 = (Q 3, Σ, 3, I 3, F 3 ) wie folgt. Idee: Hintereinanderhängen von A 1 und A 2. Q 3 = Q 1 Q 2 3 = 1 2 {(q, a, q ) q F 1 und (q 02, a, q ) 2 } { F2 F 1 falls q 02 F 2 I 3 = I 1, F 3 = (Bsp. s. Tafel) sonst F 2 Dann gilt L(A 3 ) = L(A 1 ) L(A 2 ). (Übung) Thomas Schneider Automatentheorie 1: endliche Wörter 24
7 Abgeschlossenheit unter Kleene-Hülle Und nun... Lemma 12 Sei A ein NEA über Σ. Dann gibt es einen NEA A k mit L(A k ) = L(A). Beweis: Sei A = (Q, Σ,, I, F ). Konstruieren A k = (Q k, Σ, k, I k, F k ) wie folgt. 1 Grundbegriffe 2 Anwendung: Textsuche 3 Abschlusseigenschaften Idee: Lege Schleife um A. Q k = Q {q 0 } (für ein q 0 / Q) k = {(q 0, ε, q) q I} {(q, ε, q 0 ) q F } 4 Reguläre Ausdrücke und Anwendungen 5 Charakterisierungen (ε-kanten werden aufgelöst wie im -Fall.) I k = F k = {q 0 } (Beispiel siehe Tafel) 6 Entscheidungsprobleme Dann gilt L(A k ) = L(A). (Übung) Thomas Schneider Automatentheorie 1: endliche Wörter 25 Ziel dieses Abschnitts Thomas Schneider Automatentheorie 1: endliche Wörter 26 Reguläre Sprachen Definition 13 Eine Sprache L Σ ist regulär, falls gilt: Wie können NEA-erkennbare Sprachen bequem charakterisiert werden? L = L = {ε} oder oder L = {a}, a Σ, oder L lässt sich durch (endlichmaliges) Anwenden der Operatoren,, aus den vorangehenden Fällen konstruieren. Beispiele: ({a} {b}) {a} {b} (siehe A 3 auf Folie 8) {b} {a} {a} {b} ({a} {b}) (s. A 2 auf Folie 8) Thomas Schneider Automatentheorie 1: endliche Wörter 27 Thomas Schneider Automatentheorie 1: endliche Wörter 28
8 Reguläre Ausdrücke Reguläre und NEA-erkennbare Sprachen Definition 14 Ein regulärer Ausdruck (RA) r über Σ und die zugehörige Sprache L(r) Σ werden induktiv wie folgt definiert. Beispiele: r = ist ein RA mit L(r) = r = ε ist ein RA mit L(r) = {ε} r = a, für a Σ, ist ein RA mit L(r) = {a} r = (r 1 + r 2 ), ist ein RA mit L(r) = L(r 1 ) L(r 2 ) r = (r 1 r 2 ), ist ein RA mit L(r) = L(r 1 ) L(r 2 ) r = (r 1 ), ist ein RA mit L(r ) = (L(r)) (wir lassen Klammern weg soweit eindeutig) (a + b) ab (siehe A 3 auf Folie 8) b aa b(a + b) (siehe A 2 auf Folie 8) Satz 15 (Kleene) Sei L Σ eine Sprache. 1 L ist regulär gdw. es einen RA r gibt mit L = L(r). 2 L ist regulär gdw. L NEA-erkennbar ist. Beweis. 1 Folgt offensichtlich aus Def. 13, Benutze Teil (1). : Induktion über Aufbau von r. IA: gib Automaten an, die, {ε}, {a} erkennen. IS: benutze Abschlusseigenschaften Lemmas 8, 11, 12 : siehe Tafel. Thomas Schneider Automatentheorie 1: endliche Wörter 29 Anwendungen regulärer Ausdrücke Thomas Schneider Automatentheorie 1: endliche Wörter 30 Komfortablere Syntax regulärer Ausdrücke UNIX und andere Anwendungen erweitern Syntax von RAs RAs werden verwendet, um Muster von zu suchendem Text zu beschreiben z. B.: suche alle Vorkommen von PLZ+Ort : ( ) 5 (A + + Z)(a + + z) Programme zum Suchen von Mustern im Text übersetzen RAs in NEAs/DEAs und simulieren diese wichtige Klassen von Anwendungen: lexikalische Analyse, Textsuche Thomas Schneider Automatentheorie 1: endliche Wörter 31 Hier: nur syntaktischer Zucker die Erweiterungen, die nicht aus den regulären Sprachen herausführen Alphabet Σ: alle ASCII-Zeichen RA. mit L(.) = Σ RA [a 1 a 2... a k ], Abkürzung für a 1 + a a k RAs für Bereiche: z. B. [a-z0-9], Abkü. für [ab... z ] Operator anstelle + Operator?: r? steht für ε + r Operator +: r+ steht für rr Operator {n}: r{5} steht für rrrrr Klammern und wie gehabt PLZ-Ort-Beispiel: [0-9]{5} [A-Z][a-z]* Thomas Schneider Automatentheorie 1: endliche Wörter 32
9 Anwendung: lexikalische Analyse Beispieleingabe für lex Lexer durchsucht Quelltext eines Programms nach Token: zusammengehörende Zeichenfolgen, z. B. Kennwörter, Bezeichner Ausgabe des Lexers: Token-Liste, wird an Parser weitergegeben Mit RAs: Lexer leicht programmier- und modifizierbar UNIX-Kommandos lex und flex generieren Lexer Eingabe: Liste von RA + Code Code beschreibt Ausgabe des Lexers für das jeweilige Token generierter Lexer wandelt RAs in DEAs um, um Vorkommen der Tokens zu finden (siehe Folie 15) anhand des Zustands des DEAs lässt sich bestimmen, welches Token gefunden wurde Thomas Schneider Automatentheorie 1: endliche Wörter 33 Anwendung: Finden von Mustern im Text else {return(else)} [A-Za-z][A-za-z0-9]* {<Trage gefundenen Bezeichner in Symboltabelle ein>; return(id);} >= {return(ge);} = {return(eq);} (Lexer-Generator muss Prioritäten beachten: else wird auch vom 2. RA erkannt, ist aber reserviert) Thomas Schneider Automatentheorie 1: endliche Wörter 34 Mustersuche mit regulären Ausdrücken Beispiel: Suchen von Adressen (Str. + Hausnr.) in Webseiten Solche Angaben sollen gefunden werden: Parkstraße 5 Enrique-Schmidt-Straße 12a Breitenweg 24A Knochenhauergasse aber auch solche: Straße des 17. Juni boulevard,... allee,... platz,... Postfach Am Wall 8 Mögliches Vorgehen: 1 Beschreibung des Musters mit einem einfachen RA 2 Umwandlung des RA in einen NEA 3 Implementation des NEA wie auf Folie 15 4 Test 5 Wenn nötig, RA erweitern und Sprung zu Schritt 2 Ausmaß der Variationen erst während der Suche deutlich Gesucht: einfach modifizierbare Beschreibung der Muster Thomas Schneider Automatentheorie 1: endliche Wörter 35 Thomas Schneider Automatentheorie 1: endliche Wörter 36
10 Adresssuche mit regulären Ausdrücken Und nun... So kann sich der RA entwickeln: Vorkommen von straße etc.: 1 straße str\. weg gasse Plus Name der Straße und Hausnummer: [A-Z][a-z]*(straße str\. weg gasse) [0-9]* Hausnummern mit Buchstaben (12a), -bereiche (30 32): [A-Z][a-z]*(straße str\. weg gasse) ([0-9]*[A-Za-z]-)*[0-9]*[A-za-z] und mehr: Straßennamen mit Bindestrichen Straße etc. am Anfang Plätze, Boulevards, Alleen etc. Postfächer... 1 Weil der UNIX-RA. für Σ reserviert ist, steht \. für {.} Thomas Schneider Automatentheorie 1: endliche Wörter 37 Pumping-Lemma 1 Grundbegriffe 2 Anwendung: Textsuche 3 Abschlusseigenschaften 4 Reguläre Ausdrücke und Anwendungen 5 Charakterisierungen 6 Entscheidungsprobleme Thomas Schneider Automatentheorie 1: endliche Wörter 38 Anwendung des Pumping-Lemmas Wie zeigt man, dass L nicht NEA-erkennbar (= regulär) ist? Satz 16 (Pumping-Lemma) Sei L eine NEA-erkennbare Sprache. Dann gibt es eine Konstante p N, 2 so dass für alle Wörter w L mit w p gilt: Es gibt eine Zerlegung w = xyz mit y > 0 und xy p, so dass xy i z L für alle i N. 2 Zur Erinnerung: Satz 16 (Pumping-Lemma) Wenn L eine NEA-erkennbare Sprache ist, dann gibt es eine Konstante p N, so dass für alle Wörter w L mit w p gilt: Es gibt eine Zerlegung w = xyz mit y > 0 und xy p, so dass xy i z L für alle i N. Benutzen Kontraposition: Beweis: siehe Tafel. 2 N = {0, 1, 2,... } Wenn es für alle Konstanten p N ein Wort w L mit w p gibt, so dass es für alle Zerlegungen w = xyz mit y > 0 und xy p ein i N gibt mit xy i z / L, dann ist L keine NFA-erkennbare Sprache. Bsp.: s. Tafel Thomas Schneider Automatentheorie 1: endliche Wörter 39 Thomas Schneider Automatentheorie 1: endliche Wörter 40
11 Bemerkungen zum Pumping-Lemma Der Satz von Myhill-Nerode Bedingung in Satz 16 ist notwendig dafür, dass L NEA-erkennbar ist. nicht hinreichend (Bsp.: {a m b n c n m, n 1} {b m c m m, n 0}) Pumping-L. nur zum Widerlegen von Erkennbarkeit verwendbar, nicht zum Beweisen, dass L regulär ist Notwendige und hinreichende Bedingung: Jaffes Pumping-L. Ziel: notwendige und hinreichende Bedingung für Erkennbarkeit Definition 17 Sei L Σ eine Sprache. Zwei Wörter u, v Σ sind L-äquivalent (Schreibweise: u L v), wenn für alle w Σ gilt: L ist Äquivalenzrelation uw L genau dann, wenn vw L reflexiv: offensichtlich symmetrisch: offensichtlich transitiv: offensichtlich Index von L : Anzahl der Äquivalenzklassen Thomas Schneider Automatentheorie 1: endliche Wörter 41 Der Satz von Myhill-Nerode Thomas Schneider Automatentheorie 1: endliche Wörter 42 Und nun... Satz 18 (Myhill-Nerode) L Σ is NEA-erkennbar gdw. L endlichen Index hat. 1 Grundbegriffe 2 Anwendung: Textsuche Ohne Beweis. Beispiel siehe Tafel. Interessantes Nebenprodukt des Beweises: Endlicher Index n von L = minimale Anzahl von Zuständen in einem DEA, der L erkennt. 3 Abschlusseigenschaften 4 Reguläre Ausdrücke und Anwendungen 5 Charakterisierungen 6 Entscheidungsprobleme Thomas Schneider Automatentheorie 1: endliche Wörter 43 Thomas Schneider Automatentheorie 1: endliche Wörter 44
12 Grundbegriffe Komplexität (Entscheidungs-)Problem... ist eine Teilmenge P M Beispiele: P = Menge aller Primzahlen, M = N P = Menge aller NEAs A mit L(A), M = Menge aller NEAs man stelle sich eine Blackbox vor mit Eingabe m M Ausgabe ja, falls m P, nein sonst (jede Berech. terminiert) Entscheidbarkeit: P ist entscheidbar, wenn es einen Algorithmus A gibt, der die Blackbox implementiert. ( ) Programmiersprache u. Rechnermodell sind relativ unerheblich: (Entscheidungs-)Problem... ist eine Teilmenge P M man stelle sich eine Blackbox vor mit Eingabe m M Ausgabe ja, falls m P, nein sonst Entscheidbarkeit: gibt es Alg. A, der die Blackbox implementiert? Komplexität: zusätzliche Anforderungen an Zeit-/Speicherplatzbedarf von A Polynomialzeit: Anzahl Rechenschritte von A ist pol( m ), m : Länge der Eingabe; pol ist ein festes Polynom erweiterte Churchsche These Thomas Schneider Automatentheorie 1: endliche Wörter 45 Reduktion Thomas Schneider Automatentheorie 1: endliche Wörter 46 Einige übliche Komplexitätsklassen (Entscheidungs-)Problem... ist eine Teilmenge P M man stelle sich eine Blackbox vor mit Eingabe m M Ausgabe ja, falls m P, nein sonst Polynomialzeit: Anzahl der Rechenschritte ist pol( m ), m : Länge der Eingabe; pol ist ein festes Polynom (Polynomielle) Reduktion von P M nach P M ist eine (in Polynomialzeit berechenbare) Funktion π mit π : M M m P gdw. π(m) P Skizze/Bsp.: siehe Tafel Wenn P zu P reduzierbar, dann ist P höchstens so schwer wie P. Thomas Schneider Automatentheorie 1: endliche Wörter 47 Name Bedeutung Beispiele L logarithm. Speicherplatz Grapherreichbarkeit NL nichtdetermin. log. Platz P Polynomialzeit Primzahlen NP nichtdeterminist. Polyzeit Erfüllbarkeit Auss.-logik PSPACE polynom. Speicherplatz Erfüllbarkeit QBF EXPTIME NEXPTIME EXPSPACE. Exponentialzeit nichtdet. Exponentialzeit exponentieller Platz. unentscheidbar Erfüllbarkeit Präd.-logik Thomas Schneider Automatentheorie 1: endliche Wörter 48
13 Bestimmung der Komplexität Entscheidungsprobleme für endliche Automaten Normalerweise zeigt man, dass ein Problem P M... in einer Komplexitätsklasse C liegt, indem man einen Algorithmus A findet, der P löst zeigt, dass A korrekt ist (ja/nein-antworten) und terminiert zeigt, dass A für jedes m M höchstens die C-Ressourcen braucht... A kann z. B. eine Reduktion zu einem Problem aus C sein schwer (hard) für C ist, indem man ein Problem P M findet, dass schwer für C ist und eine Reduktion von P nach P angibt vollständig für C ist, indem man zeigt, dass es in C liegt und schwer für C ist Thomas Schneider Automatentheorie 1: endliche Wörter 49 Das Leerheitsproblem Betrachten wesentliche Eigenschaften von Sprachen (Sprachen repräsentiert durch NEAs oder reguläre Ausdr.) Ist eine gegebene Sprache leer? Ist ein gegebenes Wort w in einer Sprache L? Beschreiben zwei Repräsentationen einer Sprache tatsächlich dieselbe Sprache? Wichtig für die bisher gesehenen Anwendungen (Ü: finde Gründe!) Art der Repräsentation spielt manchmal eine Rolle: Umwandlung DEA NEA: Umwandlung NEA DEA: Umwandlung reg. Ausdr. NEA: Umwandlung NEA reg. Ausdr.: konstante Zeit Exponentialzeit Wir beschränken uns im Folgenden auf NEAs. Polynomialzeit Exponentialzeit Thomas Schneider Automatentheorie 1: endliche Wörter 50 Das Wortproblem Ist definiert als {A L(A) = }. Satz 19 Das Leerheitsproblem ist entscheidbar. Ist definiert als {(A, w) w L(A)}. Satz 20 Das Wortproblem ist entscheidbar. Beweis: Siehe Tafel. Beweis: Reduktion zum Leerheitsproblem siehe Tafel. Komplexität: NL-vollständig (Wegsuche in gerichteten Graphen) Komplexität: NL-vollständig (modifizierte Wegsuche) (Reduktion liefert nur in EXPTIME ) Thomas Schneider Automatentheorie 1: endliche Wörter 51 Thomas Schneider Automatentheorie 1: endliche Wörter 52
14 Das Äquivalenzproblem Das Universalitätsproblem Ist definiert als {(A 1, A 2 ) L(A 1 ) = L(A 2 )}. Satz 21 Das Äquivalenzproblem ist entscheidbar. Ist definiert als {A L(A) = Σ }. Satz 22 Das Universalitätsproblem ist entscheidbar. Beweis: Siehe Tafel. Beweis: Übungsaufgabe. Komplexität: für DEAs in P, für NEAs PSPACE-vollständig (aus Beweis folgt nur in EXPTIME ) Komplexität: NL-vollständig (Wegsuche in gerichteten Graphen) Thomas Schneider Automatentheorie 1: endliche Wörter 53 Literatur für diesen Teil Thomas Schneider Automatentheorie 1: endliche Wörter 54 John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman. Introduction to Automata Theory, Languages and Computation. 2. Auflage, Addison-Wesley, Kapitel 1,2. Verfügbar in SUB: Zentrale a inf 420 e/028(2) dt. Versionen : 2 TB Technik n 438/101(3,2) dt. Version 2006: 2 Zentrale a inf 420 ef/238a,b Vorgängerversion von 1979: Zentrale a inf 420 e/806 oder BB Math.-MZH 19h kyb 315 e/996a oder auf dt., 1988: 2 Zentr. a kyb 308 f/352, (a) Vielen Dank. Meghyn Bienvenu. Automata on Infinite Words and Trees. Vorlesungsskript, Uni Bremen, WS 2009/10. automata/automata-notes.pdf Thomas Schneider Automatentheorie 1: endliche Wörter 55 Thomas Schneider Automatentheorie 1: endliche Wörter 56
Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern
 Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern Thomas Schneider 28. April 7. Mai 2014 Thomas Schneider Automatentheorie 1: endliche Wörter 1 Überblick 1 Grundbegriffe
Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern Thomas Schneider 28. April 7. Mai 2014 Thomas Schneider Automatentheorie 1: endliche Wörter 1 Überblick 1 Grundbegriffe
Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern
 Überblick Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern Thomas Schneider 28. April 7. Mai 2014 1 Grundbegriffe 2 Anwendung: Textsuche 3 Abschlusseigenschaften 4
Überblick Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern Thomas Schneider 28. April 7. Mai 2014 1 Grundbegriffe 2 Anwendung: Textsuche 3 Abschlusseigenschaften 4
Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern
 Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern Wintersemester 2017/18 Thomas Schneider AG Theorie der künstlichen Intelligenz (TdKI) http://tinyurl.com/ws1718-automaten
Automatentheorie und ihre Anwendungen Teil 1: endliche Automaten auf endlichen Wörtern Wintersemester 2017/18 Thomas Schneider AG Theorie der künstlichen Intelligenz (TdKI) http://tinyurl.com/ws1718-automaten
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
 Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
FORMALE SYSTEME. 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten. TU Dresden, 14. November 2016.
 FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (ii) ε ist ein regulärer Ausdruck über Σ.
 Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
2.2 Reguläre Sprachen Endliche Automaten
 2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
Homomorphismen. Defnition: Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen:
 Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Anwenundg regulärer Sprachen und endlicher Automaten
 Proseminar Theoretische Informatik Dozent: Prof. Helmut Alt Anwenundg regulärer Sprachen und endlicher Automaten Madlen Thaleiser 30. Oktober 2012 Reguläre Sprachen Regulärer Ausdruck definiert über einem
Proseminar Theoretische Informatik Dozent: Prof. Helmut Alt Anwenundg regulärer Sprachen und endlicher Automaten Madlen Thaleiser 30. Oktober 2012 Reguläre Sprachen Regulärer Ausdruck definiert über einem
Software Engineering Ergänzung zur Vorlesung
 Ergänzung zur Vorlesung Prof. Dr. Markus Müller-Olm WS 2008 2009 2.6.1 Endliche und reguläre Sprachen Endliche und reguläre Sprache: fundamental in vielen Bereichen der Informatik: theorie Formale Sprachen
Ergänzung zur Vorlesung Prof. Dr. Markus Müller-Olm WS 2008 2009 2.6.1 Endliche und reguläre Sprachen Endliche und reguläre Sprache: fundamental in vielen Bereichen der Informatik: theorie Formale Sprachen
Das Pumping-Lemma Formulierung
 Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
Theorie der Informatik
 Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Theoretische Informatik 2 bzw. Formale Sprachen und Berechenbarkeit. Sommersemester Herzlich willkommen!
 Theoretische Informatik 2 bzw. Formale Sprachen und Berechenbarkeit Sommersemester 2012 Prof. Dr. Nicole Schweikardt AG Theorie komplexer Systeme Goethe-Universität Frankfurt am Main Herzlich willkommen!
Theoretische Informatik 2 bzw. Formale Sprachen und Berechenbarkeit Sommersemester 2012 Prof. Dr. Nicole Schweikardt AG Theorie komplexer Systeme Goethe-Universität Frankfurt am Main Herzlich willkommen!
Formale Sprachen und Automaten
 Avant Propos Formale Sprachen und Automaten Sie [die Theorie der formalen Sprachen] ist ein Musterbeispiel einer informatischen Theorie, weil es ihr gelingt, einen großen Bestand an Einsichten und Zusammenhängen
Avant Propos Formale Sprachen und Automaten Sie [die Theorie der formalen Sprachen] ist ein Musterbeispiel einer informatischen Theorie, weil es ihr gelingt, einen großen Bestand an Einsichten und Zusammenhängen
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Algorithmen mit konstantem Platzbedarf: Die Klasse REG
 Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
2 2 Reguläre Sprachen. 2.2 Endliche Automaten. Übersicht
 Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Reguläre Sprachen und endliche Automaten
 Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken
 1 / 15 Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken Prof. Dr. Hans Kleine Büning FG Wissensbasierte Systeme WS 08/09 2 / 15 Deterministischer endlicher Automat (DEA) Definition 1:
1 / 15 Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken Prof. Dr. Hans Kleine Büning FG Wissensbasierte Systeme WS 08/09 2 / 15 Deterministischer endlicher Automat (DEA) Definition 1:
Musterlösung Informatik-III-Nachklausur
 Musterlösung Informatik-III-Nachklausur Aufgabe 1 (2+2+4+4 Punkte) (a) L = (0 1) 0(0 1) 11(0 1) 0(0 1) (b) Der Automat ist durch folgendes Übergangsdiagramm gegeben: 0, 1 0, 1 0, 1 0, 1 0 s q 1 1 0 0 q
Musterlösung Informatik-III-Nachklausur Aufgabe 1 (2+2+4+4 Punkte) (a) L = (0 1) 0(0 1) 11(0 1) 0(0 1) (b) Der Automat ist durch folgendes Übergangsdiagramm gegeben: 0, 1 0, 1 0, 1 0, 1 0 s q 1 1 0 0 q
DisMod-Repetitorium Tag 4
 DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
Berechenbarkeitstheorie 1. Vorlesung
 Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Zentrale Themen
Berechenbarkeitstheorie Dr. Institut für Mathematische Logik und Grundlagenforschung WWU Münster WS 15/16 Alle Folien unter Creative Commons Attribution-NonCommercial 3.0 Unported Lizenz. Zentrale Themen
Diskrete Mathematik. Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl
 OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
Herzlich willkommen!!!
 Theoretische Informatik 2 Sommersemester 2013 Prof. Dr. Georg Schnitger AG Theoretische Informatik Johann Wolfgang Goethe-Universität Frankfurt am Main Herzlich willkommen!!! 1 / 19 Kapitel 1: Einführung
Theoretische Informatik 2 Sommersemester 2013 Prof. Dr. Georg Schnitger AG Theoretische Informatik Johann Wolfgang Goethe-Universität Frankfurt am Main Herzlich willkommen!!! 1 / 19 Kapitel 1: Einführung
Die Nerode-Relation und der Index einer Sprache L
 Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Kontextfreie Sprachen
 Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Einschub: Kellerautomaten
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Einschub: Kellerautomaten
Kontextfreie Sprachen
 Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Theoretische Informatik für Medieninformatiker
 Theoretische Informatik für Medieninformatiker Jan Johannsen Lehrveranstaltung im Sommersemester 27 / 6 Organisatorisches: Jede Lehrveranstaltungsstunde gliedert sich in einen Vorlesungsteil, dessen Länge
Theoretische Informatik für Medieninformatiker Jan Johannsen Lehrveranstaltung im Sommersemester 27 / 6 Organisatorisches: Jede Lehrveranstaltungsstunde gliedert sich in einen Vorlesungsteil, dessen Länge
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
 Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Das Pumping Lemma: Ein Anwendungsbeispiel
 Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
Das Pumping Lemma: Ein Anwendungsbeispiel Beispiel: Die Palindromsprache ist nicht regulär. L = { } w {0, 1} w ist ein Palindrom Beweis: Angenommen, L ist doch regulär. Gemäß Pumping Lemma gibt es dann
Induktive Definition
 Rechenregeln A B = B A A (B C) = (A B) C A (B C) = (A B) C A (B C) = A B A C (B C) A = B A C A {ε} A = A A {ε} = A (A {ε}) = A (A ) = A A A = A + A A = A + A + {ε} = A Beispiel. Real-Zahlen = {0,..., 9}
Rechenregeln A B = B A A (B C) = (A B) C A (B C) = (A B) C A (B C) = A B A C (B C) A = B A C A {ε} A = A A {ε} = A (A {ε}) = A (A ) = A A A = A + A A = A + A + {ε} = A Beispiel. Real-Zahlen = {0,..., 9}
Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden kann.
 Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Abschlusseigenschaften
 Abschlusseigenschaften Die Klasse der regulären Sprachen hat eine große Zahl nützlicher Eigenschaften, insbesondere die folgenden Abschlusseigenschaften: Satz: Die Klasse der regulären Sprachen ist abgeschlossen
Abschlusseigenschaften Die Klasse der regulären Sprachen hat eine große Zahl nützlicher Eigenschaften, insbesondere die folgenden Abschlusseigenschaften: Satz: Die Klasse der regulären Sprachen ist abgeschlossen
Kapitel 1 Automaten: Die Grundlagen und Methoden... 23
 Vorwort...................................................... 17 Vorwort zur deutschen Auflage.............................. 21 Kapitel 1 Automaten: Die Grundlagen und Methoden..... 23 1.1 Wozu dient das
Vorwort...................................................... 17 Vorwort zur deutschen Auflage.............................. 21 Kapitel 1 Automaten: Die Grundlagen und Methoden..... 23 1.1 Wozu dient das
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2011
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2011 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Wir beschäftigen uns ab
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2011 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Wir beschäftigen uns ab
Algorithmen II Vorlesung am
 Algorithmen II Vorlesung am 17.01.013 Parametrisierte Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 17.01.013 Parametrisierte Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Satz (Abschluß unter der Stern-Operation)
 Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Die mathematische Seite
 Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
FORMALE SYSTEME. 8. Vorlesung: Minimale Automaten. TU Dresden, 6. November Markus Krötzsch Lehrstuhl Wissensbasierte Systeme
 FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
Ein deterministischer endlicher Automat (DFA) kann als 5-Touple dargestellt werden:
 Sprachen und Automaten 1 Deterministische endliche Automaten (DFA) Ein deterministischer endlicher Automat (DFA) kann als 5-Touple dargestellt werden: M = (Z,3,*,qo,E) Z = Die Menge der Zustände 3 = Eingabealphabet
Sprachen und Automaten 1 Deterministische endliche Automaten (DFA) Ein deterministischer endlicher Automat (DFA) kann als 5-Touple dargestellt werden: M = (Z,3,*,qo,E) Z = Die Menge der Zustände 3 = Eingabealphabet
Herzlich willkommen!!!
 Theoretische Informatik 2 Sommersemester 2015 Prof. Dr. Georg Schnitger AG Theoretische Informatik Goethe-Universität Frankfurt am Main Herzlich willkommen!!! 1 / 19 Kapitel 1: Einführung Einführung 2
Theoretische Informatik 2 Sommersemester 2015 Prof. Dr. Georg Schnitger AG Theoretische Informatik Goethe-Universität Frankfurt am Main Herzlich willkommen!!! 1 / 19 Kapitel 1: Einführung Einführung 2
Übungsblatt 1. Lorenz Leutgeb. 30. März 2015
 Übungsblatt Lorenz Leutgeb 30. März 205 Aufgabe. Annahmen ohne Einschränkungen: P Σ und P Γ. Per Definitionem der Reduktion: P P 2 f : Σ Γ wobei f total und berechenbar, genau so, dass: w Σ : w P f(w)
Übungsblatt Lorenz Leutgeb 30. März 205 Aufgabe. Annahmen ohne Einschränkungen: P Σ und P Γ. Per Definitionem der Reduktion: P P 2 f : Σ Γ wobei f total und berechenbar, genau so, dass: w Σ : w P f(w)
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2013
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2013 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Reguläre Ausdrücke Wozu
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2013 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Reguläre Ausdrücke Wozu
Minimalautomaten. Minimalautomaten. Frage: Ist der Äquivalenzautomat A der kleinste Automat ( Minimalautomat ) der die Sprache L(A) erkennt?
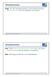 Minimalautomaten Frage: Ist der Äquivalenzautomat A der kleinste Automat ( Minimalautomat ) der die Sprache L(A) erkennt? 1 Minimalautomaten Satz: Falls A keine unerreichbaren Zustände hat, ist A der kleinste
Minimalautomaten Frage: Ist der Äquivalenzautomat A der kleinste Automat ( Minimalautomat ) der die Sprache L(A) erkennt? 1 Minimalautomaten Satz: Falls A keine unerreichbaren Zustände hat, ist A der kleinste
Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni Christian Franz
 Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni 2 Christian Franz Inhaltsverzeichnis Wiederholung: Vorlesung vom 9.6.2... Beispiele für Äquivalenzklassen... 4.5. Minimierung
Vorlesungsmitschrift zur Vorlesung Theoretische Informatik I vom 23. Juni 2 Christian Franz Inhaltsverzeichnis Wiederholung: Vorlesung vom 9.6.2... Beispiele für Äquivalenzklassen... 4.5. Minimierung
Theorie der Informatik. Theorie der Informatik P und NP Polynomielle Reduktionen NP-Härte und NP-Vollständigkeit
 Theorie der Informatik 13. Mai 2015 20. P, NP und polynomielle Reduktionen Theorie der Informatik 20. P, NP und polynomielle Reduktionen 20.1 P und NP Malte Helmert Gabriele Röger 20.2 Polynomielle Reduktionen
Theorie der Informatik 13. Mai 2015 20. P, NP und polynomielle Reduktionen Theorie der Informatik 20. P, NP und polynomielle Reduktionen 20.1 P und NP Malte Helmert Gabriele Röger 20.2 Polynomielle Reduktionen
Endliche Automaten Jörg Roth 101
 Endliche Automaten Jörg Roth 101 Wir wollen im Folgenden die Abschlusseigenschaften regulärer Sprachen betrachten. Fragestellung: Wenn wir reguläre Sprachen haben, welche binären und unären Operationen
Endliche Automaten Jörg Roth 101 Wir wollen im Folgenden die Abschlusseigenschaften regulärer Sprachen betrachten. Fragestellung: Wenn wir reguläre Sprachen haben, welche binären und unären Operationen
Operationen auf endlichen Akzeptoren und Transduktoren
 Operationen auf endlichen Akzeptoren und Transduktoren Kursfolien Karin Haenelt Karin Haenelt 2006, Operationen auf Akzeptoren und Transduktoren, 08.07.2006 ( 1 05.04.2004) 1 Notationskonventionen L reguläre
Operationen auf endlichen Akzeptoren und Transduktoren Kursfolien Karin Haenelt Karin Haenelt 2006, Operationen auf Akzeptoren und Transduktoren, 08.07.2006 ( 1 05.04.2004) 1 Notationskonventionen L reguläre
Operationen auf endlichen Automaten und Transduktoren
 Operationen auf endlichen Automaten und Transduktoren Kursfolien Karin Haenelt 1 Notationskonventionen L reguläre Sprache A endlicher Automat DEA deterministischer endlicher Automat NEA nichtdeterministischer
Operationen auf endlichen Automaten und Transduktoren Kursfolien Karin Haenelt 1 Notationskonventionen L reguläre Sprache A endlicher Automat DEA deterministischer endlicher Automat NEA nichtdeterministischer
Diskrete Mathematik. Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom
 Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Automaten und Formale Sprachen ε-automaten und Minimierung
 Automaten und Formale Sprachen ε-automaten und Minimierung Ralf Möller Hamburg Univ. of Technology Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik, Vieweg Verlag 2 Danksagung
Automaten und Formale Sprachen ε-automaten und Minimierung Ralf Möller Hamburg Univ. of Technology Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik, Vieweg Verlag 2 Danksagung
Aufgabe Mögliche Punkte Erreichte Punkte a b c d Σ a b c d Σ x1 13
 Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 2003/04 ILKD Prof. Dr. D. Wagner 14. April 2004 2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004 Hier Aufkleber
Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 2003/04 ILKD Prof. Dr. D. Wagner 14. April 2004 2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004 Hier Aufkleber
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
1.Klausur Diskrete Mathematik Seite 1 von 22
 1.Klausur Diskrete Mathematik Seite 1 von 22 1. Welche der folgenden Aussagen zum Halteproblem ist richtig? A. Jedes Problem ist auf das Halteproblem reduzierbar. B. HP ist die einzige Sprache, die rekursiv
1.Klausur Diskrete Mathematik Seite 1 von 22 1. Welche der folgenden Aussagen zum Halteproblem ist richtig? A. Jedes Problem ist auf das Halteproblem reduzierbar. B. HP ist die einzige Sprache, die rekursiv
Theoretische Informatik und Logik Übungsblatt 1 (2016S) Lösung
 Theoretische Informatik und Logik Übungsblatt (26S) en Aufgabe. Sei L = {w#w r w {, } }. Geben Sie eine deterministische Turingmaschine M an, welche die Sprache L akzeptiert. Wählen Sie mindestens einen
Theoretische Informatik und Logik Übungsblatt (26S) en Aufgabe. Sei L = {w#w r w {, } }. Geben Sie eine deterministische Turingmaschine M an, welche die Sprache L akzeptiert. Wählen Sie mindestens einen
Reguläre Ausdrücke. Karin Haenelt
 Reguläre Ausdrücke Karin Haenelt 25.04.2010 1 Inhalt Einführung Definitionen Kleene-Theorem Schreibweisen regulärer Ausdrücke Eigenschaften regulärer Sprachen 2 Was sind reguläre Ausdrücke? Reguläre Ausdrücke
Reguläre Ausdrücke Karin Haenelt 25.04.2010 1 Inhalt Einführung Definitionen Kleene-Theorem Schreibweisen regulärer Ausdrücke Eigenschaften regulärer Sprachen 2 Was sind reguläre Ausdrücke? Reguläre Ausdrücke
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten (III) 7.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch, 10.06.2015, D028,
Grundlagen der Theoretischen Informatik 3. Endliche Automaten (III) 7.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch, 10.06.2015, D028,
Automaten und Formale Sprachen
 Automaten und Formale Sprachen Einführung Ralf Möller Hamburg Univ. of Technology Übung Fr. 14:30-15:15 Max Berndt, D1025 Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik,
Automaten und Formale Sprachen Einführung Ralf Möller Hamburg Univ. of Technology Übung Fr. 14:30-15:15 Max Berndt, D1025 Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik,
Theoretische Informatik für Wirtschaftsinformatik und Lehramt
 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Eigenschaften regulärer Sprachen Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität
Theoretische Informatik für Wirtschaftsinformatik und Lehramt Eigenschaften regulärer Sprachen Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität
q 0 q gdw. nicht (q A) (q A) q i+1 q gdw. q i q oder ( a Σ) δ(q, a) i δ(q, a) L = {a n b n : n N} für a, b Σ, a b
 Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
Endliche Automaten. Grundlagen: Alphabet, Zeichenreihe, Sprache. Karin Haenelt
 Endliche Automaten Grundlagen: Alphabet, Zeichenreihe, Sprache Karin Haenelt 1 Alphabet, Zeichenreihe und Sprache Alphabet unzerlegbare Einzelzeichen Verwendung: als Eingabe- und Ausgabezeichen eines endlichen
Endliche Automaten Grundlagen: Alphabet, Zeichenreihe, Sprache Karin Haenelt 1 Alphabet, Zeichenreihe und Sprache Alphabet unzerlegbare Einzelzeichen Verwendung: als Eingabe- und Ausgabezeichen eines endlichen
TU Berlin Nachklausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2012)
 Berlin, 05. Oktober 2012 Name:... Matr.-Nr.:... TU Berlin Nachklausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2012) 1 2 3 4 5 6 7 Σ Bearbeitungszeit: 60 min.
Berlin, 05. Oktober 2012 Name:... Matr.-Nr.:... TU Berlin Nachklausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2012) 1 2 3 4 5 6 7 Σ Bearbeitungszeit: 60 min.
Theorie der Informatik
 Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Theoretische Informatik Mitschrift
 5 Eigenschaften regulärer Sprachen 51: Die Nerode-Relation Theoretische Informatik Mitschrift Definition 51: Sei L * L * * mit L :={u, v * * w *:uw L v w L }heißt Nerode-Relation von L Sei ={0,1}, L= *{00}
5 Eigenschaften regulärer Sprachen 51: Die Nerode-Relation Theoretische Informatik Mitschrift Definition 51: Sei L * L * * mit L :={u, v * * w *:uw L v w L }heißt Nerode-Relation von L Sei ={0,1}, L= *{00}
Automatentheorie und formale Sprachen
 Automatentheorie und formale Sprachen VL 4 Reguläre Ausdrücke und reguläre Sprachen Kathrin Hoffmann 10. April 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 10.4. 2012 114 Aufgabe 13:
Automatentheorie und formale Sprachen VL 4 Reguläre Ausdrücke und reguläre Sprachen Kathrin Hoffmann 10. April 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 10.4. 2012 114 Aufgabe 13:
Kapitel 2: Formale Sprachen Gliederung
 Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
11.1 Kontextsensitive und allgemeine Grammatiken
 Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
abgeschlossen unter,,,, R,
 Was bisher geschah Turing-Maschinen können Sprachen L X akzeptieren entscheiden Funktionen berechnen f : X X (partiell) Menge aller Turing-akzeptierbaren Sprachen genau die Menge aller Chomsky-Typ-0-Sprachen
Was bisher geschah Turing-Maschinen können Sprachen L X akzeptieren entscheiden Funktionen berechnen f : X X (partiell) Menge aller Turing-akzeptierbaren Sprachen genau die Menge aller Chomsky-Typ-0-Sprachen
Informatik IV. Pingo Sommersemester Dozent: Prof. Dr. J. Rothe. J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13
 Informatik IV Sommersemester 2019 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13 Website http://pingo.upb.de/ Code: 1869 J. Rothe (HHU Düsseldorf) Informatik IV 2 / 13 Frage
Informatik IV Sommersemester 2019 Dozent: Prof. Dr. J. Rothe J. Rothe (HHU Düsseldorf) Informatik IV 1 / 13 Website http://pingo.upb.de/ Code: 1869 J. Rothe (HHU Düsseldorf) Informatik IV 2 / 13 Frage
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Nico Döttling October 25, 22 Automatenminimierung Konstruktion des Äquivalenzklassenautomaten Aus der Vorlesung bekannt Überflüssige Zustände lassen sich effizient erkennen
Übung Theoretische Grundlagen Nico Döttling October 25, 22 Automatenminimierung Konstruktion des Äquivalenzklassenautomaten Aus der Vorlesung bekannt Überflüssige Zustände lassen sich effizient erkennen
Proseminar Automatentheorie. Thema: Berry Sethi Algorithmus. Von Christopher Haas
 Proseminar Automatentheorie Thema: Berry Sethi Algorithmus Von Christopher Haas Inhaltsangabe Allgemeines/Notation Ableitung regulärer Ausdruck Intuitiv Definition Beispiele Das Brzozowski-Verfahren Markierungsverfahren
Proseminar Automatentheorie Thema: Berry Sethi Algorithmus Von Christopher Haas Inhaltsangabe Allgemeines/Notation Ableitung regulärer Ausdruck Intuitiv Definition Beispiele Das Brzozowski-Verfahren Markierungsverfahren
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
1 Eliminieren von ɛ-übergängen
 1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
Ist eine algorithmische Problemstellung lösbar und wenn ja, mit welchen Mitteln? was ist eine algorithmische Problemstellung?
 Überblick 1. reguläre Sprachen endliche Automaten (deterministisch vs. nichtdeterministisch) Nichtregularität 2. Berechenbarkeit Registermaschinen/Turingmaschinen Churchsche These Unentscheidbarkeit 3.
Überblick 1. reguläre Sprachen endliche Automaten (deterministisch vs. nichtdeterministisch) Nichtregularität 2. Berechenbarkeit Registermaschinen/Turingmaschinen Churchsche These Unentscheidbarkeit 3.
Die Unentscheidbarkeit extensionaler Eigenschaften von Turingmaschinen: der Satz von Rice
 Die Unentscheidbarkeit extensionaler Eigenschaften von Turingmaschinen: der Satz von Rice Holger Arnold Dieser Text befasst sich mit der Frage, unter welchen Bedingungen das Problem, zu bestimmen, ob die
Die Unentscheidbarkeit extensionaler Eigenschaften von Turingmaschinen: der Satz von Rice Holger Arnold Dieser Text befasst sich mit der Frage, unter welchen Bedingungen das Problem, zu bestimmen, ob die
1. Welche der folgenden Aussagen zur Entscheidbarkeit beziehungsweise Unentscheidbarkeit
 1. Klausur Diskrete Mathematik Seite 1 von 22 1. Welche der folgenden Aussagen zur Entscheidbarkeit beziehungsweise Unentscheidbarkeit ist richtig? A. Keine der Aussagen. B. Eine Menge oder ihr Komplement
1. Klausur Diskrete Mathematik Seite 1 von 22 1. Welche der folgenden Aussagen zur Entscheidbarkeit beziehungsweise Unentscheidbarkeit ist richtig? A. Keine der Aussagen. B. Eine Menge oder ihr Komplement
Theoretische Informatik I
 Theoretische Informatik I Einheit 4.3 Eigenschaften von L 0 /L 1 -Sprachen 1. Abschlußeigenschaften 2. Prüfen von Eigenschaften 3. Grenzen der Sprachklassen Sprachklassen Semi-entscheidbare Sprache Sprache,
Theoretische Informatik I Einheit 4.3 Eigenschaften von L 0 /L 1 -Sprachen 1. Abschlußeigenschaften 2. Prüfen von Eigenschaften 3. Grenzen der Sprachklassen Sprachklassen Semi-entscheidbare Sprache Sprache,
4. Die lexikalische Analyse
 zerlegt Folge von Zeichen in Eingabedatei in Folge von Symbolen (Token) Scanner-Sieber-Modul Token: Typ und Inhalt übliche Token-Typen: reservierte Wörter (if, while, for, ) Bezeichner (x, dauer, name,..)
zerlegt Folge von Zeichen in Eingabedatei in Folge von Symbolen (Token) Scanner-Sieber-Modul Token: Typ und Inhalt übliche Token-Typen: reservierte Wörter (if, while, for, ) Bezeichner (x, dauer, name,..)
Formale Sprachen und endliche Automaten
 Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
4. Übung zur Vorlesung Informatik III am
 1 4. Übung zur Vorlesung Informatik III am 16.11.2007 Wiederholung Konkatenation 2 Definition Konkatenation Eine endliche Folge w von Symbolen aus Σ heißt Wort. Die Menge aller Wörter über Σ heißt Σ. Sei
1 4. Übung zur Vorlesung Informatik III am 16.11.2007 Wiederholung Konkatenation 2 Definition Konkatenation Eine endliche Folge w von Symbolen aus Σ heißt Wort. Die Menge aller Wörter über Σ heißt Σ. Sei
Formale Systeme. Büchi-Automaten. Prof. Dr. Bernhard Beckert WS 2009/2010 KIT INSTITUT FÜR THEORETISCHE INFORMATIK
 Formale Systeme Prof. Dr. Bernhard Beckert WS 2009/2010 KIT INSTITUT FÜR THEORETISCHE INFORMATIK KIT University of the State of Baden-Württemberg and National Large-scale Research Center of the Helmholtz
Formale Systeme Prof. Dr. Bernhard Beckert WS 2009/2010 KIT INSTITUT FÜR THEORETISCHE INFORMATIK KIT University of the State of Baden-Württemberg and National Large-scale Research Center of the Helmholtz
Theoretische Grundlagen des Software Engineering
 Theoretische Grundlagen des Software Engineering 1: Grundlagen, Sprachen, Automaten schulz@eprover.org Software Systems Engineering Definition Eine Definition ist eine genaue Beschreibung eines Objektes
Theoretische Grundlagen des Software Engineering 1: Grundlagen, Sprachen, Automaten schulz@eprover.org Software Systems Engineering Definition Eine Definition ist eine genaue Beschreibung eines Objektes
1.Klausur Diskrete Mathematik Seite 1 von 22
 1.Klausur Diskrete Mathematik Seite 1 von 22 1. Welche der folgenden Aussagen zum Halteproblem ist falsch? A. Für jeden nichtdeterministischen Automaten N kann entschieden werden, ob N die Eingabe akzeptiert,
1.Klausur Diskrete Mathematik Seite 1 von 22 1. Welche der folgenden Aussagen zum Halteproblem ist falsch? A. Für jeden nichtdeterministischen Automaten N kann entschieden werden, ob N die Eingabe akzeptiert,
Wie man eine Sprache versteht
 Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
Aufzählbarkeit Formale Grundlagen der Informatik 1 Kapitel 10 Aufzählbarkeit und (Un-)Entscheidbarkeit Frank Heitmann heitmann@informatik.uni-hamburg.de 11. Mai 2015 Definition 1 Eine Menge M Σ heißt (rekursiv)
Automaten und Coinduktion
 Philipps-Univestität Marburg Fachbereich Mathematik und Informatik Seminar: Konzepte von Programmiersprachen Abgabedatum 02.12.03 Betreuer: Prof. Dr. H. P. Gumm Referentin: Olga Andriyenko Automaten und
Philipps-Univestität Marburg Fachbereich Mathematik und Informatik Seminar: Konzepte von Programmiersprachen Abgabedatum 02.12.03 Betreuer: Prof. Dr. H. P. Gumm Referentin: Olga Andriyenko Automaten und
Einführung in Automatentheorie, Formale Sprachen und Berechenbarkeit
 John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman Einführung in Automatentheorie, Formale Sprachen und Berechenbarkeit 3., aktualisierte Auflage ein Imprint von Pearson Education München Boston San Francisco
John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman Einführung in Automatentheorie, Formale Sprachen und Berechenbarkeit 3., aktualisierte Auflage ein Imprint von Pearson Education München Boston San Francisco
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
 Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
1. Übungsblatt 6.0 VU Theoretische Informatik und Logik
 . Übungsblatt 6. VU Theoretische Informatik und Logik 25. September 23 Aufgabe Sind folgende Aussagen korrekt? Begründen Sie jeweils Ihre Antwort. a) Für jede Sprache L gilt: L < L (wobei A die Anzahl
. Übungsblatt 6. VU Theoretische Informatik und Logik 25. September 23 Aufgabe Sind folgende Aussagen korrekt? Begründen Sie jeweils Ihre Antwort. a) Für jede Sprache L gilt: L < L (wobei A die Anzahl
Übungsaufgaben zu Formalen Sprachen und Automaten
 Universität Freiburg PD Dr. A. Jakoby Sommer 27 Übungen zum Repetitorium Informatik III Übungsaufgaben zu Formalen Sprachen und Automaten. Untersuchen Sie das folgende Spiel: A B x x 2 x 3 C D Eine Murmel
Universität Freiburg PD Dr. A. Jakoby Sommer 27 Übungen zum Repetitorium Informatik III Übungsaufgaben zu Formalen Sprachen und Automaten. Untersuchen Sie das folgende Spiel: A B x x 2 x 3 C D Eine Murmel
Theoretische Informatik I
 Theoretische Informatik I Rückblick Theoretische Informatik I 1. Mathematische Methoden 2. Reguläre Sprachen 3. Kontextfreie Sprachen Themen der Theoretischen Informatik I & II Mathematische Methodik in
Theoretische Informatik I Rückblick Theoretische Informatik I 1. Mathematische Methoden 2. Reguläre Sprachen 3. Kontextfreie Sprachen Themen der Theoretischen Informatik I & II Mathematische Methodik in
Kontextfreie Sprachen werden von PDAs akzeptiert
 Kontextfreie Sprachen werden von PDAs akzeptiert Sei G = (Σ, V, S, P) eine kontextfreie Grammatik. Dann gibt es einen PDA A mit L(A) = L(G). Der PDA A arbeitet mit nur einem Zustand q 0, besitzt das Kelleralphabet
Kontextfreie Sprachen werden von PDAs akzeptiert Sei G = (Σ, V, S, P) eine kontextfreie Grammatik. Dann gibt es einen PDA A mit L(A) = L(G). Der PDA A arbeitet mit nur einem Zustand q 0, besitzt das Kelleralphabet
