Automaten und Formale Sprachen SoSe 2013 in Trier
|
|
|
- Gerhardt Schuster
- vor 5 Jahren
- Abrufe
Transkript
1 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier 2. Juni
2 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und reguläre Sprachen Kontextfreie Grammatiken und kontextfreie Sprachen Chomsky-Hierarchie 2
3 Endliche Automaten und reguläre Sprachen 1. Deterministische endliche Automaten 2. Nichtdeterministische endliche Automaten 3. Reguläre Ausdrücke 4. Nichtreguläre Sprachen 5. Algorithmen mit / für endliche Automaten 3
4 Eine algebraischere Betrachtungsweise von Sprachoperationen Erinnerung: Eine Sprache L Σ gehört zu REG gdw. es ein endliches Monoid (M,, e), einen Monoidmorphismus h : (Σ,, λ) (M,, e) sowie eine endliche Menge F M gibt mit L = {w Σ h(w) F}. Satz: REG ist gegen Komplementbildung abgeschlossen. Beweis: Sei L Σ durch ein endliches Monoid (M,, e), einen Monoidmorphismus h : (Σ,, λ) (M,, e) sowie eine endliche Menge F M spezifiziert. Dann spezifizieren (M,, e), h und M\F gemeinsam Σ \ L. (Beweiseinzelheiten zur Übung.) 4
5 Monoide aus Monoiden I Es seien (M,, e) und (N,, 1) Monoide. Dann kann man die Menge M N zu einem Monoid machen durch komponentenweises Anwenden der Operationen; definiere daher: (m, n) [, ](m, n ) := (m m, n n ). Satz: (M N, [, ], (e, 1)) ist ein Monoid, das Produktmonoid. Satz: Sind h M : (X,, I) (M,, e) und h N : (X,, I) (N,, 1) Monoidmorphismen, so auch der Produktmorphismus h M h N : X M N, x (h M (x), h N (x)). Beide Sätze lassen sich auf Produkte endlich vieler Monoide bzw. Morphismen verallgemeinern. In dieser Form werden wir sie im Folgenden benutzen. 5
6 Mengenoperationen als Sprachoperationen allgemein Satz: Ist f eine k-stellige Mengenoperation, so ist REG gegen f abgeschlossen. Beweis: Betrachte k reguläre Sprachen L i, spezifiziert durch endliche Monoide (M i, i, e i ), Morphismen h i und endliche Mengen F i M i. Dann spezifizieren das Produktmonoid M 1 M k, der Morphismus h 1 h k und die endliche Menge f(f 1,..., F k ) die Sprache f(l 1,..., L k ); hierbei sei F i = {(x 1,..., x k ) ( 1 j k : x j M j ) x i F i }. Mithin ist f(l 1,..., L k ) regulär. Ist speziell f der Durchschnitt, so gilt: F 1 F 2 = F 1 F 2. Schauen wir uns für diesen Fall beweistechnische Einzelheiten an: L i = {w Σ h i (w) F i } für i = 1, 2 laut Def. Für die konstruierte Sprache ist: L = {w Σ (h 1 h 2 )(w) (F 1 M 2 M 1 F 2 )}. Zu zeigen bleibt: L = L 1 L 2. w L 1 L 2 w L 1 w L 2 h 1 (w) F 1 h 2 (w) F 2 (h 1 (w), h 2 (w)) F 1 F 2 (h 1 h 2 )(w) (F 1 M 2 M 1 F 2 ). 6
7 Ein Beispiel Betrachte als endliche Monoide M 1 = (Z 2, +, 0) und M 2 = (Z 3, +, 0). Dann übersetzt der Morphismus φ aus M 1 M 2 in das Monoid M 3 = (Z 6, +, 0) gemäß: (0, 0) 0, (0, 1) 4, (0, 2) 2, (1, 0) 3, (1, 1) 1, (1, 2) 5. M 1, l 2 und {0} beschreiben die Wörter L 1 gerader Länge. M 2, l 3 und {1, 2} beschreiben die Wörter L 2, deren Länge beim Teilen durch drei nicht den Rest 0 lässt. M 1 M 2, l 2 l 3 und F = {(0, 0), (0, 1), (0, 2)} {(0, 1), (1, 1), (0, 2), (1, 2)} = {(0, 1), (0, 2)} = {0} {1, 2} beschreiben die Wörter, deren Länge gerade ist und beim Teilen durch drei den Rest 1 oder 2 lässt. Gleichwertig lässt sich L 1 L 2 durch das Monoid M 3, l 6 sowie φ(f) = {2, 4} darstellen. 7
8 Monoide aus Monoiden II Ist (M,, e) ein Monoid, so kann der Menge 2 M durch das Komplexprodukt zu einem Monoid gemacht werden. Dazu definieren wir: A B := {a b a A b B} Das zugehörige neutrale Element ist {e}. Beispiel: (Σ,, λ) ist ein Monoid, und so kann man auch als Sprachoperation auffassen. 8
9 Satz: REG ist gegen Konkatenation abgeschlossen. Beweis: Es seien L 1, L 2 REG. Wir können davon ausgehen, dass ein λ-nea A i = (Q i, Σ, δ i, Q 0,i, F i ) L i akzeptiert, der nur einen Anfangs- und einen Endzustand besitzt; der Anfangszustand hat nur ausgehende Kanten und der Endzustand nur eingehende. (Warum gibt es diese Normalform?) Wir gehen ferner davon aus, dass Q 1 Q 2 = F 1 = Q 0,2 gilt. Setze Q = Q 1 Q 2 und δ = δ 1 δ 2. Beh.: A = (Q, Σ, δ, Q 0,1, F 2 ) akzeptiert L 1 L 2. L 1 L 2 L(A) ist durch die Konstruktion einzusehen. L(A) L 1 L 2 ist die schwierigere Richtung. Wichtigen Eigenschaften von A: Jeder Pfad von Q 0,1 nach F 2 führt durch F 1 = Q 0,2. Es gibt keinen Pfad von Q 2 nach Q 1 \ F 1. (Einzelheiten zur Übung.) 9
10 REG ist gegen Konkatenation abgeschlossen: Skizze a A 1 A 2 10
11 Potenzen in Monoiden: Der Weg zum Kleene-Stern. Ist (M,, e) ein Monoid, so können wir rekursiv die n-te Potenz eines Elementes x M rekursiv festlegen durch: x 0 = e sowie x n+1 = x n x für n N. Wie wir gesehen haben, bildet auch (2 M,, {e}) ein Monoid. Somit ist auch A n für A M und n N definiert. (Leider kollidiert diese Schreibweise mit dem von dem kartesischen Mengenprodukt induzierten Potenz, aber nicht arg... ) Dann kann man A + = n 1 A n definieren und A = n 0 A n. Somit ist auch L + und L (Kleene-Stern) für L Σ festgelegt. Satz: L + (L ) ist die (das) durch L bezüglich der Konkatenation erzeugte Halbgruppe (Monoid). 11
12 Satz: REG ist gegen Kleene-Stern abgeschlossen. Beweis: Sei L REG akzeptiert durch einen λ-nea A, der nur einen Anfangs- und einen Endzustand q 0 und q f besitzt; der Anfangszustand habe nur ausgehende Kanten und der Endzustand nur eingehende. Durch Verschmelzen von q 0 und q f als neuer Anfangs- und Endzustand q 0f erhalten wir einen NEA A mit L(A ) = L. Betrachte w L(A ). Es gibt eine Folge von Zuständen p 1,..., p n (n l(w) und p 1 = p n = q 0f ), sodass für geeignete Suffixe w 1 = w,..., w n = λ von w gilt: (p i, w i ) A (p i+1, w i+1 ) sowie w i = w i+1 oder w i = aw i+1 für ein Zeichen a, für i = 1,..., n 1. Definiere J(w) = {j p j = q 0f }. Wir zeigen die Beh. durch Induktion über J(w) 1. Für J(w) = 1 haben wir w = λ vorzuliegen, also gilt sowieso w L. Ist j > 1 der erste Index mit p j = q 0f, so gilt für w = u j w j : u j L(A) = L. Ferner gibt es für w j L(A ) einen durch p j,..., p n beschriebenen Akzeptierungsweg mit J(w j ) < J(w), sodass wir hier die IV anwenden können. Also folgt w L L L. Die Inklusion L L(A ) sieht man leichter anhand der Konstruktion ein. 12
13 Reguläre Ausdrücke (ähnlich grep) Definition durch strukturelle Induktion: und a sind RA für jedes a Σ. Ist R ein RA, so auch (R). Sind R 1 und R 2 RAs, so auch R 1 R 2 und (R 1 R 2 ). Beispiel: ((b a)) aaa(bb) ist ein RA. Klammern können weggelassen werden: bindet stärker als Konkatenation, und jenes wieder stärker als Vereinigung. 13
14 Die durch einen RA beschriebene Sprache ist ebenfalls induktiv gegeben: L( ) = ; L(a) = {a}. Ist R ein RA, setze L((R) ) = (L(R)). Sind R 1 und R 2 RA, setze L(R 1 R 2 ) = L(R 1 ) L(R 2 ) und L((R 1 R 2 )) = L(R 1 ) L(R 2 ). Beispiel: L((b a) ) = {a, b} 14
15 Beispiele (1) Beschreibe die Sprache zum Ausdruck (ab )a in Mengennotation. L((ab )a) = L((ab )) L(a) = L(a) L(b ) {a} = {a} (L(b)) {a} = {a} {b} {a} = {ab n a n N} (2) Beschreibe die Sprache zum Ausdruck (a b) in Worten. Die Menge aller Wörter über {a, b}, die nicht mit a enden. 15
16 Satz: Jede RA-Sprache ist regulär. Beweis: (durch strukturelle Induktion) Endliche Sprachen sind regulär. (Dies liefert den Induktionsanfang.) Reguläre Sprachen sind gegen Kleene-Stern abgeschlossen. Reguläre Sprachen sind gegen Vereinigung und Konkatenation abgeschlossen. Beispiel: (a ab) (siehe Tafel) 16
17 Zusammenhang zwischen struktureller und vollständiger Induktion ergeben sich zumeist durch Einführung geeigneter Zählvariablen. In unserem Fall sei zu RA R die Anzahl der Operationssymbole in R notiert als: # op (R). Dies lässt sich auch wiederum strukturell induktiv definieren: # op ( ) = 0 und # op (a) = 0 für jedes a Σ. Ist R ein RA, so gilt: # op ((R) ) = # op (R) + 1. Sind R 1 und R 2 RAs, so gilt: # op (R 1 R 2 ) = # op ((R 1 R 2 )) = # op (R 1 ) + # op (R 2 )
18 Zusammenhang zwischen struktureller und vollständiger Induktion Die Beweisskizze lässt sich als Beweis durch vollständige Induktion nach # op (R) begreifen. IA: Für # op (R) = 0 gilt: R = oder R = a für ein a Σ. Die entsprechenden Sprachen bzw. {a} sind regulär. IV: Jeder RA mit höchstens n Operationssymbolen beschreibt eine reguläre Sprache. Betrachte einen RA R mit n + 1 Operationssymbolen. Hierfür sind drei Fälle möglich: (a) R = (R 1 ) ; (b) R = R 1 R 2 ; (c) R = (R 1 R 2 ). In jedem Fall gilt: # op (R 1 ) n sowie # op (R 2 ) n (falls sinnvoll). Also sind nach IV L(R 1 ) und L(R 2 ) regulär. Da die regulären Sprachen gegen Kleene Stern, Konkatenation und Vereinigung abgeschlossen sind, ist (in jedem Fall) auch L(R) regulär. 18
19 Satz: Jede reguläre Sprache ist durch einen RA beschreibbar. Beweis: Betrachte DEA A = (Q, Σ, δ, q 0, F) mit Q = {1,..., n} und q 0 = 1. R[i, j, k] RA für die Sprache, die von A akzeptiert wird, indem (1) A in Zustand i anfängt, (2) in Zustand j aufhört, und (3) zwischendurch nur Zustände aus {1,..., k} erreicht. Hinweis: Warshall/Floyd Offenbar gilt: L(A) = j F L(R[1, j, n]) = L( j FR[1, j, n]). R[i, j, 0] = x 1 x l, wobei die x l alle Beschriftungen von Kanten zwischen i und j auflisten (zusätzlich falls i = j) Für k > 0 setze rekursiv R[i, j, k] = R[i, j, k 1] R[i, k, k 1]R[k, k, k 1] R[k, j, k 1]. 19
20 Daraus ergibt sich ein Algorithmus durch dynamisches Programmieren. R[1..n, 1..n, 0..n] ist 3-dim. Array mit regulären Ausdrücken als Einträgen. Für i := 1 bis n tue: Für j := 1 bis n tue: R[i, j, 0] := a Σa Falls i = j, so setze R[i, j, 0] := R[i, j, 0]. Für k := 1 bis n tue: Für i := 1 bis n tue: Für j := 1 bis n tue: R[i, j, k] := R[i, j, k 1] R[i, k, k 1]R[k, k, k 1] R[k, j, k 1]. Damit klar: kubische Komplexität, i.z.: O(n 3 ). 20
21 Ein Beispiel (roter Zustand kann weggelassen werden, da er nicht zur Sprache beiträgt) 0 q 1 0 r 0,1 s 1 R[i, j, 0] q r s q 0 1 r 0 1 s
22 Ein Beispiel (Forts.) R[i, j, 0] q r s q 0 1 r 0 1 s 0 1 R[i, j, {q}] q r q 0 ((0 )(0 ) (0 )) = 0 1 ((0 )(0 ) 1) = 0 1 r 0 (0(0 ) (0 )) = 00 (0(0 ) 1) = 00 1 R[i, j, {q, r}] q r q 0 (0 1(00 1) 00 ) 0 1 (0 1(00 1) 00 1) = 0 1(00 1) r L(A) = L(0 (0 1(00 1) 0 )). Hinweis: Explosion EA / RA in beiden Richtungen! 22
23 Ein alternatives Verfahren (siehe Kinber/Smith) arbeitet direkt auf dem evtl. nichtdeterministischen Automatengraphen. Wichtige Konventionen: Zustandsmenge Q = {1,..., n} mit 1: Anfangszustand und n (einziger) Endzustand. Kantenbeschriftungen dürfen hierbei reguläre Ausdrücke sein. (Tatsächlich kann man auch derartige Automaten betrachten.) 23
24 Hilfsroutinen: mergearcs(i, j): Sind l 1 i,j,... lm i,j die Beschriftungen sämtlicher Kanten von i nach j im Automatengraphen, so ersetze diese m Kanten durch eine mit (l 1 i,j... lm i,j ) beschriftete. shortcut(i, j; k): Falls es nur genau eine Kante von i nach k und genau eine Kante von k nach j gibt, tue: 1. Gibt es genau eine Kante von k nach k mit Beschriftung l k,k, so tue: Ersetze einzige Kante von i nach k mit Beschriftung l i,k und einzige Kante von k nach j mit Beschriftung l k,j durch neue Kante von i nach j mit Beschriftung l i,k (l k,k ) l k,j. 2. Andernfalls: Ersetze einzige Kante von i nach k mit Beschriftung l i,k und einzige Kante von k nach j mit Beschriftung l k,j durch neue Kante von i nach j mit Beschriftung l i,k l k,j. remove(k): Lösche Knoten k und alle mit k inzidenten Kanten. 24
25 Der zweite Algorithmus zur Erzeugung äquivalenter RAs Für i := 1 bis n tue: Für j := 1 bis n tue: mergearcs(i, j) Für k := 2 bis n 1 tue: Für i := 1 bis n tue: Für j := 1 bis n tue: shortcut(i, j; k); mergearcs(i, j); remove(k). Der gewünschte reguläre Ausdruck findet sich am Schluss als Kantenbeschriftung von der (einzigen) Kante von Knoten 1 nach Knoten n. Sollte keine solche Kante existieren, so ist die Sprache leer und kann durch beschrieben werden. Vorheriges Beispiel an der Tafel! 25
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
 Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
 Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@informatik.uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@informatik.uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
 Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Organisatorisches Vorlesungen FR 10.10-11.50 im HS 13 Übungsbetrieb ab dem nächsten Mal wieder
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Organisatorisches Vorlesungen FR 10.10-11.50 im HS 13 Übungsbetrieb ab dem nächsten Mal wieder
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 7. Mai 2013 1 Organisatorisches Vorlesung FR 10.15-11.45 im F 59 Verschiebungsangebot: FR 10.10-11.40
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 7. Mai 2013 1 Organisatorisches Vorlesung FR 10.15-11.45 im F 59 Verschiebungsangebot: FR 10.10-11.40
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Homomorphismen. Defnition: Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen:
 Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Homomorphismen Σ und Γ seien zwei endliche Alphabete, und h sei eine Abbildung h : Σ Γ. Wir definieren die folgenden Sprachen: h(l) := {h(u) : u L} Γ, für jede Sprache L Σ, h 1 (M) := {u Σ : h(u) M} Σ,
Diskrete Mathematik. Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl
 OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
Formale Sprachen. Reguläre Sprachen. Rudolf FREUND, Marian KOGLER
 Formale Sprachen Reguläre Sprachen Rudolf FREUND, Marian KOGLER Endliche Automaten - Kleene STEPHEN KLEENE (99-994) 956: Representation of events in nerve nets and finite automata. In: C.E. Shannon und
Formale Sprachen Reguläre Sprachen Rudolf FREUND, Marian KOGLER Endliche Automaten - Kleene STEPHEN KLEENE (99-994) 956: Representation of events in nerve nets and finite automata. In: C.E. Shannon und
Formale Grundlagen der Informatik 1 Kapitel 5 Abschlusseigenschaften
 Formale Grundlagen der Informatik 1 Kapitel 5 Frank Heitmann heitmann@informatik.uni-hamburg.de 18. April 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/64 NFAs - Grundlagen DFAs vs. NFAs Der
Formale Grundlagen der Informatik 1 Kapitel 5 Frank Heitmann heitmann@informatik.uni-hamburg.de 18. April 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/64 NFAs - Grundlagen DFAs vs. NFAs Der
Induktive Definition
 Rechenregeln A B = B A A (B C) = (A B) C A (B C) = (A B) C A (B C) = A B A C (B C) A = B A C A {ε} A = A A {ε} = A (A {ε}) = A (A ) = A A A = A + A A = A + A + {ε} = A Beispiel. Real-Zahlen = {0,..., 9}
Rechenregeln A B = B A A (B C) = (A B) C A (B C) = (A B) C A (B C) = A B A C (B C) A = B A C A {ε} A = A A {ε} = A (A {ε}) = A (A ) = A A A = A + A A = A + A + {ε} = A Beispiel. Real-Zahlen = {0,..., 9}
Informatik III. Christian Schindelhauer Wintersemester 2006/07 3. Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 3. Vorlesung 02.11.2006 schindel@informatik.uni-freiburg.de 1 Kapitel III Reguläre Sprachen Reguläre Sprachen und Ausdrücke Informatik III
Informatik III Christian Schindelhauer Wintersemester 2006/07 3. Vorlesung 02.11.2006 schindel@informatik.uni-freiburg.de 1 Kapitel III Reguläre Sprachen Reguläre Sprachen und Ausdrücke Informatik III
Satz (Abschluß unter der Stern-Operation)
 Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken
 1 / 15 Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken Prof. Dr. Hans Kleine Büning FG Wissensbasierte Systeme WS 08/09 2 / 15 Deterministischer endlicher Automat (DEA) Definition 1:
1 / 15 Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken Prof. Dr. Hans Kleine Büning FG Wissensbasierte Systeme WS 08/09 2 / 15 Deterministischer endlicher Automat (DEA) Definition 1:
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier fernau@uni-trier.de
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M 2. p 1
 Beispiel Produktautomat p Vereinfachte Konstruktion f. NFAs Seien M,M 2 NFAs f. die Sprachen L und L 2. Konstruktion eines NFAs für L L 2 : Erzeuge Kopien von M und M 2. p q q p 2 Erzeuge neuen Startzustand
Beispiel Produktautomat p Vereinfachte Konstruktion f. NFAs Seien M,M 2 NFAs f. die Sprachen L und L 2. Konstruktion eines NFAs für L L 2 : Erzeuge Kopien von M und M 2. p q q p 2 Erzeuge neuen Startzustand
Software Engineering Ergänzung zur Vorlesung
 Ergänzung zur Vorlesung Prof. Dr. Markus Müller-Olm WS 2008 2009 2.6.1 Endliche und reguläre Sprachen Endliche und reguläre Sprache: fundamental in vielen Bereichen der Informatik: theorie Formale Sprachen
Ergänzung zur Vorlesung Prof. Dr. Markus Müller-Olm WS 2008 2009 2.6.1 Endliche und reguläre Sprachen Endliche und reguläre Sprache: fundamental in vielen Bereichen der Informatik: theorie Formale Sprachen
Beispiel Produktautomat
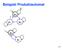 Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
Beispiel Produktautomat 0 1 p 0 p 1 p 2 q 0 q 1 445 Vereinfachte Konstruktion f. NFAs Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M
Zwei Bemerkungen zum Schluss
 Man könnte sich fragen, ob eine Typ-3 Sprache inhärent mehrdeutig sein kann (im Sinn von Einheit 8). Die Antwort lautet: NEIN. Zwei Bemerkungen zum Schluss Denn für jede Typ-3 Sprache gibt es einen DEA,
Man könnte sich fragen, ob eine Typ-3 Sprache inhärent mehrdeutig sein kann (im Sinn von Einheit 8). Die Antwort lautet: NEIN. Zwei Bemerkungen zum Schluss Denn für jede Typ-3 Sprache gibt es einen DEA,
Automaten und formale Sprachen Klausurvorbereitung
 Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Suche nach einem solchen Kreis. Endlichkeitstest. Vereinigung und Durchschnitt. Abschlusseigenschaften
 Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Endliche Automaten Jörg Roth 101
 Endliche Automaten Jörg Roth 101 Wir wollen im Folgenden die Abschlusseigenschaften regulärer Sprachen betrachten. Fragestellung: Wenn wir reguläre Sprachen haben, welche binären und unären Operationen
Endliche Automaten Jörg Roth 101 Wir wollen im Folgenden die Abschlusseigenschaften regulärer Sprachen betrachten. Fragestellung: Wenn wir reguläre Sprachen haben, welche binären und unären Operationen
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
1 Eliminieren von ɛ-übergängen
 1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
1 Eliminieren von ɛ-übergängen 1.1 Beispiel 1 (a) Ausgangspunkt: Zwei ɛ-übergänge (b) Entfernung eines ɛ-übergangs, Reduktion (c) Entfernen eines ɛ-übergangs, Reduktion Abbildung 1: Elimination von ɛ-übergängen,
2 2 Reguläre Sprachen. 2.2 Endliche Automaten. Übersicht
 Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Ogden s Lemma: Der Beweis (1/5)
 Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Reguläre Sprachen und endliche Automaten
 Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
2.2 Reguläre Sprachen Endliche Automaten
 2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
Diskrete Strukturen und Logik WiSe 2007/08 in Trier. Henning Fernau Universität Trier
 Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Für jede Sprache L X sind die folgenden Aussagen äquivalent:
 Was bisher geschah Für jede Sprache L X sind die folgenden Aussagen äquivalent: Es existiert ein NFA A mit L = L(A) (L REC(NFA)). Es existiert ein vollständiger NFA B mit L = L(B). Es existiert ein ε-nfa
Was bisher geschah Für jede Sprache L X sind die folgenden Aussagen äquivalent: Es existiert ein NFA A mit L = L(A) (L REC(NFA)). Es existiert ein vollständiger NFA B mit L = L(B). Es existiert ein ε-nfa
liefern eine nicht maschinenbasierte Charakterisierung der regulären
 Reguläre Ausdrücke 1 Ziel: L=L M für NFA M L=L(r) für einen regulären Ausdruck r Reguläre Ausdrücke über einem Alphabet Σ Slide 1 liefern eine nicht maschinenbasierte Charakterisierung der regulären Sprachen
Reguläre Ausdrücke 1 Ziel: L=L M für NFA M L=L(r) für einen regulären Ausdruck r Reguläre Ausdrücke über einem Alphabet Σ Slide 1 liefern eine nicht maschinenbasierte Charakterisierung der regulären Sprachen
Informatik III - WS07/08
 Informatik III - WS07/08 Kapitel 5 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 5 : Grammatiken und die Chomsky-Hierarchie Informatik III - WS07/08 Kapitel 5 2 Definition
Informatik III - WS07/08 Kapitel 5 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 5 : Grammatiken und die Chomsky-Hierarchie Informatik III - WS07/08 Kapitel 5 2 Definition
Grundlagen der Theoretischen Informatik, SoSe 2008
 2. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 1 Einelementiges Alphabet (4 Punkte) (a) Geben
2. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 1 Einelementiges Alphabet (4 Punkte) (a) Geben
Zusammenfassung. Beispiel. 1 Wir betrachten die folgende Signatur F = {,, +, 0, 1} sodass. 3 Wir betrachten die Identitäten E. 4 Dann gilt E 1 + x = 1
 Zusammenfassung Zusammenfassung der letzten LVA Einführung in die Theoretische Informatik Christina Kohl Alexander Maringele eorg Moser Michael Schaper Institut für Informatik @ UIBK Wintersemester 2016
Zusammenfassung Zusammenfassung der letzten LVA Einführung in die Theoretische Informatik Christina Kohl Alexander Maringele eorg Moser Michael Schaper Institut für Informatik @ UIBK Wintersemester 2016
Satz von Kleene. (Stephen C. Kleene, ) Wiebke Petersen Einführung CL 2
 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen endlichen Automaten akzeptiert wird ist regulär und jede reguläre Sprache wird von einem deterministischen endlichen
Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen endlichen Automaten akzeptiert wird ist regulär und jede reguläre Sprache wird von einem deterministischen endlichen
Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden kann.
 Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Kapitel 2: Formale Sprachen Gliederung
 Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
Grundlagen der Informatik. Prof. Dr. Stefan Enderle NTA Isny
 Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
Komplexitätstheorie WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Komplexitätstheorie WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Komplexitätstheorie Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen
Komplexitätstheorie WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Komplexitätstheorie Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Einführung in die Computerlinguistik Satz von Kleene
 Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 5. Foliensatz Wiebke Petersen Einführung CL 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen
Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 5. Foliensatz Wiebke Petersen Einführung CL 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Zusammenfassung der letzten LVA. Endliche Automaten mit Epsilon-Übergängen. Inhalte der Lehrveranstaltung (cont d)
 Zusammenfassung der letzten LVA Ein nichtdeterministischer endlicher Automat (NEA) ist ein 5-Tupel (Q, Σ, δ, S, F), sodass Q eine endliche Menge von Zustände Σ eine endliche Menge, das Eingabealphabet;
Zusammenfassung der letzten LVA Ein nichtdeterministischer endlicher Automat (NEA) ist ein 5-Tupel (Q, Σ, δ, S, F), sodass Q eine endliche Menge von Zustände Σ eine endliche Menge, das Eingabealphabet;
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie prachen (VI) 25.06.2015 Viorica ofronie-tokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie prachen (VI) 25.06.2015 Viorica ofronie-tokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen der Informatik II
 Grundlagen der Informatik II Tutorium 2 Professor Dr. Hartmut Schmeck Miniaufgabe * bevor es losgeht * Finden Sie die drei Fehler in der Automaten- Definition. δ: A = E, S, δ, γ, s 0, F, E = 0,1, S = s
Grundlagen der Informatik II Tutorium 2 Professor Dr. Hartmut Schmeck Miniaufgabe * bevor es losgeht * Finden Sie die drei Fehler in der Automaten- Definition. δ: A = E, S, δ, γ, s 0, F, E = 0,1, S = s
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Nico Döttling October 25, 22 Automatenminimierung Konstruktion des Äquivalenzklassenautomaten Aus der Vorlesung bekannt Überflüssige Zustände lassen sich effizient erkennen
Übung Theoretische Grundlagen Nico Döttling October 25, 22 Automatenminimierung Konstruktion des Äquivalenzklassenautomaten Aus der Vorlesung bekannt Überflüssige Zustände lassen sich effizient erkennen
Theoretische Grundlagen des Software Engineering
 Theoretische Grundlagen des Software Engineering 5: Reguläre Ausdrücke und Grammatiken schulz@eprover.org Software Systems Engineering Reguläre Sprachen Bisher: Charakterisierung von Sprachen über Automaten
Theoretische Grundlagen des Software Engineering 5: Reguläre Ausdrücke und Grammatiken schulz@eprover.org Software Systems Engineering Reguläre Sprachen Bisher: Charakterisierung von Sprachen über Automaten
Berechenbarkeitstheorie 4. Vorlesung
 1 Berechenbrkeitstheorie Dr. Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attribution-NonCommercil 3.0 Unported Lizenz. Reguläre Ausdrücke
1 Berechenbrkeitstheorie Dr. Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attribution-NonCommercil 3.0 Unported Lizenz. Reguläre Ausdrücke
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Einführung in die Computerlinguistik Satz von Kleene
 Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 5. Foliensatz Wiebke Petersen Einführung CL 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen
Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 5. Foliensatz Wiebke Petersen Einführung CL 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen
Automatentheorie und formale Sprachen
 Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Sommersemester 2015 16.04.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Organizatorisches Literatur Motivation und Inhalt Kurzer
Grundlagen der Theoretischen Informatik Sommersemester 2015 16.04.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Organizatorisches Literatur Motivation und Inhalt Kurzer
Formale Systeme. Endliche Automaten. Prof. Dr. Bernhard Beckert WS 2009/2010 KIT INSTITUT FÜR THEORETISCHE INFORMATIK
 Formale Systeme Prof. Dr. Bernhard Beckert WS 2009/2010 KIT INSTITUT FÜR THEORETISCHE INFORMATIK KIT University of the State of Baden-Württemberg and National Large-scale Research Center of the Helmholtz
Formale Systeme Prof. Dr. Bernhard Beckert WS 2009/2010 KIT INSTITUT FÜR THEORETISCHE INFORMATIK KIT University of the State of Baden-Württemberg and National Large-scale Research Center of the Helmholtz
F2 Zusammenfassung Letzte Tips zur Klausur
 F2 Zusammenfassung Letzte Tips zur Klausur Berndt Farwer FB Informatik, Uni HH F2-ommersemester 2001-(10.6.) p.1/15 Funktionen vs. Relationen Funktionen sind eindeutig, Relationen brauchen nicht eindeutig
F2 Zusammenfassung Letzte Tips zur Klausur Berndt Farwer FB Informatik, Uni HH F2-ommersemester 2001-(10.6.) p.1/15 Funktionen vs. Relationen Funktionen sind eindeutig, Relationen brauchen nicht eindeutig
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Sommersemester 2016 20.04.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Grundlagen der Theoretischen Informatik Sommersemester 2016 20.04.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Formale Systeme Prof. Dr. Bernhard Beckert, WS 2016/2017
 Formale Systeme Prof. Dr. Bernhard Beckert, WS 2016/2017 Endliche Automaten KIT I NSTITUT F U R T HEORETISCHE I NFORMATIK www.kit.edu KIT Die Forschungsuniversita t in der Helmholtz-Gemeinschaft Endliche
Formale Systeme Prof. Dr. Bernhard Beckert, WS 2016/2017 Endliche Automaten KIT I NSTITUT F U R T HEORETISCHE I NFORMATIK www.kit.edu KIT Die Forschungsuniversita t in der Helmholtz-Gemeinschaft Endliche
Ist eine algorithmische Problemstellung lösbar und wenn ja, mit welchen Mitteln? was ist eine algorithmische Problemstellung?
 Überblick 1. reguläre Sprachen endliche Automaten (deterministisch vs. nichtdeterministisch) Nichtregularität 2. Berechenbarkeit Registermaschinen/Turingmaschinen Churchsche These Unentscheidbarkeit 3.
Überblick 1. reguläre Sprachen endliche Automaten (deterministisch vs. nichtdeterministisch) Nichtregularität 2. Berechenbarkeit Registermaschinen/Turingmaschinen Churchsche These Unentscheidbarkeit 3.
Automaten und Coinduktion
 Philipps-Univestität Marburg Fachbereich Mathematik und Informatik Seminar: Konzepte von Programmiersprachen Abgabedatum 02.12.03 Betreuer: Prof. Dr. H. P. Gumm Referentin: Olga Andriyenko Automaten und
Philipps-Univestität Marburg Fachbereich Mathematik und Informatik Seminar: Konzepte von Programmiersprachen Abgabedatum 02.12.03 Betreuer: Prof. Dr. H. P. Gumm Referentin: Olga Andriyenko Automaten und
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
 Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Formale Systeme. Endliche Automaten. Prof. Dr. Bernhard Beckert, WS 2015/ KIT I NSTITUT F U R T HEORETISCHE I NFORMATIK
 Formale Systeme Prof. Dr. Bernhard Beckert, WS 2015/2016 Endliche Automaten KIT I NSTITUT F U R T HEORETISCHE I NFORMATIK KIT Universita t des Landes Baden-Wu rttemberg und nationales Forschungszentrum
Formale Systeme Prof. Dr. Bernhard Beckert, WS 2015/2016 Endliche Automaten KIT I NSTITUT F U R T HEORETISCHE I NFORMATIK KIT Universita t des Landes Baden-Wu rttemberg und nationales Forschungszentrum
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Sommersemester 2017 20.04.2017 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Organisatorisches Literatur Motivation und Inhalt Kurzer
Grundlagen der Theoretischen Informatik Sommersemester 2017 20.04.2017 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Organisatorisches Literatur Motivation und Inhalt Kurzer
Automatentheorie und formale Sprachen
 Automatentheorie und formale Sprachen VL 4 Reguläre Ausdrücke und reguläre Sprachen Kathrin Hoffmann 10. April 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 10.4. 2012 114 Aufgabe 13:
Automatentheorie und formale Sprachen VL 4 Reguläre Ausdrücke und reguläre Sprachen Kathrin Hoffmann 10. April 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 10.4. 2012 114 Aufgabe 13:
Formale Sprachen und endliche Automaten
 Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
A : z z A : z z : ( z, x, z ) δ
 Informatik IV, SoS2003 1 Definition 1.1 Ein Quintupel A =(X,Z,z 0,δ,Z f )heißt nichtdeterministischer endlicher Automat (NEA): 1. X, Z sind endliche nichtleere Mengen. 2. z 0 Z 4. δ Z X Z Informatik IV,
Informatik IV, SoS2003 1 Definition 1.1 Ein Quintupel A =(X,Z,z 0,δ,Z f )heißt nichtdeterministischer endlicher Automat (NEA): 1. X, Z sind endliche nichtleere Mengen. 2. z 0 Z 4. δ Z X Z Informatik IV,
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Release 1.0 Daniel Schmidt 13. 11. 2013 Inhaltsverzeichnis 1 Vorlesungsverzeichnis: 1 1.1 Vorlesungen............................................... 1 2 Definitionsverzeichnis:
Theoretische Grundlagen der Informatik Release 1.0 Daniel Schmidt 13. 11. 2013 Inhaltsverzeichnis 1 Vorlesungsverzeichnis: 1 1.1 Vorlesungen............................................... 1 2 Definitionsverzeichnis:
Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt:
 5.2 Linear beschränkte Automaten Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt: (q, c, d) δ(q, ) = c =. Ein Leerzeichen wird also nie durch ein anderes
5.2 Linear beschränkte Automaten Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt: (q, c, d) δ(q, ) = c =. Ein Leerzeichen wird also nie durch ein anderes
2.3 Abschlusseigenschaften
 2.3 Abschlusseigenschaften 2.3 Abschlusseigenschaften In diesem Abschnitt wollen wir uns mit Abschlusseigenschaften der regulären Sprachen, d.h. mit der Frage, ob, gegeben eine Operation und zwei reguläre
2.3 Abschlusseigenschaften 2.3 Abschlusseigenschaften In diesem Abschnitt wollen wir uns mit Abschlusseigenschaften der regulären Sprachen, d.h. mit der Frage, ob, gegeben eine Operation und zwei reguläre
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
 Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@informatik.uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@informatik.uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten (III) 7.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch, 10.06.2015, D028,
Grundlagen der Theoretischen Informatik 3. Endliche Automaten (III) 7.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch, 10.06.2015, D028,
c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} c) {abcabc} d) {abcbc, abc, a} c) {aa, ab, ba, bb} d) {{aa}, {ab}, {ba}, {bb}}
 2 Endliche Automaten Fragen 1. Was ergibt sich bei {a, bc} {de, fg}? a) {abc, defg} b) {abcde, abcfg} c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} 2. Was ergibt sich bei {abc, a} {bc, λ}?
2 Endliche Automaten Fragen 1. Was ergibt sich bei {a, bc} {de, fg}? a) {abc, defg} b) {abcde, abcfg} c) {abcde, abcfg, bcade, bcafg} d) {ade, afg, bcde, bcfg} 2. Was ergibt sich bei {abc, a} {bc, λ}?
Algorithmen II Vorlesung am
 Algorithmen II Vorlesung am 17.01.013 Parametrisierte Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 17.01.013 Parametrisierte Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
FORMALE SYSTEME. 8. Vorlesung: Minimale Automaten. TU Dresden, 6. November Markus Krötzsch Lehrstuhl Wissensbasierte Systeme
 FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
FORMALE SYSTEME. Wiederholung. Beispiel: NFA. Wiederholung: NFA. 4. Vorlesung: Nichtdeterministische Endliche Automaten. TU Dresden, 20.
 Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
Wiederholung FORMALE SYSTEME 4. Vorlesung: Nichtdeterministische Endliche Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme Grammatiken können Sprachen beschreiben und sie grob in Typen unterteilen
kontextfreie Grammatiken Theoretische Informatik kontextfreie Grammatiken kontextfreie Grammatiken Rainer Schrader 14. Juli 2009 Gliederung
 Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Theoretische Informatik Mitschrift
 4. Reguläre Ausdrüce Theoretische Informati Mitschrift indutive Beschreibung von Sprachen, die durch endliche Automaten erennbar sind Definition 4.1: Sei Σ ein Alphabet. (a) Die Menge RA(Σ) der regulären
4. Reguläre Ausdrüce Theoretische Informati Mitschrift indutive Beschreibung von Sprachen, die durch endliche Automaten erennbar sind Definition 4.1: Sei Σ ein Alphabet. (a) Die Menge RA(Σ) der regulären
äußere Klammern können entfallen, ebenso solche, die wegen Assoziativität von + und Konkatenation nicht notwendig sind:
 3. Reguläre Sprachen Bisher wurden Automaten behandelt und Äquivalenzen zwischen den verschiedenen Automaten gezeigt. DEAs erkennen formale Sprachen. Gibt es formale Sprachen, die nicht erkannt werden?
3. Reguläre Sprachen Bisher wurden Automaten behandelt und Äquivalenzen zwischen den verschiedenen Automaten gezeigt. DEAs erkennen formale Sprachen. Gibt es formale Sprachen, die nicht erkannt werden?
Diskrete Strukturen und Logik WiSe 2007/08 in Trier. Henning Fernau Universität Trier
 Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Diskrete Mathematik. Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom
 Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
Diskrete Mathematik Anna-Lena Rädler Christina Kohl Georg Moser Christian Sternagel Vincent van Oostrom Zusammenfassung der letzten LVA Definition Ein ɛ-nea N = (Q, Σ, δ, S, F) ist gegeben durch eine endliche
Definition 78 Ein NPDA = PDA (= Nichtdeterministischer Pushdown-Automat) besteht aus:
 4.7 Kellerautomaten In der Literatur findet man häufig auch die Bezeichnungen Stack-Automat oder Pushdown-Automat. Kellerautomaten sind, wenn nichts anderes gesagt wird, nichtdeterministisch. Definition
4.7 Kellerautomaten In der Literatur findet man häufig auch die Bezeichnungen Stack-Automat oder Pushdown-Automat. Kellerautomaten sind, wenn nichts anderes gesagt wird, nichtdeterministisch. Definition
Kontextfreie Sprachen
 Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Operationen auf endlichen Automaten und Transduktoren
 Operationen auf endlichen Automaten und Transduktoren Kursfolien Karin Haenelt 1 Notationskonventionen L reguläre Sprache A endlicher Automat DEA deterministischer endlicher Automat NEA nichtdeterministischer
Operationen auf endlichen Automaten und Transduktoren Kursfolien Karin Haenelt 1 Notationskonventionen L reguläre Sprache A endlicher Automat DEA deterministischer endlicher Automat NEA nichtdeterministischer
Diskrete Strukturen und Logik WiSe 2007/08 in Trier. Henning Fernau Universität Trier
 Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Diskrete Strukturen und Logik WiSe 2007/08 in Trier. Henning Fernau Universität Trier
 Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Grammatiken. Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V. Startsymbol S V. Kurzschreibweise G = (V, Σ, P, S)
 Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Theoretische Informatik
 Theoretische Informatik Prof. Meer, Dr. Gengler Aufgabenblatt 7 Besprechung in KW 48 / Abgabe in KW 49 Heften Sie unbedingt alle Blätter Ihrer Lösung zusammen und geben Sie oben auf dem ersten Blatt Ihren
Theoretische Informatik Prof. Meer, Dr. Gengler Aufgabenblatt 7 Besprechung in KW 48 / Abgabe in KW 49 Heften Sie unbedingt alle Blätter Ihrer Lösung zusammen und geben Sie oben auf dem ersten Blatt Ihren
10 Kellerautomaten. Kellerautomaten
 10 Kellerautomaten Bisher hatten wir kontextfreie Sprachen nur mit Hilfe von Grammatiken charakterisiert. Wir haben gesehen, dass endliche Automaten nicht in der Lage sind, alle kontextfreien Sprachen
10 Kellerautomaten Bisher hatten wir kontextfreie Sprachen nur mit Hilfe von Grammatiken charakterisiert. Wir haben gesehen, dass endliche Automaten nicht in der Lage sind, alle kontextfreien Sprachen
Endliche Automaten. Endliche Automaten 1 / 102
 Endliche Automaten Endliche Automaten 1 / 102 Endliche Automaten Endliche Automaten erlauben eine Beschreibung von Handlungsabläufen: Wie ändert sich ein Systemzustand in Abhängigkeit von veränderten Umgebungsbedingungen?
Endliche Automaten Endliche Automaten 1 / 102 Endliche Automaten Endliche Automaten erlauben eine Beschreibung von Handlungsabläufen: Wie ändert sich ein Systemzustand in Abhängigkeit von veränderten Umgebungsbedingungen?
AUTOMATENBASIERTE ALGORITHMEN UND EXAKTES 2D-PATTERN-MATCHING. Vincent Holluba
 AUTOMATENBASIERTE ALGORITHMEN UND EXAKTES 2D-PATTERN-MATCHING Vincent Holluba Gliederung 1. Einleitung und Wiederholung 2. Suchwortbaum (Trie) 3. Aho-Corasick Automat i. Matching mit Wildcards ii. 2D-Pattern
AUTOMATENBASIERTE ALGORITHMEN UND EXAKTES 2D-PATTERN-MATCHING Vincent Holluba Gliederung 1. Einleitung und Wiederholung 2. Suchwortbaum (Trie) 3. Aho-Corasick Automat i. Matching mit Wildcards ii. 2D-Pattern
Formale Sprachen (parallele und regulierte Ersetzung) SoSe 2008 in Trier. Henning Fernau Universität Trier
 Formale Sprachen (parallele und regulierte Ersetzung) SoSe 2008 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Formale Sprachen Gesamtübersicht Organisatorisches / Einführung Motivation
Formale Sprachen (parallele und regulierte Ersetzung) SoSe 2008 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Formale Sprachen Gesamtübersicht Organisatorisches / Einführung Motivation
Automaten und Formale Sprachen ε-automaten und Minimierung
 Automaten und Formale Sprachen ε-automaten und Minimierung Ralf Möller Hamburg Univ. of Technology Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik, Vieweg Verlag 2 Danksagung
Automaten und Formale Sprachen ε-automaten und Minimierung Ralf Möller Hamburg Univ. of Technology Literatur Gottfried Vossen, Kurt-Ulrich Witt: Grundkurs Theoretische Informatik, Vieweg Verlag 2 Danksagung
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
