Formale Sprachen (parallele und regulierte Ersetzung) SoSe 2008 in Trier. Henning Fernau Universität Trier
|
|
|
- Dörte Armbruster
- vor 6 Jahren
- Abrufe
Transkript
1 Formale Sprachen (parallele und regulierte Ersetzung) SoSe 2008 in Trier Henning Fernau Universität Trier 1
2 Formale Sprachen Gesamtübersicht Organisatorisches / Einführung Motivation / Erinnerung / Fragestellungen Diskussion verschiedener Sprachklassen: gesteuerte Ersetzungsverfahren parallele Ersetzungsverfahren Algebraische Ansätze: abstrakte Sprachfamilien formale Potenzreihen 2
3 Parallele Grammatiken Lindenmayer-Systeme eingeschränkter Parallelismus 3
4 Erinnerung: D0L Systeme Einfachster Typus von Lindenmayer-Systemen. Spezifiziert durch G = (Σ, h, ω), wobei: Σ Alphabet, ω Σ Axiom (Startwort), h Morphismus auf Σ, angegeben als h : Σ Σ, oder als Regelmenge P = {a w a Σ, w Σ }, die vollständig (zu jedem a Σ gibt es mindestens eine Regel mit solcher linken Seite) sein soll und auch deterministisch (zu jedem a Σ gibt es höchstens eine Regel mit solcher linken Seite) Ableitungsbegriff: x y gdw. y = h(x) (uneingeschränkt parallele Ableitung) Wie üblich: L(G) = {w Σ ω w}. 4
5 Natürliche Verallgemeinerung: 0L-Systeme Fortlassen der Determinismus-Bedingung. Formal bedeutet dies, dass wir zu jeder linken Seite a eine nicht-leere, endliche Teilmenge h(a) assoziieren. h : Σ 2 Σ lässt sich wieder als Morphismus h : Σ 2 Σ begreifen (Komplexprodukt). Mit G = (Σ, h, ω) gilt dann: Ableitungsbegriff: x y gdw. y h(x) (uneingeschränkt parallele Ableitung) Wie üblich: L(G) = {w Σ ω w}. Beispiel: Regelmenge a a, a aa, ω = a, L = {a?... } Gibt es äquivalentes D0L-System? 5
6 Weitere 0L-Sprachen Beispiel: Ist L = {w}, so sind L und L {λ} D0L-Sprachen. Tatsächlich benötigt man dafür nur entweder Regeln a a oder a λ. Beispiel: L k = {a i i N, i k} sind 0L-Sprachen, aber nur dann auch D0L- Sprachen, wenn k 1. Beweis: Hier brauchen wir beide Arten von Regeln. Wäre L 2 = {λ, a, a 2 } D0L-Sprache, so müsste a λ die Regel sein. Gleich welches Axiom gewählt würde, gilt: Läge a in der Sprache, so a 2 nicht, und läge a 2 in der Sprache, so a nicht. 6
7 Nicht-0L-Sprachen Beispiel: L = {a, a 3 } ist keine 0L-Sprache. Beweis: Angenommen, es gäbe ein 0L-System G = (Σ, h, ω) für L. Wir unterscheiden zwei Fälle: ω = a. Dann gilt: a aaa, also a 3 a 9 ω = a 3. Dann gilt: aaa a, also a λ und a a. Also ist auch a 3 a 2. Ähnlich sieht man: Beispiel: L = {a, a 4 } ist keine 0L-Sprache. Komplizierter ist schon: Beispiel: {λ, a 5, a 10 } ist keine 0L-Sprache. Beispiel: Betrachte G = ({a}, {a a 3, a a 4 }, a) und φ : a a 5, aufgefasst als Morphi. L = φ 1 (L(G)) ist keine 0L-Sprache. 7
8 Ein komplizierteres Argument Lemma: Für L = L(G) mit G = ({a, b}, {a a 2, b b 3 }, ab) gilt: L = {a 2n b 3n n N}. Dann ist L + keine 0L-Sprache. Beweis: Angenommen, G + = ({a, b}, h, ω) ist 0L-System für L +. Diskutiere ω = a r 1 bs 1... ar t bs t. Enthielte jedes nicht-leere α h(a) sowohl a als auch b s, so wäre max {max{r i 1 i t}, 2 max{ α α h({a, b})}} zur Struktur von L +. Da kein Wort in L + mit b beginnt, gilt: h(a) {b} + =. Also gibt es ein α h(a) mit α {a}. Entsprechend gilt für β h(b): β {b}. (A) λ / h(a) h(b). Gölte o.e. λ h(a), so nicht λ h(b), da λ / L +, d.h., es gäbe ein β h(b) mit β {b} + ; zusammen mit a λ ließe sich so ein Wort aus ω ableiten, das nicht zu L + gehört. (B) Wegen α h(a) für ein α {a} + gilt h(b) {b} +, denn α 2n β 3n L(G + ) für alle n N. Entsprechend folgt: h(a) {a} +. (C) Wegen (B) können aus ω nur Wörter abgeleitet werden mit t (abwechselnden) a- und b- Blöcken, zur Struktur von L +. 8
9 Satz: Die Familie der 0L-Sprachen ist nicht abgeschlossen gegen (1) Vereinigung, (2) Konkatenation, (3) Kleene-Plus, (4) Durchschnitt mit regulären Sprachen, (5) nicht-löschende Morphismen und auch nicht gegen (6) inverse Morphismen. Anti-AFL Beweis: (1) {a} und {a 3 } sind D0L-Sprachen, ihre Vereinigung ist keine 0L-Sprache. (2) {a} und {λ, a 2 } sind 0L-Sprachen, ihre Konkatenation ist keine 0L-Sprache. (3) siehe Lemma (4) {a 2n n N} ist D0L-Sprache und L = {a, a 4 } ist regulär, ihr Schnitt ist gleich L und daher nicht 0L-Sprache. (5) Betrachte φ : a a 5, aufgefasst als Morphi. Beispiel oben: L = {λ, a, aa} ist 0L-Sprache, aber φ(l) = {λ, a 5, a 10 } ist es nicht. (6) siehe obiges Beispiel 9
10 Weitere Sprachen aus 0L-Systemen: E0L-Systeme Ein E0L-System (E: extension, Erweiterung) ist ein Quadrupel G = (Σ, h, ω, ); hierbei ist U(G) = (Σ, h, ω) das unterliegende 0L-System, und Σ ist das Terminal- oder Zielalphabet. Die von G beschriebene Sprache ist L(G) = L(U(G)). Mathematische Motivation: Zwischen kontextfreien Grammatiken und 0L-Systemen gibt es zwei wesentliche Unterschiede: (1) Parallele Ableitung und (2) (Nicht-)Unterscheidung von Terminal- und Nichtterminalzeichen. E0L-Systeme isolieren den ersteren Unterschied. 10
11 Beispiele für E0L-Systeme Beispiel: G = ({S, a, b}, {S a, S b, a a 2, b b 2 }, S, {a, b}) beschreibt L(G) = {a 2n, b 2n n N}. Gibt es hierfür ein 0L-System? Beispiel: G = ({A, a, b}, {A A, A a, a a 2, b b}, AbA, {a, b}), L(G) = {a 2n ba 2m n, m N}. Lemma: Jede endliche Sprache ist E0L-Sprache. 11
12 Synchronisierte E0L-Systeme Ein E0L-System G = (Σ, h, ω, ) heißt synchronisiert gdw. a β Σ : (a β β / ). Satz: Es gibt einen Algorithmus, der ein vorgelegtes E0L-System G in ein äquivalentes synchronisiertes System Ḡ umformt. Genauer hat dieses System Ḡ = (Σ, h, ω, ) folgende Eigenschaften: (1) ω Σ \ (Startsymbol) (2) Es gibt ein Fehlersymbol F Σ \, sodass für jedes a {F} a Fdie einzige Produktion für a ist. (3) Rechte Regelseiten sind entweder Terminalwörter oder das Fehlersymbol, oder sie enthalten weder Terminalzeichen, noch das Fehler- oder Startsymbol. (4) Aus jedem Nichtterminalzeichen außer dem Fehlersymbol und möglicherweise dem Startsymbol lässt sich ein Terminalwort ableiten. Mit G ist auch Ḡ propagierend. 12
13 Synchronisierte E0L-Systeme: Anwendung Satz: Sind L 1 und L 2 E0L-Sprachen, so auch: L 1 L 2, L 1 L 2, L + 1 und L 1 R für eine beliebige reguläre Sprache R. Beweise an der Tafel. Hinweis: Normalformen sind wichtig! 13
14 EP0L versus E0L Satz: Zu jedem E0L-System H = (Σ, h, S, ) kann ein EP0L-System G = (V, g, [S, ], ) konstruiert werden mit L(H) \ {λ} = L(G). α(x): Menge der Zeichen, die in x vorkommen. Beweis: O.E.: H in Normalform, d.h., S Σ \, und L(H) ist unendlich. V = Σ 2 Σ {F}, die zweite Komponente enthält Symbole, die verschwinden sollen während der Ableitung in H. Diese Zeichenmenge rät und überprüft G. g enthält die folgenden Regeln (und nur diese): (1) Gilt b h(a) mit b Σ, so sei [b, Z ] g([a, Z]), falls Z σ(z), d.h.: x, x Σ : α(x) = Z α(x ) = Z x H x. (2) Gilt b 1... b k h(a), b i Σ, k 2, so sei [b i1, Z i1 ][b i2, Z i2 ]... [b ip, Z ip ] g([a, Z]), falls i 0 = 1 i 1 < i 2 < < i p i p+1 = k, Z σ(z), sowie Z ij = α(b ij b ij 1b ij b ij+1 1) Z für 1 j p. (3) a g([a, ]) für a. (4) g(x) = {F} für X {F}. 14
15 Weitere Sprachen aus 0L-Systemen: C0L-Systeme Es seien Σ und Σ Alphabete. Eine Abbildung g : Σ Σ heißt auch Kodierung. Kodierungen kann man auch als Morphismen zwischen frei erzeugten Monoiden auffassen. Ein C0L-System ist ein Quadrupel G = (Σ, h, ω, φ); hierbei ist U(G) = (Σ, h, ω) das unterliegende 0L-System, und φ : Σ ist eine Kodierung. Die von G beschriebene Sprache ist L(G) = φ(l(u(g))). Biologische Motivation: Ermöglicht (insbesondere, wenn < Σ ) einem beobachteten Zustand mehrere wirkliche Zustände zuzuordnen. 15
16 Ein Beispiel für ein C0L-System für L = {a n b n c n n 1}: A AA, A A B BB, B B C CC, C C seien die Regeln eines 0L-Systems mit Axiom ABC welches, zusammen mit der Kodierung A, A a, B, B b, and C, C c die Sprache L beschreibt. Genauer gilt für die n-schritt Ableitung: ABC n A(A ) n B(B ) n C(C ) n 16
17 Kodierungen und Erweiterungen Lemma: Jede C0L-Sprache ist eine E0L-Sprache. Dies gilt auch für propagierende Systeme. Beweis: Es sei G = (Σ, h, ω, φ) mit φ : Σ ein C0L-System. O.E. sei Σ =. Es gibt ein EP0L-System Ḡ = (Θ, ḡ, S, Σ) mit L(Ḡ) = L(U(G)) \ {λ}. O.E. sei Ḡ synchronisiert und Θ =. Betrachte H = (Θ, g, ), wobei g aus folgenden Regeln besteht (und nur diesen): {X φ(x) x Σ, X x ḡ} {X F X } {X x X x ḡ, x / Σ }. Es gilt: L(H) = φ(l(ḡ)) = φ(l(u(g)) \ {λ}) = φ(l(u(g))) \ {λ}. Falls λ L(G), muss H noch leicht modifiziert werden. Beobachte: Welche früheren Aussagen wurden verwendet? Aufgabe: Einfaches E0L-System für L = {a n b n c n n 1}. 17
18 Kodierungen und Erweiterungen Ohne Beweise teilen wir noch folgende Ergebnisse mit: Satz: Eine Sprache ist C0L-Sprache genau dann, wenn sie E0L-Sprache ist. Das bedeutet: Ein mathematisch/linguistisch gut motivierter Begriff stimmt im Wesentlichen mit einem biologisch gut motivierten überein. Satz: Die Familie der CP0L-Sprachen ist eine echte Teilfamilie der EP0L-Sprachen. Trennsprache: L = {a 3n, b n c n d n n 1}. Intuition? 18
19 Wachstumsmuster und Interaktion Bei sog. (i, j)l Systemen (oder kurz IL Systemen, falls die Zahlen i und j bel.), werden i Zeichen links und j Zeichen rechts von der Ersetzungsstelle mit in Betracht gezogen, was die Anwendbarkeit von Regeln angeht. Gibt es links von der Ersetzungsstelle weniger als i > 0 Zeichen in der augenblicklichen Satzform, so nimmt man an, das Sonderzeichen # werde gesehen. Genauso verfährt man am rechten Rand. 19
20 Ein Beispiel für DIL Systeme: Gabors Faultier Axiom ad, Regeln: Die Ableitung geht wie folgt: a b c d # c b a d a a b a d b a b a d c b c a ad d a b a d ad cd aad cad abd cbd acd caad abaad Gabor s sloth zeigt logarithmisches Wachstum (warum?). 20
21 Wachstumsfunktionen Zu einem vorgelegten DIL System G = (Σ, h, ω) gibt seine DIL Wachstumsfunktion g G : n w n for ω n w n die Länge des nach n Schritten abgeleiteten Wortes an. Lemma: Kein DIL System wächst schneller als exponentiell. Welche Arten von Funktionen können aber durch DIL Systeme beschrieben werden? 1. exponentielles Wachstum: Betrachte D0L System mit Regel a a 2 ; 2. polynomielles Wachstum: a ab, b b erzeugen, beginnend mit a, ab n ; 3. logarithmisches Wachstum: siehe Gabors Faultier. 21
22 Wachtumsmuster ohne Interaktion g G hängt nicht von der Abfolge der Zeichen im Axiom bzw. in rechten Regelseiten ab. Wichtig hingegen: Wie viele Zeichen welcher Art kommen vor? Diese Information kann man im sog. Parikh (Zeilen) Vektor des Axioms und in der Wachstumsmatrix der Regeln ablegen. Quadratisches Wachstum beobachten wir für ein D0L System auf den folgenden Folien: 22
23 Wachstumsfunktionen am Beispiel D0L System G = ({a, b, c}, {a abc 2, b bc 2, c c}, a). Wachstumsmatrix: M G := Die erste Zeile von M G ist der Parikh-Vektor von abc 2, die zweite der von bc 2, due dritte gehört zur Regel c c. 23
24 Wie sieht die Matrix der Parikhvektoren aus von den Wörtern, die von a, b bzw. c aus in zwei Ableitungsschritten erzeugt werden können? Diese Information erhält man einfach durch Quadrieren von M G : Beispielableitung hierzu: M 2 G = a abcc abccbcccc und (1 0 0) M 2 G = (1 2 6)
25 Algebra und Wachstumsfunktionen gehören zusammen: Ein klassisches Ergebnis aus der Matrizentheorie ist der Satz von Cayley-Hamilton: Jede Matrix befriedigt ihre eigene charakteristische Gleichung (Polynom). Daraus folgt: M n G = c 1M n 1 G + c 2M n 2 G + + c nm 0 G, was die folgende Rekursion für die Wachstumsfunktion g G liefert: g G (i + n) = c 1 g G (i + n 1) + c 2 g G (i + n 2) + + c n g G (i) (i 0 bel.). Das gestattet oft eine explizite Bestimmung von g G. 24
26 Algebra und Wachstumsfunktionen: Nochmal unser Beispiel M 3 G = = c I: Einheitsmatrix. Mit etwas Rechnen folgt: mit Anfangswerten + c 2 c 1 = 3, c 2 = 3 und c 3 = g G (i + 3) = 3g G (i + 2) 3g G (i + 1) + g G (i) g G (i) = i 2 durch Überprüfen von g G (0) = 1, g G (1) = 4 und g G (2) = 9. (i + 3) 2 = i 2 + 6i + 9 = 3(i + 2) 2 3(i + 1) 2 + i 2. + c 3 I, 25
27 Algebra und Wachstumsfunktionen: Weitere Folgerungen Lemma: Ist g eine D0L Wachstumsfunktion mit beliebig langen konstanten Intervallen, d.h. formaler: so ist g is schließlich konstant. k i : g(i) = g(i + 1) = = g(i + k), Gabors Faultier besitzt jedoch beliebig lange konstante Intervalle, d.h.: Satz: Es gibt DIL Wachstumsfunktionen, die keine D0L Wachstumsfunktionen sind. Man kann jetzt auch ganz eigentümliche Entscheidbarkeitsfragen stellen wie: Ist die Wachstumsfunktion eines vorgelegten D0L Systems polynomiell? 26
Zusammenfassung. 1 Wir betrachten die folgende Signatur F = {+,,, 0, 1} sodass. 3 Wir betrachten die Gleichungen E. 4 Dann gilt E 1 + x 1
 Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Theorie der Informatik
 Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier fernau@uni-trier.de
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
2.11 Kontextfreie Grammatiken und Parsebäume
 2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Grundlagen der Informatik II. Teil I: Formale Modelle der Informatik
 Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Diskrete Strukturen und Logik WiSe 2007/08 in Trier. Henning Fernau Universität Trier fernau@uni-trier.de
 Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit
 Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Wortproblem für kontextfreie Grammatiken
 Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
TEIL III: FORMALE SPRACHEN
 EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 TEIL III: FORMALE SPRACHEN 16. TERMERSETZUNGSSYSTEME UND CHOMSKY-GRAMMATIKEN Theoretische Informatik (SoSe 2011)
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 TEIL III: FORMALE SPRACHEN 16. TERMERSETZUNGSSYSTEME UND CHOMSKY-GRAMMATIKEN Theoretische Informatik (SoSe 2011)
Theoretische Informatik I
 Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Informatik I WS 07/08 Tutorium 24
 Info I Tutorium 24 Informatik I WS 07/08 Tutorium 24 20.12.07 Bastian Molkenthin E-Mail: infotut@sunshine2k.de Web: http://infotut.sunshine2k.de Rückblick Semi-Thue-Systeme Ein Semi-Thue-System besteht
Info I Tutorium 24 Informatik I WS 07/08 Tutorium 24 20.12.07 Bastian Molkenthin E-Mail: infotut@sunshine2k.de Web: http://infotut.sunshine2k.de Rückblick Semi-Thue-Systeme Ein Semi-Thue-System besteht
Sprachen/Grammatiken eine Wiederholung
 Sprachen/Grammatiken eine Wiederholung Was sind reguläre Sprachen? Eigenschaften regulärer Sprachen Sprachen Begriffe Symbol: unzerlegbare Grundzeichen Alphabet: endliche Menge von Symbolen Zeichenreihe:
Sprachen/Grammatiken eine Wiederholung Was sind reguläre Sprachen? Eigenschaften regulärer Sprachen Sprachen Begriffe Symbol: unzerlegbare Grundzeichen Alphabet: endliche Menge von Symbolen Zeichenreihe:
Grundlagen der Künstlichen Intelligenz
 Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Zusammenfassung. Satz. 1 Seien F, G Boolesche Ausdrücke (in den Variablen x 1,..., x n ) 2 Seien f : B n B, g : B n B ihre Booleschen Funktionen
 Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 6 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Satz 1 Seien F, G Boolesche Ausdrücke
Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 6 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Satz 1 Seien F, G Boolesche Ausdrücke
Formale Sprachen und Grammatiken
 Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Formale Sprachen und deren Grammatiken. Zusammenhang mit der Automatentheorie.
 Formale Sprachen Formale Sprachen und deren Grammatiken. Zusammenhang mit der Automatentheorie. Inhaltsübersicht und Literatur Formale Sprachen: Definition und Darstellungen Grammatiken für formale Sprachen
Formale Sprachen Formale Sprachen und deren Grammatiken. Zusammenhang mit der Automatentheorie. Inhaltsübersicht und Literatur Formale Sprachen: Definition und Darstellungen Grammatiken für formale Sprachen
Mathematische Grundlagen der Informatik 2
 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss emanuel.duss@gmail.com 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss emanuel.duss@gmail.com 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Prof. Dr. Hans J. Schneider Lehrstuhl für Programmiersprachen und Programmiermethodik Friedrich-Alexander-Universität Erlangen-Nürnberg Sommersemester 2011 I. Die
Funktionale Programmierung mit Haskell Prof. Dr. Hans J. Schneider Lehrstuhl für Programmiersprachen und Programmiermethodik Friedrich-Alexander-Universität Erlangen-Nürnberg Sommersemester 2011 I. Die
Vorlesung Theoretische Informatik
 Vorlesung Theoretische Informatik Automaten und Formale Sprachen Hochschule Reutlingen Fakultät für Informatik Masterstudiengang Wirtschaftsinformatik überarbeitet von F. Laux (Stand: 09.06.2010) Sommersemester
Vorlesung Theoretische Informatik Automaten und Formale Sprachen Hochschule Reutlingen Fakultät für Informatik Masterstudiengang Wirtschaftsinformatik überarbeitet von F. Laux (Stand: 09.06.2010) Sommersemester
11. Primfaktorzerlegungen
 78 Andreas Gathmann 11 Primfaktorzerlegungen Euch ist sicher aus der Schule bekannt, dass sich jede positive ganze Zahl a als Produkt a = p 1 p n von Primzahlen schreiben lässt, und dass diese Darstellung
78 Andreas Gathmann 11 Primfaktorzerlegungen Euch ist sicher aus der Schule bekannt, dass sich jede positive ganze Zahl a als Produkt a = p 1 p n von Primzahlen schreiben lässt, und dass diese Darstellung
Formale Sprachen. Der Unterschied zwischen Grammatiken und Sprachen. Rudolf Freund, Marian Kogler
 Formale Sprachen Der Unterschied zwischen Grammatiken und Sprachen Rudolf Freund, Marian Kogler Es gibt reguläre Sprachen, die nicht von einer nichtregulären kontextfreien Grammatik erzeugt werden können.
Formale Sprachen Der Unterschied zwischen Grammatiken und Sprachen Rudolf Freund, Marian Kogler Es gibt reguläre Sprachen, die nicht von einer nichtregulären kontextfreien Grammatik erzeugt werden können.
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten
 Inhalt 1 Einführung 2 Automatentheorie und Formale Sprachen Grammatiken Reguläre Sprachen und endliche Automaten Kontextfreie Sprachen und Kellerautomaten Kontextsensitive und Typ 0-Sprachen 3 Berechenbarkeitstheorie
Inhalt 1 Einführung 2 Automatentheorie und Formale Sprachen Grammatiken Reguläre Sprachen und endliche Automaten Kontextfreie Sprachen und Kellerautomaten Kontextsensitive und Typ 0-Sprachen 3 Berechenbarkeitstheorie
Lineare Algebra - alles was man wissen muß
 Statistik für Bioinformatiker SoSe 3 Rainer Spang Lineare Algebra - alles was man wissen muß Der Titel ist natürlich gelogen, aber was wir hier zusammengetragen haben ist zumindest ein Anfang. Weniger
Statistik für Bioinformatiker SoSe 3 Rainer Spang Lineare Algebra - alles was man wissen muß Der Titel ist natürlich gelogen, aber was wir hier zusammengetragen haben ist zumindest ein Anfang. Weniger
Bestimmung einer ersten
 Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
klar. Um die zweite Bedingung zu zeigen, betrachte u i U i mit u i = 0. Das mittlere -Zeichen liefert s
 Nachtrag zur allgemeinen Vektorraum-Theorie. 1.5.15. Direkte Summen. Sei V ein Vektorraum, seien U 1,..., U t Unterräume, wir schreiben V = U 1 U 2 U t = t i=1 U i falls die folgenden beiden Bedingungen
Nachtrag zur allgemeinen Vektorraum-Theorie. 1.5.15. Direkte Summen. Sei V ein Vektorraum, seien U 1,..., U t Unterräume, wir schreiben V = U 1 U 2 U t = t i=1 U i falls die folgenden beiden Bedingungen
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
 Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Grammatiken. Einführung
 Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen 19
 Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
Inhalt 1 inführung 2 Automatentheorie und ormale prachen Grammatiken Reguläre prachen und endliche Automaten Kontextfreie prachen und Kellerautomaten Kontextsensitive und yp 0-prachen 3 Berechenbarkeitstheorie
3.3 Eigenwerte und Eigenräume, Diagonalisierung
 3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
Formale Sprachen, reguläre und kontextfreie Grammatiken
 Formale Sprachen, reguläre und kontextfreie Grammatiken Alphabet A: endliche Menge von Zeichen Wort über A: endliche Folge von Zeichen aus A A : volle Sprache über A: Menge der A-Worte formale Sprache
Formale Sprachen, reguläre und kontextfreie Grammatiken Alphabet A: endliche Menge von Zeichen Wort über A: endliche Folge von Zeichen aus A A : volle Sprache über A: Menge der A-Worte formale Sprache
7. Formale Sprachen und Grammatiken
 7. Formale Sprachen und Grammatiken Computer verwenden zur Verarbeitung von Daten und Informationen künstliche, formale Sprachen (Maschinenspr., Assemblerspachen, Programmierspr., Datenbankspr., Wissensrepräsentationsspr.,...)
7. Formale Sprachen und Grammatiken Computer verwenden zur Verarbeitung von Daten und Informationen künstliche, formale Sprachen (Maschinenspr., Assemblerspachen, Programmierspr., Datenbankspr., Wissensrepräsentationsspr.,...)
Kapitel 4. Euklidische Ringe und die Jordansche Normalform. 4.1 Euklidische Ringe
 Kapitel 4 Euklidische Ringe und die Jordansche Normalform 4.1 Euklidische Ringe Die Ringe der ganzen Zahlen, Z, sowie Polynomringe über Körpern, K[X], wobei K ein Körper ist, haben die folgenden Gemeinsamheiten:
Kapitel 4 Euklidische Ringe und die Jordansche Normalform 4.1 Euklidische Ringe Die Ringe der ganzen Zahlen, Z, sowie Polynomringe über Körpern, K[X], wobei K ein Körper ist, haben die folgenden Gemeinsamheiten:
1. Der Begriff Informatik 2. Syntax und Semantik von Programmiersprachen. I.2. I.2. Grundlagen von von Programmiersprachen.
 1. Der Begriff Informatik 2. Syntax und Semantik von Programmiersprachen I.2. I.2. Grundlagen von von Programmiersprachen. - 1 - 1. Der Begriff Informatik "Informatik" = Kunstwort aus Information und Mathematik
1. Der Begriff Informatik 2. Syntax und Semantik von Programmiersprachen I.2. I.2. Grundlagen von von Programmiersprachen. - 1 - 1. Der Begriff Informatik "Informatik" = Kunstwort aus Information und Mathematik
Erinnerung/Zusammenfassung zu Abbildungsmatrizen
 Erinnerung/Zusammenfassung zu Abbildungsmatrizen Thomas Coutandin (cthomas@student.ethz.ch) 7. November 2 Abbildungsmatrizen Im Folgenden betrachten wir stets endlich dimensionale K-Vektorräume (K irgend
Erinnerung/Zusammenfassung zu Abbildungsmatrizen Thomas Coutandin (cthomas@student.ethz.ch) 7. November 2 Abbildungsmatrizen Im Folgenden betrachten wir stets endlich dimensionale K-Vektorräume (K irgend
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Ulrich Furbach. Sommersemester 2014
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Ulrich Furbach Institut für Informatik Sommersemester 2014 Furbach Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Ulrich Furbach Institut für Informatik Sommersemester 2014 Furbach Grundlagen d. Theoretischen Informatik:
Theoretische Informatik Mitschrift
 6. Kontextfreie Sprachen Theoretische Informatik Mitschrift Typ-2-Grammatiken: Regeln der Form A mit A N und N * Beispiel: Grammatik für arithmetische Ausdrücke G= {E,T,F },{,,,,a}, P, E, P : E ET T T
6. Kontextfreie Sprachen Theoretische Informatik Mitschrift Typ-2-Grammatiken: Regeln der Form A mit A N und N * Beispiel: Grammatik für arithmetische Ausdrücke G= {E,T,F },{,,,,a}, P, E, P : E ET T T
Seminararbeit für das SE Reine Mathematik- Graphentheorie
 Seminararbeit für das SE Reine Mathematik- Graphentheorie Der binäre Rang, der symplektische Graph, die Spektralzerlegung und rationale Funktionen Vortrag am 24.01.2012 Heike Farkas 0410052 Inhaltsverzeichnis
Seminararbeit für das SE Reine Mathematik- Graphentheorie Der binäre Rang, der symplektische Graph, die Spektralzerlegung und rationale Funktionen Vortrag am 24.01.2012 Heike Farkas 0410052 Inhaltsverzeichnis
Übungen zum Ferienkurs Lineare Algebra WS 14/15
 Übungen zum Ferienkurs Lineare Algebra WS 14/15 Linearkombinationen, Basen, Lineare Abbildungen 2.1 Lineare Unabhängigkeit Sind die folgenden Vektoren linear unabhängig? (a) 1, 2, 3 im Q Vektorraum R (b)
Übungen zum Ferienkurs Lineare Algebra WS 14/15 Linearkombinationen, Basen, Lineare Abbildungen 2.1 Lineare Unabhängigkeit Sind die folgenden Vektoren linear unabhängig? (a) 1, 2, 3 im Q Vektorraum R (b)
REG versus CF. Theorem REG ist echt in CF enthalten.
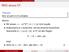 REG versus CF Theorem REG ist echt in CF enthalten. Beweis: Wir wissen: L = {a m b m m 1} ist nicht regulär. Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b}, {S}, S,
REG versus CF Theorem REG ist echt in CF enthalten. Beweis: Wir wissen: L = {a m b m m 1} ist nicht regulär. Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b}, {S}, S,
Syntax (= Satzgefüge), vgl. auch Grammatik
 1 Natürliche Sprachen Natürliche Sprachen bezeichnen wie das Wort "Sprache" ausdrückt zunächst das Gesprochene. Das Schweizerdeutsch etwa ist eine typische natürliche Sprache. Mit der Erfindung der Aufzeichnung
1 Natürliche Sprachen Natürliche Sprachen bezeichnen wie das Wort "Sprache" ausdrückt zunächst das Gesprochene. Das Schweizerdeutsch etwa ist eine typische natürliche Sprache. Mit der Erfindung der Aufzeichnung
t r Lineare Codierung von Binärbbäumen (Wörter über dem Alphabet {, }) Beispiel code( ) = code(, t l, t r ) = code(t l ) code(t r )
 Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Aufgabentypen die in der Klausur vorkommen
 Aufgabentypen die in der Klausur vorkommen können 1. Nennen Sie fünf wichtige Anwendungsgebiete der Computerlinguistik. 2. Für welches der drei Anwendungsgebiete Maschinelle Übersetzung, Rechtschreibkorrektur
Aufgabentypen die in der Klausur vorkommen können 1. Nennen Sie fünf wichtige Anwendungsgebiete der Computerlinguistik. 2. Für welches der drei Anwendungsgebiete Maschinelle Übersetzung, Rechtschreibkorrektur
1 Syntax von Programmiersprachen
 1 Syntax von Programmiersprachen Syntax ( Lehre vom Satzbau ): formale Beschreibung des Aufbaus der Worte und Sätze, die zu einer Sprache gehören; im Falle einer Programmier-Sprache Festlegung, wie Programme
1 Syntax von Programmiersprachen Syntax ( Lehre vom Satzbau ): formale Beschreibung des Aufbaus der Worte und Sätze, die zu einer Sprache gehören; im Falle einer Programmier-Sprache Festlegung, wie Programme
9. Anwendungen der Fundamentalgruppe
 76 Andreas Gathmann 9. Anwendungen der Fundamentalgruppe Nachdem wir mit Hilfe von Überlagerungen nun in der Lage sind, Fundamentalgruppen zu berechnen, wollen wir in diesem abschließenden Kapitel noch
76 Andreas Gathmann 9. Anwendungen der Fundamentalgruppe Nachdem wir mit Hilfe von Überlagerungen nun in der Lage sind, Fundamentalgruppen zu berechnen, wollen wir in diesem abschließenden Kapitel noch
4 Greedy-Algorithmen (gierige Algorithmen)
 Greedy-Algorithmen (gierige Algorithmen) Greedy-Algorithmen werden oft für die exakte oder approximative Lösung von Optimierungsproblemen verwendet. Typischerweise konstruiert ein Greedy-Algorithmus eine
Greedy-Algorithmen (gierige Algorithmen) Greedy-Algorithmen werden oft für die exakte oder approximative Lösung von Optimierungsproblemen verwendet. Typischerweise konstruiert ein Greedy-Algorithmus eine
Höhere Mathematik 3. Apl. Prof. Dr. Norbert Knarr. Wintersemester 2015/16. FB Mathematik
 Höhere Mathematik 3 Apl. Prof. Dr. Norbert Knarr FB Mathematik Wintersemester 2015/16 4. Homogene lineare Dierentialgleichungen 4.1. Grundbegrie 4.1.1. Denition. Es sei J R ein Intervall und a 0 ; : :
Höhere Mathematik 3 Apl. Prof. Dr. Norbert Knarr FB Mathematik Wintersemester 2015/16 4. Homogene lineare Dierentialgleichungen 4.1. Grundbegrie 4.1.1. Denition. Es sei J R ein Intervall und a 0 ; : :
Programmieren I. Formale Sprachen. www.kit.edu. Institut für Angewandte Informatik
 Programmieren I Formale Sprachen KIT Universität des Landes Baden-Württemberg und nationales Großforschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Formale Sprachen: Allgemeines Sprachen werden
Programmieren I Formale Sprachen KIT Universität des Landes Baden-Württemberg und nationales Großforschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Formale Sprachen: Allgemeines Sprachen werden
Entscheidungsbäume. Definition Entscheidungsbaum. Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen?
 Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Kapitel 2. Methoden zur Beschreibung von Syntax
 1 Kapitel 2 Methoden zur Beschreibung von Syntax Grammatik, die sogar Könige zu kontrollieren weiß... aus Molière, Les Femmes Savantes (1672), 2. Akt 2 Ziele Zwei Standards zur Definition der Syntax von
1 Kapitel 2 Methoden zur Beschreibung von Syntax Grammatik, die sogar Könige zu kontrollieren weiß... aus Molière, Les Femmes Savantes (1672), 2. Akt 2 Ziele Zwei Standards zur Definition der Syntax von
Optimalitätskriterien
 Kapitel 4 Optimalitätskriterien Als Optimalitätskriterien bezeichnet man notwendige oder hinreichende Bedingungen dafür, dass ein x 0 Ω R n Lösung eines Optimierungsproblems ist. Diese Kriterien besitzen
Kapitel 4 Optimalitätskriterien Als Optimalitätskriterien bezeichnet man notwendige oder hinreichende Bedingungen dafür, dass ein x 0 Ω R n Lösung eines Optimierungsproblems ist. Diese Kriterien besitzen
Entscheidungsprobleme. Berechenbarkeit und Komplexität Entscheidbarkeit und Unentscheidbarkeit. Die Entscheidbarkeit von Problemen
 Berechenbarkeit und Komlexität Entscheidbarkeit und Unentscheidbarkeit Wolfgang Schreiner Wolfgang.Schreiner@risc.uni-linz.ac.at Research Institute for Symbolic Comutation (RISC) Johannes Keler University,
Berechenbarkeit und Komlexität Entscheidbarkeit und Unentscheidbarkeit Wolfgang Schreiner Wolfgang.Schreiner@risc.uni-linz.ac.at Research Institute for Symbolic Comutation (RISC) Johannes Keler University,
Theoretische Informatik
 Theoretische Informatik für die Studiengänge Ingenieur-Informatik berufsbegleitendes Studium Lehramt Informatik (Sekundar- und Berufsschule) http://theo.cs.uni-magdeburg.de/lehre04s/ Lehrbeauftragter:
Theoretische Informatik für die Studiengänge Ingenieur-Informatik berufsbegleitendes Studium Lehramt Informatik (Sekundar- und Berufsschule) http://theo.cs.uni-magdeburg.de/lehre04s/ Lehrbeauftragter:
Kapitel 2: Formale Sprachen Gliederung
 Gliederung 0. Einleitung und Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen
Gliederung 0. Einleitung und Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen
Einführung in die Informatik Grammars & Parsers
 Einführung in die Informatik Grammars & Parsers Grammatiken, Parsen von Texten Wolfram Burgard Cyrill Stachniss 12.1 Einleitung Wir haben in den vorangehenden Kapiteln meistens vollständige Java- Programme
Einführung in die Informatik Grammars & Parsers Grammatiken, Parsen von Texten Wolfram Burgard Cyrill Stachniss 12.1 Einleitung Wir haben in den vorangehenden Kapiteln meistens vollständige Java- Programme
w a is die Anzahl der Vorkommen von a in w Beispiel: abba a = 2
 1 2 Notation für Wörter Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg w a is die Anzahl der Vorkommen von a in w Beispiel: abba
1 2 Notation für Wörter Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg w a is die Anzahl der Vorkommen von a in w Beispiel: abba
Extremwertverteilungen
 Seminar Statistik Institut für Stochastik 12. Februar 2009 Gliederung 1 Grenzwertwahrscheinlichkeiten 2 3 MDA Fréchet MDA Weibull MDA Gumbel 4 5 6 Darstellung von multivariaten, max-stabilen Verteilungsfunktionen
Seminar Statistik Institut für Stochastik 12. Februar 2009 Gliederung 1 Grenzwertwahrscheinlichkeiten 2 3 MDA Fréchet MDA Weibull MDA Gumbel 4 5 6 Darstellung von multivariaten, max-stabilen Verteilungsfunktionen
Theoretische Informatik I
 Theoretische nformatik inheit 3 Kontextfreie Sprachen 1. Kontextfreie Grammatiken 2. Pushdown Automaten 3. igenschaften kontextfreier Sprachen Theoretische nformatik inheit 3.1 Kontextfreie Grammatiken
Theoretische nformatik inheit 3 Kontextfreie Sprachen 1. Kontextfreie Grammatiken 2. Pushdown Automaten 3. igenschaften kontextfreier Sprachen Theoretische nformatik inheit 3.1 Kontextfreie Grammatiken
Grammatiken und die Chomsky-Hierarchie
 Grammatiken und die Chomsky-Hierarchie Def.: Eine Grammatik G=(Σ,V,S,R) besteht aus endlichem Alphabet Σ endlicher Variablenmenge V mit V Σ= Startsymbol SєV endlicher Menge R с (V Σ) + x(v Σ)* von Ableitungsregeln
Grammatiken und die Chomsky-Hierarchie Def.: Eine Grammatik G=(Σ,V,S,R) besteht aus endlichem Alphabet Σ endlicher Variablenmenge V mit V Σ= Startsymbol SєV endlicher Menge R с (V Σ) + x(v Σ)* von Ableitungsregeln
I. Aussagenlogik. Aussagenlogik untersucht Verknüpfungen wie "und", "oder", "nicht", "wenn... dann" zwischen atomaren und komplexen Sätzen.
 I. Aussagenlogik 2.1 Syntax Aussagenlogik untersucht Verknüpfungen wie "und", "oder", "nicht", "wenn... dann" zwischen atomaren und komplexen Sätzen. Sätze selbst sind entweder wahr oder falsch. Ansonsten
I. Aussagenlogik 2.1 Syntax Aussagenlogik untersucht Verknüpfungen wie "und", "oder", "nicht", "wenn... dann" zwischen atomaren und komplexen Sätzen. Sätze selbst sind entweder wahr oder falsch. Ansonsten
Einführung in die Kodierungstheorie
 Einführung in die Kodierungstheorie Einführung Vorgehen Beispiele Definitionen (Code, Codewort, Alphabet, Länge) Hamming-Distanz Definitionen (Äquivalenz, Coderate, ) Singleton-Schranke Lineare Codes Hamming-Gewicht
Einführung in die Kodierungstheorie Einführung Vorgehen Beispiele Definitionen (Code, Codewort, Alphabet, Länge) Hamming-Distanz Definitionen (Äquivalenz, Coderate, ) Singleton-Schranke Lineare Codes Hamming-Gewicht
Scheduling und Lineare ProgrammierungNach J. K. Lenstra, D. B. Shmoys und É.
 Scheduling und Lineare ProgrammierungNach J. K. Lenstra, D. B. Shmoys und É. Tardos Janick Martinez Esturo jmartine@techfak.uni-bielefeld.de xx.08.2007 Sommerakademie Görlitz Arbeitsgruppe 5 Gliederung
Scheduling und Lineare ProgrammierungNach J. K. Lenstra, D. B. Shmoys und É. Tardos Janick Martinez Esturo jmartine@techfak.uni-bielefeld.de xx.08.2007 Sommerakademie Görlitz Arbeitsgruppe 5 Gliederung
IT-Basics 2. DI Gerhard Fließ
 IT-Basics 2 DI Gerhard Fließ Wer bin ich? DI Gerhard Fließ Telematik Studium an der TU Graz Softwareentwickler XiTrust www.xitrust.com www.tugraz.at Worum geht es? Objektorientierte Programmierung Konzepte
IT-Basics 2 DI Gerhard Fließ Wer bin ich? DI Gerhard Fließ Telematik Studium an der TU Graz Softwareentwickler XiTrust www.xitrust.com www.tugraz.at Worum geht es? Objektorientierte Programmierung Konzepte
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
Tutorium zur theoretischen Informatik Übungsblatt 4 (2006-12-13)
 Ein verständiges Herz erwirbt Kenntnisse, und das Ohr der Weisen lauscht dem Wissen. (Die Bibel, "Buch der Sprüche", Kapitel 18 Vers 15) Inhalt 1. Empfehlenswerte Referenzen 2. Aufgabe 1 CF Grammatik für
Ein verständiges Herz erwirbt Kenntnisse, und das Ohr der Weisen lauscht dem Wissen. (Die Bibel, "Buch der Sprüche", Kapitel 18 Vers 15) Inhalt 1. Empfehlenswerte Referenzen 2. Aufgabe 1 CF Grammatik für
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Kapitel 2: Formale Sprachen Kontextfreie Sprachen. reguläre Grammatiken/Sprachen. kontextfreie Grammatiken/Sprachen
 reguläre Grammatiken/prachen Beschreibung für Bezeichner in Programmiersprachen Beschreibung für wild cards in kriptsprachen (/* reguläre Ausdrücke */)?; [a-z]; * kontextfreie Grammatiken/prachen Beschreibung
reguläre Grammatiken/prachen Beschreibung für Bezeichner in Programmiersprachen Beschreibung für wild cards in kriptsprachen (/* reguläre Ausdrücke */)?; [a-z]; * kontextfreie Grammatiken/prachen Beschreibung
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Reelle Zahlen. Mathematische Grundlagen Lernmodul 4. Stand: Oktober 2010
 Mathematische Grundlagen Lernmodul 4 Reelle Zahlen Stand: Oktober 200 Autoren: Prof. Dr. Reinhold Hübl, Professor Fakultät für Technik, Wissenschaftliche Leitung ZeMath, E-Mail: huebl@dhbw-mannheim.de
Mathematische Grundlagen Lernmodul 4 Reelle Zahlen Stand: Oktober 200 Autoren: Prof. Dr. Reinhold Hübl, Professor Fakultät für Technik, Wissenschaftliche Leitung ZeMath, E-Mail: huebl@dhbw-mannheim.de
0, v 6 = 2 2. 1, v 4 = 1. 2. span(v 1, v 5, v 6 ) = span(v 1, v 2, v 3, v 4, v 5, v 6 ) 4. span(v 1, v 2, v 4 ) = span(v 2, v 3, v 5, v 6 )
 Aufgabe 65. Ganz schön span(n)end. Gegeben sei folgende Menge M von 6 Vektoren v, v,..., v 6 R 4 aus Aufgabe P 6: M = v =, v =, v =, v 4 =, v 5 =, v 6 = Welche der folgenden Aussagen sind wahr? span(v,
Aufgabe 65. Ganz schön span(n)end. Gegeben sei folgende Menge M von 6 Vektoren v, v,..., v 6 R 4 aus Aufgabe P 6: M = v =, v =, v =, v 4 =, v 5 =, v 6 = Welche der folgenden Aussagen sind wahr? span(v,
Codierung. Auszug aus dem Skript von Maciej Liśkiewicz und Henning Fernau
 Codierung Auszug aus dem Skript von Maciej Liśkiewicz und Henning Fernau Ein bisschen Informationstheorie Betrachten wir das folgende Problem: Wie lautet eine sinnvolle Definition für das quantitative
Codierung Auszug aus dem Skript von Maciej Liśkiewicz und Henning Fernau Ein bisschen Informationstheorie Betrachten wir das folgende Problem: Wie lautet eine sinnvolle Definition für das quantitative
Primzahlzertifikat von Pratt
 Primzahlzertifikat von Pratt Daniela Steidl TU München 17. 04. 2008 Primzahltests in der Informatik "Dass das Problem, die Primzahlen von den Zusammengesetzten zu unterscheiden und letztere in ihre Primfaktoren
Primzahlzertifikat von Pratt Daniela Steidl TU München 17. 04. 2008 Primzahltests in der Informatik "Dass das Problem, die Primzahlen von den Zusammengesetzten zu unterscheiden und letztere in ihre Primfaktoren
Elemente der Analysis II
 Elemente der Analysis II Kapitel 3: Lineare Abbildungen und Gleichungssysteme Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 15. Mai 2009 1 / 35 3.1 Beispiel
Elemente der Analysis II Kapitel 3: Lineare Abbildungen und Gleichungssysteme Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 15. Mai 2009 1 / 35 3.1 Beispiel
Geometrische Mannigfaltigkeiten
 Geometrische Mannigfaltigkeiten Thilo Kuessner Abstract Kurzfassung der Vorlesung: Definitionen, Beispiele und Sätze, keine Beweise. Definition 1. Ein topologischer Raum ist eine Menge X mit einer Familie
Geometrische Mannigfaltigkeiten Thilo Kuessner Abstract Kurzfassung der Vorlesung: Definitionen, Beispiele und Sätze, keine Beweise. Definition 1. Ein topologischer Raum ist eine Menge X mit einer Familie
x 2 2x + = 3 + Es gibt genau ein x R mit ax + b = 0, denn es gilt
 - 17 - Die Frage ist hier also: Für welche x R gilt x = x + 1? Das ist eine quadratische Gleichung für x. Es gilt x = x + 1 x x 3 = 0, und man kann quadratische Ergänzung machen:... ( ) ( ) x x + = 3 +
- 17 - Die Frage ist hier also: Für welche x R gilt x = x + 1? Das ist eine quadratische Gleichung für x. Es gilt x = x + 1 x x 3 = 0, und man kann quadratische Ergänzung machen:... ( ) ( ) x x + = 3 +
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
 9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
Zusammenfassung Grundzüge der Informatik 4
 Zusammenfassung Grundzüge der Informatik 4 Sommersemester 04 Thorsten Wink 21. September 2004 Version 1.2 Dieses Dokument wurde in L A TEX 2εgeschrieben. Stand: 21. September 2004 Inhaltsverzeichnis 1
Zusammenfassung Grundzüge der Informatik 4 Sommersemester 04 Thorsten Wink 21. September 2004 Version 1.2 Dieses Dokument wurde in L A TEX 2εgeschrieben. Stand: 21. September 2004 Inhaltsverzeichnis 1
Modulabschlussklausur Analysis II
 Modulabschlussklausur Analysis II. Juli 015 Bearbeitungszeit: 150 min Aufgabe 1 [5/10 Punkte] Es sei a R und f a : R 3 R mit f a (x, y, z) = x cos(y) + z 3 sin(y) + a 3 + (z + ay a y) cos(x) a) Bestimmen
Modulabschlussklausur Analysis II. Juli 015 Bearbeitungszeit: 150 min Aufgabe 1 [5/10 Punkte] Es sei a R und f a : R 3 R mit f a (x, y, z) = x cos(y) + z 3 sin(y) + a 3 + (z + ay a y) cos(x) a) Bestimmen
13. Abzählen von Null- und Polstellen
 13. Abzählen von Null- und Polstellen 77 13. Abzählen von Null- und Polstellen Als weitere Anwendung des Residuensatzes wollen wir nun sehen, wie man ot au einache Art berechnen kann, wie viele Null- bzw.
13. Abzählen von Null- und Polstellen 77 13. Abzählen von Null- und Polstellen Als weitere Anwendung des Residuensatzes wollen wir nun sehen, wie man ot au einache Art berechnen kann, wie viele Null- bzw.
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Lösungen zu Kapitel 7
 Lösungen zu Kapitel 7 Lösung zu Aufgabe 1: Nach Definition 7.1 ist eine Verknüpfung auf der Menge H durch eine Abbildung : H H H definiert. Gilt H = {a 1,..., a m }, so wird eine Verknüpfung auch vollständig
Lösungen zu Kapitel 7 Lösung zu Aufgabe 1: Nach Definition 7.1 ist eine Verknüpfung auf der Menge H durch eine Abbildung : H H H definiert. Gilt H = {a 1,..., a m }, so wird eine Verknüpfung auch vollständig
Einfache kryptographische Verfahren
 Einfache kryptographische Verfahren Prof. Dr. Hagen Knaf Studiengang Angewandte Mathematik 26. April 2015 c = a b + a b + + a b 1 11 1 12 2 1n c = a b + a b + + a b 2 21 1 22 2 2n c = a b + a b + + a b
Einfache kryptographische Verfahren Prof. Dr. Hagen Knaf Studiengang Angewandte Mathematik 26. April 2015 c = a b + a b + + a b 1 11 1 12 2 1n c = a b + a b + + a b 2 21 1 22 2 2n c = a b + a b + + a b
Grundbegriffe der Informatik Tutorium 7
 Grundbegriffe der Informatik Tutorium 7 Tutorium Nr. 16 Philipp Oppermann 16. Dezember 2014 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Grundbegriffe der Informatik Tutorium 7 Tutorium Nr. 16 Philipp Oppermann 16. Dezember 2014 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
Algorithmen II Vorlesung am 15.11.2012
 Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
6.2 Perfekte Sicherheit
 04 6.2 Perfekte Sicherheit Beweis. H(B AC) + H(A C) = H(ABC) H(AC) + H(AC) H(C) Wegen gilt Einsetzen in die Definition gibt = H(AB C). H(A BC) = H(AB C) H(B C). I(A; B C) = H(A C) H(AB C) + H(B C). Da
04 6.2 Perfekte Sicherheit Beweis. H(B AC) + H(A C) = H(ABC) H(AC) + H(AC) H(C) Wegen gilt Einsetzen in die Definition gibt = H(AB C). H(A BC) = H(AB C) H(B C). I(A; B C) = H(A C) H(AB C) + H(B C). Da
Diskrete Mathematik für Informatiker
 Diskrete Mathematik für Informatiker Markus Lohrey Universität Siegen Wintersemester 2014/2015 Lohrey (Universität Siegen) Diskrete Mathematik Wintersem. 2014/2015 1 / 344 Organisatorisches zur Vorlesung
Diskrete Mathematik für Informatiker Markus Lohrey Universität Siegen Wintersemester 2014/2015 Lohrey (Universität Siegen) Diskrete Mathematik Wintersem. 2014/2015 1 / 344 Organisatorisches zur Vorlesung
Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung
 Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung Frank Heitmann heitmann@informatik.uni-hamburg.de 13. Mai 2014 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/17 Überblick Wir hatten
Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung Frank Heitmann heitmann@informatik.uni-hamburg.de 13. Mai 2014 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/17 Überblick Wir hatten
Compiler. Kapitel. Syntaktische Analyse. Kapitel 4. Folie: 1. Syntaktische Analyse. Autor: Aho et al.
 Folie: 1 Kapitel 4 Übersicht Übersicht Syntax: Definition 4 syn-tax: the way in which words are put together to form phrases, clauses, or sentences. Webster's Dictionary Die Syntax (griechisch σύνταξις
Folie: 1 Kapitel 4 Übersicht Übersicht Syntax: Definition 4 syn-tax: the way in which words are put together to form phrases, clauses, or sentences. Webster's Dictionary Die Syntax (griechisch σύνταξις
Prof. Dr. Jürgen Dassow Otto-von-Guericke-Universität Magdeburg. Codierungstheorie und Kryptographie
 Prof. Dr. Jürgen Dassow Otto-von-Guericke-Universität Magdeburg Fakultät für Informatik Codierungstheorie und Kryptographie Wintersemester 2008 1 2 Inhaltsverzeichnis 1 Definition und Charakterisierung
Prof. Dr. Jürgen Dassow Otto-von-Guericke-Universität Magdeburg Fakultät für Informatik Codierungstheorie und Kryptographie Wintersemester 2008 1 2 Inhaltsverzeichnis 1 Definition und Charakterisierung
Codierungstheorie Rudolf Scharlau, SoSe 2006 9
 Codierungstheorie Rudolf Scharlau, SoSe 2006 9 2 Optimale Codes Optimalität bezieht sich auf eine gegebene Quelle, d.h. eine Wahrscheinlichkeitsverteilung auf den Symbolen s 1,..., s q des Quellalphabets
Codierungstheorie Rudolf Scharlau, SoSe 2006 9 2 Optimale Codes Optimalität bezieht sich auf eine gegebene Quelle, d.h. eine Wahrscheinlichkeitsverteilung auf den Symbolen s 1,..., s q des Quellalphabets
5. Verschiedene Repräsentanten
 5. Verschiedene Repräsentanten 5.1. Die Sätze Hall und König Sei I := {1,...,n}, und sei A(I) = (A 1,...,A n ) eine Familie von Teilmengen einer endlichen Menge E. Zu K I seien A(K) := (A i : i K) und
5. Verschiedene Repräsentanten 5.1. Die Sätze Hall und König Sei I := {1,...,n}, und sei A(I) = (A 1,...,A n ) eine Familie von Teilmengen einer endlichen Menge E. Zu K I seien A(K) := (A i : i K) und
Was ist ein Compiler?
 Was ist ein Compiler? Was ist ein Compiler und worum geht es? Wie ist ein Compiler aufgebaut? Warum beschäftigen wir uns mit Compilerbau? Wie ist die Veranstaltung organisiert? Was interessiert Sie besonders?
Was ist ein Compiler? Was ist ein Compiler und worum geht es? Wie ist ein Compiler aufgebaut? Warum beschäftigen wir uns mit Compilerbau? Wie ist die Veranstaltung organisiert? Was interessiert Sie besonders?
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
