Lineare Algebra - Zusammenfassung
|
|
|
- Heike Schuster
- vor 5 Jahren
- Abrufe
Transkript
1 Lineare Algebra - Zusammenfassung Diese Zusammenfassung erhebt keinen Anspruch auf Vollständigkeit oder Korrektheit. Solltet ihr Fehler finden oder Ergänzungen haben, teilt sie mir bitte mit: richard.gebauer@student.kit.edu 1 Lineare Algebra II 1.1 Jordan-Normalform (JNF) Bestimmung der JNF Charakteristisches Polynom der Matrix bestimmen: CP A (λ) = l i=1 (λ c i) ri Algebraische Vielfachheit r i ist Länge des Jordan-Blocks zum Eigenwert c i Bestimme Eigenraum (bzw. dessen Dimension) zum Eigenwert c i : E ci = kern(a c i I) Geometrische Vielfachheit k i = dim(e ci ) ist Anzahl Jordan-Kästchen im Block zu c i Vielfachheit e i eines Linearfaktors (λ c i ) im Minimalpolynom ist Länge des größten Jordan- Kästchen im Block zum Eigenwert c i, d.h. d ci,1 = e i Jordan-Blöcke und Kästchen (innerhalb der Blöcke) nach Größe anordnen: Große zuerst c c 0 0 Jordan-Kästchen der Länge d zum EW c: J d (c) =. 0 1 c... R d d c J dci, J... dci,2 Jordan-Block zum EW c i : D i = D BiB i (A H(A,ci)) = R ri ri Jordan-Normalform von A: JNF(A) = D BB (A) = 0 0 J dci,k i D D.. 2. R..... n n D l Bestimmung der Basis für eine JNF Betrachte jeden Eigenwert c Bestimme kern(a c I) 2, kern(a c I) 3,... bis sich die Dimension des Kerns nicht mehr ändert Die kleinste Zahl für die dies so ist, sei p: kern(a c I) p = kern(a c I) p+1 p ist Vielfachheit des Linearfaktors (λ c) im Minimalpolynom Wähle Basisvektoren für kern(a c I), ergänze diese zu Basis von kern(a c I) 2, diese wiederum zu Basis von kern(a c I) 3 usw. Wähle Basisvektoren aus kern(a c I) p, die nicht in kern(a c I) p 1 enthalten sind Für jeden Vektor v bestimme: v, (A c I) v, (A c I) 2 v,..., (A c I) p 1 v Diese bilden in dieser Reihenfolge Basis des größten Jordan-Kästchen (also der Länge p) Seite 1 von 7
2 Zu einem Jordan-Kästchen der Länge k gehören Basisvektoren aus kern(a c I) k Sei also k nun die Länge des nächstgrößten Jordan-Kästchen zum EW c Wähle wieder Basisvektoren aus kern(a c I) k, die nicht in kern(a c I) k 1 liegen Bestimme für jeden dieser Vektoren v: v, (A c I) v, (A c I) 2 v,..., (A c I) k 1 v Fahre so fort, bis alle Jordan-Kästchen Basisvektoren haben Man erhält somit eine Basiswechselmatrix S = (b 1... b n ), sodass JNF(A) = S 1 A S d.h. S definiert Basisisomorphismus von B in die Std.basis: β B : x Sx = x 1 b x n b n 1.2 Skalarprodukt (SKP), Orthonormalbasis (ONB), Orthogonalprojektion Vektorraum-Paarung V, W K-VR, Abb. P : V W K Paarung, falls P linear in jedem Argument Für V = W : heißt P Bilinearform auf V P heißt nicht ausgeartet, falls w 0 0, v 0 0 : P (, w 0 ) 0, P (v 0, ) 0 Bilinearform P heißt symmetrisch, falls v, w V : P (v, w) = P (w, v) Fundamentalmatrix V, W K-VR mit Basen B = (b 1,..., b m ), C = (c 1,..., c n ), P VR-Paarung D BC (P ) := (P (b i, c j )) ij K m n P (v, w) = D B (v) T D BC (P ) D C (w) Sesquilinearform V K-VR, s : V V K heißt Sesquilinearform, falls x, y, z V, α K: s(αx + y, z) = α s(x, z) + s(y, z) und s(x, αy + z) = αs(x, y) + s(x, z) s heißt hermitesch (für K = C) bzw. symmetrisch (für K = R), falls s(y, x) = s(x, y) (schiefsymmetrisch) Skalarprodukt Schiefsymm. Sesquilinearform s heißt Skalarprodukt auf V, falls es positiv definit ist: x V : s(x, x) 0 und s(x, x) = 0 x = 0 Schreibe: x, y := s(x, y) Norm x := x, x x V Orthogonalität V VR mit Skp., und zugehöriger Norm x, y V senkrecht bzw. orthogonal x, y = 0 x y M, N V orthogonal x M, y N : x y M N B V Orthogonalsystem (OGS) x, y B : x y x y B V Orthonormalsystem (ONS) B OGS und x B : x = 1 B V Orthogonalbasis (OGB) B Basis von V und OGS B V Orthonormalbasis (ONB) B Basis von V und ONS Erhard-Schmidtsches Orthogonalisierungsverfahren Sei (b i ) i lin. unabhängig. Wollen OGS (c i ) i finden, sodass (b i ) i = (c i ) i Setze c 0 = b 0 und rekursiv: c n = b n n 1 i=0 b n, c i c i, c i c i Seite 2 von 7
3 Orthogonalraum M V. Orthogonales Komplement von M: M := {y V ; y M} Orthogonalprojektion U V endl.dim. Teilraum x V :!y U : d := x y = min{ x u ; u U} y U, x y U Definiere orthogonale Projektion auf U: π U (x) := y Es gilt: π U End stetig (V ), π 2 U = π U (unipotent), π U (x) x d heißt Abstand von x von U, z := x y Lot von x auf U, y Lotfußpunkt Sei (b 1,..., b l ) ONB von U: π U (v) = l i=1 v, b i b i Abstand d({x}, U) := z = π U (x) = x π U (x) 1.3 Adjungierte, Selbstadjungierte Adjungierte Matrix A := A T Adjungierter Homomorphismus Φ Hom(V, W ). Ψ Hom(W, V ) heißt zu Φ adjung. Hom., falls: x V, y W : Φ(x), y W = x, Ψ(y) V Schreibe: Ψ =: Φ und setze Hom a (V, W ) := {Φ : V W ; Φ existiert} Mit ONB B gilt: D BB (Φ ) = D BB (Φ) Selbstadjungierte Endomorphismen Φ End a (V ) selbstadjungiert, falls Φ = Φ Φ selbstadjungiert D BB (Φ) = DBB (Φ), d.h. hermitesch Φ selbstadjungiert Φ normal A C m m mit A = A Spec(A) R Für A hermitesch gilt: A positiv definit λ Spec(A) : λ > 0 Spektralradius V C-VR, Φ End(V ): Spektralradius ρ(φ) := sup{ λ ; λ Spec(Φ)} Norm von linearen Abbildungen A K m n : A := sup{ Ax ; x 1} Es gilt: A = ρ(a A) und für normale A mit m = n gilt: A = ρ(a) 1.4 Isometrien, Isometrienormalform (INF) Morphismus von VR mit Sesquilinearformen V 1, V 2 K-VR mit Sesquilinearformen s 1, s 2 Φ Hom(V 1, V 2 ) mit s 2 (Φ(x), Φ(y)) = s 1 (x, y) x, y V 1 (Lin.) Isometrie Φ Morphimus von VR mit Sesquilinearformen und bijektiv Isometrie Φ : (V, s) (V, s) heißt Automorphismus von s Φ Isometrie Φ End a (V ) und Φ = Φ 1 x V : x = Φ(x) y V : y Φ(y) = 1 Isometrienormalform (INF) Im unitären VR V n-dim. unitärer VR, φ : V V unitär. Dann ex. ONB aus EV von V und für alle EW gilt: λ = 1 Seite 3 von 7
4 Im euklidischen VR V n-dim eukl. VR, φ : V V orthogonal. Dann ex. ONB B von V, sodass: ( ) cos ϕ sin ϕ D BB (φ) = diag(1,..., 1, 1,..., 1, D ϕ1,..., D ϕl ) mit D ϕ := sin ϕ cos ϕ und φ hat als reelle EW nur ±1. Für komplexe EW gilt: λ EW (x 2 2Re(λ)x + 1) CP φ (x), λ = 1 Mit cos ϕ = Re(λ) bzw. sin ϕ = Im(λ) erhält man den Drehwinkel des zugehörigen Drehkästchens. Eine ONB erhält man mit den normierten EV von ±1 und für die Drehkästchen wähle v kern(x 2 2Re(λ)x + 1): (v, φ(v)) ist Basis des Drehkästchens. Noch orthonormieren: Fertig! 1.5 unitäre VR, normale Endomorphismen normale Endomorphismen Φ End a (V ) ist normal, falls Φ Φ = Φ Φ bzw.: x, y V : Φ (x), Φ (y) = Φ(x), Φ(y) Mit ONB B gilt für A := D BB (Φ) auch: Φ normal A A = A A Spektralsatz für normale Endomorphismen V endl.dim VR mit Skp., Φ End(V ) normal Falls K = R dann habe CP Φ nur reelle NS. Dann besitzt V eine ONB aus Eigenvektoren von Φ unitäre Endomorphismen Φ End(V ) unitär Φ normal und λ Spec(Φ) : λ = 1 Drehkästchennormalform V endl.dim. R-VR mit Skp., Ψ End(V ) normal. Dann gilt: CP Ψ (x) = r j=1 (x λ j) s k=1 (x λ r+k)(x + λ r+k ) mit λ 1,..., λ r R, λ r+1,..., λ r+s C \ R ONB C = {c 1,..., c r, c r+1, c r+1,..., c r+s, c r+s} von V, sodass D CC (Ψ) DrehkästchenNF hat: D CC (Ψ) = diag(λ 1,..., λ r, γ 1 D φ1,..., γ s D φs ) mit D φ := Ψ orthogonal: Siehe Isometrienormalform (INF) ( EW λ : λ = 1) 1.6 affine Geometrie, affine Abbildungen, Quadriken Affiner Raum P A : 0 + P = P ( cos φ sin φ sin φ cos φ V endl.dim. K-VR. A heißt affiner Raum mit Richtung(svektorraum) V, falls: x, y V : x + (y + P ) = (x + y) + P P, Q A :!x V : Q = x + P (Translationsvektor x = P Q) Affiner Teilraum B A, B heißt lineare Varietät in A, falls: VR U B V : B affiner Raum mit Richtung U B B = wird ebenfalls affiner Raum genannt B aff. TR von A P A : UVR U V : B = U + P K >2 P, Q B : P Q P Q B Affine Hülle von M A [M] := B aff. TR, B M Für M = {P 1,..., P m } schreibe [M] =: [P 1,..., P m ] [P 0,..., P m ] in allgemeiner Lage, falls dim[p 0,..., P m ] = m ( P 0 P i ) i=1...m linear unabhängig B ) Parallelität Affine TR B, C A sind parallel (B C), falls: U B U C oder U C U B Seite 4 von 7
5 Affines Koordinatensystem A AR mit Richtung V, dim A = n. Ein Paar K := (O, B) A {Basen von V } heißt affines Koordinatensystem mit Ursprung O D K : A K n, P D B ( OP ) die Koordinatenvektorabbildung D K : A A n (K) Koordinatendarstellung zum KS K Morphismus affiner Räume A, B AR mit Richtungen V, W. Abb ϕ : A B heißt affin, falls: Φ Hom(V, W ) : ϕ(x + P ) = Φ(x) + ϕ(p ) x V, P A Setze Hom aff (A, B) := {ϕ Abb(A, B); ϕ affin}. Es gilt: ϕ affin mit zugeh. Φ P 0 A : x V : ϕ(x + P 0 ) = Φ(x) + ϕ(p 0 ) ϕ Hom aff (A, B) zugeh. Φ =: Λ ϕ ist eindeutig ϕ affin: ϕ injektiv/surjektiv Λ ϕ injektiv/surjektiv ϕ affin und bijektiv heißt Affinität oder für A = B Automorphismus ψ : K n K m affin A K m n, a K n : ψ(x) = Ax + a, Schreibe daher: ψ =: (A, a) Fixpunkt, -raum & -richtung A AR mit Richtung V, ϕ Hom aff (A, A) P A heißt Fixpunkt von ϕ, falls ϕ(p ) = P Aff. TR B A, B heißt Fixraum von ϕ, falls ϕ(b) B UVR U V heißt Fixrichtung von ϕ, falls Λ ϕ (U) U Geradentreue Abb. A AR, Abb. φ : A A ist geradentreu, falls: G A Gerade φ(g) Gerade Es gilt: φ Affinität φ geradentreu Für dim A > 1, K = F p mit p 2 oder K = Q gilt: ϕ Affinität ϕ bijektiv und geradentreu Euklidischer Raum Abstand Paar (E,, ) mit E AR über R und Skp. auf Richtung U E = V von E von P, Q E: d(p, Q) := P Q = P Q, P Q cartesisches Koordinatensystem K = (O, B) auf euklid. Raum E mit ONB B bzgl., Bewegungen E, F euklid. Räume, ϕ : E F ϕ heißt längentreu, falls d(ϕ(p ), ϕ(q)) = d(p, Q) P, Q E ϕ heißt isometrisch, falls ϕ affin und längentreu ϕ heißt Bewegung von E, falls ϕ Aut aff (E) und isometrisch ϕ heißt eigentliche Bewegung, falls zusätzlich det(λ ϕ ) = 1 gilt Ortogonalität affiner Teilräume A B U A U B Gemeinsames Lot von A, B mit Lotfußpunkten P +, Q + : Gerade G mit G A, G B, G A = {P + }, G B = {Q + } A, B R n ATR, A, B, dim(u A +U B ) < n! gem. Lot G mit P +, Q + und d(a, B) = d(p +, Q + ) Seite 5 von 7
6 Abstandsbestimmung: Mit LGS A, B lassen sich mit Stützvektor und Basisvektoren schreiben als: A = s i=1 Rx i + x 0, B = r j=1 Ry j + y 0 Sei P + = i λ ix i + x 0, Q + = j µ jy j + y 0 Unbestimmte λ i, µ j lassen sich mit folgendem LGS ermitteln: x i, P + Q + = 0 i {1,..., s} y j, P + Q + = 0 j {1,..., r} Mit den Lotfußpunkten ergibt sich schließlich der Abstand d(a, B) = d(p +, Q + ) Abstandsbestimmung: Mit ONB Bestimme ONB {b 1,..., b t } für (U A + U B ) t Dann gilt: d(a, B) = τ=1 x o y o, b τ 2 Bewegungen von A 2 (R) Zu ϕ Aut dist (R 2 ) ex. KS L, sodass D LL (ϕ) eine der folgenden NF hat: (I, 0) = id (I, λe 1 ) Translation (λ > 0), kein Fixpunkt (D α, 0) Drehung (0 < α π), genau ein Fixpunkt (C, 0) Spiegelung an Achse, Fixpunktmenge = Achse (C, λe 1 ) Gleitspiegelung, kein Fixpunkt, genau 1 Fixgerade ( ) ( ) cosα sinα 1 0 Mit D α := und C := sinα cosα 0 1 Affine Quadrik A K n n symmetrisch, b K n, γ K, f : K n K, x x T Ax + 2b T x + γ Q := N (f) = {x K n ; f(x) = 0} Quadratische Ergänzung A K n n symmetrisch, Rang(A) = r, Char(K) 2 Dann: C GL n (K) : C T AC = diag(α 1,..., α r, 0..., 0) Trägheitssatz von Sylvester A K n n symmetrisch, Rang(A) = r K = C K = R {}}{ C GL n (C) : C T AC = diag( 1,..., 1, 0,..., 0) {}}{{}}{ C GL n (R) : C T AC = diag( 1,..., 1, 1,..., 1, 0,..., 0) und p, q durch A eindeutig bestimmt r p q Mittelpunkt f(x) = x T Ax+2b T x+γ. Falls ex., heißt Lsg. des LGS Az = b Mittelpunkt der Quadrik Seite 6 von 7
7 Affine Normalform für Quadriken mit Mittelpunkt Allg. Körper f = α 1 X α r X 2 r + K = C f = X X 2 r + { 0 falls γ = 0 1 falls γ 0 { 0 falls γ = 0 1 falls γ 0 K = R f = X X 2 p X 2 p+1... X 2 p+q + { 0 falls γ = 0 1 falls γ 0 (OBdA: p q) Affine Normalform für Quadriken ohne Mittelpunkt K = C f = X X 2 r 2X r+1 K = R f = X X 2 p X 2 p+1... X 2 p+q 2X r+1 (OBdA: p q) Affine Äquivalenz F, F quadratische Polynome affin äquivalent falls: Affinität Φ(X) = MX + t auf A n (K), Einheit e K : F (X) = e F (MX + t) Bestimmung der affinen Normalform Quadratische Ergänzung nacheinander in den einzelnen Variablen durchführen (z.b: zuerst in x, dann in y, dann in z...) Mit anderem Variablenset (affin, also höchstens linear) substituieren (z.b: u = 2x + 3z 7) Substitution beschreibt affine Transformation der Quadrik in NF: (A, a) : K n K n, X A X +a Euklidische Klassifikation Nur Orthogonale Transformationen zugelassen, d.h. C O n Spektralsatz C O n : C T AC = diag(λ 1,..., λ r, 0,..., 0) (OBdA: λ i λ i+1 ) Erhalten Normalformen: λ 1 X λ r Xr 2 λ 1 X λ r Xr λ 1 X λ r Xr 2 2X r+1 Seite 7 von 7
17. Orthogonalsysteme
 17. Orthogonalsysteme 17.1. Winkel und Orthogonalität Vorbemerkung: Sei V ein Vektorraum mit Skalaprodukt, und zugehöriger Norm, dann gilt nach Cauchy-Schwarz: x, y V \ {0} : x, y x y 1 Definition: (a)
17. Orthogonalsysteme 17.1. Winkel und Orthogonalität Vorbemerkung: Sei V ein Vektorraum mit Skalaprodukt, und zugehöriger Norm, dann gilt nach Cauchy-Schwarz: x, y V \ {0} : x, y x y 1 Definition: (a)
1. Übungsblatt: Lineare Algebra II Abgabe: 8./ in den Übungsgruppen
 Hannover, den 7. Februar 2002 Aufgabe. Übungsblatt: Lineare Algebra II Abgabe: 8./9.4.2002 in den Übungsgruppen (2, 2, 3 Punkte) Der Vektorraum V = C[, ] sei mit dem üblichen Skalarprodukt f, g = f(t)g(t)
Hannover, den 7. Februar 2002 Aufgabe. Übungsblatt: Lineare Algebra II Abgabe: 8./9.4.2002 in den Übungsgruppen (2, 2, 3 Punkte) Der Vektorraum V = C[, ] sei mit dem üblichen Skalarprodukt f, g = f(t)g(t)
Lösungsskizzen der Klausur zur Linearen Algebra im Herbst 2015
 sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 2009
 I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
21. Affine Koordinaten und affine Abbildungen
 21.1. Grundbegriffe Definition: Sei A ein affiner Raum mit Richtungs-VRm V der Dimension n. (a) Sei B die Menge aller Basen von V. Ein Paar K := (O, B) A B heißt affines Koordinatensystem, wobei O der
21.1. Grundbegriffe Definition: Sei A ein affiner Raum mit Richtungs-VRm V der Dimension n. (a) Sei B die Menge aller Basen von V. Ein Paar K := (O, B) A B heißt affines Koordinatensystem, wobei O der
T := {σ S 4 σ 3 = Id}. a) Es seien V ein Vektorraum und Φ ein Endomorphismus von V, sodass
 I. a) Es sei (G, ) eine abelsche Gruppe mit neutralem Element e G. Zeigen Sie, dass U := {g G g 3 = e G } eine Untergruppe von G ist. b) In der symmetrischen Gruppe S 4 definieren wir analog zu a) die
I. a) Es sei (G, ) eine abelsche Gruppe mit neutralem Element e G. Zeigen Sie, dass U := {g G g 3 = e G } eine Untergruppe von G ist. b) In der symmetrischen Gruppe S 4 definieren wir analog zu a) die
a b Q = b a 0 ) existiert ein Element p Q, so dass gilt: q 1 q 2 = 2 b 1 b 2 a 1 b 2 a 2 b 1 a 1 a 2 b 1 b 2 a 1 b 2 a 2 b 1 a b p = 1 det(q) C 2 2,
 Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
Wiederholungsserie II
 Lineare Algebra II D-MATH, FS 205 Prof. Richard Pink Wiederholungsserie II. Zeige durch Kopfrechnen, dass die folgende reelle Matrix invertierbar ist: 205 2344 234 990 A := 224 423 990 3026 230 204 9095
Lineare Algebra II D-MATH, FS 205 Prof. Richard Pink Wiederholungsserie II. Zeige durch Kopfrechnen, dass die folgende reelle Matrix invertierbar ist: 205 2344 234 990 A := 224 423 990 3026 230 204 9095
24. Projektive Geometrie
 24. Projektive Geometrie 24.1. Projektive Räume Zweck: Störende Ausnahmefälle der affinen Geometrie beseitigen durch geschickte Erweiterung affiner Räume zu sogenannten projektiven Räumen, wo die Ausnahmen
24. Projektive Geometrie 24.1. Projektive Räume Zweck: Störende Ausnahmefälle der affinen Geometrie beseitigen durch geschickte Erweiterung affiner Räume zu sogenannten projektiven Räumen, wo die Ausnahmen
Tutorium 7. Definition. Sei V ein C-Vektorraum. Eine Abbildung, : V V C heißt komplexes Skalarprodukt : det F k > 0 mit F k := (f i,j ) C k k
 Skalarprodukte Tutorium 7 Bemerkung. Für jeden komplexen Vektorraum V mit dim V und jede komplexe Bilinearform P auf V findet man einen Vektor v mit P (v, v) =. Es gibt also keine positiv definite Bilinearformen
Skalarprodukte Tutorium 7 Bemerkung. Für jeden komplexen Vektorraum V mit dim V und jede komplexe Bilinearform P auf V findet man einen Vektor v mit P (v, v) =. Es gibt also keine positiv definite Bilinearformen
Hinweis: Die Klausur Lineare Algebra 2 für die Fachrichtung Informatik besteht aus den Aufgaben 2.1 bis 2.4.
 Hinweis: Die Klausur Lineare Algebra 2 für die Fachrichtung Informatik besteht aus den Aufgaben 2.1 bis 2.4. Aufgabe 2.1 (8 Punkte) Es sei K ein Körper, n N, V ein 2n-dimensionaler K -Vektorraum und U
Hinweis: Die Klausur Lineare Algebra 2 für die Fachrichtung Informatik besteht aus den Aufgaben 2.1 bis 2.4. Aufgabe 2.1 (8 Punkte) Es sei K ein Körper, n N, V ein 2n-dimensionaler K -Vektorraum und U
Lineare Algebra II (NAWI) SS2014 Übungsblatt 1
 Lineare Algebra II (NAWI) SS2014 Übungsblatt 1 Aufgabe 1. Welche der folgenden Abbildungen sind Sesquilinearformen oder Bilinearformen? Welche davon sind Skalarprodukte? (a) B 1 : R R R, (x, y) xy (b)
Lineare Algebra II (NAWI) SS2014 Übungsblatt 1 Aufgabe 1. Welche der folgenden Abbildungen sind Sesquilinearformen oder Bilinearformen? Welche davon sind Skalarprodukte? (a) B 1 : R R R, (x, y) xy (b)
Lösungsskizzen zur Klausur zur Linearen Algebra II. Definitionen
 Technische Universität Berlin Sommersemester 2008 Institut für Mathematik 18 Juli 2008 Prof Dr Stefan Felsner Andrea Hoffkamp Lösungsskizzen zur Klausur zur Linearen Algebra II Aufgabe 1 (1+1+1 Punkte)
Technische Universität Berlin Sommersemester 2008 Institut für Mathematik 18 Juli 2008 Prof Dr Stefan Felsner Andrea Hoffkamp Lösungsskizzen zur Klausur zur Linearen Algebra II Aufgabe 1 (1+1+1 Punkte)
10 Unitäre Vektorräume
 10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
3 Bilinearform, Basen und Matrizen
 Lineare Algebra II 2. Oktober 2013 Mitschrift der Vorlesung Lineare Algebra II im SS 2013 bei Prof. Peter Littelmann von Dario Antweiler an der Universität zu Köln. Kann Fehler enthalten. Veröentlicht
Lineare Algebra II 2. Oktober 2013 Mitschrift der Vorlesung Lineare Algebra II im SS 2013 bei Prof. Peter Littelmann von Dario Antweiler an der Universität zu Köln. Kann Fehler enthalten. Veröentlicht
a) Ein Gruppenhomomorphismus von G nach H ist eine Abbildung Φ : G H, sodass für alle g 1, g 2 G die Gleichung Φ(g 1 g 2 ) = Φ(g 1 ) Φ(g 2 )
 I. (4 Punkte) Es seien (G, ) eine Gruppe mit neutralem Element e G und (H, ) eine weitere Gruppe. a) Geben Sie die Definition eines Gruppenhomomorphismus Φ : G H an und beweisen Sie, dass für solch einen
I. (4 Punkte) Es seien (G, ) eine Gruppe mit neutralem Element e G und (H, ) eine weitere Gruppe. a) Geben Sie die Definition eines Gruppenhomomorphismus Φ : G H an und beweisen Sie, dass für solch einen
Musterlösungen zur Linearen Algebra II Hauptklausur
 Musterlösungen zur Linearen Algebra II Hauptklausur Aufgabe. Q ist unitär genau dann, wenn gilt Q Q = I n. Daraus folgt, dass a) und c) richtig sind. Die -Matrix A := (i) zeigt, dass i.a. A A t, d.h. b)
Musterlösungen zur Linearen Algebra II Hauptklausur Aufgabe. Q ist unitär genau dann, wenn gilt Q Q = I n. Daraus folgt, dass a) und c) richtig sind. Die -Matrix A := (i) zeigt, dass i.a. A A t, d.h. b)
Klausur zur Vorlesung Lineare Algebra II, SoSe 2016,
 Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Ferienkurs zur Linearen Algebra Bilinearformen, Euklidische Vektorräume und Endomorphismen
 Technische Universität München Department of Physics Ferienkurs zur Linearen Algebra Bilinearformen, Euklidische Vektorräume und Endomorphismen Freitag, 16.03.2012 Sascha Frölich Ferienkurs Lin. Alg. -
Technische Universität München Department of Physics Ferienkurs zur Linearen Algebra Bilinearformen, Euklidische Vektorräume und Endomorphismen Freitag, 16.03.2012 Sascha Frölich Ferienkurs Lin. Alg. -
Universität Bielefeld Sommersemester Lineare Algebra 2 Übungsblatt 1
 Übungsblatt 1 Abgabe bis 10:00 Uhr am Donnerstag, den 19. April 2018, im Postfach Ihrer Tutorin bzw. Ihres Tutors. Es sei K ein beliebiger Körper. Seien V und W endlich-dimensionale K-Vektorräume, mit
Übungsblatt 1 Abgabe bis 10:00 Uhr am Donnerstag, den 19. April 2018, im Postfach Ihrer Tutorin bzw. Ihres Tutors. Es sei K ein beliebiger Körper. Seien V und W endlich-dimensionale K-Vektorräume, mit
1 Die Jordansche Normalform
 Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 4/5 A Die Jordansche Normalform Vierter Tag (9.03.205) Im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme
Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 4/5 A Die Jordansche Normalform Vierter Tag (9.03.205) Im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme
a) Zeigen Sie, dass ϕ genau dann ein Gruppenhomomorphismus ist, wenn die Verknüpfung
 Aufgabe (8 Punkte) Es sei (G, ) eine Gruppe und ϕ: G G die Abbildung, die für jedes g G durch ϕ(g) = g g =: g gegeben ist. a) Zeigen Sie, dass ϕ genau dann ein Gruppenhomomorphismus ist, wenn die Verknüpfung
Aufgabe (8 Punkte) Es sei (G, ) eine Gruppe und ϕ: G G die Abbildung, die für jedes g G durch ϕ(g) = g g =: g gegeben ist. a) Zeigen Sie, dass ϕ genau dann ein Gruppenhomomorphismus ist, wenn die Verknüpfung
1. Übungsblatt: Lineare Algebra II Abgabe: 24./ in den Übungsgruppen
 Hannover, den 0. April 2006. Übungsblatt: Lineare Algebra II Abgabe: 24./25.4.2006 in den Übungsgruppen ( ) 2 5 a) Zeigen Sie, dass A = und B = 2 ( 7 6 invertierbare Matrix T an mit T AT = B. b) Zeigen
Hannover, den 0. April 2006. Übungsblatt: Lineare Algebra II Abgabe: 24./25.4.2006 in den Übungsgruppen ( ) 2 5 a) Zeigen Sie, dass A = und B = 2 ( 7 6 invertierbare Matrix T an mit T AT = B. b) Zeigen
Lineare Algebra II (SS 13)
 Lineare Algebra II (SS 13) Bernhard Hanke Universität Augsburg 03.07.2013 Bernhard Hanke 1 / 16 Selbstadjungierte Endomorphismen und der Spektralsatz Definition Es sei (V,, ) ein euklidischer oder unitärer
Lineare Algebra II (SS 13) Bernhard Hanke Universität Augsburg 03.07.2013 Bernhard Hanke 1 / 16 Selbstadjungierte Endomorphismen und der Spektralsatz Definition Es sei (V,, ) ein euklidischer oder unitärer
Kontrollfragen und Aufgaben zur 3. Konsultation
 1 Technische Universität Ilmenau Fakultät für Mathematik und Naturwissenschaften Institut für Mathematik Prof. Dr. Michael Stiebitz Kontrollfragen und Aufgaben zur 3. Konsultation Termin: Ort: Determinante
1 Technische Universität Ilmenau Fakultät für Mathematik und Naturwissenschaften Institut für Mathematik Prof. Dr. Michael Stiebitz Kontrollfragen und Aufgaben zur 3. Konsultation Termin: Ort: Determinante
Analytische Geometrie
 21 Vorlesungen über Analytische Geometrie für Lehramtstudierende der Schulformen Grund-, Mittel- und Realschule Jens Jordan Universität Würzburg, Wintersemster 2015/16 Hier kommt noch ein schönes Bildchen
21 Vorlesungen über Analytische Geometrie für Lehramtstudierende der Schulformen Grund-, Mittel- und Realschule Jens Jordan Universität Würzburg, Wintersemster 2015/16 Hier kommt noch ein schönes Bildchen
43911: Lineare Algebra/Geometrie Prüfungstermin Herbst 2015 Lösungsvorschlag
 Dr. Erwin Schörner 49: Lineare Algebra/Geometrie Prüfungstermin Herbst 5 Lösungsvorschlag I.. a Die in Abhängigkeit vom Parameter t R für t t A t t t R und b R t + t t + t zu betrachtende Menge F t { x
Dr. Erwin Schörner 49: Lineare Algebra/Geometrie Prüfungstermin Herbst 5 Lösungsvorschlag I.. a Die in Abhängigkeit vom Parameter t R für t t A t t t R und b R t + t t + t zu betrachtende Menge F t { x
Aufgabe I.1 (4 Punkte) Gegeben seien die Matrix H := und die Menge L := {A R 4 4 A HA = H} Zeigen Sie:
 Aufgabe I (4 Punkte Gegeben seien die Matrix und die Menge Zeigen Sie: H := L := {A R 4 4 A HA = H} a L ist bezüglich der Matrizenmultiplikation eine Gruppe b Die Matrizen der Form ( E O, O B wobei E R
Aufgabe I (4 Punkte Gegeben seien die Matrix und die Menge Zeigen Sie: H := L := {A R 4 4 A HA = H} a L ist bezüglich der Matrizenmultiplikation eine Gruppe b Die Matrizen der Form ( E O, O B wobei E R
Proseminar Lineare Algebra II, SS 11. Blatt
 Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
Lineare Algebra II 8. Übungsblatt
 Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Klausurenkurs zum Staatsexamen (SS 2016): Lineare Algebra und analytische Geometrie 6
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 6): Lineare Algebra und analytische Geometrie 6 6. (Herbst, Thema, Aufgabe 4) Der Vektorraum R 4 sei mit dem Standard Skalarprodukt versehen. Der Unterraum
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 6): Lineare Algebra und analytische Geometrie 6 6. (Herbst, Thema, Aufgabe 4) Der Vektorraum R 4 sei mit dem Standard Skalarprodukt versehen. Der Unterraum
5.3 Typen und Klassifikation affiner Abbildungen
 53 Typen und Klassifikation affiner Abbildungen Definition 531 Sei A ein AR und Aff(A) die Gruppe der Affinitäten von A τ Aff(A) heißt Translation falls p, q A gilt: pτ(p) = qτ(q) Der dann von der Wahl
53 Typen und Klassifikation affiner Abbildungen Definition 531 Sei A ein AR und Aff(A) die Gruppe der Affinitäten von A τ Aff(A) heißt Translation falls p, q A gilt: pτ(p) = qτ(q) Der dann von der Wahl
Lineare Algebra I Ferienblatt
 Wintersemester 09/0 Prof. Dr. Frank-Olaf Schreyer Dr. Janko Boehm Lineare Algebra I Ferienblatt. Sei, das Euklidische Skalarprodukt auf R. Das Kreuzprodukt a b von Vektoren a, b R ist durch die Formel
Wintersemester 09/0 Prof. Dr. Frank-Olaf Schreyer Dr. Janko Boehm Lineare Algebra I Ferienblatt. Sei, das Euklidische Skalarprodukt auf R. Das Kreuzprodukt a b von Vektoren a, b R ist durch die Formel
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 42 Normale Endomorphismen Nach Satz 34.1 besitzt eine Isometrie über C eine Orthonormalbasis aus Eigenvektoren
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 42 Normale Endomorphismen Nach Satz 34.1 besitzt eine Isometrie über C eine Orthonormalbasis aus Eigenvektoren
3 Vektorräume abstrakt
 Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
7 Lineare Abbildungen und Skalarprodukt
 Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
Übungen zur Vorlesung Lineare Algebra II, SoSe 2016, Blatt 12
 Übungen zur Vorlesung Lineare Algebra II, SoSe 2016, Blatt 12 Schriftliche Aufgaben Aufgabe 1. Sei A M(n n, C). Zeigen Sie: (1) exp(a) ist invertierbar mit exp(a) 1 = exp( A). (2) Ist A M(n n, C) selbstadjungiert
Übungen zur Vorlesung Lineare Algebra II, SoSe 2016, Blatt 12 Schriftliche Aufgaben Aufgabe 1. Sei A M(n n, C). Zeigen Sie: (1) exp(a) ist invertierbar mit exp(a) 1 = exp( A). (2) Ist A M(n n, C) selbstadjungiert
4 Lineare Abbildungen Basisdarstellungen
 4 Lineare Abbildungen Basisdarstellungen (4.1) Seien V,W endlich dimensionale K-Vektorräume, und sei T : V W linear. Sei {v 1,...,v } Basis von V und {w 1,...,w M } Basis von W. Sei T (v j ) = M a kj w
4 Lineare Abbildungen Basisdarstellungen (4.1) Seien V,W endlich dimensionale K-Vektorräume, und sei T : V W linear. Sei {v 1,...,v } Basis von V und {w 1,...,w M } Basis von W. Sei T (v j ) = M a kj w
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 6
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 6 6. (Herbst, Thema, Aufgabe 4) Der Vektorraum R 4 sei mit dem Standard Skalarprodukt versehen. Der Unterraum
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 6 6. (Herbst, Thema, Aufgabe 4) Der Vektorraum R 4 sei mit dem Standard Skalarprodukt versehen. Der Unterraum
Lineare Algebra II 11. Übungsblatt
 Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
Lösungsvorschläge zur Klausur. Lineare Algebra, Herbst 2010
 Lösungsvorschläge zur Klausur Lineare Algebra, Herbst 200 I. Es seien n eine natürliche Zahl, M = {,..., n} N und S n die Gruppe der Permutationen der Menge M. Zeigen Sie: a) Für jedes a M ist H a := {σ
Lösungsvorschläge zur Klausur Lineare Algebra, Herbst 200 I. Es seien n eine natürliche Zahl, M = {,..., n} N und S n die Gruppe der Permutationen der Menge M. Zeigen Sie: a) Für jedes a M ist H a := {σ
43911: Lineare Algebra/Geometrie Prüfungstermin Frühjahr 2015 Lösungsvorschlag
 Dr. Erwin Schörner 439: Lineare Algebra/Geometrie Prüfungstermin Frühjahr 5 Lösungsvorschlag I.. Für n N mit n ist das inhomogene lineare Gleichungssystem in den n Unbekannten x,..., x n mit den n Gleichungen
Dr. Erwin Schörner 439: Lineare Algebra/Geometrie Prüfungstermin Frühjahr 5 Lösungsvorschlag I.. Für n N mit n ist das inhomogene lineare Gleichungssystem in den n Unbekannten x,..., x n mit den n Gleichungen
Klausurenkurs zum Staatsexamen (WS 2016/17): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 6/7): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 6/7): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Tutorium 4. 1 Bilinearformen. Definition. Seien U, V, W Vektorräume. Eine Abbildung Φ : V W U heißt bilinear: Bemerkung. Dies ist äquivalent zu:
 1 Bilinearformen Tutorium 4 Definition. Seien U, V, W Vektorräume. Eine Abbildung Φ : V W U heißt bilinear: Φ(αv + w, x) = α Φ(v, x) + Φ(w, x) und Φ(v, βx + y) = β Φ(v, x) + Φ(v, y) Bemerkung. Dies ist
1 Bilinearformen Tutorium 4 Definition. Seien U, V, W Vektorräume. Eine Abbildung Φ : V W U heißt bilinear: Φ(αv + w, x) = α Φ(v, x) + Φ(w, x) und Φ(v, βx + y) = β Φ(v, x) + Φ(v, y) Bemerkung. Dies ist
Kontrollfragen und Aufgaben zur 4. Konsultation
 1 Technische Universität Ilmenau Fakultät für Mathematik und Naturwissenschaften Institut für Mathematik Dr. Jens Schreyer und Prof. Dr. Michael Stiebitz Kontrollfragen und Aufgaben zur 4. Konsultation
1 Technische Universität Ilmenau Fakultät für Mathematik und Naturwissenschaften Institut für Mathematik Dr. Jens Schreyer und Prof. Dr. Michael Stiebitz Kontrollfragen und Aufgaben zur 4. Konsultation
10. Übung zur Linearen Algebra II -
 0. Übung zur Linearen Algebra II - Lösungen Kommentare an Hannes.Klarner@Fu-Berlin.de FU Berlin. SS 00. Aufgabe 7 Der ( linearen ) Abbildung ϕ : R R sei bzgl. der kanonischen Basis die Matrix zugeordnet.
0. Übung zur Linearen Algebra II - Lösungen Kommentare an Hannes.Klarner@Fu-Berlin.de FU Berlin. SS 00. Aufgabe 7 Der ( linearen ) Abbildung ϕ : R R sei bzgl. der kanonischen Basis die Matrix zugeordnet.
Musterlösungen zur Linearen Algebra II Übungsklausur
 Musterlösungen zur Linearen Algebra II Übungsklausur Aufgabe. Sei A R 3 3. Welche der folgenden Aussagen sind richtig? a Ist det(a =, dann ist A eine orthogonale Matrix. b Ist A eine orthogonale Matrix,
Musterlösungen zur Linearen Algebra II Übungsklausur Aufgabe. Sei A R 3 3. Welche der folgenden Aussagen sind richtig? a Ist det(a =, dann ist A eine orthogonale Matrix. b Ist A eine orthogonale Matrix,
Musterlösung der Klausur zur linearen Algebra II
 David Blottière SS 7 Patrick Schützdeller Universität Paderborn Julia Sauter Musterlösung der Klausur zur linearen Algebra II Aufgabe 1 Bestimmen Sie Jordan-Normalformen der folgenden Matrizen, und schreiben
David Blottière SS 7 Patrick Schützdeller Universität Paderborn Julia Sauter Musterlösung der Klausur zur linearen Algebra II Aufgabe 1 Bestimmen Sie Jordan-Normalformen der folgenden Matrizen, und schreiben
Orthonormalisierung. ein euklidischer bzw. unitärer Vektorraum. Wir setzen
 Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
5.4 Affine Abbildungen in C 2 und R 2
 5.4 Affine Abbildungen in C 2 und R 2 Notation. Wir erinnern an die affine Ähnlichkeit von Matrizen (5.3.8): L 1, L 1 AM n (K). Dann: L 1 a L 2 falls C AGL n (K) mit C 1 L 2 C = L 1. Die aus 3.2.9 bekannte
5.4 Affine Abbildungen in C 2 und R 2 Notation. Wir erinnern an die affine Ähnlichkeit von Matrizen (5.3.8): L 1, L 1 AM n (K). Dann: L 1 a L 2 falls C AGL n (K) mit C 1 L 2 C = L 1. Die aus 3.2.9 bekannte
Steilkurs Lineare Algebra 1 einige wichtige Stationen
 Steilkurs Lineare Algebra 1 einige wichtige Stationen Für einen Körper K ist ein K-Vektorraum V eine Menge mit einer kommutativen und assoziativen Verknüpfung + : V V V, für die es ein neutrales Element
Steilkurs Lineare Algebra 1 einige wichtige Stationen Für einen Körper K ist ein K-Vektorraum V eine Menge mit einer kommutativen und assoziativen Verknüpfung + : V V V, für die es ein neutrales Element
Einige Lösungsvorschläge für die Klausur zur Vorlesung
 Prof Klaus Mohnke Institut für Mathematik Einige Lösungsvorschläge für die Klausur zur Vorlesung Lineare Algebra und analtische Geometrie II* - SS 7 Aufgabe Im R mit dem Standardskalarprodukt ist die folgende
Prof Klaus Mohnke Institut für Mathematik Einige Lösungsvorschläge für die Klausur zur Vorlesung Lineare Algebra und analtische Geometrie II* - SS 7 Aufgabe Im R mit dem Standardskalarprodukt ist die folgende
4.4 Hermitesche Formen
 44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
2. Dezember Lineare Algebra II. Christian Ebert & Fritz Hamm. Skalarprodukt, Norm, Metrik. Matrizen. Lineare Abbildungen
 Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Lineare Algebra für Physiker 11. Übungsblatt
 Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Lineare Algebra II. Inhalt und Begriffe. Lineare Algebra II p. 1
 Lineare Algebra II Inhalt und Begriffe Lineare Algebra II p. 1 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen Algebra... Lineare Algebra II p. 2 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen
Lineare Algebra II Inhalt und Begriffe Lineare Algebra II p. 1 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen Algebra... Lineare Algebra II p. 2 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema, Aufgabe 4) Im R seien die beiden Ebenen E : 6 x + 4 y z = und E : + s + t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema, Aufgabe 4) Im R seien die beiden Ebenen E : 6 x + 4 y z = und E : + s + t 4 gegeben.
Tagesablauf. Allgemeine Organisation. Programm des Kompaktseminars
 Kompaktseminar Werbellinsee Sept. 2008 1 Tagesablauf 9:00 Frühstück 9:30-13:00 Erste Sitzung (mit Pausen nach Bedarf) 13:00 Mittagessen 14:30-19:00 Zweite Sitzung (mit Pausen nach Bedarf) 19:00 Abendessen
Kompaktseminar Werbellinsee Sept. 2008 1 Tagesablauf 9:00 Frühstück 9:30-13:00 Erste Sitzung (mit Pausen nach Bedarf) 13:00 Mittagessen 14:30-19:00 Zweite Sitzung (mit Pausen nach Bedarf) 19:00 Abendessen
Klausur zu. Lineare Algebra II. Viel Erfolg! Fachbereich Mathematik WS 2012/13 Dr. habil. Matthias Schneider. Bonus Note. Aufgabe
 Klausur zu Lineare Algebra II Fachbereich Mathematik WS 0/3 Dr. habil. Matthias Schneider Aufgabe 3 4 5 6 7 Bonus Note Punktzahl 4 3 3 3 3 0 erreichte Punktzahl Es sind keine Hilfsmittel zugelassen. Die
Klausur zu Lineare Algebra II Fachbereich Mathematik WS 0/3 Dr. habil. Matthias Schneider Aufgabe 3 4 5 6 7 Bonus Note Punktzahl 4 3 3 3 3 0 erreichte Punktzahl Es sind keine Hilfsmittel zugelassen. Die
Lösungsvorschlag zur LA-Klausur vom
 I. (4 Punkte) Lösungsvorschlag zur LA-Klausur vom 7.03.008 Es sei M eine Menge mit zwei Verknüpfungen und. Weiter gebe es ein Element e M, das sowohl für als auch für neutrales Element ist. Schließlich
I. (4 Punkte) Lösungsvorschlag zur LA-Klausur vom 7.03.008 Es sei M eine Menge mit zwei Verknüpfungen und. Weiter gebe es ein Element e M, das sowohl für als auch für neutrales Element ist. Schließlich
5.3 Typen und Klassifikation affiner Abbildungen
 53 Typen und Klassifikation affiner Abbildungen Definition 531 Sei A ein AR und Aff(A) die Gruppe der Affinitäten von A τ Aff(A) heißt Translation falls p, q A gilt: pτ(p) = qτ(q) Der dann von der Wahl
53 Typen und Klassifikation affiner Abbildungen Definition 531 Sei A ein AR und Aff(A) die Gruppe der Affinitäten von A τ Aff(A) heißt Translation falls p, q A gilt: pτ(p) = qτ(q) Der dann von der Wahl
Skalarprodukte. Kapitel Bilinearformen
 Kapitel 11 Skalarprodukte Das bekannte Skalarprodukt auf dem n dimensionalen Euklidischen Raum R n ist ein Spezialfall einer für viele Bereiche der linearen Algebra und der Funktionalanalysis außerordentlich
Kapitel 11 Skalarprodukte Das bekannte Skalarprodukt auf dem n dimensionalen Euklidischen Raum R n ist ein Spezialfall einer für viele Bereiche der linearen Algebra und der Funktionalanalysis außerordentlich
5.4 Affine Abbildungen in C 2 und R 2
 5.4 Affine Abbildungen in C 2 und R 2 Notation. Wir erinnern an die affine Ähnlichkeit von Matrizen (5.3.(ii)): L, L n (K). Dann: L a L 2 falls C AGL n (K) mit C L 2 C = L. Die aus 3.2.9 bekannte übliche
5.4 Affine Abbildungen in C 2 und R 2 Notation. Wir erinnern an die affine Ähnlichkeit von Matrizen (5.3.(ii)): L, L n (K). Dann: L a L 2 falls C AGL n (K) mit C L 2 C = L. Die aus 3.2.9 bekannte übliche
Modulteilprüfung Geometrie (BaM-GS), Probeklausur
 HRZ-Benutzername: Modulteilprüfung Geometrie (BaM-GS), Probeklausur Dr. Patrik Hubschmid // SoSe 2013, 4. Juli 2013 Kontrollieren Sie, ob Sie alle Blätter (8 einschlieÿlich zweier Deckblätter) erhalten
HRZ-Benutzername: Modulteilprüfung Geometrie (BaM-GS), Probeklausur Dr. Patrik Hubschmid // SoSe 2013, 4. Juli 2013 Kontrollieren Sie, ob Sie alle Blätter (8 einschlieÿlich zweier Deckblätter) erhalten
Kapitel V. Räumliche Geometrie. 1. Drehungen
 Kapitel V Räumliche Geometrie 1. Drehungen Punkte in R 3 sind durch 3 Koordinaten (x 1,x 2,x 3 ) bestimmt. Wir benützen die Matrix-Schreibweise x 1 x = x 2 x 3 Eine Drehung um die Koordinatenachse x 3
Kapitel V Räumliche Geometrie 1. Drehungen Punkte in R 3 sind durch 3 Koordinaten (x 1,x 2,x 3 ) bestimmt. Wir benützen die Matrix-Schreibweise x 1 x = x 2 x 3 Eine Drehung um die Koordinatenachse x 3
1 Analytische Geometrie und Grundlagen
 $Id: vektor.tex,v 1.44 2018/05/17 14:11:13 hk Exp $ 1 Analytische Geometrie und Grundlagen 1.6 Bewegungen und Kongruenzbegriffe Wir untersuchen gerade die Spiegelung an einer Hyperebene h R d. Ist ein
$Id: vektor.tex,v 1.44 2018/05/17 14:11:13 hk Exp $ 1 Analytische Geometrie und Grundlagen 1.6 Bewegungen und Kongruenzbegriffe Wir untersuchen gerade die Spiegelung an einer Hyperebene h R d. Ist ein
HM II Tutorium 7. Lucas Kunz. 5. Juni 2018
 HM II Tutorium 7 Lucas Kunz 5. Juni 2018 Inhaltsverzeichnis 1 Theorie 2 1.1 Orthogonalität und Orthonormalbasen.................... 2 1.2 Orthogonalraum................................. 2 1.3 Projektoren...................................
HM II Tutorium 7 Lucas Kunz 5. Juni 2018 Inhaltsverzeichnis 1 Theorie 2 1.1 Orthogonalität und Orthonormalbasen.................... 2 1.2 Orthogonalraum................................. 2 1.3 Projektoren...................................
4 Orthogonale Endormorphismen
 4 Orthogonale Endormorphismen Frage: Bei welchen Abbildungen R R bzw. R 3 R 3 bleibt der Abstand zwischen zwei Punkten erhalten? Für α R setzen wir cosα sin α D(α) = und S(α) := sin α cosα ( cos α sin
4 Orthogonale Endormorphismen Frage: Bei welchen Abbildungen R R bzw. R 3 R 3 bleibt der Abstand zwischen zwei Punkten erhalten? Für α R setzen wir cosα sin α D(α) = und S(α) := sin α cosα ( cos α sin
Institut für Analysis und Scientific Computing E. Weinmüller WS 2016
 Institut für Analysis und Scientific Computing TU Wien E. Weinmüller WS 26 L I N E A R E A L G E B R A F Ü R T P H, U E (3.64) 2. Haupttest (FR, 2..27) (mit Lösung ) Ein einfacher Taschenrechner ist erlaubt.
Institut für Analysis und Scientific Computing TU Wien E. Weinmüller WS 26 L I N E A R E A L G E B R A F Ü R T P H, U E (3.64) 2. Haupttest (FR, 2..27) (mit Lösung ) Ein einfacher Taschenrechner ist erlaubt.
Basisprüfung. 18. August 2015
 Lineare Algebra I/II D-MATH, HS 4/FS 5 Prof Richard Pink Basisprüfung 8 August 25 [6 Punkte] Betrachte den reellen Vektorraum R 3 zusammen mit dem Standardskalarprodukt, und die Vektoren 9 3 v := 6, v
Lineare Algebra I/II D-MATH, HS 4/FS 5 Prof Richard Pink Basisprüfung 8 August 25 [6 Punkte] Betrachte den reellen Vektorraum R 3 zusammen mit dem Standardskalarprodukt, und die Vektoren 9 3 v := 6, v
Determinante und Inverse
 Vorzeigeaufgaben: Determinante und Inverse Bestimmen Sie für welche a R die folgende Matrix invertierbar ist und berechnen Sie deren Inverse: A = a cos(x) sin(x) a sin(x) cos(x) Bestimmen Sie ob folgende
Vorzeigeaufgaben: Determinante und Inverse Bestimmen Sie für welche a R die folgende Matrix invertierbar ist und berechnen Sie deren Inverse: A = a cos(x) sin(x) a sin(x) cos(x) Bestimmen Sie ob folgende
Eine Affinität α eines euklidischen Raumes heißt eine Bewegung, wenn sie Abstände (und damit auch Winkel) erhält, wenn also für alle Punkte X, Y gilt:
 5 Zur Geometrie euklidischer Bewegungen 5.1 Bewegungen Eine Affinität α eines euklidischen Raumes heißt eine Bewegung, wenn sie Abstände (und damit auch Winkel) erhält, wenn also für alle Punkte X, Y gilt:
5 Zur Geometrie euklidischer Bewegungen 5.1 Bewegungen Eine Affinität α eines euklidischen Raumes heißt eine Bewegung, wenn sie Abstände (und damit auch Winkel) erhält, wenn also für alle Punkte X, Y gilt:
Klausur zur Vorlesung Lineare Algebra B im SS 2002 an der Universität Hannover
 Dozent: Prof. Dr. Wolfgang Ebeling Übungsleiter: Dr. Detlef Wille Klausur zur Vorlesung Lineare Algebra B im SS an der Universität Hannover Joachim Selke 9. Februar Lineare Algebra B SS Klausur zur Vorlesung
Dozent: Prof. Dr. Wolfgang Ebeling Übungsleiter: Dr. Detlef Wille Klausur zur Vorlesung Lineare Algebra B im SS an der Universität Hannover Joachim Selke 9. Februar Lineare Algebra B SS Klausur zur Vorlesung
1 Analytische Geometrie und Grundlagen
 Mathematische Probleme, SS 28 Dienstag 29.5 $Id: vektor.tex,v.46 28/5/29 6:4: hk Exp $ Analytische Geometrie und Grundlagen.6 Bewegungen und Kongruenzbegriffe Am Ende der letzten Sitzung hatten wir bereits
Mathematische Probleme, SS 28 Dienstag 29.5 $Id: vektor.tex,v.46 28/5/29 6:4: hk Exp $ Analytische Geometrie und Grundlagen.6 Bewegungen und Kongruenzbegriffe Am Ende der letzten Sitzung hatten wir bereits
Analysis. Lineare Algebra
 Analysis Ableitung Ableitungsregeln totale und partielle Ableitung Extremwertbestimmung Integrale partielle Integration Substitution der Variablen Koordinatentransformationen Differentialgleichungen Lineare
Analysis Ableitung Ableitungsregeln totale und partielle Ableitung Extremwertbestimmung Integrale partielle Integration Substitution der Variablen Koordinatentransformationen Differentialgleichungen Lineare
Klausurenkurs zum Staatsexamen (WS 2013/14): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
1 Analytische Geometrie und Grundlagen
 $Id: vektor.tex,v 1.24 2017/05/18 11:18:04 hk Exp $ 1 Analytische Geometrie und Grundlagen 1.6 Bewegungen und Kongruenzbegriffe In diesem Abschnitt wollen wir die Automorphismengruppe der euklidischen
$Id: vektor.tex,v 1.24 2017/05/18 11:18:04 hk Exp $ 1 Analytische Geometrie und Grundlagen 1.6 Bewegungen und Kongruenzbegriffe In diesem Abschnitt wollen wir die Automorphismengruppe der euklidischen
Institut für Analysis und Scientific Computing E. Weinmüller WS 2017
 Institut für Analysis und Scientific Computing TU Wien E. Weinmüller WS 27 L I N E A R E A L G E B R A F Ü R T P H, U E (.64) 2. Haupttest (FR, 9..28) (mit Lösung ) Ein einfacher Taschenrechner ist erlaubt.
Institut für Analysis und Scientific Computing TU Wien E. Weinmüller WS 27 L I N E A R E A L G E B R A F Ü R T P H, U E (.64) 2. Haupttest (FR, 9..28) (mit Lösung ) Ein einfacher Taschenrechner ist erlaubt.
Unter einem reellen inneren Produktraum verstehen wir einen Vektorraum V über
 9 Innere Produkte In diesem Kapitel betrachten wir immer Vektorräume über dem Körper der reellen Zahlen R oder dem Körper der komplexen Zahlen C. Definition 9.1: Sei V ein Vektorraum über R. Ein inneres
9 Innere Produkte In diesem Kapitel betrachten wir immer Vektorräume über dem Körper der reellen Zahlen R oder dem Körper der komplexen Zahlen C. Definition 9.1: Sei V ein Vektorraum über R. Ein inneres
AUFGABENSAMMLUNG ZU VEKTORRECHNUNG FÜR USW
 AUFGABENSAMMLUNG ZU VEKTORRECHNUNG FÜR USW Lineare Gleichungssysteme Lösen Sie folgende Gleichungssysteme über R: a) x + x + x = 6x + x + x = 4 x x x = x 7x x = 7 x x = b) x + x 4x + x 4 = 9 x + 9x x x
AUFGABENSAMMLUNG ZU VEKTORRECHNUNG FÜR USW Lineare Gleichungssysteme Lösen Sie folgende Gleichungssysteme über R: a) x + x + x = 6x + x + x = 4 x x x = x 7x x = 7 x x = b) x + x 4x + x 4 = 9 x + 9x x x
2. Klausur zur Linearen Algebra II
 Technische Universität Dortmund Fakultät für Mathematik Platznummer: Sommersemester 7.9.7. Klausur zur Linearen Algebra II Name: Vorname: Matrikelnummer: Studiengang: Wichtige Informationen: Prüfen Sie
Technische Universität Dortmund Fakultät für Mathematik Platznummer: Sommersemester 7.9.7. Klausur zur Linearen Algebra II Name: Vorname: Matrikelnummer: Studiengang: Wichtige Informationen: Prüfen Sie
Institut für Analysis und Scientific Computing E. Weinmüller WS 2017
 Institut für Analysis und Scientific Computing TU Wien E. Weinmüller WS 7 L I N E A R E A L G E B R A F Ü R T P H, U E (.64). Haupttest (FR, 9..8) (mit Lösung ) Ein einfacher Taschenrechner ist erlaubt.
Institut für Analysis und Scientific Computing TU Wien E. Weinmüller WS 7 L I N E A R E A L G E B R A F Ü R T P H, U E (.64). Haupttest (FR, 9..8) (mit Lösung ) Ein einfacher Taschenrechner ist erlaubt.
Abschnitt 1. Jordan Normalform
 Abschnitt Jordan Normalform Beispiel & Eigenschaften λ λ λ λ 2 λ 2 λ 2 λ 3 Voraussetzung: χ zerfällt Dann: ex. Basis, s.d. Darstellungsmatrix Jordan-Form hat Minimalpolynom µ hat Faktor zu jedem EW in
Abschnitt Jordan Normalform Beispiel & Eigenschaften λ λ λ λ 2 λ 2 λ 2 λ 3 Voraussetzung: χ zerfällt Dann: ex. Basis, s.d. Darstellungsmatrix Jordan-Form hat Minimalpolynom µ hat Faktor zu jedem EW in
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 14. Übung: Woche vom (Lin.Alg.
 Übungsaufgaben 14. Übung: Woche vom 30. 1.-3. 2. 2017 (Lin.Alg. III): Heft Ü 3: 3.2.6.a,b,l,n; 3.2.12; 3.2.13; 5.4.1; 5.4.5.c; Hinweis 1: 3. Test (Integration, analyt. Geom.) ist seit 9.1. freigeschalten
Übungsaufgaben 14. Übung: Woche vom 30. 1.-3. 2. 2017 (Lin.Alg. III): Heft Ü 3: 3.2.6.a,b,l,n; 3.2.12; 3.2.13; 5.4.1; 5.4.5.c; Hinweis 1: 3. Test (Integration, analyt. Geom.) ist seit 9.1. freigeschalten
Klausur zur Vorlesung Lineare Algebra II
 Universität zu Köln Sommersemester 06 Mathematisches Institut 9. Juli 06 Prof. Dr. P. Littelmann Dr. Teodor Backhaus Klausur zur Vorlesung Lineare Algebra II Bearbeitungszeit 80 Minuten Bitte geben Sie
Universität zu Köln Sommersemester 06 Mathematisches Institut 9. Juli 06 Prof. Dr. P. Littelmann Dr. Teodor Backhaus Klausur zur Vorlesung Lineare Algebra II Bearbeitungszeit 80 Minuten Bitte geben Sie
8 Eigenwerttheorie I 8. EIGENWERTTHEORIE I 139. Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet:
 8. EIGENWERTTHEORIE I 139 8 Eigenwerttheorie I Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet: K[x] = Abb[N, K] = {P ; P = a n x n + a n 1 x n 1 + + a 0 ; a
8. EIGENWERTTHEORIE I 139 8 Eigenwerttheorie I Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet: K[x] = Abb[N, K] = {P ; P = a n x n + a n 1 x n 1 + + a 0 ; a
Klausurenkurs zum Staatsexamen (SS 2014): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Lösung zu Serie 18. Lineare Algebra D-MATH, HS Prof. Richard Pink
 Lineare Algebra D-MATH, HS 201 Prof. Richard Pink Lösung zu Serie 18 1. Sei V,, ein endlich-dimensionaler unitärer Vektorraum. Zeige, dass zu jeder Sesquilinearform f : V V C eine eindeutige lineare Abbildung
Lineare Algebra D-MATH, HS 201 Prof. Richard Pink Lösung zu Serie 18 1. Sei V,, ein endlich-dimensionaler unitärer Vektorraum. Zeige, dass zu jeder Sesquilinearform f : V V C eine eindeutige lineare Abbildung
6 Metrische Klassifikation der Quadriken
 6 Metrische Klassifikation der Quadriken A Wiederholung von Kap V, 5 Sei A = (a ij ) eine symmetrische n n Matrix. n x 1 q(x) := x t Ax = a ij x i x j, x =. i,j=1 ist dann ein quadratisches Polynom in
6 Metrische Klassifikation der Quadriken A Wiederholung von Kap V, 5 Sei A = (a ij ) eine symmetrische n n Matrix. n x 1 q(x) := x t Ax = a ij x i x j, x =. i,j=1 ist dann ein quadratisches Polynom in
Lineare Algebra II Zwischentest
 Lineare Algebra II Zwischentest Dr. Stephan Ehlen, Dr. Chris Jennings-Shaffer, Jonathan Schürr 14.06.18 Dieser Zwischentest besteht aus 7 Aufgaben und enthält insgesamt 12 Seiten. Sie haben für die Bearbeitung
Lineare Algebra II Zwischentest Dr. Stephan Ehlen, Dr. Chris Jennings-Shaffer, Jonathan Schürr 14.06.18 Dieser Zwischentest besteht aus 7 Aufgaben und enthält insgesamt 12 Seiten. Sie haben für die Bearbeitung
Institut für Analysis und Scientific Computing E. Weinmüller WS 2017
 Institut für Analysis und Scientific Computing TU Wien E. Weinmüller WS 7 L I N E A R E A L G E B R A F Ü R T P H, U E (.64). Haupttest (FR, 9..8) (mit Lösung ) Ein einfacher Taschenrechner ist erlaubt.
Institut für Analysis und Scientific Computing TU Wien E. Weinmüller WS 7 L I N E A R E A L G E B R A F Ü R T P H, U E (.64). Haupttest (FR, 9..8) (mit Lösung ) Ein einfacher Taschenrechner ist erlaubt.
Modulteilprüfung Geometrie (BaM-GS, L3M-RF)
 Modulteilprüfung Geometrie (BaM-GS, L3M-RF) Prof. Dr. Martin Möller SoSe 2011 // 05. Juli 2011 Kontrollieren Sie, ob Sie alle Blätter (12 einschließlich zweier Deckblätter) erhalten haben, und geben Sie
Modulteilprüfung Geometrie (BaM-GS, L3M-RF) Prof. Dr. Martin Möller SoSe 2011 // 05. Juli 2011 Kontrollieren Sie, ob Sie alle Blätter (12 einschließlich zweier Deckblätter) erhalten haben, und geben Sie
Lineare Algebra I/II LVA ,
 Lineare Algebra I/II LVA 401-1151-00,401-1152-00 Prof. G. Wüstholz, C. Fuchs Lösungen zur Basisprüfung, HS08/FS09 09.02.2010 1. a) (1 Punkt) Wir beginnen mit dem charakteristischen Polynom der Matrix A:
Lineare Algebra I/II LVA 401-1151-00,401-1152-00 Prof. G. Wüstholz, C. Fuchs Lösungen zur Basisprüfung, HS08/FS09 09.02.2010 1. a) (1 Punkt) Wir beginnen mit dem charakteristischen Polynom der Matrix A:
Probeklausur Lineare Algebra für Physiker
 Fachbereich Mathematik Prof. Dr. K. Grosse-Brauckmann D. Frisch Probeklausur Lineare Algebra für Physiker SS 8 26./27.6.27 Name:..................................... Vorname:.................................
Fachbereich Mathematik Prof. Dr. K. Grosse-Brauckmann D. Frisch Probeklausur Lineare Algebra für Physiker SS 8 26./27.6.27 Name:..................................... Vorname:.................................
VII.2. INNERE PRODUKTE 227
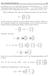 VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
