Musterlösung. Aufgaben zu Iterative Lösung Linearer Gleichungssysteme. Vordiplomskurs Numerische Methoden Sommer 2008

Beispiellösung Serie 7

D-MAVT FS 2014 K. Nipp A. Hiltebrand NUMERISCHE MATHEMATIK Beispiellösung Serie 7 1. a) Exakt: 0.005 1 1 1 0.005 1 ( 1 0 200-199 L = 200 1 Rückwärts einsetzen Lz = b : z 1 = 0.5, z 2 = 1 100 = 99 Rx =

4 Iterative Lösung Linearer Gleichungssysteme 4.1 Fixpunktiteration und Konvergenzsätze.

4 Iterative Lösung Linearer Gleichungssysteme 4.1 Fixpunktiteration und Konvergenzsätze. Wir betrachten das lineare Gleichungssystem der Form Ax = b; (4.1.1) mit A R n n reguläre Matrix und b R n gegeben,

Numerische Mathematik für Ingenieure (SoSe 2013)

Numerische Mathematik für Ingenieure (SoSe 2013) PD Dr(USA) Maria Charina Auszüge aus Vorlesungsfolien von Prof Joachim Stöckler werden verwendet Für die Bereitstellung dieses Materials und der Tex-Files

3. Lineare Gleichungssysteme

3. Lineare Gleichungssysteme 1 3.1. Problemstellung 2 3.2. Direkte Verfahren 3 3.3. Normen und Fehleranalyse 4 3.4. Iterative Verfahren 5 3.5. Konvergenz von linearen Iterationsverfahren 6 3.6. Gradienten-Verfahren

2. Lineare Gleichungssysteme: direkte und iterative Lösungsverfahren

2. Lineare Gleichungssysteme: direkte und iterative Lösungsverfahren Problem (P2): Löse Ax = b, A R n und b R. 2.1 Satz: Die folgenden Aussagen sind äquivalent: (i) Ax = b ist für jedes b eindeutig lösbar;

Musterlösung Serie 3

D-MAVT FS 0 K.Nipp NUMERISCHE MATHEMATIK Musterlösung Serie 3. a) T = (D + ωl) ( ωr + ( ω)d) A=[3 ; 3 ; 3]; D=diag(diag(A)); L=tril(A)-D; R=triu(A)-D; omega_vec=0.00:0.00:.999; rho=zeros(size(omega_vec));

5.3.5 Abstiegs & Gradientenverfahren

5.3 Iterative Lösungsverfahren für lineare Gleichungssysteme 5.3.5 Abstiegs & Gradientenverfahren Die bisher kennengelernten Iterationsverfahren zur Approximation von linearen Gleichungssystemen haben

Iterative Löser: Einführung

Iterative Löser: Einführung Im vergangenen Semester wurden folgende Löser für LGS betrachtet: LU-Zerlegung (mit und ohne Pivotisierung) QR-Zerlegung (Householder und Givens) Lösung beliebiger, regulärer,

Iterative Verfahren, Splittingmethoden

Iterative Verfahren, Splittingmethoden Theodor Müller 19. April 2005 Sei ein lineares Gleichungssystem der Form Ax = b b C n, A C n n ( ) gegeben. Es sind direkte Verfahren bekannt, die ein solches Gleichungssystem

Kapitel 2: Lineare Gleichungssysteme. 2.1 Motivation: Bildverarbeitung Sei B = (B(n, m)) ein N M stochastisches Feld mit ZVen

Kapitel 2: Lineare Gleichungssysteme 21 Motivation: Bildverarbeitung Sei B = (B(n, m)) ein N M stochastisches Feld mit ZVen B(n, m) : Ω {0,,255}, n = 1,,N, m = 1,,M dig Camera Realisierung von B η ist

Lineare Iterationsverfahren: Definitionen

Lineare Iterationsverfahren: Definitionen 1. Ein Lösungsverfahren zur Berechnung von Ax = b heißt iterativ, falls ausgehend von einem Startwert x eine Folge x k von Iterierten bestimmt wird. 2. Ein Iterationsverfahren

KAPITEL 1. Einleitung

KAPITEL 1 Einleitung Wir beschäftigen uns in dieser Vorlesung mit Verfahren aus der Numerischen linearen Algebra und insbesondere dem sogenannten Mehrgitterverfahren zur Lösung linearer Gleichungssysteme

Institut für Numerische Simulation der Universität Bonn Prof. Dr. Mario Bebendorf

Institut für Numerische Simulation der Universität Bonn Prof. Dr. Mario Bebendorf Praktikum im Sommersemester 2012 Programmierpraktikum numerische Algorithmen (P2E1) (Numerische Lösung der Wärmeleitungsgleichung)

D-MAVT NUMERISCHE MATHEMATIK FS 14 K. Nipp, A. Hiltebrand Lösung vom Test 2

D-MAVT NUMERISCHE MATHEMATIK FS 4 K Nipp, A Hiltebrand Lösung vom Test Sei A ( 3 3 ) a) Bestimmen Sie κ(a), die Kondition von A (in der -Norm): κ(a) b) Berechnen Sie den Spektralradius von A: ρ(a) 4 c)

Kapitel 3. Iterative Verfahren für LGS. 3.1 Der Banach sche Fixpunktsatz. Definition 3.1:

Kapitel 3 Iterative Verfahren für LGS 3 Der Banach sche Fixpunktsatz Sei A R n n invertierbar und das LGS A x b gegeben Ein iteratives Verfahren besteht aus einer Berechnungsvorschrift x (j+) F ( x (j))

III. Iterative Löser. III.1 Direkte Löser und ihre Nachteile. III.2 Klassische lineare Iterationsverfahren

III. Iterative Löser III.1 Direkte Löser und ihre Nachteile III.2 Klassische lineare Iterationsverfahren Typeset by FoilTEX 1 Erinnerung: Lineares Gleichungssystem bei FDM Diskretisierung einer linearen

Kapitel 8. Lineare Gleichungssysteme III: iterative Verfahren

Kapitel 8. Lineare Gleichungssysteme III: iterative Verfahren Inhalt: 8.1 Fixpunkt-Iteration 8.2 Verfahren der konjugierten Gradienten 8.3 Anwendungsbeispiel Numerische Mathematik I 323 Kap. 8: Lineare

38 Iterative Verfahren für lineare Gleichungssysteme

38 Iterative Verfahren für lineare Gleichungssysteme 38.1 Motivation Viele praktische Probleme führen auf sehr große lineare Gleichungssysteme, bei denen die Systemmatrix dünn besetzt ist, d. h. nur wenige

Klausur zu Grundlagen der Computermathematik

Prof. Dr. Klaus Höllig 14. Oktober 2010 Klausur zu Grundlagen der Computermathematik en Aufgabe 1 Geben Sie (ohne Beweis an, welche der folgenden Aussagen richtig und welche falsch sind. a Die Folge A

Klausur zu Grundlagen der Computermathematik

Prof. Dr. Klaus Höllig. März 11 Klausur zu Grundlagen der Computermathematik en Aufgabe 1 Geben Sie (ohne Beweis an, welche der folgenden Aussagen richtig und welche falsch sind. a Die Folge A n x/ A n

2. Geben Sie für das Jacobi-Verfahren eine scharfe a-priori Abschätzung für den Fehler. x (10) x p

Wiederholungsaufgaben Algorithmische Mathematik Sommersemester Prof. Dr. Beuchler Markus Burkow Übungsaufgaben Aufgabe. (Jacobi-Verfahren) Gegeben sei das lineare Gleichungssystem Ax b = für A =, b = 3.

Numerische Lineare Algebra

Numerische Lineare Algebra Vorlesung 11 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 2010 Prof. Dr. Klaus Höllig

Einführung in die numerische Mathematik

Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis

Lineare Gleichungssysteme

Lineare Gleichungssysteme Beispiel: Feder Masse System festes Ende Feder k 1 Masse m 1 k 2 m 2 k 3 m 3 k 4 festes Ende u 0 = 0 Federkraft y 1 Verschiebung u 1 y 2 u 2 y 3 u 3 y 4 u 4 = 0 Grundlagen der

Lineare Gleichungssysteme

Lineare Gleichungssysteme 4. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 17. März 2016 Lineare Gleichungssysteme 1 Wiederholung: Normen, Jacobi-Matrix,

Numerisches Rechnen. (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang. Institut für Geometrie und Praktische Mathematik RWTH Aachen

Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen

Konvergenz des Jacobi- und Gauß-Seidel-Verfahrens

Konvergenz des Jacobi- und Gauß-Seidel-Verfahrens Bachelor-Arbeit im -Fach Bachelorstudiengang Mathematik der Mathematisch-Naturwissenschaftlichen Fakultät der Christian-Albrechts-Universität zu Kiel vorgelegt

Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: b a 2 3a 1

Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche

Kapitel 6. Iterationsverfahren für lineare Gleichungssysteme

Kapitel 6 Iterationsverfahren für lineare Gleichungssysteme Falls n sehr groß ist und falls die Matrix A dünn besetzt ist (sparse), dann wählt man zur Lösung von Ax = b im Allgemeinen iterative Verfahren.

Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV Aufgabe N1 (LR-Zerlegung mit Pivotisierung) Gegeben seien R 3.

Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV 7.7.6 Aufgabe N (LR-Zerlegung mit Pivotisierung) Gegeben seien 6 8 A = 8 6 R und b = 6 R. a) Berechnen Sie die LR-Zerlegung von A mit Spaltenpivotisierung.

Kapitel 2: Lineare Gleichungssysteme. 2.1 Motivation: Bildverarbeitung Sei B = (B(n, m)) ein N M stochastisches Feld mit ZVen

Kapitel 2: Lineare Gleichungssysteme 2.1 Motivation: Bildverarbeitung Sei B = (B(n, m)) ein N M stochastisches Feld mit ZVen B(n, m) : Ω {0,...,255}, n = 1,...,N, m = 1,...,M. dig. Camera Realisierung

Übungsblatt 5 Musterlösung

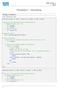MSE Mathe 4 SS Übungsblatt Musterlösung Lösung (Solution) Siehe MATLAB Codes function [x_new, it, rho] = jacobi (A, x_start, b, TOL, it_max) 3 % Set up all the quantities used during iteration 4 % Diagonal

Algorithmik kontinuierlicher Systeme

Algorithmik kontinuierlicher Systeme Iterative Verfahren (2/2) Ziel dieser Vorlesung Wie schnell können wir Gleichungssysteme lösen? O(n 3 ) LR- oder QR-Zerlegung: Immer anwendbar Standardverfahren Aber:

Begleitmaterial zur Vorlesung Numerik I

Begleitmaterial zur Vorlesung Numerik I Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik I 1 / 49 Inhalte der Numerik

2 Lineare Gleichungssysteme

2 Lineare Gleichungssysteme Wir betrachten das lineare Gleichungssystem Ax = b mit der n n-koeffizientenmatrix A und der rechten Seite b R n. Wir leiten zuerst eine Variante des Gauss-Algorithmus (LR-Zerlegung)

Musterlösungen zur Leistungsnachweisklausur vom Studiengang Informatik, Ingenieurinformatik, Lehramt

TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra

D-ITET, D-MATL Numerische Methoden SS 2006 Prof. R. Jeltsch. Musterlösung 6. x A 1 b. A 1 b A 1. x A ( A. gestört: x A 1 =

D-ITET, D-MATL Numerische Methoden SS 2006 Prof. R. Jeltsch Musterlösung 6 1. a b exakt: x = c Die Inverse von A lautet x = A 1 b x = A 1 b x A 1 b x A 1 b x A 1 b A x b x κ A b x b 3 1 A 1 = gestört:

Klausur Numerische Mathematik (für Elektrotechniker), 24. Februar 2016

Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.

MATLAB Ferienkurs WS 2010/2011

MATLAB Ferienkurs WS 2010/2011 Teil 4 von 6 Andreas Klimke, Matthias Wohlmuth Technische Universität München Fakultät Mathematik, Lehrstuhl für Numerische Mathematik Basier auf Kursunterlagen von Boris

Ausgleichsproblem. Definition (1.0.3)

Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst

Banach scher Fixpunktsatz. 1) D ist abgeschlossen und konvex; 2) f ist selbstabbildend, d.h. f(d) D;

Institut für Geometrie und Praktische Mathematik Höhere Mathematik IV (für Elektrotechniker und Technische Informatiker) - Numerik - SS 2007 Dr. S. Börm, Dr. M. Larin Banach scher Fixpunktsatz Gegeben

A 1 x = b, A 1 R m m, m := (n 1) 2, nh = 1, T I I T I. A 1 = 1 h 2 I T. T R (n 1) (n 1) und I ist die (n 1) (n 1)-Identitätsmatrix.

KAPITEL 13. Große dünnbesetzte LGS, iterative Löser Erstes Beispielproblem: die diskretisierte Poisson-Gleichung wobei A 1 x = b, A 1 R m m, m := (n 1) 2, nh = 1, A 1 = 1 h 2 T I I T I......... I T I I

7. Iterative Lösung. linearer Gleichungssysteme

7. Iterative Lösung linearer Gleichungssysteme 1 Grundlagen (1) Zur Erinnerung: Gesucht ist die Lösung eines linearen Gleichungssystems a 0,0 x 0 +a 0,1 x 1 + a 0,n 1 x n 1 = b 0 a 1,0 x 0 +a 1,1 x 1 +

Begleitmaterial zur Vorlesung Numerik II

Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik

Numerisches Rechnen. (für Informatiker) M. Grepl J. Berger & J.T. Frings. Institut für Geometrie und Praktische Mathematik RWTH Aachen

(für Informatiker) M. Grepl J. Berger & J.T. Frings Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2010/11 Problemstellung Lineare Gleichungssysteme, iterative Verfahren geg.:

Klausur DI/LA F 2006 LA : 1

Klausur DI/LA F 26 LA : Aufgabe (4+2=6 Punkte): Gegeben seien die Matrix A und der Vektor b mit λ A = λ und b = λ a) Bestimmen Sie die Werte λ R, für welche das Gleichungssystem Ax = b genau eine, keine

Finite Elemente. Dr. S.-J. Kimmerle Institut für Mathematik und Rechneranwendung Fakultät für Luft- und Raumfahrttechnik Wintertrimester 2015

Dr. S.-J. Kimmerle Institut für Mathematik und Rechneranwendung Fakultät für Luft- und Raumfahrttechnik Wintertrimester 5 Aufgabe 8 (Speichertechniken) Finite Elemente Übung 5 a) Stellen Sie die Matrix

Einführung in die Programmierung (MA8003)

Theorie 2.2: Schleifen, Vektorisierung, bedingte Ausführung Dr. Lorenz John Technische Universität München Fakultät Mathematik, Lehrstuhl für Numerische Mathematik M2 05.10.2016 Numerische Mathematik M2

Diplomvorprüfung LA H 06 VD : 1

Diplomvorprüfung LA H 6 VD : Aufgabe : (3 + + = 6 Punkte) Gegeben sei die Matrix A = a) Bestimmen Sie die Eigenwerte von A b) Bestimmen Sie alle Eigenvektoren der Matrix A c) Ist die Matrix A invertierbar?

VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.

IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei

III. Iterative Löser. III.1 Direkte Löser und ihre Nachteile. III.2 Klassische Iterationsverfahren

III. Iterative Löser III.1 Direkte Löser und ihre Nachteile III.2 Klassische Iterationsverfahren Kapitel III (0) 1 Erinnerung: Lineares Gleichungssystem bei FDM Diskretisierung einer linearen PDGL 2. Ordnung

Kapitel 5. Lineare Systeme. Lineare Systeme. Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 5/3

Kapitel 5 Lineare Systeme Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 5/2 Lineare Systeme Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure

Klausur Numerische Mathematik (für Elektrotechniker), Samstag, 19. August 2017

Verständnisfragen-Teil (5 Punkte) Jeder der 5 Verständnisfragenblöcke besteht aus 5 Verständnisfragen. Werden alle 5 Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block

Lineare Algebra und Numerische Mathematik für D-BAUG

R Käppeli L Herrmann W Wu Herbstsemester 26 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 2 Aufgabe 2 Welche der folgenden Aussagen sind korrekt? (i) Jedes

Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)

Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 5 Lineare

Numerik II. Roland Pulch

Numerik II Roland Pulch Institut für Mathematik und Informatik Mathematisch-Naturwissenschaftliche Fakultät Ernst-Moritz-Arndt-Universität Greifswald Skript zu Iterativer Lösung linearer Gleichungssysteme

Begleitmaterial zur Vorlesung Numerik I

Begleitmaterial zur Vorlesung Numerik I Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik I 1 / 55 Studienplanung Bachelor

Lineare Algebra und Numerische Mathematik D-BAUG. Winter 2013 Prof. H.-R. Künsch. , a R. det(a) = 0 a = 1.

b Musterlösung Lineare Algebra und Numerische Mathematik D-BAUG. Multiple Choice) Gegeben sei die folgende Matrix Winter 3 Prof. H.-R. Künsch A = a a) deta) = genau dann wenn gilt x a =. a =. ), a R. x

Kapitel 3 Lineare Gleichungssysteme

1. Direkte Verfahren Kapitel 3 Lineare Gleichungssysteme Grundbaustein vieler numerischer Verfahren zur Lösung von partiellen oder gewöhnlicher Differentialgleichungen und von nichtlinearen Optimierungsproblemen

Iterative Methoden zur Lösung von linearen Gleichungssystemen

Iterative Methoden zur Lösung von linearen Gleichungssystemen (13.12.2011) Ziel Können wir wir die zeitabhängige Schrödinger-Gleichung lösen? φ(t) = e iht ψ(0) Typischerweise sind die Matrizen, die das

Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17

Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und

Lineare Algebra: Determinanten und Eigenwerte

: und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b

Aufgabe 1. Berechnen Sie die absolute und die relative Kondition des Problems x f(x) für die Abbildung. x = x 2 e x 1.

Name: Matrikel-Nr.: 1 Aufgabe 1. Berechnen Sie die absolute und die relative Kondition des Problems x f(x) für die Abbildung R 3 R 2, x 1 f : x 1 + e x2 2 sin(x3 ) x = x 2 e x 1 (1 + x 2 1 + x, 2x 3 )

Lineare Algebra und Numerische Mathematik D-BAUG Winter 2013 Prof. H.-R. Künsch. Regeln Multiple Choice:

b Prüfung Lineare Algebra und Numerische Mathematik D-BAUG Winter 03 Prof. H.-R. Künsch c Alle Aufgaben haben das gleiche Gewicht. Die Lösungswege müssen, abgesehen von Aufgabe, nachvollziehbar dargestellt

Newton-Verfahren für ein Skalarfunktion

Newton-Verfahren für ein Skalarfunktion Für eine Näherungsberechnung von Nullstellen einer reellen Funktion f(x) : R R benutzt man das Newton-Verfahren: x (n+1) = x (n) f(x (n) )/f (x (n) ). Das Newton-Verfahren

Lineare Algebra und Numerische Mathematik für D-BAUG

R. Käppeli L. Herrmann W. Wu Herbstsemester 2016 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 6 Aufgabe 6.1 Berechnen Sie die Determinanten der beiden

Invertierung von Sparse Matrizen

Kapitel 8 Invertierung von Sparse Matrizen Im letzten Kapitel haben wir gesehen, wie man Sparse-Matrizen in C++ behandelt. Hier wollen wir diskutieren, wie man die Gleichung Ax = b (8.1) für eine vorgegebene

5.3 Iterative Lösungsverfahren für lineare Gleichungssysteme

5.3 Iterative Lösungsverfahren für lineare Gleichungssysteme Als zweite Hauptanwendung des Banachschen Fixpunktsatzes besprechen wir in diesem Kapitel die iterative Lösung linearer Gleichungssysteme. Die

Lineare Algebra und Geometrie II, Übungen

Lineare Algebra und Geometrie II, Übungen Gruppe (9 9 45 ) Sei A 2 Bestimmen Sie A und A Finden Sie weiters Vektoren u, v R 2 mit u und Au A, beziehungsweise v und Av A Zunächst die Berechnung der Norm

Institut für Geometrie und Praktische Mathematik

RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben).

Einführung in die Numerik

Institut für Angewandte Mathematik Universität Heidelberg http://www.numerik.uni-hd.de/ lehre/ss10/numerik0/ Zahldarstellung Normalisierte Gleitkommazahl: x = ±[m 1 b 1 + + m r b r ] b ±[es 1bs 1 + +e

A 1 A 2 A 3 A 4 A 5 A 6 A 7

Institut für Geometrie und Praktische Mathematik Numerisches Rechnen für Informatiker WS 7/8 Prof. Dr. H. Esser J. Grande, Dr. M. Larin Klausur Numerisches Rechnen für Informatiker Hilfsmittel: keine (außer

Ferienkurs Mathematik für Physiker I Blatt 3 ( )

Ferienkurs Mathematik für Physiker I WS 6/7 Ferienkurs Mathematik für Physiker I Blatt 3 (9.3.7) Aufgabe : Matrizenrechung 3 (a) Ermitteln Sie für die Matrix A = 3 4 den Ausdruck A + A + A + 6 A3. 3 4

Sommersemester 2017 Blatt 1 von 6 Studiengänge: RMM Masterstudiengang Sem. 1 und Wiederholer

HOCHSCHULE ESSLINGEN Sommersemester 07 Blatt von 6 Studiengänge: RMM Masterstudiengang Sem. und Wiederholer Prüfungsfach: Hilfsmittel: Modellbildung und Simulation Literatur, Manuskript; keine Taschenrechner

Klausur Numerisches Rechnen ( ) (Musterlösung)

Rheinisch-Westfälische Technische Hochschule Aachen Institut für Geometrie und Praktische Mathematik Numerisches Rechnen WS 01/013 Prof. Dr. M. Grepl J. Berger, P. Esser, L. Zhang Klausur Numerisches Rechnen

Algorithmik kontinuierlicher Systeme

Algorithmik kontinuierlicher Systeme Iterative Verfahren (2/2) Ziel dieser Vorlesung Wie schnell können wir Gleichungssysteme lösen? O(n 3 ) LR- oder QR-Zerlegung: Immer anwendbar Komplexität im Allgemeinen

Institut für Geometrie und Praktische Mathematik

RWTH Aachen IGPM RWTH Aachen Institut für Geometrie und Praktische Mathematik Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen

EINFÜHRUNG IN DIE NUMERISCHE MATHEMATIK II 1. Numerische Lineare Algebra. Prof. Dr. Hans Babovsky. Institut für Mathematik

EINFÜHRUNG IN DIE NUMERISCHE MATHEMATIK II 1 Numerische Lineare Algebra Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Sommer 2010 INHALTSVERZEICHNIS 1 Inhaltsverzeichnis

2.2. Übung. Einführung in die Programmierung (MA 8003)

Technische Universität München M2 - Numerische Mathematik Dr. Laura Scarabosio 2.2. Übung. Einführung in die Programmierung (MA 8003) Hinweis: Ab jetzt werden Schleifen benötigt. Aufgabe 2.2.1: Verändern

Prof. Steinwart Höhere Mathematik I/II Musterlösung A =

Prof. Steinwart Höhere Mathematik I/II Musterlösung 7..7 Aufgabe ( Punkte) (a) Bestimmen Sie die Eigenwerte und Eigenräume der Matrix A mit 3 3 A = 3 Ist die Matrix A diagonalisierbar? (b) Die Matrix A

(d) das zu Grunde liegende Problem gut konditioniert ist.

Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt

Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016

Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b

Inexakte Newton Verfahren

Kapitel 3 Inexakte Newton Verfahren 3.1 Idee inexakter Newton Verfahren Wir betrachten weiterhin das nichtlineare Gleichungssystem F (x) = mit einer zumindest stetig differenzierbaren Funktion F : R n

Lineare Algebra und Numerische Mathematik für D-BAUG

R Käppeli L Herrmann W Wu Herbstsemester Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie Aufgabe Beispiel einer Koordinatentransformation Gegeben seien zwei

Lösen der Matrizengleichung

Lösen der Matrizengleichung Oliver Deussen Lösungsverfahren K 1 letztes Kapitel: Berechnung der Formfaktoren F außerdem: B: zu berechnende Strahlung, E: gegebenes Eigenleuchten nun: Wie löst man K B =

Numerisches Programmieren (IN0019)

Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 10. Minimieren von Funktionen....................................................................................... 2 Gradienten-Abstieg

Mathematik für Ökonomen II

RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen II 3..993 (WS 9/93) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt 9 Aufgaben; pro Aufgabe sind

Lösung der Diplom-Vorprüfung Höhere Mathematik III/IV 6.8.005 1 Aufgabe N1 Gegeben seien A = 5-10 -5-10 8-10 -5-10 13 R 3 3 und b = a) Überprüfen Sie, ob die Matrix A positiv definit ist. b) Bestimmen

EINFÜHRUNG IN DIE NUMERISCHE MATHEMATIK III 1. Numerische Lineare Algebra. Prof. Dr. Hans Babovsky. Institut für Mathematik

EINFÜHRUNG IN DIE NUMERISCHE MATHEMATIK III 1 Numerische Lineare Algebra Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2017 INHALTSVERZEICHNIS 1 Inhaltsverzeichnis

eps für alle x D. 4. Die Zahl 256 ist in M(2, 4, 6, 6) exakt darstellbar.

IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H13 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei

4x 1 + 2x 2 + 3x 3 = 1, x 2 + ax 3 = 1, ax 2 + x 3 = a 1. 0 a 1 1 Wir führen nun den Gauÿalgorithmus durch:

Aufgabe 8 Punkte Bestimmen Sie die Lösungsmenge in R in Abhängigkeit von a R des folgenden linearen Gleichungssystems: 4x + x + 3x 3 =, x + ax 3 =, ax + x 3 =. Lösung. Wir schreiben das lineare Gleichungssystem

III. Iterative Löser. III.1 Direkte Löser und ihre Nachteile. III.2 Klassische Iterationsverfahren. III.3 GMRES und CG-Verfahren

III. Iterative Löser III.1 Direkte Löser und ihre Nachteile III.2 Klassische Iterationsverfahren III.3 GMRES und CG-Verfahren Kapitel III (0) 1 Erinnerung: Lineares Gleichungssystem bei FDM Diskretisierung

Mathematik für Studierende der Fachrichtungen Biologie, Chemie, Lebensmittelchemie und Erziehungswissenschaften Blatt 2

Fakultät Mathematik WS 27/8 Institut für Mathematische Stochastik / Institut für Analysis Dr. W. Kuhlisch, Dr. F. Morherr Mathematik für Studierende der Fachrichtungen Biologie, Chemie, Lebensmittelchemie

Institut für Geometrie und Praktische Mathematik

RWTH Aachen Institut für Geometrie und Praktische Mathematik Multiple-Choice-Test NumaMB F08 (30 Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine

Übungen zur Mathematik Blatt 1

Blatt 1 Aufgabe 1: Bestimmen Sie die Fourier-Reihe der im Bild skizzierten periodischen Funktion, die im Periodenintervall [ π, π] durch die Gleichung f(x) = x beschrieben wird. Zeichnen Sie die ersten

Lineare Gleichungssysteme

Lineare Gleichungssysteme 6. Vorlesung 170004 Numerische Methoden I Clemens Brand 25. März 2010 Nachträge Gliederung Nachträge it Nachträge Wichtige Begriffe Eine Zusammenfassung der Folien 8 16 der letzten

Übungsblatt 12 Musterlösung

NumLinAlg WS56 Übungsblatt 2 Musterlösung Lösung 44 (QR-Algorithmus mit Wilkinson-Shift und Deflation) a)+b) Die QR-Iteration zur Berechnung aller Eigenwerte einer Matrix A kann wie folgt implementiert

VF-3: Gegeben seien die Daten f(x 0 ), f(x 1 ),..., f(x n ) mit x 0,..., x n paarweise verschiedenen und

IGPM RWTH Aachen Verständnisfragen-Teil NumaMB F10 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Aussagen Diese sind mit wahr bzw falsch zu kennzeichnen (hinschreiben) Es müssen alle Fragen mit wahr

D-INFK Lineare Algebra HS 2014 Roman Glebov Marc Pollefeys. Serie 13

D-INFK Lineare Algebra HS 2014 Roman Glebov Marc Pollefeys Serie 13 1. Um einen Tisch sitzen 7 Zwerge. Vor jedem steht ein Becher mit Milch. Einer der Zwerge verteilt seine Milch gleichmässig auf alle