Formelsammlung MATHEMATIK Oberstufe
|
|
|
- Julia Thomas
- vor 9 Jahren
- Abrufe
Transkript
1 Formelsmmlug MATHEMATIK Oerstufe Diese Formelsmmlug erhet keie Aspruch uf Vollstädigkeit ud Richtigkeit. Sie wird ei Bedrf durch weitere Kpitel ergäzt..poteze Fktorezerleguge, R r,s R k Z m, N r s r+ s : ( ) r s r s r s r s (. ) r + * r r r 0 k m k k ( ) k r r m m k m k ( ± ) ± + ( ) ( ) ± ± + ± + + c + + c + + c + c ( )( ). + ( )(. + + ) + ( + )(. + ) ( ) gerde ( + )( ) ugerde + ( + )( ) Formelsmmlug A. Lider Seite
2 .Logrithmus Umrechuge, R + + * \{}, u, v R, r R, N, R u log u log log log 0 log( u v) logu + log v u log logu log v v log u r log u r log u log u log lg 0 e log ld log l e lim +, e log u log u log log u log l Formelsmmlug A. Lider Seite
3 .Qudrtische Gleichuge + p + q 0 4.Komplee Zhle p p ± q + + c 0 0 4c ± + p ( )( ) + p + q q ( )( ) + + c i. z +. i C, R ud i ( )( ) mit > 0 + i i + z r rg z ϕ tϕ r cos ϕ + [ O ;60 ] r siϕ z r cosϕ + i siϕ ( ) ( r; ϕ) ( r ; ϕ) ( r ; ϕ ) ( r r ; ϕ + ϕ ) ( r ; ϕ) r ; ϕ ϕ ( r ; ϕ ) r ( r; ϕ) ( r ; ϕ) ϕ 60 ( r; ϕ) r ; + k k 0,..., - - Formel vo Moivre N ( cos + i si ) cos( ) i si( ) : ϕ ϕ ϕ + ϕ Formelsmmlug A. Lider Seite
4 5. Eee Figure Dreieck Rechtwikeliges Dreieck A...Flächeihlt u...umfg A h h c h c A Stz des Pythgors + c Höhestz h p q Kthetestz Gleichseitiges Dreieck Formel vo Hero Umkreisrdius Ikreisrdius p c, q c A A 4 h s.( s ).( s ).( s c) c r 4A A p s + c h A Trpez ( ) Deltoid A e f Prllelogrmm A. h h Rhomus (Rute) e f A h Rechteck A Qudrt A d Kreis A r π u r π Kreissektor A r r πα 60 Kreisoge rπα rπα mit + + c s Formelsmmlug A. Lider Seite 4
5 6.Körper G...Ihlt der Grudfläche M...Ihlt der Mtelfläche O...Ihlt der Oerfläche A...Flächeihlt V...Volume h...höhe r...rdius Prism O G + M V G h Quder O ( + c + c) V c Würfel Zylider Pyrmide Pyrmidestumpf Kegel Kegelstumpf Kugel Kugelklotte A rπ h Kugelzoe A rπ h Kugelsektor Kugelsegmet Kugelschichte + O 6 Rumdigole: d V O r π + rπh M rπh V r πh O G + M V G h ( ) O G + G + M V h G + G G + G O r r s r s V r + h π π π M π O r π + r π + ( r + r ) πs M ( r + r ) πs ( ) V h π r + r r + r O 4r π V 4 r π O rπ h + ρπr r π V h h O rπ. h + ρ π V ( r h) hπ O rπ. h + ρ + ρ π V ρ + ρ + h 6 π ( ) Formelsmmlug A. Lider Seite 5
6 7.Wikelfuktioe - Trigoometrie Trigoometrische Grudeziehuge Werte spezieller Wikel siα Gegekthete Hypoteuse Akthete cos α Hypoteuse tα Gegekthete Akthete cotα Akthete Gegekthete si α + cos α siα tα cotα siα tα α siα 0 tα 0 cotα Qudrteregel α Qudrt I Qudrt II Qudrt III Qudrt IV siα tα cotα Reduktiosformel siα si (80 α) si (80 + α) si (60 α) si (60 + α) cos (80 α) cos (80 + α) cos (60 α) cos (60 + α) tα t (80 α) t (80 + α) t (60 α) t (60 + α) si( α ) siα ugerdefuktio siα cos(90 α) cos(90 + α) cos( α ) gerdefuktio si (90 α) si (90 + α) t ( α) tα Formelsmmlug A. Lider Seite 6
7 Umrechuge Summesätze Siusstz siα tα si siα si α α cos cos si( α ± β ) siα.cos β ±.si β cos( α ± β ).cos β siα.si β siα siα α α tα + t + t cos α si α tα ± β t( α ± β) tα tβ tα tα t α α + β α β siα + si β si cos α + β α β + cosβ cos cos α + β α β siα si β cos si α + β α β cosβ si si c R ; : : c siα : siβ : siγ siα si β siγ α α Kosiusstz + c c Flächeihlt des Dreiecks Umkreisrdius Bogemß ud Grdmß + c c cosβ c + cosγ c c A siα siβ si γ c r siα siβ si γ rd π π π π rd rd Formelsmmlug A. Lider Seite 7
8 8. Vektore ; ; Sklres Produkt Eiheitsvektore zu ϕ (, )... Wikelmß vo ud... Normlprojektio vo uf Vektorielles Produkt (Kreuzprodukt) R : ± A ± B ± ± R : ± A ± B ± ± ± r r A r r mit r R r r A r r mit r R r : R A B + : R A B + + R R A A A A : A + : A ± cosϕ 0 cosϕ 0 ; woei d c c d siϕ Formelsmmlug A. Lider Seite 8
9 9. Alytische Geometrie Drstellugsform ) A,B,C...Koorditevektore der Pukte A,B,C ) Vektor AB mit Afgspukt A ud Edpukt B,, c...ortsvektore der Pukt A, B,C g...gerde g...richtugsvektor vo g...normlvektor vo g... Eiheitsvektor zu 0 X, A, B... Koorditevektore der Pukte X, A, B g,,... Ortsvektore der Pukte X, X, X g AB B A A + AB B Astd AB der Pukte A,B AB AB B A ( B A) AB AB Mittelpukt M der Strecke AB ( ) ( ) M A + B A + AB m ( + ) S A + B + C zw. s + + c A... T A λ B woei λ λ cos ϕ V X A+ t g (mit t R) ; + t g (mit t R) Schwerpukt S des Dreiecks ABC ( ) ( ) Vektorielle Flächeformel des Dreiecks ( ) Teilugspukt T der Strecke AB eim Teilugsverhältis λ ( ) Wikelmß Volume Prllelepiped ( ) c Prmeterdrstellug Gleichug eier Gerde i der Eee Hessesche Normlform (HNF) X A + t AB (mit t R) ; X A ( X A) 0 Gleichug: + y +c 0 + t ( )(mit t R) + y +c HNF: 0 + Formelsmmlug A. Lider Seite 9
10 0.Mtrize λ λ λ λ λ + + ( λ R ) Differetil- ud Itegrlrechug Fuktio ud Aleitugsfuktio; Stmmfuktio y f() k y' f'() 0 F() y y' F() y y' k d k + C f ( ) q f '( ) q mit q Formelsmmlug A. Lider Seite 0 q q+ q d + C q + f ( ) f '( ) q mit q q F() d I + C y f ( ) e y' f '( ) e F( ) e d e + C y f ( ) y' f' ( ) l F() d + C l y f ( ) l q y' f' ( ) :, lso f() F( ) l d l + C y f ( ) log y' f' ( ) log e l F( ) log d ( l ) + C l ;
11 y f ( ) si y' f' ( ) cos F( ) si d cos + C y f ( ) cos y' f' ( ) si F( ) cosd si + C y f ( ) t y' f' ( ) cos F( ) td l cos + C y f ( ) cot y' f' ( ) si F( ) cot d l si + C Aleitugsregel ( f ± g)' f ' ± g' Aleitugsregel ( k f)' k f' k R Aleitugsregel ( f g)' f' g + f' g' Aleitugsregel f f g f g g ' ' g Ketteregel h( ) g( f ( )) h'() g'(f()) f'() Reziprokregel Itegrtiosregel Prtielle Itegrtio Itegrtio durch Sustitutio Newtosches Verfhre ' ' f '( ) f( ) f ( ) ( f ± g) f ± g k f k f (k R ) f g F g F g' f ( y) dy f( g( )) g' ( ) d f ( ) d F( ) F( ) f( ) + f '( ) e d e + C Formelsmmlug A. Lider Seite
12 . Zhlefolge Arithmetische Folge Arithmetische Folge Geometrische Folge Geometrische Folge Geometrische Folge Ziseerechug K 0... Afgskpitl K... Kpitl ch Jhre ei gzjähriger Kpitlisierug p...zisfuß rekursive Drstellug : eplizite Drstellug : s + ( + ). rekursivedrstellug : eplizitedrstellug : s + speziell ei lims K : s + + d + ( ) d q mit q < q p K q [ + ( ) d] c q woeic q q q + q + q, q mit q 0 mit q q q i 0 q i Formelsmmlug A. Lider Seite
Formelheft bfi ('11/'12/ 13)
 Formelheft fi ('/'/ ) zuletzt ktulisiert:.. Kp. Poteze S. Poteze, IR + ; r, s IR; k Z; m, IN 0 ; - k k k r s r+s r : s r-s ( r ) s r s ( ) r r r r r r k k m km m m k,, c IR ( + )² ² + + ² ( )² ² + ² (
Formelheft fi ('/'/ ) zuletzt ktulisiert:.. Kp. Poteze S. Poteze, IR + ; r, s IR; k Z; m, IN 0 ; - k k k r s r+s r : s r-s ( r ) s r s ( ) r r r r r r k k m km m m k,, c IR ( + )² ² + + ² ( )² ² + ² (
Studienkolleg bei den Universitäten des Freistaates Bayern. Übungsaufgaben zur Vorbereitung auf den. Mathematiktest
 Studiekolleg ei de Uiversitäte des Freisttes Byer Üugsufge zur Vorereitug uf de Mthemtiktest . Polyomdivisio:. Dividiere Sie! ) ( 6 8 ):( ) Lös.: ) ( 9 7 0 8 9):(6 ) Lös.: 7 9 c) ( - ):() Lös.: d) (8 9
Studiekolleg ei de Uiversitäte des Freisttes Byer Üugsufge zur Vorereitug uf de Mthemtiktest . Polyomdivisio:. Dividiere Sie! ) ( 6 8 ):( ) Lös.: ) ( 9 7 0 8 9):(6 ) Lös.: 7 9 c) ( - ):() Lös.: d) (8 9
Formelsammlung für den Mittleren uchulabschluss in uchleswig-holstein
 Formelsmmlug für de Mittlere uhulshluss i uhleswig-holstei gültig : 5/6 Figure Dreiek g rudseite g h Fläheihlt A si( ), Seite Umfgu g + + Wikel Qudrt Fläheihlt A Umfgu 4 Rehtek Seite Fläheihlt A, Seite
Formelsmmlug für de Mittlere uhulshluss i uhleswig-holstei gültig : 5/6 Figure Dreiek g rudseite g h Fläheihlt A si( ), Seite Umfgu g + + Wikel Qudrt Fläheihlt A Umfgu 4 Rehtek Seite Fläheihlt A, Seite
Mathematik (AHS) Formelsammlung für die standardisierte kompetenzorientierte schriftliche Reifeprüfung (ab Schuljahr 2017/18)
 Mthemtik (AHS Formelsmmlug für die stdrdisierte kompetezorietierte schriftliche Reifeprüfug ( Schuljhr 017/18 Std: 1. Septemer 017 1 Mege ist Elemet vo... ist icht Elemet vo Durchschitt(smege Vereiigug(smege
Mthemtik (AHS Formelsmmlug für die stdrdisierte kompetezorietierte schriftliche Reifeprüfug ( Schuljhr 017/18 Std: 1. Septemer 017 1 Mege ist Elemet vo... ist icht Elemet vo Durchschitt(smege Vereiigug(smege
Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1. Auflage (2017) S. 1/8. Dreieck Flächeninhalt: Mindestens zwei Seiten sind gleich lang.
 Aiturprüfug Bde-Württemerg: Mthemtishe Merkhilfe,. Auflge (7) S. /8 Eee Figure Dreiek Fläheihlt: A g hg gleihshekliges Dreiek Midestes zwei Seite sid gleih lg. gleihseitiges Dreiek Alle drei Seite sid
Aiturprüfug Bde-Württemerg: Mthemtishe Merkhilfe,. Auflge (7) S. /8 Eee Figure Dreiek Fläheihlt: A g hg gleihshekliges Dreiek Midestes zwei Seite sid gleih lg. gleihseitiges Dreiek Alle drei Seite sid
Formelsammlung. Angewandte Mathematik
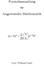 Formelsmmlug für Agewdte Mthemtik + = k= k k k ( b) b Autor: Wolfgg Kugler Formelsmmlug INHALTSVERZEICHNIS. Poteze 3. Defiitioe 3. Recheregel 3.3 Wurzel 4.4 Biomischer Lehrstz 4. Kreisfuktioe 6. Defiitioe
Formelsmmlug für Agewdte Mthemtik + = k= k k k ( b) b Autor: Wolfgg Kugler Formelsmmlug INHALTSVERZEICHNIS. Poteze 3. Defiitioe 3. Recheregel 3.3 Wurzel 4.4 Biomischer Lehrstz 4. Kreisfuktioe 6. Defiitioe
Formelheft. Sarah Leitner. Fiona Aschenbrenner. Paul Brandauer. Julia Nageler. Alwin Dürrer. Sarah Neumann. Angelina Eder.
 Formelheft der 8C ('/') ulett geädert m 9.. Fio Aschereer Pul Brduer Alwi Dürrer Ageli Eder Kord Esterm Mimili Heim Kthri Höck Christi Hörhger Fi Jicek Christi Joh Christi Jurkeit Mimili Kimmel Ev Körschild
Formelheft der 8C ('/') ulett geädert m 9.. Fio Aschereer Pul Brduer Alwi Dürrer Ageli Eder Kord Esterm Mimili Heim Kthri Höck Christi Hörhger Fi Jicek Christi Joh Christi Jurkeit Mimili Kimmel Ev Körschild
Übersicht Integralrechnung
 Vorbemerkug Übersicht Itegrlrechug Diese Übersicht fßt wesetliche Pukte der Vorlesug zusmme. Sie ersetzt icht die usführliche Vorlesugsmitschrift, weil die dort behdelte Beispiele ud Erläuteruge für die
Vorbemerkug Übersicht Itegrlrechug Diese Übersicht fßt wesetliche Pukte der Vorlesug zusmme. Sie ersetzt icht die usführliche Vorlesugsmitschrift, weil die dort behdelte Beispiele ud Erläuteruge für die
Lösungsformel für quadratische Gleichungen. = ± q + Lösungsformel für. Potenzen. negative Exponenten: gebrochene Exponenten: a a.
 HUNKLOIHDWKHPDWLN Dies ist keie Fomelsmmlug im klssische Si - die vewedete Bezeichuge wede icht eklät ud Voussetzuge fü die ültigkeit de Fomel wede i de Regel icht gegee. 7HLO,6WRIIJHELHWHHULWWHOVWXIH
HUNKLOIHDWKHPDWLN Dies ist keie Fomelsmmlug im klssische Si - die vewedete Bezeichuge wede icht eklät ud Voussetzuge fü die ültigkeit de Fomel wede i de Regel icht gegee. 7HLO,6WRIIJHELHWHHULWWHOVWXIH
Mathematik (AHS) Formelsammlung für die standardisierte kompetenzorientierte schriftliche Reifeprüfung (ab Schuljahr 2017/18)
 Mthemtik (HS Formelsmmlug für die stdrdisierte kompetezorietierte schriftliche Reifeprüfug ( Schuljhr 017/18 1 Poteze Poteze mit gzzhlige Expoete R; N\{0} R\{0}; N\{0}... 1 0 1 1 1 1 ( 1 Fktore Poteze
Mthemtik (HS Formelsmmlug für die stdrdisierte kompetezorietierte schriftliche Reifeprüfug ( Schuljhr 017/18 1 Poteze Poteze mit gzzhlige Expoete R; N\{0} R\{0}; N\{0}... 1 0 1 1 1 1 ( 1 Fktore Poteze
Grundwissen Mathematik Klasse 9
 Grudwisse Mthetik Klsse Reelle Zhle: Qudrtwurzel: ist die icht-egtive Lösug der Gleichug:. Merke: heißt Rdikd ud drf icht egtiv sei! Bsp.: 7 6, 7 7 Irrtiole Zhle: Jede Zhl, die sich icht ls Bruch drstelle
Grudwisse Mthetik Klsse Reelle Zhle: Qudrtwurzel: ist die icht-egtive Lösug der Gleichug:. Merke: heißt Rdikd ud drf icht egtiv sei! Bsp.: 7 6, 7 7 Irrtiole Zhle: Jede Zhl, die sich icht ls Bruch drstelle
1.Weiterentwicklung der Zahlvorstellung
 Grudwie Mthemtik 9.Kle Gymium SOB.Weiteretwicklug der Zhlvortellug Defiitio der Qudrtwurzel: Für 0 it diejeige icht egtive Zhl dere Qudrt ergibt. heißt Qudrtwurzel, heißt Rdikd. Beipiele: 0,5 0,5 64 8
Grudwie Mthemtik 9.Kle Gymium SOB.Weiteretwicklug der Zhlvortellug Defiitio der Qudrtwurzel: Für 0 it diejeige icht egtive Zhl dere Qudrt ergibt. heißt Qudrtwurzel, heißt Rdikd. Beipiele: 0,5 0,5 64 8
Zusammenfassung: Komplexe Zahlen
 LGÖ Ks VM Schuljhr 06/07 Zusmmefssug: Komplexe Zhle Ihltsvereichis Komplexe Zhleeee che mit komplexe Zhle Polrform komplexer Zhle 4 Wurel komplexer Zhle 6 Formel vo Crdo 8 Nullstelle ud Fktorisierug vo
LGÖ Ks VM Schuljhr 06/07 Zusmmefssug: Komplexe Zhle Ihltsvereichis Komplexe Zhleeee che mit komplexe Zhle Polrform komplexer Zhle 4 Wurel komplexer Zhle 6 Formel vo Crdo 8 Nullstelle ud Fktorisierug vo
Merkhilfe. 1 Inhalte der Mittelstufe STAATSINSTITUT FÜR SCHULQUALITÄT UND BILDUNGSFORSCHUNG MÜNCHEN. Mathematik am Gymnasium
 STAATSINSTITUT FÜR SCHULQUALITÄT UND BILDUNGSFORSCHUNG MÜNCHEN Mekhilfe Mthemtik m Gymsium Ihlte de Mittelstufe Lösugsfomel fü qudtische Gleichuge c / 4c Poteze m m s s s s s s Logithme logc log logc log
STAATSINSTITUT FÜR SCHULQUALITÄT UND BILDUNGSFORSCHUNG MÜNCHEN Mekhilfe Mthemtik m Gymsium Ihlte de Mittelstufe Lösugsfomel fü qudtische Gleichuge c / 4c Poteze m m s s s s s s Logithme logc log logc log
Formelsammlung. Angewandte Mathematik (BHS) für die standardisierte kompetenzorientierte schriftliche Reife- und Diplomprüfung (SRDP)
 Formelsmmlug für die stdrdisierte kompetezorietierte schriftliche Reife- ud Diplomprüfug SRDP Agewdte Mthemtik BHS A dem Hupttermi 09 Mi 09 ist diese Formelsmmlug die eizig zugelssee Formelsmmlug für die
Formelsmmlug für die stdrdisierte kompetezorietierte schriftliche Reife- ud Diplomprüfug SRDP Agewdte Mthemtik BHS A dem Hupttermi 09 Mi 09 ist diese Formelsmmlug die eizig zugelssee Formelsmmlug für die
Formelsammlung. Angewandte Mathematik (BHS) für die standardisierte kompetenzorientierte schriftliche Reife- und Diplomprüfung (SRDP)
 Formelsmmlug für die stdrdisierte kompetezorietierte schriftliche Reife- ud Diplomprüfug SRDP Agewdte Mthemtik BHS Diese Formelsmmlug ist dem Hupttermi 07 Mi 07 ls Hilfsmittel für die SRDP i Agewdter Mthemtik
Formelsmmlug für die stdrdisierte kompetezorietierte schriftliche Reife- ud Diplomprüfug SRDP Agewdte Mthemtik BHS Diese Formelsmmlug ist dem Hupttermi 07 Mi 07 ls Hilfsmittel für die SRDP i Agewdter Mthemtik
7.5. Aufgaben zu Skalarprodukt und Vektorprodukt
 7.. Aufgbe zu Sklrprodukt ud Vektorprodukt Aufgbe : Sklrprodukt Bereche die folgede Produkte: ) Aufgbe : Läge eies Vektors Bestimme die Läge ud de etsprechede Eiheitsvektor der folgede Vektore. =, b =,
7.. Aufgbe zu Sklrprodukt ud Vektorprodukt Aufgbe : Sklrprodukt Bereche die folgede Produkte: ) Aufgbe : Läge eies Vektors Bestimme die Läge ud de etsprechede Eiheitsvektor der folgede Vektore. =, b =,
Grundwissen Mathematik 9. Klasse. Eigenschaften - Besonderheiten - Beispiele
 Grudwisse Mthemtik 9. Klsse Theme Erweiterug des Zhlebereichs reelle Zhle Eigeschfte - Besoderheite - Beispiele Jede rtiole Zhl k ls Bruch geschriebe werde: = q p Dieser Bruch stellt etweder eie gze Zhl,
Grudwisse Mthemtik 9. Klsse Theme Erweiterug des Zhlebereichs reelle Zhle Eigeschfte - Besoderheite - Beispiele Jede rtiole Zhl k ls Bruch geschriebe werde: = q p Dieser Bruch stellt etweder eie gze Zhl,
Abschlussprüfung 2015 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Abschlussprüfug 05 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Nachtermi A 0 Für Trapeze ABC D mit de parallele Seite [AD ] ud [BC ]
Prüfugsdauer: 50 Miute Abschlussprüfug 05 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Nachtermi A 0 Für Trapeze ABC D mit de parallele Seite [AD ] ud [BC ]
Stereometrie: Übersicht
 Stereometrie: Übersicht Stereometrie ist die Lehre der dreidimensionlen Körper. Wir werden uns nun mit einigen von ihnen beschäftigen.. Prismen Ein Prism besteht us einer Grund und Deckfläche die gleich
Stereometrie: Übersicht Stereometrie ist die Lehre der dreidimensionlen Körper. Wir werden uns nun mit einigen von ihnen beschäftigen.. Prismen Ein Prism besteht us einer Grund und Deckfläche die gleich
Formelsammlung für den Mittleren Schulabschluss in Schleswig-Holstein
 Formelsmmlug für de Mittlere Shulshluss i Shleswig-Holstei gültig : 5/6 Figure Dreiek g rudseite gh h Höhe FläheihltA si( γ ), Seite Umfgu g + + γ Wikel Qudrt Fläheihlt A Umfgu 4 Rehtek Seite Fläheihlt
Formelsmmlug für de Mittlere Shulshluss i Shleswig-Holstei gültig : 5/6 Figure Dreiek g rudseite gh h Höhe FläheihltA si( γ ), Seite Umfgu g + + γ Wikel Qudrt Fläheihlt A Umfgu 4 Rehtek Seite Fläheihlt
Merkhilfe Mathematik für die Sekundarstufe II an beruflichen Schulen in Baden-Württemberg
 Für die schriftliche Fchhochschulreifeprüfug sid ur die Ihlte der Seite is 6 der Merkhilfe relevt, die icht mit eiem grue Blke mrkiert sid. Zhlemege ℕ = { ; ; ; 3 ;...} Mege der türliche Zhle ℕ = ℕ {}
Für die schriftliche Fchhochschulreifeprüfug sid ur die Ihlte der Seite is 6 der Merkhilfe relevt, die icht mit eiem grue Blke mrkiert sid. Zhlemege ℕ = { ; ; ; 3 ;...} Mege der türliche Zhle ℕ = ℕ {}
Flächenberechnung. Flächenberechnung
 Itegrlrechug Gegee sei eie Fuktio. 1 Itegrlrechug Gesucht ist die Fläche zwische der Kurve vo 0 is 1 ud der -Achse. 0 1 2 197 Wegeer Mth/5_Itegrl_k Mittwoch 04.04.2007 18:38:48 Itegrlrechug Wir eee 1 um
Itegrlrechug Gegee sei eie Fuktio. 1 Itegrlrechug Gesucht ist die Fläche zwische der Kurve vo 0 is 1 ud der -Achse. 0 1 2 197 Wegeer Mth/5_Itegrl_k Mittwoch 04.04.2007 18:38:48 Itegrlrechug Wir eee 1 um
Merkhilfe Mathematik für die Sekundarstufe II an beruflichen Schulen in Baden-Württemberg
 Merkhilfe Mthemtik für die Sekudrstufe II erufliche Schule i Bde-Württemerg Für die schriftliche Fchhochschulreifeprüfug sid ur die Ihlte der Seite is 6 der Merkhilfe relevt, die icht mit eiem grue Blke
Merkhilfe Mthemtik für die Sekudrstufe II erufliche Schule i Bde-Württemerg Für die schriftliche Fchhochschulreifeprüfug sid ur die Ihlte der Seite is 6 der Merkhilfe relevt, die icht mit eiem grue Blke
Ableitungsregeln. Produkte- und Quotientenregel. Ableitung einiger wichtiger Funktionen. Kettenregel. Vorkurs Mathematik DIFFERENTIATION
 Vorkurs Mthemtik DIFFERENTIATION Ableitugsregel (f + g) = f + g (cf) = c f, c R ( ) = (c) =, c R Dmit köe wir Polyome bleite: Beispiel. ( 5 + 3 + ) = ( 5 ) + 3( ) + () = 5 4 + 3 = 5 4 + 6 Produkte- ud
Vorkurs Mthemtik DIFFERENTIATION Ableitugsregel (f + g) = f + g (cf) = c f, c R ( ) = (c) =, c R Dmit köe wir Polyome bleite: Beispiel. ( 5 + 3 + ) = ( 5 ) + 3( ) + () = 5 4 + 3 = 5 4 + 6 Produkte- ud
sfg Quadratwurzeln a ist diejenige nichtnegative Zahl (a 0), die quadriert a ergibt: Die Zahl a unter der Wurzel heißt Radikand:
 M 9.1 Quadratwurzel a ist diejeige ichtegative Zahl (a 0), die quadriert a ergibt: a 2 = a Die Zahl a uter der Wurzel heißt Radikad: a Quadratwurzel sid ur für ichtegative Zahle defiiert: a 0 25 = 5; 81
M 9.1 Quadratwurzel a ist diejeige ichtegative Zahl (a 0), die quadriert a ergibt: a 2 = a Die Zahl a uter der Wurzel heißt Radikad: a Quadratwurzel sid ur für ichtegative Zahle defiiert: a 0 25 = 5; 81
1 Funktionen und Flächen
 Fuktioe ud Fläche. Fläche Defiitio: Die Ebee R ist defiiert als Mege aller geordete Paare vo reelle Zahle: R = {(,, R} Der erste Eitrag heißt da auch Koordiate ud der zweite Koordiate. Für zwei Pukte (,,
Fuktioe ud Fläche. Fläche Defiitio: Die Ebee R ist defiiert als Mege aller geordete Paare vo reelle Zahle: R = {(,, R} Der erste Eitrag heißt da auch Koordiate ud der zweite Koordiate. Für zwei Pukte (,,
Formelsammlung für das Fach Mathematik Stand:
 Formelsmmlug für ds Fch Mthemtik Std:.4.6 Mthemtische Symbole gleich ugleich < kleier ls kleier oder gleich > größer größer oder gleich ugefähr gleich; rud deckugsgleich; kogruet etsricht rllel sekrecht
Formelsmmlug für ds Fch Mthemtik Std:.4.6 Mthemtische Symbole gleich ugleich < kleier ls kleier oder gleich > größer größer oder gleich ugefähr gleich; rud deckugsgleich; kogruet etsricht rllel sekrecht
Ich kann den SdP anwenden, um Seitenlängen in rechtwinkligen Dreiecken zu berechnen.
 Klsse 9c Mthemtik Vorbereitung zur Klssenrbeit Nr. m.5.018 Themen: Stz des Pythgors, Qudrtische Gleichungen Checkliste Ws ich lles können soll Ich knn den Stz des Pythgors (SdP) in Worten formulieren.
Klsse 9c Mthemtik Vorbereitung zur Klssenrbeit Nr. m.5.018 Themen: Stz des Pythgors, Qudrtische Gleichungen Checkliste Ws ich lles können soll Ich knn den Stz des Pythgors (SdP) in Worten formulieren.
Strahl Eine gerade Linie, die auf einer Seite von einem Punkt begrenzt wird, (Anfangspunkt) heißt Strahl.
 1. 1. 2. Strecke B B Gerde Eine gerde, von zwei Punkten begrenzte Linie heißt Strecke. Eine gerde Linie, die nicht begrenzt ist, heißt Gerde. D.h. eine Gerde ht keine Endpunkte! 2. 3. 3. g Strhl Eine gerde
1. 1. 2. Strecke B B Gerde Eine gerde, von zwei Punkten begrenzte Linie heißt Strecke. Eine gerde Linie, die nicht begrenzt ist, heißt Gerde. D.h. eine Gerde ht keine Endpunkte! 2. 3. 3. g Strhl Eine gerde
WS 2005/06 Vorkurs: Mathematische Methoden der Physik Musterlösung von Blatt1. 2. Fall x < 2
 WS 5/6 Vorkurs: Mtemtise Metode der Pysik Musterlösug vo Bltt Aufge : 6 < < 6 8 < > Lsg.: < 7 7. Fll > : < < < <
WS 5/6 Vorkurs: Mtemtise Metode der Pysik Musterlösug vo Bltt Aufge : 6 < < 6 8 < > Lsg.: < 7 7. Fll > : < < < <
Formelsammlung Mathematik 4. Klasse
 Formelsmmlung Mthemtik 4. Klsse Inhlt Rehtek... Qurt... llgemeines Dreiek... Rehtwinkeliges Dreiek... Gleihshenkliges Dreiek... 4 Gleihseitiges Dreiek... 4 Trpez... 5 Prllelogrmm... 5 Rute Rhomus... 6
Formelsmmlung Mthemtik 4. Klsse Inhlt Rehtek... Qurt... llgemeines Dreiek... Rehtwinkeliges Dreiek... Gleihshenkliges Dreiek... 4 Gleihseitiges Dreiek... 4 Trpez... 5 Prllelogrmm... 5 Rute Rhomus... 6
Flächenmaße : 1 m 2 = 100 dm 2 = cm 2. 1 a = 100 m 2 1 ha = 100 a = m 2. Dreieck. A = 1 2 g h. u = a+b+c+d. Trapez.
 Römische Zhlzeiche I õ V õ 5 X õ 0 L õ 50 C õ00 D õ 500 M õ 000 Zhlereiche z türliche Zhle z gze Zhle z rtiole Zhle Ø reelle Zhle griechische uchste Ø komplexe Zhle z lph z et g G z Gmm d D z Delt e E
Römische Zhlzeiche I õ V õ 5 X õ 0 L õ 50 C õ00 D õ 500 M õ 000 Zhlereiche z türliche Zhle z gze Zhle z rtiole Zhle Ø reelle Zhle griechische uchste Ø komplexe Zhle z lph z et g G z Gmm d D z Delt e E
II Orientieren und Bewegen im Raum
 Schüleruchseiten II Orientieren und ewegen im Rum Erkundungen Seite Seite ( ), ( ), D ( ), E ( ), F ( ), G ( ), H ( ) Ich sehe ws, ws Du nicht siehst Individuelle Lösungen Rechnen mit Vektoren uftrg )
Schüleruchseiten II Orientieren und ewegen im Rum Erkundungen Seite Seite ( ), ( ), D ( ), E ( ), F ( ), G ( ), H ( ) Ich sehe ws, ws Du nicht siehst Individuelle Lösungen Rechnen mit Vektoren uftrg )
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam ARBEITSBLATT 2-6 GEOMETRISCHE KÖRPER 1) DAS PRISMA
 . Semester ARBEITSBLATT -6 GEOMETRISCHE KÖRPER 1) DAS PRISMA Definition: Prismen hben deckungsgleiche (kongruente), prllele und eckige Grund- und Deckflächen. Die Seitenknten sind lle gleich lng und zueinnder
. Semester ARBEITSBLATT -6 GEOMETRISCHE KÖRPER 1) DAS PRISMA Definition: Prismen hben deckungsgleiche (kongruente), prllele und eckige Grund- und Deckflächen. Die Seitenknten sind lle gleich lng und zueinnder
Kapitel IV Euklidische Vektorräume. γ b
 Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
Abschlussprüfung 2016 an den Realschulen in Bayern
 Prüfugsdauer: 150 Miute Abschlussprüfug 016 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A 1 Haupttermi A 10 Die gleichscheklige Dreiecke ABC habe die Base AB
Prüfugsdauer: 150 Miute Abschlussprüfug 016 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A 1 Haupttermi A 10 Die gleichscheklige Dreiecke ABC habe die Base AB
Analysis II für Studierende der Ingenieurwissenschaften
 Fchbereich Mthemtik der Uiversität Hmburg SoSe 2015 Dr. K. Rothe Alysis II für Studierede der Igeieurwisseschfte Hörslübug mit Beispielufgbe zu Bltt 3 Recheregel für Potezreihe Stz: Die Potezreihe g(z
Fchbereich Mthemtik der Uiversität Hmburg SoSe 2015 Dr. K. Rothe Alysis II für Studierede der Igeieurwisseschfte Hörslübug mit Beispielufgbe zu Bltt 3 Recheregel für Potezreihe Stz: Die Potezreihe g(z
A. Zahleneinteilung. r a b
 Aus FUNKSCHAU 14/1953 (Blatt 1+) ud 17/1953 (Blatt 3), im Origial -spaltig. Digitalisiert 07/016 vo Eike Grud für http://www.radiomuseum.org mit freudlicher Geehmigug der FUNKSCHAU- Redaktio. Die aktuelle
Aus FUNKSCHAU 14/1953 (Blatt 1+) ud 17/1953 (Blatt 3), im Origial -spaltig. Digitalisiert 07/016 vo Eike Grud für http://www.radiomuseum.org mit freudlicher Geehmigug der FUNKSCHAU- Redaktio. Die aktuelle
Abschlussprüfung 2015 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute bschlussprüfug 05 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: ufgabe Haupttermi.0 Gegebe sid rechtwiklige Dreiecke BM mit M 4 cm ud de Hypoteuse
Prüfugsdauer: 50 Miute bschlussprüfug 05 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: ufgabe Haupttermi.0 Gegebe sid rechtwiklige Dreiecke BM mit M 4 cm ud de Hypoteuse
Abschlussprüfung 2017 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute bschlussprüfug 07 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: ufgabe Haupttermi.0 Trapeze BD mit de parallele Seite D ud B rotiere um die Gerade
Prüfugsdauer: 50 Miute bschlussprüfug 07 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: ufgabe Haupttermi.0 Trapeze BD mit de parallele Seite D ud B rotiere um die Gerade
AT AB., so bezeichnet man dies als innere Teilung von
 Teilverhältisse Aus der Geometrie der Dreiecke ket ma die Aussage, dass der Schwerpukt T eies Dreiecks die Seitehalbierede im Verhältis : teilt. Für die Strecke AT ud TM gilt gemäß der Abbildug AT : TM
Teilverhältisse Aus der Geometrie der Dreiecke ket ma die Aussage, dass der Schwerpukt T eies Dreiecks die Seitehalbierede im Verhältis : teilt. Für die Strecke AT ud TM gilt gemäß der Abbildug AT : TM
1 Das Skalarprodukt und das Kreuzprodukt
 Das Skalarprodukt ud das Kreuzprodukt Wir betrachte zu x = de Ausdruck y t x : = x Grud: Die rechte Seite der Gleichug ist: y t x = (y tx +... + (y ty { t x } y +... + x y x + x y (x y +... + x y x x t
Das Skalarprodukt ud das Kreuzprodukt Wir betrachte zu x = de Ausdruck y t x : = x Grud: Die rechte Seite der Gleichug ist: y t x = (y tx +... + (y ty { t x } y +... + x y x + x y (x y +... + x y x x t
Vektorrechnung. Ronny Harbich, 2003
 Vektorrechug Ro Hrich, 2003 Eiführug Ihlt Defiitio Betrg Sklrmultipliktio Nullvektor Gegevektor Eiheitsvektor Additio Sutrktio Gesetze Defiitio Ei Vektor ist eie Mege vo Pfeile, die gleichlg (kogruet),
Vektorrechug Ro Hrich, 2003 Eiführug Ihlt Defiitio Betrg Sklrmultipliktio Nullvektor Gegevektor Eiheitsvektor Additio Sutrktio Gesetze Defiitio Ei Vektor ist eie Mege vo Pfeile, die gleichlg (kogruet),
Komplexe Zahlen Ac '16
 Komplexe Zhle Ac '16 I der Mege der reelle Zhle ist die Gleichug x² = -1 icht lösr. Ahilfe schfft eie Zhlereichserweiterug vo der Mege uf die Mege der sogete komplexe Zhle. Die Mege der komplexe Zhle esteht
Komplexe Zhle Ac '16 I der Mege der reelle Zhle ist die Gleichug x² = -1 icht lösr. Ahilfe schfft eie Zhlereichserweiterug vo der Mege uf die Mege der sogete komplexe Zhle. Die Mege der komplexe Zhle esteht
I PLANIMETRIE. 1 Winkel. 2 Dreiecke. Lösungen zu Übungen 1. Lösungen zu Übungen 2. Lösungen zu Übungen 1
 I PLANIMETRIE Winkel Lösungen zu Üungen. ) 8 β α + γ ) ϕ 8 β. ) α 7 ) α 5 ; β c) α 5 d) α ; β. α. ε 78 5. ) α 58 ; β ; γ 6 ) α ; γ 76 c) α 6 ; β d) α 6 6. ) β α ; β ) β α ; β 5 7. ) ε 8 α ) α + β ε 8.
I PLANIMETRIE Winkel Lösungen zu Üungen. ) 8 β α + γ ) ϕ 8 β. ) α 7 ) α 5 ; β c) α 5 d) α ; β. α. ε 78 5. ) α 58 ; β ; γ 6 ) α ; γ 76 c) α 6 ; β d) α 6 6. ) β α ; β ) β α ; β 5 7. ) ε 8 α ) α + β ε 8.
Abschlussprüfung 2010 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Abschlussprüfug 00 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A A.0 I eiem Hadbuch zur Wetterkude fide Sie im Kapitel Erdatmosphäre die
Prüfugsdauer: 50 Miute Abschlussprüfug 00 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A A.0 I eiem Hadbuch zur Wetterkude fide Sie im Kapitel Erdatmosphäre die
Lösungen Mathematik II
 Lösungen Mthemtik II Geometrie für Berufsmturitätsschulen,. Auflge Druckdtum: August I PLANIMETRIE Winkel Lösungen zu Üungen. ) 8 β α + γ ) ϕ 8 β. ) α 7 ) α 5 ; β c) α 5 d) α ; β. α. ε 78 5. ) α 58 ;
Lösungen Mthemtik II Geometrie für Berufsmturitätsschulen,. Auflge Druckdtum: August I PLANIMETRIE Winkel Lösungen zu Üungen. ) 8 β α + γ ) ϕ 8 β. ) α 7 ) α 5 ; β c) α 5 d) α ; β. α. ε 78 5. ) α 58 ;
Analysis I Probeklausur 2
 WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch
WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch
Vektoren. Definition. Der Betrag eines Vektors. Spezielle Vektoren
 Vektoren In nderen Bereichen der Nturwissenschften treten Größen uf, die nicht nur durch eine Zhlenngbe drgestellt werden können, wie Krft, die Geschwindigkeit. Zur vollständigen Beschreibung z.b. der
Vektoren In nderen Bereichen der Nturwissenschften treten Größen uf, die nicht nur durch eine Zhlenngbe drgestellt werden können, wie Krft, die Geschwindigkeit. Zur vollständigen Beschreibung z.b. der
dominik erdmann ingenieurinformatik fh bingen
 INHALTSVERZEICHNIS ANALYSIS domiik erdm igeieuriformtik fh bige INHALTSVERZEICHNIS ANALYSIS domiik erdm igeieuriformtik fh bige I DIE REELLEN ZAHLEN Grudlge. Megelehre. Smbole der Mthemtik. Aiome der Alsis
INHALTSVERZEICHNIS ANALYSIS domiik erdm igeieuriformtik fh bige INHALTSVERZEICHNIS ANALYSIS domiik erdm igeieuriformtik fh bige I DIE REELLEN ZAHLEN Grudlge. Megelehre. Smbole der Mthemtik. Aiome der Alsis
Großdruck. ohne Beispiele. (a + b) = a + 2ab + b. (a - b) = a - 2ab + b. (a + b) (a - b) = a - b. Zeitspannen: erste binomische Formel:
 16 7 8 9 4 5 6 1 2 3 1 2 13 14 15 5 6 1 2 3 4 b c A B 3 4 5 6 7 8 9 10 11 12 17 18 19 20 21 22 23 24 25 C 13 14 15 16 9 10 11 12 7 8 2 2 2 erste binomische Formel: ( + b) + 2b + b 2 2 2 zweite binomische
16 7 8 9 4 5 6 1 2 3 1 2 13 14 15 5 6 1 2 3 4 b c A B 3 4 5 6 7 8 9 10 11 12 17 18 19 20 21 22 23 24 25 C 13 14 15 16 9 10 11 12 7 8 2 2 2 erste binomische Formel: ( + b) + 2b + b 2 2 2 zweite binomische
Aufgabensammlung der höheren Mathematik
 Aufgbensmmlung der höheren Mthemtik von Vsili P. Minorski 5., ktulisierte Auflge Hnser München 2008 Verlg C.H. Beck im Internet: www.beck.de ISBN 978 3 446 466 Zu Inhltsverzeichnis schnell und portofrei
Aufgbensmmlung der höheren Mthemtik von Vsili P. Minorski 5., ktulisierte Auflge Hnser München 2008 Verlg C.H. Beck im Internet: www.beck.de ISBN 978 3 446 466 Zu Inhltsverzeichnis schnell und portofrei
Abschlussprüfung 2012 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Abschlussprüfug 0 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A cos 6 A 0 Die Pfeile OP ( ) ud OQ ( ) cos cos spae für [0 ;80 ] Dreiecke
Prüfugsdauer: 50 Miute Abschlussprüfug 0 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A cos 6 A 0 Die Pfeile OP ( ) ud OQ ( ) cos cos spae für [0 ;80 ] Dreiecke
0.1 E: Der Haupsatz der Mineralogie
 0. E: Der Haupsatz der Mieralogie Satz: I eiem Kristall gibt es ur,,3,4 ud 6-zählige Symmetrie. Defiitio: Seie u, v 0 zwei Vektore, die icht auf eier Gerade liege. Die Mege heißt Gitter. Satz: Die Vektore
0. E: Der Haupsatz der Mieralogie Satz: I eiem Kristall gibt es ur,,3,4 ud 6-zählige Symmetrie. Defiitio: Seie u, v 0 zwei Vektore, die icht auf eier Gerade liege. Die Mege heißt Gitter. Satz: Die Vektore
Arbeitsblatt Geometrie / Trigonometrie
 Fchhochschule Nordwestschweiz (FHNW) Hochschule für Technik Institut für Mthemtik und Nturwissenschften Arbeitsbltt Geometrie / Trigonometrie Dozent: - rückenkurs Mthemtik 2016 Modul: Mthemtik Dtum: 2016
Fchhochschule Nordwestschweiz (FHNW) Hochschule für Technik Institut für Mthemtik und Nturwissenschften Arbeitsbltt Geometrie / Trigonometrie Dozent: - rückenkurs Mthemtik 2016 Modul: Mthemtik Dtum: 2016
Übungsaufgaben zu Analysis 1 Lösungen von Blatt XII vom sin(nx) n sin(x). sin(ax) a sin(x) z = re iϕ = r(cos(ϕ) + i sin(ϕ)) z n = w
 Prof. Dr. Moritz Kaßma Fakultät für Mathematik Witersemester 04/05 Uiversität Bielefeld Übugsaufgabe zu Aalysis Lösuge vo Blatt XII vom 5.0.5 Aufgabe XII. 3 Pukte) Beweise Sie, dass für alle R ud N die
Prof. Dr. Moritz Kaßma Fakultät für Mathematik Witersemester 04/05 Uiversität Bielefeld Übugsaufgabe zu Aalysis Lösuge vo Blatt XII vom 5.0.5 Aufgabe XII. 3 Pukte) Beweise Sie, dass für alle R ud N die
1.7 Inneres Produkt (Skalarprodukt)
 Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
Sinus- + Cosinus-Funktion und komplexe Wurzel
 Dr. Siegfried Echterhoff Aalysis 1 Vorlesug WS 08 09 6 Polarkoordiate Sius- + Cosius-Fuktio ud komplexe Wurzel 6.1 Im folgede seik 1 1 := {z C z = 1} der Kreis i C mit Radius 1 ud Mittelpukt 0. Wir defiiere
Dr. Siegfried Echterhoff Aalysis 1 Vorlesug WS 08 09 6 Polarkoordiate Sius- + Cosius-Fuktio ud komplexe Wurzel 6.1 Im folgede seik 1 1 := {z C z = 1} der Kreis i C mit Radius 1 ud Mittelpukt 0. Wir defiiere
Abschlussprüfung 2017 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Abschlussprüfug 07 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Nachtermi A.0 Trapeze ABCD rotiere um die Achse AD. Die Wikel 45 ;90 DCB
Prüfugsdauer: 50 Miute Abschlussprüfug 07 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Nachtermi A.0 Trapeze ABCD rotiere um die Achse AD. Die Wikel 45 ;90 DCB
Abschlussprüfung 2016 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Abschlussprüfug 06 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Nachtermi A 0 Gegebe sid der Pukt O0 0 ud die Pfeile OP 4si 5cos A Zeiche
Prüfugsdauer: 50 Miute Abschlussprüfug 06 a de Realschule i Bayer Mathematik I Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Nachtermi A 0 Gegebe sid der Pukt O0 0 ud die Pfeile OP 4si 5cos A Zeiche
Vektorrechnung Produkte
 Vektorrechnung Produkte Die Luft fliesst von ussen gegen ds Zentrum des Tiefdruckgeiets üer Islnd Wegen der Erdrottion eginnt die Luft zu rotieren Die ewegte Luft nimmt Wolken uf ihrem Weg mit zeigt uns
Vektorrechnung Produkte Die Luft fliesst von ussen gegen ds Zentrum des Tiefdruckgeiets üer Islnd Wegen der Erdrottion eginnt die Luft zu rotieren Die ewegte Luft nimmt Wolken uf ihrem Weg mit zeigt uns
Abschlussprüfung 2014 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Name: Abschlussprüfug 204 a de Realschule i Bayer Mathematik I Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Haupttermi A 0 Gegebe ist das rechtwiklige Dreieck ABC mit der Hypoteuse
Prüfugsdauer: 50 Miute Name: Abschlussprüfug 204 a de Realschule i Bayer Mathematik I Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Haupttermi A 0 Gegebe ist das rechtwiklige Dreieck ABC mit der Hypoteuse
