Darstellende Geometrie
|
|
|
- Ida Kranz
- vor 9 Jahren
- Abrufe
Transkript
1 Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig
2 Inhaltsverzeichnis 1 Projektionsarten Zentralprojektion Parallelprojektion und Normalprojektion Kotierte Projektion Zugeordnete Normalrisse Axonometrie Zentralprojektion Bestimmungselemente Spurpunkte und Fluchtpunkte Zugeordnete Normalrisse Grundriss und Aufriss Kreuzriss Ordner Übung: Konstruktion des Kreuzrisses Übung: Konstruktion eines Zentralrisses (I) Bild eines Punktes Fluchtpunkte waagerechter Geraden Übung: Konstruktion eines Zentralrisses (II) Fluchtpunkte beliebiger Geraden Sichtbarkeit Grundelemente der Normalprojektion Darstellung von Punkten Darstellung von Geraden Hauptlinie erster Art oder Höhenlinie Hauptlinie zweiter Art oder Frontlinie Hauptlinie dritter Art Projizierende Geraden Übung: Konstruktion von Spurpunkten Darstellung von Ebenen Erstprojizierende (grundrissprojizierende) Ebene Zweitprojizierende (aufrissprojizierende) Ebene Doppeltprojizierende Ebene Höhen- oder Schichtebene Frontebene Pultebene Hauptlinien von Ebenen Übung: Konstruktion von Spurgeraden Lage zweier Geraden im Raum Zwei Geraden schneiden sich
3 INHALTSVERZEICHNIS Zwei Geraden sind parallel Zwei Geraden sind windschief Übung: Konstruktion von Inzidenzen (I) Übung: Konstruktion von Inzidenzen (II) Übung: Konstruktion von Inzidenzen (III) Übung: Konstruktion von Inzidenzen (IV) Sichtbarkeit Übung: Konstruktion von Lagen (I) Übung: Konstruktion von Lagen (II) Neigungswinkel Geraden Ebenen und Fallgeraden Platonische Körper Übung: Schnittfigur Spurgeraden einer Ebene Schnittpunkt mit einer Geraden Seitenrisse Die Seitenrissebene Übung: Konstruktion eines Seitenrisses Doppelter Seitenriss Übung: Konstruktion eines doppelten Seitenrisses Übung: Projizierendmachen von Geraden Übung: Drehen eines Punktes um eine Achse Übung: Konstruktion einer Gerade Übung: Projizierendmachen von Ebenen Übung: Neigungswinkel einer Ebene Übung: Entzerren durch Umprojizieren (I) Übung: Entzerren durch Umprojizieren (II) Kotierte Projektion Die kotierte Projektion Übung: Konstruktion eines Seitenrisses Geraden Übung: Konstruktion einer Graduierung Ebenen Übung: Konstruktion von Ebenen Übung: Konstruktion von Schnittgeraden Übung: Konstruktion von Schnittpunkten Erste Grundaufgabe Übung: Straße abböschen Zweite Grundaufgabe Übung: Konstruktion einer Serpentine Dritte Grundaufgabe Übung: Teich anlegen Bezeichnungen 89 9 Literatur 90
4 Kapitel 1 Projektionsarten Wie sehen wir 3-dimensionale Objekte und wie können wir sie (2-dimensional) so zeichnen, dass sie möglichst gut erkennbar sind? 3
5 KAPITEL 1. PROJEKTIONSARTEN Zentralprojektion Die Zentralprojektion ist dem natürlichen Sehvorgang nachgebildet. Ein Bildpunkt P ergibt sich als Schnittpunkt der Bildebene π mit dem Projektionsstrahl durch den Augpunkt Z und den Dingpunkt P. Der Bildpunkt P heißt auch Riss von P. Z P P π Die Abbildung heißt Zentralprojektion, das entstehende Bild heißt Zentralriss. Bei der Zentralprojektion werden Geraden im Raum auf Geraden im Bild abgebildet: Die Abbildung ist geradentreu. Die Zentralprojektion liefert eine Abbildung von einem Objekt, welches für uns relativ anschaulich ist. Allerdings ist es oft schwierig, die wahren Größenverhältnisse des Objektes aus einer Zentralprojektion abzulesen. Ein Beispiel für einen Zentralriss ist der Schatten eines Gegenstandes bei künstlicher Beleuchtung mit einer nahezu punktförmigen Lichtquelle; Die Lichtquelle ist dabei der Augpunkt. Ein weiteres Beispiel ist die Fotographie eines Objektes; Der Augpunkt ist dabei die Linse der Kamera.
6 KAPITEL 1. PROJEKTIONSARTEN Parallelprojektion und Normalprojektion Bei der Parallelprojektion ergibt sich der Bildpunkt P als Schnittpunkt der Bildebene π mit dem Projektionsstrahl durch den Dingpunkt P. Alle Projektionsstrahlen sind parallel. Die Richtung der Projektionsstrahlen bestimmt das entstehende Bild. Der Bildpunkt P wird wieder auch Riss von P genannt. P P π Die Abbildung heißt Parallelprojektion, das entstandene Bild Parallelriss. Wieder werden Geraden im Raum auf Geraden im Bild abgebildet: Auch diese Abbildung ist geradentreu. Die Parallelprojektion entspricht nicht dem Sehvorgang und liefert Bilder, die für uns nicht immer sehr anschaulich sind. Aber die Parallelprojektion hat den Vorteil, dass die Größenverhältnisse des Objektes einfacher aus dem Bild abzulesen sind als bei der Zentralprojektion, denn das Bild wird nicht verzerrt. Bei der schiefen Parallelprojektion treffen die Projektionsstrahlen schief auf die Bildebene. Bei der Normalprojektion treffen die Projektionsstrahlen senkrecht auf die Bildebene. Das entstandene Bild heißt dann auch Normalriss. Aus einem Normalriss lassen sich am leichtesten die wahren Größen von Strecken und Winkeln des Originals ermitteln. Der Normalriss ist daher zur Herstellung von technischen Zeichnungen am besten geeignet.
7 KAPITEL 1. PROJEKTIONSARTEN Kotierte Projektion Die kotierte Projektion ist eine Variante der Normalprojektion: Es wird ein Objekt auf eine horizontale Bildebene projiziert und dann wird zusätzlich an jeden Bildpunkt die Entfernung des Originalpunktes von der Bildebene als Kote geschrieben (Französisch a cote de = neben ). Dabei muss für die Höhe ein Maßstab angegeben werden. Die kotierte Projektion wird vorwiegend für Geländedarstellungen verwendet. Ein zweiter Anwendungsbereich sind Dachausmittlungen.
8 KAPITEL 1. PROJEKTIONSARTEN Zugeordnete Normalrisse Das Objekt wird auf zwei zueinander senkrecht stehende Bildebenen, genannt Grund- und Aufrissebene, senkrecht projiziert. Klappt man nun die Rissebenen um eine Rissachse in die Zeichenebene, so spricht man von zugeordneten Normalrissen. Das Objekt ist durch zwei seiner Normalrisse eindeutig bestimmt. Aufrisstafel π 2 A =B A Rissachse (12) B A Grundrisstafel π 1 B A B gedrehte Grundrisstafel π 1
9 KAPITEL 1. PROJEKTIONSARTEN Axonometrie Mithilfe der Axonometrie kann man eher anschauliche Bilder erstellen. Es wird das Objekt mit einem dreidimensionalen Koordinatensystem auf die Bildebene projiziert.
10 Kapitel 2 Zentralprojektion Hier werden einige Eigenschaften und bestimmende Elemente der Zentralprojektion vorgestellt. 2.1 Bestimmungselemente Das folgende Bild enthält die wesentlichen Elemente einer Zentralprojektion. l H h d Z P P s π S π π V Z l π π V π S H d h s Projektionszentrum oder Auge der Zentralprojektion Hauptsehstrahl Bildebene Verschwindungsebene Standebene Hauptpunkt der Perspektive Distanz des Auges von der Bildebene Horizont Standlinie Bei einer Zentralprojektion kann jedem Punkt, der nicht auf der Verschwindungsebene liegt, ein Bild zugeordnet werden. Verschiedene Punkte im Objekt können das gleiche Bild haben. Sie sind dann im Bild nicht mehr zu unterscheiden. 9
11 KAPITEL 2. ZENTRALPROJEKTION Spurpunkte und Fluchtpunkte Sei g 1 eine Gerade, die nicht parallel zur Bildebene π verläuft. Dann hat g 1 einen Spurpunkt S g1 : Dies ist der Punkt, in dem sich g 1 mit der Bildebene π schneidet. Der Verschwindungspunkt von g 1 ist der Punkt, in dem sich g 1 mit der Verschwindungsebene π V schneidet. Weiter gibt es eine Gerade g, die parallel zu g 1 verläuft und durch den Augpunkt Z geht. Der Fluchtpunkt F g1 von g 1 ist der Punkt, in dem g die Bildebene π schneidet. Ist g 2 eine Gerade, die parallel zu g 1 verläuft, so haben g 1 und g 2 den gleichen Fluchtpunkt. Es gilt also F g1 = F g2. Das wird in dem folgenden Bild demonstriert. π V π Z g 2 F V g2 g S g2 g 2 V g1 g 1 S g1 g 1 S g1, S g2 Spurpunkte der Geraden g 1 und g 2 V g1, V g2 Verschwindungspunkte der Geraden g 1 und g 2 g1, g2 Bilder der Geraden g 1 und g 2 g Gerade durch Z parallel zu g 1 und g 2 F = F g1 = F g2 Fluchtpunkt der Geraden g 1 und g 2 Man kann an dem Bild auch erkennen, dass die Bilder paralleler Geraden nicht parallel sind. Die beiden Bilder schneiden sich im gemeinsamen Fluchtpunkt. Man kann auch erkennen, dass das Bild jeder Gerade durch den Spurpunkt und den Fluchtpunkt verläuft.
12 Kapitel 3 Zugeordnete Normalrisse In technischen Zeichnungen wird normalerweise die Normalprojektion verwendet. Dabei wird das Objekt wird auf zwei zueinander sekrecht stehenden Bildebenen senkrecht projiziert. Die beiden Bildebenen heißen Grundriss und Aufriss. Zusammen sind es die zugeordneten Normalrisse. 11
13 KAPITEL 3. ZUGEORDNETE NORMALRISSE Grundriss und Aufriss Aufrisstafel π 2 A =B A Rissachse (12) B A Grundrisstafel π 1 B A B gedrehte Grundrisstafel π 1 Zu einem Punkt A ist A sein Grundriss und A sein Aufriss. Diese Bezeichnungsweise muss immer beibehalten werden! Der Grundriss wird dann aus seiner natürlichen horizontalen Lage nach unten gedreht, so dass er mit dem Aufriss in einer Ebene liegt. Das wird auch Verebnung genannt.
14 KAPITEL 3. ZUGEORDNETE NORMALRISSE Kreuzriss Manchmal gibt es noch eine dritte Bildebene, die senkrecht zu Grund- und Aufriss steht: den Kreuzriss. Diese wird dann in der Verebnung nach links gedreht, so dass auch diese Tafel mit Grund- und Aufriss in einer Ebene liegt. Der Kreuzriss eines Punktes P wird mit P bezeichnet. gedrehte Kreuzrisstafel π 3 P ord(p) P π 2 π 3 P P ord(p) H O P π 1 H P gedrehte Grundrisstafel π 1 π 1, π 2, π 3 Grund-, Auf- und Kreuzrissebene (π 1 π 2 π 3 π 1 ) P Dingpunkt P, P, P Grund-, Auf- und Kreuzriss von P Die Rissachsen heißen: (12) für π 1 π 2, (13) für π 1 π 3, und (23) für π 2 π Ordner Zwei zugeordnete Normalrisse eines Punktes P liegen immer auf einer Geraden senkrecht zur Rissachse. Diese Gerade heißt auch Ordner von P und wird mit ord(p) bezeichnet. Ordner sind ein wichtiges Hilfsmittel in Konstruktionen. So ist zum Beispiel der Kreuzriss P aus Grund- und Aufriss P und P konstruierbar, denn P liegt auf einem Ordner mit P und es gilt OH = OH.
15 KAPITEL 3. ZUGEORDNETE NORMALRISSE Übung: Konstruktion des Kreuzrisses Ein Objekt ist gegeben in Grund- und Aufriss. Wir wollen dazu den Kreuzriss konstruieren. Aufgabe Konstruktion Übertrage Punkte einzeln mit Hilfe ihrer Ordner.
16 KAPITEL 3. ZUGEORDNETE NORMALRISSE 15 Lösung 3.5 Übung: Konstruktion eines Zentralrisses (I) Gegeben seien der Grundriss und der Aufriss eines Objektes. Wir wollen eine anschauliche Darstellung des Objektes konstruieren. Wie kann man das machen? Eine Möglichkeit dazu ist die Konstruktion einer Zentralprojektion des Objektes, denn die Zentralprojektion ist in der Regel anschaulicher als die Darstellung in den zugeordneten Normalrissen. Um eine Zentralprojektion konstruieren zu können, brauchen wir die Angabe des Augpunktes und der Bildebene der Zentralprojektion. Diese sollen mit in Grund- und Aufriss eingetragen sein: Z und Z seien Grund- und Aufriss des Augpunktes Z. g sei die Schnittgerade der Zentralriss-Bildebene mit der Grundrissebene. Die Zentralrissebene soll senkrecht auf der Grundrissebene stehen.
17 KAPITEL 3. ZUGEORDNETE NORMALRISSE 16 Wir gehen die Aufgabe nun so an, dass wir den gegebenen Grund- und Aufriss auf die linke Seite eines Papiers zeichnen, auf der rechten Seite soll der Zentralriss entstehen. Der erste Schritt in der Kontruktion des Zentralrisses ist eine Drehung des Grundrisses, so dass g und die Rissachse parallel liegen. Der gedrehte Grundriss ist Teil der neuen Konstruktion und wird auf die rechte Seite gezeichnet. Vorlage Z Rissachse Z g g Z
18 KAPITEL 3. ZUGEORDNETE NORMALRISSE 17 Vorbereitungen Linker Teil: Grund- und Aufriss Rechter Teil: Zentralriss Z Horizont Rissachse g gedrehter Grundriss, so dass g und g parallel sind Z g g Z Z Aufriss des Augpunktes Z Grundriss des Augpunktes g Schnittgerade der Zentralrissebene mit der Grundrissebene g Verlängerung der Rissachse Horizont Parallele zur Rissachse durch Z
19 KAPITEL 3. ZUGEORDNETE NORMALRISSE Bild eines Punktes Gegeben: Punkt P in Grundriss P und Aufriss P Gesucht: Zentralriss P des Punktes P P P Z p P Rissachse s = ord(p ) t P P P Z g g P Z P Schnittpunkt von g und P Z s, t Senkrechte zur Rissachse durch P P Schnittpunkt von P Z und s p Parallele zur Rissachse durch P P Schnittpunkt von p und t
20 KAPITEL 3. ZUGEORDNETE NORMALRISSE Fluchtpunkte waagerechter Geraden Gegeben: Gerade h, die parallel zur Grundrissebene ist. (Der Aufriss h ist also parallel zur Rissachse) Gesucht: Fluchtpunkt F von h (und aller zu h parallelen Geraden). Z F Horizont Rissachse h s h h F g p Z p Parallele zu h durch Z F Schnittpunkt von g und p s Senkrechte zur Rissachse durch F F Schnittpunkt des Horizonts mit s
21 KAPITEL 3. ZUGEORDNETE NORMALRISSE 20 Konstruktion Mit Hilfe der Konstruktion von Fluchtpunkten von Geraden und Bildern von Punkten kann man nun den gesamten Zentralriss schnell herleiten. Schritte: Konstruiere die Fluchtpunkte der waagerechten Geraden; Da parallele Geraden den gleichen Fluchtpunkt haben, gibt es zwei Fluchtpunkte in dieser Konstruktion. (F 1 und F 2 ). Wähle 3 Eckpunkte des Quaders, die nicht auf einer Fläche liegen, und konstruiere ihre Bilder. (A, B, C ). Konstruiere das Bild der Dachspitze (D ). Nun können alle anderen Eckpunkte und alle Verbindungsgeraden abgeleitet werden als Schnittpunkte. Dabei ist zu beachten, dass Geraden, die senkrecht auf dem Grundriss stehen, auch senkrechte (und damit parallele) Bilder im Zentralriss haben.
22 KAPITEL 3. ZUGEORDNETE NORMALRISSE 21 Lösung Z Rissachse Z g g Z
23 KAPITEL 3. ZUGEORDNETE NORMALRISSE Übung: Konstruktion eines Zentralrisses (II) Hier soll der Zentralriss eines Quaders konstruiert werden, wobei der Quader und die Angaben über Augpunkt und Zentralrissebene wieder in Grund- und Aufriss gegeben sind. Hier gibt es keine waagerechten Geraden, die ausgenutzt werden könnten. Daher wird jetzt vorgestellt, wie man Fluchtpunkte beliebiger Geraden konstruiert. Vorlage Z Rissachse Z g g Z
24 KAPITEL 3. ZUGEORDNETE NORMALRISSE Fluchtpunkte beliebiger Geraden S r F q Z h s 1 s 2 Rissachse S 1 p 1 Z h h g g S 2 p 2 Z p 1, p 2 Parallele zu h durch Z S 1, S 2 Schnittpunkte von p 1 und p 2 mit g s 1, s 2 Senkrechte zur Rissachse durch S 1 und S 2 q Parallele zu h durch Z S Schnittpunkt von s 1 und q r Parallele zur Rissachse durch S F Schnittpunkt von r und s 2
25 KAPITEL 3. ZUGEORDNETE NORMALRISSE 24 Konstruktion Damit ist die Konstruktion nun analog zur Übung (I): Konstruiere 3 Fluchtpunkte von Graden. (F 1, F 2, F 3 ). Wähle 3 Eckpunkte des Quaders, die nicht auf einer Fläche liegen (hier: wähle sie auf dem Horizont; dies vereinfacht die Konstruktion), und konstruiere ihre Bilder. (A, B, C ). Finde alle anderen Ecken als Schnittpunkte von Geraden. (Dabei führen neue Punkte auch zu neuen Geraden von den Fluchtpunkten aus.) Lösung Z Rissachse Z g g Z
26 KAPITEL 3. ZUGEORDNETE NORMALRISSE Sichtbarkeit Im Zentralriss ist sichtbar, was vom Augpunkt aus sichtbar ist. Im Zentralriss werden sichtbare Kanten durchgezeichnet, unsichtbare werden gestrichelt gezeichnet. Übung: Zeichne in den Übungen 3.5 und 3.6 die unsichtbaren Kanten gestrichelt.
27 Kapitel 4 Grundelemente der Normalprojektion Normalrisse sind ein wichtiges Instrument, um Zeichnungen eines räumlichen Objektes umkehrbar eindeutig zu machen und damit das räumlich Objekt erfassen zu können. Normalrisse werden für alle maßgerechten Zeichnungen eingesetzt, die Grundlage für die Entwurfs- und Ausführungsplanung sind. Mit Hilfe der Normalrisse kann die Lage der verschiedenen Bauteile zueinander und im Raum sowie die wahre Gestalt und Größe der Bauteile ermittelt werden. Die Methode der Normalrisse kann benutzt werden, um räumliche Probleme in der Zeichnung zu lösen. Zum Beispiel können die Schnittlinien und Anschlüsse von verschiedenen Gebäudeteilen damit berechnet werden. Um sich der Methode der Normalrisse systematisch zu nähern, wird hier zuerst eine Einführung in die geometrischen Grundelemente Punkt, Gerade und Ebene in Normalrissen behandelt. Danach werden diese Grundelemente zueinander in Beziehung gesetzt. Es wird zum Beispiel untersucht, ob ein Punkt in einer Ebene liegt oder in welcher Geraden sich zwei Ebenen schneiden. Wir betrachten im Folgenden immer die Darstellung durch Grund- und Aufriss, also die Zweitafelprojektion. 26
28 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Darstellung von Punkten Ein Punkt P wird auf zwei Bildpunkte abgebildet: P im Grundriss und P im Aufriss. Die beiden Punkte P und P liegen auf einem Ordner senkrecht zur Rissachse (12). Meistens sollte das abgebildete Objekt über der Grundrissebene und vor der Aufrissebene liegen. Es kann aber auch passieren, dass ein Punkt unter der Grundrissebene oder hinter der Aufrissebene liegt. Daher ist es erforderlich, immer die Bezeichnungen P und P zu verwenden. Verschiedene Lagen von Punkten: P P P P P P P P P P (12) P P P auf Aufrissebene P hinter Aufrissebene P auf Grundrissebene und hinter Aufrissebene P unter Grundrissebene Vereinbarung über die Sichtbarkeit einzelner Punkte: A liegt über B: A verdeckt B C liegt vor D: C verdeckt D
29 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Darstellung von Geraden Eine Gerade g ist bestimmt durch zwei Punkte auf der Geraden. Die Lage einer Geraden im Raum kann gekennzeichnet werden mit Hilfe der Durchstoßpunkte der Geraden durch die Rissebenen π 1 und π 2. Der Durchstoßpunkt der Geraden g mit der Grundrissebene wird Grundrissspurpunkt S 1 genannt. Der Durchstoßpunkt der Geraden g mit der Aufrissebene wird Aufrissspurpunkt S 2 genannt. Es gilt: S 1 liegt auf g, und S 1 liegt auf g und der Rissachse (12). S 2 liegt auf g und der Rissachse (12), und S 2 liegt auf g. Ist P ein Punkt auf g, so liegt P auf g und P auf g. Außerdem liegen P und P auf dem Ordner ord(p). Aufrissebene π 2 g (12) P S 2 =S 2 S 2 =S 2 g ord(s g 2 ) ord(s 2 ) P ord(p) ord(p) (12) S 1 S 1 P ord(s 1 ) S 1 =S 1 g P Grundrissebene π 1 S 2 ord(s 1 ) g P S 2 S 1 =S Hauptlinie erster Art oder Höhenlinie Ist eine Gerade g parallel zur Grundrissebene, so heißt sie Hauptlinie 1. Art oder Höhenlinie oder Höhengerade. Ob eine Gerade eine Höhenlinie ist, kann im Aufriss festgestellt werden. Eine Höhenlinie erscheint im Aufriss parallel zur Rissachse. g P g P g g P Rissachse g P
30 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Hauptlinie zweiter Art oder Frontlinie Ist eine Gerade g parallel zur Aufrissebene, so heißt sie Hauptlinie 2. Art oder Frontlinie oder Frontgerade. Ob eine Gerade eine Frontlinie ist, kann im Grundriss festgestellt werden. Eine Frontlinie erscheint im Grundriss parallel zur Rissachse. g g g Rissachse P P g P g P Hauptlinie dritter Art Ist eine Gerade g parallel zur Kreizrissebene, so heißt sie Hauptlinie 3. Art. Diese spezielle Lage kann man in Grund- und Aufriss nicht ablesen. B B B g g =g g g g A Rissachsen A =B A g A
31 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Projizierende Geraden Ist eine Gerade g senkrecht zu einer der Rissebenen und parallel zu den anderen, so heißt sie projizierend. Man unterscheidet die grundrissprojizierenden, die aufrissprojizierenden und die kreuzrissprojizierenden Geraden. Ist g grundrissprojizierend, so steht g senkrecht auf der Grundrissebene und verläuft parallel zu Aufund Kreuzrissebene. Die Gerade g erscheint dann als Punkt im Grundriss und verläuft im Aufriss senkrecht zur Rissachse. Ist g aufrissprojizierend, so steht g senkrecht auf der Aufrissebene und verläuft parallel zu Grundund Kreuzrissebene. Die Gerade g erscheint dann als Punkt im Aufriss und verläuft im Grundriss senkrecht zur Rissachse. Ist g kreuzrissprojizierend, so steht g senkrecht auf der Kreuzrissebene und verläuft parallel zu Grundund Aufrissebene. Die Gerade g verläuft dann als waagerechte Linie in Grund- und Aufriss. g P=g P=g g Rissachse Rissachse Rissachsen P=g g g g senkrecht zur Grundrissebene π 1 g senkrecht zur Aufrissebene π 2 g senkrecht zur Kreuzrissebene π 3
32 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Übung: Konstruktion von Spurpunkten Aufgabe Sei P ein Punkt auf der Geraden g. Konstruieren Sie den Aufriss von P und die Spurpunkte von g. g (12) g P Konstruktion P liegt auf ord(p) und auf g. S 1 liegt auf g und auf (12). S 1 liegt auf g und auf ord(s 1 ). S 2 liegt auf g und auf (12). S 2 liegt auf g und auf ord(s 2 ). 4.4 Darstellung von Ebenen Eine Ebene kann bestimmt werden durch zwei Geraden g und h, die entweder parallel sind oder sich schneiden: ε = gh; eine Gerade g und einen Punkt P, der nicht auf g liegt: ε = gp; drei Punkte, die nicht auf einer Geraden liegen (ε = PQR). π 2 ε s 2 s 2 (12) s 1 π 1 s 1 Die Schnittgeraden s 1 und s 2 der Ebene ε mit den Rissebenen heißen Spurgeraden oder kurz Spuren der Ebene. Man unterscheidet die Grundrissspur und die Aufrissspur. Die Spuren der Ebene ε schneiden sich auf der Rissachse.
33 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Erstprojizierende (grundrissprojizierende) Ebene Ist eine Ebene senkrecht zur Grundrissebene, so heißt sie erstprojizierend oder grundrissprojizierend. Ihr Grundriss ist in diesem Falle eine Gerade und gleich der Grundrissspur. s 2 s Zweitprojizierende (aufrissprojizierende) Ebene Ist eine Ebene senkrecht zur Aufrissebene, so heißt sie zweitprojizierend oder aufrissprojizierend. Ihr Aufriss ist in diesem Falle eine Gerade und gleich der Aufrissspur. s 2 s Doppeltprojizierende Ebene Ist eine Ebene parallel zur Kreuzrissebene, so heißt sie doppeltprojizierend. Ihr Grund- und ihr Aufriss sind jeweils Geraden, die gleich der Grund- und Aufrissspur sind und außerdem senkrecht zur Rissachse (12) verlaufen. s 2 s 1
34 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Höhen- oder Schichtebene Ist eine Ebene parallel zur Grundrissebene, so heißt sie Höhenebene oder Schichtebene. Ihr Aufriss ist eine Gerade parallel zur Rissachse (12) und diese ist gleich der Aufrissspur. s Frontebene Ist eine Ebene parallel zur Aufrissebene, so heißt sie Frontebene. Ihr Grundriss ist eine Gerade parallel zur Rissachse (12) und diese ist gleich der Grundrissspur. s Pultebene Ist eine Ebene senkrecht zur Kreuzrissebene, so heißt sie Pultebene. Ihr Kreuzriss ist eine Gerade. Ihre Grund- und Aufrissspuren sind Geraden parallel zur Rissachse (12). s 2 s 1
35 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Hauptlinien von Ebenen Eine Teilgerade einer Ebene heißt Hauptlinie, wenn sie parallel zu einer der Rissebenen verläuft. f h s 2 (12) (12) h f s 1 h ist parallel zur Grundrissebene. f ist parallel zur Aufrissebene. 4.5 Übung: Konstruktion von Spurgeraden Aufgabe Sei ε = ab eine Ebene. Konstruieren Sie die Spurgeraden von ε. b (12) a a b Konstruktion Konstruiere zuerst die Spurpunkte S 1 (a),s 2 (a),s 1 (b),s 2 (b) der Geraden a und b. Die Spurgeraden von ε sind dann die Verbindungsgeraden S 1 (a)s 1 (b) und S 2 (a)s 2 (b).
36 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Lage zweier Geraden im Raum Zwei verschiedene Geraden g und h im Raum können drei unterschiedliche Lagen zueinander einnehmen: g und h schneiden sich, g und h sind parallel, oder g und h sind windschief Zwei Geraden schneiden sich Wenn zwei Geraden g und h sich schneiden, dann schneiden sich auch ihre Grundrisse g und h in einem Punkt P und ihre Aufrisse g und h in einem Punkt P. Weiter sind dann P und P Grundund Aufriss des Schnittpunktes P von g und h und daher liegen P und P auf einem Ordner. g P h Ordner g P h Zwei Geraden sind parallel Sind zwei Geraden g und h parallel und nicht projizierend, so sind g, g, h und h Geraden und es gilt g h und g h. Sind zwei Geraden g und h projizierend, so sind sie parallel, falls sie senkrecht auf derselben Rissebene stehen.
37 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Zwei Geraden sind windschief Zwei Geraden g und h sind windschief, wenn sie weder parallel zueinander sind noch sich schneiden. Es kann passieren, dass sich ihr Grund- und ihr Aufriss schneiden, aber die Schnittpunkte liegen dann nicht auf einem Ordner. Schreibe: G 1 = H 1 = g h im Grundriss. G 2 = H 2 = g h im Aufriss. Für die Schnittpunkte der beiden Geraden in Grund- und Aufriss ist die Frage der Sichtbarkeit zu klären. Die jeweils verdeckte Gerade wird unterbrochen gezeichnet. Es gilt: G 1 unter H 1 im Aufriss ( g liegt unter h ) = g unterbrochen. G 2 unter H 2 im Grundriss ( g liegt vor h ) = h unterbrochen. g g liegt vor h G 2=H 2 H 1 G 1 h H 2 G 1=H 1 G h 2 g g liegt unter h Bei allen Konstruktionen muss auf den Unterschied zwischen wahren und scheinbaren Schnittpunkten geachtet werden. Nur mindestens zwei zugeordnete Normalrisse können die Lage im Raum eindeutig kennzeichnen. Liegen zwei Geraden in einer Ebene, so sind sie entweder parallel, oder sie schneiden sich. Windschief können sie in diesem Fall nicht sein.
38 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Übung: Konstruktion von Inzidenzen (I) Aufgabe Gegeben sei eine Ebene, definiert durch zwei sich schneidende Geraden a und b, und der Grundriss g einer in ab enthaltenen Geraden g. Gesucht ist der Aufriss g von g. a (12) g b b a Konstruktion g schneidet beide Geraden a und b. Sei P der Schnittpunkt von g mit a und Q der Schnittpunkt von g mit b. Die Grundrisse P und Q sind dann die Schnittpunkte von g mit a und von g mit b. Die Aufrisse P und Q können durch die Ordner von P und O und deren Schnittpunkt mit a und b konstruiert werden. Lösung (12) g P Q g Q P a b b a
39 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Übung: Konstruktion von Inzidenzen (II) Aufgabe Gegeben sei eine Ebene, definiert durch ihre Spurgeraden s 1 und s 2, und der Grundriss g einer in der Ebene enthaltenen Geraden g. Gesucht ist der Aufriss g von g. s 2 (12) s 1 g Konstruktion Dies ist ein Spezialfall der Übung Inzidenzen (I): Wieder ist eine Ebene durch zwei Geraden gegeben, nur sind die Geraden jetzt die Spurgeraden. In Grund- und Aufriss erscheint daher nur jeweils eine Gerade. Die beiden anderen Grund- und Aufrisse s 2 und s 1 entsprechen gerade der Rissachse (12). Damit kann nun genau wie in der Übung Inzidenzen (I) verfahren werden. Lösung g s 2 B = B (12) A B s 1 A = A g
40 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Übung: Konstruktion von Inzidenzen (III) Aufgabe Gegeben sei eine Ebene ab und der Grundriss P eines Punktes auf ab. Gesucht ist der Aufriss P von P. b (12) a a P b Konstruktion Wähle eine Gerade g in der Ebene ab durch den Punkt P. Zeichne zunächst nur g und erhalte die Schnittpunkte A von g mit a und B von g mit b. Konstruiere nun g nach (Inzidenzen I). Dann liegt P auf g und auf dem Ordner ord(p ). Damit kann P konstruiert werden. Diese Konstruktion wird auch als Angittern von P bezeichnet. Lösung B g b P (12) A A ord(p) a a P B g b
41 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Übung: Konstruktion von Inzidenzen (IV) Aufgabe Gegeben sind Grund- und Aufriss einer Dachfläche sowie der Grundriss eines Dachflächenfensters. Gesucht ist der Aufriss des Dachflächenfensters. (12) Konstruktion Hier können die Konstruktionen von Inzidenzen verwendet werden. Es gibt dazu verschiedene Möglichkeiten: Konstruiere den Aufriss der 4 Geraden des Dachfesterns nach Inzidenzen (I). Konstruiere den Aufriss der 4 Ecken des Dachfesterns nach Inzidenzen (III). Schneller geht es mit der folgenden Variante: Konstruiere den Aufriss von zwei parallelen Geraden des Dachfensterns nach Inzidenzen (I). Konstruiere die 4 Ecken des Dachfensters nun mit Hilfe ihrer Ordner: jede Ecke liegt auf einer der konstruierten Geraden und auf ihrem Ordner.
42 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION 41 Lösung ε B Q P g 1 A D R g 2 S C (12) B Q g 1 P ε A D R g 2 S C 4.11 Sichtbarkeit Im Grundriss ist sichtbar, was bei Blick von vorne sichtbar ist. (Lese aus Aufriss ab!) Im Aufriss ist sichtbar, was bei Blick von vorne sichtbar ist. (Lese aus Grundriss ab!)
43 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Übung: Konstruktion von Lagen (I) Aufgabe Gegeben sei eine Gerade g und eine Ebene ab in Grund- und Aufriss. Die Ebene ab sei nicht erstprojizierend, d.h. sie sei nicht senkrecht zur Grundrissebene. Weiter sei g nicht in ab. Gesucht ist der Durchstoßpunkt P von g mit ab, d.h. der Schnittpunkt der Geraden mit der Ebene. g b (12) a a g b Konstruktion Konstruiere zuerst die in ab enthaltene Gerade h mit h = g nach Inzidenzen (I). Diese Gerade h heißt auch Deckgerade von g. P liegt auf g, also liegt P auf h. P ist dann der Schnittpunkt von h und g. P erhält man über den Ordner von P. Anschließend an die Konstruktion entscheide über die Sichtbarkeit der Geraden g. Nicht sichtbare Teile von g und g werden gestrichelt eingezeichnet. Lösung g h b P (12) a a P g = h b
44 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Übung: Konstruktion von Lagen (II) Aufgabe Gegeben seien zwei Ebenen in Grundriss und Aufriss. Gesucht ist die Schnittgerade der beiden Ebenen. (12) Konstruktion Diese Aufgabe wird auf Lagen (I) zurückgeführt: Man bestimme geeignete Teilgeraden der ersten Ebene sowie die Durchstoßpunkte in der zweiten Ebene. Die Verbindungsgerade zweier solcher Punkte ist die gesuchte Schnittgerade.
45 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION 44 Lösung ε 1 P 1 k P 2 g 2 h 1 h 2 ε 2 g 1 (12) ε 2 P 2 g 2=h 2 k P 1 g 1=h 1 ε 1 g 1 ε 2 (Kante) h 1 Deckgerade von g 1 in ε 1 P 1 g 1 ε 2 g 2 ε 1 (Kante) h 2 Deckgerade von g 1 in ε 2 P 2 g 2 ε 1 k = P 1 P 2
46 KAPITEL 4. GRUNDELEMENTE DER NORMALPROJEKTION Neigungswinkel Geraden Der Neigungswinkel einer Geraden g gegen die Grundrissebene ist der Winkel β g zwischen g und dem Grundriss g : g (12) β g g Ebenen und Fallgeraden In einer Ebene µ liegen Geraden g mit unterschiedlichen Neigungswinkeln. Der größte vorkommende Winkel β g wird als Neigungswinkel der Ebene β µ angesehen. Wenn g in µ enthalten ist und senkrecht zur Grundrissspur s 1 von µ steht, dann heißt g eine Fallgerade von µ. Es gilt: Der Neigungswinkel von µ ist der Neigungswinkel einer Fallgeraden von µ. h µ β h β g =β µ g s 2 g (12) h s 1 β h < β g β g = β µ
47 Kapitel 5 Platonische Körper In diesem Kapitel werden die Methoden aus den vorherigen Kapiteln angewendet, um Schnittfiguren durch gewisse Objekte zu konstruieren. Als Objekte werden die platonischen Körper herangezogen. Dies sind konvexe Polyeder, bei denen an jeder Ecke q reguläre kongruente p-ecke zusammenstoßen. Es gibt fünf Platonische Körper: 46
48 KAPITEL 5. PLATONISCHE KÖRPER 47 p = q = 3: Tetraeder p = 4, q = 3: Hexaeder, Würfel p = 3, q = 4: Oktaeder p = 5, q = 3: Dodekaeder p = 3, q = 5: Ikosaeder
49 KAPITEL 5. PLATONISCHE KÖRPER Übung: Schnittfigur Die Gerade s 1 ist die Grundrissspur einer Ebene mit der Neigung 30. Konstruieren Sie den Schnitt des Tetraeders mit der Ebene. Zeichnen Sie sichtbare Kanten durchgezogen, unsichtbare gestrichelt. Aufgabe s 1
50 KAPITEL 5. PLATONISCHE KÖRPER Spurgeraden einer Ebene Gegeben: Grundrissspur s 1 und Neigungswinkel β einer Ebene Gesucht: Aufrissspur s 2 der Ebene B k t p D s 2 B r Rissachse A =A q β s 1 C s 1 Grundrissspur der Ebene A = A Schnittpunkt von s 1 und der Rissachse B Punkt auf der Rissachse p Parallele zu s 1 durch B q Senkrechte zu s 1 durch B C Schnittpunkt von s 1 und q β Neigungswinkel der Ebene r Gerade durch C im Winkel β zu q D Schnittpunkt von p und r k Kreis um B mit dem Radius B D t Senkrechte zur Rissachse durch B B Schnittpunkt von t und k s 2 Gerade durch A und B
51 KAPITEL 5. PLATONISCHE KÖRPER Schnittpunkt mit einer Geraden Gegeben: Grund- und Aufriss einer Geraden g sowie Spurgeraden s 1 und s 2 einer Ebene Gesucht: Grund- und Aufriss des Schnittpunktes P von Ebene und Gerade A g r P t h s 2 A B Rissachse P g =h s 1 u B Sei h eine Deckgerade von g, d.h. eine Gerade in der Ebene, die den gleichen Grundriss wie g hat. Damit ist der Grundriss von h gegeben und wir konstuieren zuerst den Aufriss von h nach Inzidenzen (II). Der Schnittpunkt von g und h liegt in der Ebene und ist damit P. Nun erhalte P über den Ordner von P.
52 KAPITEL 5. PLATONISCHE KÖRPER 51 g =h Grundriss der Geraden g und h A Schnittpunkt von h und der Rissachse r Senkrechte zur Rissachse durch A A Schnittpunkt von r und s 2 B Schnittpunkt von h und s 1 u Senkrechte zur Rissachse durch B B Schnittpunkt von u und der Rissachse h Gerade durch A und B P Schnittpunkt von g und h t Senkrechte zur Rissachse durch P P Schnittpunkt von t und g Konstruktion Für die Lösung der Aufgabe nehmen wir jede Kante des Polyeders und berechnen den Schnittpunkt. Die Verbindung aller dieser Schnittpunkte ist dann die gesuchte Schnittfigur. Ein paar Bemerkungen dazu: Die Deckgerade h zu einer Gerade g kann für alle Kanten mit gleichem Grundriss gleichzeitig benutzt werden. Ist h parallel zur Rissachse, so ist h parallel zu s 2. Ist h parallel zu s 1, so ist h parallel zur Rissachse. Die Konstruktion kann auch mit h = g von oben nach unten durchgeführt werden.
53 KAPITEL 5. PLATONISCHE KÖRPER 52 Lösung
54 Kapitel 6 Seitenrisse Manchmal ist es sehr nützlich, neben der Grund-, Auf- und Kreuzrissebene eine neue Rissebene, genannt Seitenrissebene, einzuführen. Zum Beispiel kann man damit manchmal ein Objekt anschaulicher darstellen oder es können Maßaufgaben leichter gelöst werden. Die Konstruktion des Seitenrisses aus einer Zweitafelprojektion wird umprojizieren genannt. 53
55 KAPITEL 6. SEITENRISSE Die Seitenrissebene So wie Grund- und Aufriss immer senkrecht aufeinander stehen, muss auch die neue Seitenrissebene π 4 senkrecht auf einer der bisherigen Rissebenen stehen (also π 4 π 1 oder π 4 π 2 oder π 4 π 3 ). P IV Seitenrissebene π 4 Aufrissebene π 2 P P alte Rissachse neue Rissachse Grundrissebene π 1 P P P IV alte Rissachse (14) neue Rissachse a neuer Ordner alter Ordner P a (12) Im Beispiel steht die Seitenrissebene senkrecht auf der Grundrissebene. Nach dem Umprojizieren ist der Aufriss überflüssig geworden und kann daher weggelassen werden. Man nennt in diesem Fall die Aufrissebene auch wegfallende Rissebene. Die Rissachse zwischen Grund- und Aufrissebene heißt wegfallende Rissachse. Ein Seitenriss kann in der Zweitafelprojektion durch die Angabe einer neuen Rissachse eingeführt werden. Es gilt: Der Abstand des neuen Risses von der neuen Rissachse ist gleich dem Abstand des alten Risses von der alten Rissachse. Mit (12) als wegfallende Rissachse und (14) als neue Rissachse ergibt sich daher: P IV liegt auf ord(p ) bzgl. (14) mit abst(p IV, (14)) = abst(p, (12)). Die Richtung, in welcher die Abtragung erfolgt, ist nicht festgelegt. Hat man sich aber bei einem Objekt für die Richtung entschieden, so liegt die Richtung für alle Objekte fest.
56 KAPITEL 6. SEITENRISSE Übung: Konstruktion eines Seitenrisses Aufgabe Konstruieren Sie den Seitenriss (Aufrissebene π 2 = wegfallende Rissebene). E = H F = G A = D B = C (12) S D = H C = G S A = E B = F (14) Konstruktion Übertrage jede Ecke des Objektes einzeln. Zur Übertragung einer Ecke benutze ihren Ordner aus dem Grundriss und den Abstand von der Rissachse aus dem Aufriss.
57 KAPITEL 6. SEITENRISSE 56 Lösung E = H F = G A = D B = C D IV H IV C IV G IV (12) D = H S C = G S IV E IV A IV F IV B IV S A = E B = F (14)
58 KAPITEL 6. SEITENRISSE Doppelter Seitenriss Man kann die Erstellung eines Seitenrisses auch mehrfach anwenden. Durch zweifaches Anwenden kann man jede beliebige Ebene zur Rissebene machen. π 2 π 4 (45) (12) (14) π 1 π 5 Die erste Seitenrissebene π 4 steht senkrecht zur Grundrissebene π 1 und ersetzt die alte Aufrissebene π 2. Die zweite Seitenrissebene π 5 steht auf der ersten Seitenrissebene π 4 senkrecht und ersetzt die Grundrissebene π 1. (14) P (45) (12) a P Ordner Ordner b a P IV b Ordner P V Ziele des doppelten Seitenrisses sind eine anschauliche Darstellung eines Objektes (zum Beispiel in einer gewünschten Blickrichtung) oder die Ermittlung der wahren Gestalt einer ebenen Figur.
59 KAPITEL 6. SEITENRISSE Übung: Konstruktion eines doppelten Seitenrisses Aufgabe Konstruieren Sie den doppelten Seitenriss des Würfels. E = F G = H (45) (12) A = B C = D A = E C = G B = F D = H (14)
60 KAPITEL 6. SEITENRISSE 59 Lösung B V A V E V F V DV C V H V E = F G = H G V E IV (45) A = B C = D A IV G IV (12) A = E C = G C IV B IV F IV H IV B = F D = H D IV (14)
61 KAPITEL 6. SEITENRISSE Übung: Projizierendmachen von Geraden Erinnerung: Eine Gerade ist projizierend, wenn sie senkrecht auf einer Rissebene steht und parallel zu den anderen (Auf- und Kreuzriss) ist. Aufgabe Mache die Gerade g projizierend. g (12) g Konstruktion Wähle zunächst eine Seitenrissebene π 4 parallel zu g und senkrecht zur Grundrissebene. Die Gerade g ist dann eine Frontlinie bezüglich π 4. (Der Schritt entfällt, wenn g schon eine Frontlinie ist). Wähle dann eine Seitenrissebene π 5 senkrecht zu g und π 4. Die Gerade g ist dann π 5 -projizierend. Im Beispiel: Wähle (14) parallel zu g, zum Beispiel durch (14) = g. Konstruiere g IV mittels zweier Punkte P und Q auf g. Wähle (45) senkrecht zu g IV. Dann ist g V ein Punkt. Notation: π 1 = Grundrissebene; π 2 = Aufrissebene; π 3 = Kreuzrissebene; π 4 = erste Seitenrissebene; π 5 = zweite Seitenrissebene.
62 KAPITEL 6. SEITENRISSE 61 Lösung g P a Q b (12) P V = Q V = g V Q b (45) (14) g P a Q IV g IV P IV 6.6 Übung: Drehen eines Punktes um eine Achse Aufgabe Man drehe den Punkt P um 50 um die Achse g. Der gedrehte Punkt heiße Q. P (12) g P g Konstruktion Mache die Gerade g projzierend und drehe dann. Im Normalriss auf π 5 erscheint die Drehung von P unverzerrt als Drehung von P V um den Punkt g V. Im Seitenriss π 4 ist der Riss des Bildpunkts von Q auf der Senkrechten zu g IV durch P IV zu finden. α Q V g V P V (45) Q IV P IV g IV
63 KAPITEL 6. SEITENRISSE 62 Lösung (12) (14) A A P P B g g B B IV A V =B V =g V Q V P V 50 A IV P IV (45) g IV 6.7 Übung: Konstruktion einer Gerade Aufgabe Die Gerade g enthält den Punkt A und hat gegen die Grundrissebene den Neigungswinkel 30. Konstruiere g. (12) g A = A Konstruktion Wir konstruieren eine zu g parallele Seitenrissebene. Der Winkel von g IV zur Rissachse (14) ist dann der gegebene Neigungswinkel. Lösung g B b (12) (14) g b B 30 A = A = A IV g IV B IV
64 KAPITEL 6. SEITENRISSE Übung: Projizierendmachen von Ebenen Erinnerung: Eine Ebene ist projizierend, wenn sie senkrecht auf einer Rissebene steht, also ihr Riss eine Gerade ist. Aufgabe Eine Ebene sei durch zwei Geraden a und b gegeben. Mache die Ebene ε = ab projizierend. a b (12) b a Konstruktion Wir konstruieren zuerst eine Höhenlinie h in ε. Danach führen wir einen Seitenriss senkrecht zu h ein. Dann ist ε IV eine Gerade und ε ist projizierend bezüglich der neuen Rissebene. Wähle h parallel zur Rissachse (12). Konstruiere h nach Inzidenz (I). Wähle (14) senkrecht zu h. Ist g in ε enthalten, so ist g IV = ε IV oder g IV ist ein Punkt auf ε IV. Lösung B h A a x y C b b (12) B h C A a y x C IV A IV =B IV =h IV ε IV (14)
65 KAPITEL 6. SEITENRISSE Übung: Neigungswinkel einer Ebene Aufgabe Eine Ebene ε sei durch ihre Spuren s 1 und s 2 gegeben. Bestimme den Neigungswinkel von ε gegen die Grundrissebene. s 2 (12) s 1 Konstruktion Wir machen ε projizierend. Dann ist der Winkel von ε IV zur Rissachse gleich dem Neigungswinkel. Lösung s 2 A = A x x g s 1 α (12) = h A B=B =B =B IV s 1 = h = h ε IV (14)
66 KAPITEL 6. SEITENRISSE Übung: Entzerren durch Umprojizieren (I) Aufgabe Konstruieren Sie die wahre Gestalt des Schnitts µ des Trichters mit der Ebene ε = UV W. A = D B = C S (12) D C W Konstruktion S V U A B Mache zuerst die Ebene ε projizierend. Dann ist ε IV eine Gerade. Dann führe einen neuen Seitenriss parallel zu ε ein. Wähle die Rissachse parallel zu ε IV, zum Beispiel als (45) = ε IV. µ V zeigt nun µ in wahrer Gestalt und Größe.
67 KAPITEL 6. SEITENRISSE 66 Lösung A = D B = C D U b W V S a c W C P h (12) (14) U S V A B x P z y a c (45) = µ IV W IV h V IV y z V V W V µ V b U IV x U V
68 KAPITEL 6. SEITENRISSE Übung: Entzerren durch Umprojizieren (II) Aufgabe Gegeben ist die Grundrissspur s 1 einer Ebene mit der Neigung 60 zur Grundrissebene und ein Fünfeck, das in dieser Ebene liegt. Konstruieren Sie die wahre Gestalt des Fünfecks. s 1
69 KAPITEL 6. SEITENRISSE 68 Konstruktion Sei P ein Punkt des Fünfecks. Wir suchen den Punkt P in der wahren Gestalt des Fünfecks. a t P C a r P B q p β s 1 A s 1 Grundrissspur der Ebene A Punkt auf s 1 p Senkrechte zu s 1 durch A β Neigungswinkel der Ebene q Gerade durch A im Winkel β zu p r Senkrechte zu p durch P B Schnittpunkt von q und r t Senkrechte zu q durch B C Schnittpunkt von r und p a Abstand von P und C P Punkt auf t im Abstand a von B
70 KAPITEL 6. SEITENRISSE 69 Lösung Die Lösung der Aufgabe kann nun erreicht werden, indem jeder Eckpunkt des Fünfecks übertragen wird. s 1
71 Kapitel 7 Kotierte Projektion 7.1 Die kotierte Projektion Bei der kotierten Projektion wird jeder Raumpunkt P durch seinen Grundriss P und seine Kote, d.h. den Abstand von P zur Grundrissebene, dargestellt. Dabei wird für die Höhen immer ein Maßstab angegeben. D Kotierte Projektion 7 1 A 7 A C D A (1) C 1 D (7) C (1) Grundrissebene B = B B (0) 70
72 KAPITEL 7. KOTIERTE PROJEKTION Übung: Konstruktion eines Seitenrisses Aufgabe Zeichnen Sie den Seitenriss des folgenden Walmdachs. A (1) D (1) E (5) F (5) Rissachse (14) Maßstab: B (1) C (1) Konstruktion Die Kote eines Punktes P entspricht dem Abstand von P und der Rissachse (12) und damit auch dem Abstand von P IV zur Rissachse (14). Um einen Punkt P aus der kotierten Projektion in den Seitenriss zu übertragen, kann sein Ordner benutzt werden und mit der Kote der Abstand des Bildpunktes von der Rissachse (14) ermittelt werden.
73 KAPITEL 7. KOTIERTE PROJEKTION 72 Lösung E A F B D A (1) D (1) E (5) F (5) C Rissachse (14) Maßstab: B (1) C (1)
74 KAPITEL 7. KOTIERTE PROJEKTION Geraden Eine Gerade g wird in der kotierten Projektion als graduierte Gerade dargestellt: (2) (3) i (4) (5) (6) g Punkte P auf g mit ganzzahliger Kote heißen Hauptpunkte der Geraden g. Der Abstand zwischen den Grundrissen benachbarter Hauptpunkte heißt das Intervall i von g. g β 1 k (k + 1) g (0) β (k) i Grundrissebene Für den Winkel β zwischen der Grundrissebene und der Geraden g gilt: tanβ = 1/i. Dieser Wert heißt auch Anstieg, Böschung, Steigung oder Gefälle von g. Gelegentlich wird der Anstieg als Prozentwert p% angegeben: p = 100/i. (Wegen 100/100 = 1 = tan 45 entspricht einer Steigung von 100% der Winkel β = 45.) Erinnerung: Eine parallel zur Grundrissebene verlaufende Gerade g heißt Höhengerade oder Höhenlinie. Dafür schreibt man hier auch g = g(z), wenn g in Höhe z verläuft. Ist z ganzzahlig, so heißt g = g(z) Haupthöhengerade oder Hauptschichtengerade.
75 KAPITEL 7. KOTIERTE PROJEKTION Übung: Konstruktion einer Graduierung Aufgabe Bestimmen Sie die Graduierung der Verbindungsgeraden g der Punkte A und B. g A (3,7) B (2,2) Maßstab: Konstruktion Man wähle g = (14) und konstruiere A IV, B IV und g IV. In der Seitenrissebene können die Höhen der Gerade, insbesondere die Hauptpunkte und damit das Intervall, leicht abgelesen werden. Lösung g (4) A (3, 7) i (3) B (2, 2) (2) (1) g IV i = 3 B IV Maßstab A IV
76 KAPITEL 7. KOTIERTE PROJEKTION Ebenen Ebenen werden in der kotierten Projektion durch ihre Hauptschichtengeraden h(z), z Z (Z = Menge der ganzen Zahlen), dargestellt. Die resultierende Parallelschar {h (z) : z Z} heißt Hauptschichtenplan der Ebene. ε f f h(z) h (k + 2) h (k + 1) Grundrissebene β h (0) = h(0) h (k) h (k 1) f h (z) h (k 2) Eine Fallgerade f ist eine Gerade mit der stärksten Neigung gegen die Grundrissebene. Jede Fallgerade steht senkrecht auf jeder Hauptschichtengerade; dies gilt auch im Grundriss. Eine Fallgerade wird im Grundriss durch einen Doppelstrich angegeben und in Fallrichtung der Ebene orientiert. Es gilt: Durch eine graduierte Fallgerade ist die Ebene eindeutig bestimmt. Der Anstieg (Böschung, Steigung) der Ebene ist gegeben durch tanβ = 1/i. Die Zahl i heißt Intervall der Ebene.
77 KAPITEL 7. KOTIERTE PROJEKTION Übung: Konstruktion von Ebenen Aufgabe Konstruieren Sie die Ebene durch die Punkte A, B und C sowie deren Anstieg. B ( 2) C (1) A (3) Konstruktion Eine der Seiten des Dreiecks (ABC) werden graduiert und damit wird der Hauptschichtenplan der Ebene bestimmt. Der Anstiegswinkel β wird in einem Seitenriss einer beliebigen Fallgeraden bestimmt.
78 KAPITEL 7. KOTIERTE PROJEKTION 77 Lösung B ( 2) h( 1) h(0) β C (1) h(1) h(2) A (3) g IV h(3) g
79 KAPITEL 7. KOTIERTE PROJEKTION Übung: Konstruktion von Schnittgeraden Aufgabe Man bestimme die Schnittgerade s der durch die Hauptschichtenpläne {h (z)} und {k (z)} gegebenen Ebenen δ und ε. k (6) k (5) k (4) k (3) k (2) h (0) h (1) h (2) h (3) h (4) h (5) Konstruktion Bestimme zwei Schnittpunkte von Geraden mit gleicher Kote und verbinde diese Schnittpunkte. Lösung k (6) k (5) k (4) s k (3) k (2) h (0) h (1) h (2) h (3) h (4) h (5)
80 KAPITEL 7. KOTIERTE PROJEKTION Übung: Konstruktion von Schnittpunkten Aufgabe Man bestimme den Schnittpunkt P der durch den Hauptschichtenplan {h (z)} gegebenen Ebene ε mit der graduierten Geraden g. (2) (1) g h (4) h (3) (4) (3) h (2) 3 4 (5) h (1) 5 Konstruktion Lege eine Ebene µ definiert durch den Hauptschichtenplan {k (z)}, durch g, so dass g die Fallgerade von µ ist. Bestimme die Schnittgerade s von ε mit µ. Der gesuchte Punkt liegt auf s und auf g und damit kann P bestimmt werden. Nun muss noch die Kote von P berechnet werden. Dazu wähle g als neue Rissachse (14) und berechne g IV und P IV. Nun kann die Kote von P als Abstand a von P IV und der Rissachse abgelesen werden. Lösung k (3) 4 P IV k (2) a (4) (5) k (1) (2) (3) P g IV 1 g = (14) (1) h (4) h (3) h (2) s h (1)
81 KAPITEL 7. KOTIERTE PROJEKTION Erste Grundaufgabe Gegeben sei eine Gerade g und zwei Zahlen i und j. Die Zahl j bestimme den Anstieg µ von g durch tan µ = 1/j. Gesucht ist eine Ebene durch g mit Anstieg β, wobei tanβ = 1/i gelte. Vorüberlegung Sei ε eine Lösung der Aufgabe. Dann hat ε den Anstieg β und damit ist β die Neigung aller Fallgeraden f von ε. Also muss β > µ oder β = µ gelten, sonst hat die Aufgabe keine Lösung. Im Fall β = µ ist g eine Fallgerade von ε. Daher steht der Hauptschichtenplan von ε senkrecht auf g und kann damit leicht eingezeichnet werden. Außerdem gibt es in diesem Fall nur eine Lösung. Im Fall β > µ sind genau zwei Lösungen zu erwarten, die von g aus gesehen nach verschiedenen Seiten abfallen. Ein Teil des Problems besteht darin, unter diesen Lösungen diejenige zu erkennen, die möglicherweise gewünscht wird. Meist benötigt man nur eine (durch g begrenzte) Hälfte der gesuchten Ebene, und es ist vorgegeben, auf welcher Seite von g sie liegt, und ob sie gegenüber g ansteigt oder abfällt. Vor Beginn der Konstruktion sollte man also feststellen, welche der beiden Lösungen gesucht wird. Lösung 1 Lösung 2 g
82 KAPITEL 7. KOTIERTE PROJEKTION 81 Konstruktion im Fall β > µ = 0 Im Fall β > µ = 0 ist g eine Höhengerade und wird als g(x) bezeichnet. (g ist parallel zur Grundrissebene). Dann ist der Hauptschichtenplan {h (k)} der gesuchten Ebene parallel zu g. Das Intervall zwischen h (k) und h (k + 1) ist gerade i. Damit kann der Schichtenplan gezeichnet werden. Beachte: Es gibt zwei Lösungen, je nachdem in welche Richtung die Ebene von g aus abfällt. Lösung 1 Lösung 2 h (k + 4) h (k + 3) h (k + 2) h (k + 1) g (x) h (k) h (k 1) h (k 2) h (k 1) h (k) g (x) h (k + 1) h (k + 2) Konstruktion im Fall β > µ > 0 Wähle zunächst auf g zwei beliebige Punkte P = P(u) und Q = Q(m) mit verschiedenen Koten u und m. Zeichne: Kreis k um P mit Radius r = i m u ; Tangente h an k durch Q ; Gerade f durch P senkrecht zu h. Dann ist h der Grundriss einer Höhengerade mit Kote m, d.h. es gilt h = h (m). Die Gerade f ist der Grundriss einer Geraden f durch P, welche h(m) schneidet. Daher hat die Ebene gh(m) die Fallgerade f und ihr Anstieg ist m u /r = 1/i. Die Ebene gh(m) ist daher die gesuchte Ebene. g Lösung 1 k Lösung 2 k g P (u) r h (u) h (m) P r f Q (m) Q f h (m) h (u)
83 KAPITEL 7. KOTIERTE PROJEKTION 82 Variante für Halbebenen: Lösung 1 g Lösung 2 g Q (m) P (u) r f h (m) Q (m) r P (u) h (u) f 7.10 Übung: Straße abböschen Aufgabe Böschen Sie die ebene Straße mit den Randgeraden g 1 und g 2 gegen das ebene Gelände mit der Fallgerade f ab. Verwenden Sie das Intervall i = 0, 5 sowohl für den Abtrag als auch für den Auftrag. (8) (11) (10) (9) (10) (11) (9) (12) (8) (13) (7) (6) f (14) g 1 g 2
84 KAPITEL 7. KOTIERTE PROJEKTION 83 Konstruktion Zunächst legen wir einen Hauptschichtenplan für das Gelände an. Dieser lässt sich an der Fallgeraden f ablesen. Dann bestimmen wir die Schnittpunkte der Straßenkante mit dem Gelände. D.h. wir bestimmen die Schnittpunkte der Geraden g 1 und g 2 mit der Gelände-Ebene. Nun legen wir die Hauptschichtenpläne der Böschungsflächen an. Dazu müssen wir Ebenen durch g 1 und g 2 mit einem durch i gestimmten Neigungswinkel konstruieren. Das ist also eine Anwendung der ersten Grundaufgabe. Nun müssen wir noch die Böschungsebenen mit der Geländeebene schneiden, um den Plan zu vervollständigen. Dazu müssen wir jeweils den Schnitt zwischen zwei Ebenen ermitteln. Lösung (9) (10) (11) (12) (8) i (8) (9) (10) (11) (10) (9) P 2 (8) (9) (10) Q (11) (12) i (8) (9) (10) (11) (8) (13) r (7) (6) r P 1 (14) g 1 f (6) (7) (8) (9) (10) (11) g 2
85 KAPITEL 7. KOTIERTE PROJEKTION Zweite Grundaufgabe Aufgabe Gegeben sei eine Ebene ε mit Anstieg tanβ = 1/i, ein Punkt P dieser Ebene sowie der Anstieg tan µ = 1/j. Konstruiere alle Geraden g durch den Punkt P, die in ε enthalten sind und deren Anstieg 1/j beträgt. Konstruktion Sei {h (z)} der Schichtenplan von ε und sei P gegeben als P (u). Man wähle eine Kote m verschieden von u. Jede der gesuchten Geraden g schneidet die Höhenschichtenlinie h(m) von ε in einem Punkt Q. Ist r der Abstand von P und Q, so hat g den Anstieg m u /r. Also müssen wir Q auf einem Kreis um P mit Radius r = j m u suchen. Für µ < β gibt es zwei, für µ = β eine und für µ > β keine Lösungen. Lösung k = k (P,r) r = j m u P (u) h (u) h (m) Zweite Lösung Erste Lösung
86 KAPITEL 7. KOTIERTE PROJEKTION Übung: Konstruktion einer Serpentine Aufgabe Vorgelegt ist eine Ebene durch ihre Graduierung {h (u)} sowie zwei Punkte A,B dieser Ebene. Gesucht ist ein Weg ( Serpentine ) mit halbem Anstieg auf der Ebene, der von A nach B führt. (3) (4) A (4) (5) 0 15 mm (6) (7) B (8) (9) 4 5 Lösung (3) (4) r A (4) (5) 0 15 mm (6) (7) mm B r (8) (9) 5
87 KAPITEL 7. KOTIERTE PROJEKTION Dritte Grundaufgabe Aufgabe Gegeben seien drei Punkte P, Q und R mit Höhenangabe und Anstiege m und n der Ebenen µ und ν. Gesucht sind die Haupthöhengeraden t 1,t 2,... der Ebene µ mit PQ µ, die Haupthöhengeraden s 1,s 2,... der Ebene ν mit QR ν und die Schnittgerade u von µ und ν. Lösung r 2 P 1 R R 2 k 2 t 3 P s 3 t 2 s 2 s 1 Q t 1 u r 1 Q 1 k 1 Q 2 P 1, Q 1 Punkte auf PQ mit ganzzahliger Höhe r 1 Intervall von µ = 1/m (Maßstab beachten) k 1 Kreis um Q 1 mit Radius r 1 t 1 Tangente an k 1 durch P 1 s 2, s 3,... Parallele zu s 1 jeweils im Abstand r 1 Q 2, R 2 Punkte auf QR mit ganzzahliger Höhe r 2 Intervall von ν = 1/n (Maßstab beachten) k 2 Kreis um R 2 mit Radius r 2 s 1 Tangente an k 2 durch Q 2 t 2, t 3,... Parallele zu t 1 jeweils im Abstand r 2 u Gerade durch Q und die Schnittpunkte der Haupthöhenlinien mit jeweils gleicher Höhe Der Kreis k 1 kann auch um P 1 geschlagen werden. Die Tangente t 1 verläuft dann durch Q 1 (analog für k 2 ). Welche der jeweils beiden möglichen Tangenten ausgewählt wird, hängt von der Richtung des Anstiegs der Ebenen ab.
88 KAPITEL 7. KOTIERTE PROJEKTION Übung: Teich anlegen Aufgabe In schrägem Gelände soll ein Teich angelegt werden. Das Ufer mit dem Gefälle 1:5 beginnt innerhalb des Dreiecks. An den Ecken des Dreiecks ist die Höhe des Geländes über der Wasseroberfläche angegeben. Wo befindet sich die Wasserlinie? Meter (1,5) (2) (1)
89 KAPITEL 7. KOTIERTE PROJEKTION 88 Lösung (2) 5 m (1) Meter (1,5) (1) (0) (0) (1) (0) (1) 5 m (2) (1)
90 Kapitel 8 Bezeichnungen Punkte werden mit lateinischen Großbuchstaben bezeichnet, zum Beispiel: P,Q,P 3,Q 7,... Geraden und krumme Linien werden mit lateinischen Kleinbuchstaben bezeichnet. Zum Beispiel: g,h,u 9,...; Längen haben die gleiche Bezeichnung. Ebenen und ebene Figuren sowie Winkel werden mit griechischen Kleinbuchstaben bezeichnet, zum Beispiel: α,β,γ 4,... Krumme Flächen werden mit griechischen Großbuchstaben bezeichnet, zum Beispiel: Γ, Ω 5,... : zum Beispiel P g: Der Punkt P liegt auf der Geraden g. : zum Beispiel g π: Die Gerade g ist in der Ebene π enthalten. : zum Beispiel g π: Die Gerade g ist parallel zur Ebene π. : zum Beispiel g h: Die Gerade g steht senkrecht auf der Geraden h. : zum Beispiel g h: Schnittpunkt der Geraden g und h oder die leere Menge, falls g und h sich nicht schneiden. Verneinungen:,,,. P Q: Verbindungsgerade von P und Q. PQ: (Länge der) Verbindungsstrecke zwischen P und Q. Pg: Verbindungsebene des Punktes P und der Geraden g. gh: Verbindungsebene der Geraden g und h (falls diese existiert). PQR: Verbindungsebene der Punkte P, Q und R (falls P, Q und R nicht kollinear) (ABC): Dreieck mit Eckpunkten A, B, C. k(m,r): Kreis um Mittelpunkt M mit Radius r. k(m, P): Kreis um Mittelpunkt M durch Punkt P. (P,g): Parallele zu g durch P. (P,g): Senkrechte auf g durch P. (P,ε): Ebene parallel zu ε durch P. (g, h): Winkel zwischen g und h. (g,ε): Winkel zwischen Gerade g und Ebene ε. abst(, ): Abstand zwischen zwei Objekten (Punkt, Gerade, Ebene,... ). dreh(p,h): Drehung eines Punktes P um eine Gerade h. ord(p): Ordner des Punktes P. paff (P;a,X,X ): perspektive Affinität von P bzgl. Affinitätsachse a und affin zugeordnetem Punktepaar X,X. 89
91 Kapitel 9 Literatur [1] G. Bär: Geometrie, 2. Aufl. Teubner, Stuttgart, [2] R. Fucke, K. Kirch, H. Nickel: Darstellende Geometrie für Ingenieure, 16. Aufl. Fachbuchverlag, Leipzig, [3] O. Giering, O. Kozinowski, H. Seybold: Konstruktive Ingenieurgeometrie. Hanser, München, [4] J. Hoschek, G. Spreitzer: Aufgaben zur Darstellenden Geometrie. BI, Zürich, [5] W.-D. Klix: Konstruktive Geometrie, darstellend und analytisch. Fachbuchverlag, Leipzig, [6] C. Leopold: Geometrische Grundlagen der Architektendarstellung, 2. Aufl. Kohlhammer, Stuttgart, [7] E. Müller, E. Kruppa: Lehrbuch der darstellenden Geometrie, 6. Aufl. Springer, Berlin, [8] F. Rehbock: Darstellende Geometrie, 3. Aufl. Springer, Berlin, [9] F. Rehbock: Geometrische Perspektive, 2. Aufl. Springer, Berlin, [10] F. Reutter: Darstellende Geometrie 1, 12. Aufl. G. Braun, Karlsruhe, [11] R. Reutter: Darstellende Geometrie 2, 5. Aufl. G. Braun, Karlsruhe, [12] E. Schörner: Darstellende Geometrie, 3. Aufl. Hanser, München, [13] E. Stiefel: Lehrbuch der darstellenden Geometrie, 3. Aufl. Birkhäuser, Basel, [14] K. Strubecker: Vorlesungen über Darstellende Geometrie, 2. Aufl. Vandenhoeck & Ruprecht, Göttingen, [15] W. Wunderlich: Darstellende Geometrie I. BI, Mannheim, [16] W. Wunderlich: Darstellende Geometrie II. BI, Mannheim,
Elemente der Zweitafelprojektion
 Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss
Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss
Grundrissebene und Aufrissebene
 Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
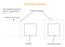 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 30. August 2017 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 30. August 2017 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 5. März 2018 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
9"+#5(00(),(& 7(8.(5+%(
 !"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
!"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Darstellende Geometrie
 Darstellende Geometrie für Architekten und Bauingenieure Version: Wintersemester 2007/08 Erste Fassung: Prof. Dr. Harald Löwe Vorliegende Fassung: Prof. Dr. Rainer Löwen Technische Universität Braunschweig
Darstellende Geometrie für Architekten und Bauingenieure Version: Wintersemester 2007/08 Erste Fassung: Prof. Dr. Harald Löwe Vorliegende Fassung: Prof. Dr. Rainer Löwen Technische Universität Braunschweig
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Hans Walser. Raumgeometrie. Modul 4 Die Ebene
 Hans Walser Raumgeometrie Modul 4 Die Ebene Hans Walser: Modul 4, Die Ebene ii Modul 4 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002 Überarbeitung Sommer 2003 Fehlerkorrekturen,
Hans Walser Raumgeometrie Modul 4 Die Ebene Hans Walser: Modul 4, Die Ebene ii Modul 4 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002 Überarbeitung Sommer 2003 Fehlerkorrekturen,
Kapitel 4: Zeichnerische Darstellung von Körpern. Darstellung von Körpern in der Ebene. Ziel bei der Darstellung von räumlichen Figuren (Körpern):
 Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 31. August 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 31. August 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Termin: 9. September zugel. Hilfsmittel:
 Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Univ.-Prof. Dr.-Ing. Mike Sieder Univ.-Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2011 Name: Matrikelnummer:
Technische Universität München Lehrstuhl für Holzbau und Baukonstruktion Univ.-Prof. Dr.-Ing. Mike Sieder Univ.-Prof. Dr.-Ing. Stefan Winter Methoden der Darstellung Prüfung Herbst 2011 Name: Matrikelnummer:
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Termin: 14. September 2012 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten vor Beginn der
Prüfungsfach: Termin: 14. September 2012 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten vor Beginn der
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Technische Darstellung
 Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
DARSTELLENDE GEOMETRIE I
 DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
Figur in der Bildfläche bzw. Bildebene
 2 ABBILDUNGSMETHODEN 2.1 Projektionsarten Um dreidimensionale Objekte wie Gebäude, Stadträume oder Bauteile darzustellen, werden diese auf eine Bildfläche bzw. eine Bildebene abgebildet. Der hierbei verwendete
2 ABBILDUNGSMETHODEN 2.1 Projektionsarten Um dreidimensionale Objekte wie Gebäude, Stadträume oder Bauteile darzustellen, werden diese auf eine Bildfläche bzw. eine Bildebene abgebildet. Der hierbei verwendete
Geometrische Grundlagen der. Architekturdarstellung
 Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Seite 1 Einleitung Elemente der Darstellenden Geometrie 13. Lernkontrolle A 1 15
 Inhaltsverzeichnis Seite 1 Einleitung 13 2 Elemente der Darstellenden Geometrie 13 Lernkontrolle A 1 15 3 Projektionsarten und Verfahren 15 3.1 Projektionsvorgang 15 3.2 Projektionsarten 16 3.2.1 Zentralprojektion
Inhaltsverzeichnis Seite 1 Einleitung 13 2 Elemente der Darstellenden Geometrie 13 Lernkontrolle A 1 15 3 Projektionsarten und Verfahren 15 3.1 Projektionsvorgang 15 3.2 Projektionsarten 16 3.2.1 Zentralprojektion
Durchstoßpunkt Gerade Ebene. Vorkurs Darstellende Geometrie. Erstprojizierende Hilfsebene ν durch g. Teil I. Lösung mit erstprojizierender Hilfsebene
 Durchstoßpunkt Gerade Ebene Vorkurs Darstellende Geometrie Durchstoßpunkt Gerade Ebene Bestimmen Sie den Durchstoßpunkt D der Geraden g mit der Ebene ε. Hans-Peter Schröcker Arbeitsbereich Geometrie und
Durchstoßpunkt Gerade Ebene Vorkurs Darstellende Geometrie Durchstoßpunkt Gerade Ebene Bestimmen Sie den Durchstoßpunkt D der Geraden g mit der Ebene ε. Hans-Peter Schröcker Arbeitsbereich Geometrie und
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Methoden der Darstellung Termin: 7. März 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 11.30 Uhr 12.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Methoden der Darstellung Termin: 7. März 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 11.30 Uhr 12.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Ziel bei der Darstellung von räumlichen Figuren (Körpern): Startseite
 Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Geometrie 1. 1.)Geometrische Grundkonstruktionen. Halbierung einer Strecke, Mittelsenkrechte. Teilung einer Strecke. Winkelhalbierung.
 Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Die Konstruktion der Schnittgeraden zweier Ebenen ist auf unterschiedliche Art und Weise möglich:
 Ebene Ebene Zwei Ebenen sind entweder Elemente eines Parallelenebenenbüschels oder sie schneiden einander. Im letzteren Fall existiert eine eindeutig bestimmte eigentliche Gerade als Schnittmenge beider
Ebene Ebene Zwei Ebenen sind entweder Elemente eines Parallelenebenenbüschels oder sie schneiden einander. Im letzteren Fall existiert eine eindeutig bestimmte eigentliche Gerade als Schnittmenge beider
Darstellende Geometrie Übungen. Tutorial. Übungsblatt: Perspektive Rekonstruktion - FSI
 Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
4^ Springer Vieweg. Geometrische Grundlagen der Architekturdarstellung. Cornelie Leopold. 5V überarbeitete und erweiterte Auflage.
 Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 5V überarbeitete und erweiterte Auflage Unter Mitwirkung von Andreas Matievits 4^ Springer Vieweg Affinität INHALTSVERZEICHNIS Vorwort
Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 5V überarbeitete und erweiterte Auflage Unter Mitwirkung von Andreas Matievits 4^ Springer Vieweg Affinität INHALTSVERZEICHNIS Vorwort
Darstellung dreidimensionaler Figuren in der Ebene. Schrägbild
 Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Die Zentralprojektion
 Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
KOP1_1_28. Lüftungsschacht
 Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Thomae. Perspektive und Axonometrie
 Thomae. Perspektive und Axonometrie Reiner Thomae Perspektive und Axonometrie 7. Auflage Verlag W Kohlhammer Die Deutsche Bibliothek - CIP-Einheitsaufnahme Thomae, Reiner: Perspektive und Axonometrie/Reiner
Thomae. Perspektive und Axonometrie Reiner Thomae Perspektive und Axonometrie 7. Auflage Verlag W Kohlhammer Die Deutsche Bibliothek - CIP-Einheitsaufnahme Thomae, Reiner: Perspektive und Axonometrie/Reiner
iek Institut für Entwerfen und Konstruieren
 Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
G1.02 In jedes der drei Muster hat sich ein Fehler eingeschlichen. Kennzeichne diesen, indem du den Bereich mit roter Farbe einringelst!
 1 Muster (Teil 1) G1.01 Vervollständige das Muster, sodass der gesamte Raster ausgefüllt ist! Verwende dazu ein Geodreieck und einen gespitzten Bleistift oder einen Druckbleistift mit einer 0,5 mm HB-Mine
1 Muster (Teil 1) G1.01 Vervollständige das Muster, sodass der gesamte Raster ausgefüllt ist! Verwende dazu ein Geodreieck und einen gespitzten Bleistift oder einen Druckbleistift mit einer 0,5 mm HB-Mine
Modul: Ausgewählte Kapitel der Didaktik der Mathematik
 Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
2.3.1 Rechtshändiges und linkshändiges Koordinatensystem
 2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
Hans Walser. Raumgeometrie. Modul 4 Die Ebene Lernumgebung Teil 2
 Hans Walser Raumgeometrie Modul 4 Die Ebene Lernumgebung Teil 2 Hans Walser: Modul 4, Die Ebene. Lernumgebung. Teil 2 ii Inhalt 1 Abstand Punkt / Ebene... 1 2 Abstand... 2 3 Neigungswinkel... 3 4 Neigungswinkel...
Hans Walser Raumgeometrie Modul 4 Die Ebene Lernumgebung Teil 2 Hans Walser: Modul 4, Die Ebene. Lernumgebung. Teil 2 ii Inhalt 1 Abstand Punkt / Ebene... 1 2 Abstand... 2 3 Neigungswinkel... 3 4 Neigungswinkel...
Projektion. FG Borrego - TU Berlin Architekturdarstellung und Gestaltung Collaborative Design Laboratory
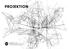 Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Aufgabenstellung zur Wahlfachübung 4
 Darstellende Geometrie für Architekten III Institut für Geometrie und Prakt. Mathematik RWTH Aachen 4.2 Prismen Geometrie der Formen Übung 4 Seite 1 Aufgabenstellung zur Wahlfachübung 4 Hausübung zum Thema
Darstellende Geometrie für Architekten III Institut für Geometrie und Prakt. Mathematik RWTH Aachen 4.2 Prismen Geometrie der Formen Übung 4 Seite 1 Aufgabenstellung zur Wahlfachübung 4 Hausübung zum Thema
Grundsätzliche Konstruktionshilfen:
 Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Schriftliche Reifeprüfung Darstellende Geometrie
 SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
Wo viel Licht ist, ist starker Schatten.
 Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Legt man die vom Betrachter aus gesehen vor den, wird die spätere Konstruktion kleiner als die Risse. Legt man die hinter das Objekt, wird die perspek
 Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Der Hauptsatz der Axonometrie, Aufbauverfahren
 Axonometrie Der Hauptsatz der Axonometrie, Aufbauverfahren Gegeben seien ein kartesisches Rechtssystem (U, E x, E y, E z ) und eine Bildebene π derart, daÿ bezüglich einer Parallelprojektion p keine Koordinatenebene
Axonometrie Der Hauptsatz der Axonometrie, Aufbauverfahren Gegeben seien ein kartesisches Rechtssystem (U, E x, E y, E z ) und eine Bildebene π derart, daÿ bezüglich einer Parallelprojektion p keine Koordinatenebene
Geometrie-Dossier Kreis 2
 Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Bild 1: Gegeben ist der in der Zentralperspektive zentrale Fluchtpunkt, der Distanzpunkt und der Grundriss des zu zeichnenden Vierecks.
 Bild 1: Gegeben ist der in der Zentralperspektive zentrale, der und der Grundriss des zu zeichnenden Vierecks. Die Breite des Vierecks trägt man auf der ab und verbindet die Schnittpunkte mit dem zentralen
Bild 1: Gegeben ist der in der Zentralperspektive zentrale, der und der Grundriss des zu zeichnenden Vierecks. Die Breite des Vierecks trägt man auf der ab und verbindet die Schnittpunkte mit dem zentralen
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
6.4.3 Frontalperspektive
 102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
KOP1_1_8. Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen.
 Titel Risszeichnen Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen. Relevante(r) Deskriptor(en) Die Schülerinnen und Schüler können Konstruktionsaufgaben mittels geeigneter Abbildungsverfahren
Titel Risszeichnen Die Schülerinnen und Schüler können normgerechte Zeichnungen lesen. Relevante(r) Deskriptor(en) Die Schülerinnen und Schüler können Konstruktionsaufgaben mittels geeigneter Abbildungsverfahren
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover
 Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Hochschule München Fakultät 03. Skript zur Darstellenden Geometrie. Nach Vorlagen von Prof. Dr. Schwägerl und Prof. Dr. Schulz
 Fakultät 03 Skript zur Darstellenden Geometrie Nach Vorlagen von Prof. Dr. Schwägerl und Prof. Dr. Schulz Stand: September 2018 Inhaltsverzeichnis 2 Vorwort Mit großer Freunde können wir nun der Fachschaft
Fakultät 03 Skript zur Darstellenden Geometrie Nach Vorlagen von Prof. Dr. Schwägerl und Prof. Dr. Schulz Stand: September 2018 Inhaltsverzeichnis 2 Vorwort Mit großer Freunde können wir nun der Fachschaft
Dipl, ng (FH) Darstellende
 Kamprath-Reihe Technik Dipl, ng (FH) Darstellende Josef Vogelmann Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 6. Auflage Vogel Buchverlag Inhaltsverzeichnis 1. Einleitung
Kamprath-Reihe Technik Dipl, ng (FH) Darstellende Josef Vogelmann Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 6. Auflage Vogel Buchverlag Inhaltsverzeichnis 1. Einleitung
Die Übereckperspektive mit zwei Fluchtpunkten
 Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Einerseits: Zentralperspektive
 VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen
 Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
D a r s t e l l u n g s g r u n d l a g e n a m L e h r s t u h l G D A Perspektive konstruieren
 D a r s t e l l u n g s g r u n d l a g e n a m L e h r s t u h l G D A Perspektive konstruieren T u t o r i u m s h e f t N o. I I Technische Universität Dortmund Lehrstuhl Grundlagen der Architektur
D a r s t e l l u n g s g r u n d l a g e n a m L e h r s t u h l G D A Perspektive konstruieren T u t o r i u m s h e f t N o. I I Technische Universität Dortmund Lehrstuhl Grundlagen der Architektur
Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT
 Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT 1 Anmerkung Prof. Lenz ist bereits pensioniert. Im Unterricht
Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT 1 Anmerkung Prof. Lenz ist bereits pensioniert. Im Unterricht
Klausur zur Einführung in die Geometrie im SS 2002
 Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Perspektive Vertiefung
 Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
D C. Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
 V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
SRP DG am BG und BRG Wieselburg 2017/2018, Seite 1 von 7, Name:
 SRP DG am BG und BRG Wieselburg 2017/2018, Seite 1 von 7, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2017/2018 8AD und 8BD, Realgymnasium mit
SRP DG am BG und BRG Wieselburg 2017/2018, Seite 1 von 7, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2017/2018 8AD und 8BD, Realgymnasium mit
Josef Vogelmann Darstellende Geometrie
 Josef Vogelmann Darstellende Geometrie Kamprath-Reihe Technik Dipl.-Ing. (FH) Josef Vogelmann Darstellende Geometrie Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 5. Auflage
Josef Vogelmann Darstellende Geometrie Kamprath-Reihe Technik Dipl.-Ing. (FH) Josef Vogelmann Darstellende Geometrie Die Lehre vom richtigen Zeichnen eine Grundlage des technischen Zeichnens 5. Auflage
Stereometrie. Rainer Hauser. Dezember 2010
 Stereometrie Rainer Hauser Dezember 2010 1 Einleitung 1.1 Beziehungen im Raum Im dreidimensionalen Euklid schen Raum sind Punkte nulldimensionale, Geraden eindimensionale und Ebenen zweidimensionale Unterräume.
Stereometrie Rainer Hauser Dezember 2010 1 Einleitung 1.1 Beziehungen im Raum Im dreidimensionalen Euklid schen Raum sind Punkte nulldimensionale, Geraden eindimensionale und Ebenen zweidimensionale Unterräume.
Einige Fragen aus den Elementen der Darstellenden Geometrie,
 Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und
Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A Bremen. Die Kursübersicht für das Fach Mathematik
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
4.22 Buch XI der Elemente
 4.22 Buch XI der Elemente In Buch XI werden die Grundbegriffe der räumlichen Geometrie eingeführt und für viele Propositionen aus den Büchern I und VI die entsprechende dreidimensionale Aussagen bewiesen.
4.22 Buch XI der Elemente In Buch XI werden die Grundbegriffe der räumlichen Geometrie eingeführt und für viele Propositionen aus den Büchern I und VI die entsprechende dreidimensionale Aussagen bewiesen.
Polyeder, Konvexität, Platonische und archimedische Körper
 Unter einem Polyeder verstehen wir einen zusammenhängenden Teil des dreidimensionalen Raumes der durch Polygone begrenzt wird. Seine Oberfläche besteht also aus Punkten (Ecken genannt), Strecken (Kanten
Unter einem Polyeder verstehen wir einen zusammenhängenden Teil des dreidimensionalen Raumes der durch Polygone begrenzt wird. Seine Oberfläche besteht also aus Punkten (Ecken genannt), Strecken (Kanten
Lösungen. Christian Haas. Perspektiven. Ausbildungseinheit für Anlagen- und Apparatebauer/innen. Reform Lernziele:
 Perspektiven Ausbildungseinheit für Anlagen- und Apparatebauer/innen EFZ Reform 2013 4 Lösungen Lernziele: Einfache Werkstücke perspektivisch darstellen Von Normalprojektionen die Perspektive zeichnen
Perspektiven Ausbildungseinheit für Anlagen- und Apparatebauer/innen EFZ Reform 2013 4 Lösungen Lernziele: Einfache Werkstücke perspektivisch darstellen Von Normalprojektionen die Perspektive zeichnen
Aufgaben zur Übung der Anwendung von GeoGebra
 Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Jahresplanung Vorschlag 1
 Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
2.6. Aufgaben zu Kongruenzabbildungen
 Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
14 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE. x y
 4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
37 II.1. Abbildungen
 37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
Darstellende Geometrie Übungen. Tutorial 06. Übungsblatt: Schatten - Perspektive 04. Wohnhaus
 Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial 06 Übungsblatt: Schatten - Perspektive 04 Wohnhaus Fluchtpunkte und Fluchtspuren (Abb. 01) 1. Zuerst werden die fehlenden Fluchtpunkte
Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial 06 Übungsblatt: Schatten - Perspektive 04 Wohnhaus Fluchtpunkte und Fluchtspuren (Abb. 01) 1. Zuerst werden die fehlenden Fluchtpunkte
Kapitel 1. Koordinaten im Raum. 1.1 Schrägbilder - Kavalier-Perspektive Koordinaten
 Kapitel Koordinaten im Raum Schrägbilder - Kavalier-Perspektive Koordinaten Im Raum benötigt man drei Angaben, um die Lage eines Punktes zu beschreiben So beschreiben Geographen durch N5 0"E07 38 7"H5m
Kapitel Koordinaten im Raum Schrägbilder - Kavalier-Perspektive Koordinaten Im Raum benötigt man drei Angaben, um die Lage eines Punktes zu beschreiben So beschreiben Geographen durch N5 0"E07 38 7"H5m
Mathematische Probleme, SS 2016 Freitag $Id: convex.tex,v /05/13 14:42:55 hk Exp $
 $Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
$Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
Anschauliche Parallelrisse und Hauptrisse
 Anschauliche Parallelrisse und Hauptrisse Seit frühester Kindheit wirst du im täglichen Leben immer wieder mit Bildern konfrontiert, sei es in Form von Bauanleitungen oder Produktinformationen. Du solltest
Anschauliche Parallelrisse und Hauptrisse Seit frühester Kindheit wirst du im täglichen Leben immer wieder mit Bildern konfrontiert, sei es in Form von Bauanleitungen oder Produktinformationen. Du solltest
1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO
 1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO 128-24. Ordnen Sie den gekennzeichneten Linien die korrekten Linienarten zu! A B C D F G J K Verwenden Sie dazu die in
1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO 128-24. Ordnen Sie den gekennzeichneten Linien die korrekten Linienarten zu! A B C D F G J K Verwenden Sie dazu die in
Parallelprojektive Schattenbilder von Körpern mit Cabri 3D
 Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Ein Beitrag zur Perspektive mit gekippter Grundebene
 Ein Beitrag zur Perspektive mit gekippter Grundebene Von Georg GLAESER, Wien Herrn Prof. Dr. E. Frisch zum 65. Geburtstag gewidmet. Zusammenfassung Die Perspektive mit gekippter Grundebene wird wegen ihres
Ein Beitrag zur Perspektive mit gekippter Grundebene Von Georg GLAESER, Wien Herrn Prof. Dr. E. Frisch zum 65. Geburtstag gewidmet. Zusammenfassung Die Perspektive mit gekippter Grundebene wird wegen ihres
Institut für Mathematik Geometrie und Lineare Algebra J. Schönenberger-Deuel
 Lösungen Übung 6 Aufgabe 1. a.) Idee: Gesucht sind p, q mit pq = 6 2 und p + q = 13. Dies entspricht genau der Situation im Höhensatz. Konstruktion: 1. Punkte A, B mit AB = 13 2. Gerade g AB mit dist(g,
Lösungen Übung 6 Aufgabe 1. a.) Idee: Gesucht sind p, q mit pq = 6 2 und p + q = 13. Dies entspricht genau der Situation im Höhensatz. Konstruktion: 1. Punkte A, B mit AB = 13 2. Gerade g AB mit dist(g,
Rotation eines Punktes um eine Achse allgemeiner Lage
 Rotation eines Punktes um eine chse allgemeiner Lage Es gibt eine allgemein, in der arstellenden Geometrie übliche Methode, dieses eispiele zu lösen: 1) chse in Wahrer Größe darstellen - ein weiterer Seitenriss
Rotation eines Punktes um eine chse allgemeiner Lage Es gibt eine allgemein, in der arstellenden Geometrie übliche Methode, dieses eispiele zu lösen: 1) chse in Wahrer Größe darstellen - ein weiterer Seitenriss
11: Die Euler sche Polyederformel für planare Graphen
 Chr.Nelius: Graphentheorie (WS 2016/17) 38 11: Die Euler sche Polyederformel für planare Graphen (11.1) BEM: a) Ein Polyeder (auch Vielflach oder Vielflächner) ist ein geometrischer Körper, der nur von
Chr.Nelius: Graphentheorie (WS 2016/17) 38 11: Die Euler sche Polyederformel für planare Graphen (11.1) BEM: a) Ein Polyeder (auch Vielflach oder Vielflächner) ist ein geometrischer Körper, der nur von
